Path Planning and Tracking Control for Unmanned Surface Vehicle Based on Adaptive Differential Evolution Algorithm

Abstract

With the growing demand for safe obstacle avoidance and precise trajectory tracking in the autonomous navigation of unmanned surface vessels (USVs), this paper investigates an adaptive differential evolution approach for integrated path planning and tracking control. In the path planning stage, an elite archive mechanism is first incorporated into the mutation process, and the scaling factor F and crossover rate $CR$ are adaptively adjusted to enhance population diversity and global search capability. Then, the International Regulations for Preventing Collisions at Sea (COLREGs) are embedded into the algorithmic framework to reinforce collision avoidance performance in complex encounter scenarios. A multi-objective fitness function combining six performance criteria is subsequently constructed to evaluate individual path points, thereby identifying high-quality solutions that ensure both safe navigation and route efficiency. In the tracking control stage, the optimally generated reference trajectory is then employed as the input command for the vessel’s motion control subsystem. A fuzzy logic system is introduced to approximate unknown nonlinear dynamics, and an adaptive fuzzy logic controller is designed to guarantee accurate tracking of the planned path. Finally, simulation tests are used to show the algorithm’s efficiency and usefulness.

1. Introduction

With the continuous advancement of technologies, including the Marine Internet of Things (Marine IoT) [1], big data, and cloud computing, the field of intelligent navigation has garnered increasing attention. In the context of complex and dynamic maritime environments, one of the critical technical challenges lies in achieving safe and economically viable vessel route planning from origin to destination. This involves not only ensuring high-precision trajectory tracking control but also maintaining overall safe navigation. Such challenges have prompted significant academic interest in recent years [2].

Research on vessel path planning has seen significant advancements with the application of various intelligent optimization algorithms aimed at enhancing performance. Zheng et al. [3] developed a hierarchical framework that integrates genetic algorithms (GAs) with adaptive elite selection and fuzzy probability sets, thereby improving the global search capability and convergence speed. Wang et al. [4] proposed a particle swarm optimization algorithm (PSO) incorporating adversarial learning to adjust inertial weights, effectively mitigating premature convergence. LYRIDIS [5] introduced an ant colony optimization algorithm (ACO) enhanced by fuzzy logic, demonstrating superior convergence efficiency and path optimality, which facilitates efficient real-time local path planning for unmanned surface vessels (USVs) in restricted waters. However, despite the distinct advantages of these methods, such as straightforward parameter tuning in PSO, heuristic probabilistic search in ACO that helps avoid local optima, and the robust global search capability in GAs, these techniques often suffer from limited convergence efficiency in complex environments. As a result, they often fail to meet the requirements for high-real-time applications. Moreover, due to computational constraints, their application in scenarios demanding real-time local path planning remains restricted.

To address the limitations of the aforementioned methods, the differential evolution (DE) algorithm has emerged as a promising solution. Introduced by Storn and Price in 1997 [6], DE is a stochastic, population-based search algorithm inspired by biological evolution. It is known for its simple parameterization, real-time tracking of individual solutions, and autonomous adjustment of the search strategy, relying solely on fitness information without prior domain knowledge. These characteristics make DE effective for solving multi-objective optimization problems in complex environments. As a result, DE has attracted significant research interest, leading to enhanced versions. For example, Tanabe et al. [7] proposed a DE variant with a memory mechanism for control parameters, guiding future iterations using historically effective parameter sets. Sun et al. [8] introduced separate strategy pools for exploration and exploitation, where mutation strategies dynamically acquire resources through cooperation and competition, improving resource utilization and algorithm performance. In hybrid approaches, Yu et al. [9] integrated DE with the gray wolf optimizer (GWO) to mitigate the risk of local optima, improving convergence behavior. However, despite these advancements, the application of improved DE algorithms in intelligent collision and obstacle avoidance for USVs remains underexplored, and collision risk in maritime practices is not fully addressed in current studies [10,11].

Furthermore, research on vessel path planning and control has increasingly incorporated multidisciplinary approaches to address the complex challenges in dynamic maritime environments. Teng et al. [12] approached the efficiency of path planning by integrating a repulsive potential function that considers target distance, along with an adaptive step size mechanism, into the artificial potential field (APF) method. This enabled precise trajectory tracking in complex environments by combining a line-of-sight (LOS) guidance strategy with a non-singular terminal sliding mode control method. Liu et al. [13] addressed path planning for USVs in confined waters by using a probabilistic mapping approach and designing a predictive controller for accurate trajectory tracking. Wang [14] enhanced the traditional artificial potential field method by introducing virtual target points and developing a robust tracking controller based on LOS guidance, which enabled USVs to perform tasks under disturbances. Precup et al. [15] integrated GWO with fuzzy control, demonstrating improved performance in path planning and tracking systems. Zhang [16] proposed a collaborative framework that integrates a planning method compliant with the International Regulations for Preventing Collisions at Sea (COLREGs) with a composite LOS and neural network controller, demonstrating significant engineering applicability in simulations under varying sea states. However, despite these advancements, current intelligent navigation systems for USVs continue to face challenges in the completeness, robustness, and smoothness of path planning and control algorithms, and unresolved issues persist regarding the abstraction of tracking control signals.

Based on the analysis provided, this paper proposes an integrated path planning and tracking control method for USVs using a composite adaptive differential evolution algorithm (CRI-DE). This method enhances both path planning and tracking accuracy by introducing an elite archiving mechanism to improve population diversity and prevent premature convergence. Additionally, it integrates a fuzzy logic control system for improved tracking performance. COLREGs are incorporated to optimize obstacle avoidance in complex maritime scenarios. The primary innovations of this paper are as follows:

(1)

In comparison with the existing research on collision avoidance strategies [17,18,19], this paper introduces an elite archiving mechanism and adaptive adjustments of the scaling factor F and crossover factor $CR$, which effectively improve population diversity and prevent premature convergence. Moreover, by integrating COLREGs into the algorithm design, the method enhances autonomous obstacle avoidance in complex maritime scenarios. A multi-objective fitness function is used, which incorporates factors such as voyage distance, collision risk, and vessel maneuverability. This significantly improves the rationality, safety, and feasibility of the planned paths.

(2)

The primary contribution of this paper lies in the control aspect. In comparison with traditional path tracking methods [20,21,22], a systematic framework is developed to model USV motion based on the path coordinates generated by CRI-DE. A fuzzy logic system is employed for adaptive control, ensuring an effective match between the USV’s motion trajectory and the planned command signals. This approach overcomes the limitation of conventional algorithms that often neglect dynamic environmental disturbances, thus achieving high-precision integrated path planning and tracking control for USVs.

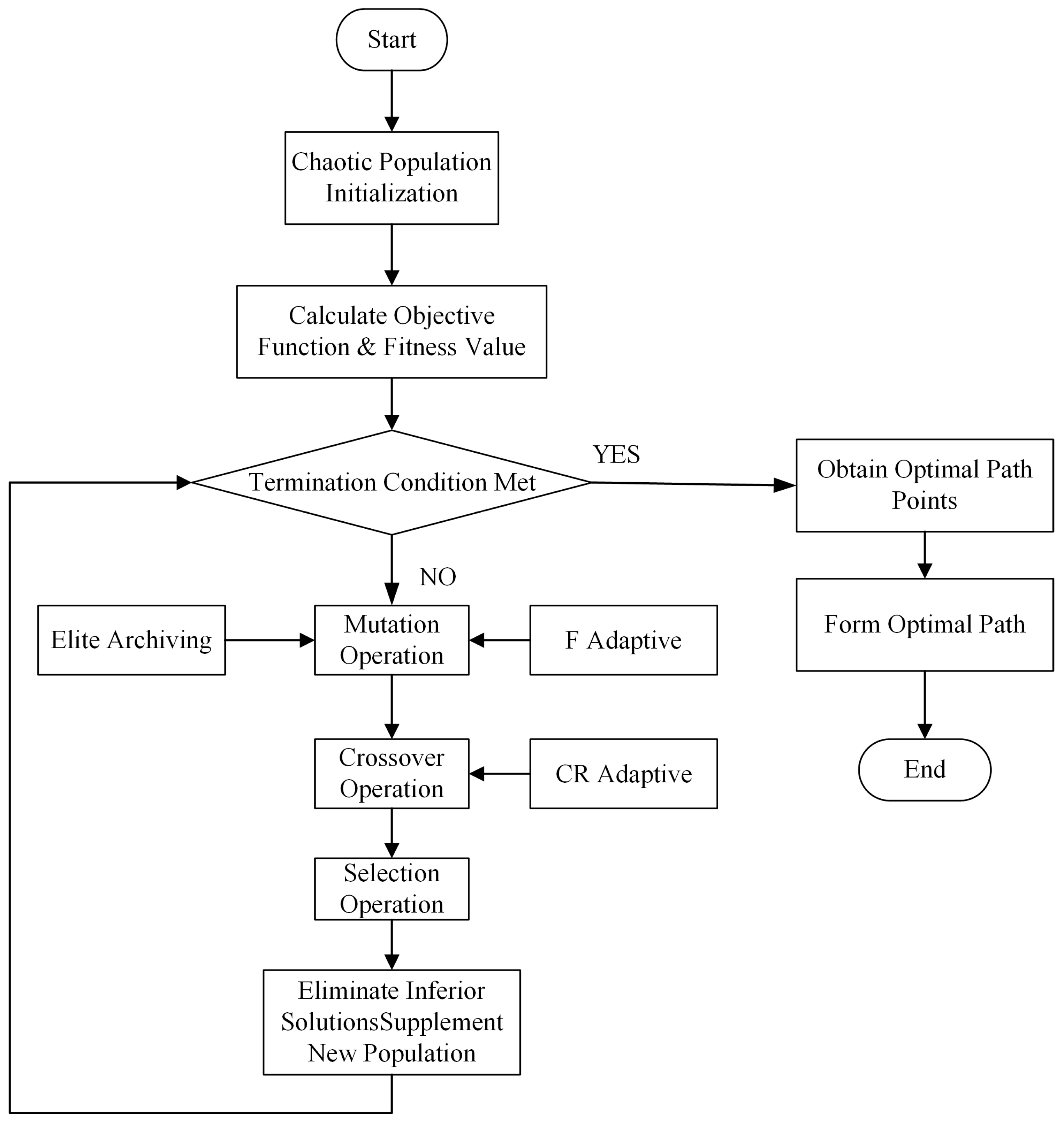
2. Path Planning for USVs Based on Adaptive Differential Evolution

This chapter introduces the framework for path planning of USVs using the Adaptive differential evolution algorithm. Section 2.1 provides an overview of the differential evolution (DE) algorithm, explaining its key components and operations. Section 2.2 discusses various strategies for improving the DE algorithm to enhance its performance in the context of USV path planning.

2.1. Differential Evolution Algorithm

The DE algorithm is a stochastic optimization technique inspired by the principles of biological evolution. It operates through an iterative process involving five fundamental stages: population initialization, fitness evaluation, differential mutation, crossover, and selection.

2.1.1. Population Initialization

The initial population size is denoted by $NP$ and is determined based on the problem complexity. Each individual in the population is represented as a Q-dimensional vector, where each dimension is initialized randomly within the prescribed boundaries. The mathematical representation of the initial population is expressed as follows:

$$X_i=\left(x_{i1},x_{i2},\dots ,x_{ij},\dots ,x_{iQ}\right), i=1,2,\dots ,NP,$$

(1)

The initialization for the j-th dimension of the i-th individual is given by

$$x_{ij}=x_{\min ,j}+rand(0,1)·(x_{\max ,j}-x_{\min ,j}),$$

(2)

where $x_{\max ,j}$ and $x_{\min ,j}$ represent the lower and upper bounds of the j-th dimension, and rand(0,1) denotes a random number within the range (0,1).

2.1.2. Fitness Evaluation

The formulation of the fitness function is intrinsically linked to the optimization objective. In this study, the fitness function is designed to evaluate the quality of each candidate path point. A smaller fitness value corresponds to a higher-quality solution and, consequently, greater overall fitness.

2.1.3. Differential Mutation

The fundamental operation of mutation involves generating new individuals through the recombination of differential vectors. Specifically, three distinct individuals are randomly selected from the current population, and a mutant vector is generated based on their vector differences. The mutation strategy is defined as follows:

$$v_i\left(g\right)=x_{r1}\left(g\right)+F\times \left(x_{r2}\left(g\right)-x_{r3}\left(g\right)\right),$$

(3)

where $x_{r1}\left(g\right), x_{r2}\left(g\right), x_{r3}\left(g\right)$ are three different vectors randomly selected from the population at the g-th generation, and F is the scaling factor. $v_i\left(g\right)$ denotes the resulting mutant vector [23].

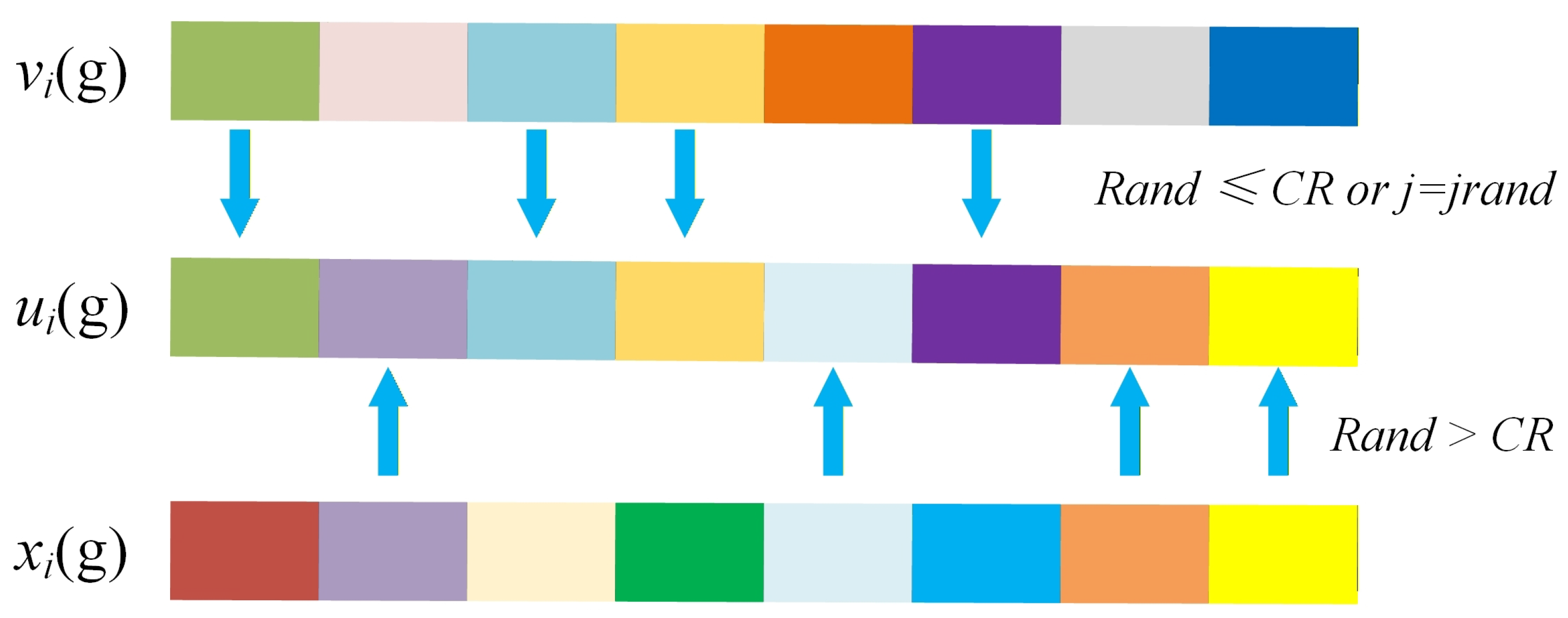
2.1.4. Crossover Operation

The crossover operation serves to enhance genetic diversity within a population and promote the exchange and integration of information among distinct individuals. By combining features from multiple parent vectors, this process enables exploration of uncharted regions in the solution space. The crossover is performed as follows:

$$u_{ij}(g+1)=\left\{\begin{array}{cc}{v}_{ij}\left(g\right),\hfill & rand\le CRorj=j_{rand}\hfill \\ x_{ij}\left(g\right),\hfill & else\hfill \end{array}\right.,$$

(4)

Here, $u_{ij}(g+1)$ denotes the new vector generated after crossover, and the crossover factor $CR$ ranges between 0 and 1. The crossover process is illustrated in Figure 1.

2.1.5. Selection Operations

The selection operation operates on a greedy strategy to retain individuals with higher fitness, thereby propelling the population toward superior solutions. Compared to other evolutionary algorithms, the selection mechanism in differential evolution is relatively straightforward, thereby enhancing computational efficiency. The selection criterion is defined as follows:

$$x_i(g+1)=\left\{\begin{array}{cc}{u}_i\left(g\right),\hfill & f\left(u_i\left(g\right)\right)\le f\left(x_i\left(g\right)\right)\hfill \\ x_i\left(g\right),\hfill & else\hfill \end{array}\right.,$$

(5)

Here, $f\left(u_i\left(g\right)\right)$ and $f\left(x_i\left(g\right)\right)$ denote the fitness value of the individual $x_i$ and the fitness value of the trial vector $u_i$ at the g-th generation, respectively.

2.2. Improvement Strategies for Differential Evolution Algorithms

In this study, an adaptive differential evolution algorithm, referred to as CRI-DE, is developed to improve path planning performance under complex encounter conditions. To enrich population diversity and reduce premature convergence, an elite archive mechanism is incorporated into the mutation stage together with adaptive adjustment strategies for both the scaling factor F and the crossover rate $CR$. In addition, COLREGs are embedded in the algorithm framework to strengthen autonomous decision-making for collision avoidance. During the assessment of collision risk, a multi-objective fitness function is constructed on the basis of six main criteria, namely, total voyage distance, steering angle, collision risk level, compliance with COLREGs, evasion timing, and vessel maneuverability. This fitness function supports the selection of path points with high quality and therefore improves the rationality, safety, and efficiency of the planned routes. Throughout the optimization process, potential collision risks between the USV and both moving targets and static obstacles are considered in a comprehensive manner to ensure safer and more reliable path planning. The overall framework of the proposed CRI-DE algorithm is shown in Figure 2.

2.2.1. Elite Archive Strategy

The mutation strategy adopted in this study is $DE/rand/2.$ This strategy employs two differential vectors to generate mutant individuals, providing stronger global exploration ability and greater population diversity compared to other schemes, which contributes to escaping local optima. Although it features a flexible structure and ease of implementation, it lacks sufficient guidance toward high-quality solutions. To address this limitation, an elite archive mechanism is integrated into the strategy to better balance local exploitation and global search. This improved mutation operator is utilized in the proposed algorithm.

Specifically, the current population N is ranked based on fitness values. The top P individuals form the elite set G, while the remaining (N–P) individuals are assigned to the non-elite set. The modified mutation operation is defined as follows:

$${\nu }_i\left(g\right)=x_{r1}^G+F\times (x_{r2}^G-x_{r3}^B)+F\times (x_{r4}^G-x_{r5}^B),$$

(6)

$$G\cup B=N,G\cap B=\varnothing ,\left(N-P\right)u_i\left(g\right)x_i\left(g\right).$$

(7)

Individuals $x_{r1}^G$, $x_{r2}^G$, and $x_{r4}^G$ are randomly selected from the elite set G, whereas individuals $x_r{3}^B$ and $x_{r5}^B$ are drawn from the non-elite set $B.$ The fundamental concept of this archiving mechanism is as follows: utilize G to guide the search in an evolutionary manner toward high-quality regions, thereby accelerating convergence, and to leverage B for maintaining population diversity. During each iteration, if the fitness of a newly generated individual $u_i\left(g\right)$ surpasses that of its corresponding original individual $x_i\left(g\right)$, sets G and B remain unchanged. Otherwise, update according to the following rules:

(1)

If $u_i\left(g\right)$ was originally a member of G, it directly replaces its counterpart in G.

(2)

If $u_i\left(g\right)$ is not a member of G but exhibits superior fitness compared with the worst individual in G, it replaces that worst individual. The replaced individual is subsequently transferred to B, and the original counterpart of $u_i\left(g\right)$ is removed from B.

2.2.2. Adaptive Factors

When the scaling factor F is excessively large, individual perturbations are amplified [24], which helps maintain population diversity and enhances the algorithm’s capability to escape local optima. Although this improves global exploration performance, it simultaneously slows down the convergence process. Conversely, a smaller F reduces individual movement steps, strengthens local exploration capabilities, and accelerates convergence, but it may lead to a loss of population diversity. To balance global exploration and convergence efficiency, this study introduces an adaptive update strategy for the scaling factor F, expressed as follows:

$$F_g=\left\{\begin{array}{c}{F}_1,F_0·\sum _{i=1}^{M}f\left(x_i^g\right)/\sum _{i=1}^{M}f\left(x_i^0\right)\le F_1\hfill \\ F_0·{\displaystyle \frac{{\sum }_{i=1}^{M}f\left(x_i^g\right)}{{\sum }_{i=1}^{M}f\left(x_i^0\right)}},else\hfill \end{array}\right.,$$

(8)

Here, $F_0$ and $F_{\mathrm{l}}$ denote the scaling factors in the first and second iterations, respectively, while $F_{\mathrm{g}}$ represents the value at the g-th iteration. $f\left(x_i^g\right)$ and $f\left(x_i^0\right)$ indicate the fitness values of the i-th individual in the g-th generation and the initial generation, respectively.

The magnitude of the crossover factor $CR$ directly influences the proportion of variation information transmitted to the original individuals [25]. Higher values facilitate the retention of more variation information, while lower values promote independence among individuals, thereby enhancing search diversity. To balance these two effects, this paper further proposes an adaptive $CR$ adjustment strategy:

$$C{R}_n=\left\{\begin{array}{cc}C{R}_1,\hfill & f\left(x_n^g\right)>f\left({\overline{x}}^g\right)\hfill \\ C{R}_0·{\displaystyle \frac{(C{R}_1-C{R}_0)(f\left({\overline{x}}^g\right)-f\left(x_n^g\right))}{f\left({\overline{x}}^g\right)-f\left(x_{\min }^g\right)}},\hfill & f\left(x_n^g\right)\le f\left({\overline{x}}^g\right)\hfill \end{array}\right.,$$

(9)

where $f\left(x_n^g\right)$ denotes the fitness of the n-th individual, $f\left({\overline{x}}^g\right)$ represents the average fitness of the population, and $f\left(x_{\min }^g\right)$ is the minimum value among them.

2.2.3. Collision Risk Index Model

This paper utilizes the Collision Risk Index (CRI) as a safe metric within the fitness function for evaluating path points. The CRI is a fuzzy evaluation metric that quantifies the probability of a collision between vessels, with its value ranging from 0 to 1 [26]. This metric is influenced not only by objective factors such as vessel speed and heading but also, to some extent, by the subjective judgment of the operator. A CRI value of 1 indicates that a collision is nearly unavoidable, whereas a value of 0 corresponds to a completely safe situation. Higher CRI values represent greater collision risk.

Three key factors were selected to construct the CRI model: Distance to Closest Point of Approach (DCPA), Time to Closest Point of Approach (TCPA), and Distance Between Vessels (D). Accordingly, the collision risk factor set is defined as follows:

$$M=\left\{\begin{array}{c}DCPA,TCPA,D\end{array}\right\}.$$

(10)

The membership functions for each factor are defined as follows.

First, the traditional DCPA membership function was modified to comprehensively account for mutual intrusion between the own ship (OS)’s domain and the target ship (TS)’s domain [27]. The modified DCPA membership function $u_d$ is defined as

$$u_d=\left\{\begin{array}{cc}1,\hfill & DCPA<r_1\Vert n_1>0\Vert n_2>0\hfill \\ {\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}\sin \left[{\displaystyle \frac{180°}{r_2-r_1}}\left(DCPA-{\displaystyle \frac{r_2+r_1}{2}}\right)\right],\hfill & r_1<DCPA<r_2\hfill \\ 0,\hfill & DCPA\ge r_2\hfill \end{array}\right.,$$

(11)

where $n_1$ represents the number of intersection points between the relative motion line of the own vessel with respect to the target vessel and the boundary of the target vessel’s domain, and $n_2$ denotes the number of intersections between the relative motion line of the target vessel relative to the own vessel and the boundary of the own vessel’s domain.

The TCPA membership function $u_t$ is expressed as

$$u_t=\left\{\begin{array}{cc}1,\hfill & \mathrm{TCPA}\le t_1\hfill \\ {\left({\displaystyle \frac{t_2-\left|TCPA\right|}{t_2-t_1}}\right)}^2,\hfill & t_1<\mathrm{TCPA}\le t_2\hfill \\ 0,\hfill & \mathrm{TCPA}>t_2,\mathrm{DCPA}>d_2\hfill \end{array}\right.,$$

(12)

where the critical thresholds $t_1$ and $t_2$ are dynamically adjusted based on the avoidance distances $D_1$, $D_2$ and the relative bearing $RB$. $d_1$ denotes the minimum safe passing distance for the give-way vessel, and $d_2$ represents the effective distance within which vessels can execute collision avoidance maneuvers [28].

The membership function $u_D$ for the inter-vessel distance is defined as follows:

$$u_D=\left\{\begin{array}{cc}1,\hfill & 0\le D\le d_1\hfill \\ \\ {\left({\displaystyle \frac{d_2-D}{d_2-d_1}}\right)}^2,\hfill & d_1<D\le d_2\hfill \\ \\ 0,\hfill & D>d_2\hfill \end{array}\right.,$$

(13)

Weights are assigned according to the relative importance of each factor to CRI, forming the weight set $W=\left\{w_d,w_t,w_D\right\}.$ The weight relationships satisfy $w_d>w_t>w_D$, and the sum of all weights equals 1. The collision risk level is ultimately calculated through the following weighted evaluation:

$$CRI=w_d{u}_d+w_t{u}_t+w_D{u}_D.$$

(14)

2.2.4. Fitness Function

To achieve effective path planning for USVs, this paper constructs a multi-objective optimization model. Its fitness function integrates six critical factors: collision risk, steering angle, total voyage distance, compliance with COLREGs, avoidance timing, and vessel maneuverability. For objectives with different attributes, corresponding path decomposition methods are employed. The entire path is divided into multiple way points. By evaluating the performance of each way point, the computational burden is reduced, and the reuse of high-quality way points is promoted, thereby enhancing algorithm efficiency.

Specifically, the path decomposition strategies are categorized into two types: one is based on geometric relationships, applicable to total voyage distance and steering angle, computed from the relative positions between consecutive way points; the other is based on state relationships, applicable to continuously varying factors like collision risk, COLREGs compliance, avoidance timing, and vessel maneuverability. This approach treats the state of a specific way point as representative of the entire path segment to enhance path smoothness.

In the total voyage objective function, voyage economy is converted into the sum of Euclidean distances between way points. For each way point, its contribution is defined as the sum of the normalized distance to the current segment and the estimated distance to the endpoint segment:

$$F_1={\displaystyle \frac{\sqrt{{\left(x_i-x_{i-1}\right)}^2+{\left(y_i-y_{i-1}\right)}^2}}{\sqrt{{\left(x_n-x_{i-1}\right)}^2+{\left(y_n-y_{i-1}\right)}^2}}}+{\displaystyle \frac{\sqrt{{\left(x_n-x_i\right)}^2+{\left(y_n-y_i\right)}^2}}{\sqrt{{\left(x_n-x_{i-1}\right)}^2+{\left(y_n-y_{i-1}\right)}^2}}}.$$

(15)

The objective function for the steering angle aims to minimize the frequency and magnitude of steering maneuvers during navigation, enhancing maneuvering efficiency and safety. The steering angle at way point i is computed using the vector angle formula, and the objective function requires its absolute value:

$$F_2=\left|arccos\left({\displaystyle \frac{\left(x_i-x_{i-1},y_i-y_{i-1}\right)·{\left(x_n-x_i,y_n-y_i\right)}^T}{∥\left(x_i-x_{i-1},y_i-y_{i-1}\right)·\left(x_n-x_i,y_n-y_i\right)∥}}\right)\right|.$$

(16)

To adhere to the collision avoidance principles of “early, substantial, wide, and clear” maneuvering, the collision risk must be continuously evaluated and minimized throughout the entire voyage. The safe objective function is therefore formulated as follows:

$$F_3=\max CRI.$$

(17)

Based on the description of encounter scenarios [28], the relative orientation of the target ship, denoted as $T_R$, is divided into three distinct regions: 355–005°, 005–67.5°, and 67.5–112.5°. In these regions, the own ship is required to take proactive measures to avoid a collision. Conversely, when $T_R$ lies within the two regions of 112.5–247.5° and 247.5–355°, the own ship should maintain its current course and speed. This approach is aligned with the COLREGs, and the following objective function is formulated accordingly:

$$F_4=\left\{\begin{array}{cc}1\hfill & {000}^{\circ }\le T_R\le 112.5^{\circ }\mathrm{or}{355}^{\circ }\le T_R\le {005}^{\circ }\hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right..$$

(18)

The collision risk threshold is established at 0.5. Once this value is exceeded, the give-way vessel must immediately take evasive action. The objective function for collision avoidance timing is

$$F_5=\left\{\begin{array}{cc}1\hfill & CRI\ge 0.5\hfill \\ 0\hfill & CRI<0.5\hfill \end{array}\right..$$

(19)

Although small vessels are more maneuverable due to their small size, they are more susceptible to external forces like wind and waves, which can cause instability at high speeds. This necessitates a higher maneuverability coefficient of 1.0 for small vessels. Medium vessels, with moderate speed and better stability, are less affected by such forces and can perform smoother maneuvers at lower speeds, justifying a coefficient of 0.9. Large and extra-large vessels are more stable and capable of handling large rudder angles, leading to a higher coefficient of 1.1. The objective function for USV maneuverability is formulated as follows:

$$F_6=\left\{\begin{array}{cc}1.0,\hfill & \mathrm{small}\mathrm{USVs}\hfill \\ 0.9,\hfill & \mathrm{medium}\mathrm{USVs}\hfill \\ 1.1,\hfill & \mathrm{large}\mathrm{and}\mathrm{extra}-\mathrm{large}\mathrm{USVs}\hfill \end{array}\right..$$

(20)

Ultimately, the aforementioned objective functions are integrated into an overall fitness function through weighting and constraint formulation. Collision risk is assigned the highest weight as a safety factor, followed by economic objectives. COLREGs compliance, evasion timing, and vessel maneuverability are incorporated as constraints in multiplicative constraints. A lower fitness value indicates superior overall path performance

$$Fitness=\left(\begin{array}{c}{\omega }_1{F}_1+{\omega }_2{F}_2+{\omega }_3{F}_3\end{array}\right)·F_4·F_5·F_6.$$

(21)

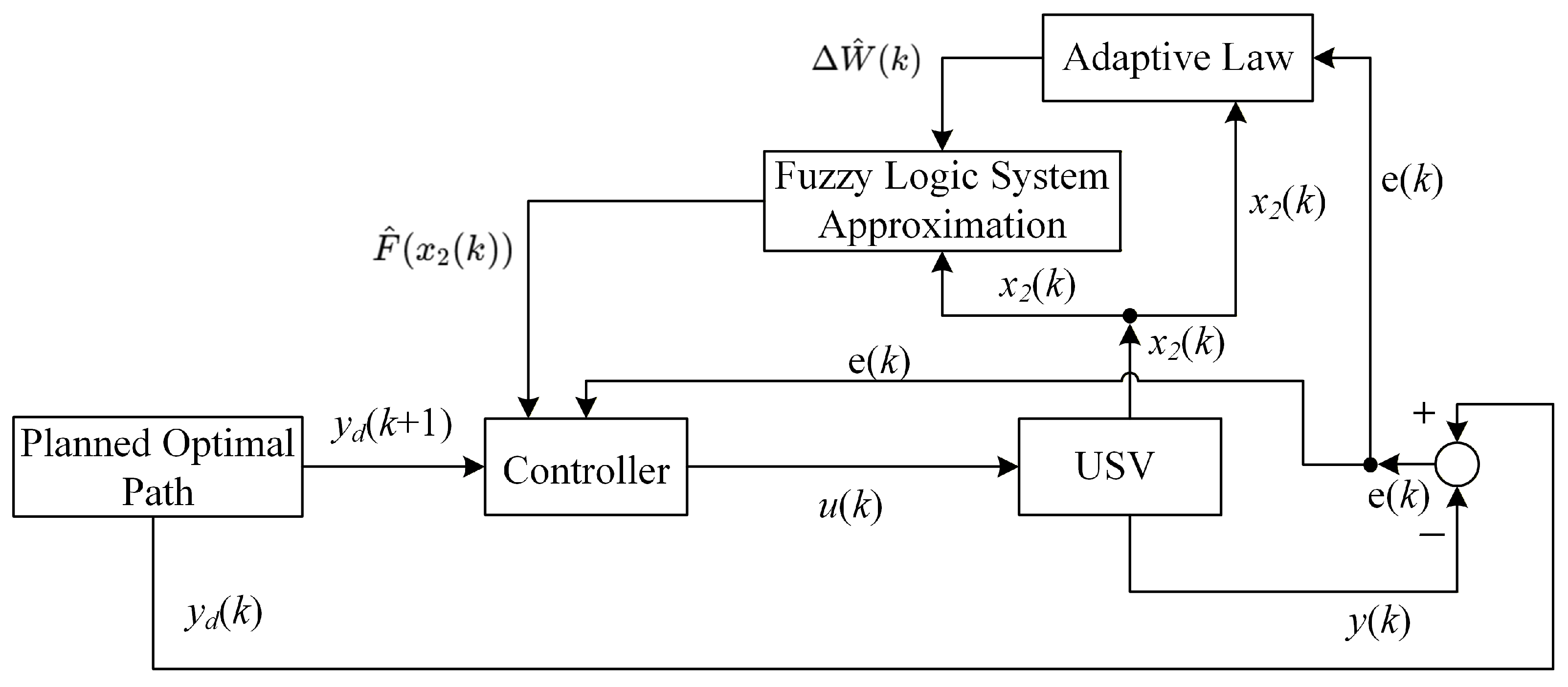
3. Path Tracking Control for USVs

This chapter focuses on the control systems used for path tracking of USVs, specifically addressing ship heading motion. Section 3.1 introduces the mathematical model of the ship’s heading motion. Section 3.2 discusses the design of the adaptive fuzzy logic controller for the ship’s motion control. Finally, Section 3.3 provides an analysis of the system’s stability to ensure the effectiveness and reliability of the proposed control system.

3.1. Mathematical Model of Ship Heading Motion

In continuous systems, the nonlinear control system for ship heading can be described by the dynamic relationship between rudder angle $\delta$ and heading $\varphi$ [29], generally expressed as:

$$\ddot{\varphi }+{\displaystyle \frac{1}{T}}H\left(\dot{\varphi }\right)={\displaystyle \frac{K}{T}}\delta ,$$

(22)

where K represents the vessel’s turning ability index, T denotes the vessel’s tracking performance index, and $H\left(\dot{\varphi }\right)$ is a nonlinear function of $\dot{\varphi }$, approximated as $H\left(\dot{\varphi }\right)=b_1\dot{\varphi }+b_2{\dot{\varphi }}^3+b_3{\dot{\varphi }}^5+\cdots$, where coefficient $b_i(i=1,2,3,\cdots )$ is a constant. By defining the state variable $x_1=\varphi$, $x_2=\dot{\varphi }$ and control input $u={\displaystyle \frac{K\delta }{T}}$, the original continuous model can be discretized to establish a nonlinear discrete system model for vessel heading [30]:

$$\left\{\begin{array}{c}{x}_1(k+1)=x_2\left(k\right),\hfill \\ x_2(k+1)=F\left(x_2\left(k\right)\right)+u\left(k\right),\hfill \\ y\left(k\right)=x_1\left(k\right).\hfill \end{array}\right.$$

(23)

For the second discrete system in (23), the following relationship holds:

$$y\left(k\right)\triangleq x_2\left(k\right),$$

(24)

which results in the corresponding discrete form:

$$y(k+1)=F\left(y\right(k\left)\right)+u\left(k\right).$$

(25)

In this system, $x_i(i=1,2)$ denotes the state variable; $u\left(k\right)$ and $y\left(k\right)$ represent the control input and system output, respectively; the nonlinear function $F\left(x_2\left(k\right)\right)=(-1/T)H\left(x_2\left(k\right)\right)$ remains unknown.

Further, the tracking error is defined as

$$e\left(k\right)=y_d\left(k\right)-y\left(k\right).$$

(26)

Based on [31] and practical navigation experience, the optimal path formed by the preceding planning is mathematically modeled to derive the following input control signal:

$$y_d\left(k\right)=\arctan {\displaystyle \frac{x}{y}}+\pi ,y_d\left(k\right)\in ({\displaystyle \frac{\pi }{2}},{\displaystyle \frac{3\pi }{2}}),$$

(27)

where $y_d\left(k\right)$ denotes the ideal reference signal and $(x,y)$ represent the position coordinates of USVs in a given coordinate system.

The control objective of this study is to design an adaptive controller $u\left(k\right)$ such that the vessel heading motion tracks the planned command signal $y_d\left(k\right)$ produced by the path planner. From (23), the system output satisfies $y\left(k\right)=x_1\left(k\right)$ and the unknown nonlinearity enters the dynamics through the yaw-rate state $x_2\left(k\right)$ via the term $F\left(x_2\left(k\right)\right)$. The block diagram of the controller design is shown in Figure 3.

Assumption 1.

State variables $x_1\left(k\right)$ and $x_2\left(k\right)$ are measurable.

Assumption 2.

For any time step $k\ge 0$, the desired reference signal $y_d\left(k\right)$ is bounded.

$$|y_d\left(k\right)|\le {\overline{y}}_d,|\Delta y_d\left(k\right)|\le \Delta {\overline{y}}_d,$$

where $\Delta y_d\left(k\right)\triangleq y_d(k+1)-y_d\left(k\right)$, and ${\overline{y}}_d,\Delta {\overline{y}}_d$ are positive constants.

Accordingly, in Section 3.2 we construct the adaptive fuzzy controller by approximating and compensating $F\left(x_2\left(k\right)\right)$ based on measurable signals $x_1\left(k\right)$ and $x_2\left(k\right)$ (Assumption 1). This design allows the yaw-rate dynamics to be regulated while ensuring that the heading response $x_1\left(k\right)$ follows the planned command $y_d\left(k\right)$.

Under Assumption 2, where $y_d\left(k\right)$ and its time derivatives are bounded, the closed-loop system is designed to achieve semiglobal uniform ultimate boundedness, with the tracking error converging to a neighborhood of the origin.

In Figure 3, the summing junction computes the heading tracking error $e\left(k\right)=y_d\left(k\right)-y\left(k\right)$. The error $e\left(k\right)$ is split by a branching node (black dot) to feed both the controller and the adaptive law, avoiding multiple outputs from a summing junction. The fuzzy approximator produces $\widehat{F}\left(x_2\left(k\right)\right)$, while the adaptive law updates the weight vector $\widehat{W}\left(k\right)$, maintaining the single error structure.

3.2. Design of Adaptive Fuzzy Logic System Controller for Vessels

According to the universal approximation theorem [32], a fuzzy logic system is employed to approximate and compensate the unknown nonlinear term $F\left(y\left(k\right)\right)$ in the system:

$$\widehat{F}\left(y\left(k\right)\right)=\widehat{W}{\left(k\right)}^{T}h\left[y\left(k\right)\right],$$

(28)

where $\widehat{W}\left(k\right)$ is the fuzzy weight vector and $h_j$ is the fuzzy basis function vector, typically implemented using a Gaussian membership function:

$$h_j=\exp \left({\displaystyle \frac{{∥x-c_j∥}^2}{2{{\sigma }_j}^2}}\right),$$

(29)

where $c_j={[c_{j1},\dots ,c_{jq}]}^T$ is the fuzzy rule center vector and ${\sigma }_j$ is the width parameter. Assuming there exists an optimal fuzzy weight vector $W^{*}$ such that the fuzzy logic system approximation error ${\Delta }_F\left(x\right)$ satisfies $|{\Delta }_F\left(x\right)|<{\epsilon }_F$, the fuzzy approximation error can be expressed as

$$\begin{array}{cc}\hfill \tilde{F}\left(y\left(k\right)\right)& =F\left[y\left(k\right)\right]-\widehat{F}\left[y\left(k\right)\right]\hfill \\ \hfill & =-\tilde{W}{\left(k\right)}^{T}h\left[y\left(k\right)\right]-{\Delta }_F\left[y\left(k\right)\right],\hfill \end{array}$$

(30)

where $\tilde{W}\left(k\right)=\widehat{W}\left(k\right)-W^{*}$.

Based on this, the control law is designed as

$$u\left(k\right)=y_d(k+1)-\widehat{F}\left(y\left(k\right)\right)-{\beta }_{1}e\left(k\right),{\beta }_1>0.$$

(31)

Substituting these into the system model yields the error dynamics equation:

$$e(k+1)=y_d(k+1)-y(k+1)=y_d(k+1)-\left(F\left(y\right(k\left)\right)+u\left(k\right)\right)=\tilde{F}\left(y\left(k\right)\right)-{\beta }_{1}e\left(k\right)$$

(32)

Move Equation (32) to the left and rewrite it as follows:

$$e\left(k\right)+{\beta }_{1}e(k-1)=\tilde{F}\left(y(k-1)\right).$$

(33)

Then define the following equation:

$$\Psi \left(z^{-1}\right)=1+{\beta }_1{z}^{-1},$$

(34)

The error function becomes

$$e\left(k\right)=\Psi \left(z^{-1}\right)\tilde{F}\left(y(k-1)\right).$$

(35)

Further introducing the filtering error function [30],

$$e_1\left(k\right)=\gamma [e\left(k\right)-{\Psi }^{-1}\left(z^{-1}\right)\eta \left(k\right)],\gamma >0,$$

(36)

Rearranging yields the following recursive relationship:

$$e_1(k-1)={\displaystyle \frac{\gamma \{\tilde{F}\left[x(k-1)\right]-\eta \left(k\right)\}-e_1\left(k\right)}{{\beta }_1}}.$$

(37)

Based on [33], the adaptive control law is designed as

$$\Delta \widehat{W}\left(k\right)=\left\{\begin{array}{cc}{\displaystyle \frac{\gamma }{\tau {\beta }_1^2}}h\left[x(k-1)\right]e_1\left(k\right),\hfill & |e_1\left(k\right)|>{\epsilon }_F/D\hfill \\ 0,\hfill & |e_1\left(k\right)|\le {\epsilon }_F/D\hfill \end{array}\right.,$$

(38)

where D is the gain constant, $\Delta \widehat{W}\left(k\right)=\widehat{W}\left(k\right)-\widehat{W}(k-1)$.

3.3. Stability Analysis

To address stability issues in discrete-time systems, this study employs Lyapunov theory for analysis [34]. First, we define the discrete-time Lyapunov function:

$$V\left(k\right)=e_1^2\left(k\right)+\rho {\tilde{W}}^T\left(k\right)\tilde{W}\left(k\right),$$

(39)

The first-order difference of this function is expressed as

$$\begin{array}{cc}\hfill \Delta V\left(k\right)& =V\left(k\right)-V(k-1)\hfill \\ & =e_1^2\left(k\right)-e_1^2(k-1)+\hfill \\ & \tau \left[{\tilde{W}}^T\left(k\right)+{\tilde{W}}^T(k-1)\right]\left[\tilde{W}\left(k\right)-\tilde{W}(k-1)\right],\hfill \end{array}$$

(40)

where $\tau$ is a strictly positive definite design parameter. To verify stability, we must derive the relationship between error dynamics and parameter update rates. Substituting $e_{\mathrm{i}}(k-1)$ from Equation (37) into the Lyapunov function’s difference expression yields [35]

$$\begin{array}{cc}& \Delta V\left(k\right)=-V_1+{\displaystyle \frac{2\gamma \left\{\tilde{F}\left[x(k-1)\right]-\eta \left(k\right)\right\}{e}_1\left(k\right)}{{\beta }_1^2}}\hfill \\ & +\tau [\Delta {\widehat{W}}^T\left(k\right)+2{\tilde{W}}^T(k-1)]\Delta \widehat{W}\left(k\right),\hfill \end{array}$$

(41)

where $\gamma$ is the adjustment parameter, and $\tau$ satisfies the non-negativity condition:

$$\tau ={\displaystyle \frac{{e_1}^2\left(k\right)(1-{\beta }_1^2)}{{{\beta }_1}^2}}+{\displaystyle \frac{{\gamma }^2\left\{\tilde{F}\left[x(k-1)\right]-\eta {\left(k\right)}^2\right\}}{{{\beta }_1}^2}}\ge 0,$$

(42)

Substituting adaptive law (38) into the Lyapunov function difference expression yields two simplified cases:

$$\Delta \eta \left(k\right)=\left\{\begin{array}{c}-V_1-{\displaystyle \frac{2\gamma }{{\beta }_1^2}}\left\{{\Delta }_F\left[x(k-1)\right]+\eta \left(k\right)\right\}{e}_1\left(k\right)\hfill \\ \\ +{\left({\displaystyle \frac{\gamma }{\sqrt{\tau }{\beta }_1^2}}\right)}^2{h}^{T}h{e}_1^2\left(k\right),\left|e_1\left(k\right)\right|>{\epsilon }_F/D,\hfill \\ \\ -V_1-{\displaystyle \frac{2\gamma }{{\beta }_1^2}}\{{\tilde{W}}^T(k-1)h+\eta \left(k\right)+\hfill \\ \\ {\Delta }_F\left[x(k-1)\right]e_1\left(k\right)\},\left|e_1\left(k\right)\right|\le {\epsilon }_F/D.\hfill \end{array}\right.$$

(43)

To ensure asymptotic convergence of the tracking error, an auxiliary control signal $\eta \left(k\right)={\eta }_1\left(k\right)+{\eta }_2\left(k\right)$ is designed, where

$${\eta }_1\left(k\right)={\displaystyle \frac{\gamma }{2\tau {\beta }_1^2}}{h}^T\left[x(k-1)\right]h\left[x(k-1)\right]e_1\left(k\right),$$

(44)

$${\eta }_2\left(k\right)=D{e}_1\left(k\right),$$

(45)

Substituting this into the error dynamics equation yields an explicit expression for the error function:

$$e_1\left(k\right)={\displaystyle \frac{-{\beta }_1{e}_1(k-1)+\gamma \left[e\left(k\right)+{\beta }_{1}e(k-1)\right]}{1+\gamma \left[{\eta }_1^{\prime }\left(k\right)+D\right]}},$$

(46)

If $\mid e_1\left(k\right)\mid >{\epsilon }_F/D$, substituting Equation (43) into Equation (38) gives

$$\begin{array}{cc}\hfill \Delta V\left(k\right)& =-V_1-{\displaystyle \frac{2\gamma }{{\beta }_1^2}}\left\{{\Delta }_F\left[x(k-1)\right]+D{e}_1\left(k\right)\right\}{e}_1\left(k\right)\hfill \\ & \le -{\displaystyle \frac{2\gamma }{{\beta }_1^2}}\left\{{\Delta }_F\left[x(k-1)\right]+D{e}_1\left(k\right)\right\}{e}_1\left(k\right).\hfill \end{array}$$

(47)

Based on the assumption $\mid {\Delta }_F\left(x\right)\mid <{\epsilon }_F$, and when $|e_1\left(k\right)|>{\epsilon }_F/D$, we have

$$\mid e_1\left(k\right)\mid >{\displaystyle \frac{\mid {\Delta }_F\left[x(k-1)\right]\mid }{D}},e_1^2\left(k\right)>-{\displaystyle \frac{{\Delta }_F\left[x(k-1)\right]e_1\left(k\right)}{D}}.$$

(48)

Therefore, $\left\{{\Delta }_F\left[x(k-1)\right]+D{e}_1\left(k\right)\right\}{e}_1\left(k\right)>0$, and thus $\Delta V\left(k\right)<0$ satisfies the Lyapunov stability condition.

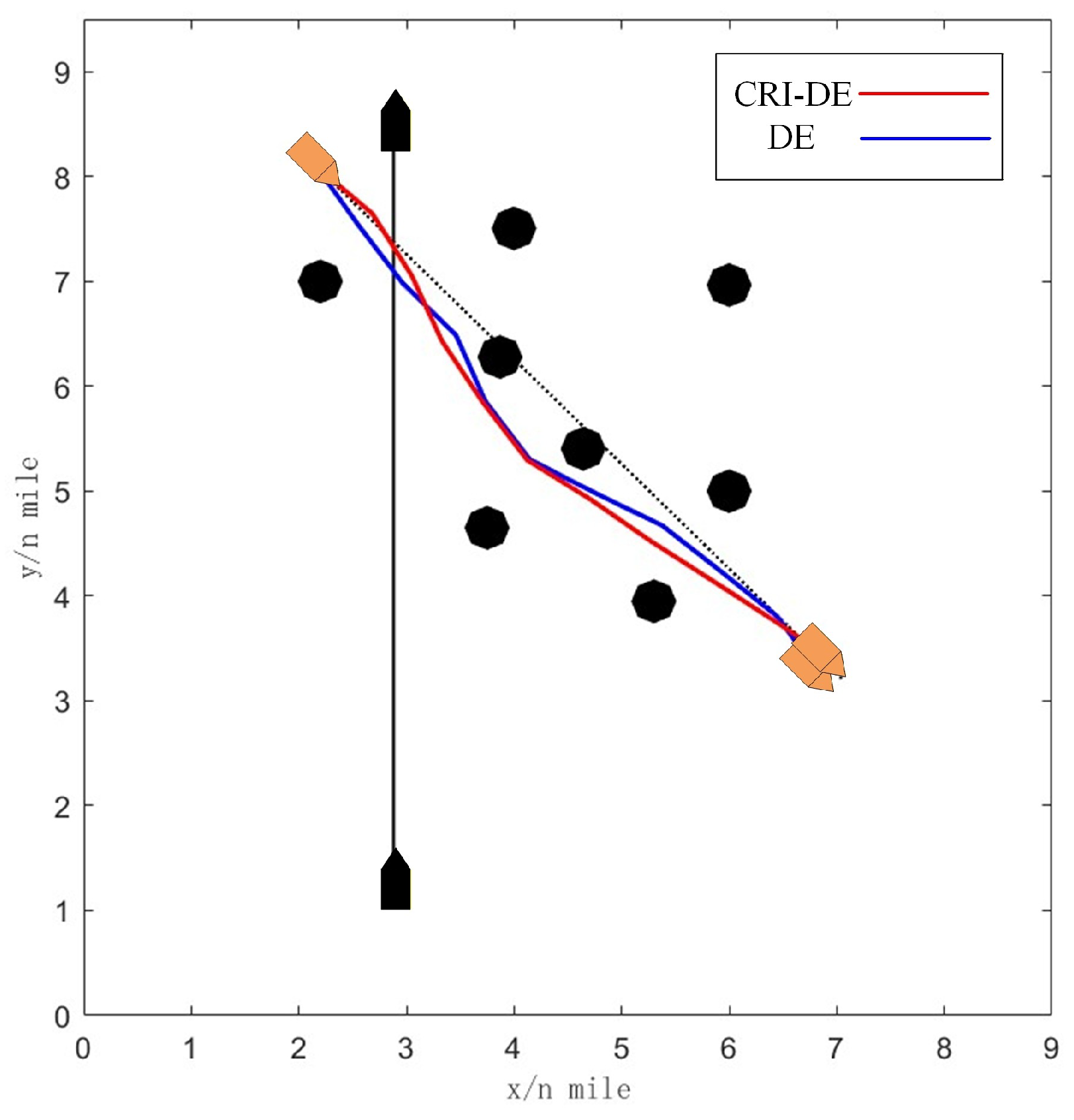
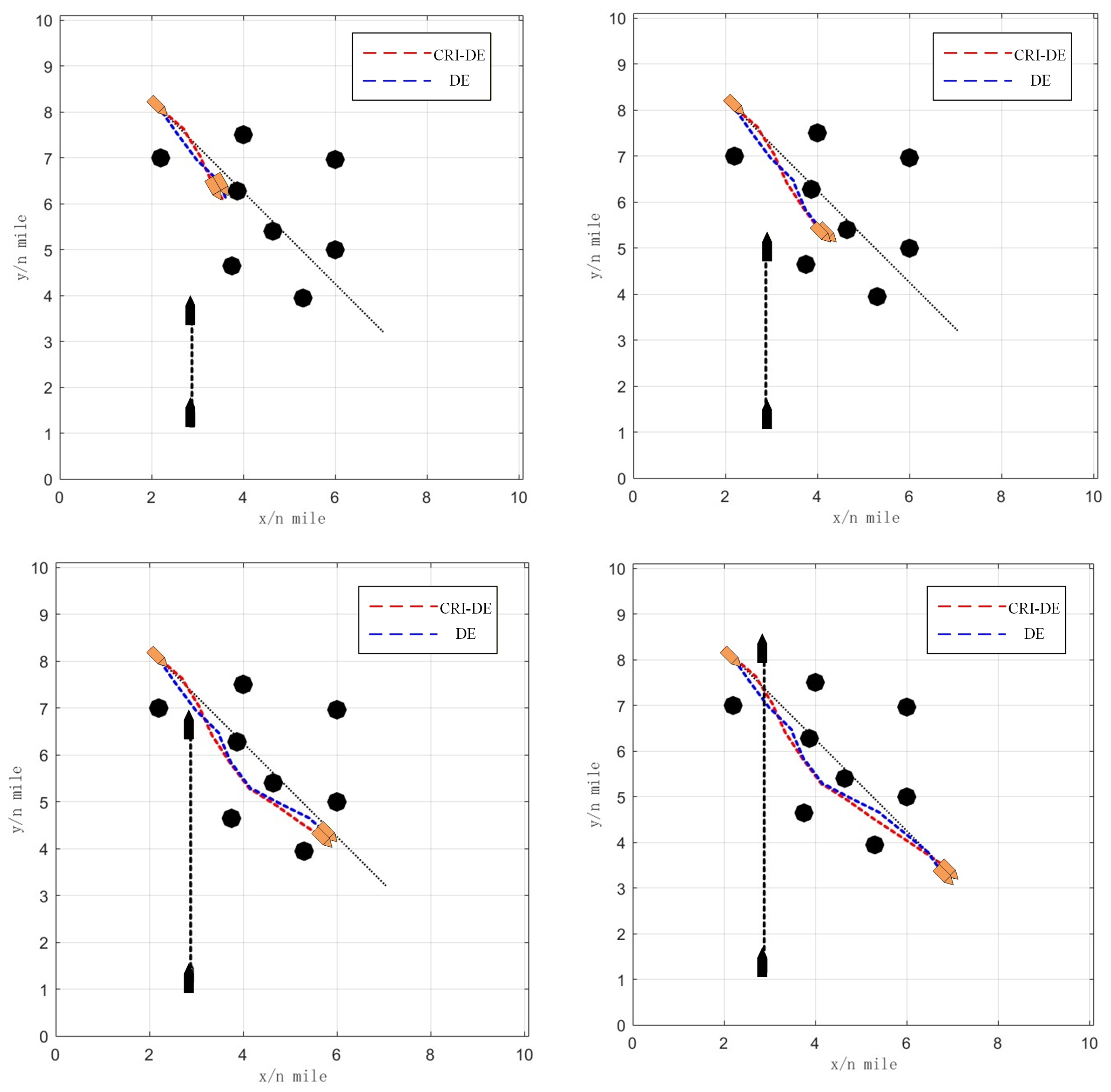
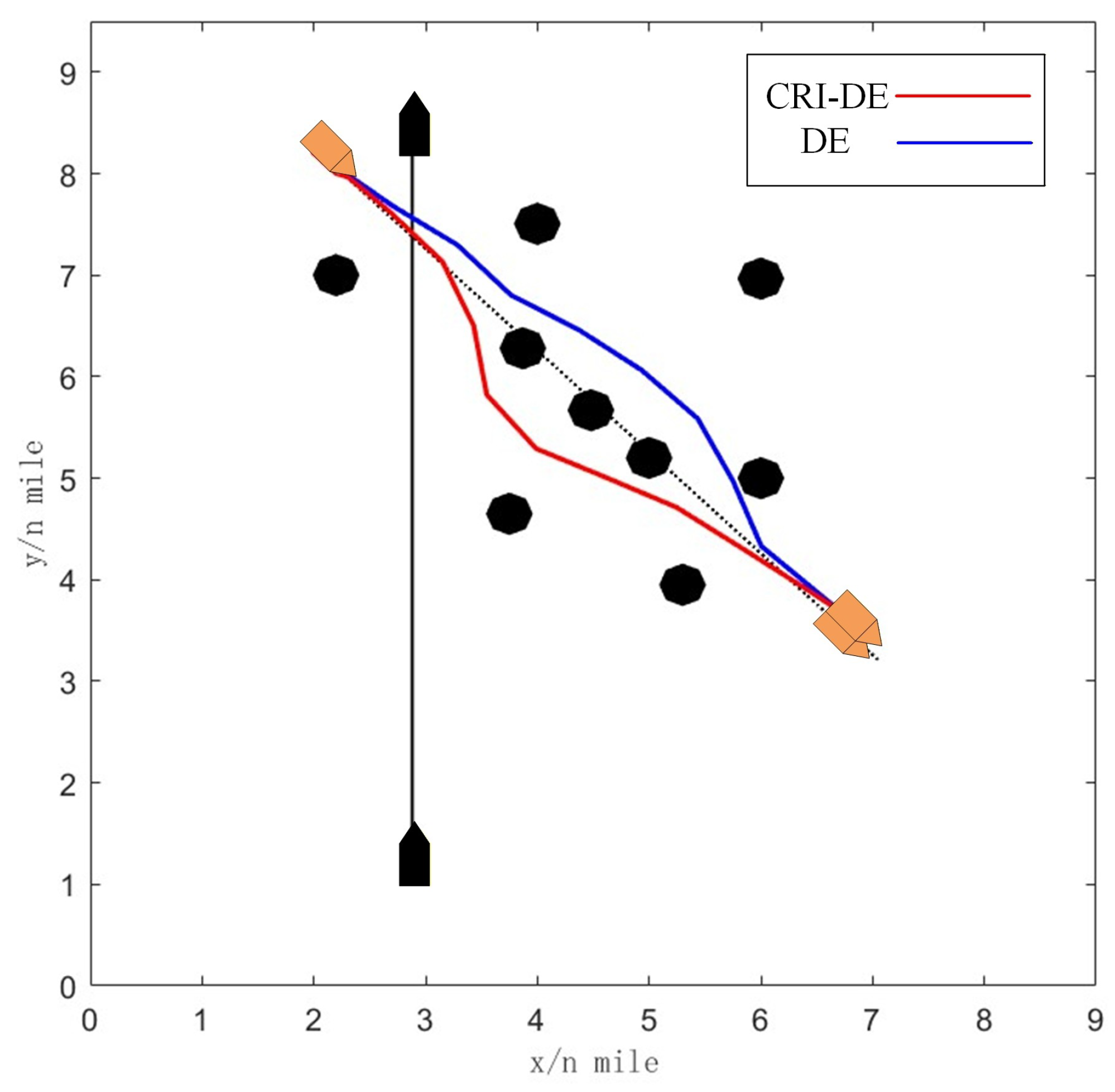
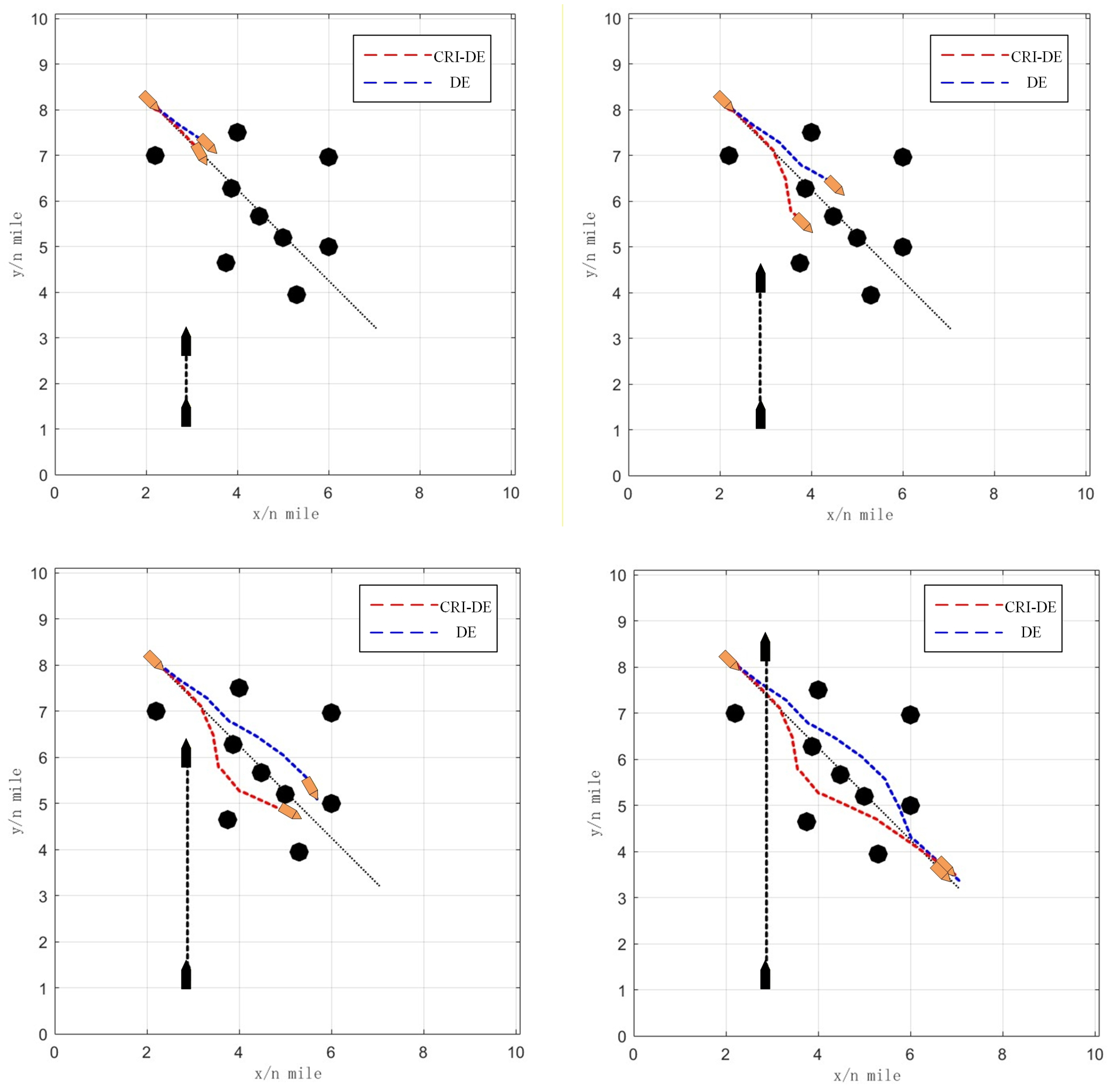
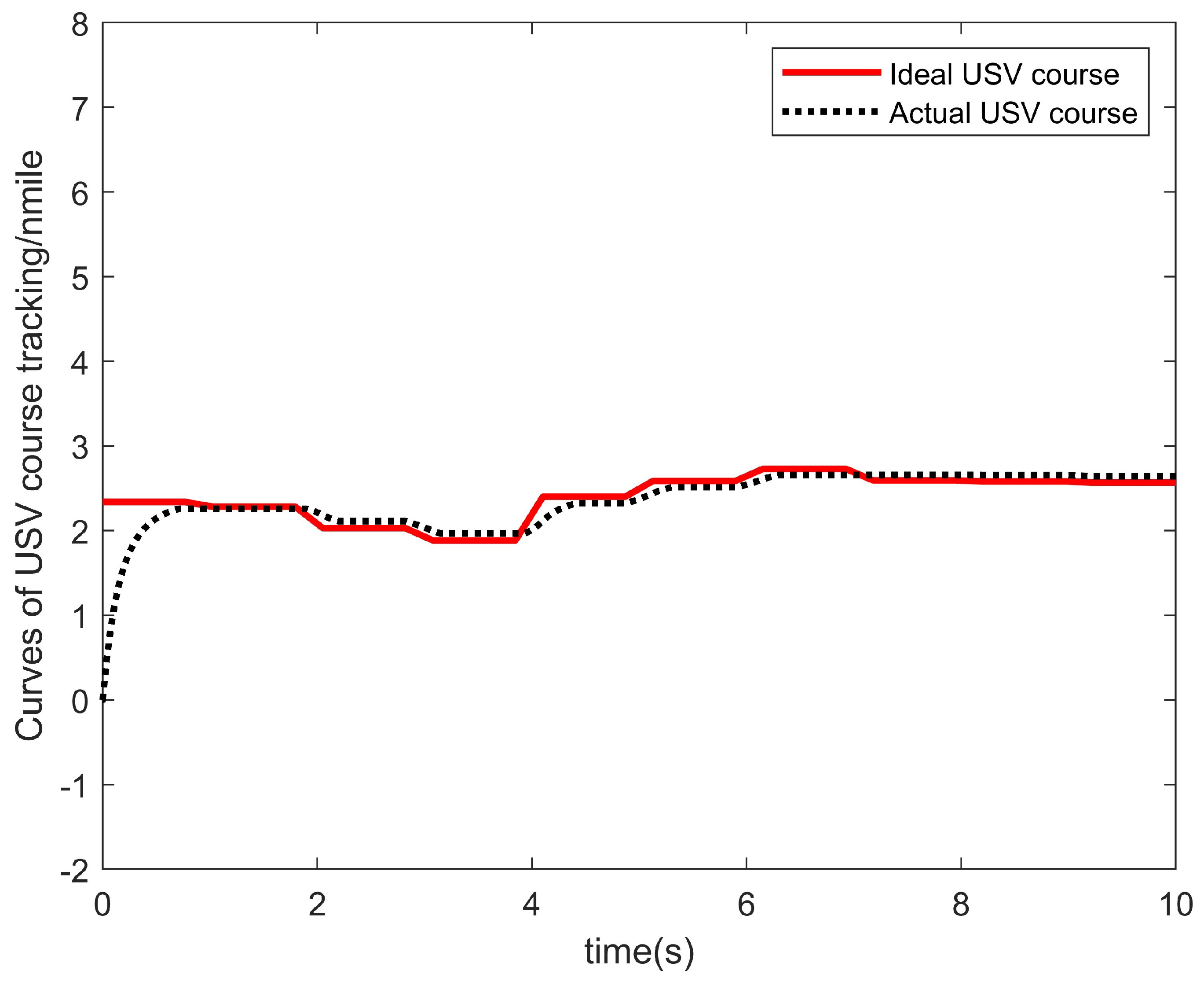
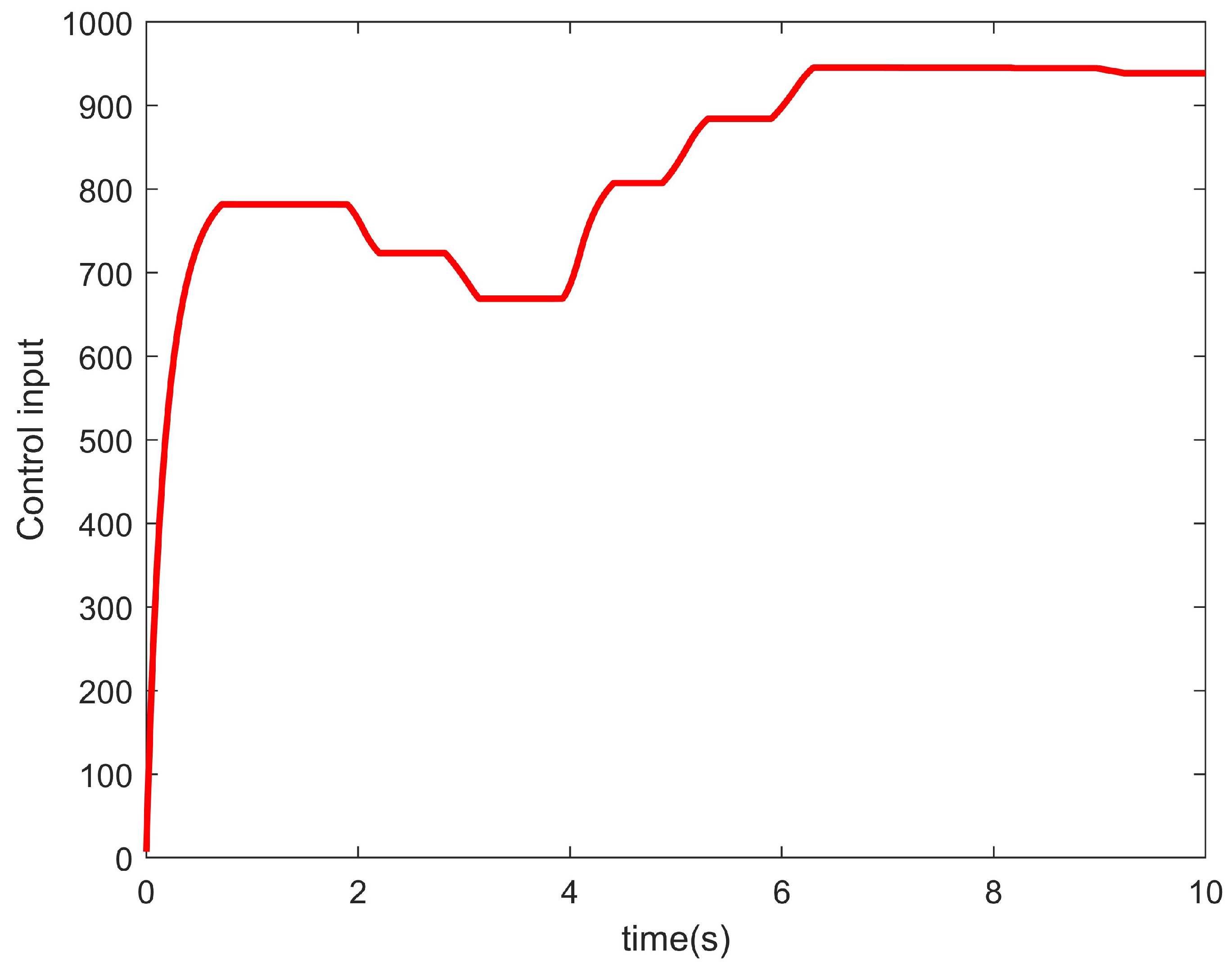
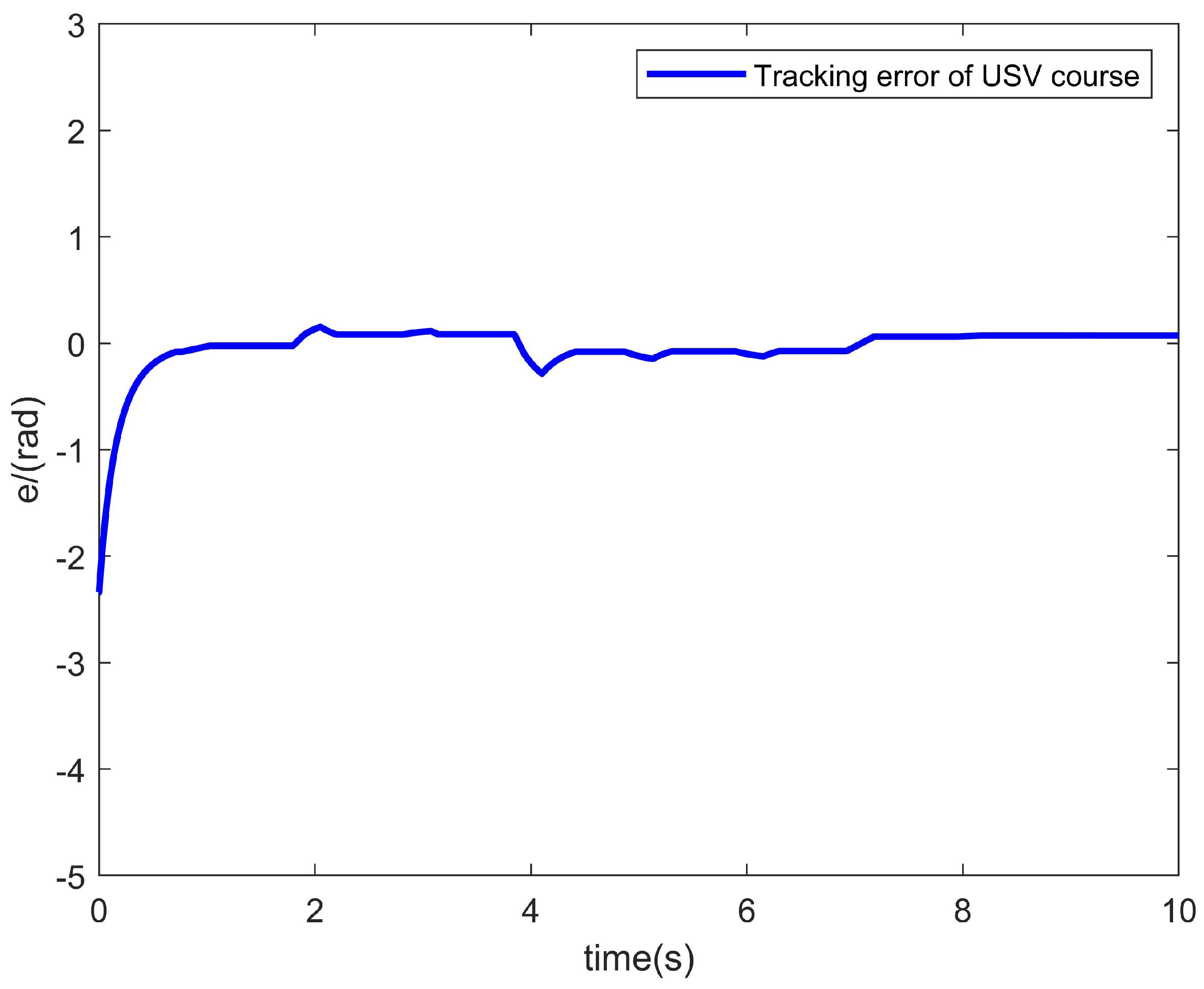
4. Simulation Result

The simulation experiments were carried out in MATLAB 2023b using standard hardware, specifically a computer with an Intel Core i5 CPU and 16 GB of RAM. To validate the practical effectiveness of the proposed adaptive DE algorithm for USV path planning and to evaluate the vessel’s ability to follow the desired trajectory and the accuracy of the control system, path planning and tracking control simulations were performed. The experimental environment consisted of open water with good visibility, where the effects of wind, waves, and currents were neglected. In the absence of external factors such as water currents, the difference between the ship’s course and heading is considered negligible. Therefore, the course used in this model was effectively equivalent to the heading.

Case 1. A comparative study was conducted between the standard DE algorithm and the proposed adaptive DE algorithm. To ensure fairness and consistency, both algorithms used the same parameter settings. The parameters and initial states of the experimental subjects are presented in

Table 1. Ship parameters.

Parameter	OS	TS
Length between perpendiculars/m	189	105
Beam/m	27.8	18
Draft/m	11.0	5.4
Block coefficient	0.720	0.5595
Rudder area/m2	38	11.8
Water density/m3	1.025	1.025
Displacement/t	29,268.3	5735.5
Metacentric height/m	1.8	−0.51

and

Table 2. Initial state of experimental subjects.

Ship	Initial Heading/°	Initial Speed/kn	Distance from OS/n Mile
OS	135°	8	0
TS	0°	8	6.90
Obstacle	none	none	none

. The iteration count was $M=100$, the population size was $NP=50$, and the population dimension was $Q=10$. The weighting coefficients were ${\omega }_1=0.4,{\omega }_2=0.1,{\omega }_3=0.5$ for both algorithms.

The simulation environment consisted of a square region with a side length of 9 nautical miles (n miles). In this region, eight octagonal obstacles were randomly distributed for scenario S1 and nine octagonal obstacles for scenario S2. Each obstacle had a radius of 0.21 nautical miles. The defined Euclidean coordinate system set the initial position of the vessel at (2, 8), with the target position located at (7, 3.5).

Scenario S1 involved a two-vessel encounter where TS formed a crossing situation with OS and static obstacles were present along the intended course. In scenario S2, a two-vessel encounter occurred, where TS formed a crossing situation with OS but with one additional static obstacle compared to S1. Static obstacles were distributed along the intended course for both scenarios, where S1 had eight obstacles and S2 had nine.

In the S1 scenario, the efficiency, effectiveness, and applicability of the proposed adaptive DE algorithm and the standard DE algorithm were compared by running each algorithm independently for 30 trials, as shown in

Table 3. Results of simulation experiments of S1 scenario.

Algorithm	CRI-DE	DE
Average Fitness Value	0.9597	1.0033
Best Fitness Value	0.8851	0.9512
Fitness Std. Dev.	0.4391	0.4539
Computation Time/Seconds	4.5780	3.6609
Minimum Distance to Target Ship/Nautical Miles	1.36	1.34
Minimum Distance to Obstacle/Nautical Miles	0.82	0.81
Maximum Yaw Distance/Nautical Miles	0.58	0.76

.

Among the randomly selected simulation results, the path planning outcomes obtained by the standard DE algorithm and the proposed adaptive DE algorithm in the S1 scenario are shown in Figure 4 and Figure 5. Table 3 summarizes the optimal value, average value, and standard deviation of the fitness values from 30 trials, reflecting the effectiveness of each algorithm. These results also include the minimum distance between the USV and dynamic vessels or static obstacles, representing the safety of the planned path, the maximum yaw distance indicating the economic viability, and the computation time reflecting the efficiency.

The results demonstrate that the improved DE algorithm consistently achieves smaller fitness values with a more uniform distribution and lower optimal values, indicating better stability. The adaptive DE algorithm also plans shorter, more optimal paths compared to the standard DE algorithm. While the standard DE algorithm has a shorter running time, it produces larger yaw distances, suggesting that it sacrifices path efficiency for speed. These findings confirm that the proposed adaptive DE algorithm not only improves the collision avoidance performance but also offers superior path planning efficiency, thus validating its overall superiority.

In the S2 scenario, the efficiency, effectiveness, and applicability of the proposed adaptive DE algorithm and the standard DE algorithm were compared by running each algorithm independently for 30 trials, as shown in

Table 4. Results of simulation experiments of S2 situation.

Algorithm	CRI-DE	DE
Average Fitness Value	1.2064	1.2796
Best Fitness Value	1.1476	1.2335
Fitness Std. Dev.	0.4867	0.4280
Computation Time/Seconds	4.5852	3.7689
Minimum Distance to Target Ship/Nautical Miles	1.20	1.22
Minimum Distance to Obstacle/Nautical Miles	0.85	0.81
Maximum Yaw Distance/Nautical Miles	0.71	0.71

.

A randomly selected simulation result from one of the trials is presented in Figure 6 and Figure 7. Based on the data in Table 4, it can be observed that the proposed adaptive DE algorithm achieves smaller average and optimal fitness values, although with slightly larger standard deviation. This indicates that the algorithm is effective in this scenario, but its stability slightly decreases as the number of obstacles increases.

In terms of computation time, the proposed adaptive DE algorithm performs similarly to the S1 scenario, requiring only about 4.58 s, which indicates high efficiency. However, as the collision avoidance scenario becomes more complex, the computation time of the standard DE algorithm increases. Regarding safety, both algorithms are able to ensure safe avoidance of the target ship and static obstacles, with the proposed adaptive DE algorithm achieving a slightly larger avoidance distance. Specifically, the minimum distance from the target ship is 0.85 nautical miles. Considering the data from both algorithms in Table 4, the proposed adaptive DE algorithm outperforms the standard DE algorithm in both computation speed and algorithm performance. It also exhibits good economic performance. However, there is still room for improvement in terms of algorithm stability.

Case 2. The optimal path planned in Case 1 was further processed and used as the input signal for path tracking control. To facilitate subsequent analysis, the position coordinates along the planned path were subjected to a mathematical transformation. Let $\mathcal{P}$ denote the heading angle of USVs, $(x,y)$ represent the position coordinates in the current coordinate system, and $\phi$ be the angle between the vessel’s forward direction and the horizontal plane. According to maritime practice and Ref. [36], the heading angle derived from Equation (49) is taken as the ideal heading reference value, given by

$${\phi }_d=\arctan {\displaystyle \frac{x}{y}}+\pi ,\phi \in ({\displaystyle \frac{\pi }{2}},{\displaystyle \frac{3\pi }{2}}).$$

(49)

In this experiment, the “YuKun” vessel was selected as the simulation object, with the main particulars given as length 189.0 m, beam 27.8 m, full load draft 11.0 m, block coefficient 0.720, and speed 8 kn. Additional calculations yielded the parameters of the discrete nonlinear heading model as $b_1=0.6,b_2=5,K=0.2,T=64$.

In the simulation test, the initial value of the controlled object was set to 0, and the ideal tracking signal was $y_d\left(k\right)={\phi }_d.$ The error variable $e_1\left(k\right)$ was computed using Equation (43). The control law followed Equation (31), and the adaptive law used Equation (38). The control parameters were set to ${\beta }_{\mathrm{l}}=0.008,\gamma =0.0045,\tau =0.001$, $D=5000,{\epsilon }_F=0.003$. The simulation results of the path tracking control are shown in Figure 8, Figure 9 and Figure 10.

Figure 8, Figure 9 and Figure 10 show that during course tracking, the heading angle of the USV remains essentially coincident with the planned route, without noticeable deviation. This demonstrates that under the control of the adaptive fuzzy logic controller, the vessel achieves accurate path tracking and completes the maneuver from the starting point to the target point. Moreover, when ${\phi }_d$ varies within interval $(\pi /2,3\pi /2)$, the system consistently maintains excellent tracking performance.

5. Discussion

This study addresses the challenges of path planning and tracking control for USVs, leveraging fuzzy logic and differential evolution algorithms. While the method exhibits promising results in simulations, its real-world applicability remains limited by environmental factors such as ocean currents, wind, and waves, which were not fully accounted for in the current model. These dynamic factors, along with the presence of irregularly shaped obstacles, must be considered for the method to be adapted to more complex, real-world environments.

The simplified assumptions of the system model, such as ignoring nonlinear disturbances and assuming ideal obstacle-free conditions, limit the robustness of the approach. Real-world conditions, such as moving obstacles and varying environmental forces, are not reflected in the initial simulations. In future work, improving obstacle modeling and introducing adaptive mechanisms for real-time environmental changes will enhance the system’s practical applicability. Moreover, the system’s failure boundaries, particularly under extreme operational conditions like high-density traffic or severe weather, need to be further explored.

Path planning performance is another area of concern. While the algorithm effectively plans optimal paths under ideal conditions, it may face difficulties in environments with multiple dynamic obstacles or sudden changes in vessel motion. Incorporating real-time decision-making processes and more advanced obstacle avoidance strategies will be critical in improving path planning reliability.

Lastly, constraints such as minimum distance from obstacles and vessel maneuvering regulations need to be incorporated into the model for comprehensive real-world implementation. Future developments should focus on extending the adaptive framework to consider maritime safety rules and constraints, ensuring the USVs can operate autonomously and safely under various conditions.

6. Conclusions

This study focuses on enhancing path planning and tracking control of USVs using an adaptive differential evolution algorithm. The approach effectively resolves the slow convergence and stagnation issues of traditional algorithms, enabling optimal path generation. The adaptive fuzzy controller designed for the vessel’s heading control compensates for environmental disturbances and model inaccuracies, making the framework robust.

While the proposed method shows strong simulation results, real-world implementation will face challenges related to computational limitations, particularly when transitioning from desktop simulations (MATLAB) to real-time applications. The performance of real-time systems often involves lower computational power, which needs to be addressed in future work to ensure efficient implementation.

Simulation results demonstrate the effectiveness of the algorithm, proving its ability to generate stable and precise paths in autonomous navigation. The method outperforms traditional path planning techniques in terms of convergence speed and the ability to avoid local minima, making it a promising solution for USV navigation in both simulations and potential real-world applications.