Research on Dual-Motor Redundant Compensation for Unstable Fluid Load of Control Valves

Abstract

Control valves are widely applied in nuclear power, offshore oil/gas extraction, and chemical engineering, but suffer from issues like pressure oscillation, flow control accuracy degradation, and motor overload due to unstable fluid loads (e.g., nuclear reactions in power plants and complex marine climates). This paper proposes a dual-motor redundant compensation method to address these challenges. The core lies in a control strategy where a single main motor drives the valve under normal conditions, while a redundant motor intervenes when load torque exceeds a preset threshold—calculated via the valve core’s fluid load model. By introducing excess load torque as positive feedback to the current loop, the method coordinates torque output between the two motors. AMESim and Matlab/Simulink joint simulations compare single-motor non-compensation, single-motor compensation, and dual-motor schemes. Results show that under inlet pressure step changes, the dual-motor compensation scheme shortens the stabilization time of the valve’s controlled variable by 40%, reduces overshoot by 65%, and decreases motor torque fluctuation by 50%. This redundant design enhances fault tolerance, providing a novel approach for reliability enhancement of deep-sea oil/gas control valves.

1. Introduction

In nuclear power, offshore oil and gas extraction, chemical engineering, and other fields, control valves, as key equipment, directly determine the safety of systems. In engineering applications, control valves face numerous challenges from complex operating conditions [1]. For example, unique effects from nuclear reactions in nuclear power plants and complex, variable marine climates significantly affect the fluids controlled by control valves, potentially causing severe fluctuations in controlled parameters (such as fluid pressure and flow rate). To ensure controlled parameters remain stable, the opening of control valves requires continuous dynamic adjustment. This adjustment process is not arbitrary but results from real-time, automatic feedback mechanisms within the control system. When control valves are in processes such as startup, shutdown, or adjustment, fluid flow inside the valve exhibits unsteady characteristics [2]. At this point, valve opening is not determined by a single factor but by the comprehensive interaction and constraints of multiple factors, including inlet fluid, outlet fluid, and valve driving force. More complexly, these factors themselves have a close feedback relationship with valve opening: changes in valve opening affect these factors, and vice versa [2,3,4].

The stability issue of control valves under complex operating conditions is essentially closely related to the propagation mechanism of pressure pulsations in hydraulic system dynamics and the coupling effect of the valve’s nonlinear behavior. Recent studies in the field of hydraulic system dynamics have shown that the generation of pressure pulsations is the result of the combined action of external mechanical vibration excitation, the internal nonlinear response of the valve, and system impedance characteristics [5,6]. The intricate interplay weaves a tight link between the flow properties of the fluid within the valve and the motion of internal parts like the valve spool. This coupling effect causes the valve core to bear unstable and oscillating additional coupling loads. The existence of such additional coupling loads complicates the operating conditions faced by control valves and introduces potential risks to their safe and stable operation.

When unstable fluid loads combine with the valve’s intrinsic load, the torque needed by the actuator might go beyond the safety limit. In engineering design, to protect crucial components such as the sealing surface of the valve stem, the maximum output torque of the actuator is generally set to 1.8 times the standard load, which serves as a protective measure [2]. When the superimposed unstable fluid load causes the total load to exceed this threshold, abnormal conditions such as actuator jamming and control lag occur, reducing valve control accuracy and causing a sudden increase in motor load torque beyond the actuator’s maximum output capacity, leading to faults like winding overheating, transmission component wear, or even motor seizing. If a motor failure occurs in offshore or deep-sea environments, timely replacement to restore system operation is difficult, potentially triggering safety accidents such as oil and gas leaks. The hydrocarbon leakage and explosion accident at a refinery in Texas, USA, resulted from a control valve drive motor failure that prevented the valve from opening and closing normally. The isomerization reaction in the unit required precise control of material flow and pressure, but the control valve motor failure disrupted the scheduled material flow, ultimately causing massive hydrocarbon leakage. The leaked hydrocarbons ignited and exploded upon contact with an open flame, resulting in significant casualties and property damage [7].

To address such challenges, research on unstable fluid loads in valves is necessary, and relevant studies have been conducted. Stosiak et al. focused on the suppression of broadband pressure pulsations in hydraulic systems as their research direction, proposed a hybrid suppression scheme integrating passive branched dampers and active control, established relevant theoretical models and experimental systems, and verified that this scheme can effectively cover pressure pulsations in low- to high-frequency bands and reduce system operating noise [8]. Li et al. [9] took marine electro-hydraulic control valves as the research object and found through AMESim simulations that load variations in valve cavity pressure area and damping orifice diameter significantly affect the response speed of control valves. Li et al. [10] established a collaborative simulation model for pneumatic ABS in commercial vehicles, confirming that overload leads to failure of key components in brake valves. Guo et al. [11] designed a valve-controlled cylinder servo system based on the ADRC algorithm, constructed a Matlab-AMESim collaborative simulation model, and studied dynamic responses under multiple working conditions. Han et al. [2] carried out theoretical derivation of unstable fluid loads in cone valves, adopted AMESim-Matlab joint simulation, and investigated the fluid oscillation characteristics during the movement of cone valves. Zhang et al. [12] proposed a novel control valve spool design, effectively suppressing unstable loads and reducing the jamming frequency caused by excessive fluid velocity. Tecza et al. [13] analyzed the unsteady fluid dynamics of steam turbine throttle valves through CFD simulations and optimized the valve structure accordingly. Simic et al. [14] constructed a new fluid model for small regulating valves and optimized their geometric shapes. Existing studies have laid a certain research foundation in the composition, calculation, and monitoring of unstable fluid loads, which helps reduce the adverse effects caused by unstable fluid loads. However, research on enhancing the ability of valves to cope with extreme working conditions and improving valve reliability remains very limited.

To solve these issues, this paper innovatively proposes a scheme that deeply integrates dual-motor redundant drive with load compensation. This scheme integrates multiple advantages, demonstrating excellent performance in improving system performance and reliability. From the perspective of reliability, the dual-motor redundant system provides robust guarantees for stable control valve operation. In complex and variable actual operating conditions, although motor failure is a low-probability event, it often paralyzes the entire control system. The dual-motor redundant design in this scheme acts as “double insurance” for control valve operation. When one motor fails due to sudden issues (e.g., overload, short circuit), the other can immediately take over within a very short time, seamlessly switching to normal operation to ensure precise and stable valve movements, avoiding production interruptions or safety accidents caused by motor failures, thus ensuring sufficient fault tolerance of the control system. In terms of driving force and control flexibility, the dual-motor drive mode shows unparalleled advantages. Under extreme conditions with excessive unstable fluid loads, traditional single-motor drive systems often struggle to provide sufficient torque to drive the valve core, reducing adjustment accuracy or even rendering the valve inoperable. In contrast, the dual-motor drive system in this scheme achieves precise synchronous operation of the two motors through advanced collaborative control algorithms. When high-torque output is required, the two motors work together to provide strong driving force, ensuring rapid and accurate valve core movement, thereby achieving precise fluid control. Additionally, the flexible control of dual motors offers more possibilities for system optimization, allowing real-time adjustment of motor output power and speed according to different operating conditions to implement more intelligent and personalized control strategies.

2. Theoretical Model

During normal operation, when affected by conditions such as nuclear reactions in nuclear power plants and complex marine climates, controlled parameters of pipeline systems (e.g., fluid pressure or flow rate) may change drastically. To maintain the stability of controlled parameters, the opening of control valves is constantly adjusted, resulting from real-time, automatic feedback within the control system. During dynamic processes such as valve opening, closing, and adjustment, the flow field inside the valve displays notable unsteady characteristics. As a critical state parameter, valve core opening arises from coupled interactions among multiple factors, including throttled inlet flow patterns, outlet fluid properties, and valve driving force. These influencing factors, in turn, are dynamically constrained by the valve core opening. This bidirectional coupling between flow field characteristics and the motion state of internal components (e.g., the valve core) makes it challenging to accurately predict fluid-induced loads prior to system operation. Owing to this strong coupling effect, an oscillating fluid load with unsteady characteristics is generated on the valve core surface. These fluid-driven dynamic loads interact nonlinearly with the control valve’s inherent base load, giving rise to additional coupled loads that exert complex influences on the valve system’s dynamic behaviors. When the total load—encompassing the superimposed unstable fluid load—acts on the valve core, it may result in the driving torque needed by the valve exceeding the actuator’s maximum output torque. In such situations, the actuator might either cease to function or work irregularly, thereby undermining the valve’s stability and reliability.

In order to rid control valves of the impact from unstable fluid loads and boost their operational reliability, it is essential to examine the forces acting on the valve core, calculate the overall load borne by the valve once unstable fluid loads have been superimposed, and subsequently take active measures to counteract this load—all with the aim of attaining precise control over the valve.

Figure 1 illustrates how the cone valve system and its control volume are divided. This conical valve system is made up of a valve itself, an actuator, a controller, and a detection sensor. The area outlined by the red dashed line in the figure represents the selected control volume, which is enclosed by the surfaces ${\mathrm{S}}_1$, ${\mathrm{S}}_2$, ${\mathrm{S}}_3$, and ${\mathrm{S}}_4$. In the diagram, $\mathrm{q}$ denotes the flow through the control valve after throttling, ${\mathrm{Q}}_1$ stands for the valve’s inlet flow, and ${\mathrm{Q}}_2$ indicates the valve’s outlet flow (unit: m³/s); ${\mathrm{d}}_1$ represents the inner diameter of the valve cavity at the inlet (unit: m); $\theta$ (unit: °) denotes the half-cone angle of the valve core; ${\mathrm{S}}_1$, ${\mathrm{S}}_2$, ${\mathrm{S}}_3$, and ${\mathrm{S}}_4$, respectively, correspond to each surface of the defined control volume within the valve; ${\mathrm{A}}_1$ signifies the cross-sectional area of the valve inlet; ${\mathrm{A}}_2$ indicates the surface area of the defined control volume ${\mathrm{S}}_2$ (unit: m²); ${\mathrm{P}}_1$ refers to the valve’s inlet pressure; ${\mathrm{P}}_2$ denotes the valve’s outlet pressure (unit: Pa); $\mathrm{y}$ signifies the displacement of the valve core; ${\mathrm{y}}_1$ corresponds to the distance from the valve seat to the surface of the defined control volume s1; and ${\mathrm{y}}_2$ refers to the distance from the tip of the control valve core to the seat when the valve is fully closed (unit: m). Based on the above, the formula for the fluid load acting on the conical valve core can be derived as [2]

$$\begin{array}{c}{\mathrm{F}}_{\mathrm{load}}={\mathrm{F}}_{\mathrm{static}}+{\mathrm{F}}_{\mathrm{unstable}}\hfill \\ ={\mathrm{P}}_1{\mathrm{A}}_1-\pi {\mathrm{d}}_1{\mathrm{yP}}_2\sin \theta \cos \theta +\rho {\displaystyle \frac{{\mathrm{Q}}_1^2}{{\mathrm{A}}_1}}-{\displaystyle \frac{{\rho \mathrm{q}}^2\cos \theta }{{\mathrm{A}}_2}}+{\rho \mathrm{y}}_1\stackrel{·}{\mathrm{q}}-{\displaystyle \frac{1}{2}}{\rho \sin }^2\theta \stackrel{·}{\mathrm{q}}\mathrm{y}\hfill \\ -\ddot{\mathrm{y}}\left({\left(0.5{\mathrm{d}}_1-\mathrm{ysin}\theta \cos \theta \right)}^2 \left({\mathrm{y}}_2+\mathrm{y}+{\displaystyle \frac{{\mathrm{d}}_1\cot \theta }{3}}\right)\rho \pi -{\rho \mathrm{y}}_1{\mathrm{A}}_1\right)-\stackrel{·}{\mathrm{y}}\left({\displaystyle \frac{1}{2}}{\rho \mathrm{qsin}}^2\theta \right)\hfill \\ -{\stackrel{·}{\mathrm{y}}}^2\left({\left(0{.5\mathrm{d}}_1-\mathrm{ysin}\theta \cos \theta \right)}^2-2\sin \theta \cos \theta \left(0.5{\mathrm{d}}_1-\mathrm{ysin}\theta \cos \theta \right)\left({\mathrm{y}}_2+\mathrm{y}+{\displaystyle \frac{{\mathrm{d}}_1\cot \theta }{3}}\right)\right)\hfill \end{array}$$

(1)

In Equation (1), $\rho$ represents the density of the fluid in the valve (unit: kg/m³); ${\mathrm{F}}_{\mathrm{load}}$ is the total load on the valve core; ${\mathrm{F}}_{\mathrm{static}}$ is the static fluid load on the valve core; and ${\mathrm{F}}_{\mathrm{unstable}}$ is the unstable fluid load on the valve core (unit: N) [2].

To ensure the control valve functions properly, the matching actuator must be capable of delivering adequate torque. That said, if the output torque of the chosen actuator greatly surpasses the total load, it may give rise to excessively strong force and undue amplitude during control processes. This may trigger impacts with parts such as the valve stem and valve sealing surfaces, leading to damage. As a result, actuators are typically selected with their maximum output torque set to 1.8 times the regular load.

3. Dual-Motor Redundant Compensation System

3.1. Structure of Control Valve System

In the dual-motor redundant compensation system of this study, the analysis object is selected as a control valve with a cone valve core, and the comparison of the 3D structures between the ordinary control valve and the dual-motor control valve is shown in Figure 2.

In Figure 2, the control valve on the left is an ordinary one, which uses a single-motor-driven gear rack to convert the motor’s rotational motion into the linear motion of the valve stem; the control valve on the right is a dual-motor redundant-driven one, where the two motors drive in parallel to control the vertical movement of the valve core. As shown in the diagram, the two permanent magnet synchronous servo motors (PMSMs) are configured in a parallel drive arrangement. When the motors are started, power is transmitted to the valve core through the gearbox to adjust the valve opening. The valve consists of components such as the valve cavity, valve core, and valve stem [15]. Flow and pressure sensors are fitted at both the inlet and outlet of the valve, with the function of monitoring real-time variations in fluid flow rate and pressure. These sensors transmit flow and pressure information to the control system, which compares the real-time feedback data with preset target values and adjusts motor output parameters in real time, thereby achieving precise control of the valve opening [16,17].

The PMSM control system is structured, from the innermost to the outermost layer, with a current loop, speed loop, and position loop, constituting a closed-loop feedback control architecture—a typical three-loop nested control system that allows for rapid response and precise adjustment [2].

In this research, the current loop is employed for control purposes. The current loop functions by receiving the error value of the current signal, outputting a reference voltage, which subsequently undergoes coordinate transformation (Park/Clark transformation) and inverter (SVPWM) processing. Regulating the stator current allows for swift adjustment of the motor’s output, enabling the motor to start with maximum current so as to accommodate the control valve’s operation under various conditions. The vector control schematic of the two motors is shown in Figure 3:

In the figure, ${\mathrm{\omega }}_1$ represents the angular velocity of the main motor rotor, and ${\mathrm{\omega }}_2$ represents the angular velocity of the auxiliary motor rotor; ${\mathrm{\omega }}_{01}$ denotes the set angular velocity for the main motor rotor, and ${\mathrm{\omega }}_{02}$ denotes the set angular velocity for the auxiliary motor rotor; ${\theta }_1$ represents the angle between the main motor’s A-phase winding axis and the d-axis in the d/q coordinate system, ${\theta }_2$ represents the angle between the auxiliary motor’s A-phase winding axis and the d-axis in the d/q coordinate system, and $\theta$ denotes the set value of this angle; ${\mathrm{u}}_{\mathrm{d}1}$, ${\mathrm{u}}_{\mathrm{q}1}$ represent the voltage components of the main motor’s stator windings in the d/q coordinate system, and ${\mathrm{u}}_{\mathrm{d}2}$, ${\mathrm{u}}_{\mathrm{q}2}$ represent those of the auxiliary motor; ${\mathrm{u}}_{\alpha 1}$, ${\mathrm{u}}_{\beta 1}$ represent the voltage components of the main motor’s stator windings in the α/β coordinate system, and ${\mathrm{u}}_{\alpha 2}$, ${\mathrm{u}}_{\beta 2}$ represent those of the auxiliary motor; ${\mathrm{i}}_{\mathrm{a}1}$, ${\mathrm{i}}_{\mathrm{b}1}$, ${\mathrm{i}}_{\mathrm{c}1}$ represent the excitation currents generated by the main motor’s stator ABC three-phase windings, and ${\mathrm{i}}_{\mathrm{a}2}$, ${\mathrm{i}}_{\mathrm{b}2}$, ${\mathrm{i}}_{\mathrm{c}2}$ represent those of the auxiliary motor; ${\mathrm{i}}_{\mathrm{d}1}$, ${\mathrm{i}}_{\mathrm{q}1}$ represent the current components of the main motor’s stator windings in the d/q coordinate system, and ${\mathrm{i}}_{\mathrm{d}2}$, ${\mathrm{i}}_{\mathrm{q}2}$ represent those of the auxiliary motor; ${\mathrm{i}}_{\mathrm{d}01}$, ${\mathrm{i}}_{\mathrm{q}01}$ denote the set current components of the main motor’s stator windings, and ${\mathrm{i}}_{\mathrm{d}02}$, ${\mathrm{i}}_{\mathrm{q}02}$ denote those of the auxiliary motor; ${\mathrm{i}}_{\alpha 1}$, ${\mathrm{i}}_{\beta 1}$ represent the current components of the main motor’s stator windings in the α/β coordinate system, and ${\mathrm{i}}_{\alpha 2}$, ${\mathrm{i}}_{\beta 2}$ represent those of the auxiliary motor. The current control method for the motor in this study adopts the ${\mathrm{i}}_{\mathrm{d}}=0$ control scheme where the d-axis current is zero [2].

When the two motors run concurrently in parallel drive, speed asynchrony will induce impact loads on the gear transmission mechanism, aggravating mechanical wear and even resulting in transmission jamming. Excessive speed discrepancies between the two motors will also lead to uneven electromagnetic torque output between the main and auxiliary motors, inducing unstable power output and impairing the compensation effect on unstable fluid loads. To achieve speed synchronization between the two motors, appropriate control strategies are required to tackle such speed discrepancies. Currently, the most commonly adopted approach in dual-motor control systems to resolve this issue is motor cross-coupling control, as illustrated in the red section of Figure 3. Specifically, the speed difference between the two motors is first calculated; this difference is then compensated for, and the compensated signal is fed into both motors, thereby enabling signal interaction between their respective control systems.

In this study, the speed of the main motor (PMSM1) can be designated as the reference speed for the auxiliary motor (PMSM2). After calculating the speed difference in the auxiliary motor relative to the main motor, the obtained difference is output to the speed controller for compensation processing, then fed back to the motor to adjust the auxiliary motor’s speed, thus realizing speed synchronization of the dual motors.

Based on the fundamental principles of motors, the equation describing the motion of a permanent magnet synchronous motor (PMSM) is specified as [2]

$$\begin{array}{c}\mathrm{J}{\displaystyle \frac{{\mathrm{d}\omega }_{\mathrm{m}}}{\mathrm{dt}}}{=\mathrm{T}}_{\mathrm{e}}{-\mathrm{T}}_{\mathrm{L}}-\mathrm{B}\\ {\omega }_{\mathrm{m}}{\mathrm{T}}_{\mathrm{e}}={\displaystyle \frac{3}{2}}{\mathrm{p}}_{\mathrm{n}}\left[{\psi }_{\mathrm{f}}{\mathrm{i}}_{\mathrm{q}}+\left({\mathrm{L}}_{\mathrm{d}}{-\mathrm{L}}_{\mathrm{q}}\right){\mathrm{i}}_{\mathrm{d}}{\mathrm{i}}_{\mathrm{q}}\right]\end{array}$$

(2)

where $\mathrm{J}$ is the moment of inertia, kg·m²; ${\omega }_{\mathrm{m}}$ is the mechanical angular velocity of the motor, rad/s; ${\mathrm{T}}_{\mathrm{e}}$ is the electromagnetic torque of the motor, N·m; ${\mathrm{T}}_{\mathrm{L}}$ is the load torque, N·m; $\mathrm{B}$ is the damping coefficient; ${\mathrm{p}}_{\mathrm{n}}$ is the number of pole pairs of the motor; ${\psi }_{\mathrm{f}}$ is the permanent magnet flux linkage, Wb; ${\mathrm{I}}_{\mathrm{q}}$ is the q-axis current, A [2]; ${\mathrm{L}}_{\mathrm{d}}$, ${\mathrm{L}}_{\mathrm{q}}$ are the self-inductance coefficients of the stator winding, H. Usually, for PMSM, ${\mathrm{L}}_{\mathrm{d}}$ = ${\mathrm{L}}_{\mathrm{q}}$. Therefore, in Equation (2), the calculation equation for motor electromagnetic torque is [18]

$${\mathrm{T}}_{\mathrm{e}}=1{.5\mathrm{p}}_{\mathrm{n}}{\psi }_{\mathrm{f}}{\mathrm{i}}_{\mathrm{q}}$$

(3)

Equation (3) makes it evident that a linear mapping correlation exists between motor electromagnetic torque ${\mathrm{T}}_{\mathrm{e}}$ and q-axis current ${\mathrm{i}}_{\mathrm{q}}$. Based on this relationship, continuous adjustable regulation of motor output torque can be achieved by changing the q-axis current.

For converting motor output torque $\mathrm{T}$ to driving force $\mathrm{F}$ acting on the valve stem:

$$\mathrm{F}={\displaystyle \frac{2\mathrm{T}\cdot \mathrm{i}}{\mathrm{r}}}$$

(4)

In Equation (4), $\mathrm{i}$ is the transmission ratio of the gearbox, and $\mathrm{r}$ is the radius of the pinion.

3.2. Principle of Dual-Motor Redundant Compensation

Figure 4 shows a schematic diagram of the dual-motor redundant compensation system.

Comprising components such as motors, gearboxes, and valve stems, the actuator converts the motor’s rotational motion into the linear movement of the valve core. It is equipped with high-precision position control and rapid torque response capabilities. The valve stem is connected to the parallel transmission mechanism in the gearbox. The two motors control valve stem displacement through a parallel transmission mechanism with a reducer function to adjust valve opening. The configuration of the speed-reducing component ensures that the motor’s high-speed, low-torque output is converted into the low-speed, high-torque movement needed for the valve core to operate. Sensors real-time monitor post-valve-controlled variables and valve core displacement information, transmitting them to the control system to enable timely regulation of the dual motors, thereby achieving control of the controlled variables.

Under normal operating conditions, only a single motor operates to satisfy the routine operational demands of the control valve, thereby reducing energy consumption. When the load undergoes sudden changes and compensation is required, the motor’s load torque is derived via Equation (1), monitored in real time, and subsequently compared against the preset compensation activation value. If the load torque exceeds this preset activation value, the auxiliary motor is activated to output power in conjunction with the main motor. The flowchart of the dual-motor compensation mechanism is presented in Figure 5.

Where ${\mathrm{T}}_{\mathrm{emax}}$ is the maximum output electromagnetic torque of the servo motor; ${\mathrm{T}}_{\mathrm{Lmax}}$ is the set compensation activation value; $\mathrm{e}$ is the differential signal output by the PID; ${\mathrm{T}}_{\mathrm{L}}$ is the load torque; ${\mathrm{I}}_{\mathrm{q}1}$ and ${\mathrm{I}}_{\mathrm{q}2}$ are the current signals of the main motor and the auxiliary motor, respectively. The compensation activation value is preset as ${\mathrm{T}}_{\mathrm{Lmax}}$, and ${\mathrm{T}}_{\mathrm{Lmax}}$ < ${\mathrm{T}}_{\mathrm{emax}}$. The system monitors the motor load torque in real time. When ${\mathrm{T}}_{\mathrm{L}}$ < ${\mathrm{T}}_{\mathrm{Lmax}}$, in such scenarios, only the primary motor operates. The PID controller computes a differential signal e based on the discrepancy between real-time flow and target flow, and this signal is then fed into the motor—thus achieving single-motor control under these circumstances. When ${\mathrm{T}}_{\mathrm{L}}$ > ${\mathrm{T}}_{\mathrm{Lmax}}$, the main motor struggles to provide sufficient power, so the auxiliary motor is started. The difference between ${\mathrm{T}}_{\mathrm{L}}$ and ${\mathrm{T}}_{\mathrm{emax}}$ is calculated, then processed by the PID controller to obtain a control signal [2]. This signal is superimposed with e to generate the compensation superimposed signal e + ev that can make the motor provide the total torque required by the system. The main motor receives signal e, responsible for the primary power output; the auxiliary motor receives signal ev, responsible for outputting the torque exceeding the single-motor load, achieving superimposed torque output of the two motors.

In contrast to single-motor load compensation, dual-motor parallel drive is capable of providing more ample power, reacting more swiftly to sudden load changes, markedly enhancing the dynamic performance of the control valve, and ensuring its stable operation even under extreme working conditions. The two motors are identical in type, both boasting adequate power and torque output capabilities. This ensures that a single motor, when operating independently, can satisfy the normal operational needs of the control valve; meanwhile, when the two motors work in tandem, they can provide more sufficient compensation power to cope with more extreme working conditions. A corresponding parallel transmission mechanism and control system are configured to achieve independent control and collaborative operation of the two motors. The parallel transmission mechanism is capable of achieving synchronous operation of the motors or independent driving of either one, while the control system can produce suitable control signals based on load conditions and control strategies to regulate the respective operating strategies of the two motors. The schematic diagram of dual-motor compensation incorporating unstable fluid loads is presented in Figure 6.

The red section in Figure 6 denotes the load compensation module incorporated into the dual motors. The entire system primarily consists of a PID controller, a load compensation module, a fluid load calculation module, a dual-motor speed synchronization control module, two permanent magnet synchronous servo motors (PMSM1 and PMSM2), and detection sensors.

When the valve is in operation, sensor-collected data—such as the control valve’s inlet pressure, outlet pressure, and valve core displacement—are sent to the fluid load calculation module. Based on Equation (1), this module calculates the real-time total load exerted on the valve core (including the superimposed unstable fluid load) and then converts it into the motor’s load torque. The load torque is then assessed; when the compensation condition is fulfilled, the dual-motor compensation mechanism is activated. The distribution strategy for the compensation component is as follows: based on the difference between the load torque and the compensation activation value, an additional control signal is calculated. This signal is superimposed with the differential signal e output by the PID, then input separately to the two motors, thereby achieving reasonable distribution of the compensation amount between the dual motors.

4. Construction of Joint Simulation Model Based on AMESim and Matlab/Simulink

The compensation system is constructed using AMESim 2020.1 and Matlab/Simulink 2020a. In the modeling of the control valve system, components such as the valve cavity and parallel transmission mechanism are built in AMESim, utilizing its hydraulic library and mechanical library for construction; the control system and motor-related components are constructed in Simulink, including the PID controller, PMSM model, and load compensation module, among others.

4.1. AMESim Model Construction

In the AMESim component library, the corresponding components can be directly selected to build the hydraulic and transmission parts [19]. As shown in Figure 7, this is the model constructed in AMESim.

During the construction process, it is necessary to model the mass of the valve core and valve stem, which can be represented by a mass block from the component library [20]. The conversion of rotational motion into linear motion of the valve core can be achieved using a rack-and-pinion module. A gear set is employed to construct the parallel transmission structure, enabling the parallel operation of the motors [21]. Inlet and outlet pressure sources are configured, with water specified as the working medium. Flow meters, pressure gauges, and displacement sensors are integrated to monitor pressure, flow rate, and valve core displacement. The parameters of each component are set according to the requirements of the actual system, such as the radius of the rack pinion and the transmission reduction ratio [22].

4.2. Matlab/Simulink Model Construction

The Matlab/Simulink model comprises a valve control system, a PMSM module, a data exchange module, and a load calculation module. The control system is made up of components like a PID controller and a comparison element, while the PMSM module incorporates elements such as a speed and current controller, coordinate transformation, an output module, and an inverter [23,24].

The module for calculating fluid load and load torque is capable of determining the overall load acting on the valve core. It does so by leveraging the theoretical model of fluid load on the valve core, along with data like pressure and displacement transmitted from AMESim and then proceeds to compute the motor’s load torque in further steps. The model constructed in Matlab/Simulink is illustrated in Figure 8, with ${\mathrm{p}}_1$ representing the inlet pressure of the control valve, ${\mathrm{p}}_2$ denoting the outlet pressure of the control valve, and $\mathrm{xp}$ standing for the spool displacement of the control valve.

After the simulation starts, the module for data exchange between the two software is shown in Figure 9. Through this module, AMESim transmits information such as the real-time simulation results of valve inlet and outlet pressures, valve core displacement, post-valve flow rate, and pressure to Simulink. Simulink performs calculations based on the information obtained from AMESim, generates motor control signals, etc., and then feeds them back to AMESim.

A load compensation module is incorporated at the input terminal of the current loop, and a cooperative control algorithm for dual motors is developed. When the load torque surpasses the compensation capability of a single motor, both motors are activated simultaneously. The auxiliary motor then takes charge of the torque output that exceeds the main motor’s capacity, thereby ensuring efficient and stable operation. Figure 10 depicts the setup of the motor load compensation module. In this illustration, the intended flow rate downstream of the valve is established at 5000 L/min. This target undergoes a comparison with the real-world flow rate downstream of the valve, and a PID controller is employed to calculate a control signal. This control signal is then fed into the motor load compensation module. Concurrently, the load torque is input into the load compensation calculation module.

The motor load compensation module is capable of calculating compensation values based on the load torque and PID output shaft current. It then feeds the current signal into the motor’s current loop for control, thus achieving real-time compensation of the current loop.

The control system module and the PMSM module are shown in Figure 11, which are the model building of the load compensation module and the two motors.

The red box in the diagram represents the motor load compensation module, which computes the q-axis current needed by the motors and sends it to both units. The blue and green boxes, on the other hand, correspond to the model construction of the main motor and auxiliary motor (PMSM), respectively. These modules encompass components such as an inverter module, a filter module, a coordinate transformation module, and a load module.

After the simulation starts, AMESim first transmits the initial valve inlet and outlet pressure, valve core displacement, and other parameters to Simulink. Simulink calculates the initial control signal of the motor according to these parameters, and feeds it back to AMESim to drive the valve core to start moving. AMESim real-time monitors the changes in the valve inlet and outlet pressure, valve core displacement, and the flow and pressure after the valve, and transmits these data to Simulink. Simulink calculates the new control signal of the motor according to the received data, and judges whether to start the dual-motor compensation and calculates the compensation amount according to the load compensation strategy. Simulink sends the updated motor control signals and compensation signals back to AMESim. In response to these signals, AMESim adjusts the motor’s output torque and the valve core’s movement, thereby achieving dynamic control and load compensation for the control valve system [2].

5. Result Analysis

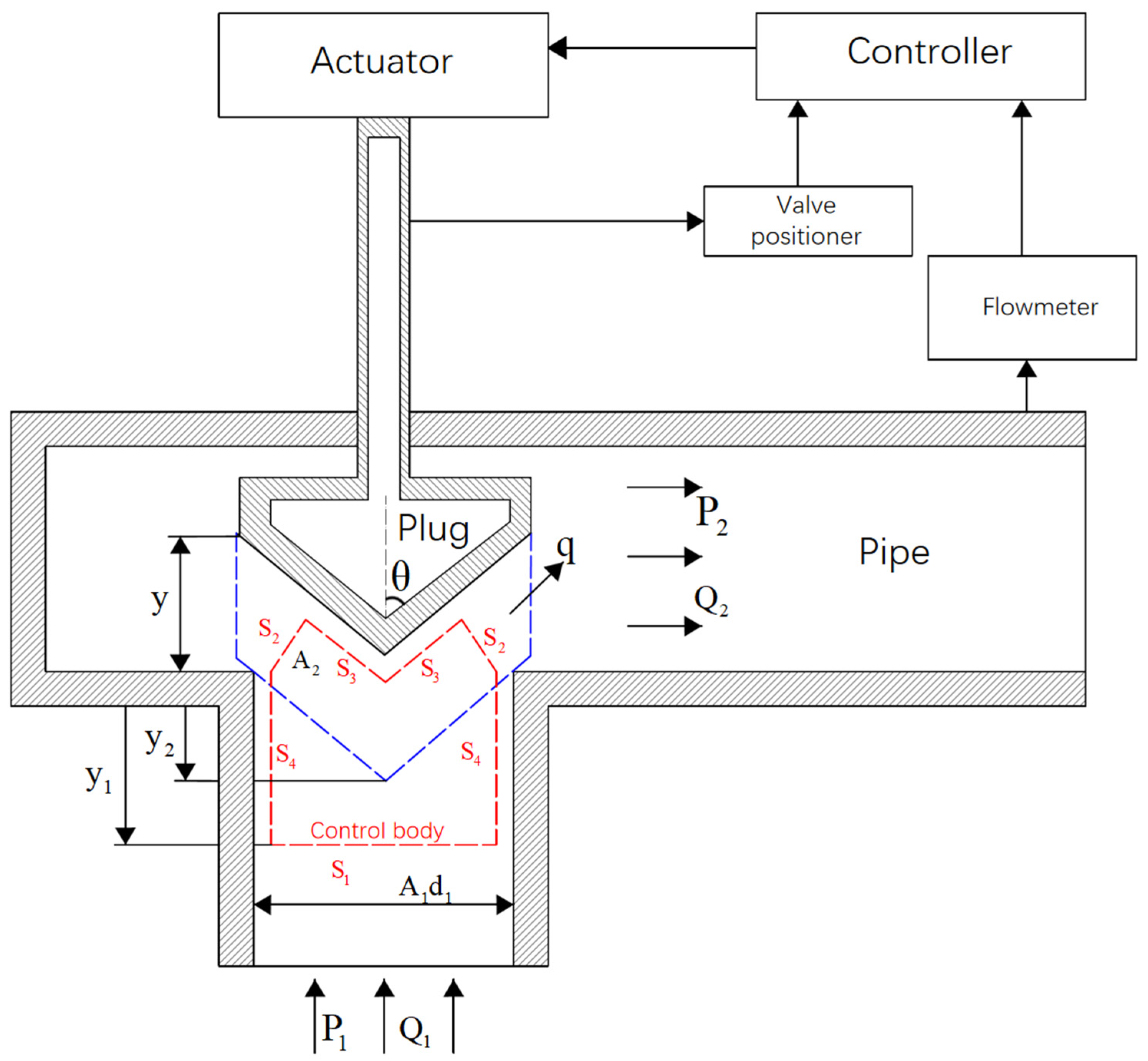
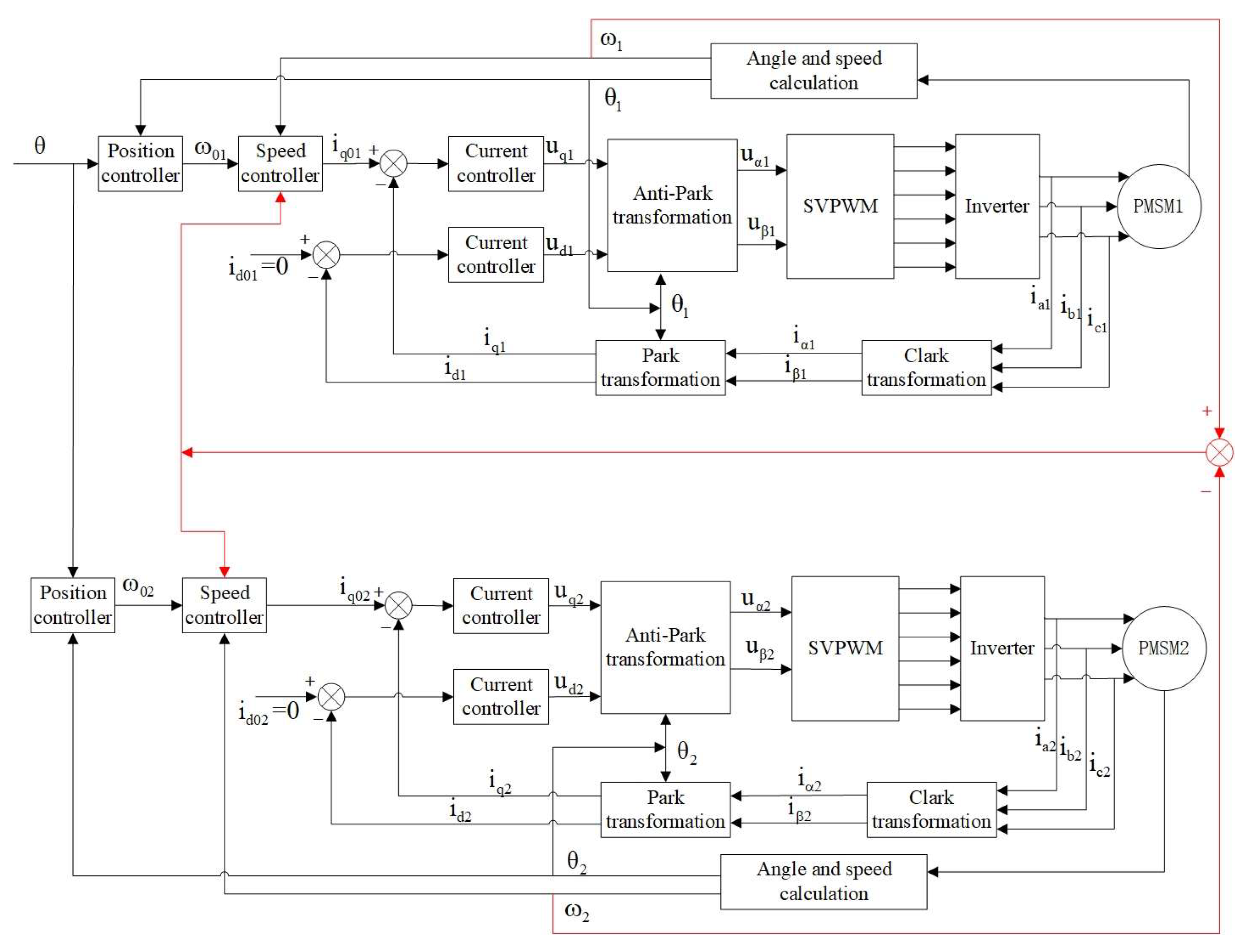
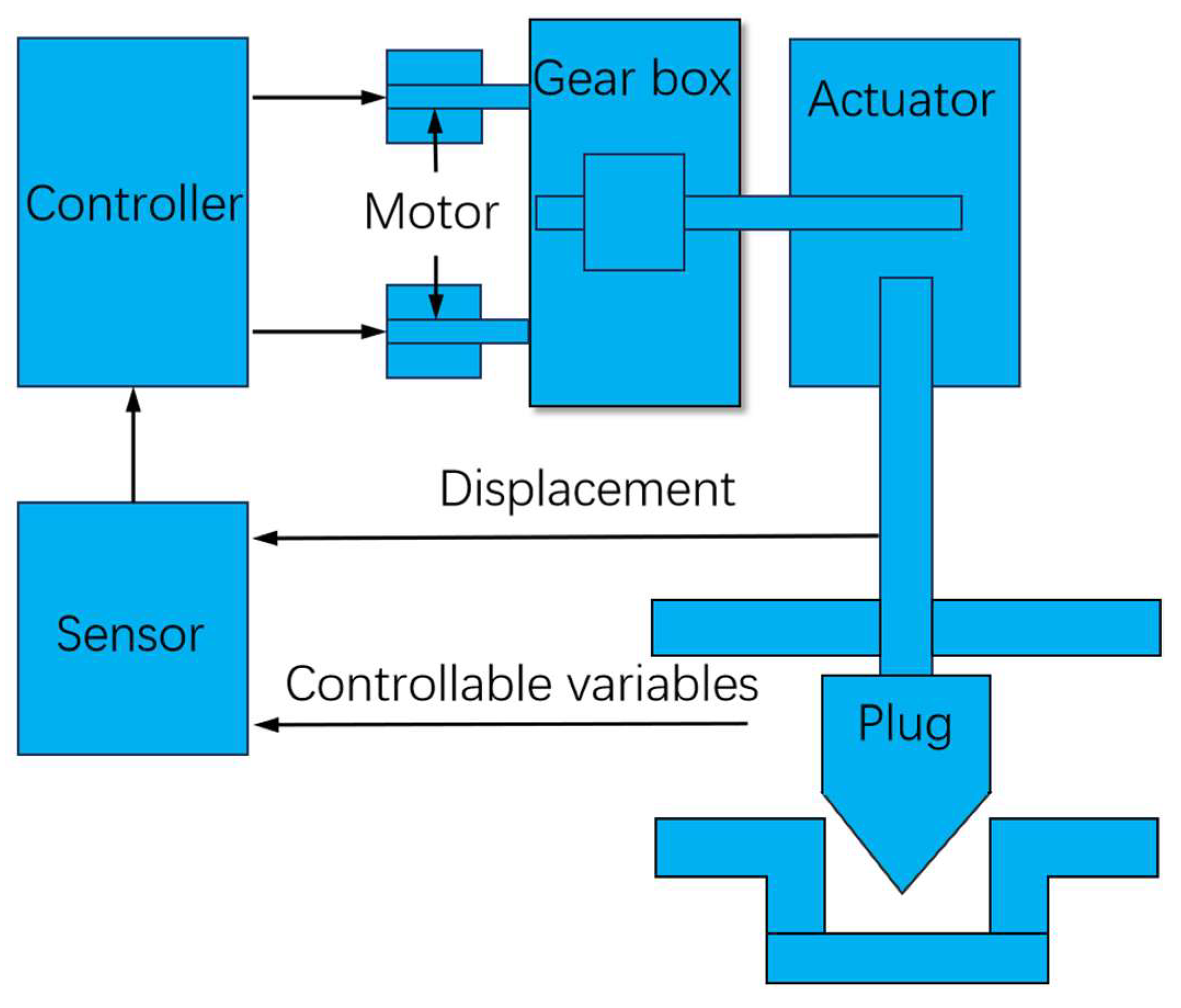
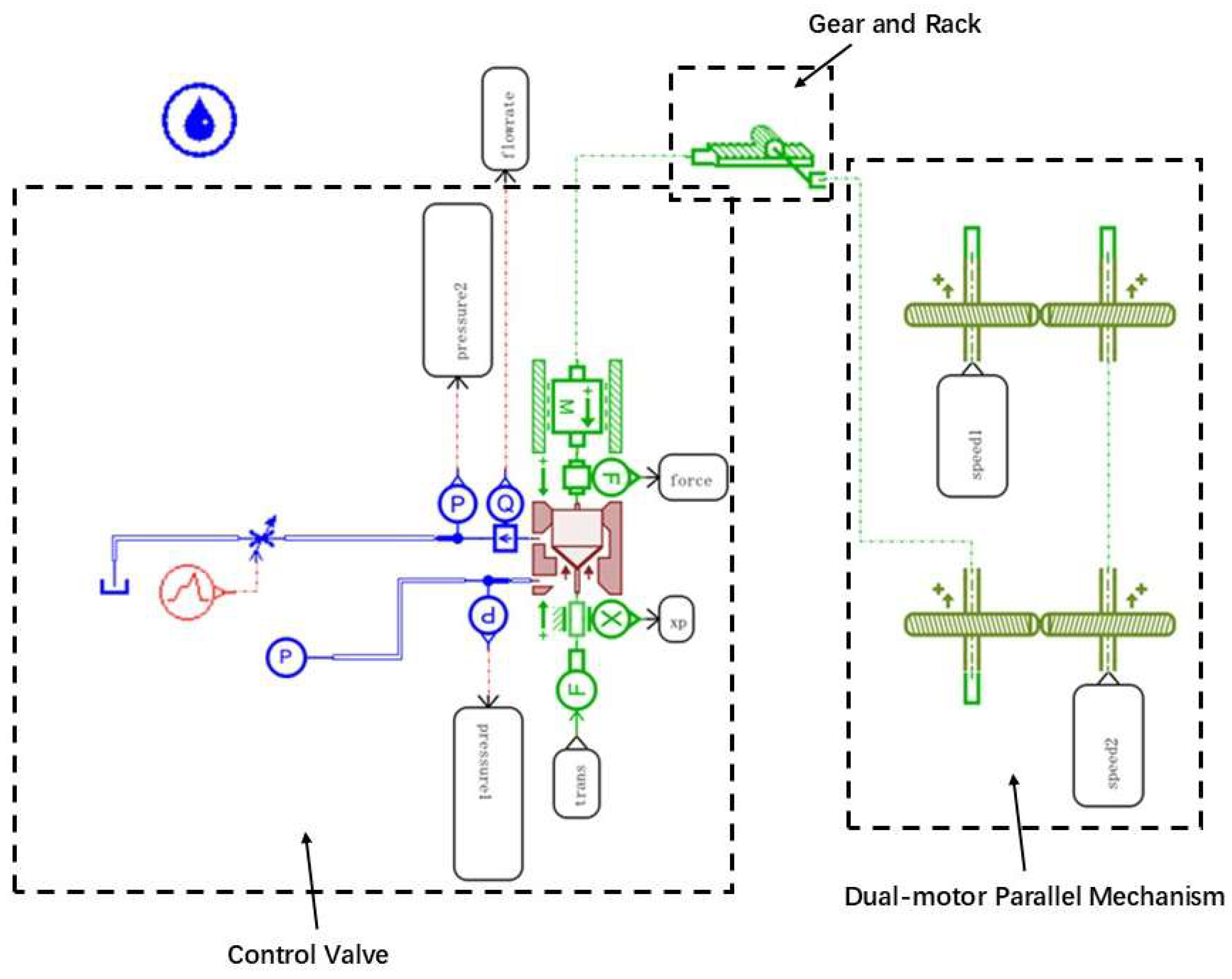
5.1. Influence Analysis of Dual-Motor Compensation on Control Effect

The core objective of this study is to verify the suppression effect of the “dual-motor redundant compensation strategy” on unstable fluid loads, rather than directly reproducing the compressible characteristics of oil and gas media. Therefore, water can be selected as the medium for simulation experiments during the simulation process. Specifically, as a typical incompressible fluid, water has stable and easily obtainable physical property parameters such as density (approximately 980 kg/m³ at room temperature) and viscosity (approximately 0.001 Pa·s at room temperature). This can eliminate the interference of complex factors caused by pressure changes in compressible fluids (e.g., oil and gas), such as density fluctuations and pressure wave propagation delay, and avoid multi-variable coupling from masking the core effects of the load torque calculation model, compensation threshold triggering logic, and dual-motor coordinated control—thereby efficiently verifying the suppression effect of the compensation method on unstable fluid loads. Meanwhile, in the scenario of deep-sea oil and gas exploitation, the fluid inside the control valve mostly operates under a low Mach number (Ma < 0.3) flow state. Under this condition, the density change rate of the compressible fluid is less than 5%, and its flow laws (e.g., throttling effect, flow field distribution) are highly similar to those of water. In subsequent work, it is only necessary to replace the fluid physical property parameters in the simulation model to adapt to actual oil and gas media.

The settings of sensor bandwidth and accuracy in this study are as follows: the post-valve flow sensor is assumed to have a bandwidth of 100 Hz and an accuracy of ±0.5% full scale (FS); the valve inlet and outlet pressure sensors are assumed to have a bandwidth of 200 Hz and an accuracy of ±0.2% FS; the valve core displacement sensor is assumed to have a bandwidth of 500 Hz and an accuracy of ±0.01 mm. These assumptions are based on existing mature technologies and can meet the core requirement of “real-time monitoring-dynamic compensation” in this study.

During the simulation, the post-valve flow is chosen as the regulated variable, with relevant parameters configured on the AMESim platform. The valve’s inlet pressure is set to 5 bar, the initial displacement of the valve core is configured as 0.005 m, the initial post-valve flow is set to 0 L/min, and the target post-valve flow is set to 5000 L/min. In this setup, the post-valve flow in each simulation scenario stabilizes within 1 s. Therefore, once the flow rate downstream of the valve stabilizes at the target value of 5000 L/min, an abrupt change is applied to the valve’s inlet pressure. To be specific, at the 1-s mark, the inlet pressure of the valve is increased to 15 bar. It is confirmed that each simulation scenario reaches the final outcome—either control failure or stable maintenance of the control target at the set value—within 1 s. As a result, the simulation length on the Simulink platform is set to 2 s. The control valve’s actuator dynamically adjusts the valve core’s displacement based on the signal output by the PID controller to adapt to the pressure surge. The diagram of the applied inlet pressure is shown in Figure 12; as depicted, the valve’s inlet pressure remains at 5 bar from 0 to 1 s and shifts abruptly to 15 bar at 1 s. In the study, “pressure step changes at the inlet” is selected as a typical extreme operating condition. This choice is based on its characteristics of “high occurrence frequency in practical engineering (e.g., the impact of complex marine climates on upstream pipelines mentioned in Section 1. Introduction) and clear disturbance characteristics”, which facilitates the quantitative verification of the proposed scheme’s effectiveness. In essence, the proposed scheme is a “general compensation solution centered on dynamic load response”. The core of the scheme is to calculate load torque in real time and quickly mobilize dual motors for coordinated compensation to respond to load changes; its universality lies in adapting to various extreme conditions (e.g., inlet pressure mutations, fluid property changes, multi-disturbance coupling) in nuclear power, deep-sea oil and gas fields, etc., without modifying the overall structure. Specific parameter settings are detailed in

Table 1. Simulation modeling parameters.

Parameter	Value
Radius of the rack gear	value
Reduction ratio of the rack and pinion	10 mm
Inlet pressure of the control valve	50:1
Outlet pressure of the control valve	5~15 bar
Mass of the valve core	0 bar
Diameter of the control valve	20 kg
Half-cone angle of the valve core	250 mm
Moment of inertia of the motor	45°
Armature inductance of the motor	0.003 kg·m2
Magnetic flux linkage of the motor	0.000835 H
Viscous damping of the motor	0.1827
Number of pole pairs of the motor	0.008 N·m·s

below:

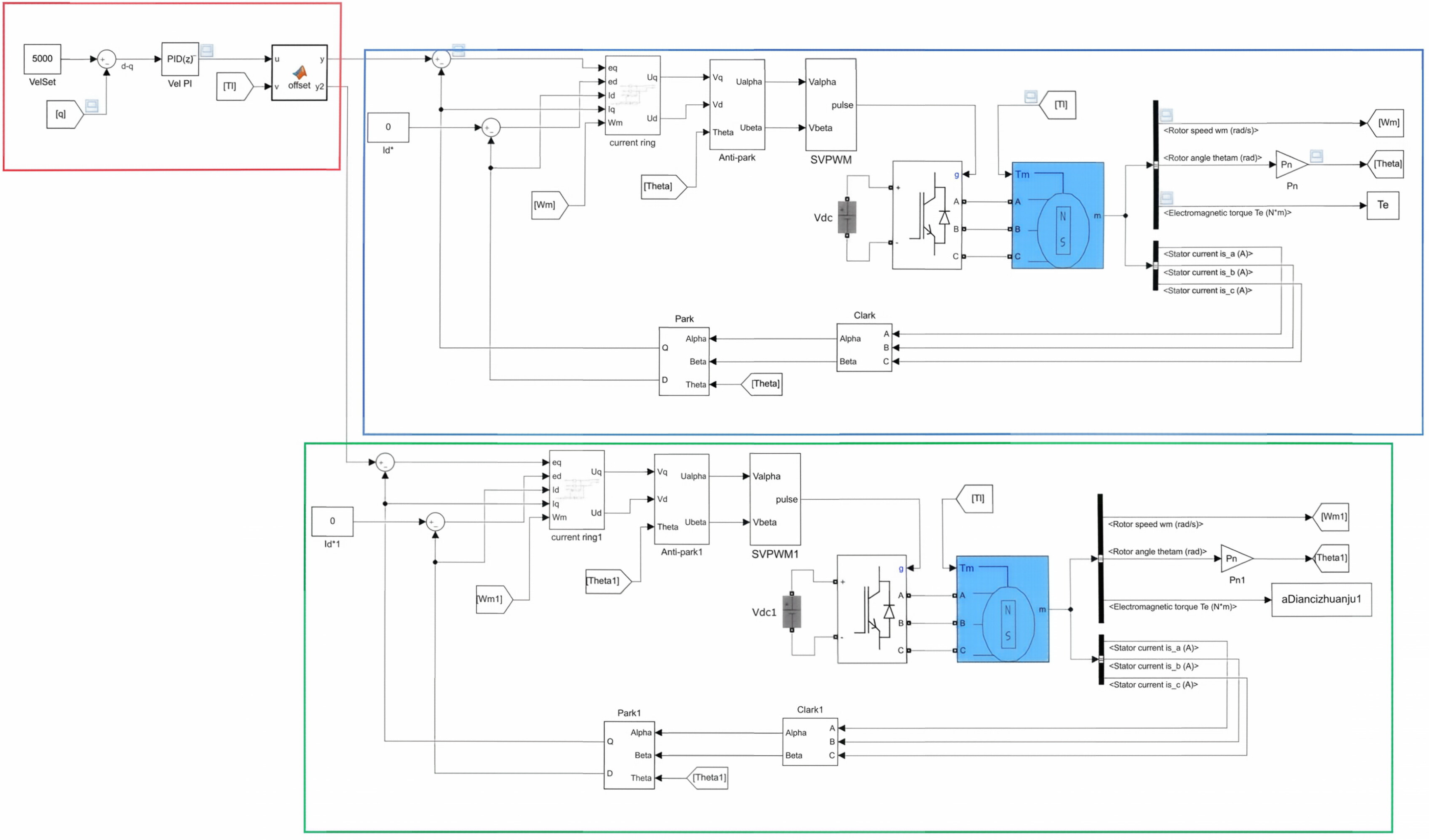
Next, a comparison will be made of the system performance across three scenarios: single-motor drive without a compensation algorithm, single-motor drive with a compensation algorithm, and dual-motor drive with a compensation algorithm. This comparison will take place when the inlet fluid pressure of the valve undergoes an abrupt change from 5 bar to 15 bar at the 1-s mark. The comparison of the flow after the valve with single-motor non-compensation, single-motor compensation, and dual-motor compensation is shown in Figure 13:

Where Figure 13a is the flow diagram after the valve in the case of single-motor non-compensation algorithm, Figure 13b is the flow diagram after the valve in the case of single-motor compensation algorithm, and Figure 13c is the flow diagram after the valve in the case of dual-motor compensation algorithm.

Since no abrupt change occurs in the valve inlet pressure before the first second, the total load on the valve core is lower than the set compensation activation value at this time. Therefore, irrespective of whether the compensation algorithm is enabled, the changing pattern of the flow curve downstream of the valve stays the same, with both attaining the preset stable value of 5000 L/min at 0.77 s. At the beginning, the flow rises rapidly and overshoots, reaching the maximum value of 6750 L/min at 0.18 s, exceeding the target flow by 35%. Then, after PID adjustment, the flow gradually falls back and approaches the target value, and stabilizes at about 5000 L/min at 0.77 s.

At the 1-s timestamp, the inlet pressure of the control valve starts to increase, and this leads the downstream flow rate of the valve to surge abruptly to 10,000 L/min, which is twice the target flow rate. Under the action of PID, the flow rate starts to adjust back. At this point, the curve changes under three scenarios—single-motor without compensation, single-motor with compensation, and dual-motor with compensation—exhibit significant differences. In the scenario without compensation, the flow rate is difficult to adjust back, with a slow change in slope, and the servo motor struggles during the adjustment process. By the 2-s mark, the flow rate reaches roughly 13,600 L/min, which is 172% higher than the target flow rate and thus fails to meet the set target. In the case of single-motor compensation, although the servo motor can perform compensation adjustment, due to the excessive amplitude of pressure mutation, an overshoot phenomenon occurs. The single motor with the compensation algorithm fails to converge the overshoot; after 0.5 s of oscillation, the post-valve flow rate cannot stabilize at the target value. Eventually, at 1.5 s, the flow rate stagnates at 0 L/min, and the adjustment process fails to complete successfully. In the case of dual-motor compensation, after the load mutation, the flow rate drops rapidly, showing a significant change. Due to the excessive inlet pressure mutation, an overshoot phenomenon also occurs. After 0.7 s of oscillation, the post-valve flow rate reaches the target value at 1.7 s and remains basically stable thereafter.

In order to further reveal the reasons for the phenomenon in Figure 13, the following analyzes the motor electromagnetic torque of single-motor non-compensation, single-motor compensation, and dual-motor compensation, as shown in Figure 14:

Here, Figure 14a shows the electromagnetic torque curve of the motor when using a single-motor without a compensation algorithm; Figure 14b presents the electromagnetic torque curve of the motor under the scenario of a single-motor with a compensation algorithm; Figure 14c displays the electromagnetic torque curve of the main motor in the case of a dual-motor compensation algorithm; and Figure 14d illustrates the electromagnetic torque curve of the auxiliary motor under the dual-motor compensation algorithm.

Figure 14 compares the changes in motor electromagnetic torque under four scenarios: single-motor without compensation, single-motor with compensation, and dual-motor compensation (including the main motor and the auxiliary motor). During the phase from 0 to 1 s (when the valve inlet pressure does not mutate), the auxiliary motor in the dual-motor compensation scenario is not activated (Figure 14d). The torque variation trends of the single-motor without compensation (Figure 14a), single-motor with compensation (Figure 14b), and the main motor in dual-motor compensation (Figure 14c) are consistent: they first oscillate in the range of −100 to 125 N·m, then exhibit damped oscillation after 0.44 s, and stabilize at −12 N·m at 0.77 s. At this point, the post-valve flow rate reaches the target value.

During the phase after 1 s (when the valve inlet pressure mutates to 15 bar), the motor electromagnetic torque of the single-motor without compensation (Figure 14a) oscillates significantly at high frequency in the range of −175 to 25 N·m, tends to stabilize after 1.65 s, and stabilizes at 10 N·m at 1.75 s. However, the post-valve flow rate exceeds the target value by 170%, resulting in control failure. For the single-motor with compensation (Figure 14b), the motor electromagnetic torque fluctuates in the range of −148 to 60 N·m; the post-valve flow rate drops to 0 L/min at 1.5 s, and thereafter the motor still oscillates within this range but fails to adjust the flow rate, leading to compensation failure. For the dual-motor compensation (Figure 14c,d), the electromagnetic torques of the main and auxiliary motors fluctuate in the range of −160 to 30 N·m; the torques of the main and auxiliary motors stabilize synchronously at 1.8 s, and the post-valve flow rate reaches the target value without any failure.

The comparison of the motor speed of single-motor non-compensation, single-motor compensation, and dual-motor compensation is shown in Figure 15:

In this context, Figure 15a depicts the motor speed profile for the scenario involving a single-motor without a compensation algorithm; Figure 15b illustrates the motor speed profile when a single motor is used with a compensation algorithm; Figure 15c shows the speed profile of the main motor under the dual-motor compensation algorithm; and Figure 15d illustrates the rotational speed curve of the auxiliary motor when the dual-motor compensation algorithm is applied.

During the phase from 0 to 1 s (when the valve inlet pressure does not mutate), the auxiliary motor in the dual-motor compensation scenario is not activated (Figure 15d). The speed variation trends of the single-motor without compensation (Figure 15a), single-motor with compensation (Figure 15b), and the main motor in dual-motor compensation (Figure 15c) are consistent: all quickly reach a maximum value of 260 rad/s, then drop to 0 rad/s at 0.18 s (at this point, the valve core opening is maximum and the flow rate reaches its peak), rise to a maximum negative value of −250 rad/s (overshoot) at 0.25 s, exhibit damped oscillation after 0.44 s, and stabilize at 0 rad/s at 0.77 s—corresponding to the post-valve flow rate reaching the target value.

During the phase after 1 s (when the valve inlet pressure mutates to 15 bar), the motor speed of the single-motor without compensation (Figure 15a) first rises rapidly to approximately 225 rad/s and oscillates around this value, drops sharply at 1.65 s, reaches 0 rad/s at 1.75 s and then reverses direction with the speed increasing continuously, and finally reaches a maximum negative value of −250 rad/s at 1.86 s. In this case, the post-valve flow rate exceeds the target value by 170%, failing to achieve regulation. For the single-motor with compensation (Figure 15b), the motor rotates in the reverse direction, reaches a minimum negative value of −145 rad/s at 1.2 s, and drops to 0 rad/s at 1.6 s (overshoot); thereafter, it rotates forward and oscillates around 250 rad/s, but the post-valve flow rate drops to 0 L/min after 1.6 s, making regulation impossible. For the dual-motor compensation (Figure 15c,d), the main and auxiliary motors rotate in the reverse direction, reach a minimum negative value of −148 rad/s at 1.3 s, drop to 0 rad/s at 1.16 s, and then rotate forward; after 0.7 s of oscillation, the speed stabilizes at 0 rad/s, and at this point, the post-valve flow rate also stabilizes at the target value of 5000 L/min.

Under extreme working conditions, the dual-motor compensation scheme can quickly respond to load changes, realize the cooperative adjustment of dual-motor torque in the form of positive feedback, and improve the dynamic response capability and operation stability of the valve. In general, the flow stabilization effect of dual-motor compensation is more significant than that of single-motor non-compensation and single-motor compensation, and it shows better regulation performance and stability in the face of pressure mutation scenarios. At the same time, the dual-motor redundant design can make the other motor immediately take over the work when one motor is damaged, significantly enhancing the system reliability, and providing a new idea for the reliability optimization of control valves for deep-sea oil and gas extraction.

5.2. Influence Analysis of Variable Transmission Ratio on Dual-Motor Compensation Control Effect

After studying the influence of dual-motor compensation on the control effect, we study the influence of the transmission ratio on the compensation effect by changing the transmission ratio between the gear connected to the motor and the gear on the output shaft in the AMESim model. When the dual motor is turned on for compensation, the flow change at the inlet of the valve is kept as shown in Figure 12.

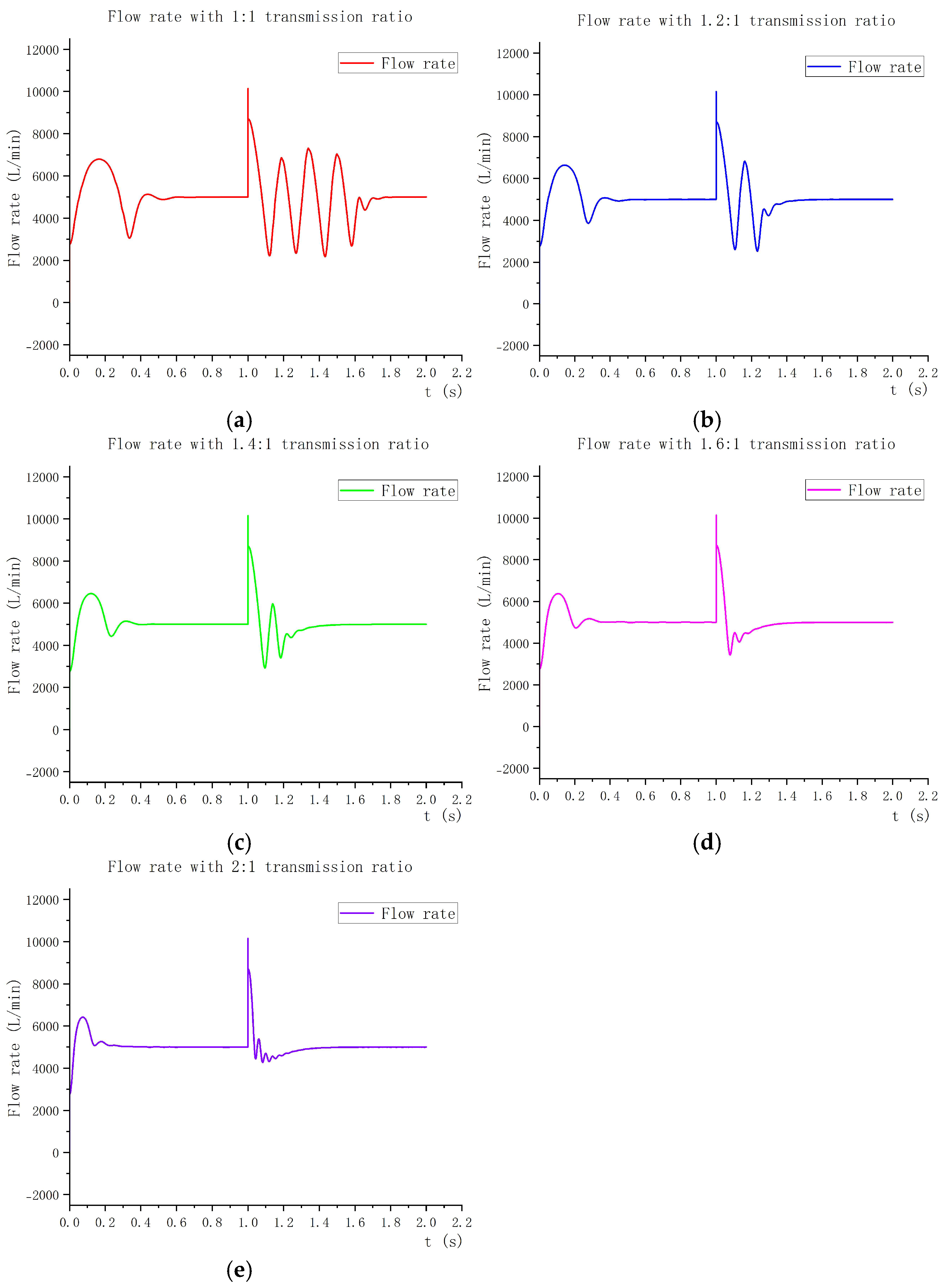
The comparison of the flow after the valve with the dual-motor compensation algorithm under different transmission ratios is shown in Figure 16. It is found in the simulation that the influence on the control result is not significant when the transmission ratio exceeds 1.6:1, and the control result deteriorates with an excessively large transmission ratio. For instance, as shown in Figure 16e, when the transmission ratio is set to 2:1, the control effect on the post-valve flow does not show obvious improvement, and the oscillation frequency and times even increase between 1 s and 1.3 s. Therefore, the transmission ratios are set to 1:1, 1.2:1, 1.4:1, and 1.6:1, respectively, to analyze the influence of variable transmission ratios.

In the 0–1 s initial phase, the valve inlet pressure is 5 bar. During this period, the servo motor’s load torque is lower than the actuator’s maximum output torque. The flow variation trends under different transmission ratios are roughly consistent, yet a larger transmission ratio means the motor supplies greater torque to the transmission system, allowing the post-valve flow to stabilize at the target flow rate more quickly. Specifically, when the transmission ratio is 1:1, the flow reaches stability at the target rate at 0.77 s; with a 1.2:1 ratio, it stabilizes at 0.65 s; at 1.4:1, stabilization occurs at 0.55 s; and at 1.6:1, it stabilizes at 0.5 s. Additionally, it can be observed that when adjusting the post-valve flow, the overshoot of the post-valve flow beyond the target flow will gradually diminish as the transmission ratio increases. This results in smaller flow fluctuations, enabling a more significant reduction in the impact of unstable flow.

At the 1-s instant, the inlet pressure of the control valve rises, bringing about an abrupt shift in load. Meanwhile, the flow rate surges to 10,000 L/min in an instant, which is 100% higher than the target flow rate. Under the action of PID, the flow begins to recover. At this time, the curve changes under different transmission ratios also show significant differences: for the 1:1 transmission ratio, the flow recovery is slow, the flow after the valve oscillates repeatedly, and after 0.7 s of multiple oscillations, the flow after the valve stabilizes at the target flow; for the 1.2:1 transmission ratio, the number of oscillations and overshoot of the flow after the valve are significantly reduced, and after 0.5 s of oscillation, at the 1.5 s moment, the flow after the valve stabilizes at the target flow; for the 1.4:1 transmission ratio, the number of oscillations and overshoot of the flow after the valve are even less, and after 0.4 s of oscillation, at the 1.4 s moment, the flow after the valve stabilizes at the target flow; for the 1.6:1 transmission ratio, the flow after the valve drops rapidly, and after a very short period of 0.35 s of oscillation, it stabilizes at the target flow. In general, within the given transmission ratio range, with the increase in the transmission ratio, the control effect of the motor on the flow after the valve is better. In addition to the faster adjustment speed, the fluctuation range of the flow after the valve in the adjustment process is also smaller.

The comparison of the motor speeds of the main motor and the auxiliary motor driven by dual-motor compensation under different transmission ratios is shown in Figure 17 and Figure 18:

Between 0 and 1 s, the compensation start standard is not reached, and the auxiliary motor is not started. At the 1:1 transmission ratio, the speed quickly reaches the maximum value of 260 rad/s. At this time, the flow after the valve is higher than the target value, so the motor speed begins to decrease under the PID adjustment. At the 0.18 s moment, the speed is 0 rad/s. At this point, both the valve opening and the flow rate hit their maximums. To bring the flow rate back down to the target value, the motor initiates reversal under the regulation of the PID controller, causing the valve opening to keep decreasing. By the 0.25-s mark, it reaches a maximum reverse speed of −250 rad/s. After many oscillation changes, the flow after the valve approaches the target flow continuously and finally stabilizes at 5000 L/min. At the 1 s moment, the inlet pressure of the valve rises to 15 bar. At this time, the valve opening needs to be reduced. Through PID adjustment, the motor reverses. At the 1.3 s moment, the motor speed reaches the reverse minimum of −148 rad/s, and then the motor speed decreases. At the 1.16 s moment, the motor speed decreases to 0 rad/s. The motor speed oscillates continuously, the rotation direction of the motor also changes continuously, and the flow after the valve also changes around the target flow value. After 0.7 s of oscillation, the motor speed stabilizes at 0 rad/s, and at this time, the flow after the valve also stabilizes at the target flow value of 5000 L/min.

It can be seen from Figure 17 and Figure 18 that in the adjustment process of the same working condition from 0 to 1 s, with the increase in the transmission ratio, the speed of the main motor decreases from the maximum of 260 rad/s at the 1:1 transmission ratio to the maximum of 242 rad/s at the 1.6:1 transmission ratio, and the maximum speed decreases by 6.9%. After the overshoot phenomenon occurs, the 1:1 transmission ratio can reach −255 rad/s, while the 1.6:1 transmission ratio is only −150 rad/s, and the speed change range of the motor is reduced by 23.9%. And with the increase in the transmission ratio, the speed of stabilizing to the target flow is faster, and the speed change in the motor is less fluctuated. After the disturbance of 15 bar occuring at the 1 s moment, with the increase in the transmission ratio, the speed fluctuations of the main and auxiliary motors are significantly reduced. In the case of 1:1 transmission ratio, it needs to go through 0.8 s of repeated oscillation and stabilize at the target value at the 1.8 s moment. But in the case of 1.6:1 transmission ratio, it only needs to go through 0.4 s of a small amount of oscillation and can stabilize at the target value at the 1.4 s moment. The oscillation time is reduced by 50%. The increase in the transmission ratio has a significant impact on the improvement of the performance of the motor control valve, which greatly reduces the speed change time and amplitude of the motor, can effectively reduce the probability of motor failure, and increase the service life of the motor.

The comparison of the gear torque under the dual-motor compensation drive with different transmission ratios is shown in Figure 19:

It can be seen from Figure 19 that at the 1 s moment, when the inlet pressure suddenly changes to 15 bar, due to the excessive change, the compensation algorithm is turned on, and the auxiliary motor begins to intervene. At this juncture, the torque between the motor and the main shaft’s transmission gear starts to shift, with such changes aligning with both the motor’s rotational speed and the flow rate variations downstream of the valve. At the 1:1 transmission ratio, the torque between the gears fluctuates violently and the size and positive and negative of the torque will change greatly, and it takes 0.9 s to reach stability. With the increase in the transmission ratio, the degree of fluctuation will gradually decrease. At the 1.6:1 transmission ratio, it can reach stability after 0.5 s of fluctuation, and the number of torque direction changes will be significantly reduced. Excessive torque fluctuation of the gear will cause the contact stress between the tooth surfaces to change frequently, which is easy to cause failure forms such as tooth surface fatigue wear and pitting. When the torque fluctuation decreases, the stress change on the tooth surface is relatively stable, which slows down the fatigue process of the tooth surface material, thus prolonging the service life of the gear. At the same time, the reduction in the number of torque direction changes makes the change frequency of the force direction of the gear teeth decrease, reduces the possibility of fatigue cracks in the root of the gear teeth due to repeatedly bearing alternating stress, and further prolongs the service cycle of the gear.

5.3. Sensitivity Analysis of Fluid Density

To verify the robustness of the dual-motor compensation system against key medium parameters, a sensitivity analysis was conducted with fluid density as the research object. Considering the two core application scenarios of this study—deep-sea oil and gas exploitation and nuclear power—the variation range of fluid density needs to cover both the “simulation benchmark (water)” and “actual industrial media” to ensure the engineering reference value of the sensitivity analysis. The simulation in the previous section defaults to using the density of water (980 kg/m³) as the benchmark, while in practical scenarios, the density of oil and gas media varies significantly: the density of light crude oil generally ranges from 820 to 880 kg/m³, so 850 kg/m³ was selected as the typical value; the density of heavy crude oil mostly falls between 920 and 980 kg/m³, thus 950 kg/m³ was set as the representative value; additionally, special crude oil containing sand or with high viscosity is often encountered in deep-sea exploitation, whose maximum density can reach 1100 kg/m³, so this value was included to cover extreme medium conditions. In summary, the analysis range of fluid density was finally determined to be 850–1100 kg/m³, with four sets of parameters set to fully cover the actual medium density range of the target application scenarios, and the diagram below shows the post-valve flow rate under different fluid densities.

From the Figure 20, it can be seen that as the fluid density increases, both the post-valve flow rate stabilization time and the overshoot only undergo slight changes, with no order-of-magnitude changes observed. This indicates that the model has low sensitivity to changes in fluid density. Even at the maximum density, the dual-motor compensation can still achieve flow rate stabilization, which proves that the dual-motor compensation strategy remains effective under actual operating conditions with varying fluid densities.

6. Conclusions

To address the issues of diminished adjustment precision and reliability in control valves resulting from unstable fluid loads in complex environments, this study puts forward a dual-motor collaborative compensation approach based on redundant motors. By means of load compensation via dual motors, both the stability and dynamic response capacity of the valve under extreme operating conditions have been notably enhanced. The key research findings are summarized as follows:

Under the extreme working condition of sudden change in the inlet pressure of the valve, the dual-motor compensation system can quickly respond to the load change and significantly shorten the stable time of the flow after the valve by cooperatively adjusting the electromagnetic torque. Compared with the single-motor non-compensation and single-motor compensation schemes, the dual-motor compensation makes the flow after the valve return to the target value within 1.7 s, and has higher stability, avoiding overshoot and jamming phenomena.

By real-time monitoring of the motor load torque and introducing the compensation algorithm, the dual-motor system can dynamically allocate the compensation amount when the load changes suddenly, ensuring the cooperative work of the two motors. The simulation results show that the electromagnetic torque and speed regulation under the dual-motor compensation are more stable, effectively overcoming the problem of insufficient torque of the single-motor compensation.

The study on the transmission ratio found that increasing the transmission ratio can improve the control effect of the motor on the flow after the valve, speed up the adjustment speed, and reduce the fluctuation range of the flow after the valve in the adjustment process. At the same time, the speed change fluctuation and stable time of the motor are reduced, and the torque fluctuation of the transmission part gear is reduced, which helps to prolong the service life of the motor and gear.

In future work, experimental verification of the model will be conducted. Currently, a complete test bench for single-motor controlled valves is available, which provides a hardware and control logic foundation for subsequent verification. A dual-motor transmission system will be built based on this test bench in the later stage.

At the hardware level, permanent magnet synchronous servo motors (PMSMs) consistent with the parameters described in this study, high-precision flow/pressure sensors, and cone valve structures will be selected. A dual-motor parallel transmission mechanism (including a gearbox and a rack-and-pinion module) will be additionally built, while the hydraulic circuit and detection modules of the existing test bench will be reused.

In terms of operating condition simulation, the key operating conditions described in this study (such as the sudden pressure change scenario where the valve inlet pressure jumps from 5 bar to 15 bar at 1 s) will be reproduced on the test bench. Meanwhile, different load conditions will be simulated by adjusting circuit parameters.

In the data acquisition and comparison phase, real-time data from the test bench—including post-valve flow rate, motor electromagnetic torque, rotational speed, and gear torque—will be collected and quantitatively compared with the simulation results from the AMESim-Matlab/Simulink co-simulation. This will verify the consistency of core indicators (e.g., flow rate stabilization time and torque fluctuation amplitude) under dual-motor compensation. Additionally, parameters such as the transmission ratio (adjusted from 1:1 to 1.6:1) and compensation activation threshold will be modified to verify the model’s adaptability to multiple operating conditions on the test bench, ensuring that the model can accurately reflect the dynamic response characteristics of the actual system.