Robust Sliding Mode Motion Control for an Integrated Hydromechatronic Actuator

Abstract

Electro-hydraulic servoactuators have great potential in mobile robotics due to their robustness, high bandwidth and power density, but compared with electromechanical actuators, they can be inefficient and more difficult to integrate into systems. The Integrated Smart Actuator (ISA) developed by Moog Controls Ltd. is a hydromechatronic device that aims to address these issues by combining a novel efficient servovalve, cylinder, sensors and control electronics into a single component. The aim of this work was to develop a robust motion control algorithm that can make integration of the ISA into a robotic system straightforward by requiring minimal controller set-up despite variations in the load characteristics. The proposed controller is a sliding mode controller with a varying boundary layer that contains two robustness parameters and a single bandwidth parameter that defines the response. The controller outperforms a conventional high-performance linear controller in terms of tracking performance and its robustness to variations in the load mass and fluid bulk modulus. The response when the system was subject to some unachievable demand trajectories, such as large step demands, was found to be poor, and an online velocity, acceleration and jerk limited trajectory filter was demonstrated to rectify this issue. The successful implementation of a robust motion controller enables this highly novel integrated actuator to live up to its ‘smart’ epithet.

1. Introduction

Electro-hydraulic servos are widely used actuators consisting of a servovalve, piston and feedback loop. The combination of a high bandwidth, large force capability and mechanical robustness mean they can be found in many industrial applications, including material testing machines [1,2,3], aircraft primary flight controls [4,5], flight simulators [6], robotics [4], the dynamic testing of components in hardware-in-the-loop systems [7] and earthquake-simulating shaker tables [8].

The use of hydraulics in mobile robotics is quite appealing due to the dynamic performance and power density achievable compared with electromagnetic actuation. However, it comes with reduced efficiency due to the flow throttling and leakage within the servovalve and challenges with control design due to nonlinearities in the pressure–flow relationship, friction, parameter uncertainties, including the temperature-dependent fluid properties, low damping and high order dynamics, particularly when the valve response cannot be neglected.

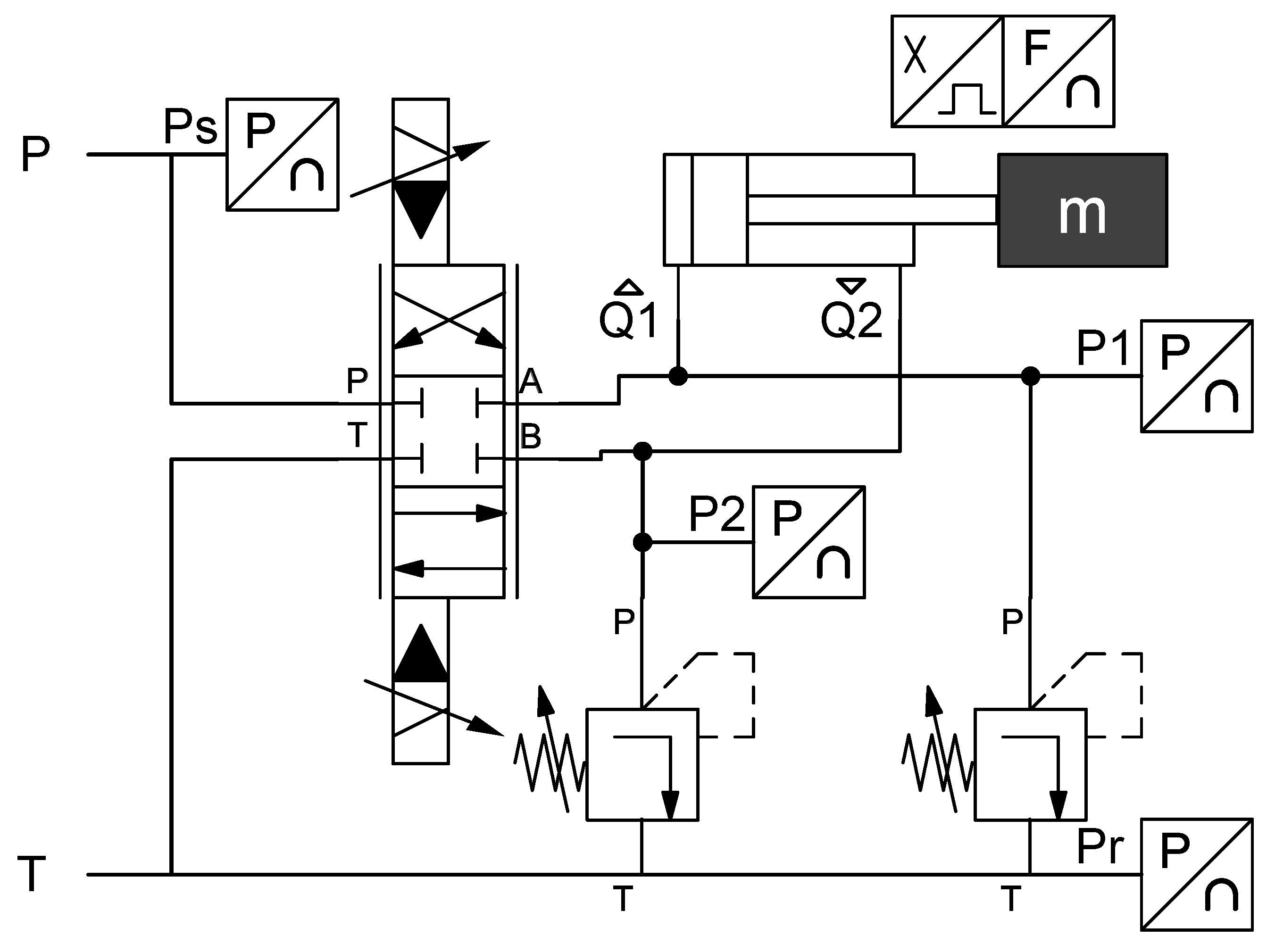
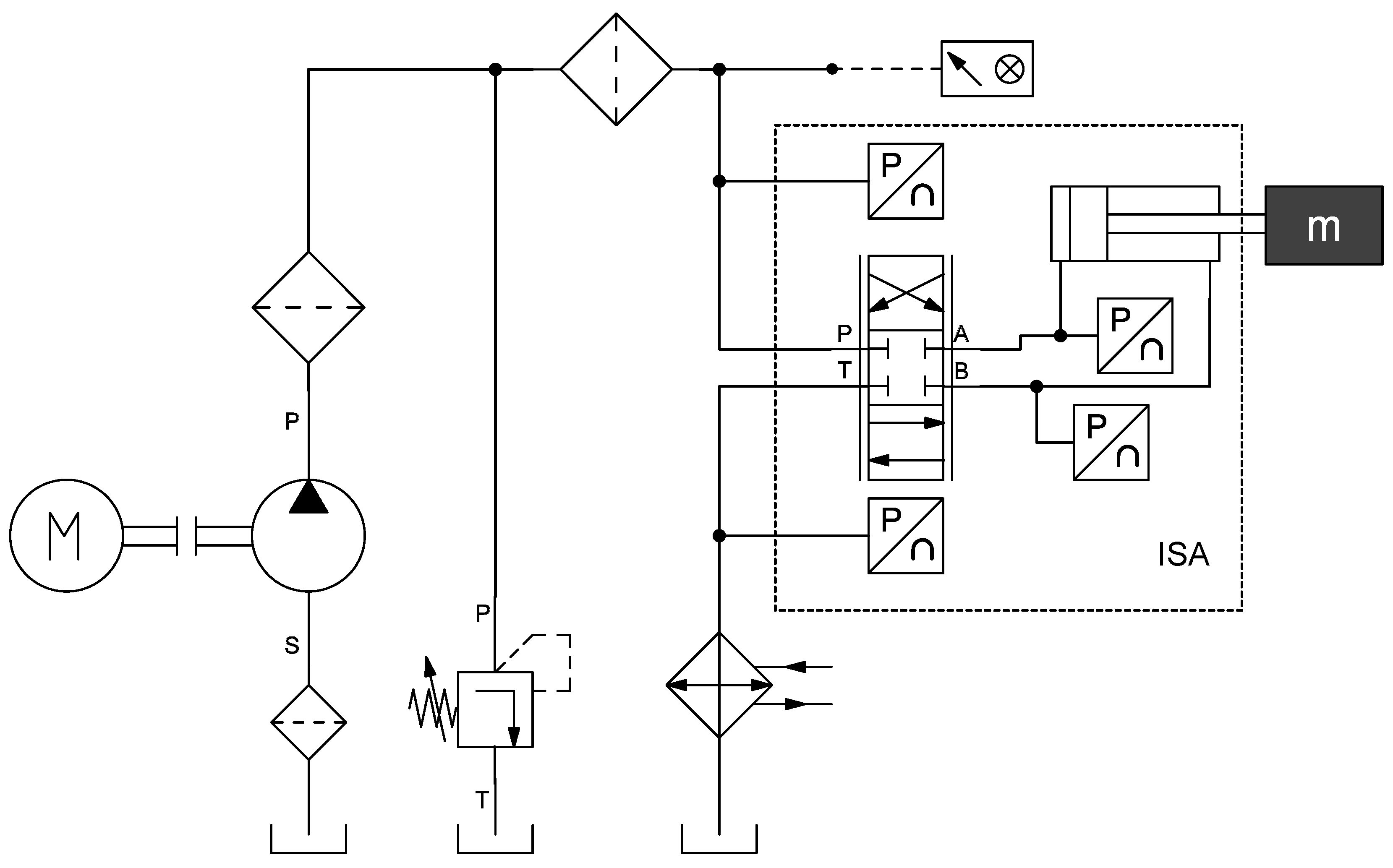
The Integrated Smart Actuator (ISA), developed by Moog [9] and shown in Figure 1, is a single actuation component consisting of a servovalve, actuator, sensors and control electronics in an additively manufactured titanium body. It is specifically designed for mobile robotics, with a compact and lightweight design for easy mechanical integration into a system. It also aims to address energy losses with a low-leakage nozzle-flapper pilot stage valve design. A detailed description can be found in [10]. The specifications are presented in

Table 1. ISA specifications.

Property	Value	Units
Stroke	100	mm
Closed length (between rod ends)	295	mm
Piston diameter	21.5	mm
Rod diameter	12	mm
Supply pressure	200	bar
Maximum force extension	7260	N
Maximum force retraction	5000	N
Nominal spool flow rate	7	lpm
Dry weight	1.6	kg

and the hydraulic schematic in Figure 2.

The aim of this work is to develop a control algorithm that can use the known characteristics of the ISA and the integrated sensors (position, force, spool position, torque motor current and supply and return and chamber pressures) to deal with the unknown or uncertain parts of the system, like the load it is attached to. With a suitable controller, the ISA could be a ‘plug-and-play’ device that requires minimal tuning to set up within a system.

The control method used in this work is based on sliding mode control, which has been applied a number of times to electro-hydraulic servos. The key differentiator is the method of dealing with the chattering effect caused by unmodelled delays and discrete sampling. Ghazali et al. [11] used a hyperbolic tangent sigmoid function for the boundary layer. The approach in [12] switched between two fixed magnitude boundary layers, depending on the absolute value of the tracking error, and it was able to both improve tracking and reduce chattering compared with a conventional SMC. More advanced approaches include using a time-varying gain combined with either a fixed [13] or varying boundary layer [14]. Gdoura et al. [15] used an adaptive surface and an adaptive gain. Fung [16] proposed a two-phase controller to improve the transient reaching phase when the system is approaching the sliding surface which, combined with a boundary layer, was able to remove chatter. Feng et al. [17] added disturbance and model uncertainty compensation using an adaptive radial basis function-based neural network, which was demonstrated to outperform both PID and conventional sliding mode control in tracking and disturbance rejection on an excavator.

In other applications of sliding mode control to hydraulic actuators, the authors of [18] demonstrated insensitivity to a load disturbance force for a slow-moving system.  In [19], an SMC was applied to a hydraulic press test bed, but the focus was on demand input shaping to reduce vibration rather than investigating robustness.  An SMC was demonstrated for hydraulic actuators in a robot leg in [20], showing acceptable performance across both stance and swing phases.

Other methods applied to electro-hydraulic actuators to deal with parametric uncertainty include gain scheduling [21], H-Infinity [22] and combining adaptive control with pole placement [23] and backstepping [24,25].

A common challenge when implementing these methods is tuning the control parameters, which can be numerous and unintuitive. The approach in this work aims to keep control parameters to a minimum, with a simple tuning process to deliver robust motion control performance.

2. System Modelling

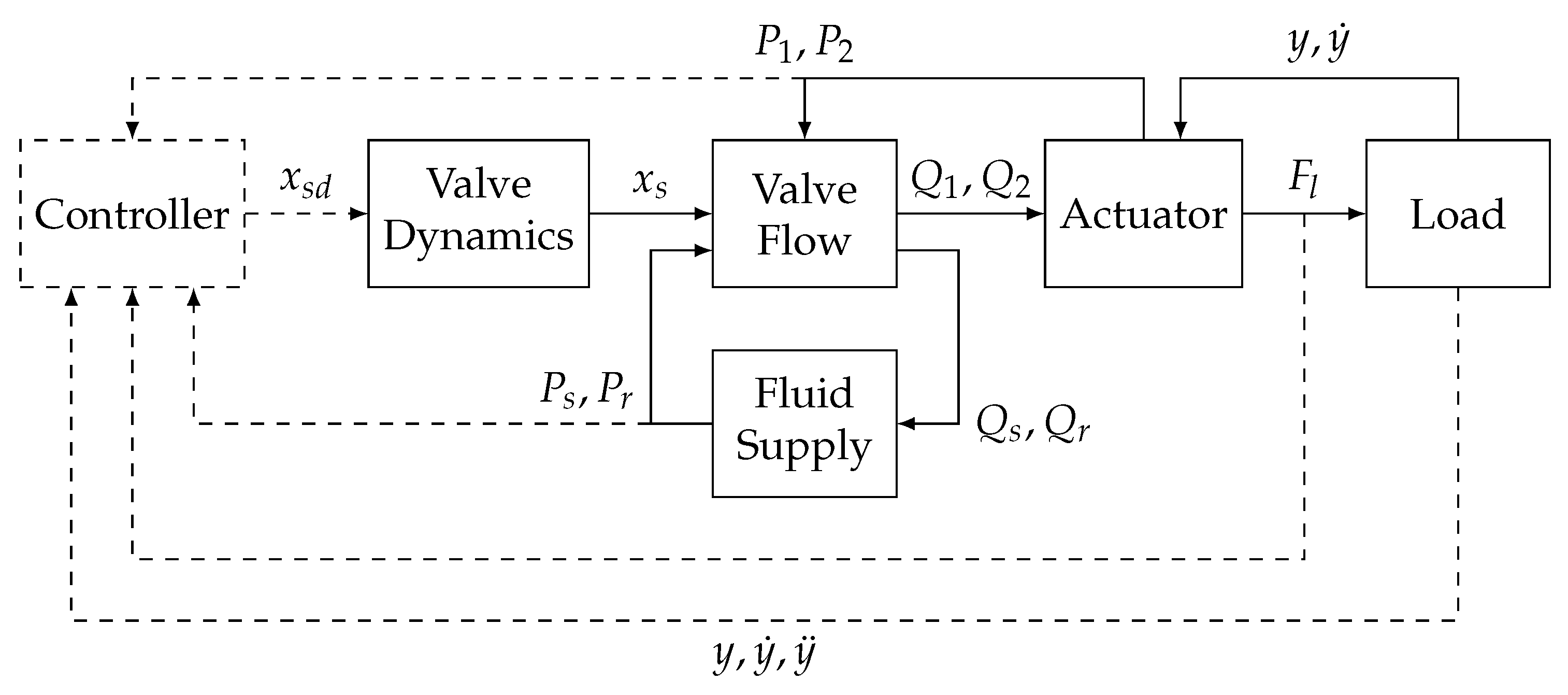
A summary of the system modelling is presented here. For a more detailed discussion, see [26]. An overview of each component of the model and the interaction between them is shown in Figure 3.

2.1. Servovalve

The servovalve dynamic model maps the spool position demand $x_{sd}$ to the spool position $x_s$. A second-order transfer function with a rate limit $R_{lim}$ to represent saturation of the torque motor current and a time delay $\tau$ to encompass unmodelled torque motor dynamics is used. The model is shown in Equation (1), where ${\omega }_s$ is the natural frequency and ${\zeta }_s$ is the damping ratio:

$$\begin{array}{c}{\displaystyle \frac{x_s}{x_{sd}}}={\displaystyle \frac{{\omega }_s^2}{s^2+2{\zeta }_s{\omega }_{s}s+{\omega }_s^2}}{e}^{-\tau s}\\ \left|{\dot{x}}_s\right|\le R_{lim}\end{array}$$

(1)

The servovalve spool is cut such that for a given spool displacement from the centre position, the velocity of the piston in each direction matches, as opposed to the typical configuration of the same area for each land. Each land also has a 2.5 times larger cross-section after 25% spool displacement and an overlap at the centre. 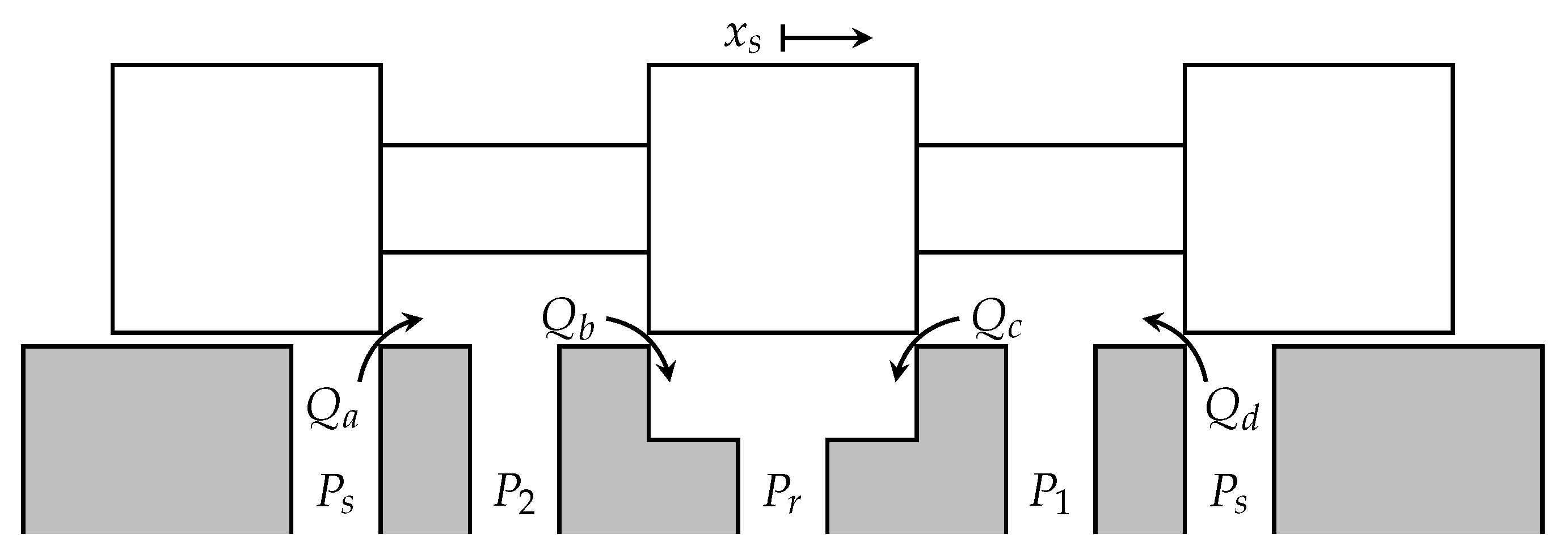Due to the asymmetric nature of the lands and some slight differences during manufacturing, each land is modelled individually based on experimental data, with the land area split into three piece-wise equations, as shown for land d in Equation (2). A diagram of the spool pressure ports and flows is shown in Figure 4. Each flow $Q_x$ corresponds to the land area $A_x$.

$$A_d\left(x_s\right)=\left\{\begin{array}{cc}\gamma e^{{\displaystyle \frac{k{x}_s}{2}}}\hfill & x_s\le x_t\left(a\right)\hfill \\ w_1{x}_s+A_s\hfill & x_t<x_s\le x_b\left(b\right)\hfill \\ {\displaystyle \frac{A_{d2}{A}_{sat}}{\sqrt{A_{d2}^2+A_{sat}^2}}}\hfill & x_b<x_s\left(c\right)\hfill \end{array}\right.$$

(2)

The piece-wise model consists of three regions split at spool breakpoints $x_t$ and $x_b$. These are (1) the leakage region where the land is effectively closed, but some leakage occurs (Equation (2a)), modelled as an exponential characterised by $\gamma$ and k; (2) the linear region where the area increases linearly with the spool position, proportional to $w_1$ (Equation (2b)) and offset by $A_t$ to account for leakage; and (3) the saturation region where the area increases linearly but the flow tapers off due to pressure drops in the valve body (Equation (2c)). The body saturation losses are modelled as a fixed orifice $A_{sat}$ in series with the linearly varying area $A_{d2}$.

With equivalent models for each land area, the flow across each of the lands for a given pressure drop, and therefore the flows in the actuator chambers $Q_1$ and $Q_2$, are therefore

$$\begin{array}{c}{Q}_1=k_v{A}_d\left(x_s\right)\sqrt[]{\Delta P_d}-k_v{A}_c\left(x_s\right)\sqrt[]{\Delta P_c}\\ Q_2=k_v{A}_b\left(x_s\right)\sqrt[]{\Delta P_b}-k_v{A}_a\left(x_s\right)\sqrt[]{\Delta P_a}\end{array}$$

(3)

where $P_x$ is the pressure drop, $A_x$ is the effective area across land x and $k_v$ is the flow constant given by

$$k_v=C\sqrt[]{{\displaystyle \frac{2}{\rho }}}$$

(4)

where C is the orifice coefficient and $\rho$ is the fluid density.

2.2. Actuator and Load

The equations relating the pressures $P_1$ and $P_2$ to the flows to and from the actuator and its motion are shown in Equation (5):

$$\begin{array}{c}{Q}_1(x_s,P_1)-A_1\dot{y}={\dot{P}}_1{\displaystyle \frac{V_1\left(y\right)}{{\beta }_e}}\\ A_2\dot{y}-Q_2(x_s,P_2)={\dot{P}}_2{\displaystyle \frac{V_2\left(y\right)}{{\beta }_e}}\end{array}$$

(5)

where $A_n$ and $v_n$ are the chamber areas and volumes, respectively, y is the piston position and ${\beta }_e$ is the effective fluid bulk modulus.

The friction acting between the piston and the actuator body is modelled as Stribeck friction, as shown in Equation (6), where $\sigma$ is the viscous coefficient, $F_c$ is the Coulomb friction, $F_s$ is the static friction and $c_s$ is the exponential coefficient. The equation of motion of the piston and load is then given by Equation (7), where m is the combined mass of the piston and the load and $F_l$ is the disturbance force:

$$F_f=\sigma \dot{y}+sign\left(\dot{y}\right)\left(F_c+F_s{e}^{-{\displaystyle \frac{|\dot{y}|}{c_s}}}\right)$$

(6)

$$(P_1{A}_1-P_2{A}_2)-F_l-F_f=m\ddot{y}$$

(7)

2.3. Full Model

The state space model representing the full system is shown in Equation (8), where the states $\mathit{x}=[x_1,x_2,x_3,x_4,x_5]=[y,\dot{y},\ddot{y},x_s,\dot{x_s}]$ and the control input $u=x_{sd}$:

$$\dot{\mathit{x}}=\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\\ {\dot{x}}_3\\ {\dot{x}}_4\\ {\dot{x}}_5\end{array}\right]=\left[\begin{array}{c}{x}_2\\ x_3\\ h\left(x_1\right)-g(x_1,x_2)-{\dot{F}}_f-{\dot{F}}_l\\ x_5\\ v(x_4,x_5)\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ b_s\end{array}\right]u$$

(8)

where

$$\begin{array}{cc}\hfill v(x_4,x_5)& =-2{\zeta }_s{\omega }_s{x}_5-{\omega }_s^2{x}_4,\left|x_5\right|\le R_{lim}\hfill \\ \hfill h(x_1,x_4)& ={\displaystyle \frac{{\beta }_e{A}_1}{m{V}_1\left(x_1\right)}}{Q}_1(x_4,P_1)+{\displaystyle \frac{{\beta }_e{A}_2}{m{V}_2\left(x_1\right)}}{Q}_2(x_4,P_2)\hfill \\ \hfill g(x_1,x_2)& ={\displaystyle \frac{{\beta }_e}{m}}\left({\displaystyle \frac{A_1^2}{V_1\left(x_1\right)}}+{\displaystyle \frac{A_2^2}{V_2\left(x_1\right)}}\right)x_2\hfill \\ \hfill b_s& ={\omega }_s^2{e}^{-\tau s}\hfill \end{array}$$

(9)

3. Control Law Derivation

3.1. Controller Model

The proposed control method uses a sliding mode controller (SMC) with a varying boundary layer [27]. The controller is designed using a simplified model of the system that assumes the servovalve dynamics are significantly faster than the rest of the system and thus can be ignored, and the input to the system becomes $u=x_s$. The system states are $\mathit{x}=[x_1,x_2,x_3]=[y,\dot{y},\ddot{y}]$:

$$\dot{\mathit{x}}=\left[\begin{array}{c}{x}_2\\ x_3\\ -g(x_1,x_2)-{\dot{F}}_f-{\dot{F}}_l\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ b(x_1,u)\end{array}\right]$$

(10)

where

$$\begin{array}{cc}\hfill g(x_1,x_2)=& {\displaystyle \frac{{\beta }_e}{m}}\left({\displaystyle \frac{A_1^2}{V_1\left(x_1\right)}}+{\displaystyle \frac{A_2^2}{V_2\left(x_1\right)}}\right)x_{2}l\hfill \\ \hfill b(x_1,u)=& {\displaystyle \frac{{\beta }_e{A}_1}{m{V}_1\left(x_1\right)}}{Q}_1(u,P_1)+{\displaystyle \frac{{\beta }_e{A}_2}{m{V}_2\left(x_1\right)}}{Q}_2(u,P_2)\hfill \end{array}$$

(11)

For the design of the sliding mode controller, it is required that the system model is input-affine, i.e., the input is linear. This requires changing it from the current form of $b(\mathit{x},u)$ to $b_l\left(\mathit{x}\right)u$, where $b_l\left(\mathit{x}\right)$ is the new linear control term.

This implies that

$$b_l\left(\mathit{x}\right)={\displaystyle \frac{b(\mathit{x},u)}{u}}$$

(12)

and therefore

$$b_l\left(\mathit{x}\right)={\displaystyle \frac{{\beta }_e{A}_1}{m{V}_1\left(x_1\right)u}}{Q}_1(u,P_1)+{\displaystyle \frac{{\beta }_e{A}_2}{m{V}_2\left(x_1\right)u}}{Q}_2(u,P_2)$$

(13)

The $g\left(\mathit{x}\right)$ and $b_l\left(\mathit{x}\right)$ terms are assumed to be uncertain but with known error bounds, with the estimates of each being $\widehat{g}\left(\mathit{x}\right)$ and $\widehat{b}\left(\mathit{x}\right)$, respectively. The error associated with the actuator velocity feedback term $g\left(\mathit{x}\right)$ is additive and bounded by G (Equation (14)). The error associated with the control gain $b_l\left(\mathit{x}\right)$ is multiplicative and bounded by B (Equation  (15)).

$F_d$ represents the combined friction and force disturbance, with a derivative bounded by F, as per Equation (16):

$$|\widehat{g}-g|\le G$$

(14)

$${\displaystyle \frac{1}{B}}\le {\displaystyle \frac{b_l}{{\widehat{b}}_l}}\le B$$

(15)

$$|{\dot{F}}_d|\le F$$

(16)

3.2. Derivation

The following derivation of the sliding mode controller is based on [27,28].

The position demand is $y_d$, and the tracking error e is given by

$$e=y_d-y$$

(17)

The sliding surface s represents the desired error dynamics of the system, chosen with critically damped poles:

$$s=\ddot{e}+2\lambda \dot{e}+{\lambda }^{2}e=0$$

(18)

where $\lambda$ defines the location of the poles.

For the system to achieve the desired asymptotic error dynamics behaviour, it needs to remain on the surface s. The control objective transforms into a stabilisation of s.

The first step in approaching this stabilisation problem is to construct a Lyapunov function V of s that is positive for all $s\ne 0$, in which

$$V={\displaystyle \frac{1}{2}}{s}^2$$

(19)

and choose a control law that ensures that the time derivative of the Lyapunov function is always negative:

$$\dot{V}\le -\eta \left|s\right|$$

(20)

where $\eta$ is a positive constant.

The control law that satisfies this will always drive the system towards $s=0$.

From Equations (18) and (19), the derivative of V is given by

$$\begin{array}{c}\hfill \dot{V}=s\dot{s}=s\left(\stackrel{⃛}{e}+2\lambda \ddot{e}+{\lambda }^2\dot{e}\right)=s\left({\stackrel{⃛}{y}}_d-\stackrel{⃛}{y}+2\lambda \ddot{e}+{\lambda }^2\dot{e}\right)\le -\eta \left|s\right|\end{array}$$

(21)

Substituting in $\stackrel{⃛}{y}$ from Equation (10) yields

$$s\left({\stackrel{⃛}{y}}_d-b_l\left(\mathit{x}\right)u+g\left(\mathit{x}\right)+{\dot{F}}_d+2\lambda \ddot{e}+{\lambda }^2\dot{e}\right)\le -\eta \left|s\right|$$

(22)

The control law for u contains an estimate of the control signal required to achieve $\dot{s}=0$, $\widehat{u}$ and a robust switching component $K\left(\mathit{x}\right)sgn\left(s\right)$:

$$u={\displaystyle \frac{1}{{\widehat{b}}_l\left(\mathit{x}\right)}}\left(\widehat{u}+K\left(\mathit{x}\right)sgn\left(s\right)\right)$$

(23)

$\widehat{u}$, also known as the equivalent control, is given by

$$\widehat{u}=\left({\stackrel{⃛}{y}}_d+\widehat{g}\left(\mathit{x}\right)+2\lambda \ddot{e}+{\lambda }^2\dot{e}\right)$$

(24)

To satisfy the condition in Equation (22), the gain K needs to be chosen by considering the uncertainties presented in Equations (14) and (15).

Substituting in the control law from Equation (23) into Equation (22) leads to

$$\begin{array}{c}\hfill s({\stackrel{⃛}{y}}_d-{\displaystyle \frac{b_l}{{\widehat{b}}_l}}\left({\stackrel{⃛}{y}}_d+\widehat{g}+2\lambda \ddot{e}+{\lambda }^2\dot{e}+K\left(\mathit{x}\right)sgn\left(s\right)\right))\left.+g+{\dot{F}}_d+2\lambda \ddot{e}+{\lambda }^2\dot{e}\right)\le -\eta \left|s\right|\end{array}$$

(25)

It can be shown that ([26])

$$K\left(\mathit{x}\right)\ge \left(B\left(\mathit{x}\right)-1\right)\left|\widehat{u}\right|+B\left(\mathit{x}\right)\left(G\left(\mathit{x}\right)+\eta +F\right)$$

(26)

The above states a clear requirement for stability of the system in terms of the bounded modelling uncertainties and external disturbances.

3.3. Varying Boundary Layer

The chattering effect of the standard sliding mode controller caused by the switching control signal is often countered by using a boundary layer. The proposed controller uses a varying boundary layer such that the switching part of the control law becomes

$$\overline{K}\left(\mathit{x}\right)sat\left({\displaystyle \frac{s}{\varphi }}\right)$$

(27)

where $\varphi$ is the boundary layer thickness. The saturation function is defined as follows:

$$sat\left({\displaystyle \frac{s}{\varphi }}\right)=\left\{\begin{array}{cc}sgn\left({\displaystyle \frac{s}{\varphi }}\right)\hfill & \left|{\displaystyle \frac{s}{\varphi }}\right|\ge 1\hfill \\ {\displaystyle \frac{s}{\varphi }}\hfill & \left|{\displaystyle \frac{s}{\varphi }}\right|<1\hfill \end{array}\right.$$

(28)

The varying boundary layer can take advantage of situations with reduced uncertainty whilst maintaining stability guarantees. The stability condition from Equation (20) is adjusted such that the distance to the boundary layer always decreases when s is outside:

$$\dot{V}\le (\dot{\varphi }-\eta )\left|s\right|$$

(29)

This change to the stability criterion requires modification of the switching gain $K\left(\mathit{x}\right)$. According to Equation (30), the new gain $\overline{K}\left(\mathit{x}\right)$ must satisfy

$$\begin{array}{cc}\hfill & \overline{K}\left(\mathit{x}\right)\ge \left|\left({\displaystyle \frac{{\widehat{b}}_l}{b_l}}-1\right)\left({\stackrel{⃛}{y}}_d+2\lambda \ddot{e}+{\lambda }^2\dot{e}+\widehat{g}\right)+{\displaystyle \frac{{\widehat{b}}_l}{b_l}}\left((g-\widehat{g})-{\dot{F}}_d\right)\right|+{\displaystyle \frac{{\widehat{b}}_l}{b_l}}(\eta -\dot{\varphi })\hfill \end{array}$$

(30)

The boundary layer dynamics are set to match those of $\lambda$ such that no further parameters are required for tuning. It can be shown [27] that with these constraints, the switching gain $\overline{K}\left(\mathit{x}\right)$ is

$$\overline{K}\left(\mathit{x}\right)=K\left(\mathit{x}\right)-K\left({\mathit{x}}_{\mathit{d}}\right)+{\displaystyle \frac{\lambda \varphi }{B\left({\mathit{x}}_{\mathit{d}}\right)}}$$

(31)

and the evolution on the boundary layer $\varphi$ is given by

$$\dot{\varphi }=\left\{\begin{array}{cc}-\lambda \varphi +B\left({\mathit{x}}_{\mathit{d}}\right)K\left({\mathit{x}}_{\mathit{d}}\right)\hfill & K\left({\mathit{x}}_{\mathit{d}}\right)\ge {\displaystyle \frac{\lambda \varphi }{B\left({\mathit{x}}_{\mathit{d}}\right)}}\hfill \\ -{\displaystyle \frac{\lambda }{B^2\left({\mathit{x}}_{\mathit{d}}\right)}}\varphi +{\displaystyle \frac{K\left({\mathit{x}}_{\mathit{d}}\right)}{B\left({\mathit{x}}_{\mathit{d}}\right)}}\hfill & K\left({\mathit{x}}_{\mathit{d}}\right)<{\displaystyle \frac{\lambda \varphi }{B\left({\mathit{x}}_{\mathit{d}}\right)}}\hfill \end{array}\right.$$

(32)

The final control law is

$$u={\displaystyle \frac{1}{{\widehat{b}}_l\left(\mathit{x}\right)}}\left(\widehat{u}+\overline{K}\left(\mathit{x}\right)sat\left({\displaystyle \frac{s}{\varphi }}\right)\right)$$

(33)

3.4. Linearising the Control Gain

The control law presented in Equation (33) is based on the assumption that $b_l\left(\mathit{x}\right)$ and therefore $\widehat{b_l}\left(\mathit{x}\right)$ are independent of u. In Equation (13), this can be seen to be false.

In (33), the control law can be rearranged as follows:

$$\widehat{b}(\mathit{x},u)={\widehat{b}}_l\left(\mathit{x}\right)u=\left(\widehat{u}+\overline{K}\left(\mathit{x}\right)sgn\left(s\right)\right)$$

(34)

where $\widehat{u}$, $\overline{K}\left(\mathit{x}\right)$ and s can all be calculated without knowledge of the control input estimate $\widehat{b}(\mathit{x},u)$. Therefore, it is required to find the inverse of $\widehat{b}(\mathit{x},u)$ for a value of u that satisfies (34). Thus, $\widehat{b}(\mathit{x},u)$ is equal to

$$\begin{array}{cc}\hfill \widehat{b}(\mathit{x},u)=& {\displaystyle \frac{{\beta }_e{A}_1}{m{V}_1\left(x_1\right)}}{Q}_1(u,P_1)+{\displaystyle \frac{{\beta }_e{A}_2}{m{V}_2\left(x_1\right)}}{Q}_2(u,P_2)\hfill \end{array}$$

(35)

which, for a particular piston position and system pressures across each land (land pressure drops), varies nonlinearly with u.

In order to cancel u from Equation (35), the land area equations are estimated with a piecewise linear model, which gives six linear regions for $\widehat{b}(\mathit{x},u)$:

$$\widehat{b}(\mathit{x},u)=\left\{\begin{array}{cc}\widehat{b}(\mathit{x},u_{b4})+K_6(u-u_{b4})\hfill & u<u_{b4}\hfill \\ \widehat{b}(\mathit{x},u_{b3})+K_5(u-u_{b3})\hfill & u_{b4}\le u<u_{b3}\hfill \\ K_{4}u\hfill & u_{b3}\le u<0\hfill \\ K_{1}u\hfill & 0\le u\le u_{b1}\hfill \\ \widehat{b}(\mathit{x},u_{b1})+K_2(u-u_{b1})\hfill & u_{b1}<u\le u_{b2}\hfill \\ \widehat{b}(\mathit{x},u_{b2})+K_3(u-u_{b2})\hfill & u_{b2}<u\hfill \end{array}\right.$$

(36)

The gradients of each region, from $K_1$ to $K_6$, are based on the linearised land areas, the constants in Equation (35) and the instantaneous pressure and piston position measurements. The breakpoints in the piecewise linear model are zero and from $u_{b1}$ to $u_{b4}$.

The process for calculating u is as follows:

1.

Calculate the value of $X=\widehat{u}+\overline{K}\left(\mathit{x}\right)sgn\left(s\right)$.

2.

Calculate the gradients of the piecewise linear model from $K_1$ to $K_6$.

3.

Calculate the value of $\widehat{b}(\mathit{x},u)$ at each breakpoint from $u_{b1}$ to $u_{b4}$.

4.

Determine the correct region based on the value of X and from $\widehat{b}(\mathit{x},u_{b1})$ to $\widehat{b}(\mathit{x},u_{b4})$.

5.

Calculate u in this region based on Equation (36) and X.

The following is a pseudocode implementation of the algorithm to calculate the control signal u based on a set of measurements:

$X=\widehat{u}+\overline{K}\left(\mathit{x}\right)sgn\left(s\right)$	▹ Calculate the desired value of $\widehat{b}$
$K_1...K_6=...$	▹ Calculate the gradients of $\widehat{b}$
$\widehat{b}(\mathit{x},u_{b1})...\widehat{b}(\mathit{x},u_{b4})=...$	▹ Calculate $\widehat{b}$ at the breakpoints
	▹ Find the correct region and assign the value of u
if $X\ge 0$ then
if $X\le \widehat{b}(\mathit{x},u_{b1})$ then
$u={\displaystyle \frac{X}{K_1}}$
else if $X\le \widehat{b}(\mathit{x},u_{b1})$ then
$u={\displaystyle \frac{X-\widehat{b}(\mathit{x},u_{b1})}{K_2}}-u_{b1}$
else
$u={\displaystyle \frac{X-\widehat{b}(\mathit{x},u_{b2})}{K_3}}-u_{b2}$
end if
else
if $X\ge \widehat{b}(\mathit{x},u_{b3})$ then
$u={\displaystyle \frac{X}{K_4}}$
else if $X\ge \widehat{b}(\mathit{x},u_{b4})$ then
$u={\displaystyle \frac{X-\widehat{b}(\mathit{x},u_{b3})}{K_5}}-u_{b3}$
else
$u={\displaystyle \frac{X-\widehat{b}(\mathit{x},u_{b4})}{K_6}}-u_{b4}$
end if
end if

4. Simulation Results

The model described by the block diagram in Figure 5 and Equations (8) and (9) was implemented in Simulink to test the controller. The controller was compared against a standard high-performance linear control design in both the time and frequency domains and for robustness to parametric uncertainty.

The linear controller was designed around a linearised version of Equation (10), shown in Equations (37)–(39), where c is the viscous friction coefficient, $V_{01}$ and $V_{02}$ are the chamber volumes at midstroke and ${\dot{y}}_{ss}$ is the steady state velocity at spool position $u_{ss}$. The linear model is based on a spool position below the dual-gain breakpoint, with control outputs greater than the dual-gain breakpoint adjusted before being applied to the plant to compensate for this nonlinearity:

$${\displaystyle \frac{y}{u}}={\displaystyle \frac{b_0}{s\left(s^2+cs+g_0\right)}}$$

(37)

$$g_0={\displaystyle \frac{{\beta }_e}{m}}\left({\displaystyle \frac{A_1^2}{V_{01}}}+{\displaystyle \frac{A_2^2}{V_{02}}}\right)$$

(38)

$$b_0={\displaystyle \frac{{\dot{y}}_{ss}{g}_0}{u_{ss}}}$$

(39)

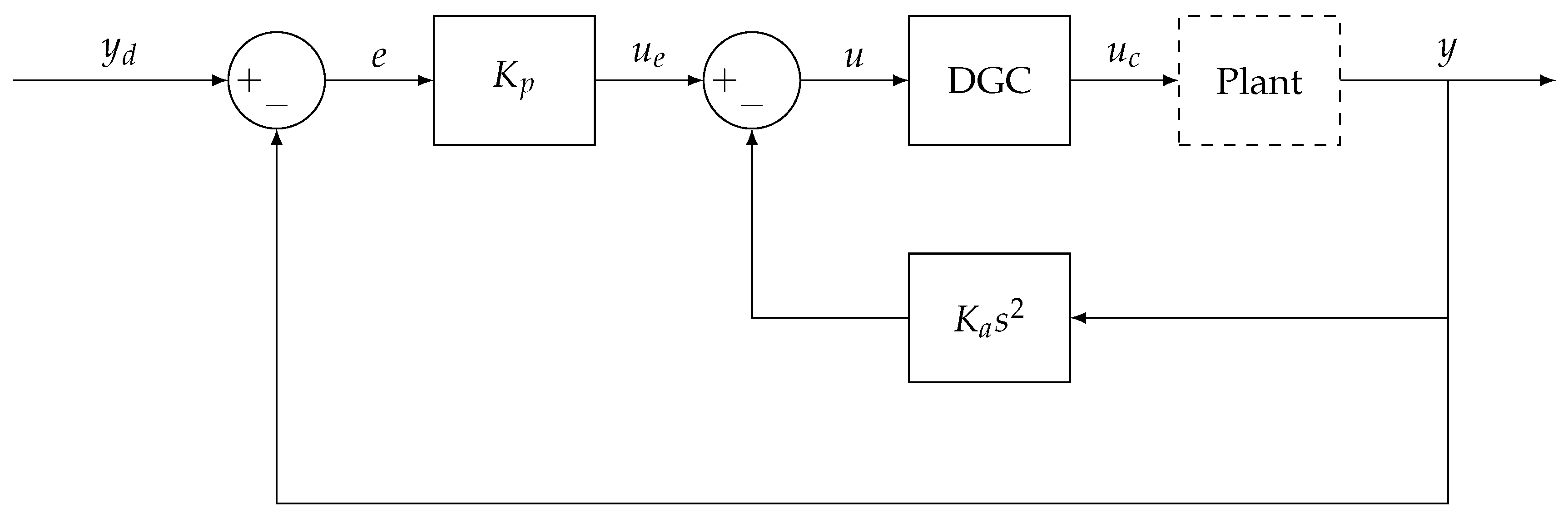
The linear controller consisted of an acceleration feedback term $K_a$ added to increase the open loop damping to 0.7 and a proportional feedback term $K_p$ tuned for a phase margin of 60 ° [4].

4.1. SMC Controller Tuning

The proposed controller has four variable terms that can be tuned to impact the response: the uncertainty terms B and G, the error dynamics $\lambda$ and $\eta$. B represents the multiplicative uncertainty in the gain $b_l\left(\mathit{x}\right)$ and is a combination of parametric uncertainties in the bulk modulus, spool area and load mass and the measurement uncertainty in the pressures, as shown in

Table 2. Uncertainty components of B.

Property	Error/%
Bulk Modulus	20
Spool Areas	10
Load Mass	10
Pressure Measurement	2
Total (B)	48

. The total uncertainty was 48%, and thus the value of B was fixed at 1.48.

G represents the uncertainty in the velocity feedback term $g\left(\mathit{x}\right)$, shown in Equation (40) (neglecting the leakage term). Uncertainty in the load mass and bulk modulus were considered, for a total of 32%. However, G is an additive error such that it changes with the state $\mathit{x}$ according to Equation (41):

$$\begin{array}{c}\hfill g\left(\mathit{x}\right)={\displaystyle \frac{{\beta }_e}{m}}\left({\displaystyle \frac{A_1^2}{V_1\left(x_1\right)}}+{\displaystyle \frac{A_2^2}{V_2\left(x_1\right)}}\right)x_2\end{array}$$

(40)

$$\begin{array}{c}\hfill G\left(\mathit{x}\right)=0.32{\displaystyle \frac{{\beta }_e}{m}}\left({\displaystyle \frac{A_1^2}{V_1\left(x_1\right)}}+{\displaystyle \frac{A_2^2}{V_2\left(x_1\right)}}\right)x_2\end{array}$$

(41)

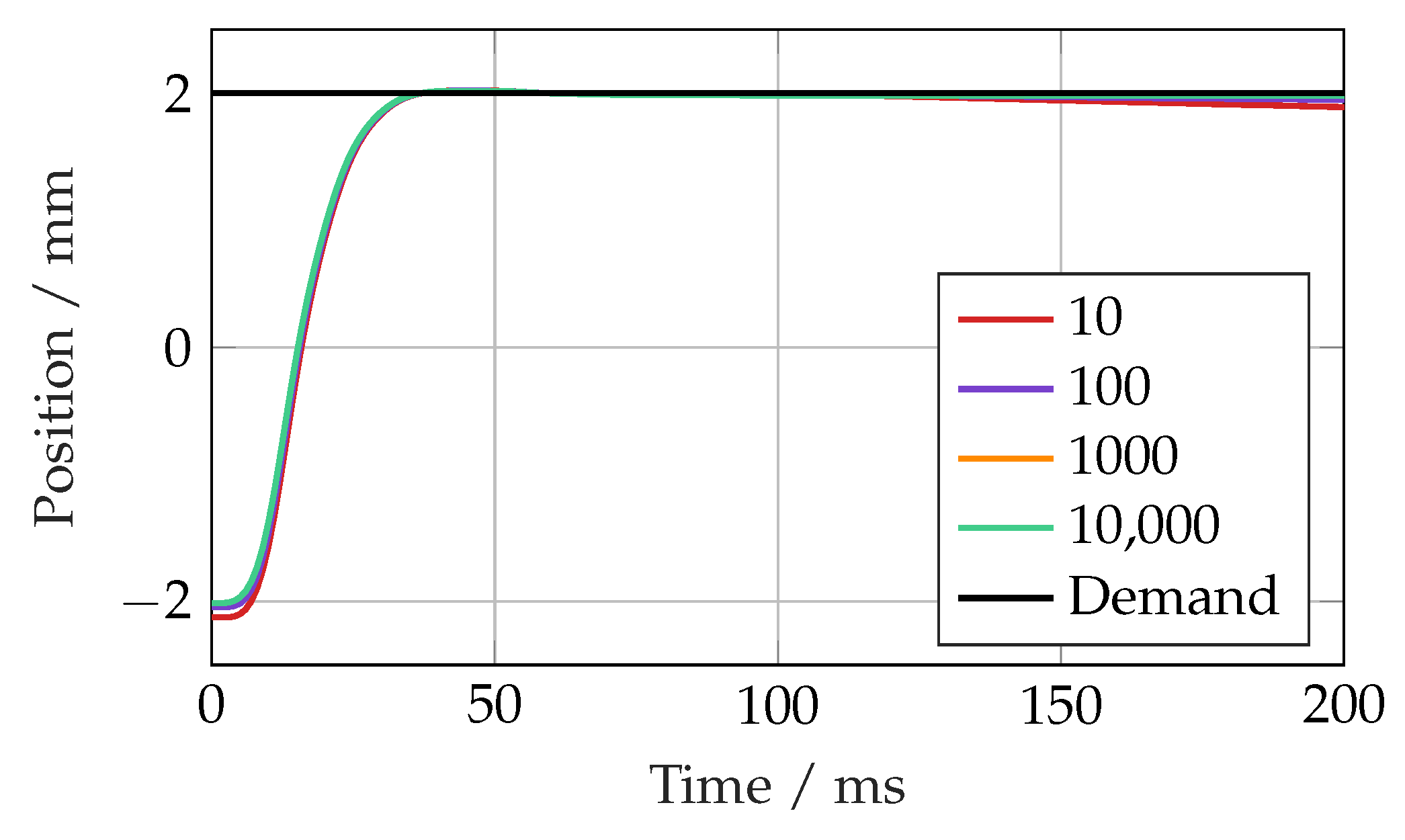
The $\eta$ term is combined with the unknown force disturbance F such that its purpose is to both attract the system to boundary layer when it is outside and compensate for any unmodelled disturbance. It is important that $\eta$ is not too large; otherwise, the robustness properties of the controller are lost [27]. Shown in Figure 6 is the simulated step response of the system with different order of magnitude values for $\eta$. This was found to have a small impact on the response time and steady-state error. A value of $\eta =500$ was chosen as larger values had a diminishing impact on the response.

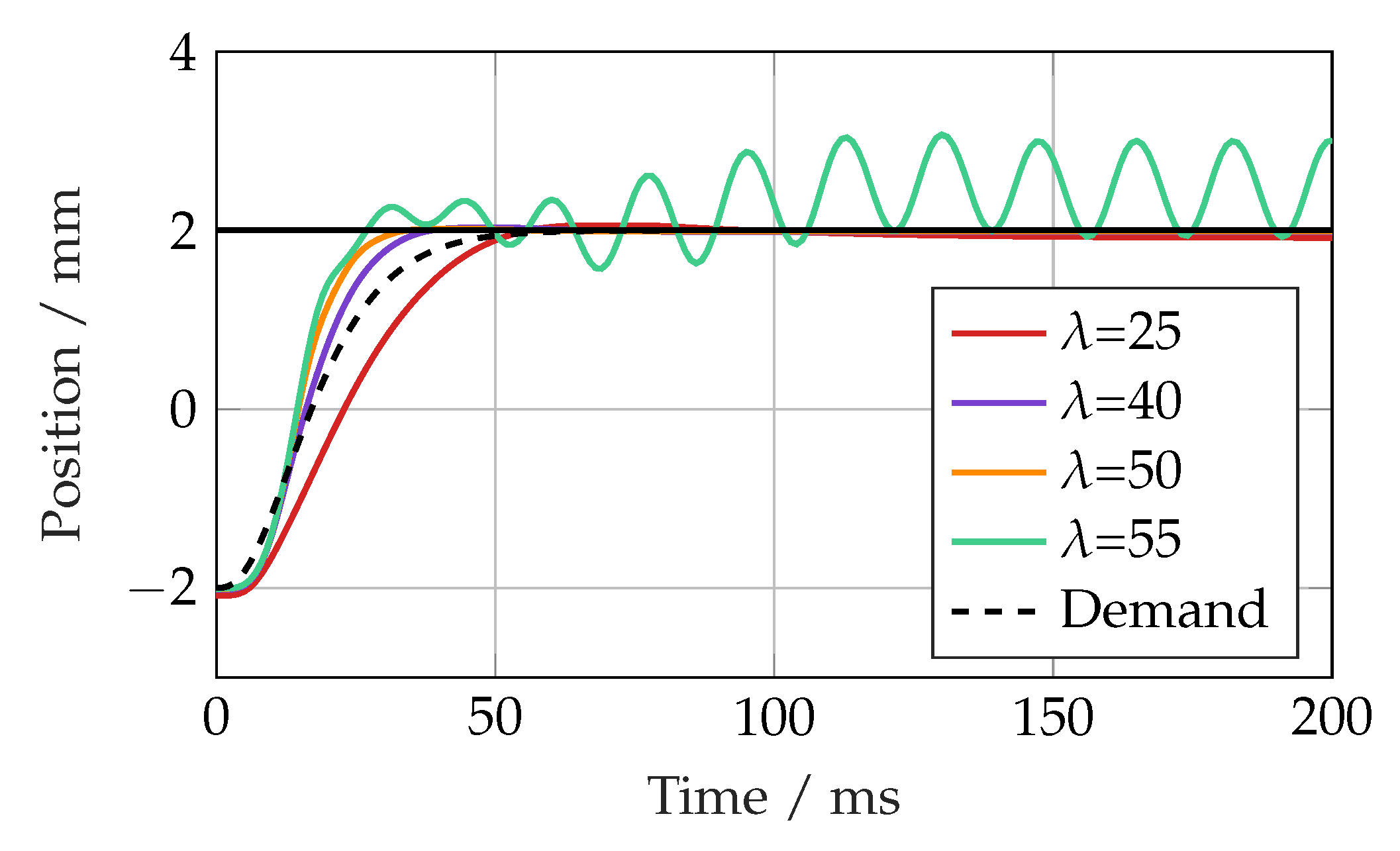
The final parameter is $\lambda$, which has the most significant impact on the control performance as it defines the characteristics of the error dynamics. The main limitations on the selection of $\lambda$ are the unmodelled dynamics, time-delays and the sample rate of the controller. The sample-rate in this case was 10 kHz, which was sufficiently fast to have no impact, leaving just the servovalve dynamics as the critical limitation.

Figure 7 shows how the step response changed with $\lambda$. As would be expected, the response was faster as $\lambda$ increased up to a point at which it became too aggressive. The performance deteriorated between $\lambda =50$ and $\lambda =55$ to the point where it was on the limit of stability.

From these results, a value of 45 Hz was chosen for $\lambda$, giving a fast response with no overshoot, and it was also found to work well for the experimental set-up. The response also closely matched that of the linear controller, which allowed comparisons to be made between the robustness of the linear controller and SMC with similar tuning.

4.2. Performance Comparison

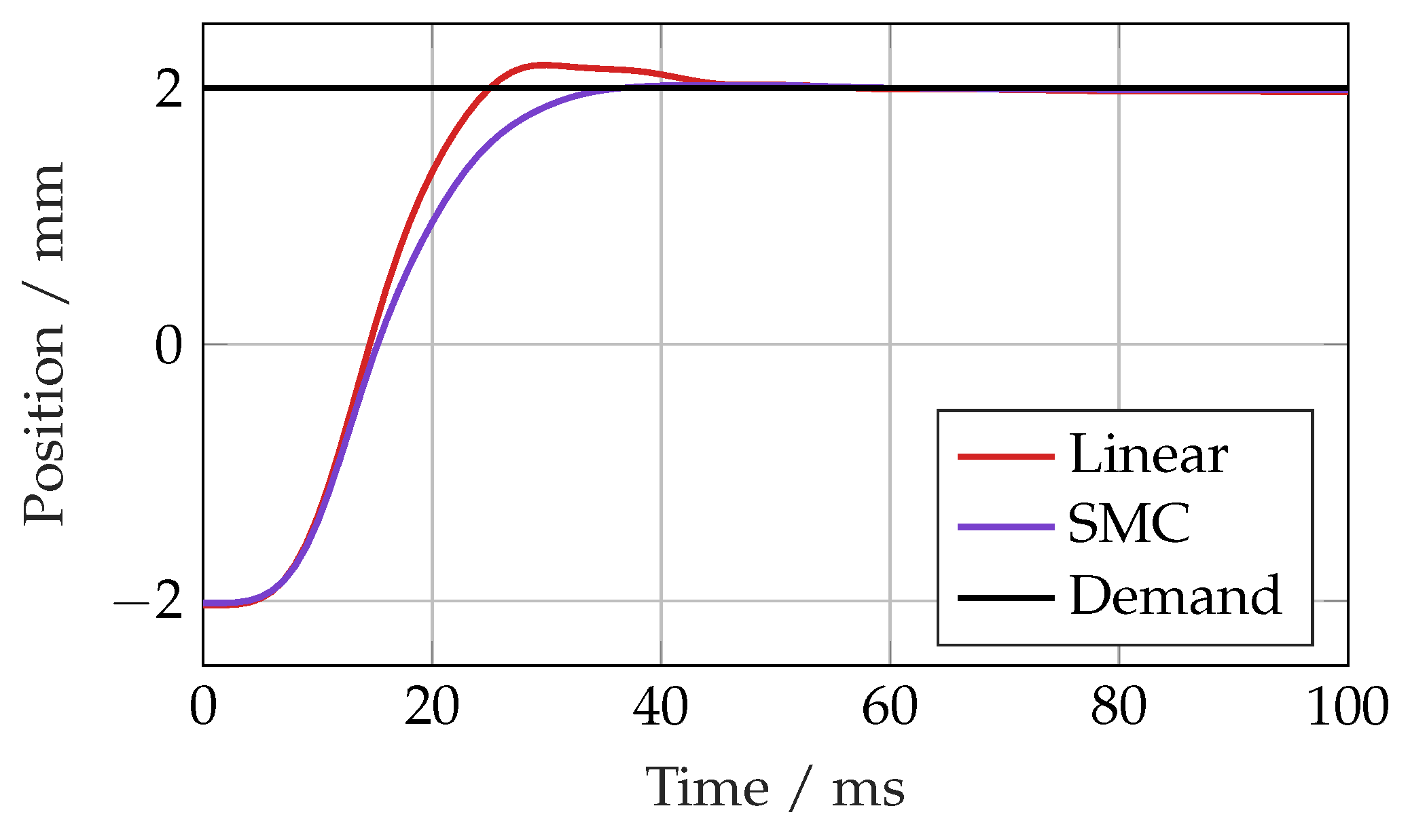
To test the performance of the sliding mode controller, it was compared to the linear controller in both the time and frequency domains. The simulated step response of each controller is shown in Figure 8. The responses were broadly similar, although the linear controller exhibited a small overshoot due to the tuning method used. The time domain results are summarised in

Table 3. Simulation performance metrics.

Metric	Linear	SMC
Rise Time (ms)	13	16
Settling Time (ms)	43	31
Overshoot (%)	5	1
Bandwidth (1 mm) (Hz)	28	44

.

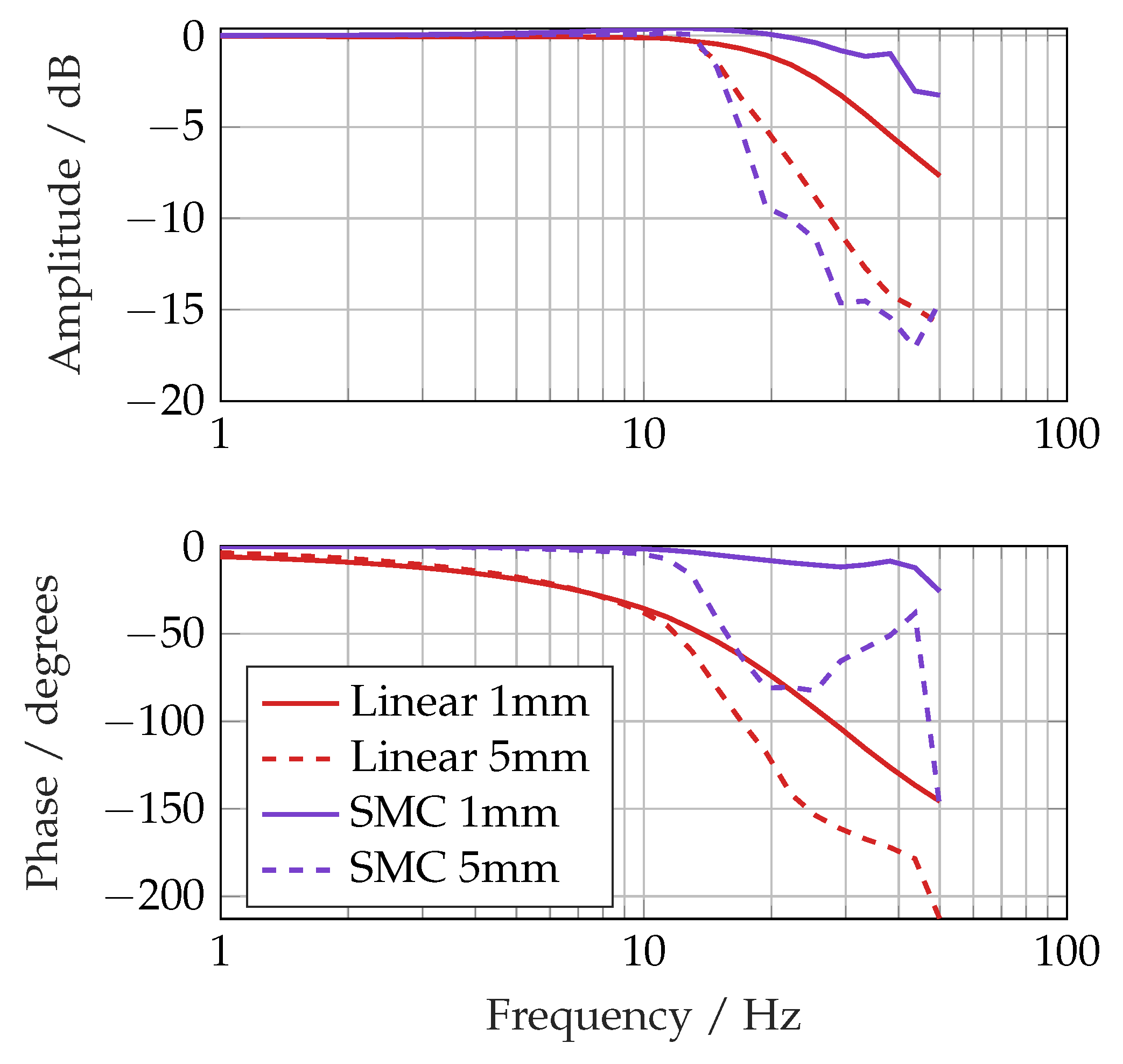
The frequency responses in Figure 9 demonstrate the performance advantage of the sliding mode controller, which had a bandwidth (−3 dB) of 44 Hz against 28 Hz with a 1 mm demand signal. The phase lag at a 1 mm amplitude was also far better, only reaching 25 ° at 50 Hz compared with 150 ° for the linear controller. The main reason for this is probably the nonlinear model-based feedforward terms in the control signal.

4.3. Robustness Comparison

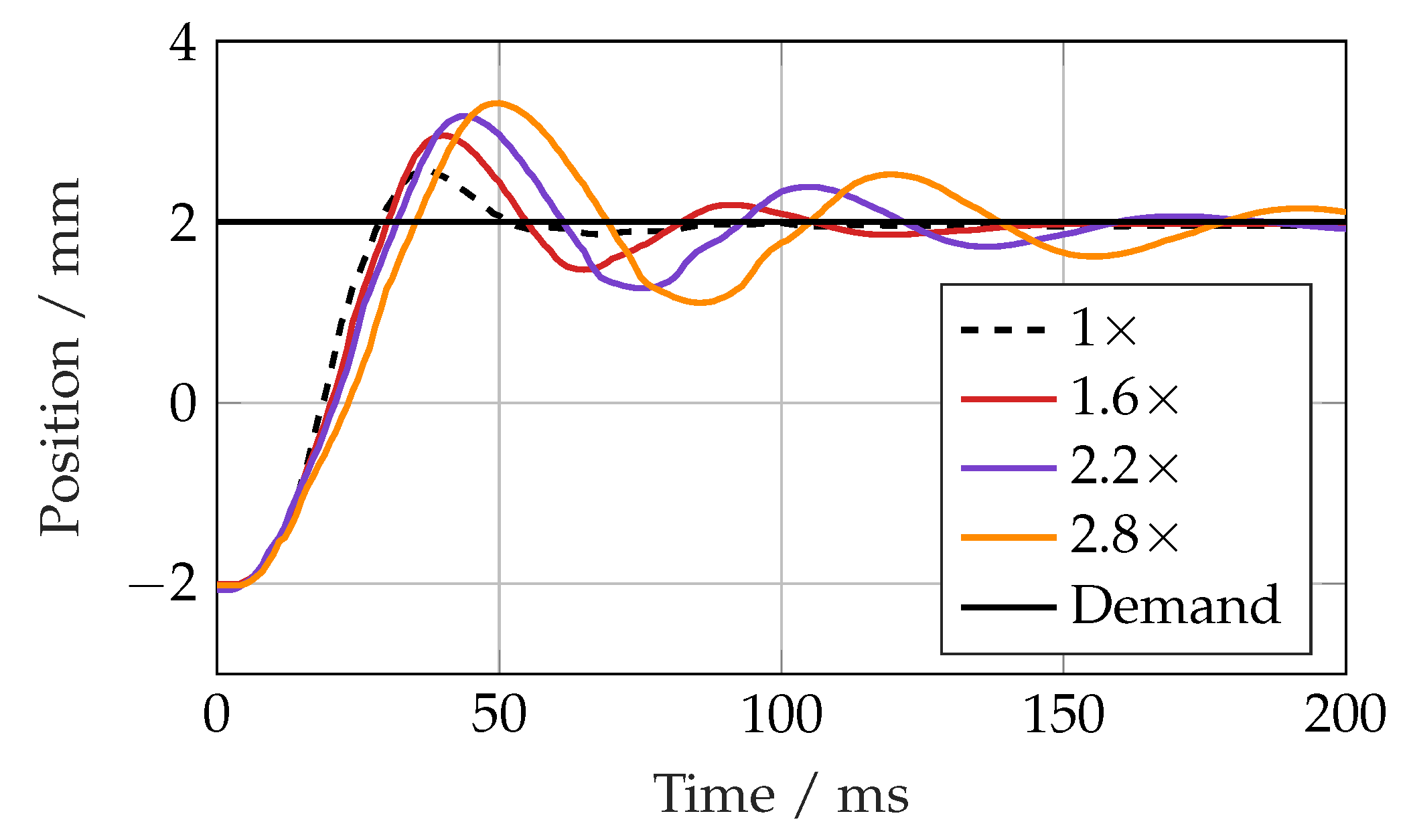
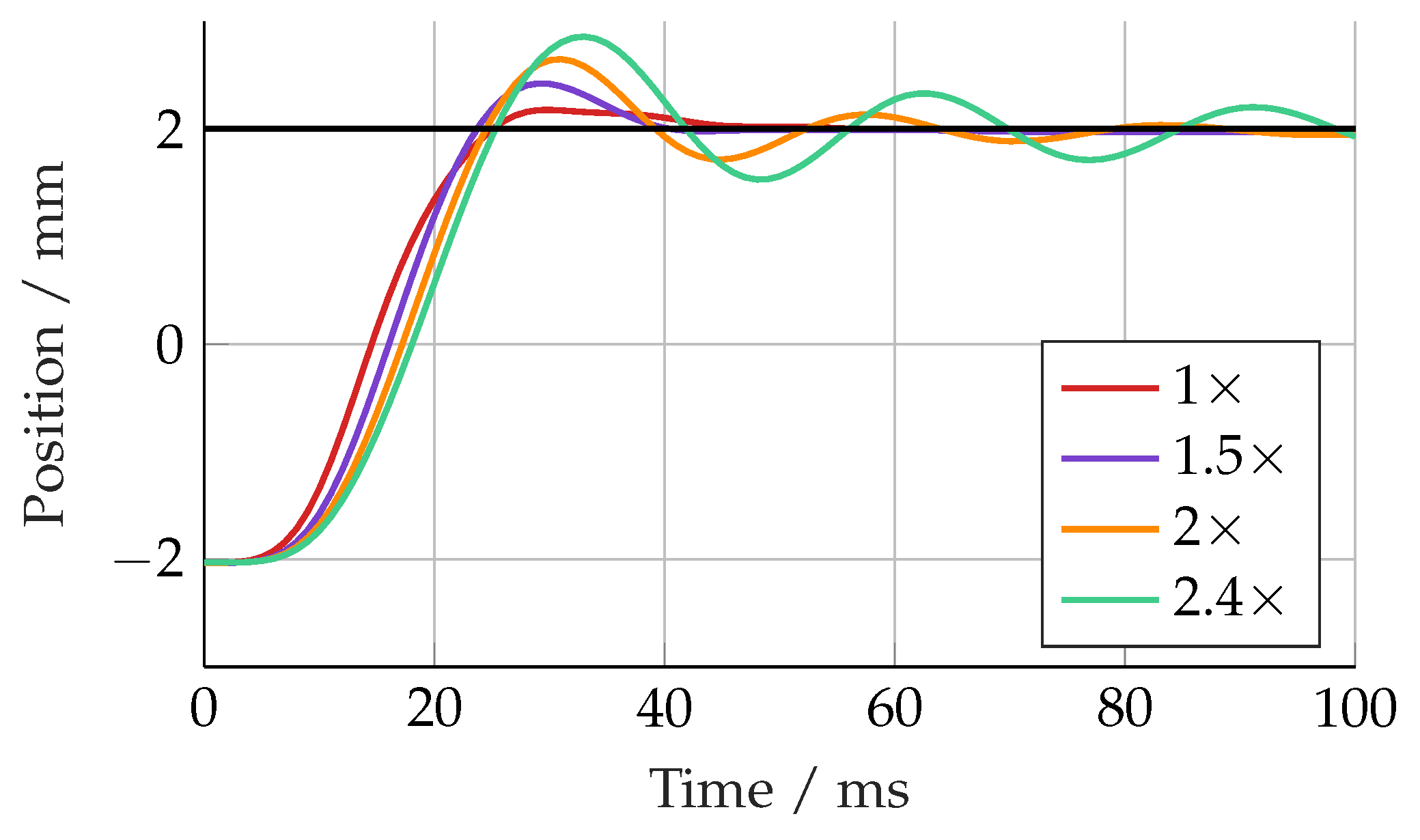
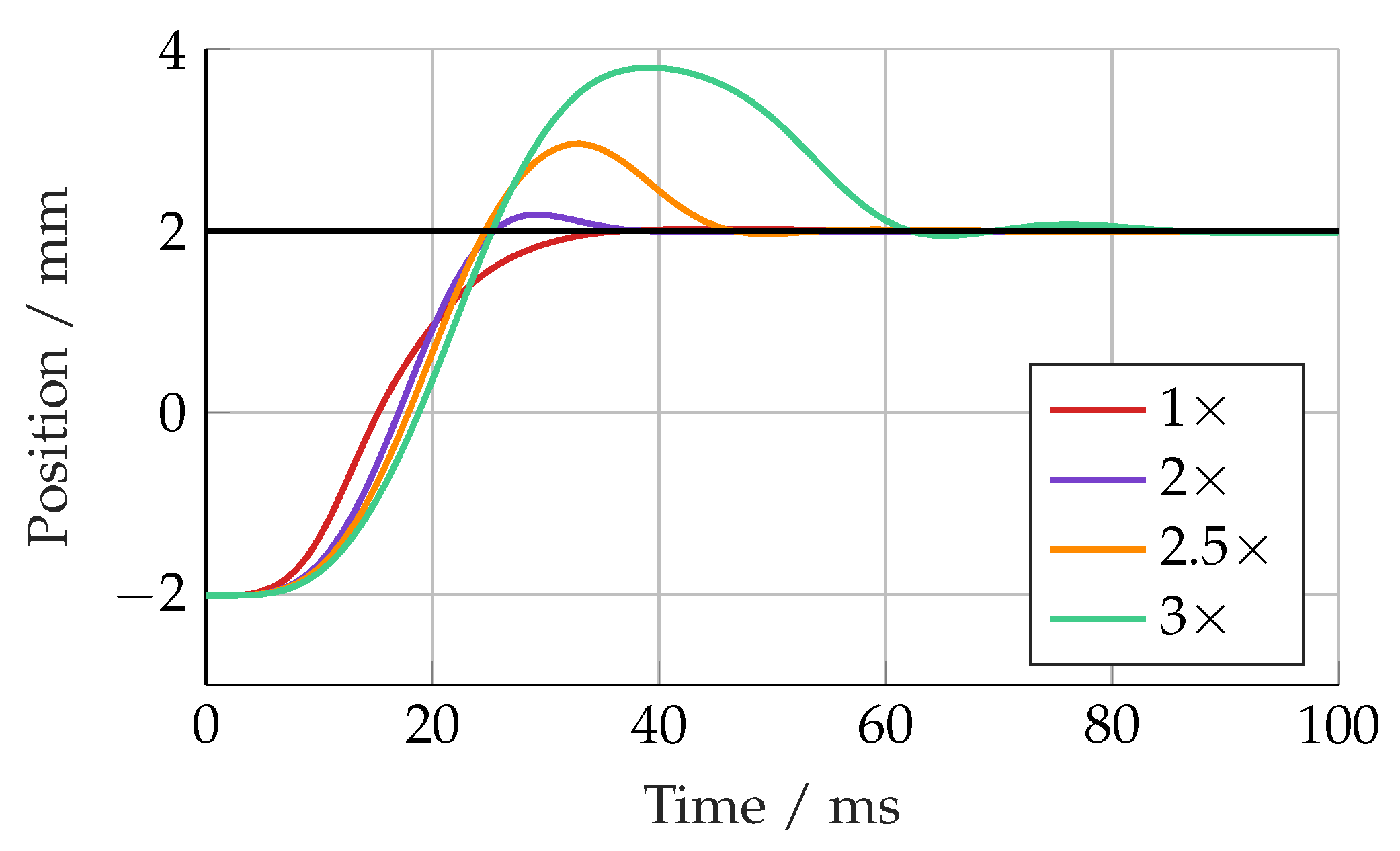
To test the robustness of the controllers, the bulk modulus and load mass were varied from their nominal values used during the control design. The step response of each controller with increasing mass is shown in Figure 10 and Figure 11. The linear controller response became more oscillatory with an increasing mass up to 2.5× (192 kg), at which point it became unstable. The SMC response was quite different, with increasing overshoot with an increasing load mass. Up to 3× the nominal load (231 kg), there was no sign of instability, but the overshoot was 1.8 mm, equivalent to 45%.

At smaller masses, both controllers were limited by the bandwidth of the valve. As the mass decreased, the actuator natural frequency approached that of the valve, making high-performance control extremely challenging. The linear controller and SMC were found to become unstable at 46 and 31 kg, respectively.

Altering the bulk modulus changed the stiffness of the actuator and therefore the natural frequency. Figure 12 shows the step response of each controller with 50% and 150% of the nominal bulk modulus value. The linear controller showed more deviation from the nominal response, particularly with a lower bulk modulus, causing some oscillations.

5. Experimental Set-Up

The ISA was mounted horizontally on a test bed attached to a pivoting beam which acted as the inertial load, as shown in Figure 13. The equivalent mass acting on the actuator due to the rotational inertia of the beam was 77 kg, which could be increased by adding mass to the end of the beam.

The hydraulic supply was a 24 lpm pump at a fixed supply pressure of 200 bar. The full circuit is shown in Figure 14.

The nested loop control architecture for the ISA onboard STM32F7 microcontroller-based controller is shown in Figure 15. Each of the current, spool and position loops operate at 10 kHz. Sensor data and other signals are streamed back to a host PC at 1 kHz for logging. An overview of the sensors is shown in

Table 4. ISA sensors.

Quantity	Sensor	Range	Resolution	Sample Rate
Piston Position	Absolute Encoder	100 mm	1 $\mathsf{\mu }$m	1 kHz
Spool position	Hall effect	$\pm 0.6$ mm	12-bit	10 kHz
Force	Strain Gauge	−5000 to 7260 N	12-bit	10 kHz
Pressures	Strain Gauge	0 to 200 bar	12-bit	10 kHz
Torque Motor Current	Current	$\pm 20$ mA	12-bit	10 kHz

. The analog sensors were sampled using the microcontroller’s 12 bit ADC.

6. Experimental Results

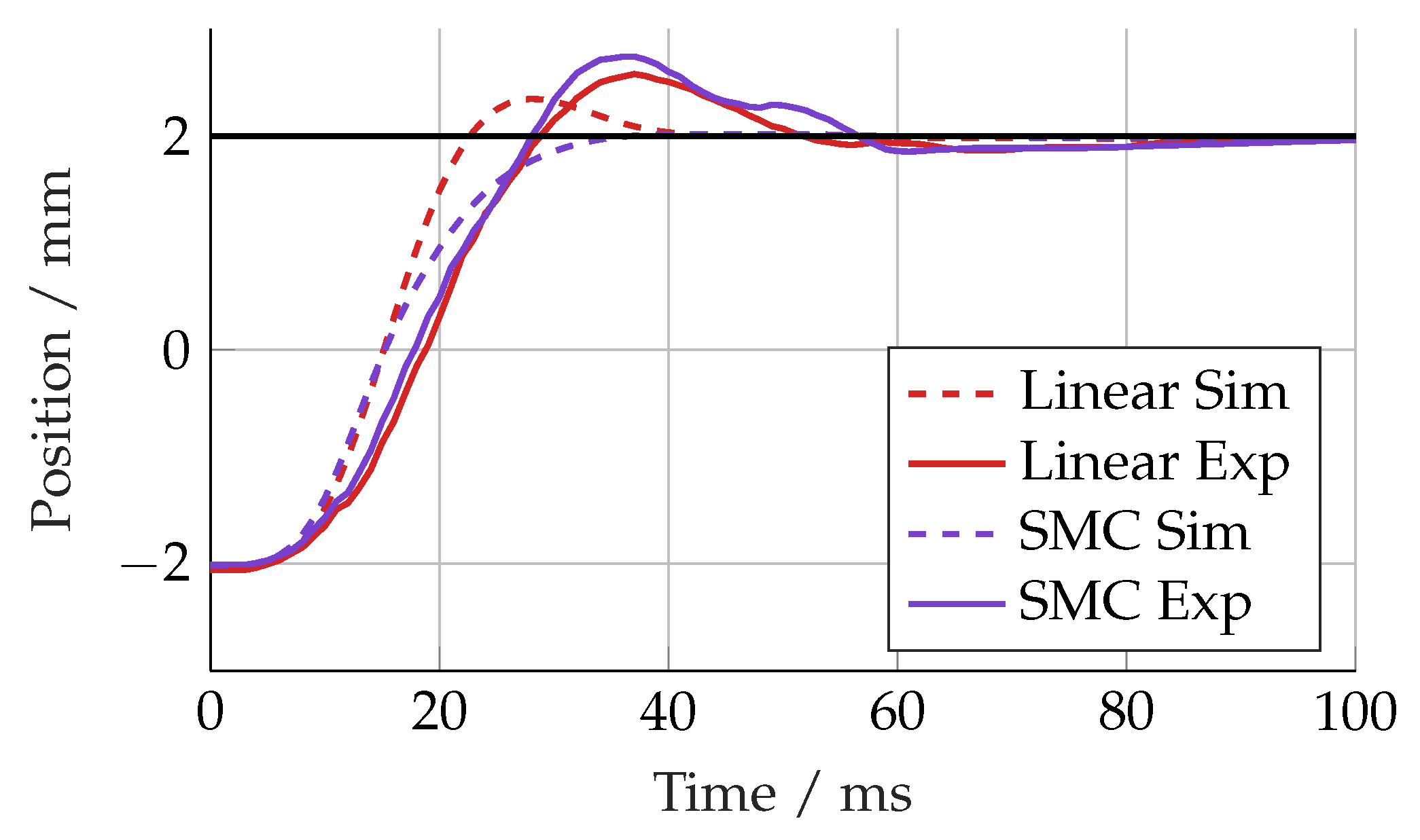
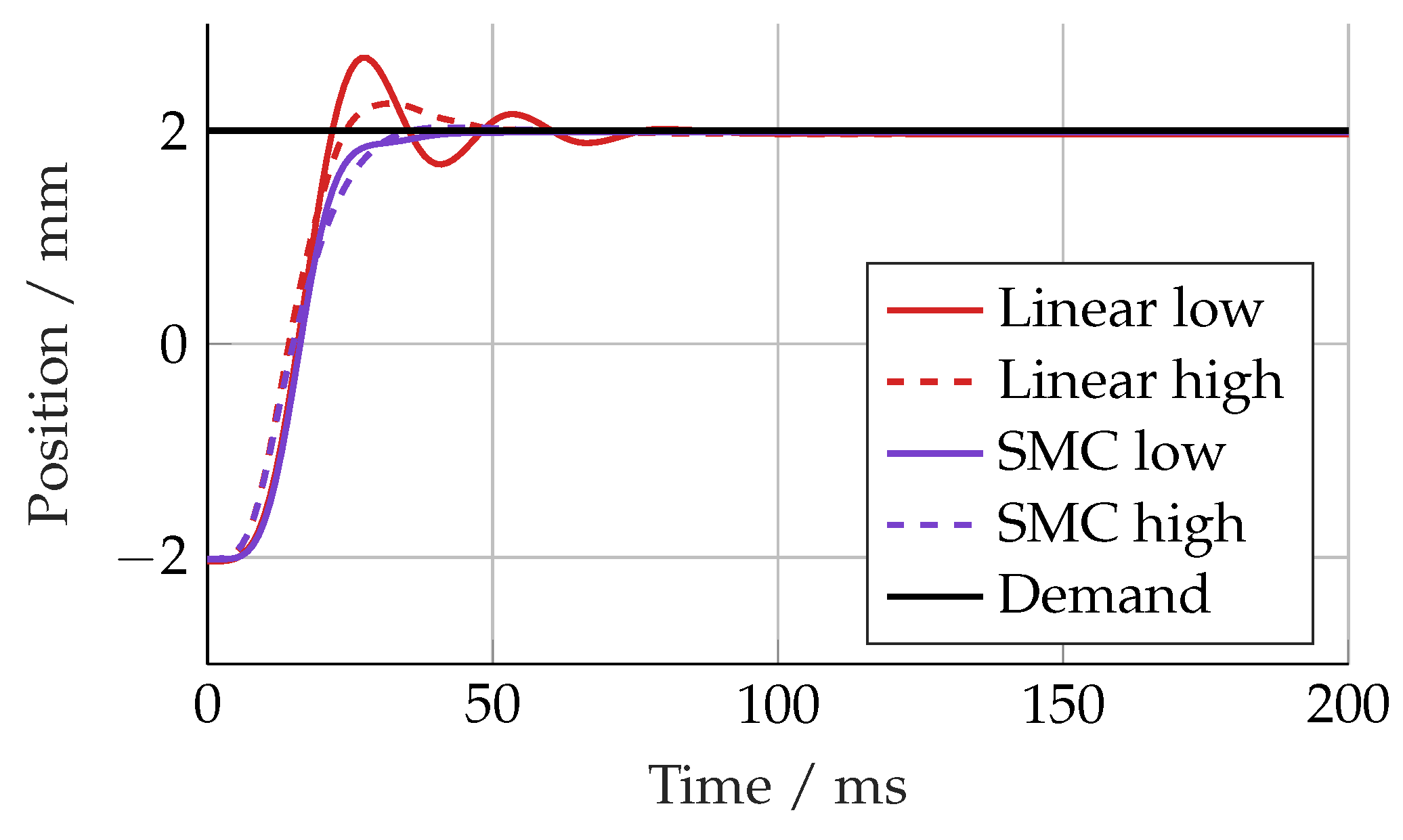
For the experimental testing, the same control parameters were used as for the simulations. The step response of each controller compared to the simulation results is shown in Figure 16. Each controller responded more slowly with a larger overshoot, suggesting either a parametric error or unmodelled dynamics in the simulation model.

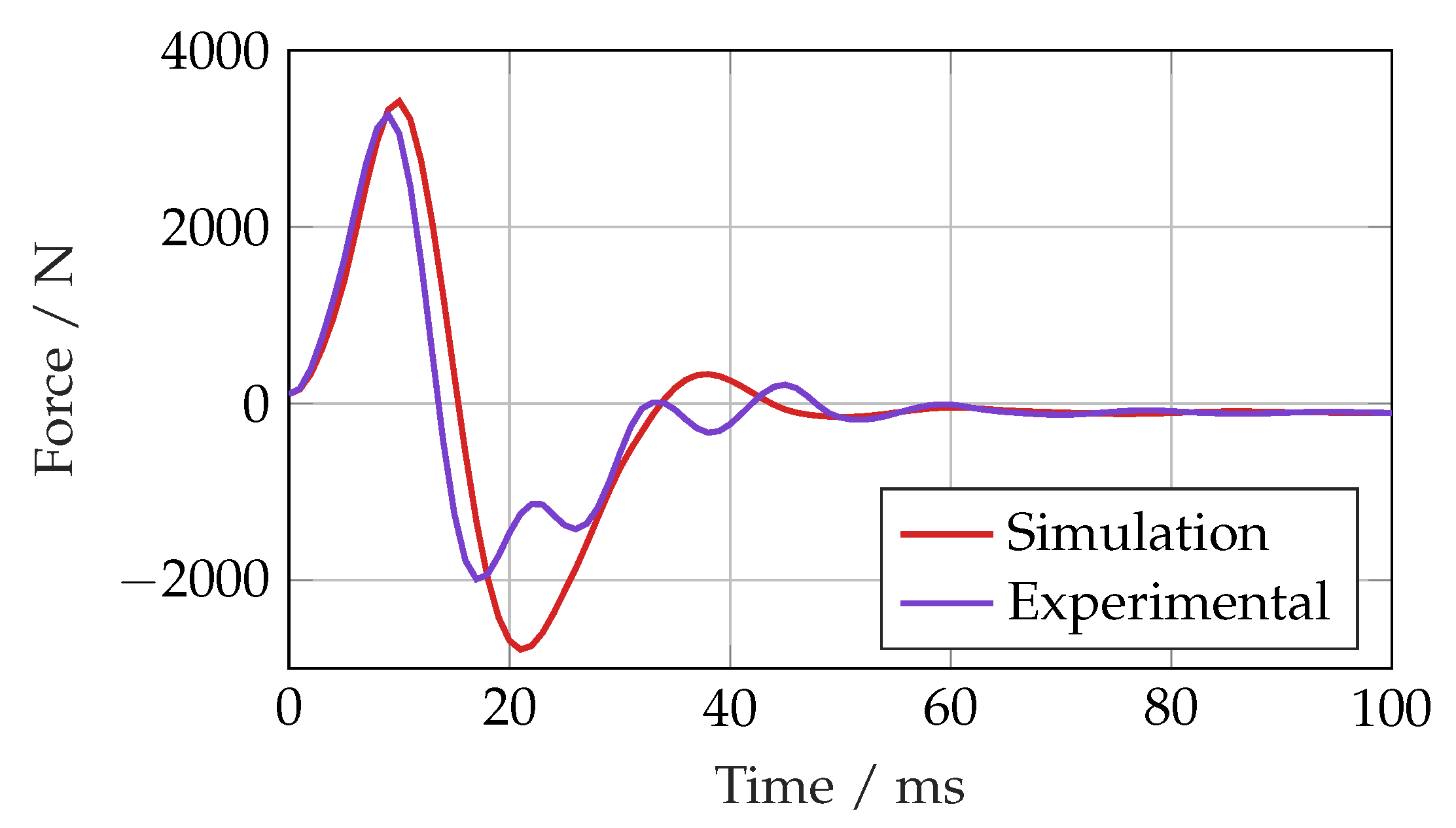
When observing the actuator force measurement during a step position demand for both the simulation and experiment with the SMC, shown in Figure 17, the responses were broadly similar, but there was clearly a higher frequency component to the experimental data. This would suggest that there is compliance between either the ISA and the test bed or the ISA and the load.

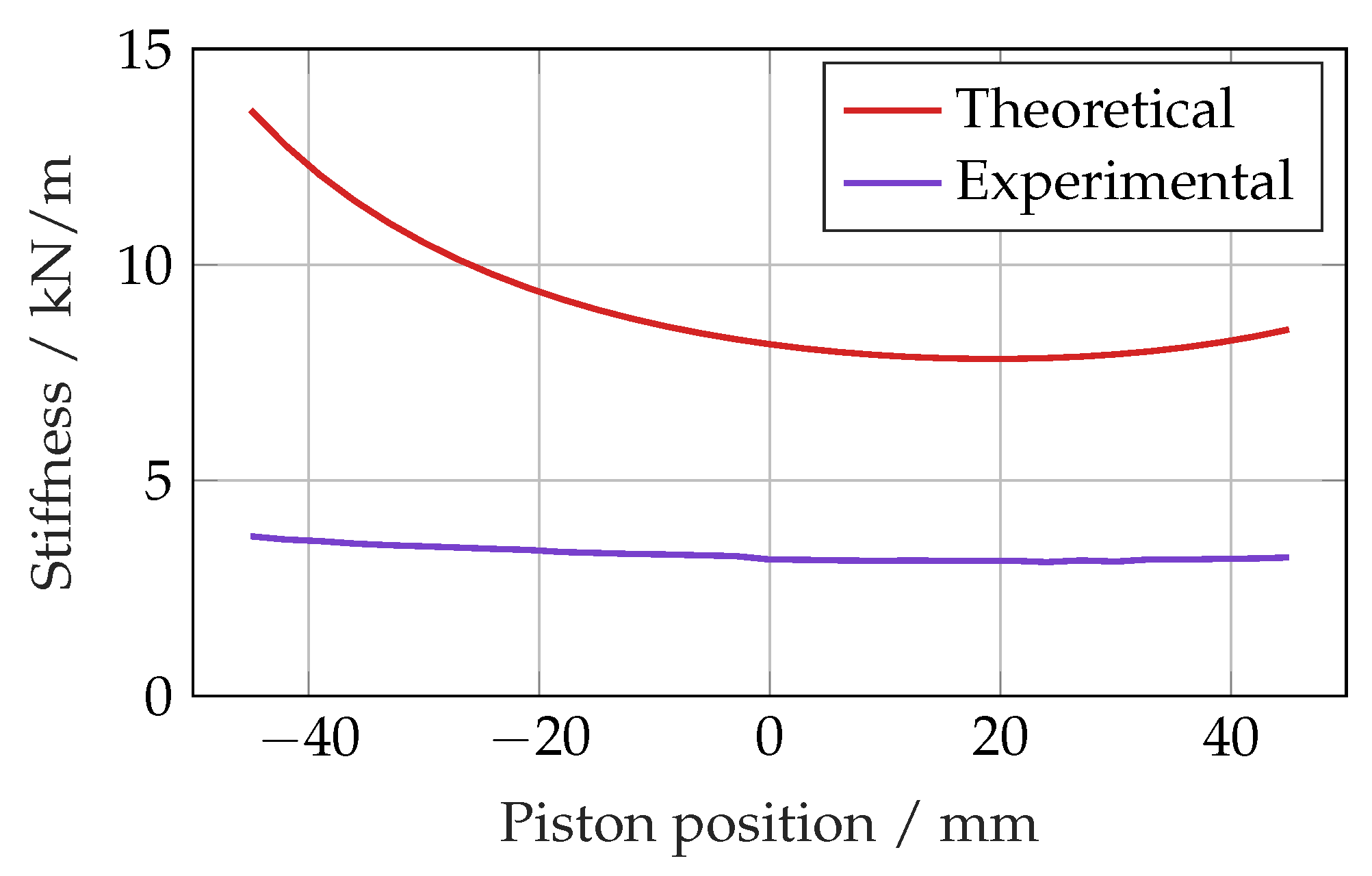
To determine the stiffness of the experimental set-up, the actuator was accelerated to a steady velocity and then suddenly stopped at a range of piston positions. The frequency of the resulting oscillation along with the load mass was used to determine the stiffness, shown in Figure 18, alongside the theoretical value. The experimentally determined stiffness was clearly much lower and approximately equivalent to a 4.65 kN/mm spring in series with the fluid in the actuator, likely due to compliance in the couplings between the ISA and the mounts.

The extra compliance explains the slower response compared with the simulation and may also explain the similar experimental response of each controller, with both limited by the reduced stiffness.

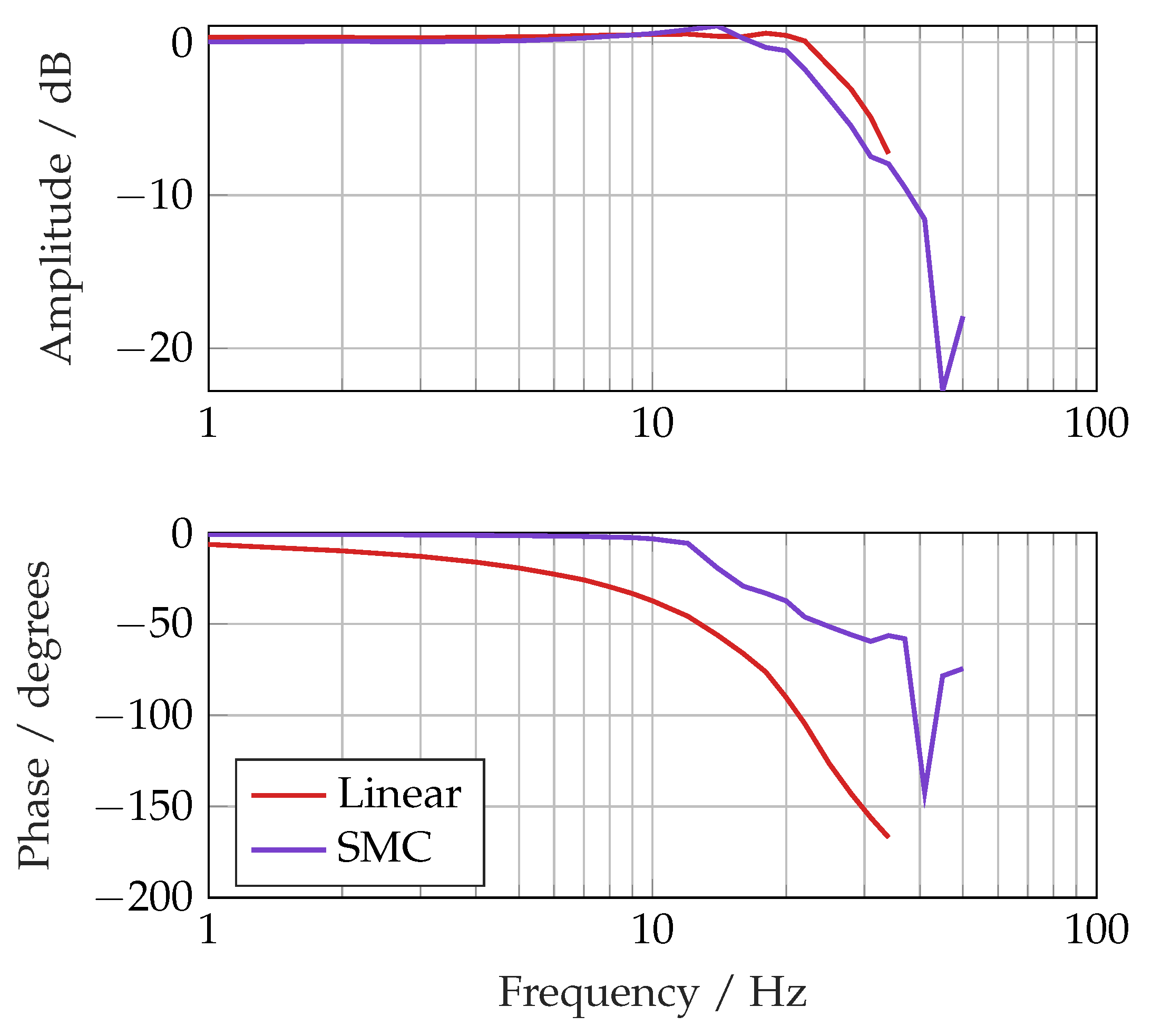
6.1. Performance Comparison

Figure 16 shows that the step responses of each controller were quite similar, as confirmed by the rise time, settling time and overshoot in

Table 5. Experimental performance metrics.

Metric	Linear	SMC
Rise Time (ms)	16	16
Settling Time (ms)	80	75
Overshoot (%)	14	19
Bandwidth (1 mm) (Hz)	19	38

. However, in the frequency domain, the SMC demonstrated better performance, with a $-{90}^{\circ }$ bandwidth of 38 Hz against 19 Hz for the linear controller with a 1 mm amplitude demand, shown in Figure 19. The good phase response can also be seen in the tracking performance at 10 Hz in Figure 20.

6.2. Robustness

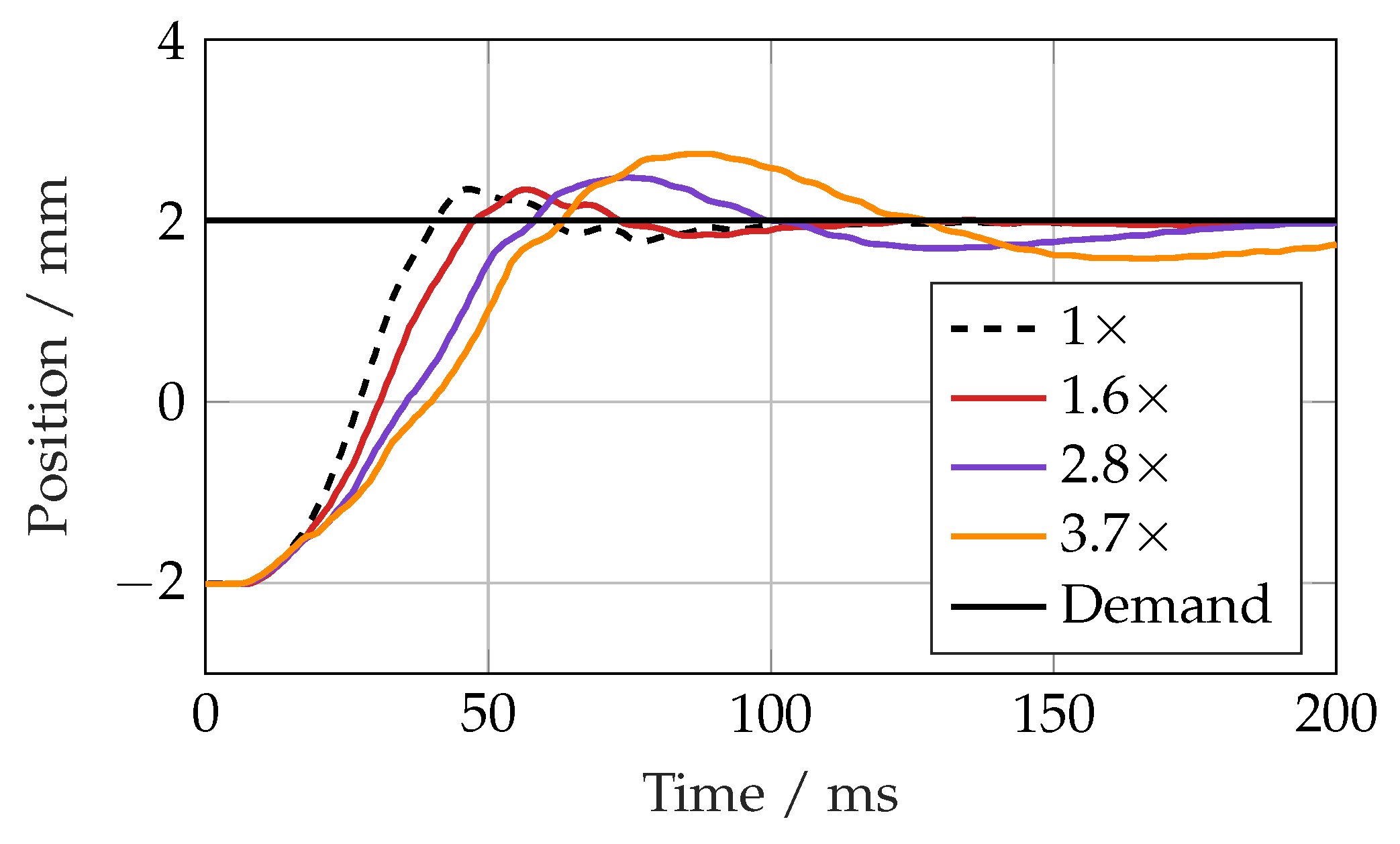
To test the robustness of each controller, extra mass was added to the beam to increase it from the nominal value of 77 kg. Similar to the simulation results, the linear controller Figure 21 showed increasing oscillations, whilst the SMC showed gradually increasing overshoot but no instability (Figure 22). At a 285 kg load mass (3.7 times the nominal amount), the linear controller became unstable, but the SMC response remained reasonable, albeit with an overshoot of 0.8 mm (20%).

7. Trajectory Filtering for SMC

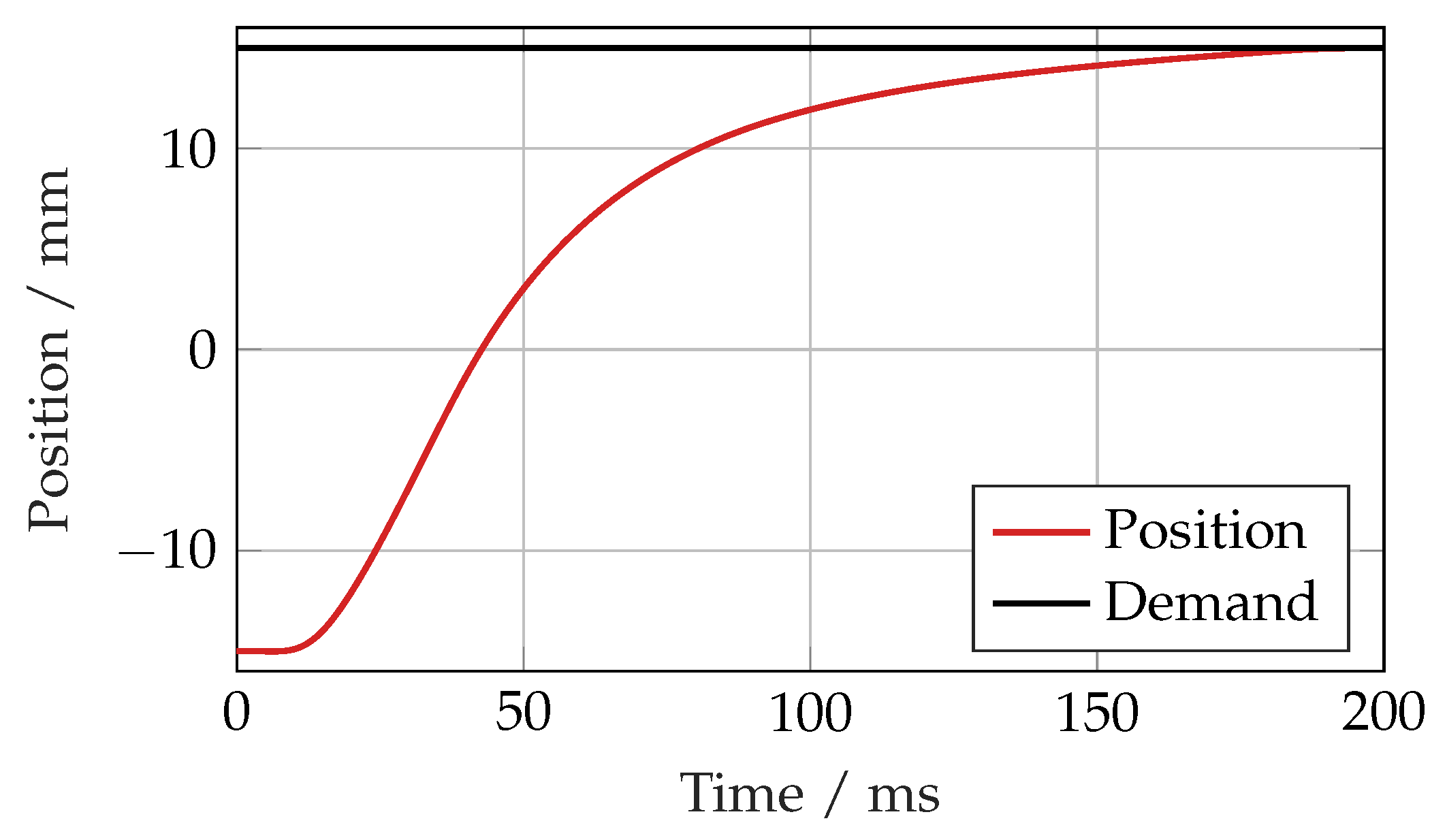
Whilst the SMC responded well to the demand signals presented thus far, it was found that particular unachievable demand signal trajectories such as a large step caused a rather slow response, as shown in the simulation results in Figure 23. This is likely to be due to a windup effect in the control signal caused by a sustained error between the position, velocity and acceleration and their desired values.

It is common in robotic systems to use a trajectory generator to create smooth and achievable demand signals for a robot joint to move from one position to another. Since the controller can take arbitrary input demands, a filter is placed before the controller to shape the demand such that it is within the capabilities of the actuator. A fourth-order linear filter is sufficient to create smooth position, velocity, acceleration and jerk signals required by the controller and implicitly contain these signals, as implemented in Figure 24.

With the filter configured as four matching poles at 10 Hz, the simulation response to a large step change then closely followed the trajectory sent to the controller, shown in Figure 25. However, this severely limited the performance of the controller to the chosen bandwidth of the filter. A better solution is to constrain the trajectory according the limits of the actuator.

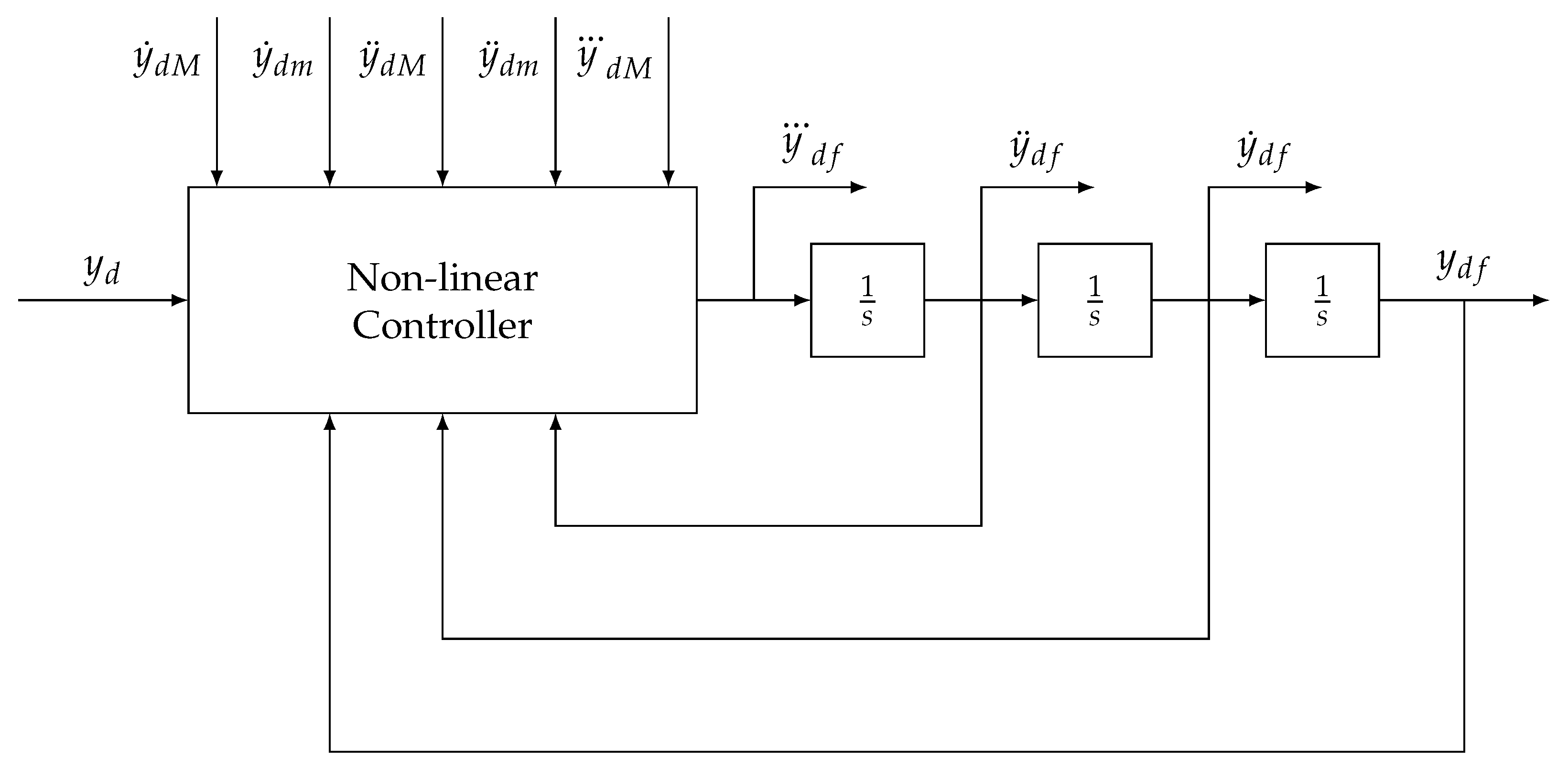
The approach to constrained trajectory generation proposed in [29] is able to consider asymmetric constraints to velocity and acceleration, as well as a jerk limit to filter an input demand and produce a position demand and its derivatives. The premise of the filter is a triple integrator system controlled by a nonlinear switching controller, shown in the block diagram in Figure 26.

The velocity and acceleration limits were chosen based on the known characteristics of the system. The velocity limit was set to 450 mm/s based on the maximum velocity of the actuator, which was found experimentally. The acceleration constraints were based on the minimum and maximum values that the piston pressures could take to supply the flow required to match the demand velocity. For example, if the filtered velocity demand is positive (${\dot{y}}_d>0$), then the flow into the piston side chamber is

$$Q_1={\dot{y}}_d{A}_1=K_v{A}_d\sqrt{P_s-P_1}$$

(42)

Assuming that the valve is open fully such that the flow area is $A_{dM}$, the maximum piston pressure $P_{1M}$ is given by

$$P_{1M}=P_s-{\left({\displaystyle \frac{{\dot{y}}_d{A}_1}{K_v{A}_{dM}}}\right)}^2$$

(43)

Similarly, the minimum pressure on the annulus side $P_{2m}$ is given by

$$P_{2m}=P_r+{\left({\displaystyle \frac{{\dot{y}}_d{A}_2}{K_v{A}_{cM}}}\right)}^2$$

(44)

The maximum acceleration ${\ddot{y}}_{dM}$ that the actuator can apply on the load mass is then

$${\ddot{y}}_{dM}={\displaystyle \frac{P_{1M}{A}_1-P_{2m}{A}_2}{m}}$$

(45)

If the demand velocity is negative, then the pressure drops across the spool lands are assumed to take their maximum values such that $P_2=0$ and $P_1=P_s$. The maximum acceleration is therefore given by

$${\ddot{y}}_{dM}={\displaystyle \frac{P_s{A}_1}{m}}$$

(46)

The minimum accelerations can be found in a similar manner, as summarised in

Table 6. Trajectory generation acceleration limits.

Direction	Minimum	Maximum
Extension	$-{\displaystyle \frac{P_s{A}_2}{m}}$	${\displaystyle \frac{P_{1M}{A}_1-P_{2m}{A}_2}{m}}$
Retraction	${\displaystyle \frac{P_{1m}{A}_1-P_{2M}{A}_2}{m}}$	${\displaystyle \frac{P_s{A}_1}{m}}$

.

The final limit, the maximum jerk, is symmetrical and fixed. There is a trade-off between a fast reponse and a chattering effect due to the switching nature of the filter, which can be tuned by the jerk limit. This is performed heuristically, with a value of 2 × 10⁶ (mm/s³) found to work well.

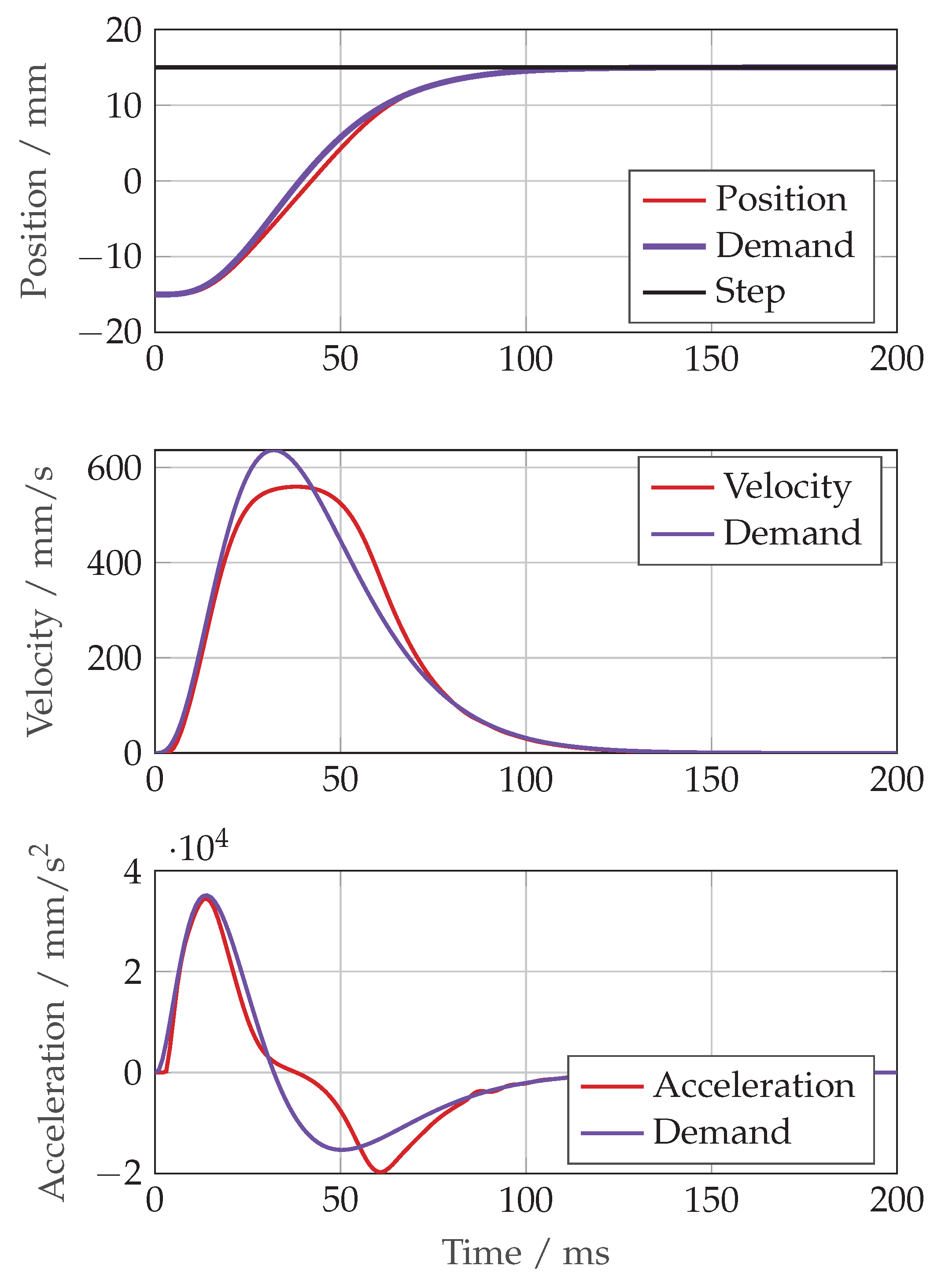
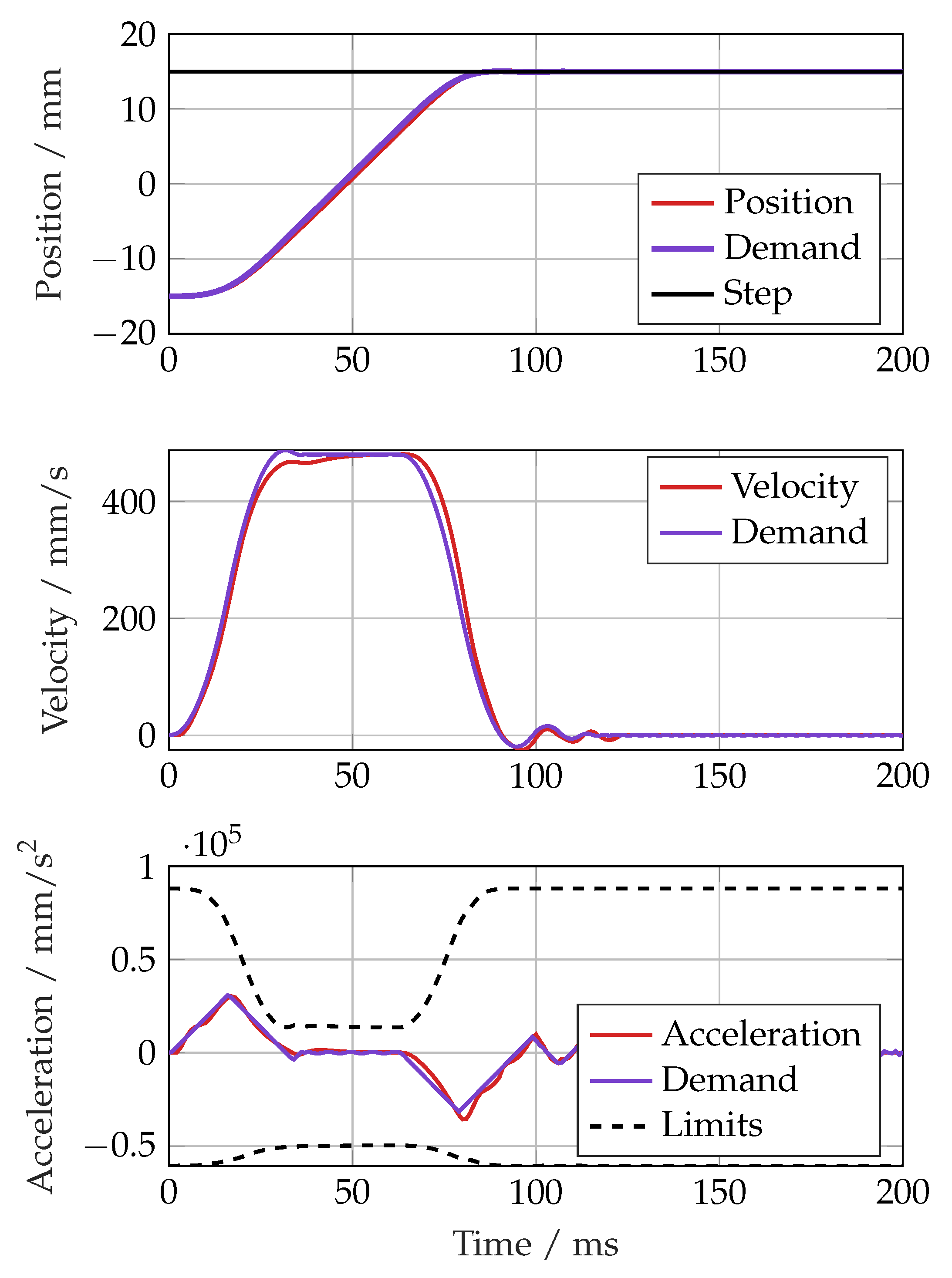
The same large step demand using the constrained trajectory generator is shown in Figure 27. The controller was able to effectively track the filtered trajectory and reached the position demand in 80 ms instead of 100 ms.

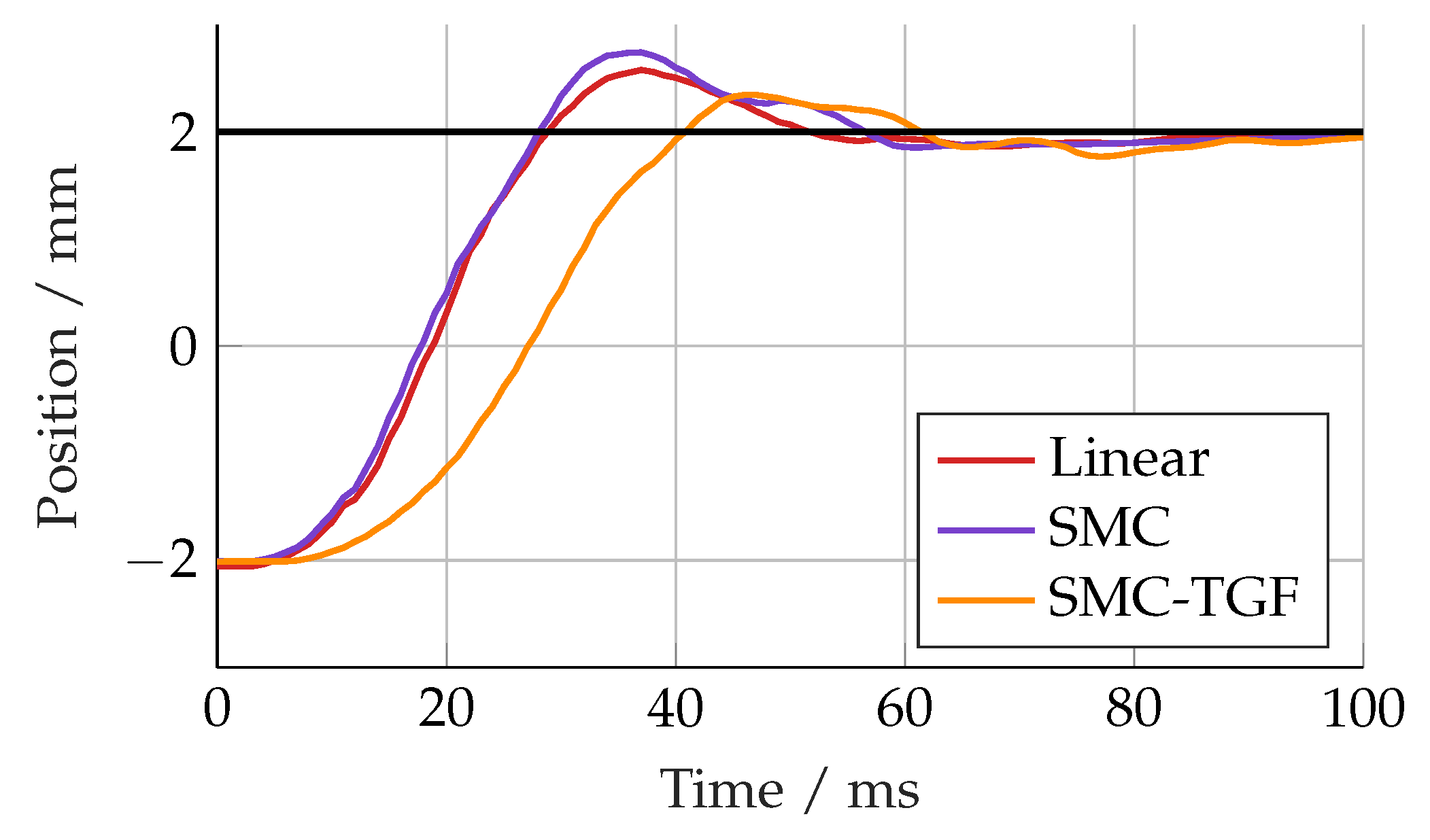
It was found experimentally that the switching component of the filter produced significant chattering in the response of the system. To rectify this, a linear filter with a cutoff frequency of 200 Hz was placed in series with the trajectory filter. This effectively removed the chattering, but the response was slower than the controller without any trajectory filtering, as shown in Figure 28.

8. Conclusions

This paper presented the application of a varying boundary layer sliding mode controller to a novel integrated hydraulic actuator known as the ISA. The controller was chosen for its robustness to parametric uncertainty and disturbances and its varying boundary layer for dealing with the typical issue of chattering without adding any extra tuning parameters. It has been shown to have a relatively simple tuning process, with variables B and G based on parametric uncertainty that can be determined based on engineering judgment, $\eta$ based on experimental trials, though its value is not at all critical, and a single dominant tuning parameter $\lambda$ that can be chosen to give a trade-off between performance and robustness.

The controller was shown to outperform a high-performance linear proportional plus acceleration feedback controller, particularly in terms of tracking performance, with low phase lag at high frequencies. The SMC also exhibited superior robustness to variations in the load mass and fluid bulk modulus.

The controller was found to exhibit undesirable behaviour for some unachievable trajectories. A velocity-, acceleration- and jerk-constrained trajectory filter was shown to effectively remove this behaviour, at the cost of a slightly slower response and some chattering for other types of trajectories. Experimentally, a linear filter was also required to remove the chattering effect.

The plant model developed includes both actuator and valve dynamics and a nonlinear spool flow characteristic. The experimental response of the system exhibited additional unmodelled dynamics due to compliance in the connections between the actuator and the load or test rig. Nevertheless, the model proved adequate for controller development.

The ISA has a novel low-leakage servovalve pilot stage, a consequence of which is that the valve has a relatively low bandwidth. Valve dynamics were neglected during the control design. This was found to limit performance at higher actuator-load natural frequencies, and exploring methods for including valve response in the design may help mitigate this issue.

The key objective of this work was to develop and investigate an actuator motion control method which is insensitive to load characteristics. Thus, it was not simply about designing a controller which gave a good closed-loop position response with known, fixed-load dynamics. As has been shown, a linear proportional controller with acceleration feedback can be tuned to give quite good performance when the load dynamics are fixed. It is critical that an actuator can be used in a new system with unmodelled or varying load characteristics without requiring significant time and expertise to retune or redesign the controller. This is usually achieved with electrical actuation using auto-tuning algorithms, but such algorithms have not been successfully developed for electrohydraulic actuators. Hence, despite their superior power density, application of electrohydraulic actuation to (for example) new robotic systems requires significant control design effort. The ISA used in this research, through its hardware integration of cylinder, valve, sensors and electronics, overcomes some of the challenges in applying electrohydraulic actuation. With the actuator and sensor characteristics well defined, it is only the load which is unknown, and the development of load-insensitive control becomes tractable. With just one major tuning parameter and good robustness to load variations demonstrated, the developed SMC is a promising step towards enabling ‘plug-and-play’ motion control for integrated high-performance electrohydraulic actuators, such as the ISA used in this work.