Intelligent Fault Diagnosis for Rotating Machinery via Transfer Learning and Attention Mechanisms: A Lightweight and Adaptive Approach
Abstract
1. Introduction
- Over-parameterization: Most TL models inherit cumbersome architectures, hindering edge-device deployment.
- Attention Mechanism Limitations: Existing attention modules (e.g., SE, CBAM) introduce excessive parameters or fail to capture cross-scale fault features effectively.
- Dynamic Adaptation: Few methods consider the real-time variability of mechanical signals, leading to suboptimal performance under non-stationary conditions.
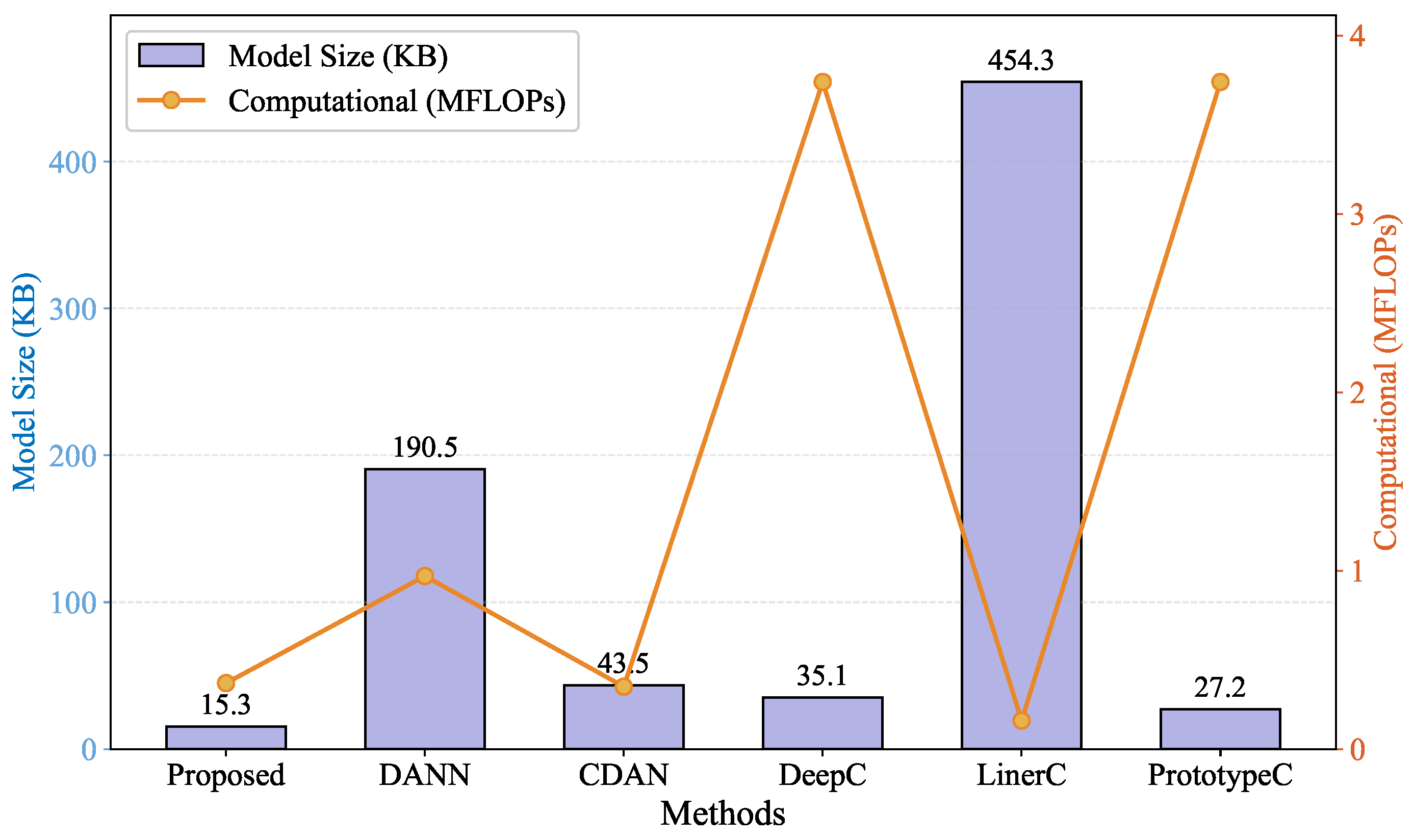
- Propose a lightweight CNN self attention feature extractor that reduces parameter overhead. (Our method demonstrates a superior performance compared to DANN and CDAN, reducing model size by 91.97% and 64.83%, respectively.) In addition, it effectively enhances discriminative feature learning, particularly under variable speed conditions.
- Design a pseudo-label domain adaptation strategy for transfer learning in response to distribution shifts caused by changes in rotational speed.
- Experimental validation on the CWRU, JNU, and SEU datasets, showing % higher accuracy than state-of-the-art methods under variable noise levels.
2. Related Work on TL for Rotating Machinery
2.1. Statistical Alignment Based Method
2.2. Adversarial Generative-Based Method
2.3. Pre-Training Strategies
3. Materials and Methods
3.1. Dataset Partitioning for Source and Target Domains in TL
3.2. CNN–Attention Model
- 1.
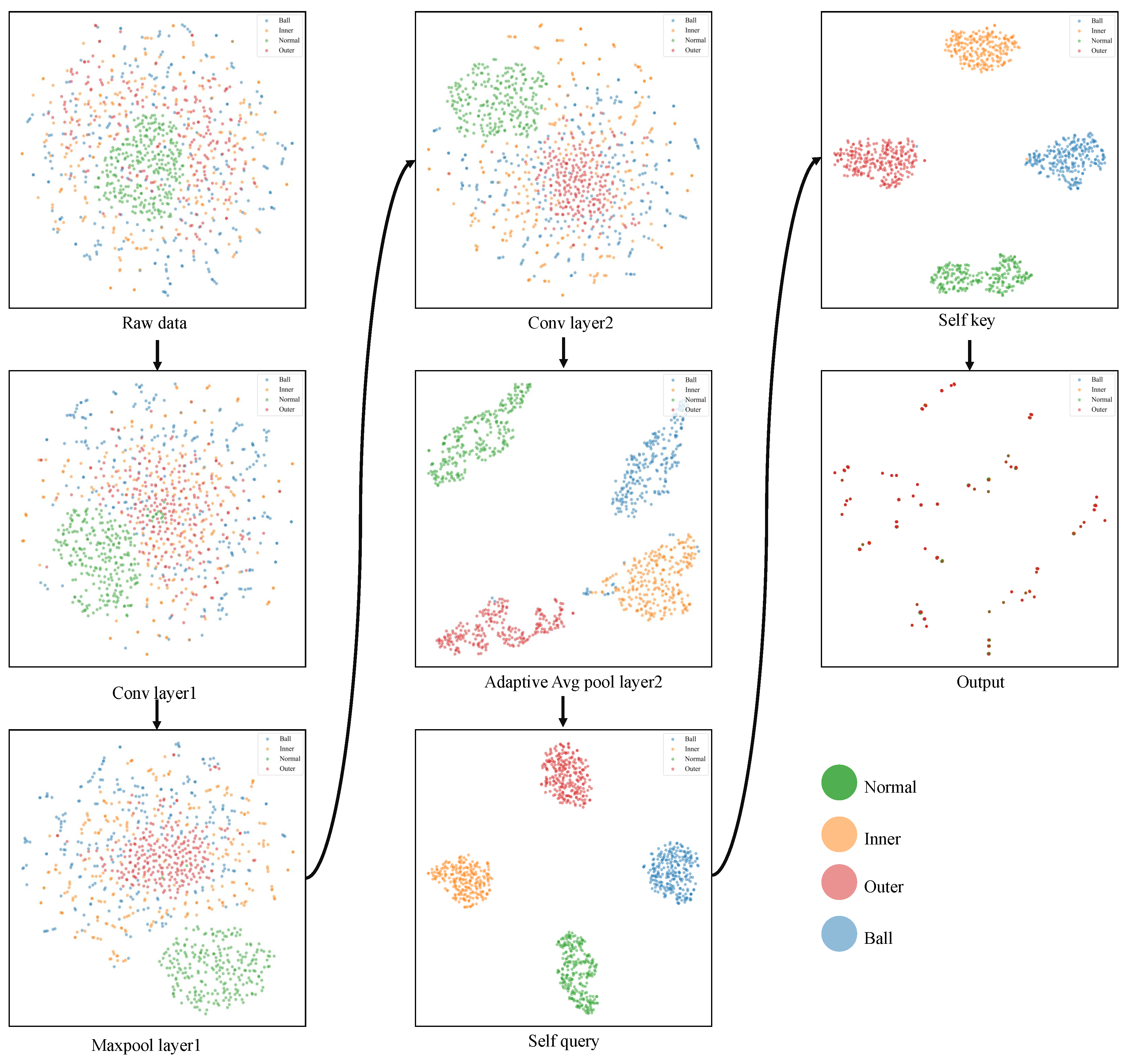
- To improve training efficiency while ensuring accuracy, a lightweight CNNs feature extractor was designed. This lightweight design reduces computational complexity by employing a streamlined convolutional layer structure, which consequently reduces training time [44]. The structure achieves high accuracy while converging faster, significantly accelerating the training process.The model extracts deeper features from the input raw signals and outputs them as feature vectors. The constructed model consists of two convolutional layers, each with two batch normalization layers to accelerate training efficiency and enhance generalization capability. Two ReLU activation functions enable the model to learn more complex feature relationships. The two convolution layers are Conv1 and Conv2 in Figure 1. Global average pooling is applied to obtain a feature vector from Conv2.
- 2.
- The classifier model incorporates the self-attention mechanism to dynamically adjust the extracted features. This allows the model to focus more on the feature regions useful for classification, thereby enhancing detection performance. Given the feature vector Z as input, the input to the classifier is the feature vector, which is linearly transformed to obtain and K, as shown in Equations (5) and (6) below:where the input of the classifier is , and the feature vector is .Therefore, the attention weight coefficient is computed asNext, the feature vector is weighted using the attention weight coefficient:Finally, a fully connected layer outputs the logits for the 4 categories, which are used to identify fault types. The convolutional layers, linear layers, and batch normalization of the model are then initialized appropriately to ensure the stability of the training process.Compared to Squeeze-and-Excitation (SE) and Convolutional Block Attention Module (CBAM), the scaled dot-product attention mechanism offers several advantages for fault diagnosis in rotating machinery. First, it dynamically captures long-range dependencies in vibration signals without introducing excessive parameters, which is critical for lightweight models. SE and CBAM, while effective in vision tasks, often fail to model cross-scale fault features efficiently due to their localized attention mechanisms. Second, the dot-product attention explicitly computes interactions between all feature positions, enabling the model to focus on discriminative fault patterns under variable speed conditions. This is particularly important for bearing faults, where fault signatures may span multiple frequency bands. Finally, the self-attention mechanism assigns adaptive weights to features according to their relevance to the fault type, which markedly diminishes the need for manual feature engineering and overcomes a principal shortcoming of traditional methods.
3.3. Loss Function and Fine-Tuning Strategy
- CNN, serving as the fundamental feature extractor, employed to discern local spatio-temporal patterns within the raw vibration signals.
- Self-attention dynamically assigns feature importance to address the issue of key feature drift under variable operating conditions.
- The pseudo-label method leverages the source-domain model to generate pseudo-labels for the target domain, thereby addressing the unsupervised domain adaptation problem.
- MMD loss aligns the feature distributions of the source and target domains by employing a multi-kernel radial basis function metric.
- Focal loss facilitates equilibrium in the label distribution to mitigate model overfitting.
4. Experiments and Discussion
4.1. Dataset Description
4.2. Experimental Setup
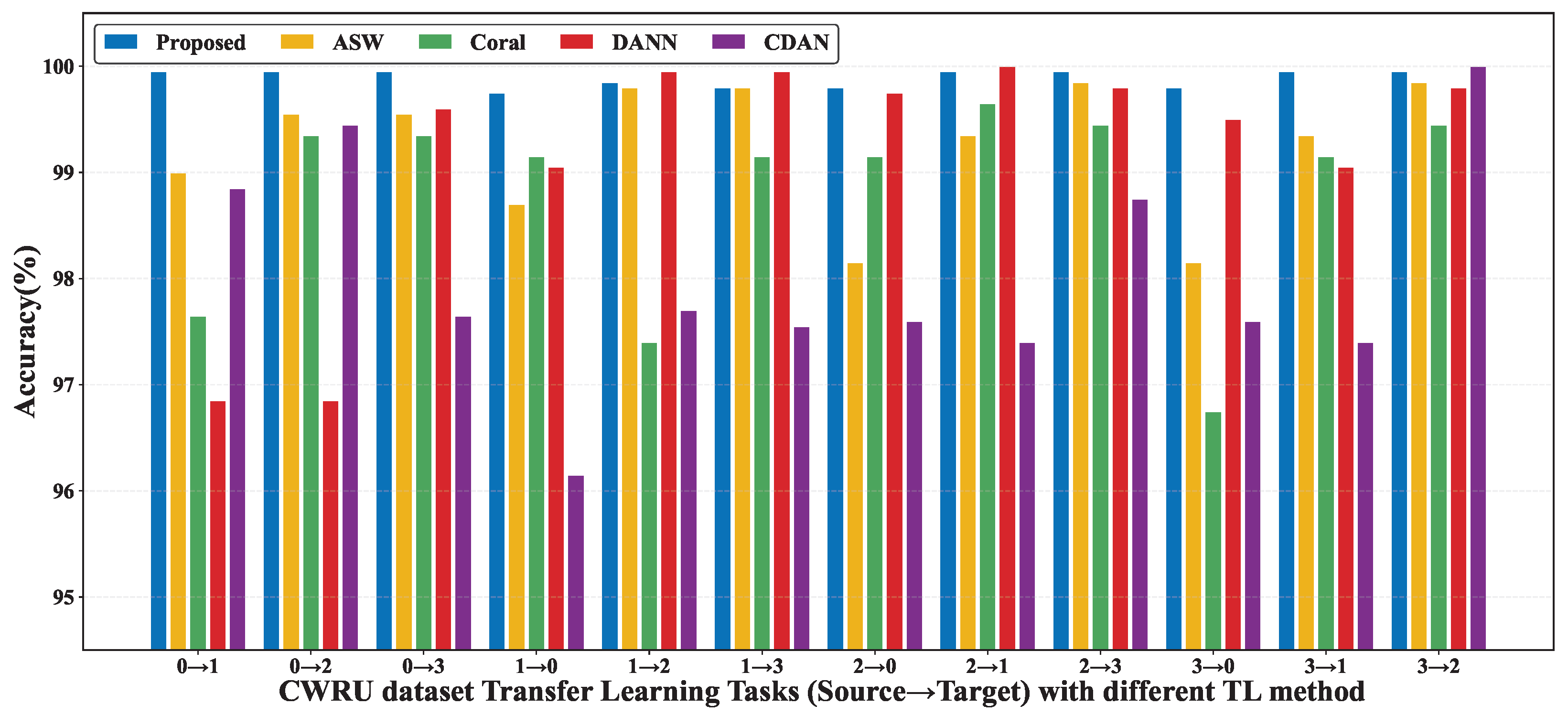
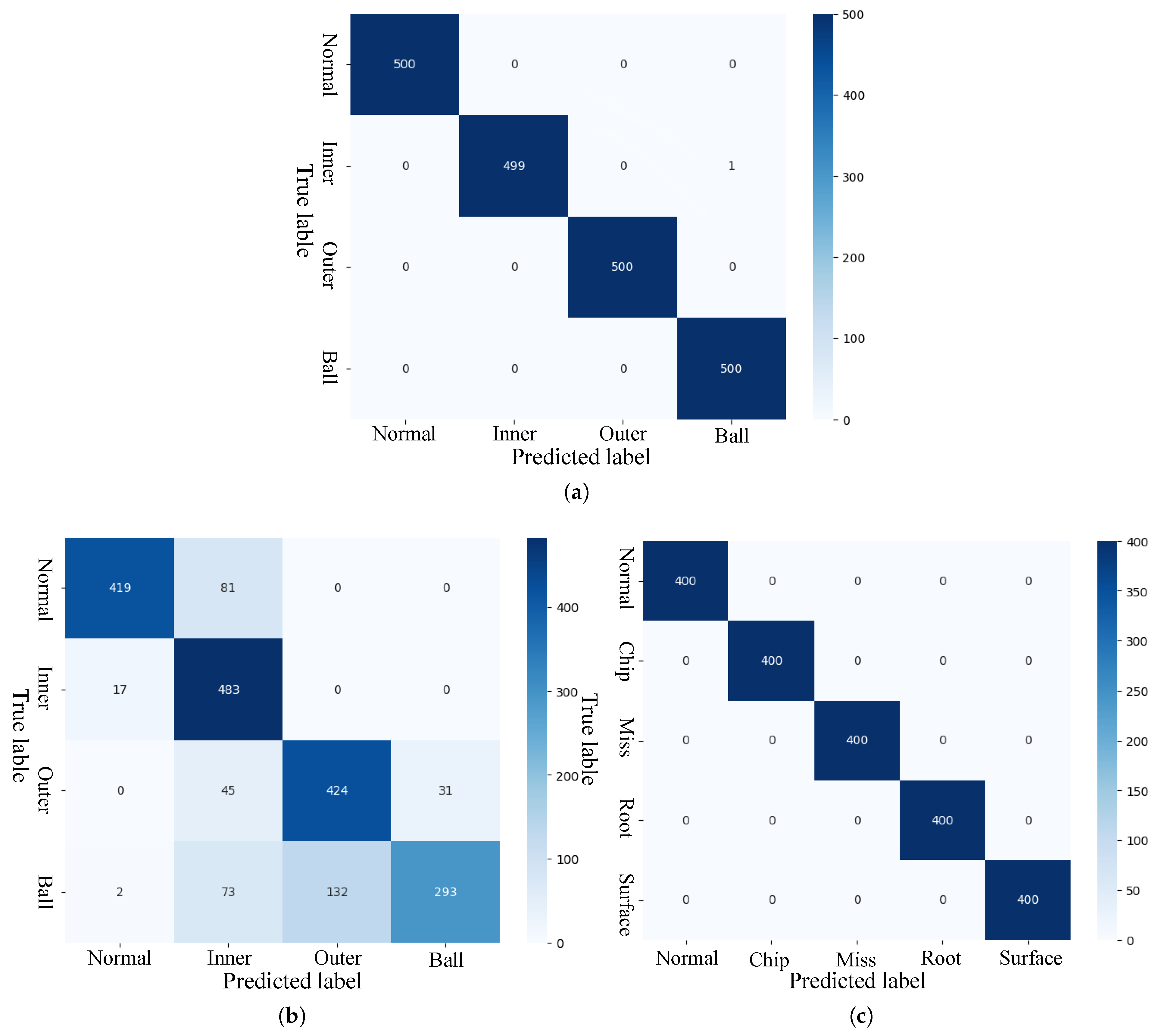
4.3. Bearing Fault Diagnosis Under Various Working Conditions
4.4. Comparison of Training Efficiency of Different Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Converso, G.; Gallo, M.; Murino, T.; Vespoli, S. Predicting Failure Probability in Industry 4.0 Production Systems: A Workload-Based Prognostic Model for Maintenance Planning. Appl. Sci. 2023, 13, 1938. [Google Scholar] [CrossRef]
- Fu, C.; Sinou, J.J.; Zhu, W.; Lu, K.; Yang, Y. A state-of-the-art review on uncertainty analysis of rotor systems. Mech. Syst. Signal Process. 2023, 183, 109619. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, L.; Shu, L.; Jing, X.; Zhang, Z. SILF Dataset: Fault Dataset for Solar Insecticidal Lamp Internet of Things Node. Sensors 2025, 25, 2808. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Jiang, B.; Pillay, P.; Rakheja, S. A Comprehensive Review on Signal-Based and Model-Based Condition Monitoring of Wind Turbines: Fault Diagnosis and Lifetime Prognosis. Proc. IEEE 2022, 110, 754–806. [Google Scholar] [CrossRef]
- Aqamohammadi, A.R.; Niknam, T.; Shojaeiyan, S.; Siano, P.; Dehghani, M. Deep Neural Network with Hilbert–Huang Transform for Smart Fault Detection in Microgrid. Electronics 2023, 12, 499. [Google Scholar] [CrossRef]
- Hu, C.; Wu, J.; Sun, C.; Chen, X.; Nandi, A.K.; Yan, R. Unified Flowing Normality Learning for Rotating Machinery Anomaly Detection in Continuous Time-Varying Conditions. IEEE Trans. Cybern. 2025, 55, 221–233. [Google Scholar] [CrossRef] [PubMed]
- Jeong, E.; Yang, J.H.; Lim, S.C. Deep Neural Network for Valve Fault Diagnosis Integrating Multivariate Time-Series Sensor Data. Actuators 2025, 14, 70. [Google Scholar] [CrossRef]
- Jung, H.; Choi, S.; Lee, B. Rotor Fault Diagnosis Method Using CNN-Based Transfer Learning with 2D Sound Spectrogram Analysis. Electronics 2023, 12, 480. [Google Scholar] [CrossRef]
- Huang, D.; Zhang, W.A.; Guo, F.; Liu, W.; Shi, X. Wavelet Packet Decomposition-Based Multiscale CNN for Fault Diagnosis of Wind Turbine Gearbox. IEEE Trans. Cybern. 2023, 53, 443–453. [Google Scholar] [CrossRef]
- Gawde, S.; Patil, S.; Kumar, S.; Kamat, P.; Kotecha, K.; Abraham, A. Multi-fault diagnosis of Industrial Rotating Machines using Data-driven approach: A review of two decades of research. Eng. Appl. Artif. Intell. 2023, 123, 106139. [Google Scholar] [CrossRef]
- Nie, L.; Ren, Y.; Wu, R.; Tan, M. Sensor Fault Diagnosis, Isolation, and Accommodation for Heating, Ventilating, and Air Conditioning Systems Based on Soft Sensor. Actuators 2023, 12, 389. [Google Scholar] [CrossRef]
- Guo, C.; Sun, Y.; Yu, R.; Ren, X. Deep Causal Disentanglement Network with Domain Generalization for Cross-Machine Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2025, 74, 3512616. [Google Scholar] [CrossRef]
- Younesi, A.; Ansari, M.; Fazli, M.; Ejlali, A.; Shafique, M.; Henkel, J. A Comprehensive Survey of Convolutions in Deep Learning: Applications, Challenges, and Future Trends. IEEE Access 2024, 12, 41180–41218. [Google Scholar] [CrossRef]
- LI, G.; GENG, H.; XIE, F.; XU, C.; XU, Z. Ensemble Deep Transfer Learning Method for Fault Diagnosis of Waterjet Pump Under Variable Working Conditions. Ship Boat 2025, 36, 103. [Google Scholar] [CrossRef]
- Sun, B.; Saenko, K. Deep coral: Correlation alignment for deep domain adaptation. In Proceedings of the Computer Vision–ECCV 2016 Workshops, Amsterdam, The Netherlands, 8–10, 15–16 October 2016; Proceedings, Part III 14. Springer: Cham, Switzerland, 2016; pp. 443–450. [Google Scholar] [CrossRef]
- Borgwardt, K.M.; Gretton, A.; Rasch, M.J.; Kriegel, H.P.; Schölkopf, B.; Smola, A.J. Integrating structured biological data by Kernel Maximum Mean Discrepancy. Bioinformatics 2006, 22, e49–e57. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Liang, W.; He, F. Research on rolling bearing fault diagnosis based on parallel depthwise separable ResNet neural network with attention mechanism. Expert Syst. Appl. 2025, 286, 128105. [Google Scholar] [CrossRef]
- Cui, J.; Li, Y.; Zhang, Q.; Wang, Z.; Du, W.; Wang, J. Multi-layer adaptive convolutional neural network unsupervised domain adaptive bearing fault diagnosis method. Meas. Sci. Technol. 2022, 33, 085009. [Google Scholar] [CrossRef]
- An, Y.; Zhang, K.; Chai, Y.; Zhu, Z.; Liu, Q. Gaussian Mixture Variational-Based Transformer Domain Adaptation Fault Diagnosis Method and Its Application in Bearing Fault Diagnosis. IEEE Trans. Ind. Informatics 2024, 20, 615–625. [Google Scholar] [CrossRef]
- Ding, P.; Jia, M.; Ding, Y.; Zhao, X. Statistical Alignment-Based Metagated Recurrent Unit for Cross-Domain Machinery Degradation Trend Prognostics Using Limited Data. IEEE Trans. Instrum. Meas. 2021, 70, 3511212. [Google Scholar] [CrossRef]
- Chen, X.; Shao, H.; Xiao, Y.; Yan, S.; Cai, B.; Liu, B. Collaborative fault diagnosis of rotating machinery via dual adversarial guided unsupervised multi-domain adaptation network. Mech. Syst. Signal Process. 2023, 198, 110427. [Google Scholar] [CrossRef]
- Kim, T.; Chai, J. Fault Diagnosis of Bearings with the Common-Domain Data. IEEE Access 2022, 10, 45457–45470. [Google Scholar] [CrossRef]
- Xiao, H.; Dong, L.; Wang, W.; Ogai, H. Distribution Sub-Domain Adaptation Deep Transfer Learning Method for Bridge Structure Damage Diagnosis Using Unlabeled Data. IEEE Sensors J. 2022, 22, 15258–15272. [Google Scholar] [CrossRef]
- Zhang, J.; Pei, G.; Zhu, X.; Gou, X.; Deng, L.; Gao, L.; Liu, Z.; Ni, Q.; Lin, J. Diesel engine fault diagnosis for multiple industrial scenarios based on transfer learning. Measurement 2024, 228, 114338. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, T. Deep Convolutional Neural Network Using Transfer Learning for Fault Diagnosis. IEEE Access 2021, 9, 43889–43897. [Google Scholar] [CrossRef]
- Farag, M.M. Towards a Standard Benchmarking Framework for Domain Adaptation in Intelligent Fault Diagnosis. IEEE Access 2025, 13, 24426–24453. [Google Scholar] [CrossRef]
- Tang, S.; Ma, J.; Yan, Z.; Zhu, Y.; Khoo, B.C. Deep transfer learning strategy in intelligent fault diagnosis of rotating machinery. Eng. Appl. Artif. Intell. 2024, 134, 108678. [Google Scholar] [CrossRef]
- Ibrahim, A.; Anayi, F.; Packianather, M. New Transfer Learning Approach Based on a CNN for Fault Diagnosis. Eng. Proc. 2022, 24, 16. [Google Scholar] [CrossRef]
- Zhu, C.; Lin, W.; Zhang, H.; Cao, Y.; Fan, Q.; Zhang, H. Research on a Bearing Fault Diagnosis Method Based on an Improved Wasserstein Generative Adversarial Network. Machines 2024, 12, 587. [Google Scholar] [CrossRef]
- Shakiba, F.M.; Shojaee, M.; Azizi, S.M.; Zhou, M. Transfer Learning for Fault Diagnosis of Transmission Lines. arXiv 2022, arXiv:2201.08018. [Google Scholar] [CrossRef]
- Wang, Q.; Michau, G.; Fink, O. Domain Adaptive Transfer Learning for Fault Diagnosis. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Paris), Paris, France, 2–5 May 2019; pp. 279–285. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Wang, Y.; Zhou, Y.; Jia, L. Machinery Fault Diagnosis for Imbalanced Samples via Coupled Generative Adversarial Networks. In Proceedings of the 2024 43rd Chinese Control Conference (CCC), Kunming, China, 28–31 July 2024; pp. 8951–8956. [Google Scholar] [CrossRef]
- Zhao, B.; Cheng, C.; Peng, Z.; He, Q.; Meng, G. Hybrid Pre-Training Strategy for Deep Denoising Neural Networks and Its Application in Machine Fault Diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 3526811. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, J.; Xu, P.; Liang, Y.; Dai, Y.; Gao, T.; Bai, Y. Bearing Fault Diagnosis for Cross-Condition Scenarios Under Data Scarcity Based on Transformer Transfer Learning Network. Electronics 2025, 14, 515. [Google Scholar] [CrossRef]
- Asutkar, S.; Chalke, C.; Shivgan, K.; Tallur, S. TinyML-enabled edge implementation of transfer learning framework for domain generalization in machine fault diagnosis. Expert Syst. Appl. 2023, 213, 119016. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, Z.; Liu, S. Improving Performance of Seismic Fault Detection by Fine-Tuning the Convolutional Neural Network Pre-Trained with Synthetic Samples. Energies 2021, 14, 3650. [Google Scholar] [CrossRef]
- Di Maggio, L.G. Intelligent Fault Diagnosis of Industrial Bearings Using Transfer Learning and CNNs Pre-Trained for Audio Classification. Sensors 2023, 23, 211. [Google Scholar] [CrossRef]
- Chakraborty, S.; Uzkent, B.; Ayush, K.; Tanmay, K.; Sheehan, E.; Ermon, S. Efficient Conditional Pre-training for Transfer Learning. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022; pp. 4240–4249. [Google Scholar] [CrossRef]
- Udmale, S.S.; Singh, S.K.; Singh, R.; Sangaiah, A.K. Multi-Fault Bearing Classification Using Sensors and ConvNet-Based Transfer Learning Approach. IEEE Sensors J. 2020, 20, 1433–1444. [Google Scholar] [CrossRef]
- Pei, X.; Zheng, X.; Wu, J. Rotating Machinery Fault Diagnosis Through a Transformer Convolution Network Subjected to Transfer Learning. IEEE Trans. Instrum. Meas. 2021, 70, 2515611. [Google Scholar] [CrossRef]
- Dai, X.; Gao, Z. From Model, Signal to Knowledge: A Data-Driven Perspective of Fault Detection and Diagnosis. IEEE Trans. Ind. Inform. 2013, 9, 2226–2238. [Google Scholar] [CrossRef]
- Ding, Q.; Zheng, F.; Liu, L.; Li, P.; Shen, M. Swift Transfer of Lactating Piglet Detection Model Using Semi-Automatic Annotation Under an Unfamiliar Pig Farming Environment. Agriculture 2025, 15, 696. [Google Scholar] [CrossRef]
- Dong, F.; Yang, J.; Cai, Y.; Xie, L. Transfer learning-based fault diagnosis method for marine turbochargers. Actuators 2023, 12, 146. [Google Scholar] [CrossRef]
- Lin, Y.C.; Huang, Y.C. Streamlined Deep Learning Models for Move Prediction in Go-Game. Electronics 2024, 13, 93. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Van Huynh, N.; Chu, N.H.; Saputra, Y.M.; Hoang, D.T.; Nguyen, D.N.; Pham, Q.V.; Niyato, D.; Dutkiewicz, E.; Hwang, W.J. Transfer Learning for Wireless Networks: A Comprehensive Survey. Proc. IEEE 2022, 110, 1073–1115. [Google Scholar] [CrossRef]
- Hao, S.; Li, J.; Ma, X.; Sun, S.; Tian, Z.; Li, T.; Hou, Y. A Photovoltaic Hot-Spot Fault Detection Network for Aerial Images Based on Progressive Transfer Learning and Multiscale Feature Fusion. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4709713. [Google Scholar] [CrossRef]
- Zeng, Y.; Sun, B.; Xu, R.; Qi, G.; Wang, F.; Zhang, Z.; Wu, K.; Wu, D. Multirepresentation Dynamic Adaptive Network for Cross-Domain Rolling Bearing Fault Diagnosis in Complex Scenarios. IEEE Trans. Instrum. Meas. 2025, 74, 3522716. [Google Scholar] [CrossRef]
- Lv, K.; Yang, Y.; Liu, T.; Gao, Q.; Guo, Q.; Qiu, X. Full parameter fine-tuning for large language models with limited resources. arXiv 2023, arXiv:2306.09782. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Q.; Yu, X.; Sun, C.; Wang, S.; Yan, R.; Chen, X. Applications of Unsupervised Deep Transfer Learning to Intelligent Fault Diagnosis: A Survey and Comparative Study. IEEE Trans. Instrum. Meas. 2021, 70, 3525828. [Google Scholar] [CrossRef]
- Neupane, D.; Seok, J. Bearing Fault Detection and Diagnosis Using Case Western Reserve University Dataset with Deep Learning Approaches: A Review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- AlShalalfeh, A.; Shalalfeh, L. Bearing Fault Diagnosis Approach Under Data Quality Issues. Appl. Sci. 2021, 11, 3289. [Google Scholar] [CrossRef]
- Li, C.; Mo, L.; Yan, R. Fault Diagnosis of Rolling Bearing Based on WHVG and GCN. IEEE Trans. Instrum. Meas. 2021, 70, 3519811. [Google Scholar] [CrossRef]
- Qian, C.; Jiang, Q.; Shen, Y.; Huo, C.; Zhang, Q. An intelligent fault diagnosis method for rolling bearings based on feature transfer with improved DenseNet and joint distribution adaptation. Meas. Sci. Technol. 2021, 33, 025101. [Google Scholar] [CrossRef]
- Fanai, H.; Abbasimehr, H. A novel combined approach based on deep Autoencoder and deep classifiers for credit card fraud detection. Expert Syst. Appl. 2023, 217, 119562. [Google Scholar] [CrossRef]
- Rymarczyk, D.; Struski, Ł.; Górszczak, M.; Lewandowska, K.; Tabor, J.; Zieliński, B. Interpretable Image Classification with Differentiable Prototypes Assignment. In Proceedings of the Computer Vision—ECCV 2022, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 351–368. [Google Scholar] [CrossRef]
- Evron, I.; Moroshko, E.; Buzaglo, G.; Khriesh, M.; Marjieh, B.; Srebro, N.; Soudry, D. Continual Learning in Linear Classification on Separable Data. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; Krause, A., Brunskill, E., Cho, K., Engelhardt, B., Sabato, S., Scarlett, J., Eds.; PMLR: Cambridge, MA, USA, 2023; Volume 202, Proceedings of Machine Learning Research. pp. 9440–9484. [Google Scholar]
- Liu, C.; Gryllias, K. Simulation-Driven Domain Adaptation for Rolling Element Bearing Fault Diagnosis. IEEE Trans. Ind. Inform. 2022, 18, 5760–5770. [Google Scholar] [CrossRef]
- Jiao, X.; Zhang, J.; Cao, J. A Bearing Fault Diagnosis Method Based on Dual-Stream Hybrid-Domain Adaptation. Sensors 2025, 25, 3686. [Google Scholar] [CrossRef]
- Jeong, H.; Kim, S.; Seo, D.; Kwon, J. Source-Free Domain Adaptation Framework for Rotary Machine Fault Diagnosis. Sensors 2025, 25, 4383. [Google Scholar] [CrossRef]







| Operating Condition | Normal | Ball | Inner Race | Outer Race | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | B_07 | B_014 | B_021 | IR_07 | IR_014 | IR_021 | OR_07 | OR_014 | OR_021 | |
| 1730/rpm | Normal_0 | B007_0 | B014_0 | B021_0 | IR007_0 | IR014_0 | IR021_0 | OR007_0 | OR014_0 | OR021_0 |
| 1750/rpm | Normal_1 | B007_1 | B014_1 | B021_1 | IR007_1 | IR014_1 | IR021_1 | OR007_1 | OR014_1 | OR021_1 |
| 1772/rpm | Normal_2 | B007_2 | B014_2 | B021_2 | IR007_2 | IR014_2 | IR021_2 | OR007_2 | OR014_2 | OR021_2 |
| 1797/rpm | Normal_3 | B007_3 | B014_3 | B021_3 | IR007_3 | IR014_3 | IR021_3 | OR007_3 | OR014_3 | OR021_3 |
| Source Domain | Label | 0 | 1 | 2 | 3 |
| Content | Normal | Ball | Inner race | Outer race | |
| Target Domain | Label | N/A | |||
| Content | No labeled data | ||||
| Operating Condition | Normal | Chip/Ball | Miss/Comb | Root/Inner | Surface/Outer |
|---|---|---|---|---|---|
| gear 20 kHz_0V | Normal_0 | Chip_0 | Miss_0 | Root_0 | Surface_0 |
| gear 30 kHz_2V | Normal_1 | Chip_1 | Miss_1 | Root_1 | Surface_1 |
| Bearing 20 kHz_0V | Normal_0 | Ball_0 | Comb_0 | Inner_0 | Outer_0 |
| Bearing 30 kHz_2V | Normal_1 | Ball_1 | Comb_1 | Inner_1 | Outer_1 |
| Source Domain | Label | 0 | 1 | 2 | 3 | 4 |
| Content | Normal | Chip /Ball | Miss /Comb | Root /Inner | Surface /Outer | |
| Target Domain | Label | N/A | ||||
| Content | No labeled data | |||||
| Operating Condition | Normal | Ball | Inner Race | Outer Race |
|---|---|---|---|---|
| 600/rpm | Normal_0 | Ball_0 | Inner_0 | Outer_0 |
| 800/rpm | Normal_1 | Ball_1 | Inner_1 | Outer_1 |
| 1000/rpm | Normal_2 | Ball_2 | Inner_2 | Outer_2 |
| Source Domain | Label | 0 | 1 | 2 | 3 |
| Content | Normal | Ball | Inner race | Outer race | |
| Target Domain | Label | N/A | |||
| Content | No labeled data | ||||
| Module | Layer | Filter Size | Filter Number | Stride | Padding |
|---|---|---|---|---|---|
| CNN feature extractor | Conv1d+BN+ReLU | 3 | 32 | 1 | 1 |
| MaxPool1d | 2 | – | 2 | – | |
| Conv1d+BN+ReLU | 3 | 64 | 1 | 1 | |
| AdaptivePool | – | – | – | – | |
| Layer | Input dimension | Output dimension | |||
| Self-attention Classifier | Query | 64 | 64 | ||
| Key | 64 | 64 | |||
| Softmax | – | – | |||
| Weighted sum | – | – | |||
| FC | 64 | 4 | |||
| Module | Layer | Input Dimension | Output Dimension |
|---|---|---|---|
| Deep fully connected classifier (DeepC [54]) | Linear | 64 | 32 |
| BN+ReLU+Dropout | 32 | 32 | |
| Linear | 32 | 4 | |
| Softmax | – | – | |
| Prototype classifier (PrototypeC [55]) | Prototypes | 64 | 4 |
| Linear classifier (LinearC [56]) | Linear | 64 | 4 |
| Softmax | – | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yang, X.; Li, T.; She, L.; Guo, X.; Yang, F. Intelligent Fault Diagnosis for Rotating Machinery via Transfer Learning and Attention Mechanisms: A Lightweight and Adaptive Approach. Actuators 2025, 14, 415. https://doi.org/10.3390/act14090415
Wang Z, Yang X, Li T, She L, Guo X, Yang F. Intelligent Fault Diagnosis for Rotating Machinery via Transfer Learning and Attention Mechanisms: A Lightweight and Adaptive Approach. Actuators. 2025; 14(9):415. https://doi.org/10.3390/act14090415
Chicago/Turabian StyleWang, Zhengjie, Xing Yang, Tongjie Li, Lei She, Xuanchen Guo, and Fan Yang. 2025. "Intelligent Fault Diagnosis for Rotating Machinery via Transfer Learning and Attention Mechanisms: A Lightweight and Adaptive Approach" Actuators 14, no. 9: 415. https://doi.org/10.3390/act14090415
APA StyleWang, Z., Yang, X., Li, T., She, L., Guo, X., & Yang, F. (2025). Intelligent Fault Diagnosis for Rotating Machinery via Transfer Learning and Attention Mechanisms: A Lightweight and Adaptive Approach. Actuators, 14(9), 415. https://doi.org/10.3390/act14090415







