Abstract
This paper deals with the design and the robustness analysis of a model predictive control (MPC) for the position tracking of primary flight movables driven by electro-mechanical actuators. This study is, in particular, focused on a rotary electro-mechanical actuator (EMA) by UMBRAGROUP, employing a patented mechanical transmission based on a differential ball-screw mechanism characterized by a huge gear ratio. To obtain a baseline reference, conventional PID regulators were initially optimized by using multi-objective cost functions based on tracking accuracy, load disturbance rejection, and power consumption. The position regulator was then replaced by an MPC regulator, designed to balance performance, computational resources, and safety constraints. A nonlinear physics-based simulation model of the EMA, entirely developed in the Matlab–Simulink environment and validated with experiments, was used to compare the two control strategies. The simulation results in both the time and frequency domains highlight that the MPC solution provides faster and more accurate position tracking, improved dynamic stiffness, and reduced power absorption. Finally, the robustness against model uncertainties of the MPC was addressed by imposing random and combined deviations of model parameters from the nominal values (via Monte Carlo analysis). The results demonstrate that the implementation of MPC control laws could enhance the stability and the reliability of EMAs, thus supporting their application for safety-critical flight control functions.
1. Introduction
In recent years, the aerospace sector has undergone a progressive shift toward the electrification of onboard systems, driven by the need to improve energy efficiency, reduce environmental impact, and optimize system integration [1]. The more electric aircraft (MEA) concept seeks to replace traditional hydraulic and pneumatic systems with electrically powered alternatives, offering benefits in terms of weight reduction, maintenance costs, and sustainability [2,3,4]. Nevertheless, given the present power density storage technology [5], the feasibility of achieving all-electric aircraft (AEA) is currently limited to urban air mobility (UAM) applications, such as the emerging market of urban air taxi (UAT) and electrical vertical take-off and landing (eVTOL) vehicles [6]. A key enabling technology within this transformation is the electro-mechanical actuator [7], which converts electrical energy into mechanical motion using an electric motor and mechanical transmission, hence, without relying on hydraulic fluids, eliminating leakage risks, and simplifying system architecture. Significant progress in enabling components—such as electric machines [8], power electronics [9], and materials of mechanical elements [10]—has notably increased the technology readiness level (TRL) of these systems. Although the feasibility of EMAs in aerospace applications has been demonstrated in terms of load capacity, dynamic performance, and health-monitoring capabilities [11,12,13,14,15], their deployment in safety-critical flight controls or landing gears still raises concerns related to reliability, fault tolerance, and compliance with airworthiness certification standards [16,17]. To address these functions, several architectural solutions have been proposed, including simplex configurations with passive fail-safe mechanisms and more complex redundant fault-tolerant architectures involving dual motors, independent control paths, or differential mechanisms. Nevertheless, actuator reliability depends not only on hardware redundancy but also on the control and monitoring strategies implemented [18]. Robust and high-performance controllers are essential to ensure system stability and disturbance rejection under variable conditions and partial faults [19]. Classical control approaches, such as proportional–integral (PI) or linear–quadratic regulator (LQR) schemes, are widely employed in aerospace applications due to their simplicity, reliability, and deterministic behavior. However, these methods operate on current or past states and measurements, and are, hence, limited in managing future disturbances or constraints. In contrast, model predictive control has emerged as a powerful alternative, enabling the anticipation of future system behavior through internal prediction models and the explicit handling of input and state constraints within the control action optimization window [20,21]. Eren et al. [22] provide a comprehensive review of MPC techniques for aircraft and spacecraft system applications, focusing on safety-critical applications and fault-tolerant control, observing that the complexity of nonlinear formulations is a challenge for practical implementation in safety-critical functions. Although RTCA DO-178C does not restrict the choice of control techniques from a certification standpoint [23], the software implementation of PI controllers is generally easier to validate due to their interpretability and limited branching logic, making modified condition/decision coverage (MC/DC) relatively straightforward. In contrast, for MPC involving model nonlinearities or constrained real-time optimization, the highly complex logic, numerical challenges, and recursive solver behavior may significantly increase the verification effort, particularly in applications subject to a higher development assurance level (DAL) classification.
MPC has been studied in the context of aircraft flight mechanics for load alleviation functions [24] and dynamic system modeling [25], spacecraft enhancement dynamics [26], and UAV maneuver optimization [27,28]. MPC has also demonstrated promising results in governing permanent magnet synchronous motors (PMSMs), functioning as a speed controller [29], MIMO direct quadrature current regulator [30], and direct torque controller (DTC) [31]. Additionally, Hasan et al. [32] employed MPC as a speed regulator for electromagnetic actuators, integrated with a PI position controller. Nevertheless, the use of MPC for position control in safety-critical EMAs remains a promising yet open research topic. The main barriers are associated with the nonlinear and coupled dynamics of electro-mechanical systems, the need for real-time implementation on embedded hardware with limited computational resources, and the rigorous certification requirements in aviation environments.
The main objective of this work was to assess the feasibility and advantages of applying MPC to a rotary EMA developed by UMBRAGROUP for primary flight control applications by comparing its performance and robustness with those of conventional control laws.
This paper is articulated as follows: The first part is dedicated to the description of the EMA architecture and to the development of a detailed model integrating both electrical and mechanical subsystems based on first physical principles. Subsequently, the classical PI-based cascade of position, speed, and current regulators is designed through a multi-objective optimization. A linear time-invariant (LTI) MPC then replaces the PI position regulator, while keeping other loops unchanged. Comprehensive simulations with a nonlinear model in Simulink assess the performance of PI- and MPC-controlled EMAs in the time and frequency domains, also evaluating robustness against individual and coupled parameter deviations and model uncertainties, as well as the power absorption and computational resource requirements. Finally, the key findings are discussed, highlighting differences between the two approaches, along with suggestions for future refinements.
2. Materials and Methods
2.1. System Description
The reference architecture for this study was a rotary fail-safe EMA (Figure 1), based on a differential ball-screw patented by UMBRAGROUP (UG) [33], within the CleanSky 2 program [34]. The closed-loop control of EMAs designed for secondary flight surfaces primarily focuses on disturbance rejection requirements, minimizing position deviations from the commanded setpoint when external loads act on the surface. Conversely, the position-tracking behavior under load is the key performance requirement that an actuator specifically designed for primary flight controls must meet. In this last case, the position control loop should operate at higher bandwidths (e.g., 2–10 Hz), ensuring precise tracking, while the output shaft speed typically ranges between 10 and 60 degrees per second.

Figure 1.
Rotary EMA (UG patent) and electronic control units (ECUs).
The specific case study investigated the rotary EMA architecture integrated into the rudder actuation system of a medium-sized eVTOL vehicle featuring a V-tail configuration. In such a layout, the rudder functions as a primary flight control surface, contributing to both yaw and pitch control during cruise and transition phases. Consequently, the actuator must ensure high dynamic performance, particularly in terms of frequency response, position-tracking accuracy, and robustness against aerodynamic disturbances.
2.2. System Dynamics Modeling
High-fidelity nonlinear models of EMAs are widely used to accurately reproduce the behavior of a real system. Such model-based approaches have become increasingly relevant in the context of digital twin development, enabling simulation-based analysis and verification for monitoring and control algorithms. The developed nonlinear model of the EMA, illustrated in Figure 2, includes two main sections: the electro-mechanical section and the digital electronics section, each comprising multiple functional blocks. The electro-mechanical section consists of the following components:
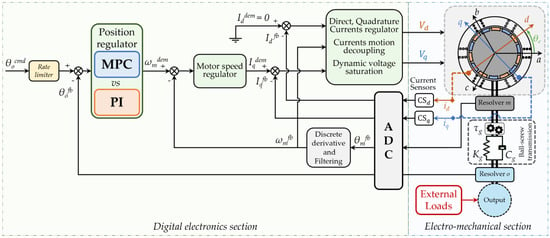
Figure 2.
Block diagram of EMA closed-loop control architecture.
- Three-phase surface-mounted permanent magnet synchronous motor (S-PMSM) current dynamics in the direct-quadrature (d–q) reference frame;
- UMBRAGROUP-patented mechanical transmission based on a high transmission ratio differential ball-screw mechanism, including its internal stiffness and resonance;
- Mechanical free-play of the transmission;
- Coulomb and viscous friction;
- Rotational dynamics of the output shaft, including the reference aircraft surface inertia and external load effects.
The digital electronics section includes:
- Three nested control loops acting on direct and quadrature motor currents, motor speed, and output shaft position;
- Control nonlinearities (saturations and a rate limiter on position command);
- Sensor dynamics, latencies, resolution, and noise;
- Resolver sensors for motor and output shaft position feedback;
- Motor speed reconstruction from angular positions;
- Hall effect sensors for current measurement;
- Digital signal processing performed at 10 kHz.
The model is implemented in Simulink (version 2024b) using the ODE4 Runge–Kutta solver with a fixed integration step of 10−5 s.
2.2.1. Electro-Mechanical Section
The electro-mechanical section includes three main dynamic contributions: the electric motor with d–q axes current dynamics (1), the rotor-side one-degree-of-freedom (DOF) rotational motion (2), and the output shaft with 1-DOF rotational dynamics (3). These equations are coupled through the compliant mechanical transmission, modeled with lumped spring–damper parameters, assuming low structural damping. Mechanical friction is modeled as lumped on the motor shaft and includes both viscous and Coulomb contributions [35]. A load-dependent friction term proportional to the motor torque is also included. Mechanical free-play nonlinearity is introduced into the transmission by means of a symmetric dead-zone model [36] acting on the relative angular displacement (4).
Vd, Vq and Id, Iq are, respectively, the direct and quadrature voltages and currents. Lph and Rph are the motor phase inductance and resistance, nd is the number of pole pairs, and Ke is the back-electromotive force constant of the PMSM. θm and θo are, respectively, the angular positions of the motor and the output shaft, and Jm and Jo are the associated inertias. Kg and Cg represent the torsional stiffness and damping of the differential ball-screw drivetrain with gear ratio τg. The motor torque constant kt is equal to Ke for the S-PMSM. Bm is the viscous friction coefficient, while Tc and ωc are the parameters of the Coulomb–tanh friction model illustrated in Figure 3. The torque-induced drag is included through a scaling term proportional to the motor torque Tm, governed by the coefficient Kfl. Text is the external torque acting on the output shaft, accounting for load disturbances and aerodynamic actions. Finally, the parameter θfp defines the half-width of the free-play dead zone.
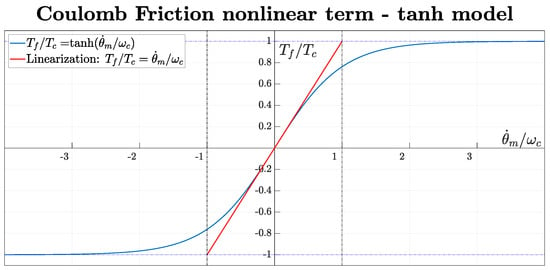
Figure 3.
Coulomb–tanh friction model and its linearization around equilibrium.
The proposed model represents a balance between accuracy and complexity, consistent with the current objective of comparing control strategies rather than developing a high-fidelity simulation framework. More advanced EMA models usually include three-phase current dynamics, with space vector pulse width modulation (SVPWM) and field-oriented control (FOC) [37], to represent real-time switching behavior accurately. While the overall friction behavior is inspired by experimental trends observed in similar actuators, some parameters are defined through engineering assumptions in the absence of experimental data (Coulomb velocity). PMSM iron losses and thermal effects were not explicitly modeled; however, the variation in key parameters with temperature—such as phase resistance and viscous friction—was implicitly accounted for through the parameter ranges considered in the robustness analysis presented in the following sections. Sensor noise was not experimentally characterized in terms of variance; thus, it was approximated based on the nominal resolution. The parameters used in the electro-mechanical section of the simulation model are listed in Table 1.

Table 1.
Parameters of electro-mechanical section.
2.2.2. Digital Electronics Section
The digital control section of the model includes two main parts.
- Control laws: The EMA output position command is, first, rate-limited at the maximum output shaft speed ωomax and then compared with the resolver feedback. The position error is fed to the position regulator, which generates a motor speed request. This is compared with the value derived from the motor resolver position feedback and fed to the motor speed regulator, which outputs a quadrature current demand. The direct current, instead, has a fixed null reference to achieve maximum torque per ampere (MTPA) control for the S-PMSM [38], assuming Ld = Lq = Lph. The baseline design, position, speed, and current regulators have a proportional–integral structure with saturation and an anti-windup scheme. In the MPC-based control, only the position regulator is replaced with an MPC, maintaining the other control laws unchanged. Additionally, the current regulator integrates the decoupling technique. By reformulating Equation (1), the relationships in (5) can be established, linking the voltages Vdreg, Vqreg, calculated by the current regulator, to their post-decoupling counterparts Vddec, Vqdec. This approach ensures that the current dynamics along the d–q axes remain unaffected by motor speed variations, leading to the independent behavior of the d and q currents. Equation (5) assumes that discrepancies between actual and measured values of currents and speed remain minimal, alongside low variations in electrical constants, thus ensuring an effective decoupling. Finally, the voltages are dynamically saturated according to Constraint (6).
- Sensor processing: The rotor and output shaft positions are measured through resolver angular sensors, while the d–q currents are acquired with Hall effect current sensors. In the real EMA, each motor phase current is measured, and then the d–q currents are calculated in the digital control section via Clarke–Park transformation (7).
The analog signals first pass through continuous-time first-order low-pass filters representing the bandwidth limitations of the sensor dynamics. A complete digital acquisition chain is implemented, with its characteristics detailed in Table 2, including finite resolution effects due to analog-to-digital conversion. Each sensor output is quantized according to the ADC bit depth and full-scale range, and additive white noise is superimposed. The signals are then digitized through sample-and-hold functions operating at a 10 kHz rate.

Table 2.
Sensor characteristics.
2.3. Conventional Control Laws Optimization
Conventional proportional–integral controllers are commonly used for their simplicity and capability to achieve zero steady-state tracking error. The general continuous-time transfer function is given by Equation (8).
The two parameters (for each control loop) to be selected are as follows:
- 1.
- The proportional gain: KP;
- 2.
- The zero of the integrator: zI.
These parameters are tuned to meet the stability and closed-loop performance requirements reported in Table 3. It is worth noting that the bandwidths of the three control loops are designed to be separated by one decade in order to obtain disjointed dynamics.

Table 3.
Control loop design requirements.
- PI controllers are designed through an optimization procedure based on a reduced-order linear time-invariant model of the EMA, derived from Equations (1)–(5). This model neglects mechanical nonlinearities, such as angular free-play, and imposes zero Coulomb and load-dependent friction, since its linearization would generate unrealistically high values for ω > ωc. The electrical model is reduced by neglecting the d-axis current dynamics and retaining only the quadrature current state, resulting in, a mono-phase equivalent model of the electrical machine (9). The sensor section is modeled in continuous time using only first-order low-pass filters to capture bandwidth limitations. Figure 4 illustrates the key degrees of freedom of this reduced electro-mechanical model.
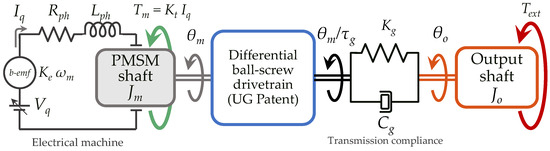 Figure 4. Reduced EMA model for PIs and MPC tuning.
Figure 4. Reduced EMA model for PIs and MPC tuning.
This approach enables the systematic definition and minimization of performance-oriented cost functions, with the goal of identifying the optimal controller parameters that guarantee accurate position tracking and effective load disturbance rejection with minimal energy consumption. This also provides a consistent basis for comparison with the MPC-based control strategy. The controller design is framed as a multi-objective optimization problem and employs a Monte Carlo search method to explore a broader design space than directional minimization approaches. Within this framework, each cost function, Ji, quantifies a specific performance metric of the EMA under predefined test conditions. A total of six cost functions are defined based on the EMA response in the following two scenarios:
- 1.
- The position-tracking test: The commanded output position is a step of θos = 1 deg, with no external load applied. The cost function measures the squared tracking error between the output position and the reference command (10). Similarly, is linked to the deviation of the motor speed from the regulator reference (11). The cost function quantifies the normalized electric power absorption. Since it includes the open-loop input voltage Vq, this metric reflects the required effort to achieve the desired tracking performance.
- 2.
- The load disturbance rejection test: The position command is set to the equilibrium condition (i.e., θocmd = 0 deg), while an external torque step of Text = 1 Nm is applied. The three corresponding cost functions are analogously defined in (13)–(15).
Finally, the global cost function is defined as a weighted linear combination of the individual terms Ji, normalized by their respective minimum values to ensure comparability among different metrics (16). The minimum of Equation (16) yields the optimal placement of the PI controller zeros.
To facilitate further result interpretation and to clarify the adopted weight assignment convention, it is useful to group each pair of cost functions associated with a specific performance metric: position tracking (17), speed tracking (18), and power consumption (19).
The controller optimization is carried out in the MATLAB environment, based on a state-space representation of the EMA LTI model. The procedure consists of the following main steps:
- 1.
- Zeros placement variation: A common variation vector for zero placement is defined and applied equally across all control loops. The zero location is varied as fractions of the respective closed-loop design bandwidths, within the range of [0.1–0.5], to ensure a minimal impact of the zero on the bandwidth itself. The Monte Carlo-based algorithm generates a large number of zeros placement combinations for the three nested control loops.
- 2.
- Feed-forward design and stability verification: For each configuration, the feed-forward transfer function is constructed by cascading with the open-loop transfer function from its output to the EMA system output in the corresponding control loop. The proportional gain is then automatically calculated by enforcing that the cut-off frequency of the feed-forward transfer function matches the predefined closed-loop bandwidth. Stability margins are checked, and if they meet the required specifications, the state-space LTI closed-loop model of the EMA system is constructed.
- 3.
- Time-domain simulation and cost function evaluation: The position closed-loop EMA is simulated under position-tracking and disturbance rejection tests; consequently, the values of the six cost functions are evaluated for each zeros configuration.
- 4.
- Normalization of cost functions: For each cost function, the minimum value across all combinations is identified to allow its normalization. This ensures consistent comparison across metrics with different physical units and scales.
- 5.
- Weight definition for multi-objectives cost function: Given the focus on primary flight control applications, the optimization strategy prioritizes position-tracking performance over secondary objectives. Accordingly, the weights associated with motor speed tracking and power consumption are fixed to small values (20); conversely, the weights associated with position-tracking cost functions are allowed to vary within a discrete set of values (21) to be treated as tunable parameters within the optimization process.Only combinations satisfying the constraint are valid. This approach effectively incorporates weights tuning into the overall optimization framework, thereby expanding the dimensionality of the parameters space and enabling a balanced trade-off among the multiple performance objectives.
- 6.
- Computation of the global cost function: For each valid combination of zero placements and cost function weights, the global cost function Jw is evaluated according to (16).
- 7.
- Optimal design identification: The optimal controllers configuration is identified as the one that minimizes the global cost function, ensuring the best trade-off among the considered performance metrics.
2.4. Model Predictive Controller Development
An MPC for EMA position regulation was developed based on the standard theory of discrete-time, LTI, state-space formulation for single-input–single-output model-based predictive control [39]. This control approach represents a novel strategy in aerospace EMA applications. Its objective is to optimize the system performance by predicting future behavior and computing control actions accordingly. This technique relies on a dynamic model of the plant and solves an optimization problem at each time step to minimize a cost function while satisfying system constraints. The implementation of an MPC algorithm requires the following elements:
- Information on the current and previous states of the system;
- A mathematical model of the plant to predict its future evolution;
- An optimization criterion (typically a quadratic cost function).
The MPC strategy is based on three core concepts, displayed in Figure 5:
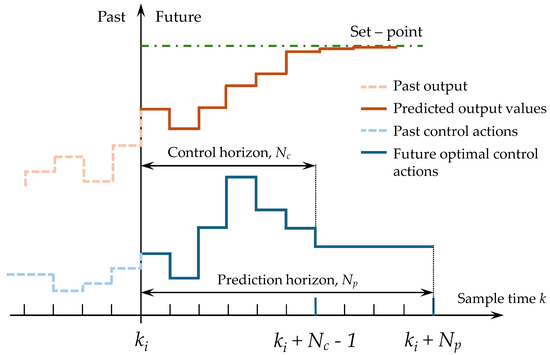
Figure 5.
Model predictive control fundamentals.
- 1.
- The prediction horizon (Np) defines the finite time span (in terms of discrete time steps k) over which the future system output is predicted, using the plant model and current state information. A longer prediction horizon allows the controller to capture a more comprehensive understanding of the system evolution, though increasing the complexity of the algorithm.
- 2.
- The control horizon (Nc) denotes the finite time window over which the future control inputs u(k) are optimized, i.e., for k = ki, …, ki + Nc − 1, where ki is the initial time. Nc is constrained by computational costs and the need to balance predictive accuracy with real-time implementation. Thus, Nc is usually smaller than Np, and for k > ki + Nc − 1, the control input is assumed to remain constant. The selection of an appropriate control horizon is crucial as it directly influences the controller ability to anticipate and regulate the system behavior effectively.
- 3.
- Receding horizon control: A dynamic optimization framework enables the controller to adapt its control strategy in real-time by recalculating control inputs at each time step, based on the most recent state information, to enhance robustness against model inaccuracies and external perturbations and to maintain system stability. Mathematically, at time k, the MPC computes an optimal sequence of control actions over the full control horizon; however, only the first input u(k) is applied to the plant. In the next time step, the system state is updated, and a new optimization is performed.
2.4.1. Discrete-Time LTI MPC Formulation
The design of a model predictive controller is based on a mathematical model of the plant, with its algorithm complexity increasing as the model becomes more detailed or nonlinear. A basic MPC formulation relies on a discrete-time, LTI, SISO, state-space model (the extension to multiple-input–multiple-output (MIMO) systems is straightforward), whose embedded dynamic equations are formulated as (22) and (23), where k is the actual time sample, xm(k) is the vector of states at time k with length n1, u(k) and y(k) are, respectively, the input and output at the current time (both scalar for SISO), and Am(n1 × n1), Bm(n1 × 1), and Cm(1 × n1) are the plant state-space representation matrices with constant parameters. Due to the receding horizon technique, the Dm matrix is always null, since the input cannot directly affect the output in the same time step. If the dynamic model is nonlinear, the matrices can be obtained via linearization around an equilibrium point.
Expressing the variation in the input and states within two consecutive time samples (24), it is possible to rearrange the dynamic Equations (22) and (23) in incremental terms as (25) and (26).
Defining the so-called augmented states vector (27), the augmented state-space LTI model of the plant is obtained as (28)–(30) and used to design the MPC controller and for the calculation of future states and outputs.
2.4.2. Prediction Within One Optimization Window
At each discrete time step ki > 0, the MPC algorithm solves an optimization problem to compute the Nc future increments of the control variable Δu(ki), …, Δu(ki + Nc − 1). Based on this control sequence, using the augmented model, the algorithm then predicts, sequentially, the future states (31) and the output (32) of the system over the prediction horizon Np (i.e., the optimization window). The notation x(k|ki) denotes the predicted state for future time k = ki + 1, …, ki + Np carried out at time ki. By defining two vectors containing all Np values of input (33) and output (34), the dynamic equation used for output prediction can be rewritten in a compact, state-space-like form as (35). Remarkably, the F and Φ matrices depend only on the augmented model matrices, defined as constant, enabling a significant simplification of the MPC code generation.
2.4.3. Optimization Criterion
The control objective of the MPC is to minimize the deviation between the predicted output and a reference signal r(ki), which is assumed to remain constant over the prediction horizon (36). This goal is achieved by computing the optimal sequence of control increments ΔU that minimizes a convex quadratic cost function (37). The first part aims to minimize the tracking error e(ki) = r(ki) − y(ki), while the second term penalizes excessive control effort by weighting the magnitude of ΔU. This trade-off is regulated by a tunable parameter rw ≥ 0, embedded in the diagonal input-weighting matrix , where is the identity matrix. The input-weight parameter rw governs the balance between tracking performance and control effort. Setting rw = 0 results in a purely performance-oriented controller, neglecting the cost of control variation. Conversely, larger rw values yield smoother control inputs by limiting abrupt variations, thus producing a more conservative response.
By substituting Equation (35) into (37), the expanded expression shown in (38) is obtained.
By setting the gradient of the cost function with respect to ΔU to zero, and considering the problem’s convex and quadratic structure, a unique global minimum is guaranteed, which corresponds to the optimal control trajectory (39). The term in (39) is commonly referred to as the Hessian matrix, whose existence is guaranteed by the problem construction. Since both Φ and are constant matrices in this formulation, the resulting Hessian matrix is also constant.
2.4.4. Model Predictive Position Controller Design
The first design decision involves choosing how to integrate the model predictive controller. Since classical EMA architectures consist of three nested loops, one option would be to replace all of them with a single MPC regulator. However, this strategy introduces significant challenges: internal saturation limits (e.g., maximum motor speed and current), typically enforced by external saturation blocks, must be explicitly addressed as hard constraints on system states, inputs, and outputs. This approach would require solving a constrained optimization problem with linear inequalities constraints. Although MPC algorithms can address this task using quadratic programming methods, such as Hildreth’s algorithm [40], the associated computational complexity and potential constraints conflicts make this solution unsuitable for safety-critical applications. Preliminary control laws design and further optimization of PI controllers highlighted a strong dependence of the EMA’s closed-loop performance on the tuning of the position regulator, while motor speed and current regulators have a secondary influence. Based on this evidence, the MPC was employed as the position regulator, in cascade with the optimized PI controllers for speed and current loops. Aerospace applications impose a trade-off between embedded model accuracy and necessary computational resources. Certification requirements in safety-critical systems limit the use of complex or unverified algorithms. Therefore, the embedded model must be kept as simple as possible while still capturing the essential EMA dynamics. To fulfil these requirements, the MPC was developed without internal constraints and based on a simplified LTI model. Specifically, since the MPC operates as a position regulator, its embedded model corresponds to the speed closed-loop EMA shown in Figure 6, represented by the transfer function (40) and discretized at a 10 kHz sampling rate. Referring to Figure 6, the open-loop model of the EMA corresponds to the five-states representation also used for PI optimization (Figure 4). The inclusion of current and speed loop integrators adds two additional states. An additional state results from the discrete-time derivative and filtering used in speed reconstruction, yielding a total of eight states (41). These additional states are not directly measurable but can be computed from the PI regulators’ internal variables and sensor processing at the previous time step. The output speed ωo is estimated using the same approach applied to calculate the motor speed from the position feedback.
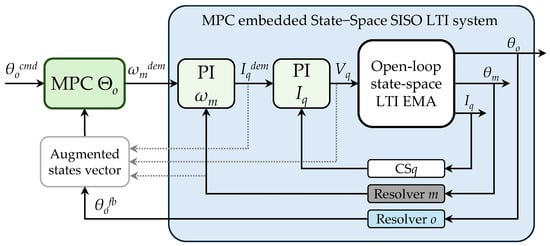
Figure 6.
MPC embedded model and control scheme.
In the absence of a formal procedure to determine an optimal configuration for MPC parameters (Nc, Np, and rw) a priori, the design was carried out through an iterative refinement. A series of closed-loop simulations were conducted in both the time and frequency domains, progressively adjusting the tuning parameters based on the observed performance, until satisfactory tracking accuracy and closed-loop stability were achieved with minimal control effort. In particular, the MPC was tuned to achieve a position loop bandwidth of approximately 2 Hz, as measured in unloaded frequency response tests, while ensuring an overshoot of less than 5% in response to unit step commands. This iterative process led to some key considerations:
- A short control horizon (Nc = 5) proved sufficient, as longer values did not significantly improve performance;
- A long prediction horizon (Np = 500) was necessary to properly capture the system dynamics and generate effective control actions;
- Given the incremental nature of the MPC law, the input-weighting factor should remain small (rw = 10−3) to prevent over-smooth inputs, thereby preserving actuator responsiveness and ensuring adequate control authority.
In the nonlinear Simulink model, the MPC is implemented via a custom MATLAB function that computes the optimal control trajectory, as expressed in (39). The necessary matrices in (42), being constant in this formulation, are precomputed and loaded into the code. By opting for a significantly reduced control horizon, these matrices are of a small dimension. To compute ΔUopt, the MPC block requires the reference input r(k) = θocmd(k) and the augmented states vector (27); therefore, state values at both the current and previous time steps are needed. Finally, the MPC applies only the first element of the control increment vector to compute the optimal speed reference, as defined in Equation (43). Finally, the MPC output is externally saturated to avoid a more complex constrained optimization procedure, and it is sent to the motor speed regulator in cascade.
2.5. Performance Comparison and Robustness Analysis
To substantiate the differences between the two control strategies, the following simulations in the time and frequency domains are performed using the nonlinear dynamic model described in Section 2.2 and implemented in the Simulink environment.
- 1.
- The EMA unloaded position-tracking response is assessed in the frequency domain with harmonic commands of a 1 deg amplitude.
- 2.
- In the loaded position-tracking tests, aerodynamic actions on the control surface are modeled as an equivalent torsional spring with constant stiffness Kaero, acting on the EMA output shaft (44).
The tests are conducted using sinusoidal commands with amplitudes of 0.1 deg, 1 deg, and 10 deg. Also, to assess the dynamic behavior in the presence of actuator and control loop saturations, a loaded step-tracking test with a large deflection amplitude (10 deg) is performed.
- 3.
- The EMA dynamic compliance is derived, imposing harmonic and step-like loads of a 1 Nm amplitude.
To quantify the energetic benefit of MPC, the percentage energy reduction is defined as in (45), where the energy terms (EMPC and EPI) are evaluated according to the respective power integral (46).
To assess the robustness of the control strategies, a reference test sequence is designed. The actuator is first commanded to track and hold a 1 deg position step command under aerodynamic spring load. Subsequently, an external load step of 1 Nm is applied on the output shaft to evaluate the ability to reject gust disturbances. The robustness analysis is conducted in two phases. First, a comprehensive single-parameter sensitivity analysis is carried out by individually varying several parameters of the EMA nonlinear model. Due to the high inherent robustness of both controllers, only the most relevant results are reported, related to the variation in the following parameters:
- The PMSM phase resistance Rph as a function of the windings temperature;
- The PMSM torque constant kt;
- The friction torque multiplier Kf;
- The equivalent aerodynamic spring load stiffness Kaero.
Figure 7 displays the ten selected points for each parameter along with their mean values (used as the baseline) and the standard deviation.
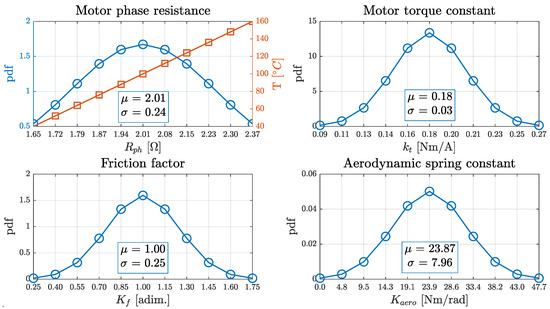
Figure 7.
Gaussian variation in the parameters included in the robustness analysis.
As a second step, focusing on MPC, a multi-parameter robustness analysis is performed to account for potential nonlinear interactions among uncertainties. A Monte Carlo-like approach is employed to generate 103 combinations of the parameters kt, Kf, and Kaero. The MPC robustness is then evaluated in comparison with the baseline performance. Key statistic metrics include the deviation in the position-tracking error (47) and the deviation in the electrical power consumption (48), providing a quantitative assessment of tracking accuracy and energy efficiency under uncertainty. For each Monte Carlo run and for both performance metrics, the four statistical moments (the mean, the standard deviation, the skewness, and the kurtosis) are computed over the simulation timespan Nsim. This analysis intended to support a statistical robustness evaluation by estimating the likely distribution of performance metrics across a representative range of uncertain conditions.
3. Results
3.1. Proportional–Integral Controller Optimization
Figure 8, Figure 9 and Figure 10 provide a concise overview of the main trends observed in the PI cost functions. Figure 8 shows the individual cost terms plotted against the normalized locations of the zeros placement: the x-axis reports , the y-axis reports , and the different surfaces correspond to different values of . The results from both the position-tracking and disturbance rejection tests suggest that, for each performance metric, the corresponding pair of cost functions exhibited similar trends, hence, the definitions (17)–(19) illustrated in Figure 9. Conversely, position- and speed-related cost functions displayed opposite trends: combinations that minimized inevitably increased , emphasising the necessity of a multi-objective optimization. The current loop zero had only a marginal influence on the power cost index of the disturbance rejection tests. Finally, Figure 10 locates every controller design in the three-dimensional space (, , ). The plane (49) is tangent to the Pareto front of the multi-objective optimization exactly at a single point (highlighted), which, therefore, represents the global optimum and the recommended zero placement configuration for PI design, reported numerically in Table 4.
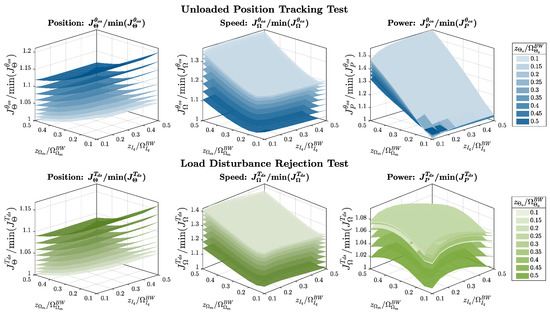
Figure 8.
Cost functions’ variation with PIs’ zeros placement.
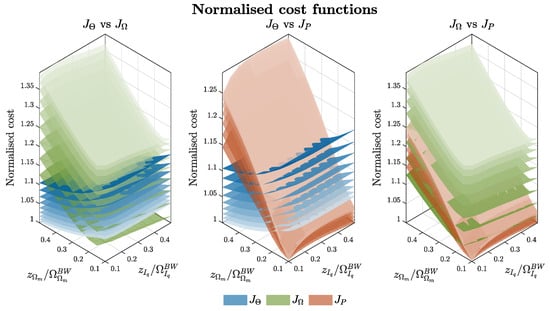
Figure 9.
Normalized cost functions comparison (increasing shade color with position loop zero).
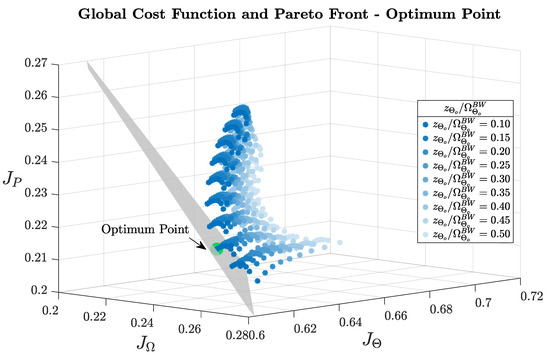
Figure 10.
Global cost function and optimum point.

Table 4.
Optimized PI controllers’ parameters.
3.2. PI and MPC-Based Control Performance Comparison
3.2.1. Unloaded Position-Tracking Tests
The Bode diagram in Figure 11 compares the MPC- and PI-based systems’ frequency responses during unloaded position-tracking tests. The acceptance mask for the frequency response is defined as follows.
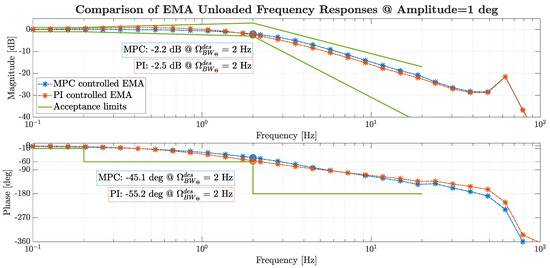
Figure 11.
Unloaded frequency response with 1 deg command amplitude.
- At frequencies lower than 0.2 Hz, the magnitude shall remain within ±1 dB, while the phase shall be higher than −10 deg.
- For frequencies between 0.2 Hz and 2 Hz, a linear increase in the magnitude is allowed till ±3 dB at the design bandwidth, whereas the phase shall remain above −60 deg.
- Beyond 2 Hz and up to 20 Hz, the magnitude is expected to decay with a slope between −20 dB/dec and −40 dB/dec, while the phase must be greater than −180 deg.
While both architectures achieved the nominal position-loop bandwidth, the MPC-controlled EMA exhibited a flatter gain profile and reduced phase lag up to approximately 6 Hz, suggesting enhanced dynamic performance. Moreover, both systems exhibited a resonance peak around 60 Hz due to mechanical transmission compliance, located well beyond the closed-loop position bandwidth. Notably, the peak amplitude was strongly attenuated, despite the absence of explicit deformation compensation loops.
The computational effort required by both control strategies was evaluated using the Simulink Profiler tool, which measured the execution time of the MPC and PI blocks during a one-second simulation with a step-like position command, performed under identical hardware conditions (an ASUS FX607VU laptop, an Intel Core i7-13620H processor, and single-threaded execution). Despite its higher algorithmic complexity, the MPC controller exhibited a low computational load, requiring only 2.23 μs per iteration, compared with 0.80 μs for the PI controller, indicating the feasibility of MPC real-time implementation without extra processing resources at a typical control rate (e.g., 10 kHz).
3.2.2. Loaded Position-Tracking Tests
Figure 12 shows the loaded frequency response at increasing levels of command amplitude. At 0.1 deg, typical of aircraft stability augmentation functions, the PI controller suffered early gain attenuation and phase lag, while MPC maintained full sensitivity at small commands. At 1 deg, representative of typical autopilot commands, both controllers met the performance requirements. Under extreme maneuvers (10 deg), saturation effects caused both to exceed the acceptance limits.
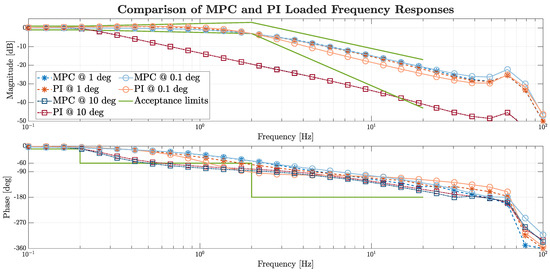
Figure 12.
Frequency response under aerodynamic loads.
Figure 13 illustrates the time-domain response obtained during the loaded step-tracking test with a large deflection amplitude (10 deg). Although actuator and regulator saturation led to performance limitations in both architectures, the MPC-controlled system—despite not including an explicit anti-windup scheme—exhibited a shorter settling time, reduced overshoot, and, consequently, faster position error compensation compared with the PI-based counterpart, for which an anti-windup strategy was required, indicating adequate robustness in nonlinear operating conditions.
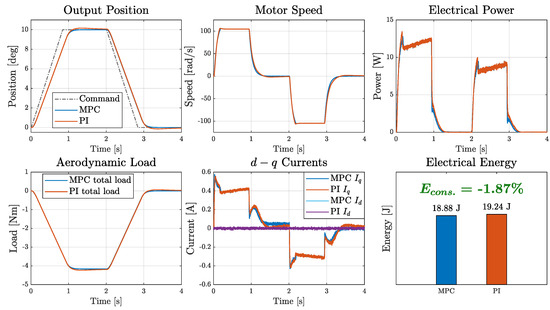
Figure 13.
Saturation effects under large deflections (10 deg) and aerodynamic loads.
3.2.3. Load Disturbance Rejection Tests
The response of the EMA to a step-like gust disturbance is shown in Figure 14. Despite a comparable peak in the output position, the MPC-controlled actuator returned to equilibrium significantly faster, demonstrating superior damping. This improved rejection capability was further confirmed by the motor speed and current profiles: while PI induced strong oscillations, the MPC ensured smoother transients. In addition, energy consumption was reduced by approximately 20%, highlighting MPC as a promising solution also for aircraft secondary control surfaces.
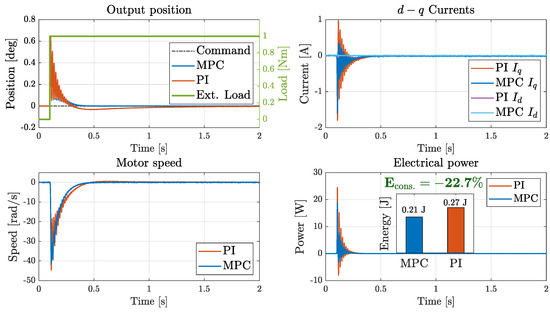
Figure 14.
Rejection to 1 Nm step of external load.
The Bode diagram of the EMA dynamic compliance, defined as the transfer function from external torque input to the angular displacement, is illustrated in Figure 15. Around the design bandwidth, the MPC achieved slightly greater load attenuation and a higher phase lead, enabling faster compensation of the disturbance. At low frequencies, PI outperformed MPC due to better phase anticipation. In the high frequency range, the responses of the two controllers converged, as the actuator resonance mode dominated the overall dynamics.
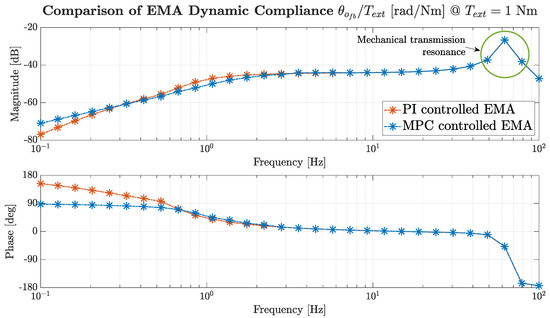
Figure 15.
Dynamic compliance at 1 Nm harmonic load input.
3.3. Robustness Analysis
The time-domain responses of MPC- and PI-controlled EMAs under single-parameter variation are illustrated in Figure 16, Figure 17, Figure 18 and Figure 19. Figure 16 illustrates the effect of temperature-induced variation in the motor phase resistance. While the overall dynamic response remained robust for both controllers, the increased resistance led to higher Joule losses, which reflected directly in the power and energy consumption, with the MPC efficiency gain over the PI widening as temperature increased.
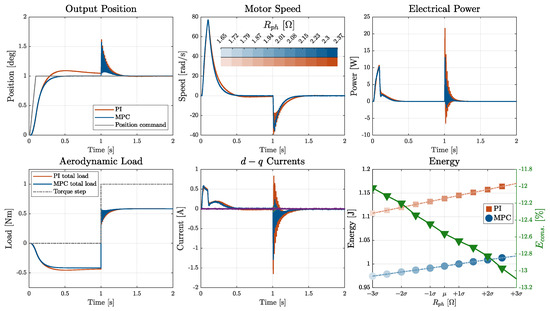
Figure 16.
Motor phase resistance effect of MPC- and PI-controlled EMAs.
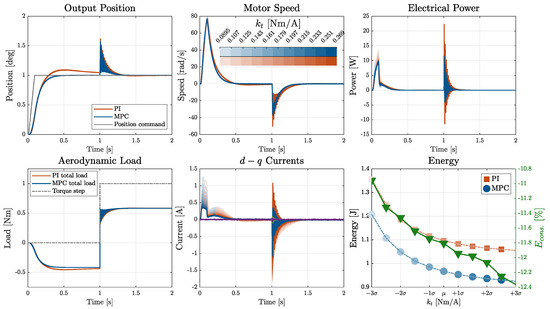
Figure 17.
Motor torque constant effect on MPC- and PI-controlled EMAs.
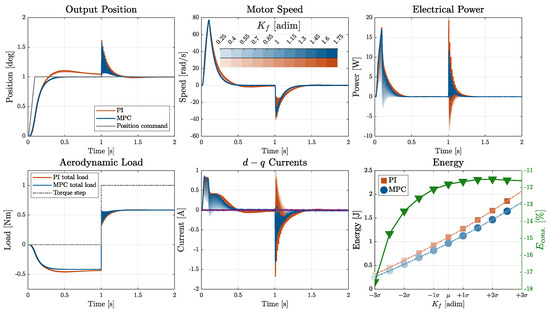
Figure 18.
Friction multiplier effect on MPC- and PI-controlled EMAs.
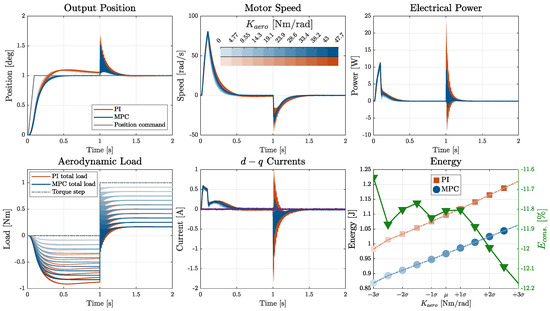
Figure 19.
Aerodynamic spring load stiffness effect on MPC- and PI-controlled EMAs.
Considering the variation in the motor torque constant (Figure 17), both control strategies exhibited strong robustness in the output position response. However, significant sensitivity was observed in the electrical quantities. At lower values of the torque constant kt, a higher quadrature current is required to generate the same motor torque, resulting in increased power peaks in both systems. Nevertheless, in this extreme scenario, the relative energy saving achieved by the MPC strategy became even more evident, highlighting its superior efficiency.
Uncertainty in the friction coefficients (Figure 18) introduced noticeable deviations, not only in the electrical but also in the mechanical responses. Deviations in the output position became significant, particularly for the PI controller, highlighting its higher sensitivity to friction-induced drag. The MPC controller, instead, exhibited improved consistency in position tracking and faster recovery following the disturbance, while showing reduced energy consumption, especially under severe parameter deviations.
Unlike the previous cases, variations in Kaero (Figure 19) influenced the external load model rather than the intrinsic characteristics of the actuator. The MPC controller was able to leverage this variation more effectively, slightly enhancing its energy efficiency from the unloaded condition up to the maximum aerodynamic load.
The second phase of the analysis focused on a detailed robustness characterization of the MPC with respect to combined variations in the most influential parameters, kt, Kf, and Kaero. Figure 20 shows the statistical distribution of the position error deviation across all Monte Carlo simulations, in terms of the mean, standard deviation, skewness, and kurtosis. The distribution of the mean value, centered near zero with a slight positive bias, indicated that the tracking performance was generally preserved. The standard deviation revealed a multi-modal profile, suggesting the presence of distinct sensitivity clusters due to the discrete influence of the Kaero. The skewness values were broadly distributed around zero, showing no dominant direction asymmetry. The high kurtosis observed across the dataset confirmed a leptokurtic distribution, characterized by a non-negligible occurrence of extreme outliers. These cases represented critical parameter combinations that led to significant deviations in tracking performance.
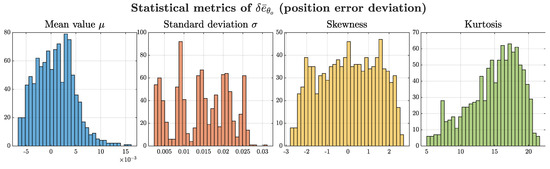
Figure 20.
Statistical metrics of position error deviation under combined parameter variations.
To better understand the interaction between uncertain parameters and their impact on control performance, the statistical metrics of the position error deviation were mapped over the kt − Kf plane and layered with Kaero values (Figure 21). The mean and standard deviation plots revealed a reduction in control effectiveness under conditions of low electro-mechanical coupling combined with high friction and external loads.
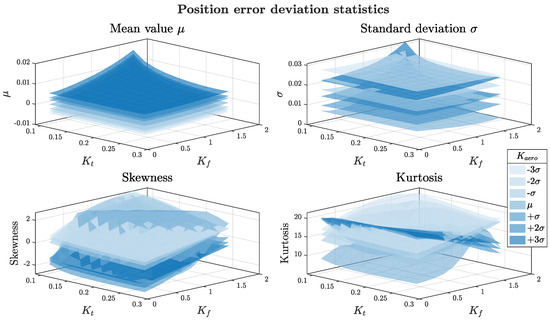
Figure 21.
Dependency of the position error deviation statistical metrics on the three parameters.
The power consumption deviation metrics are summarized in Figure 22. The distribution of the mean values was predominantly non-negative and slightly right-skewed, indicating that most uncertain configurations tended to increase average power consumption compared with the nominal scenario. Notably, a secondary mode with negative values emerged, suggesting that a subset of parameter combinations can also lead to net energy savings. This behavior aligned with the bimodal trend observed in the skewness plot. The heavy-tailed standard deviation suggested nonlinear amplification of power fluctuations under uncertainty. The kurtosis appeared strongly leptokurtic, with frequent extreme outliers. This reflected the system’s susceptibility to large energetic deviations under specific uncertainty conditions, in contrast with the more constrained behavior observed in the position error analysis.
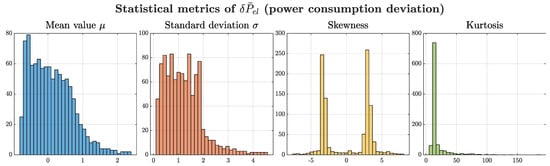
Figure 22.
Statistical metrics of the power consumption deviation under combined parameter variations.
Figure 23 is useful for identifying specific regions where strong power performance degradation occurred. Similarly to the position trend, the mean and standard deviation increased significantly for low kt and high Kf, highlighting a critical region for EMA robustness. The skewness confirmed highly asymmetric and heavy-tailed behavior in the same region. Interestingly, the combined influence of extreme values of Kaero and kt appeared secondary in terms of means and standard deviations but had a significant impact on kurtosis, suggesting that certain parameter combinations might have amplified rare, yet extreme, power deviations.
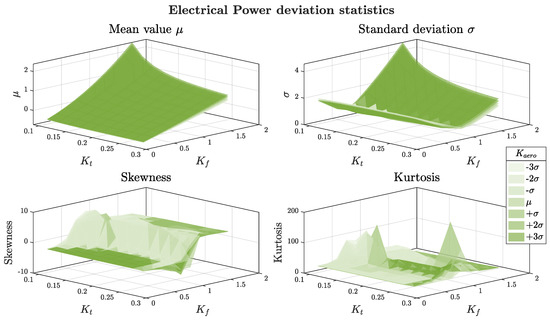
Figure 23.
Dependency of the power deviation statistical metrics on the three parameters.
4. Discussion
This study provides a comprehensive assessment of the performance and robustness of conventional PI-based and advanced MPC strategies applied to an electro-mechanical actuator for primary flight control surfaces. The findings highlight distinct response patterns between conventional PI-based and model predictive control strategies, driven by their respective structural characteristics and interaction with system dynamics. To ensure a fair assessment, the baseline PI controller was first tuned through a multi-objective optimization procedure, balancing dynamic response and power consumption. Nevertheless, the MPC controller consistently outperformed the PI architecture in terms of both dynamic response and energy efficiency, across test scenarios representative of primary and secondary flight control applications. Notably, this was obtained without a significant increase in computational cost, as the simulation times remained comparable.
The comparison of PI and MPC robustness under single-parameter variations highlighted a major degradation in PI performance under high friction, a low torque constant, and stiff aerodynamic loads. In contrast, the MPC demonstrated greater overall stability, enabled by its predictive formulation, even relying on a non-adaptive embedded model.
The robustness characterization of the MPC design was further assessed via Monte Carlo analysis over a multidimensional uncertainty space. The results confirmed that control effectiveness was not uniformly distributed across the uncertainty space but, rather, influenced by nonlinear interactions between electro-mechanical and external load conditions. It also enabled the identification of critical parameter regions and rare but impactful deviations on position tracking accuracy and power consumption, which are especially relevant for control system design targeting certification and fault resilience in aerospace applications.
Although this study covered a broad range of single and combined parameter variations, some limitations remain. Mechanical degradation and failure modes were not included in the current model and may further influence the robustness envelope. Simulation model refinements are planned to account for power electronics switching effects and provide a more accurate description of friction dynamics. While the current MPC formulation does not incorporate real-time linearization or uncertainty estimation, such features could enhance robustness, although their computational impact must be carefully evaluated. Experimental testing on physical EMA hardware is expected to complement the simulation-based findings and provide insight into real-world performance under operational constraints.
5. Conclusions
This study proposed a simplified and real-time implementable MPC strategy for electro-mechanical actuators in aerospace applications. The control architecture was validated through an extensive simulation campaign, demonstrating improved tracking performance, energy efficiency, and load disturbance rejection compared with an optimized PI benchmark. The robustness-oriented methodology confirmed the MPC’s reliability under both individual and combined parameter variations, supporting its suitability for both primary and potentially secondary flight control surfaces.
Author Contributions
Conceptualization and methodology, M.L. and G.D.R.; software, M.L.; validation, M.L., M.N., and G.D.R.; formal analysis, M.N. and G.D.R.; investigation, M.L. and G.D.R.; resources, M.N. and N.B.; data curation, M.L.; writing—original draft preparation, M.L.; writing—review and editing, G.D.R.; visualization, M.N. and N.B.; supervision, M.N., N.B., and G.D.R.; project administration, M.N., N.B., and G.D.R.; funding acquisition, M.N. and N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Authors Marco Lucarini, Marco Nardeschi and Nicola Borgarelli were employed by the company UMBRAGROUP SpA. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sarlioglu, B.; Morris, C.T. More Electric Aircraft: Review, Challenges, and Opportunities for Commercial Transport Aircraft. IEEE Trans. Transp. Electrif. 2015, 1, 54–64. [Google Scholar] [CrossRef]
- Buticchi, G.; Wheeler, P.; Boroyevich, D. The More-Electric Aircraft and Beyond. Proc. IEEE 2023, 111, 356–370. [Google Scholar] [CrossRef]
- Schäfer, A.W.; Barrett, S.R.H.; Doyme, K.; Dray, L.; Gnadt, A.R.; Self, R.; O’Sullivan, A.; Synodinos, A.P.; Torija, A.J. Technological, economic and environmental prospects of all-electric aircraft. Nat. Energy 2019, 4, 160–166. [Google Scholar] [CrossRef]
- Sahoo, S.; Zhao, X.; Kyprianidis, K. A Review of Concepts, Benefits, and Challenges for Future Electrical Propulsion-Based Aircraft. Aerospace 2020, 7, 44. [Google Scholar] [CrossRef]
- Johannisson, J.; Asp, L.E.; Carlstedt, D.; Zenkert, D.; Johansen, M.; Carlson, J.; Willgert, M. Structural Batteries for Aeronautic Applications—State of the Art, Research Gaps and Technology Development Needs. Aerospace 2022, 9, 7. [Google Scholar] [CrossRef]
- Barzkar, A.; Ghassemi, M. Electric Power Systems in More and All Electric Aircraft: A Review. IEEE Access 2020, 8, 169314–169332. [Google Scholar] [CrossRef]
- Savy, M. Control Surface Actuation for High Aspect Ratio Wings. In Proceedings of the Recent Advances in Aerospace Actuation Systems and Components, Toulouse, France, 25–28 September 2023. [Google Scholar]
- D’Andrea, M.; Di Domenico, G.; Pizzoni, L.; Borgarelli, N. Electromagnetic Design of a Fault-Tolerant Electromechanical Actuator for Landing Gear. In Proceedings of the 2022 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 22–24 June 2022; pp. 677–682. [Google Scholar] [CrossRef]
- Salas, F. Electronics in Harsh Environment Reliability Update. In Proceedings of the Recent Advances in Aerospace Actuation Systems and Components, Toulouse, France, 25–28 September 2023. [Google Scholar]
- Pispola, G.; Corradi, G.; Lavatelli, A.; Telteu, D. Advances in Mechanical Transmission Design for Flight Control EMAS. In Proceedings of the Recent Advances in Aerospace Actuation Systems and Components, Toulouse, France, 21–23 May 2025. [Google Scholar]
- Di Rito, G.; Galatolo, R.; Schettini, F. Experimental and simulation study of the dynamics of an electro-mechanical landing gear actuator. In Proceedings of the 30th Congress of the International Council of the Aeronautical Sciences (ICAS), Daejeon, Republic of Korea, 25–30 September 2016. [Google Scholar]
- Di Rito, G.; Kovel, R.; Nardeschi, M.; Borgarelli, N.; Luciano, B. Minimisation of Failure Transients in a Fail-Safe Electro-Mechanical Actuator Employed for the Flap Movables of a High-Speed Helicopter-Plane. Aerospace 2022, 9, 527. [Google Scholar] [CrossRef]
- Di Rito, G.; Luciano, B.; Borgarelli, N.; Nardeschi, M. Model-Based Condition-Monitoring and Jamming-Tolerant Control of an Electro-Mechanical Flight Actuator with Differential Ball Screws. Actuators 2021, 10, 230. [Google Scholar] [CrossRef]
- Di Rito, G.; Luciano, B.; Borgarelli, N.; Nardeschi, M. Health-Monitoring of a Jamming Tolerant Electro-Mechanical Actuator with Differential Ball Screws. In Proceedings of the 8th IEEE International Workshop on Metrology for Aerospace, Pisa, Italy, 22–24 June 2020. [Google Scholar] [CrossRef]
- Arriola, D.; Thielecke, F. Model-based design and experimental verification of a monitoring concept for an active-active electromechanical aileron actuation system. Mech. Syst. Signal Process. 2017, 94, 322–345. [Google Scholar] [CrossRef]
- Maré, J.-C. Review and Analysis of the Reasons Delaying the Entry into Service of Power-by-Wire Actuators for High-Power Safety-Critical Applications. Actuators 2021, 10, 233. [Google Scholar] [CrossRef]
- Biagetti, F.; Borgarelli, N.; Malleret, F.; Pelliccia, S. Fault-Tolerant Electric Actuation: A Condition to Make Electric Platforms Certifiable. In Proceedings of the Vertical Flight Society’s 80th Annual Forum & Technology Display, Montréal, QC, Canada, 7–9 May 2024. [Google Scholar]
- Barambones, O.; Cortajarena, J.A.; Alkorta, P. New Control Schemes for Actuators. Actuators 2024, 13, 99. [Google Scholar] [CrossRef]
- Di Rito, G.; Kovel, R.; Luciano, B.; Salvi, F.; Nardeschi, M. Failure Transients Characterization for the Qualification of the Fail-Safe EMA Used for the Airbus RACER Flap Movables. In Proceedings of the Recent Advances in Aerospace Actuation Systems and Components, Toulouse, France, 21–23 May 2025. [Google Scholar]
- Rawlings, J.B.; Mayne, D.Q.; Diehl, M. Model Predictive Control: Theory, Computation, and Design, 2nd ed.; Nob Hill Publishing: Madison, WI, USA, 2017. [Google Scholar]
- Camacho, E.F.; Bordons, C. Model Predictive Control, 2nd ed.; Springer: London, UK, 2007; pp. 1–408. [Google Scholar]
- Eren, U.; Prach, A.; Kocer, B.; Raković, S.V.; Kayacan, E.; Açıkmeşe, B. Model Predictive Control in Aerospace Systems: Current State and Opportunities. J. Guid. Control Dyn. 2017, 40, 1541–1566. [Google Scholar] [CrossRef]
- RTCA. DO-178C: Software Considerations in Airborne Systems and Equipment Certification; RTCA, Inc.: Washington, DC, USA, 2011. [Google Scholar]
- Kopf, M.; Bullinger, E.; Giesseler, H.; Adden, S.; Findeisen, R. Model Predictive Control for Aircraft Load Alleviation: Opportunities and Challenges. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 2417–2424. [Google Scholar] [CrossRef]
- Dunham, W.; Hencey, B.; Girard, A.R.; Kolmanovsky, I. Distributed Model Predictive Control for More Electric Aircraft Subsystems Operating at Multiple Time Scales. IEEE Trans. Control Syst. Technol. 2020, 28, 2177–2190. [Google Scholar] [CrossRef]
- Hegrenæs, Ø.; Gravdahl, J.; Tøndel, P. Spacecraft Attitude Control Using Explicit Model Predictive Control. Automatica 2005, 41, 2107–2114. [Google Scholar] [CrossRef]
- Ru, P.; Subbarao, K. Nonlinear Model Predictive Control for Unmanned Aerial Vehicles. Aerospace 2017, 4, 31. [Google Scholar] [CrossRef]
- Garcia, G.A.; Keshmiri, S.S.; Stastny, T. Robust and Adaptive Nonlinear Model Predictive Controller for Unsteady and Highly Nonlinear Unmanned Aircraft. IEEE Trans. Control Syst. Technol. 2015, 23, 1620–1627. [Google Scholar] [CrossRef]
- Chai, S.; Wang, L.; Rogers, E. Model Predictive Control of a Permanent Magnet Synchronous Motor. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 1928–1933. [Google Scholar] [CrossRef]
- Spatola, S.; Pastorelli, M.A. Predictive Control of Permanent Magnets Synchronous Motors. Master’s Thesis, Politecnico di Torino, Turin, Italy, 2019. [Google Scholar]
- Cimini, G.; Bernardini, D.; Bemporad, A.; Levijoki, S. Online Model Predictive Torque Control for Permanent Magnet Synchronous Motors. In Proceedings of the IEEE International Conference on Industrial Technology, Seville, Spain, 17–19 March 2015; pp. 2308–2313. [Google Scholar] [CrossRef]
- Hasan, M.D.S.; Hafni, A.E.; Kennel, R. Position Control of an Electromagnetic Actuator Using Model Predictive Control. In Proceedings of the 2017 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics, Pilsen, Czech Republic, 11–13 September 2017; pp. 37–41. [Google Scholar] [CrossRef]
- Borgarelli, N.; Pizzoni, L. Rotary Mechanical Screw Transmission. EP4042039, 9 October 2019. [Google Scholar]
- Research and Development–European Commission, Clean Aviation, CleanSky2 Demonstrators, RACER Compound Helicopter. Available online: https://www.clean-aviation.eu/clean-sky-2/key-demonstrators/racer-compound-helicopter (accessed on 30 June 2025).
- Andersson, S.; Söderberg, A.; Björklund, S. Friction models for sliding dry, boundary and mixed lubricated contacts. Tribol. Int. 2007, 40, 580–587. [Google Scholar] [CrossRef]
- Chen, S.; Tang, J.; Luo, C.; Wang, Q. Nonlinear dynamic characteristics of geared rotor bearing systems with dynamic backlash and friction. Mech. Mach. Theory 2011, 46, 466–478. [Google Scholar] [CrossRef]
- Yao, H.; Yan, Y.; Shi, T.; Zhang, G.; Wang, Z.; Xia, C. A Novel SVPWM Scheme for Field-Oriented Vector-Controlled PMSM Drive System Fed by Cascaded H-Bridge Inverter. IEEE Trans. Power Electron. 2021, 36, 8988–9000. [Google Scholar] [CrossRef]
- Sul, S. Control of Electric Machine Drive Systems, 1st ed.; Wiley-IEEE Press: Piscataway, NJ, USA, 2011; ISBN 978-0470590799. [Google Scholar]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB, 1st ed.; Springer: London, UK, 2009. [Google Scholar] [CrossRef]
- Hildreth, C. A quadratic programming procedure. Nav. Res. Logist. 1957, 4, 79–85. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).