Fault Diagnosis Method of Micro-Motor Based on Jump Plus AM-FM Mode Decomposition and Symmetrized Dot Pattern
Abstract
1. Introduction
2. Basic Theory of JMD-SDP-ICNN
2.1. The Principle of Jump Plus AM-FM Mode Decomposition
- To effectively extract the oscillatory components from the signal, the bandwidth of the oscillatory components must be minimized. The optimization equation that employs the VMD algorithm is as follows:where denotes the partial derivative with respect to time, and is the center frequency associated with each mode. represents the analytic signal, and refers to the Hilbert transform. estimates the bandwidth of the oscillatory mode of the signal.
- The extraction of the jump component from the signal is accomplished by applying a reparametrized and rescaled minimax concave penalty term [22]. By imposing constraints on the derivative of the jump component, this approach enhances the representation of discontinuities while effectively preserving the amplitude of the piecewise continuous signal component.where represents the first derivative of the jump term, and is defined as a piecewise quadratic function as follows [23]:where the parameter alters the degree of nonconvexity. When , the minimax concave penalty term is defined as and , whereas tends toward the pseudo-norm.
- To extract the jump and oscillation variables from , we combined from Equation (2) and from Equation (3), using the parameters and to balance the two terms. Simultaneously, an auxiliary variable was introduced to address the issue of non-differentiability in the term. This approach allows the formulation of the problem using the following optimization equation:
2.2. The SDP Method
2.3. ICNN Method
2.4. Overall Process of JMD-SDP-ICNN
3. Experimental Analysis and Verification
3.1. Experimental Setup
3.2. Data Acquisition
4. Fault Diagnosis Analysis of Micro-Motor
- (1)
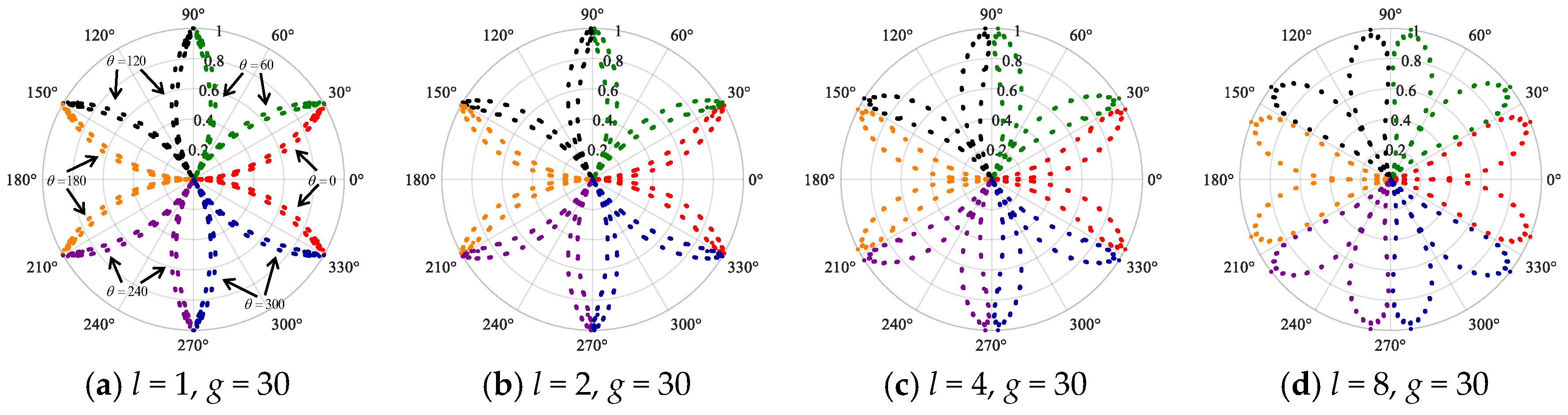
- Comparison and verification of different SDP parameter selection schemes
- (2)
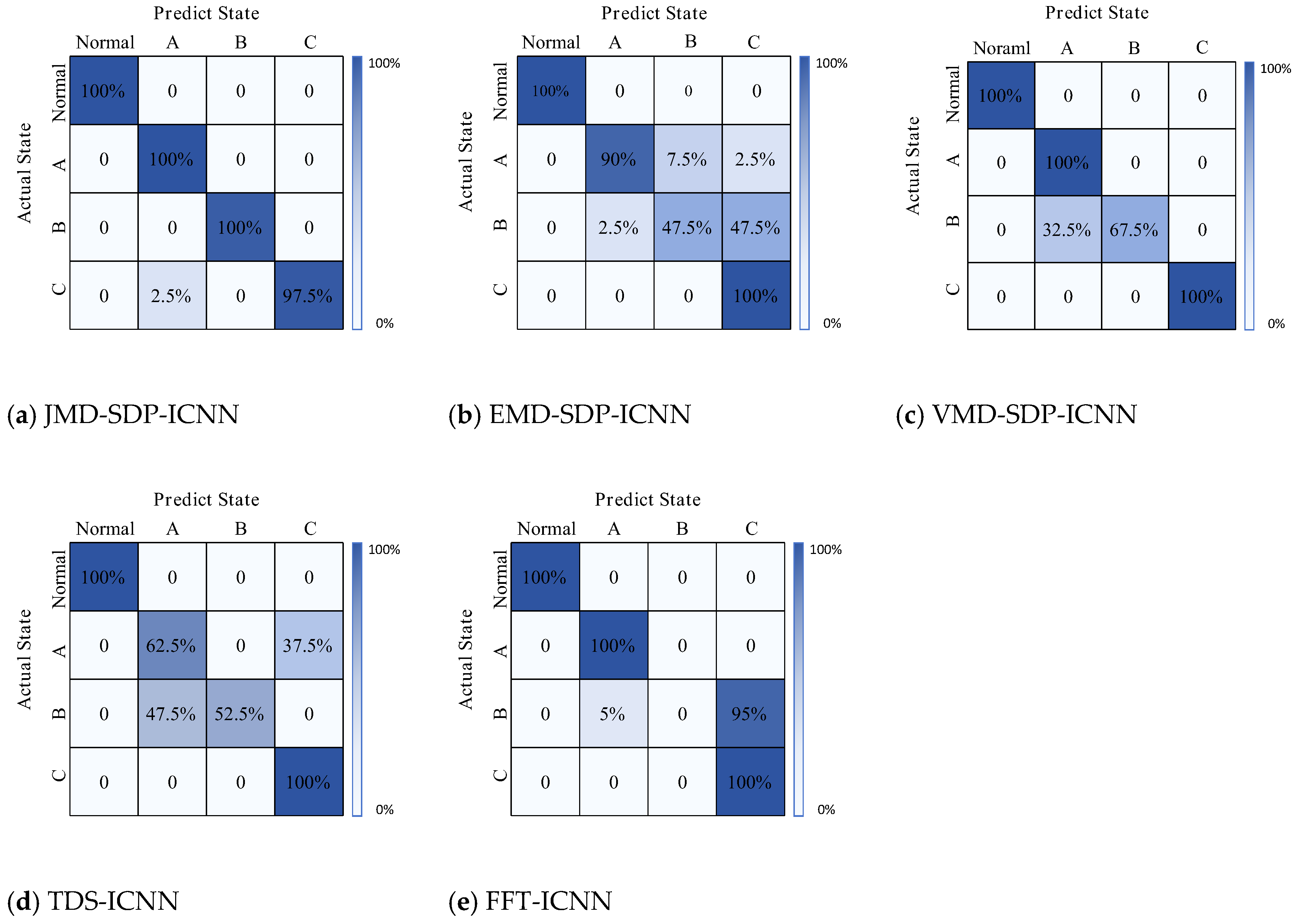
- Comparison and verification of different decomposition approaches
- (3)
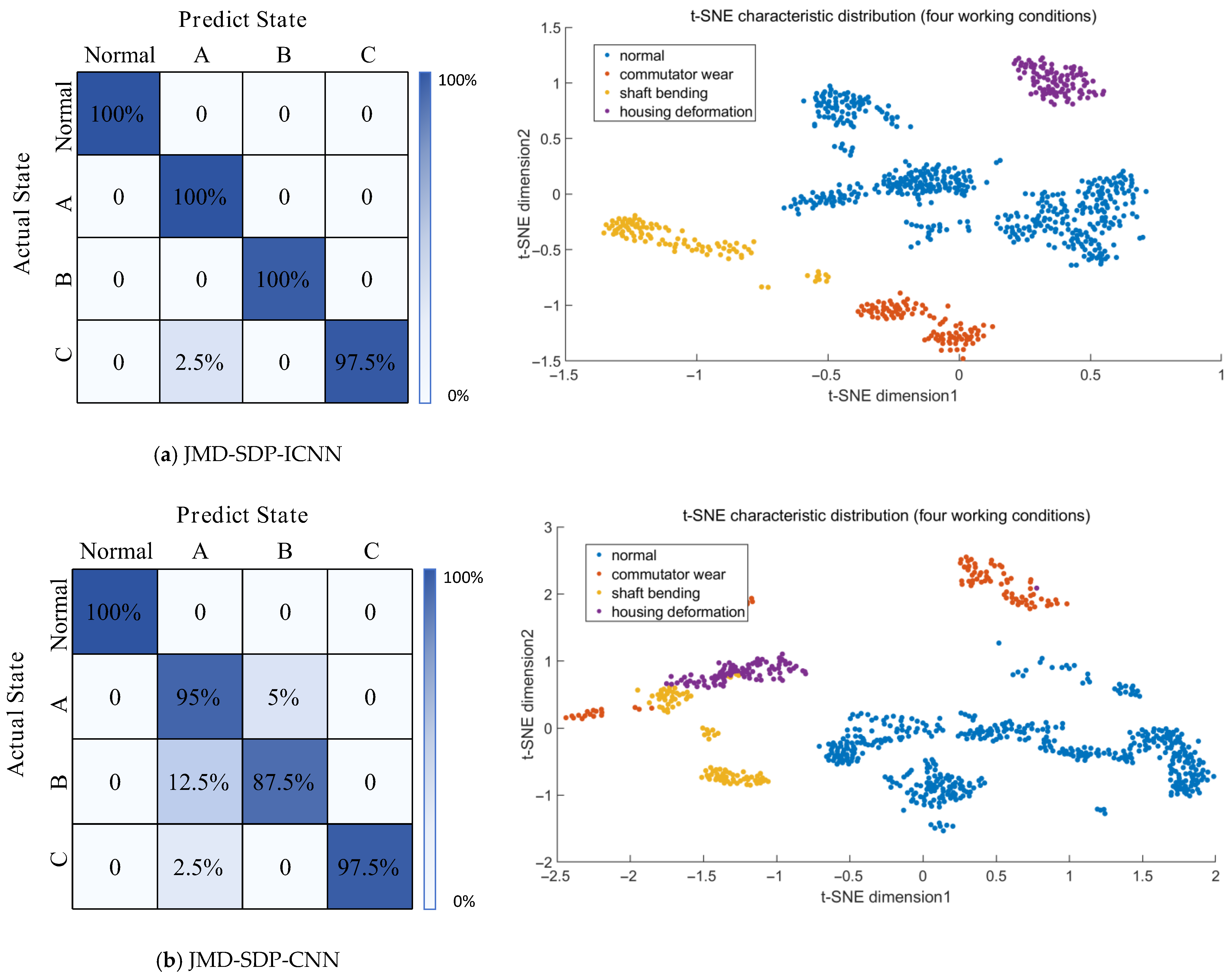
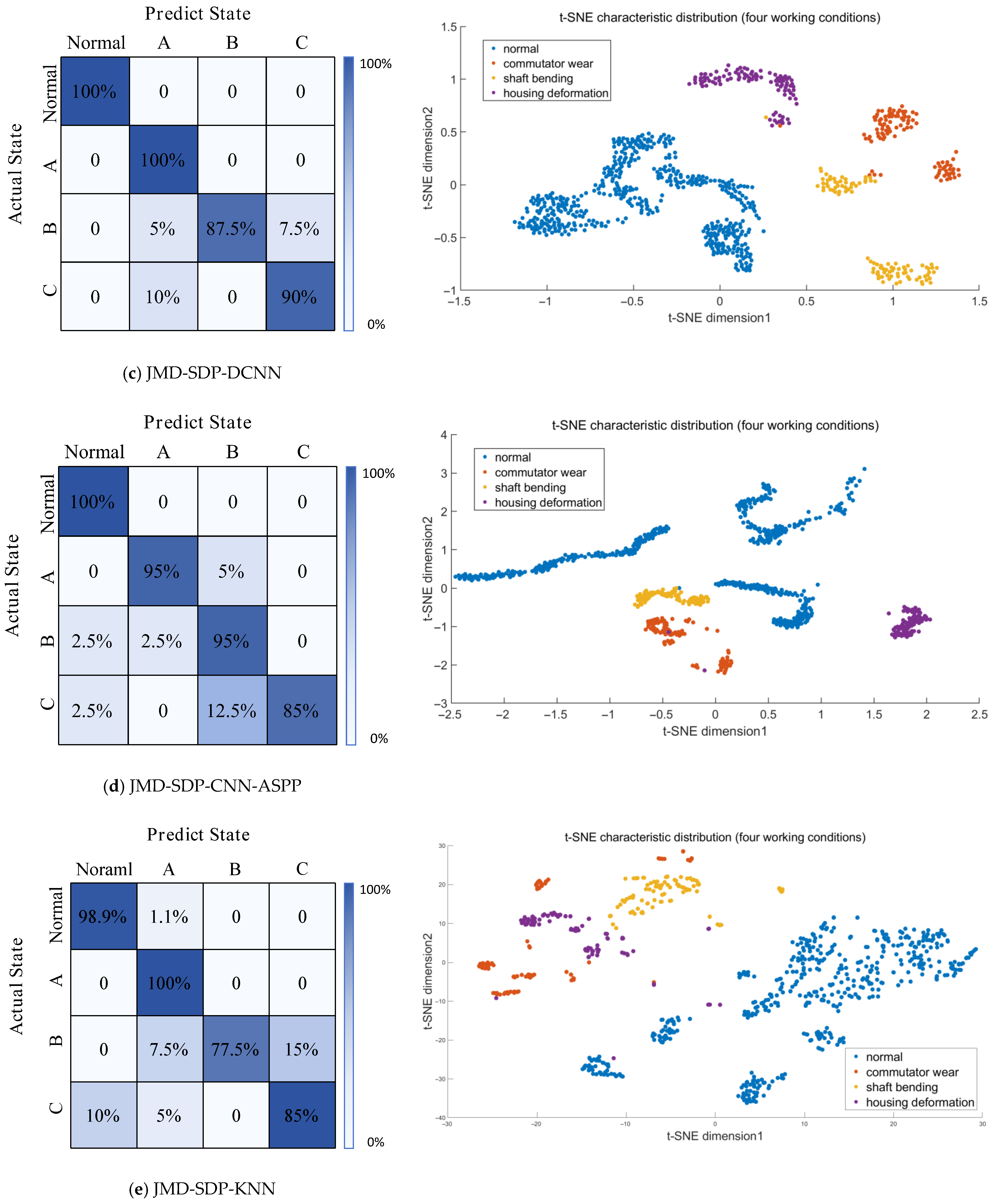
- Comparison and verification of different trained models
- (4)
- Comparison and verification of another public dataset
5. Conclusions
- (1)
- Firstly, the JMD method was employed to effectively solve the problem of signal aliasing, which is often encountered in traditional signal processing. This method offers distinct advantages, particularly in handling jump signals. By constructing non-stationary signals for verification, it is demonstrated that the method is especially suitable for separating characteristic components of motor fault signals.
- (2)
- Secondly, the multi-channel SDP visualization method was introduced to effectively convert the selected IMF components into 2D faulty petal images in polar space. This technique enhances the clarity of signal features and supports intuitive fault classification.
- (3)
- At last, we proposed an ICNN method with the LeakyReLU activation function to replace the traditional CNN to identify SDP images. This modification allows the network to continue receiving gradient updates even when it encounters negative inputs during training, ultimately enhancing the stability and performance of the fault type identification model.
- (4)
- The ICNN fault classification model was used to classify the generated SDP images efficiently. Through experimental verification, this method performs well in multiple fault classification tests, and the accuracy rates on the self-built platform and the CWRU public dataset reached 99.2381% and 99.9091%, respectively, which has significant advantages compared with other methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, H.; Ye, M.; Nelson, B.J.; Wang, X. A Selectively Controllable Triple-Helical Micromotor. IEEE Robot. Autom. Lett. 2024, 9, 4742–4749. [Google Scholar] [CrossRef]
- Niu, Y.; Jin, X.; Wen, Z. Research on Command and Control Technology in Small-UAV Defense System. In Proceedings of the 2021 International Conference on Computer Information Science and Artificial Intelligence, Kunming, China, 17–19 September 2021; pp. 673–677. [Google Scholar] [CrossRef]
- Sawa, K.; Ueno, T.; Nakano, K.; Toya, K. Effects of Brush Spring Force on Brush Wear and Arc Behaviors of Small DC Motor. In Proceedings of the 2023 IEEE 68th Holm Conference on Electrical Contacts (HOLM), Seattle, WA, USA, 4–11 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Gretskov, A.; Boyarkina, U.; Vorokh, D. Application of Radio-Wave Motion Transducers to Measure the Parameters of Bending Vibrations of a Turbine Unit Shaft. In Proceedings of the 2024 IEEE Ural-Siberian Conference on Biomedical Engineering, Radioelectronics and Information Technology (USBEREIT), Yekaterinburg, Russia, 13–15 May 2024; pp. 241–244. [Google Scholar] [CrossRef]
- Wu, J.; Xu, Q.; Xu, L. A Study on Winding MMF Harmonic and Vibration of Polyphase Motor. In Proceedings of the 2021 Power System and Green Energy Conference (PSGEC), Shanghai, China, 20–22 August 2021; pp. 732–737. [Google Scholar] [CrossRef]
- Javorskyj, I.; Yuzefovych, R.; Lychak, O.; Trokhym, G.; Varyvoda, M. Methods of Periodically Non-Stationary Random Processes for Vibrations Monitoring of Rolling Bearing with Damaged Outer Race. Digit. Signal Process. 2024, 145, 104343. [Google Scholar] [CrossRef]
- Han, J.; Song, J.H. Phase Current-Balance Control Using DC-Link Current Sensor for Multiphase Converters with Discontinuous Current Mode Considered. IEEE Trans. Ind. Electron. 2016, 63, 4020–4030. [Google Scholar] [CrossRef]
- Chen, C.; Li, H.; Feng, Y.; Chen, J.; Cai, S.; Yin, J. Research on Low Temperature Characteristics and Application of Temperature Sensor in Alpine Region. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 1551–1556. [Google Scholar] [CrossRef]
- Gu, J.; Peng, Y. An Improved Complementary Ensemble Empirical Mode Decomposition Method and Its Application in Rolling Bearing Fault Diagnosis. Digit. Signal Process. 2021, 113, 103050. [Google Scholar] [CrossRef]
- Chen, J.; Li, S.; Zhu, J.; Liu, M.; Li, R.; Cui, X.; Li, L. Significant Wave Height Prediction Based on Variational Mode Decomposition and Dual Network Model. Ocean Eng. 2025, 323, 120533. [Google Scholar] [CrossRef]
- Nazari, M.; Korshøj, A.R.; ur Rehman, N. Jump Plus AM-FM Mode Decomposition. IEEE Trans. Signal Process 2024, 73, 1081–1093. [Google Scholar] [CrossRef]
- Gbashi, S.M.; Adedeji, P.A.; Olatunji, O.O.; Madushele, N. Optimal Feature Selection for a Weighted K-Nearest Neighbors for Compound Fault Classification in Wind Turbine Gearbox. Results Eng. 2025, 25, 103791. [Google Scholar] [CrossRef]
- Ren, H.; Liu, S.; Qiu, B.; Guo, H.; Zhao, D. A Novel Intelligent Fault Diagnosis Method of Bearing Based on Multi-Head Self-Attention Convolutional Neural Network. Artif. Intell. Eng. Des. Anal. Manuf. AIEDAM 2024, 38, e9. [Google Scholar] [CrossRef]
- Pickover, C.A. On the use of symmetrized dot patterns for the visual characterization of speech waveforms and other sampled data. J. Acoust. Soc. Am. 1986, 80, 955–960. [Google Scholar] [CrossRef]
- Xian, X.; Tang, H.; Tian, Y.; Liu, Q.; Fan, Y. Performance Analysis of Different Machine Learning Algorithms for Identifying and Classifying the Failures of Traction Motors. J. Phys. Conf. Ser. 2021, 2095, 012058. [Google Scholar] [CrossRef]
- Zhu, X.; Hou, D.; Zhou, P.; Han, Z.; Yuan, Y.; Zhou, W.; Yin, Q. Rotor Fault Diagnosis Using a Convolutional Neural Network with Symmetrized Dot Pattern Images. Meas. J. Int. Meas. Confed. 2019, 138, 526–535. [Google Scholar] [CrossRef]
- Rani, S.; Memoria, M.; Almogren, A.; Bharany, S.; Joshi, K.; Altameem, A.; Rehman, A.U.; Hamam, H. Deep Learning to Combat Knee Osteoarthritis and Severity Assessment by Using CNN-Based Classification. BMC Musculoskelet. Disord. 2024, 25, 817. [Google Scholar] [CrossRef] [PubMed]
- Goh, K.W.; Surono, S.; Afiatin, M.Y.F.; Mahmudah, K.R.; Irsalinda, N.; Chaimanee, M.; Onn, C.W. Comparison of Activation Functions in Convolutional Neural Network for Poisson Noisy Image Classification. Emerg. Sci. J. 2024, 8, 592–602. [Google Scholar] [CrossRef]
- Wang, L.H.; Zhao, X.P.; Wu, J.X.; Xie, Y.Y.; Zhang, Y.H. Motor Fault Diagnosis Based on Short-Time Fourier Transform and Convolutional Neural Network. Chin. J. Mech. Eng. 2017, 30, 1357–1368. [Google Scholar] [CrossRef]
- Xing, Y.; Li, H. Rolling Bearing Fault Diagnosis Based on Model Migration. In Intelligent Computing Theories and Application; Lecture Notes in Computer Science; Springer Nature: Berlin, Germany, 2022; Volume 13393, pp. 135–146. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhang, C.H. Nearly Unbiased Variable Selection Under Minimax Concave Penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef]
- Cicone, A.; Huska, M.; Kang, S.H.; Morigi, S. JOT: A Variational Signal Decomposition into Jump, Oscillation and Trend. IEEE Trans. Signal Process. 2022, 70, 772–784. [Google Scholar] [CrossRef]
- Wu, B.; Tang, W.; Zhou, Z.; Tan, Y.; Chen, S.; Feng, Y. An Improved Adaptive EMD-SVD Method for Railway Bridge Dynamic LG-Strain Processing under Moving Trainloads. Structures 2025, 80, 109777. [Google Scholar] [CrossRef]
- Long, Z.; Guo, J.; Ma, X.; Wu, G.; Rao, Z.; Zhang, X.; Xu, Z. Motor Fault Diagnosis Based on Multisensor-Driven Visual Information Fusion. ISA Trans. 2024, 155, 524–535. [Google Scholar] [CrossRef]
- González, J.; Oro, J.M.F.; Delgado, L.; Méndez, D.; Argüelles, K.M.; Velarde-suárez, S.; Rodríguez, D. Symmetrized Dot Pattern Analysis for the Unsteady Vibration State in a Sirocco Fan Unit. Appl. Acoust. 2019, 152, 1–12. [Google Scholar] [CrossRef]
- Xu, X.; Liu, H.; Zhu, H.; Wang, S. Fan Fault Diagnosis Based on Symmetrized Dot Pattern Analysis and Image Matching. J. Sound Vib. 2016, 374, 297–311. [Google Scholar] [CrossRef]
- Gu, Y.; Zeng, L.; Qiu, G. Bearing Fault Diagnosis with Varying Conditions Using Angular Domain Resampling Technology, SDP and DCNN. Measurement 2020, 156, 107616. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, W.; Li, H. Tool Wear Prediction Method Based on Symmetrized Dot Pattern and Multi-Covariance Gaussian Process Regression. Measurement 2022, 189, 110466. [Google Scholar] [CrossRef]
- Shiney, S.A.; Seetharaman, R.; Sharmila, V.J.; Prathiba, S. Deep Learning Based Gasket Fault Detection: A CNN Approach. Sci. Rep. 2025, 15, 4776. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. An Optimized VMD Method and Its Applications in Bearing Fault Diagnosis. Measurement 2020, 166, 108185. [Google Scholar] [CrossRef]









| Methods | JMD | EMD | VMD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IMFs | IMF1 | IMF2 | IMF3 | V | IMF1 | IMF2 | IMF3 | V | IMF1 | IMF2 | IMF3 | V |
| R | 0.9932 | 0.9590 | 0.7528 | 1.0000 | 0.7962 | 0.5511 | 0.7297 | 0.6055 | 0.0012 | 0.2417 | 0.7173 | 0.9535 |
| RMSE | 0.3294 | 0.4055 | 0.9944 | 0.0119 | 2.2932 | 2.1980 | 1.3113 | 7.2384 | 3.4138 | 3.5563 | 1.0478 | 2.3941 |
| MAE | 0.2753 | 0.3391 | 0.8466 | 0.0082 | 0.8992 | 0.6251 | 0.3333 | 3.8500 | 2.8361 | 2.8383 | 0.4316 | 0.8700 |
| Parameters | Voltage | Current | Rotational Speed | Length | Diameter of Housing | Shaft Diameter |
|---|---|---|---|---|---|---|
| Value | 3.7 V | 150 mA | 30,000 rpm | 20 mm | 8.5 mm | 1 mm |
| IMFs | Correlation Coefficient Ri | Energy Ei | Xi | Ranking |
|---|---|---|---|---|
| IMF1 | 0.6384 | 18.66% | 0.4125 | 1 |
| IMF2 | 0.3381 | 3.85% | 0.1883 | 2 |
| IMF3 | 0.2059 | 0.80% | 0.1069 | 3 |
| IMF4 | 0.1333 | 0.82% | 0.0708 | 4 |
| IMF5 | 0.1234 | 0.36% | 0.0635 | 5 |
| IMF6 | 0.0168 | 0.01% | 0.0084 | 6 |
| Parameter Sets | g = 60, l = 8 | g = 90, l = 8 | g = 90, l = 2 | g = 60, l = 2 |
|---|---|---|---|---|
| Accuracy | 99.2381% | 80.4762% | 81.9048% | 84.3809% |
| Schematic diagram |  | 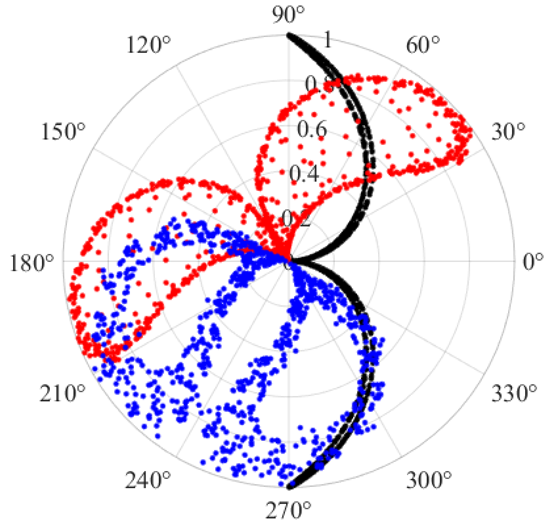 |  | 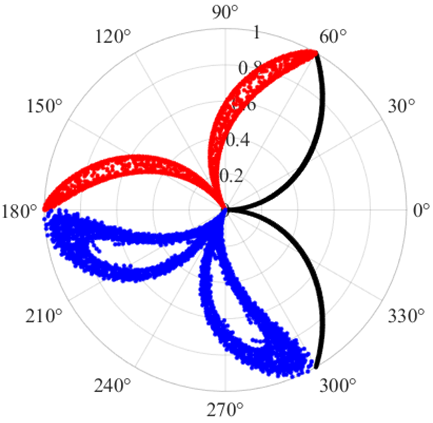 |
| Models | JMD-SDP-ICNN | EMD-SDP-ICNN | VMD-SDP-ICNN | TDS-ICNN | FFT-ICNN |
|---|---|---|---|---|---|
| Accuracy | 99.2381% | 88.2857% | 94.2857% | 83.8095% | 80.9524% |
| Models | Accuracy | Training Time (s) | Number of Iterations |
|---|---|---|---|
| JMD-SDP-ICNN | 99.2381% | 10 | 375 |
| JMD-SDP-CNN | 94.9424% | 14 | 250 |
| JMD-SDP-DCNN | 97.5238% | 37 | 250 |
| JMD-SDP-CNN-ASPP | 95.3333% | 141 | 1500 |
| JMD-SDP-KNN | 92.3810% | 22 | / |
| Models | JMD-SDP-ICNN | JMD-SDP-CNN | JMD-SDP-DCNN | JMD-CNN-ASPP | JMD-KNN |
|---|---|---|---|---|---|
| Accuracy | 99.9091% | 98.6364% | 98.8182% | 98.0909% | 96.3636% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Z.; Bai, Y.; Yu, J.; Chen, J. Fault Diagnosis Method of Micro-Motor Based on Jump Plus AM-FM Mode Decomposition and Symmetrized Dot Pattern. Actuators 2025, 14, 405. https://doi.org/10.3390/act14080405
Gu Z, Bai Y, Yu J, Chen J. Fault Diagnosis Method of Micro-Motor Based on Jump Plus AM-FM Mode Decomposition and Symmetrized Dot Pattern. Actuators. 2025; 14(8):405. https://doi.org/10.3390/act14080405
Chicago/Turabian StyleGu, Zhengyang, Yufang Bai, Junsong Yu, and Junli Chen. 2025. "Fault Diagnosis Method of Micro-Motor Based on Jump Plus AM-FM Mode Decomposition and Symmetrized Dot Pattern" Actuators 14, no. 8: 405. https://doi.org/10.3390/act14080405
APA StyleGu, Z., Bai, Y., Yu, J., & Chen, J. (2025). Fault Diagnosis Method of Micro-Motor Based on Jump Plus AM-FM Mode Decomposition and Symmetrized Dot Pattern. Actuators, 14(8), 405. https://doi.org/10.3390/act14080405






