Continuous Estimation of sEMG-Based Upper-Limb Joint Angles in the Time–Frequency Domain Using a Scale Temporal–Channel Cross-Encoder
Abstract
1. Introduction
- This study constructs a sEMG–elbow-angle dataset consisting of over 100,000 samples collected from seven healthy subjects, providing a valuable data resource for continuous joint-angle estimation research.
- A fixed Input Scaling operation is applied to amplify the time–frequency features, which accelerates model convergence and improves the accuracy of angle estimation.
- We propose a novel STCCE, built upon a Transformer architecture, that integrates multi-scale temporal and channel attention mechanisms to effectively model the mapping from time–frequency sEMG features to joint angles.
2. Experiment Setup and Data Collection
2.1. Experiment Platform
2.2. Participants
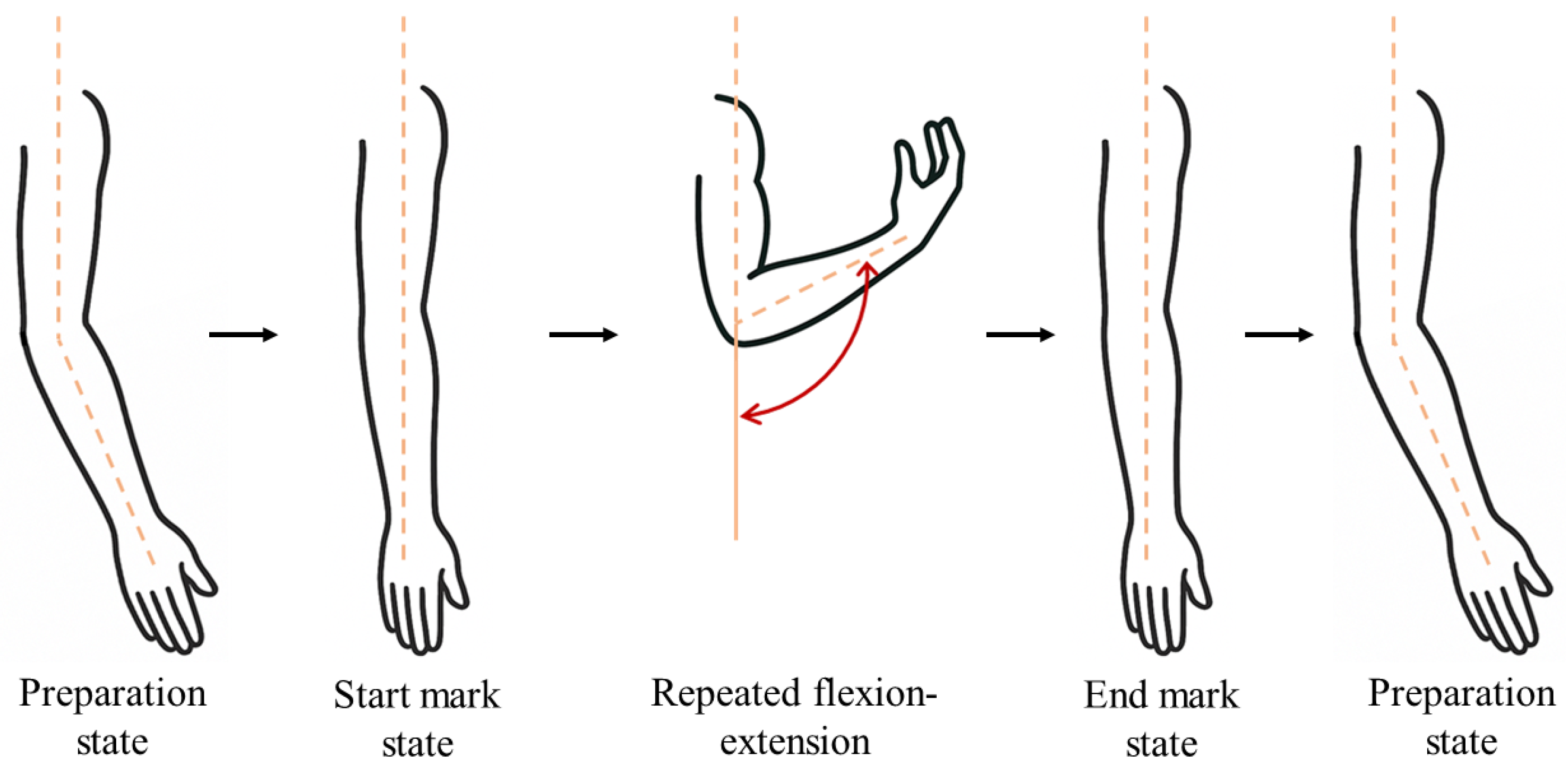
2.3. Data Acquisition
- Preparation state: The forearm hangs naturally with the palm facing forward, and the elbow flexion angle is approximately .
- Start mark state: The forearm is extended to .
- Repeated flexion-extension: Starting from the Start mark state, perform the arm flexion and extension k times repeatedly. The maximum flexion angle is approximately 140°–150°; the minimum angle is (some participants showed a brief hyperextension of the arm, with an actual angle less than ; however, we still treated it as , because such a condition does not occur during rehabilitation exercises.).
- End mark state: The last forearm extension to during the repetition process.
- Restore to preparation state: The subject relaxes, and the elbow flexion angle is maintained at approximately .
2.4. Data Trimming
2.5. Data Preprocessing
3. Method
3.1. Dataset Construction
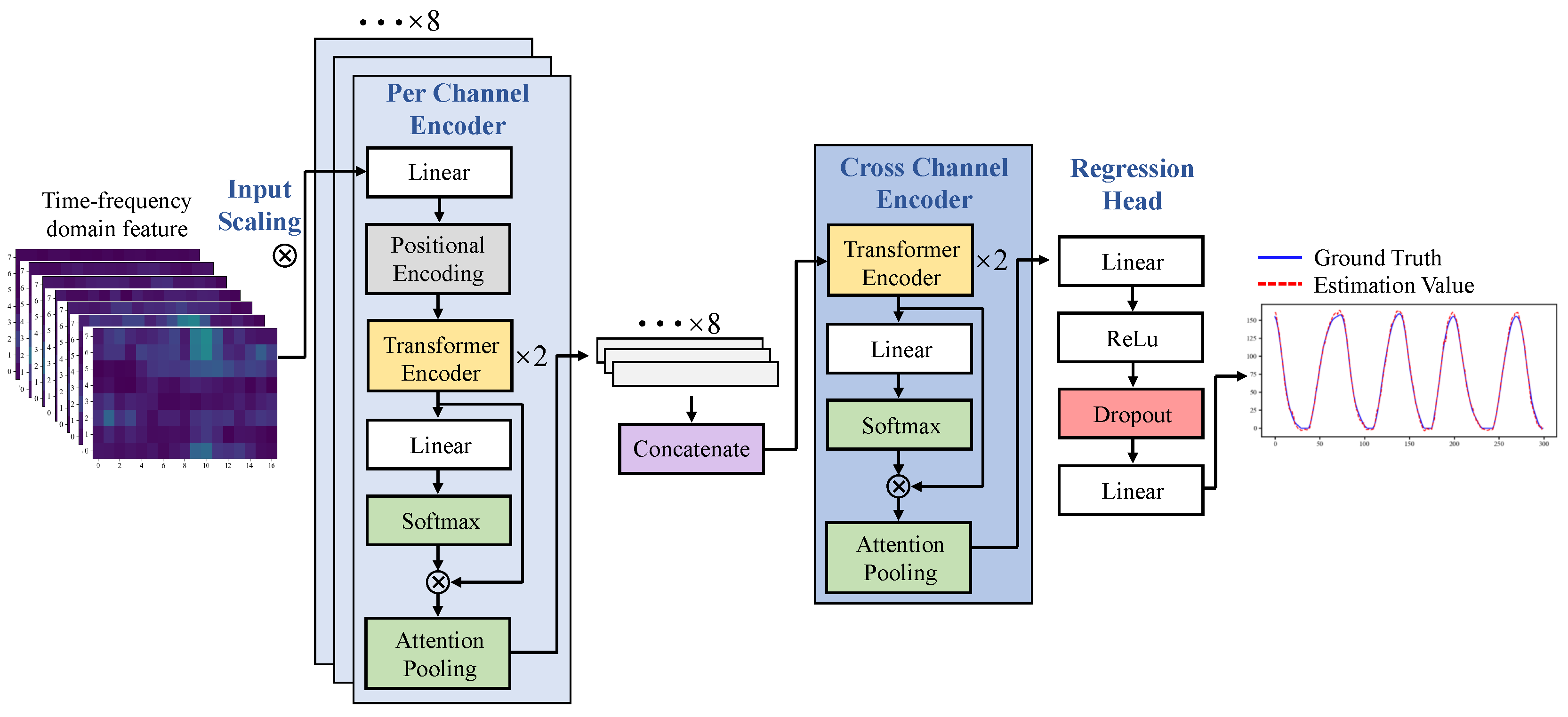
3.2. Proposed Model
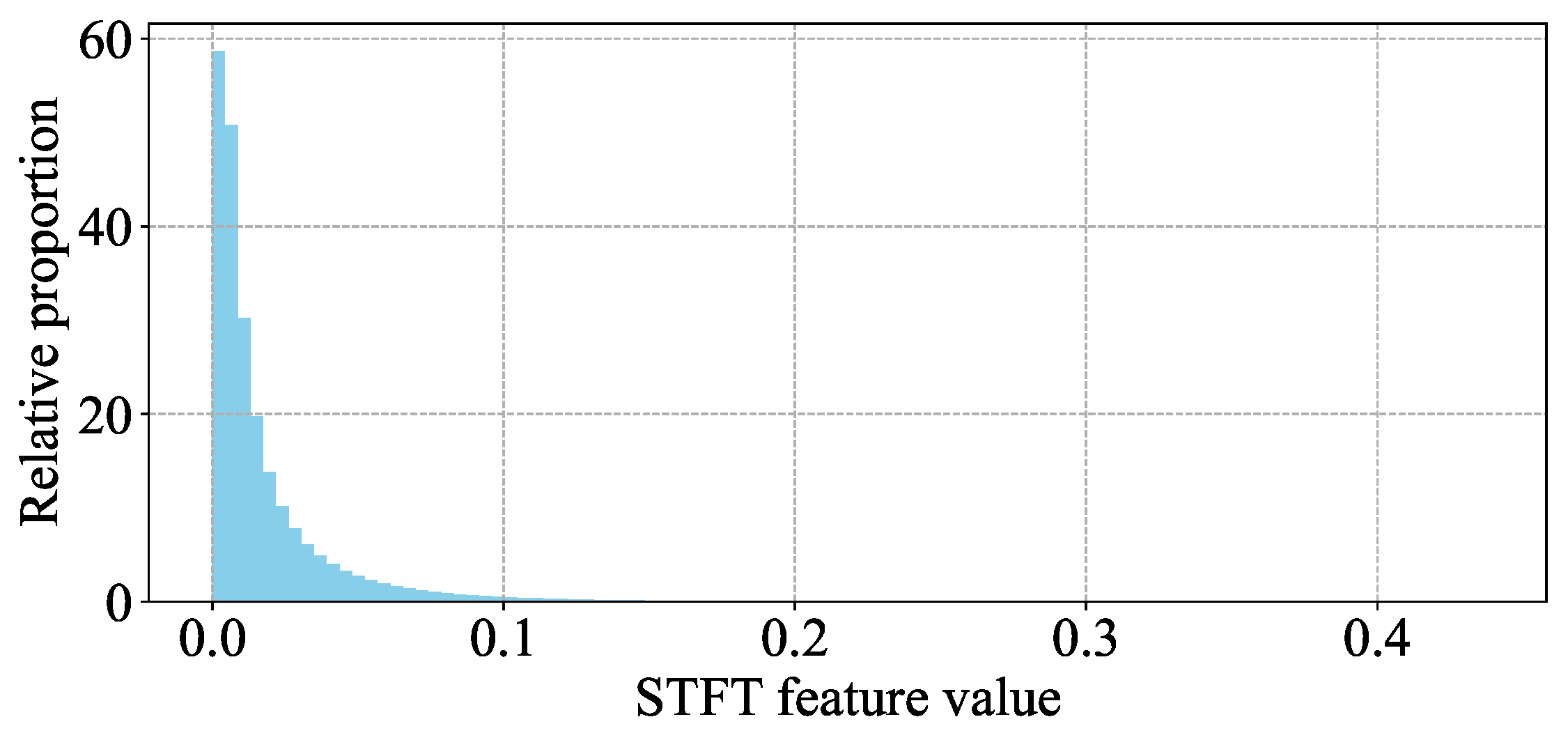
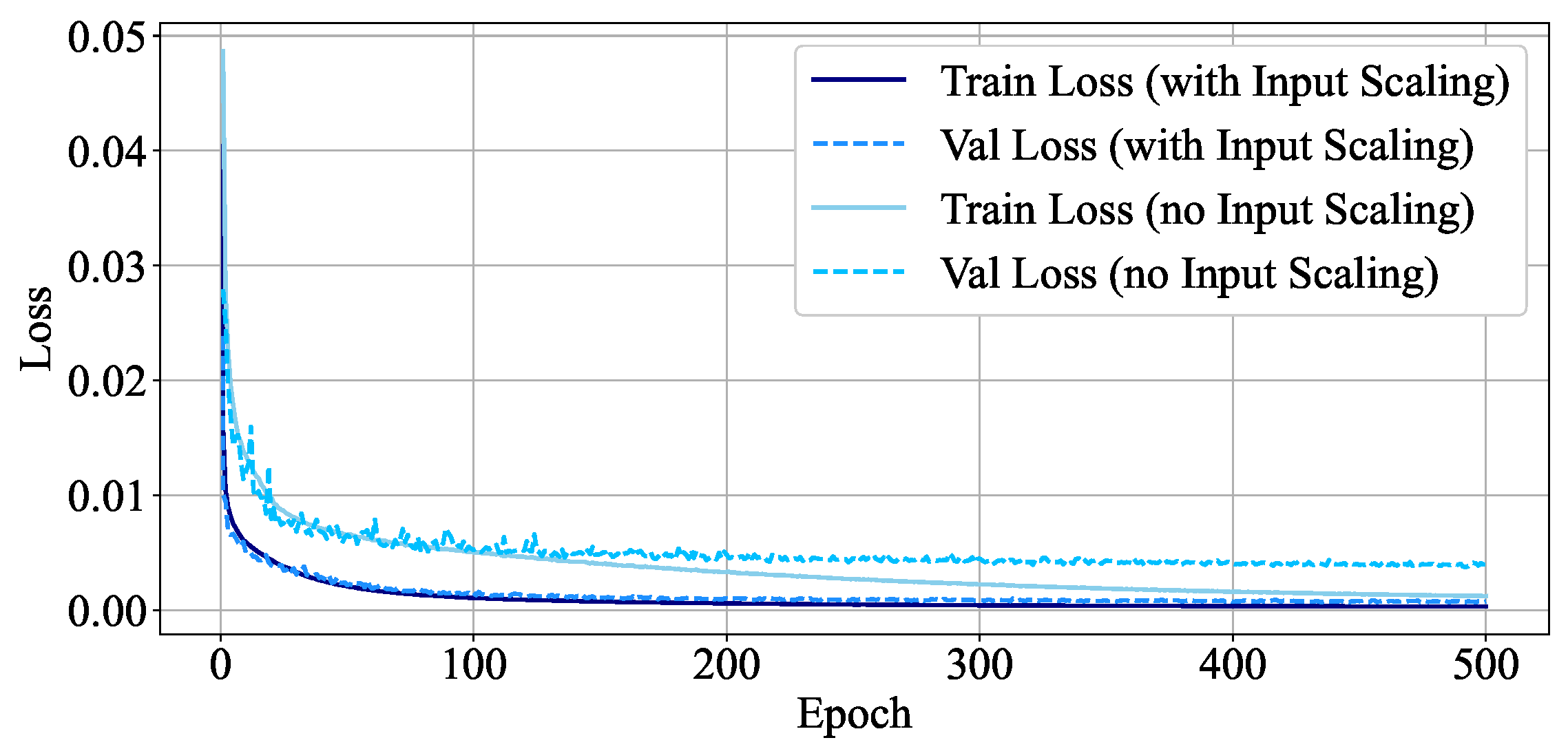
3.2.1. Input Scaling
3.2.2. Per-Channel Temporal Attention Encoder
3.2.3. Cross-Channel Attention Encoder
3.2.4. Regression Head
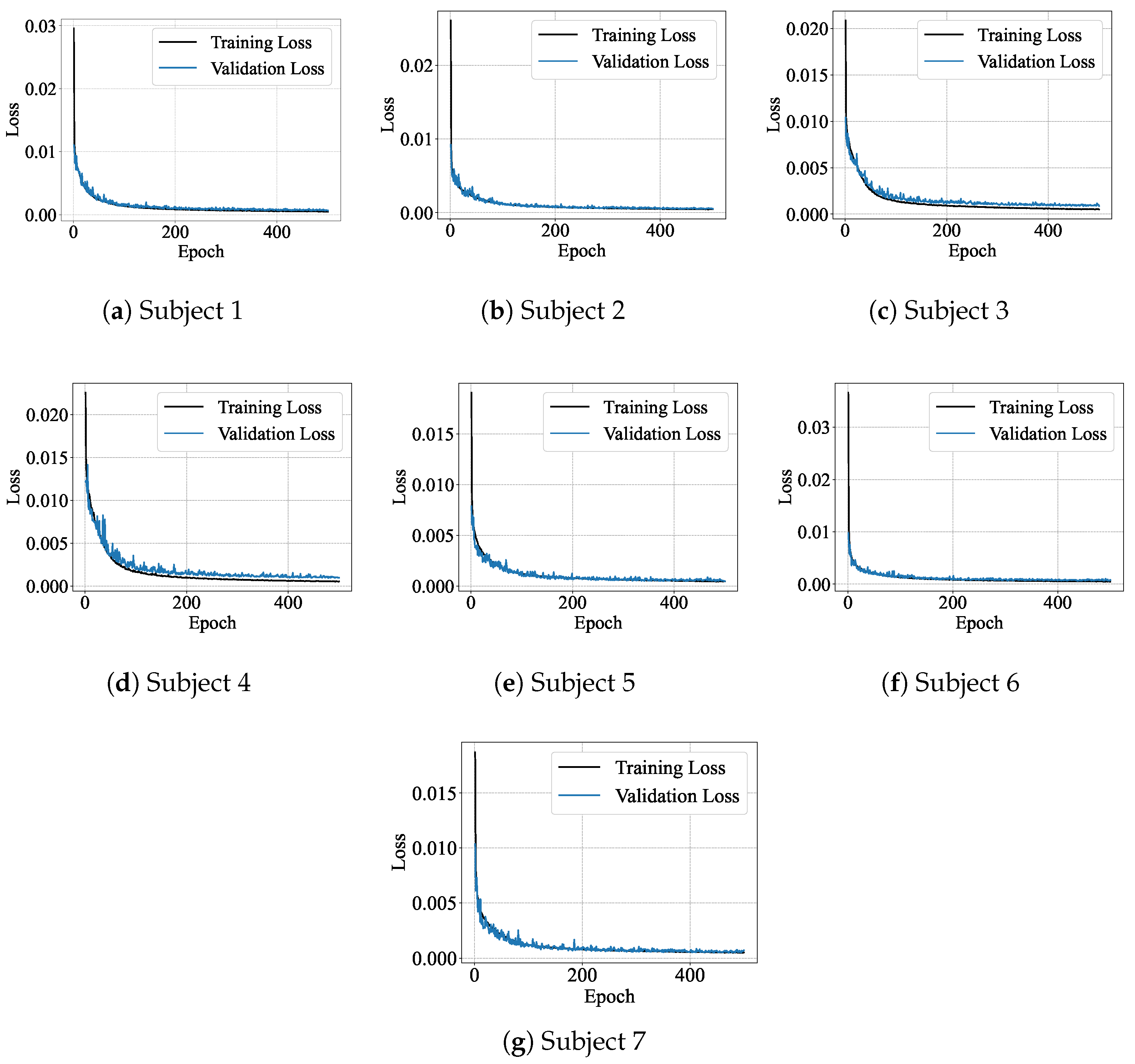
3.3. Implementation and Training
3.4. Evaluation Metric
4. Results and Discussion
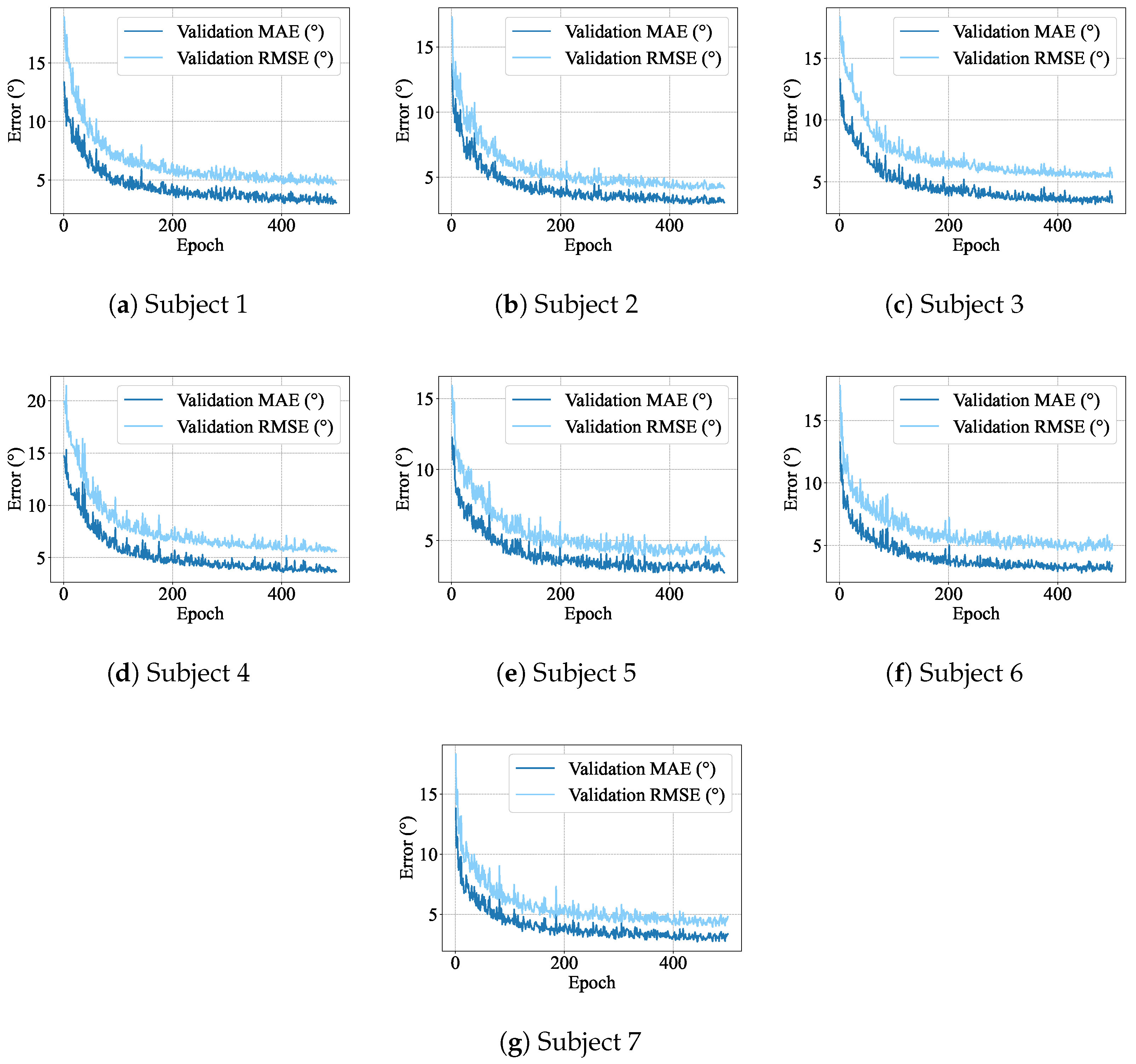
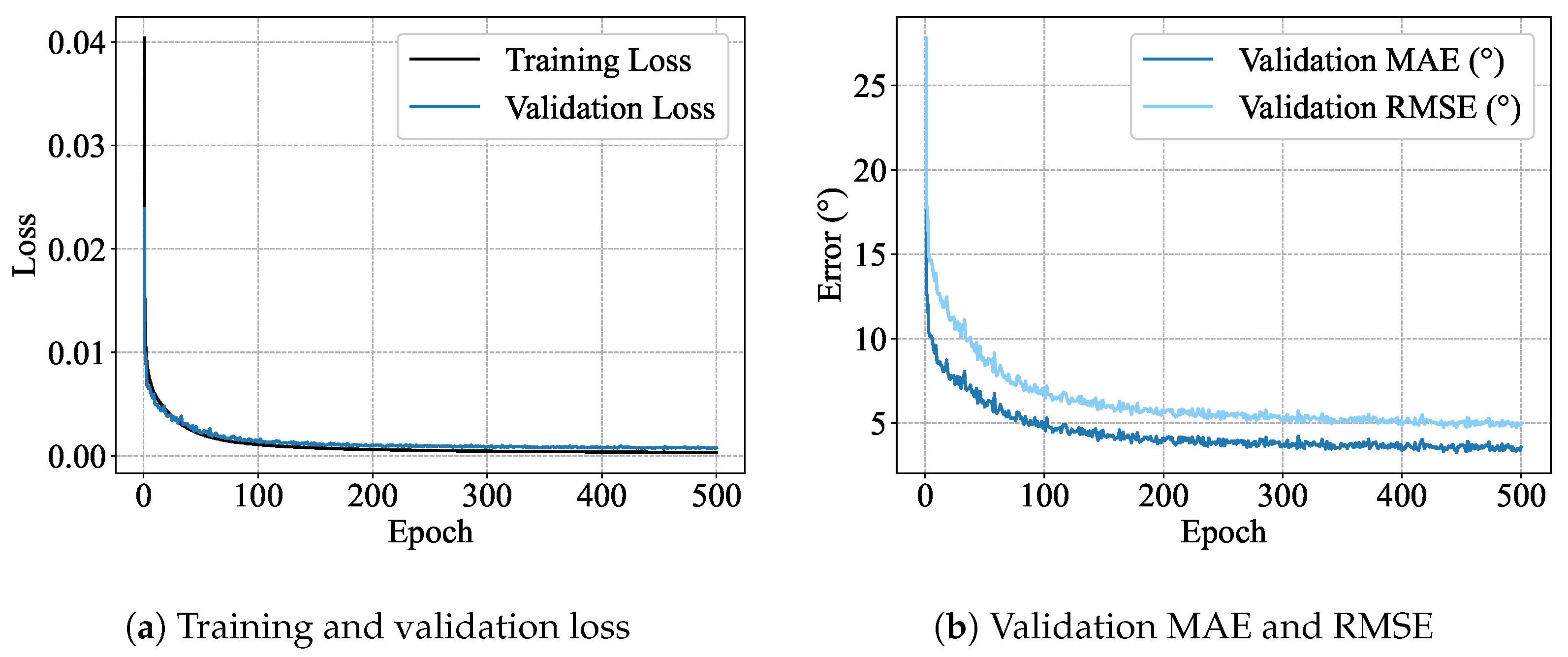
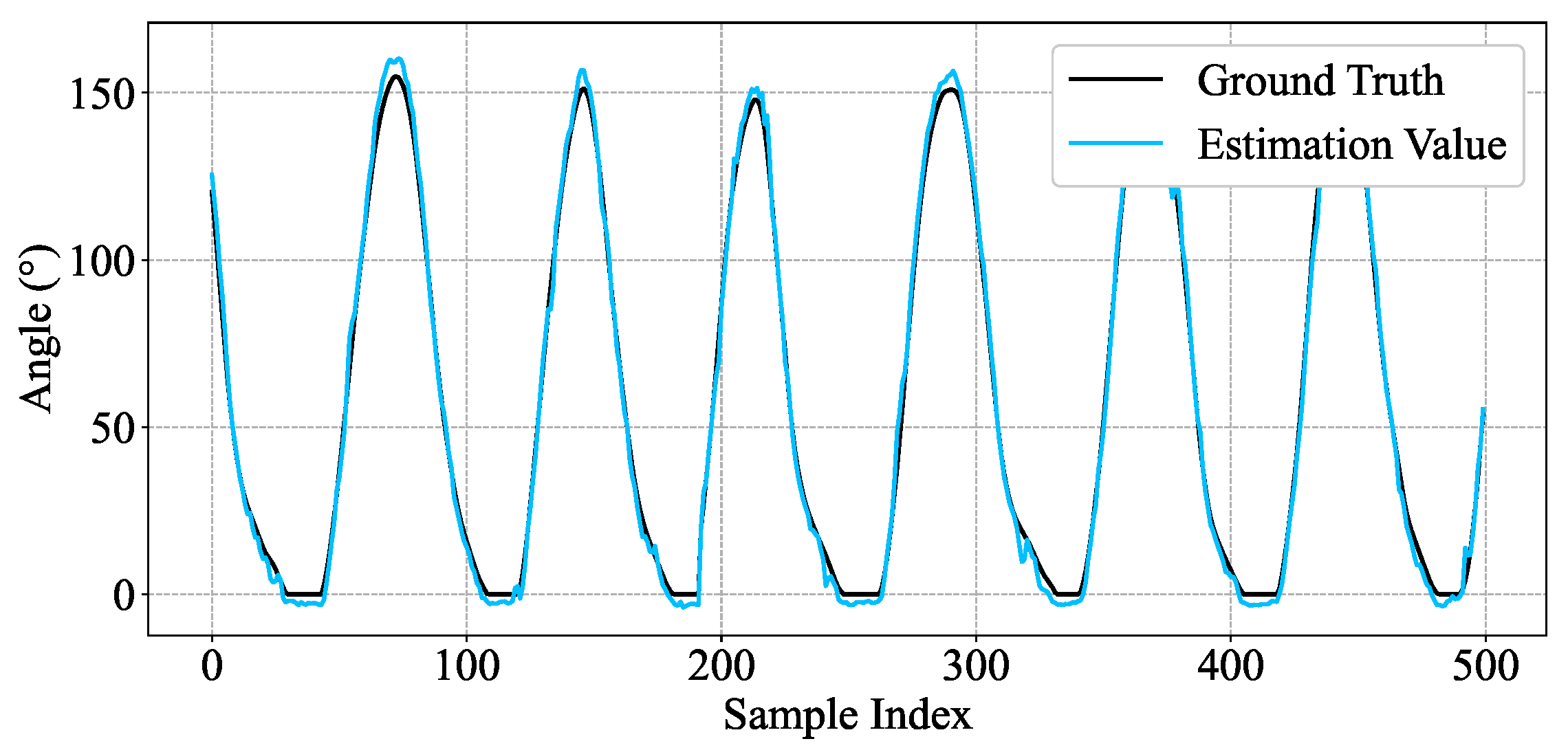
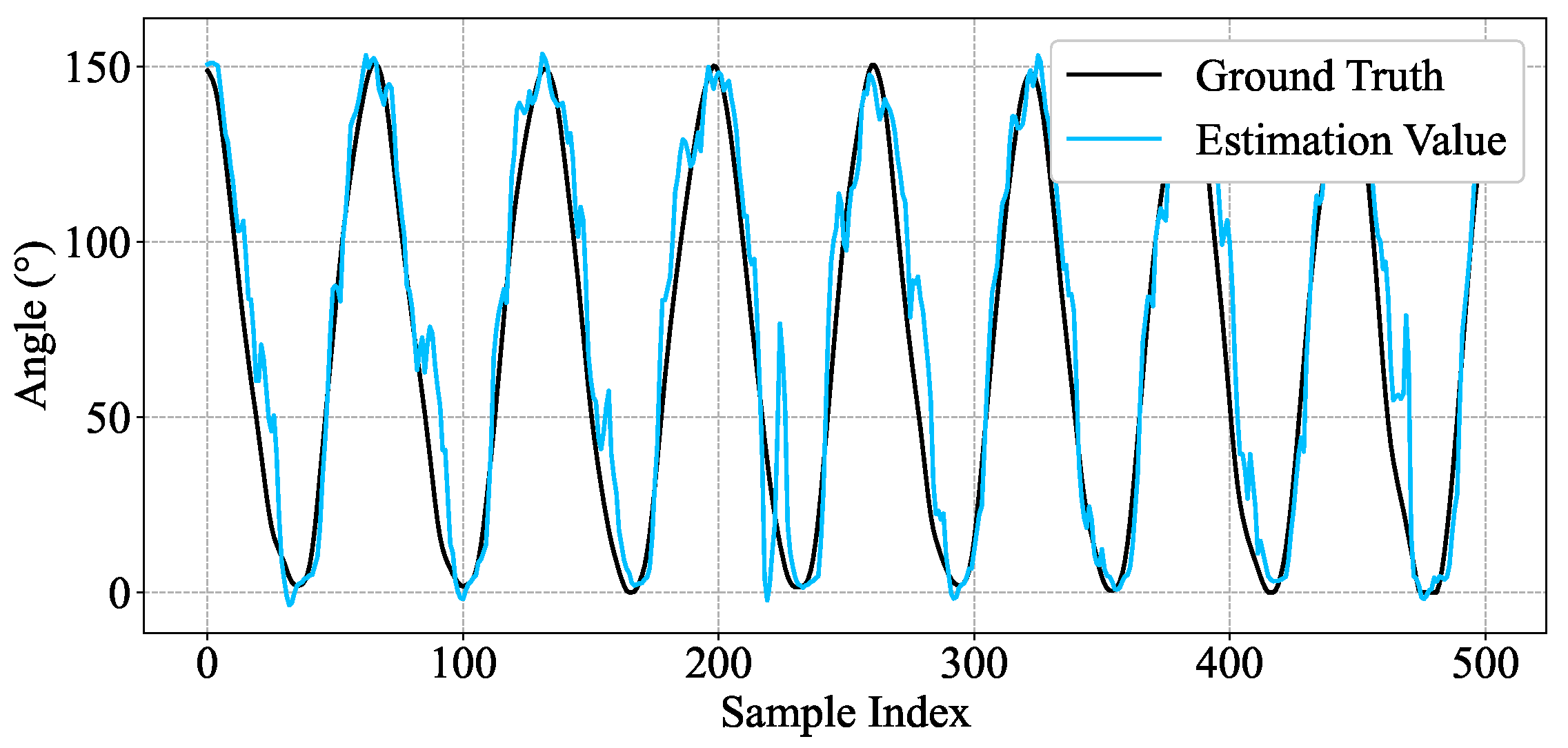
4.1. Single-Subject
4.2. Multi-Subject
4.3. Inter-Subject
4.4. Compared to Other Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| sEMG | Surface electromyographic |
| STFT | Short-Time Fourier Transform |
| STCCE | Scale Temporal-Channel Cross Encoder |
| ZC | Zero Crossing |
| MAV | Mean Absolute Value |
| WL | Waveform Length |
| SSC | Slope Sign Changes |
| DASDV | Absolute Standard Deviation Value |
| IEMG | Integrated EMG |
| VMD | Variational Mode Decomposition |
| WPT | Wavelet Packet Transform |
| DWT | Wavelet Transform |
| WOA | Whale Optimization Algorithm |
| SVR | Support Vector Regression |
| ANNs | Artificial Neural Networks |
| LSTM | Long Short-Term Memory |
| BiLSTM | Bidirectional LSTM |
| CNNs | Convolutional Neural Networks |
| TS-CNN | Two-stream multi-scale Convolutional Neural Network |
| SDK | Myo Software Development Kit |
| RMSE | Mean Square Error |
| Coefficient of Determination | |
| CC | Pearson Correlation Coefficient |
| TCA | Transfer Component Analysis |
| DANN | Domain-Adversarial Neural Network |
References
- Feigin, V.L.; Brainin, M.; Norrving, B.; Martins, S.; Sacco, R.L.; Hacke, W.; Fisher, M.; Pandian, J.; Lindsay, P. World Stroke Organization (WSO): Global Stroke Fact Sheet 2022. Int. J. Stroke 2022, 17, 18–29. [Google Scholar] [CrossRef]
- Ersoy, C.; Iyigun, G. Boxing Training in Patients with Stroke Causes Improvement of Upper Extremity, Balance, and Cognitive Functions but Should It Be Applied as Virtual or Real? Top. Stroke Rehabil. 2021, 28, 112–126. [Google Scholar] [CrossRef]
- Anwer, S.; Waris, A.; Gilani, S.O.; Iqbal, J.; Shaikh, N.; Pujari, A.N.; Niazi, I.K. Rehabilitation of Upper Limb Motor Impairment in Stroke: A Narrative Review on the Prevalence, Risk Factors, and Economic Statistics of Stroke and State of the Art Therapies. Healthcare 2022, 10, 190. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhao, P.; Li, X.; Zhang, L.; Zhou, Y.; Wang, S. Design of MMSD Six-Bar Rehab Device toward the Realization of Multiple Gait Trajectories with One Adjustable Parameter. IEEE/ASME Trans. Mechatron. 2024, 29, 4309–4319. [Google Scholar] [CrossRef]
- Song, W.; Zhao, P.; Li, X.; Zhang, Y.; Wang, S. Data-Driven Design of a Six-Bar Lower-Limb Rehabilitation Mechanism Based on Gait Trajectory Prediction. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 31, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Zhang, Y.; Guan, H.; Li, X.; Wang, S. Design of a Single-Degree-of-Freedom Immersive Rehabilitation Device for Clustered Upper-Limb Motion. J. Mech. Robot. 2021, 13, 031006. [Google Scholar] [CrossRef]
- Zhao, P.; Zhu, L.; Zi, B.; Zhang, Y.; Wang, S. Design of Planar 1-DOF Cam-Linkages for Lower-Limb Rehabilitation via Kinematic-Mapping Motion Synthesis Framework. J. Mech. Robot. 2019, 11, 041006. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, H.; Teng, Z.; Xie, L.; Song, A. Design of a Robotic Rehabilitation System for Mild Cognitive Impairment Based on Computer Vision. J. Eng. Sci. Med. Diagn. Ther. 2020, 3, 021108. [Google Scholar] [CrossRef]
- Inoue, Y.; Kuroda, Y.; Yamanoi, Y.; Okajima, Y.; Tsuji, T. Development of Wrist Separated Exoskeleton Socket of Myoelectric Prosthesis Hand for Symbrachydactyly. Cyborg Bionic Syst. 2024, 5, 0141. [Google Scholar] [CrossRef]
- Kuroda, Y.; Yamanoi, Y.; Jiang, H.; Inoue, Y.; Tsuji, T. Toward Cyborg: Exploring Long-Term Clinical Outcomes of a Multi-Degree-of-Freedom Myoelectric Prosthetic Hand. Cyborg Bionic Syst. 2025, 6, 0195. [Google Scholar] [CrossRef]
- Hu, K.; Ma, Z.; Zou, S.; Zhu, Y.; Tao, B.; Zhang, D. Impedance Sliding-Mode Control Based on Stiffness Scheduling for Rehabilitation Robot Systems. Cyborg Bionic Syst. 2024, 5, 0099. [Google Scholar] [CrossRef]
- Chen, W.; Song, W.; Chen, H.; Xie, L.; Wang, S. Motion Synthesis for Upper-Limb Rehabilitation Motion with Clustering-Based Machine Learning Method. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 8–14 November 2019; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 59407, p. V003T04A066. [Google Scholar]
- Qassim, H.M.; Wan Hasan, W.Z. A Review on Upper Limb Rehabilitation Robots. Appl. Sci. 2020, 10, 6976. [Google Scholar] [CrossRef]
- Colombo, R.; Pisano, F.; Micera, S.; Mazzone, A.; Delconte, C.; Carrozza, M.C.; Dario, P.; Minuco, G. Robotic Techniques for Upper Limb Evaluation and Rehabilitation of Stroke Patients. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 311–324. [Google Scholar] [CrossRef] [PubMed]
- Ghai, S.; Ghai, I.; Lamontagne, A. Virtual Reality Training Enhances Gait Poststroke: A Systematic Review and Meta-Analysis. Ann. N. Y. Acad. Sci. 2020, 1478, 18–42. [Google Scholar] [CrossRef] [PubMed]
- Ghai, S.; Ghai, I. Effects of (Music-Based) Rhythmic Auditory Cueing Training on Gait and Posture Post-Stroke: A Systematic Review & Dose-Response Meta-Analysis. Sci. Rep. 2019, 9, 2183. [Google Scholar]
- Zhang, T.; Sun, H.; Zou, Y. An Electromyography Signals-Based Human-Robot Collaboration System for Human Motion Intention Recognition and Realization. Robot. Comput.-Integr. Manuf. 2022, 77, 102359. [Google Scholar] [CrossRef]
- Zhang, X.; Qu, Y.; Zhang, G.; Wang, Z.; Chen, C.; Xu, X. Review of sEMG for Exoskeleton Robots: Motion Intention Recognition Techniques and Applications. Sensors 2025, 25, 2448. [Google Scholar] [CrossRef]
- Khairuddin, I.M.; Sidek, S.N.; Majeed, A.P.P.A.; Razman, M.A.M.; Puzi, A.A.; Yusof, H.M. The Classification of Movement Intention through Machine Learning Models: The Identification of Significant Time-Domain EMG Features. PeerJ Comput. Sci. 2021, 7, e379. [Google Scholar] [CrossRef]
- Li, Z.Y.; Zhao, X.G.; Zhang, B.; Ding, Q.C.; Zhang, D.H.; Han, J.D. Review of sEMG-Based Motion Intent Recognition Methods in Non-Ideal Conditions. Acta Autom. Sin. 2021, 47, 955–969. [Google Scholar]
- Li, L.L.; Cao, G.Z.; Liang, H.J.; Zhang, Y.P.; Cui, F. Human Lower Limb Motion Intention Recognition for Exoskeletons: A Review. IEEE Sens. J. 2023, 23, 30007–30036. [Google Scholar] [CrossRef]
- Liu, H.; Tao, J.; Lyu, P.; Tian, F. Human-Robot Cooperative Control Based on sEMG for the Upper Limb Exoskeleton Robot. Robot. Auton. Syst. 2020, 125, 103350. [Google Scholar] [CrossRef]
- Kiguchi, K.; Hayashi, Y. An EMG-Based Control for an Upper-Limb Power-Assist Exoskeleton Robot. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 1064–1071. [Google Scholar] [CrossRef]
- Aung, Y.M.; Al-Jumaily, A. Estimation of Upper Limb Joint Angle Using Surface EMG Signal. Int. J. Adv. Robot. Syst. 2013, 10, 369. [Google Scholar] [CrossRef]
- Ding, Z.; Yang, C.; Tian, Z.; Yi, C.; Fu, Y.; Jiang, F. sEMG-Based Gesture Recognition with Convolution Neural Networks. Sustainability 2018, 10, 1865. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, G.; Han, B.; Wang, Z.; Zhang, T. sEMG-Based Human Motion Intention Recognition. J. Robot. 2019, 2019, 3679174. [Google Scholar] [CrossRef]
- Wei, W.; Wong, Y.; Du, Y.; Hu, Y.; Kankanhalli, M.; Geng, W. A Multi-Stream Convolutional Neural Network for sEMG-Based Gesture Recognition in Muscle-Computer Interface. Pattern Recognit. Lett. 2019, 119, 131–138. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, Z.Q.; Xie, S.Q. Continuous Motion Intention Prediction Using sEMG for Upper-Limb Rehabilitation: A Systematic Review of Model-Based and Model-Free Approaches. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 1487–1504. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Wang, Y.; Gao, Y.; Zhu, Y.; Zhao, J. Continuous Estimation of Joint Angle from Electromyography Using Multiple Time-Delayed Features and Random Forests. Biomed. Signal Process. Control 2018, 39, 303–311. [Google Scholar] [CrossRef]
- Raj, R.; Sivanandan, K.S. Comparative Study on Estimation of Elbow Kinematics Based on EMG Time Domain Parameters Using Neural Network and ANFIS NARX Model. J. Intell. Fuzzy Syst. 2017, 32, 791–805. [Google Scholar] [CrossRef]
- Karheily, S.; Moukadem, A.; Courbot, J.B.; Abdeslam, D.O. sEMG time–frequency features for hand movements classification. Expert Syst. Appl. 2022, 210, 118282. [Google Scholar] [CrossRef]
- Adzkia, M.; Setiawan, A.W.; Arland, F. Comparation Classification of EMG Signals in the Time Domain and Time-Frequency Domain. In Proceedings of the 2023 International Conference on Electrical Engineering and Informatics (ICEEI), Bandung, Indonesia, 10–11 October 2023; IEEE: New York, NY, USA, 2023; pp. 1–5. [Google Scholar]
- Wen, L.; Xu, J.; Li, D.; Pei, X.; Wang, J. Continuous Estimation of Upper Limb Joint Angle from sEMG Based on Multiple Decomposition Feature and BiLSTM Network. Biomed. Signal Process. Control 2023, 80, 104303. [Google Scholar] [CrossRef]
- Alazrai, R.; Alabed, D.; Alnuman, N.; Khalifeh, A.; Mowafi, Y. Continuous Estimation of Hand’s Joint Angles from sEMG Using Wavelet-Based Features and SVR. In Proceedings of the 4th Workshop on ICTs for Improving Patients Rehabilitation Research Techniques, Lisbon, Portugal, 13–14 October 2016; pp. 65–68. [Google Scholar]
- Jiang, H.; Yamanoi, Y.; Chen, P.; Wang, X.; Chen, S.; Xu, Y.; Li, G.; Yokoi, H.; Jing, X. TF2AngleNet: Continuous Finger Joint Angle Estimation Based on Multidimensional Time–Frequency Features of sEMG Signals. Biomed. Signal Process. Control 2025, 107, 107833. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Liu, J.; Chen, W. Estimation of Joint Angle Using sEMG Based on WOA-SVR Algorithm. In Proceedings of the 2023 IEEE 18th Conference on Industrial Electronics and Applications (ICIEA), Ningbo, China, 18–22 August 2023; IEEE: New York, NY, USA, 2023; pp. 1674–1679. [Google Scholar]
- Aung, Y.M.; Al-Jumaily, A. sEMG Based ANN for Shoulder Angle Prediction. Procedia Eng. 2012, 41, 1009–1015. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Y. Artificial Neural Network Prediction of Angle Based on Surface Electromyography. In Proceedings of the 2011 International Conference on Control, Automation and Systems Engineering (CASE), Singapore, 30–31 July 2011; IEEE: New York, NY, USA, 2011; pp. 1–3. [Google Scholar]
- Graves, A. Long Short-Term Memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Graves, A.; Schmidhuber, J. Framewise Phoneme Classification with Bidirectional LSTM and Other Neural Network Architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Z.; Ai, Q.; Chen, K.; Ma, L.; Liu, Q.; Meng, W. Simultaneous and Continuous Motion Estimation of Upper Limb Based on sEMG and LSTM. In Proceedings of the 14th International Conference on Intelligent Robotics and Applications (ICIRA 2021), Yantai, China, 22–25 October 2021; Springer: Cham, Switzerland, 2021. Part I. pp. 313–324. [Google Scholar]
- Ma, C.; Lin, C.; Samuel, O.W.; Guo, W.; Zhang, H.; Greenwald, S.; Xu, L.; Li, G. A Bi-Directional LSTM Network for Estimating Continuous Upper Limb Movement from Surface Electromyography. IEEE Robot. Autom. Lett. 2021, 6, 7217–7224. [Google Scholar] [CrossRef]
- Hajian, G.; Morin, E. Deep Multi-Scale Fusion of Convolutional Neural Networks for EMG-Based Movement Estimation. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 486–495. [Google Scholar] [CrossRef]
- Silva-Acosta, V.C.; Román-Godínez, I.; Torres-Ramos, S.; Salido-Ruiz, R.A. Automatic Estimation of Continuous Elbow Flexion–Extension Movement Based on Electromyographic and Electroencephalographic Signals. Biomed. Signal Process. Control 2021, 70, 102950. [Google Scholar] [CrossRef]
- Li, H.; Guo, S.; Wang, H.; Bu, D. Subject-Independent Continuous Estimation of sEMG-Based Joint Angles Using Both Multisource Domain Adaptation and BP Neural Network. IEEE Trans. Instrum. Meas. 2022, 72, 1–10. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Pan, S.J.; Tsang, I.W.; Kwok, J.T.; Yang, Q. Domain Adaptation via Transfer Component Analysis. IEEE Trans. Neural Netw. 2010, 22, 199–210. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-Adversarial Training of Neural Networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]

| Subjects | Gender | Age | Height (m) | Weight (kg) |
|---|---|---|---|---|
| 1 | male | 27 | 1.86 | 72 |
| 2 | male | 23 | 1.80 | 68 |
| 3 | male | 24 | 1.68 | 68 |
| 4 | male | 26 | 1.75 | 70 |
| 5 | female | 27 | 1.70 | 58 |
| 6 | female | 26 | 1.63 | 55 |
| 7 | female | 24 | 1.64 | 56 |
| Subjects | Training Set (70%) | Validation Set (15%) | Test Set (15%) | Shape |
|---|---|---|---|---|
| 1 | 11,089 | 2376 | 2377 | Input: [7, 8, 17] Output: [1] |
| 2 | 8354 | 1790 | 1791 | |
| 3 | 9696 | 2078 | 2078 | |
| 4 | 10,371 | 2222 | 2223 | |
| 5 | 9695 | 2078 | 2078 | |
| 6 | 10,977 | 2352 | 2353 | |
| 7 | 12,019 | 2576 | 2576 |
| Subjects | MAE | RMSE | CC | |
|---|---|---|---|---|
| 1 | 0.9928 | 0.9965 | ||
| 2 | 0.9926 | 0.9964 | ||
| 3 | 0.9910 | 0.9956 | ||
| 4 | 0.9884 | 0.9942 | ||
| 5 | 0.9933 | 0.9968 | ||
| 6 | 0.9933 | 0.9969 | ||
| 7 | 0.9951 | 0.9977 |
| Subjects | MAE | RMSE | CC | |
|---|---|---|---|---|
| Multi-subject | 0.9915 | 0.9962 |
| Subjects | MAE | RMSE | CC | |
|---|---|---|---|---|
| L1 | 0.8397 | 0.9178 | ||
| L2 | 0.8542 | 0.9314 | ||
| L3 | 0.8445 | 0.9408 | ||
| L4 | 0.7572 | 0.8909 | ||
| L5 | 0.7315 | 0.8569 | ||
| L6 | 0.7799 | 0.8861 | ||
| L7 | 0.8915 | 0.9464 |
| Research | Method | Scenarios | MAE | RMSE | CC | |
|---|---|---|---|---|---|---|
| [44] | LSTM | Single-subject | 0.9221 | 0.9600 | ||
| Multi-subject | 0.9165 | 0.9574 | ||||
| Inter-subject | 0.8046 | 0.8951 | ||||
| [33] | BiLSTM | Single-subject | 0.9219 | 0.9601 | ||
| Multi-subject | 0.9154 | 0.9568 | ||||
| Inter-subject | 0.7797 | 0.8964 | ||||
| This paper | STCCE | Single-subject | 0.9924 | 0.9963 | ||
| Multi-subject | 0.9915 | 0.9962 | ||||
| Inter-subject | 0.8141 | 0.9100 |
| Methods | Scenarios | T-Statistic | p-Value |
|---|---|---|---|
| LSTM vs. STCCE | Single-subject | ||
| Multi-subject | |||
| Inter-subject | |||
| BiLSTM vs. STCCE | Single-subject | ||
| Multi-subject | |||
| Inter-subject |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Chen, H.; Cheng, X.; Zhao, P. Continuous Estimation of sEMG-Based Upper-Limb Joint Angles in the Time–Frequency Domain Using a Scale Temporal–Channel Cross-Encoder. Actuators 2025, 14, 378. https://doi.org/10.3390/act14080378
Han X, Chen H, Cheng X, Zhao P. Continuous Estimation of sEMG-Based Upper-Limb Joint Angles in the Time–Frequency Domain Using a Scale Temporal–Channel Cross-Encoder. Actuators. 2025; 14(8):378. https://doi.org/10.3390/act14080378
Chicago/Turabian StyleHan, Xu, Haodong Chen, Xinyu Cheng, and Ping Zhao. 2025. "Continuous Estimation of sEMG-Based Upper-Limb Joint Angles in the Time–Frequency Domain Using a Scale Temporal–Channel Cross-Encoder" Actuators 14, no. 8: 378. https://doi.org/10.3390/act14080378
APA StyleHan, X., Chen, H., Cheng, X., & Zhao, P. (2025). Continuous Estimation of sEMG-Based Upper-Limb Joint Angles in the Time–Frequency Domain Using a Scale Temporal–Channel Cross-Encoder. Actuators, 14(8), 378. https://doi.org/10.3390/act14080378








