Study on Optimal Adaptive Meta-Model and Performance Optimization of Built-In Permanent Magnet Synchronous Motor

Abstract

To overcome the limitations of single-objective optimization in permanent magnet synchronous motor (PMSM) performance enhancement, this study proposes an adaptive moving least squares (AMLS) for a 12-pole/36-slot built-in PMSM. Through comprehensive exploration of the design space, a systematic approach is established for holistic motor performance improvement. The Gaussian weight function is modified to improve the model’s fitting accuracy, and the decay rate of the control weight is optimized. The optimal adaptive meta-model for the built-in PMSM is selected based on the coefficient of determination. Subsequently, sensitivity analysis is conducted to identify the parameters that most significantly influence key performance indicators, including torque ripple, stator core loss, electromagnetic force amplitude, and average output torque. These parameters are then chosen as the optimal design variables. A multi-objective optimization framework, built upon the optimal adaptive meta-model, is developed to address the multi-objective optimization problem. The results demonstrate increased output torque, along with reductions in stator core loss, torque ripple, and radial electromagnetic force, thereby significantly improving the overall performance of the motor.

1. Introduction

Permanent magnet synchronous motors (PMSMs) exhibit superior attributes such as high efficiency, power density, and precision controllability [1,2]. These advantages have contributed to the widespread adoption of PMSMs in various fields, including industrial automation, transportation, and home appliances. As performance indicators such as power density, overload capacity, and lightweight design continue to improve, the electromagnetic load on the motor also increases, leading to a corresponding rise in vibration intensity [3,4,5]. Moreover, the motor’s performance can be severely compromised when exposed to high temperatures for extended periods, as limited installation space and inadequate heat dissipation can lead to the degradation of the permanent magnets. Therefore, ensuring safe and reliable operation of permanent magnet synchronous motors (PMSMs) remains a critical industrial priority, driving accelerated interdisciplinary research in design optimization.

Reducing torque ripple is critical for enhancing the operational smoothness, vibration, and noise performance of permanent magnet and reluctance motors, driving research into various solutions based on electromagnetic design optimization and control strategies. Rafaq et al. [6] systematically investigated torque ripple generation mechanisms and proposed a current waveform modulation strategy for effective suppression; Yamashita et al. [7], focusing on synchronous reluctance motors, combined iron loss sensitivity analysis using the adjoint variable method with topology optimization via the level set method to improve torque characteristics while minimizing iron losses.

Research has been focusing on optimizing diverse structural parameters to achieve high efficiency, high torque, and robust operation. For instance, Xing and Zezhic [8] studied a 60-slot/4-pole IPMSM with a non-uniform air gap, systematically considering geometric structure, permanent magnet (PM) arrangement, and rotor flux barrier design. They proposed an optimization method to achieve the optimal PM arrangement for a U-shaped rotor, successfully reducing both torque ripple and electromagnetic vibration intensity. Naik et al. [9] applied the meta-heuristic Rao algorithm combined with the finite element method to investigate the impact of air gap magnetic flux density, electromagnetic torque, and flux density on IPMSM efficiency under varying stator slot configurations and operating conditions. Zhu et al. [10] conducted topology optimization on dual-armature flux-switched permanent magnet (DA-FSPM) motors (featuring U-type, E-type, and C-type), performing detailed parameter analysis encompassing copper loss distribution, magnetic pole radius, stator tooth radius, and yoke thicknesses to maximize average torque. Furthermore, Reyes et al. [11] highlighted the influence of input parameter uncertainty on motor performance and employed a 2D finite element surrogate model for the robust optimization design of permanent magnet-assisted synchronous reluctance motors. Their study demonstrated the necessity of robust strategies for achieving both optimal and stable performance under consistent operating conditions. Collectively, these studies illustrate that PMSM design optimization is a complex, multi-parameter, multi-objective process spanning geometry, materials, electromagnetics, and control, requiring simultaneous consideration of deterministic performance and robustness.

In multi-objective optimization studies, the complex nonlinear relationships between design variables and objective functions necessitate the development of accurate mathematical models, which are critical for effective problem-solving. Significant efforts have thus been dedicated to high-precision modeling techniques [12,13,14]. Xu et al. [15] established a mathematical model for the built-in PMSM used in traction drives. They conducted a multi-objective optimization design based on flat wire winding technology, which effectively suppressed torque ripple and validated the proposed methodology; Sun et al. [16], addressing the dynamic performance and energy consumption of PMSMs under complex operating conditions, developed a finite element characterization method using equivalent points on the speed–torque plane and proposed a multi-objective structural optimization method to simultaneously reduce torque ripple and energy consumption. To address computational burden, Kim et al. [17] proposed an adaptive response surface method that minimizes finite element evaluations required for determining the response surface parameters. By optimizing computation time based on the structure of the computing cluster, this method enabled efficient reliability evaluation of power electronic modules; Zhang et al. [18] integrated adaptive response surfaces with a Gaussian global harmony search algorithm into a double-loop framework, demonstrating its global optimization capability using NASA aircraft stiffener plates.

Current research on PMSM performance enhancement primarily emphasizes single-dimensional approaches—whether through structural topology optimization, electromagnetic theory refinement, or advanced control techniques. While effective for specific performance metrics, these conventional methods often neglect synergistic improvements across multiple operational parameters. To bridge this critical gap, this investigation establishes a comprehensive optimization framework through systematic analysis of a 12-pole/36-slot built-in PMSM.

The main contributions of the study are as follows:

• We conduct large-scale exploration of the design space through DOE sampling, making large-scale exploration of the interaction between electromagnetic structures possible.
• Leveraging sampling data obtained from large-scale design space exploration via design of experiments (DOE), we develop a high-fidelity predictive metamodel that closely approximates the actual system’s behavior.
• Sensitivity analysis is conducted on critical optimization design parameters to identify those exhibiting the highest sensitivity to the target performance metrics, which are subsequently selected as primary design variables.

The proposed methodology not only enhances the output torque, but also achieves concurrent reductions in stator core loss, torque ripple, and radial electromagnetic force, thereby delivering a significant improvement in overall motor performance efficiency.

2. The Best Predictive Metamodel for PMSM

The Moving Least Squares (MLS) method employs kernel-based weighting to prioritize proximal data points for localized approximation. Enhanced by an AMLS approach, this framework dynamically adjusts weight functions, basis functions, and algorithm parameters in response to local data characteristics, noise levels, and cross-validation metrics.

The optimal adaptive metamodel is constructed via MFS-MLS methodology, integrating Moving Frame Method with Moving Least Squares. The MFS-MLS methodology was selected owing to its distinctive capabilities in addressing PMSM-specific optimization challenges, characterized by three key features:

Local Adaptability: Achieved via an adaptive moving-window mechanism employing modified Gaussian weighting functions (refer to Section 2), which facilitates a dynamic response to localized nonlinearities within electromagnetic field distributions, crucial for accurately capturing abrupt variations in torque ripple and radial force density.

Computational Efficiency: Attained through the resolution of localized least-squares problems (refer to Equations (8)–(11)), this approach obviates the need for computationally burdensome inversions of large-scale covariance matrices, as required in Gaussian processes, thereby diminishing computational overhead in high-dimensional design spaces (e.g., 7 variables as indicated in

Table 1. Initial value of the variable and the range of change.

Variables	Initial Value	Range of Variation
O2 (mm)	24.27	19.41~29.12
Rib (mm)	9.00	7.20~10.80
Hm (mm)	44.00	35.20~42.80
Bm(mm)	7.50	6.00~9.00
Bs0 (mm)	2.50	2.00~3.00
Bs1 (mm)	10.11	8.01~12.13
Hs0 (mm)	1.50	1.20~1.80

).

Multi-Fidelity: Integration facilitated by scaling function a₀(x) (Equation (2)) to incorporate low-fidelity data, a capability absent in pure interpolation methods such as radial basis functions (RBFs).

For the sampled data point set {(x_i,y_i)}, the error is minimized by fitting a polynomial function P(x) to approximate the true model. The polynomial model’s predicted response P(x) is mathematically expressed as:

$$P(x)=a_0+a_{1}x+a_2{x}^2+\dots +a_n{x}^n$$

(1)

where x represents the vector of design variables within the n-dimensional design space, and $a_0,a_1,a_2,\dots ,a_n$ denote the polynomial coefficients. To overcome limitations of conventional regression methods, this work develops an MFS-MLS model.

The high-precision prediction metamodel for PMSM, constructed using the MLS method, acknowledges that not all sample points hold equal significance when estimating the regression coefficients. Therefore, when constructing the loss function, each squared residual is assigned a weight that varies based on the distance between the point to be predicted and each observed data point. Moreover, the coefficients of the moving least squares model are functions of the input x. At each predicted point x_new, the coefficients are computed using the sample points within the neighborhood of x_new. This neighborhood defines the influence domain of the point x_new, with sample points outside this domain being excluded. As the prediction point moves, the influence domain adjusts accordingly.

This approach enables the high-fidelity analysis model to automatically determine both the size of the influence domain based on the sample points and the varying scale factors of the predicted points, providing enhanced flexibility and accuracy. The expression is mathematically defined as follows [19]:

$$\begin{array}{c}{\widehat{y}}_H(x)=a_0(x)y_L(x)+{\displaystyle \sum _{i=1}^m{a}_i}(x)p_i(x)\\ =a(x{)}^{\mathrm{T}}p(x)\end{array}$$

(2)

where $y_L\left(x\right)$ is a function of the design variable X, $a_0\left(x\right)$ is the scaling function of the low-fidelity model $y_L\left(x\right)$, and $a_i\left(x\right)$ is the coefficient of the basis function. The coefficient vector is augmented to form the equation that includes $a_0\left(x\right)$ and ${\mathit{a}}_{\mathit{i}}\left(x\right)$,$i=\mathrm{1,2},...,m.$ Here, m represents the number of terms in the basis function. The term ${\sum }_{i=1}^m{\mathit{a}}_{\mathit{i}}\left(x\right){\mathit{p}}_{\mathit{i}}\left(x\right)$ is defined as the difference function. ${\mathit{P}}_{\mathit{i}}\left(x\right)$is a monomial basis function, which is extended to form the integrated vector $\mathit{p}\left(x\right)={\left[y_L\left(x\right)p_1\left(x\right)\dots p_m\left(x\right)\right]}^T$.

In the absence of specific knowledge about the properties of real functions, linear and quadratic polynomials are typically used as basic functions [20]. A complete quadratic basis function can be written as $\tilde{\mathit{p}}\left(x\right)=[1x_1{x}_2{x}_1^2{x}_1{x}_2{x}_2^2{]}^T$. Therefore, the ensemble vector $\mathit{p}\left(x\right)$ can be expressed as $\mathit{p}\left(x\right)={\left[y_L\left(x\right)p\left(x\right)\right]}^T$. To compute the coefficient vector $\mathit{a}\left(x\right)$, an objective function $J\left(a\right)$, consisting of weighted discrete $L_2$ norms, must be minimized.

$$\begin{gathered} J\left(a\right)=\sum _{j=1}^{n_H}w\left(x-x_j\right){\left[{\widehat{y}}_H\left(x_j\right)-y_H\left(x_j\right)\right]}^2 \\ ={\sum }_{j=1}^{n_H}w\left(x-x_j\right){\left[a\left(x{)}^{T}p\right(x)-y_H\left(x_j\right)\right]}^2 \end{gathered}$$

(3)

where $x_j\left(\mathrm{j}=\mathrm{1,2},\dots ,n_H\right)$ represents the $n_H$ high-fidelity sampling points near the evaluation point $X$, and $w\left(x-x_j\right)$ is the weighting function applied to the samples.

Equation (3) is expressed in matrix form as

$$J\left(a\right)={\left(\begin{array}{c}\mathit{P}a-y_H\end{array}\right)}^{T}W\left(x\right)\left(\begin{array}{c}\mathit{P}a-y_H\end{array}\right)$$

(4)

where

$${\mathit{y}}_H={\left[\begin{array}{c}{y}_H\left({\mathit{x}}_1\right)y_H\left({\mathit{x}}_2\right)\dots y_H\left({\mathit{x}}_{n_H}\right)\end{array}\right]}^T$$

(5)

$$\left.P=\left[\begin{array}{cccc}{y}_L\left(x_1\right)& p_1\left(x_1\right)& \dots & p_m\left(x_1\right)\\ y_L\left(x_2\right)& p_1\left(x_2\right)& \dots & p_m\left(x_2\right)\\ ⋮& ⋮& \ddots & ⋮\\ y_L\left(x_{n_H}\right)& p_1\left(x_{n_H}\right)& \dots & p_m\left(x_{n_H}\right)\end{array}\right.\right]$$

(6)

with

$$\left.\mathrm{W}\left(\mathrm{x}\right)=\left[\begin{array}{cccc}\mathrm{w}\left(\mathrm{x}-{\mathrm{x}}_1\right)& 0& ...& 0\\ 0& \mathrm{w}\left(\mathrm{x}-{\mathrm{x}}_2\right)& ...& 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& ...& \mathrm{w}\left(\mathrm{x}-{\mathrm{x}}_{{\mathrm{n}}_{\mathrm{H}}}\right)\end{array}\right.\right]$$

(7)

Taking the derivative of Equation (4) with respect to a(x) and setting it to zero yields:

$$A\left(x\right)a\left(x\right)=B\left(x\right)y_H$$

(8)

where

$$\mathit{A}\left(\mathit{x}\right)=P^{T}W\left(x\right),B\left(x\right)=P^{T}W\left(x\right)$$

(9)

Consequently, the solution for a(x) is:

$$a\left(x\right)=A^{-1}\left(x\right)B\left(x\right)y_H$$

(10)

Substituting a(x) back into Equation (2), we obtain the estimated response:

$${\widehat{y}}_H\left(x\right)=p^T\left(x\right)A^{-1}\left(x\right)B\left(x\right)y_H$$

(11)

As shown in Equation (11), the parameter k is adjusted to control the decay speed of the Gaussian weight function $w\left(x-x_j\right)$, which represents the weight of each sample point. This adjustment allows the model to better adapt to varying data distributions and enhances fitting accuracy.

The Gaussian weight function is given by [21]:

$$\mathrm{w}\left(x-x_j\right)=\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{C{\left(‖x-x_j‖\right)}^2}{{2k}^{2{\sigma }^2}}})$$

(12)

where $C\left(‖x-x_j‖\right)$ is a constant influencing the effect of the Euclidean distance between points x and $x_i$, and $k,\mathsf{\sigma }$ are the standard deviation of the Gaussian distribution.

3. The Kriging Surrogate Model

In multidisciplinary and multi-objective optimization, the relationship between dependent and independent variables is explored using surrogate modeling. Surrogate modeling has become an indispensable tool across engineering, scientific, and economic domains for approximating complex simulations and experimental processes, enabling accelerated computation, cost reduction, and data-driven optimization. Among prevalent surrogate techniques—including polynomial regression, support vector machines, and neural networks—the Kriging model distinguishes itself through its capacity to provide minimum-variance unbiased predictions while delivering quantitative uncertainty estimates.

The Kriging framework assumes stationarity, where the covariance between any two points depends solely on their spatial separation rather than absolute position:

$$C\left(x,x_j\right)=C\left(‖x-x_j‖\right)$$

(13)

where $C\left(x,x_j\right)$denotes the covariance kernel function.

The goal of Kriging interpolation is to determine a set of weighting coefficients that minimize the prediction error $\widehat{f}\left(x\right)$, which can be expressed as follows:

$$\widehat{f}(x)={\displaystyle \sum ^n{\lambda }_i}{y}_i$$

(14)

where ${\lambda }_i$ is the weighting coefficient; $y_i$ is the objective function value at the known data point $y_i$.

The weighting coefficients are determined by solving the Kriging equation

$$C\lambda =c\left(x\right)$$

(15)

where C is the covariance matrix between training samples, λ is the weight vector, and $\mathbf{c}\left(\mathrm{x}\right)$ is the covariance vector between the prediction point $x$ and training data.

The coefficient of determination is an index used to assess the fitting accuracy of a polynomial regression model. It is defined as the percentage of variation explained by the fitted value of the response parameter, with its value ranging from 0 to 1. The closer the value is to 1, the better the model’s fitting performance. Its expression is:

$$R^2=1-{\displaystyle \frac{S{S}_{\mathrm{res}}}{S{S}_{\mathrm{tot}}}}$$

(16)

where the sum of squared residuals $S{S}_{\mathrm{res}}$ is the sum of the squared differences between the observed and predicted values;$S{S}_{\mathrm{tot}}$ is the total sum of squares, representing the sum of the squared differences between the observations and the mean of the observations.

Considering models of varying complexity, the adjusted coefficient of determination $R_{adj}$ is expressed as

$$R_{adj}^2=1-{\displaystyle \frac{\left(1-{\mathrm{R}}^2\right)\cdot \left(\mathrm{n}-1\right)}{\mathrm{n}-\mathrm{m}-1}}$$

(17)

where n is the number of samples and m is the number of independent variables.

In the study, the sample space is partitioned, and the coefficient of determination is calculated using the cross-validation algorithm. The predicted values ${\widehat{y}}_{\mathrm{i}}$ are obtained through the regression model. By evaluating and combining the predictive qualities of both the interpolation and regression models, the optimal adaptive meta-model that meets the required criteria is determined based on the coefficient of determination. As shown in Figure 1, the predicted coefficients for total COP all reached over 90%, meeting the high precision requirement for a multi-objective optimization problem.

4. Sensitivity Analysis

Table 2. The main structure parameters of the motor.

Parameters	Value	Parameters	Value
Power rating/kW	65	Rotor inner diameter/mm	180
Rated voltage/V	900	Axial length/mm	42
Rated speed/rpm	4300	Minimum air gap/mm	0.75
Stator outer diameter/mm	360	Maximum air gap/mm	5.2
Stator inner diameter/mm	254.1	Number of poles	12

lists the key structural parameters of the motor under study in this paper.

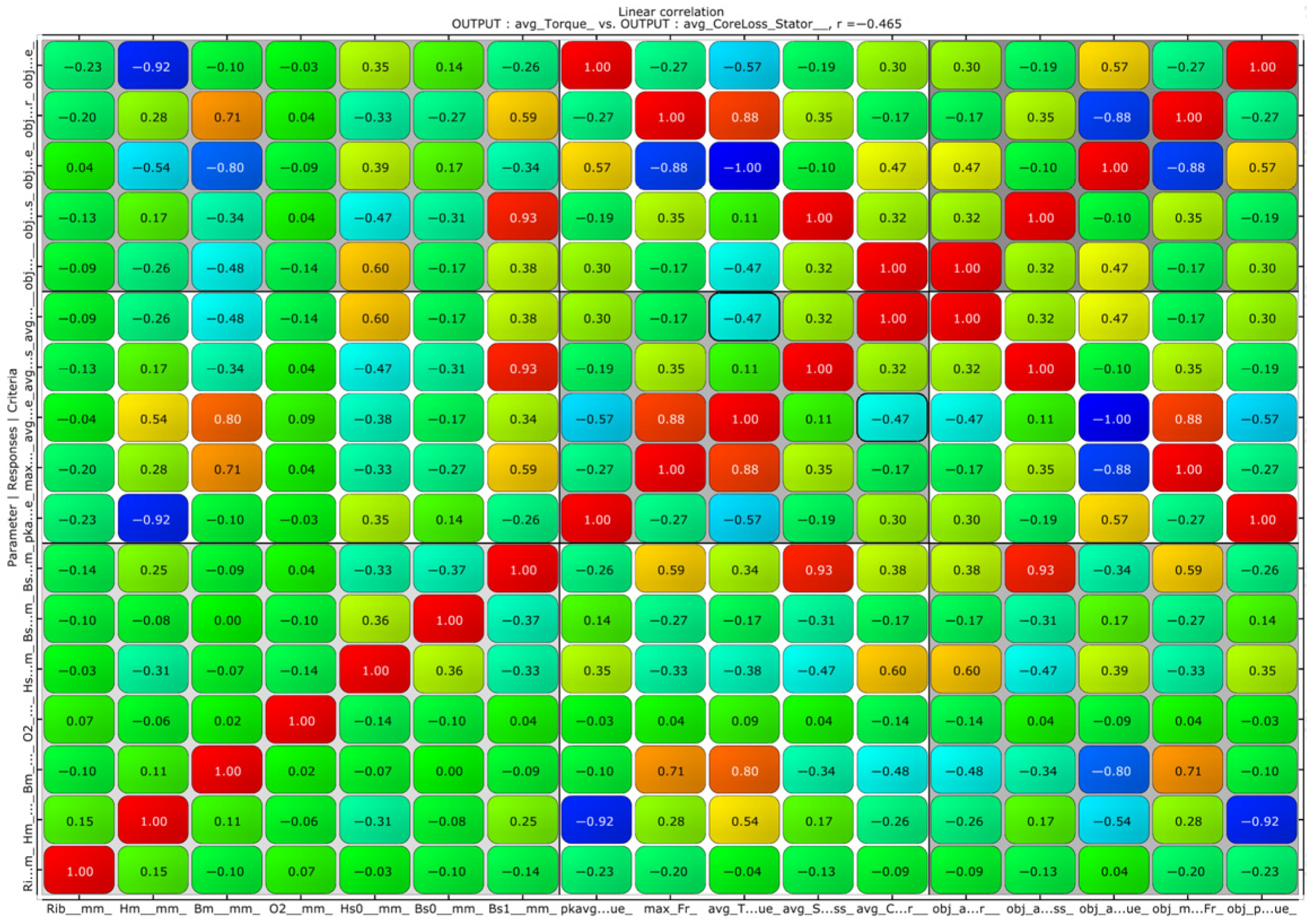
In the optimal predictive adaptive metamodel, uncertainty in the input parameters may lead to uncertainty in the model output parameters. To further improve the quality of the best fit, sensitivity analysis is essential prior to conducting the multi-objective optimization design, which employs local gradient-based derivatives to assess the primary influence of design variables on motor performance. This approach is suitable due to the approximately linear relationship observed between key motor performance and structural parameters within the optimized design domain, reducing the need for higher-order sensitivity analysis. Further, the inherent ability of the multi-objective optimization algorithm to explore interactions via Pareto solutions compensates for the relative simplicity of this sensitivity method. Additionally, the tenfold increase in samples required for Sobol indices compared to gradient-based methods was deemed prohibitively expensive given Finite Element Method simulation costs. The correlation coefficients in Figure 2 represent normalized partial derivatives; their sign indicates the influence direction (e.g., increasing B_m decreases torque ripple but increases radial force). The correlation coefficient between the optimization variables and the objective function f is defined as follows.

$${\gamma }_{ij}={\displaystyle \frac{\partial f}{\partial x_j}}$$

(18)

where $x_j$ is the j-th optimization variable, and ${\gamma }_{ij}$ represents the correlation coefficient between $x_j$ and f.

The structural parameters of the motor are shown in Figure 3. Based on previous research, torque ripple, stator core loss, electromagnetic force amplitude, and output average torque are chosen as the performance optimization objectives. The key structural parameters that influence the motor’s performance, such as slot width B_s0, slot heart width B_s1, slot height H_s0, permanent magnet width H_m, slot spacing Rib between adjacent poles, distance O₂ between the bottom of the permanent magnet and the inner circle of the rotor, and permanent magnet thickness $B_m$, are selected as the optimization design variables. The initial values and ranges of the variables initially selected in the experimental design are presented in Table 1. Design variable boundaries in multi-objective optimization are defined by physical constraints and electromagnetic viability. As Table 1 shows, physical constraints set mechanical integrity lower bounds and saturation prevention upper bounds to avoid lamination distortion during stamping. Electromagnetic constraints limit flux leakage while maintaining greater than 70% slot-fill factor for feasible winding.

Sensitivity analysis was performed on the four objectives concerning the seven design variables, yielding the correlation coefficients between the optimization objectives and design variables, as shown in Figure 3. The positive and negative signs of the sensitivity coefficients indicate the direction of the correlation between the parameters and the objectives. Specifically, a positive coefficient indicates a positive correlation, while a negative coefficient indicates a negative correlation. The absolute value of the sensitivity coefficient reflects the magnitude of the influence that parameter changes have on the optimization objective. The larger the absolute value, the more significant the influence of the parameter on the objective.

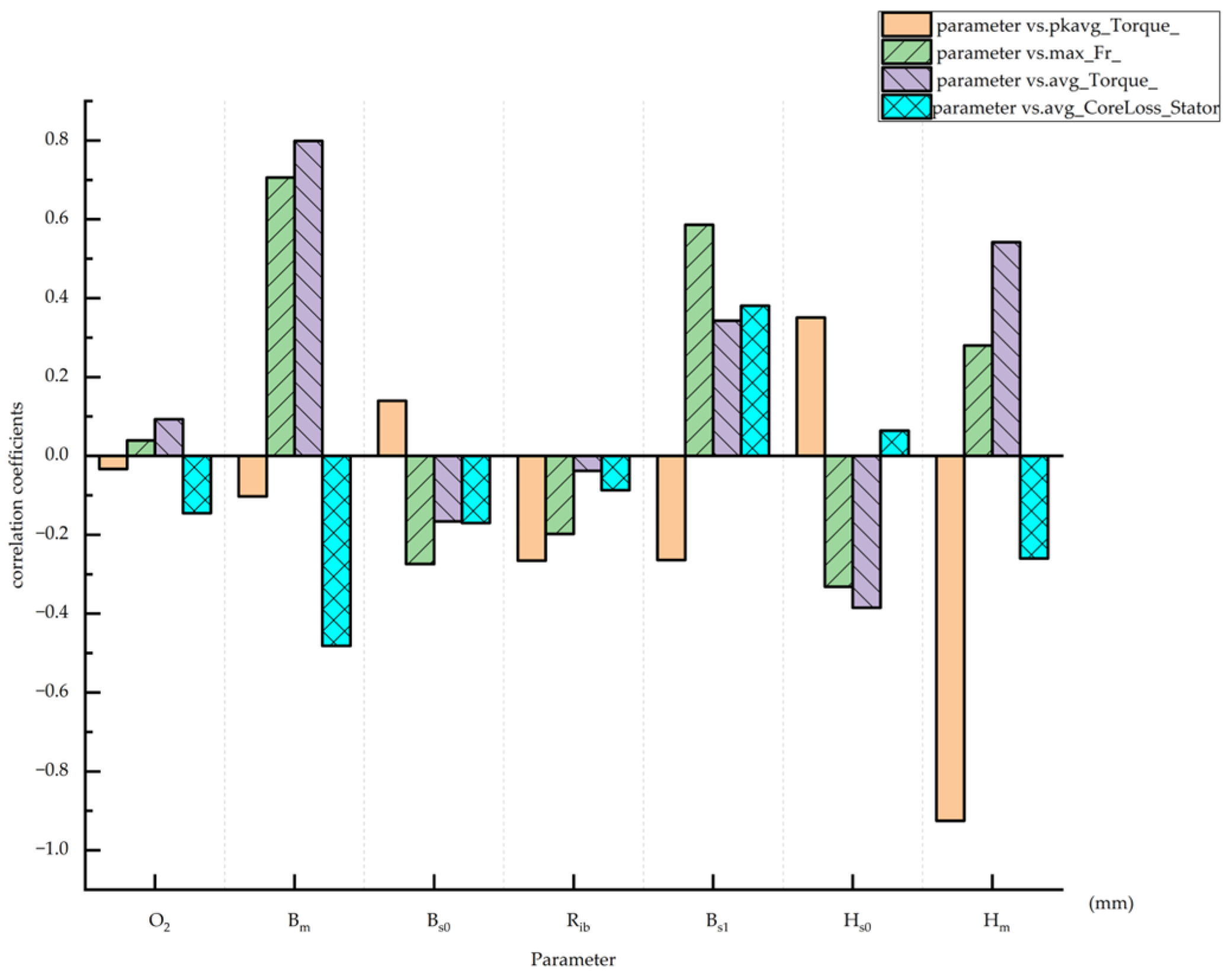
Figure 4 demonstrates notable differences in the sensitivities of various design variables across the objectives. For instance, stator core loss is predominantly affected by the slot height H_s0, slot core width B_s1, and permanent magnet thickness B_m, while it is less affected by the slot width B_s0 and the distance between the magnet bottom and the inner rotor circle. The output torque is influenced not only by the permanent magnet thickness B_m and permanent magnet width H_m, but also by the slot height H_s0 and slot core width B_s1. The variables that have the greatest impact on the radial electromagnetic force are the permanent magnet thickness B_m and the slot core width B_s1; while torque ripple is primarily dependent on the magnet width H_m, it is also affected by H_s0, B_s1, and the slot spacing R_ib of the magnets at adjacent poles.

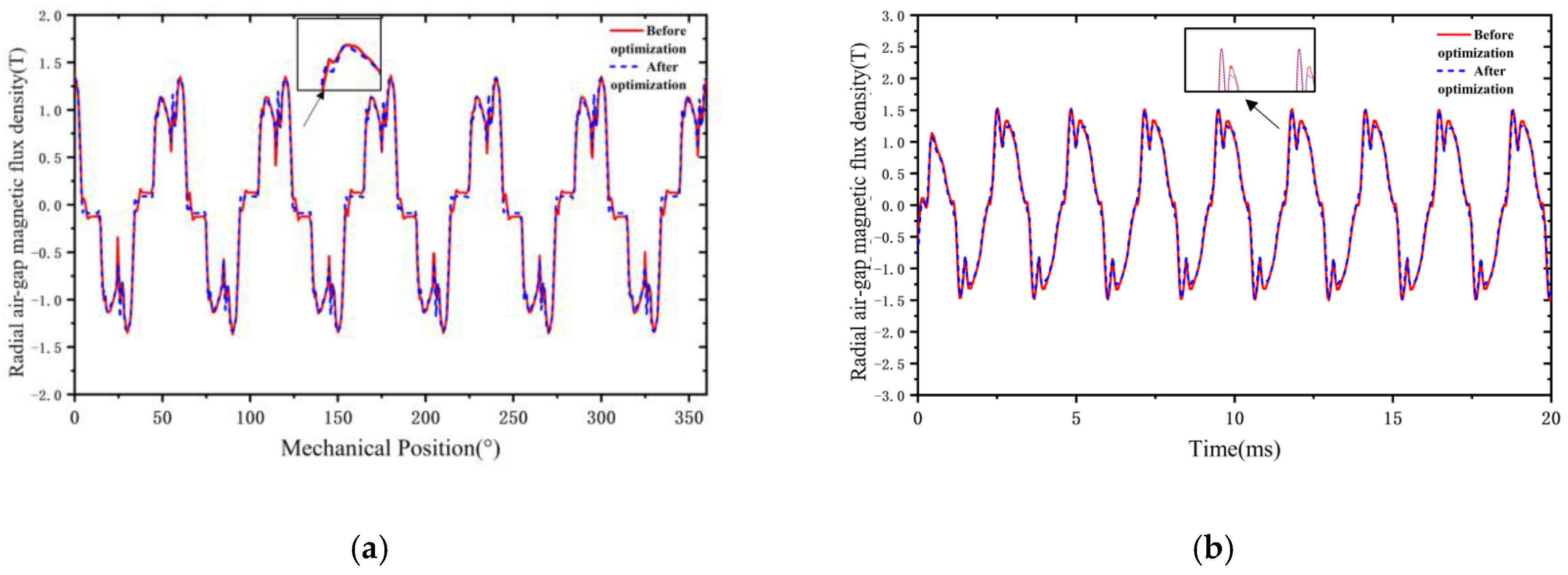
This is largely because the slot spacing between adjacent magnets influences the harmonic distribution of the air-gap magnetic field in the permanent magnet synchronous motor, along with factors such as the rotor distance O₂ and the slot spacing R_ib between adjacent poles.

5. Multi-Objective Optimization Model of PMSM Performance

Based on the results of the sensitivity analysis, the selected optimization design variables are the permanent magnet thickness B_m, permanent magnet width H_m, slot height H_s0, and slot core width B_s1. The optimized parameters of the multi-objective genetic algorithm (MOGA) are listed in Table 2, with their formulation as follows:

$$\begin{array}{c}find\to X=\{B_m,H_m,H_{s0},B_{s1}\}\\ \begin{array}{c}\mathit{min}:avg\left(CoreLoss\right(stator\left)\right)\\ \mathit{min}:pkavg\left(Torque\right)\end{array}\\ \mathit{min}:max\left(Fr\right)\\ \mathit{max}:avg\left(Torque\right)\\ s.t.:6.75\mathrm{mm}\text{≤}{B}_m\le 8.25\mathrm{mm}\\ 39.6\mathrm{mm}\text{≤}{H}_m\le 48.4\mathrm{mm}\\ 1.35\mathrm{mm}\text{≤}{H}_{s0}\le 1.65\mathrm{mm}\\ 9.10255\mathrm{mm}\text{≤}{B}_{s1}\le 11.1253\mathrm{mm}\end{array}$$

(19)

where avg(CoreLoss(stator)) is the average value of the stator core loss of the motor under rated operating conditions, avg(Torque) is the average output torque, pkavg(Torque) represents the torque ripple, and max(Fr) denotes the peak amplitude of the radial electromagnetic force.

The efficacy of NSGA-II is substantially contingent upon the initial parameters, as evidenced in

Table 3. The parameters of optimization objectives and variables.

Parameter	Values	Parameter	Values
Population size	100	Crossover ratio	0.95
Maximum number of iterations	60	Mutation rate	0.05
Percentage stability	70	Maximum allowed Pareto percentage	20

. The population size N necessitates a proportional adjustment in accordance with the objective dimension M and the design variables D. In the context of this study, which encompasses four objectives (M = 4) and four design variables (D = 4), the minimum population size Nmin is established at 64, though empirically expanded to 100 to augment diversity. The maximum permissible percentage of the Pareto front is increased to 20% to preserve a distribution of trade-off solutions. To mitigate the sparsity of solutions in high-dimensional spaces, to improve the efficiency of global search, and to avoid local entrapment, the crossover probability is fixed at 0.95. The maximum iteration count and the mutation probability are pivotal factors that influence computational efficiency, convergence of solutions, and the quality of optimization. These parameters necessitate a thorough evaluation, taking into account the complexity of the problem, the size of the population, the computational resources available, the landscape of the objectives, and the rate of change of the Pareto front. Consequently, the maximum iteration count is set at 60, with the mutation probability at 0.05. Based on sensitivity analysis, parameters such as slot width and permanent magnet thickness exhibit a high degree of sensitivity with respect to torque and iron loss. Therefore, the percentage stability is configured at 70.

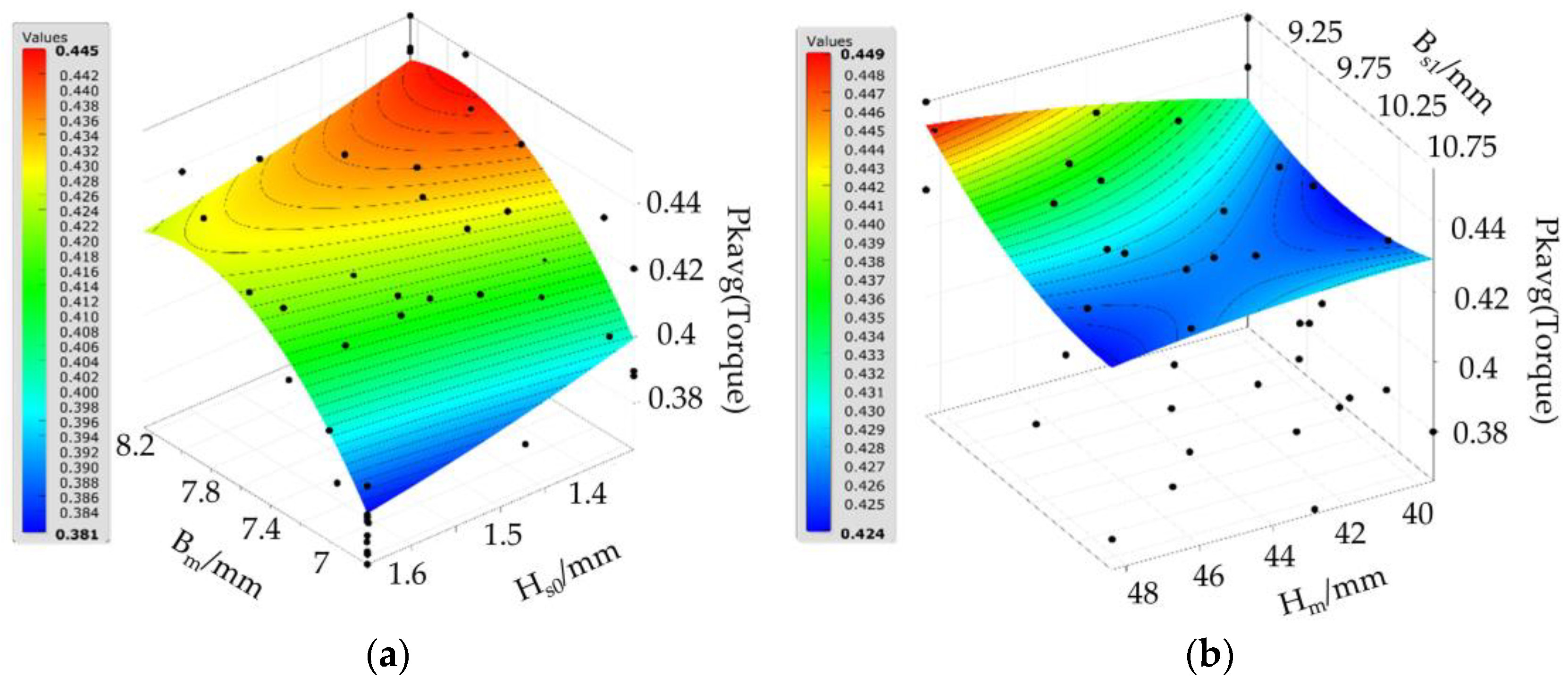
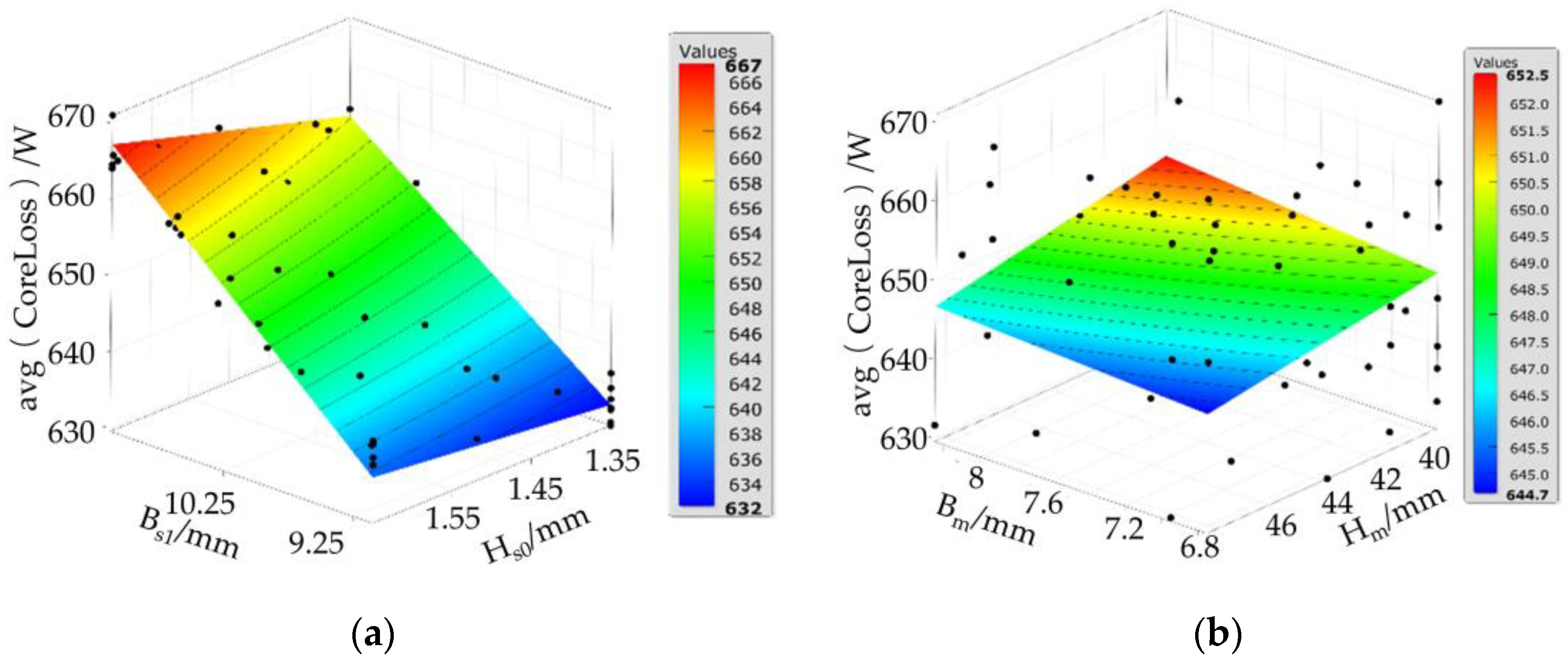
The response surfaces in Figure 5, Figure 6 and Figure 7 are based on regression analysis using the MFS-MLS method. The 3D response surface of the stator core loss is shown in Figure 5. The average stator core loss ranges from 630 W to 670 W. As illustrated in Figure 5a, the average stator core loss increases gradually with both the slot core width B_s1 and slot height H_s0, reaching a maximum value of 667 W, with a steep gradient on the response surface. From Figure 5b, as the permanent magnet thickness B_m increases and the magnet width H_m decreases, the average stator core loss also tends to increase, reaching a maximum value of 652.5 W, although the gradient in this region is less steep.

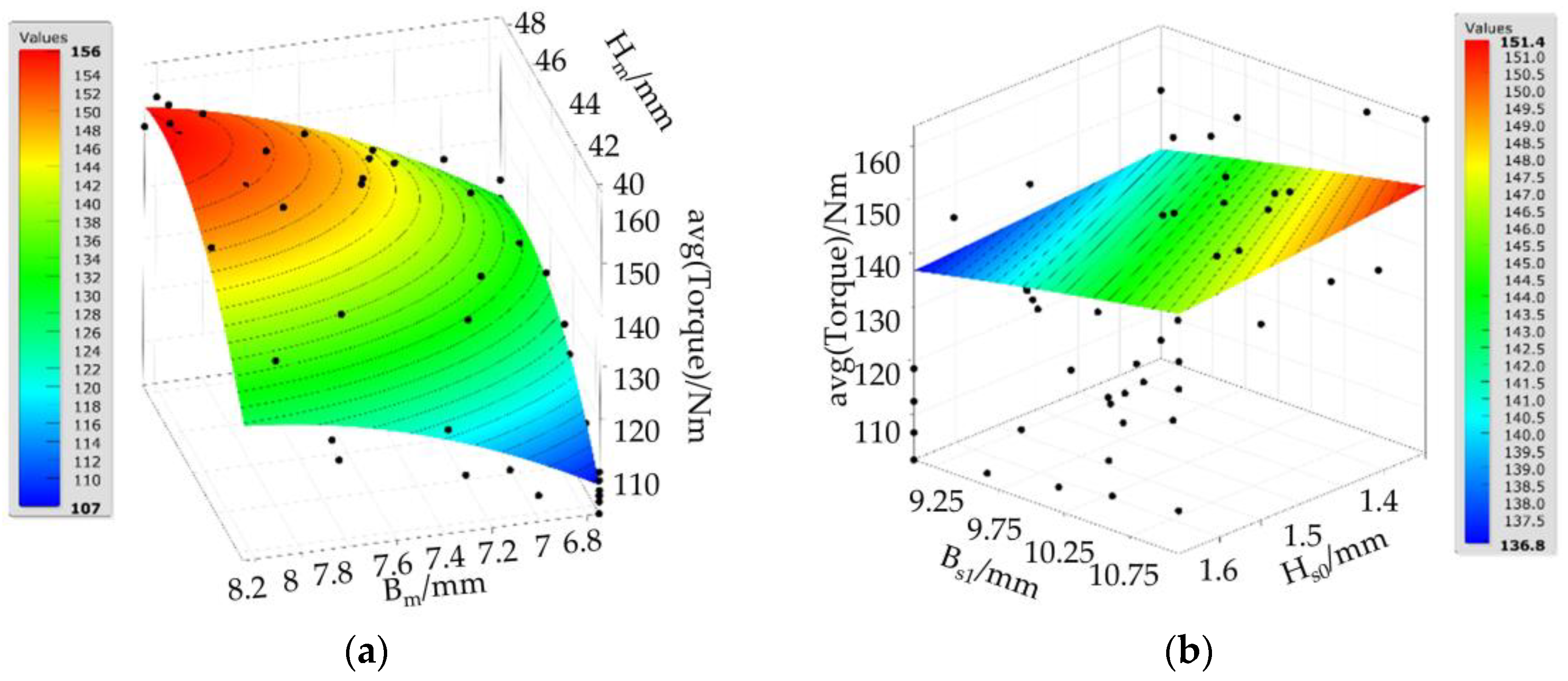
The 3D response surface of the average output torque is depicted in Figure 6. As shown, increasing both the thickness B_m and width H_m of the permanent magnet results in a gradual increase in the average output torque, with a steep response surface gradient. Additionally, the torque increases as the slot core width B_s1 expands from 9.25 mm to 10.75 mm, while the slot height H_s0 decreases from 1.6 mm to 1.35 mm.

Figure 7 displays the 3D response surface of the torque ripple. As observed in Figure 6a, increasing B_m from 6.8 mm to 8.2 mm and decreasing H_s0 from 1.6 mm to 1.35 mm causes the torque ripple to increase, with a notable steep gradient. In Figure 6b, reducing B_s1 10.75 mm to 9.25 mm and increasing H_m increases from 40 mm to 48 mm initially decreases the torque ripple, but further increases in Hm lead to a rise in ripple.

Figure 8 illustrates the 3D response surface of the radial electromagnetic force amplitude on the circle. Enlarging both the slot core width B_s1 from 9.25 mm to 10.75 mm and the magnet width H_m from 40 mm to 48 mm, as well as increasing the magnet thickness B_m from 6.8 mm to 8.2 mm and decreasing H_s0 from 1.6 mm to 1.35 mm, leads to a corresponding increase in the radial electromagnetic force.

As shown in

Table 4. An empirical comparison using the same DOE samples to evaluate MFS-MLS against three common techniques.

	MFS-MLS	Kriging	RBF	Neural Network
R2 (avg. torque)	0.982	0.975	0.963	0.958
R2 (torque ripple)	0.961	0.949	0.932	0.941
Training time (s)	28	65	42	120
Sensitivity to noise	Low	Moderate	High	Moderate

, we conducted an empirical comparison using the same DOE samples (Section 3) to evaluate MFS-MLS against three common techniques. Table 4 demonstrates that MFS-MLS achieved superior R² values for torque-related responses due to its adaptive weighting mechanism. In contrast, Kriging exhibited limitations in handling non-stationary responses, notably the abrupt variations in electromagnetic force at H_m = 46.3 mm. Furthermore, neural networks required a training dataset three times larger than MFS-MLS to attain comparable accuracy, rendering them computationally prohibitive within the 60-iteration MOGA framework.

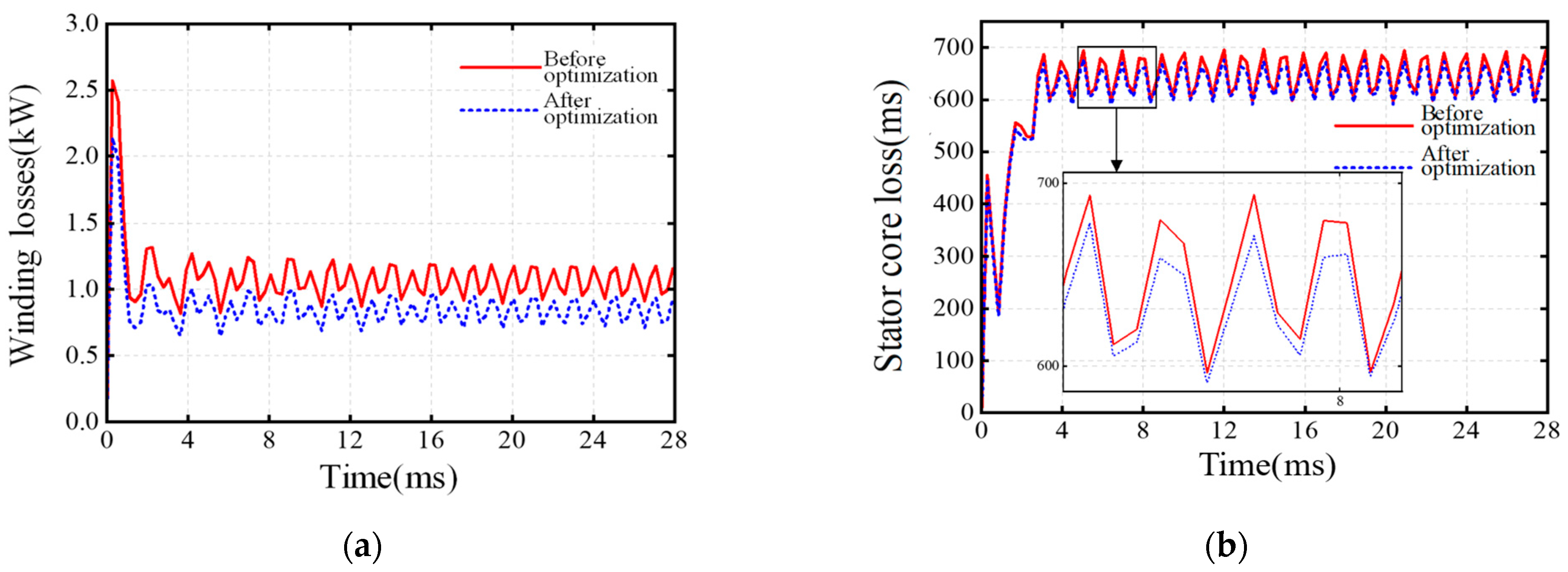
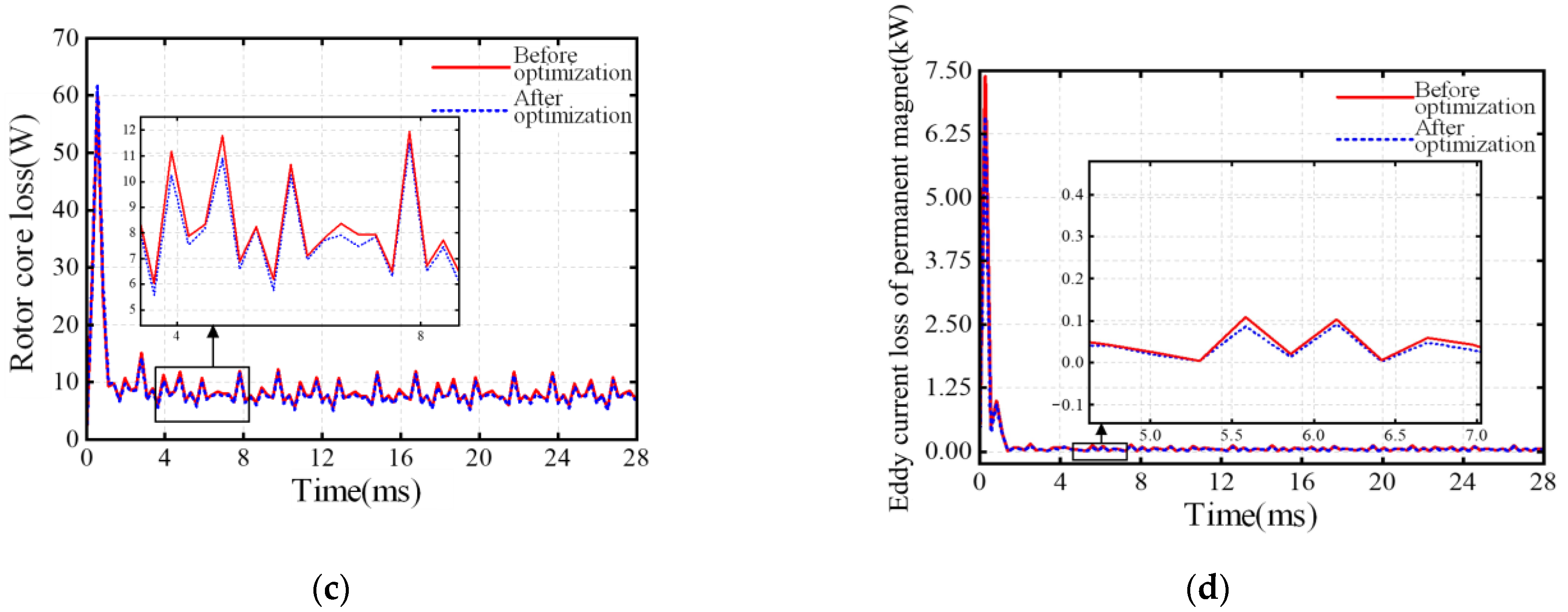
The structural parameters of the PMSM before and after optimization are summarized in

Table 5. Motor structural parameters before and after optimization.

Optimization Variable	Before Optimization	After Optimization
Hm (mm)	44.000	46.338
Bm(mm)	7.500	6.914
Bs1 (mm)	10.114	9.324
Hs0 (mm)	1.500	1.495

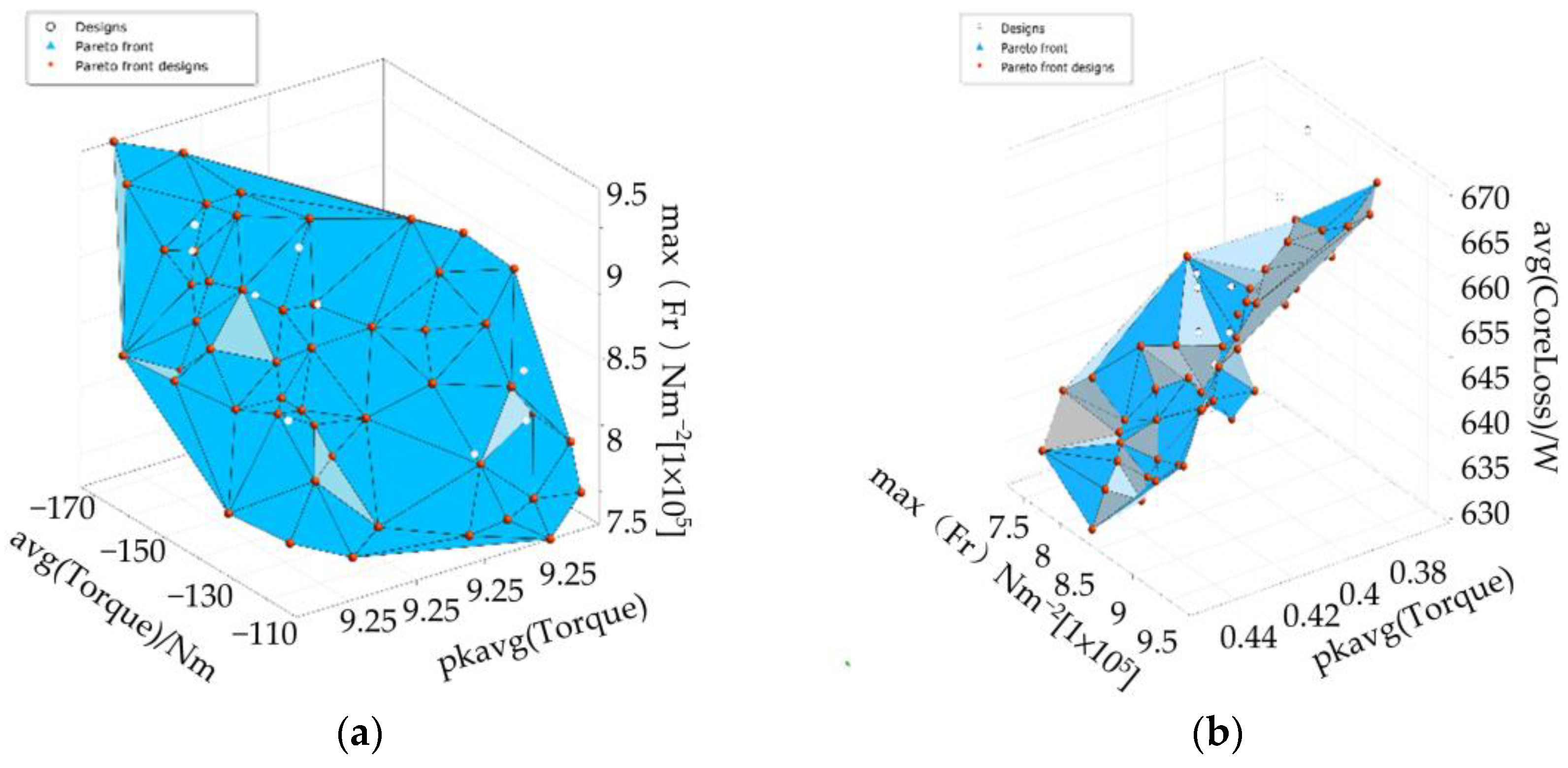
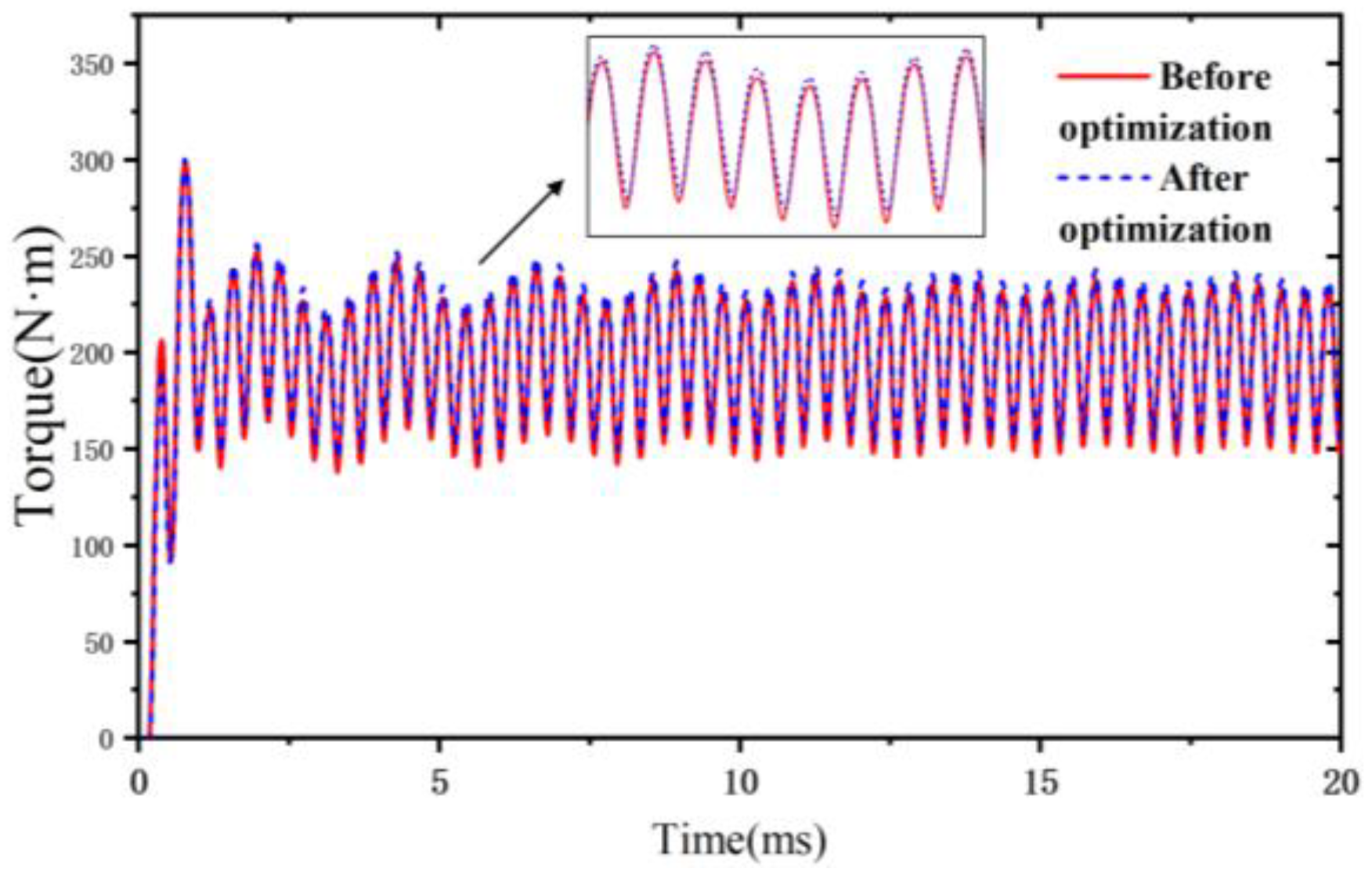
. The optimized design parameters are as follows: the width of the permanent magnet H_m is 46.338 mm, the thickness of the permanent magnet B_m is 6.914 mm, the width of the slot core B_s1 is 9.324 mm, and the height of the slot H_s0 is 1.495 mm. The Pareto front of the multi-objective optimization for the PMSM is depicted in Figure 8. As shown, decreasing the average output torque concurrently reduces both the torque ripple and the radial electromagnetic force. Conversely, increasing the radial electromagnetic force tends to decrease torque ripple but results in higher stator core losses.

Figure 9 presents a comprehensive illustration of the characteristics of the Pareto front, encompassing the following: (1) complete coverage of core loss (ranging from 630 W to 670 W), achievement of 90% of the torque target (spanning from 0.38 N·m to 0.44 N·m), and a comprehensive representation of the force density spectrum (varying between 7.5 N/m² and 9.5 × 10⁵ N/m²), with an irregular polyhedral structure that confirms a balanced trade-off among multiple objectives; (2) the formation of a continuous front (depicted by red dots) devoid of discontinuities, juxtaposed with densely distributed design points (indicated by blue triangles). This configuration displays continuous distributions across objectives, uniform spacing of core loss (without clustering), dispersed torque solutions (absence of dense regions), and stepwise intervals for force density (exhibiting balanced spacing). The integrated continuity results in optimal spacing metrics (less than 0.1) and a high hypervolume (HV exceeding 0.85), collectively substantiating the superior quality of solutions for motor optimization design.

6. Comparison of Main Performance Indexes of PMSM Before and After Optimization

To validate the effectiveness of the optimization results, a comparative analysis of the motor’s electromagnetic performance before and after optimization was performed.

6.1. Loss Optimization

Figure 10 illustrates the comparison of various losses in the PMSM before and after optimization. Following the optimization, the winding copper loss decreases from 1052 W to 828 W, reflecting a reduction of approximately 21%. The stator core loss is reduced from 647 W to 634 W, the rotor core loss decreases slightly from 8 W to 7.54 W, and the eddy current loss in the permanent magnet is lowered from 47.4 W to 37.9 W.

6.2. Torque Performance Optimization

The torque fluctuation coefficient is expressed as follows:

$$k={\displaystyle \frac{T_{max}-T_{min}}{T_{avg}}}\times 100\%$$

(20)

where Tmax is the maximum value of output torque, Tmin is the maximum value of output torque, and Tavg is the average value of output torque.

Figure 11 illustrates that the mean torque prior to optimization was 194.44 N∙m, accompanied by a torque fluctuation coefficient of 51.57%, as computed using Equation (20). Subsequent to a sudden increase in load, an overshoot of 120 N∙m was observed, and the settling time was determined to be 8.3 milliseconds. Following optimization, the mean torque was observed to decrease to 201.742 N∙m, while the torque fluctuation coefficient diminished to 48.48%, signifying a reduction of 3.09%. Additionally, the overshoot was mitigated to 45 N∙m, and the settling time was reduced to 3.1 milliseconds.

6.3. Radial Electromagnetic Force Optimization

The comparison of the radial electromagnetic force in the PMSM before and after optimization is presented in Figure 12. As shown in Figure 12a, the maximum radial electromagnetic force density before optimization is 729,845 N/m², which decreases to 717,952 N/m² after optimization. Figure 12b shows that at a specific point on the stator tooth surface, the maximum radial electromagnetic force density drops from 1,008,578 N/m² to 961,496 N/m² post-optimization, indicating a significant reduction in electromagnetic force intensity.

6.4. Flux Density Analysis Optimization

The comparison of the flux density in the PMSM before and after optimization is shown in Figure 13. The magnetic flux density attains its maximum values at approximately ±1.5 T around 100 and 250 degrees, whereas the minimum values approach zero at 0, 150, and 300 degrees within the mechanical position range of 0–350 degrees. The optimized design diminishes the peak values to approximately ±1.0 T with the minimum levels nearing ±0.5 T, markedly reducing the overall fluctuation amplitude, as illustrated in the magnified box area.

The amplitude of the magnetic flux density prior to optimization, represented by the solid line, is approximately ±3.0 T within the 0 to 20 millisecond range, exhibiting pronounced high-frequency oscillations. In contrast, for post-optimization, denoted by the dashed line, the amplitude has been reduced to ±2.0 T, and the fluctuations are notably more subdued, as indicated by the arrow in the vicinity of 10 milliseconds.

The optimization results markedly enhance the spatial uniformity and dynamic attributes of the radial air gap flux density, mitigate the periodic fluctuation and localized distortion of the motor flux density, achieve a more balanced magnetic field distribution, suppress high-frequency oscillations, and yield a more stable dynamic response. These improvements exert a beneficial influence on motor efficiency, noise levels, and reliability.

7. Conclusions and Future Works

• In contrast to the methodologies delineated in the extant literature, this paper introduces an adaptive Moving Least Squares (MFS-MLS) metamodel characterized by high precision. The enhancement of the Gaussian weight function and the adaptive moving window mechanism bolsters the dynamic local adaptability, effectively addressing the challenge faced by conventional models in capturing nonlinear abrupt changes within electromagnetic fields, such as torque ripple and radial force density.
• The integration of a scaling function facilitates the incorporation of low-fidelity true data, surmounting the constraints inherent to pure interpolation methods and achieving a synthesis of multi-fidelity true data. The resolution of local least squares problems circumvents the computational burden associated with the inversion of large-scale covariance matrices in Gaussian processes, thereby enhancing computational efficiency within high-dimensional design spaces and optimizing the overall computational performance.
• The synchronization of optimization objectives, encompassing torque, iron loss, and electromagnetic force, transcends the constraints of unidimensional optimization prevalent in existing research. This methodology yields a 3.09% reduction in torque ripple, a 4.67% diminution in radial electromagnetic force density, and a 13 W reduction in stator iron loss.

In the future, the following research will be investigated. For example, the impact of ±5% tolerances (typical for mass production) on key parameters (e.g., B_m, H_s0) using Monte Carlo simulations, and the simulation of performance at ±10% deviations of H_m and B_m.