Integrated Intelligent Control for Trajectory Tracking of Nonlinear Hydraulic Servo Systems Under Model Uncertainty
Abstract
1. Introduction
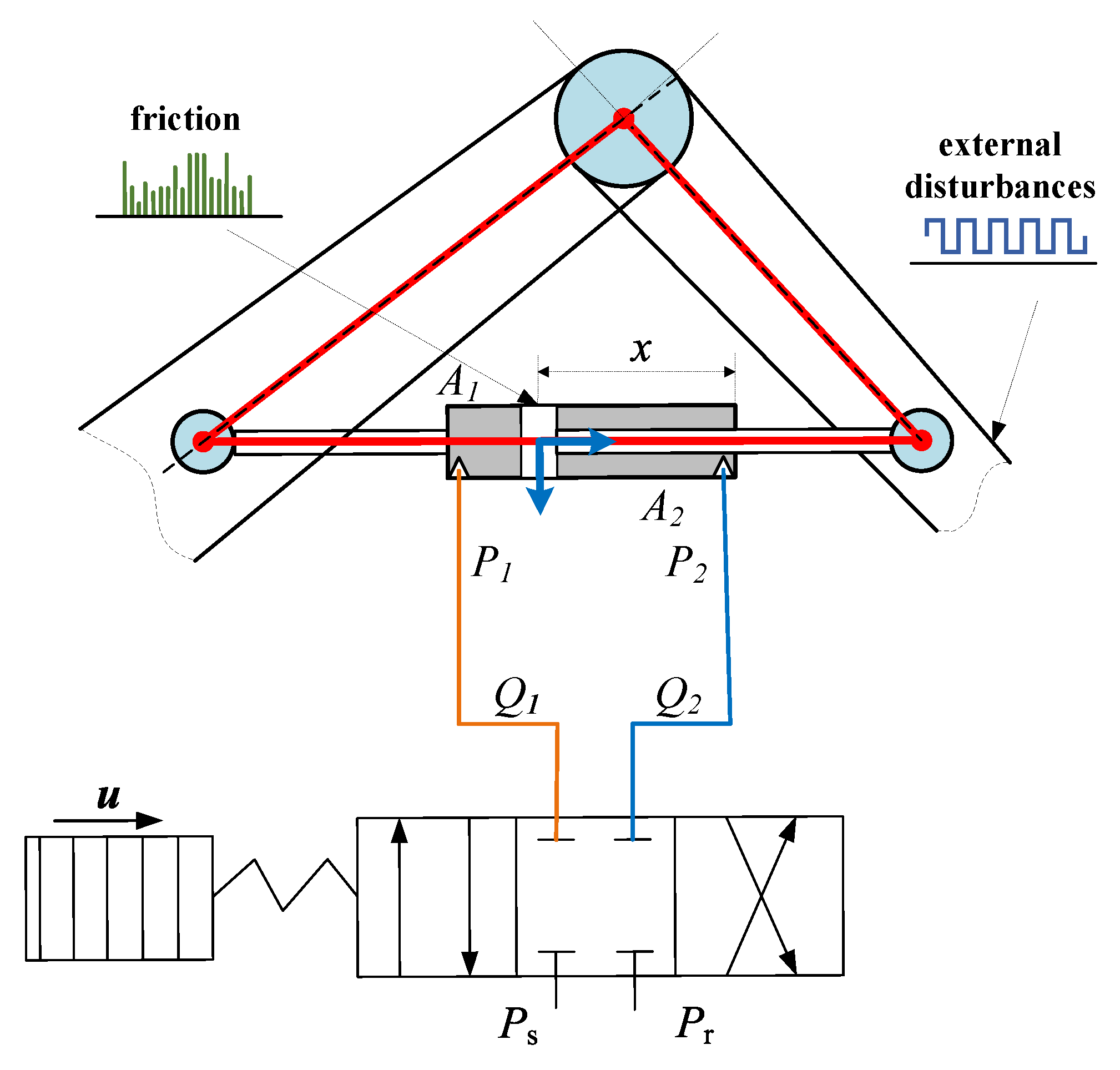
2. Problem Formulation and Dynamic Model
3. Model-Predictive Controller Design
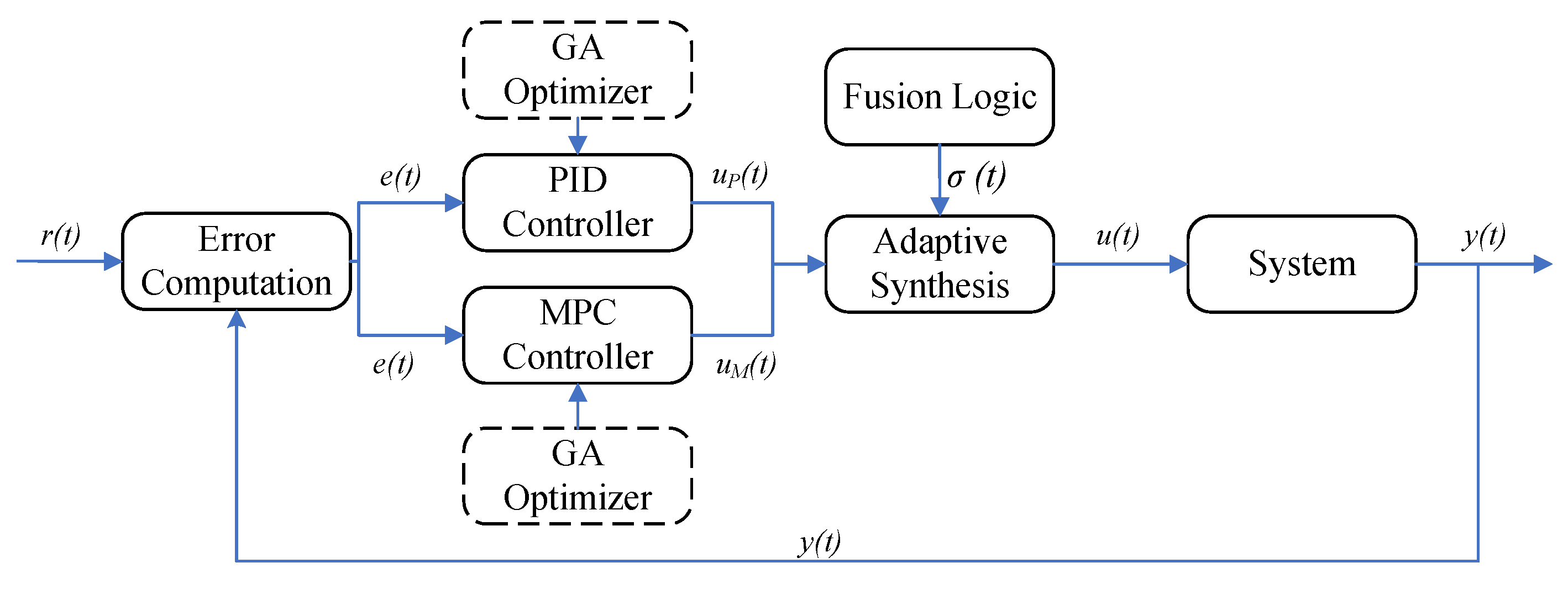
4. Integrated PID–MPC Controller
4.1. Fusion Architecture
4.2. Adaptive Gain Tuning via Projection
4.3. Cost-Aware Blending and Online Implementation
Motivation and Intuition Behind the Blending Law
- Small results in overly conservative blending, where hovers near 0.5 and dilutes both control benefits;
- Very large (e.g., >50) leads to quasi-discrete switching, producing oscillations similar to mode-chatter;
- values below 0.2 slow the adaptation rate and degrade transient performance;
- The chosen nominal setting (, ) achieves stable and responsive adaptation.
5. Rigorous Stability and Performance Analysis of the Hybrid Loop
5.1. Switched System Modeling and Preliminaries
- a sinusoidal input disturbance: on s;
- parametric variation in plant matrices A, B simulating model mismatch;
- Gaussian sensor noise with variance .
5.2. Input-to-State Stability via Multiple Lyapunov Functions
5.3. Performance via LMI Conditions
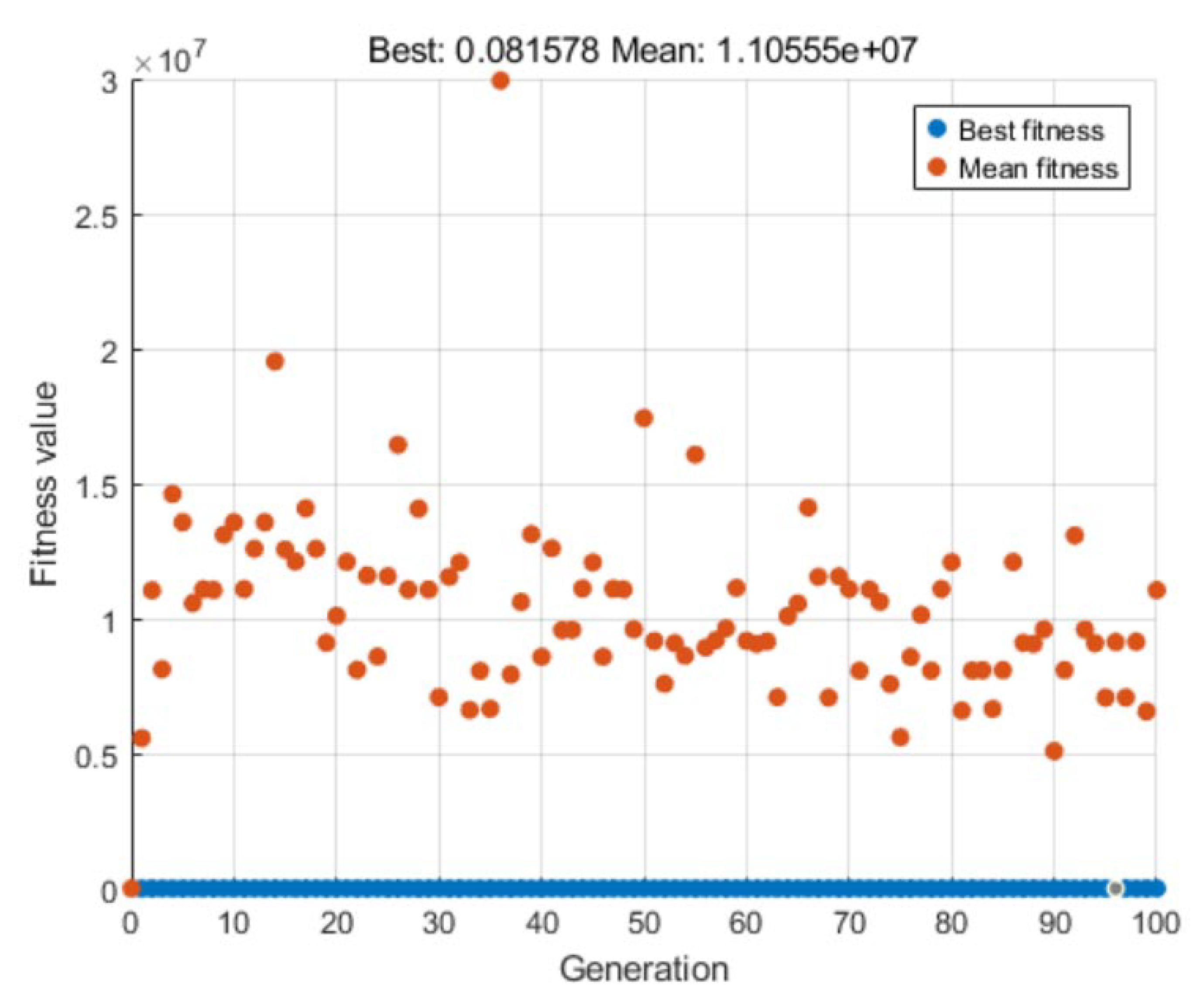
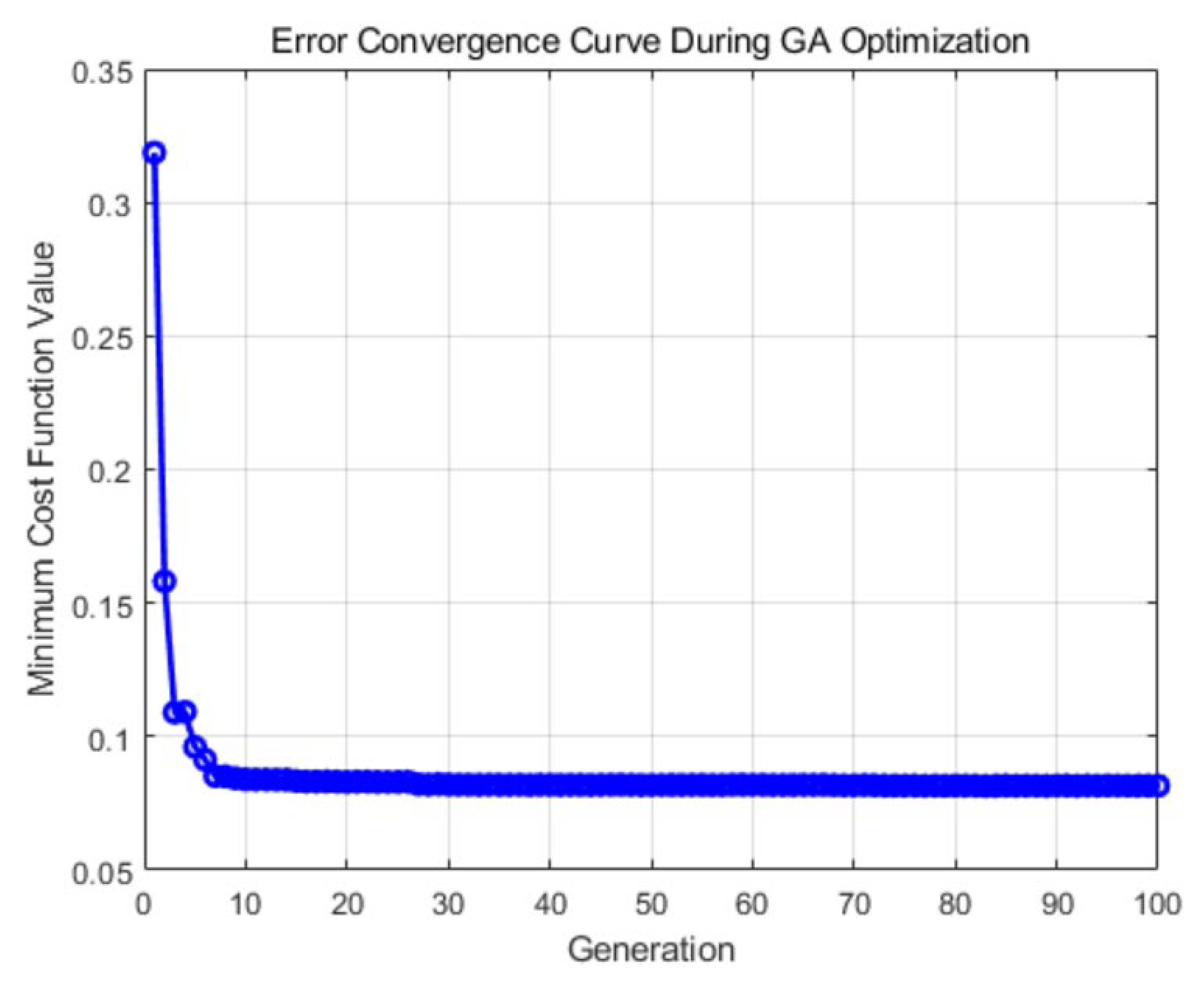
6. Simulation Experiments and Results Analysis
6.1. Digital-Twin Platform and Experiment Setup
Discussion on Advanced Benchmark Controllers
- Multi-dimensional variable configuration for energy efficiency. As presented in [32], the powertrain of electro-hydraulic systems can be co-optimized across electrical, mechanical, and hydraulic domains to minimize energy loss. While such methods improve efficiency, they typically rely on extensive system-level modeling and are less reactive to unmodeled disturbances.
- Adaptive neural network output feedback under event-triggered switching. The method proposed in [33] employs neural approximators and multiple event triggers to address nonlinear switched dynamics. These approaches achieve impressive robustness but often require significant training data and high computational overhead, which may limit real-time deployment on embedded hardware.
6.2. Simulation Results and Analysis
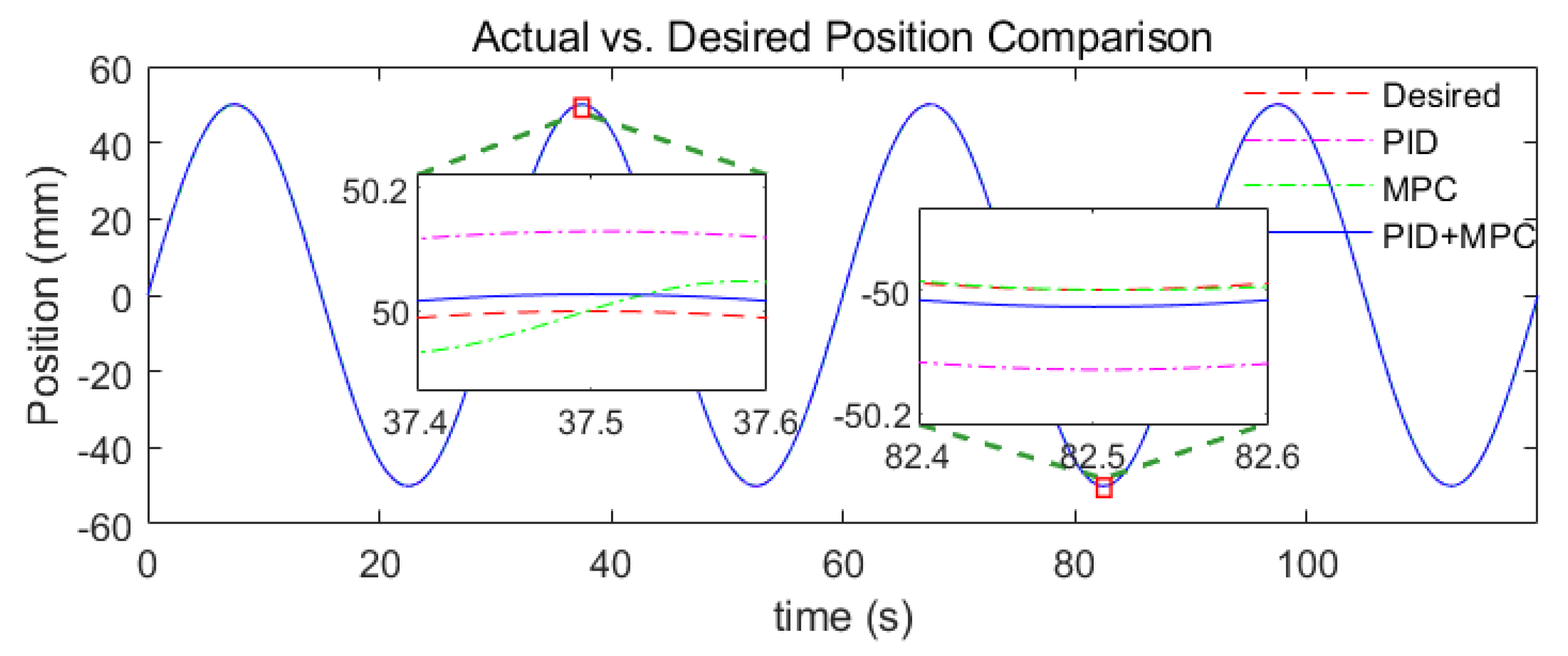
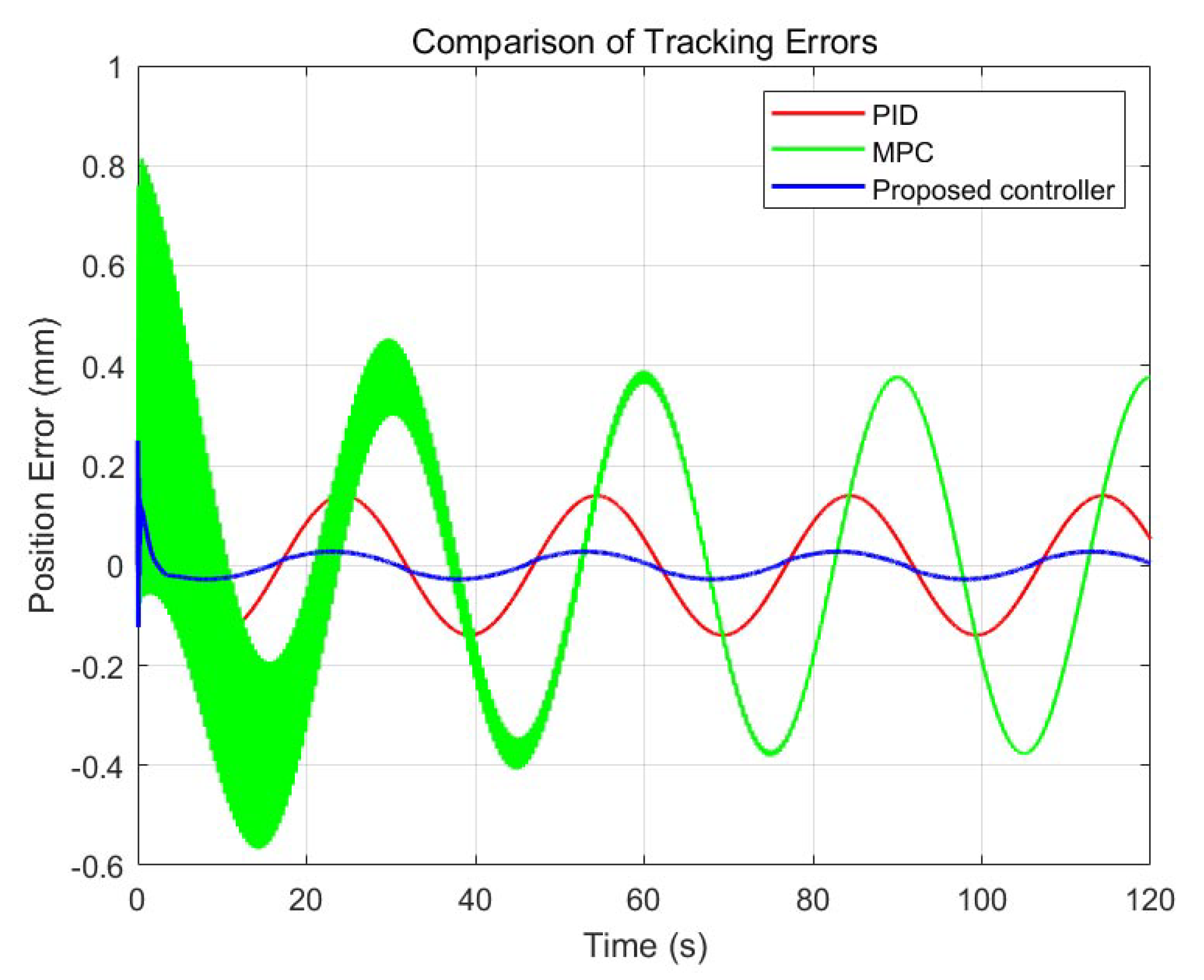
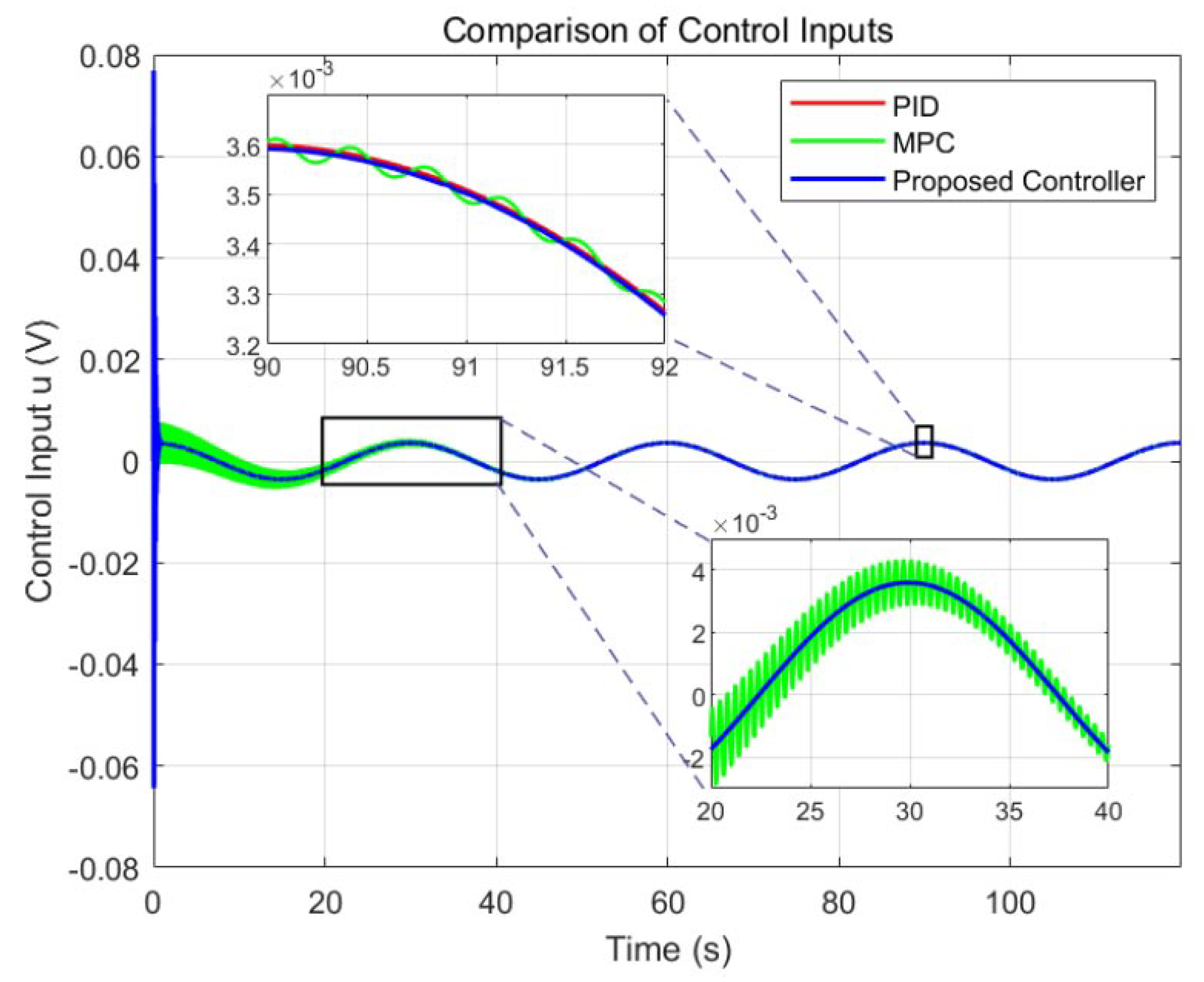
6.2.1. Comparative Experiment of Three Controllers Under No-Friction Disturbance
Ringing Behavior in MPC Control
- Model mismatch and prediction error accumulation. The MPC controller operates on a linearized internal model, whereas the true hydraulic system exhibits strong nonlinearities, including friction, leakage, and flow saturation. These unmodeled dynamics introduce a mismatch between predicted and actual trajectories, causing the optimizer to overcompensate in the following steps.
- Underdamped tuning and insufficient terminal penalty. Although the cost weights are optimized using a genetic algorithm, the resulting controller may still lack sufficient damping for rapid trajectory transitions. This underdamped configuration manifests as oscillatory corrections in both tracking error and control input.
- Delayed response to fast disturbances. The MPC optimization process requires several sampling intervals to update its solution, especially under constraints. As a result, the controller reacts sluggishly to high-frequency reference variations or measurement noise, which explains the high-frequency ringing visible in early stages of the tracking task.
- Absence of high-bandwidth feedback loop. Unlike the fusion controller, the standalone MPC lacks a fast inner-loop (such as PID) that could suppress transient oscillations in real-time. The result is an observable periodic overshoot in error and control effort during trajectory execution.
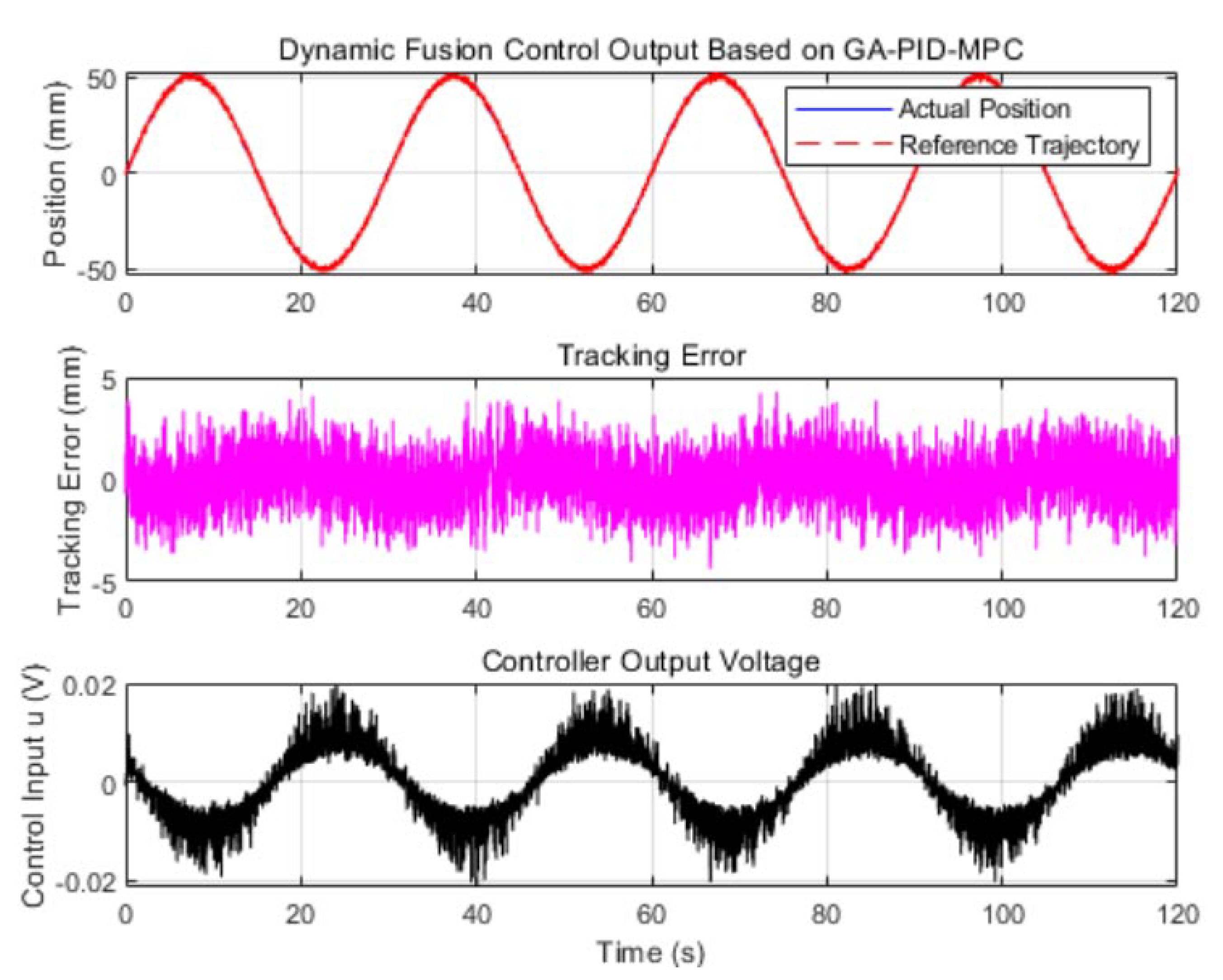
6.2.2. Experiment of the Proposed Controller Under Significant Frictional Disturbance
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Comprehensive Symbol Table
| Symbol | Description | Unit |
|---|---|---|
| Piston displacement/system state vector | m or – | |
| Velocity of piston | m/s | |
| , | Chamber pressures | MPa |
| Load pressure: | MPa | |
| Control input to servo valve | V | |
| Valve spool displacement | mm | |
| , | Valve flow gains | varies |
| Effective bulk modulus | GPa | |
| Static friction force | kN | |
| Viscous damping coefficient | Ns/m | |
| m | Equivalent piston–load mass | kg |
| Internal leakage flow | L/min | |
| Lumped disturbance (friction, noise, etc.) | – | |
| PID gain vector: | varies | |
| Blending coefficient between PID and MPC | – | |
| , | Cost function under PID and MPC modes | – |
| Learning rate matrix for gain adaptation | – | |
| Blending update gains | – | |
| Q, R, P | MPC cost weights and terminal penalty | varies |
| MPC prediction horizon | s | |
| Controller sampling period | s | |
| Augmented hybrid system state | – | |
| Mode indicator (1 = PID dominant, 2 = MPC) | – | |
| Closed-loop dynamics under mode i | – | |
| Lyapunov function for mode i | – | |
| Minimum average dwell time | s | |
| Maximum admissible disturbance amplitude | – | |
| performance gain bound | – | |
| Performance output: | – |
References
- Wang, J.; Yang, J.; Fang, D.; Wu, G.; Xue, Y.; Yang, M. Development of a bionic multi-chamber hydraulic cylinder for improving energy efficiency. Mechatronics 2024, 99, 103149. [Google Scholar] [CrossRef]
- Bakırcıoğlu, V.; Çabuk, N.; Jond, H.B.; Kalyoncu, M. Optimization-driven design and experimental validation of a hydraulic robot leg mechanism. Measurement 2025, 250, 117096. [Google Scholar] [CrossRef]
- Yu, B.; Li, H.; Ma, G.; Liu, X.; Chen, C.; Zheng, B.; Ba, K.; Kong, X. Design and matching control strategy of electro-hydraulic load-sensitive hydraulic power unit for legged robots. Energy 2024, 313, 133730. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Prentkovskis, O.; Deptuła, A.; Skačkauskas, P. Research of vibrations effect on hydraulic valves in military vehicles. Def. Technol. 2023, 30, 111–125. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Ivannikova, V.; Maskeliūnaitė, L. The impact of mechanical vibrations on pressure pulsation, considering the nonlinearity of the hydraulic valve. J. Low Freq. Noise Vib. Act. Control 2024, 44, 706–719. [Google Scholar] [CrossRef]
- Lovrec, D.; Tic, V.; Tasner, T. Dynamic behaviour of different hydraulic drive concepts-comparison and limits. Int. J. Simul. Model 2017, 16, 448–457. [Google Scholar] [CrossRef]
- Chai, T.; Dreyer, J.T.; Singh, R. Time domain responses of hydraulic bushing with two flow passages. J. Sound Vib. 2014, 333, 693–710. [Google Scholar] [CrossRef]
- Ma, L.; Huang, Q.; Ma, L.; Ma, Q.; Zhang, W.; Han, H. Structural Design and Dynamic Characteristics of Overloaded Horizontal Servo Cylinder for Resisting Dynamic Partial Load. Chin. J. Mech. Eng. 2019, 32, 11. [Google Scholar] [CrossRef]
- Aboelhassan, A.; Abdelgeliel, M.; Zakzouk, E.E.; Galea, M. Design and Implementation of model predictive control based PID controller for industrial applications. Energies 2020, 13, 6594. [Google Scholar] [CrossRef]
- Sun, Y.; Wan, Y.; Ma, H.; Liang, X. Compensation control of hydraulic manipulator under pressure shock disturbance. Nonlinear Dyn. 2023, 111, 11153–11169. [Google Scholar] [CrossRef]
- Chen, Z.; Zha, H.; Peng, K.; Yang, J.; Yan, J. A design method of optimal PID-based repetitive control systems. IEEE Access 2020, 8, 139625–139633. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, J.; Qiu, L.; Liu, X.; Wu, W.; Fang, Y. Subspace Predictor-Based Predictive Voltage Control for Power Converters. IEEE Trans. Ind. Electron. 2025, 72, 7659–7671. [Google Scholar] [CrossRef]
- Amiri, M.; Hosseinzadeh, M. Practical considerations for implementing robust-to-early termination model predictive control. Syst. Control Lett. 2025, 196, 106018. [Google Scholar] [CrossRef]
- Calogero, L.; Pagone, M.; Cianflone, F.; Gandino, E.; Karam, C.; Rizzo, A. Neural Adaptive MPC with Online Metaheuristic Tuning for Power Management in Fuel Cell Hybrid Electric Vehicles. IEEE Trans. Autom. Sci. Eng. 2025, 22, 11540–11553. [Google Scholar] [CrossRef]
- Yang, X.; Ge, Y.; Zhu, W.; Deng, W.; Zhao, X.; Yao, J. Adaptive Motion Control for Electro-hydraulic Servo Systems With Appointed-Time Performance. IEEE/ASME Trans. Mechatron. 2025. [Google Scholar] [CrossRef]
- Li, D.; Lu, K.; Cheng, Y.; Wu, H.; Handroos, H.; Yang, S.; Zhang, Y.; Pan, H. Nonlinear model predictive control—Cross-coupling control with deep neural network feedforward for multi-hydraulic system synchronization control. ISA Trans. 2024, 150, 30–43. [Google Scholar] [CrossRef] [PubMed]
- Yao, Z.; Yao, J. Exponential Asymptotic Prescribed Performance Control of Electro-Hydrostatic Actuators. IEEE Trans. Ind. Electron. 2025. [Google Scholar] [CrossRef]
- He, J.; Zhou, L.; Li, C.; Li, T.; Huang, J.; Su, S. Control Strategy of Hydraulic Servo Control Systems Based on the Integration of Soft Actor-Critic and Adaptive Robust Control. IEEE Access 2024, 12, 63629–63643. [Google Scholar] [CrossRef]
- Cao, D.X.; Duan, X.J.; Guo, X.Y.; Lai, S.K. Design and performance enhancement of a force-amplified piezoelectric stack energy harvester under pressure fluctuations in hydraulic pipeline systems. Sens. Actuators Phys. 2020, 309, 112031. [Google Scholar] [CrossRef]
- Battarra, M.; Mucchi, E. On the relation between vane geometry and theoretical flow ripple in balanced vane pumps. Mech. Mach. Theory 2020, 146, 103736. [Google Scholar] [CrossRef]
- Jiang, S.; Huang, F.; Liu, W.; Huang, Y.; Chen, Y. A Double Closed-Loop Digital Hydraulic Cylinder Position System Based on Global Fast Terminal Sliding Mode Active Disturbance Rejection Control. IEEE Access 2024, 12, 80138–80152. [Google Scholar] [CrossRef]
- Chen, J.; Pan, H.; Zhang, K.; Lan, H.; Xu, X.; Luo, W. Predictive control approach incorporating incremental learning. Appl. Intell. 2025, 55, 401. [Google Scholar] [CrossRef]
- Zhang, H.; Assawinchaichote, W.; Shi, Y. New PID parameter autotuning for nonlinear systems based on a modified monkey–multiagent DRL algorithm. IEEE Access 2021, 9, 78799–78811. [Google Scholar] [CrossRef]
- Arpacik, O.; Ankarali, M.M. An efficient implementation of online model predictive control with field weakening operation in surface mounted PMSM. IEEE Access 2021, 9, 167605–167614. [Google Scholar] [CrossRef]
- Bøhn, E.; Gros, S.; Moe, S.; Johansen, T.A. Optimization of the model predictive control meta-parameters through reinforcement learning. Eng. Appl. Artif. Intell. 2023, 123, 106211. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Pub. Co.: Redwood City, CA, USA, 1989. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- The MathWorks, Inc. MATLAB Optimization Toolbox: Quadprog Function Documentation; The MathWorks, Inc.: Natick, MA, USA, 2023. [Google Scholar]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; PTR Prentice-Hall: Upper Saddle River, NJ, USA, 1996; Volume 1. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991; Volume 199. [Google Scholar]
- Hespanha, J.P.; Morse, A.S. Stability of switched systems with average dwell-time. In Proceedings of the 38th IEEE Conference on Decision and Control (Cat. No. 99CH36304), Phoenix, AZ, USA, 7–10 December 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 3, pp. 2655–2660. [Google Scholar]
- Jin, R.; Li, L.; Liang, X.; Zou, X.; Yang, Z.; Ge, S.S.; Huang, H. Energy-efficient design of the powertrain for mechanical-electro-hydraulic equipment via configuring multidimensional controllable variables. Renew. Sustain. Energy Rev. 2024, 201, 114511. [Google Scholar] [CrossRef]
- Wang, F.; Long, L. Adaptive NN Output Feedback Control of Switched Nonlinear Systems via Multiple Event-Triggering Communications. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 3906–3916. [Google Scholar] [CrossRef]

| Symbol | Description | Unit |
|---|---|---|
| Piston displacement/state vector | m or – | |
| Control input voltage to servo valve | V | |
| Tracking error: | m | |
| Chamber pressures | MPa | |
| Load pressure | MPa | |
| PID gains: | varies | |
| PID/MPC blending factor | – | |
| Sampling interval | s |
| Parameter | Value | Unit |
|---|---|---|
| Equivalent mass m | 10 | kg |
| Viscous damping | 2 | N·s/m |
| Effective piston area A | 0.01 | m2 |
| Bulk modulus | Pa | |
| Supply pressure | Pa | |
| Tank pressure | 0 | Pa |
| Stroke length L | 1.0 | m |
| Fluid density | 850 | kg/m3 |
| Orifice gain | 0.75 | L/min/mm1/2 |
| Static friction | 5000 | N |
| Stribeck velocity | 0.01 | m/s |
| Sampling interval | 0.001 | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Zhang, J.; Zhang, H. Integrated Intelligent Control for Trajectory Tracking of Nonlinear Hydraulic Servo Systems Under Model Uncertainty. Actuators 2025, 14, 359. https://doi.org/10.3390/act14080359
Zhou H, Zhang J, Zhang H. Integrated Intelligent Control for Trajectory Tracking of Nonlinear Hydraulic Servo Systems Under Model Uncertainty. Actuators. 2025; 14(8):359. https://doi.org/10.3390/act14080359
Chicago/Turabian StyleZhou, Haoren, Jinsheng Zhang, and Heng Zhang. 2025. "Integrated Intelligent Control for Trajectory Tracking of Nonlinear Hydraulic Servo Systems Under Model Uncertainty" Actuators 14, no. 8: 359. https://doi.org/10.3390/act14080359
APA StyleZhou, H., Zhang, J., & Zhang, H. (2025). Integrated Intelligent Control for Trajectory Tracking of Nonlinear Hydraulic Servo Systems Under Model Uncertainty. Actuators, 14(8), 359. https://doi.org/10.3390/act14080359






