Abstract
This study presents a quasi-static optimization framework for the pressure-based control of a multi-segment soft continuum manipulator. The proposed method circumvents traditional curvature and length-based modeling by directly identifying the quasi-static input–output relationship between actuator pressures and the 6-DoF end-effector pose. Experimental data were collected using a high-frequency electromagnetic tracking system under monotonic pressurization to minimize hysteresis effects. Transfer functions were identified for each coordinate–actuator pair using the System Identification Toolbox in MATLAB, and optimal actuator pressures were computed analytically by solving a constrained quadratic program via a manual active-set method. The resulting control strategy achieved sub-millimeter positioning error while minimizing the number of actuators engaged. The approach is computationally efficient, sensor-minimal, and fully implementable in open-loop settings. Despite certain limitations due to sensor nonlinearity and actuator hysteresis, the method provides a robust foundation for feedforward control and the real-time deployment of soft robots in quasi-static tasks.
1. Introduction
Soft continuum manipulators have emerged as a focal point in robotic research due to their intrinsic mechanical compliance, high adaptability, and suitability for operation in constrained or deformable environments. Constructed from elastomeric materials and actuated through internal pressure, such systems offer continuous deformation capabilities beyond the limits of traditional rigid-link mechanisms. Consequently, their applications span various domains, including endoscopic procedures [1], physical human–robot interaction [2,3] and coordinated manipulation in multi-agent systems [4].
However, due to their distributed compliance and nonlinear material behavior, the accurate control of soft manipulators remains a significant challenge. Thus, a study by Garcia et al. [1] demonstrated a 3-DOF pneumatic robot capable of achieving complex spatial configurations using pressure modulation. However, their open-loop calibration approach was imperfect and could not be fully utilized for different task conditions.
Similarly, Wang et al. [2] introduced a feedback-based trajectory control framework based on kinematic models, yet orientation regulation and actuator constraints were not considered. A broader synthesis by Tejada et al. [4] highlighted the lack of unified modeling strategies for multi-segment designs, citing scalability, real-time stability, and geometric predictability limitations.
In scenarios where actuation is slow and quasi-static, dynamic effects such as inertia and damping may be safely neglected. Under these conditions, control formulations based on static equilibrium become appropriate, particularly for high-precision positioning applications. However, the pressure–position relationship in soft systems remains highly nonlinear and affected by such dependent material features, leading to hysteresis. For example, Chen et al. [5] investigated hysteresis-aware neural models and confirmed their relevance in predicting quasi-static deformations. In addition, Rabiee et al. [6] observed a sharp drop in accuracy when the coupling effects were ignored, thus emphasizing the importance of segmental calibration in multi-section actuators. In support of the quasi-static assumption, Haggerty et al. [7] showed that inertial effects can be disregarded without compromising fidelity in many typical soft robotic tasks.
Given these challenges, considerable effort has been devoted to modeling quasi-static behavior via data-driven techniques. In particular, Sapai et al. [8] employed deep neural networks trained on synthetic data to predict deformation under varying pressure configurations. While accurate within the training domain, the resulting models showed poor generalization to real-world systems. Similarly, Nadizar et al. [9] evaluated evolved neural controllers for configuration estimation, reporting performance degradation under structural or environmental variation. Moreover, Zhang et al. [10] demonstrated ML-based proprioceptive sensing for estimating curvature states, albeit with significant calibration overhead and limited robustness to sensor drift.
While forward modeling techniques have been extensively studied, significantly less attention has been paid to the inverse quasi-static control problem—the computation of pressure inputs that achieve a desired terminal pose under equilibrium conditions. Existing approaches include learning-based and optimization-based methods. For example, Garg et al. [11] implemented safe reinforcement learning combined with covariance matrix adaptation to optimize control policies. However, the approach did not guarantee convergence to target poses with minimal steady-state error. In another effort, Chen et al. [12] proposed an adaptive Jacobian controller that allows for real-time gain adjustment, yet the method lacked a formal optimization framework. Furthermore, Cao et al. [13] introduced an AI-driven co-design pipeline to jointly synthesise structure and controller, though the resulting models were computationally intensive and difficult to interpret.
However, despite all the advances, there are still fundamental problems related to transparency, constraint integration, and physical plausibility.
As shown by the studies of George Thuruthel et al. [14] and Kim et al. [15], the use of black box models in machine learning has challenges that manifest themselves in high data requirements and a lack of physical justification. Chen et al. [16] added that existing learning-based controllers rarely account for actuation limits and often underperform when generalized to multi-segment geometries. Complementing this view, Hsieh and Hou [17] evaluated nonlinear transfer functions in bionic soft systems, identifying instability issues when extrapolating beyond training data.
In response, several hybrid approaches have been proposed to combine the strengths of data-driven modeling and physically interpretable control. Papageorgiou et al. [18] applied sparse system identification to derive reduced-order models and incorporated sliding-mode control for enhanced robustness, although without an explicit optimization objective. Yang et al. [19] developed an online optimization-enhanced controller for continuum robots; however, the model was empirical and not grounded in static equilibrium theory. A comparative evaluation by Grube et al. [20] concluded that model-based methods consistently outperform learning-based strategies in scenarios requiring high positioning accuracy and real-time constraint satisfaction.
Despite some success in static control applications, most contributions remain limited in scope. Wang et al. [21] designed a geometry-driven closed-loop controller for position regulation, omitting orientation tracking. Morales-Enríquez et al. [22] developed a data-driven controller for a single-link actuator, which was not extended to multi-segment configurations. Peña Fernández [23] formulated an optimal control law via dynamic programming for compliant manipulators, but the work lacked system identification from real measurements. A recent review by Chen et al. [16] underscored the absence of constrained, interpretable, and experimentally verified frameworks for solving the inverse static problem in soft robots.
Taken together, these studies illustrate that while ML and hybrid approaches have advanced the field, significant limitations remain in terms of generalizability, interpretability, and integration of physical constraints. The reliance on large datasets, limited support for constraint-aware optimization, and insufficient validation on multi-segment configurations underscore a persistent research gap.
The present study introduces a model-based inverse quasi-static control framework for a two-segment pneumatic soft continuum manipulator to address these limitations. The objective is to compute the pressure input vector that minimizes pose error—defined over position and orientation—under static equilibrium constraints. Quasi-static input–output relationships are obtained via system identification using experimentally acquired pressure–pose datasets. These mappings are then embedded into a constrained optimization problem that enforces actuation limits while minimizing end-effector deviation from the target configuration.
The paper is organized into four sections. Section 1 introduces the motivation for developing an optimization-based control strategy for soft continuum manipulators, emphasizing the challenges associated with nonlinear material behavior, actuation uncertainty, and structural compliance. Section 2 describes the experimental setup and data acquisition methodology, including system calibration, high-frequency pose tracking, and mapping pressure inputs to end-effector displacements under quasi-static conditions. Section 3 presents the system identification and optimization results, covering the derivation of quasi-static input–output models, analytical formulation of the inverse control problem, and validation of the proposed method. Finally, Section 4 provides a critical discussion of the results, highlights limitations related to sensor artefacts and actuator hysteresis, and concludes by outlining the implications of the work for future control architectures in soft robotics.
2. Materials and Methods
2.1. Experimental Setup
For the study, the experimental platform shown in Figure 1 was used to empirically characterize the quasi-static relationships between action and posture in a pneumatic manipulator with a soft continuum. Each experiment applies a predefined pressure vector to the actuators, inducing segmental deformation through axial contraction of pneumatic artificial muscles [24]. Following a transient response, the system reaches a static equilibrium, at which point the end-effector configuration is recorded. Repetition across a structured pressure grid produces a dataset suitable for quasi-static model identification and inverse control formulation.

Figure 1.
Experimental setup.
The platform consists of three functional subsystems to achieve this goal, including the actuator, control and data acquisition interface, and measurement module units. These subsystems work in concert to ensure consistent actuation and synchronized data measurement [25].
The actuation unit comprises two serially connected continuum segments. Each segment includes three symmetrically arranged pneumatic artificial muscles (FESTO DMSP-10-400N-RM-CM, Esslingen am Neckar, Germany) capable of up to 25% axial shortening under positive pressure. Differential pressurization allows for planar and compound bending. Pressure is modulated via six independent proportional regulators (FESTO VEAB-L-26-D9-Q4-V1-1R1), each controlled by a 0–10 V analog input and operating in the 0–600 kPa range. The regulators exhibit a response time below 20 ms and maintain a control accuracy of ±1% full scale. Compressed air is supplied from a constant-pressure source (AIRSTAR AC401/50, New York, NY, USA), and power distribution is managed by a stabilized laboratory DC supply (KORAD KD3005D, Guangdong, China).
The control and acquisition interface uses a Humusoft MF634 (Prague, Czech Republic) real-time I/O board integrated with MATLAB/Simulink (Version R2023b). The system provides 16-bit analog outputs and supports synchronous data acquisition at rates up to 10 kHz. Analog signals are dispatched to the regulators at fixed intervals, and pressure values are held constant during pose acquisition to ensure consistency in static equilibrium conditions.
End-effector position and orientation are recorded using a Viper electromagnetic tracking system (Polhemus, Colchester, VT, USA) [26]. A six-degree-of-freedom sensor is rigidly attached to the distal tip of the manipulator. The tracker operates at sampling frequencies up to 960 Hz, providing <0.8 mm RMS positional error and <0.1° angular resolution. The measurement system is robust to occlusion and independent of external lighting conditions.
As an integrated architecture, the system enables repeatable quasi-static actuation experiments, high-resolution 6-DoF pose capture, and structured input–output data acquisition.
2.2. Data Collection and Mapping
The system was operated under quasi-static conditions to characterize the mapping between actuator pressure and manipulator configuration empirically. Pressure input was incrementally varied across a structured grid of combinations, while depressurization sequences were intentionally omitted to avoid the influence of hysteresis phenomena inherent to soft continuum structures. The experimental cycle proceeded through a deterministic sequence of pressure application, mechanical deformation, pose acquisition, stabilization detection, and data recording. This process is summarized schematically in Figure 2.
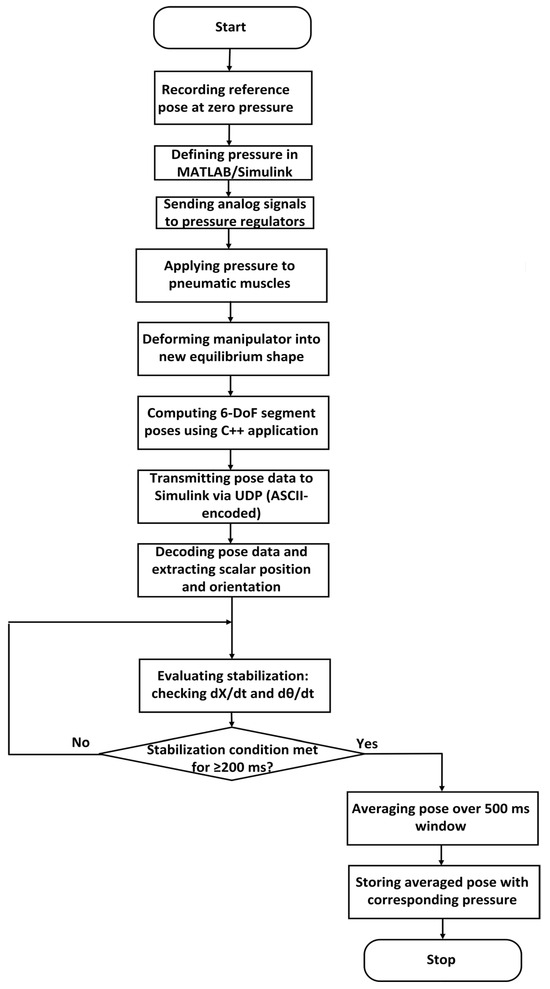
Figure 2.
Block diagram of data acquisition cycle.
Each data acquisition cycle began with geometric calibration to ensure the consistency and physical relevance of all measurements. The unloaded, depressurized manipulator was recorded to define a zero-reference configuration. Zero reference is defined by three coordinates and three angles: x, y, and z coordinates and pitch, yaw, and roll angles. Before starting the movement, this data is collected by the software for 5 s, where the average value of each value is then taken to begin counting the deviation from the zero value. Sensors in each segment of the robot measure the relative position to the source [26].
All subsequent pose measurements were computed as displacements relative to this reference, effectively isolating pressure-induced deformation while eliminating static offsets and long-term drift.
Following calibration, actuation was performed in an open-loop manner. Pressure vectors were generated within the MATLAB/Simulink environment and transmitted via analog output channels through the Humusoft MF634 interface to six independent pneumatic regulators. Each regulator controlled a dedicated actuator, inducing axial contraction and differential bending across the manipulator structure. No feedback from the measurement subsystem was used to adjust input signals, ensuring strict decoupling between actuation and observation.
Pose acquisition was performed using two electromagnetic tracking sensors, one per segment. A custom C++ application interfaced with the Viper SDK to obtain real-time curvature measurements converted into absolute 6-DoF pose estimates using a pre-calibrated geometric model. The resulting data were transmitted to Simulink via UDP using ASCII encoding and decoded into scalar position and orientation components for further processing.
Pause stabilization was verified in real time by monitoring temporal derivatives to guarantee that only equilibrium configurations were captured. A configuration was considered stable when translational and rotational velocity norms remained below 0.1 mm/s and 0.05°/s, respectively, for a continuous 200 ms interval. Once these conditions were satisfied, a 500 ms time-averaging window was applied to suppress high-frequency noise and improve measurement fidelity.
Each pressure configuration was repeated twenty times to ensure statistical robustness and enable reliable filtering. Final values were computed by averaging the stabilized pose measurements across trials, discarding any outliers exceeding predefined variance thresholds.
The resulting dataset consists of filtered, temporally aligned 6-DoF pose vectors corresponding to each input pressure combination. These measurements serve as the empirical foundation for the system identification and control synthesis developed in the subsequent section.
2.3. System Identification
A quasi-static system identification procedure was employed to model the relationship between actuator pressure inputs and the resulting spatial configuration of the soft manipulator. The system is assumed to operate under quasi-static conditions, with negligible dynamic and hysteretic effects due to monotonic actuation and stabilization-based data acquisition. As a result, the manipulator is treated as a memoryless nonlinear system in which the equilibrium configuration is defined solely by the current input pressures.
Let the actuator input vector be defined as Equation (1):
The corresponding end-effector position can be described as (2):
In Equation (2), only translational coordinates are considered, while orientation angles (φ, θ, ψ) are intentionally excluded. This assumption is justified by the task formulation, which focuses exclusively on achieving target positions in Cartesian space. The orientation at the final pose is assumed to be either unobservable, non-actuated, or irrelevant to the application.
The identification problem is formulated as a quasi-static mapping (3).
In Equation (3), μ: R6→R3 is a nonlinear, component-wise continuous function. Each scalar output is modeled as a function of all six pressure inputs, resulting in a set of three multi-input–single-output (MISO) models.
Before selecting the appropriate model, the estimation of alternative models was performed by using the System Identification Toolbox in MATLAB. The reliability of the identified models was ensured by comparing the obtained transfer functions and the model’s response to a single pulse in the MATLAB System Identification Toolbox. During this, each of the models was compared with the standard. Among them, the models that could not be identified at some points were immediately discarded. After the models are discarded, the model that can provide the maximum accuracy is selected, which tends to 100%.
A continuous-time transfer function was identified for each coordinate using the tfest algorithm applied to steady-state data. Although tfest is typically employed for dynamic system modeling, it can be adapted to quasi-static scenarios by focusing on input–output pairs recorded after complete stabilization. Internally, the algorithm performs prediction error minimization to fit a rational transfer function of the form
Under quasi-static conditions, the influence of dynamic terms is suppressed, and the model effectively represents the steady-state sensitivity of the system to input variations.
The transfer function order was limited to three to preserve analytical tractability and ensure robust control performance. Higher-order models were excluded due to the emergence of oscillatory terms and reduced numerical stability. The final quasi-static representation for each coordinate took the form
In Equation (5), are scalar input gains, and is a constant offset. These coefficients were estimated by least-squares minimization within the identification routine.
However, in the full dynamic formulation, each coordinate was described as a linear combination of pressure-dependent subsystems, each governed by its own transfer function:
X from Equation (6) denotes the output coordinate under consideration (e.g., X, Y, Z, pitch, yaw, roll) for which the pressure-dependent transfer functions Gxj (s) are defined. The x indicates the output variable being modeled as a function of each input pressure pj. Therefore, the identified class of models serves as a control-compatible representation of the quasi-static behavior of the manipulator with subsequent optimization.
2.4. Optimal Control Formulation
The inverse quasi-static control problem for the continuum soft manipulator can be formulated as an optimization task aimed at determining the actuator pressures required to precisely position the end-effector at a desired point in space. Mathematically, the control objective is defined through the minimization of the following quadratic cost function:
In Equation (7), is the vector of actuator input pressures, is the target end-effector position, represents the quasi-static gain matrix determined from the experimental data, and presents an offset vector derived from initial calibration.
Considering physical limitations of the actuators, the pressures are constrained within feasible bounds, typically expressed as
For mathematical convenience and rigorous analytical treatment, the optimization problem can be explicitly reformulated into the standard quadratic form:
In Equation (9), the symmetric positive semi-definite matrix and vector are explicitly defined as (10) and (11):
To ensure transparency, reproducibility, and interpretability of the solution method, the optimization problem is solved analytically by applying the Karush–Kuhn–Tucker (KKT) conditions explicitly. This manual analytical approach consists of several clearly defined sequential steps:
First, active constraints are hypothesized by assuming one or more actuator pressures reach their boundary values (0 or 500 kPa):
Second, a reduced linear system is constructed by removing equations and unknowns corresponding to the active constraints. Denoting the set of free (non-constrained) variables as pr, the resulting reduced linear equation system takes the form
In Equation (13), and represent the reduced matrices and vectors derived from Q and f.
Third, the solution of this reduced linear system is obtained explicitly using Gaussian elimination. The system is first transformed into an upper-triangular form (14):
This is followed by a direct backward substitution (15):
Fourth, to ensure physical feasibility, each computed actuator pressure is projected back onto the allowable range using the operation
Finally, the full vector of optimal actuator pressures is reconstructed by incorporating previously fixed boundary pressures, ensuring a complete and feasible pressure distribution for the soft manipulator control.
3. Results
3.1. Model Validation
To reconstruct the spatial response of the soft manipulator, individual transfer functions were identified for each of the 18 actuator–coordinate pairings. Each model captures the dynamic mapping from the input pressure applied to a pneumatic muscle to the resulting displacement of the end-effector along the X, Y, or Z axis.
The System Identification Toolbox carried out data fitting and model selection in MATLAB. For each pair, 3–5 s or third-order candidate models were generated and evaluated using the normalized root mean square error (NRMSE) criterion. The final selection was based on multiple factors, such as best numerical fit, minimal overshoot, physical plausibility, and smoothness of response. All accepted models were restricted to a maximum of a third order to avoid numerical instability and unphysical oscillations. In cases where the best fit was below 30%, models were retained if they preserved monotonic and directionally consistent behavior concerning pressure input.
The final selected models are listed in Table 1, with one transfer function provided per coordinate and actuator channel.

Table 1.
Complete transfer function table.
Each identified model has the canonical form
It relates the pressure input pj (s) of the j-th actuator to the displacement component xi (s) along a given axis. The overall response of each spatial coordinate is thus formulated as a linear combination of individual actuator contributions (18)–(20).
To demonstrate the quality of the model approximation, Figure 3, Figure 4 and Figure 5 present comparisons between measured and simulated trajectories for actuator 1 along the X, Y, and Z axes, respectively.
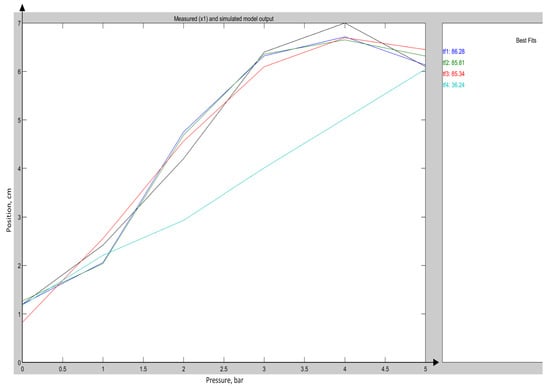
Figure 3.
Comparisons between measured and simulated trajectories for actuator 1 along the X-axis.
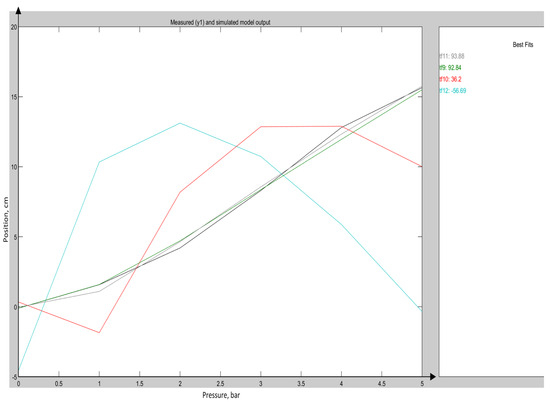
Figure 4.
Comparisons between measured and simulated trajectories for actuator 1 along the Y-axis.
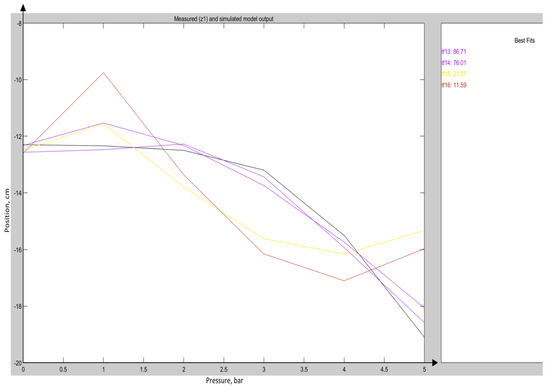
Figure 5.
Comparisons between measured and simulated trajectories for actuator 1 along the Z-axis.
The models show strong alignment with empirical data, including transitions and consistent steady-state values. Validation plots for the remaining actuator–coordinate pairs are provided in the Supplementary Materials (Figures S1–S15).
It is worth noting that in several cases—especially for Z-axis responses or actuators with weak mechanical influence—the best-fit accuracy dropped below 30%. These discrepancies are partially attributed to the limitations of the electromagnetic tracking system used for pose estimation. As discussed in Section 2.2 and further detailed in the Discussion, the sensor may produce polarity inversions and localized discontinuities when crossing the center of the magnetic field. Nevertheless, the selected models were physically plausible, directionally valid, and sufficient for use in the control framework.
The validated transfer functions serve as the foundation for the optimal control formulation presented in the next section.
3.2. Quasi-Static Optimization Results and Control Strategy
To evaluate the effectiveness of the proposed inverse quasi-static control framework, the target Cartesian position is
Equation (21) was selected as a representative end-effector configuration. The optimization objective was formulated as a least-squares minimization problem with bounded pressure inputs
In the equation, is the matrix of DC gains derived from the experimentally identified quasi-static transfer functions for each actuator–coordinate pair, and is a constant vector accounting for the manipulator’s calibrated baseline offset. All values are expressed in centimeters and kilopascals.
Rewriting the cost function in canonical quadratic form:
This yields a strictly convex optimization problem over a convex feasible set.To obtain an interpretable closed-form solution and reduce numerical sensitivity, we employed a manually constructed active-set strategy, where actuator 5 was fixed at its lower bound kPa, as it contributed minimally in prior numerical experiments.
With this constraint enforced, the reduced quadratic system in (26) and (27) was solved analytically using the Gaussian elimination method:
The resulting reduced optimal pressure vector is
This result demonstrates a highly sparse actuation profile, where only two muscles (actuators 4 and 6) require significant input pressure. Actuators 1, 2, and 3 receive residual numerical artefacts that are below the regulator resolution and thus are rounded to 0 kPa.The quasi-static prediction error obtained by substituting into the model can be described with Equation (29):
Thus, this strategy demonstrates that the optimal pressure vector enables sub-millimeter accuracy in reaching the target configuration.
4. Discussion and Conclusions
The inverse quasi-static control strategy results demonstrate that high-precision positioning of a continuum soft manipulator can be achieved under quasi-static assumptions without dynamic modeling or closed-loop feedback. The system consistently converged to the desired spatial configurations with sub-millimeter accuracy using experimentally identified transfer functions and an analytical optimization approach. The simplicity and interpretability of the method, along with the sparsity of the resulting actuation profiles, offer practical advantages for real-time implementation and low-power operation.
However, certain limitations were encountered, and one of the most critical concerns was the behavior of the electromagnetic tracker used for pose acquisition. Although the sensor offers high temporal and spatial resolution, its measurements are susceptible to field distortions and discontinuities, particularly when the manipulator crosses the central symmetry axis of the magnetic field.
Another methodological simplification involved bypassing curvature-based models and direct actuator length estimation, which was motivated by experimental constraints and theoretical reasoning, such as the structural complexity of pneumatic, specifically embedded sensing.
Furthermore, curvature-based formulations depend on assumptions about material homogeneity and constant-radius bending, which are often violated in practice. Instead, the quasi-static modeling approach directly maps pressure inputs to end-effector positions, avoiding the uncertainties associated with intermediate kinematic representations. While this greatly simplifies identification and control, it restricts the model’s generality and limits its application to purely forward (pressurization-only) movements.
Hysteresis effects posed another important constraint. Due to the inherent viscoelasticity and internal friction within the pneumatic actuators, the manipulator displays irreversibility under unloading. All identification and validation experiments were conducted under strictly monotonic pressure increases to ensure reproducibility. As a result, the current model does not generalize to bidirectional or cyclic actuation scenarios. Future work can address this limitation by explicitly modeling hysteresis loops or using hybrid system representations.
From an optimization standpoint, the proposed active-set formulation allowed for efficient and transparent computation of the optimal pressure vector. The solution reveals that in many configurations, only a subset of actuators needs to be energized to achieve the desired pose. This should be taken into account in the design of the control system.
Although this method is limited to quasi-static tasks, it can serve as a feedforward component in more complex hierarchical controllers, such as model predictive control frameworks.
Regarding practical constraints, the pressure range was limited to 500 kPa to prevent plastic deformation or long-term degradation of the actuator materials. Although this limit was sufficient for most tasks, specific configurations may require higher force generation or more aggressive pressurization. Therefore, actuator durability and fatigue under repeated cycling remain important for future validation.
In conclusion, this work presents a complete pipeline for the optimization-based control of a soft continuum robot using quasi-static input–output models. The results confirm that achieving accurate and repeatable positioning is feasible using only pressure commands and an external tracking system, even without curvature modeling. The approach provides a foundation for practical soft robot control with minimal sensor requirements and reduced computational overhead. Future research will extend the model to include dynamic effects, feedback integration, and adaptive identification.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/act14070352/s1, Figures S1–S15.
Author Contributions
Conceptualization, M.M.; methodology, O.S. and S.S.; software, O.S.; validation, S.S.; formal analysis, O.S., A.I. and M.M.; investigation, O.S., S.S., A.I. and M.M.; resources, A.I.; data curation, O.S., S.S., A.I. and M.M.; writing—original draft preparation, O.S. and A.I.; writing—review and editing, S.S. and M.M.; visualization, O.S.; supervision, S.S.; project administration, A.I.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the EU NextGenerationEU through the Recovery and Resilience Plan for Slovakia under projects No. 09I03-03-V03-00075, No. 09I03-03-V01-00095, and by the projects VEGA 1/0061/23 and KEGA 063TUKE-4/2025, granted by the Ministry of Education, Research, Development and Youth of the Slovak Republic. This paper was supported by the project SGS-2025-026 titled “Artificial Intelligence Algorithms in Sustainable Manufacturing”, solved within the framework of the Internal Grant Agency of the University of West Bohemia in Pilsen and was also carried out within the project “Intensification of production processes and development of intelligent product quality control systems in smart manufacturing” (State reg. no. 0122U200875, Ministry of Education and Science of Ukraine).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Garcia, M.; Esquen, A.-C.; Sabbagh, M.; Grace, D.; Schneider, E.; Ashuri, T.; Voicu, R.C.; Tekes, A.; Amiri Moghadam, A.A. Soft Robots: Computational Design, Fabrication, and Position Control of a Novel 3-DOF Soft Robot. Machines 2024, 12, 539. [Google Scholar] [CrossRef]
- Wang, B.; Sun, H.; Du, J.; Yi, Z.; Liu, X.; Hua, D.; Li, Z.; Chauhan, S.; Vashishtha, G. Kinematic Modelling and Closed-Loop Control of a Novel Soft Continuum Robot. Knowl.-Based Syst. 2025, 316, 113367. [Google Scholar] [CrossRef]
- Andrusyshyn, V.; Andrusyshyn, I.; Židek, K.; Ivanov, V.; Piteľ, J.; Trojan, J. Creating a Digital Twin of the ABB Yumi Robot to Improve the Human-Robot Interaction Experience. In Proceedings of the 2024 25th International Carpathian Control Conference (ICCC), Krynica Zdrój, Poland, 22–24 May 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Tejada, J.C.; Toro-Ossaba, A.; López-Gonzalez, A.; Hernandez-Martinez, E.G.; Sanin-Villa, D. A Review of Multi-Robot Systems and Soft Robotics: Challenges and Opportunities. Sensors 2025, 25, 1353. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Xia, Y.; Liu, J.; Liu, J.; Tang, W.; Chen, J.; Gao, F.; Ma, L.; Liao, H.; Wang, Y.; et al. Hysteresis-Aware Neural Network Modeling and Whole-Body Reinforcement Learning Control of Soft Robots. Soft Robot. 2025, in press. [Google Scholar]
- Rabiee, S.; Nalkenani, S.S.; Sharifi, I. Curvature Tracking of a Double Section Soft Bending Actuator Using MPC Method. In Proceedings of the 2023 11th RSI International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 19–21 December 2023; pp. 377–383. [Google Scholar]
- Haggerty, D.A.; Banks, M.J.; Kamenar, E.; Cao, A.B.; Curtis, P.C.; Mezić, I.; Hawkes, E.W. Control of Soft Robots with Inertial Dynamics. Sci. Robot. 2023, 8, eadd6864. [Google Scholar] [CrossRef] [PubMed]
- Sapai, S.; Loo, J.Y.; Ding, Z.Y.; Tan, C.P.; Baskaran, V.M.; Nurzaman, S.G. A Deep Learning Framework for Soft Robots with Synthetic Data. Soft Robot. 2023, 10, 1224–1240. [Google Scholar] [CrossRef] [PubMed]
- Nadizar, G.; Medvet, E.; Nichele, S.; Pontes-Filho, S. An Experimental Comparison of Evolved Neural Network Models for Controlling Simulated Modular Soft Robots. Appl. Soft Comput. 2023, 145, 110610. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, T.-H.; Truby, R.L.; Chin, L.; Rus, D. Machine Learning Best Practices for Soft Robot Proprioception. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 2564–2571. [Google Scholar]
- Garg, S.; Goharimanesh, M.; Sajjadi, S.; Janabi-Sharifi, F. Autonomous Control of Soft Robots Using Safe Reinforcement Learning and Covariance Matrix Adaptation. Eng. Appl. Artif. Intell. 2025, 153, 110791. [Google Scholar] [CrossRef]
- Chen, Z.; Ren, X.; Hamamatsu, Y.; Ciuti, G.; Stefanini, C. A Generalized Adaptive Jacobian Controller for Soft Robots. Soft Robot. 2024, in press. [Google Scholar]
- Cao, Y.; Xu, B.; Li, B.; Fu, H. Advanced Design of Soft Robots with Artificial Intelligence. Nano-Micro Lett. 2024, 16, 214. [Google Scholar] [CrossRef] [PubMed]
- Thuruthel, T.G.; Falotico, E.; Beccai, L.; Iida, F. Editorial: Machine Learning Techniques for Soft Robots. Front. Robot. AI 2021, 8, 726774. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Kim, S.-H.; Kim, T.; Kang, B.B.; Lee, M.; Park, W.; Ku, S.; Kim, D.; Kwon, J.; Lee, H.; et al. Review of Machine Learning Methods in Soft Robotics. PLoS ONE 2021, 16, e0246102. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Renda, F.; Le Gall, A.; Mocellin, L.; Bernabei, M.; Dangel, T.; Ciuti, G.; Cianchetti, M.; Stefanini, C. Data-Driven Methods Applied to Soft Robot Modeling and Control: A Review. IEEE Trans. Autom. Sci. Eng. 2025, 22, 2241–2256. [Google Scholar] [CrossRef]
- Hsieh, P.-Y.; Hou, J.-H. Comparative Evaluation of Learning Models for Bionic Robots: Non-Linear Transfer Function Identifications. Soft Comput. 2024, in press. [Google Scholar]
- Papageorgiou, D.; Sigurðardóttir, G.Þ.; Falotico, E.; Tolu, S. Sliding-Mode Control of a Soft Robot Based on Data-Driven Sparse Identification. Control Eng. Pract. 2024, 144, 105836. [Google Scholar] [CrossRef]
- Yang, L.; Zheng, Y.; Sun, Y.; Chen, X. Online Optimization Enhanced Closed-Loop Control of Multi-Section Continuum Robots. Robot. Auton. Syst. 2025, 189, 104986. [Google Scholar] [CrossRef]
- Grube, M.; Wieck, J.C.; Seifried, R. Comparison of Modern Control Methods for Soft Robots. Sensors 2022, 22, 9464. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chortos, A. Control Strategies for Soft Robot Systems. Adv. Intell. Syst. 2022, 4, 2100165. [Google Scholar] [CrossRef]
- Morales-Enríquez, D.A.; Guzmán-López, J.; Aguilar-Ramírez, R.A.; Lorenzo-Martínez, J.L.; Sapién-Garza, D.; Cortez, R.; Lozada-Castillo, N.; Luviano-Juárez, A. Data-Based Modeling and Control of a Single Link Soft Robotic Arm. Biomimetics 2025, 10, 294. [Google Scholar] [CrossRef] [PubMed]
- Peña Fernández, C.A. Control of Flexible Manipulator Robots Based on Dynamic Confined Space of Velocities: Dynamic Programming Approach. J. Robot. Control 2022, 3, 743–753. [Google Scholar] [CrossRef]
- Tóthová, M.; Piteľ, J.; Mižáková, J. Electro-Pneumatic Robot Actuator with Artificial Muscles and State Feedback. Appl. Mech. Mater. 2014, 460, 23–31. [Google Scholar] [CrossRef]
- Sokolov, O.; Hosovsky, A.; Sokolov, S.; Pitel, B. Study on the Piecewise Constant Curvature Kinematic Model of a Two-Segment Robot. MM Sci. J. 2024, 8011–8018. [Google Scholar] [CrossRef]
- Polhemus Innovation in Motion. Available online: https://polhemus.com/viper/ (accessed on 3 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).