Fuzzy Adaptive Control for a 4-DOF Hand Rehabilitation Robot
Abstract
1. Introduction
2. Materials and Methods
2.1. Medical Protocol for Robotic-Assisted Hand Rehabilitation
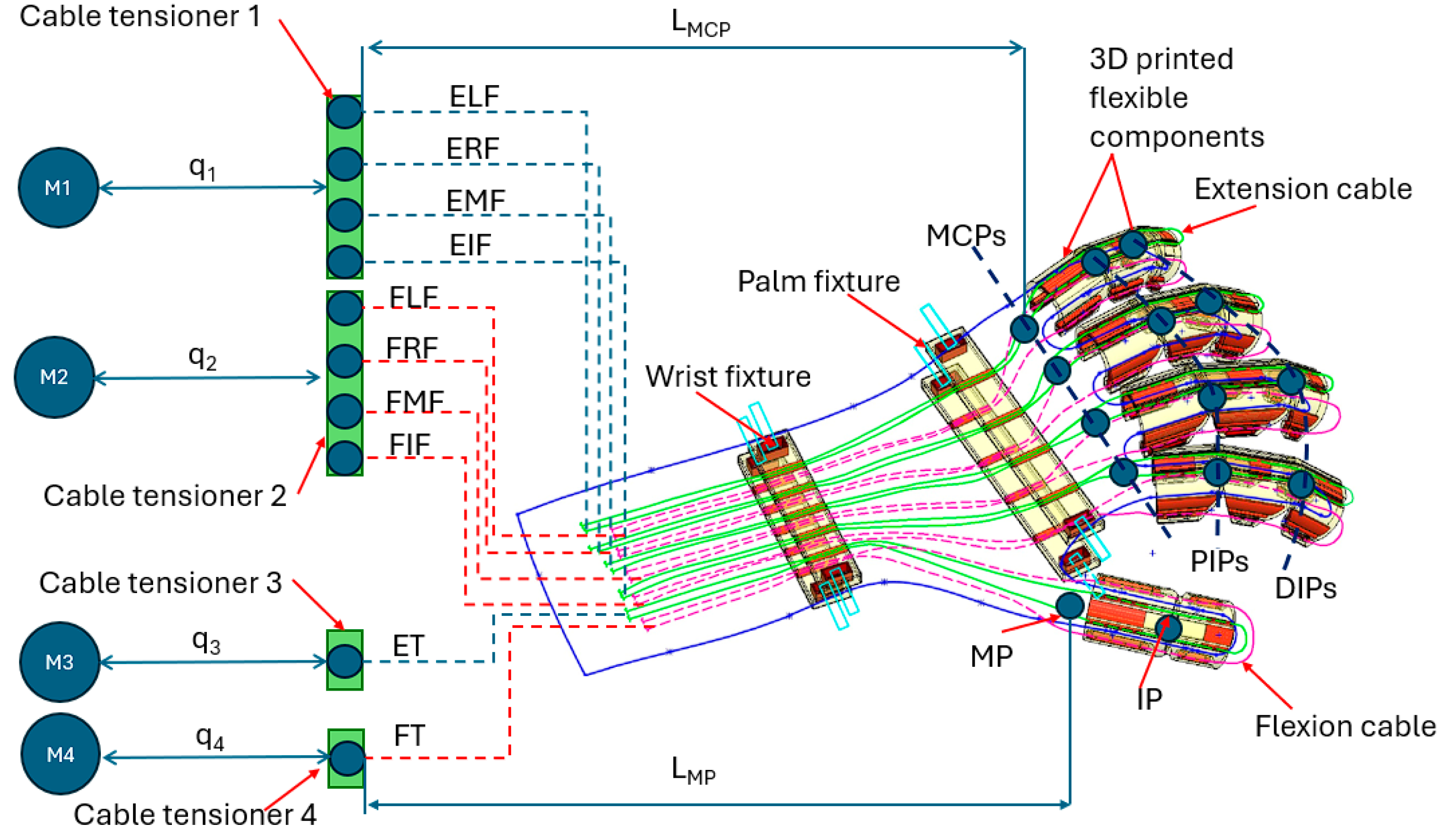
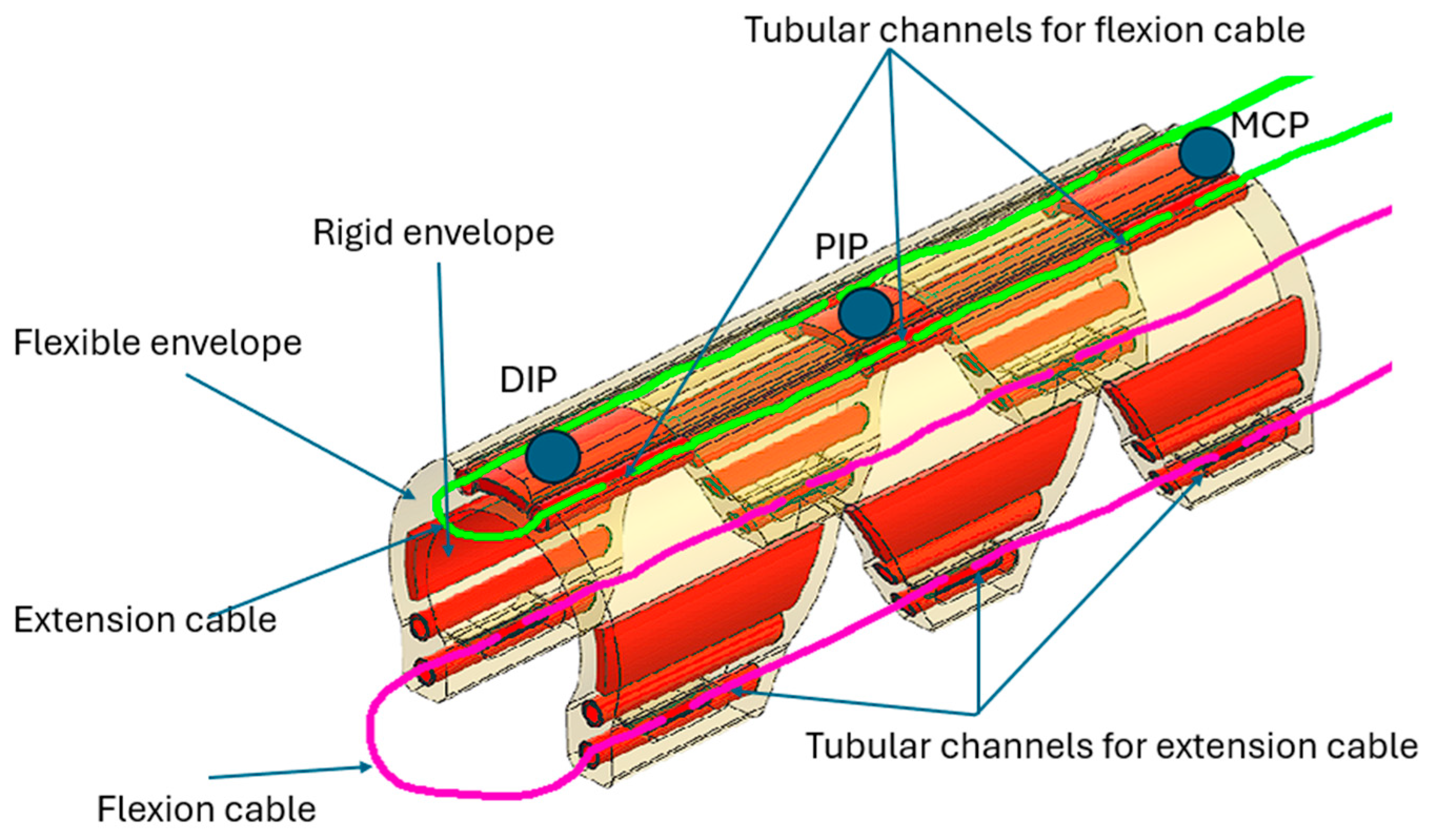
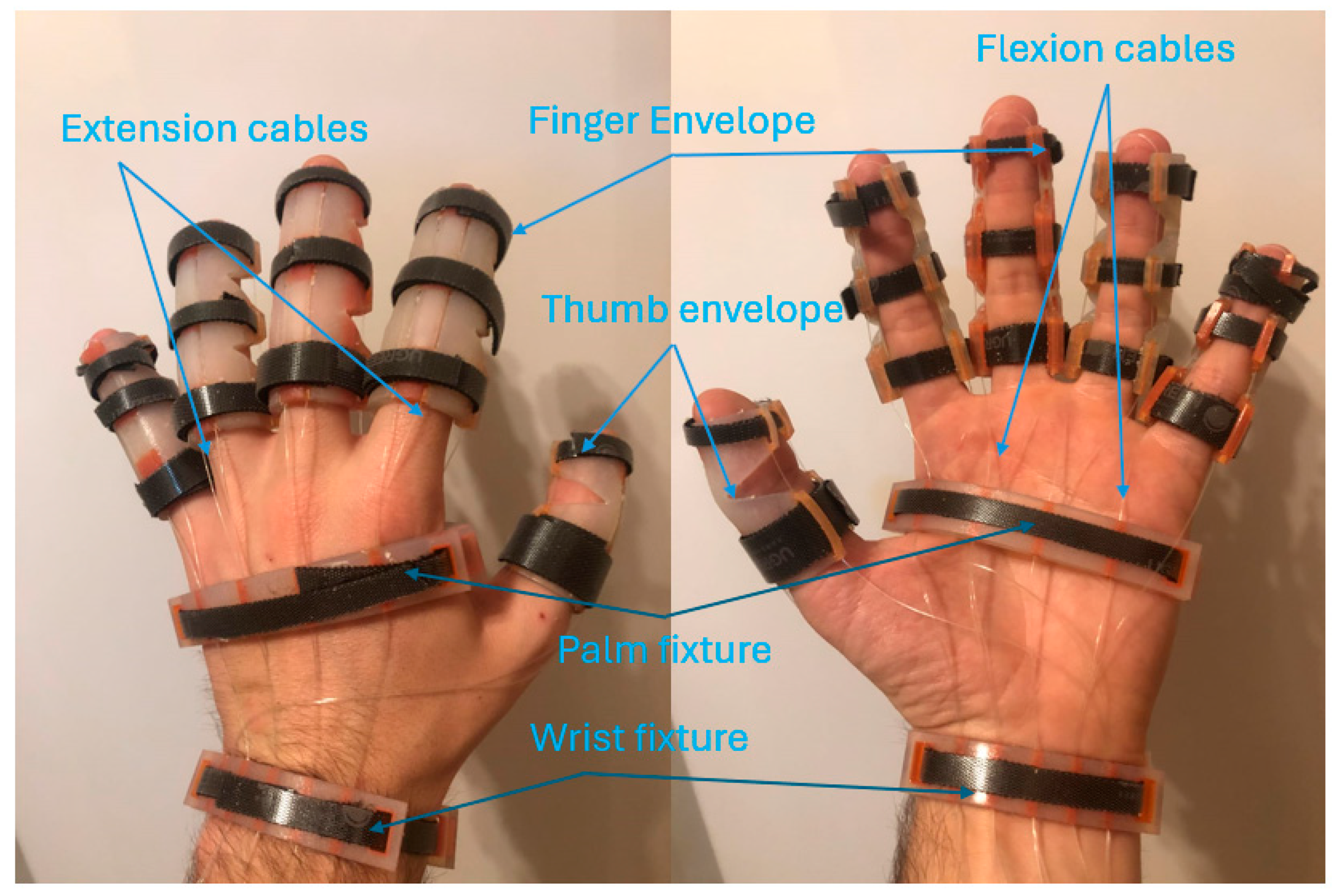
2.2. Description of the Hand Rehabilitation Robot
2.3. Robot–Patient Interaction Modes
- a.
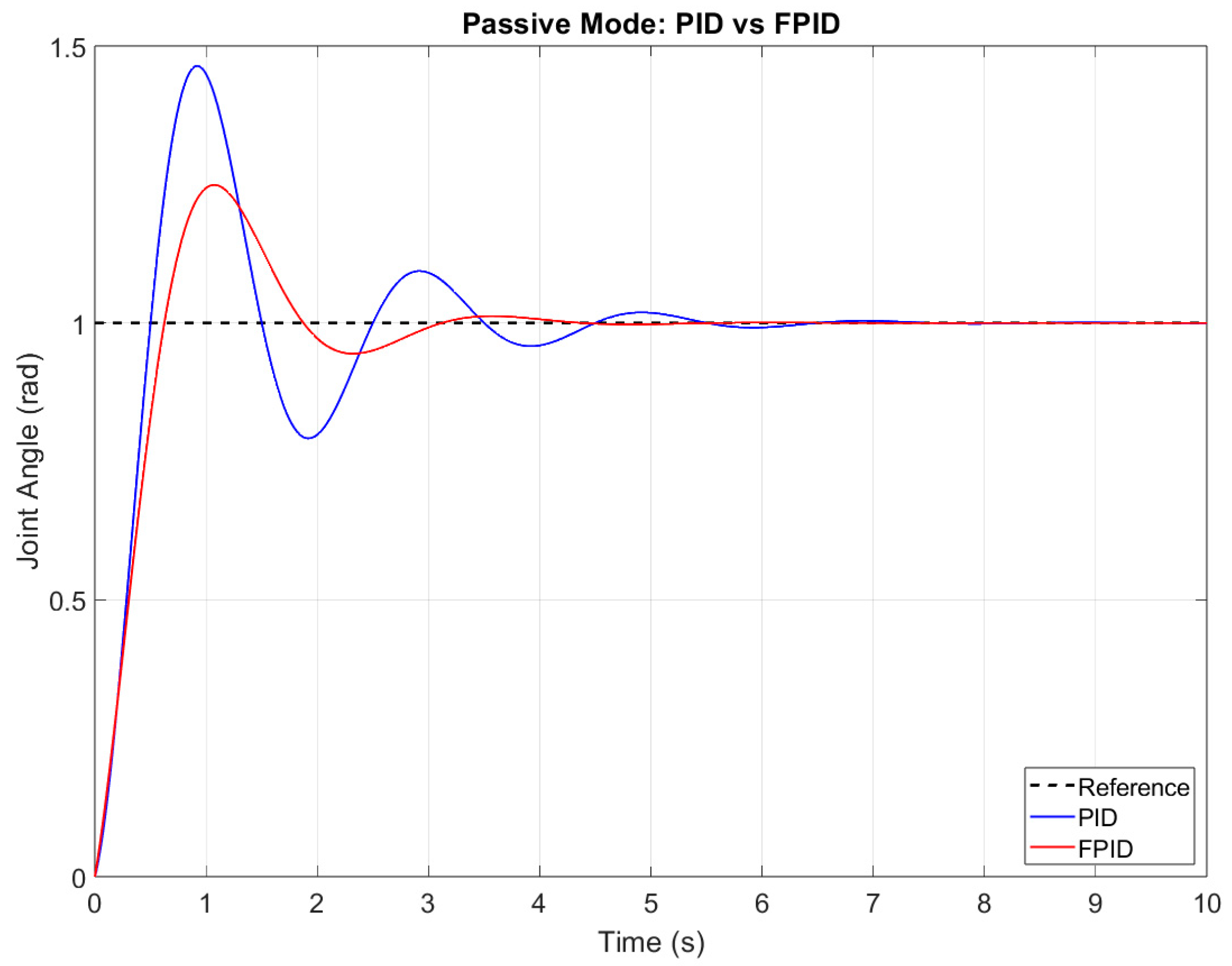
- Passive rehabilitation mode: the robot is responsible for moving the finger through a predefined trajectory, with minimal or no patient effort. Key characteristics of this mode include that patient input is minimal, meaning that the robot drives the motion; the controller follows a precomputed trajectory (position or joint angle profile); and the system continuously monitors the torque (via servomotor encoder) and intervenes if excessive force is detected to protect the patient.
- b.
- Active–Assistive Rehabilitation Mode: the patient initiates movement, and the robot helps to complete or smooth the motion. The key aspects are as follow: a measurable patient-generated force or a small change in joint angle signals to the controller that assistance is needed; the controller must sense when the patient has begun moving and then provide an “assisting” torque to help overcome any insufficiencies; and the controller monitors both the deviation from the desired trajectory and the patient’s applied force.
- c.
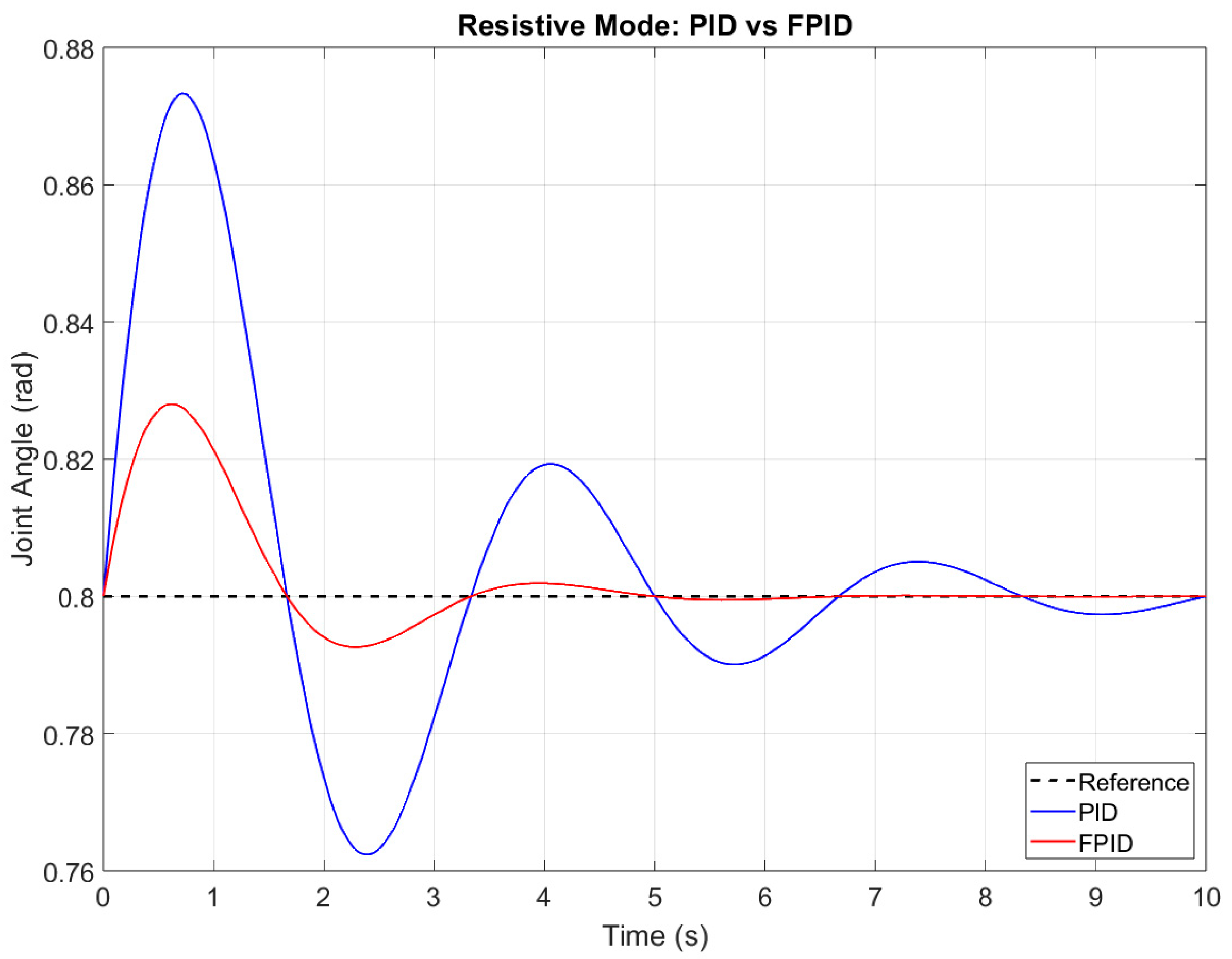
- Resistive Rehabilitation Mode: resistive mode is used to help build muscle strength. Here, the robot intentionally opposes the patient’s movement: the control output includes a resistance component that increases the required patient torque; the magnitude of resistance is tuned to provide safe yet challenging forces; and the controller monitors the patient’s applied torque so that the resistance can be adjusted in real time.
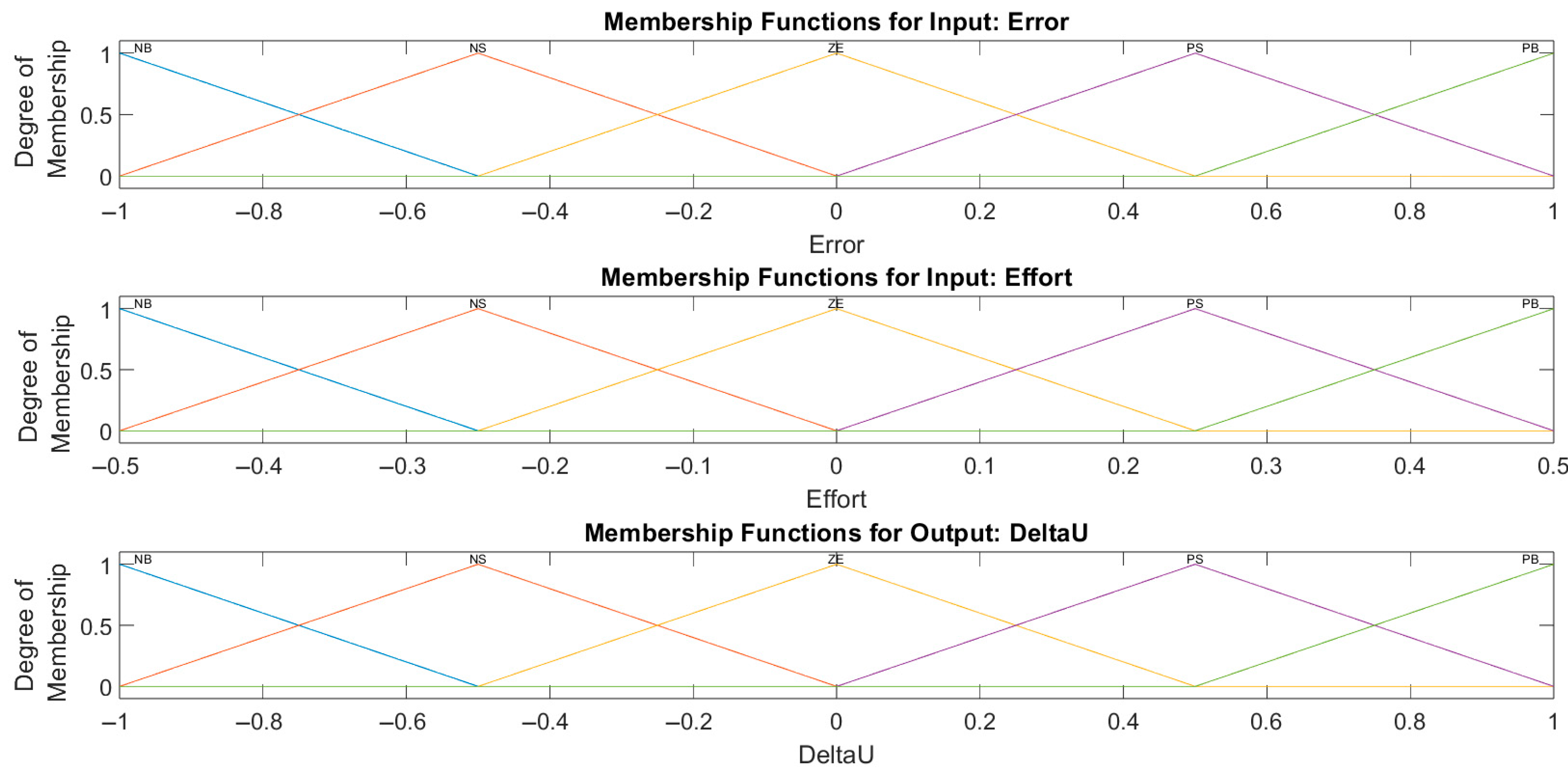
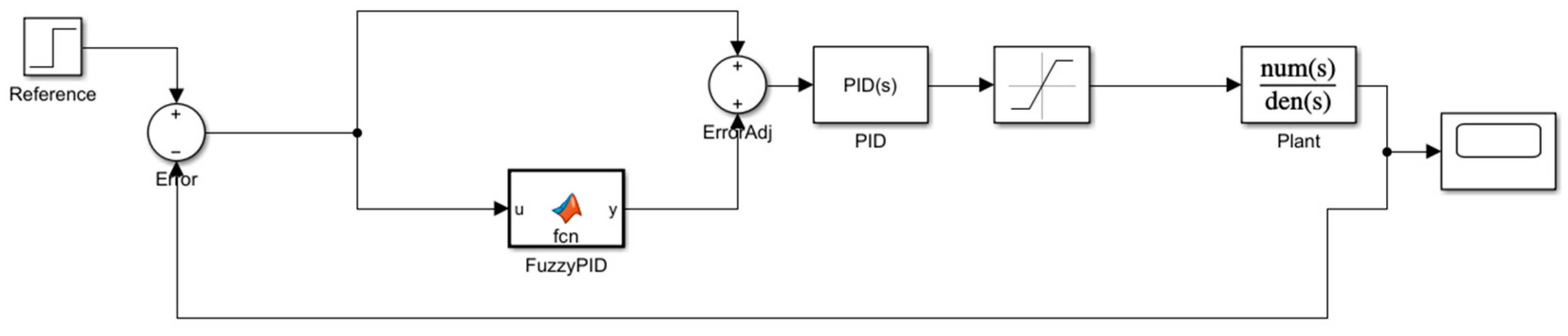
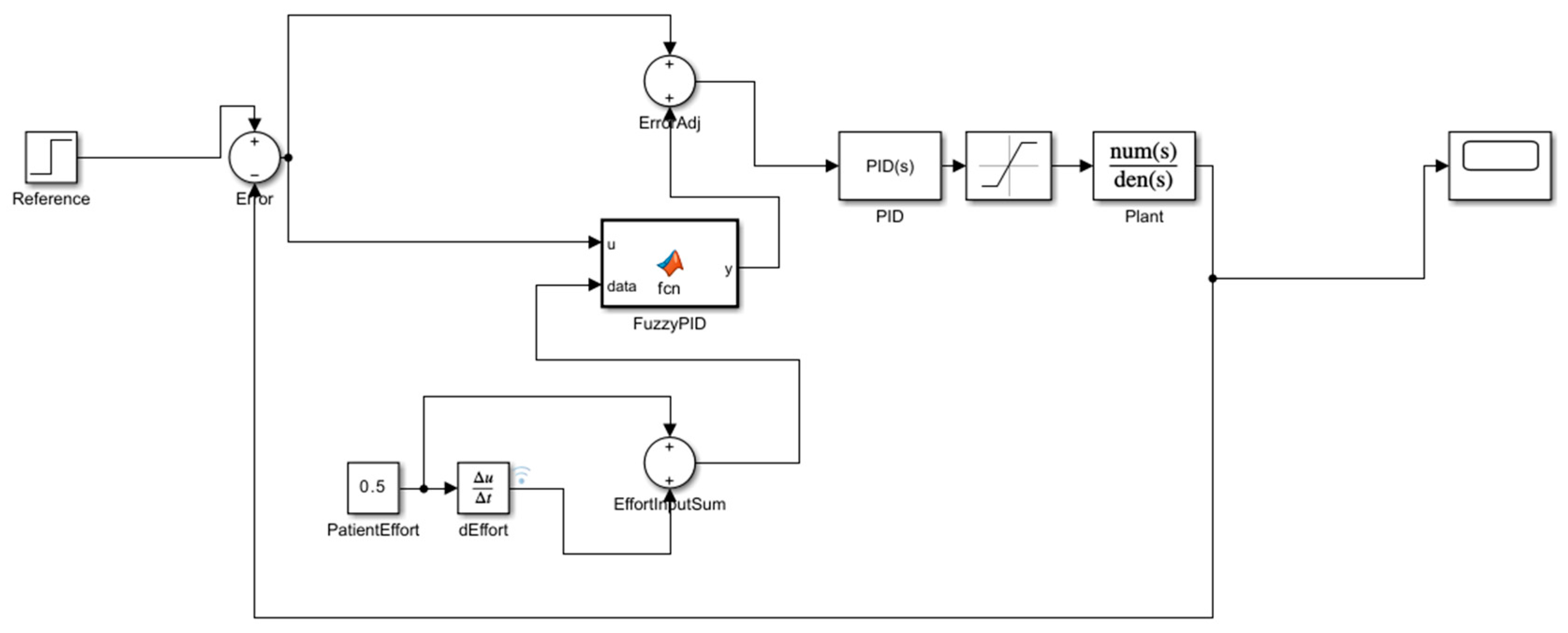
2.4. Design of the Fuzzy-PID Controller
- Tracking error (e): the difference between the desired and actual joint angle.
- Effort (eef): a measure of patient generated effort.
- Output Adjustment (Δu): the output of the fuzzy controller is used as a gain scheduling signal for PID gains such as Kp, Ki, and Kd.
- NB: centred at −Emax, with support [−Emax, −Emax/2]
- NS: centred at −Emax/2, with support [−Emax, 0]
- ZE: centred at 0, with support [−Emax/2, Emax/2]
- PS: centred at Emax/2, with support [0, Emax]
- PB: centred at Emax, with support [Emax/2, Emax]
- NB: large negative adjustment.
- NS: small negative adjustment.
- ZE: no adjustment.
- PS: small positive adjustment.
- PB: large positive adjustment.
- Passive Mode (Mode 1): active when the estimated torque remains below τ_passive. The robot executes pre-programmed trajectories without assistance from the patient.
- Active–Assistive Mode (Mode 2): triggered when torque exceeds τ_passive + τ_hys, indicating voluntary motion initiation. The robot provides assistive force proportional to patient input.
- Resistive Mode (Mode 3): engaged when torque exceeds τ_resistive + τ_hys, signaling the ability to handle load-bearing tasks. The controller applies graded resistance to strengthen musculature.
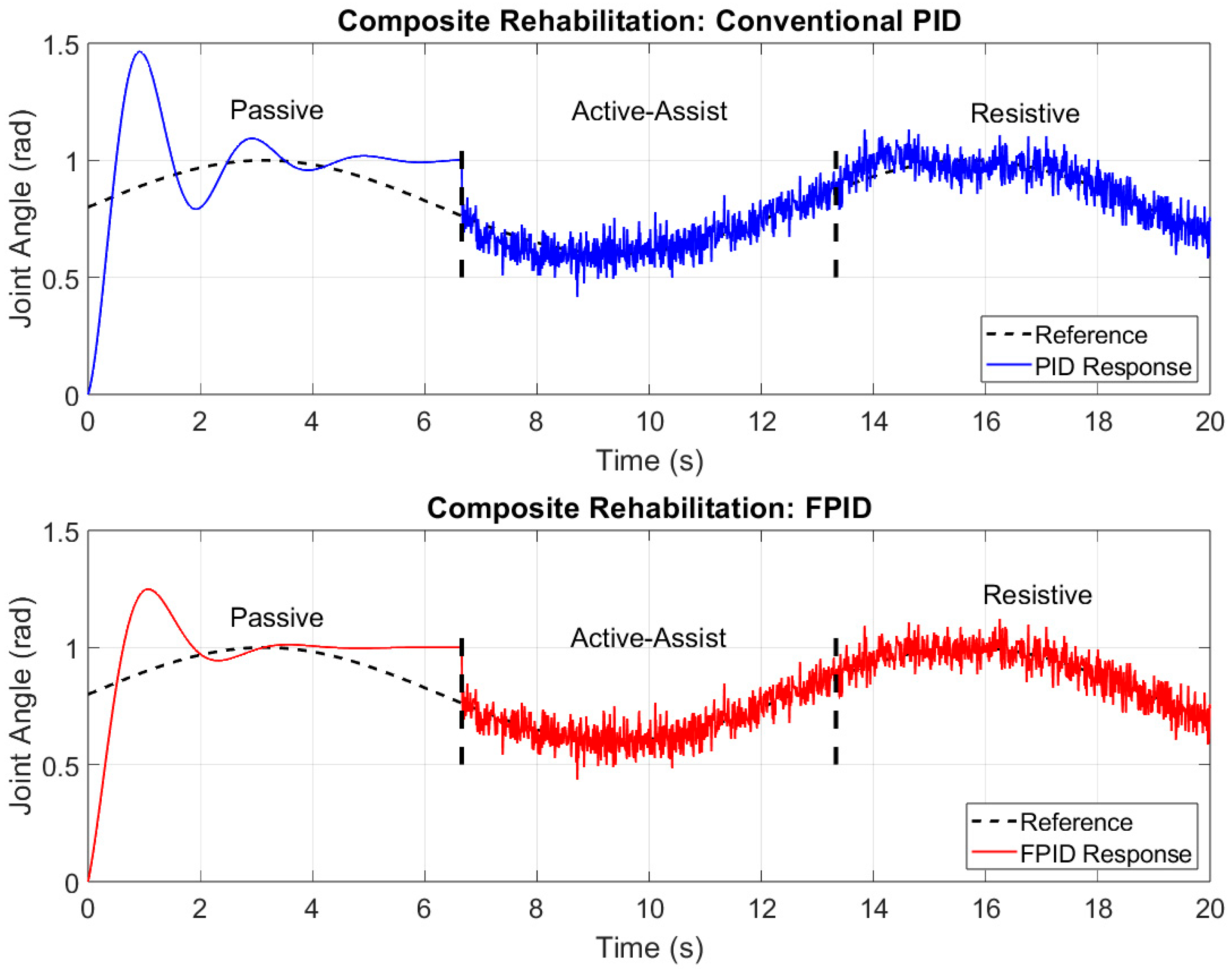
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kamper, D.G.; Fischer, H.C.; Cruz, E.G.; Rymer, W.Z. Weakness Is the Primary Contributor to Finger Impairment in Chronic Stroke. Arch. Phys. Med. Rehabil. 2006, 87, 1262–1269. [Google Scholar] [CrossRef] [PubMed]
- Bonzano, L.; Sormani, M.P.; Tacchino, A.; Abate, L.; Lappuci, C.; Mancardi, G.L.; Uccelli, A. Bove, Marco, Quantitative Assessment of Finger Motor Impairment in Multiple Sclersosis. PLoS ONE 2013, 8, e65225. [Google Scholar] [CrossRef] [PubMed]
- Anwer, S.; Waris, A.; Gilani, S.O.; Iqbal, J.; Shaikh, N.; Pujari, A.N.; Niazi, I.K. Rehabilitation of Upper Limb Motor Impairment in Stroke: A Narrative Review on the Prevalence, Risk Factors, and Economic Statistics of Stroke and State of the Art Therapies. Healthcare 2022, 10, 190. [Google Scholar] [CrossRef] [PubMed]
- Dalton, E.J.; Jamwal, R.; Augoustakis, L.; Hill, E.; Johns, H.; Thijs, V.; Hayward, K.S. Prevalence of Arm Weakness, Pre-Stroke Outcomes and Other Post-Stroke Impairments Using Routinely Collected Clinical Data on an Acute Stroke Unit. Neurorehabilit. Neural Repair 2024, 38, 148–160. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Nakamichi, R.; Nakahara, R.; Nishida, K.; Ozaki, T. The Effectiveness of Rehabilitation after Open Surgical Release for Trigger Finger: A Prospective, Randomized, Controlled Study. J. Clin. Med. 2023, 12, 7187. [Google Scholar] [CrossRef] [PubMed]
- Waszczykowski, M.; Dziankowska-Bartkowiak, B.; Podgórski, M.; Fabis, J.; Waszczykowski, A. Role and effectiveness of complex and supervised rehabilitation on overall and hand function in systemic sclerosis patients—One-year follow-up study. Sci. Rep. 2021, 11, 15174. [Google Scholar] [CrossRef] [PubMed]
- Landry, M.D.; Hack, L.M.; Coulson, E.; Freburger, J.; Johnson, M.P.; Katz, R.; Kerwin, J.; Smith, M.H.; “Bud” Wessman, H.C.; Venskus, D.G.; et al. Workforce Projections 2010–2020: Annual Supply and Demand Forecasting Models for Physical Therapists Across the United States. Phys. Ther. 2016, 96, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Leonardis, D.; Barsotti, M.; Loconsole, C.; Solazzi, M.; Troncossi, M.; Mazzotti, C.; Castelli, V.P.; Procopio, C.; Lamola, G.; Lamola, C.; et al. An EMG-Controlled robotic hand exoskeleton for bilateral rehabilitation. IEEE Trans. Haptics 2015, 8, 140–151. [Google Scholar] [CrossRef] [PubMed]
- Gherman, B.; Zima, I.; Vaida, C.; Tucan, P.; Pisla, A.; Birlescu, I.; Machado, J.; Pisla, D. Robotic Systems for Hand Rehabilitation—Past, Present and Future. Technologies 2025, 13, 37. [Google Scholar] [CrossRef]
- Ratz, R.; Conti, F.; Muri, R.M.; Marchal-Crespo, L. A Novel Clinical-Driven Design for Robotic Hand Rehabilitation: Combining Sensory Training, Effortless Setup, and Large Range of Motion in a Palmar Device. Front. Neurorobotics 2021, 15, 748196. [Google Scholar] [CrossRef] [PubMed]
- Mahfouz, D.M.; Shehata, O.M.; Morgan, E.I.; Arrichiello, F. A Comprehensive Review of Control Challenges and Methods in End-Effector Upper-Limb Rehabilitation Robots. Robotics 2024, 13, 181. [Google Scholar] [CrossRef]
- Li, X.; Peng, Y.; Chen, Z. Review of Adaptive Control for Stroke Lower Limb Exoskeleton Rehabilitation Robots. Front. Neurorobotics 2023, 17, 1186175. [Google Scholar] [CrossRef] [PubMed]
- Baud, R.; Manzoori, A.R.; Ijspeert, A.; Bouri, M. Review of Control Strategies for Lower-Limb Exoskeletons to Assist Gait. J. Neuroeng. Rehabil. 2021, 18, 119. [Google Scholar] [CrossRef] [PubMed]
- Ghafoori, S.; Rabiee, A.; Norouzi, M.; Jouaneh, M.; Abiri, R. A Novel Seamless Magnetic-Based Actuating Mechanism for End-Effector-Based Robotic Rehabilitation Platforms. arXiv 2024, arXiv:2404.01441. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Nolan, K.J.; Zanotto, D. Shaping Individualized Impedance Landscapes for Gait Training via Reinforcement Learning. arXiv 2021, arXiv:2109.02109. [Google Scholar] [CrossRef]
- Wang, H.; Shen, H.; Han, Y.; Zhou, W.; Wang, J. Effect of Robot-Assisted Training for Lower Limb Rehabilitation on Lower Limb Function in Stroke Patients: A Systematic Review and Meta-Analysis. Front. Hum. Neurosci. 2025, 19, 1549379. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.U.A.; Ajmal, H.M.S.; Hassan, H.A.; Azam, A.; Malik, E. A Soft Robotic Sleeve for Physiotherapy: Improving Elbow Rehabilitation in Baseball Pitchers. Physiother. Res. Int. 2025, 30, e70025. [Google Scholar] [CrossRef] [PubMed]
- Pezeshki, L.; Sadeghian, H.; Mohebbi, A.; Keshmiri, M.; Haddadin, S. Personalized Assistance in Robotic Rehabilitation: Real-Time Adaptation via Energy-Based Performance Monitoring. IEEE Trans. Autom. Sci. Eng. 2025, 22, 1234–1245. [Google Scholar] [CrossRef]
- Lejeune, T.; Nuic, D.; Dehem, S.; Previnaire, J.-G.; Cuenot, C.; Debugne, T.; Kaps, J.; Paul, B.; Pean, V.; Sanz Perez, S.; et al. Hands-Free Atalante Exoskeleton in Post-Stroke Gait and Balance Rehabilitation: A Safety Study. J. Neuroeng. Rehabil. 2025, 22, 82. [Google Scholar] [CrossRef] [PubMed]
- Duanmu, D.; Wen, R.; Li, X.; Huang, W.; Hu, Y. Development of Assistive Donning Device of Robotic Hand Glove Inspired by the Venus Flytrap. Mech. Based Des. Struct. Mach. 2025, 53, 2487171. [Google Scholar] [CrossRef]
- Roy, R.; Islam, M.; Rashid, M.; Mounis, S.; Ahsan, M.M.; Ahad, M.T.; Siddique, Z.; Kouzani, A.Z.; Mahmud, M.A.P. Investigation of 2DOF PID Controller for Physio-Therapeutic Application for Elbow Rehabilitation. Appl. Sci. 2021, 11, 8617. [Google Scholar] [CrossRef]
- Saleem, O.; Ahmad, K.R.; Iqbal, J. Fuzzy-Augmented Model Reference Adaptive PID Control Law Design for Robust Voltage Regulation in DC–DC Buck Converters. Mathematics 2024, 12, 1893. [Google Scholar] [CrossRef]
- Maxim, A.; Pauca, O.; Caruntu, C.-F. Distributed Model Predictive Control and Coalitional Control Strategies—Comparative Performance Analysis Using an Eight-Tank Process Case Study. Actuators 2023, 12, 281. [Google Scholar] [CrossRef]
- Xiao, W.; Chen, K.; Fan, J.; Hou, Y.; Kong, W.; Dan, G. AI-driven rehabilitation and assistive robotic system with intelligent PID controller based on RBF neural networks. Neural Comput. Appl. 2023, 35, 16021–16035. [Google Scholar] [CrossRef]
- Borase, R.P.; Maghade, D.K.; Sondkar, S.Y.; Pawar, S.N. A Review of PID Control, Tuning Methods and Applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Tong, L.; Cui, D.; Wang, C.; Peng, L. A Novel Zero-Force Control Framework for Post-Stroke Rehabilitation Training Based on Fuzzy-PID Method. Intell. Robot. 2024, 4, 125–145. [Google Scholar] [CrossRef]
- Hu, Y.; Meng, J.; Li, G.; Zhao, D.; Feng, G.; Zuo, G.; Liu, Y.; Zhang, J.; Shi, C. Fuzzy Adaptive Passive Control Strategy Design for Upper-Limb End-Effector Rehabilitation Robot. Sensors 2023, 23, 4042. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Guo, J. Disturbance Rejection Model Predictive Control of Lower Limb Rehabilitation Exoskeleton. Sci. Rep. 2023, 13, 19463. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Tang, M.; Wang, W.; Zhang, Y.; An, B. Trajectory Tracking Control of Wearable Upper Limb Rehabilitation Robot Based on Laguerre Model Predictive Control. Robot. Auton. Syst. 2024, 179, 104745. [Google Scholar] [CrossRef]
- Brown, D.F.; Xie, S.Q. Model Predictive Control with Optimal Modelling for Pneumatic Artificial Muscle in Rehabilitation Robotics: Confirmation of Validity Though Preliminary Testing. Biomimetics 2025, 10, 208. [Google Scholar] [CrossRef] [PubMed]
- Geonea, I.D.; Tarnita, D.; Pisla, D.; Carbone, G.; Bolcu, A.; Tucan, P.; Georgescu, M.; Tarniță, D.N. Dynamic Analysis of a Spherical Parallel Robot Used for Brachial Monoparesis Rehabilitation. Appl. Sci. 2021, 11, 11849. [Google Scholar] [CrossRef]
- Lou, Y.; Lin, H.; Quan, P.; Wei, D.; Di, S. Robust Adaptive Control of Fully Constrained Cable-Driven Serial Manipulator with Multi-Segment Cables Using Cable Tension Sensor Measurements. Sensors 2021, 21, 1623. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Li, Z.; Cui, X.; Zhang, J.; Bai, S. Mechanical Design and Kinematic Modeling of a Cable-Driven Arm Exoskeleton Incorporating Inaccurate Human Limb Anthropomorphic Parameters. Sensors 2019, 19, 4461. [Google Scholar] [CrossRef] [PubMed]
- Vaida, C.; Birlescu, I.; Pîșla, A.; Carbone, G.; Plitea, N.; Ulinici, I.; Gherman, B.; Puskas, F.; Tucan, P.; Pîșla, D. RAISE—An Innovative Parallel Robotic System for Lower Limb Rehabilitation. In New Trends in Medical and Service Robotics; Carbone, G., Ceccarelli, M., Pîșla, D., Eds.; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2018; pp. 293–302. [Google Scholar]
- Vaida, C.; Plitea, N.; Carbone, G.; Birlescu, I.; Ulinici, I.; Pîșla, A.; Pîșla, D. Innovative development of a spherical parallel robot for upper limb rehabilitation. Int. J. Mech. Robot. Syst. 2018, 4, 256. [Google Scholar] [CrossRef]
- Fardipour, S.; Hadadi, M. Investigation of Therapeutic Effects of Wearable Robotic Gloves on Improving Hand Function in Stroke Patients: A Systematic Review. Curr. J. Neurol. 2022, 21, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Yang, X.; Li, D.; Ma, Z.; Liu, Z.; Bai, X.; Mao, Z. Predicting flow status of a flexible rectifier using cognitive computing. Expert Syst. Appl. 2025, 264, 125878. [Google Scholar] [CrossRef]
- Mao, Z.; Kobayashi, R.; Nabae, H.; Suzumori, K. Multimodal Strain Sensing System for Shape Recognition of Tensegrity Structures by Combining Traditional Regression and Deep Learning Approaches. IEEE Robot. Autom. Lett. 2024, 9, 10050–10056. [Google Scholar] [CrossRef]
- Birouaș, F.I.; Țarcă, R.C.; Dzitac, S.; Dzitac, I. Preliminary Results in Testing of a Novel Asymmetric Underactuated Robotic Hand Exoskeleton for Motor Impairment Rehabilitation. Symmetry 2020, 12, 1470. [Google Scholar] [CrossRef]
- Tohanean, N.; Tucan, P.; Vanta, O.-M.; Abrudan, C.; Pintea, S.; Gherman, B.; Burz, A.; Banica, A.; Vaida, C.; Neguran, D.A.; et al. The Efficacity of the NeuroAssist Robotic System for Motor Rehabilitation of the Upper Limb—Promising Results from a Pilot Study. J. Clin. Med. 2023, 12, 425. [Google Scholar] [CrossRef] [PubMed]
- Connelly, L.; Stoykov, M.E.; Jia, Y.; Toro, M.L.; Kenyon, R.V.; Kamper, D.G. Use of a pneumatic glove for hand rehabilitation following stroke. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 2434–2437. [Google Scholar] [CrossRef]
- Fischer, H.C.; Triandafilou, K.M.; Thielbar, K.O.; Ochoa, J.M.; Lazzaro, E.D.; Pacholski, K.A.; Kamper, D.G. Use of a portable assistive glove to facilitate rehabilitation in stroke survivors with severe hand impairment. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 344–351. [Google Scholar] [CrossRef] [PubMed]
- van Ommeren, A.L.; Radder, B.; Buurke, J.H.; Kottink, I.R.; Holmberg, J.; Sletta, K.; Prange-Lasonder, G.B.; Rietman, J.S. The effect of prolonged use of a wearable soft-robotic glove post stroke—A proof-of-principle. In Proceedings of the 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Enschede, The Netherlands, 26–29 August 2018. [Google Scholar]
- Prange-Lasonder, G.B.; Radder, B.; Kottink, A.I.R.; Melendez-Calderon, A.; Buurke, J.H.; Rietman, J.S. Applying a soft-robotic glove as assistive device and training tool with games to support hand function after stroke: Preliminary results on feasibility and potential clinical impact. In Proceedings of the IEEE International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 1401–1406. [Google Scholar] [CrossRef]
- Zhu, Y.; Gong, W.; Chu, K.; Wang, X.; Hu, Z.; Su, H. A Novel Wearable Soft Glove for Hand Rehabilitation and Assistive Grasping. Sensors 2022, 22, 6294. [Google Scholar] [CrossRef] [PubMed]
- Barfi, M.; Karami, H.; Faridi, F.; Sohrabi, Z.; Hosseini, M. Improving robotic hand control via adaptive Fuzzy-PI controller using classification of EMG signals. Heliyon 2022, 8, e11931. [Google Scholar] [CrossRef] [PubMed]
- Hao, X.; Xin, Z.; Huang, W.; Wan, S.; Qiu, G.; Wang, T.; Wang, Z. Deep reinforcement learning enhanced PID control for hydraulic servo systems in injection molding machines. Sci. Rep. 2025, 15, 23005. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Su, S.; Wang, H.; Chen, F.; Yin, B. Online PID Tuning Strategy for Hydraulic Servo Control Systems via SAC-Based Deep Reinforcement Learning. Machines 2023, 11, 593. [Google Scholar] [CrossRef]



| Protocol Parameter | PRAIMP | AARIMP | RSRIMP |
|---|---|---|---|
| Sessions | 15–20 min per session, 3–5 sessions per week. | 15–20 min per session, 3–5 sessions per week. | 15–20 min per session, 3–5 sessions per week. |
| Repetitions | 2–3 sets of 10–15 repetitions per movement cycle. | 2–3 sets of 10–15 repetitions per movement cycle. | 3 sets of 10–15 repetitions per movement cycle, focusing on gradually increasing resistance. |
| Motion execution | The robotic system moves the fingers through predefined arcs while maintaining joint safety. Also maintains the stretch for 2 s to preserve ROM. | The patient initiates movement while the robotic device provides adjustable assistance based on the detected effort. | The device now introduces graded resistance to challenge the patient’s muscles during active movement. |
| MCP Joint | Passive flexion up to 80–90° and extension to neutral (0–10°). | Aim for active movement toward 80–90° flexion (with assistance) and controlled return to neutral. | Active movement against resistance, targeting the same arc (flexion up to 80–90° and return to neutral) with emphasis on strength. |
| PIP Joint | Flexion up to 90–100° and extension to 0–10° | Active-assisted flexion targeting 90–100° with gradual extension to 0–10°. | Active flexion toward 90–100° with resistance, ensuring controlled extension to 0–10°. |
| DIP Joint | Flexion up to 60–70°. | Active-assisted flexion approaching 60–70°, progressing toward independent control. | Active flexion of 60–70° with resistance to build fine motor control and muscular endurance. |
| Thumb | Oppositional movements: Guide the thumb in abduction and opposition, aiming for contact with the small finger (approximating a 50° opposition angle). | Assisted opposition and abduction to achieve a 50° opposition angle, reinforcing the initiation of thumb-to-small finger contact. | Resistance-based opposition and abduction training to reinforce a 50° opposition angle, promoting strength and fine control. |
| Monitoring | Monitor for discomfort or signs of increased spasticity. Adjust the device’s speed and range if any pain or discomfort is reported. | Closely monitor the patient’s initiation effort, movement smoothness, and any discomfort; adjust the level of robotic assistance as needed to ensure safety. | Monitor for signs of fatigue, discomfort, or improper technique; adjust resistance levels and provide feedback to maintain proper movement quality. |
| Notation | Description |
|---|---|
| θ1 | MCP angle |
| θ1 | PIP angle |
| θ1 | DIP angle |
| L11 | length from MCP to PIP |
| L12 | length from PIP to DIP |
| L13 | length from DIP to fingertip |
| q1 | finger extension active joint |
| q2 | finger flexion active joint |
| LMCP | from cable tensioner 1 and 2 to finger MCP |
| α1 | CMC angle |
| α2 | MP angle |
| α3 | IP angle |
| L21 | length from CMC to MP |
| L22 | length from MP to IP |
| L23 | length from IP to thumb tip |
| q3 | thumb extension active joint |
| q4 | thumb flexion active joint |
| LMP | length from cable tensioner to MP |
| D | pulley diameter |
| e/eeff | NB | NS | ZE | PS | PB |
| NB | NB | NB | NB | NS | ZE |
| NS | NB | NB | NS | ZE | PS |
| ZE | NB | NS | ZE | PS | PB |
| PS | NS | ZE | PS | PB | PB |
| PB | ZE | PS | PB | PB | PB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tucan, P.; Vanta, O.-M.; Vaida, C.; Ciupe, M.; Sebeni, D.; Pisla, A.; Stiole, S.; Lupu, D.; Major, Z.; Gherman, B.; et al. Fuzzy Adaptive Control for a 4-DOF Hand Rehabilitation Robot. Actuators 2025, 14, 351. https://doi.org/10.3390/act14070351
Tucan P, Vanta O-M, Vaida C, Ciupe M, Sebeni D, Pisla A, Stiole S, Lupu D, Major Z, Gherman B, et al. Fuzzy Adaptive Control for a 4-DOF Hand Rehabilitation Robot. Actuators. 2025; 14(7):351. https://doi.org/10.3390/act14070351
Chicago/Turabian StyleTucan, Paul, Oana-Maria Vanta, Calin Vaida, Mihai Ciupe, Dragos Sebeni, Adrian Pisla, Simona Stiole, David Lupu, Zoltan Major, Bogdan Gherman, and et al. 2025. "Fuzzy Adaptive Control for a 4-DOF Hand Rehabilitation Robot" Actuators 14, no. 7: 351. https://doi.org/10.3390/act14070351
APA StyleTucan, P., Vanta, O.-M., Vaida, C., Ciupe, M., Sebeni, D., Pisla, A., Stiole, S., Lupu, D., Major, Z., Gherman, B., Bulbucan, V., Zima, I., Machado, J., & Pisla, D. (2025). Fuzzy Adaptive Control for a 4-DOF Hand Rehabilitation Robot. Actuators, 14(7), 351. https://doi.org/10.3390/act14070351










