Gaussian Process Regression-Based Fixed-Time Trajectory Tracking Control for Uncertain Euler–Lagrange Systems
Abstract
1. Introduction
2. Preliminaries
2.1. Gaussian Process Regression
2.2. Fixed-Time Stability Theory
3. Problem Statement
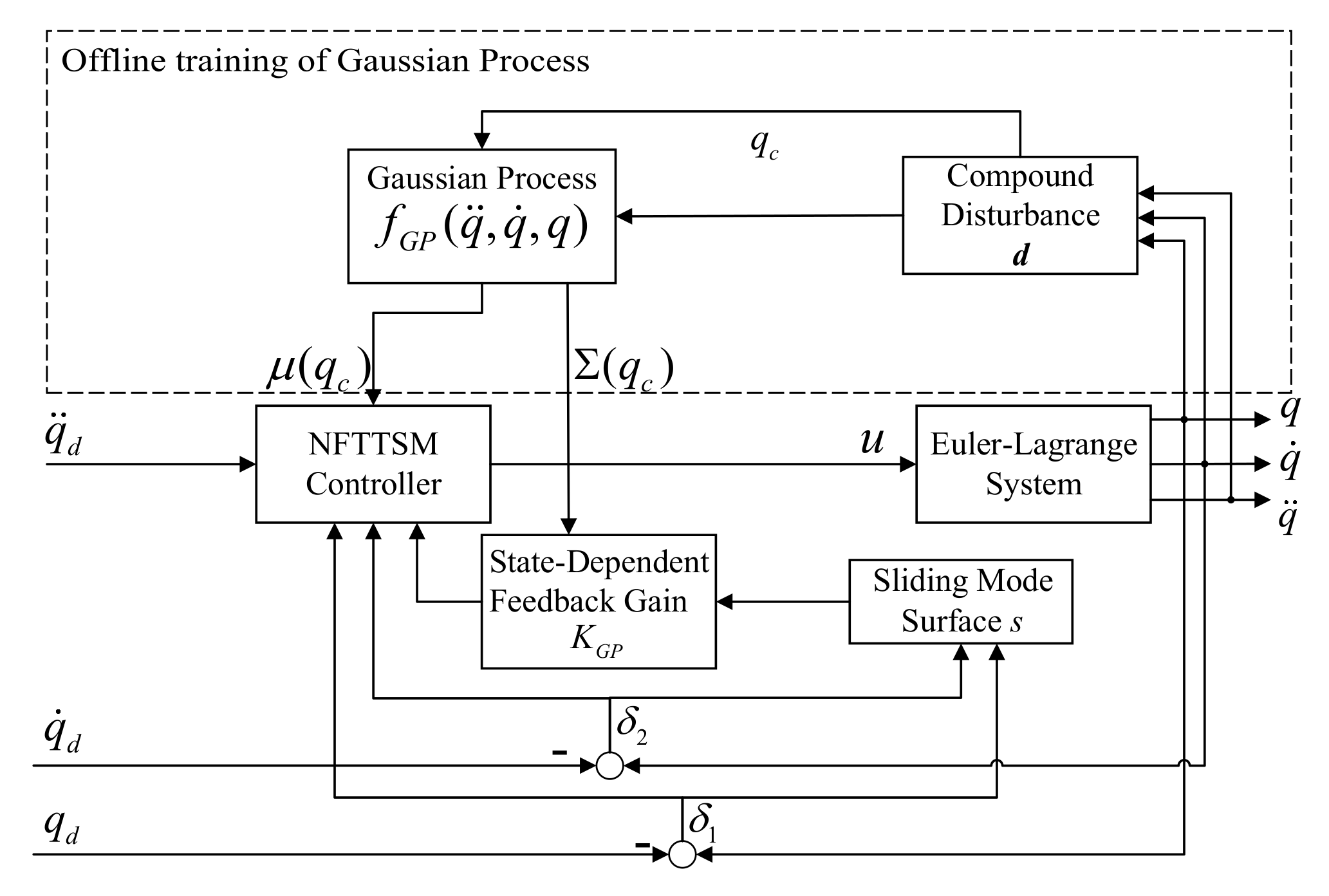
4. Controller Design and Stability Analysis
| Algorithm 1 Data Generation for GP Learning. |
|
5. Numerical Simulation and Comparisons
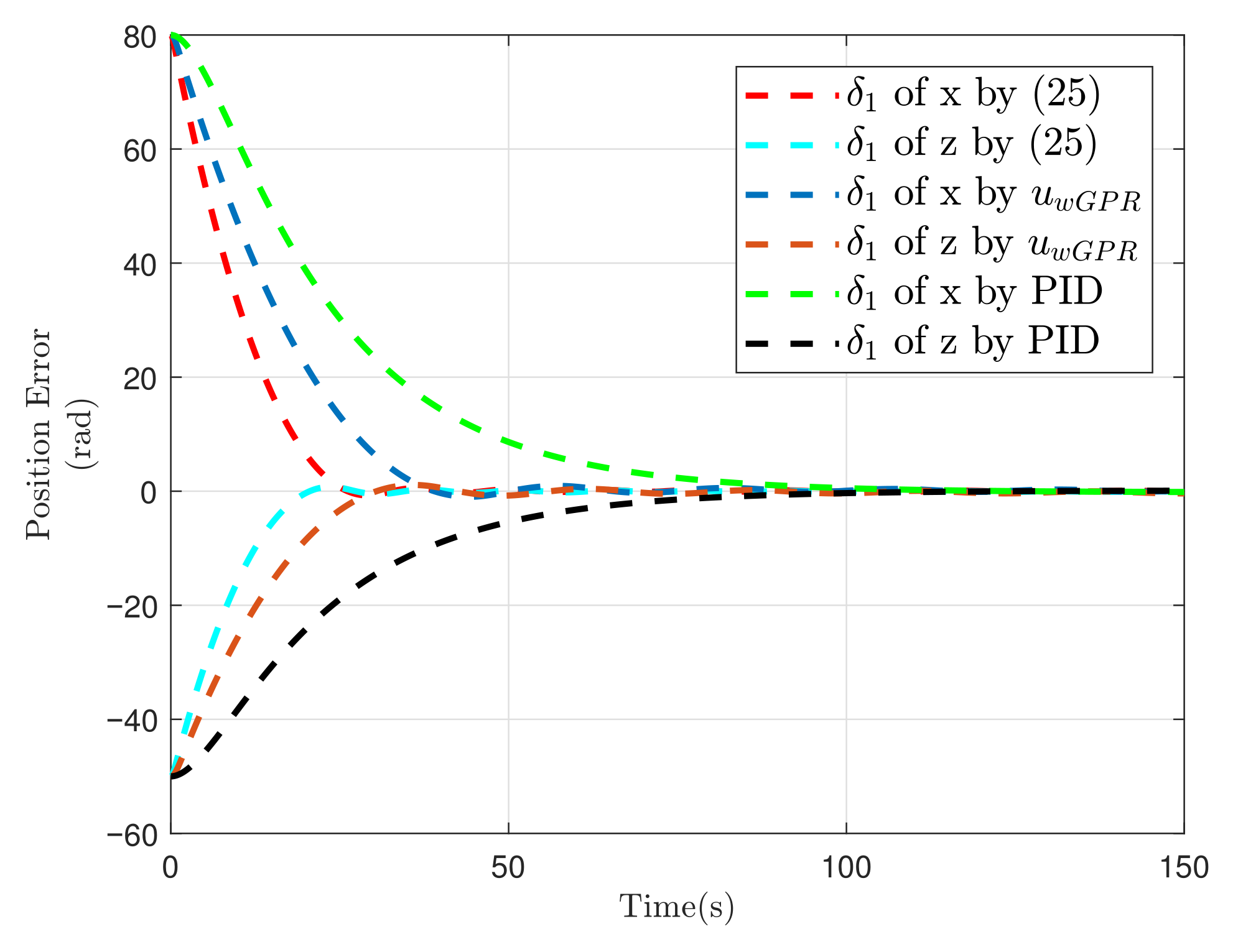
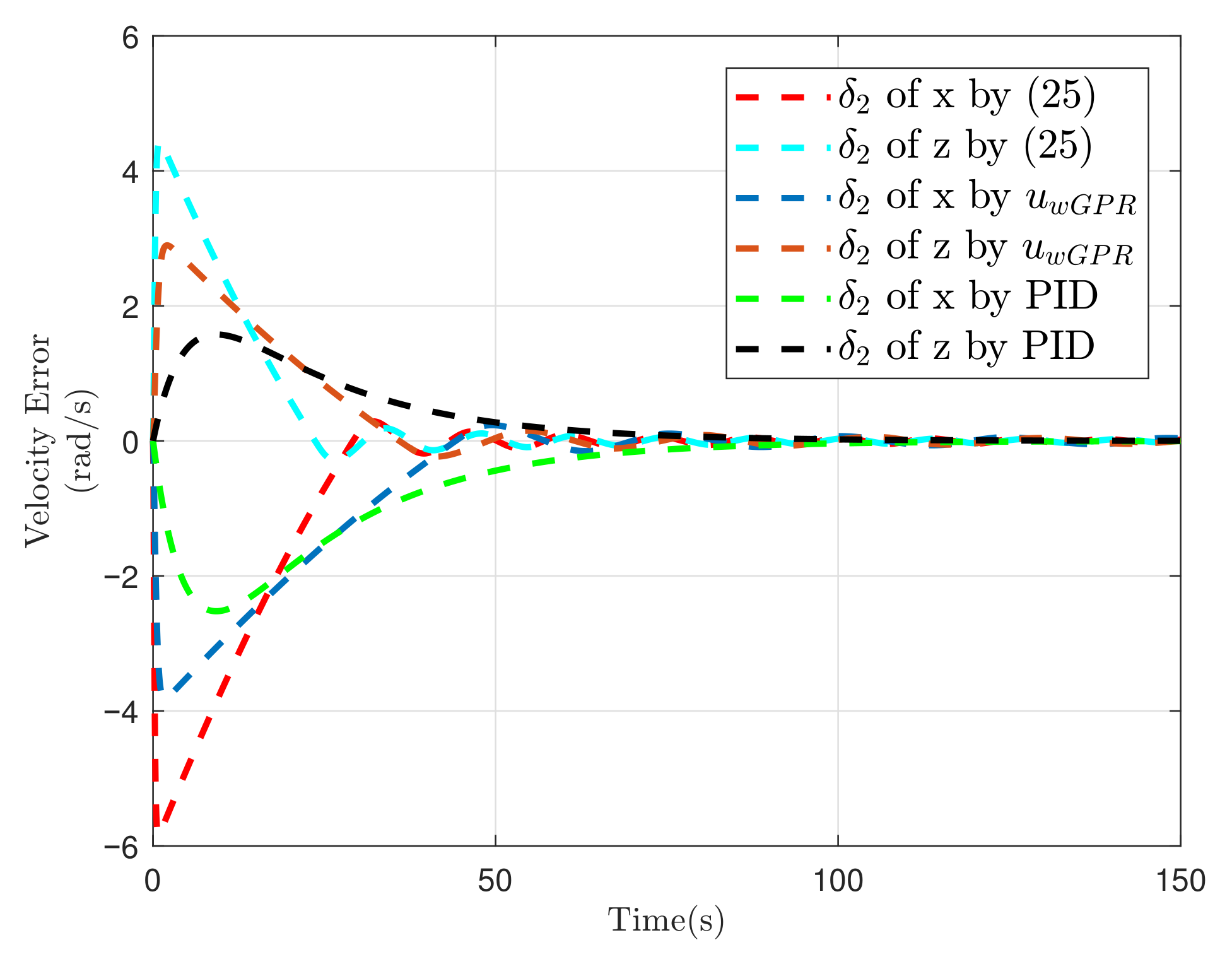
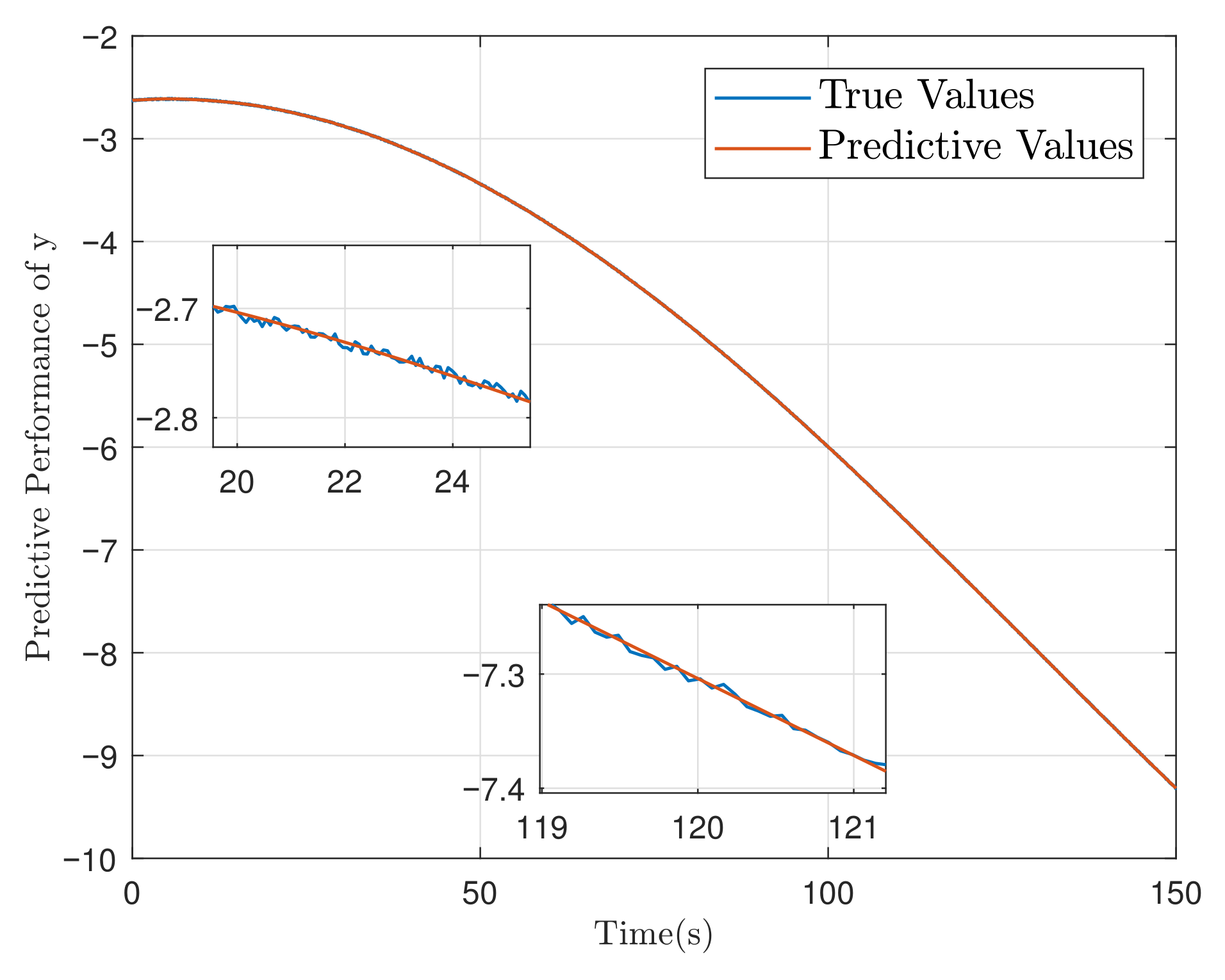
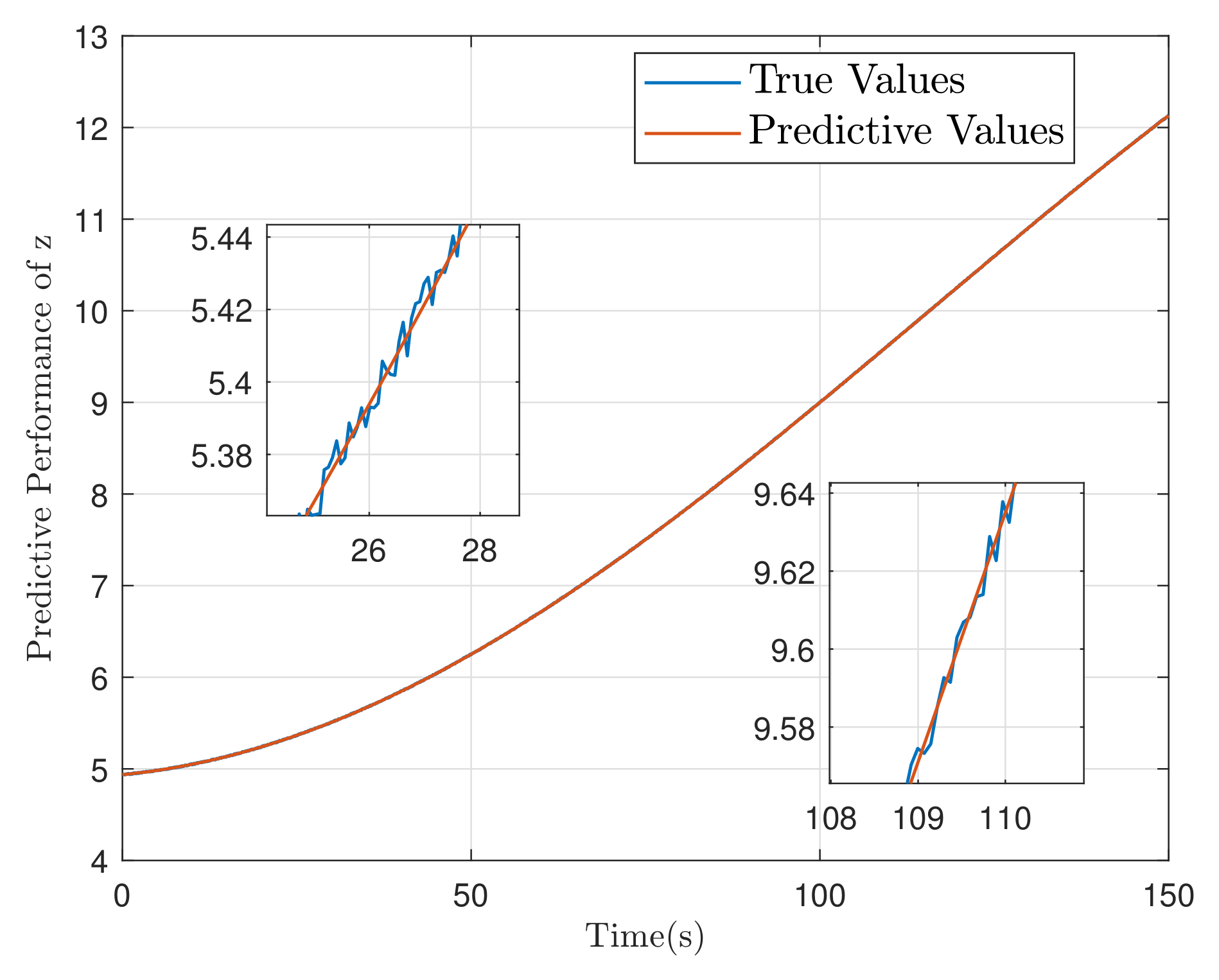
5.1. Simulation of Spacecraft Rendezvous Mission
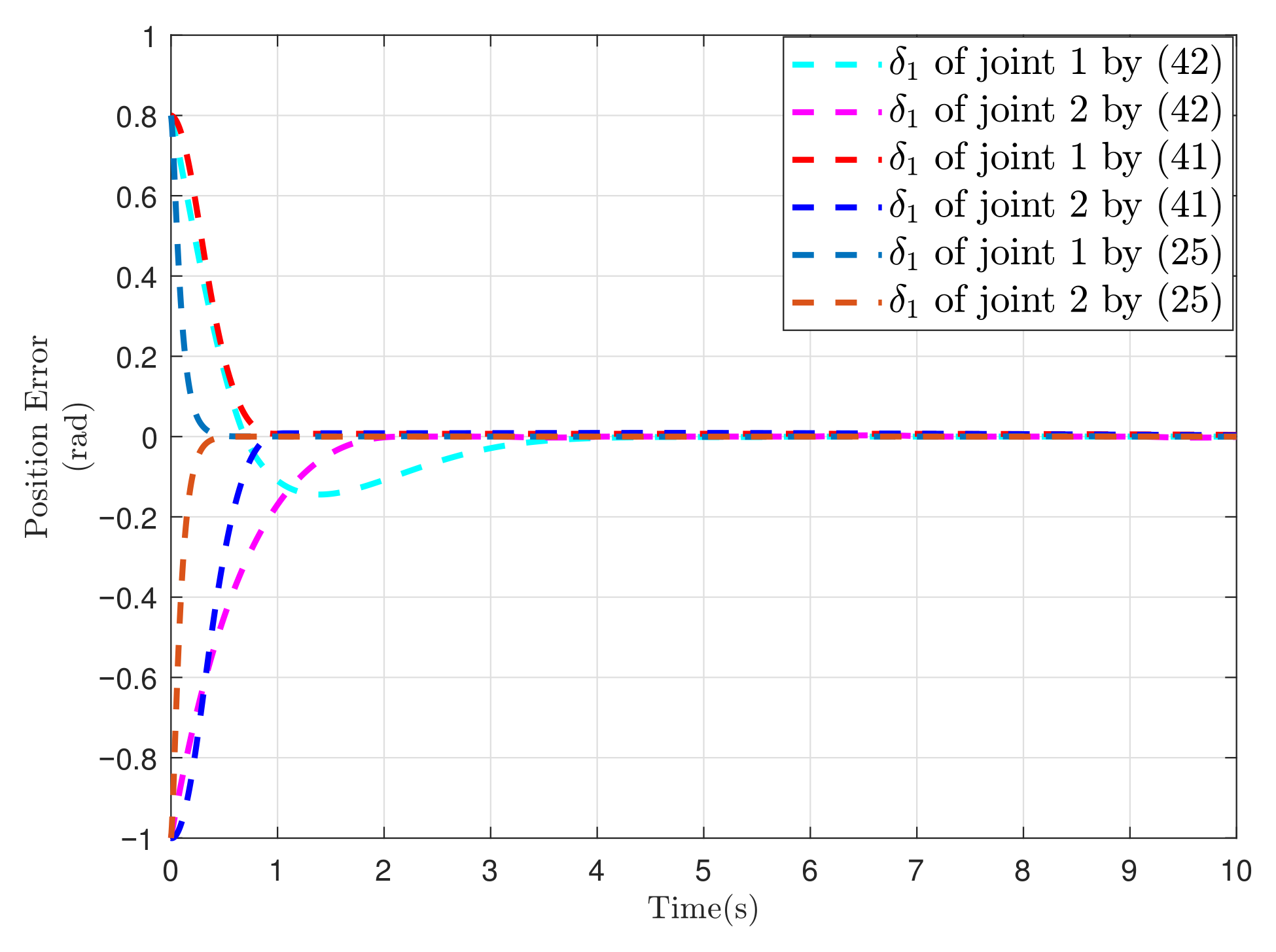
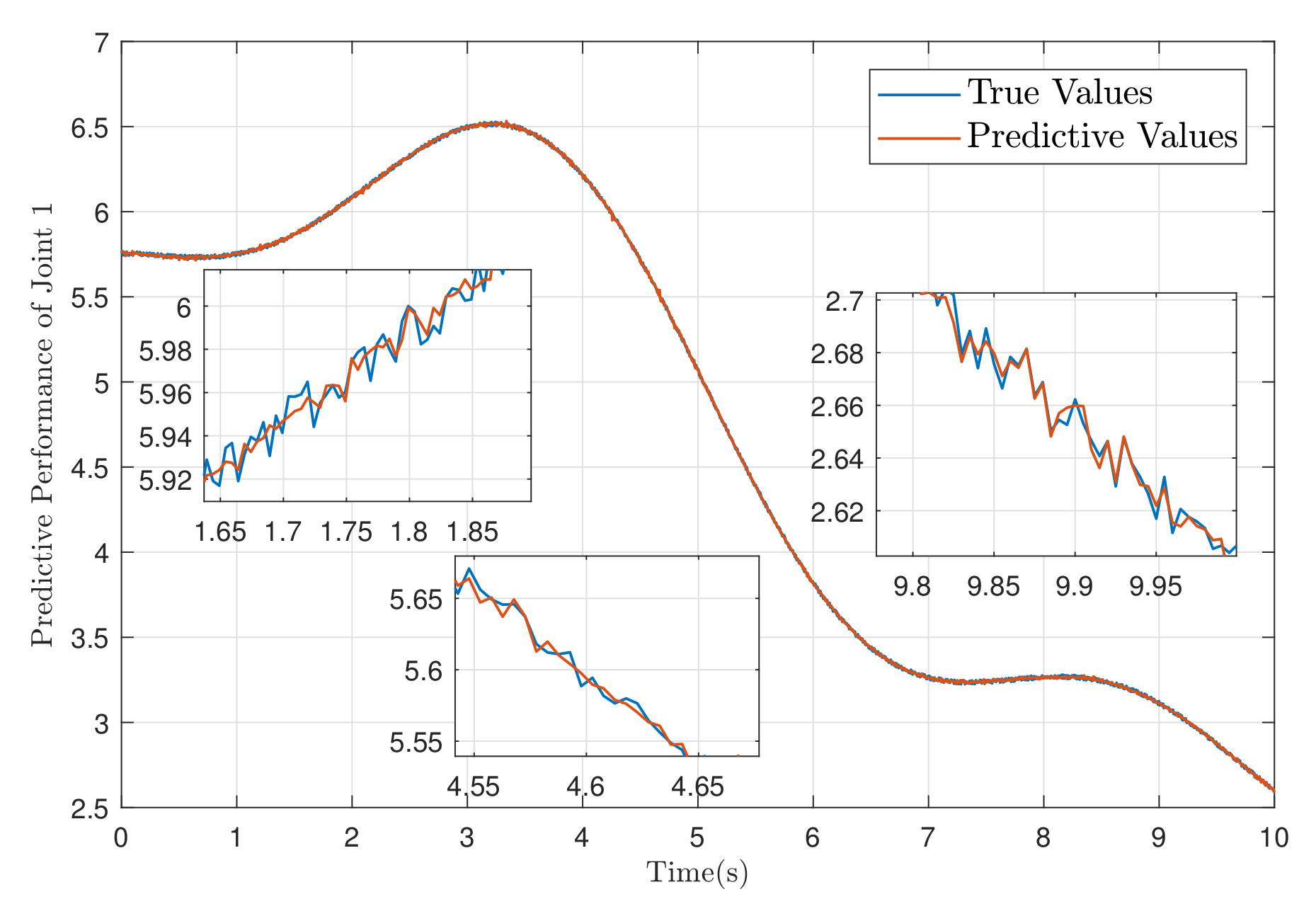
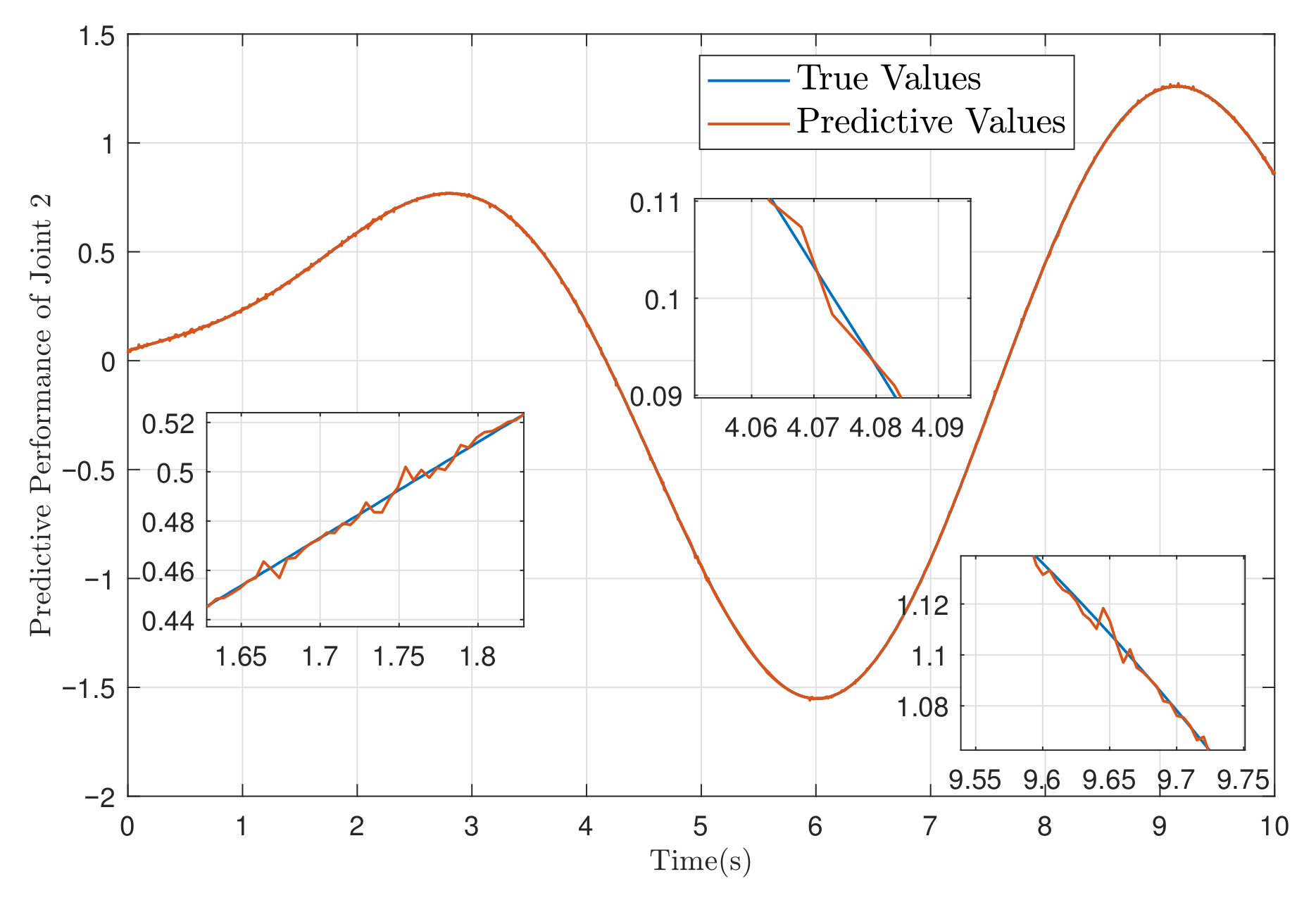
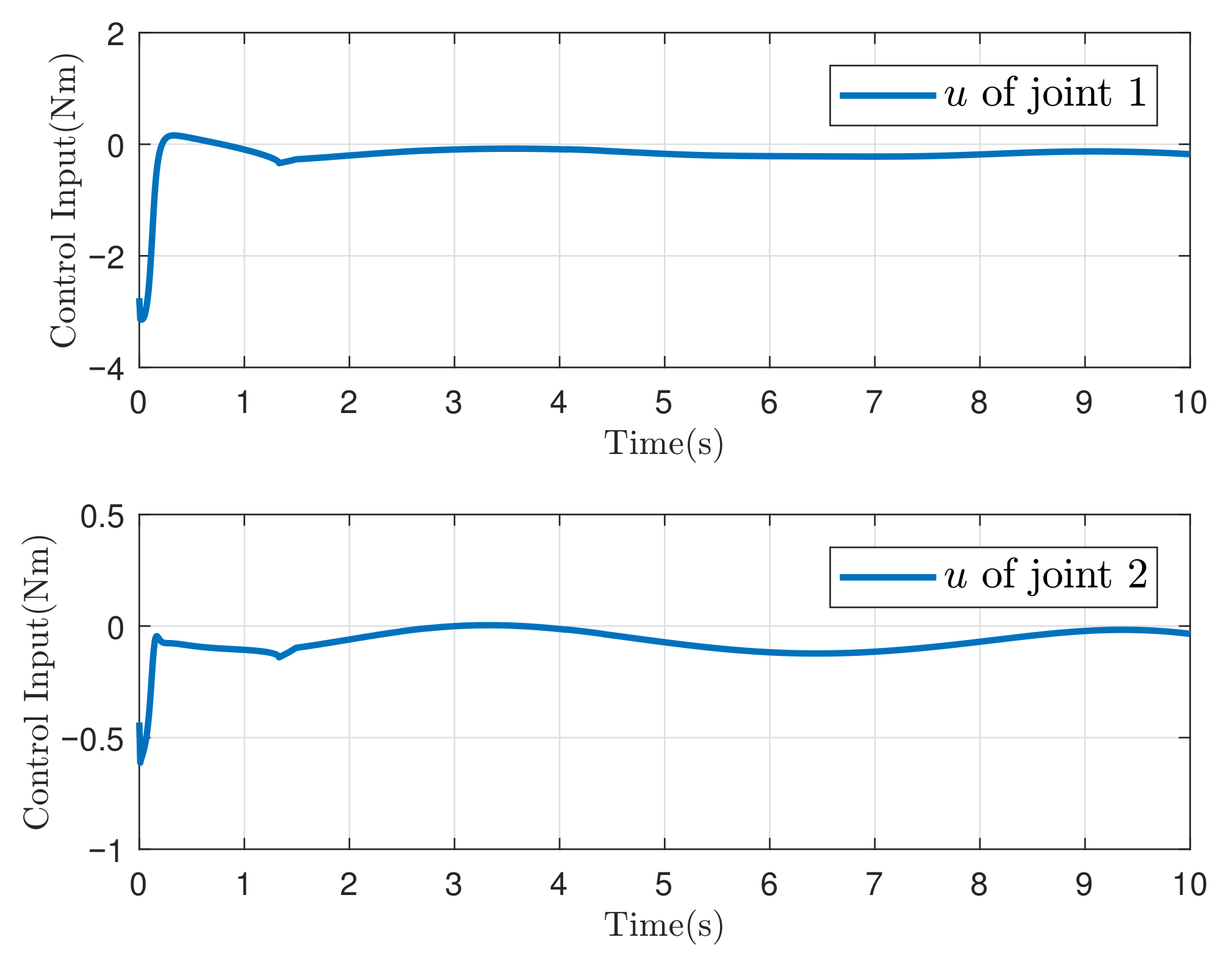
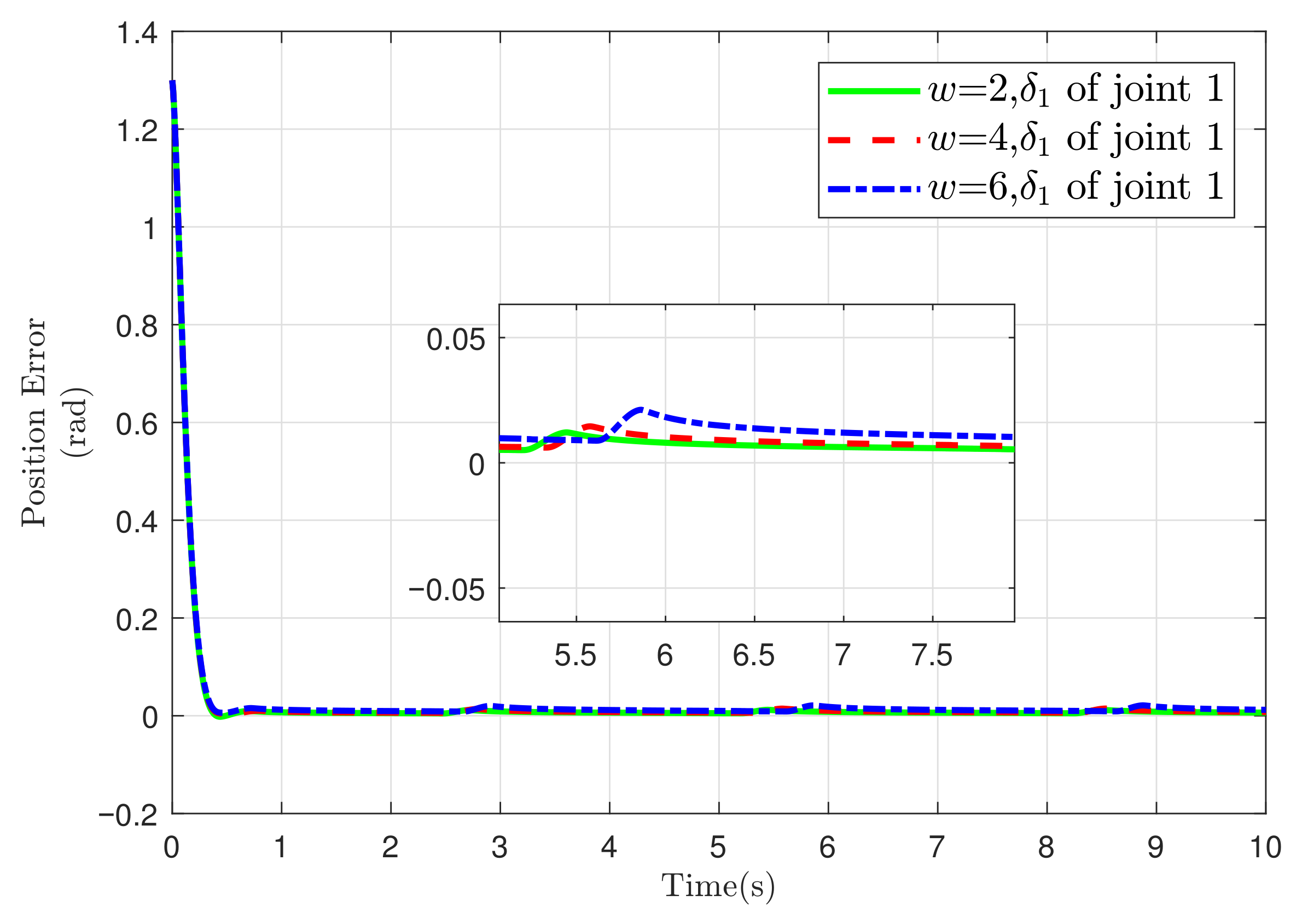
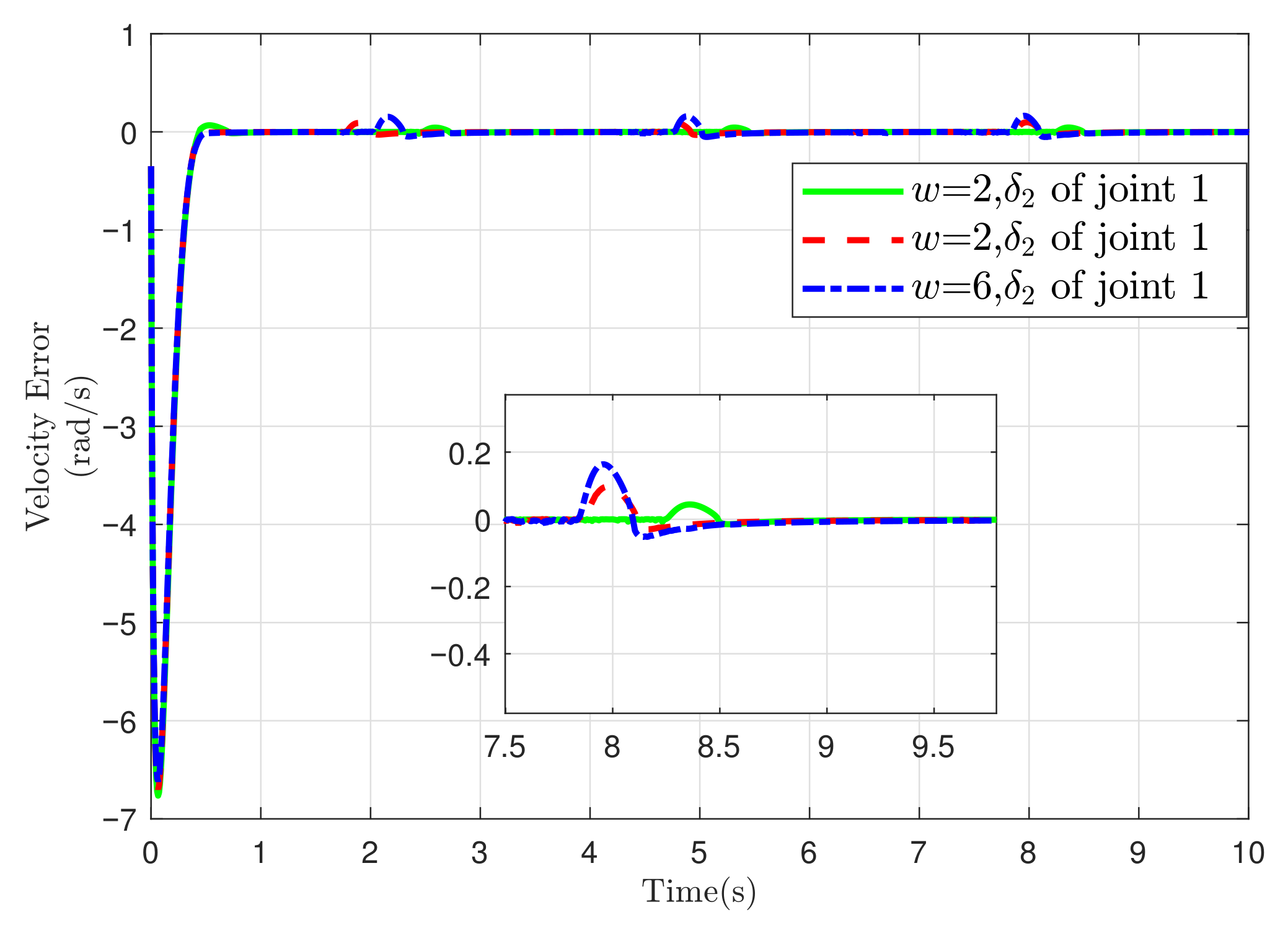
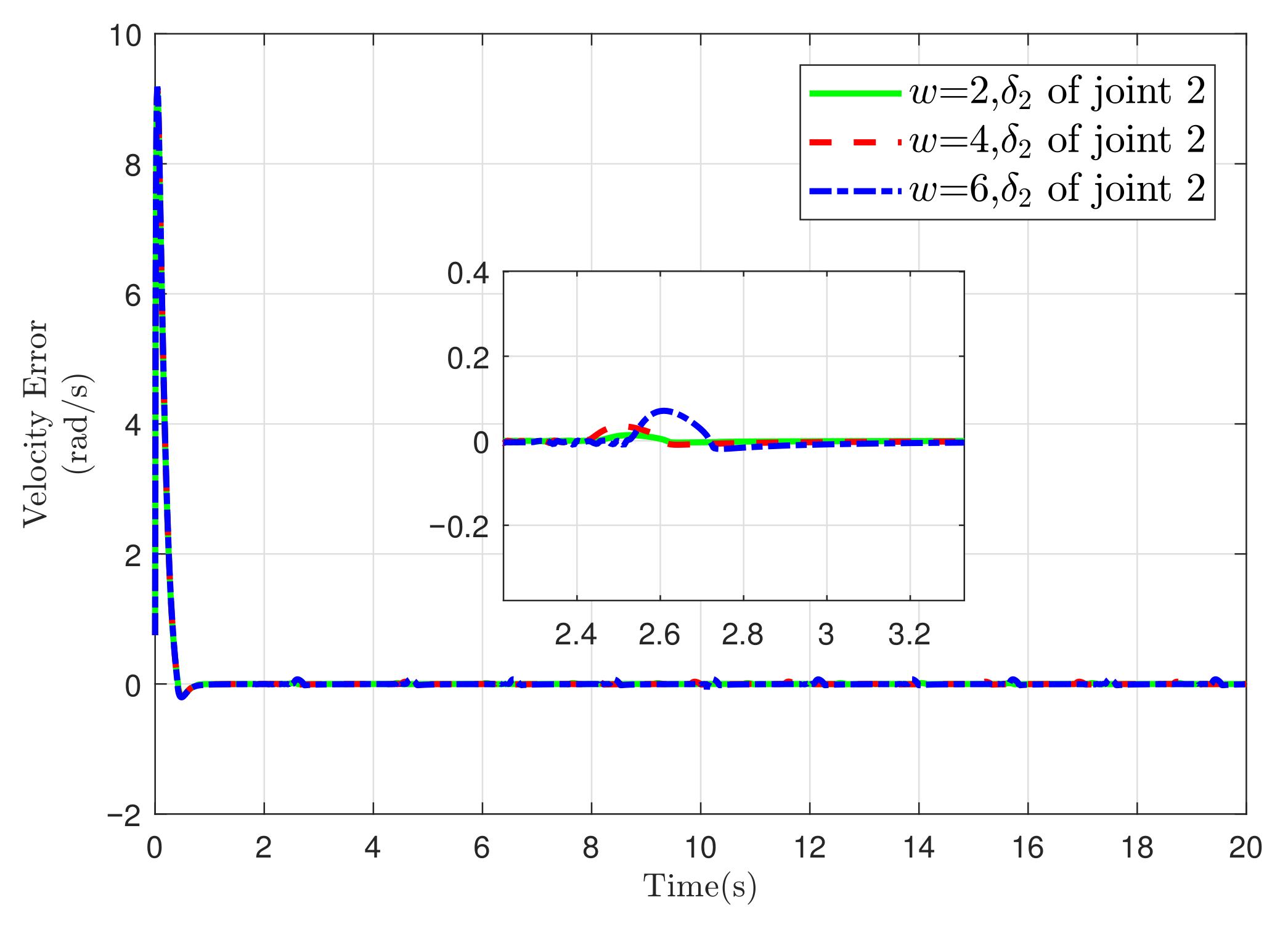
5.2. Simulation of Two-Link Robotic Manipulator
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, X.; Man, Z. Multi-input uncertain linear systems with terminal sliding-mode control. Automatica 1998, 34, 389–392. [Google Scholar] [CrossRef]
- Sun, L.; Liu, Y. Extended state observer augmented finite-time trajectory tracking control of uncertain mechanical systems. Mech. Syst. Signal Process. 2020, 139, 106374. [Google Scholar] [CrossRef]
- Rouhani, E.; Erfanian, A. A finite-time adaptive fuzzy terminal sliding mode control for uncertain nonlinear systems. Int. J. Control. Autom. Syst. 2018, 16, 1957–1964. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Z. Finite-time sliding mode trajectory tracking control of uncertain mechanical systems. Asian J. Control. 2017, 19, 399–404. [Google Scholar] [CrossRef]
- Andrieu, V.; Praly, L. Homogeneous approximation, recursive observer design and output feedback. Siam J. Control. Optim. 2008, 47, 1814–1850. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control. 2012, 57, 2106–2110. [Google Scholar] [CrossRef]
- Zuo, Z. Non-singular fixed-time terminal sliding mode control of non-linear system. IET Control Theory Appl. 2015, 9, 545–552. [Google Scholar] [CrossRef]
- Zuo, Z.; Tian, B.; Defoort, M.; Ding, Z. Fixed-time consensus tracking for multiagent system with high-order integrator dynamics. IEEE Trans. Autom. Control. 2018, 63, 563–570. [Google Scholar] [CrossRef]
- Zuo, Z.; Han, Q.; Ge, X.; Zhang, X. An overview of recent advances in fixed-time cooperative control of multiagent systems. IEEE Trans. Ind. Inform. 2018, 14, 2322–2334. [Google Scholar] [CrossRef]
- Cao, S.; Sun, L.; Jiang, J.; Zuo, Z. Reinforcement learning-based fixed-time trajectory tracking control for uncertain robotic manipulators with input saturation. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 4584–4595. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Y.; Che, W.; Hou, Z. Adaptive NN-based event-triggered containment control for unknown nonlinear networked systems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 2742–2752. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Han, Y.; Zhu, S.; Zeng, Z. Neural network-based fixed-time tracking and containment control of second-order heterogeneous nonlinear multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 11565–11579. [Google Scholar] [CrossRef] [PubMed]
- Xiao, B.; Zhang, H.; Chen, Z.; Cao, L. Fixed-time fault-tolerant optimal attitude control of spacecraft with performance constraint via reinforcement learning. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7715–7724. [Google Scholar] [CrossRef]
- Williams, C.K.I.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Deisenroth, M.; Fox, D.; Rasmussen, C. Gaussian processes for data-efficient learning in robotics and control. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 408–423. [Google Scholar] [CrossRef]
- Beckers, T.; Umlauft, J.; Kulić, D.; Hirche, S. Stable Gaussian process based tracking control of Euler–Lagrange systems. Automatica 2019, 103, 390–397. [Google Scholar] [CrossRef]
- Cen, R.; Jiang, T.; Tang, P. Modified Gaussian process regression based adaptive control for quadrotors. Aerosp. Sci. Technol. 2021, 110, 106483. [Google Scholar] [CrossRef]
- Umlauft, J.; Hirche, L. An uncertainly-based control Lyapunov approach for control-affine systems modeled by Gaussian process. IEEE Control Syst. Lett. 2018, 2, 483–488. [Google Scholar] [CrossRef]
- Han, F.; Yi, J. Stable learning-based tracking control of underactuated balance robots. IEEE Robot. Autom. Lett. 2021, 6, 1543–1550. [Google Scholar] [CrossRef]
- Beckers, T.; Umlauft, J.; Hirche, S. Stable model-based control with Gaussian process regression for robot manipulators. IFAC-PapersOnLine 2017, 50, 3877–3884. [Google Scholar] [CrossRef]
- Li, T.; Sun, L.; Jiang, J. Gaussian process-based adaptive sliding mode tracking control for robotic manipulators. In Proceedings of the 2022 WRC Symposium on Advanced Robotics and Automation, Beijing, China, 19 August 2022. [Google Scholar]
- Srinivas, N.; Krause, A.; Kakade, S.M.; Seeger, M.W. Information-theoretic regret bounds for Gaussian process optimization in the bandit setting. IEEE Trans. Inf. Theory 2012, 58, 3250–3265. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. Siam J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Attitude stabilization of rigid spacecraft with finite-time convergence. Int. J. Robust Nonlinear Control 2011, 21, 686–702. [Google Scholar] [CrossRef]
- Zuo, Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks. Automatica 2015, 54, 305–309. [Google Scholar] [CrossRef]
- Huang, Y.; Jia, Y. Fixed-time consensus tracking control for second-order multi-agent systems with bounded input uncertainties via NFFTSM. IET Control Theory Appl. 2017, 11, 2900–2909. [Google Scholar] [CrossRef]
- Ravichandran, T.; Wang, D.W.L.; Heppler, G.R. Stability and robustness of a class of nonlinear controllers for robot manipulators. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June 2004. [Google Scholar]
- Jiang, B.; Hu, Q.; Friswell, M.I. Fixed-time rendezvous control of spacecraft with a tumbling target under loss of actuator effectiveness. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1576–1586. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, X. Terminal sliding-mode controllers for spacecraft-integrated attitude and position motion using the power of twistors. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8502–8520. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, P.; Lee, C.; Tóth, R. Attitude takeover control for noncooperative space targets based on Gaussian processes with online model learning. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 3050–3066. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, B.; Duan, G. Robust gain scheduled control of spacecraft rendezvous system subject to input saturation. Aerosp. Sci. Technol. 2015, 42, 442–450. [Google Scholar] [CrossRef]
- Boukattaya, M.; Mezghani, N.; Damak, T. Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems. ISA Trans. 2018, 77, 1–19. [Google Scholar] [CrossRef]
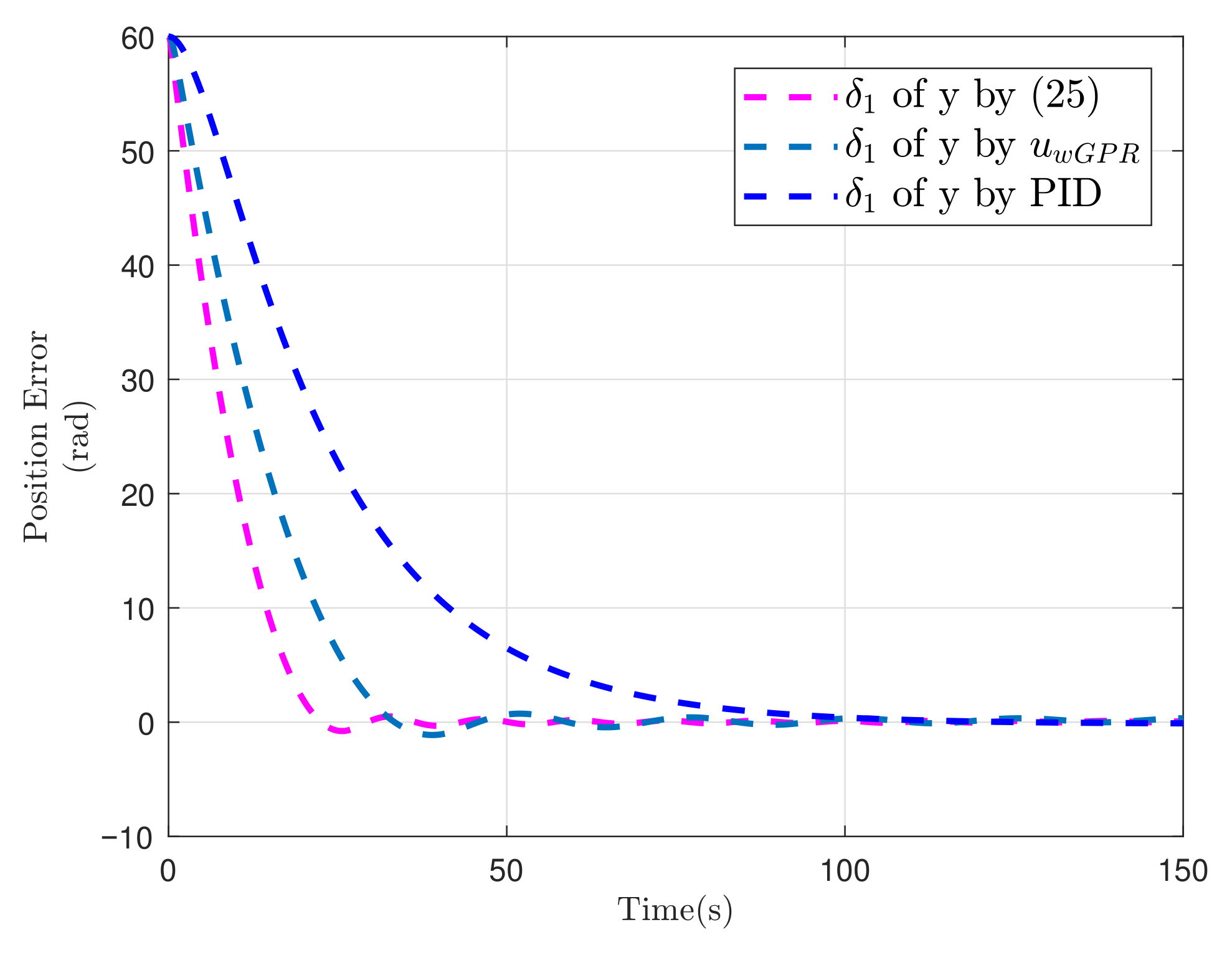
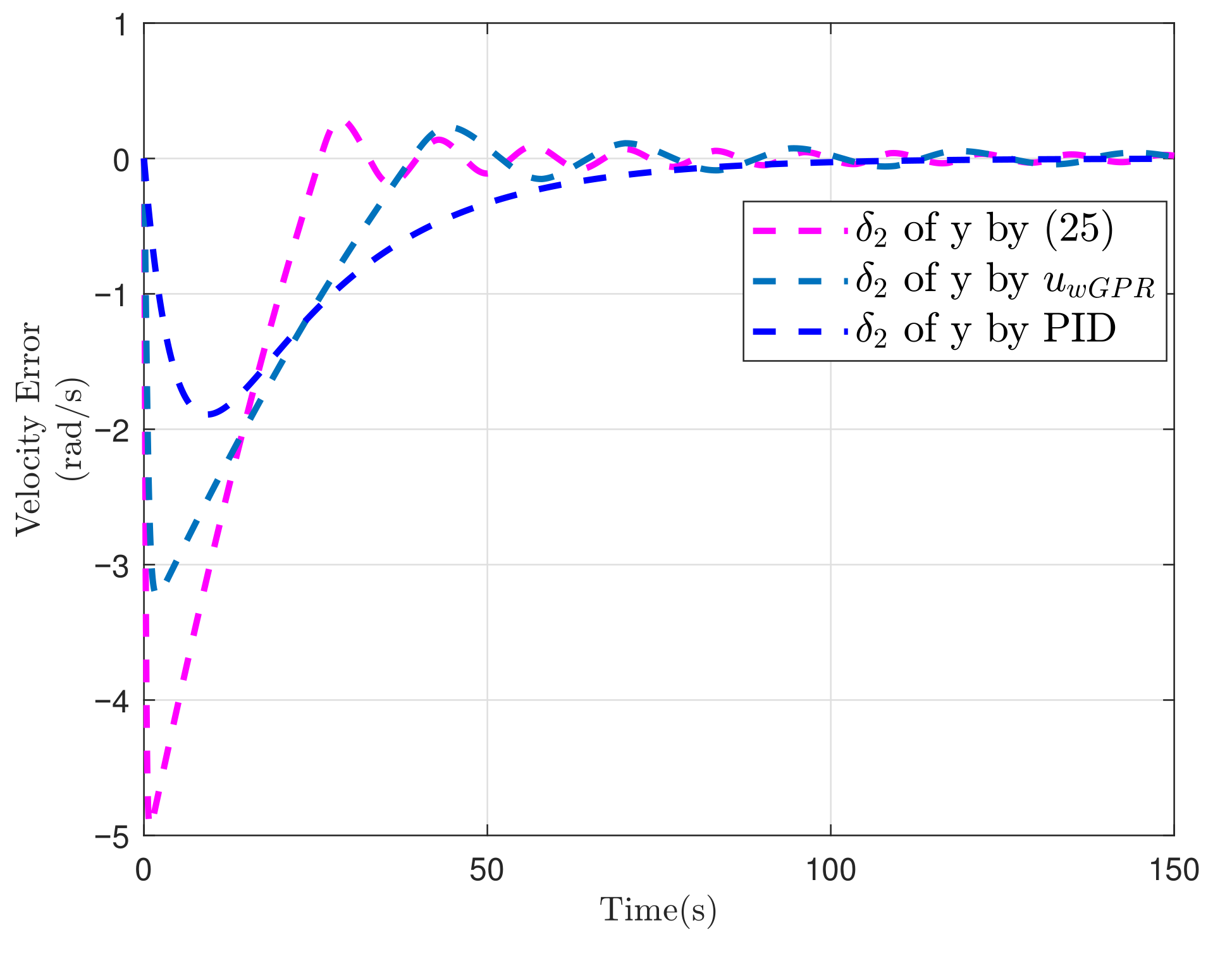
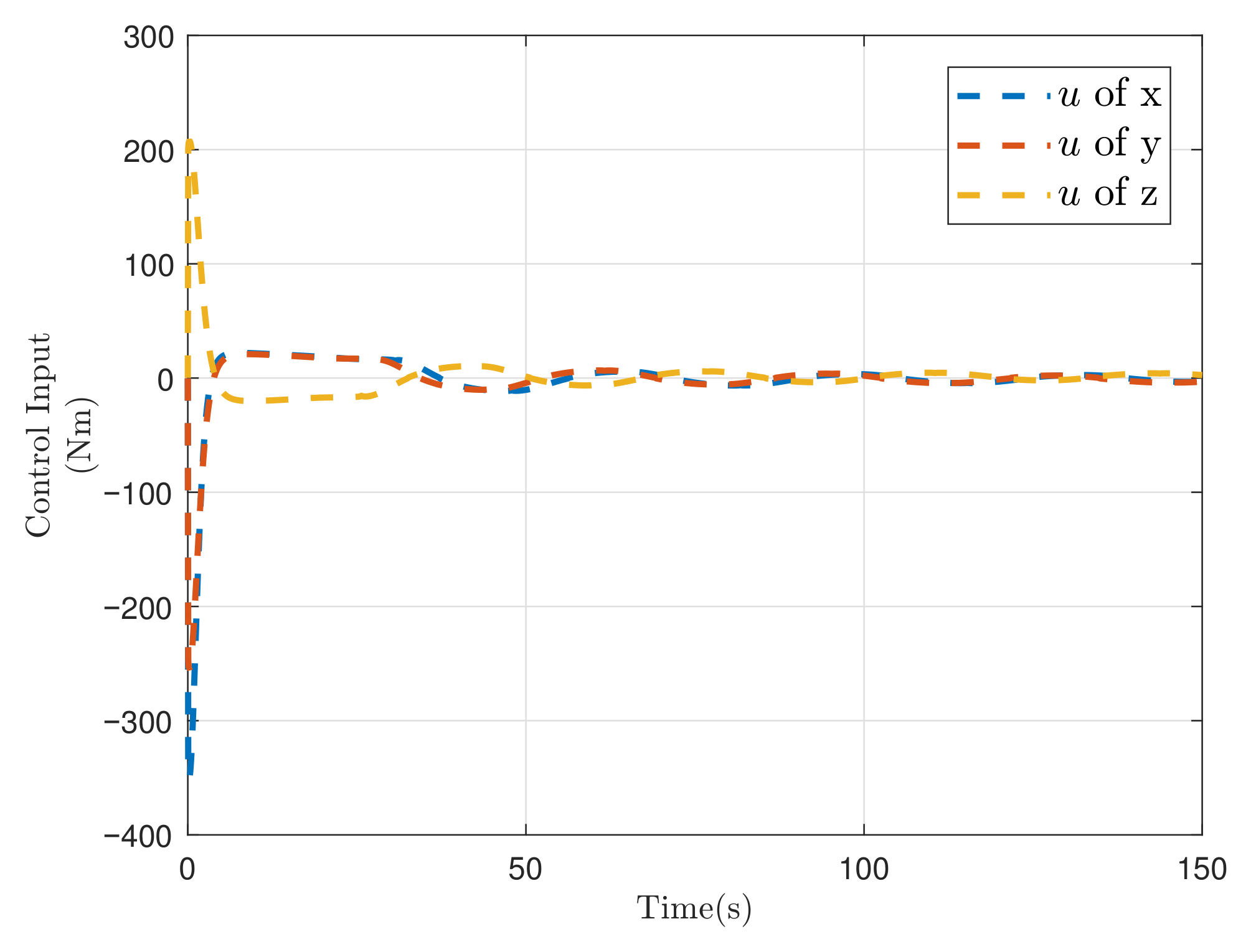
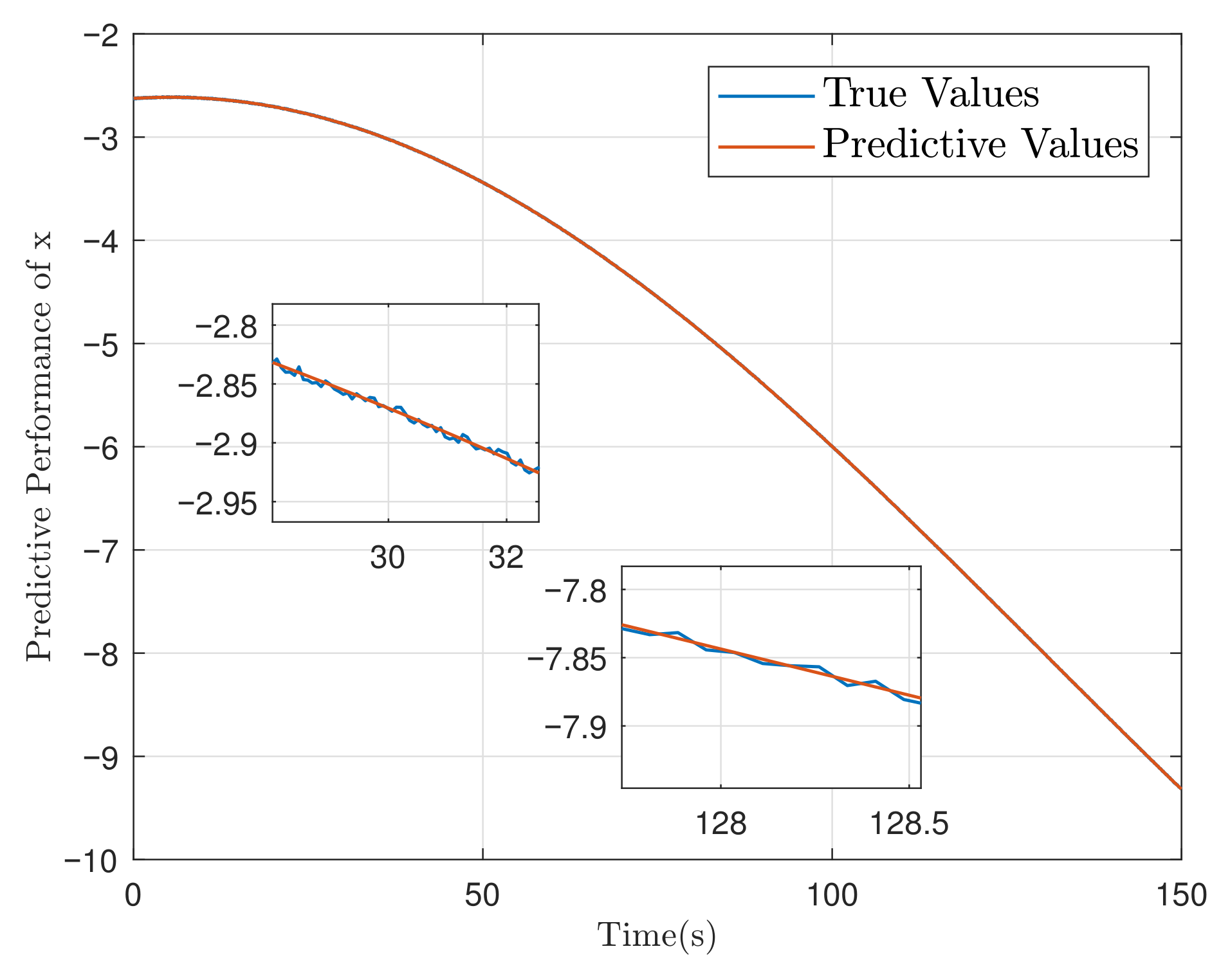





| Controller | Controller (25) | Controller | Controller PID | ||||||
|---|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | x | y | z | |
| IAE | 758.9 | 506.3 | 393.4 | 1.1 | 779.5 | 610.5 | 1.9 | 1.4 | 1.2 |
| ITAE | 6.1 | 3.8 | 3.0 | 1.4 | 9.2 | 7.5 | 4 | 3 | 2.5 |
| /(s) | 58.3 | 65.2 | 59.0 | 72.7 | 84.50 | 75.4 | 120.4 | 125.3 | 120.4 |
| /(s) | 125.6 | 145.8 | 123.5 | 134.4 | 143.8 | 136.4 | 143.5 | 146.7 | 142.8 |
| /(rad) | 0.062 | 0.122 | 0.245 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Chen, T.; Sun, L. Gaussian Process Regression-Based Fixed-Time Trajectory Tracking Control for Uncertain Euler–Lagrange Systems. Actuators 2025, 14, 349. https://doi.org/10.3390/act14070349
Li T, Chen T, Sun L. Gaussian Process Regression-Based Fixed-Time Trajectory Tracking Control for Uncertain Euler–Lagrange Systems. Actuators. 2025; 14(7):349. https://doi.org/10.3390/act14070349
Chicago/Turabian StyleLi, Tong, Tianqi Chen, and Liang Sun. 2025. "Gaussian Process Regression-Based Fixed-Time Trajectory Tracking Control for Uncertain Euler–Lagrange Systems" Actuators 14, no. 7: 349. https://doi.org/10.3390/act14070349
APA StyleLi, T., Chen, T., & Sun, L. (2025). Gaussian Process Regression-Based Fixed-Time Trajectory Tracking Control for Uncertain Euler–Lagrange Systems. Actuators, 14(7), 349. https://doi.org/10.3390/act14070349