A Computational Intelligence-Based Proposal for Cybersecurity and Health Management with Continuous Learning in Chemical Processes
Abstract
1. Introduction
2. Understanding Fuzzy Clustering: Core Features
2.1. Fuzzy C-Means (FCM)
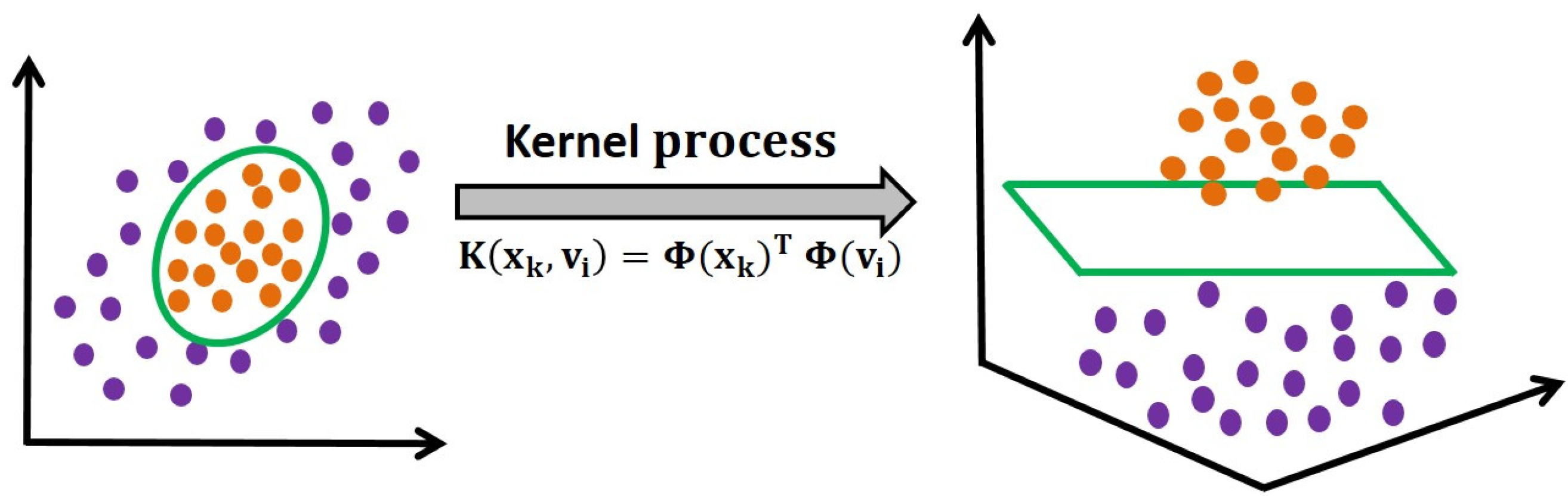
2.2. Kernel Fuzzy C-Means
| Algorithm 1: Kernelized Fuzzy C-Means (KFCM) |
| Input: data X, number of classes g, parameters
. Output: matrix U, class centers V. Assign random entries to matrix U during initialization. for Update the centroid of every classification by using Equation (11). Compute the distances based on Equation (7). Update matrix U using Equation (10). Verify if the following termination condition is satisfied: end for |
2.3. Type-2 FCM Algorithm (T2FCM) and Its Kernel Variant (KT2FCM)
| Algorithm 2: KT2FCM |
| Input: dataset X, number of classifications g, parameters . Output: matrix U, class centers V. Assign random entries to matrix U during initialization. Compute A based on Equation (12). for Revise the centroid of each classification using Equation (18). Compute the distances based on Equation (14). Update matrix A using Equation (17). Verify if the termination condition is satisfied: end for |
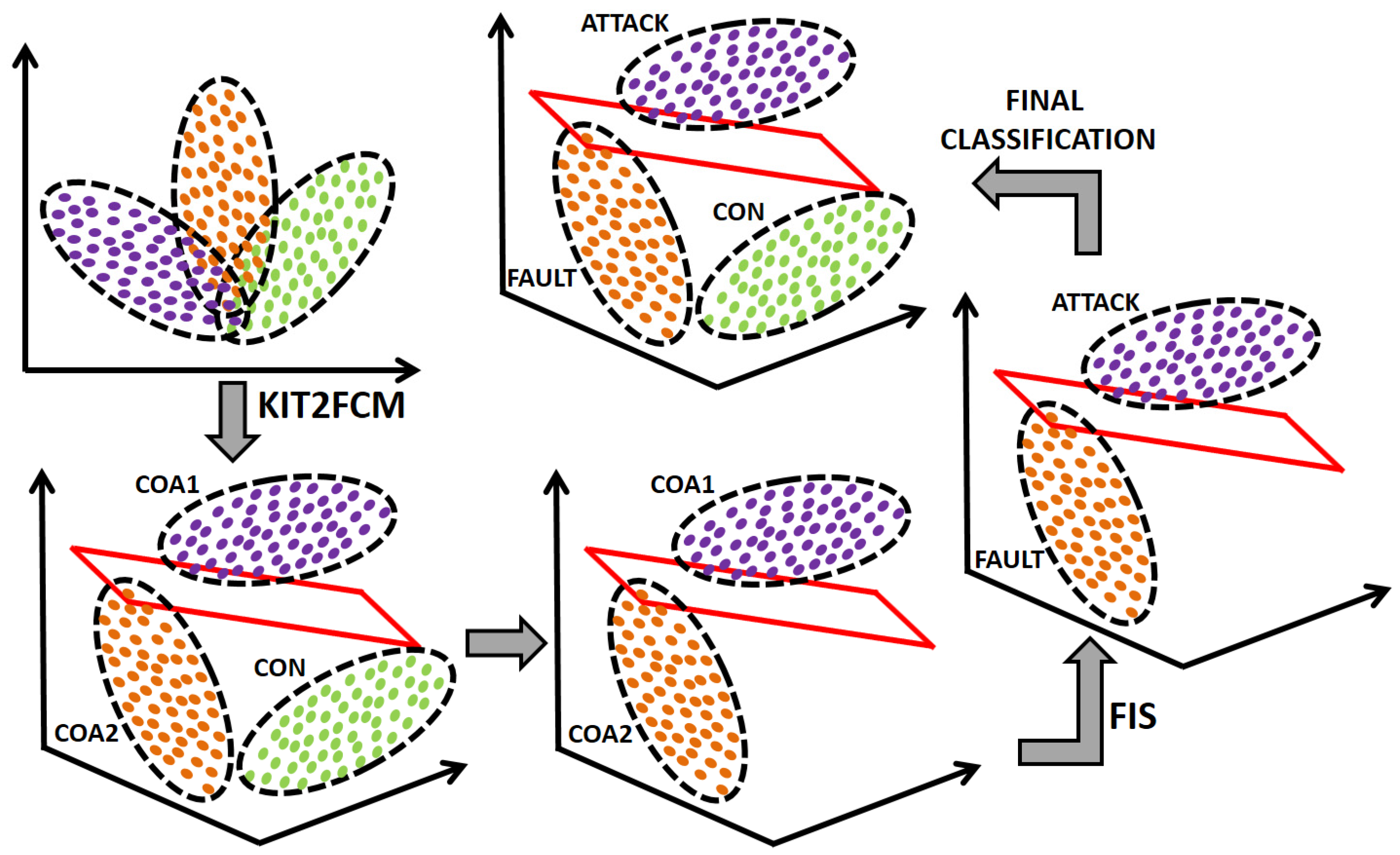
2.4. Interval Type-2 FCM (IT2FCM) and Its Kernel Variant (KIT2FCM)
| Algorithm 3: KIT2FCM |
| Input: dataset X, number of classes g, parameters . Output: matrix U, class centers V. Assign random entries to the lower matrix and upper in the initialization for Revise the centroid of each classification using Equation (11) for and . Compute the distances based on Equation (14). Update and using Equation (10) for and Update the cluster centers: . Type-reduce the interval Type-2 fuzzy partition matrix as . Verify if the termination condition is satisfied: end for |
2.5. Density-Oriented Fuzzy C-Means (DOFCM)
| Algorithm 4: DOFCM to determine the presence of a new class |
| Input: Dataset with outliers X, number of clusters c, Output: Filtered dataset without outliers Xp Compute the neighborhood radius. Compute using Equation (25). Determine . Compute using Equation (24). Using the specified value of , identify outliers according to Equation (26). |
3. Proposed Monitoring Scheme
3.1. Offline Training
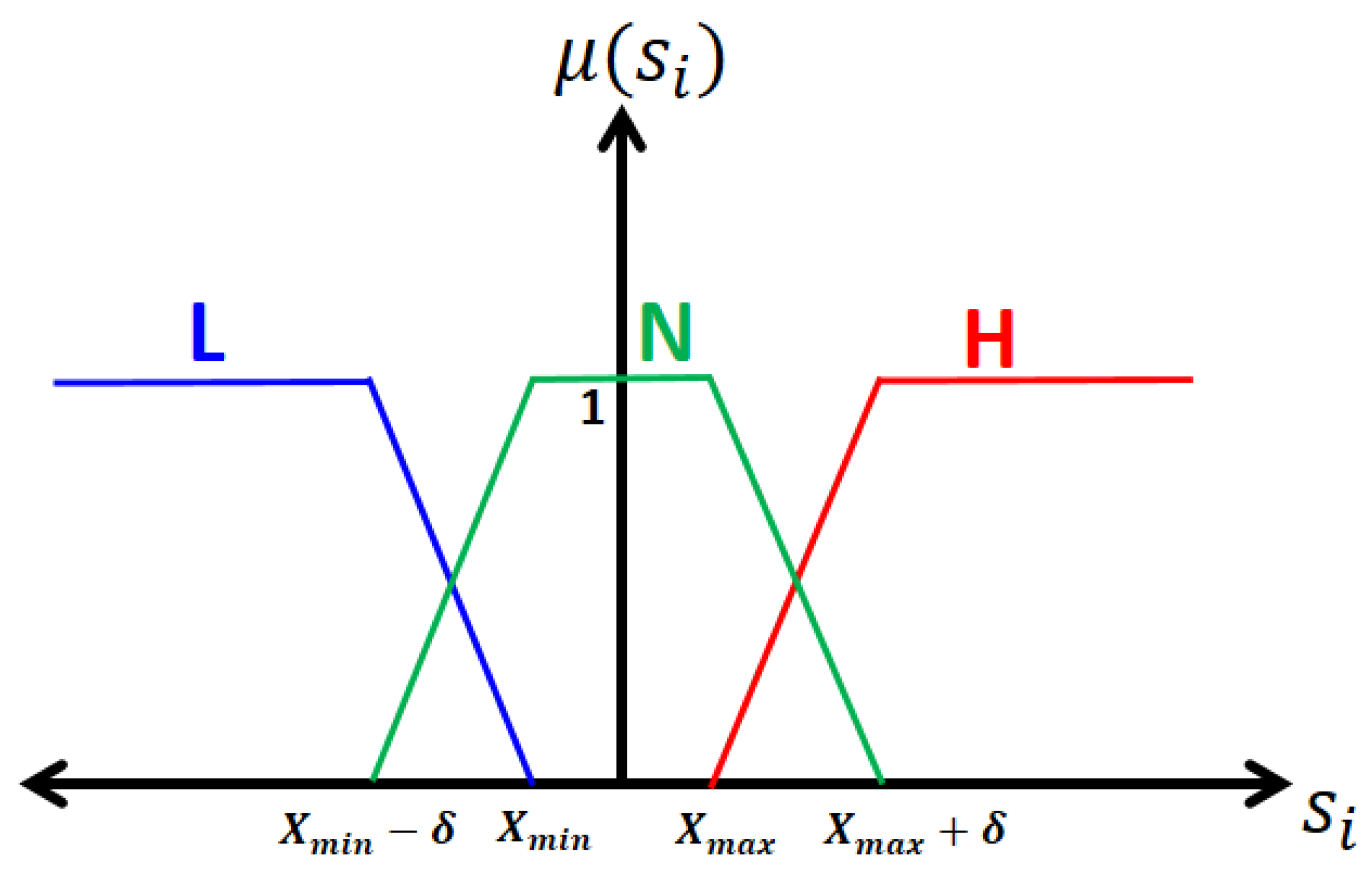
- n denotes the number of symptom variables in the process.
- i = 1 (FS low), 2 (FS normal), and 3 (FS high).
- j = 1 (Fault) and 2 (Attack)
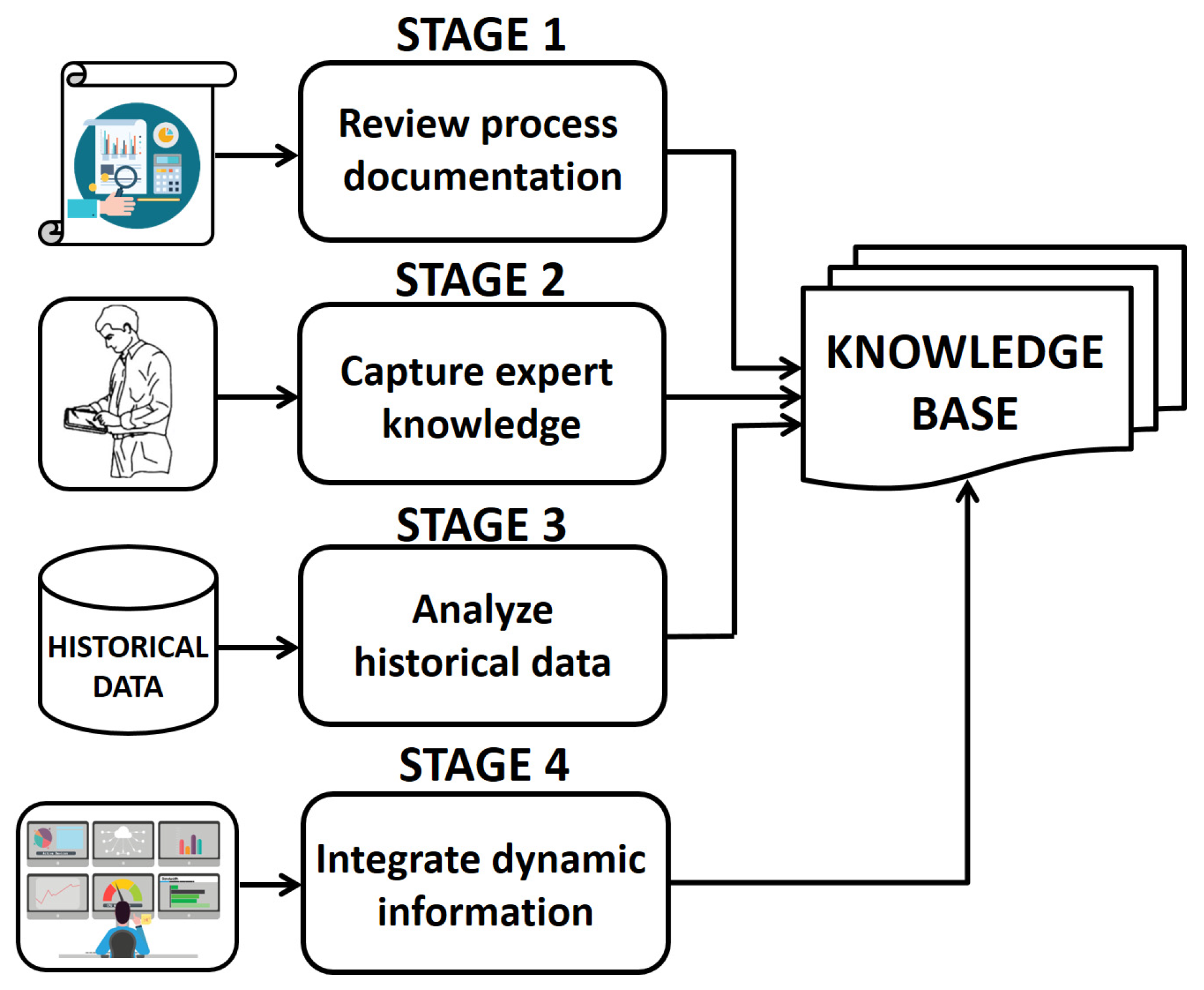
- Review process documentation: review manuals, standard operating procedures, safety protocols, repair records, previous incident reports, and design specifications.
- Capture expert knowledge: Conduct interviews with experts in the operation of the process; capture undocumented knowledge from experienced personnel through direct observation.
- Analyze historical data: Examine the most common problems with variable symptoms, common errors, and successful resolutions based on operational data and maintenance records.
- Integrate dynamic information: Integrate data from the monitoring system to feed the knowledge base with dynamic information.
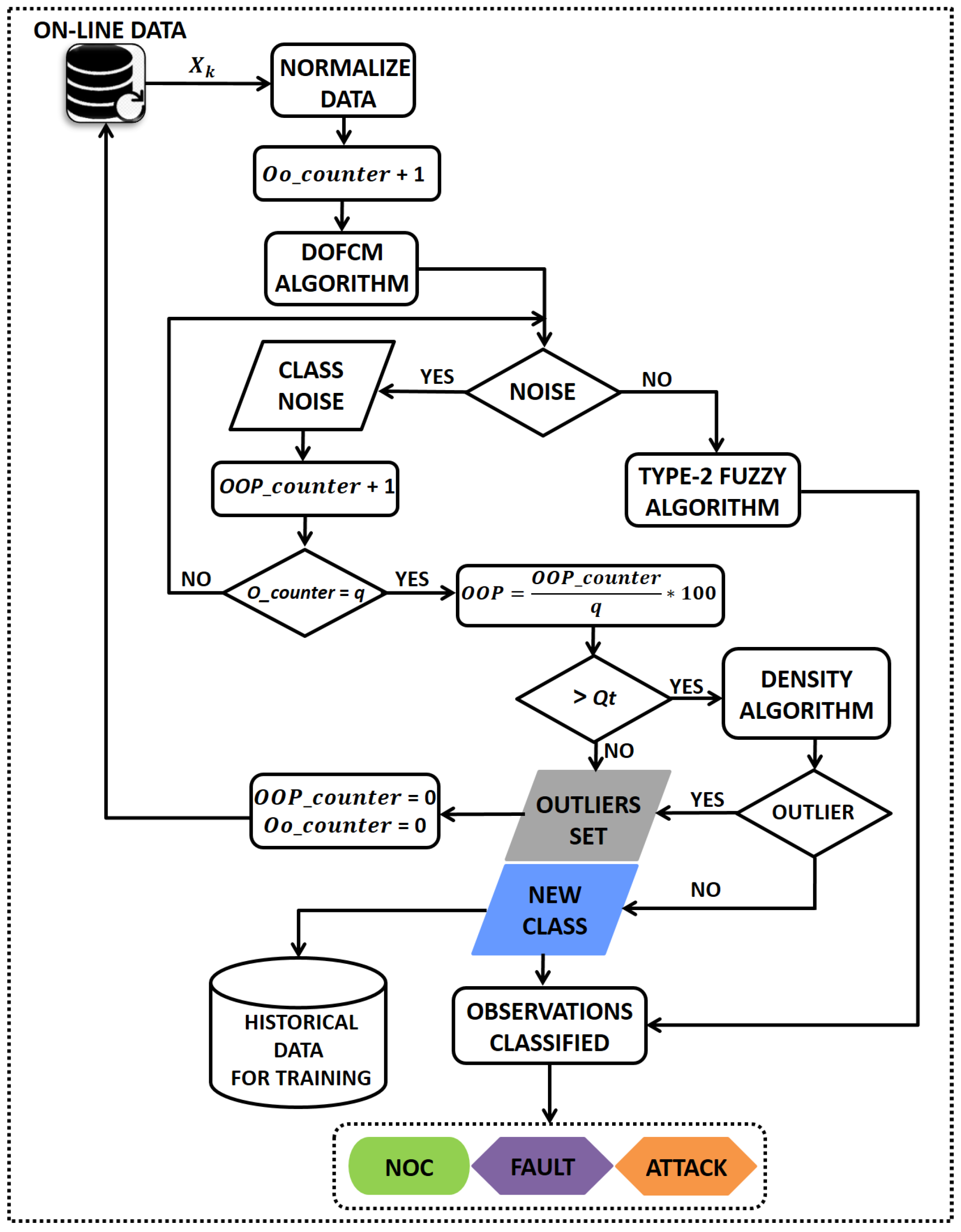
3.2. Online Analysis
| Algorithm 5: Online analysis |
| Input: data , class centers V, f,
,
, Output: Current State, New event Select q Select Qt Initialize OO counter = 0 Initialize OOP counter = 0 for Increment OO counter by 1 Compute using Equation (25) Compute using Equation (24) if q ≠ Coutlier then Calculate the distances from the sample l to the class centers. Calculate the membership degree of sample l to the g classes. Assign observation l to a class according to Equation (31). else Store observation q in Cnoise Increment the OOP counter by 1 end if end for Compute OOP = (OOP counter) x 100/q if OOP > Qt then Apply the DOFCM algorithm for Cnoise assuming two classes (New Event, Outlier) if Cnoise ≠ Coutlier then Create a new pattern Identify the new pattern: Fault or Attack Store in the historical database for training else Delete Cnoise Reset the OO counter and OOP counter to 0 end if else Delete Cnoise Reset the OO counter and OOP counter to 0 end if |
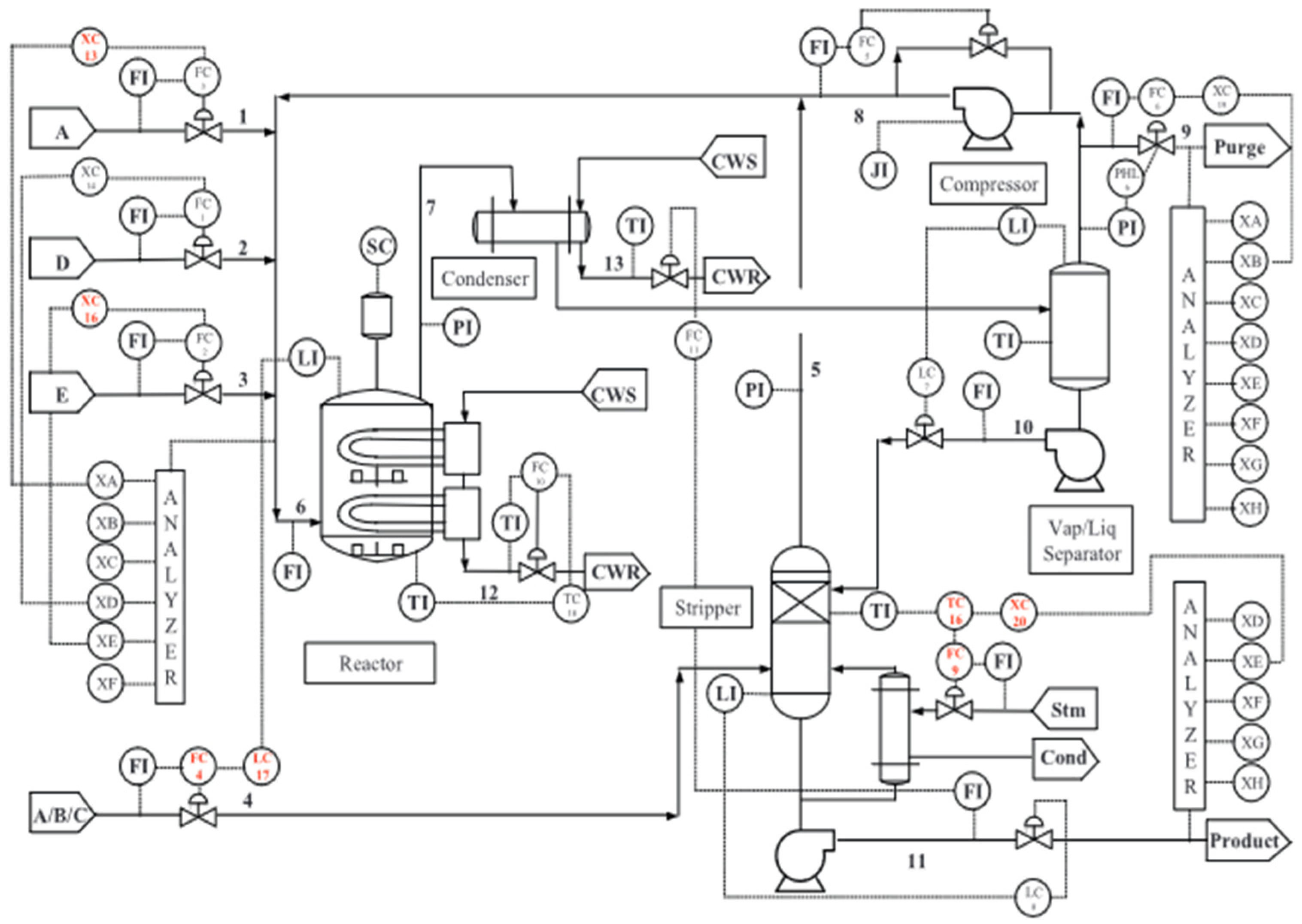
4. Case Study: Tennessee Eastman Process
4.1. Process Description
4.2. Experimental Design
4.3. Discussion of the Experimental Results
Offline Training
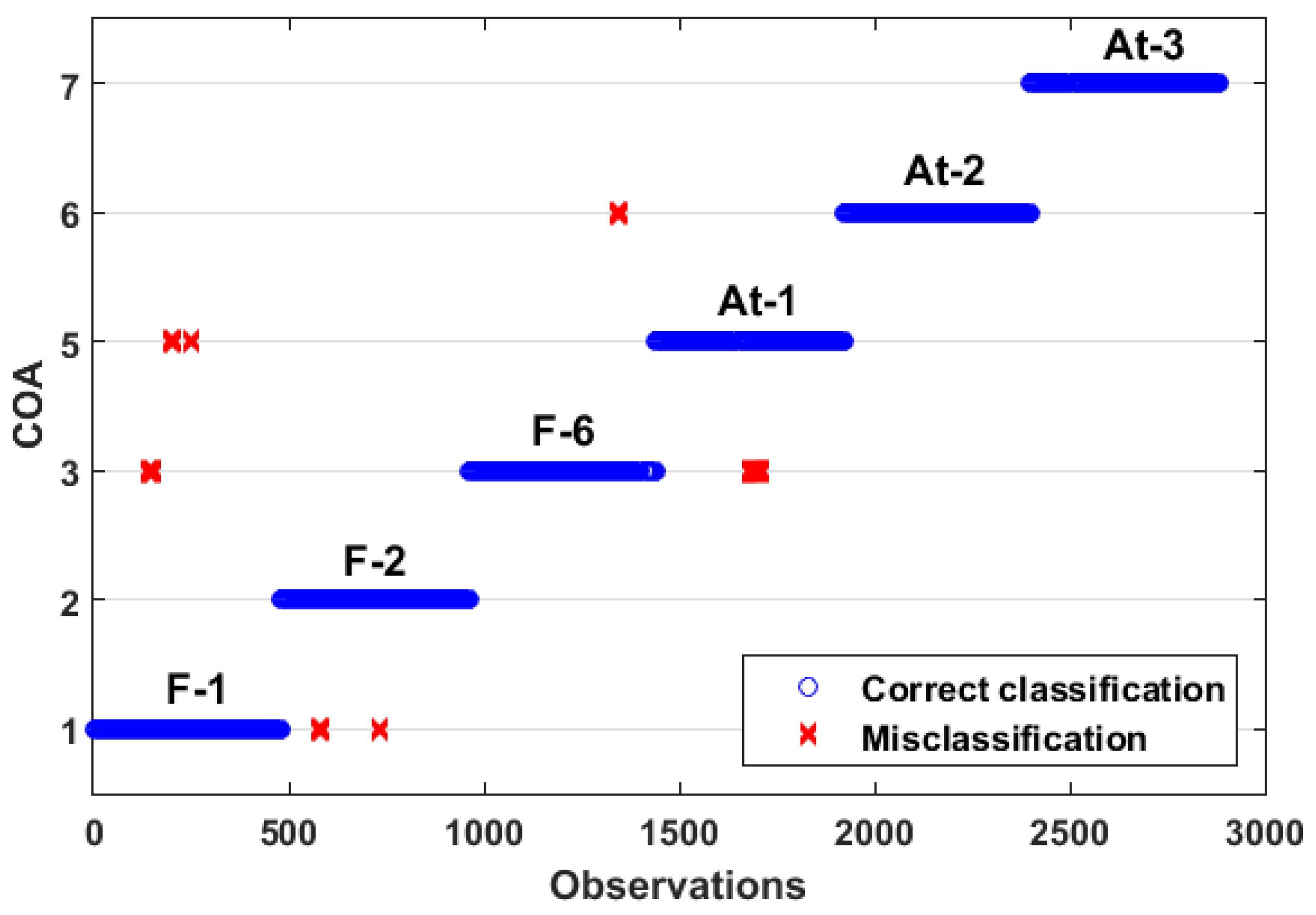
4.4. Online Analysis
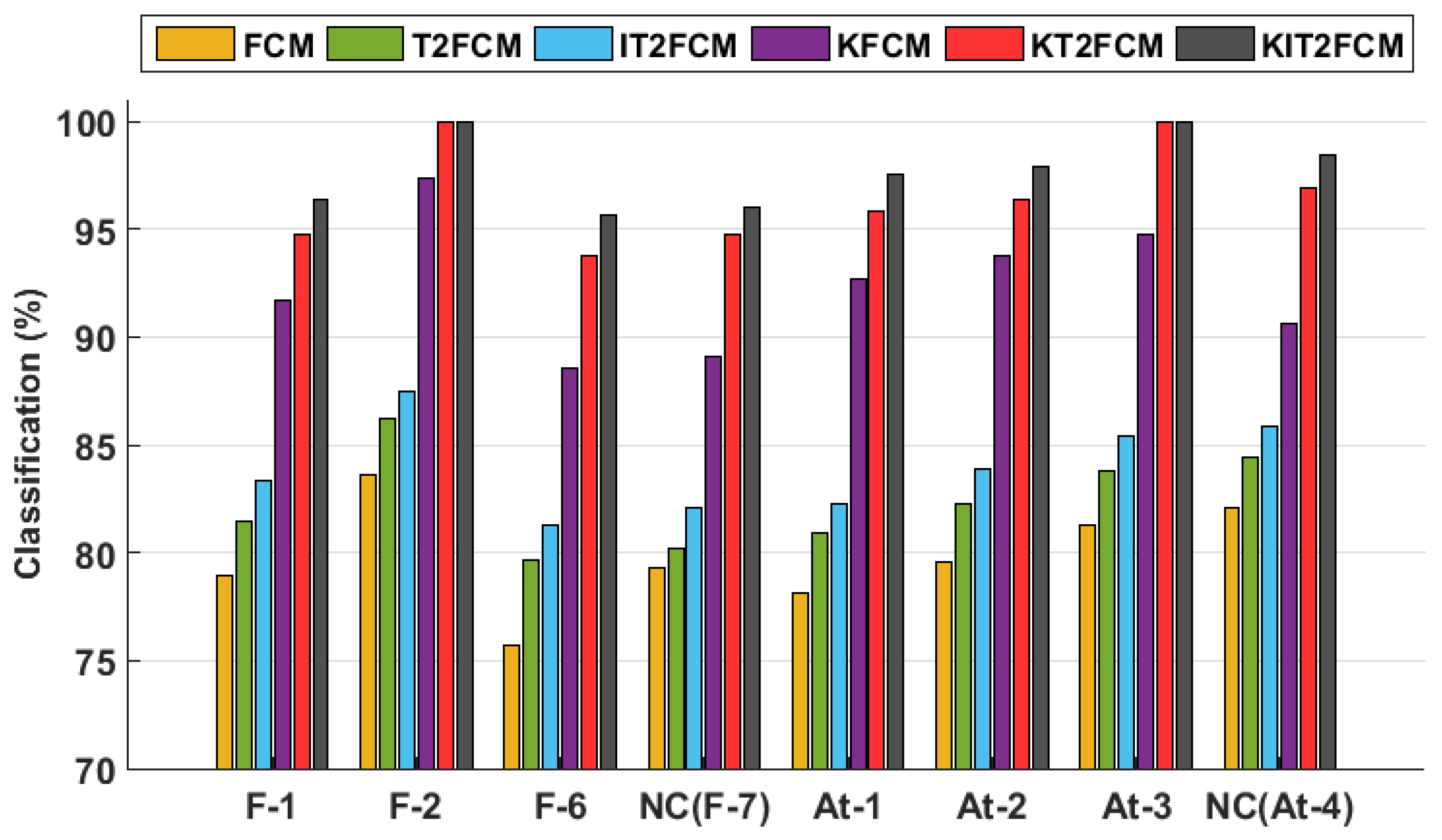
5. Comparative Analysis of Performances
5.1. Comparison with Analogous Condition-Monitoring Algorithms
- Statistical Tests
- Friedman Test
- Wilcoxon Test
5.2. With Recent Algorithms
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Macas, M.; Wu, C.; Fuertes, W. A survey on deep learning for cybersecurity: Progress, challenges, and opportunities. Comput. Netw. 2022, 212, 109032. [Google Scholar] [CrossRef]
- Bashendy, M.; Tantawy, A.; Erradi, A. Intrusion response systems for cyber-physical systems: A comprehensive survey. Comput. Secur. 2023, 124, 102984. [Google Scholar] [CrossRef]
- Alanazi, M.; Mahmood, A.; Morshed, M.J. SCADA vulnerabilities and attacks: A review of the state of the art and open issues. Comput. Secur. 2023, 125, 103028. [Google Scholar] [CrossRef]
- Alladi, T.; Chamola, V.; Zeadally, S. Industrial Control Systems: Cyberattack trends and countermeasur. Comput. Commun. 2020, 155, 1–8. [Google Scholar] [CrossRef]
- Azzam, M.; Pasquale, L.; Provan, G.; Nuseibeh, B. Forensic readiness of industrial control systems under stealthy attacks. Comput. Secur. 2023, 125, 103010. [Google Scholar] [CrossRef]
- Parker, S.; Wu, Z.; Christofides, P.D. Cybersecurity in process control, operations, and supply chain. Comput. Chem. Eng. 2023, 171, 108169. [Google Scholar] [CrossRef]
- Fernandes, M.; Corchado, J.M.; Marreiros, G. Machine learning techniques applied to mechanical fault diagnosis and fault prognosis in the context of real industrial manufacturing use-cases: A systematic literature review. Appl. Intell. 2022, 52, 14246–14280. [Google Scholar] [CrossRef]
- Li, W.; Huang, R.; Li, J.; Liao, Y.; Chen, Z.; He, G.; Yan, R.; Gryllias, K. A perspective survey on deep transfer learning for fault diagnosis in industrial scenarios: Theories, applications and challenges. Mech. Syst. Signal Process. 2022, 167, 108487. [Google Scholar] [CrossRef]
- Lv, H.; Chen, J.; Pan, T.; Zhang, T.; Feng, Y.; Liu, S. Attention mechanism in intelligent fault diagnosis of machinery: A review of technique and application. Measurement 2022, 199, 111594. [Google Scholar] [CrossRef]
- Mu, B.; Scott, J.K. Set-based fault diagnosis for uncertain nonlinear systems. Comput. Chem. Eng. 2024, 180, 108479. [Google Scholar] [CrossRef]
- Quian, J.; Song, Z.; Yao, Y.; Zhu, Z.; Zhang, X. A review on autoencoder based representation learning for fault detection and diagnosis in industrial processes. Chemom. Intell. Lab. Syst. 2022, 231, 104711. [Google Scholar] [CrossRef]
- Vidal-Puig, S.; Vitale, R.; Ferrer, A. Data-driven supervised fault diagnosis methods based on latent variable models: A comparative study. Chemom. Intell. Lab. Syst. 2019, 187, 41–52. [Google Scholar] [CrossRef]
- Doing, D.; Han, Q.L.; Xiang, Y.; Zhang, X.M. New Features for Fault Diagnosis by Supervised Classification. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar]
- Zang, P.; Wen, G.; Dong, S.; Lin, H.; Huang, X.; Tian, X.; Chen, X. A novel multiscale lightweight fault diagnosis model based on the idea of adversarial learning. Neurocomputing 2018, 275, 1674–1683. [Google Scholar]
- Camps-Echevarría, L.; Llanes Santiago, O.; Campos Velho, H.F.d.; Silva Neto, A.J.d. Fault Diagnosis Inverse Problems. In Fault Diagnosis Inverse Problems: Solution with Metaheuristics; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Kravchik, M.; Demetrio, L.; Biggio, L.; Shabtai, A. Practical Evaluation of Poisoning Attacks on Online Anomaly Detectors in Industrial Control System. Comput. Secur. 2022, 122, 102901. [Google Scholar] [CrossRef]
- Zhou, J.; Zhu, Y. Fault isolation based on transfer-function models using an MPC algorithm. Comput. Chem. Eng. 2022, 159, 107668. [Google Scholar] [CrossRef]
- Prieto-Moreno, A.; Llanes-Santiago, O.; García-Moreno, E. Principal components selection for dimensionality reduction using discriminant information applied to fault diagnosis. J. Process Control 2015, 33, 4–24. [Google Scholar] [CrossRef]
- Lundgren, A.; Jung, D. Data-driven fault diagnosis analysis and open-set classification of time-series data. Control Eng. Pract. 2022, 121, 105006. [Google Scholar] [CrossRef]
- Taqvi, S.A.A.; Zabiri, H.; Tufa, L.D.; Uddinn, F.; Fatima, S.A.; Maulud, A.S. A review on data-driven learning approaches for fault detection and diagnosis in chemical process. ChemBioEng Rev. 2021, 8, 39–259. [Google Scholar] [CrossRef]
- Kumar, N.; Mohan Mishra, V.; Kumar, A. Smart grid and nuclear power plant security by integrating cryptographic hardware chip. Nucl. Eng. Technol. 2021, 53, 3327–3334. [Google Scholar] [CrossRef]
- Hadroug, N.; Hafaifa, A.; Alili, B.; Iratni, A.; Chen, X. Fuzzy Diagnostic Strategy Implementation for Gas Turbine Vibrations Faults Detection: Towards a Characterization of Symptom Fault Correlations. J. Vib. Eng. Technol. 2022, 10, 225–251. [Google Scholar] [CrossRef]
- Chi, Y.; Dong, Y.; Wang, Z.Y.; Yu, F.R.; Leung, V.C.M. Knowledge-Based Fault Diagnosis in Industrial Internet of Things: A Survey. IEEE Internet Things J. 2022, 9, 12886–12900. [Google Scholar] [CrossRef]
- Rodríguez-Ramos, A.; Bernal-de-Lázaro, J.M.; Cruz-Corona, C.; Silva Neto, A.J.; Llanes-Santiago, O. An approach to robust condition monitoring in industrial processes using pythagorean memberships grades. Ann. Braz. Acad. Sci. 2022, 94, e20200662. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.; Tang, J. Harnessing fuzzy neural network for gear fault diagnosis with limited data labels. Int. J. Adv. Manuf. Tech. 2021, 115, 1005–1019. [Google Scholar] [CrossRef]
- Fan, Y.; Ma, T.; Xiao, F. An improved approach to generate generalized basic probability assignment based on fuzzy sets in the open world and its application in multi-source information fusion. Appl. Intell. 2021, 51, 3718–3735. [Google Scholar] [CrossRef]
- Pan, H.; Xu, H.; Zheng, J.; Su, J.; Tong, J. Multi-class fuzzy support matrix machine for classification in roller bearing fault diagnosis. Adv. Eng. Inform. 2021, 51, 101445. [Google Scholar] [CrossRef]
- Yang, X.; Yu, F.; Pedrycz, W. Typical Characteristic-Based Type-2 Fuzzy C-Means Algorithm. IEEE Trans. Fuzzy Syst. 2021, 29, 1173–1187. [Google Scholar] [CrossRef]
- Yin, Y.; Sheng, Y.; Qin, J. Interval type-2 fuzzy C-means forecasting model for fuzzy time series. Appl. Soft Comput. 2022, 129, 109574. [Google Scholar] [CrossRef]
- Li, Q.; Chen, B.; Chen, Q.; Li, X.; Qin, Z.; Chu, F. HSE: A plug-and-play module for unified fault diagnosis foundation models. Inf. Fusion 2025, 123, 103277. [Google Scholar] [CrossRef]
- Amin, T.; Halim, S.Z.; Pistikopoulos, S. A holistic framework for process safety and security analysis. Comput. Chem. Eng. 2022, 165, 107693. [Google Scholar] [CrossRef]
- Syfert, M.; Ordys, A.; Koscielny, J.M.; Wnuk, P.; Mozaryn, J.; Kukielka, K. Integrated approach to diagnostics of failures and cyber-attacks in industrial control systems. Energies 2022, 15, 6212. [Google Scholar] [CrossRef]
- Dai, S.; Zha, L.; Liu, J.; Xie, X.; Tian, E. Fault detection filter design for networked systems with cyber attacks. Appl. Math. Comput. 2022, 412, 126593. [Google Scholar] [CrossRef]
- Müller, N.; Bao, K.; Matthes, J.; Heussen, K. Cyphers: A cyberphysical event reasoning system providing real-time situational awareness for attack and fault response. Comput. Ind. 2023, 151, 103982. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In 2nd ACM SIGKDD; AAAI Press: Washington, DC, USA, 1996; pp. 226–231. [Google Scholar]
- Bathelt, A.; Ricker, N.L.; Jelali, M. Revision of the Tennessee Eastman Process model. IFAC Pap. OnLine 2015, 48, 309–314. [Google Scholar] [CrossRef]
- Melo, A.; Câmara, M.M.; Clavijo, N.; Pinto, J. Open benchmarks for assessment of process monitoring and fault diagnosis techniques: A review and critical analysis. Comput. Chem. Eng. 2022, 165, 107964. [Google Scholar] [CrossRef]
- Rodríguez-Ramos, A.; Ortiz, F.J.; Llanes-Santiago, O. A proposal of Robust Condition Monitoring Scheme for Industrial Systems. Comput. Sist. 2023, 27, 223–235. [Google Scholar] [CrossRef]
- García, S.; Herrera, F. An extension on statistical comparisons of classifiers over multiple datasets for all pairwise comparisons. J. Mach. Learn. Res. 2008, 9, 2677–2694. [Google Scholar]
- Zhang, Z.; Zhao, J. A deep belief network based fault diagnosis model for complex chemical processes. Comput. Chem. Eng. 2017, 107, 395–407. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, J. Deep convolutional neural network model based chemical process fault diagnosis. Comput. Chem. Eng. 2018, 115, 185–197. [Google Scholar] [CrossRef]
- Zhang, S.; Bi, K.; Qiu, T. Bidirectional recurrent neural network based chemical process fault diagnosis. Ind. Eng. Chem.Res. 2020, 59, 824–834. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, J. Process topology convolutional network model for chemical process fault diagnosis. Process Saf. Environ. Prot. 2021, 150, 93–109. [Google Scholar] [CrossRef]





| Fault | Process Variable | Type |
|---|---|---|
| Fault 1 (F-1) | A/C feed ratio, B composition constant | step |
| Fault 2 (F-2) | B composition, A/C ratio constant | step |
| Fault 6 (F-6) | A feed loss | step |
| Fault 7 (F-7) | C header pressure loss-reduced availability | step |
| Type of Attack | Magnitude of the Sensor Under Attack | Symptom Variables | Description | Impact |
|---|---|---|---|---|
| Attack 1 (At-1) | VMe(1) [+2.35] | VMe(1), VMe(7), VMe(8), VMe(3) | For three hours, the actual value is incremented by a factor of 2.35 | HRP or LSL: shutdown |
| Attack 2 (At-2) | VMe(14) [+7] | VMe(12), VMe(14), VMe(15), VMa(7), VMa(8) | For 2.88 h the actual value increases by 7 | HSL: shutdown |
| Attack 3 (At-3) | VMe(14) [−7] | VMe(12), VMe(14), VMe(15), VMa(7), VMa(8) | For 2.02h the actual value decreases by 7 | LSL: shutdown |
| Attack 4 (At-4) | VMe(14) [22.9] | VMe(12), VMe(15), VMa(7) | The value is set to 22.9 for 1.9 h | LSL: shutdown |
| CON | COA1 | COA2 | COA3 | COA5 | COA6 | COA7 | TA (%) | |
| CON | 480 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| COA1 | 0 | 465 | 15 | 0 | 0 | 0 | 0 | 96.88 |
| COA2 | 0 | 0 | 480 | 0 | 0 | 0 | 0 | 100 |
| COA3 | 2 | 5 | 0 | 460 | 13 | 0 | 0 | 95.83 |
| COA5 | 0 | 2 | 0 | 8 | 470 | 0 | 0 | 97.92 |
| COA6 | 0 | 0 | 0 | 0 | 0 | 480 | 0 | 100 |
| COA7 | 0 | 0 | 0 | 0 | 0 | 0 | 480 | 100 |
| AVE | 98.66 |
| F-1 | F-2 | F-6 | At-1 | At-2 | At-3 | |
|---|---|---|---|---|---|---|
| VMe(1) | H | N | L | H | N | N |
| VMe(3) | N | H | N | N | N | N |
| VMe(4) | L | H | N | N | N | N |
| VMe(7) | N | N | H | L | N | N |
| VMe(8) | N | N | N | L | N | N |
| VMe(10) | N | H | N | N | N | N |
| VMe(11) | N | N | L | N | N | N |
| VMe(12) | N | N | N | N | H | L |
| VMe(13) | N | N | H | N | N | N |
| VMe(14) | N | N | N | N | H | L |
| VMe(15) | N | N | N | N | L | H |
| VMe(16) | N | N | H | N | N | N |
| VMe(18) | H | L | N | N | N | N |
| VMe(19) | H | L | N | N | N | N |
| VMe(20) | N | N | L | N | N | N |
| VMe(21) | N | N | N | N | N | N |
| VMe(22) | N | H | L | N | N | N |
| VMe(23) | N | N | L | N | N | N |
| VMe(25) | N | N | H | N | N | N |
| VMe(28) | N | L | N | N | N | N |
| VMe(29) | N | N | L | N | N | N |
| VMe(31) | N | N | H | N | N | N |
| VMe(33) | N | N | N | N | N | N |
| VMe(34) | N | L | N | N | N | N |
| VMe(35) | N | N | L | N | N | N |
| VMe(36) | N | N | L | N | N | N |
| VMe(38) | N | N | H | N | N | N |
| VMe(39) | N | L | N | N | N | N |
| VMa(2) | N | H | N | N | N | N |
| VMa(3) | H | N | H | L | N | N |
| VMa(4) | L | N | N | N | N | N |
| VMa(5) | N | N | L | N | N | N |
| VMa(6) | N | H | L | N | N | N |
| VMa(7) | H | N | N | N | L | H |
| VMa(8) | N | N | N | N | L | H |
| VMa(9) | N | L | N | N | N | N |
| VMa(10) | N | N | H | N | N | N |
| CON | F-1 | F-2 | F-6 | NC(F-7) | At-1 | At-2 | At-3 | NC(At-4) | TA (%) | |
| CON | 960 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| F-1 | 0 | 925 | 23 | 0 | 12 | 0 | 0 | 0 | 0 | 96.35 |
| F-2 | 0 | 0 | 960 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| F-6 | 3 | 9 | 0 | 918 | 5 | 25 | 0 | 0 | 0 | 95.63 |
| NC(F-7) | 3 | 18 | 10 | 0 | 922 | 0 | 0 | 7 | 0 | 96.06 |
| At-1 | 0 | 8 | 0 | 16 | 0 | 936 | 0 | 0 | 0 | 97.50 |
| At-2 | 0 | 0 | 0 | 0 | 0 | 0 | 940 | 0 | 20 | 97.92 |
| At-3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 960 | 0 | 100 |
| NC(At-4) | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 0 | 945 | 98.44 |
| AVE | 97.99 |
| FCM | ||||||||||
| CON | F-1 | F-2 | F-6 | F-7 | At-1 | At-2 | At-3 | At-4 | TA(%) | |
| CON | 800 | 0 | 0 | 90 | 70 | 0 | 0 | 0 | 0 | 83.33 |
| F-1 | 0 | 758 | 120 | 0 | 82 | 0 | 0 | 0 | 0 | 78.96 |
| F-2 | 0 | 90 | 803 | 0 | 67 | 0 | 0 | 0 | 0 | 83.65 |
| F-6 | 41 | 45 | 0 | 727 | 57 | 90 | 0 | 0 | 0 | 75.73 |
| F-7 | 22 | 77 | 51 | 0 | 761 | 0 | 0 | 49 | 0 | 79.27 |
| At-1 | 0 | 94 | 0 | 116 | 0 | 750 | 0 | 0 | 0 | 78.13 |
| At-2 | 0 | 0 | 0 | 0 | 0 | 0 | 764 | 0 | 196 | 79.58 |
| At-3 | 38 | 52 | 0 | 0 | 90 | 0 | 0 | 780 | 0 | 81.25 |
| At-4 | 0 | 0 | 0 | 0 | 0 | 0 | 172 | 0 | 788 | 82.08 |
| AVE | 80.22 | |||||||||
| T2FCM | ||||||||||
| CON | F-1 | F-2 | F-6 | F-7 | At-1 | At-2 | At-3 | At-4 | TA (%) | |
| CON | 825 | 0 | 0 | 78 | 57 | 0 | 0 | 0 | 0 | 85.94 |
| F-1 | 0 | 782 | 103 | 0 | 75 | 0 | 0 | 0 | 0 | 81.46 |
| F-2 | 0 | 82 | 828 | 0 | 50 | 0 | 0 | 0 | 0 | 86.25 |
| F-6 | 34 | 39 | 0 | 765 | 42 | 80 | 0 | 0 | 0 | 79.69 |
| F-7 | 20 | 75 | 50 | 0 | 770 | 0 | 0 | 45 | 0 | 80.21 |
| At-1 | 0 | 83 | 0 | 100 | 0 | 777 | 0 | 0 | 0 | 80.94 |
| At-2 | 0 | 0 | 0 | 0 | 0 | 0 | 790 | 0 | 170 | 82.29 |
| At-3 | 35 | 45 | 0 | 0 | 76 | 0 | 0 | 804 | 0 | 83.75 |
| At-4 | 0 | 0 | 0 | 0 | 0 | 0 | 150 | 0 | 810 | 84.38 |
| AVE | 82.77 | |||||||||
| IT2FCM | ||||||||||
| CON | F-1 | F-2 | F-6 | F-7 | At-1 | At-2 | At-3 | At-4 | TA (%) | |
| CON | 838 | 0 | 0 | 70 | 52 | 0 | 0 | 0 | 0 | 87.29 |
| F-1 | 0 | 800 | 92 | 0 | 68 | 0 | 0 | 0 | 0 | 83.33 |
| F-2 | 0 | 75 | 840 | 0 | 45 | 0 | 0 | 0 | 0 | 87.50 |
| F-6 | 30 | 35 | 0 | 780 | 40 | 75 | 0 | 0 | 0 | 81.25 |
| F-7 | 17 | 68 | 45 | 0 | 788 | 0 | 0 | 42 | 0 | 82.08 |
| At-1 | 0 | 73 | 0 | 97 | 0 | 790 | 0 | 0 | 0 | 82.29 |
| At-2 | 0 | 0 | 0 | 0 | 0 | 0 | 805 | 0 | 155 | 83.85 |
| At-3 | 32 | 40 | 0 | 0 | 68 | 0 | 0 | 820 | 0 | 85.42 |
| At-4 | 0 | 0 | 0 | 0 | 0 | 0 | 136 | 0 | 824 | 85.83 |
| AVE | 84.32 | |||||||||
| KFCM | ||||||||||
| CON | F-1 | F-2 | F-6 | F-7 | At-1 | At-2 | At-3 | At-4 | TA(%) | |
| CON | 940 | 0 | 0 | 12 | 8 | 0 | 0 | 0 | 0 | 97.92 |
| F-1 | 0 | 880 | 50 | 0 | 30 | 0 | 0 | 0 | 0 | 91.67 |
| F-2 | 0 | 15 | 935 | 0 | 10 | 0 | 0 | 0 | 0 | 97.40 |
| F-6 | 10 | 16 | 0 | 850 | 34 | 50 | 0 | 0 | 0 | 88.54 |
| F-7 | 14 | 40 | 26 | 0 | 855 | 0 | 0 | 25 | 0 | 89.06 |
| At-1 | 0 | 30 | 0 | 40 | 0 | 890 | 0 | 0 | 0 | 92.71 |
| At-2 | 0 | 0 | 0 | 0 | 0 | 0 | 900 | 0 | 60 | 93.75 |
| At-3 | 10 | 15 | 0 | 0 | 25 | 0 | 0 | 910 | 0 | 94.79 |
| At-4 | 0 | 0 | 0 | 0 | 0 | 0 | 90 | 0 | 870 | 90.63 |
| AVE | 92.94 | |||||||||
| KT2FCM | ||||||||||
| CON | F-1 | F-2 | F-6 | F-7 | At-1 | At-2 | At-3 | At-4 | TA(%) | |
| CON | 960 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| F-1 | 0 | 910 | 30 | 0 | 20 | 0 | 0 | 0 | 0 | 94.79 |
| F-2 | 0 | 0 | 960 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| F-6 | 5 | 13 | 0 | 900 | 10 | 32 | 0 | 0 | 0 | 93.75 |
| F-7 | 4 | 24 | 12 | 0 | 910 | 0 | 0 | 10 | 0 | 94.79 |
| At-1 | 0 | 17 | 0 | 23 | 0 | 920 | 0 | 0 | 0 | 95.83 |
| At-2 | 0 | 0 | 0 | 0 | 0 | 0 | 925 | 0 | 35 | 96.35 |
| At-3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 960 | 0 | 100 |
| At-4 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 0 | 930 | 96.88 |
| AVE | 96.93 | |||||||||
| KIT2FCM | ||||||||||
| CON | F-1 | F-2 | F-6 | F-7 | At-1 | At-2 | At-3 | At-4 | TA(%) | |
| CON | 960 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| F-1 | 0 | 925 | 23 | 0 | 12 | 0 | 0 | 0 | 0 | 96.35 |
| F-2 | 0 | 0 | 960 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| F-6 | 3 | 9 | 0 | 918 | 5 | 25 | 0 | 0 | 0 | 95.63 |
| F-7 | 3 | 18 | 10 | 0 | 922 | 0 | 0 | 7 | 0 | 96.04 |
| At-1 | 0 | 8 | 0 | 16 | 0 | 936 | 0 | 0 | 0 | 97.50 |
| At-2 | 0 | 0 | 0 | 0 | 0 | 0 | 940 | 0 | 20 | 97.92 |
| At-3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 960 | 0 | 100 |
| At-4 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 0 | 945 | 98.44 |
| AVE | 97.99 | |||||||||
| O vs. P | O vs. Q | O vs. R | O vs. S | O vs. W | P vs. Q | P vs. R | P vs. S | P vs. W | Q vs. R | Q vs. S | Q vs. W | R vs. S | R vs. W | S vs. W | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | |
| 55 | 55 | 55 | 55 | 55 | 50 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 55 | 50 | |
| T | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | |
| Winner | 2 | 3 | 4 | 5 | 6 | 3 | 4 | 5 | 6 | 4 | 5 | 6 | 5 | 6 | 6 |
| Algorithm | Number of Wins | Rank |
|---|---|---|
| O | 0 | 6 |
| P | 1 | 5 |
| Q | 2 | 4 |
| R | 3 | 3 |
| S | 4 | 2 |
| W | 5 | 1 |
| Fault | Process Variable | Type |
|---|---|---|
| Fault 3 (F-3) | D feed temperature (stream 2) Reactor cooling water inlet | step |
| Fault 9 (F-9) | D feed temperature (stream 2) | random |
| Fault 15 (F-15) | Condenser cooling water valve | sticking |
| CON | F-3 | F-9 | F-15 | TA (%) | |
| CON | 915 | 13 | 11 | 21 | 95.31 |
| F-3 | 39 | 891 | 20 | 10 | 92.81 |
| F-9 | 50 | 31 | 854 | 25 | 88.96 |
| F-15 | 74 | 32 | 35 | 819 | 85.31 |
| AVE | 90.60 |
| Fault | DBN(%) | DCNN(%) | BiGRU(%) | PTCN(%) | KIT2FCM (%) |
|---|---|---|---|---|---|
| F-3 | 95.00 | 91.70 | 93.50 | 88.04 | 92.81 |
| F-9 | 57.00 | 58.40 | 80.70 | 66.01 | 88.96 |
| F-15 | 0.00 | 28.00 | 54.10 | 0.35 | 85.31 |
| AVE | 50.66 | 59.36 | 76.10 | 51.46 | 89.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez Ramos, A.; Rivera Torres, P.J.; Llanes-Santiago, O. A Computational Intelligence-Based Proposal for Cybersecurity and Health Management with Continuous Learning in Chemical Processes. Actuators 2025, 14, 329. https://doi.org/10.3390/act14070329
Rodríguez Ramos A, Rivera Torres PJ, Llanes-Santiago O. A Computational Intelligence-Based Proposal for Cybersecurity and Health Management with Continuous Learning in Chemical Processes. Actuators. 2025; 14(7):329. https://doi.org/10.3390/act14070329
Chicago/Turabian StyleRodríguez Ramos, Adrián, Pedro Juan Rivera Torres, and Orestes Llanes-Santiago. 2025. "A Computational Intelligence-Based Proposal for Cybersecurity and Health Management with Continuous Learning in Chemical Processes" Actuators 14, no. 7: 329. https://doi.org/10.3390/act14070329
APA StyleRodríguez Ramos, A., Rivera Torres, P. J., & Llanes-Santiago, O. (2025). A Computational Intelligence-Based Proposal for Cybersecurity and Health Management with Continuous Learning in Chemical Processes. Actuators, 14(7), 329. https://doi.org/10.3390/act14070329






