Adaptive Linear Active Disturbance Rejection Cooperative Control of Multi-Point Hybrid Suspension System
Abstract
1. Introduction
- (1)
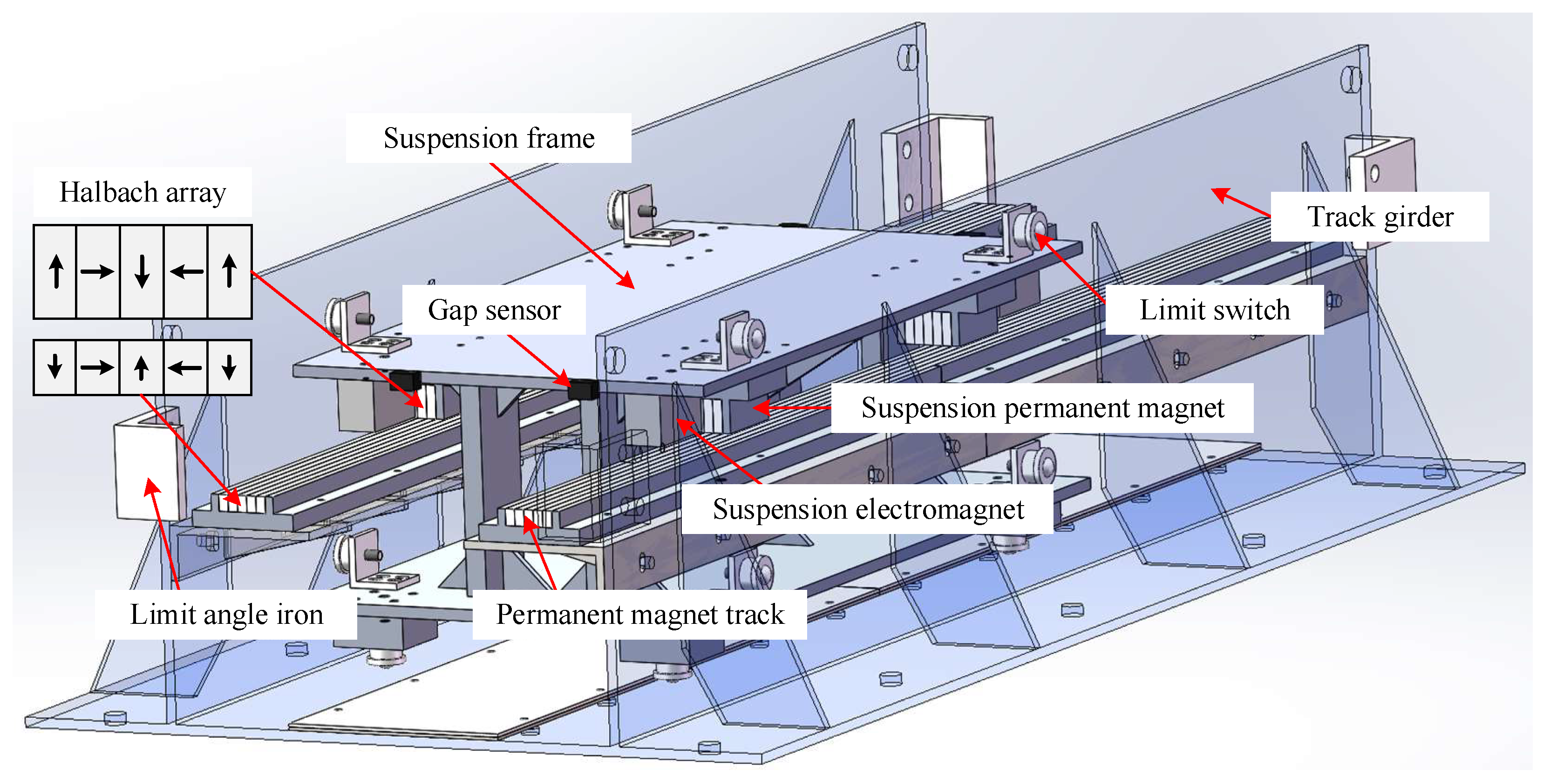
- The structure and working principle of the hybrid suspension system are analyzed, the single-point and multi-point hybrid suspension system models are established, respectively, and the coupling relationship between multiple suspension points is deduced.
- (2)
- Aiming at the uncertainties caused by the permanent magnet–electromagnetic combination, such as the enhancement in system nonlinearity and the increase in magnetic field coupling, ALESO is designed to simultaneously improve the dynamic response performance and noise rejection of the hybrid suspension system.
- (3)
- Aiming at the lack of synchronization coordination mechanism in independent control mode, the CCC is designed and integrated into the linear error feedback control law of the ALADRC algorithm to realize the cross-coupling of the suspension gap and its rate of change to enhance the synchronous coordination of the multi-point suspension system.
- (4)
- A multi-point permanent magnet electromagnetic hybrid suspension experimental platform is built to carry out single-point suspension, unilateral suspension, and four-point suspension experiments to verify the effectiveness of the control algorithm designed in this paper.
2. Multi-Point Hybrid Suspension System Modeling
2.1. Structure and Principle Analysis of Hybrid Suspension System
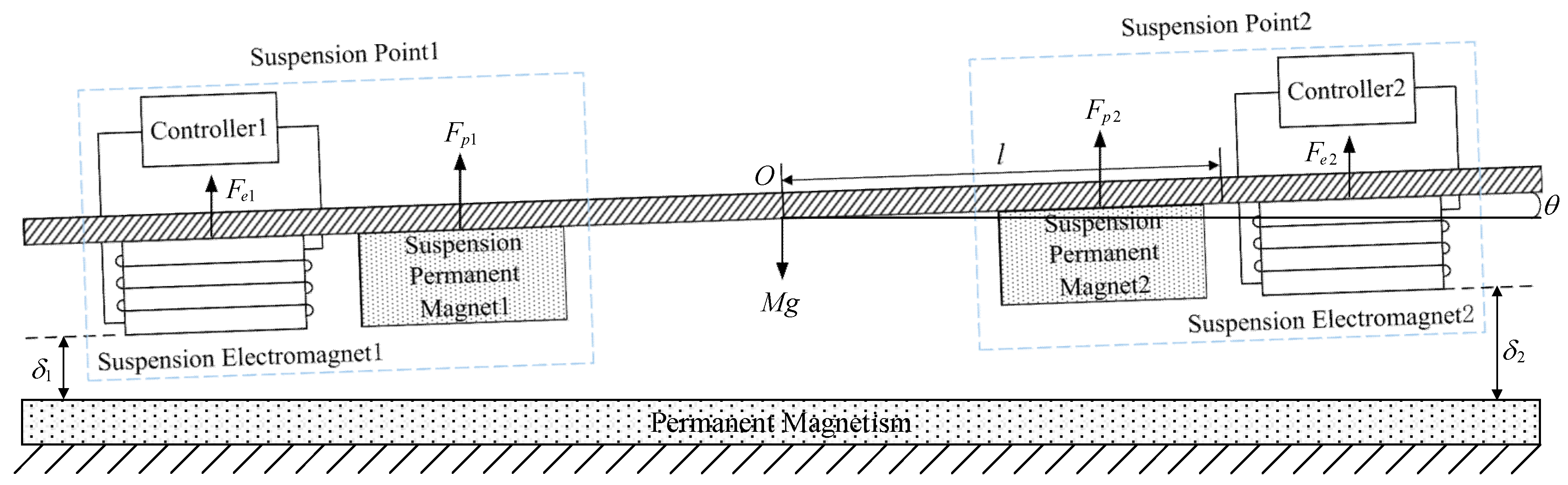
2.2. Single-Point Hybrid Suspension System Model
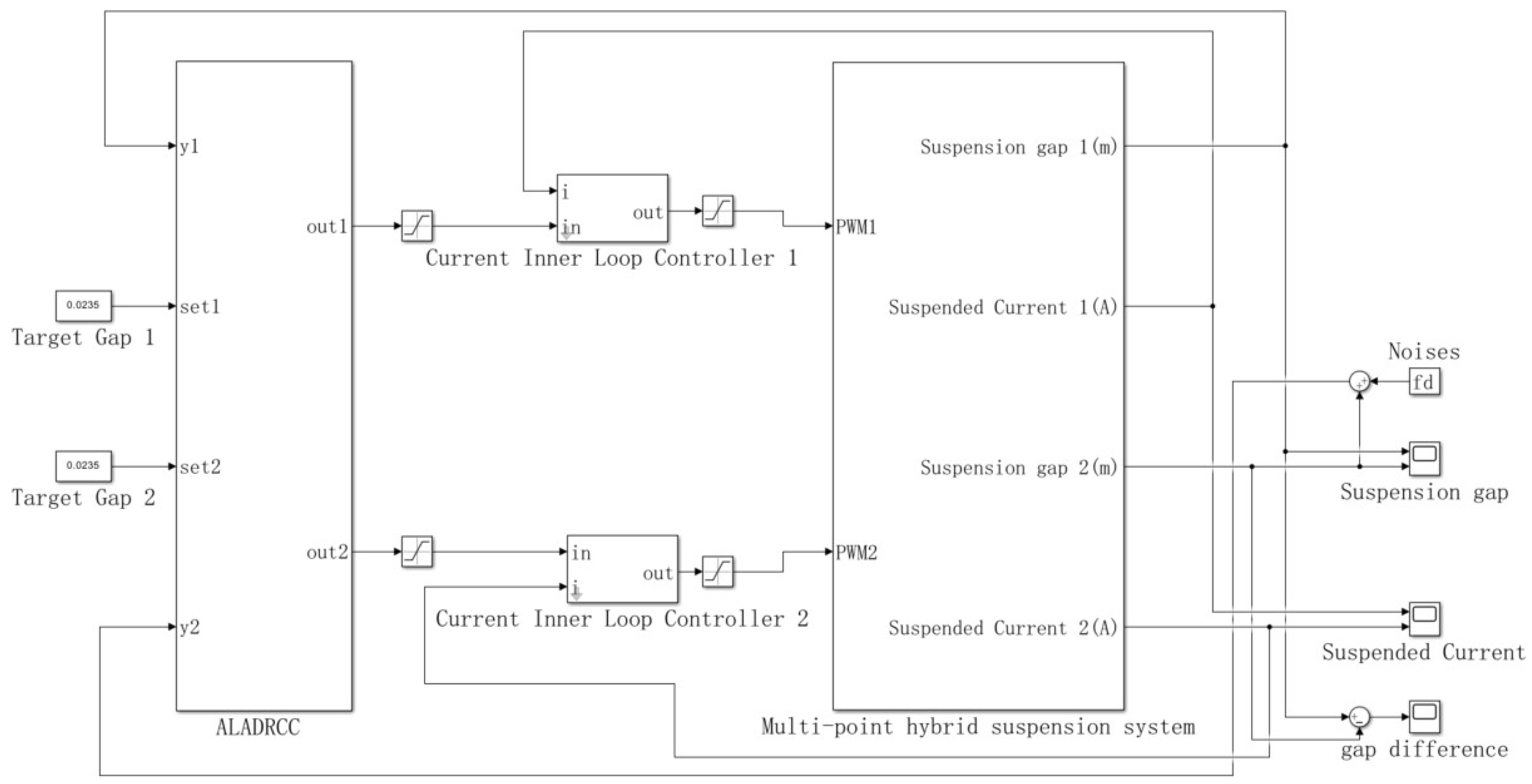
2.3. Multi-Point Hybrid Suspension System Model
- (1)
- The mass of the unilateral suspension frame is uniformly distributed throughout its structure, and the center of gravity coincides with its geometric center;
- (2)
- There is no coupling between the permanent magnetic field and the electromagnetic field;
- (3)
- The suspension is rigid and undeformed, and the effect of transverse force is neglected;
- (4)
- Neglect of remanent magnetism, remanent magnetization, magnetic saturation phenomena, and no magnetic leakage.
3. Controller Design
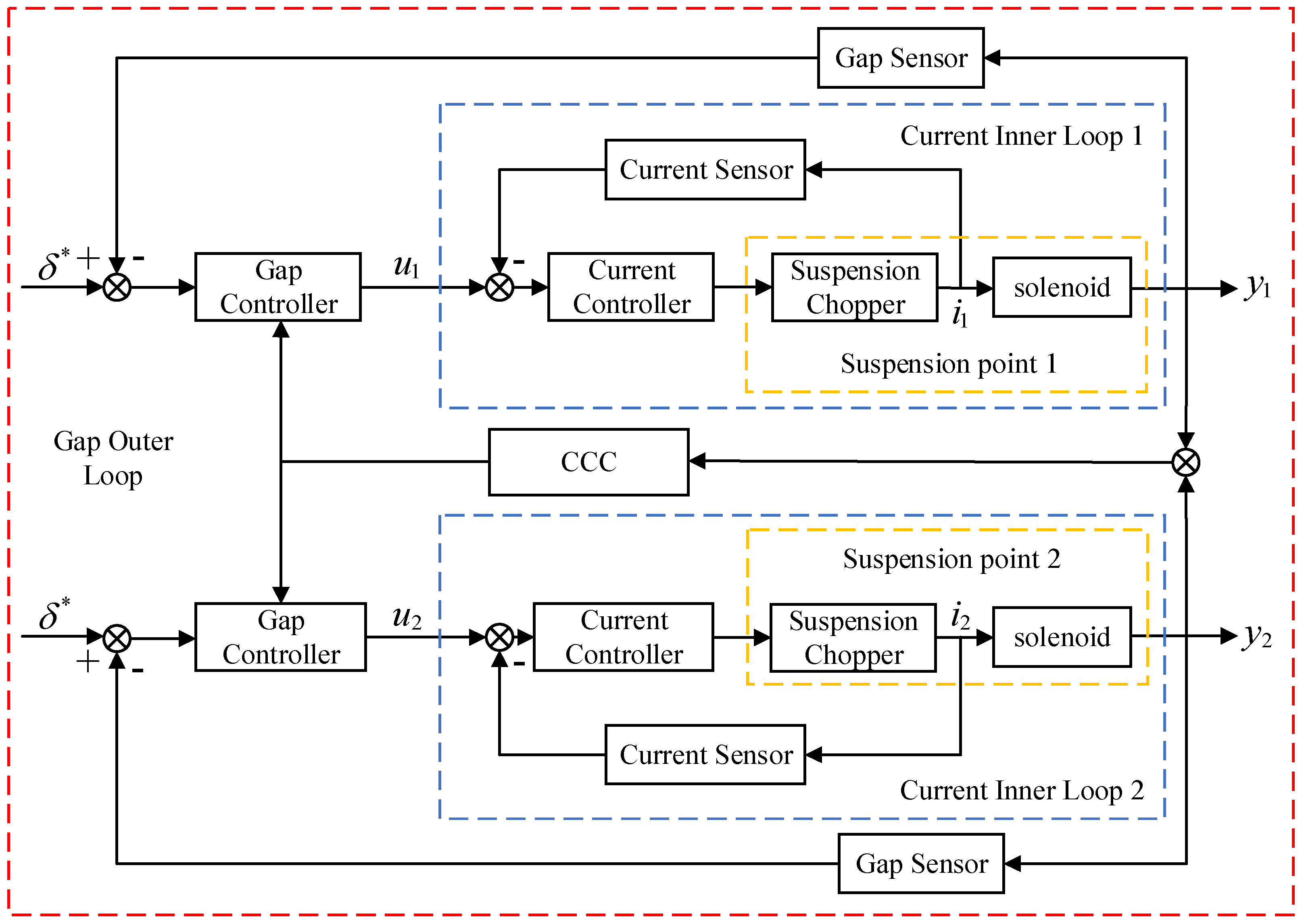
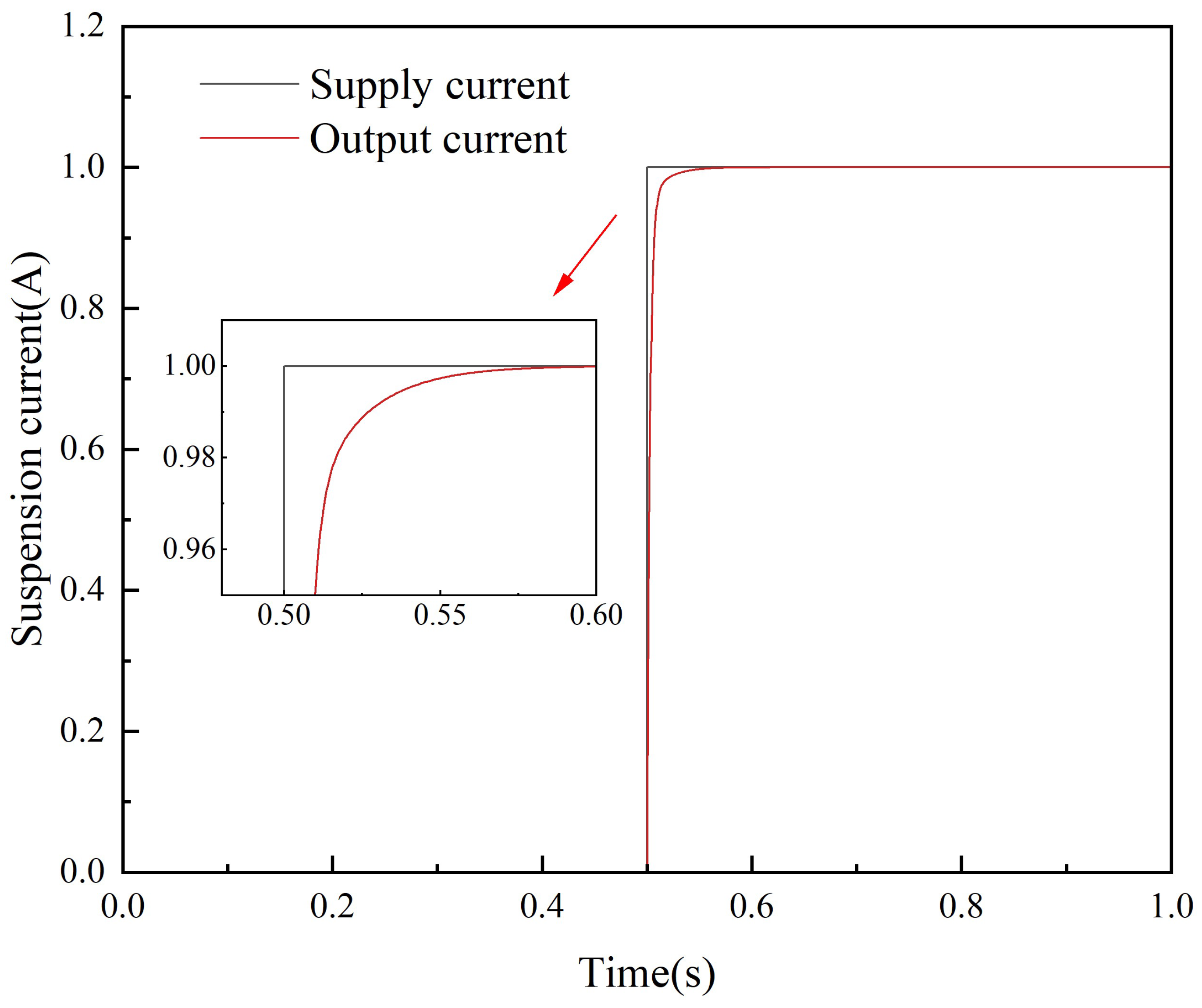
3.1. Current Inner Loop PI Controller Design
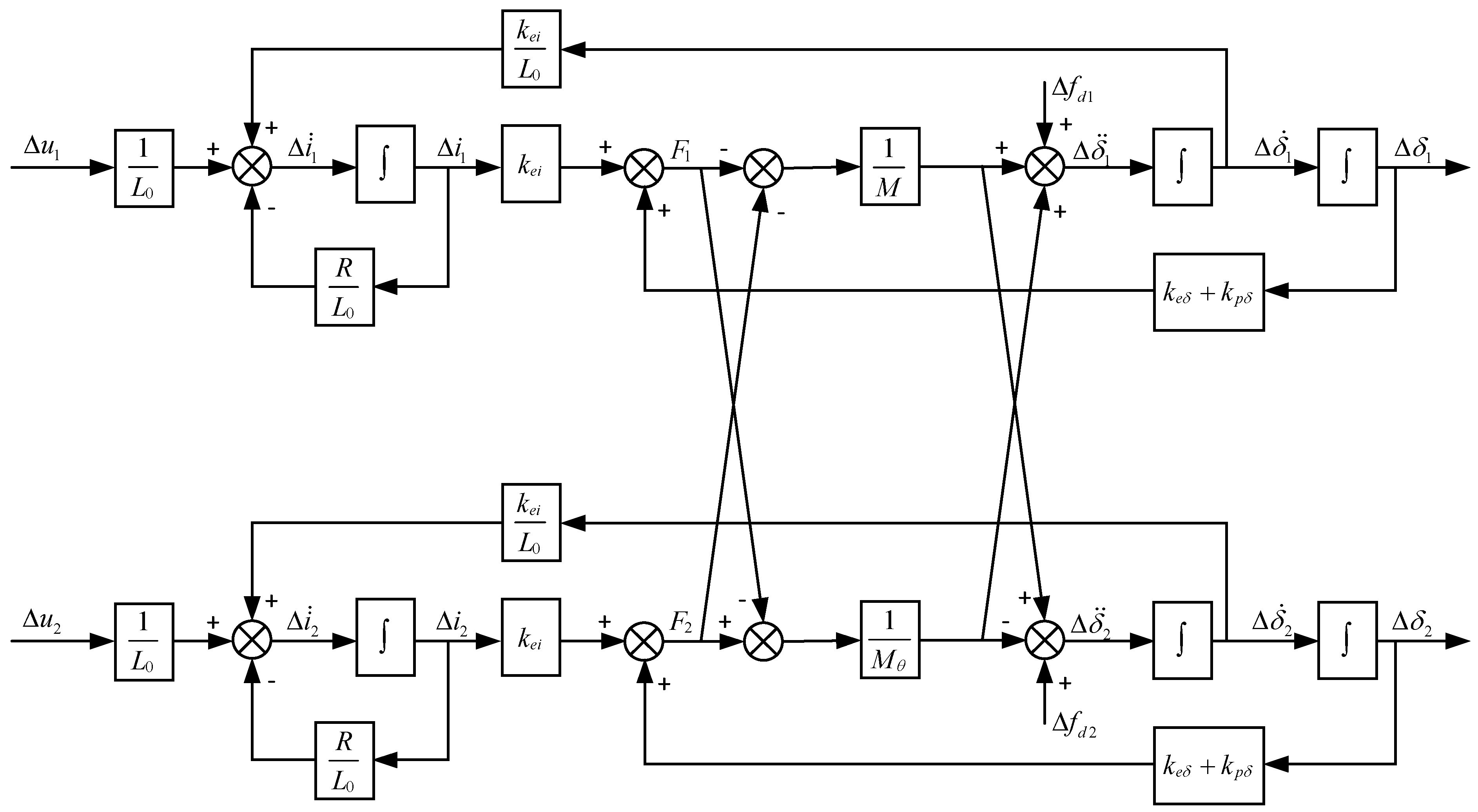
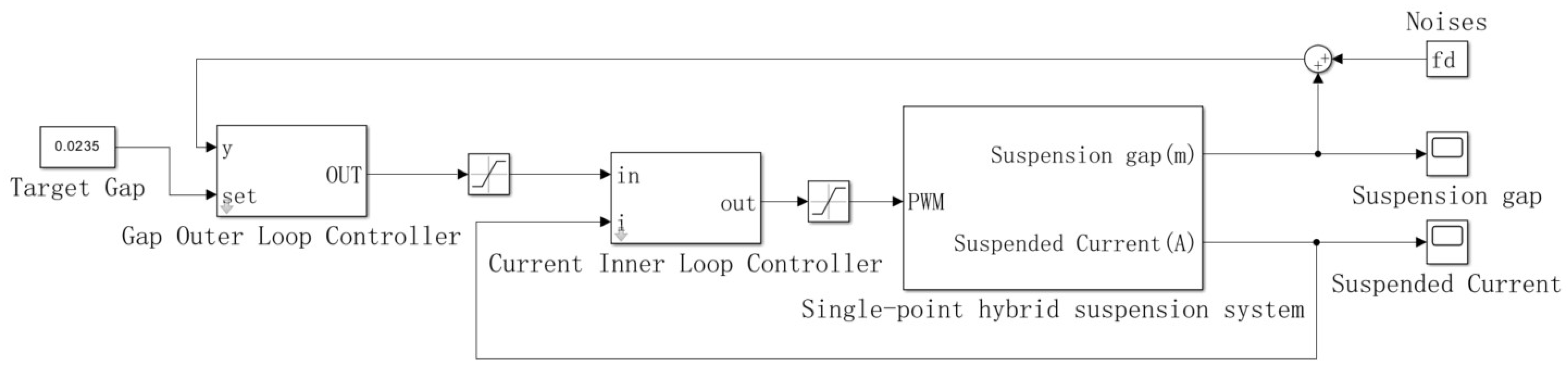
3.2. Gap Outer Loop ALADRCC Controller Design
3.3. Parameter Calibration
- (1)
- According to the simulation in Section 3.1, it can be seen that , which can satisfy the current tracking performance requirements of the suspension system.
- (2)
- The sampling period is set to 0.5 ms, then the sampling step size s; increase can enhance the filtering effect, increase when the noise is large, and decrease when the response is slow, with a typical range of 0.1~2.0; increase can speed up the tracking speed, but too large will cause oscillations, according to the set value of the change in the frequency of the adjustment, with a typical range of 50~300.
- (3)
- An increase in the value of improves the system response, but too much of it would introduce the effect of high-frequency noise. The value of should ensure that the system has good dynamic performance and fast responses when disturbed to be selected according to the actual system; should ensure that the system has good steady-state performance and that the suspension gap fluctuations and current ripple are small when the system is stabilized, ensuring low noise sensitivity, to be selected according to the actual system; For , the larger the bandwidth, the faster the response speed; this paper uses the simulation and experimental selection of = 2.
- (4)
- is the controller bandwidth. According to the relationship between the response of the closed-loop system and the performance index, the regulation formula of can be expressed as follows: , where is the system rise time. In the case of incomplete model information, is usually set as a large initial value, then and are adjusted to make the system stable. Then, the value of is gradually reduced to optimize the system’s immunity to disturbances and the dynamic response performance. are the system cross-coupling coefficients, the corresponding value of zero indicates independent control of multiple points; the larger the corresponding value is, the more synergistic it is, but the value is too large to cause system oscillations. For the cross-coupling coefficients of the system, the larger the corresponding value, the stronger the synergy, but values that are too large will cause system oscillation. Rectification time should be gradually increased under the premise of ensuring the stability of the system.
4. Simulation Analysis
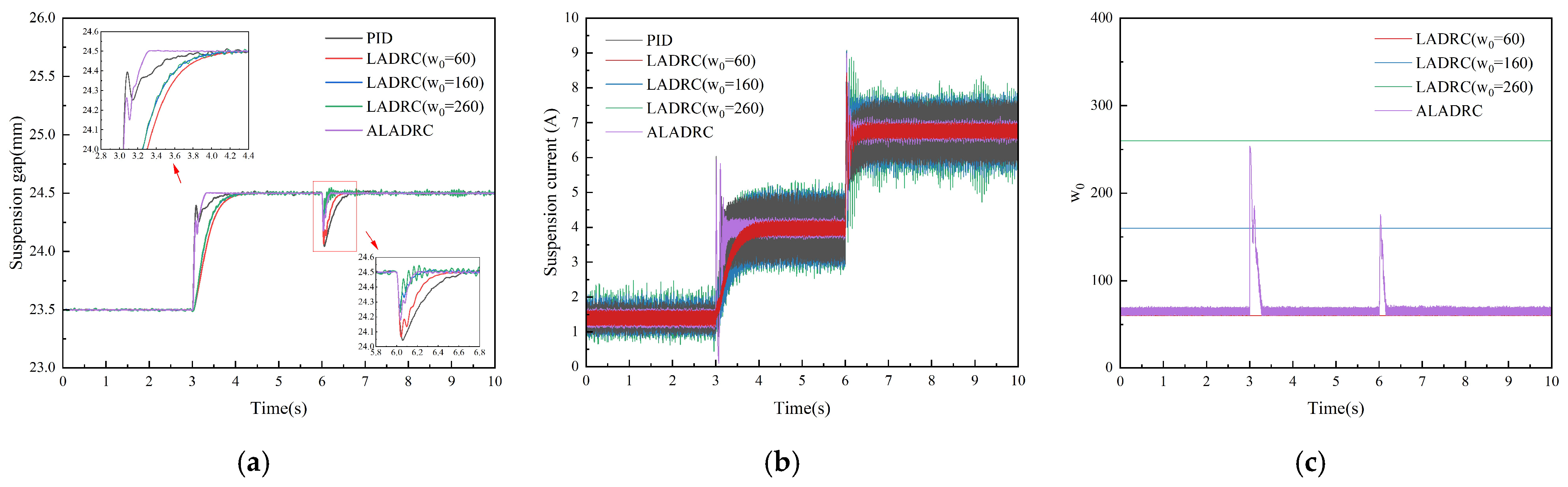
4.1. Single-Point Suspension Immunity Simulation Experiment
4.2. Multi-Point Suspension Synergy Simulation Experiment
5. Results
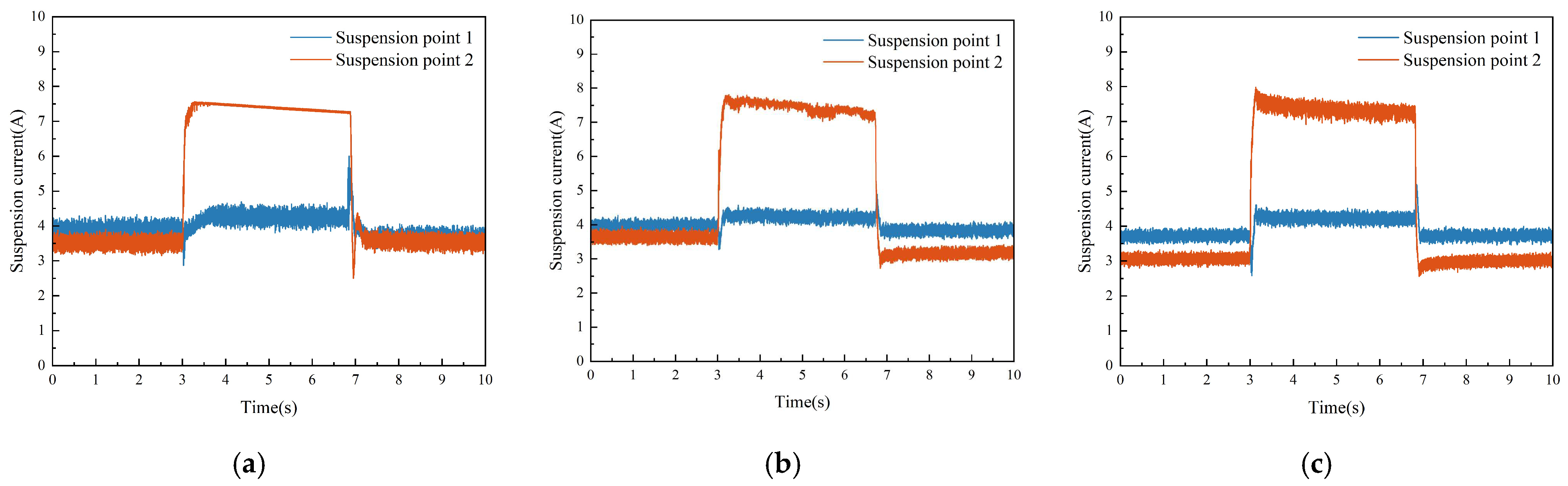
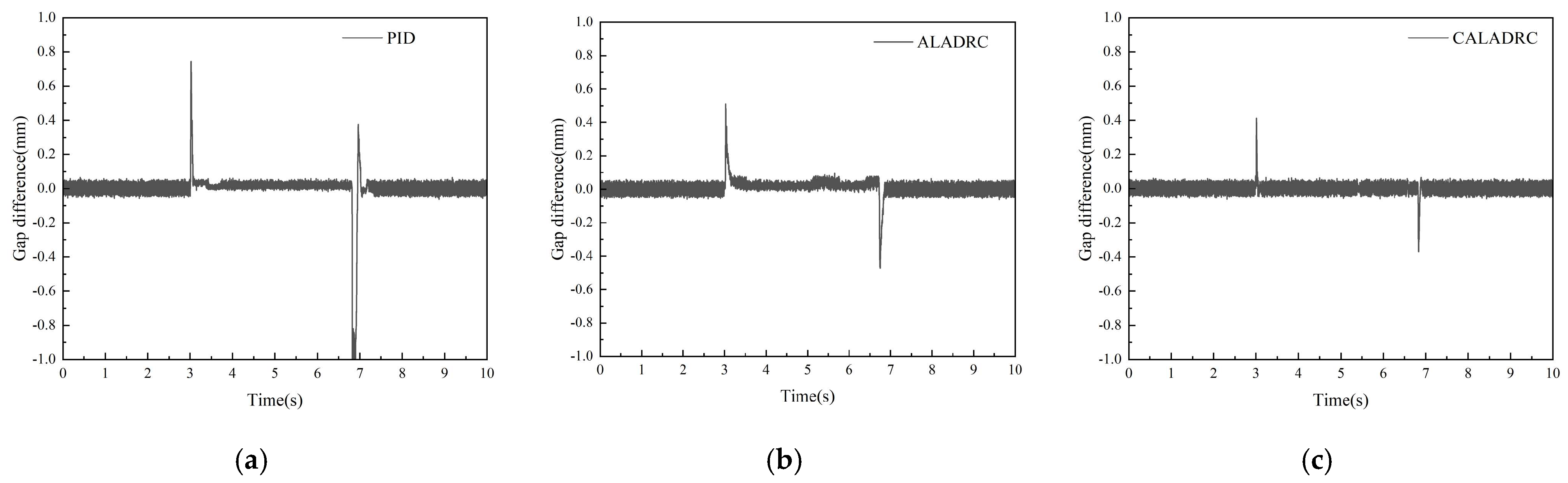
5.1. Single-Point Suspension Immunity Experiment
5.2. Unilateral Suspension Immunity Experiment
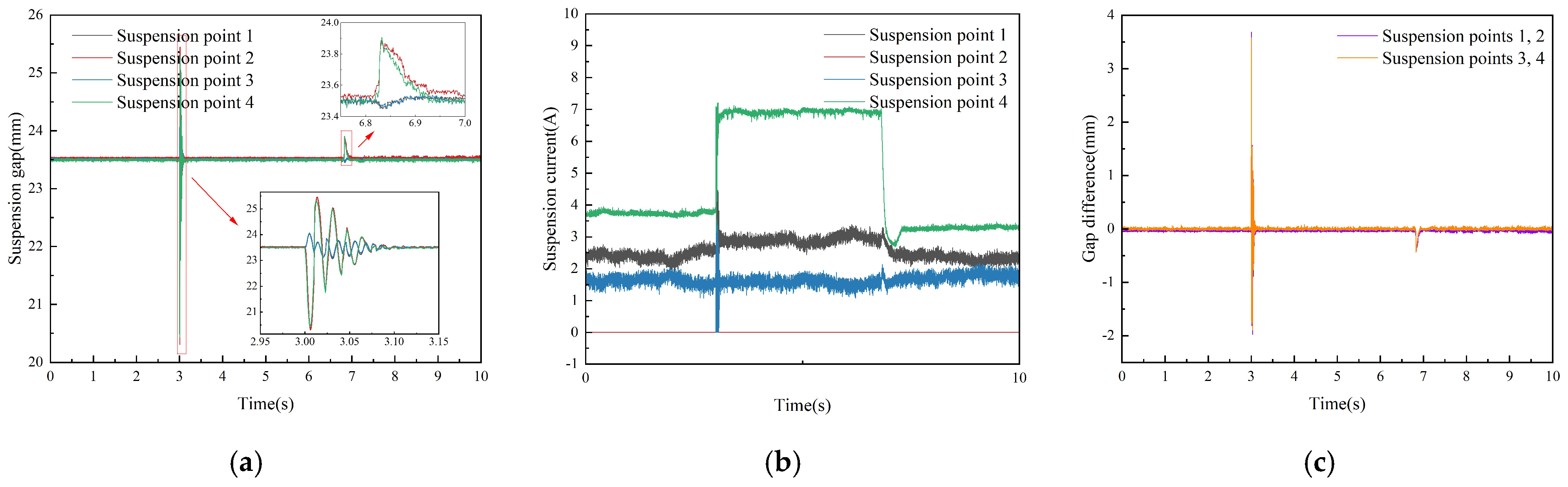
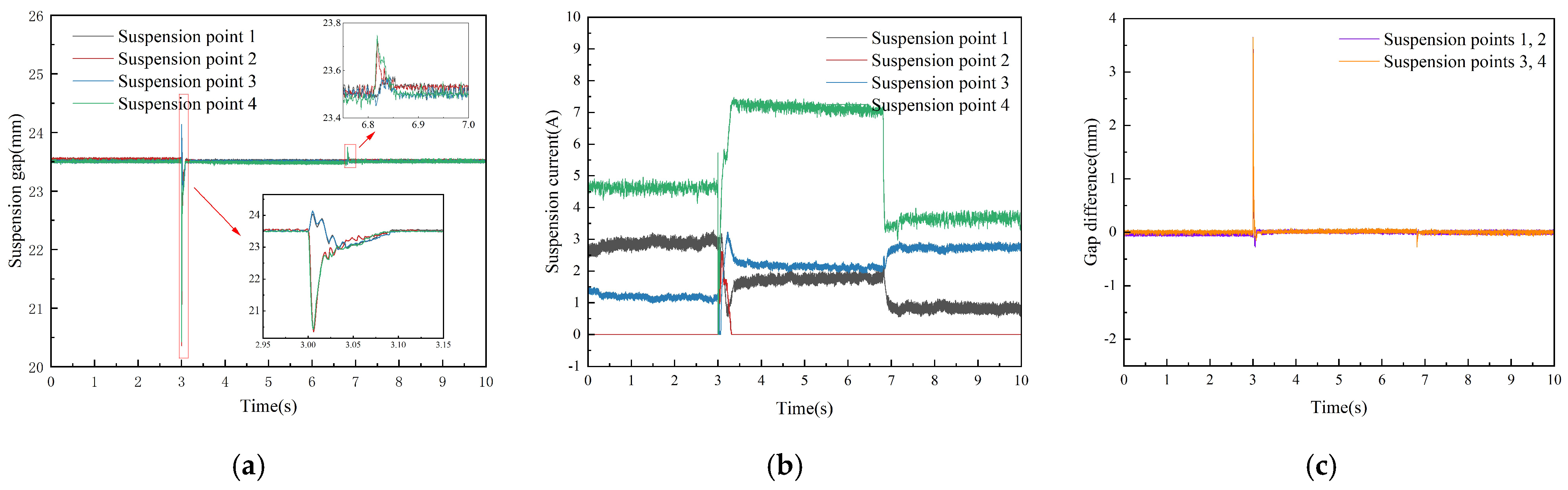
5.3. Four-Point Suspension Immunity Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, W.B.; Xiao, L.Y.; Wang, S.; Zhang, J.Y. Summary of Research on Levitation-guidance Modes in Maglev Rail Transportation Technology. Adv. Technol. Electr. Eng. Energy 2022, 41, 45–60. [Google Scholar]
- Gao, T.; Yang, J.; Zhou, F.Z.; Cao, Z.H. Design and Analysis of a Permanent Magnet Electromagnetic Hybrid Levitation Control Experiment Based on COMSOL. Exp. Technol. Manag. 2024, 41, 165–174. [Google Scholar]
- Wang, Y.G.; Yang, J.; Cui, Y.M. Characteristic Analysis of Permanent Magnet Electromagnetic Hybrid Suspension Guidance System for Maglev Train. Electr. Driv. Locomot. 2021, 6, 1–8. [Google Scholar]
- Liang, Z.H.; Wu, H.B.; Yang, X.; Li, Q.J. Application of Fuzzy-PID Control Algorithm to Hybrid Maglev System. J. Shenyang Polytech. Univ. 2008, 1, 32–37. [Google Scholar]
- Yang, J.; Qin, Y.; Wang, Y.Z.; Zhang, Z.L. Improved Sliding Mode Control Method for Permanent Magnet Electromagnetic Hybrid Magnetic Levitation Ball. J. Hunan Univ. Nat. Sci. 2023, 50, 200–209. [Google Scholar]
- Hu, W.J.; Zhou, Y.H.; Zhang, Z.L.; Fujita, H. Model Predictive Control for Hybrid Levitation Systems of Maglev Trains With State Constraints. IEEE Trans. Veh. Technol. 2021, 70, 9972–9985. [Google Scholar] [CrossRef]
- Han, W.J.; Tan, W. Tuning of Linear Active Disturbance Rejection Controllers Based on PID Tuning Rules. Control. Decis. 2021, 36, 1592–1600. [Google Scholar]
- Song, X.J.; Li, L.Q.; Xue, W.C.; Song, K.; Xin, B. Active Disturbance Rejection Decoupling Control for Nonlinear MIMO Uncertain Systems with Application to Path Following of Self-driving Bus. Control Eng. Pract. 2023, 133, 105432. [Google Scholar] [CrossRef]
- Wang, J.S.; Jiang, Q.L.; Luo, Y.; Liu, T.F. Active Disturbance Rejection Generalized Predictive Control for Magnetic Levitation System. J. Harbin Inst. Technol. 2022, 54, 141–150. [Google Scholar]
- Qin, Y.; Yang, J.; Guo, H.Q.; Wang, Y.Z. Fuzzy Linear Active Disturbance Rejection Control Method for Permanent Magnet Electromagnetic Hybrid Suspension Platform. Appl. Sci. 2023, 13, 2631. [Google Scholar] [CrossRef]
- Liu, Z.T.; Lin, W.Y.; Yu, X.H.; Rodríguez-Andina, J.J.; Gao, H.J. Approximation-Free Robust Synchronization Control for Dual-Linear-Motors-Driven Systems With Uncertainties and Disturbances. IEEE Trans. Ind. Electron. 2022, 69, 10500–10509. [Google Scholar] [CrossRef]
- Hu, N.T.; Chen, L.Y.; Chen, C.S. Novel Cross-Coupling Position Command Shaping Controller Using H∞ in Multiaxis Motion Systems. IEEE Trans. Ind. Electron. 2022, 69, 13099–13110. [Google Scholar] [CrossRef]
- Shang, W.W.; Xie, F.; Zhang, B.; Cong, S.; Li, Z.J. Adaptive Cross-Coupled Control of Cable-Driven Parallel Robots With Model Uncertainties. IEEE Robot. Autom. Lett. 2020, 5, 4110–4117. [Google Scholar] [CrossRef]
- Ling, J.H.; Lu, Y.B.; Pi, D.Y.; Yin, J.D.; Zhang, W.C.; Wang, F.A.; Feng, J.W.; Zhou, C.B. A Decentralized Cooperative Control Framework for Active Steering and Active Suspension: Multi-Agent Approach. IEEE Trans. Transp. Electrif. 2022, 8, 1414–1429. [Google Scholar] [CrossRef]
- Feng, J.W.; Liang, J.H.; Lu, Y.B.; Zhang, W.C.; Pi, D.W.; Yin, G.D.; Xu, L.W.; Peng, P.; Zhou, C.B. An Integrated Control Framework for Torque Vectoring and Active Suspension System. Chin. J. Mech. Eng. 2024, 37, 75–86. [Google Scholar] [CrossRef]
- Li, Q.N.; Xu, D.H. Gap Cross-coupling Control for 4-Electromagnet Supported Steel Plate Magnetic Suspension System. Proc. CSEE 2010, 30, 129–134. [Google Scholar]
- Xu, J.Q.; Lin, G.B.; Chen, C.; Rong, L.J.; Ji, W. Modeling and Control of Multi-point Levitation of Maglev Vehicle Under Loading Disturbance. J. Tongji Univ. Nat. Sci. 2020, 48, 1353–1363. [Google Scholar]
- Wang, M.Q.; Hao, Z.Y.; He, Y.X.; Zeng, S.H.; Qi, Z.; Liu, P.F. Active Disturbance Rejection Backstepping Cross-Coupling Controller Design for a Magnetic Levitation Vehicle Suspension Frame. IEEE Trans. Transp. Electrif. 2025, 11, 4634–4644. [Google Scholar] [CrossRef]
- Zhang, D.D.; Sun, Y.G.; Jia, N.; Sun, W. Adaptive Fuzzy Super-twisting Sliding Mode Control for the Multi-electromagnets Levitation System of Maglev Vehicles: Design and Experiments. IEEE Trans. Intell. Veh. 2024; early access. [Google Scholar]
- Huang, X.Y.; Kang, J.S.; Ding, H.; Xia, C.; Huang, D.X.; Wang, F.X. Adjacent Cross-Coupling Control for Magnetic Levitation System With Ultra-Local Sliding Mode Algorithm. IEEE Trans. Veh. Technol. 2025, 74, 2418–2428. [Google Scholar] [CrossRef]
- Zhao, C.; Sun, F.; Pei, W.Z.; Jin, J.J.; Xu, F.C.; Zhang, X.Y. Independent Cascade Control Method for Permanent Magnetic Levitation Platform. J. Southwest. Jiaotong Univ. 2022, 57, 618–626. [Google Scholar]





| Parameter | Value |
|---|---|
| 17.6 | |
| 35.2 | |
| 3 | |
| 0.4 | |
| 500 | |
| 2.4 | |
| 0.005 | |
| 23 | |
| 23.5 | |
| 9.8 |
| PID | LADRC | ALADRC |
|---|---|---|
| Performance | PID | LADRC ( = 60) | LADRC ( = 160) | LADRC ( = 260) | ALADRC | |
|---|---|---|---|---|---|---|
| (1) Step response | Regulation time | 861 ms | 1187 ms | 1014 ms | 1007 ms | 320 ms |
| Maximum fluctuation | 0.456 mm | 0.429 mm | 0.276 mm | 0.241 mm | 0.321 mm | |
| Steady-state current ripple | 1.997 A | 0.444 A | 2.273 A | 2.663 A | 0.557 A | |
| (2) Load perturbation | Regulation time | 616 ms | 450 ms | 225 ms | 122 ms | 179 ms |
| Maximum fluctuation | 0.456 mm | 0.429 mm | 0.276 mm | 0.241 mm | 0.321 mm | |
| Steady-state current ripple | 1.926 A | 0.525 A | 2.444 A | 3.041 A | 0.754 A | |
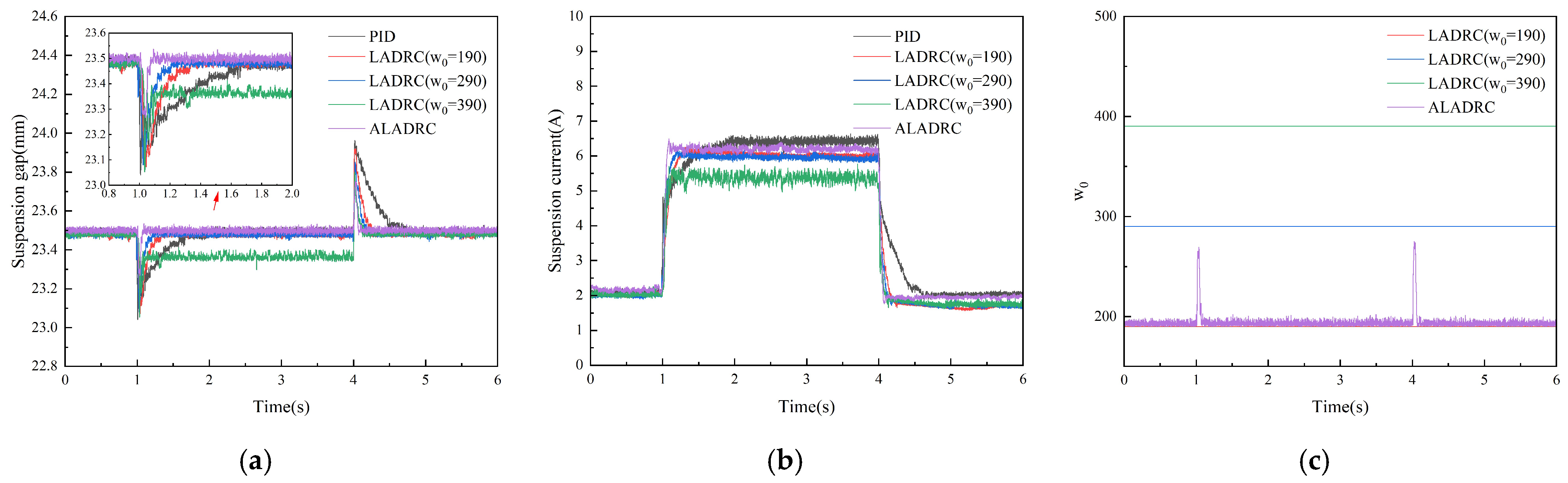
| PID | LADRC | ALADRC |
|---|---|---|
| Performance | PID | LADRC ( = 190) | LADRC ( = 290) | LADRC ( = 390) | ALADRC |
|---|---|---|---|---|---|
| Regulation time | 632 ms | 365 ms | 226 ms | - | 91 ms |
| Maximum fluctuation | 1.959 mm | 1.928 mm | 1.919 mm | 1.936 mm | 1.726 mm |
| Steady-state current ripple | 0.464 A | 0.151 A | 0.242 A | 0.486 A | 0.212 A |
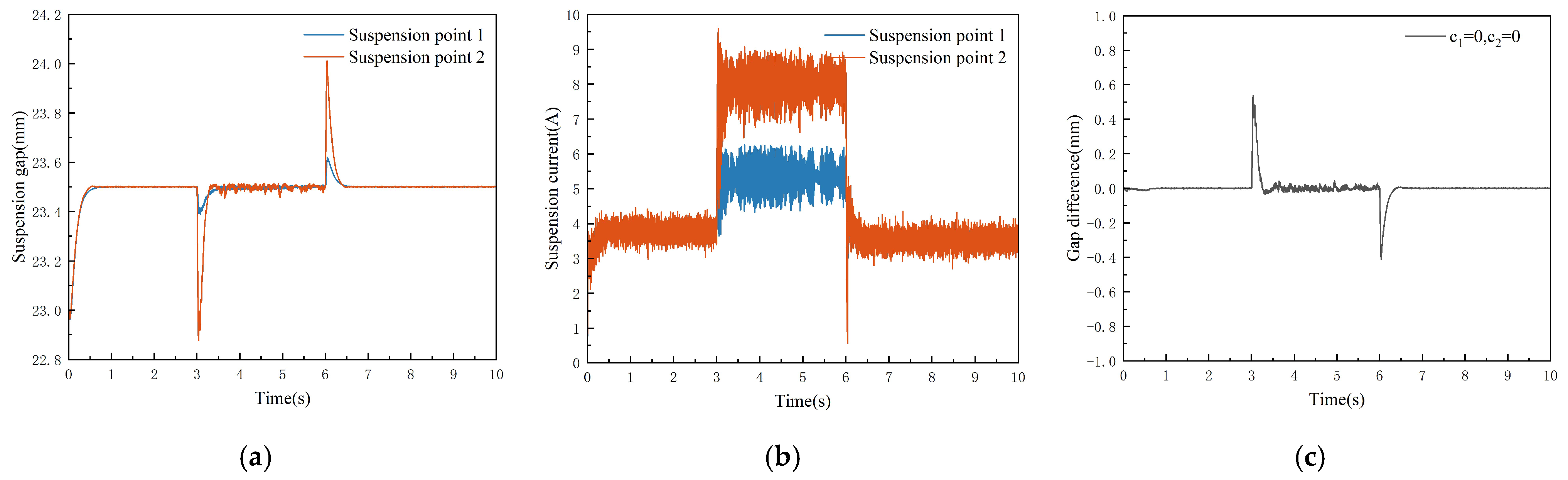
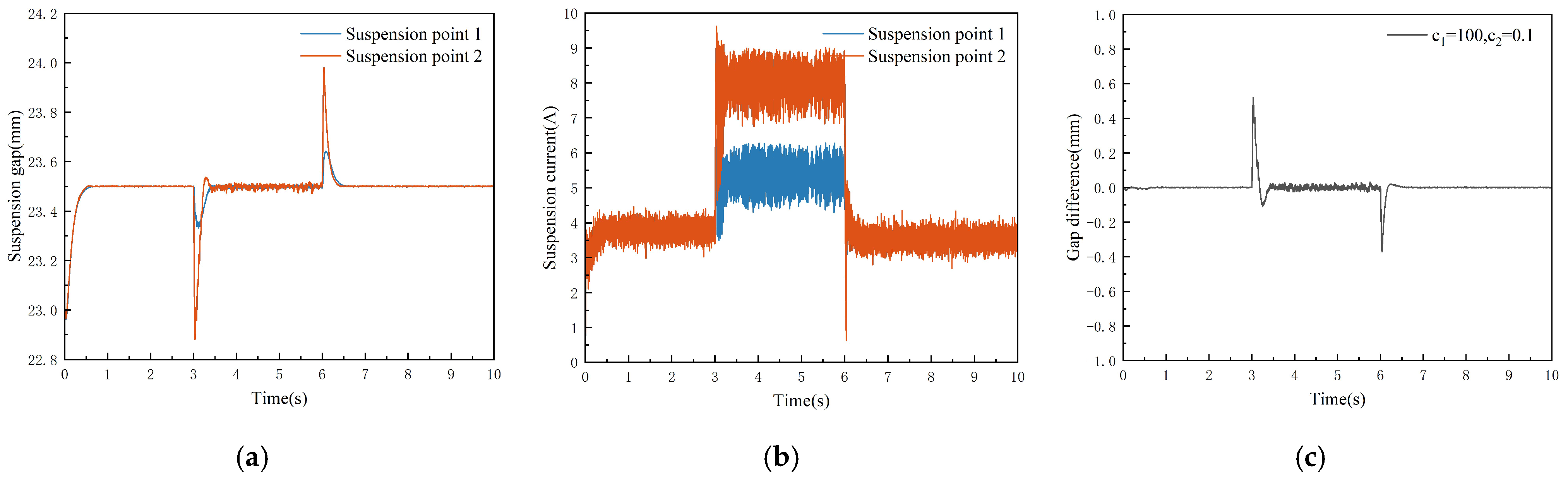
| Suspension Point | PID | ALADRC | ALADRCC |
|---|---|---|---|
| 1 | |||
| 2 |
| Performance | PID | ALADRC | ALADRCC |
|---|---|---|---|
| Regulation time | 157 ms | 175 ms | 126 ms |
| Maximum fluctuation | 0.829 mm | 0.547 mm | 0.442 mm |
| Steady-state error | 0.02 mm | 0.02 mm | 0 |
| Steady-state current ripple | 0.733 A | 0.513 A | 0.631 A |
| Maximum suspension gap difference | 0.744 mm | 0.511 mm | 0.413 mm |
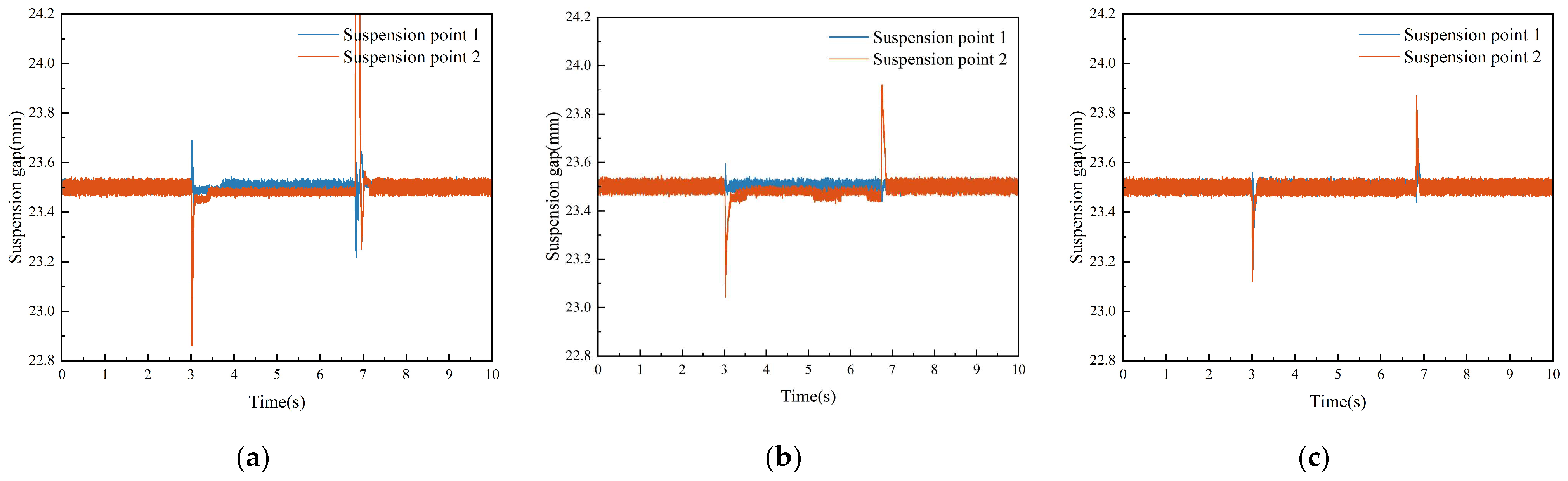
| Suspension Point | PID | ALADRCC |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
| Performance | PID | ALADRCC | |
|---|---|---|---|
| (1) Load shock | Regulation time | 92 ms | 89 ms |
| Maximum fluctuation | 5.144 mm | 3.781 mm | |
| Steady-state current ripple | 0.521 A | 0.384 A | |
| Maximum suspension gap difference between suspension point 1 and suspension point 2 | 3.682 mm | 3.653 mm | |
| Maximum suspension gap difference between suspension point 3 and suspension point 4 | 3.569 mm | 3.651 mm | |
| (2) Remove load | Regulation time | 114 ms | 53 ms |
| Maximum fluctuation | 0.437 mm | 0.276 mm | |
| Steady-state current ripple | 0.518 A | 0.373 A | |
| Maximum suspension gap difference between suspension point 1 and suspension point 2 | 0.397 mm | 0.204 mm | |
| Maximum suspension gap difference between suspension point 3 and suspension point 4 | 0.402 mm | 0.236 mm | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Yang, J.; Zhou, F. Adaptive Linear Active Disturbance Rejection Cooperative Control of Multi-Point Hybrid Suspension System. Actuators 2025, 14, 312. https://doi.org/10.3390/act14070312
Yang S, Yang J, Zhou F. Adaptive Linear Active Disturbance Rejection Cooperative Control of Multi-Point Hybrid Suspension System. Actuators. 2025; 14(7):312. https://doi.org/10.3390/act14070312
Chicago/Turabian StyleYang, Shuai, Jie Yang, and Fazhu Zhou. 2025. "Adaptive Linear Active Disturbance Rejection Cooperative Control of Multi-Point Hybrid Suspension System" Actuators 14, no. 7: 312. https://doi.org/10.3390/act14070312
APA StyleYang, S., Yang, J., & Zhou, F. (2025). Adaptive Linear Active Disturbance Rejection Cooperative Control of Multi-Point Hybrid Suspension System. Actuators, 14(7), 312. https://doi.org/10.3390/act14070312







