Design and Optimization of a Large-Air-Gap Voice Coil Motor with Enhanced Thermal Management for Magnetic Levitation Vibration Isolation in a Vacuum †
Abstract
:1. Introduction
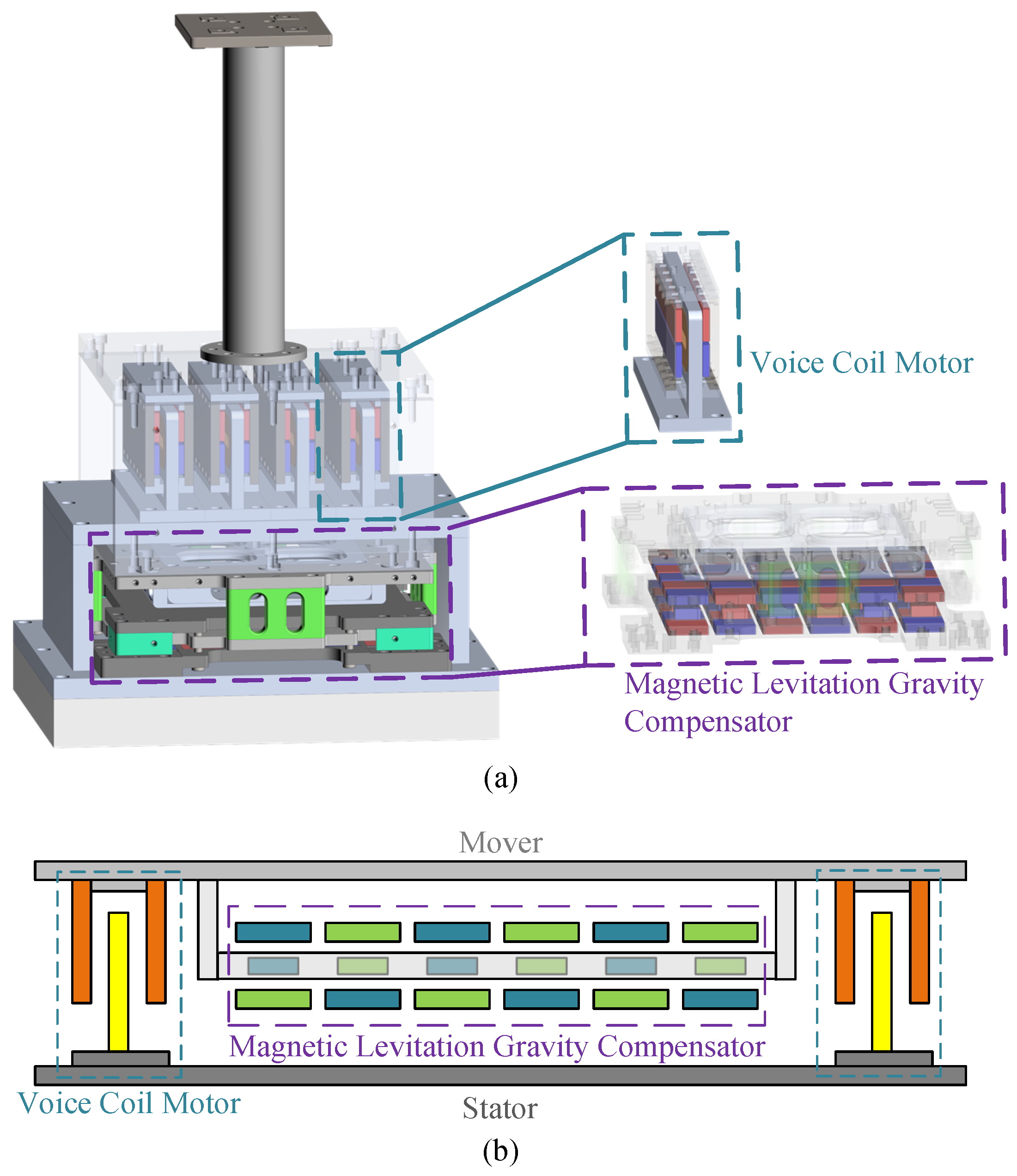
2. Structure and Magnetic Field Analysis of the LAG-VCM
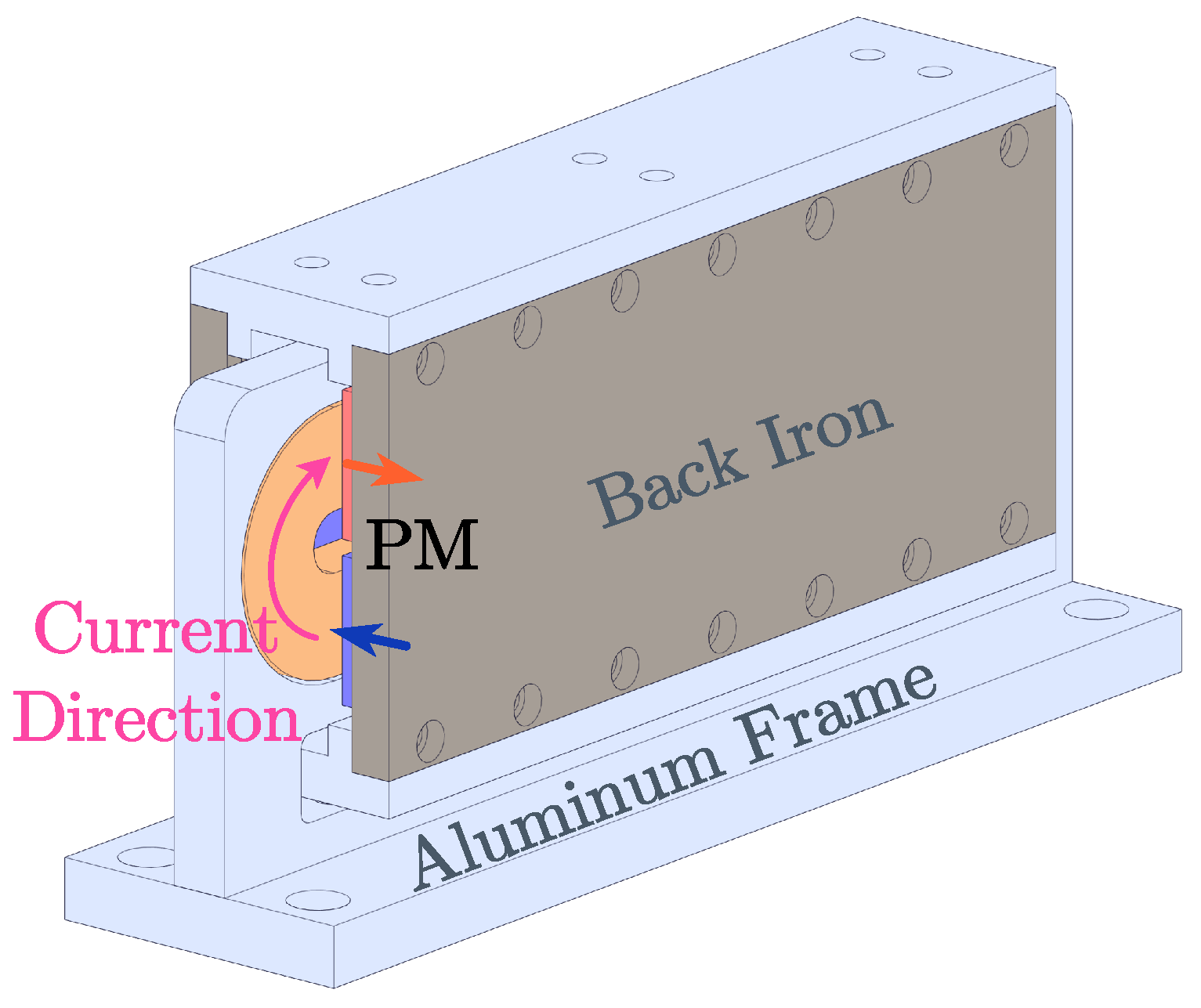
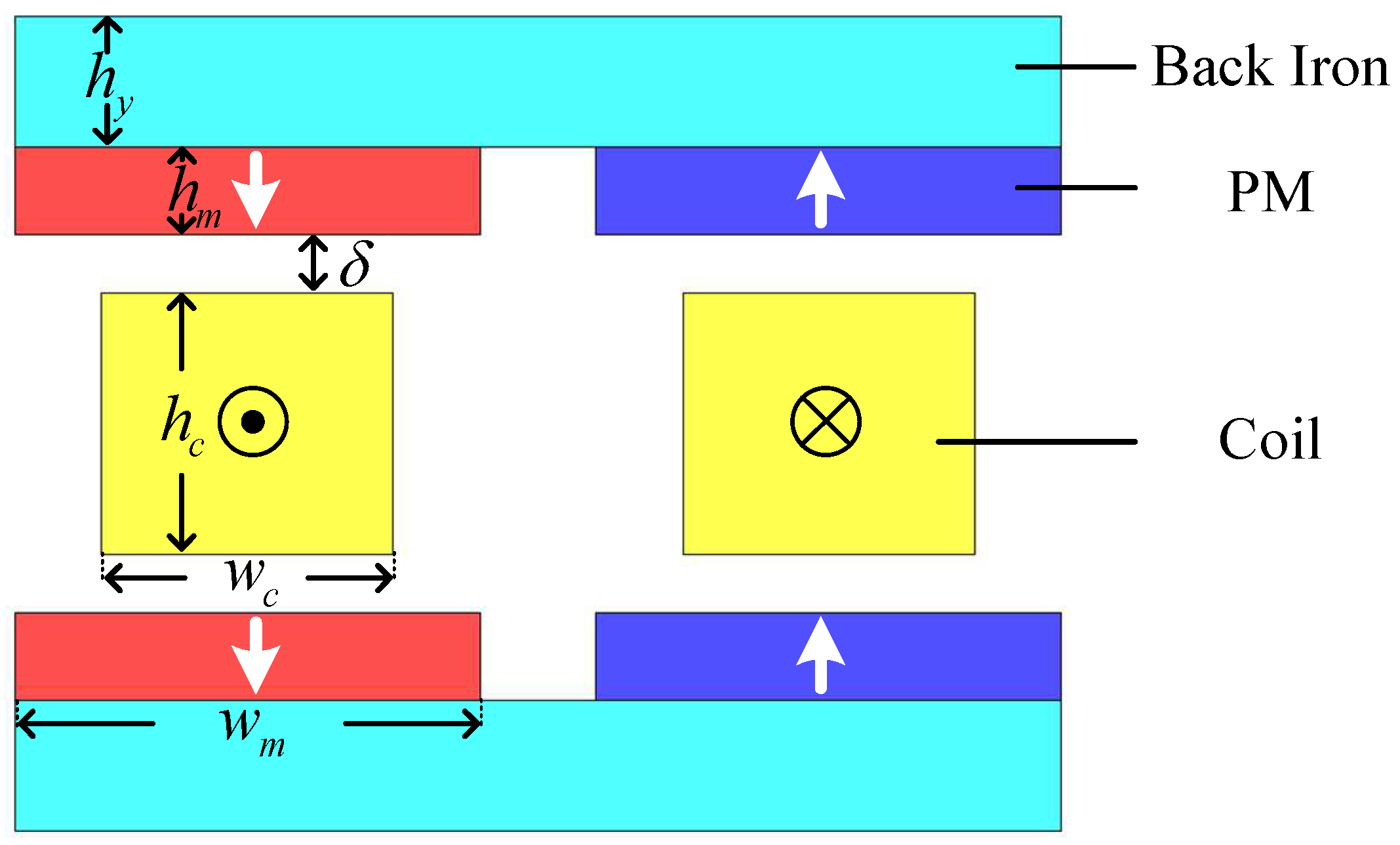
2.1. The Structure of the LAG-VCM
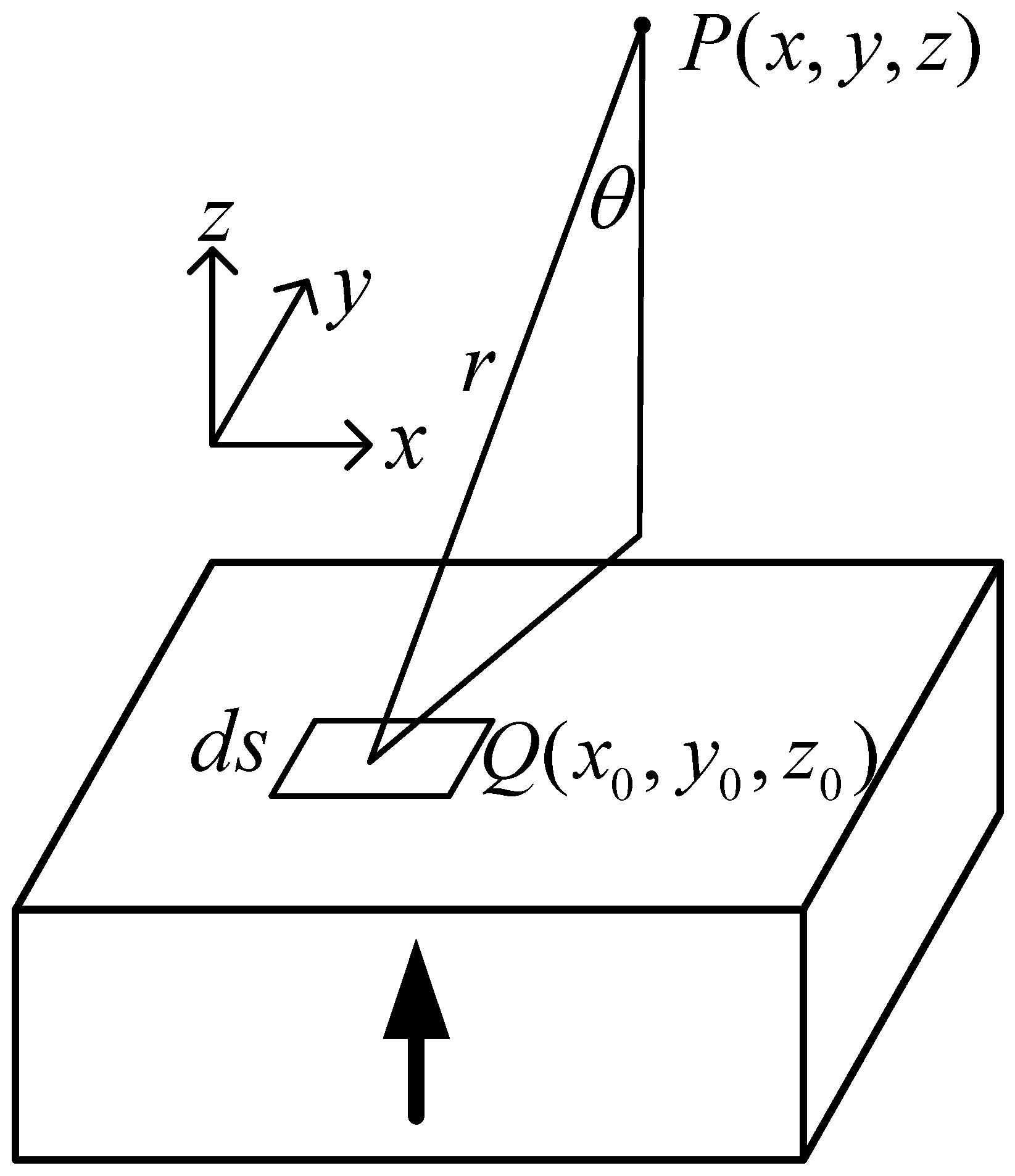
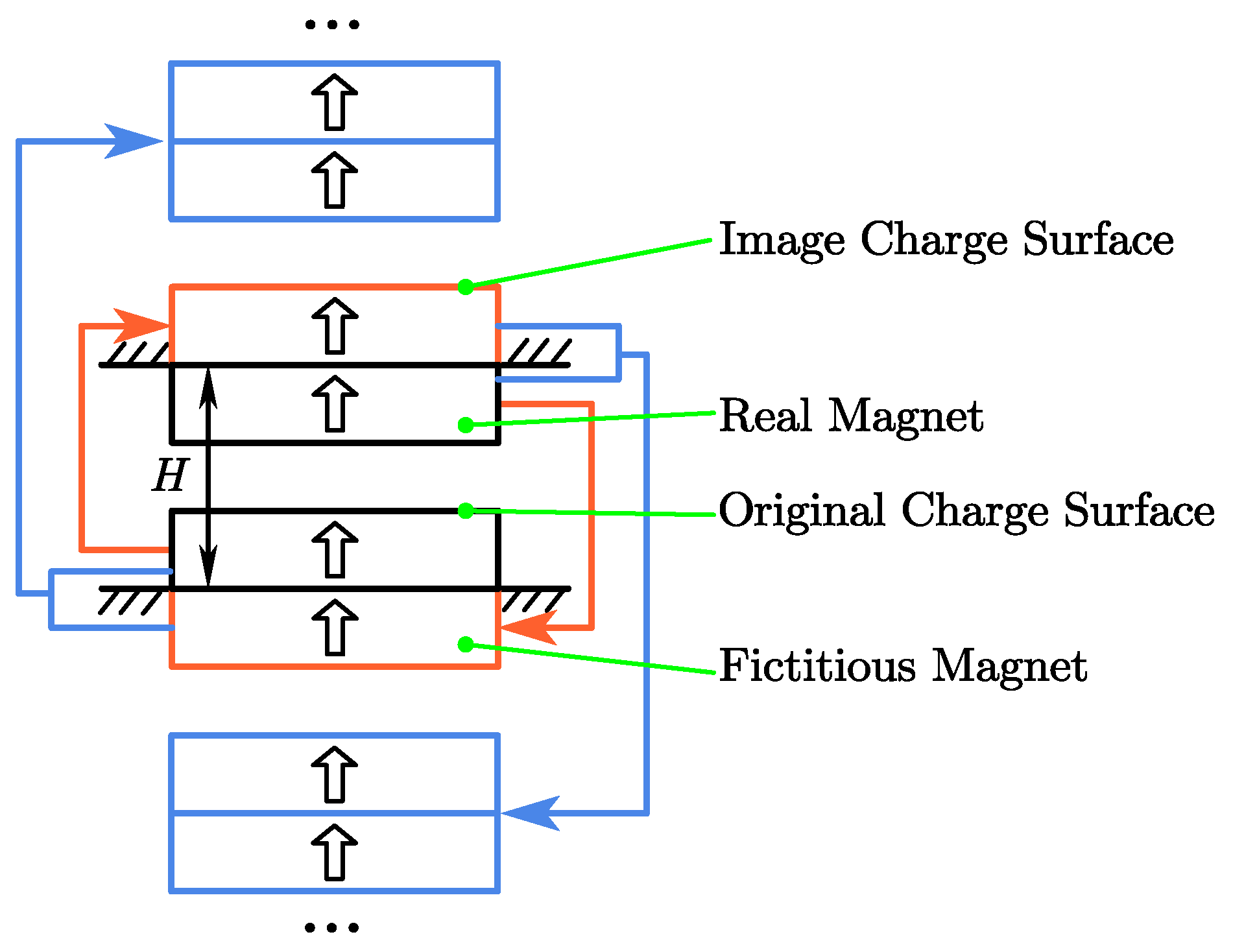
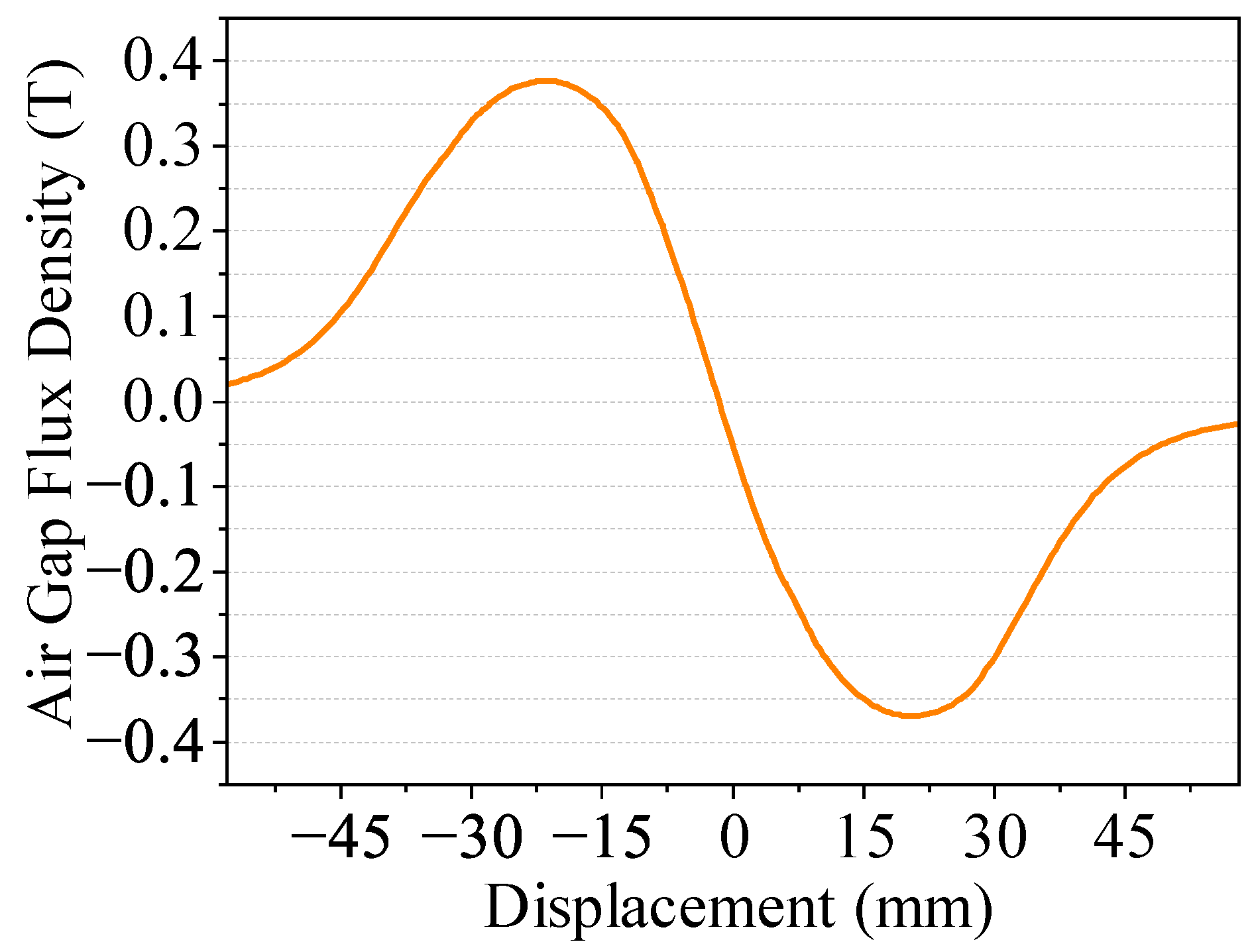
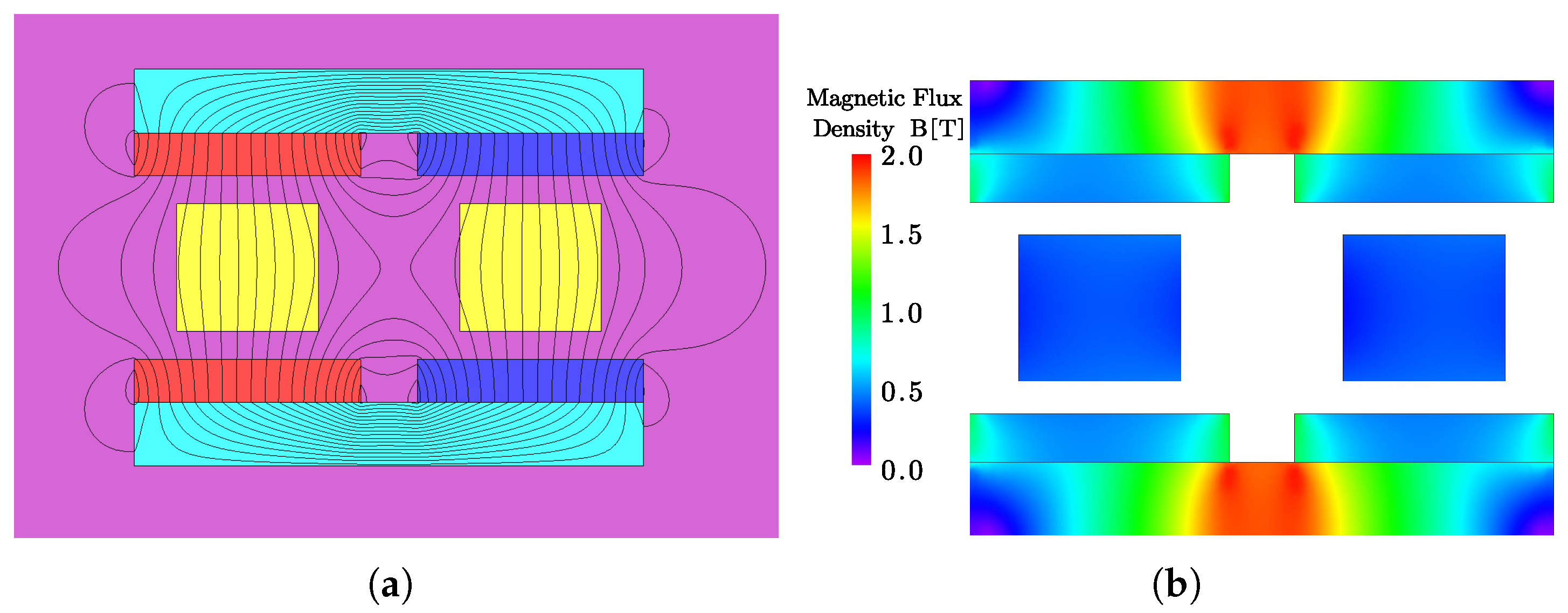
2.2. Magnetic Field Analysis of the LAG-VCM
3. Finite Element Analysis and Optimization of the LAG-VCM
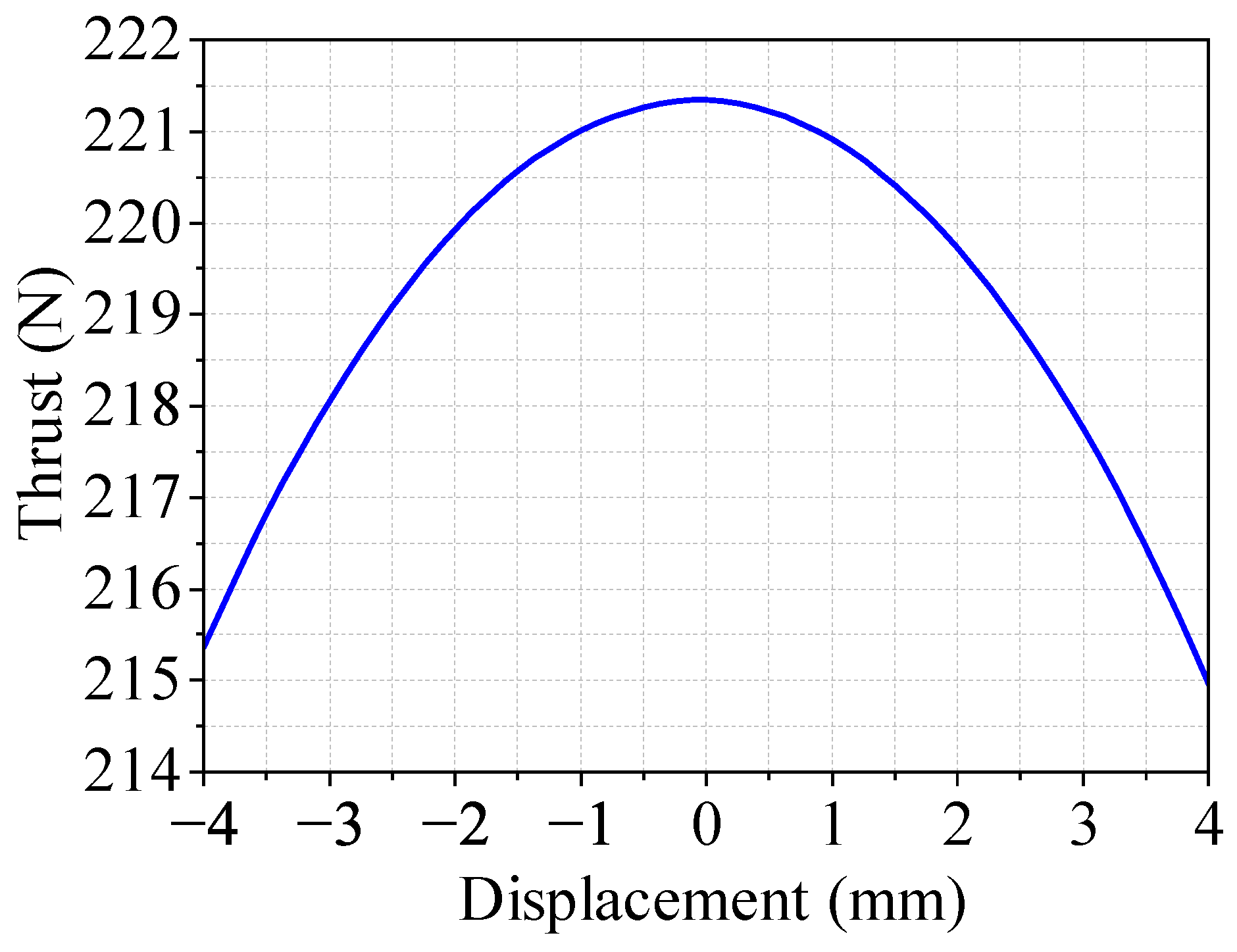
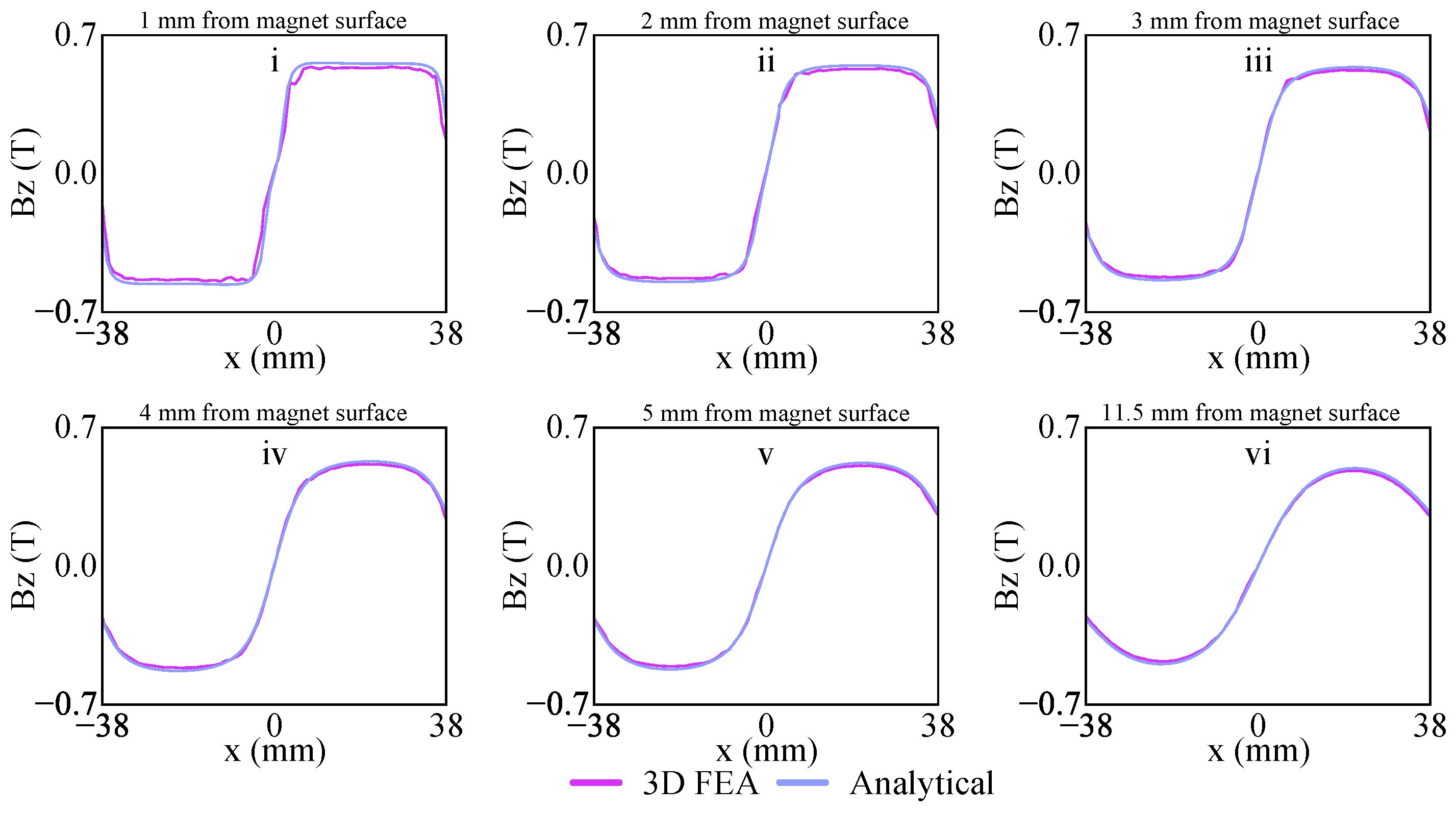
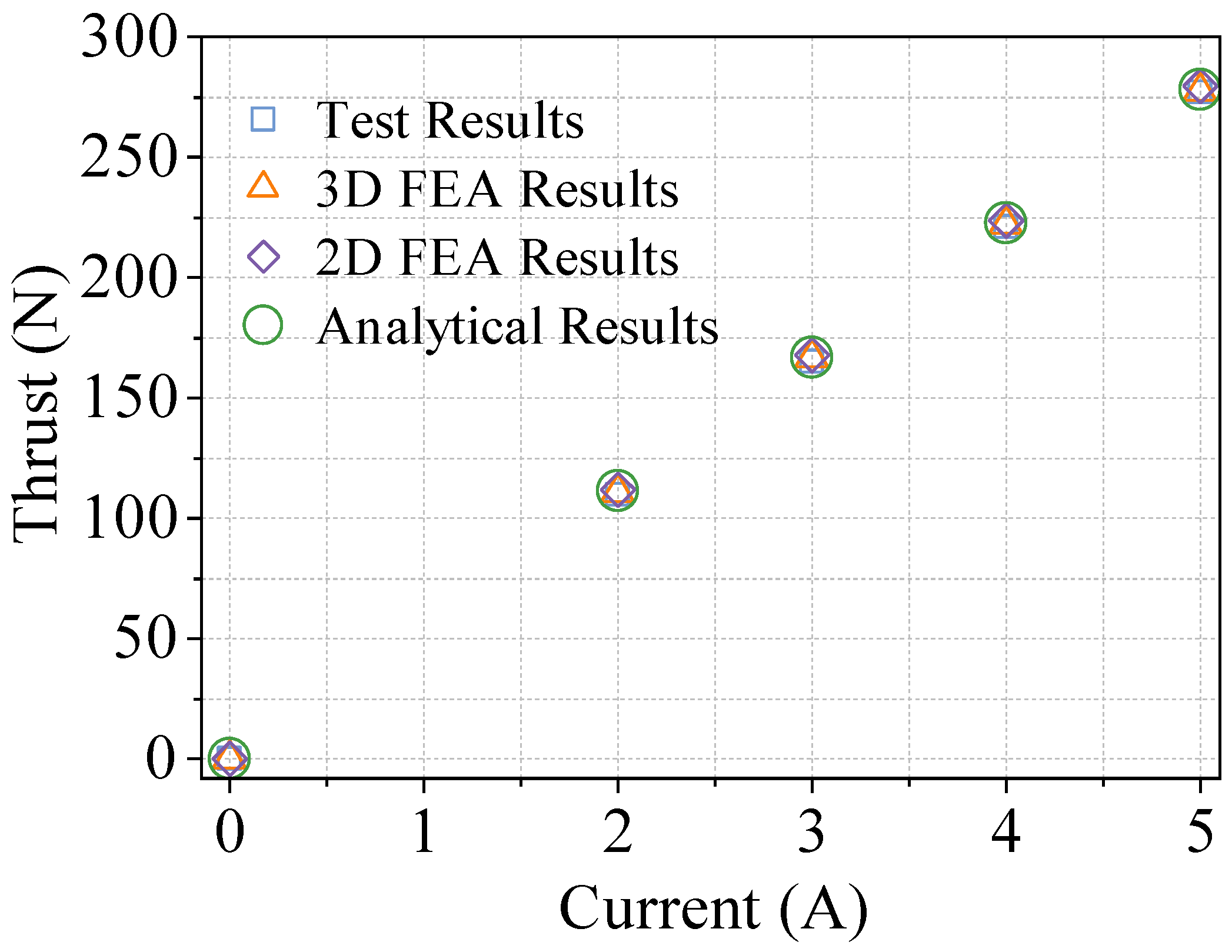
3.1. Finite Element Analysis Validation of the LAG-VCM
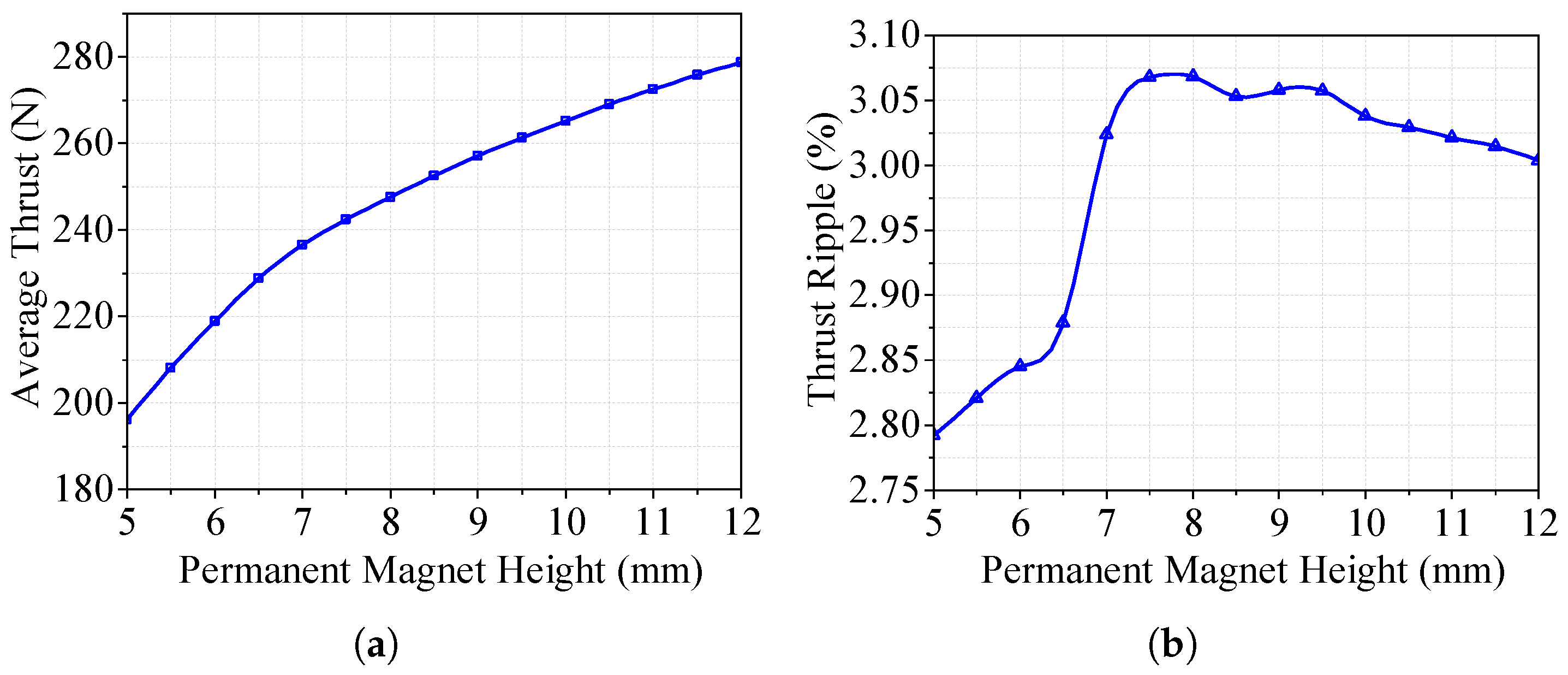
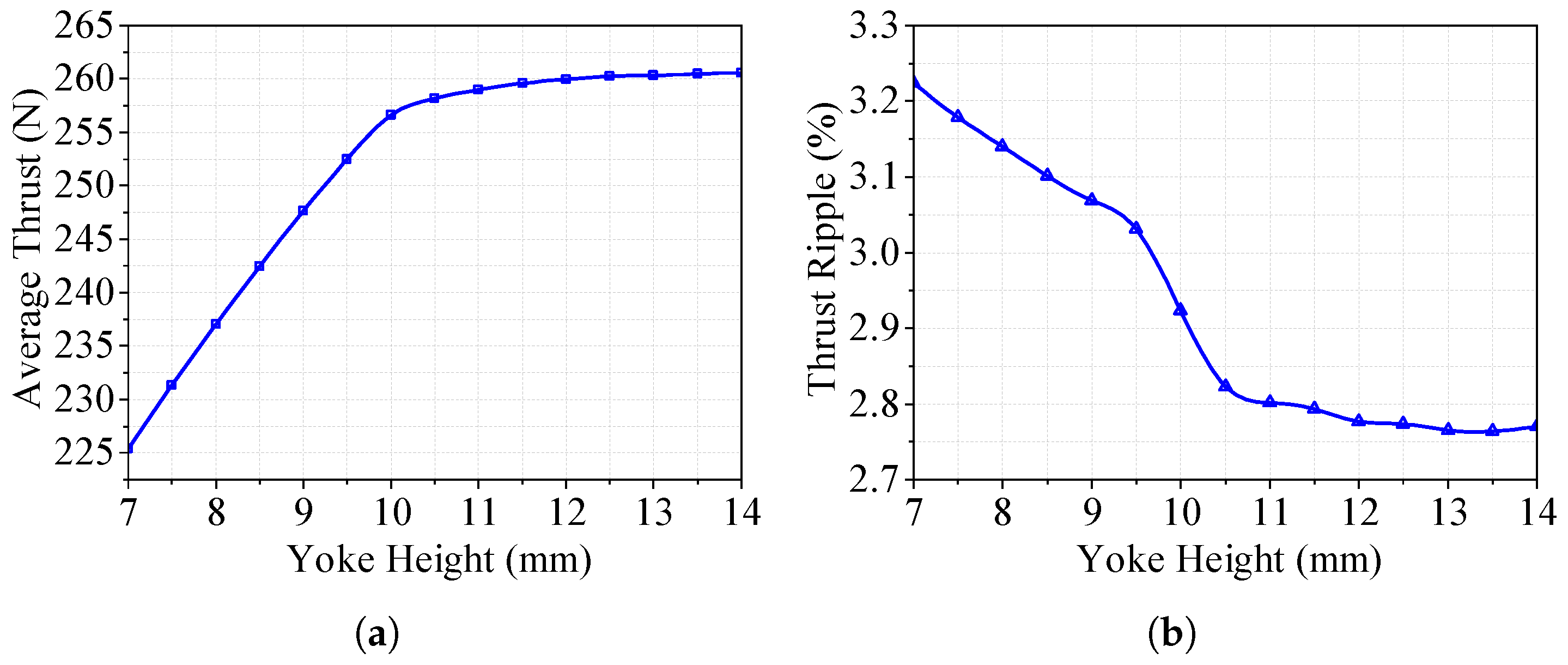
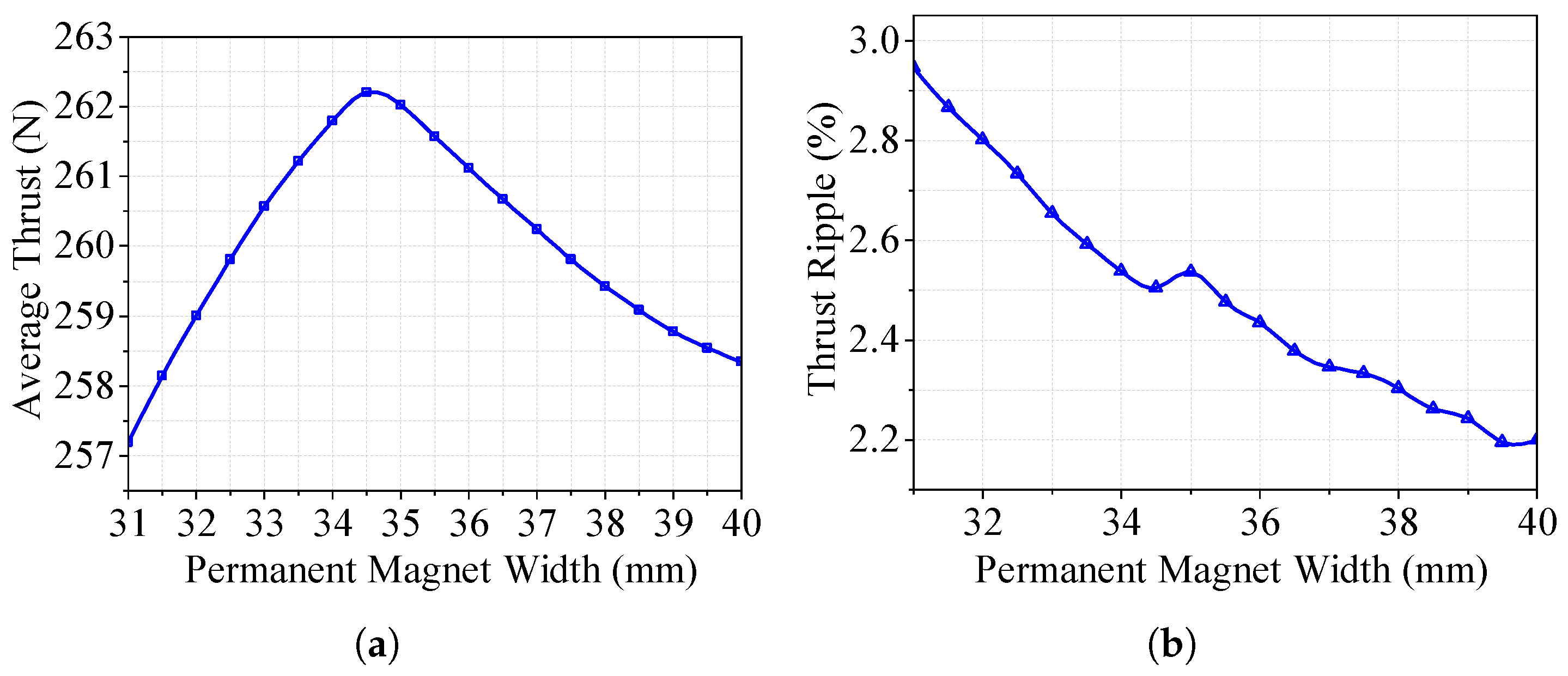
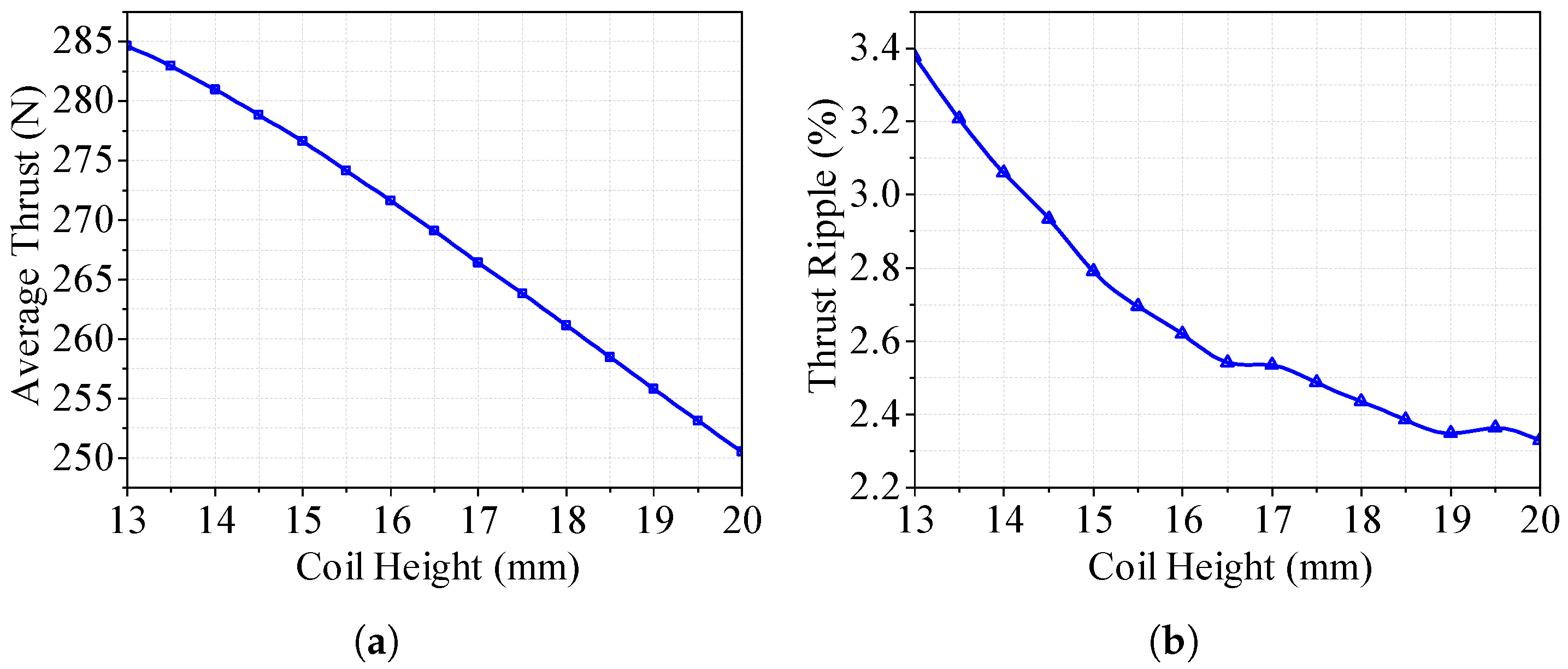
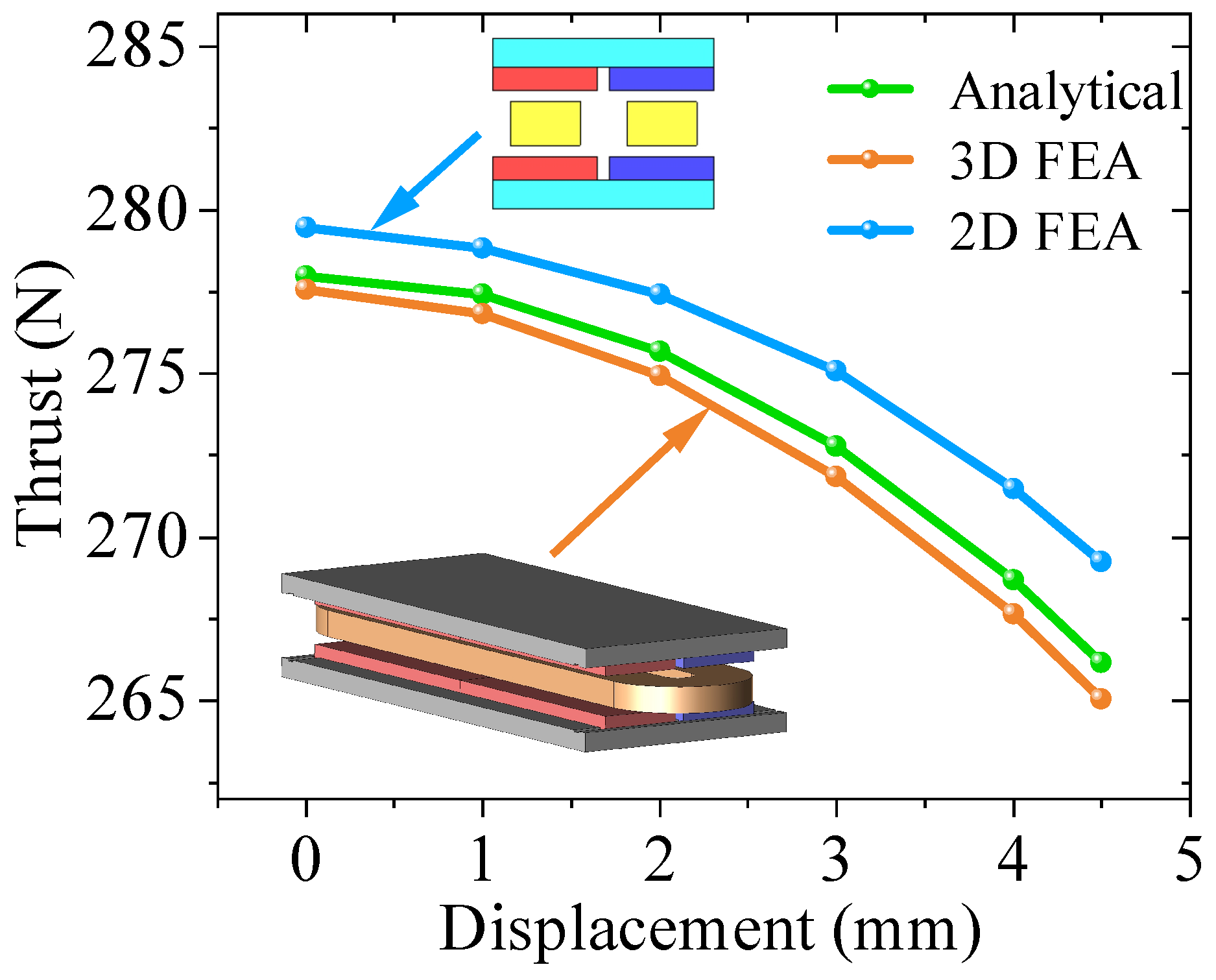
3.2. Finite Element Optimization of the LAG-VCM
4. Thermal Analysis and a Cooling Strategy for a Vacuum-Operated Voice Coil Motor
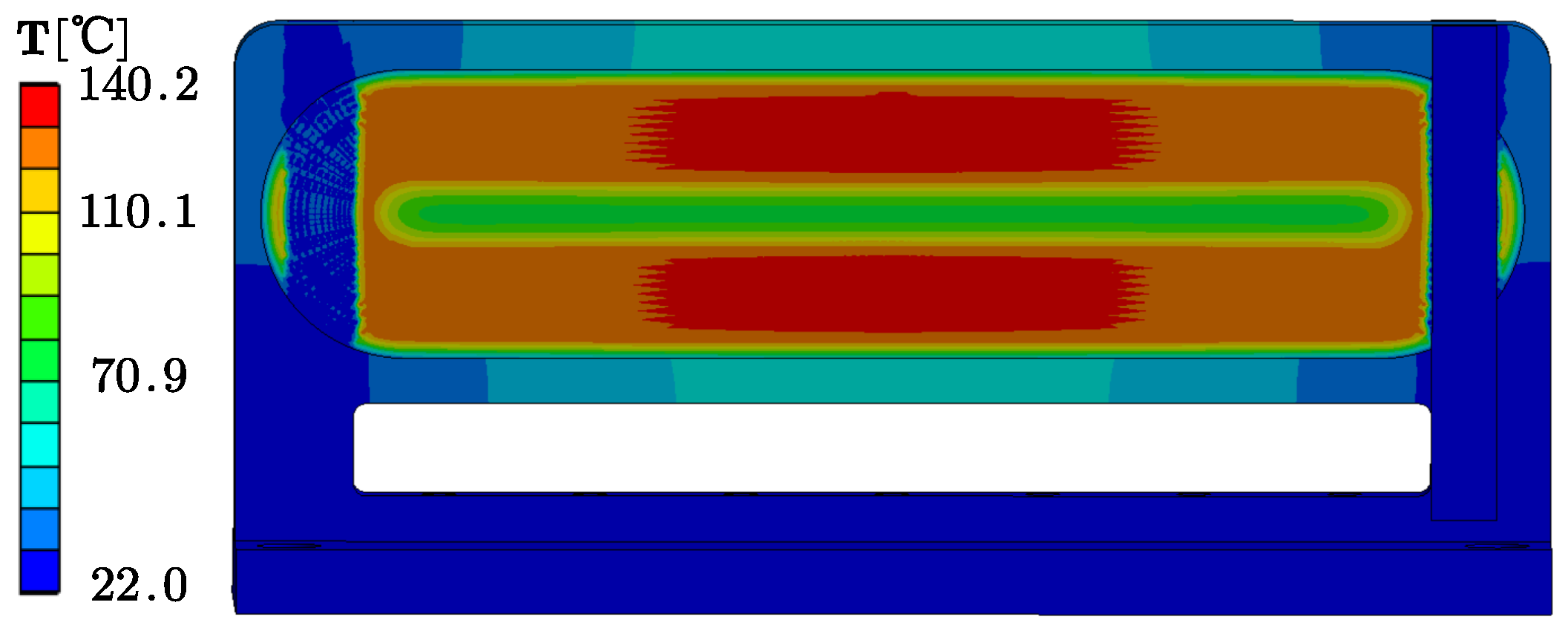
4.1. Introduction and Baseline Analysis
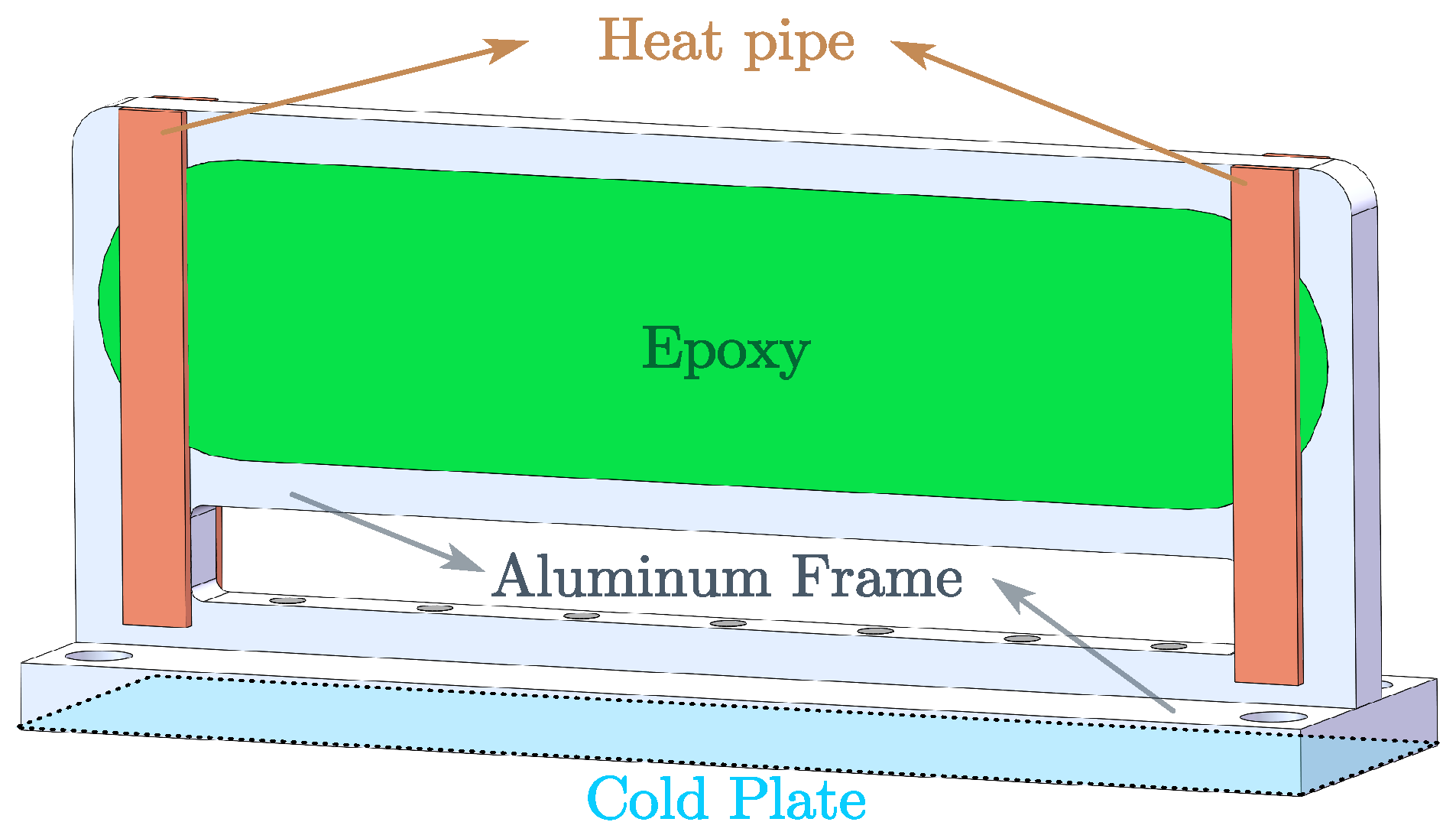
4.2. Proposed Heat Pipe Cooling Enhancement
5. The LAG-VCM Prototype and Experimentation
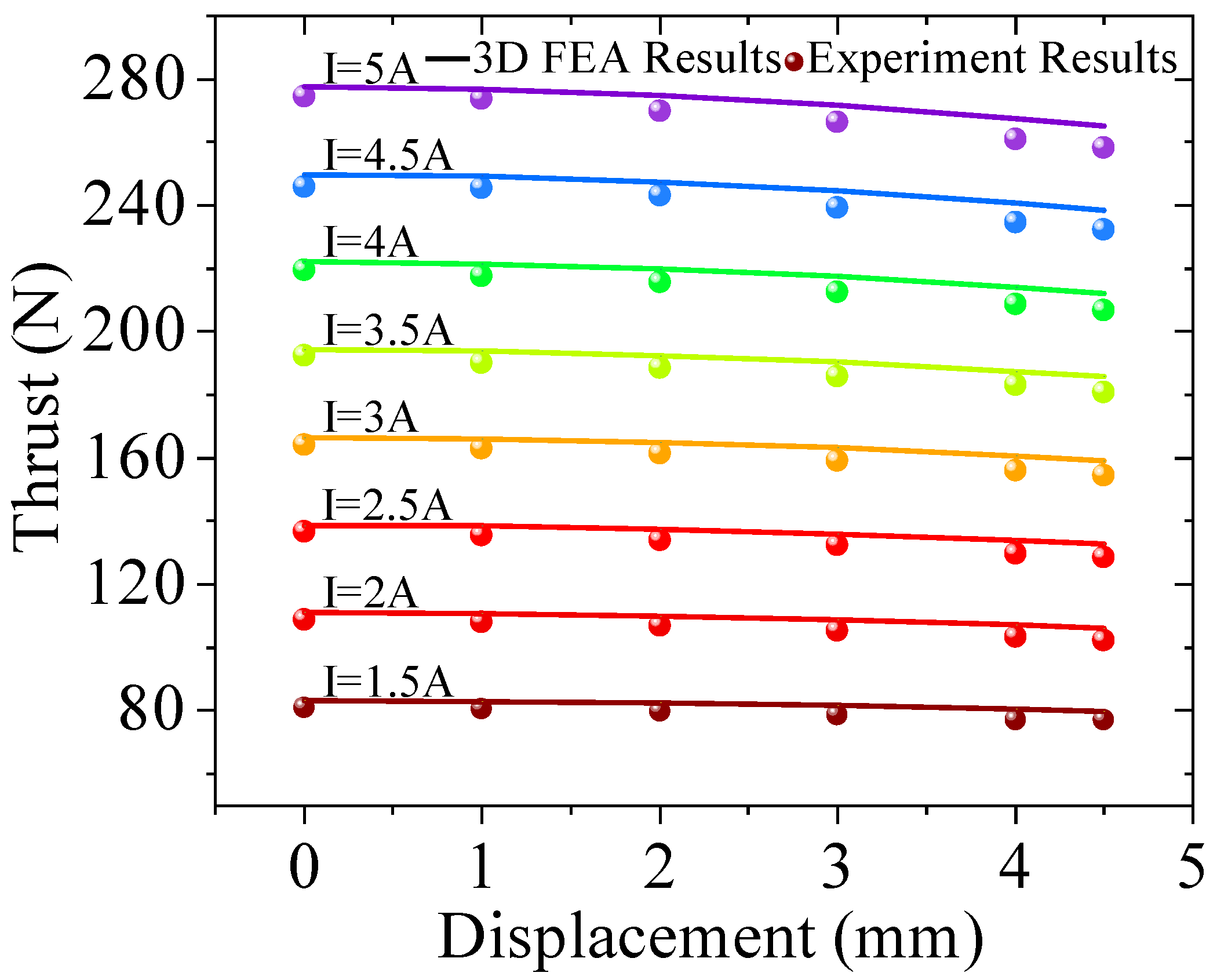
5.1. The Thrust Test of the LAG-VCM Prototype
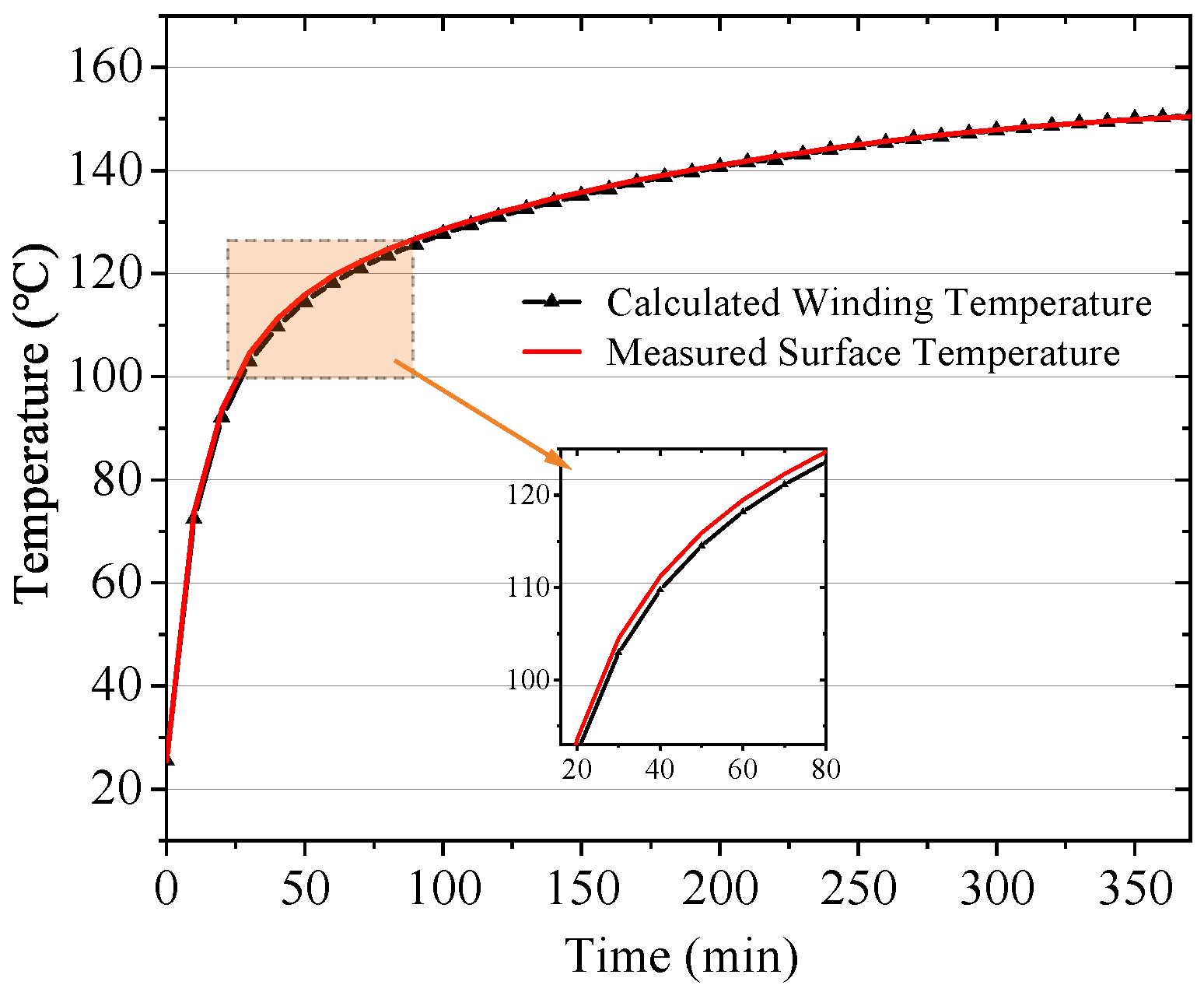
5.2. The Temperature Test of the LAG-VCM Prototype
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LAG-VCM | Large-air-gap voice coil motor |
| FEA | Finite element analysis |
References
- Ling, Y.; Wu, S.; Gu, J.; Lai, H. A novel ring spring vibration isolator for metro superstructure. Appl. Sci. 2021, 11, 8422. [Google Scholar] [CrossRef]
- Araki, Y.; Asai, T.; Kimura, K.; Maezawa, K.; Masui, T. Nonlinear vibration isolator with adjustable restoring force. J. Sound Vib. 2013, 332, 6063–6077. [Google Scholar] [CrossRef]
- Voigtländer, B.; Coenen, P.; Cherepanov, V.; Borgens, P.; Duden, T.; Tautz, F.S. Low vibration laboratory with a single-stage vibration isolation for microscopy applications. Rev. Sci. Instrum. 2017, 88, 023703. [Google Scholar] [CrossRef] [PubMed]
- Qu, D.; Liu, X.; Liu, G.; Bai, Y.; He, T. Analysis of vibration isolation performance of parallel air spring system for precision equipment transportation. Meas. Control 2019, 52, 291–302. [Google Scholar] [CrossRef]
- Law, M.; Wabner, M.; Colditz, A.; Kolouch, M.; Noack, S.; Ihlenfeldt, S. Active vibration isolation of machine tools using an electro-hydraulic actuator. CIRP J. Manuf. Sci. Technol. 2015, 10, 36–48. [Google Scholar] [CrossRef]
- Henderson, J.-P.; Plummer, A.; Johnston, N. An electro-hydrostatic actuator for hybrid active-passive vibration isolation. Int. J. Hydromechatronics 2018, 1, 47–71. [Google Scholar] [CrossRef]
- Xu, D.; Yu, Q.; Zhou, J.; Bishop, S.R. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2013, 332, 3377–3389. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wang, Z.; Wu, C.; Wang, S.; Zhang, W. Lever-type quasi-zero stiffness vibration isolator with magnetic spring. J. Sound Vib. 2022, 527, 116865. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, R.; Yang, Q.; Lee, H.P.; Chai, K. A semi-active electromagnetic quasi-zero-stiffness vibration isolator. Int. J. Mech. Sci. 2023, 252, 108357. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, J.; Jing, Y.; Cao, X.; Yuan, S.; Luo, J.; Pu, H. A novel permanent magnet vibration isolator with wide stiffness range and high bearing capacity. Mechatronics 2024, 98, 103119. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, J.; Bian, X.; Zou, L.; Liang, S.; Wang, L. Study on Performance of an air spring isolator for large-scale precision optical micro-vibration isolation. In Proceedings of the 3rd International Conference on Information Technologies and Electrical Engineering, Changde, China, 3–5 December 2020; pp. 173–178. [Google Scholar]
- Zhang, H.; Lou, Y.; Zhou, L.; Kou, Z.; Mu, J. Modeling and Optimization of a Large-Load Magnetic Levitation Gravity Compensator. IEEE Trans. Ind. Electron. 2022, 70, 5055–5064. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Ahn, D. Analysis of high force voice coil motors for magnetic levitation. Actuators 2020, 9, 133. [Google Scholar] [CrossRef]
- Lee, K.-M. Design and analysis of a vertically moving voice coil motor with gravity compensation for semiconductor equipment. Sens. Actuators A Phys. 2022, 344, 113735. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Liu, C.-S.; Yeh, C.-N. Design and Simulation of Novel 3-DOF Spherical Voice Coil Motor. Actuators 2021, 10, 155. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, M.; Zhou, H.; Duan, J.-A. Design and analysis of a novel two-degree-of-freedom voice coil motor. IEEE/ASME Trans. Mechatronics 2019, 24, 2908–2918. [Google Scholar] [CrossRef]
- Zhang, H.; Kou, B.; Ge, Q.; Liu, Y. Design and analysis of a high thrust linear voice coil motor using for the stiffness test of linear motor servo system. IEEE Trans. Magn. 2021, 58, 1–5. [Google Scholar] [CrossRef]
- Chi, F.; Wu, L.; Yang, X. Optimum design of voice coil motor using for nano-stage in lithographic equipment. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 2540–2543. [Google Scholar]
- Zhang, Z.-J.; Zhou, H.-B.; Duan, J.-A.; Kou, B.-Q. Design and analysis of two-degree-of-freedom voice coil motors for linear-rotary motion. In Proceedings of the 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–6. [Google Scholar]
- Chen, Y.-D.; Fuh, C.-C.; Tung, P.-C. Application of voice coil motors in active dynamic vibration absorbers. IEEE Trans. Magn. 2005, 41, 1149–1154. [Google Scholar] [CrossRef]
- Li, L.; Pan, D.; Liu, J.; Wang, M.; Guo, Q.; Peng, E. Analysis and modeling of air-core monopole linear motor for nanopositioning system. IEEE Trans. Magn. 2013, 49, 3977–3980. [Google Scholar] [CrossRef]
- Mu, J.; Zhang, H. Design and Optimization of Large Air-Gap Voice Coil Motor for Application in Magnetic Levitation Platform. In Proceedings of the 11th Chinese Symposium on Magnetic Levitation Technology and Vibration Control (CSMLVC11), Changsha, China, 4–7 August 2023; p. 231. [Google Scholar]
- Ravaud, R.; Lemarquand, G.; Lemarquand, V.; Depollier, C. Analytical calculation of the magnetic field created by permanent-magnet rings. IEEE Trans. Magn. 2008, 44, 1982–1989. [Google Scholar] [CrossRef]
- Ravaud, R.; Lemarquand, G.; Lemarquand, V.; Depollier, C. Permanent magnet couplings: Field and torque three-dimensional expressions based on the Coulombian model. IEEE Trans. Magn. 2009, 45, 1950–1958. [Google Scholar] [CrossRef]
- Rakotoarison, H.L.; Yonnet, J.-P.; Delinchant, B. Using Coulombian approach for modeling scalar potential and magnetic field of a permanent magnet with radial polarization. IEEE Trans. Magn. 2007, 43, 1261–1264. [Google Scholar] [CrossRef]
- Lee, S.-H.; Park, S.-B.; Kwon, S.-O.; Lee, J.-Y.; Lee, J.-J.; Hong, J.-P.; Hur, J. Characteristic analysis of the slotless axial-flux type brushless DC motors using image method. IEEE Trans. Magn. 2006, 42, 1327–1330. [Google Scholar]
- Zhang, H.; Kou, B.; Zhang, H.; Jin, Y. A Three-Degree-of-Freedom Short-Stroke Lorentz-Force-Driven Planar Motor Using a Halbach Permanent-Magnet Array With Unequal Thickness. IEEE Trans. Ind. Electron. 2015, 62, 3640–3650. [Google Scholar] [CrossRef]





| Design Requirement | Short Designation | Value | Units |
|---|---|---|---|
| Continuous Thrust | 250 | N | |
| Peak Thrust | 300 | N | |
| Rated Current | 5 | A | |
| Single-Side Air Gap | 4 | mm | |
| Maximum Dimensions | - | 160 × 100 × 320 | mm |
| Symbol | Quantity | Value | Units |
|---|---|---|---|
| Remanence | 1.385 | T | |
| Coercivity | 1073 | kA/m | |
| Relative permeability | 1.027 | – | |
| PM width | 36 | mm | |
| PM height | 8 | mm | |
| Polar pitch | 40 | mm | |
| Coil width | 24 | mm | |
| Coil height | 15 | mm | |
| Yoke height | 11 | mm | |
| N | Coil turns | 264 | – |
| Electromagnetic air gap | 4 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, J.; Zhang, H. Design and Optimization of a Large-Air-Gap Voice Coil Motor with Enhanced Thermal Management for Magnetic Levitation Vibration Isolation in a Vacuum. Actuators 2025, 14, 301. https://doi.org/10.3390/act14060301
Mu J, Zhang H. Design and Optimization of a Large-Air-Gap Voice Coil Motor with Enhanced Thermal Management for Magnetic Levitation Vibration Isolation in a Vacuum. Actuators. 2025; 14(6):301. https://doi.org/10.3390/act14060301
Chicago/Turabian StyleMu, Junren, and He Zhang. 2025. "Design and Optimization of a Large-Air-Gap Voice Coil Motor with Enhanced Thermal Management for Magnetic Levitation Vibration Isolation in a Vacuum" Actuators 14, no. 6: 301. https://doi.org/10.3390/act14060301
APA StyleMu, J., & Zhang, H. (2025). Design and Optimization of a Large-Air-Gap Voice Coil Motor with Enhanced Thermal Management for Magnetic Levitation Vibration Isolation in a Vacuum. Actuators, 14(6), 301. https://doi.org/10.3390/act14060301






