State Observer-Based Sampled-Data Control for Path Tracking of Autonomous Agricultural Tractor †
Abstract
1. Introduction
2. System Portrayal and Mathematical Construction
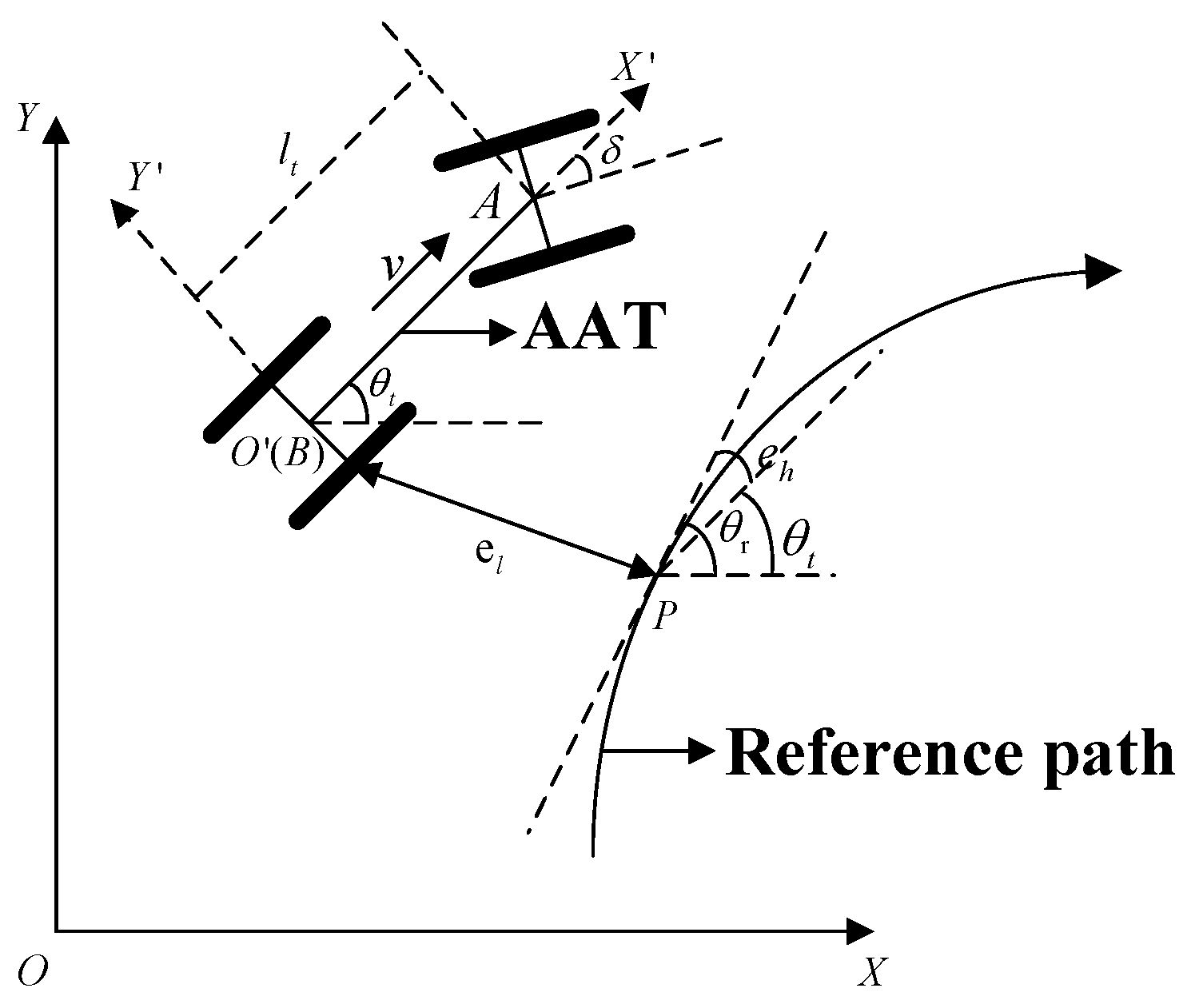
2.1. Symbol Definition and Issue Description
2.2. Ideal Model
2.3. Offset Model
3. Control Design
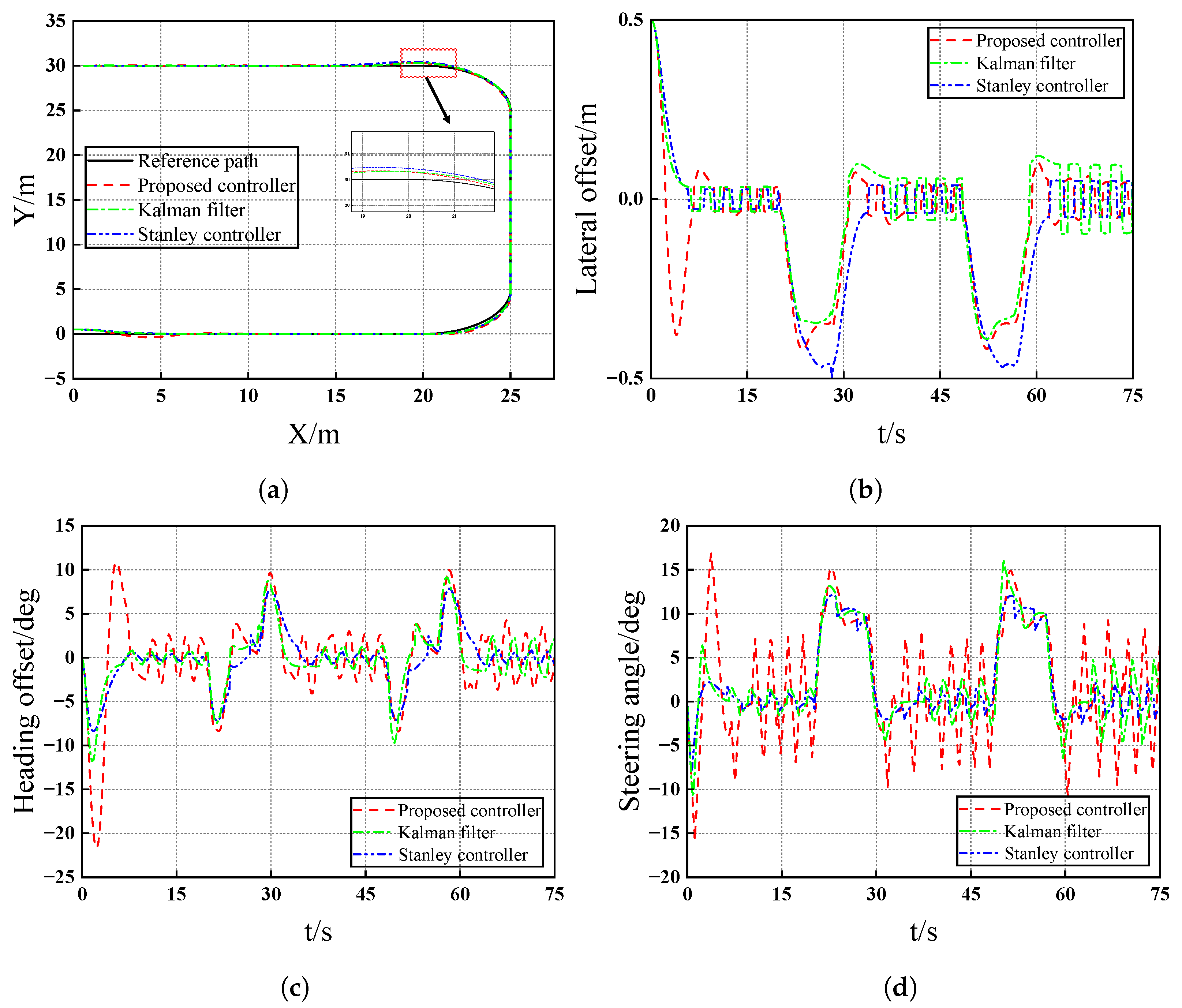
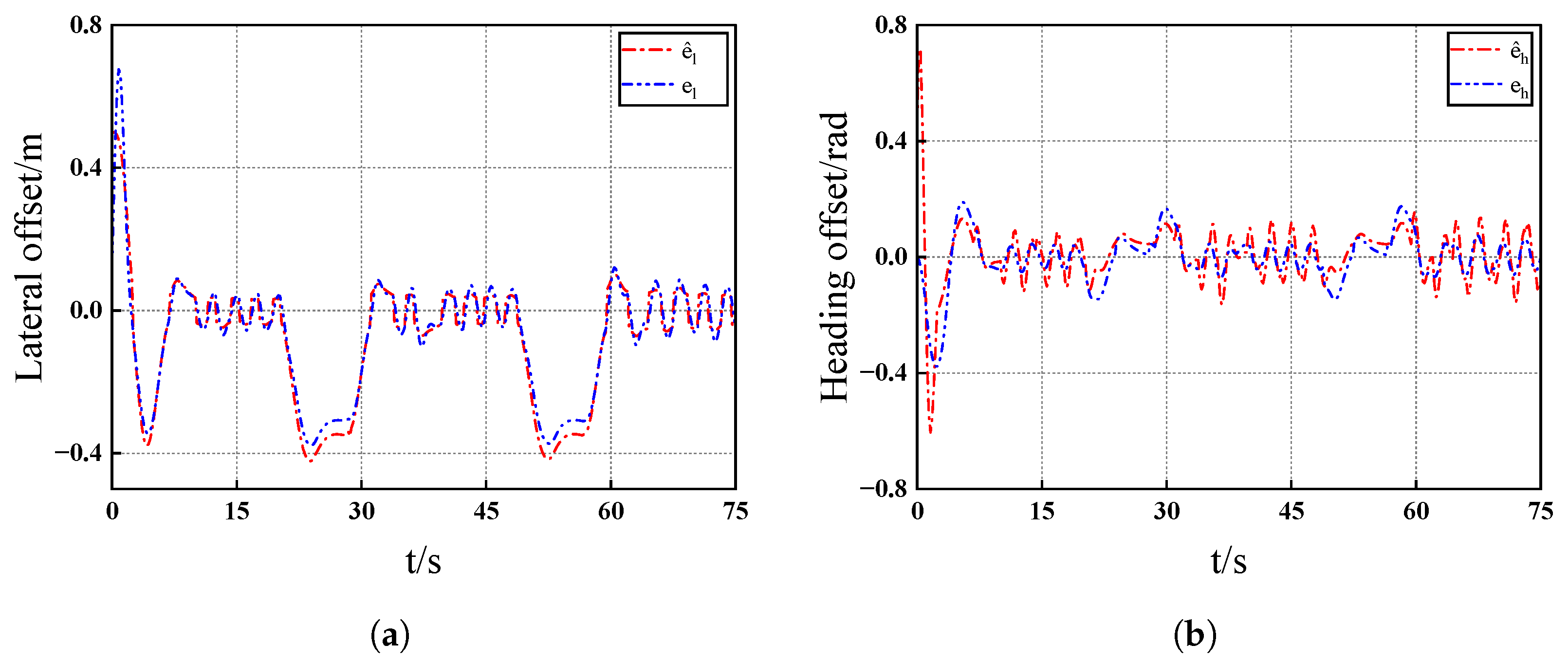
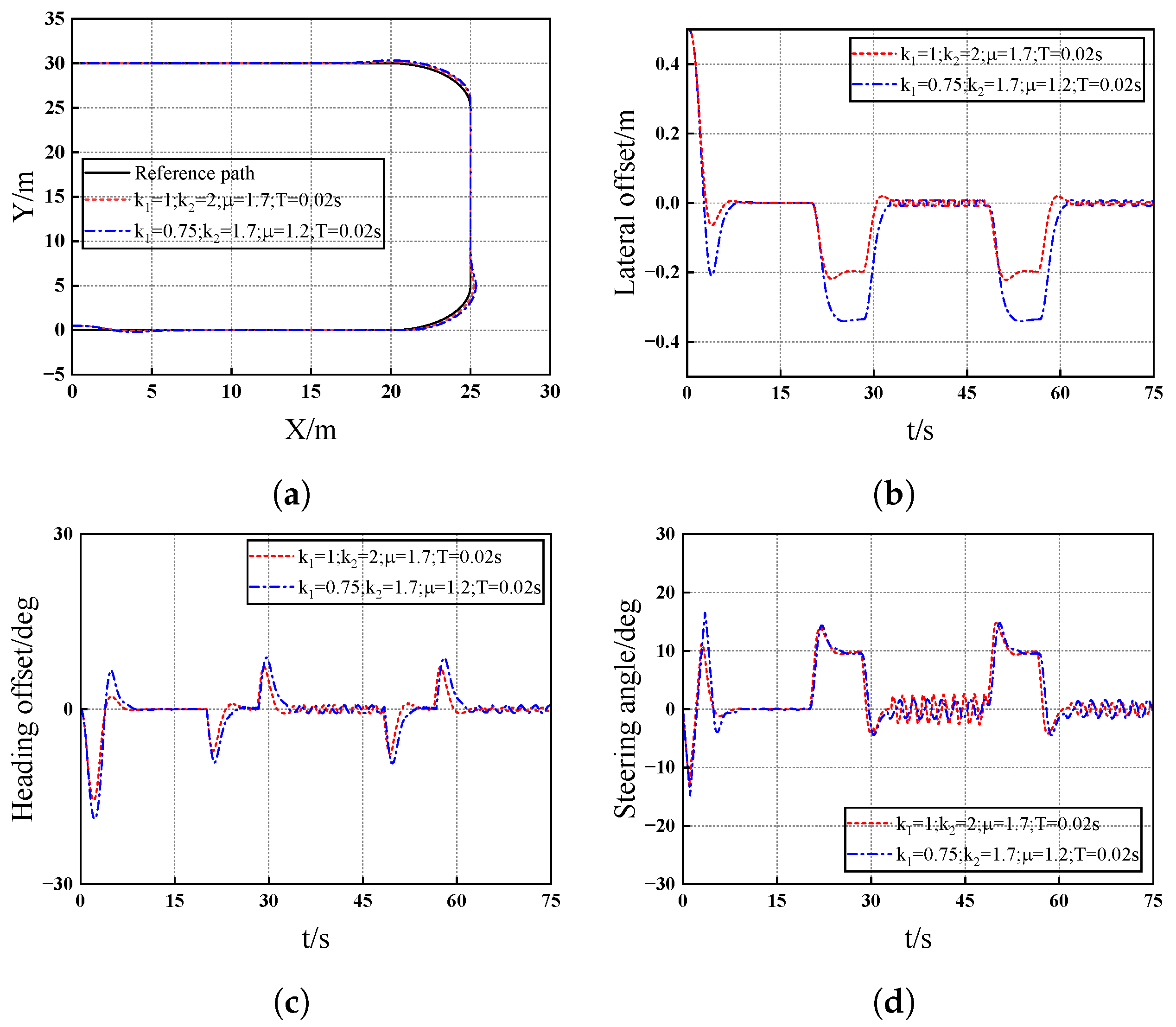
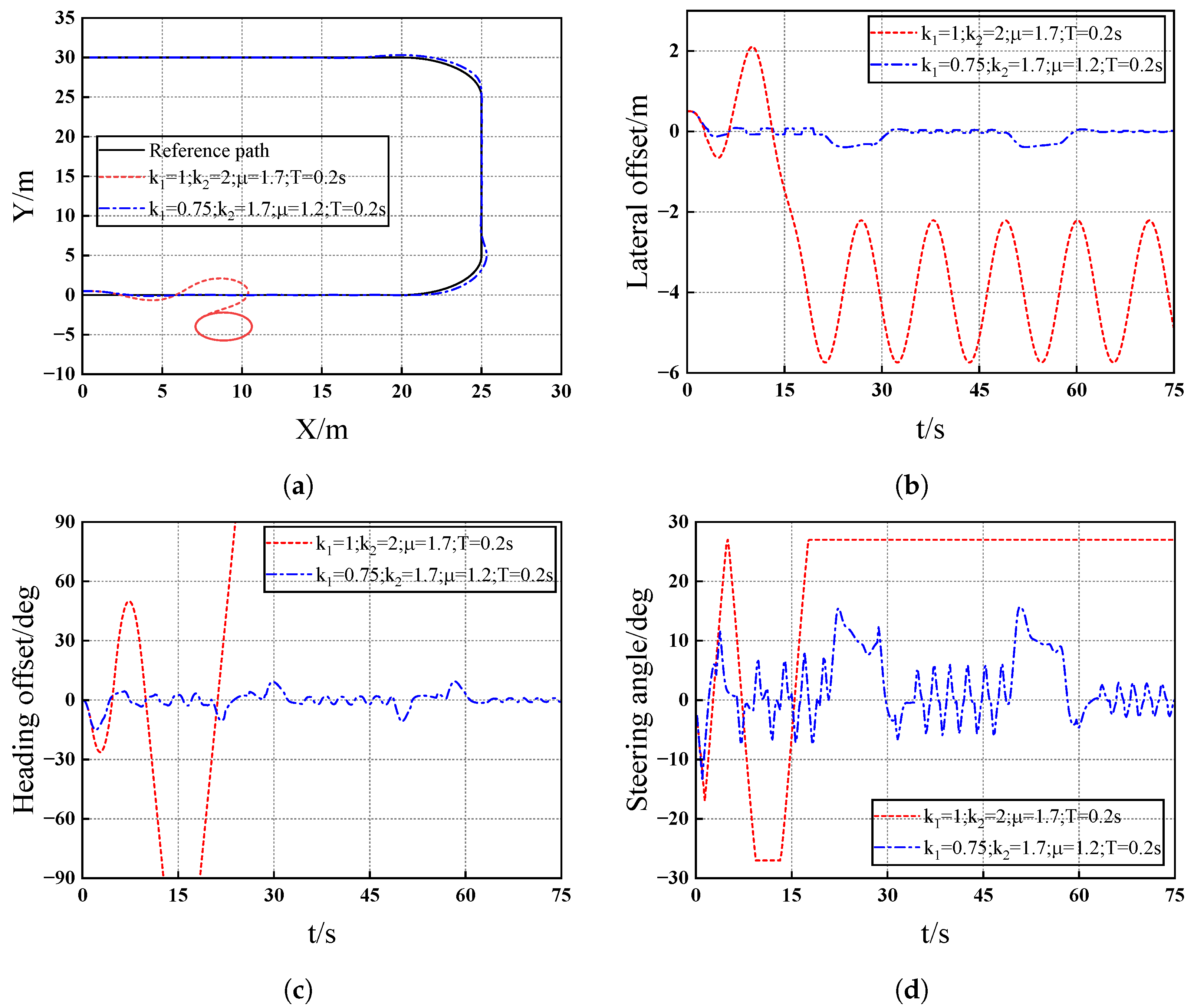
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, Q.; Liu, D.; Mao, H.; Shen, B.; Li, M. Wind-induced response of rice under the action of the downwash flow field of a multi-rotor UAV. Biosyst. Eng. 2021, 203, 60–69. [Google Scholar] [CrossRef]
- Ji, W.; Pan, Y.; Xu, B.; Wang, J. A Real-Time Apple Targets Detection Method for Picking Robot Based on ShufflenetV2-YOLOX. Agriculture 2023, 12, 856. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, L.; Zhou, X.; Yao, K.S.; Tian, Y.; Nirere, A. A method of information fusion for identification of rice seed varieties based on hyperspectral imaging technology. J. Food Process. Eng. 2021, 44, 13797. [Google Scholar] [CrossRef]
- Ding, Z.; Tang, Z.; Zhang, B.; Ding, C. Vibration response of metal plate and shell structure under multi-source excitation with welding and bolt connection. Agriculture 2024, 14, 816. [Google Scholar] [CrossRef]
- Thanpattranon, P.; Ahamed, T.; Takigawa, T. Navigation of autonomous tractor for orchards and plantations using a laser range finder: Automatic control of trailer position with tractor. Biosyst. Eng. 2016, 147, 90–103. [Google Scholar] [CrossRef]
- Hu, J.; Gao, L.; Bai, X.; Li, T.; Liu, X. Review of research on automatic guidance of agricultural vehicles. Trans. Chin. Soc. Agric. Eng. 2015, 31, 1–10. [Google Scholar]
- Chen, C.; Liu, X.Q.; Liu, C.J.; Pan, Q. Development of the precision feeding system for sows via a rule-based expert system. Int. J. Agric. Biol. Eng. 2023, 16, 187–198. [Google Scholar] [CrossRef]
- Ji, W.; Zhang, T.; Xu, B.; He, G. Apple recognition and picking sequence planning for harvesting robot in a complex environment. J. Agric. Eng. 2023, 55, 1549. [Google Scholar] [CrossRef]
- Backman, J.; Piirainen, P.; Oksanen, T. Smooth turning path generation for agricultural vehicles in headlands. Biosyst. Eng. 2015, 139, 76–86. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, Z.; Ali, S.; Yang, N.; Fu, S.; Zhang, Y. Multi-class detection of cherry tomatoes using improved YOLOv4-Tiny. Int. J. Agric. Biol. Eng. 2023, 16, 225–231. [Google Scholar] [CrossRef]
- Zhu, W.; Sun, J.; Wang, S.; Shen, J.; Yang, K.; Zhou, X. Identifying field crop diseases using transformer-embedded convolutional neural network. Agriculture 2022, 12, 1083. [Google Scholar] [CrossRef]
- Zhu, Y.; Cui, B.; Yu, Z.; Gao, Y.; Wei, X. Tillage Depth Detection and Control Based on Attitude Estimation and Online Calibration of Model Parameters. Agriculture 2024, 14, 2130. [Google Scholar] [CrossRef]
- Ji, W.; Wang, J.; Xu, B.; Zhang, T. Apple Grading Based on Multi-Dimensional View Processing and Deep Learning. Foods 2023, 12, 2117. [Google Scholar] [CrossRef] [PubMed]
- Chang, X.H.; Liu, Y.; Shen, M. Resilient control design for lateral motion regulation of intelligent vehicle. IEEE/ASME Trans. Mechatron. 2019, 24, 2488–2497. [Google Scholar] [CrossRef]
- Lenain, R.; Deremetz, M.; Braconnier, J.B.; Thuilot, B.; Rousseau, V. Robust sideslip angles observer for accurate off-road path tracking control. Adv. Robot. 2017, 31, 453–467. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Li, M.; Shang, Z. Dynamic Measurement Method for Steering Wheel Angle of Autonomous Agricultural Vehicles. Agriculture 2024, 14, 1602. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Lenain, R.; Thuilot, B.; Cariou, C.; Martinet, P. Adaptive control for car like vehicles guidance relying on RTK GPS: Rejection of sliding effects in agricultural applications. In Proceedings of the International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 115–120. [Google Scholar]
- Mei, K.; Ding, S.; Dai, X.; Chen, C. Design of second-order sliding-mode controller via output feedback. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 54, 4371–4380. [Google Scholar] [CrossRef]
- Mei, K.; Ding, S.; Yu, X. A generalized supertwisting algorithm. IEEE Trans. Cybern. 2023, 53, 3951–3960. [Google Scholar] [CrossRef]
- Sun, J.; Xu, S.; Ding, S.; Pu, Z.; Yi, J. Adaptive conditional disturbance negation-based nonsmooth-integral control for PMSM drive system. IEEE/ASME Trans. Mechatron. 2024, 29, 3602–3613. [Google Scholar] [CrossRef]
- Li, J.; Shang, Z.; Li, R.; Cui, B. Adaptive Sliding Mode Path Tracking Control of Unmanned Rice Transplanter. Agriculture 2022, 12, 1225. [Google Scholar] [CrossRef]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Ding, S.; Zhang, B.; Mei, K.; Park, J.H. Adaptive fuzzy SOSM controller design with output constraints. IEEE Trans. Fuzzy Syst. 2021, 30, 2300–2311. [Google Scholar] [CrossRef]
- Liu, L.; Ding, S.; Yu, X. Second-order sliding mode control design subject to an asymmetric output constraint. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 1278–1282. [Google Scholar] [CrossRef]
- Yuan, J.; Ding, S.; Mei, K. Fixed-time SOSM controller design with output constraint. Nonlinear Dyn. 2020, 102, 1567–1583. [Google Scholar] [CrossRef]
- Mei, K.; Liu, J.; Ding, S. Output feedback SOSM control of constrained systems with unmatched uncertainties. IEEE Trans. Autom. Sci. Eng. 2024, 22, 7786–7797. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Ding, S.; Xia, J.; Xing, G. Adaptive disturbance observer-based fixed-time nonsingular terminal sliding mode control for path-tracking of unmanned agricultural tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Cui, B.; Cui, X.; Wei, X.; Zhu, Y.; Ma, Z.; Zhao, Y.; Liu, Y. Design and Testing of a Tractor Automatic Navigation System Based on Dynamic Path Search and a Fuzzy Stanley Model. Agriculture 2024, 14, 2136. [Google Scholar] [CrossRef]
- Li, H.; Mei, K.; Ding, S.; Ding, C.; Sun, J. Sampled-Data Output Feedback Control for Path Tracking of Unmanned Agricultural Vehicles. In Proceedings of the First International Conference on Advanced Robotics, Control, and Artificial Intelligence: ICARCAI 2024, Perth, Australia, 9–12 December 2024; Lecture Notes in Networks and Systems. Springer: Berlin/Heidelberg, Germany, 2025; Volume 1376. [Google Scholar]
- Qian, C.; Du, H. Global output feedback stabilization of a class of nonlinear systems via linear sampled-data control. IEEE Trans. Autom. Control. 2012, 57, 2934–2939. [Google Scholar] [CrossRef]
- Zeng, H.B.; Zhai, Z.L.; Xiao, H.Q.; Wang, W. Stability analysis of sampled-data control systems with constant communication delays. IEEE Access 2018, 7, 111–116. [Google Scholar] [CrossRef]
- Liu, W.; Lim, C.; Shi, P.; Xu, S. Sampled-data fuzzy control for a class of nonlinear systems with missing data and disturbances. Fuzzy Sets Syst. 2017, 306, 63–86. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, Y.; Zheng, W.; Zou, Y. Stability of Sampled-data systems with packet losses: A nonuniform sampling interval approach. IEEE Trans. Cybern. 2023, 53, 7648–7658. [Google Scholar] [CrossRef] [PubMed]
- Tsinias, J. A theorem on global stabilization of nonlinear systems by linear feedback. Syst. Control. Lett. 1991, 17, 357–362. [Google Scholar] [CrossRef]
- Qian, C.; Lin, W. Output feedback control of a class of nonlinear systems: A nonseparation principle paradigm. IEEE Trans. Autom. Control. 2002, 47, 1710–1715. [Google Scholar] [CrossRef]
- Marsh, A. Past Forward: The Starting Line for Self-Driving Cars: 20 Years Ago, Stanley Won the DARPA Grand Challenge, But the Tech is Still Niche. IEEE Spectr. 2025, 1–4. [Google Scholar]
- Jin, X.; Chen, W.; Ma, H.; Kong, J.; Su, T.; Bai, Y. Parameter-Free State Estimation Based on Kalman Filter with Attention Learning for GPS Tracking in Autonomous Driving System. Sensors 2023, 23, 8650. [Google Scholar] [CrossRef]
- Ligeza, P. Reconstructing the trajectory of the object’s motion on the basis of measuring the components of its velocity. Measurement 2023, 221, 113546. [Google Scholar] [CrossRef]
| Notations | Descriptions | Dimension |
|---|---|---|
| Lateral offset | -/m | |
| Heading offset | -/rad | |
| Turning angle of front wheel | -/rad | |
| Wheelbase | 0.9 m | |
| Real angle of AAT | -/rad | |
| Planned angle at tracking point | -/rad | |
| v | Velocity of AAT | 1 m/s |
| Curvature of reference path | - |
| Couple | Parameters Choice |
|---|---|
| Couple 1 | ; ; |
| Couple 2 | ; ; |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Mei, K.; Ma, L.; Ding, S.; Ding, C. State Observer-Based Sampled-Data Control for Path Tracking of Autonomous Agricultural Tractor. Actuators 2025, 14, 300. https://doi.org/10.3390/act14060300
Li H, Mei K, Ma L, Ding S, Ding C. State Observer-Based Sampled-Data Control for Path Tracking of Autonomous Agricultural Tractor. Actuators. 2025; 14(6):300. https://doi.org/10.3390/act14060300
Chicago/Turabian StyleLi, Haozhe, Keqi Mei, Li Ma, Shihong Ding, and Chen Ding. 2025. "State Observer-Based Sampled-Data Control for Path Tracking of Autonomous Agricultural Tractor" Actuators 14, no. 6: 300. https://doi.org/10.3390/act14060300
APA StyleLi, H., Mei, K., Ma, L., Ding, S., & Ding, C. (2025). State Observer-Based Sampled-Data Control for Path Tracking of Autonomous Agricultural Tractor. Actuators, 14(6), 300. https://doi.org/10.3390/act14060300






