Three-Dimensional Modelling and Validation for the Ultra-High-Speed EDS Rocket Sled with PM Halbach Array
Abstract
1. Introduction
2. Structural Design of the Rocket Sled
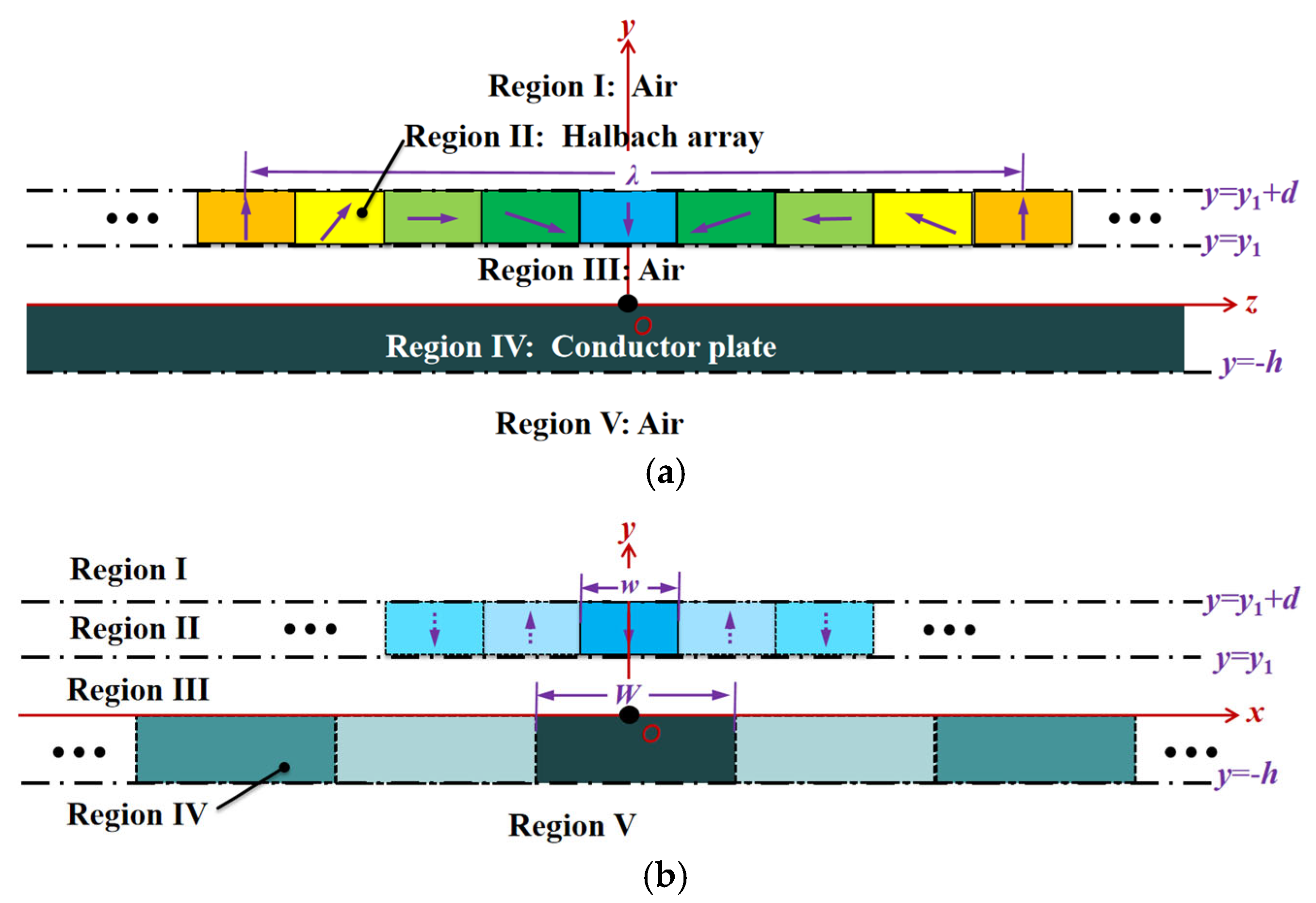
3. Three-Dimensional Electromagnetic Modelling
3.1. Magnetization Vector Expansion
3.2. Governing Equations in Each Region
3.3. General Solutions to Governing Equations
3.4. Boundary Conditions
3.5. Analytic Formulas of Electromagnetic Forces
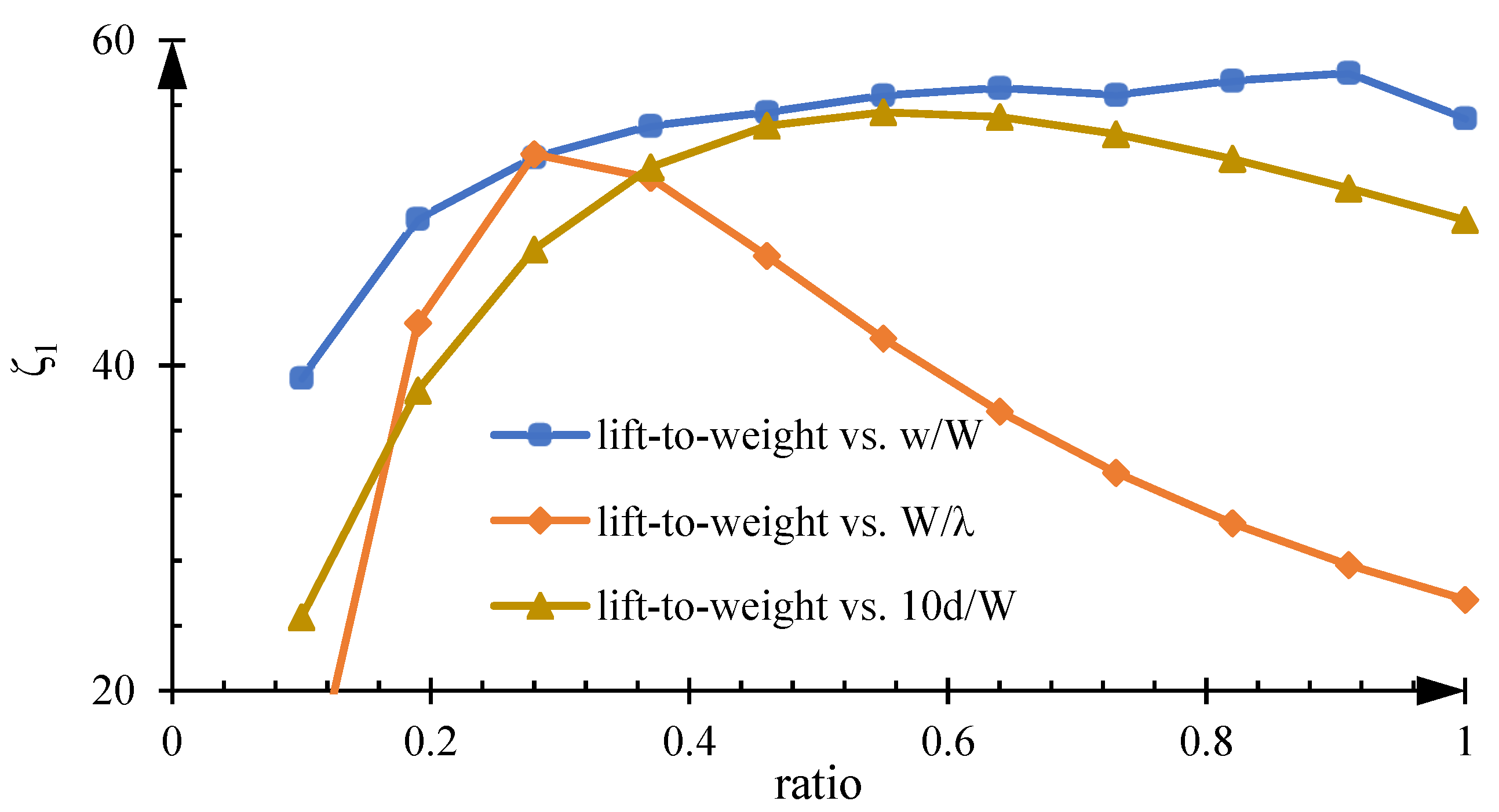
4. Structural Optimization
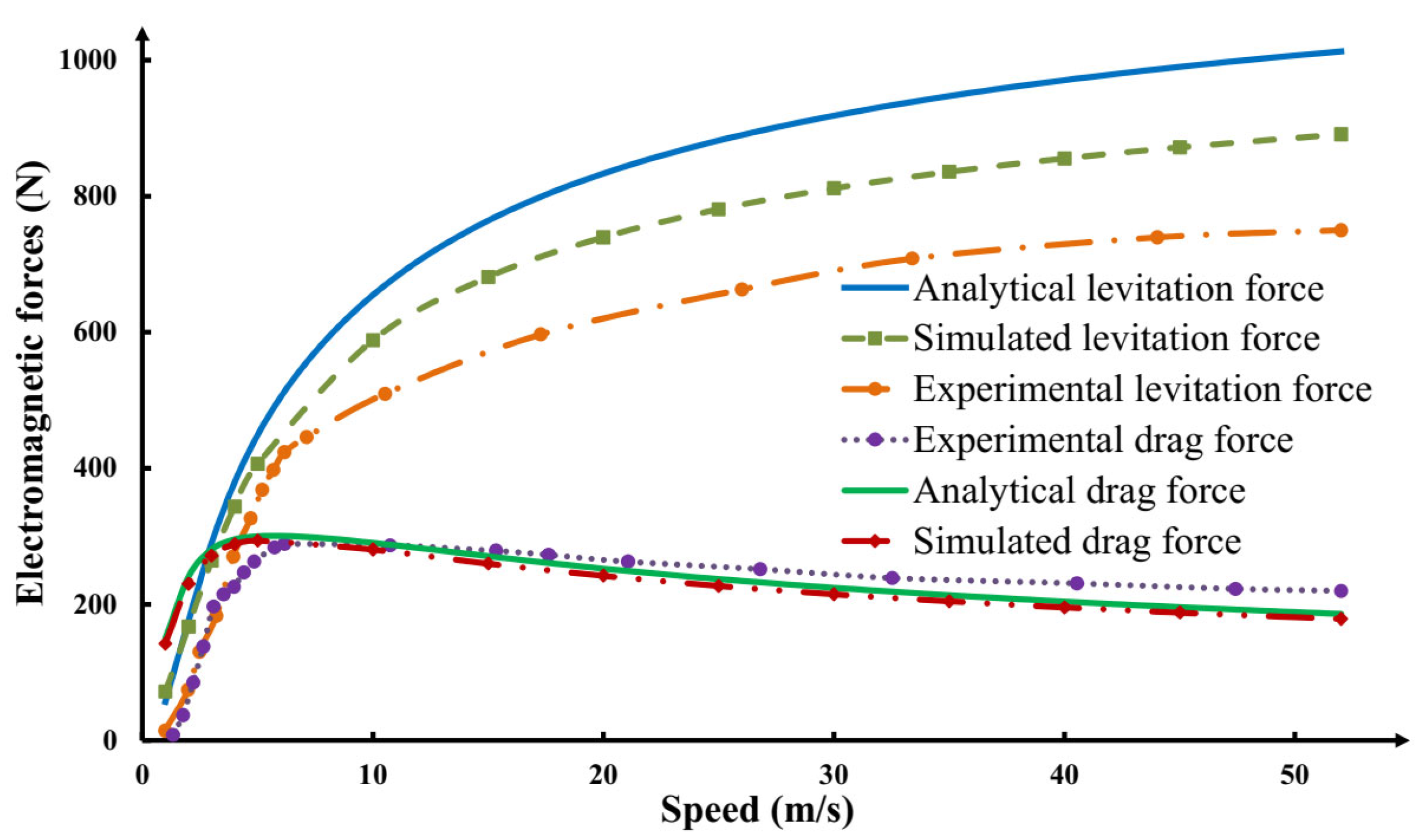
5. Simulation Verification
6. Experimental Verification
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Long, Z.Q.; Li, X.L.; Cheng, H. Research on Permanent-Electromagnetic Levitation Technology and Application; Shanghai Scientific and Technical Publishers: Shanghai, China, 2019. [Google Scholar]
- Cinnamon, J.D.; Palazotto, A.N.; Szmerekovsky, A.G. Further Refinement of Material Models for Hypervelocity Gouging Impacts. AIAA J. 2018, 46, 317–327. [Google Scholar] [CrossRef]
- Hooser, M. 6 DoF Model of the Holloman High Speed Test Track Maglev Sled. In Proceedings of the US Air Force T&E Days, Nashville, Tennessee, 2–4 February 2010; p. 1706. [Google Scholar]
- Minto, D. Recent increases in hypersonic test capabilities at the Holloman High Speed Test Track. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2000; p. 154. [Google Scholar]
- Hsu, Y.; Langhorn, A.; Ketchen, D.; Holland, L.; Minto, D.; Doll, D. Magnetic levitation upgrade to the Holloman high speed test track. IEEE Trans. Appl. Supercond. 2009, 19, 2074–2077. [Google Scholar] [CrossRef]
- Gurol, H.; Ketchen, D.; Holland, L.; Minto, D.; Hooser, M.; Bosmajian, N. Status of the Holloman high speed MagLev test track (HHSMTT). In Proceedings of the 30th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2655. [Google Scholar]
- Xuesong, Q.; Qianyuan, S.; Zikang, S.; Yuhang, L.; Bin, W. Analysis of the magnetic levitation characteristics of the vertical Halbach array in a permanent magnet rotor. Nonlinear Dyn. 2025, 113, 397–412. [Google Scholar] [CrossRef]
- Li, Q.; Ma, C.; Gao, F. Nonlinear model for Halbach array axial flux permanent magnet motor in stator and rotor reference frames based on harmonic modeling technique. IEEE Trans. Magn. 2024, 60, 8201811. [Google Scholar] [CrossRef]
- Vatani, M.; Chulaee, Y.; Mohammadi, A.; Stewart, D.R.; Eastham, J.F.; Ionel, D.M. On the optimal design of coreless AFPM machines with Halbach array rotors for electric aircraft propulsion. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 19–21 June 2024; pp. 1–6. [Google Scholar]
- Hu, Y.P.; Long, Z.Q.; Xu, Y.S.; Wang, Z.Q. Control-oriented modeling for the electrodynamic levitation with permanent magnet Halbach array. Int. J. Appl. Electromagn. Mech. 2021, 67, 375–3921. [Google Scholar] [CrossRef]
- Shi, H.; Deng, Z.; Ke, Z.; Li, Z.; Zhang, W. Linear permanent magnet electrodynamic suspension system: Dynamic characteristics, magnetic-mechanical coupling and field test. Measurement 2024, 225, 113960. [Google Scholar] [CrossRef]
- Shi, H.; Ke, Z.; Zheng, J.; Xiang, Y.; Ren, K.; Lin, P.; Li, K.; Liang, L.; Deng, Z. An effective optimization method and implementation of permanent magnet electrodynamic wheel for Maglev car. IEEE Trans. Veh. Technol. 2023, 72, 8369–8381. [Google Scholar] [CrossRef]
- Sun, H.; Cheng, S.S. A cylindrical Halbach array magnetic actuation system for longitudinal robot actuation across 2D workplane. IEEE Robot. Autom. Lett. 2024, 9, 5847–5854. [Google Scholar] [CrossRef]
- Shi, H.; Wu, S.; Ke, Z.; Deng, Z.; Zhang, W. Speed-Range-Based Novel Guideway Configuration with Variable Material and Thickness for PMECB. IEEE Trans. Instrum. Meas. 2024, 73, 2514913. [Google Scholar] [CrossRef]
- Hirde, A.; Khardenavis, A.; Banerjee, R.; Bose, M.; Hari, V.S.P.K. Energy and emissions analysis of the hyperloop transportation system. Environ. Dev. Sustain. 2023, 25, 8165–8196. [Google Scholar] [CrossRef]
- Wang, B.; Luo, S.; Ma, W.; Li, G.; Wang, Z.; Xu, J.; Zhang, X. A fast dynamic model of a two-sided permanent magnet electrodynamic suspension system in a maglev train. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2023, 237, 996–1008. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, K.; Zhang, H. Effect of the passive damping plate on the vertical stability of permanent magnet electrodynamic suspension system. IET Electr. Power Appl. 2024, 18, 107–115. [Google Scholar] [CrossRef]
- Flankl, M.; Wellerdieck, T.; Tüysüz, A.; Kolar, J.W. Scaling laws for electrodynamic suspension in high-speed transportation. IET Electr. Power Appl. 2018, 12, 357–364. [Google Scholar] [CrossRef]
- Qin, W.; Ma, Y.; Lv, G.; Wang, F.; Zhao, J. New Levitation Scheme with Traveling Magnetic Electromagnetic Halbach Array for EDS Maglev System. IEEE Transactions on Magnetics 2022, 58, 8300106. [Google Scholar] [CrossRef]
- Liu, J.; Cao, T.; Deng, Z.; Shi, H.; Liang, L.; Wu, X.; Jiang, S. Damping characteristics improvement of permanent magnet electrodynamic suspension by utilizing the end-effect of onboard magnets. Electr. Eng. 2024, 106, 15–29. [Google Scholar] [CrossRef]
- Long, Z.Q.; He, G.; Xue, S. Study of EDS & EMS Hybrid Suspension System with Permanent-Magnet Halbach Array. IEEE Trans. Magn. 2011, 47, 4717–4724. [Google Scholar]
- Hu, Y.P.; Long, Z.Q.; Zeng, J.; Wang, Z.Q. Analytical Optimization of Electrodynamic Suspension for Ultrahigh-Speed Ground Transportation. IEEE Trans. Magn. 2021, 57, 8000511. [Google Scholar] [CrossRef]




| M | 2 | 4 | 6 | 8 | 10 | 12 |
| 0.41 | 0.81 | 0.91 | 0.95 | 0.97 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Chen, B.; Lin, G.; Wang, Z. Three-Dimensional Modelling and Validation for the Ultra-High-Speed EDS Rocket Sled with PM Halbach Array. Actuators 2025, 14, 225. https://doi.org/10.3390/act14050225
Hu Y, Chen B, Lin G, Wang Z. Three-Dimensional Modelling and Validation for the Ultra-High-Speed EDS Rocket Sled with PM Halbach Array. Actuators. 2025; 14(5):225. https://doi.org/10.3390/act14050225
Chicago/Turabian StyleHu, Yongpan, Baojun Chen, Guobin Lin, and Zhiqiang Wang. 2025. "Three-Dimensional Modelling and Validation for the Ultra-High-Speed EDS Rocket Sled with PM Halbach Array" Actuators 14, no. 5: 225. https://doi.org/10.3390/act14050225
APA StyleHu, Y., Chen, B., Lin, G., & Wang, Z. (2025). Three-Dimensional Modelling and Validation for the Ultra-High-Speed EDS Rocket Sled with PM Halbach Array. Actuators, 14(5), 225. https://doi.org/10.3390/act14050225








