The Design of a Turning Tool Based on a Self-Sensing Giant Magnetostrictive Actuator
Abstract
1. Introduction
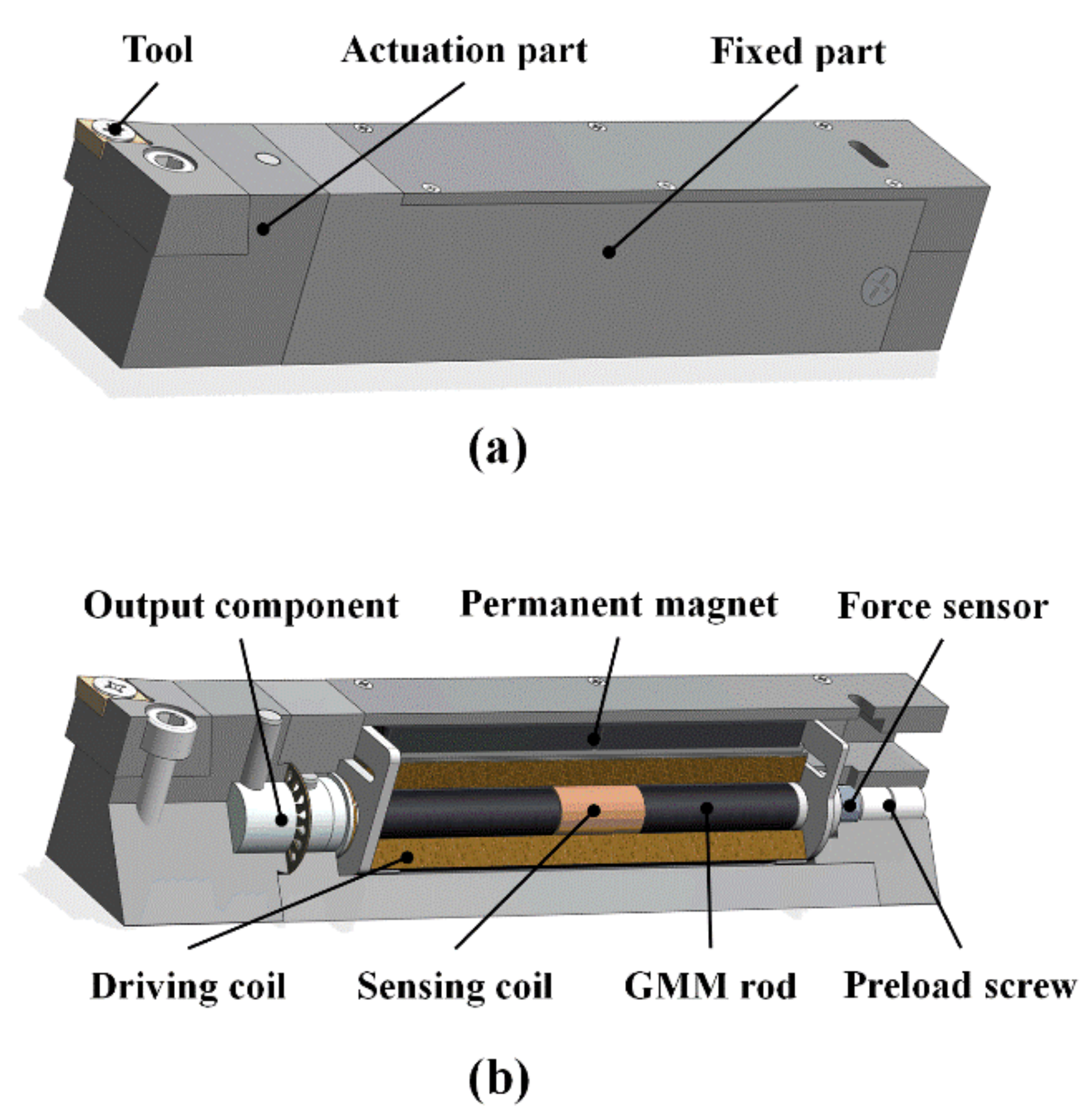
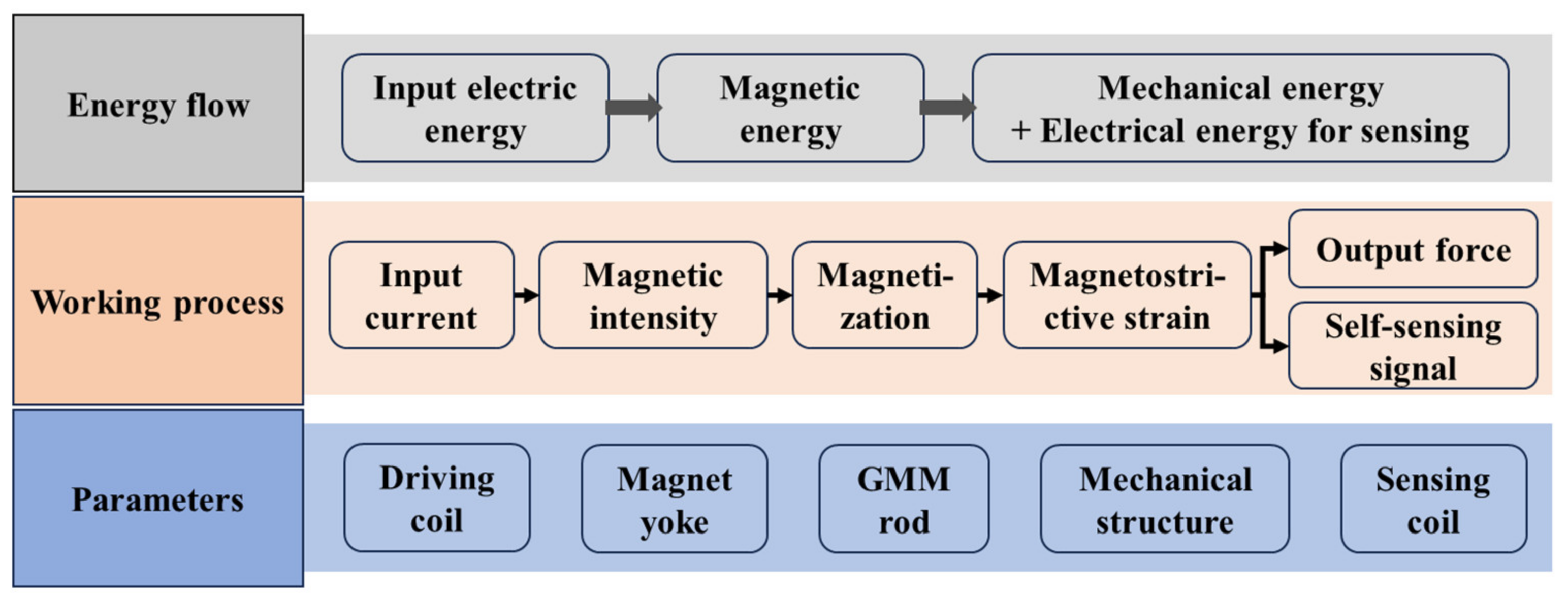
2. Working Principle and Structure Scheme
3. Optimization of Structural Parameters
3.1. Parameter Analysis
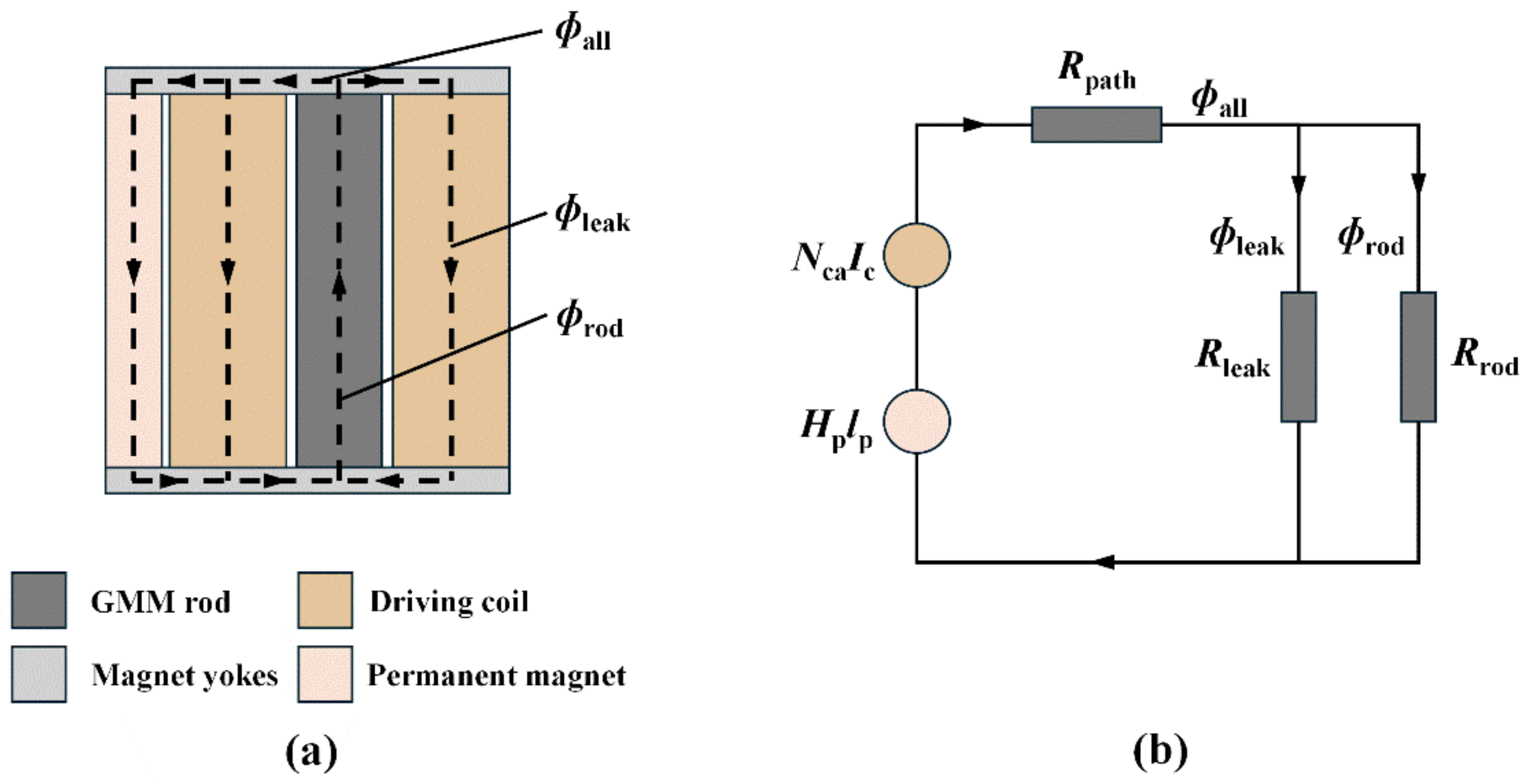
- Drive coil energy loss analysis
- II.
- Drive magnetic field strength analysis
- III.
- Energy loss analysis of the magnetic yoke
- IV.
- Analysis of sensor coil design parameters
- V.
- Natural frequency analysis of the system
- VI.
- Quality analysis of key components
3.2. Multi-Objective Parameter Optimization Model and Results
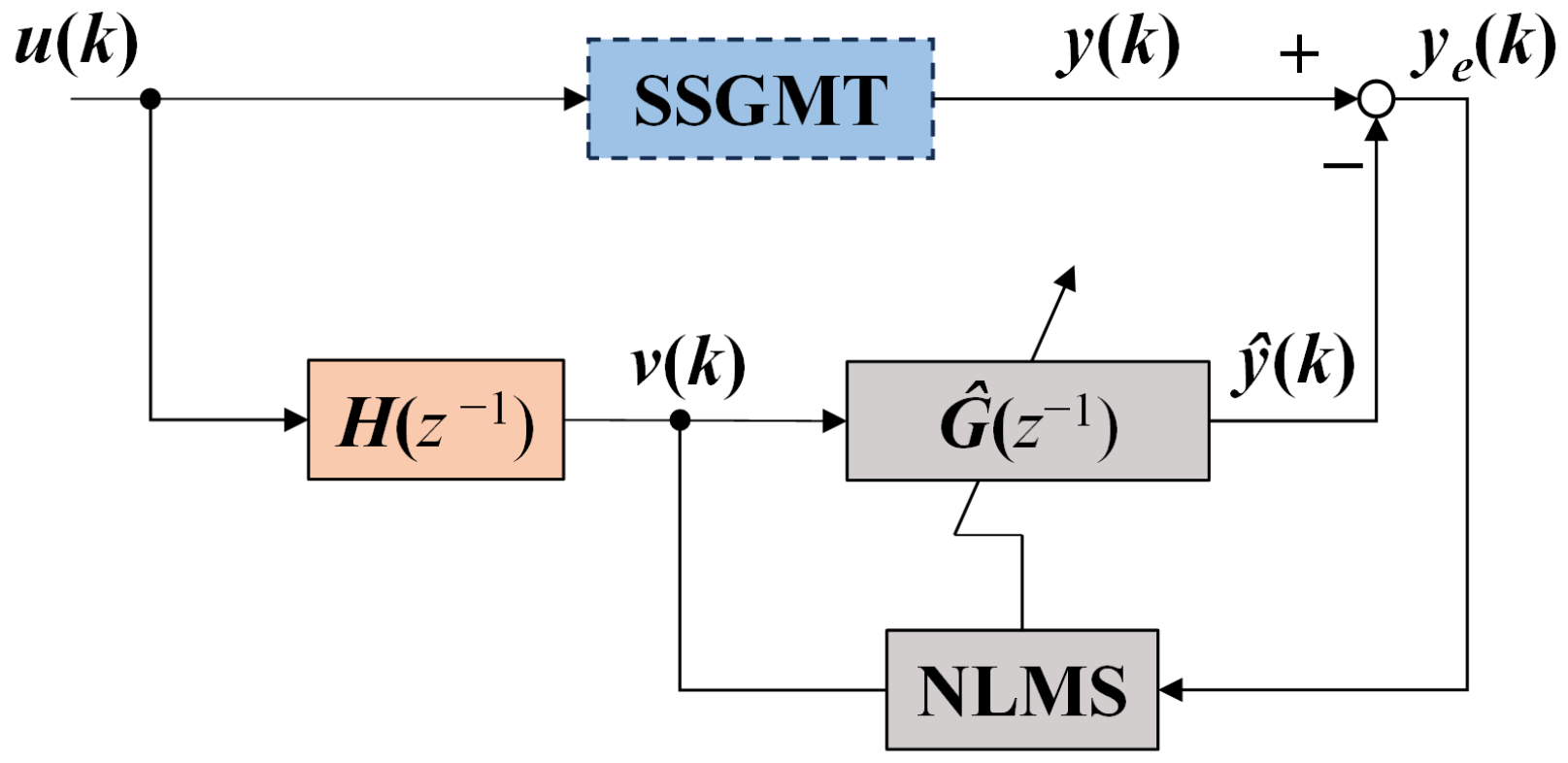
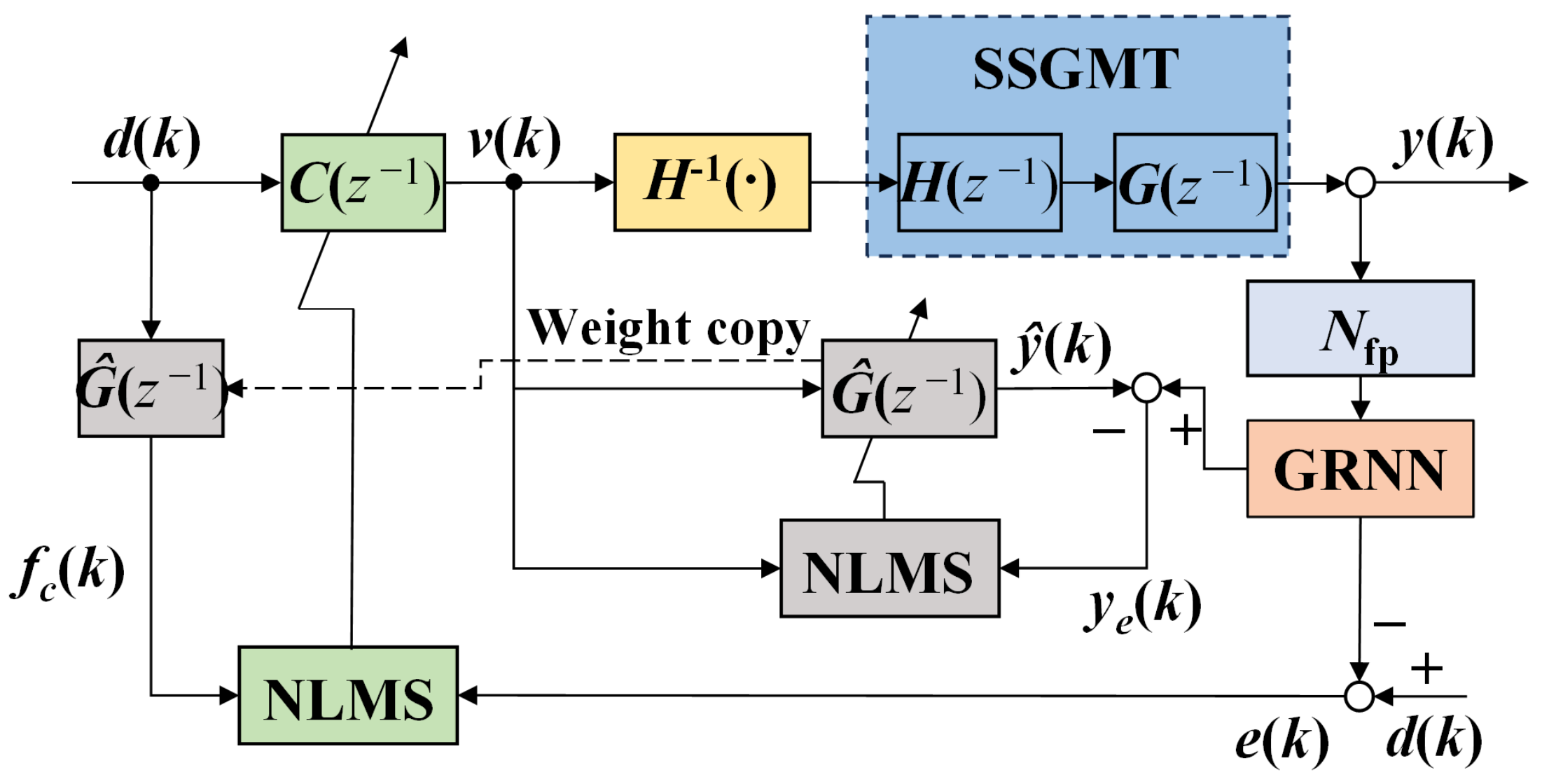
4. Controller Design
5. Experimental Verification
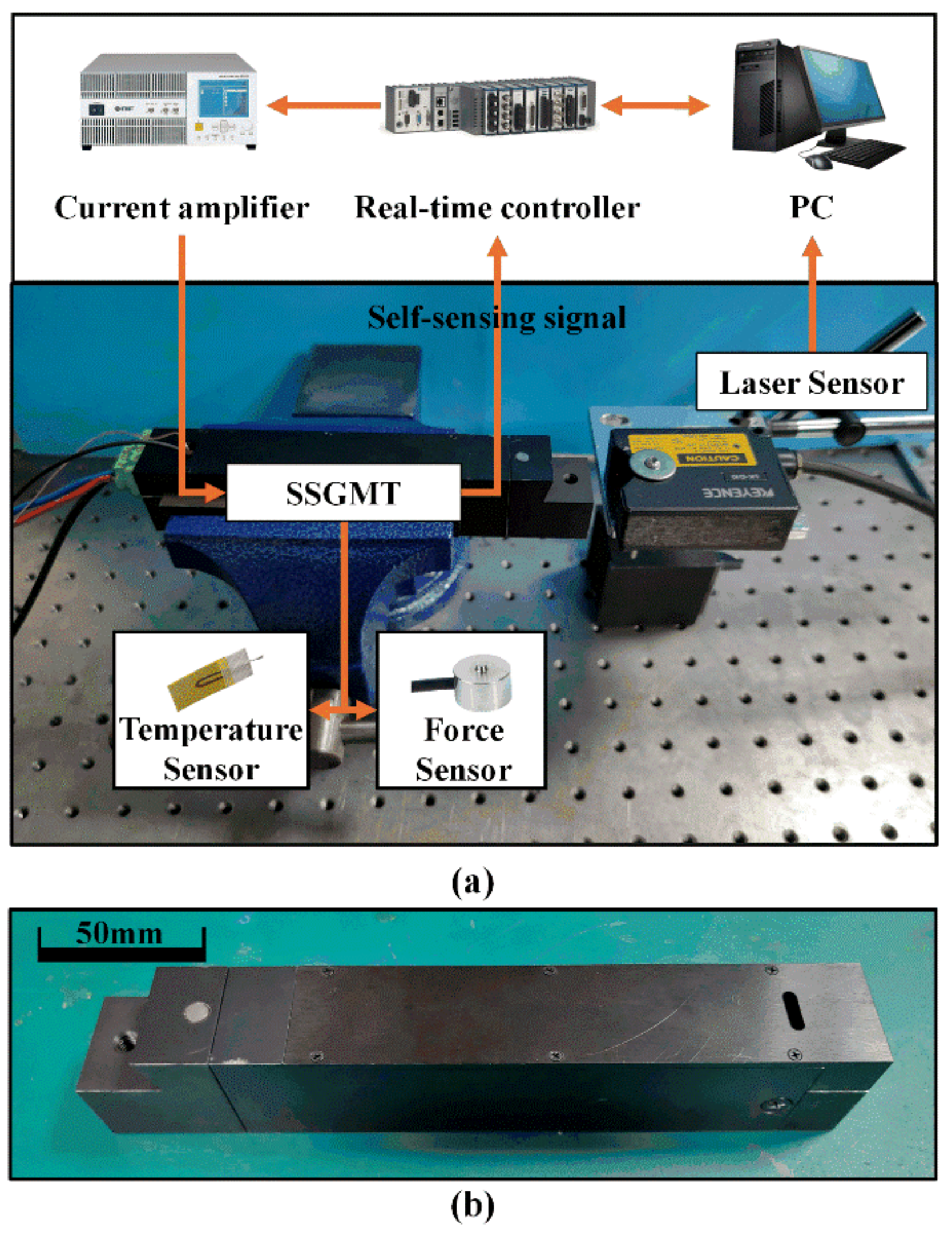
5.1. Experimental Setup
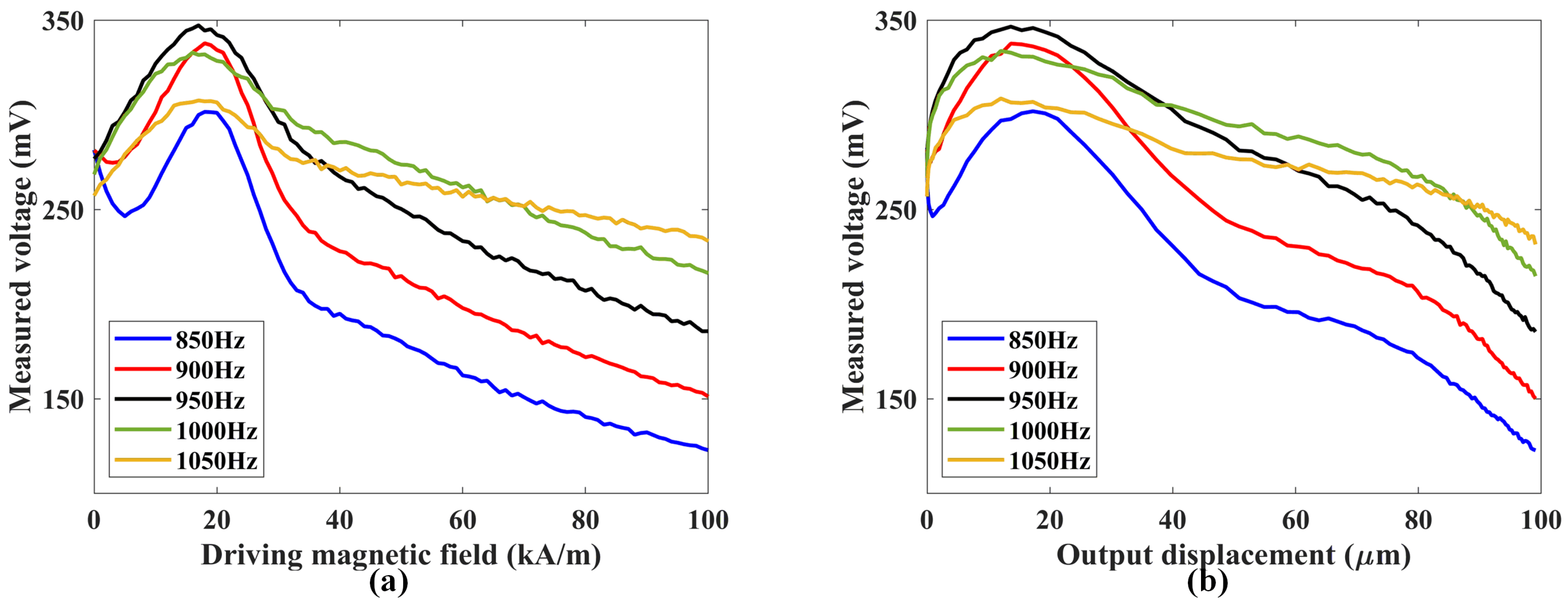
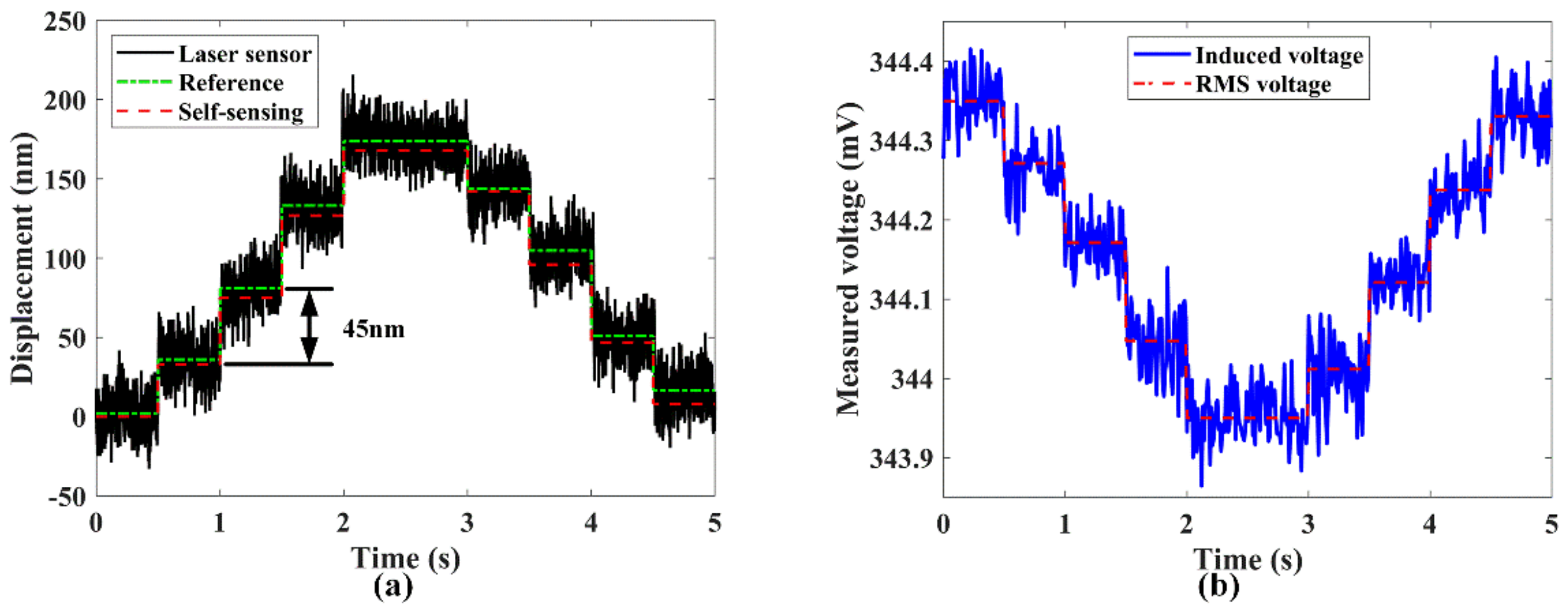
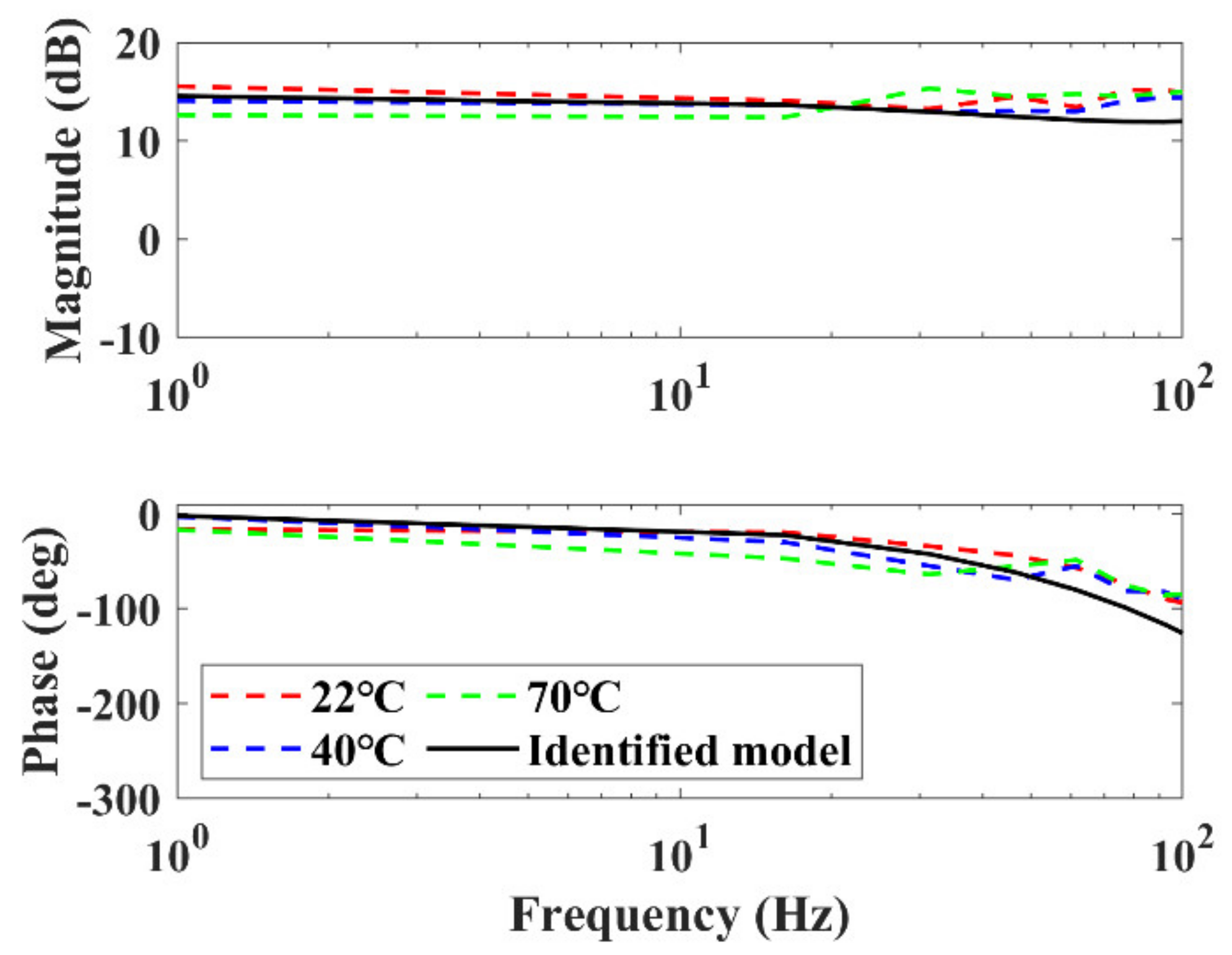
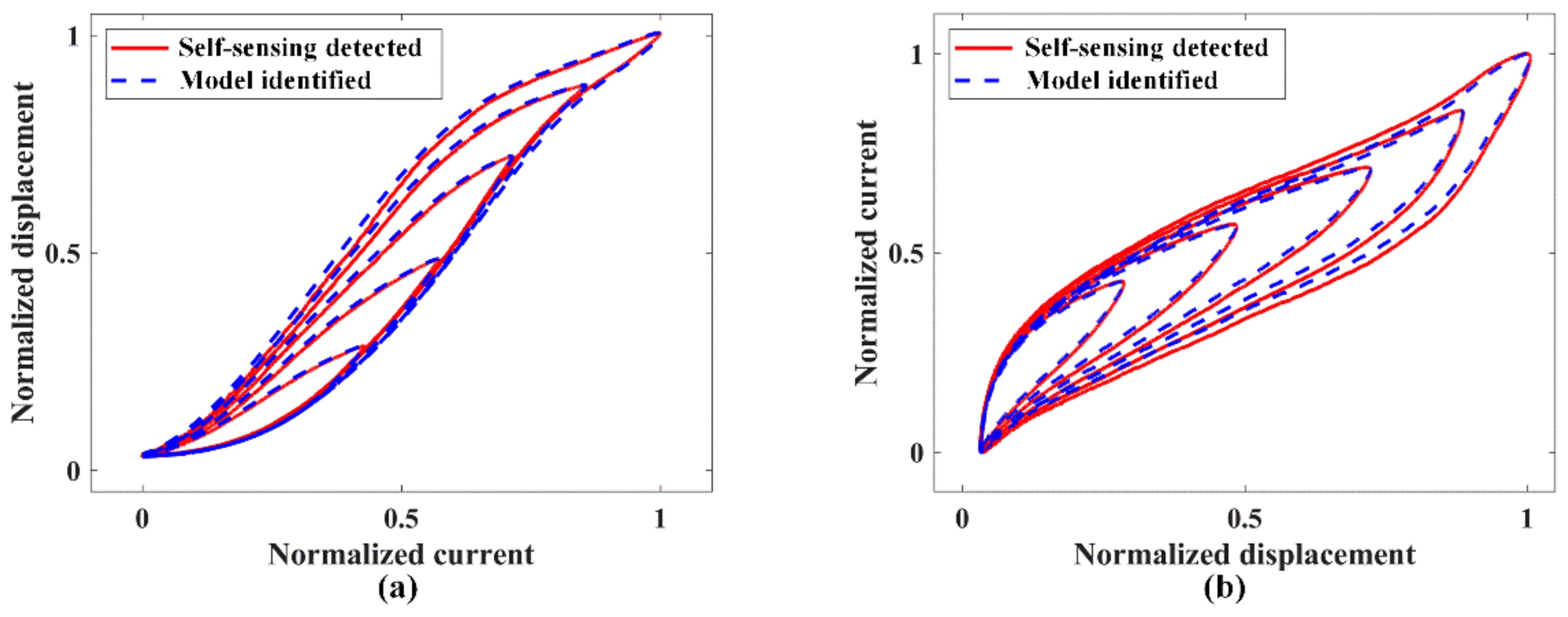
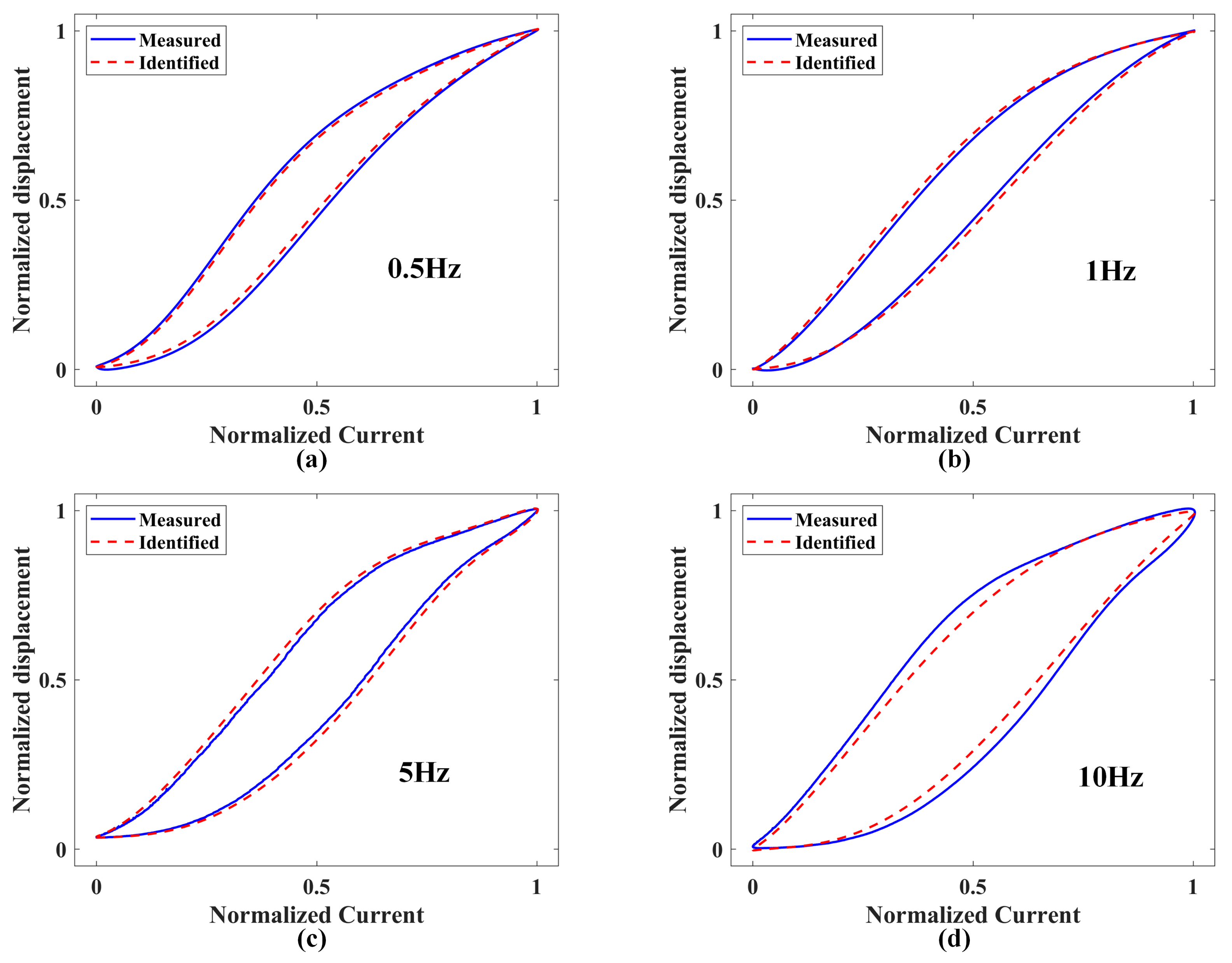
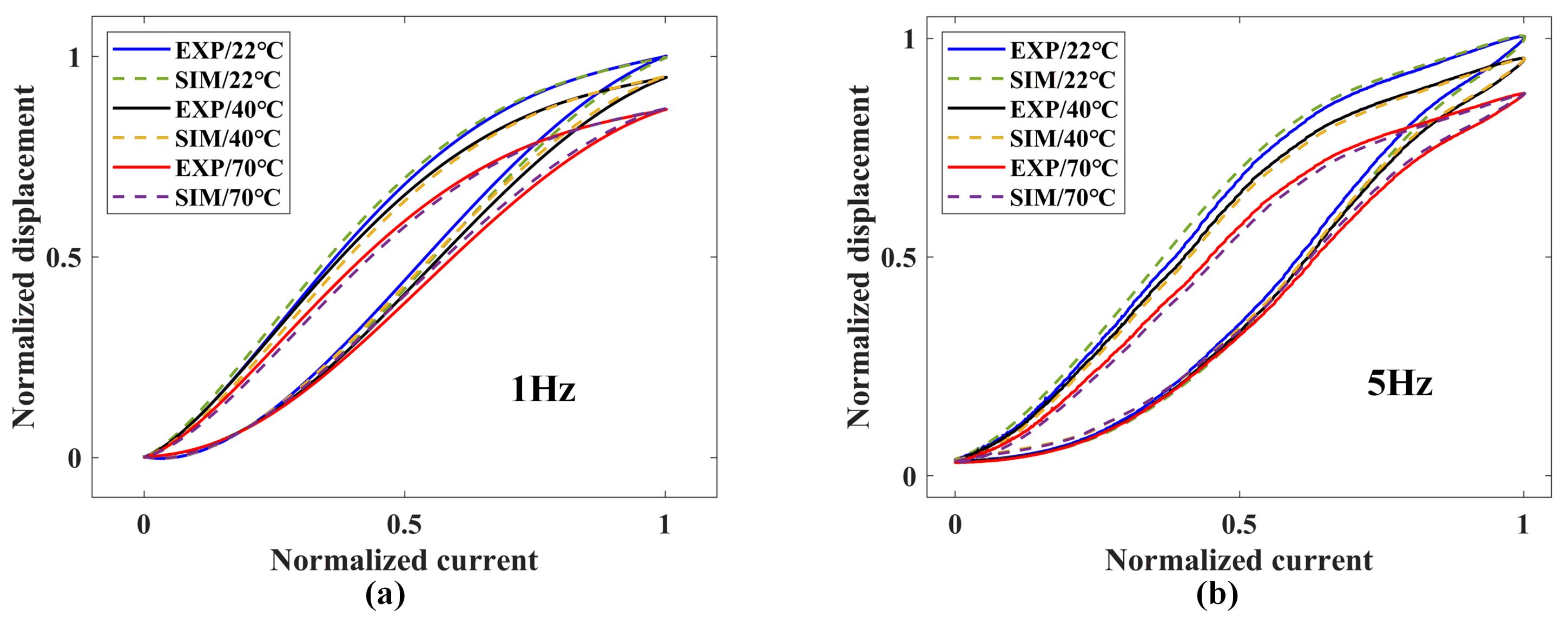
5.2. Self-Sensing Output Displacement Performance Test
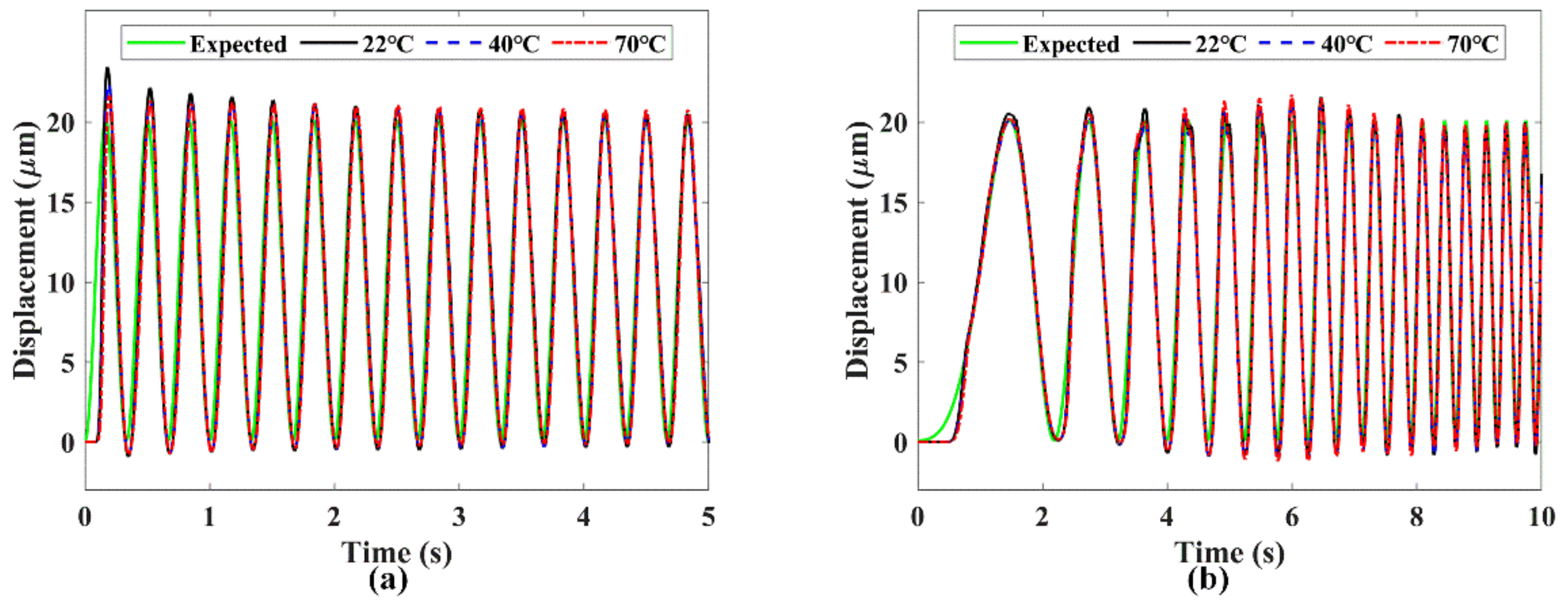
5.3. Trajectory Tracking Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bleicher, F.; Biermann, D.; Drossel, W.-G.; Moehring, H.-C.; Altintas, Y. Sensor and Actuator Integrated Tooling Systems. CIRP Ann. 2023, 72, 673–696. [Google Scholar] [CrossRef]
- Zhou, C.; Guo, K.; Sun, J. An Integrated Wireless Vibration Sensing Tool Holder for Milling Tool Condition Monitoring with Singularity Analysis. Measurement 2021, 174, 109038. [Google Scholar] [CrossRef]
- Bleicher, F.; Ramsauer, C.M.; Oswald, R.; Leder, N.; Schoerghofer, P. Method for Determining Edge Chipping in Milling Based on Tool Holder Vibration Measurements. CIRP Ann. 2020, 69, 101–104. [Google Scholar] [CrossRef]
- Zhang, P.; Gao, D.; Lu, Y.; Ma, Z.; Wang, X.; Song, X. Cutting Tool Wear Monitoring Based on a Smart Toolholder with Embedded Force and Vibration Sensors and an Improved Residual Network. Measurement 2022, 199, 111520. [Google Scholar] [CrossRef]
- Mohamed, A.; Hassan, M.; M’Saoubi, R.; Attia, H. Tool Condition Monitoring for High-Performance Machining Systems—A Review. Sensors 2022, 22, 2206. [Google Scholar] [CrossRef]
- Mishra, D.; Pattipati, K.R.; Bollas, G.M. Intelligent Feature Engineering for Monitoring Tool Health in Machining. In Industry 4.0 Driven Manufacturing Technologies; Kumar, A., Kumar, P., Liu, Y., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 37–67. ISBN 978-3-031-68271-1. [Google Scholar]
- Deshpande, S.; Araujo, A.C.; Lagarrigue, P. Identification of Material Layer During Helical Milling Process on Aerospace Stacks Using Spindle Power Data; Elsevier: Amsterdam, The Netherlands, 2025. [Google Scholar]
- Hu, S.; Yang, Y.; Bao, W.; Nie, Y. Research on the Control System and Method of Cutting Arms for Digital Twin Driven Excavation Equipment. In Proceedings of the 2024 9th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 19–21 April 2024; pp. 1475–1480. [Google Scholar]
- Huber, J.E.; Fleck, N.A.; Ashby, M.F. The Selection of Mechanical Actuators Based on Performance Indices. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1997, 453, 2185–2205. [Google Scholar] [CrossRef]
- Ceyssens, F.; Sadeghpour, S.; Fujita, H.; Puers, R. Actuators: Accomplishments, Opportunities and Challenges. Sens. Actuators A Phys. 2019, 295, 604–611. [Google Scholar] [CrossRef]
- Wang, S.; Rong, W.; Wang, L.; Xie, H.; Sun, L.; Mills, J.K. A Survey of Piezoelectric Actuators with Long Working Stroke in Recent Years: Classifications, Principles, Connections and Distinctions. Mech. Syst. Signal Process. 2019, 123, 591–605. [Google Scholar] [CrossRef]
- De Vicente, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R. Magnetorheological Fluids: A Review. Soft Matter 2011, 7, 3701–3710. [Google Scholar] [CrossRef]
- Maiwald, D.; Bucht, A.; Zorn, W.; Drossel, W.-G. Development Approach of Actuators for High Loads Based on Shape Memory Alloys. In Proceedings of the ASME 2020 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Virtual, Online, 15 September 2020. [Google Scholar]
- Yoshioka, H.; Shinno, H.; Sawano, H. A Newly Developed Rotary-Linear Motion Platform with a Giant Magnetostrictive Actuator. CIRP Ann. 2013, 62, 371–374. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, X.; Liu, Z.; Wang, R.; Zhu, L. Development of a Piezoelectrically Actuated Two-Degree-of-Freedom Fast Tool Servo with Decoupled Motions for Micro-/Nanomachining. Precis. Eng. 2014, 38, 809–820. [Google Scholar] [CrossRef]
- Li, H.; Ibrahim, R.; Cheng, K. Design and Principles of an Innovative Compliant Fast Tool Servo for Precision Engineering. Mech. Sci. 2011, 2, 139–146. [Google Scholar] [CrossRef]
- Huang, W.-W.; Li, L.; Zhu, Z.; Zhu, L.-M. Modeling, Design and Control of Normal-Stressed Electromagnetic Actuated Fast Tool Servos. Mech. Syst. Signal Process. 2022, 178, 109304. [Google Scholar] [CrossRef]
- Yoshioka, H.; Kojima, K.; Toyota, D. Micro Patterning on Curved Surface with a Fast Tool Servo System for Micro Milling Process. CIRP Ann. 2020, 69, 325–328. [Google Scholar] [CrossRef]
- Xie, D.; Yang, Y.; Zhang, Y.; Yang, B. Precision Positioning Based on Temperature Dependence Self-Sensing Magnetostrictive Actuation Mechanism. Int. J. Mech. Sci. 2024, 272, 109174. [Google Scholar] [CrossRef]
- Xie, D.; Yang, Y.; Yang, B. Self-Sensing Magnetostrictive Actuator Based on ΔE Effect: Design, Theoretical Modeling and Experiment. Smart Mater. Struct. 2022, 31, 055007. [Google Scholar] [CrossRef]
- Kim, H.-S.; Lee, K.-I.; Lee, K.-M.; Bang, Y.-B. Fabrication of Free-Form Surfaces Using a Long-Stroke Fast Tool Servo and Corrective Figuring with on-Machine Measurement. Int. J. Mach. Tools Manuf. 2009, 49, 991–997. [Google Scholar] [CrossRef]
- Zhong, E.; Wang, S.; Zhai, C.; Li, W. Improved Non-Singular Fast Terminal Sliding Mode Control with Hysteresis Compensation for Piezo-Driven Fast Steering Mirrors. Actuators 2025, 14, 170. [Google Scholar] [CrossRef]
- Sun, X.; Liu, Y.; Hu, W.; Sun, T.; Hu, J. Design Optimization of a Giant Magnetostrictive Driving System for Large Stroke Application Considering Vibration Suppression in Working Process. Mech. Syst. Signal Process. 2020, 138, 106560. [Google Scholar] [CrossRef]
- Sun, X.; Wei, H.; Liu, Y.; Wang, Z.; Jun, H. Integrated Design and Simulation of a Giant Magnetostrictive Driving Positioning and Vibration Suppression System. J. Syst. Simul. 2021, 33, 358–365. [Google Scholar] [CrossRef]
- Barbisio, E.; Fiorillo, F.; Ragusa, C. Predicting Loss in Magnetic Steels under Arbitrary Induction Waveform and with Minor Hysteresis Loops. IEEE Trans. Magn. 2004, 40, 1810–1819. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle Swarm Optimization Algorithm: An Overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent Advances in Micro-Vibration Isolation. Mech. Syst. Signal Process. 2015, 56–57, 55–80. [Google Scholar] [CrossRef]
- Kuhnen, K. Modeling, Identification and Compensation of Complex Hysteretic Nonlinearities: A Modified Prandtl-Ishlinskii Approach. Eur. J. Control. 2003, 9, 407–418. [Google Scholar] [CrossRef]

| Parameter | Value Range | Result | Selected Value |
|---|---|---|---|
| rm (mm) | [4, 8] | 4.6 | 5 |
| ra2 (mm) | [8, 15] | 10.7 | 11 |
| lca (mm) | [100, 110] | 104.6 | 105 |
| dca (mm) | [0.25, 0.5] | 0.38 | 0.4 |
| lcs (mm) | [18, 25] | 20.3 | 20 |
| ty (mm) | [1.5, 3] | 2.2 | 2 |
| Parameter | Value Range |
|---|---|
| ŵH | [1.4208, −0.9671, −0.0229, 0.0435, 0.1561, −1.7034, 1.0543, −2.2107, 1.6592, −2.4592] |
| ŵp | [−7.9794, −5.3456, 5.0142, −0.8762, 3.3423] |
| Temperature (°C) | Sinusoidal Trajectory | Sweep Trajectory | ||
|---|---|---|---|---|
| RMS (µm) | RRMS (%) | RMS (µm) | RRMS (%) | |
| 22 | 0.976 | 2.37 | 1.056 | 2.60 |
| 40 | 1.038 | 2.53 | 1.129 | 2.79 |
| 70 | 1.113 | 2.70 | 1.259 | 3.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, D.; Wu, Q.; Zhang, Y.; Yang, Y.; Yang, B.; Zhang, C. The Design of a Turning Tool Based on a Self-Sensing Giant Magnetostrictive Actuator. Actuators 2025, 14, 302. https://doi.org/10.3390/act14060302
Xie D, Wu Q, Zhang Y, Yang Y, Yang B, Zhang C. The Design of a Turning Tool Based on a Self-Sensing Giant Magnetostrictive Actuator. Actuators. 2025; 14(6):302. https://doi.org/10.3390/act14060302
Chicago/Turabian StyleXie, Dongjian, Qibo Wu, Yahui Zhang, Yikun Yang, Bintang Yang, and Cheng Zhang. 2025. "The Design of a Turning Tool Based on a Self-Sensing Giant Magnetostrictive Actuator" Actuators 14, no. 6: 302. https://doi.org/10.3390/act14060302
APA StyleXie, D., Wu, Q., Zhang, Y., Yang, Y., Yang, B., & Zhang, C. (2025). The Design of a Turning Tool Based on a Self-Sensing Giant Magnetostrictive Actuator. Actuators, 14(6), 302. https://doi.org/10.3390/act14060302









