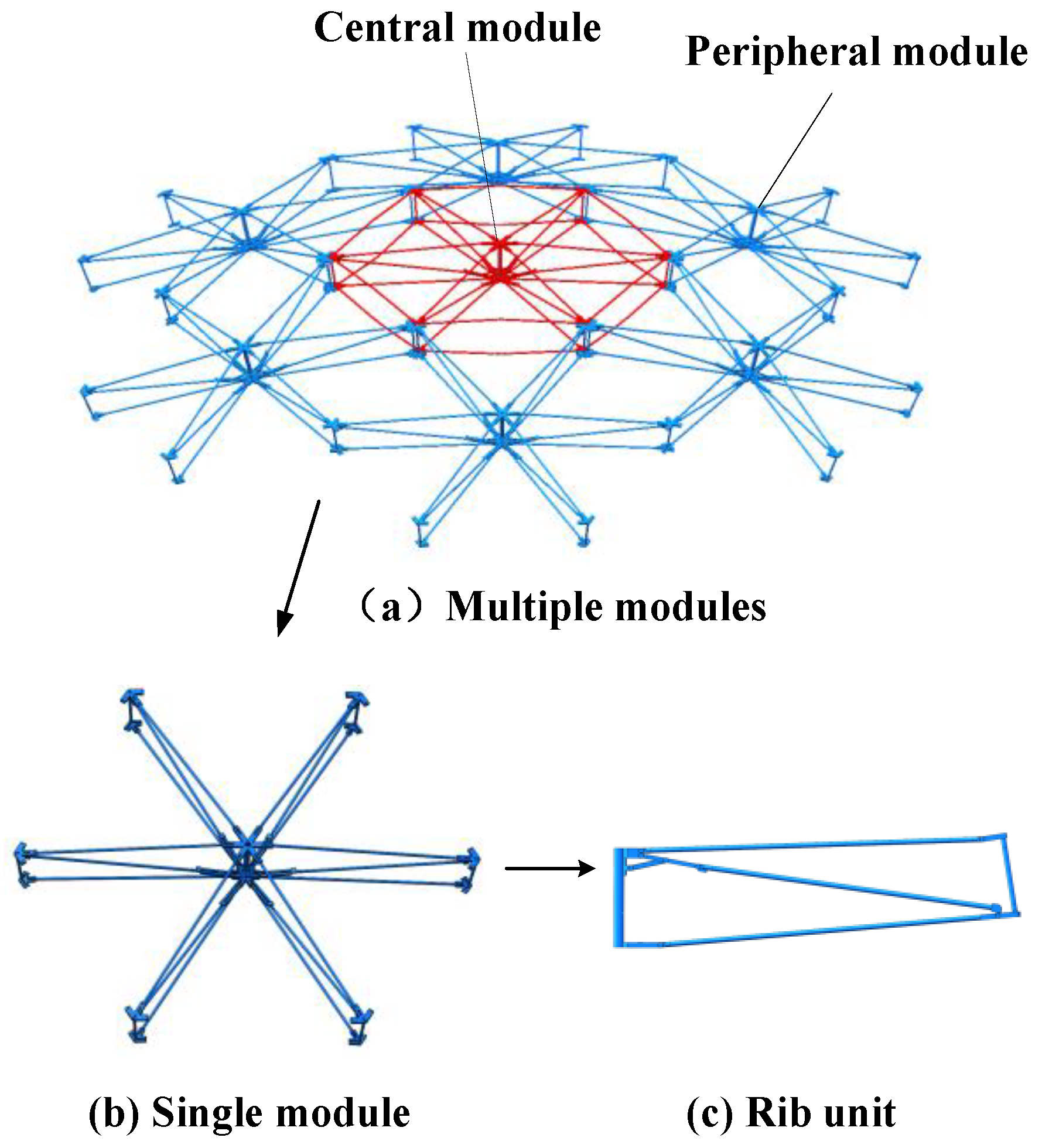
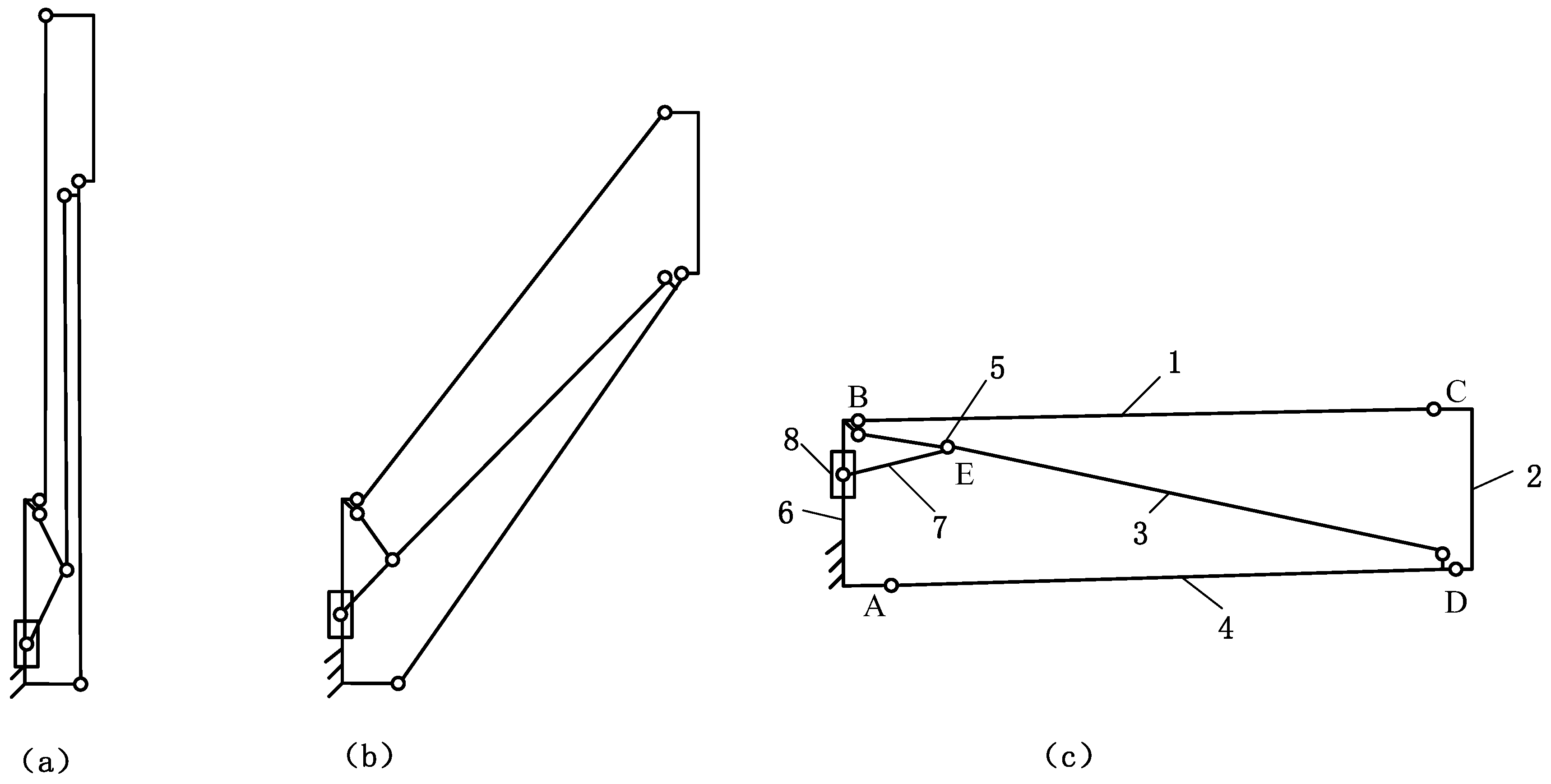
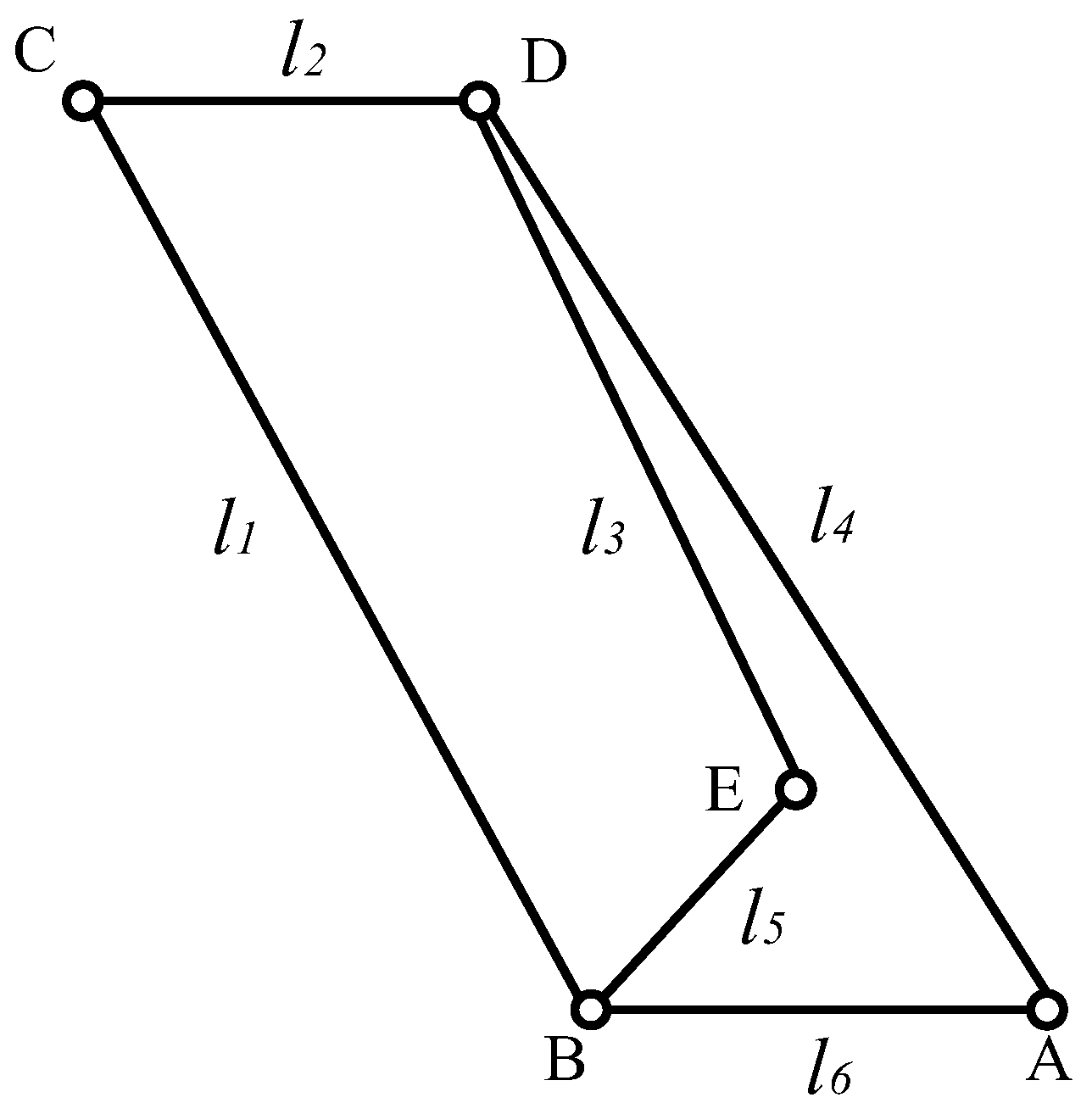
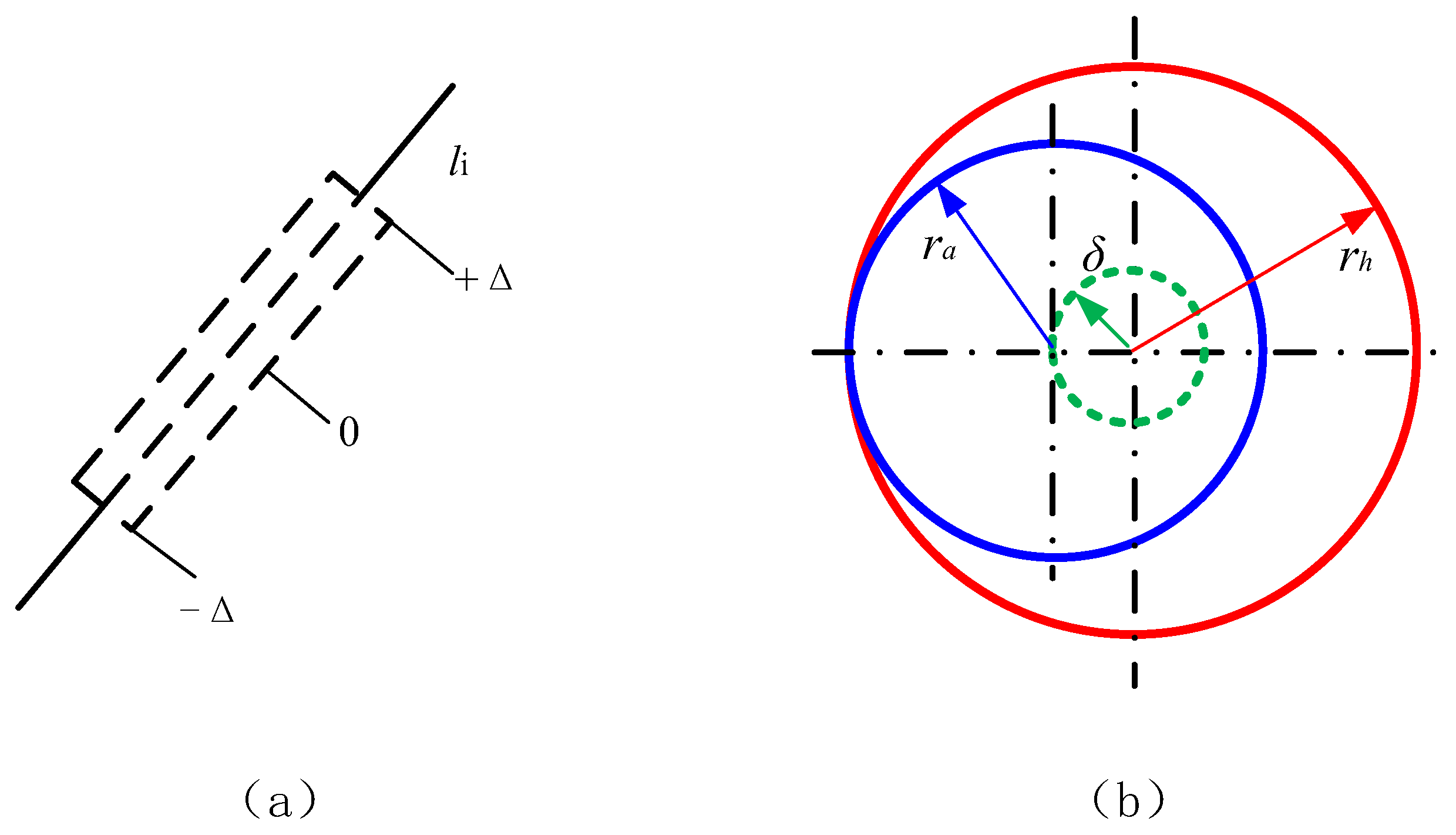
In modern radar, communication, and remote sensing technologies, reflector antennas serve as one of the core components, with their performance directly influencing the sensitivity, selectivity, and anti-interference capability of the system. Due to their complex geometric structures and multi-band sharing features, multi-frequency band reflector antennas have become a research hotspot in recent years [
1]. However, the deployment accuracy of such antennas has long been a critical factor limiting their practical applications. With the rise of modular deployable antenna technology, their potential in radar, communication, and remote sensing applications is gradually being recognized, but achieving a high-accuracy design for modular deployable antennas remains an urgent challenge [
2]. Precise antenna deployment requires not only highly consistent geometric positioning and orientation of reflector elements but also involves multi-faceted co-optimization of material properties, structural stiffness, and antenna-matching networks [
3]. Therefore, improving the deployment accuracy of modular deployable antennas not only requires breakthroughs in theoretical research but also the development of efficient and reliable numerical simulation and optimization methods. This study focuses on the accuracy design of modular deployable antennas, exploring novel ideas and methods to address the deployment accuracy challenges of multi-frequency band reflector antennas.
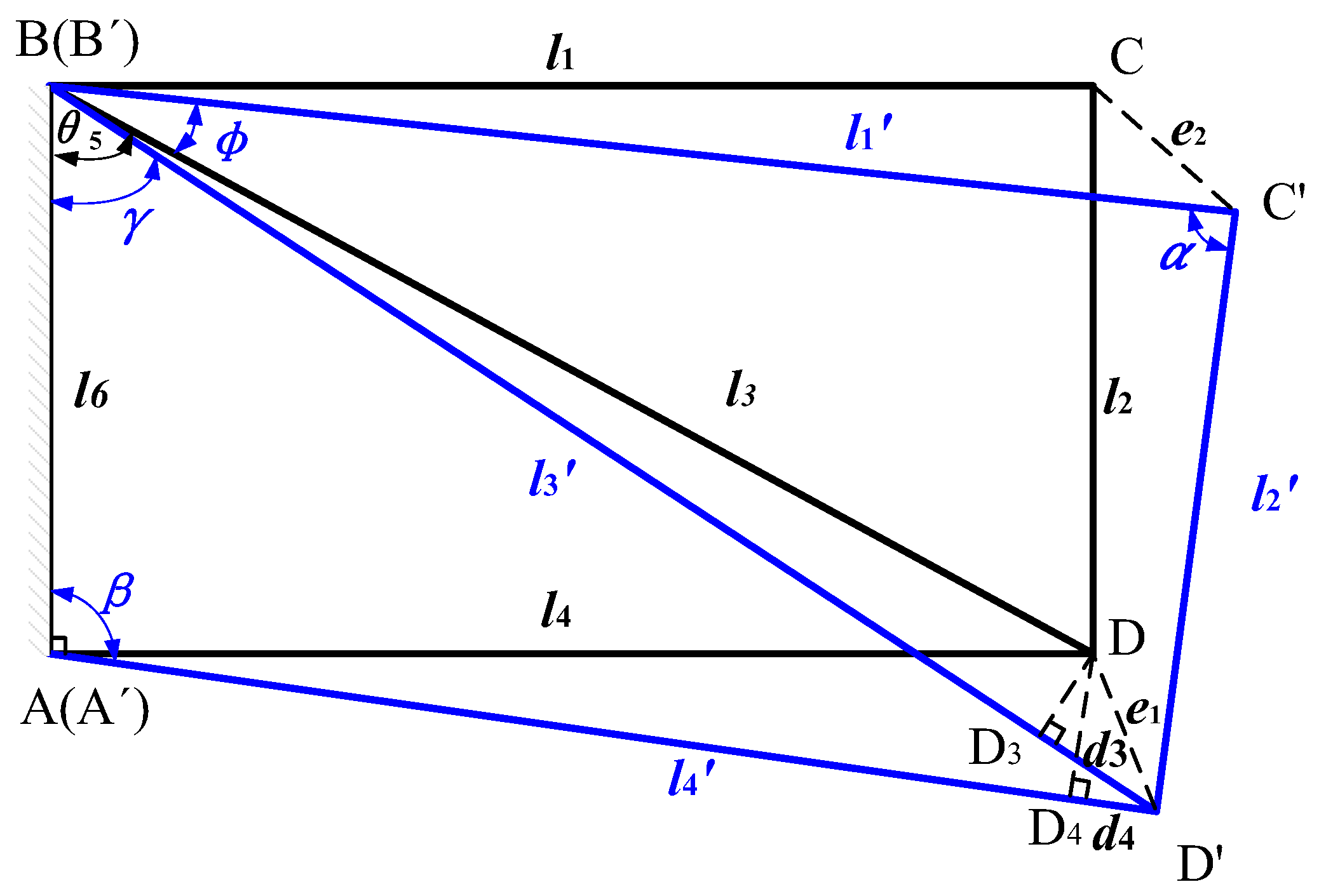
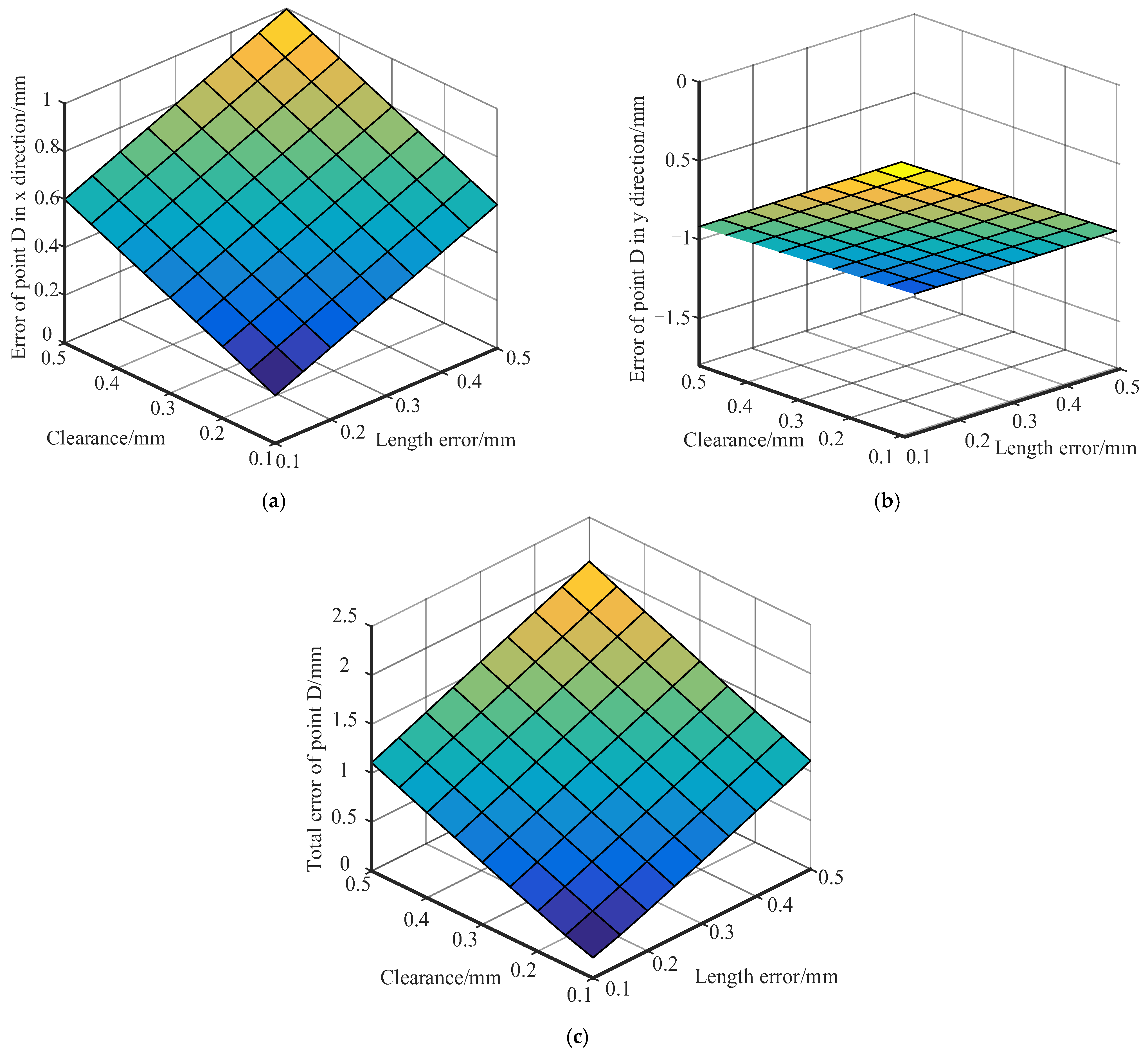
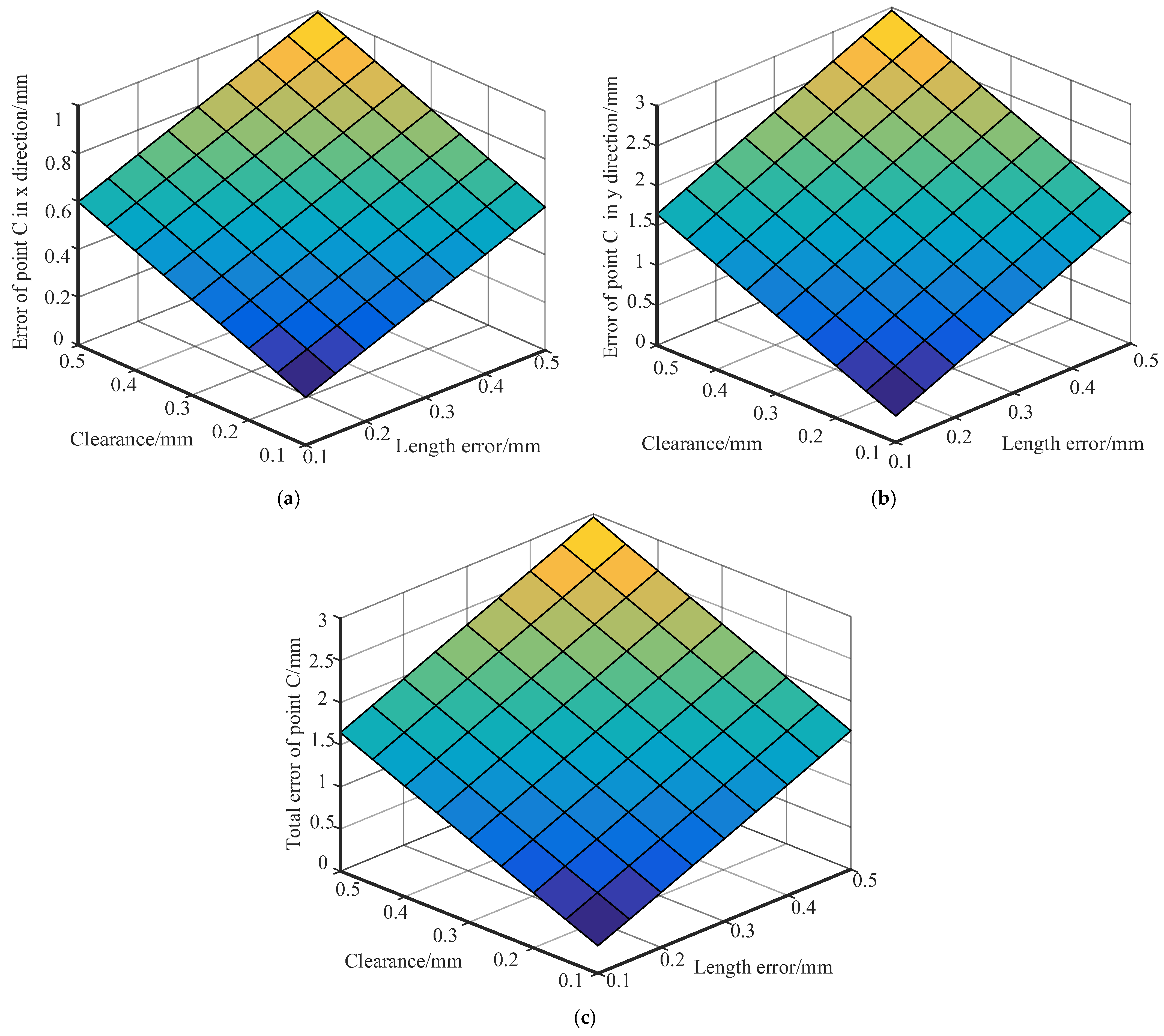
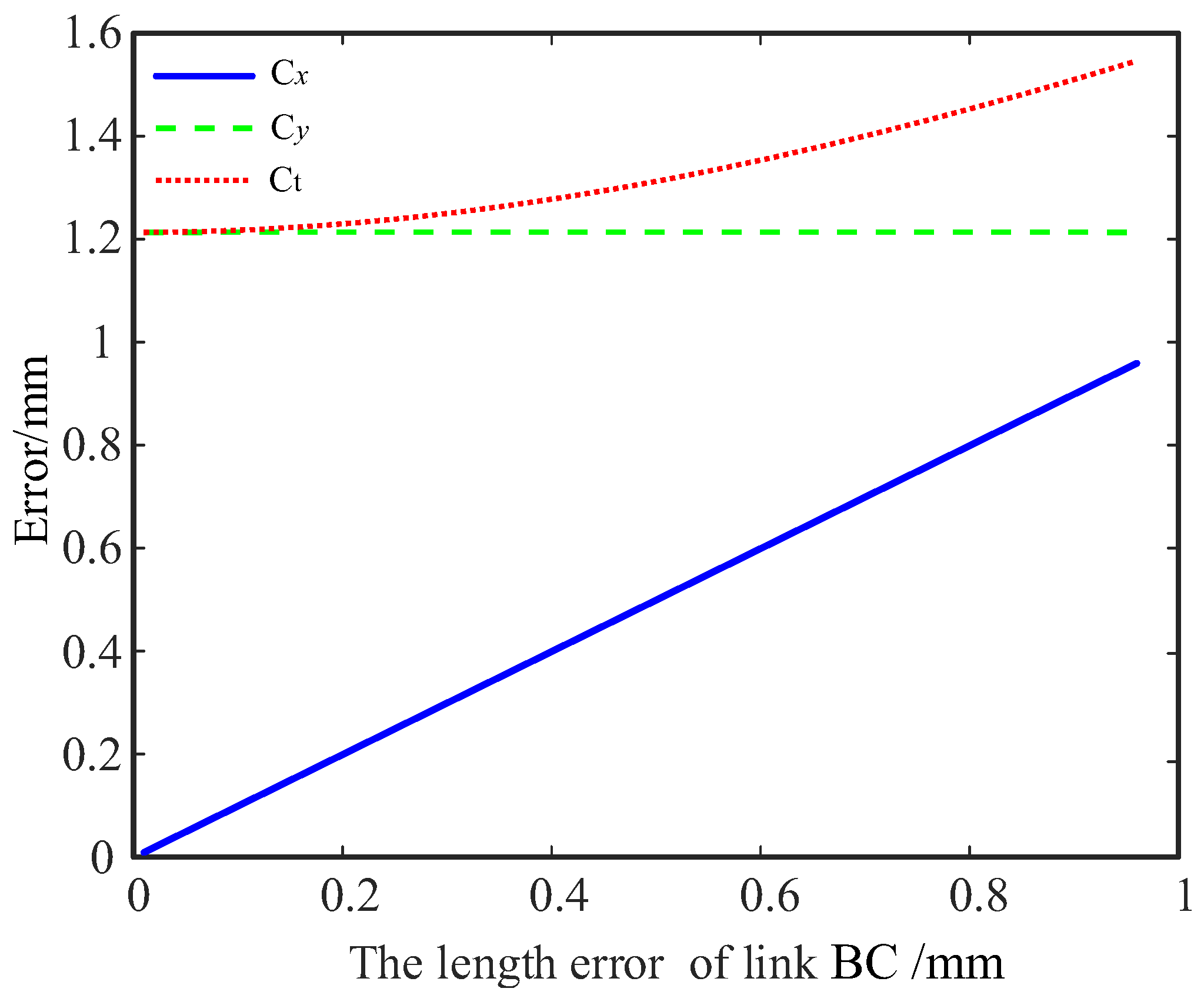
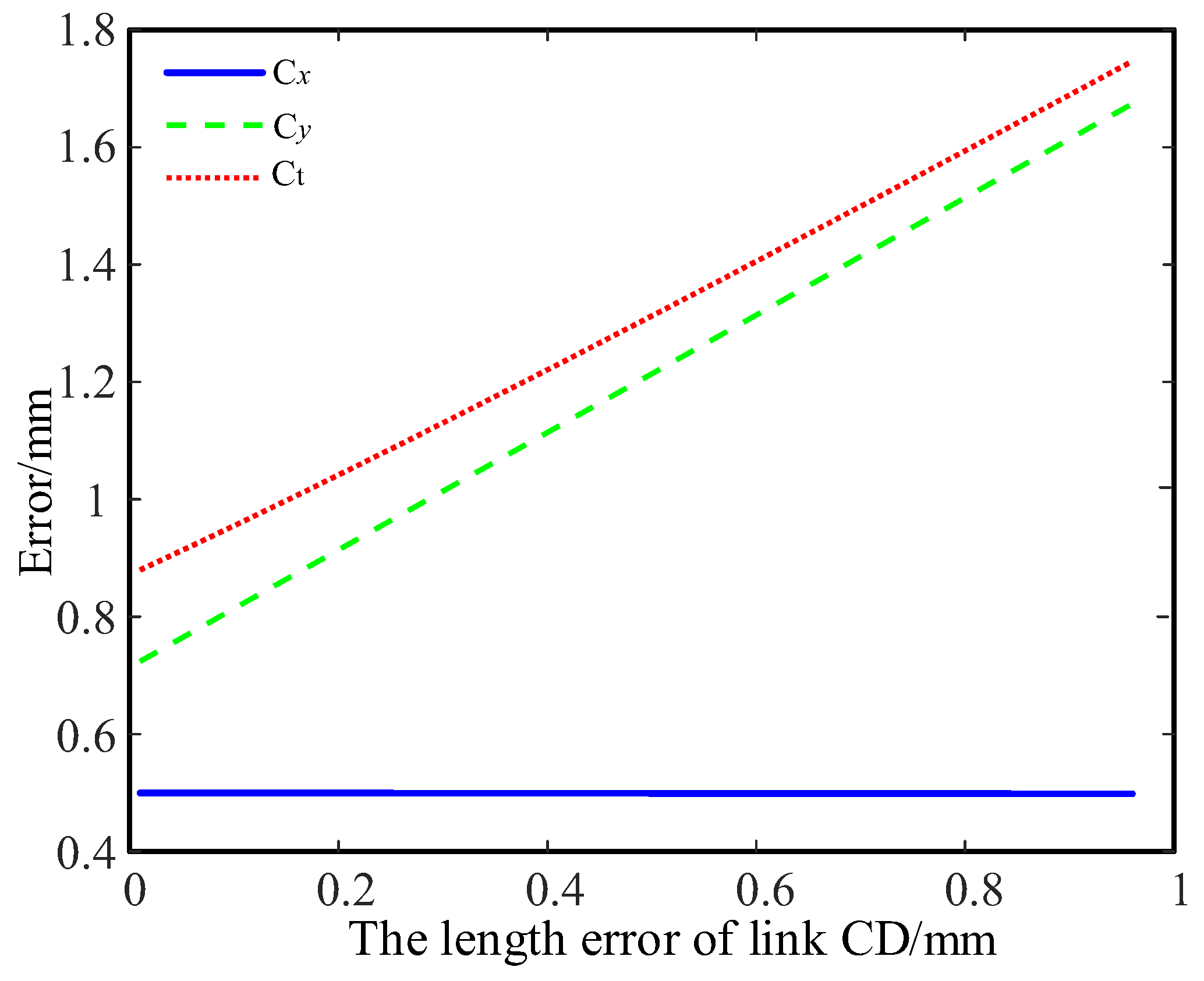
The deployment accuracy of modular deployable antennas is influenced by various factors, including machining accuracy, assembly accuracy, structural deformation, and component wear. Among these, rod length error and hinge gap error are the primary factors affecting the positional accuracy of the deployment mechanism [
4]. The accuracy design of modular deployable antennas is a crucial approach for enhancing deployment accuracy, with accuracy analysis and accuracy synthesis being its main components. Accuracy analysis aims to reveal the impact of various errors on the end accuracy. While accuracy synthesis is to formulate or reasonably allocate various error parameters according to the unfolding accuracy requirements of a specified mechanism, which is the inverse problem of mechanism accuracy analysis [
5]. At present, several research institutions and scholars worldwide have conducted in-depth research on this topic.
In terms of the accuracy analysis of mechanisms, Ding et al. [
6] proposed an accuracy analysis method based on matrix block modeling, decomposing complex deployment models into several single-loop mechanism computational models to separately evaluate the impact of hinge gaps on accuracy. Liu et al. [
7] introduced a direct linearization method, expressing component tolerances, hinge gaps, and deformation errors as linear vectors to establish a vector-loop model for mechanism closure, and calculated the positional deviation of the closed vector loop through homogeneous transformation matrices. Dong et al. [
8] proposed a modeling approach for mechanisms with hinge gaps based on massless rod models; this method employed the D-H method [
9] to construct geometric relationship models for three closed loops of an antenna and integrated the massless rod model into the mechanism’s error model. Chen et al. [
4] developed an accuracy analysis method that simultaneously accounts for hinge gaps and rod length error, by applying screw theory; they equated hinge gap and rod length error to virtual screws, established a comprehensive error model, and calculated the positional deviation at the open-chain output point using homogeneous transformation matrices. Ding et al. [
10] employed the vector differential method to create an error model for a six-degree-of-freedom parallel mechanism considering hinge gaps; they also proposed a pose accuracy analysis method based on Sobol sequence quasi-Monte Carlo simulation. Hafezipour et al. [
11] examined the effects of link dimension deviations and hinge gaps on the positional accuracy of spatial mechanisms and robotic end effector, proposed an error modeling formulation based on the direct linearization method. Some studies [
12,
13,
14,
15] conducted geometric error modeling and sensitivity analysis for parallel robots, identifying the primary factors influencing the accuracy of parallel mechanisms; Liu et al. [
16,
17] established an error model for a 4/2-type Stewart mechanism that considers bearing clearance and dimensional errors in the driving branches, based on the error model; they conducted a sensitivity analysis of various error components of the mechanism. In terms of the accuracy synthesis of mechanisms, Ni et al. [
18] designed a fully rotational parallel robot and modeled its errors, then conducted parameter tolerance design using a minimum-cost model. Liu et al. [
19] performed accuracy synthesis for the TriMule hybrid mechanism, with the objective function aimed at minimizing manufacturing costs and accuracy requirements as constraints. Han et al. [
20] established configuration optimization design criteria based on a sensitivity analysis of various parameters affecting the end accuracy of parallel mechanisms, enabling a multi-objective accuracy optimization design for the main structural parameters of parallel mechanisms. Gao et al. [
5] employed genetic algorithms for the optimized allocation of parameter tolerances for a 7-DOF robotic arm, with error minimization as the objective function and manufacturing costs as constraints. Yao et al. [
21] constructed an accuracy synthesis model to minimize manufacturing costs under accuracy constraints and solved the optimization problem using genetic algorithms. Wu et al. [
22] established an error model for a 3-DOF parallel robot using the closed-loop vector method, conducting sensitivity analysis via the Sobol sequence-based quasi-Monte Carlo (Sobol-QMC) method, to formulate an accuracy synthesis objective function targeting minimal manufacturing costs, and determine reasonable tolerance ranges for various errors using genetic algorithms.
Currently, most domestic and foreign scholars use screw theory or differential methods for precision analysis, but there are many limitations. For example, the differential method requires establishing a multi-single error model first when solving precision problems for complex models, and then combining the mechanism’s position equation for differential solving, making the process extremely complex. Screw theory expresses errors using screws and represents the posture of components through coordinate homogeneous transformations, but when dealing with multi-loop coupled models, the coordination relationships between loops are not considered, which will lead to imprecise error analysis. Based on geometric relationships, this paper establishes a multi-loop error model, converts the deformation coordination of coupled loops into a nonlinear equation group, and solves it by using numerical solution methods.