Time-Jerk Optimal Robotic Trajectory Planning Under Jerk and Continuity Constraints via Convex Optimization

Abstract

This paper proposes a robot trajectory planning method focused on time and jerk optimization under compound constraints. First, the robot path-tracking task is parameterized by incorporating both kinematic and dynamic constraints in joint and Cartesian spaces, establishing a time-optimal trajectory optimization model. To achieve C³ continuity in joint motion, joint-motion continuity conditions are analyzed, and optimization variables are reconstructed using piecewise cubic splines with corresponding continuity constraints. Considering the nonlinear and nonconvex characteristics of jerk constraints, the time-optimal planning model is decomposed into two second-order cone programming (SOCP) subproblems, achieving linear convexification of the original problem. Additionally, the objective function is improved to optimize both time and joint jerk simultaneously. Experimental results confirm that the proposed method effectively improves robot efficiency and trajectory smoothness.

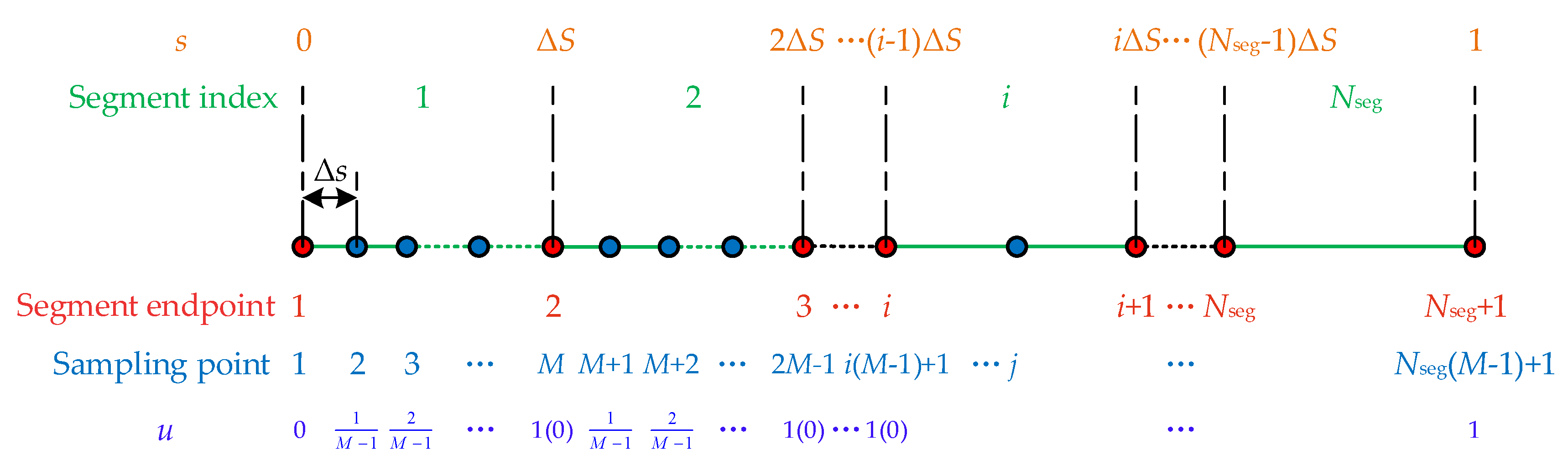
1. Introduction

With the advancement of robotics technology, robotic manipulators are increasingly used in various fields of production and manufacturing due to their high flexibility and low cost. Motion planning is one of the essential technologies in robotic applications and a key research focus. Research on robot motion planning mainly involves two stages: path planning and trajectory planning. A robot path refers to the geometric description of the robot’s posture and position in the workspace, typically defined by the pose at given path points or specific path lengths. A robot trajectory is the time parameterization of the path, generally expressed as the robot’s pose as a function of time.

Robot trajectory planning generally encompasses two primary task types: point-to-point (PTP) tasks and path-following (PF) tasks. In PTP trajectory planning, only the initial and target poses of the robot are specified. As a result, planning is typically conducted in the joint space, with a focus on task feasibility and execution efficiency. This type of planning is commonly employed in simple robotic operations, such as material handling. In contrast, the PF trajectory planning requires the robot to move along a predefined path. In addition to feasibility and efficiency, it places greater emphasis on the quality of motion execution, including path accuracy and motion smoothness. Such planning is widely adopted in precision-critical applications, such as robotic milling, welding, and polishing. Consequently, compared with PTP tasks, PF trajectory planning imposes more stringent requirements on motion quality and involves more complex constraints.

For path-following trajectory planning tasks, researchers have proposed several methods. Some have introduced curve-based feedrate scheduling (CBFS) methods, which are well developed in CNC machining, into robotic trajectory planning, such as S-curve-based and polynomial-based feedrate scheduling methods [1,2,3,4]. Xu et al. [5] proposed a dynamic window-based look-ahead feedrate scheduling method using an S-curve profile, achieving feedrate planning for a six-degree-of-freedom robot under kinematic constraints. Li et al. [6] generated an initial feedrate profile using B-splines and then adjusted it in regions that violated kinematic constraints to produce a feasible trajectory. These CBFS methods offer clearly defined constraints and high computational efficiency and are widely applied to online feedrate scheduling in both CNC and robotic machining. However, CBFS can not optimize the trajectory and therefore cannot fully exploit the robot motion capabilities. Other researchers have used dynamic programming (DP) to address trajectory planning. Kaserer et al. [7] formulated an optimization problem incorporating jerk constraints and motor models, and proposed an improved DP algorithm with phase-plane interpolation to ensure derivative continuity and generate smooth executable trajectories. Wu et al. [8] transformed the energy-optimal trajectory planning problem into a multi-stage decision problem and solved it using DP. Similarly, Ding et al. [9] applied DP in the discrete domain to search for approximately optimal trajectories under kinematic and dynamic constraints. However, due to the exhaustive search nature of dynamic programming in the discrete domain, these methods often suffer from low planning efficiency. In addition, some studies have adopted numerical integration methods [10,11,12,13] to iteratively generate time-optimal trajectory. To achieve trajectory planning with various performance objectives, researchers have increasingly formulated the problem as an optimization model and applied corresponding solution methods, targeting objectives such as time optimality [14], energy efficiency [15], jerk minimization [16], or multi-objective optimization [17,18].

In optimization-based trajectory planning, the problem is typically formulated as an infinite-dimensional optimization model, which is then discretized through path sampling into a finite-dimensional form. Despite this transformation, the resulting problem remains nonlinear and high-dimensional due to the complexity of robotic kinematics and dynamics. To address these challenges, some researchers have reformulated the trajectory planning problem as a convex optimization model to leverage its computational advantages. Debrouwere et al. [19] and Lin et al. [20] demonstrated that joint torque rate constraints disrupt problem convexity. By expressing these nonconvex constraints as differences in convex functions, they reformulated the problem with convex–concave constraints and solved it using sequential convex programming. Ma et al. [21] employed convex optimization to compute forward and backward maximum velocity curves (MVCs), solving a finite number of convex subproblems at each path point to obtain time-optimal trajectories. Zhang et al. [22] applied sequential quadratic programming (SQP) to generate smooth and time-optimal manipulator trajectories. Liu et al. [23] and Nagy et al. [24] linearized nonlinear constraints and adopted linear programming (LP) to minimize the sum of velocities at sampled points, achieving time-optimal solutions. Wu et al. [25] and Shen et al. [26] formulated the time-optimal trajectory planning problem in the standard form of second-order cone programming (SOCP) and subsequently solved it using SOCP methods. Compared with other optimization-based approaches, convex optimization offers simpler formulations and faster computation. Moreover, the availability of commercial convex solvers further reduces the complexity and computational cost of solving convexified trajectory planning problems.

One of the key challenges in robot trajectory planning is to obtain an optimal solution under complex and diverse constraints. These constraints mainly include joint-space and Cartesian-space constraints. Joint-space constraints refer to the kinematic and dynamic limits of joints, while Cartesian-space constraints pertain to the kinematic limitations of the end-effector within the workspace. Some trajectory planning methods for path-following tasks consider only joint-space constraints [7,21,27,28,29,30]. However, for path-following tasks, especially in robotic machining applications, the quality of task execution is directly affected by the motion of the end-effector, making it necessary to impose additional kinematic constraints on the end-effector motion [5,31,32]. In some studies, only joint velocity, acceleration, and torque limits are considered, while jerk constraints are omitted [19,29,33,34]. Several researchers have demonstrated that incorporating joint jerk constraints in trajectory planning can effectively suppress vibration during robot operation and improve trajectory smoothness [28,30,32]. Furthermore, most of the above methods operate in the discrete domain, where pseudo-acceleration is often assumed constant and the square of pseudo-velocity is modeled as a linear function. This simplification causes joint torques at the boundaries of discrete intervals to become nonlinear and discontinuous, leading to severe vibration and jerks in the resulting trajectory [25,35]. Therefore, ensuring the continuity of joint motion is also essential in trajectory planning.

This paper proposes a time-jerk optimal trajectory planning (TJOTP) method for robots, considering compound constraints and joint motion continuity. To enhance the completeness of constraint modeling, an optimization framework is established for path-following tasks under compound constraints, incorporating both joint jerk limits and Cartesian-space kinematic constraints of the end-effector (EE). To reduce jerk and improve motion smoothness, sufficient conditions for achieving the C³ continuity of joint trajectories are analyzed, and the trajectory optimization problem is reformulated using cubic spline interpolation. A direct transcription method is adopted to construct a finite-dimensional optimization problem. To further suppress joint jerk and enhance motion smoothness, a jerk evaluation term is introduced into the objective function, yielding a time and jerk co-optimization model. To improve the planning efficiency, constraint tightening and convex relaxation techniques are applied to linearize the model, enabling its solution via SOCP. Experimental results validate the effectiveness of the proposed method in optimizing both execution time and joint jerk under compound constraints.

The remainder of the manuscript is structured as follows. In Section 2, the time-optimal trajectory planning (TOTP) problem under compound constraints is modeled. The TOTP model is first formulated, followed by an analysis of the C³ continuity requirement for joint motion. To fulfill this requirement, segmented cubic splines are employed to reconstruct the TOTP model. The infinite-dimensional problem in the continuous domain is then converted into a finite-dimensional problem in the discrete domain through direct transcription. In Section 3, the TOTP problem with nonlinear and non-convex jerk constraints is decomposed into two second-order cone programming problems. A jerk evaluation term is introduced into the objective function, leading to the formulation and solution of a time-and-jerk optimal trajectory planning problem. In Section 4, the effectiveness of the proposed method is demonstrated through experimental validation. Section 5 provides the conclusions.

2. Formulation of Time-Optimal Trajectory Planning

2.1. Modeling of TOTP with Compound Kinematic

2.1.1. Parameterization of the Path

For path-following tasks, the goal of TOTP for robots is to determine appropriate velocity, acceleration, and jerk profiles along a given path. For a specified path of a robotic manipulator with N joints, the joint trajectory can be represented as a function of the path length l, denoted by Q(l). To ensure generality, the path length is first normalized to the interval [0, 1]. Then, the normalized path length is further expressed as a function of time t, leading to

$$l(t)=L\cdot s(t)$$

(1)

where L denotes the total length of the path and $s(t)\in [0,1]$ represents the normalized arc length. In particular, s(t) = 0 and s(t) = 1 correspond to the start and end of the path, respectively. The first, second, and third derivatives of the normalized arc length with respect to time t are defined as pseudo-velocity, pseudo-acceleration, and pseudo-jerk, respectively, and are expressed as

$$\dot{s}(t)={\displaystyle \frac{ds}{dt}},\ddot{s}(t)={\displaystyle \frac{d^{2}s}{d{t}^2}},\stackrel{⃛}{s}(t)={\displaystyle \frac{d^{3}s}{d{t}^3}}$$

(2)

According to the chain rule of differentiation, the angular velocity, angular acceleration, and angular jerk of the robot joint at path-length parameter s can be computed as

$$\left\{\begin{array}{l}\dot{Q}(s)=Q_s(s)\dot{s}\hfill \\ \ddot{Q}(s)=Q_s(s)\ddot{s}+Q_{ss}(s){\dot{s}}^2\hfill \\ \stackrel{⃛}{Q}(s)=3Q_{ss}(s)\dot{s}\ddot{s}+Q_s(s)\stackrel{⃛}{s}+Q_{sss}(s){\dot{s}}^3\hfill \end{array}\right.$$

(3)

where $Q_s(s)$, $Q_{ss}(s)$ and $Q_{sss}(s)$ denote the first, second, and third derivatives of the joint path with respect to path-length parameter s, respectively. $Q_s(s)=dQ/ds$, $Q_{ss}(s)=d^{2}Q/d{s}^2$, $Q_{sss}(s)=d^{3}Q/d{s}^3$.

Similarly, the feedrate, acceleration, and jerk of the robot EE in Cartesian space at “s” can be obtained based on the chain rule as

$$\left\{\begin{array}{l}\dot{l}(s)={\displaystyle \frac{dl}{dt}}={\displaystyle \frac{dl}{ds}}\cdot {\displaystyle \frac{ds}{dt}}=L\dot{s}\hfill \\ \ddot{l}(s)={\displaystyle \frac{d}{dt}}\left(L{\displaystyle \frac{ds}{dt}}\right)=L\ddot{s}\hfill \\ \stackrel{⃛}{l}(s)={\displaystyle \frac{d}{dt}}\left(L{\displaystyle \frac{d^{2}s}{d{t}^2}}\right)=L\stackrel{⃛}{s}\hfill \end{array}\right.$$

(4)

For a serial multi-joint manipulator, the dynamic equations can be formulated using the Lagrangian method as

$$\tau =M(Q)\ddot{Q}+C(Q)(\dot{Q}\circ \dot{Q})+B(Q)(\dot{Q}\times \dot{Q})+G(Q)+{\tau }_f(Q)\mathrm{sgn}(\dot{Q})$$

(5)

where $\tau \in {ℝ}^N$ denotes the joint torque vector, $M(Q)\in {ℝ}^{N\times N}$ is the inertia matrix, $C(Q)\in {ℝ}^{N\times N}$ is the centrifugal matrix, $B(Q)\in {ℝ}^{N\times N(N-1)/2}$ is the Coriolis matrix, $G(Q)\in {ℝ}^N$ represents the torque induced by gravity, and ${\tau }_f(Q)\mathrm{sgn}(\dot{Q})$ denotes the Coulomb friction torque vector. The terms $\dot{Q}\circ \dot{Q}\in {ℝ}^N$ and $\dot{Q}\times \dot{Q}\in {ℝ}^{N(N-1)/2}$ represent the Hadamard product and the velocity cross product, respectively. $\dot{Q}\circ \dot{Q}={[{{\dot{Q}}_1}^2,{{\dot{Q}}_2}^2,\dots ,{{\dot{Q}}_N}^2]}^{\mathrm{T}}$, $\dot{Q}\times \dot{Q}={[{\dot{Q}}_1{\dot{Q}}_2,{\dot{Q}}_1{\dot{Q}}_3,\dots ,{\dot{Q}}_{N-1}{\dot{Q}}_N]}^{\mathrm{T}}$,where ${\dot{Q}}_N$ denotes the N-th component of the angular velocity vector.

By substituting Equation (3) into Equation (5), the time–path decoupled form of the dynamic model can be obtained as

$$\begin{array}{l}\tau =M(Q)(Q_s\ddot{s}+Q_{ss}{\dot{s}}^2)+(C(Q)(Q_s\circ Q_s)+B(Q)(Q_s\times Q_s)){\dot{s}}^2+G(Q)\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}+{\tau }_f(Q)\mathrm{sgn}(Q_s)\mathrm{sgn}(\dot{s})\end{array}$$

(6)

For the convenience of expression and the construction of the optimization model, Equation (6) is reformulated as

$$\tau (s)=m(Q(s))\ddot{s}+c(Q(s)){\dot{s}}^2+g(Q(s))$$

(7)

where

$$\left\{\begin{array}{l}m(Q(s))=M(Q(s))Q_s\hfill \\ c(Q(s))=M(Q(s))Q_{ss}+C(Q(s))(Q_s\circ Q_s)+B(Q(s))(Q_s\circ Q_s)\hfill \\ g(Q(s))=G(Q(s))+{\tau }_f(Q)\mathrm{sgn}(Q_s)\hfill \end{array}\right.$$

(8)

2.1.2. Constraints in Trajectory Planning for Path-Following Tasks

The robot trajectory planning problem for a given path is a compound-constrained optimization problem that involves joint kinematic constraints, dynamic constraints, and Cartesian-space kinematic constraints.

1.

Kinematic constraints in joint space

During path-following tasks, the robot must satisfy kinematic constraints in joint space, which mainly include limitations on joint angular velocity and angular acceleration. Let ${\dot{Q}}_{\max }\in {ℝ}^N$ and ${\ddot{Q}}_{\max }\in {ℝ}^N$ denote the upper bounds of angular velocity and angular acceleration, respectively. Since these constraints are typically symmetric about zero, the corresponding lower bounds are given by $-{\dot{Q}}_{\max }$ and $-{\ddot{Q}}_{\max }$. Accordingly, the joint angular velocity and acceleration constraints can be formulated as

$$-{\dot{Q}}_{\max }\le \dot{Q}(s)\le {\dot{Q}}_{\max }\hspace{0.33em}\hspace{0.33em}\iff \hspace{0.33em}\hspace{0.33em}-{\dot{Q}}_{\max }\le Q_s(s)\dot{s}\le {\dot{Q}}_{\max }$$

(9)

$$-{\ddot{Q}}_{\max }\le \ddot{Q}(s)\le {\ddot{Q}}_{\max }\hspace{0.33em}\hspace{0.33em}\iff \hspace{0.33em}\hspace{0.33em}-{\ddot{Q}}_{\max }\le Q_s(s)\ddot{s}+Q_{ss}(s){\dot{s}}^2\le {\ddot{Q}}_{\max }$$

(10)

In addition to joint velocity and acceleration constraints, joint jerk (the second derivative of angular velocity) is also considered in the formulation of joint-space kinematic constraints, in order to reduce vibration and impact caused by abrupt acceleration or deceleration of robot joints. Let ${\stackrel{⃛}{Q}}_{\max }\in {ℝ}^N$ denote the upper bound of joint jerk. The joint jerk constraints can then be expressed as

$$-{\stackrel{⃛}{Q}}_{\max }\le \stackrel{⃛}{Q}(s)\le {\stackrel{⃛}{Q}}_{\max }\iff -{\stackrel{⃛}{Q}}_{\max }\le 3Q_{ss}(s)\dot{s}\ddot{s}+Q_s(s)\stackrel{⃛}{s}+Q_{sss}(s){\dot{s}}^3\le {\stackrel{⃛}{Q}}_{\max }$$

(11)

2.

Dynamic constraints in joint space

The joint torque is a critical physical quantity that characterizes the actual output capability of the actuators. To ensure that the planned trajectory can be reliably executed by all joint actuators throughout the motion, the joint torque must remain within the motion capability range of the robot. Therefore, joint torque limits are introduced in this work as dynamic constraints in the trajectory planning model. Let ${\tau }_{\max }$ and $-{\tau }_{\max }$ denote the upper and lower bounds of joint torque, respectively. The joint torque constraints in the trajectory planning problem can thus be formulated as

$$-{\tau }_{\max }\le \tau (s)\le {\tau }_{\max }\iff -{\tau }_{\max }\le m(Q(s))\ddot{s}+c(Q(s)){\dot{s}}^2+g(Q(s))\le {\tau }_{\max }$$

(12)

3.

Kinematic constraints in Cartesian space

For paths with curvature, the influence of geometric characteristics on the EE feedrate must be taken into account during trajectory. In regions of high curvature, the dynamic behavior of motion may be significantly affected. To ensure both accuracy and stability during execution, the feedrate of the EE must be constrained. Specifically, the maximum permissible EE feedrate can be calculated as [36]

$$V_{\max }(s)=\left(\min {\displaystyle \frac{2}{T_s}}\sqrt{{\displaystyle \frac{1}{\kappa {(s)}^2}}-{\left({\displaystyle \frac{1}{\kappa (s)}}-{\epsilon }_{\mathrm{chord}}\right)}^2},\sqrt{{\displaystyle \frac{A{n}_{\max }}{\kappa (s)}}},\sqrt[3]{{\displaystyle \frac{J{n}_{\max }}{\kappa {(s)}^2}}},F\right)$$

(13)

where $T_s$ denotes the trajectory interpolation period, $\kappa (s)$ is the curvature of the path at parameter s, and ${\epsilon }_{\mathrm{chord}}$ is the chord error constraint. $A{n}_{\max }$, $J{n}_{\max }$, and F represent the maximum normal acceleration, maximum normal jerk, and commanded feedrate, respectively. Therefore, the EE velocity constraint in the trajectory planning problem can be expressed as

$$\dot{l}(s)\le V_{\max }(s)\hspace{0.33em}\hspace{0.33em}\iff \hspace{0.33em}\hspace{0.33em}L\dot{s}\le V_{\max }(s)$$

(14)

Similarly, based on the chain rule of differentiation, the acceleration and jerk constraints of the end-effector can be expressed as

$$\left\{\begin{array}{c}\left|\ddot{l}(s)\right|\le A_{\max }\\ \left|\stackrel{⃛}{l}(s)\right|\le J_{\max }\end{array}\right.\iff \left\{\begin{array}{c}L\left|\ddot{s}\right|\le A_{\max }\\ L\left|\stackrel{⃛}{s}\right|\le J_{\max }\end{array}\right.$$

(15)

where $A_{\max }$ and $J_{\max }$ represent the given maximum acceleration and maximum jerk of the EE, respectively.

For the time-optimal trajectory planning (TOTP) problem, the objective of trajectory optimization is to minimize the total execution time, which can be obtained by integrating the pseudo-velocity, expressed as

$$T={\displaystyle {\int }_0^{T}1dt}={\displaystyle {\int }_{s(0)}^{s(T)}\frac{dt}{ds}ds}={\displaystyle {\int }_0^1\frac{1}{\dot{s}}ds}$$

(16)

Based on the characteristics of the time-optimal trajectory planning objective and the associated constraints, the pseudo-state variables are defined to simplify the problem formulation as

$$\alpha (s)={\displaystyle \frac{d^{2}s}{d{t}^2}}=\ddot{s},\hspace{0.33em}\beta (s)={\left({\displaystyle \frac{ds}{dt}}\right)}^2={\dot{s}}^2,\hspace{0.33em}\gamma (s)={\displaystyle \frac{\stackrel{⃛}{s}}{\dot{s}}}$$

(17)

By integrating the objective function and the constraints involved in robot trajectory planning, and substituting Equation (17), the time-optimal trajectory planning (TOTP) problem can be formulated as an optimization model with $\alpha (s)$, $\beta (s)$, and $\gamma (s)$ as decision variables:

$$\begin{array}{l}\underset{\alpha (s),\beta (s),\gamma (s)}{\min \hspace{0.33em}T}=\min {\displaystyle {\int }_0^1\frac{1}{\sqrt{\beta (s)}}ds}\\ s.t.\left\{\begin{array}{c}-{\dot{Q}}_{\max }\le Q_s(s)\sqrt{\beta (s)}\le {\dot{Q}}_{\max }\\ -{\ddot{Q}}_{\max }\le Q_s(s)\alpha (s)+Q_{ss}(s)\beta (s)\le {\ddot{Q}}_{\max }\\ -{\stackrel{⃛}{Q}}_{\max }\le \sqrt{\beta (s)}(3Q_{ss}(s)\alpha (s)+Q_s(s)\gamma (s)+Q_{sss}(s)\beta (s))\le {\stackrel{⃛}{Q}}_{\max }\\ -{\tau }_{\max }\le m(Q(s))\alpha (s)+c(Q(s))\beta (s)+g(Q(s))\le {\tau }_{\max }\\ L\sqrt{\beta (s)}\le V_{\max }(s),L\left|\alpha (s)\right|\le A_{\max },L\sqrt{\beta (s)}\left|\gamma (s)\right|\le J_{\max }\\ \dot{Q}(0)=O,\dot{Q}(1)=O\\ s(0)=0,s(T)=1\\ s\in [0,1]\\ \beta (s)\ge 0\end{array}\right.\end{array}$$

(18)

where $\dot{Q}(0)$ and $\dot{Q}(1)$ denote the joint angular velocity at the start and end of the path, respectively. Since this work focuses on trajectory planning along the entire given path, both the initial and terminal joint velocities are set to zero, i.e., $\dot{Q}(0)=O$ and $\dot{Q}(1)=O$.

2.2. Continuity Constraints Based on Cubic Splines

For the TOTP problem defined in Equation (18), some researchers [23,24] discretize the path and apply convex optimization methods in the discrete domain to obtain the optimal decision variables. Analysis of these approaches reveals that the squared pseudo-velocity is often treated as a piecewise linear function, which results in the pseudo-acceleration being a piecewise constant function. This leads to discontinuities in the joint motion commands received by the robot during task execution [25]. These discontinuities may cause mechanical vibrations or abrupt changes in acceleration, particularly in machining scenarios where high trajectory smoothness is required, thereby compromising machining quality and reducing the service life of the robot system.

To address the above issue, the constraints in Equation (18) are further extended in this work. A cubic spline interpolation method is proposed to reconstruct the decision variables, and continuity constraints are imposed on the spline functions to ensure C³ continuity of the joint trajectories. This method can effectively guarantee the continuity and smoothness of the trajectory, enhance the dynamic feasibility of the planned motion, and avoid motion instability caused by discontinuities in the decision variables.

2.2.1. Analysis of C³ Continuity Requirements for Joint Trajectories

According to the chain rule of differentiation, the robot joint velocity, acceleration, and jerk can be explicitly expressed by the decision variables $\alpha (s)$, $\beta (s)$, and $\gamma (s)$:

$$\left\{\begin{array}{l}\dot{Q}(s)=Q_s(s)\sqrt{\beta (s)}\hfill \\ \ddot{Q}(s)=Q_s(s)\alpha (s)+Q_{ss}(s)\beta (s)\hfill \\ \stackrel{⃛}{Q}(s)=\sqrt{\beta (s)}(3Q_{ss}(s)\alpha (s)+Q_s(s)\gamma (s)+Q_{sss}(s)\beta (s))\hfill \end{array}\right.$$

(19)

According to the properties of continuous functions, the following is stated: (a) the result of addition, subtraction, multiplication, or division of continuous functions preserves the same order of continuity; and (b) if the outer function is continuous up to the required order and the inner function is also continuous to the same order within its domain, then their composite function will have the same order of continuity. In other words, both basic operations and functional compositions preserve the continuity order of a function. Therefore, based on the analysis of Equation (19), to ensure the continuity of $\dot{Q}(s)$, $\ddot{Q}(s)$, and $\stackrel{⃛}{Q}(s)$, the following conditions must be satisfied: (a) $Q_s(s)$, $Q_{ss}(s)$, and $Q_{sss}(s)$ are continuous, which implies that the given path must be C³ continuous with respect to the path length; and (b) the decision variables $\alpha (s)$, $\beta (s)$, and $\gamma (s)$ are continuous.

With regard to the C³ continuity requirement of the path, a wide range of existing methods for robotic path design and smoothing have been developed to achieve high-order continuity with respect to arc length, such as spline interpolation in joint space or path smoothing techniques in Cartesian space. As a result, the continuity of the path is relatively easy to satisfy. This aspect is not the focus of this section and will not be discussed in detail. The following discussion will focus on methods for ensuring the continuity of the decision variables.

Let ${\beta }_s(s)$ and ${\beta }_{ss}(s)$ denote the first- and second-order derivatives of $\beta (s)$ with respect to s, respectively; then, we have

$$\left\{\begin{array}{c}{\beta }_s={\displaystyle \frac{d}{ds}}({\dot{s}}^2)=2\dot{s}{\displaystyle \frac{d}{ds}}(\dot{s})=2\dot{s}{\displaystyle \frac{d(\dot{s})}{dt}}{\displaystyle \frac{dt}{ds}}=2\dot{s}\ddot{s}{\displaystyle \frac{1}{\dot{s}}}=2\ddot{s}\\ {\beta }_{ss}={\displaystyle \frac{d}{ds}}(\ddot{s})=2s{\displaystyle \frac{d}{ds}}(\ddot{s})=2{\displaystyle \frac{d(\ddot{s})}{dt}}{\displaystyle \frac{dt}{ds}}=2\stackrel{⃛}{s}{\displaystyle \frac{1}{\dot{s}}}\end{array}\right.$$

(20)

By combining Equations (17) and (20), we obtain

$$\beta (s)=\beta (s),\hspace{0.33em}\hspace{0.33em}\alpha (s)={\displaystyle \frac{1}{2}}{\beta }_s(s),\hspace{0.33em}\hspace{0.33em}\gamma (s)={\displaystyle \frac{1}{2}}{\beta }_{ss}(s)$$

(21)

According to the above equation, to ensure the continuity of the decision variables, $\beta (s)$ should be at least C2 continuous with respect to the parameter s.

2.2.2. Reconstruction of Decision Variables Based on Piecewise Cubic Splines

To achieve C2 continuity of the $\beta (s)$, piecewise cubic splines are introduced to interpolate $\beta (s)$. The parameter $s\in [0,1]$ is uniformly divided into $N_{\mathrm{seg}}$ segments, and the length of each segment is $\Delta S=1/N_{\mathrm{seg}}$. This division yields $N_{seg}+1$ segment endpoints, denoted as $s_1,s_2,s_3,\dots ,s_{N_{\mathrm{seg}}},s_{N_{\mathrm{seg}}+1}$, where $s_1=0$ and $s_{N_{\mathrm{seg}}+1}=1$. The decision variable $\beta (s)$ can then be represented as a piecewise function:

$$\beta (s)=\left\{\begin{array}{cc}{\beta }_1(s),& s\in [s_1,s_2]\\ {\beta }_2(s)& s\in [s_2,s_3]\\ ⋮& ⋮\\ {\beta }_i(s)& s\in [s_i,s_{i+1}]\\ ⋮& ⋮\\ {\beta }_{N_{\mathrm{seg}}}(s)& s\in [s_{N_{\mathrm{seg}}},s_{N_{\mathrm{seg}}+1}]\end{array}\right.$$

(22)

where ${\beta }_i(s)$ denotes the cubic polynomial function corresponding to the i-th segment. For convenience in subsequent computation and constraint formulation, the parameter “s” is normalized within the i-th segment as

$$u=u(s)=(s-s_i)/\Delta S,\hspace{0.33em}\hspace{0.33em}s\in [s_i,s_{i+1}]$$

(23)

Subsequently, a cubic polynomial function with respect to u is constructed within each segment. For the i-th segment, the decision variable ${\beta }_i(s)$ can be computed from u as

$${\beta }_i(s)=[\begin{array}{cccc}{u}^3& u^2& u& 1\end{array}]\left[\begin{array}{c}{a}_i\\ b_i\\ c_i\\ d_i\end{array}\right]\hspace{0.33em}\mathrm{with}\hspace{0.33em}u={\displaystyle \frac{(s-s_i)}{\Delta S}},s\in [s_i,s_{i+1}]$$

(24)

where a_i, b_i, c_i, and d_i represent the coefficients of the cubic, quadratic, linear, and constant terms for the i-th cubic polynomial segment, respectively. Based on Equation (21), the decision variables $\alpha (s)$ and $\gamma (s)$ in the i-th segment can be expressed as

$${\alpha }_i(s)={\displaystyle \frac{1}{2\Delta s}}[\begin{array}{cccc}3u^2& u& 1& 0\end{array}]\left[\begin{array}{c}{a}_i\\ b_i\\ c_i\\ d_i\end{array}\right]\hspace{0.33em}\mathrm{with}\hspace{0.33em}u={\displaystyle \frac{(s-s_i)}{\Delta S}},s\in [s_i,s_{i+1}]$$

(25)

$${\gamma }_i(s)={\displaystyle \frac{1}{2\Delta s^2}}[\begin{array}{cccc}6u& 1& 0& 0\end{array}]\left[\begin{array}{c}{a}_i\\ b_i\\ c_i\\ d_i\end{array}\right]\hspace{0.33em}\mathrm{with}\hspace{0.33em}u={\displaystyle \frac{(s-s_i)}{\Delta S}},s\in [s_i,s_{i+1}]$$

(26)

After piecewise cubic spline interpolation, the C2 continuity of $\beta (s)$ within each segment ensures the continuity of the decision variables $\alpha (s)$, $\beta (s)$, and $\gamma (s)$. However, at the endpoints of each segment, additional constraints must be imposed to ensure the continuity of the decision variables across both sides of the boundary. Specifically, the function values, first- and second-order derivatives on the left and right sides of each segment endpoint, must be equal, which can be expressed as

$$\left\{\begin{array}{cc}{\beta }_i(s_{i+1})={\beta }_{i+1}(s_{i+1})& \forall i=1,\cdots ,N_{\mathrm{seg}}-1\\ {\alpha }_i(s_{i+1})={\alpha }_{i+1}(s_{i+1})& \forall i=1,\cdots ,N_{\mathrm{seg}}-1\\ {\gamma }_i(s_{i+1})={\gamma }_{i+1}(s_{i+1})& \forall i=1,\cdots ,N_{\mathrm{seg}}-1\end{array}\right.$$

(27)

To ensure a smooth start and stop of the robot trajectory, boundary constraints have been imposed on $\beta (s)$ by setting its values to zero at the start and end of the path. This guarantees that the joint velocity at the beginning and end of the trajectory is zero. Based on this, to further improve smoothness during the start and stop phases, the pseudo-acceleration is also set to zero at the start and end of the path. The corresponding constraint can be expressed as $\alpha (0)=0,\alpha (1)=0$.

In the above, piecewise cubic splines were introduced to reconstruct the decision variables $\alpha (s)$, $\beta (s)$ and $\gamma (s)$ in Equation (18). As a result, the original decision variables in the TOTP optimization model are replaced by the spline coefficient vectors $a$, $b$, $c$, and $d$. Therefore, the original TOTP model needs to be reformulated. The affine relationships between the decision variables and the spline coefficient vectors are incorporated into the optimization model, along with the continuity constraints. The resulting TOTP model is given by

$$\begin{array}{l}\underset{a,b,c,d}{\min \hspace{0.33em}T}={\displaystyle {\int }_0^1\frac{1}{\sqrt{\beta (s)}}ds}\\ s.t.\left\{\begin{array}{c}{\beta }_i(s)=p(s)\\ {\alpha }_i(s)=0.5p_s(s)\\ {\gamma }_i(s)=0.5p_{ss}(s)\\ -{\dot{Q}}_{\max }\le Q_s(s)\sqrt{\beta (s)}\le {\dot{Q}}_{\max }\\ -{\ddot{Q}}_{\max }\le Q_s(s)\alpha (s)+Q_{ss}(s)\beta (s)\le {\ddot{Q}}_{\max }\\ -{\stackrel{⃛}{Q}}_{\max }\le \sqrt{\beta (s)}(3Q_{ss}(s)\alpha (s)+Q_s(s)\gamma (s)+Q_{sss}(s)\beta (s))\le {\stackrel{⃛}{Q}}_{\max }\\ -{\tau }_{\max }\le m(Q(s))\alpha (s)+c(Q(s))\beta (s)+g(Q(s))\le {\tau }_{\max }\\ {\beta }_i(s_{i+1})={\beta }_{i+1}(s_{i+1}),\hspace{0.33em}\forall i=1,\cdots ,N_{\mathrm{seg}}-1\\ {\alpha }_i(s_{i+1})={\alpha }_{i+1}(s_{i+1}),\hspace{0.33em}\forall i=1,\cdots ,N_{\mathrm{seg}}-1\\ {\gamma }_i(s_{i+1})={\gamma }_{i+1}(s_{i+1}),\hspace{0.33em}\forall i=1,\cdots ,N_{\mathrm{seg}}-1\\ \beta (0)=0,\beta (1)=1,\alpha (0)=0,\alpha (1)=0\\ L\sqrt{\beta (s)}\le V_{\max }(s),L\left|\alpha (s)\right|\le A_{\max },L\sqrt{\beta (s)}\left|\gamma (s)\right|\le J_{\max }\\ s(0)=0,s(T)=1\\ \beta (s)\ge 0\\ s\in [0,1]\end{array}\right.\end{array}$$

(28)

2.2.3. Discretization of the Trajectory Optimization Model

The optimization problem described in Equation (28) is infinite-dimensional in the continuous domain. In practical engineering applications, it is difficult to obtain an analytical solution directly. In this section, a direct transcription method is adopted to discretize the problem, resulting in a large-scale finite-dimensional optimization model in the discrete domain. As illustrated in Figure 1, the machining path is first divided into $N_{\mathrm{seg}}$ cubic spline segments. Then, within each segment, the path-length parameter is further uniformly sampled, and kinematic and dynamic constraints are imposed at each sampling point. Suppose the number of discrete points in each spline segment is M. For a given path, the above discretization yields $N_{\mathrm{seg}}$ spline segments, $N_{\mathrm{seg}}+1$ segment endpoints, and the total number of sampling points is $N_{\mathrm{point}}=N_{\mathrm{seg}}(M-1)+1$, with a uniform sampling interval of $\Delta s=1/N_{seg}$.

For the j-th discrete point on the discretized path, the index of the spline segment to which it belongs can be calculated as

$$N_{\mathrm{ide}}=\left\{\begin{array}{cc}{\displaystyle \frac{j}{M-1}}& if\hspace{0.33em}\mathrm{mod}(j,M-1)=0\\ \mathrm{floor}({\displaystyle \frac{j}{M-1}})+1& else\end{array}\right.$$

(29)

where $\mathrm{mod}(\cdot )$ denotes the modulo operation, which returns the remainder of a division, and $\mathrm{floor}(\cdot )$ represents the floor function. For the $N_{\mathrm{ide}}$-th spline segment, the normalized parameter corresponding to the j-th discrete point within the segment can be calculated as

$$u_j=\left\{\begin{array}{cc}M-1& if\hspace{0.33em}\mathrm{mod}(j,M-1)=0\\ \mathrm{mod}(j,M-1)& else\end{array}\right.$$

(30)

Therefore, after path discretization, for the j-th discrete point, we have

$$\left\{\begin{array}{l}{\beta }_j=a_{N_{\mathrm{ide}}}{u_j}^3+b_{N_{\mathrm{ide}}}{u_j}^2+c_{N_{\mathrm{ide}}}{u}_j+d_{N_{\mathrm{ide}}}\hfill \\ {\alpha }_j=3a_{N_{\mathrm{ide}}}{u_j}^2+b_{N_{\mathrm{ide}}}{u}_j+c_{N_{\mathrm{ide}}}\hfill \\ {\gamma }_j=6a_{N_{\mathrm{ide}}}{u}_j+b_{N_{\mathrm{ide}}}\hfill \end{array}\right.$$

(31)

For the objective function T in the TOTP model described by Equation (28), the trapezoidal integration rule is used to discretize it as

$$\begin{array}{l}T={\displaystyle {\int }_0^1\frac{1}{\sqrt{\beta (s)}}ds}\Rightarrow T={\displaystyle \sum _{j=1}^{N_{\mathrm{point}}-1}{\displaystyle {\int }_{s_j}^{s_{j+1}}\frac{1}{\sqrt{\beta (s)}}ds}}\\ \Rightarrow T=2\Delta s{\displaystyle \sum _{j=1}^{N_{\mathrm{point}}-1}\frac{1}{\sqrt{{\beta }_j}+\sqrt{{\beta }_{j+1}}}}\end{array}$$

(32)

As a result, the discretized form of Equation (28) is obtained as

$$\begin{array}{l}\underset{a,b,c,d}{\min \hspace{0.33em}T}=2\Delta s{\displaystyle \sum _{j=1}^{N_{\mathrm{point}}-1}\frac{1}{\sqrt{{\beta }_j}+\sqrt{{\beta }_{j+1}}}}\\ s.t.\left\{\begin{array}{c}{\beta }_j=a_{N_{\mathrm{ide}}}{u_j}^3+b_{N_{\mathrm{ide}}}{u_j}^2+c_{N_{\mathrm{ide}}}{u}_j+d_{N_{\mathrm{ide}}}\\ {\alpha }_j=3a_{N_{\mathrm{ide}}}{u_j}^2+b_{N_{\mathrm{ide}}}{u}_j+c_{N_{\mathrm{ide}}}\\ {\gamma }_j=6a_{N_{\mathrm{ide}}}{u}_j+b_{N_{\mathrm{ide}}}\\ -{\dot{Q}}_{\max }\le Q_s\sqrt{{\beta }_j}\le {\dot{Q}}_{\max }\\ -{\ddot{Q}}_{\max }\le Q_s{\alpha }_j+Q_{ss}{\beta }_j\le {\ddot{Q}}_{\max }\\ -{\stackrel{⃛}{Q}}_{\max }\le \sqrt{{\beta }_j}(3Q_{ss}{\alpha }_j+Q_s{\gamma }_j+Q_{sss}{\beta }_j)\le {\stackrel{⃛}{Q}}_{\max }\\ -{\tau }_{\max }\le m(Q){\alpha }_j+c(Q){\beta }_j+g(Q)\le {\tau }_{\max }\\ {\beta }_i(s_{i+1})={\beta }_{i+1}(s_{i+1}),\hspace{0.33em}\forall i=1,\cdots ,N_{\mathrm{seg}}-1\\ {\alpha }_i(s_{i+1})={\alpha }_{i+1}(s_{i+1}),\hspace{0.33em}\forall i=1,\cdots ,N_{\mathrm{seg}}-1\\ {\gamma }_i(s_{i+1})={\gamma }_{i+1}(s_{i+1}),\hspace{0.33em}\forall i=1,\cdots ,N_{\mathrm{seg}}-1\\ {\beta }_1=0,{\beta }_{N_{\mathrm{point}}}=1,{\alpha }_0=0,{\alpha }_{N_{\mathrm{point}}}=0\\ L\sqrt{{\beta }_j}\le V_{\max }^j,L\left|{\alpha }_j\right|\le A_{\max },L\sqrt{{\beta }_j}\left|{\gamma }_j\right|\le J_{\max }\\ s(0)=0,s(T)=1\\ {\beta }_j\ge 0\\ s\in [0,1]\end{array}\right.\end{array}$$

(33)

3. Problem-Solving via SOCP

In the optimization problem described by Equation (33), the objective function is convex, and all constraints, except for the jerk constraints, are also convex. Therefore, the convex optimization approach is employed to solve the trajectory planning problem. Given the non-convex nature of the jerk constraints, a two-stage SOCP method is proposed in this section. The problem in Equation (33) is decomposed into two convex subproblems, each solved using SOCP. In the first stage, a trajectory planning problem without jerk constraints (TOTP-2C) is solved. In the second stage, the optimal solution obtained from the first stage is used to convexify the jerk constraints, and a jerk evaluation term is incorporated into the objective function. Based on this, a time-and-jerk optimal trajectory planning model (TJOTP-3C) that considers jerk constraints is formulated and solved.

3.1. Modeling and Solution of the TOTP-2C Problem

When jerk constraints are not considered, the optimization model in Equation (33) becomes a convex problem. Due to the presence of square root and fractional terms in the objective function, second-order cone programming (SOCP) is adopted for efficient solution. Compared with linear programming (LP) and nonlinear programming (NLP), SOCP offers greater modeling capability and is especially suitable for handling optimization problems that involve norm terms, fractional terms, or square root terms. A standard SOCP formulation consists of a linear objective function and second-order cone constraints, and may also include linear equality and inequality constraints, enabling efficient solutions for complex but convex optimization models.

Although the objective function in Equation (33) is convex, it is nonlinear. To improve computational efficiency, auxiliary variables $f_j\le \sqrt{{\beta }_j}$ and $e_j\ge 1/(f_j+f_{j+1})$ are introduced to linearize the original function, resulting in a linear objective function expressed as

$$\begin{array}{l}\min \hspace{0.33em}2\Delta s{\displaystyle \sum _{j=1}^{N_{\mathrm{point}}-1}\frac{1}{\sqrt{{\beta }_j}+\sqrt{{\beta }_{j+1}}}\hspace{0.33em}}\iff \hspace{0.33em}\min \hspace{0.33em}2\Delta s{\displaystyle \sum _{j=1}^{N_{\mathrm{point}}-1}{e}_j}\\ \left\{\begin{array}{l}{f}_j\le \sqrt{{\beta }_j}\hfill \\ e_j\ge {\displaystyle \frac{1}{f_j+f_{j+1}}}\hfill \end{array}\right.\hspace{0.33em}\hspace{0.33em}\iff \hspace{0.33em}\hspace{0.33em}\left\{\begin{array}{c}{‖\left[\begin{array}{c}2f_j\\ {\beta }_j-1\end{array}\right]‖}_2\le {\beta }_j+1\\ {‖\left[\begin{array}{c}2\\ f_j+f_{j+1}-e_j\end{array}\right]‖}_2\le f_j+f_{j+1}+e_j\end{array}\right.\end{array}$$

(34)

The velocity constraints in joint space and Cartesian space are also nonlinear but convex. Their linearized forms are given as

$$\begin{array}{l}-{\dot{Q}}_{\max }\le Q_s\sqrt{{\beta }_j}\le {\dot{Q}}_{\max }\iff \left\{\begin{array}{c}{(Q_s^1)}^2{\beta }_j\le {{\dot{Q}}_{\max }^1}^2\\ ⋮\\ {(Q_s^N)}^2{\beta }_j\le {{\dot{Q}}_{\max }^N}^2\end{array}\right.\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\iff (Q_s\circ Q_s)\sqrt{{\beta }_j}\le {\dot{Q}}_{\max }\circ {\dot{Q}}_{\max }\end{array}$$

(35)

$$L\sqrt{{\beta }_j}\le v_{\max }^j\iff L^2{\beta }_j\le {v_{\max }^j}^2$$

(36)

At this point, the SOCP model for the TOTP-2C problem has been fully formulated and can be expressed as

$$\begin{array}{l}\underset{a,b,c,d}{\min \hspace{0.33em}T}=2\Delta s{\displaystyle \sum _{j=1}^{N_{\mathrm{point}}-1}{e}_j}\\ s.t.\left\{\begin{array}{c}(Q_s\circ Q_s)\sqrt{{\beta }_j}\le {\dot{Q}}_{\max }\circ {\dot{Q}}_{\max }\\ -{\ddot{Q}}_{\max }\le Q_s{\alpha }_j+Q_{ss}{\beta }_j\le {\ddot{Q}}_{\max }\\ -{\tau }_{\max }\le m(Q){\alpha }_j+c(Q){\beta }_j+g(Q)\le {\tau }_{\max }\\ {\beta }_1=0,{\beta }_{N_{\mathrm{point}}}=1,{\alpha }_0=0,{\alpha }_{N_{\mathrm{point}}}=0\\ L^2{\beta }_j\le {v_{\max }^j}^2,-A_{\max }\le L{\alpha }_j\le A_{\max }\\ {\beta }_j\ge 0,f_j\ge 0,e_j\ge 0\\ {‖\left[\begin{array}{c}2f_j\\ {\beta }_j-1\end{array}\right]‖}_2\le {\beta }_j+1\\ {‖\left[\begin{array}{c}2\\ f_j+f_{j+1}-e_j\end{array}\right]‖}_2\le f_j+f_{j+1}+e_j\\ ⋮\end{array}\right.\end{array}$$

(37)

Equation (37) conforms to the standard SOCP form after linearization. Due to the structured formulation of SOCP, many mature convex optimization tools are available for solving large-scale SOCP problems efficiently. A wide range of commercial and open-source solvers provide native support for SOCP, including MOSEK, GUROBI, SCS, ECOS, and SDPT3. Among these, MOSEK demonstrates strong numerical stability and fast convergence, making it particularly suitable for trajectory optimization problems involving a large number of variables and complex constraint structures. In this study, MOSEK is selected as the solver for SOCP problems.

3.2. Modeling and Solution of the TJOTP-3C Problem

This section extends the TOTP-2C model by introducing jerk constraints to reduce impact during robot motion. In addition, to prevent potential issues caused by improper jerk bounds, the jerk evaluation term is added to the objective function. On this basis, a time and jerk optimal trajectory planning (TJOTP-3C) problem is formulated. This approach aims to suppress jerk effects and improve the smoothness of robot motion.

Based on Equation (33), the jerk constraint for the k-th joint of a manipulator with N joints can be reformulated as

$$\sqrt{{\beta }_j}\left|3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j\right|\le {\stackrel{⃛}{Q}}_{\max }^k$$

(38)

The nonlinearity and non-convexity of the above constraint undermine the convexity of the trajectory planning problem. To enable the use of the SOCP method, the jerk constraint needs to be transformed into the linear convex form.

The TOTP-3C problem is formulated by adding jerk constraints to the TOTP-2C model. Therefore, the solution $\beta \in {ℝ}^{N_{\mathrm{point}}}$ that satisfies the constraints of the TOTP-3C also satisfies those of the TOTP-2C problem. Let $\beta *\in {ℝ}^{N_{\mathrm{point}}}$ denote the optimal solution of the TOTP-2C problem; we have $\sqrt{{\beta }_j}\le \sqrt{{\beta }_j^{*}},\forall j$ [23]. This property can be used to linearize the original joint jerk constraint as follows:

• If $3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j\ge 0$, then for the k-th joint of the robot, there exists

  $$\sqrt{{\beta }_j}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)\le \sqrt{{\beta }_j^{*}}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)$$

  (39)

In this case, the joint jerk constraint can be tightened as

$$\begin{array}{c}\sqrt{{\beta }_j}\left|3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j\right|\le {\stackrel{⃛}{Q}}_{\max }^k\\ \Updownarrow \\ \sqrt{{\beta }_j}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)\le {\stackrel{⃛}{Q}}_{\max }^k\\ \Updownarrow \\ \sqrt{{\beta }_j^{*}}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)\le {\stackrel{⃛}{Q}}_{\max }^k\end{array}$$

(40)

2.

If $3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j<0$, there exists

$$\sqrt{{\beta }_j}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)\ge \sqrt{{\beta }_j^{*}}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)$$

(41)

In this case, the joint jerk constraint can be tightened as

$$\sqrt{{\beta }_j^{*}}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)\ge -{\stackrel{⃛}{Q}}_{\max }^k$$

(42)

By combining Equations (40) and (42), the linearized form of the original joint jerk constraint is obtained as

$$-{\stackrel{⃛}{Q}}_{\max }\le \sqrt{{\beta }_j^{*}}(3Q_{ss}{\alpha }_j+Q_s{\gamma }_j+Q_s{\beta }_j)\le {\stackrel{⃛}{Q}}_{\max }$$

(43)

where ${\beta }_j^{*}$ is known. The resulting constraint is linear and convex, and is directly compatible with the standard SOCP form, allowing for efficient computation. By applying the same constraint-tightening method, the linearized form of the EE jerk constraint is obtained as

$$-J_{\max }\le L\sqrt{{\beta }_j^{*}}{\gamma }_j\le J_{\max }$$

(44)

It is important to note that due to the constraint tightening used to linearize the original joint and EE jerk constraints, the resulting solution is approximately time-optimal rather than strictly optimal. As a result, the theoretical optimality of time minimization is partially compromised. However, considering the trade-off between computational efficiency and execution performance, this approach offers a practical and effective solution for trajectory planning in real-world robotic applications.

In addition to enforcing jerk constraints, this work incorporates a joint jerk evaluation metric into the objective function, together with execution time, to formulate a weighted multi-objective optimization model. This approach enables a more balanced trade-off between execution efficiency and trajectory smoothness. By explicitly penalizing jerk in the objective, the resulting trajectory not only satisfies the jerk constraints but also actively suppresses joint jerk, leading to improved motion quality and overall planning performance.

By introducing a joint jerk evaluation metric into the objective function in a weighted form, the time-jerk evaluation function is constructed as

$$\min \hspace{0.33em}\mathrm{obj}=T+{\displaystyle \sum _{j=1}^{N_{\mathrm{point}}}{J}_j}$$

(45)

where $J_j$ represents the jerk index at the j-th discrete point, calculated as the sum of absolute joint jerk values, that is

$$J_j={\displaystyle \sum _{k=1}^N\left|{\stackrel{⃛}{Q}}_j^k\right|}={\displaystyle \sum _{k=1}^N\sqrt{{\beta }_j}\left|3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j\right|}$$

(46)

It can be observed that $J_j$ is a non-convex function. To enable convex reformulation, the optimal solution ${\beta }_j^{*}$ of the TOTP-2C is introduced, and $J_j$ is transformed into

$$J_j=\sqrt{{\beta }_j^{*}}{\displaystyle \sum _{k=1}^N\left|3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j\right|}$$

(47)

Although Equation (47) does not directly represent the joint jerk, the preceding analysis suggests that minimizing $J_j$ can help suppress the actual joint jerk, given that $\sqrt{{\beta }_j}\le \sqrt{{\beta }_j^{*}},\forall j$. Moreover, since Equation (47) involves absolute value operations, auxiliary variables $o_j^k\ge 0$ are introduced to linearize the objective function. The resulting linear objective function is expressed as

$$\begin{array}{l}\min \hspace{0.33em}\mathrm{obj}=T+{\displaystyle \sum _{j=1}^{N_{\mathrm{point}}}{\displaystyle \sum _{k=1}^N{o}_j^k}}\\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{l}{o}_j^k\ge -\sqrt{{\beta }_j^{*}}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)\hfill \\ o_j^k\ge \sqrt{{\beta }_j^{*}}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^i{\beta }_j)\hfill \\ o_j^k\ge 0\hfill \end{array}\right.\end{array}$$

(48)

Equation (48) involves both the time evaluation term and jerk evaluation term, which differ in physical units and numerical scales. To eliminate the impact of these differences on the optimization process, normalization is applied. In addition, although the jerk evaluation term is included, the primary objective remains the minimization of execution time. To prevent the jerk evaluation term from disproportionately influencing the optimization, a weighting factor $\mu$ is introduced to balance its contribution. This design provides flexibility to accommodate varying requirements across different robotic applications. The final objective function of the TJOTP-3C problem is designed as

$$\min \hspace{0.33em}\mathrm{obj}={\displaystyle \frac{T}{T^{*}}}+\mu \left({\displaystyle \sum _{j=1}^{N_{\mathrm{point}}}{\displaystyle \sum _{k=1}^N{o}_j^k}}\right)/\left({\displaystyle \sum _{j=1}^{N_{\mathrm{point}}}{J}_j^{*}}\right)$$

(49)

where $T^{*}$ and $J_j^{*}$ denote the time evaluation term and the jerk evaluation term, respectively, computed from the optimal solution of the TOTP-2C problem. By integrating the linear jerk constraints and the proposed objective function into the TOTP-2C framework, the resulting optimization model for TJOTP-3C is formulated as

$$\begin{array}{l}\underset{a,b,c,d}{\min \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\mathrm{obj}}=2\Delta s{\displaystyle \sum _{j=1}^{N_{\mathrm{point}}-1}{e}_j}+\mu {\displaystyle \sum _{j=1}^{N_{\mathrm{point}}}{\displaystyle \sum _{k=1}^N{o}_j^k}}\\ s.t.\hspace{0.33em}\left\{\begin{array}{c}(Q_s\circ Q_s)\sqrt{{\beta }_j}\le {\dot{Q}}_{\max }\circ {\dot{Q}}_{\max }\\ -{\ddot{Q}}_{\max }\le Q_s{\alpha }_j+Q_{ss}{\beta }_j\le {\ddot{Q}}_{\max }\\ -{\tau }_{\max }\le m(Q){\alpha }_j+c(Q){\beta }_j+g(Q)\le {\tau }_{\max }\\ -{\stackrel{⃛}{Q}}_{\max }\le \sqrt{{\beta }_j^{*}}(3Q_{ss}{\alpha }_j+Q_s{\gamma }_j+Q_s{\beta }_j)\le {\stackrel{⃛}{Q}}_{\max }\\ L^2{\beta }_j\le {v_{\max }^k}^2,-A_{\max }\le L{\alpha }_j\le A_{\max },-J_{\max }\le L\sqrt{{\beta }_j^{*}}{\gamma }_j\le J_{\max }\\ {\beta }_1=0,{\beta }_{N_{\mathrm{point}}}=1,{\alpha }_0=0,{\alpha }_{N_{\mathrm{point}}}=0\\ {\beta }_j\ge 0,f_j\ge 0,e_j\ge 0,o_j^k\ge 0\\ {‖\left[\begin{array}{c}2f_j\\ {\beta }_j-1\end{array}\right]‖}_2\le {\beta }_j+1\\ {‖\left[\begin{array}{c}2\\ f_j+f_{j+1}-e_j\end{array}\right]‖}_2\le f_j+f_{j+1}+e_j\\ o_j^k\ge -\sqrt{{\beta }_j^{*}}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)\\ o_j^k\ge \sqrt{{\beta }_j^{*}}(3Q_{ss}^k{\alpha }_j+Q_s^k{\gamma }_j+Q_{sss}^k{\beta }_j)\\ k=1,\cdots ,N\\ j=1,\cdots ,N_{\mathrm{point}}\end{array}\right.\end{array}$$

(50)

Equation (50) also conforms to the standard form of SOCP, and can therefore be solved using MOSEK.

4. Experimental Validation

This section validates the effectiveness of the proposed trajectory planning method using the serial 6R robot AN5, as illustrated in Figure 2. The DH (Denavit–Hartenberg) parameters of the AN5 robot are summarized in

Table 1. The modified D-H parameters of the AN5 robot.

Link i	ai−1 (mm)	αi−1 (rad)	di (mm)
1	0	0	139
2	0	π/2	114
3	−280	0	0
4	−240	0	−12
5	0	π/2	102
6	0	−π/2	100

. The algorithm was implemented on a personal laptop equipped with an Intel Core i5-8300H CPU (2.30 GHz) and 8 GB of RAM. Three sets of experiments were conducted to verify the following aspects: (a) the effectiveness of the proposed C³ continuity constraints, (b) the effectiveness of the time-jerk optimization, and (c) the comparative performance of the proposed TJOTP-3C method.

It is worth noting that the paths used in the validation experiments were generated using a custom-developed linear path local smoothing method with C³ continuity. Both the position and posture paths are C³ continuous with respect to the path length. This satisfies the first sufficient condition for achieving C³ continuity in the joint trajectory, namely that the given path itself must be C³ continuous. The paths used in this study are all defined in the Cartesian space. As shown in Figure 3, the position and posture of the robot EE are represented by the position ${[x,y,z]}^{\mathrm{T}}$ of the EE coordinate system {TCP} in the robot base coordinate system {B}, and the ZYX Euler angles ${[\varphi ,\theta ,\psi ]}^{\mathrm{T}}$. The homogeneous transformation matrix from {TCP} to the robot base coordinate system {B} can be calculated as

$$T_{TCP}^B=\left[\begin{array}{cc}{R}_{TCP}^B& P_{TCP}^B\\ 0& 1\end{array}\right], P_{TCP}^B=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$

(51)

where $P_{TCP}^B$ represents the position vector of the EE with respect to the base coordinate system, and $R_{TCP}^B$ represents the rotation matrix of the EE with respect to the base coordinate system, which determines the EE posture. It can be calculated from the ZYX Euler angles as

$$R_{TCP}^B=\mathrm{rotz}(\psi )\mathrm{roty}(\theta )\mathrm{rotx}(\varphi )=\left[\begin{array}{ccc}{c}_{\theta }{c}_{\psi }& c_{\psi }{s}_{\varphi }{s}_{\theta }-c_{\varphi }{s}_{\psi }& s_{\varphi }{s}_{\psi }+c_{\varphi }{c}_{\psi }{s}_{\theta }\\ c_{\theta }{s}_{\psi }& c_{\varphi }{c}_{\psi }+s_{\varphi }{s}_{\theta }{s}_{\psi }& c_{\varphi }{s}_{\theta }{s}_{\psi }-c_{\psi }{s}_{\varphi }\\ -s_{\theta }& c_{\theta }{s}_{\varphi }& c_{\varphi }{c}_{\theta }\end{array}\right]$$

(52)

where $\mathrm{rotz}(\cdot )$, $\mathrm{roty}(\cdot )$ and $\mathrm{rotx}(\cdot )$ denote the rotation matrices about the fixed x-, y-, and z-axes of the coordinate system, respectively. According to the inverse kinematics model of the robot, the joint angles can be determined from the Cartesian-space path, i.e., $Q=\mathrm{ik}(T_{TCP}^B)$, where $\mathrm{ik}(\cdot )$ represents the inverse kinematics function of the robot.

4.1. Validation of Continuity Constraint Effectiveness

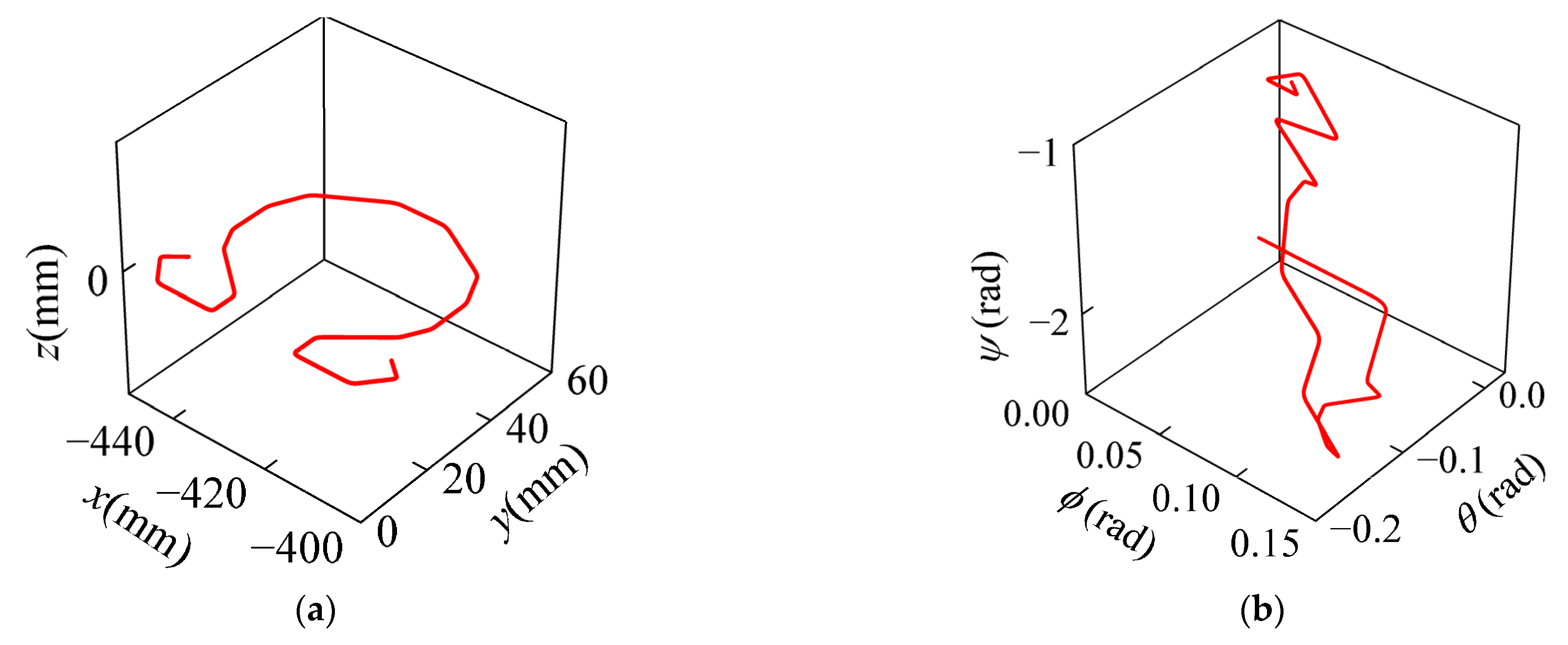
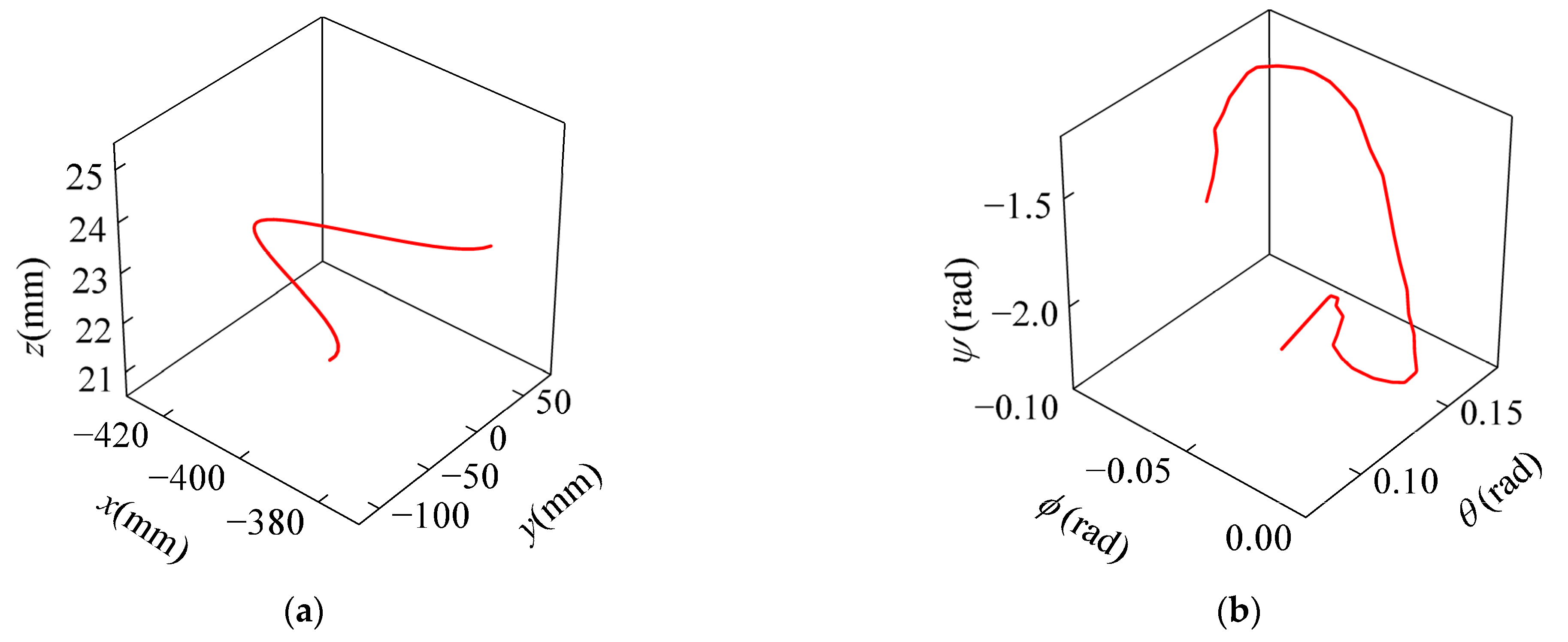
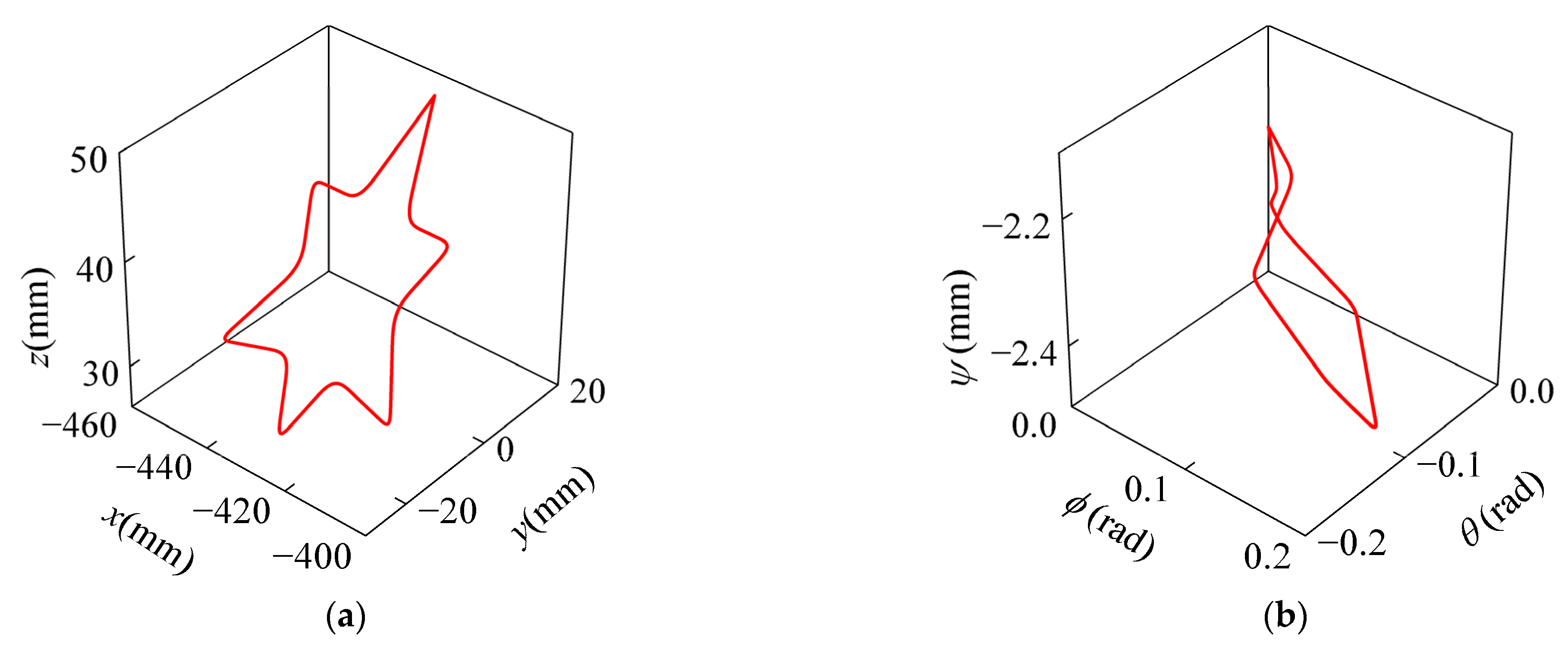
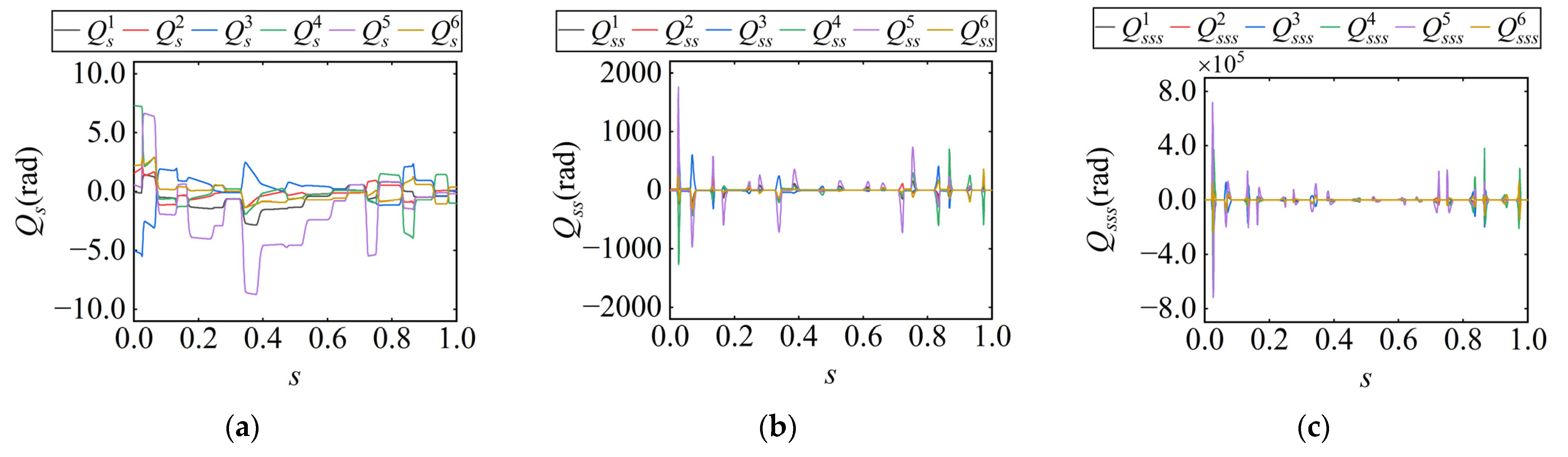
To validate the effectiveness of the continuity constraints, the butterfly-shaped EE path shown in Figure 4 is used as a test case. Based on the Cartesian path shown in Figure 4, the corresponding joint path $Q(s)$ can obtained through the robot’s inverse kinematics. By differentiating the joint path, the first-, second-, and third-order derivatives with respect to the path parameter s, namely $Q_s(s)$, $Q_{ss}(s)$ and $Q_{sss}(s)$, are computed, as illustrated in Figure 5. It can be observed that the values of $Q_s(s)$, $Q_{ss}(s)$ and $Q_{sss}(s)$ vary with the path parameter s. According to Equation (3), given the joint-space kinematic limits, if $Q_s(s)$, $Q_{ss}(s)$ and $Q_{sss}(s)$ are large at a certain point along the path, the velocity, acceleration, and jerk in Cartesian space must be reduced to ensure that the joint motion remains within the allowable limits.

The trajectory planning results are compared under two conditions: with continuity constraints (TOTP-2C) and without continuity constraints (TOTP-2). The time-optimal trajectory planning model with continuity constraints is provided in Equation (37). In the model without continuity constraints, pseudo-acceleration is typically estimated from the pseudo-velocity squared using a finite difference formula [23,24], that is

$${\alpha }_j={\displaystyle \frac{{\beta }_{j+1}-{\beta }_j}{2\Delta s}}$$

(53)

When Equation (53) is used, the pseudo-velocity becomes a piecewise linear function and the pseudo-acceleration becomes piecewise constant [25]. In this case, the pseudo-velocity is only C0 continuous, and the pseudo-acceleration is discontinuous. Such conditions can lead to sudden jumps in both acceleration and jerk in the resulting trajectory.

For the omega-shaped path, the upper limits of joint velocity and acceleration are set to ${\dot{Q}}_{\max }={[0.2,0.2,0.2,0.2,0.2,0.2]}^{\mathrm{T}}\mathrm{rad}/\mathrm{s}$ and ${\ddot{Q}}_{\max }={[0.5,0.5,0.5,0.5,0.5,0.5]}^{\mathrm{T}}{\mathrm{rad}/\mathrm{s}}^2$, respectively. The commanded feedrate of the EE is F = 10 mm/s, the maximum allowable acceleration is A_max = 100 mm/s², and the chord error constraint is set to ${\epsilon }_{\mathrm{chord}}=0.01\mathrm{mm}$. In the TOTP-2C method, the path is divided into 150 cubic spline segments, with 10 discrete points sampled per segment, resulting in a total of 1351 discrete points along the entire path. The number of discrete points in the TOTP-2 method is also set to 1351 to ensure a fair comparison.

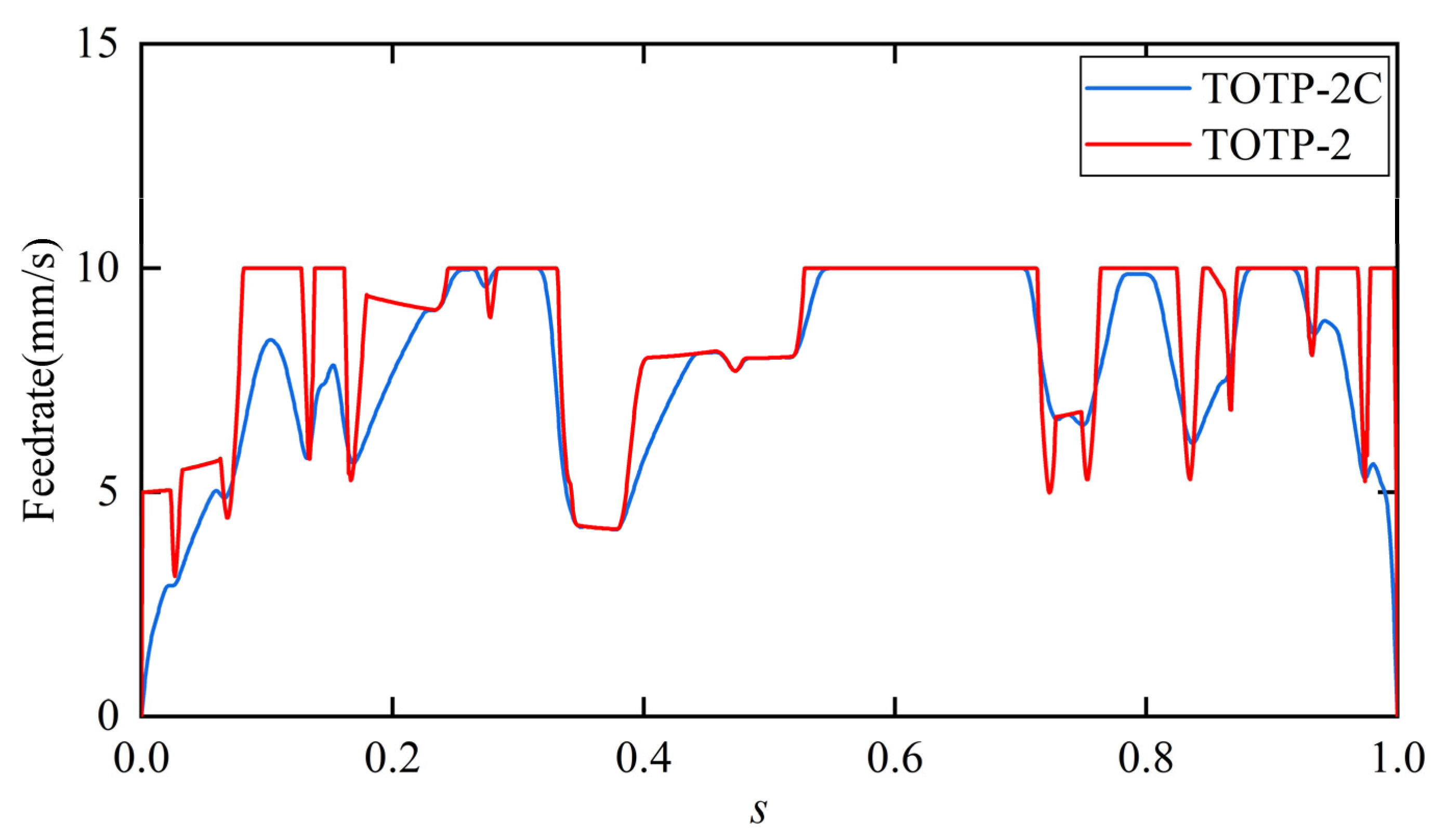
The feedrate profiles generated by the TOTP-2 and TOTP-2C methods are shown in Figure 6. As observed, both methods produce feedrate curves with similar overall trends. However, in certain regions, the feedrate generated by TOTP-2 is slightly higher than that of TOTP-2C. The total execution time of the trajectory generated by the TOTP-2C method is 22.69 s, compared to 24.36 s for the TOTP-2 method. Although the inclusion of continuity constraints slightly increases the execution time, the feedrate curve produced by TOTP-2C is noticeably smoother. This improved smoothness contributes to enhanced trajectory quality and reduced vibration during robot motion.

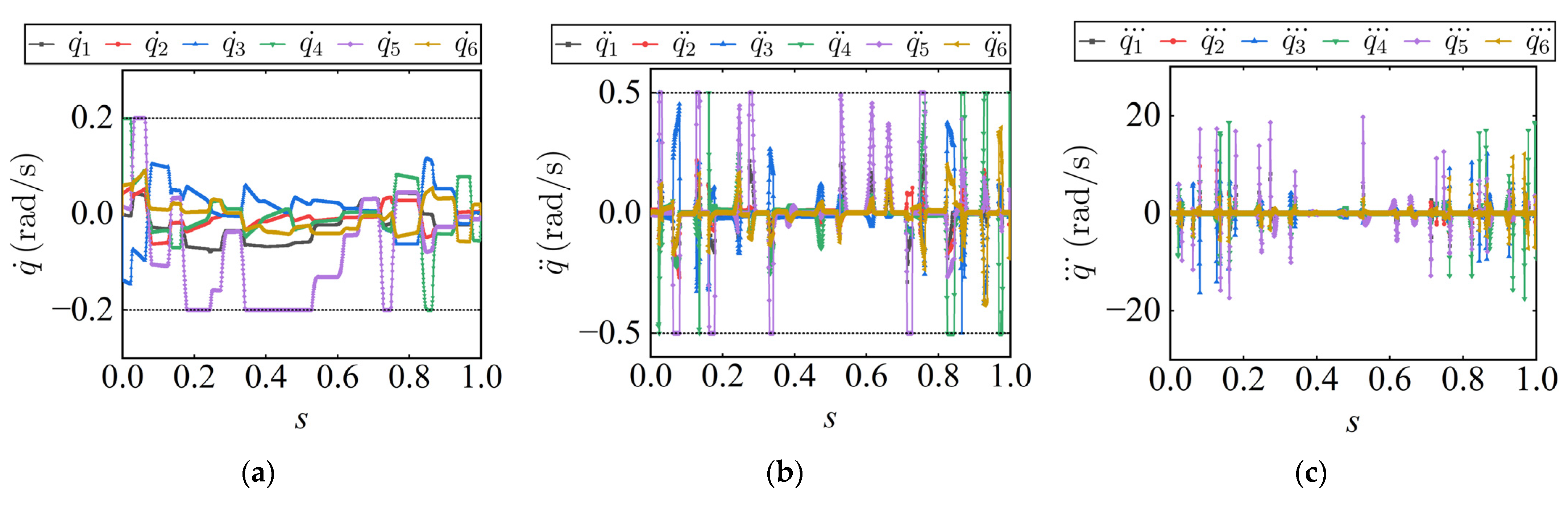
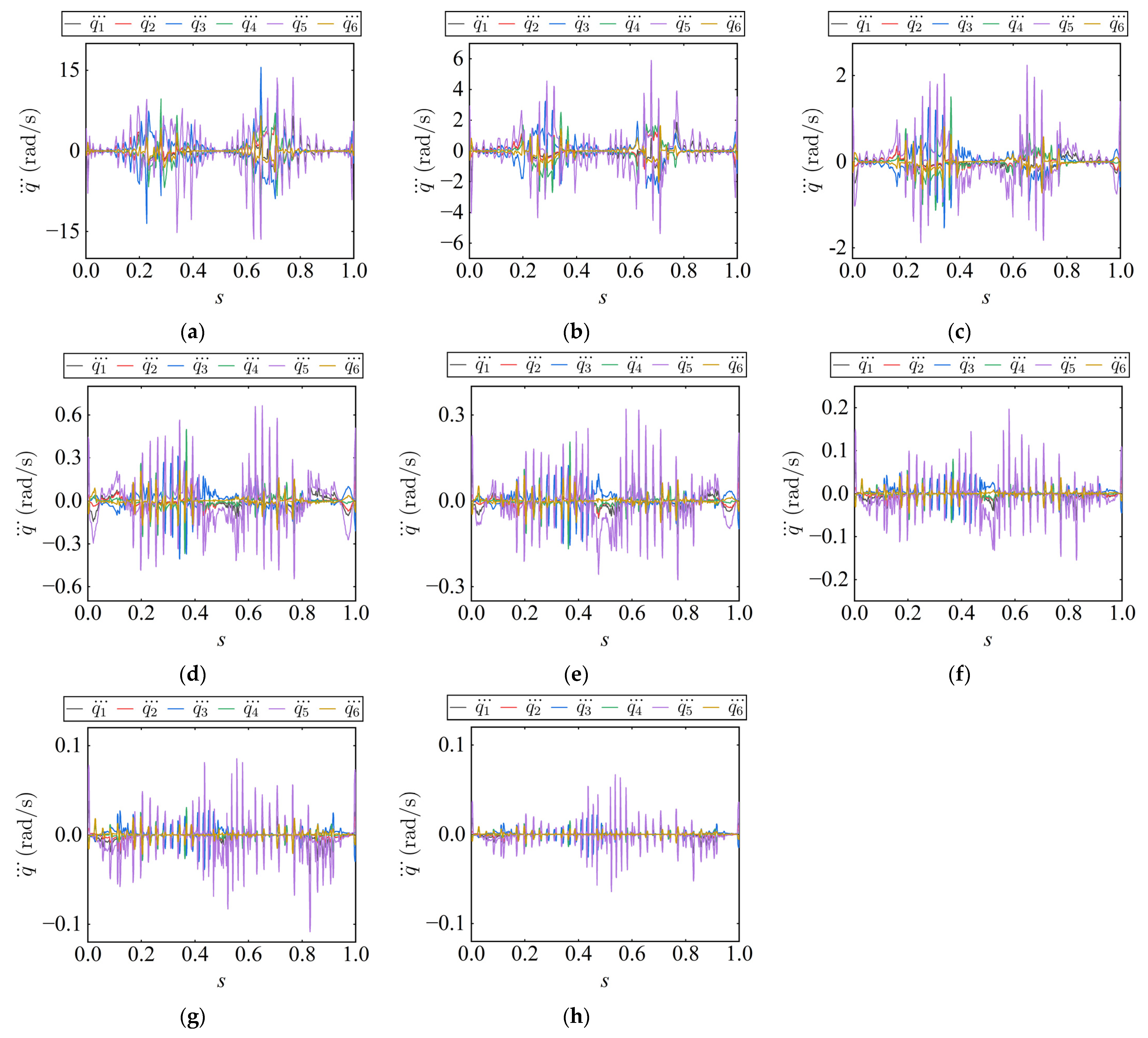
Figure 7 and Figure 8 show the joint velocity, acceleration, and jerk profiles generated by the TOTP-2C and TOTP-2 methods. While both methods produce velocity curves with good continuity, the TOTP-2C method exhibits clear advantages in higher-order continuity. In particular, the acceleration and jerk profiles from TOTP-2C display smooth transitions at discrete points without noticeable discontinuities. In contrast, the acceleration and jerk profiles generated by the TOTP-2 method show abrupt changes at discrete points, especially in the jerk curve, which features sharp corners that indicate discontinuous behavior.

A further comparison of the jerk profiles generated by TOTP-2C and TOTP-2 shows that, although neither method applies jerk constraints and both share the same velocity and acceleration limits, the jerk variation range for TOTP-2C is approximately −9.17 to 7.66 rad/s³, while that for TOTP-2 reaches −17.46 to 19.75 rad/s³, indicating significantly larger fluctuations. This is mainly due to the fact that TOTP-2C produces a continuous and smoother acceleration profile, which leads to more gradual changes in acceleration and avoids abrupt transitions. As a result, the jerk values remain within a smaller and more stable range. Overall, the TOTP-2C method not only ensures higher-order continuity of the trajectory but also delivers superior smoothness, which helps to improve control performance and enhance the dynamic stability of the actuator during execution.

4.2. Validation of the Time-Jerk Multi-Objective Optimization Effectiveness

To assess the effectiveness of the proposed TJOTP-3C method in optimizing both execution time and joint jerk, the cosine-shaped EE path in Figure 9 is selected for trajectory planning. The first-, second-, and third-order derivatives of the joint path with respect to the path parameter s are shown in Figure 10. The weighting factor $\mu$ in the Equation (50) is assigned different values to examine its influence on the planning results. The TJOTP-3C method is applied for each setting. The discretization step size remains the same as in the previous experiment, and the constraint parameters are summarized in

Table 2. Constraint parameters for the cos-shaped path.

Constraints	Joint 1	Joint 2	Joint 3	Joint 4	Joint 5	Joint 6
Joint velocity limit (rad/s)	0.07	0.07	0.07	0.07	0.07	0.07
Joint acceleration limit (rad/s2)	0.7	0.7	0.7	0.7	0.7	0.7
Joint jerk limit (rad/s3)	20	20	20	20	20	20
Joint torque limit (Nm)	60	60	60	20	20	20
Command feedrate of EE (mm/s)	15
Command acceleration of EE (mm/s2)	100
Command jerk of EE (mm/s3)	1000
Chord error limit (mm)	0.0001

.

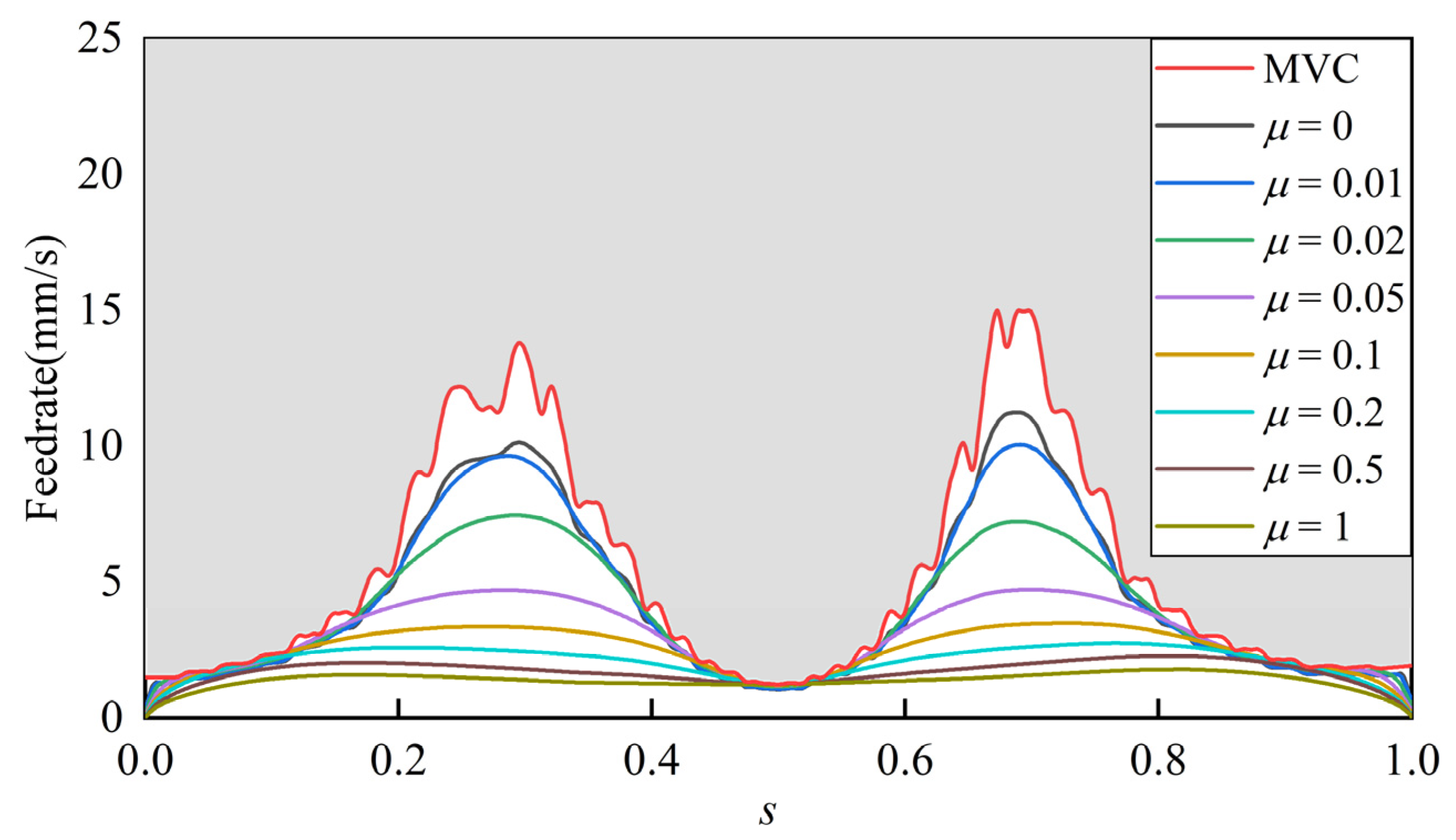
The feedrate profiles under different values of $\mu$ are shown in Figure 11, where MVC represents the maximum velocity curve considering joint velocity, joint acceleration, and EE feedrate constraints. As the value of $\mu$ increases, the jerk evaluation term contributes more heavily to the objective function in TJOTP-3C, resulting in a lower feedrate but smoother velocity curves. The corresponding joint jerk profiles are also presented in Figure 12. It can be clearly seen that increasing $\mu$ leads to a gradual reduction in joint jerk, confirming the effectiveness of the jerk optimization strategy. This indicates that, beyond satisfying hard jerk constraints, the method can further suppress dynamic disturbances and enhance trajectory smoothness.

However, analysis of both the feedrate and jerk profiles reveals a trade-off. While a higher value of $\mu$ reduces joint jerk, it increases the trajectory execution time. This reflects the inherent conflict between time efficiency and jerk minimization. Therefore, in practical applications, the choice of $\mu$ should be determined based on the specific task requirements. For tasks with high demands on execution efficiency and relatively low sensitivity to motion-induced disturbances, such as robotic handling tasks, a smaller value of $\mu$ is more appropriate. For tasks where smooth motion is more critical and execution time is less of a concern, such as robotic milling, polishing, and other machining operations, a larger value of $\mu$ can be selected to reduce joint jerk and improve machining quality.

4.3. Validation of the TJOTP-3C Method via Method Comparison

To evaluate the effectiveness of the proposed TJOTP-3C optimization method, trajectory planning is performed on the star-shaped path shown in Figure 13 using the proposed approach. The first-, second-, and third-order derivatives of the joint path with respect to the path parameter “s” are shown in Figure 14. The kinematic and dynamic constraints in both the joint space and Cartesian space are defined as listed in

Table 3. Constraint parameters for the star-shaped path.

Constraints	Joint 1	Joint 2	Joint 3	Joint 4	Joint 5	Joint 6
Joint velocity limit (rad/s)	0.08	0.08	0.08	0.08	0.08	0.08
Joint acceleration limit (rad/s2)	0.2	0.2	0.2	0.2	0.2	0.2
Joint jerk limit (rad/s3)	20	20	20	20	20	20
Joint torque limit (Nm)	60	60	60	20	20	20
Command feedrate of EE (mm/s)	15
Command acceleration of EE (mm/s2)	40
Command jerk of EE (mm/s3)	400
Chord error limit (mm)	0.002

.

In the TJOTP-3C method, the path discretization parameters are kept consistent with those used in the previous two experiments. To demonstrate the advantages of the proposed approach, two other trajectory planning methods are selected for comparison. The first is the time-optimal trajectory planning method based on linear programming (TOTP-LP) proposed by Liu et al. [23]. Although this method considers only constraints in joint space, it belongs to the class of convex optimization methods, similar to the proposed approach, and is therefore adopted as a comparison method to validate the effectiveness of the continuity constraints in TJOTP-3C. The second is a CBFS-based method proposed by Jia et al. [37]. Ref [37] defined regions where the maximum velocity curve falls below the commanded feedrate as velocity-sensitive regions. In these regions, the end-effector feedrate is kept constant. In contrast, S-curve acceleration and deceleration profiles are applied in non-sensitive regions to ensure smooth speed transitions. As CBFS is a representative feedrate scheduling strategy in trajectory planning, this method is used as another comparative approach. Originally designed for five-axis CNC machining without considering joint-space constraints, the method is adapted in this study by introducing the proportional adjustment strategy [5] to ensure compatibility with joint kinematic constraints. In addition, the trigonometric acceleration and deceleration profile are used in place of the S-curve profile in Ref [37] to achieve C³ continuity in the trajectory.

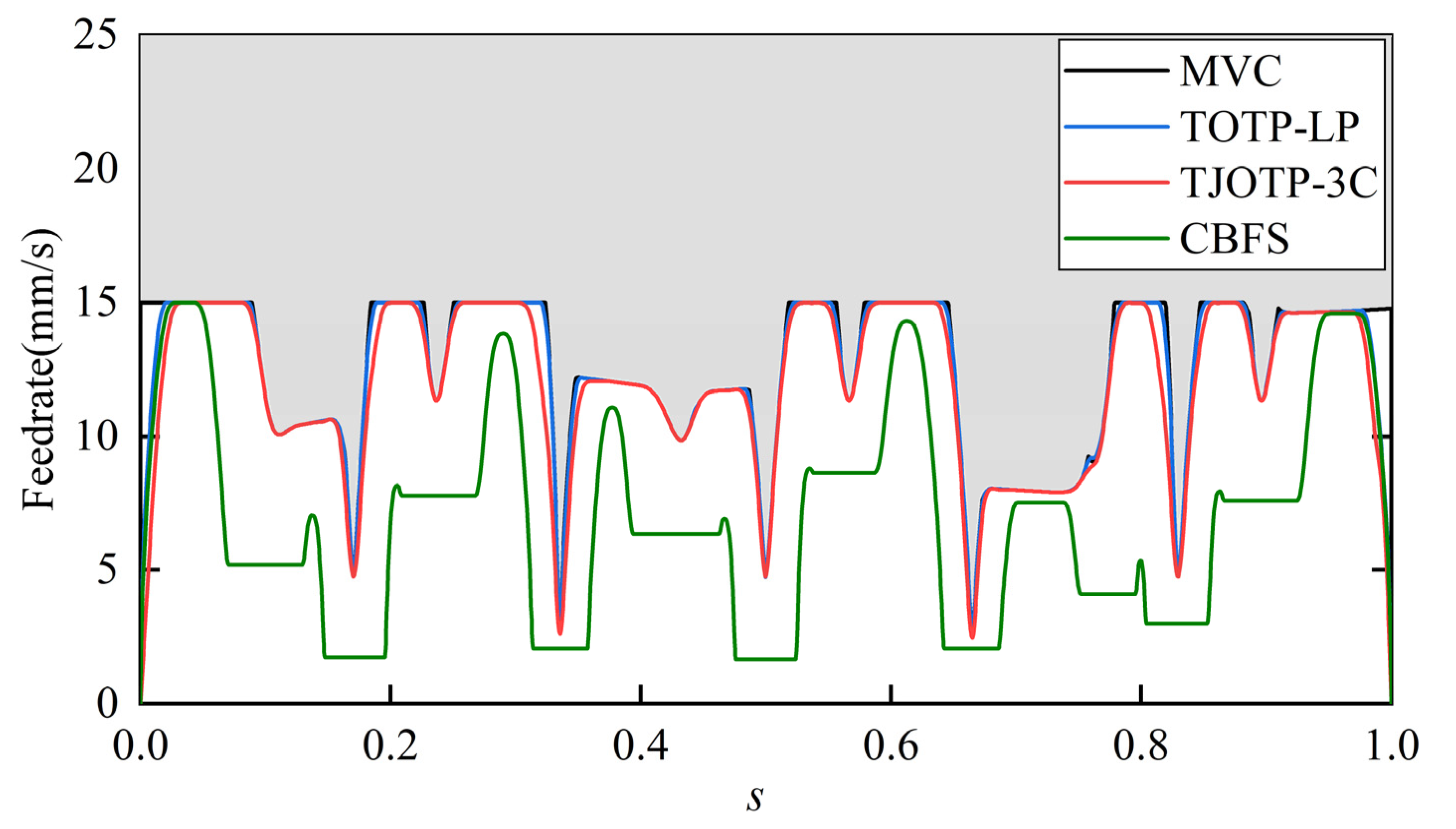
Under identical constraints and sampling parameters, the trajectory of the star-shaped path is planned using the TJOTP-3C, TOTP-LP, and CBFS methods. To eliminate the influence of the jerk-related term in the TJOTP-3C objective function on the comparative analysis, the weighting factor is set to $\mu =0$. The resulting feedrate profiles in Cartesian space for the three methods are shown in Figure 15. In Figure 15, MVC denotes the maximum velocity curve that satisfies joint velocity and acceleration constraints as well as the commanded feedrate of the end-effector. It can be observed that the feedrate profile generated by the TOTP-LP method is closest to the MVC, indicating that it achieves the highest trajectory execution efficiency. In contrast, the feedrate profiles generated by the TJOTP-3C and CBFS methods fall below that of TOTP-LP, suggesting longer overall execution. After mapping the trajectories from the parameter domain to the time domain, the trajectory durations for TOTP-LP, TJOTP-3C, and CBFS are 14.68 s, 15.23 s, and 36.76 s, respectively. Among the three methods, TOTP-LP yields the shortest duration, followed by TJOTP-3C, while CBFS results in the longest.

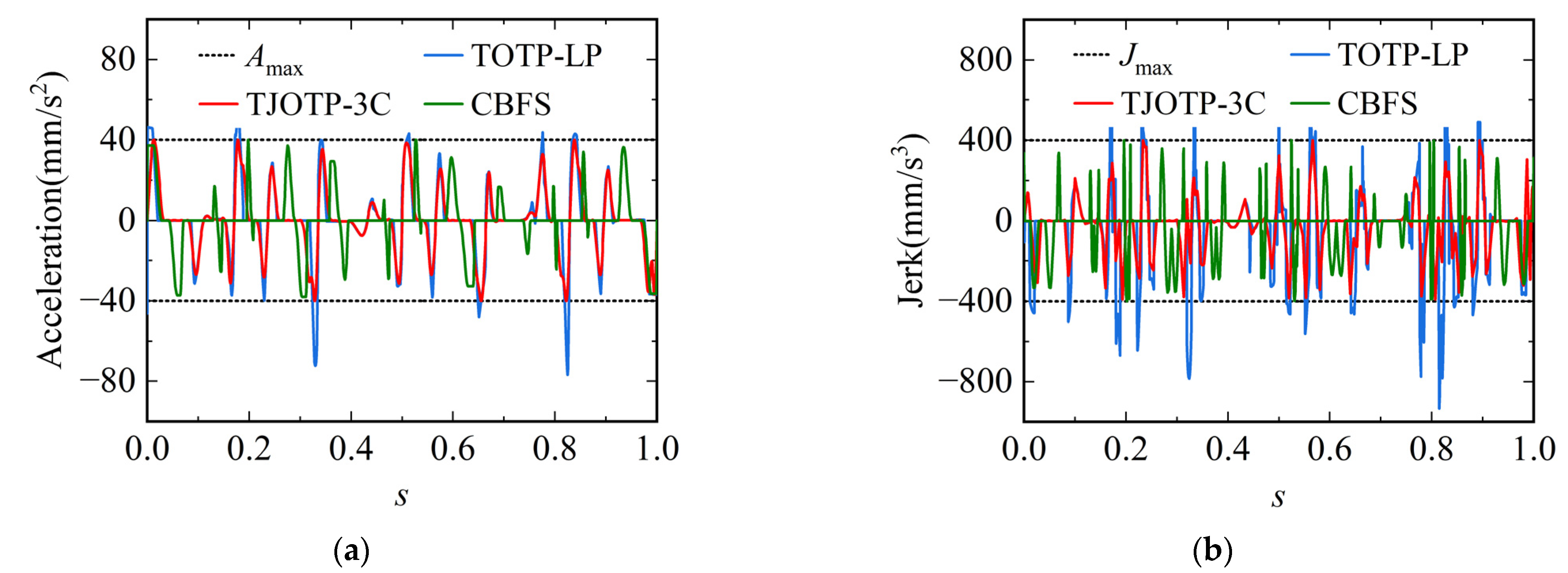
Although the TOTP-LP method provides higher trajectory execution efficiency, it imposes full kinematic and dynamic constraints only in the joint space. In the Cartesian space, TOTP-LP can constrain feedrate but lacks the ability to limit EE acceleration and jerk. As a result, the trajectory generated by TOTP-LP shows violations of the EE acceleration and jerk constraints, as illustrated in Figure 16. In contrast, both the TJOTP-3C and CBFS methods apply full kinematic constraints in both joint and Cartesian spaces, ensuring that the end-effector velocity, acceleration, and jerk remain within their respective limits. Additionally, the TJOTP-3C method explicitly incorporates continuity constraints, while the CBFS method employs a trigonometric acceleration profile that is inherently C³ continuous. These characteristics lead to smoother trajectories, which reduce jerk and vibration when compared to the C1 continuous trajectory produced by TOTP-LP.

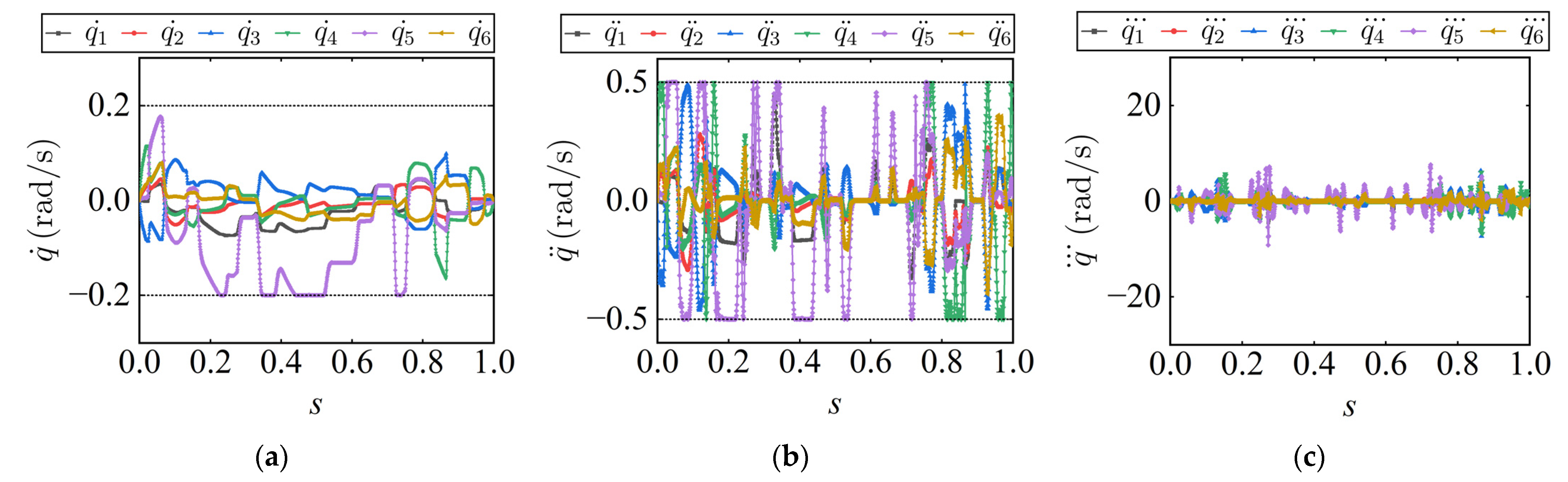
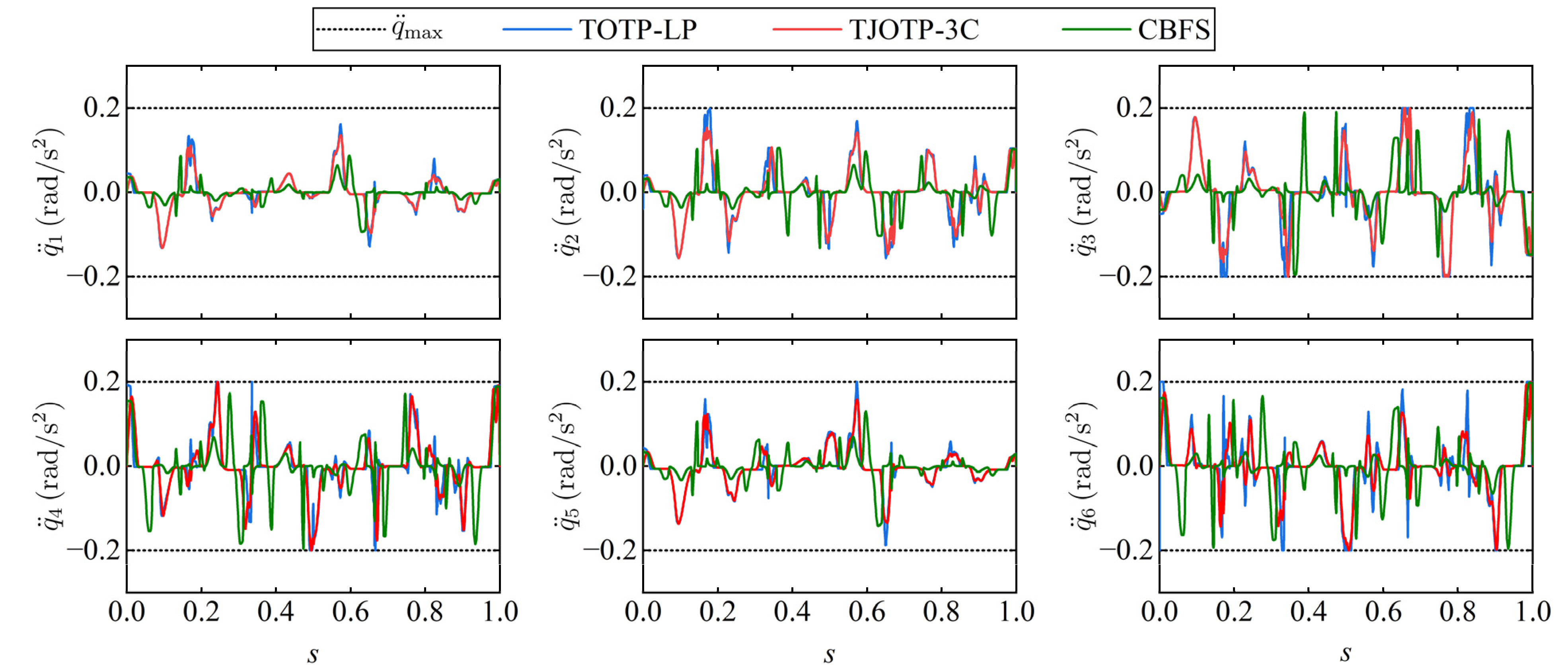
By applying inverse kinematics, the trajectories generated by the TOTP-LP, TJOTP-3C, and CBFS methods are transformed into joint space. The corresponding joint angular velocity, acceleration, and jerk profiles are shown in Figure 17, Figure 18 and Figure 19, respectively. All three methods produce joint trajectories that satisfy the specified constraint limits, confirming the effectiveness of the compound constraint strategy proposed in this study.

As illustrated in Figure 17, the joint velocity curves produced by the TOTP-LP and TJOTP-3C methods are nearly identical. This similarity arises from the fact that both methods are time-optimal and formulated using convex optimization. Aside from the EE acceleration, jerk, and continuity constraints uniquely imposed by TJOTP-3C, the two approaches share the same formulation, resulting in comparable trajectories. However, due to the absence of continuity constraints, the velocity profiles of TOTP-LP are less smooth, and its acceleration and jerk curves contain more pronounced sharp points. The CBFS method is inherently based on a C³ continuous curve, naturally resulting in relatively smooth trajectories. However, it does not make full use of the joint kinematic constraints, which explains why its execution time is longer than that of both the TOTP-LP and TJOTP-3C methods. To quantitatively evaluate trajectory smoothness, the standard deviation (STD) values of joint velocity, acceleration, and jerk are reported in

Table 4. Comparison of joint velocity, acceleration, and jerk STD values under different methods.

STD	Methods	Joint 1	Joint 2	Joint 3	Joint 4	Joint 5	Joint 6
STD of velocity	TOTP-LP	0.017	0.034	0.052	0.056	0.026	0.057
	TJOTP-3C	0.016 (5.88%)	0.031 (8.82%)	0.050 (3.85%)	0.054 (3.57%)	0.025 (3.85%)	0.055 (3.51%)
	CBFS	0.008 (52.9%)	0.018 (47.1%)	0.025 (5139%)	0.028 (50.0%)	0.011 (57.7%)	0.026 (54.4%)
STD of acceleration	TOTP-LP	0.034	0.052	0.069	0.057	0.039	0.059
	TJOTP-3C	0.032 (5.88%)	0.047 (9.62%)	0.063 (8.70%)	0.055 (3.51%)	0.037 (5.13%)	0.054 (8.47%)
	CBFS	0.017 (50.0%)	0.029 (44.2%)	0.043 (37.7%)	0.049 (14.0%)	0.023 (41.0%)	0.049 (17.0%)
STD of jerk	TOTP-LP	0.028	0.045	0.064	0.058	0.035	0.068
	TJOTP-3C	0.020 (28.57%)	0.032 (28.9%)	0.045 (59.7%)	0.045 (22.4%)	0.026 (25.7%)	0.048 (29.4%)
	CBFS	0.013 (53.57%)	0.024 (46.7%)	0.036 (43.8%)	0.040 (31.0%)	0.019 (45.7%)	0.040 (41.2%)

Notes: The values in parentheses represent the percentage reduction compared to the reference method (TOTP-LP). A positive value indicates that the result is smaller than that of the reference method, while a negative value indicates a larger result.

. Benefiting from the enforcement of C³ continuity, both CBFS and TJOTP-3C achieve lower RMS values than TOTP-LP across all motion levels, indicating smaller fluctuations and enhanced smoothness.

Taken as a whole, TJOTP-3C achieves more favorable results than the other two methods. The TOTP-LP method generates time-optimal trajectories but only ensures velocity continuity, resulting in limited smoothness that may lead to impacts and vibrations during execution. Moreover, it cannot constrain end-effector acceleration and jerk in Cartesian space. The CBFS method produces smoother, high-order continuous trajectories, but its velocity profile adjustment lacks flexibility and it does not support time optimization. As a result, it yields longer execution durations and lower machining efficiency. In addition, CBFS cannot incorporate the robot dynamic constraints. In contrast, TJOTP-3C accounts for a complete set of constraints in path-following tasks, supports execution time optimization, and generates smooth trajectories. From the perspectives of constraint completeness, execution time, and trajectory smoothness, TJOTP-3C provides a more balanced and effective solution than the other two methods. It not only inherits the time-optimization capability of TOTP-LP but also shares the ability of CBFS to generate smooth, high-order continuous trajectories.

5. Conclusions

This paper presented a trajectory planning method, TJOTP-3C, for robotic path-following tasks under compound constraints. The method integrated time optimization, jerk minimization, and continuity enhancement into a unified optimization framework, and was solved using the second-order cone programming (SOCP) approach. The main conclusions are summarized as follows:

• Jerk constraints were considered in both joint space and Cartesian space, enabling the computation of time-optimal trajectories under complete 3rd-order kinematic constraints.
• Continuity constraints based on piecewise cubic splines were introduced to improve the smoothness of joint trajectories, ensuring C³ continuity of joint motion.
• A multi-objective function was designed, allowing the proposed TJOTP-3C algorithm to optimize execution time and jerk simultaneously.
• Experimental results demonstrated that the proposed method effectively minimized task duration while maintaining the high-order continuity of joint trajectories.