Abstract
A continuously variable transmission can improve the energy efficiency of actuators with rotary output by providing an optimum transmission ratio. A continuously variable transmission based on circumferentially arranged disks (CAD CVT) is a new type of CVT that is highly beneficial for applications requiring large torques, like heavy road transport. However, its major drawback is that its efficiency drops in the low torque region. To overcome this problem, the current paper proposes an improved mechanical design in which the force on traction disks is changed according to the instantaneous torque requirement, thus resulting in improved efficiency in low torque regions. Furthermore, a hydraulic-actuation-based control system has been designed to ensure the optimum control of the improved mechanical design. The improved mechanical design of the CAD CVT is named CAD CVT-II, which is highly beneficial for variable torque applications such as road transport and wind turbines.
1. Introduction
CVTs are widely used in different fields to provide an optimum transmission ratio, resulting in improved efficiency and a smoother transition between gear ratios. They improve the energy efficiency of IC engines [], mobile robots [], wind turbines [,], hybrid hydraulic excavators [], hybrid electric vehicles [], and pure electric vehicles []. Furthermore, traction-based CVTs can improve the safety of human operators working in a robot-interactive environment because of their ability to slip when subjected to over-torque [,]. Traction-based CVTs could also be helpful for damage-free robot–crop interaction [].
So far, different types of CVTs have been developed, and they can be broadly classified as ratcheting-type CVTs, traction-based CVTs, belt and chain-based CVTs, etc.
Belt-type CVTs are the most widely used commercially available CVTs for land transport. Numerous works have been performed on different designs/configurations and analyses of belt-type CVTs [,]. Extensive research has been conducted to optimally control various parameters of a belt-type CVT, such as clamping force control and gear ratio control. Verbelen et al. [] utilized an adaptive PI controller for a slip-controlled belt CVT. They linearized the equations of slip dynamics of the CVT. The linearization resulted in the reduction of high-order nonlinear equations to first-order functions. The first-order transfer functions were easily controlled through a PI controller. Simulation results showed that the proposed controller was robust against torque and speed variations. Kim et al. [] proposed control for metal belt CVTs considering shift dynamics and ratio valve on/off characteristics. Feed-forward PID control was adopted for line pressure, whereas for ratio control, fuzzy logic is suggested. Guang-Bin et al. [] proposed an integrated control strategy for the optimization of CVT efficiency based on clamping force control. They utilized a PID controller for optimal clamping force control. Pulles et al. [] proposed a control method for a belt CVT that measures and controls slip in the CVT to minimize clamping force so that efficiency can be improved. However, at the same time, the controller ensures that the clamping force is enough to prevent slippage, which could damage the system. They used a robust PID controller with maximum gain while ensuring that the closed-loop system remained stable. Ye et al. [] investigated a new type of belt CVT called an EMCVT. In the EMCVT, instead of a hydraulic system, a DC motor was used to push the driving pulley so that a gear ratio change could be realized. Dual closed-loop controllers for position and speed were used. A fuzzy controller controlled the position loop, whereas a PI controller controlled the speed loop.
Numerous techniques have been developed for the control and optimization of different parameters of vehicles. These techniques could be helpful for the control and optimization of CVTs. Chen et al. [] proposed a novel coordination controller for chassis coordination control of a six-wheeled independent drive, an autonomous ground vehicle, by combining a quantum particle swarm optimization algorithm and a model predictive control algorithm for better computational efficiency. Jing Zhao et al. [] have proposed a constrained fractional-order model predictive controller for four-wheel independent drive autonomous ground vehicles. Chen et al. [] have proposed a trajectory and velocity planning method for vehicles based on a segmented three-dimensional Quartic Bezier Curve. Liu et al. [] proposed a model predictive control system based on direct yaw moment control for an autonomous 4WD agricultural electric vehicle. Moreover, accurate rotary angle sensors and design optimization techniques are essential for the development of an effective control system [,].
Fu et al. [] have developed a control algorithm for the braking of hydraulic excavators. They investigated load-braking laws through model analysis and developed an open-loop control algorithm called Command Reshaping. In the new algorithm, the small opening time of the valve is prolonged. Shi et al. [] developed an algorithm that fuses data from the pressure–position model and vehicle-dynamics-based model to improve pressure estimation of the master cylinder of the braking system of vehicles. Shi et al. [] developed a novel model predictive control approach for electro-hydraulic braking by wire. A quadratic polynomial was utilized to fit a relationship between piston position and cylinder pressure.
Numerous designs of traction-based CVTs have been proposed. The list comprises the W-CVT developed by Chen et al. [], PD-CVT developed by Kazerounian et al. [], CTC–CVT developed by Komatsubara [], Motion CVT developed by Carter et al. [], Hydraulic Traction CVT developed by Shen et al. [], B-CVT developed by Ghaiblu et al. [], NS CVT developed by Chao et al. [], DH CVT [], Spherical CVT [], Nu Vinci CVT [], Half Toroidal CVT [], and Full Toroidal CVT [].
The current research continues our previous work on the CAD CVT []. During the analysis of the CAD CVT, it was observed that it provides numerous advantages over existing commercially available CVTs, like high torque capacity and the achievement of negative gear ratios without requiring an additional set of gears or clutches. However, it has one main problem. The efficiency of the CAD CVT drops in the low torque region. The current research proposes an improved mechanical design of a CAD CVT that improves efficiency in the low torque regions.
The current article consists of (1) Introduction, (2) Materials and Methods, (3) Results and Discussion, and (4) Conclusion.
The Materials and Methods section is divided into (1) Analysis of CAD CVT, (2) Mechanical Design of Improved CAD CVT (CAD CVT-II), (3) Analysis of CAD CVT-II, (4) Design of Control System for CAD CVT-II, (5) Analysis of Control System of CAD CVT-II.
The scope of the current article is limited to the following:
- Analysis of a CAD CVT in the low torque region.
- Proposal of a new mechanical design that overcomes the problem of low efficiency faced by a CAD CVT in low torque regions while maintaining its fundamental theme.
- Development of a stable control system for the force applied to the traction disks of a CAD CVT according to the instantaneous torque requirement.
The main research contributions/innovations of the current article are as follows:
- New/improved mechanical design of a CAD CVT with better efficiency in low torque regions.
- Design of a stable hydraulic-actuation-based control system for the improved mechanical design of a CAD CVT.
2. Materials and Methods
2.1. Problem Statement
The problem is the need to improve the energy efficiency of a CAD CVT during variable torque, especially in low torque regions.
2.2. Analysis of CAD CVT
An analysis of a CAD CVT is performed to check its energy efficiency in the low torque region and identify potential causes of efficiency drops.
2.2.1. Analysis of CAD CVT Efficiency During Variable-Torque Operation
For a better understanding, some figures of a CAD CVT [] are reproduced here. Figure 1a is a 3D model with two transparent sides for the visualization of internal components. Figure 1b is an exploded view of the CAD CVT with components numbered. Figure 2 demonstrates the basic working principle, and Figure 3 shows the manufactured model.

Figure 1.
(a) Three-dimensional model of CAD CVT ([], Figure 2) with two sides transparent for better visualization. (b) Exploded view of CAD CVT [].

Figure 2.
Working principle of CAD CVT ([], Figure 5) for gear ratio change. (a) Forward. (b) Neutral. (c) Reverse.

Figure 3.
Manufactured model of CAD CVT ([] Figure 21) with four traction disks. (a) Output side (b) Input Side.
In [], the torque capacity of a CAD CVT having four circumferentially arranged disks at the transmission ratio TR = −1 is given, as shown below.
In the above equation, n denotes the number of circumferentially arranged disks (traction disks) ‘7a’, ‘7b’, ‘7c’, and ‘7d’. Ro represents the radius of the output disk ‘16’. Fn denotes the axial force applied to the traction disks. μkt represents the coefficient of kinematic friction. The above variables are fixed for the CAD CVT and cannot be changed during operation. Similarly, total friction losses of the CAD CVT [] are as follows:
In the above equation, PTotal denotes the total frictional losses of the CAD CVT. ωCAD represents the rotational speed of traction disks. 2a denotes the contact length at the traction points of the traction disks. μss represents the coefficient of static friction. μr denotes the coefficient of rolling friction. μbb represents the coefficient of friction of the ball bearing. μpb denotes the coefficient of friction of the pin bearing. μtb represents the coefficient of friction of the thrust bearing. Rdi denotes the distance between the center of the traction disks to the traction point between the traction disks and input disk ‘4’. d1 represents the distance from the center of ball bearings ‘9a’, ‘9b’, ‘9c’, and ‘9d’ to the tractive surface of the respective traction disks. d2 denotes the distance between ball bearings ‘9a’, ‘9b’, ‘9c’, ‘9d’ and pin bearings ‘13a’, ‘13b’, ‘13c’, ‘13d’, respectively. Rbb represents the radius of the ball bearing. Rpb denotes the radius of the pin bearing. Rtb represents the radius of the thrust bearing.
Suppose Tc is the maximum torque capacity that the CAD CVT can handle. In the real world, especially in the transport sector, the torque requirement varies, and the CVT may be subject to torque, τo, as follows:
The efficiency of the CAD CVT [] is represented as follows:
and the total input power of the CAD CVT [] is
So, the efficiency of CAD CVT becomes
In Equation (6), ωo denotes the rotational speed of the output shaft of the CAD CVT, which can also be represented as []
and
Putting the values of Equations (7) and (8) into Equation (2), we will obtain
We assume that
where
Now, we assume that
So, Equation (10) becomes
In the case of CAD CVT, Fn cannot be changed during operation. It is fixed at the assembly stage. Consequently, we can write Equation (13) as
where
Putting Equation (15) into Equation (6), we can obtain
and Equation (16) can be written as
So, we plot a graph of efficiency versus applied torque at the output as shown in Figure 4. The applied torque, τo, is varied from 0 to the maximum torque capacity Tc, as per Equation (1) for Fn = 5000 N, Tc = 90 Nm. Moreover, values of the parameters of the CAD CVT are given in Table 1.
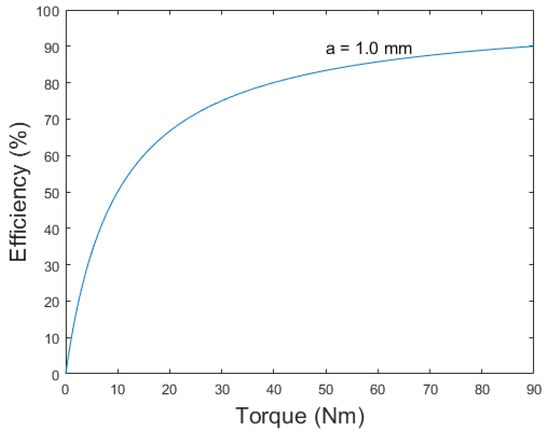
Figure 4.
Efficiency of CAD CVT during variable torque. 2a = contact length.

Table 1.
CAD CVT parameters [] with values.
It can be observed that the efficiency is maximum when the torque applied is maximum, and the efficiency drops in the lower torque region.
2.2.2. Root Cause of Efficiency Drop
The root cause of the efficiency drop in the low torque region is that maximum force is applied to the traction disks irrespective of the torque requirement at the output shaft. Therefore, frictional losses, dependent on the force applied to traction disks, remain constant. The ratio between useful output and frictional losses in the low torque region becomes very low.
This problem can be resolved by proportionally reducing the force on traction disks according to torque requirements at the output shaft.
However, as shown in Figure 5, the current design of the CAD CVT does not allow for changing the torque applied to the caps during operation.

Figure 5.
CAD CVT. Caps can be tightened like a nut to a predetermined torque at the assembly stage only. During operation, the axial force applied by nuts to traction disks is constant and cannot be changed.
2.3. Mechanical Design of the Proposed CAD CVT-II
Following the establishment of the problem statement and identification of the root cause of the problem in the CAD CVT, critical design parameters were developed. Based on these parameters, a novel mechanical design was proposed in which the axial force, Fn, applied to traction disks for controlling traction force is dynamically controlled. The new proposed mechanical design is named CAD CVT-II. The following paragraphs explain the critical design parameters, 3D models and configuration, and working principles.
2.3.1. Critical Design Parameters
The problem can be solved by incorporating design features in CAD CVT that fulfill the following criteria:
- Fn, the force applied to the traction disks, can be controlled during operation.
- The new design should apply equal force to all traction disks simultaneously.
- The new design should be such that it can measure the applied torque during operation and adjust the Fn accordingly during operation.
- The new design should be added as an additional feature to the existing CAD CVT so that the mathematical equations derived for the CAD CVT [] are also valid for the new design.
2.3.2. Three-Dimensional Model of the Proposed CAD CVT-II
To better visualize and communicate the design, a 3D model of CAD CVT-II has been developed. The caps of the CAD CVT have been replaced with hydraulic cylinders. The pistons of hydraulic cylinders apply force to traction disks. By controlling pressure in hydraulic cylinders, the force on traction disks is controlled.
Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 show different views of CAD CVT-II. Figure 11 shows an exploded view of the CAD CVT [] for comparison.

Figure 6.
Schematic view of CAD CVT-II. Arrows show the direction of observation. i.e., standing at the tail and looking in direction of arrow head. When the input shaft moves clockwise, CAD 1 and CAD 2 move anti-clockwise. This results in anti-clockwise movement of the output shaft. Pressure in hydraulic cylinders determines the axial force applied to traction disks.

Figure 7.
Three-dimensional model of the proposed CAD CVT-II with two sides transparent for better visualization.

Figure 8.
View of CAD CVT-II cut by a plane.

Figure 9.
Two-dimensional view of CAD CVT-II cut by a plane.

Figure 10.
Exploded view of CAD CVT-II. Components enclosed in the red box are additional/modified components not available in the CAD CVT [].
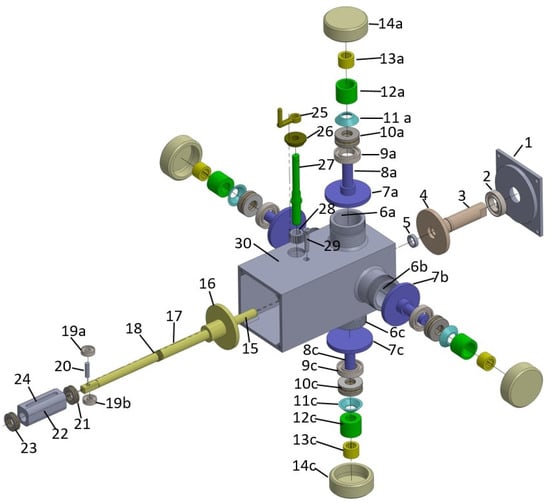
Figure 11.
Exploded view of the CAD CVT with four circumferentially arranged disks (traction disks) [] given for better comparison with CAD CVT-II given in the previous Figure 10.
2.3.3. Configuration of the Proposed CAD CVT-II
To better understand the configuration of the proposed CAD CVT-II, a 3D model of the proposed CAD CVT-II with four traction points has been selected. An exploded view of CAD CVT-II has been numbered, as shown in Figure 10. A description of each numbered component is given in Table 2.

Table 2.
The description of part numbers shown in Figure 10.
2.3.4. Operating Principle of the Proposed CAD CVT-II
The main operating principle of CAD CVT-II is similar to that of the CAD CVT. The significant difference is that in the CAD CVT, the force Fn applied to traction disks is fixed and cannot be changed during operation, whereas in CAD CVT-II, the force Fn applied to traction disks can be varied by controlling pressure in the secondary cylinders through a hydraulic system.
Figure 10 shows an exploded view of CAD CVT-II.
Parts ‘1’ to ‘34’ are the same in the CAD CVT and CAD CVT-II, except for parts ‘14a’, 14b’, ‘14c’, and ‘14d’. In the CAD CVT, these parts represent caps, whereas in CAD CVT-II, these caps have been replaced with secondary cylinders.
Part ‘11a’, ‘11b’, ‘11c’ and ‘11d’ represent disk springs in the CAD CVT. In CAD CVT-II, they have been replaced by simple metallic spacers. Since the hydraulic actuation system of CAD CVT-II already has a set of disk springs represented by part ‘44’, and these disk springs effectively apply a continuous force on the traction disks through the hydraulic fluid, there is no need to have additional disk springs in series. Moreover, the replacement of disk springs with a simple spacer significantly reduces the complexity of the transfer function of the control system.
Parts ‘35’ to ‘39’ are additional components that are part of CAD CVT-II; however, they are not available in the CAD CVT.
The input to CAD CVT-II is given at input shaft ‘3’, which results in the rotary motion of disk ‘4’ attached to input shaft ‘3’. Disk ‘4’ is in traction contact with four circumferentially arranged disks (traction disks), ‘7a’, ‘7b’, ‘7c’, and ‘7d’, resulting in the rotary motion of the traction disks. Since the traction disks are in traction contact with output disk ‘16’, the rotary motion of the traction disks results in the rotary motion of output disk ‘16’. Output disk ‘16’ is rigidly attached to output shaft ‘17’; consequently, the rotary motion of output disk ‘16’ results in the rotary motion of output shaft ‘17’.
The transmission ratio between input shaft ‘3’ and output shaft ‘17’ is decided by the position of the traction point of output disk ‘16’ on traction disks ‘7a’, ‘7b’, ‘7c’, and ’7d’.
To change the transmission ratio, output shaft ‘17’ slides axially through a rack and pinion mechanism represented by rack ‘24’ and pinion ‘28’. The axial movement of output shaft ‘17’ results in the axial movement of output disk ‘16’. In this way, the radius of the traction point on traction disks is changed. Figure 10 highlights this phenomenon.
The torque capacity of both the CAD CVT and CAD CVT-II is determined by the axial force applied to traction disks.
In CAD CVT-II, ‘14a’, ‘14b’, ‘14c’, and ‘14d’ are secondary hydraulic cylinders. ‘35a’, ‘35b’, ‘35c’, and ‘35d’ are pistons of the secondary hydraulic cylinders. ‘36a’, ‘36b’, ‘36c’, and ‘36d’ are lip seals of the pistons. When hydraulic fluid is transmitted to the secondary hydraulic cylinders through steel pipes ‘40a’, ‘40b’, ‘40c’, and ‘40d’, it results in a force applied by the pistons ‘35a’, ‘35b’, ‘35c’, ‘35d’ on disk springs/spacers ‘12a’, ‘12b’, ‘12c’, ‘12d’. The force is effectively transferred to traction disks ‘7a’, ‘7b’, ‘7c’’7d’ and through spacers ‘11a’, ‘11b’, ‘11c’, ‘11d’ and thrust bearings ‘10a’, ‘10b’, ‘10c’, ‘10d’.
The torque capacity of CAD CVT-II can be determined from the force applied by the pistons of the secondary cylinders on traction disks due to pressure in the secondary cylinders. For details, see Appendix D.
2.4. Analysis of CAD CVT-II During Variable Torque
The main advantage of CAD CVT-II over the standard CAD CVT is that in CAD CVT-II, Fn is a function of output torque and can be controlled during operation through the hydraulically actuated system, which controls the position of the motor with the help of torque, pressure, and position sensors.
From [] (Equation (28)), we can write
If Fn is a function of , then we can write
From Equations (15) and (16), we can write
Equation (20) is based on the assumption that frictional losses in the CAD CVT, which are not dependent on Fn, are almost negligible compared to frictional losses that are dependent on Fn.
Equation (20) can be further simplified as
Putting the value of Fn from Equation (19) in Equation (21), we obtain
Equation (22) can be further simplified as
For numerical values of the parameters, see Table 1. Equation (25) shows that the efficiency of CAD CVT-II is constant throughout its operating range. Figure 12 shows a comparative analysis of the efficiency of CAD CVT vs. CAD CVT-II.

Figure 12.
The efficiency of the CAD CVT (benchmark) vs. CAD CVT-II (proposed). It can be observed that the efficiency of CAD CVT-II remains maximum throughout its operating range.
2.5. Design of Control System for CAD CVT-II
The control system of CAD CVT-II must consist of the following:
- A hydraulic actuation system to control hydraulic pressure in the cylinders of CAD CVT-II. Consequently, the force on traction disks can be regulated.
- A dynamic torque sensor must be attached to the CVT’s output. Consequently, the instantaneous required torque can be measured.
- Pressure sensors in the secondary cylinders (at least one). Consequently, any fluid leakage is detected.
2.5.1. Design of Energy-Efficient Hydraulic Actuation System
To design an energy-efficient hydraulic actuation system for CAD CVT-II, we have to design a novel hydraulic actuation system that has the following characteristics:
- The hydraulic actuation system motor must run only when a change in torque is required.
- The position of the motor can precisely control the pressure. Consequently, pressure acts as a function of the position of the motor.
- The motor must maintain its position during the off state to conserve energy.
Details of the design criteria and novel features of the hydraulic actuation system are given in Appendix A.
2.5.2. Three-Dimensional Model of Energy-Efficient Hydraulic Actuation System
Figure 13 and Figure 14 show a 3D model of an energy-efficient hydraulic actuation system designed using the above-mentioned design features. Table 3 describes the part numbers shown in Figure 13.

Figure 13.
Three-dimensional model of the hydraulic actuation system of CAD CVT-II cut by a plane in the center for better visualization.

Figure 14.
Three-dimensional model of the hydraulic actuation system of CAD CVT-II.

Table 3.
The description of part numbers shown in Figure 13.
2.5.3. Working Principle of the Energy-Efficient Hydraulic Actuation System
Refer to the 3D model of CAD CVT-II in Figure 10 and the 3D model of the hydraulic actuation system in Figure 13. The hydraulic actuation system consists of an electric motor, a power screw, a set of disk springs, and a hydraulic cylinder.
When electric motor ‘50’ is energized, it rotates gear ‘49’. The rotation of gear ‘49’ results in the rotation of gear ‘48’. The rotation of gear ‘48’ results in the rotation of power screw ‘46’. The rotation of power screw ‘46’ results in the axial movement of piston ‘45’. The axial movement of piston ‘45’ compresses the set of disk springs ‘44’. Disk springs ‘44’ apply a force on piston ‘42’, which is proportional to the displacement of disk springs ‘44’. The force applied on piston ‘42’ by disk springs ‘44’ is transferred to the hydraulic fluid in primary cylinder ‘41’ through piston ‘42’. The pressure generated in primary cylinder ‘41’ is transferred through metallic pipes ‘40a’, ‘40b’, ‘40c’, and ‘40d’ to secondary cylinders ‘14a’, ‘14b’, ‘14c’, and ‘14d’. In the secondary cylinders, the pressure is transformed into an axial force applied to traction disks ‘7a’, ‘7b’, ‘7c’, and ‘7d’.
The pressure in the primary and secondary cylinders is proportional to the angular displacement of the electric motor. The use of gears, power screws, and a primary hydraulic cylinder of smaller diameter as compared to the diameter of the secondary hydraulic cylinders in a series results in a very high mechanical advantage of the system. Because of the high mechanical advantage, an electric motor of a small power is able to produce a very high force of up to 5KN on the traction disks.
Because of the self-locking capability of the power screw mechanism, the hydraulic actuation system is usually off. The electric motor of the hydraulic actuation system is operated when a change in torque is detected at the output shaft. This results in a high energy efficiency of the system.
2.6. Analysis of the Control System of CAD CVT-II
2.6.1. Overview
The control system of CAD CVT-II consists of a set of sensors and the hydraulic actuation system. The sensors include pressure sensors, a dynamic torque sensor, and a position sensor for the angular displacement of the electric motor.
The electrically actuated hydraulic system of CAD CVT-II consists of an electric motor which in turn drives a power screw. The power screw transforms the rotary motion of the electric motor into linear motion of a piston that presses against a set of disk springs. The disk springs apply a force on a piston, which creates pressure in the hydraulic fluid of the primary cylinder. The pressure in the hydraulic cylinder is proportional to the force Fn applied to traction disks, which in turn is proportional to the torque handling capacity at the output shaft.
When torque at the output shaft changes, the dynamic torque sensor detects it. From the new torque value, a new reference position of the electric motor is calculated. As the motor achieves its new position, it creates a new pressure in the hydraulic cylinders, which corresponds to the new torque that was recently detected.
Because of the self-locking capability of the power screw, the electric motor operates only when a change in torque at the output shaft is detected; otherwise, it remains off.
To control the hydraulic actuation system of CAD CVT-II, a mathematical model of the system has been established. From the mathematical model, a transfer function has been derived. Since this is a new system, a PID controller has been applied to check whether the proposed control system can be stabilized with a basic controller.
The derivation of the transfer function and the results of the PID controller are given in the following sections.
Details of the control system, mathematical modeling, and transfer function derivation are given in Appendix B.
2.6.2. Transfer Function of Control System
The transfer function of the control system has been derived by first developing a mathematical relation considering the torque required by the power screw to lift a load, which is given in following equation:
In the above equation, ‘Ts’ is the torque required to raise a load ‘L’, and rm is the diameter of threads.
Next, the spring force, viscous force, and force on accelerating masses of the hydraulic actuation system were considered and put in the above equation. The final equation is given below.
In above equation, Ts is the torque required to operate the power screw of the hydraulic actuation system. Ts is the load that is to be driven by the electric motor of the hydraulic actuation system. In addition to Ts, the electric motor also faces internal loads like rotor inertia and viscous friction. The torque experienced by the electric motor is as follows:
In the above equation, Tm is the mechanical torque experienced by the electric motor.
To derive a transfer function, the torque Tm was equated to the torque generated by the DC motor by the current flowing through it. This resulted in the following transfer function:
where , , , and . Numerical values of parameters of the hydraulic actuation system are given in Table 4.

Table 4.
Parameters of the hydraulic actuation system of CAD CVT-II driven by a brushed DC motor, Model No. Maxon 148867 [].
By putting the values in the transfer function described in Equation (29), we can obtain the actual transfer function as follows:
Furthermore, the following equation shows the relationship between the angular displacement ( of the hydraulic actuation system’s electric motor and the torque capacity ( of CAD CVT-II:
2.6.3. Control System Dynamic Response Evaluation
The transfer function of the system is defined in Equation (30). Now, if we multiply and divide Equation (30) by 105, we obtain
Following dominant pole analysis and further simplification, Equation (32) can be written as
Now, we evaluate the system’s response based on the above transfer function.
- I.
- Analysis of System Response to PID Controller
The system’s responses to a PID controller, represented by the transfer function in Equation (33), were obtained using the PID block of SIMULINK. The values of control parameters like Proportional, Integral, and Derivative constants were obtained by using the built-in Auto Tuner application of SIMULINK. The values obtained are P = 1.50008, I = 69.08334, and D = 0.00450. The SIMULINK model, along with other control parameters, is given in Appendix D.
The response of the system to a unit function is given in Figure 15. The Y-axis represents the angular displacement of the electric motor of the hydraulic actuation system. One radian corresponds to a torque change of 4.15 Nm. The system is initially at zero. When a reference of one radian is given, it crosses its required value at about 40 ms and then slightly overshoots. Finally, it settles at about 110 ms. Keeping in view the mechanical nature of our system, the response of the system is very good.

Figure 15.
Step response of the system to a PID controller. Here, 1 radian corresponds to a torque of 4.15 Nm.
As shown in Figure 16, the system is initially at zero. Then, a step value of 21.69 radians is given to the system. The value of 21.69 radians corresponds to a value of 90 Nm, which is the maximum design torque of CAD CVT-II. The above graph shows the worst-case scenario that our system may experience. The system crosses the reference value at about 70 ms and finally settles at about 150 ms. It can be observed that the response of the system to such a large sudden change is quite good.

Figure 16.
Response of the system to a value of 21.69 radians using a PID controller. Here, 21.69 radians corresponds to a torque of 90 Nm, which is the maximum design torque of the system.
To check the limits of our system, we gave a reference of 50 radians as input. The response is given in Figure 17. It can be observed that the system tries to achieve the value but flattens off at about 28 radians. At 28 radians, the motor stalls as it has reached its maximum torque value.
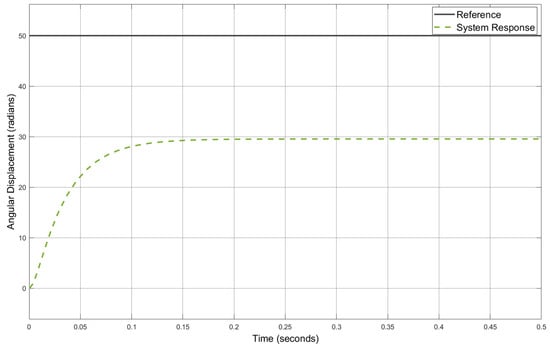
Figure 17.
Response of the system to a value of 50 radians using a PID controller.
The hydraulic actuation system consists of an electric motor that has a maximum operating voltage of 24 V. We wanted to check the response of the system to a motor that has the same characteristics and parameters but operates at 48 V. For this, we changed the saturation limits in the PID block to 48 V. The result is shown in Figure 18.

Figure 18.
Response of the system to a value of 50 radians using a PID controller when the saturation voltage is changed to 48 V from 24 V.
The reference of 50 radians, which was previously not achievable, has now been achieved.
In the transfer function, the numerator represents the torque constant of the electric motor of the hydraulic actuation system. Moreover, the coefficient of the variable with degree 1 in the denominator is also dominated by the value of the torque constant. In order to check the effect of increasing the value of the torque constant of the motor, we multiply the numerator and the coefficient of the variable with degree 1 by 2 as shown below.
The response of the system represented by Equation (34) is shown in Figure 19. This system is operated at 24 V. A motor with a high torque constant has a higher torque value. Therefore, unlike the motor that we have selected for our system, which stalled at about 28 radians, the motor with a high torque constant achieved the value of 50 radians in spite of being operated at 24 V.

Figure 19.
Response of the system to a value of 50 radians using a PID controller when the torque constant of the system is increased.
In the transfer function, the value of the constant in the denominator is dominated by the product of spring constant and pitch of the power screw. If we increase this value, it means that either we have increased the spring constant of the disk spring that is being pressed by the electric motor through the power screw provided the pitch remains constant or we have increased the pitch of the power screw provided the spring constant remains constant. In both cases, the electric motor will face more load per revolution and is expected to stall earlier. To verify this, we multiply the constant in the denominator of the transfer function by 2 to obtain the following equation:
The system response to the transfer function of Equation (35) is shown in Figure 20. It can be observed that the system achieves a maximum value of around 15 radians and then flattens off.

Figure 20.
Response of the system to a value of 50 radians using a PID controller when the spring constant is increased.
The results shown in Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 clearly show that the control system is stable. It has a good response time, keeping in view the intended application. Furthermore, the results are in accordance with the physical interpretation of the system.
- II.
- Effect of Tracking Error on Energy Efficiency
The energy efficiency of CAD CVT-II, given by Equation (21), is as follows:
The above equation shows the efficiency of CAD CVT-II under ideal conditions when there is no tracking error. However, during the analysis of the control system of CAD CVT-II, it has been observed that there will always be some tracking error during the transition period. Assume a worst-case scenario in which the reference is set at a 10% higher value than required, i.e., the CVT is operating at a 10% higher torque setting than is required. In such a scenario, Equation (36) will become
From Equations (24) and (37), we can write
Equation (38) shows that the efficiency of CAD CVT-II will slightly decrease compared to ideal conditions, as shown in Figure 21. However, the overall efficiency will remain constant throughout the operating range. The graph in Figure 21 shows that the efficiency decrease is only 0.8%, which is very small.

Figure 21.
Efficiency vs. torque of CAD CVT (blue), CAD CVT-II under ideal tracking conditions (red), CAD CVT-II with 10% offset from ideal torque reference (black).
- III.
- Tracking Strategy
It is obvious from Figure 21 that setting the reference value slightly higher than required, let us say 5% or 10%, will have a minimal effect on the energy efficiency of CAD CVT-II. However, a major advantage of this strategy is that we can ignore minor variations in torque. The hydraulic actuation system that has been designed in this article has a major advantage in that its electric motor normally remains off. It activates when it finds a difference between the reference torque and the actual torque.
All vehicles experience minor torque variations. If we have to activate our hydraulic actuation system for each small change, then it will result in efficiency loss due to frequent motor ON/OFF. If we set the reference 10% higher, then the system become activated only when a significant torque variation is observed. This will result in an energy-efficient system.
2.7. Comparison with Current Commercial CVTs
Currently, the most widely used commercial CVT is the Push Belt CVT, which is widely used in present-day cars. After the Push Belt CVT, the Toroidal CVT is considered to be the most viable CVT, although it is still in the initial stages of commercialization. Numerous other CVT designs are available in the literature, but these two are considered to be the most successful designs. A qualitative comparison of the CAD CVT and CAD CVT-II with the Push Belt CVT and Toroidal CVT is given in Table 5.

Table 5.
Qualitative comparison of the proposed CAD CVT-II with state-of-the-art commercially available CVTs.
3. Results and Discussion
Equation (17) shows that during variable-torque application, the efficiency of the CAD CVT drops. The corresponding graph is shown in Figure 4. At maximum torque, the efficiency is maximum. As the operating torque reduces, the efficiency drops. The drop in efficiency has an exponential trend as the operating torque approaches zero.
The root cause of the efficiency drop in the low torque region is that maximum force is applied to the traction disks of the CAD CVT, irrespective of the torque requirement at the output shaft. Therefore, frictional losses, dependent on the force applied to traction disks, remain constant. In the low torque region, the ratio between useful output and frictional losses becomes very low, resulting in low efficiency. The reason for applying maximum force to the traction disks of the CAD CVT at the assembly stage is that during operation, we cannot change the force on the traction disks of the CAD CVT. Therefore, to be able to cope with the maximum possible torque during operation, maximum force is applied to the traction disks of the CAD CVT.
This paper proposes an improved mechanical design of a CAD CVT to solve the efficiency problem caused by a drop in the efficiency of the CAD CVT. In the improved mechanical design, the force on traction disks can be varied according to dynamic torque requirements. For the sake of differentiation, the improved mechanical design is named CAD CVT-II.
During the design of CAD CVT-II, the design of the original CAD CVT was retained except for only two changes. They are as follows: (1) Caps ‘14a’, ‘14b’, ‘14c’, and ‘14d’ of the CAD CVT were replaced. (2) Disk springs ‘11a’, ‘11b’, ‘11c’, and ‘11d’ of the CAD CVT were replaced with simple metallic spacers.
The caps of the CAD CVT were replaced with hydraulic cylinders containing axially movable pistons so that force could be applied to traction disks during operation. This change does not affect the equations derived for the original CAD CVT.
Similarly, disk springs were replaced with metallic bushes because the set of disk springs used in the hydraulic actuation system achieves the function of disk springs. Furthermore, replacing the disk springs with bushes significantly simplifies the control system’s transfer function.
The use of a hydraulic system provides numerous advantages. The foremost among them is the ability to provide equal force to all traction disks simultaneously, which effectively prevents slippages that may arise otherwise.
Equation (24) and Figure 12 show the efficiency of CAD CVT-II. It is constant and independent of the torque applied to the CVT. Equation (24) signifies that CAD CVT-II has solved the efficiency drop problem faced by the CAD CVT.
The main reason for efficiency improvement in CAD CVT-II is that when we are unable to change the force on traction disks during operation, we have to apply a maximum design force to traction disks at the assembling stage so that the CVT can handle the full torque range. The CAD CVT suffers from different frictional losses, like spin losses and rolling friction losses at contact points between traction disks and input and output disks. These frictional losses are dependent on the force applied to the traction disks. When we apply the maximum design force to the traction disks, these frictional losses become maximum. For a constant rotation speed of the output shaft, the output power of the CVT is proportional to the output torque. Therefore, during low-torque operation, the ratio between useful output and wasted energy due to friction becomes low. This results in a low efficiency of the CAD CVT. To overcome this problem, in CAD CVT-II, we change the force on traction disks in such a manner that the relative ratio between the valuable power of the CVT and frictional losses due to traction disks remains constant.
CAD CVT-II’s control system consists of a set of pressure sensors, a dynamic torque sensor, and a hydraulic actuation system. The control system continuously monitors torque at the output shaft and adjusts the force on traction disks accordingly by varying pressure in the secondary cylinders through the hydraulic actuation system.
The hydraulic actuation system uses a multi-prong approach to achieve a very high force with a very-low-power electric motor so that energy can be conserved. Firstly, it uses spur gears to increase the torque of the motor at the input of the power screw. The power screw performs two functions. Firstly, it transforms torque into a linear force and simultaneously amplifies the force. The hydraulic system further amplifies the force provided by the power screw because the diameter of the primary cylinder is smaller than the diameter of the secondary cylinders.
An essential feature of the hydraulic actuation system of CAD CVT-II is the self-locking mechanism of the square thread power screw. Because of the self-locking mechanism, the electric motor of the hydraulic actuation system is usually off. It is actuated when there is a change in torque at the output shaft of the CVT. This results in energy saving and improved energy efficiency of the system.
A unique and novel feature of the proposed hydraulic actuation system is that, unlike the traditional hydraulic actuation system used for brake and clutch actuation, there is no fluid movement in the current system. This further improves the system’s energy efficiency.
In addition to that, the current system skillfully utilizes a set of disk springs to convert the slow response of a power screw into a fast response. The set of spur gears enables us to match the torque availability of off-the-shelf electric motors and the torque requirement of the hydraulic actuation system. The use of multiple disk springs in series enables us to optimize the system’s accuracy and response time.
The transfer function is essential for checking the control system’s stability and response. To derive the transfer function, the whole system was mathematically modeled. The transfer function of the system is given by Equation (29).
Equation (32) is the transfer function derived after putting in the numerical values. After dominant pole analysis, Equation (32) was simplified to a second-order system, as shown by Equation (33). Since this is a new system for which modeling has been done for the first time, it was prudent to apply the most straightforward control technique to the system. The system response to a PID controller under different conditions was evaluated and is given in Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20. Figure 15 shows a step response of the system. The step response corresponds to a value of one radian displacement of the electric motor of the hydraulic actuation system. The system stabilizes in 110 ms, which is a very good response for a mechanical system such as a CVT. To check the worst-case scenario that the system may face, it was given a reference value of 21.69 radians, which corresponds to a maximum design torque of 90 Nm. As shown in Figure 16, the system achieves the desired value and stabilizes in about 150 ms. This demonstrates that the system can handle all types of torque changes in the desired range effectively. To check the system limitations, a reference value of 50 radians was given to the system. It can be observed in Figure 17 that the system tries to achieve the value but stalls at about 28 radians. This result is in accordance with the physical characteristics of the system. This shows that when the electric motor rotates 28 radians, it becomes stalled. This is because it has reached its maximum torque capacity, beyond which it is unable to press the spring through the power screw. The response of the system to various inputs demonstrates that it is stable and highly responsive to all torque changes in the desired range of 0–21.8 radians. Furthermore, the maximum value that the system can achieve is 28 radians. The results in Figure 18, Figure 19 and Figure 20 show that the system can be easily designed for any other value by changing different parameters like the electric motor torque constant, saturation voltage of the electric motor, spring constant, and pitch of the power screw. Increasing the value of the torque constant or saturation voltage of the motor increases the ability of the system to achieve a higher value. Increasing the spring constant, the pitch of the power screw, or both decreases the system ability to achieve a higher value.
Equation (38) shows the efficiency of the system when the reference value is offset by 10% from the ideal. It can be observed that a decrease in efficiency is observed. But this decrease in efficiency is only about 0.8%, which is minimal. This characteristic of the system can be highly beneficial because, by offsetting our reference value by about 10%, we can effectively ignore small variations in torques that may cause excessive ON/OFF of the electric motor of the hydraulic actuation system.
4. Conclusions and Future Work
Despite the fast development of EVs, diesel-driven heavy transport will remain the backbone of freight transportation for the foreseeable future. Although a CVT can improve the efficiency of both EVs and diesel-driven transport, its importance for diesel-driven transport is more pronounced because of its ability to reduce the negative environmental impact of fossil fuels. Therefore, there is an urgency to develop a CVT for heavy transport vehicles.
The CAD CVT is the only CVT that can be designed for very large torques, so it has the potential to become the CVT of choice for heavy land transport. However, during analyses of the CAD CVT, it was observed that its efficiency drops in the low torque region. Therefore, for the CAD CVT to be implemented in heavy transport vehicles, this deficiency must be removed.
The current research proposes an improved mechanical design of a CAD CVT that significantly increases efficiency in the low torque region.
The major contributions/innovations of current research are highlighted as follows:
- Analyses of CAD CVT efficiency during variable-torque applications were performed. During analyses of the CAD CVT, it was observed that it has low energy efficiency in low torque regions.
- An improved mechanical design of a CAD CVT that is maximally efficient throughout its operating range was proposed. The new CVT was named CAD CVT-II.
- In CAD CVT-II, the force on the circumferentially arranged disks can be varied according to instantaneous torque requirements, thus resulting in improved efficiency in the low torque region.
- A hydraulic-actuation-based control system has been designed to provide control of CAD CVT-II. The novel features of the control system are as follows:
- There is almost negligible fluid movement in the hydraulic actuation system, which improves energy efficiency.
- The hydraulic actuation system has a self-locking capability, due to which it can be operated only when required; otherwise, it remains off. This also improves its energy efficiency.
- The proposed control system of CAD CVT-II can be controlled by a PID controller and is highly responsive.
The newly proposed mechanical design of CAD CVT-II, along with its control system, has significantly improved efficiency in the low torque region as compared to its predecessor (CAD CVT). This major efficiency improvement brings us closer to the realization of CVTs in heavy land transport. It will significantly impact the energy efficiency of heavy land transport, such as trucks and trailers, resulting in reduced environmental pollution and transportation costs. Moreover, CAD CVT-II is also beneficial for electric vehicles, robots, and wind turbines.
The current paper proposes the design, analysis, and mathematical modeling of CAD CVT–II. In our future work, we will fabricate and experimentally verify the proposed CAD CVT-II. After experimental verification, the CVT shall be implemented in a vehicle.
Author Contributions
Conceptualization, M.B. and Q.Z.; Methodology, M.B. and Q.Z.; Software, G.F., A.E., and M.K.N.; Validation, M.B.; Formal Analysis, M.B., Q.Z., S.R.Q., G.F., and M.K.N.; Investigation, M.B.; Resources, Q.Z.; Data Curation, M.B., S.R.Q., and M.K.N.; Writing—Original Draft, M.B.; Writing—Review and Editing, A.E. and S.K.; Visualization, M.B.; Supervision, Q.Z.; Project Administration, Q.Z.; Funding Acquisition, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
Funding was provided by the National Natural Science Foundation of China with project grant No. 52171299.
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Design of Energy-Efficient Hydraulic Actuation System
Appendix A.1. Development of Design Criteria
Appendix A.1.1. Problem Statement
The problem is that of designing a novel hydraulic actuation system that can meet the following criteria:
- Consumes energy when a pressure change is required. Otherwise, it remains off and does not consume energy.
- Has a fast response time.
- Acts as a torque-to-force converter.
- Acts as a torque-to-force amplifier. That is, it should be able to produce a very high force with a motor with a very low torque.
- Is able to vary pressure and hence force throughout its range, even when the secondary piston has no movement.
- Does not move the hydraulic fluid to reduce energy losses. It should merely act as a force transfer medium.
The hydraulic actuation system’s characteristics, summarized above, require a unique design that is not readily available in the literature.
Appendix A.1.2. Design Features of Hydraulic Actuation System
The following design features have been incorporated into the hydraulic actuation system to design an energy-efficient actuation system for CAD CVT-II.
- I.
- Simple power screw
A simple power screw has been selected as the primary driving mechanism. It provides the following advantages:
- It maintains its position when the electric motor is off. This enables the motor to remain off when there is no torque change.
- It provides a very high mechanical advantage, which enables us to drive the mechanism using an electric motor with very low torque and low power.
The major drawback of the high mechanical advantage of the power screw is that it slows the response time, mainly when the power screw is used for rotary to linear position control.
- II.
- Disk Springs
The slow response of the power screw has been resolved by converting the linear movement of the screw to force through a spring of a large spring constant. Large spring constants are provided by disk springs. However, the axial movement provided by disk springs is so tiny that a slight angular movement of the power screw can result in full compression of the spring. This severely reduces the accuracy of the system. To overcome the problem, a set of disk springs in a series arrangement has been used. This provides the capability to optimize the system’s accuracy and response time.
- III.
- Spur Gears
Disk springs are commercially available with quantized values. The pitch of the power screw has a specific range to be able to resist back driving. Furthermore, electric motors are commercially available with quantized torque values. In such circumstances, to match the torque requirement of the hydraulic actuation system with the torque that can be provided by the electric motor, a set of spur gears is provided in the hydraulic actuation system.
- IV.
- Disk Spring Placement
We have different options for disk spring placement. Each option has advantages and disadvantages, which are summarized as follows:
- In the original CAD CVT, a single disk spring is placed immediately behind each CAD. If we do not disturb the original design of the CAD CVT, then we will have two sets of disk springs, one inside the CVT and one inside the hydraulic actuation system. This arrangement results in the movement of hydraulic fluid entrapped between two sets of disk springs. Unlike traditional systems used for brake or clutch actuation, hydraulic fluid should not move in the desired system.
- If we remove disk springs from the hydraulic actuation system, we lose the ability to optimize accuracy and response time. Moreover, the problem of fluid movement will persist.
- If we place the disk springs of the hydraulic actuation system along with the disk spring of the CAD CVT, then the ability to optimize the response time and accuracy is maintained. However, the fluid movement persists.
- If we only remove the disk spring from the CAD CVT and replace it with a solid metallic bush, the fluid movement will stop. Moreover, the ability to optimize response time and accuracy is maintained.
Appendix B. Control System Mathematical Modeling
In this section, the mathematical model of CAD CVT-II driven by the hydraulic actuation system, shown in the following figure, is developed. The mathmatical model of the control system is developed by deriving equations of square thread power screws. Then torque required by the power screw to press the set of disk springs is calculated. Finally, the torque needed for the electric motor to operate the system is derived. Using the equations of the brushed DC motor and the torque required by the motor to operate CAD CVT-II, a transfer function of the system is derived. The detailed derivation of the steps mentioned above is given in the following sections.
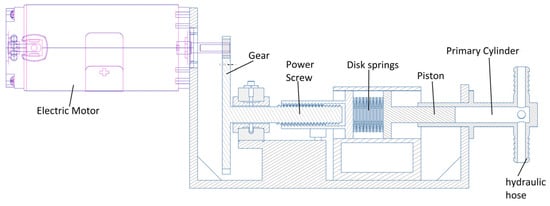
Figure A1.
The hydraulic actuation system of CAD CVT-II.
Appendix B.1. Power Screw Equations
In the current design, the power screw has square threads. If load ‘L’ has to be moved by the power screw in the linear direction, then the required torque can be calculated as follows.
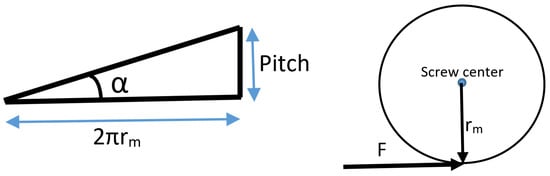
Figure A2.
Geometric relationship of essential parameters of power screw.

Figure A3.
Geometrical relationship of different forces acting on power screw.
From Figure A2 and Figure A3 above, we can write
where L is the load to be lifted by the power screw.
Equation (A1) can be written as
Similarly, we can write
The torque, Ts, required by the power screw for raising the Load L is
Equation (A5) can be written as
Putting the value of Fnorm from Equation (A3) in Equation (A6), we obtain
which can be further simplified as
where Ts denotes the torque required to raise the load L. rm represents the mean radius of the screw. α denotes the pitch angle defined as tan (α) = (pitch/2πrm). L represents the load to be lifted by the power screw.
Appendix B.2. Torque Requirement of Power Screw
Now, we assume the following:
- The hydraulic fluid is incompressible.
- The hydraulic fluid is transmitted from the primary cylinder to the secondary cylinders through steel pipes so that volumetric variation in the steel hoses and the primary and secondary cylinders can be assumed to be negligible.
Then, we can write
where Ks denotes the equivalent spring constant of the disk springs, m3 represents the mass of the piston being pressed by the power screw against the disk springs, x denotes the displacement of the piston, and b3 indicates the viscous coefficient and is a constant that represents resisting force being applied to the piston when it moves with a velocity.
Suppose θ2 is the angular displacement of the power screw, and θ1 is the angular displacement of the motor shaft. Consequently, we can write
where
If kg denotes the gear ratio between the gear attached to the motor and the gear attached to the power screw, we can write
Now we can write Equation (A9) as
So, we obtain
From Equations (A8) and (A14), we can obtain
Now, we assume that
Consequently, Equation (A15) can be written as
Appendix B.3. Torque Requirement of Motor
Let Tm denote the torque applied at the shaft of the motor. Consequently, we can write
where j1 represents the inertia moment of the electric motor rotor, j2 denotes the inertia moment of the power screw and the gear attached to the power screw, b1 represents the viscous coefficient of the electric motor, and b2 indicates the viscous coefficient of the power screw plus the gear attached to the power screw.
From Equations (A10) and (A12), we can infer
Putting the value of Equation (A19) in Equation (A18), we obtain
Putting the value of Ts from Equation (A17) into Equation (A21), we obtain
Equation (A22) can be rearranged as
Now, we assume that
Consequently, we write Equation (A23) as
Appendix B.4. Transfer Function
The electric motor driving the system is a brushed DC motor, and we can write the following for it:
where kt represents the torque constant of the motor and i is the current in the motor. Consequently, we can write
where Lind indicates the motor’s inductance.
From Equations (A27) and (A28), we can write
Calculating the Laplace transform of Equation (A30), we can obtain
Equation (A31) can be written as
By calculating the Laplace transform of Equation (A29), we can obtain
Consequently, Equation (A33) can be written as
By equating Equations (A32) and (A34), we can obtain
If kt and ke are in the SI units, then
Consequently, we can rewrite Equation (A35) as
which can also be written as
with further abstraction
and simplifies as
This implies that
where , , , and .

Table A1.
Parameters of the hydraulic actuation system of CAD CVT-II driven by brushed DC motor Model No. Maxon 148867 [].
Table A1.
Parameters of the hydraulic actuation system of CAD CVT-II driven by brushed DC motor Model No. Maxon 148867 [].
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Pitch | 2 mm | J2 | kg m2 |
| rm | 5.5 mm | b2 | Nm/rad/s |
| α | k | Nm/A | |
| Kp | m/rad | Lind | H |
| Kg | R | 0.299 Ω | |
| Ks | 1,117,777 N/m | J1 | kg m2 |
| b3 | N/m/s | μs | 0.15 |
| m3 | 0.94 kg | b1 | Nm/rad/s |
By putting the values in the transfer function described in Equation (A41), we can obtain the actual transfer function as
Appendix C. Torque vs. Pressure
The torque capability of CAD CVT-II can be determined from pressure by first selecting the force exerted by the piston of the secondary cylinders on the traction disks. The following equation can easily find the force:
In Equation (A43), the Fseal is proportional to pressure and equal to kseal x Pressure. Kseal is a constant representing the slope of the graph between the frictional force experienced by the seal and the pressure inside the cylinder. After Fn is found, the torque can be calculated through Equation (A1). The range of force on the CAD of CAD CVT-II and some other related parameters are given in Table A2.

Table A2.
Values of essential parameters of CAD CVT-II.
Table A2.
Values of essential parameters of CAD CVT-II.
| Parameter | Value/Range |
|---|---|
| CAD CVT-II torque range | 0 to 90 Nm |
| Diameter of secondary cylinders | 36 mm |
| Pressure range | 0 to 50 Bar |
| Range of force on traction disks | 0 to 5 KN |
| Traction disks’ contact length | 2 mm |
| Traction disks’ stress at the contact point | 1.3 GPa |
| Traction disks’ material | SS 304 |
Appendix D. SIMULINK Model of CAD CVT-II PID Controller
The SIMULINK model of CAD CVT-II PID controller is given in Figure A4. The PID controller is obtained by using the PID controller block of SIMULINK as shown in Figure A5. The main input required for the PID controller block is the transfer function of the system we want to control. The control parameters of the PID controller are tuned by using the Auto Tuner application of SIMULINK as shown in Figure A6. This application automatically determines the optimum parameters of the system represented by the transfer function.

Figure A4.
SIMULINK model of PID controller for CAD CVT-II.

Figure A5.
SIMULINK block of PID controller.
Figure A6.
SIMULINK Auto Tuner application for tuning the control parameters of the PID controller.
References
- Carbone, G.; Mangialardi, L.; Mantriota, G. A Comparison of the Performances of Full and Half Toroidal Traction Drives. Mech. Mach. Theory 2004, 39, 921–942. [Google Scholar] [CrossRef]
- Kim, J.; Park, F.C.; Park, Y. Design, Analysis and Control of a Wheeled Mobile Robot with a Nonholonomic Spherical CVT. Int. J. Rob. Res. 2002, 21, 409–426. [Google Scholar] [CrossRef]
- Sheng, Y.; Escobar-Naranjo, D.; Stelson, K.A. Feasibility of Hydrostatic Transmission in Community Wind Turbines. Actuators 2023, 12, 426. [Google Scholar] [CrossRef]
- Cotrell, J. Assessing the Potential of a Mechanical Continuously Variable Transmission for Wind Turbines; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2005.
- Nguyen, V.H.; Do, T.C.; Ahn, K.K. Investigation and Optimization of Energy Consumption for Hybrid Hydraulic Excavator with an Innovative Powertrain. Actuators 2023, 12, 382. [Google Scholar] [CrossRef]
- Jawad, Q.A.; Ali, A.K. Comparison of CVT Performance with the Manual and Automatic Transmission for Evaluation the Fuel Consumption and Exhaust Emissions. Basrah J. Eng. Sci. 2020, 20, 15–22. [Google Scholar] [CrossRef]
- Ruan, J.; Walker, P.D.; Wu, J.; Zhang, N.; Zhang, B. Development of Continuously Variable Transmission and Multi-Speed Dual-Clutch Transmission for Pure Electric Vehicle. Adv. Mech. Eng. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Mobedi, E.; Ismet, M.C.D. A Continuously Variable Transmission System Designed for Human-Robot Interfaces. In Proceedings of the Asian MMS Conference; Springer Nature: Berlin, Germany, 2018. [Google Scholar]
- Mobedi, E.; Dede, M.İ.C. Geometrical Analysis of a Continuously Variable Transmission System Designed for Human-Robot Interfaces. Mech. Mach. Theory 2019, 140, 567–585. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, J.; Xu, Z.; Yuan, S.; Li, P.; Wang, J. Development Status and Trend of Agricultural Robot Technology. Int. J. Agric. Biol. Eng. 2021, 14, 1–19. [Google Scholar] [CrossRef]
- Micklem, J.D.; Longmore, D.K.; Burrows, C.R. Modelling of the Steel Pushing V-Belt Continuously Variable Transmission. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1994, 208, 13–27. [Google Scholar] [CrossRef]
- Lin, X.; Peng, Y.; Hong, R.; Wang, Y. Research on a Novel Discrete Adjustable Radiuses Type Continuously Variable Transmission. Meccanica 2022, 57, 1155–1171. [Google Scholar] [CrossRef]
- Verbelen, F.; Haemers, M.; De Viaene, J.; Derammelaere, S.; Stockman, K.; Sergeant, P. Adaptive PI Controller for Slip Controlled Belt Continuously Variable Transmission. IFAC-PapersOnLine 2018, 51, 101–106. [Google Scholar] [CrossRef]
- Kim, T.; Kim, H. Low-Level Control of Metal Belt CVT Considering Shift Dynamics and Ratio Valve On-off Characteristics. KSME Int. J. 2000, 14, 645–654. [Google Scholar] [CrossRef]
- Guang-bin, W.; Yan-hui, L.; Xiao-wei, X. Optimization of CVT Efficiency Based on Clamping Force Control. IFAC-PapersOnLine Conf. Pap. Arch. 2018, 51, 898–903. [Google Scholar] [CrossRef]
- Pulles, R.J.; Bonsen, B.; Veenhuizen, P.A.; Steinbuch, M. Slip Controller Design and Implementation in a Continuously Variable Transmission. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; SAE International: Warrendale, PA, USA, 2005. [Google Scholar]
- Ye, M.; Liu, Y.G.; Cheng, Y. Modeling and Ratio Control of an Electromechanical Continuously Variable Transmission. Int. J. Automot. Technol. 2016, 17, 225–235. [Google Scholar] [CrossRef]
- Chen, T.; Xu, X.; Cai, Y.; Chen, L.; Li, K. QPSOMPC-Based Chassis Coordination Control of 6WIDAGV for Vehicle Stability and Trajectory Tracking. J. Frankl. Inst. 2025, 362, 107458. [Google Scholar] [CrossRef]
- Zhao, J.; Li, R.; Zheng, X.; Li, W.; Hu, C.; Liang, Z.; Wong, P.K. Constrained Fractional-Order Model Predictive Control for Robust Path Following of FWID-AGVs with Asymptotic Prescribed Performance. IEEE Trans. Veh. Technol. 2025, 74, 2692–2705. [Google Scholar] [CrossRef]
- Chen, T.; Cai, Y.; Chen, L.; Xu, X. Trajectory and Velocity Planning Method of Emergency Rescue Vehicle Based on Segmented Three-Dimensional Quartic Bezier Curve. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3461–3475. [Google Scholar] [CrossRef]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model Predictive Control System Based on Direct Yaw Moment Control for 4wid Self-Steering Agriculture Vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Li, M.; Shang, Z. Dynamic Measurement Method for Steering Wheel Angle of Autonomous Agricultural Vehicles. Agriculture 2024, 14, 1602. [Google Scholar] [CrossRef]
- Xu, G.; Fang, H.; Song, Y.; Du, W. Optimal Design and Analysis of Cavitating Law for Well-Cellar Cavitating Mechanism Based on MBD-DEM Bidirectional Coupling Model. Agriculture 2023, 13, 142. [Google Scholar] [CrossRef]
- Fu, W.; Lu, W.; Liu, H.; Yuan, X.; Zeng, D. Smooth Braking Control of Excavator Hydraulic Load Based on Command Reshaping. ISA Trans. 2025, 158, 674–685. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Xiong, L.; Yu, Z. Pressure Estimation of the Electro-Hydraulic Brake System Based on Signal Fusion. Actuators 2021, 10, 240. [Google Scholar] [CrossRef]
- Shi, Q.; He, L. A Model Predictive Control Approach for Electro-Hydraulic Braking by Wire. IEEE Trans. Ind. Inform. 2023, 19, 1380–1388. [Google Scholar] [CrossRef]
- Chen, X.; Hang, P.; Wang, W.; Li, Y. Design and Analysis of a Novel Wheel Type Continuously Variable Transmission. Mech. Mach. Theory 2017, 107, 13–26. [Google Scholar] [CrossRef]
- Kazerounian, K.; Furu-Szekely, Z. Parallel Disk Continuously Variable Transmission (PDCVT). Mech. Mach. Theory 2006, 41, 537–566. [Google Scholar] [CrossRef]
- KOMATSUBARA, H.; KURIBAYASHI, S. Research and Development of Cone to Cone Type CVT (1st Report, Fundamental Structure, Speed Change Mechanism and Design of CTC-CVT). Trans. JSME 2017, 83, 16-00477. (In Japanese) [Google Scholar] [CrossRef]
- Carter, J. The Design and Analysis of an Alternative Traction Drive CVT. In Proceedings of the SAE 2003 World Congress & Exhibition, Detroit, MI, USA, 3–6 March 2003. [Google Scholar]
- Shen, C.J.; Yuan, S.H.; Hu, J.B.; Wu, W.; Wei, C.; Chen, X. Principle and Characteristics of Original Hydraulic Traction Drive CVT. J. Cent. South Univ. 2014, 21, 1654–1659. [Google Scholar] [CrossRef]
- Ghariblu, H.; Behroozirad, A.; Madandar, A. Traction and Efficiency Performance of Ball Type CVTs. Int. J. Automot. Eng. 2014, 4, 738–748. [Google Scholar]
- Li, C.; Li, H.; Li, Q.; Zhang, S.; Yao, J. Modeling, Kinematics and Traction Performance of No-Spin Mechanism Based on Roller-Disk Type of Traction Drive Continuously Variable Transmission. Mech. Mach. Theory 2019, 133, 278–294. [Google Scholar] [CrossRef]
- Drescher, D.; Naves, M.; de Vries, T.J.A.; Buijze, M.; Stramigioli, S. Power Split Based Dual Hemispherical Continuously Variable Transmission. Actuators 2017, 6, 15. [Google Scholar] [CrossRef]
- Kim, J.; Park, F.C.; Park, Y.; Shizuo, M. Design and Analysis of a Spherical Continuously Variable Transmission. J. Mech. Des. 2002, 124, 21–29. [Google Scholar] [CrossRef]
- Tomaselli, M.; Bottiglione, F.; Lino, P.; Carbone, G. NuVinci Drive: Modeling and Performance Analysis. Mech. Mach. Theory 2020, 150, 103877. [Google Scholar] [CrossRef]
- Verbelen, F.; Derammelaere, S.; Sergeant, P.; Stockman, K. Half Toroidal Continuously Variable Transmission: Trade-off between Dynamics of Ratio Variation and Efficiency. Mech. Mach. Theory 2017, 107, 183–196. [Google Scholar] [CrossRef]
- Delkhosh, M.; Foumani, M.S. Multi-Objective Geometrical Optimization of Full Toroidal CVT. Int. J. Automot. Technol. 2013, 14, 707–715. [Google Scholar] [CrossRef]
- Bilal, M.; Zhu, Q.; Qureshi, S.R.; Elahi, A.; Nadeem, M.K.; Khan, S. A Novel Continuously Variable Transmission with Circumferentially Arranged Disks (CAD CVT). Actuators 2024, 13, 208. [Google Scholar] [CrossRef]
- Available online: www.maxongroup.com (accessed on 1 December 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).