Adaptive Fixed-Time Tracking Control of Cart–Pendulum Robotic Systems with Bias Actuator Dynamics
Abstract
1. Introduction
- (1)
- Our approach differs from conventional neural network parameter estimation techniques discussed in [27] by implementing a filtering mechanism that captures estimation error data from system signals in real-time. We develop adaptive estimation protocols to precisely identify unknown dynamic parameters through this mechanism.
- (2)
- While traditional sliding mode methodologies described in [30] provide a foundation, our work extends these principles through an integrated approach incorporating parameter estimation. This strategy overcomes limitations in conventional sliding mode techniques’ reaching phases and effectively compensates for actuator dynamics effects while maintaining precise control performance.
- (3)
- Differing from the studies in [18] and acknowledging practical operational constraints, our control strategy incorporates time-bounded convergence principles, minimizing initial state dependency on settling duration and establishing predetermined convergence timeframes. This enhancement significantly strengthens robotic trajectory tracking resilience against bias actuator dynamics. Moreover, the conservative design that assumes the dynamic parameter shown in [25] is overcome by adaptive adjustment designs in this paper.
2. Research Model with Preliminaries
2.1. Kinematic and Dynamic Formulation of Cart–Pendulum Robotic Architecture
2.2. Lemmas
2.3. Bias Actuator Dynamics
2.4. Control Intents
3. Adaptive Parameter Estimation and Sliding Surface Control Synthesis
3.1. Neural Network-Based Parameter Identification for Dynamics Characterization
3.2. Time-Bounded Convergent Sliding Mode Control Strategy
4. Watermelon Manipulator Case Study and Control Performance Evaluation
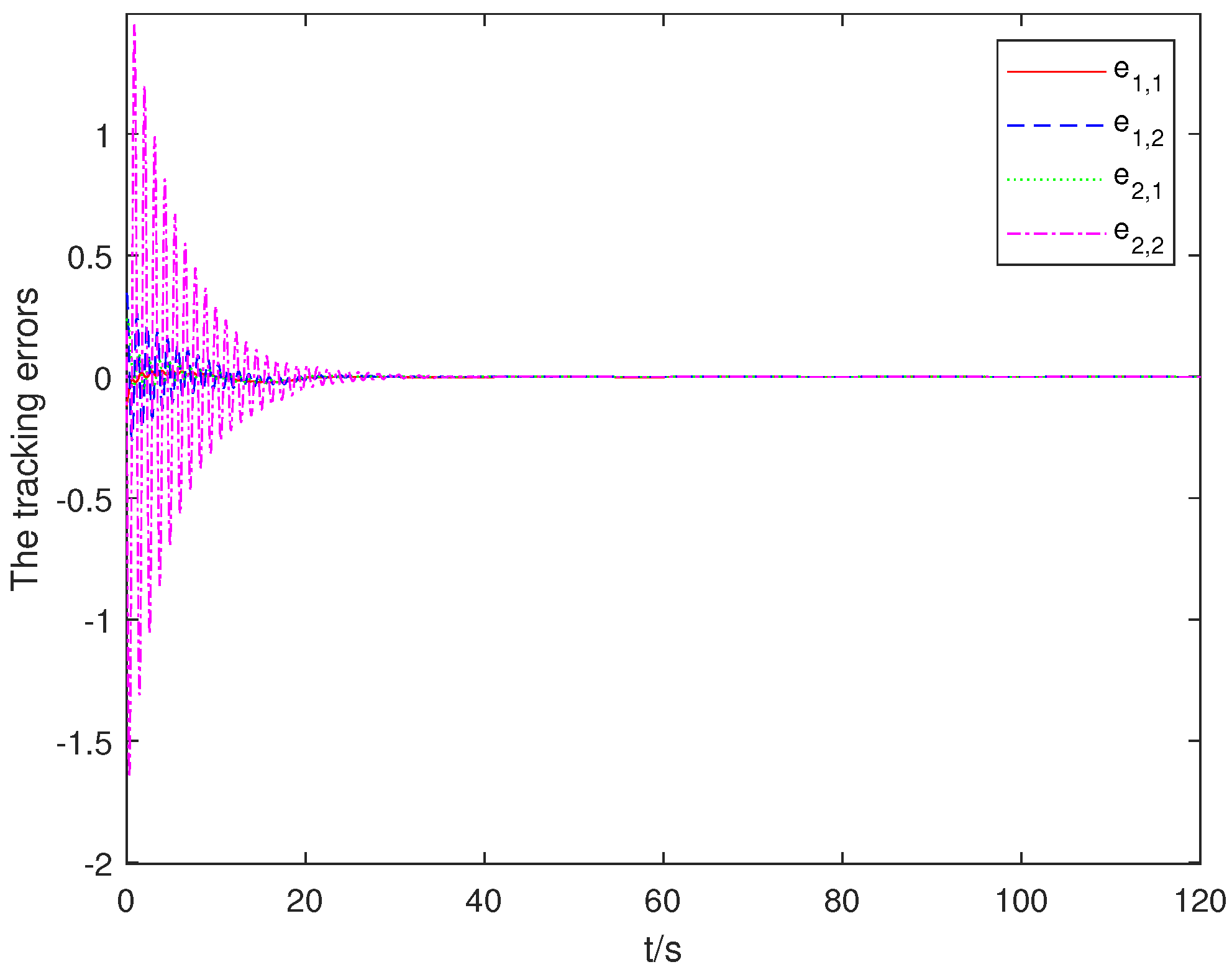
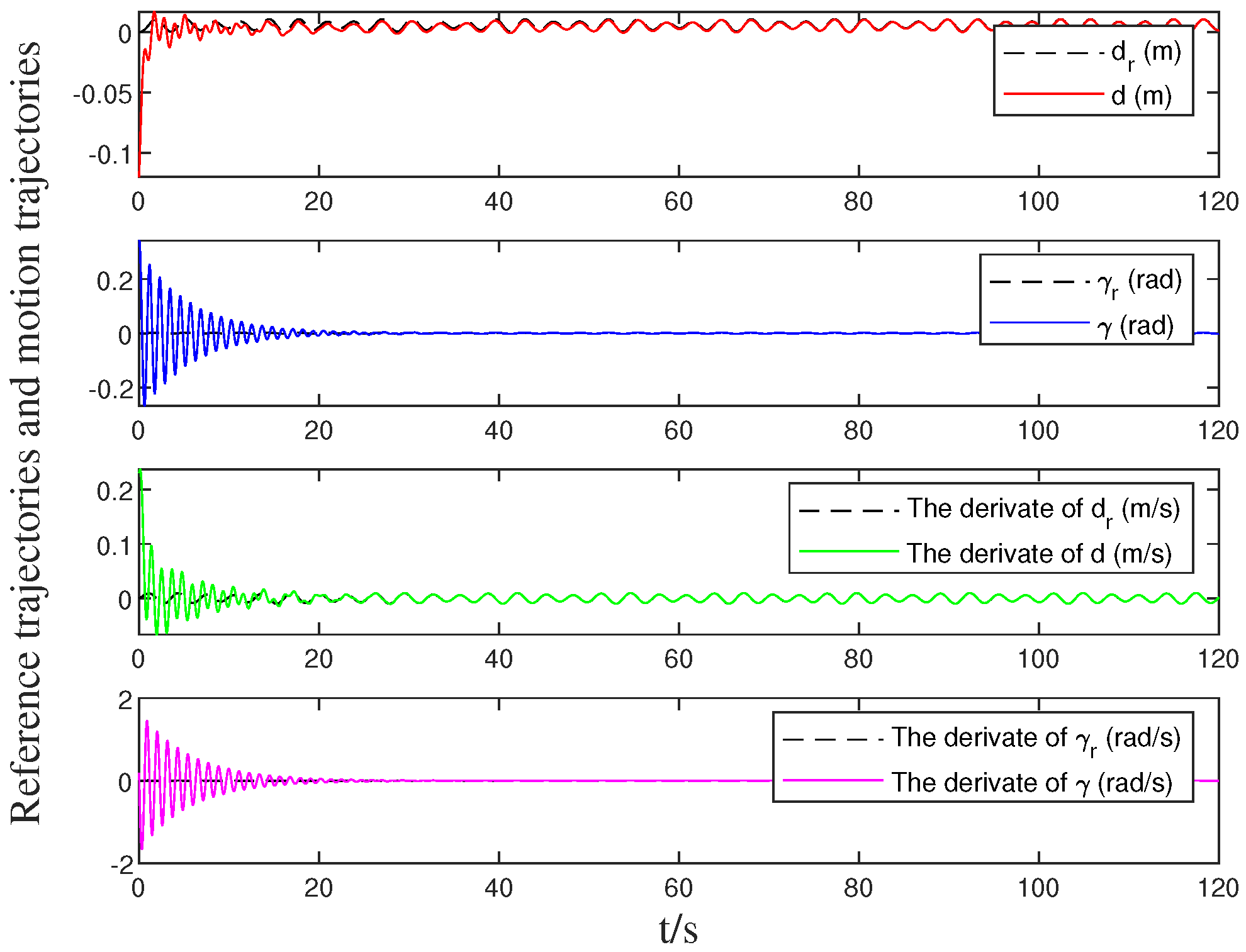
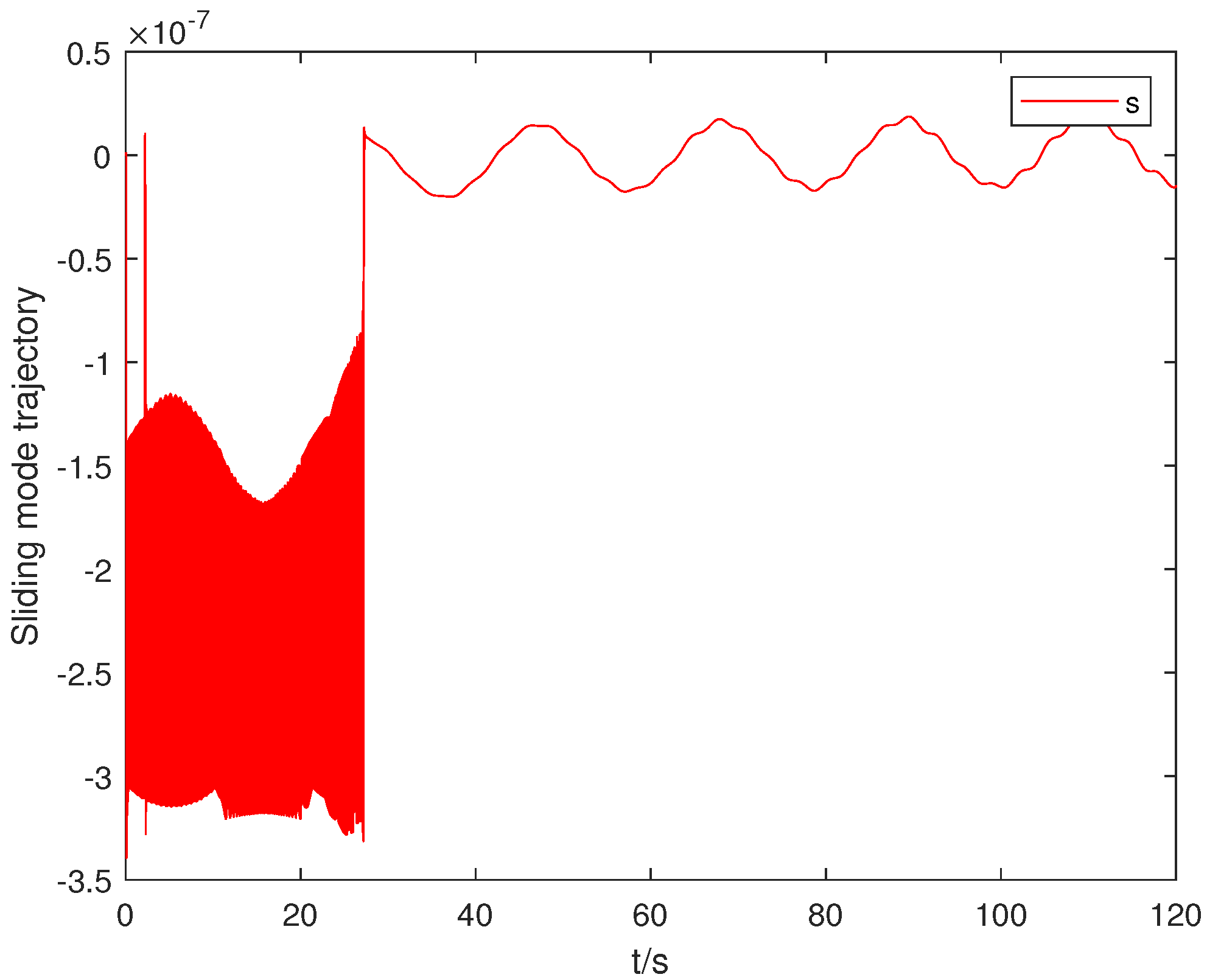
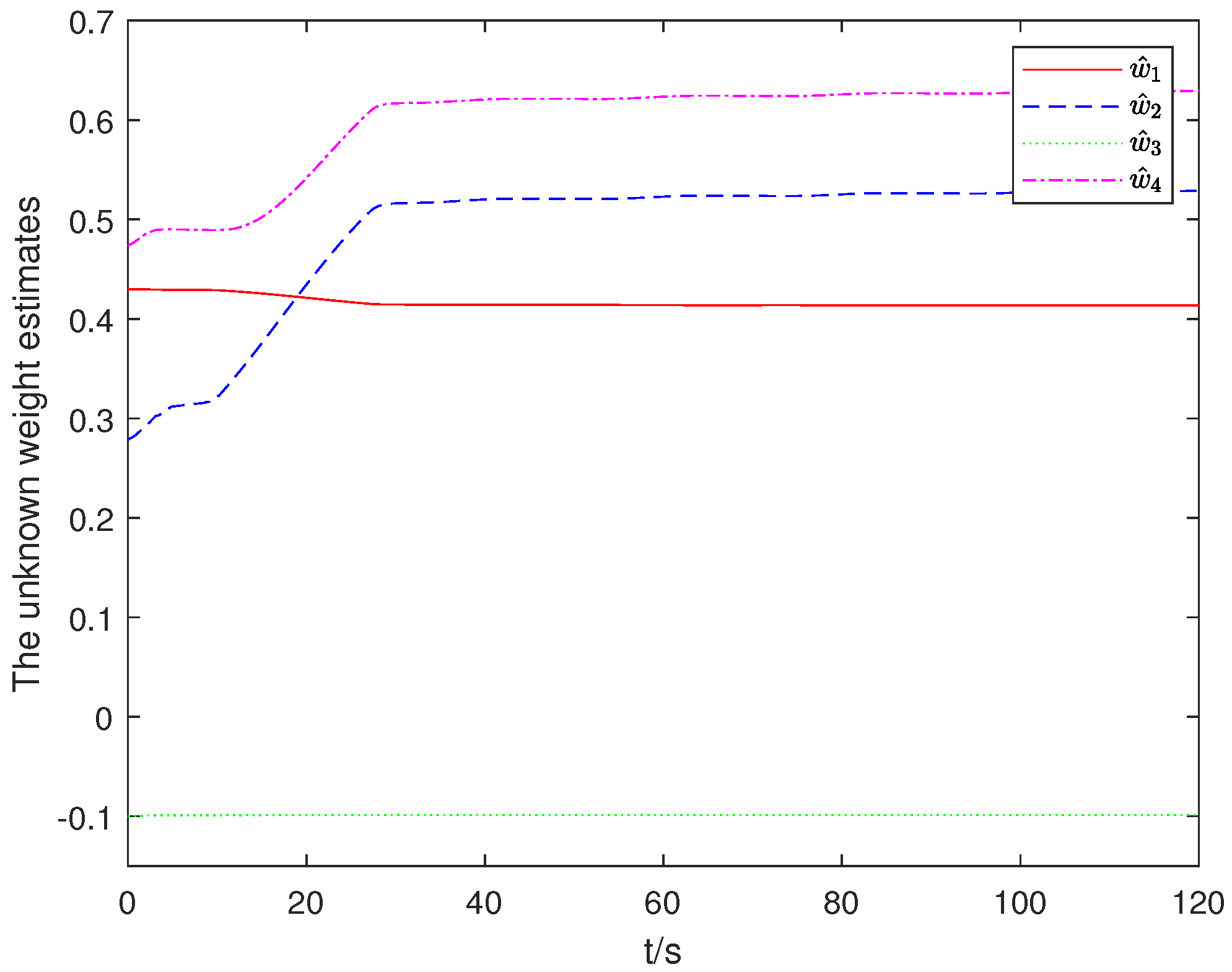
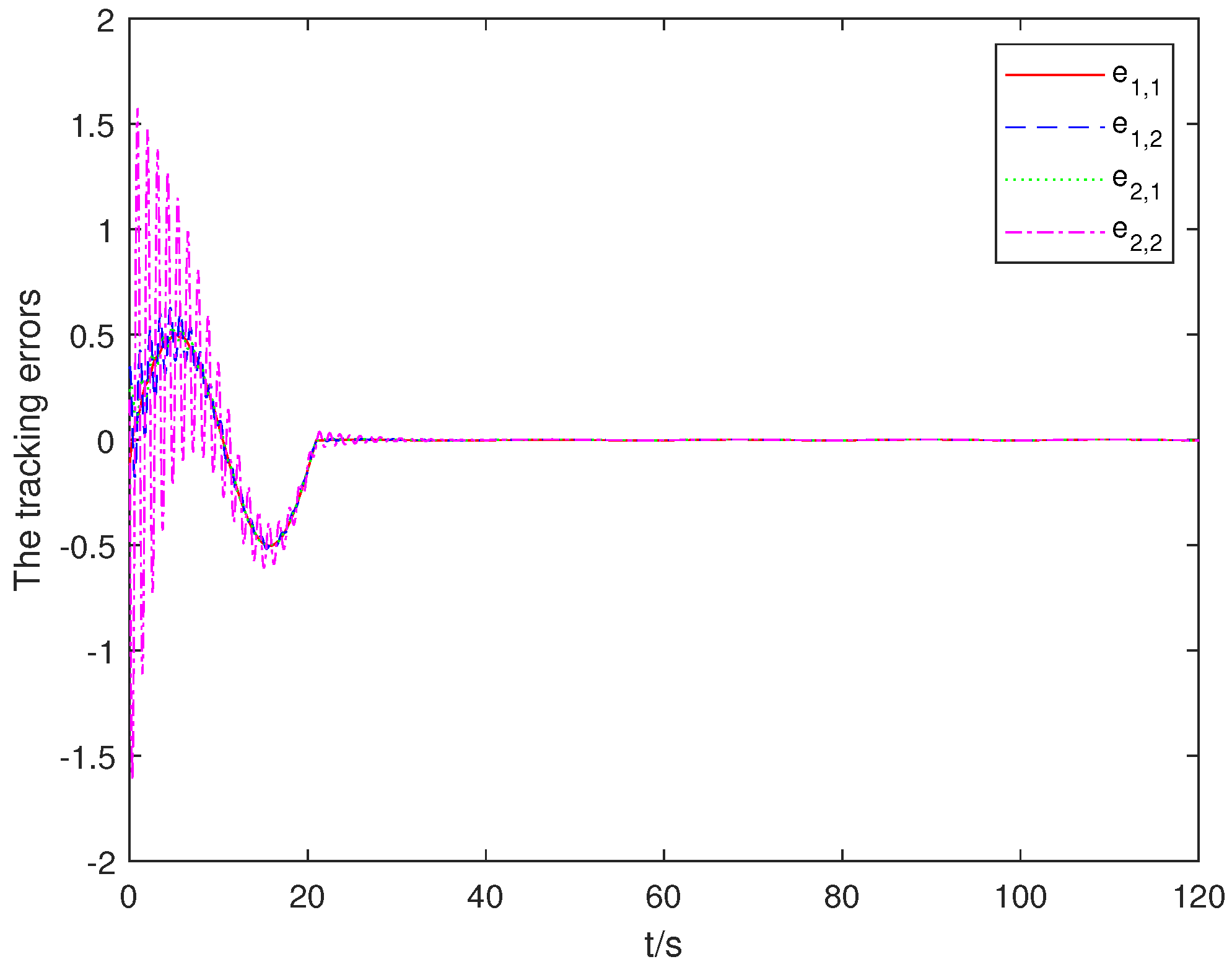
4.1. Simulation Results
4.2. Comparative Analysis
- The filtering-based parameter estimation approach enables accurate identification of the unknown actuator dynamics compared with methods relying solely on disturbance observers, effectively addressing the challenge of nonlinear actuator behavior.
- The integrated sliding surface design eliminates the reaching phase present in conventional sliding mode controllers, reducing transient tracking errors and providing consistent convergence behavior.
- The fixed-time control law guarantees convergence within a predictable time bound, independent of initial conditions, which is critical for time-sensitive applications.
- The computational complexity is higher than conventional nonadaptive sliding mode methods due to the real-time neural network operations and filter dynamics, potentially limiting applicability in extremely resource-constrained systems.
- The control performance depends on appropriate selection of neural network structure (number of neurons, centers, widths) and adaptive/controller gains, requiring careful tuning.
- While simulations demonstrated robust performance, extreme actuator failures significantly exceeding the approximation capabilities of the neural network could potentially compromise system stability.
5. Conclusions
- Automated harvesting systems operating in variable soil and crop conditions.
- Factory automation systems subject to maintenance-related actuator degradation.
- Collaborative robots working alongside humans, where predictable timing is essential for safety.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Faheem, M.; Liu, J.; Chang, G.; Ahmad, I.; Peng, Y. Hanging force analysis for realizing low vibration of grape clusters during speedy robotic post-harvest handling. Int. J. Agric. Biol. Eng. 2021, 14, 62–71. [Google Scholar] [CrossRef]
- Xu, S.; Yu, H.; Wang, H.; Chai, H.; Ma, M.; Chen, H.; Zheng, W.X. Simultaneous diagnosis of open-switch and current sensor faults of inverters in IM drives through reduced-order interval observer. IEEE Trans. Ind. Electron. 2024, 72, 6485–6496. [Google Scholar] [CrossRef]
- Jin, X.; Che, W.; Wu, Z.; Wang, H. Analog control circuit designs for a class of continuous-time adaptive fault-tolerant control systems. IEEE Trans. Cybern. 2020, 52, 4209–4220. [Google Scholar] [CrossRef]
- Jin, X.; Hou, Y.; Wu, X.; Chi, J. Adaptive ELM-based time-constrained control of uncertain robotic manipulators with minimum learning computation. IEEE Trans. Emerg. Top. Comput. 2025, 1–12. [Google Scholar] [CrossRef]
- Jin, X.; Lü, S.; Yu, J. Adaptive NN-based consensus for a class of nonlinear multiagent systems with actuator faults and faulty networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 3474–3486. [Google Scholar] [CrossRef]
- Jin, X.; Wang, S.; Qin, J.; Zheng, W.X.; Kang, Y. Adaptive fault-tolerant consensus for a class of uncertain nonlinear second-order multi-agent systems with circuit implementation. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 65, 2243–2255. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Xia, J.; Xing, G. Adaptive disturbance observer-based fixed time nonsingular terminal sliding mode control for path-tracking of unmanned agricultural tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Xu, S.; Zheng, Z.; Wang, L.; Wang, H.; Chai, Y.; Ma, M.; Zheng, W.X. Multiple open-switch fault diagnosis of grid-connected three-phase inverters under unknown parameter conditions using ICRLS and disturbance sliding mode observer. IEEE Trans. Power Electron. 2025, 40, 8631–8647. [Google Scholar] [CrossRef]
- Gao, M.; Ding, L.; Jin, X. ELM-based adaptive faster fixed-time control of robotic manipulator systems. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 4646–4658. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, Q.; Mehmood, A.; Kirmani, S.A.M.; Mechali, O. Neuro-adaptive fast integral terminal sliding mode control design with variable gain robust exact differentiator for under-actuated quadcopter UAV. ISA Trans. 2022, 120, 293–304. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.; Zhou, M.; Jiang, X. Non-cooperative spacecraft proximity control considering target behavior uncertainty. Astrodynamics 2022, 6, 399–411. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, J.; Su, J.; Li, M.; Xu, M.; Bai, S. Relative orbit transfer using constant-vector thrust acceleration. Acta Astronaut. 2025, 229, 715–735. [Google Scholar] [CrossRef]
- Yogi, S.C.; Tripathi, V.K.; Behera, L. Adaptive integral sliding mode control using fully connected recurrent neural network for position and attitude control of quadrotor. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5595–5609. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, W.; Liu, L.; Li, D.; Tong, S.; Chen, C.L.P. Adaptive neural network control for a class of nonlinear systems with function constraints on states. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 2732–2741. [Google Scholar] [CrossRef]
- Wang, X.; Ding, D.; Ge, X.; Han, Q. Neural-network-based control for discrete-time nonlinear systems with denial-of-service attack: The adaptive event-triggered case. Int. J. Robust Nonlinear Control 2022, 32, 2760–2779. [Google Scholar] [CrossRef]
- Deng, C.; Jin, X.; Che, W.; Wang, H. Learning-based distributed resilient fault-tolerant control method for heterogeneous MASs under unknown leader dynamic. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 5504–5513. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Jin, X.; Deng, C.; Che, W. Adaptive sliding-mode path-following control of cart-pendulum robots with false data injection attacks. Actuators 2023, 12, 24. [Google Scholar] [CrossRef]
- Mondal, R.; Dey, J. A novel design methodology on cascaded fractional order (FO) PI-PD control and its real time implementation to cart-inverted pendulum System. ISA Trans. 2022, 130, 565–581. [Google Scholar] [CrossRef]
- Jin, X.; Hou, Y. Adaptive event-triggered finite-time tracking control for a class of perturbed quadrotor unmanned aerial vehicles. IEEE Trans. Intell. Veh. 2024, 1–15. [Google Scholar] [CrossRef]
- Jin, X.; Liu, J.; Wu, X.; Chi, J.; Deng, C. Fixed-time linear quadratic adaptive sliding mode control for a class of cart-pendulum robots. Optim. Control Appl. Methods 2022, 43, 1735–1752. [Google Scholar] [CrossRef]
- Basin, M.V.; Ramírez, P.C.R.; Guerra-Avellaneda, F. Continuous fixed-time controller design for mechatronic systems with incomplete measurements. IEEE/ASME Trans. Mechatronics 2017, 23, 57–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Sun, C. Fixed-time sliding mode output tracking control for second-order switched systems with power integrators. Comput. Electr. Eng. 2021, 96, 107503. [Google Scholar] [CrossRef]
- Zhou, B.; Huang, B.; Su, Y.; Zheng, Y.; Zheng, S. Fixed-time neural network trajectory tracking control for underactuated surface vessels. Ocean Eng. 2021, 236, 109416. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Z.; Jin, X. Adaptive fixed-time sliding-mode trajectory tracking control of a cart-pendulum robot against actuator attacks. In Proceedings of the 2024 International Conference on Intelligent Computing, Tianjin, China, 5–8 August 2024; pp. 119–129. [Google Scholar]
- Ma, Y.-S.; Che, W.-W.; Deng, C.; Wu, Z.-G. Observer-based event-triggered containment control for MASs under DoS attacks. IEEE Trans. Cybern. 2022, 52, 13156–13167. [Google Scholar] [CrossRef]
- Jin, X.; Haddad, W.M.; Jiang, Z.; Kanellopoulos, A.; Vamvoudakis, K.G. An adaptive learning and control architecture for mitigating sensor and actuator attacks in connected autonomous vehicle platoons. Int. J. Adapt. Control Signal Process. 2019, 33, 1788–1802. [Google Scholar] [CrossRef]
- Jin, X.; Zhao, X.; Yu, J.; Wu, X.; Chi, J. Adaptive fault-tolerant consensus for a class of leader-following systems using neural network learning strategy. Neural Netw. 2020, 121, 474–483. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z.; Jin, X.; Huang, Y.; Kong, H.; Yu, M.; Ping, Z.; Sun, Z. Adaptive integral terminal sliding mode control for automobile electronic throttle via an uncertainty observer and experimental validation. IEEE Trans. Veh. Technol. 2018, 67, 8129–8143. [Google Scholar] [CrossRef]
- Wang, H.; Mi, C.; Cao, Z.; Zheng, J.; Man, Z.; Jin, X.; Tang, H. Precise discrete-time steering control for robotic fish based on data-assisted technique and super-twisting-like algorithm. IEEE Trans. Ind. Electron. 2020, 67, 10587–10599. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Z.; Gao, H.; Wang, G. Robust adaptive recursive sliding mode attitude control for a quadrotor with unknown disturbances. ISA Trans. 2022, 122, 114–125. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J.; Wang, H.; Xu, F.; Wang, X.; Liang, B. Recursive sliding mode control with adaptive disturbance observer for a linear motor positioner. Mech. Syst. Signal Process. 2021, 146, 107014. [Google Scholar] [CrossRef]
- Sakai, S.; Osuka, K.; Fukushima, H.; Iida, M. Watermelon harvesting experiment of a heavy material handling agricultural robot with LQ control. IEEE/RSJ Int. Conf. Intell. Robot. Syst. 2002, 1, 769–774. [Google Scholar]
- Hoshino, Y.; Rathnayake, N.; Dang, L.; Rathnayake, U. Cascaded-ANFIS and its successful real-world applications. In Fuzzy Logic-Advancements in Dynamical Systems, Fractional Calculus, and Computational Techniques; IntechOpen: London, UK, 2024; pp. 1–23. [Google Scholar]

| System Parameters | Symbol | Measurement Unit |
|---|---|---|
| Robot positional displacement | d | |
| Pendulum angular position | ||
| Pendulum moment of inertia | ||
| Gravity center offset | ||
| Cart mass | ||
| Cart damping coefficient | ||
| Pendulum mass | ||
| Pendulum damping coefficient | ||
| System actuation input | u | |
| Gravitational acceleration | g |
| Method | Theoretical Convergence Time | Actual Convergence Time | Convergence Ratio | RMSE () | Max Overshoot () |
|---|---|---|---|---|---|
| Proposed method | ∼106.1 s | ∼40 s | ∼2.65 | ∼ | ∼ rad |
| Basin et al. [22] | 1768.6 s | 28–38 s | 46.5–63.2 | N/A | N/A |
| Zhang et al. [23] | Fixed-time (bound not specified) | N/A | N/A | N/A | N/A |
| Zhou et al. [24] | Fixed-time (comparable) | N/A | N/A | N/A | N/A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Zhao, X.; Jin, X.; Wang, H. Adaptive Fixed-Time Tracking Control of Cart–Pendulum Robotic Systems with Bias Actuator Dynamics. Actuators 2025, 14, 245. https://doi.org/10.3390/act14050245
Chen S, Zhao X, Jin X, Wang H. Adaptive Fixed-Time Tracking Control of Cart–Pendulum Robotic Systems with Bias Actuator Dynamics. Actuators. 2025; 14(5):245. https://doi.org/10.3390/act14050245
Chicago/Turabian StyleChen, Shuo, Xuansen Zhao, Xiaozheng Jin, and Hai Wang. 2025. "Adaptive Fixed-Time Tracking Control of Cart–Pendulum Robotic Systems with Bias Actuator Dynamics" Actuators 14, no. 5: 245. https://doi.org/10.3390/act14050245
APA StyleChen, S., Zhao, X., Jin, X., & Wang, H. (2025). Adaptive Fixed-Time Tracking Control of Cart–Pendulum Robotic Systems with Bias Actuator Dynamics. Actuators, 14(5), 245. https://doi.org/10.3390/act14050245








