Model-Based Control Allocation During State Transitions of a Variable Recruitment Fluidic Artificial Muscle Bundle
Abstract
1. Introduction
2. Modeling
2.1. FAM Model Including Resistive Effects During Compression
2.2. Hydraulic System Model
3. Controller Design
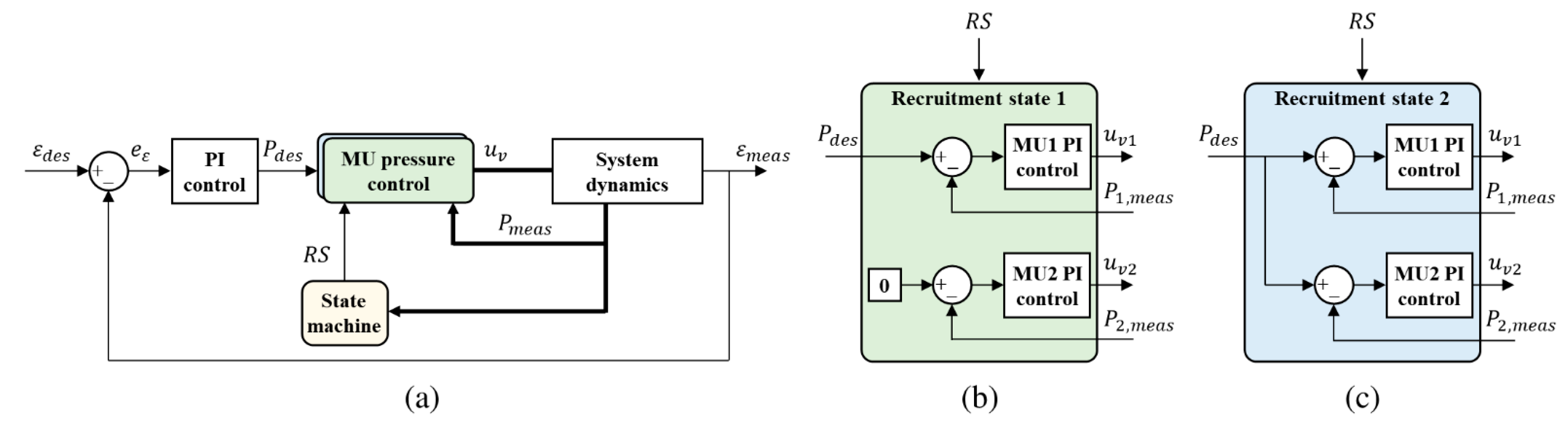
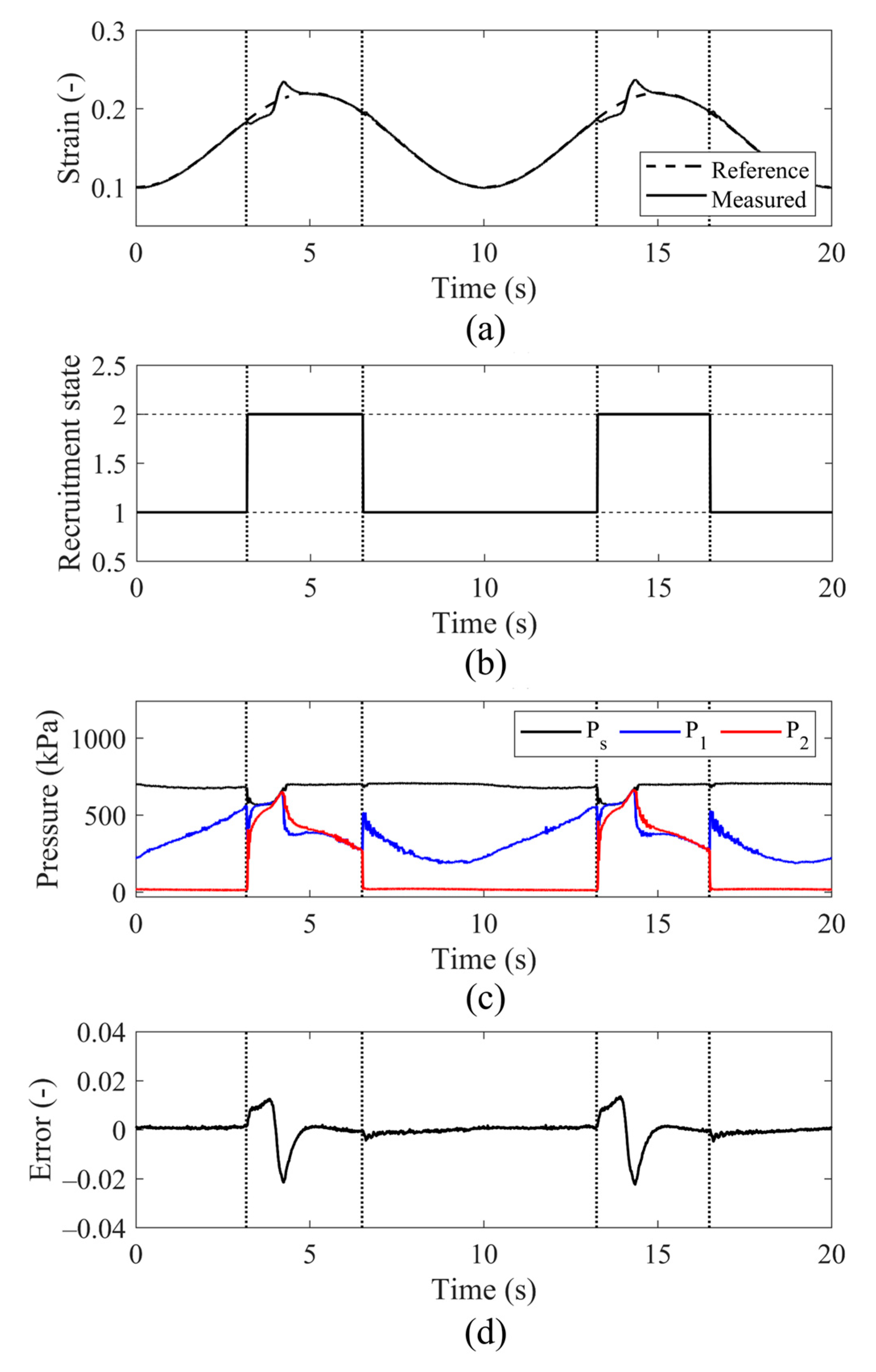
3.1. Baseline Scheme: Cascaded PI-PI Control Using Pressure Thresholds for State Transitions
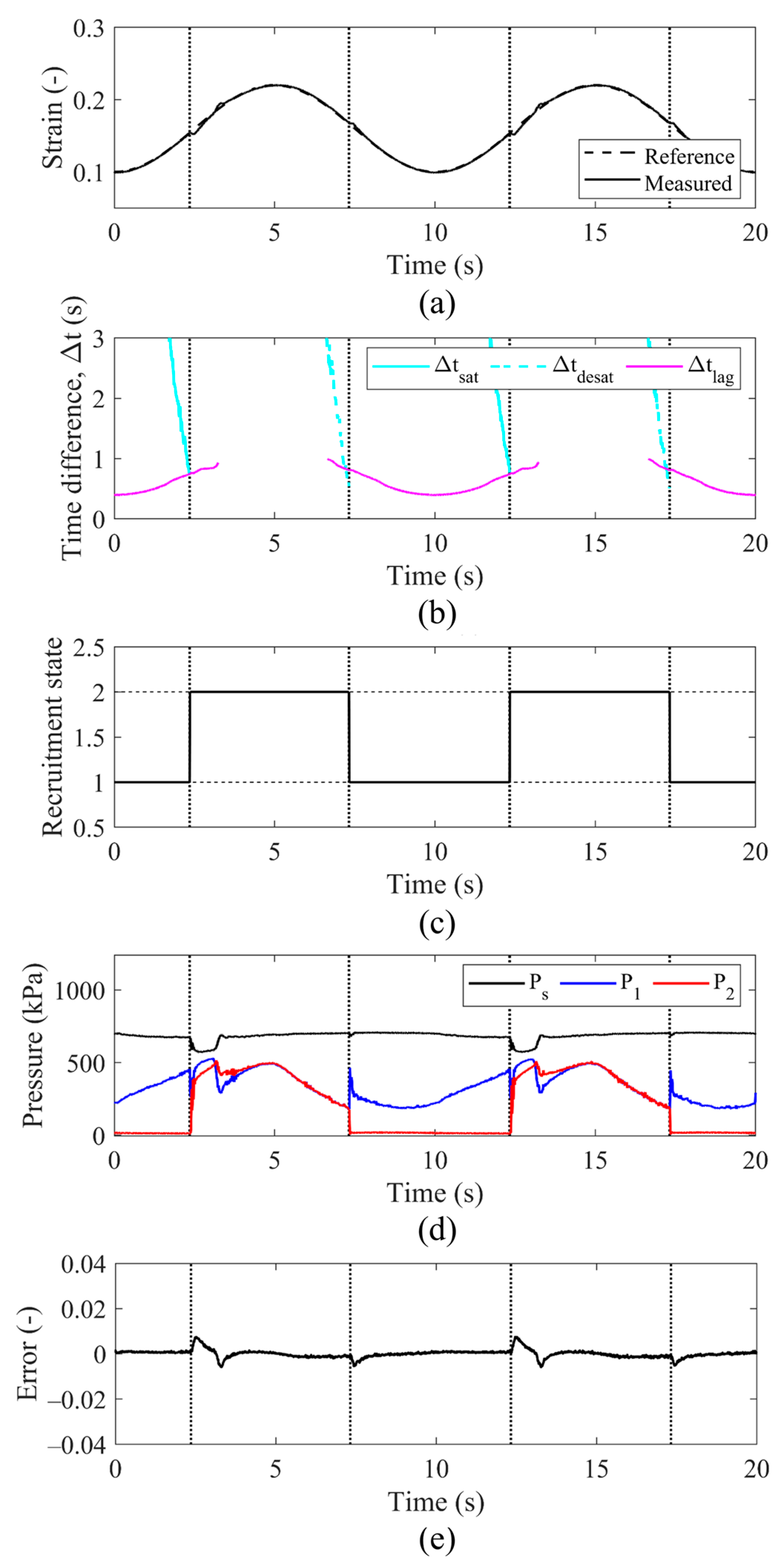
3.2. Proposed Scheme: Cascaded PI-PI Control with Lag and Pressure Compensation
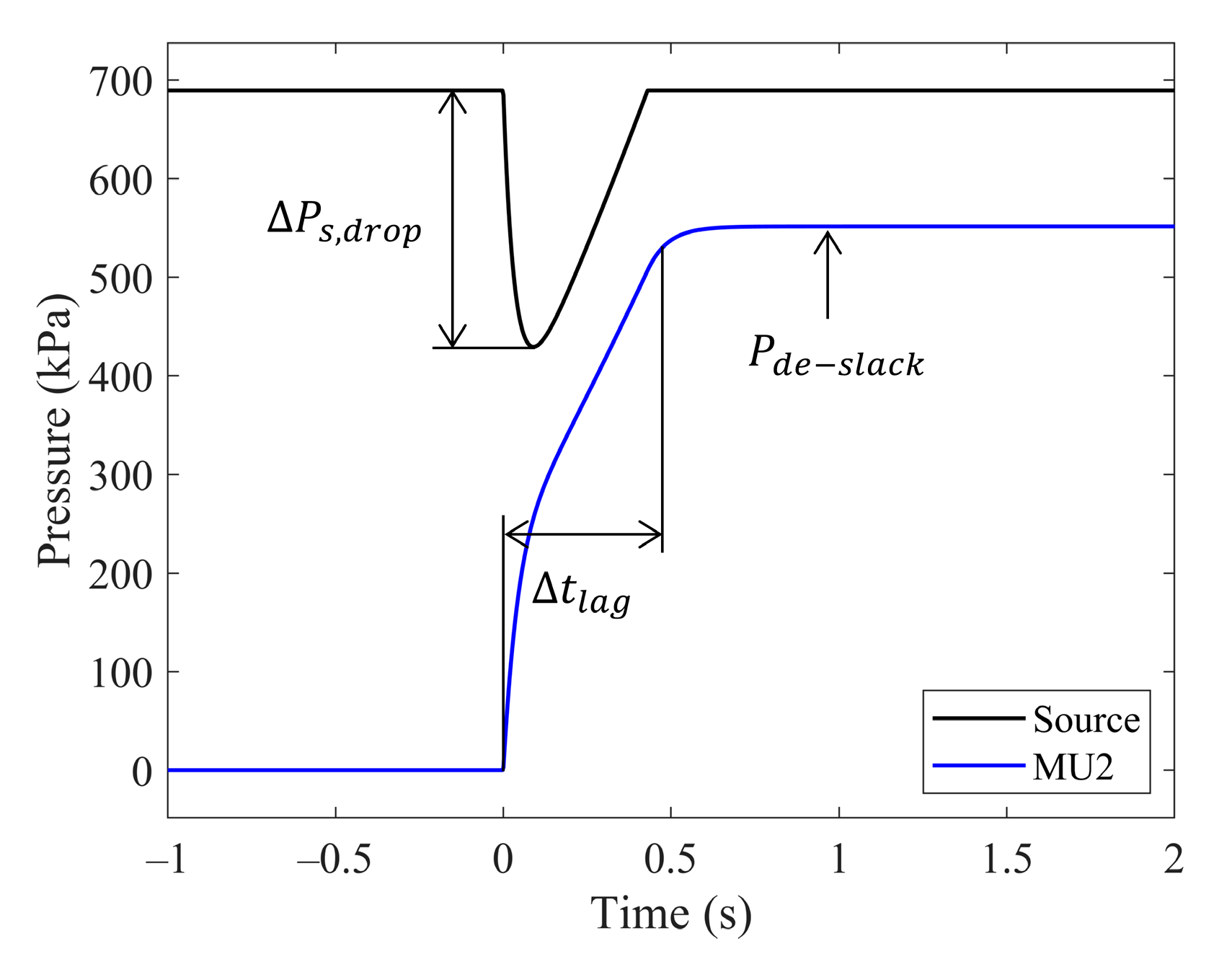
3.2.1. Pressure Compensation
3.2.2. Lag Compensation
4. Experiment Setup
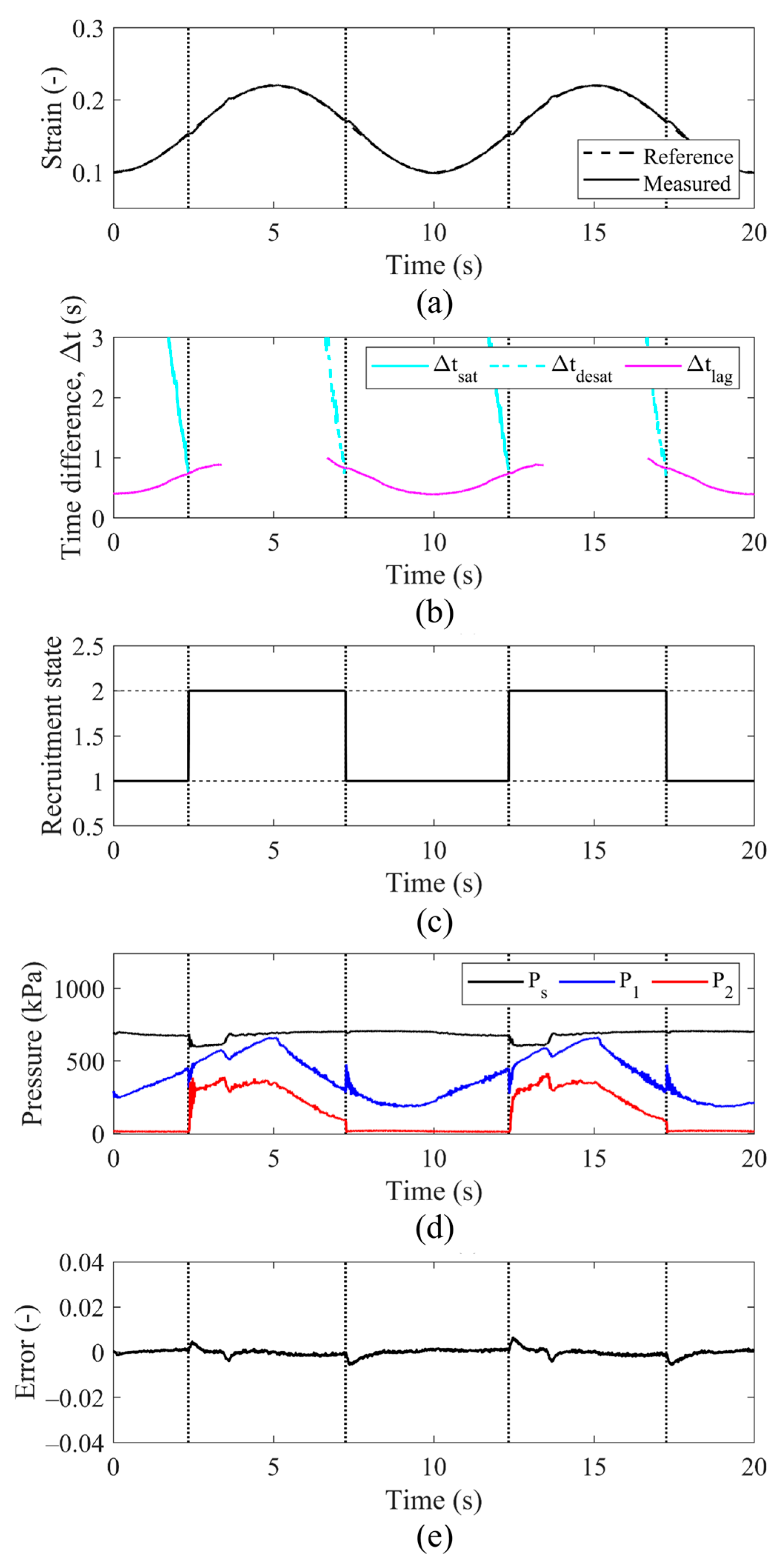
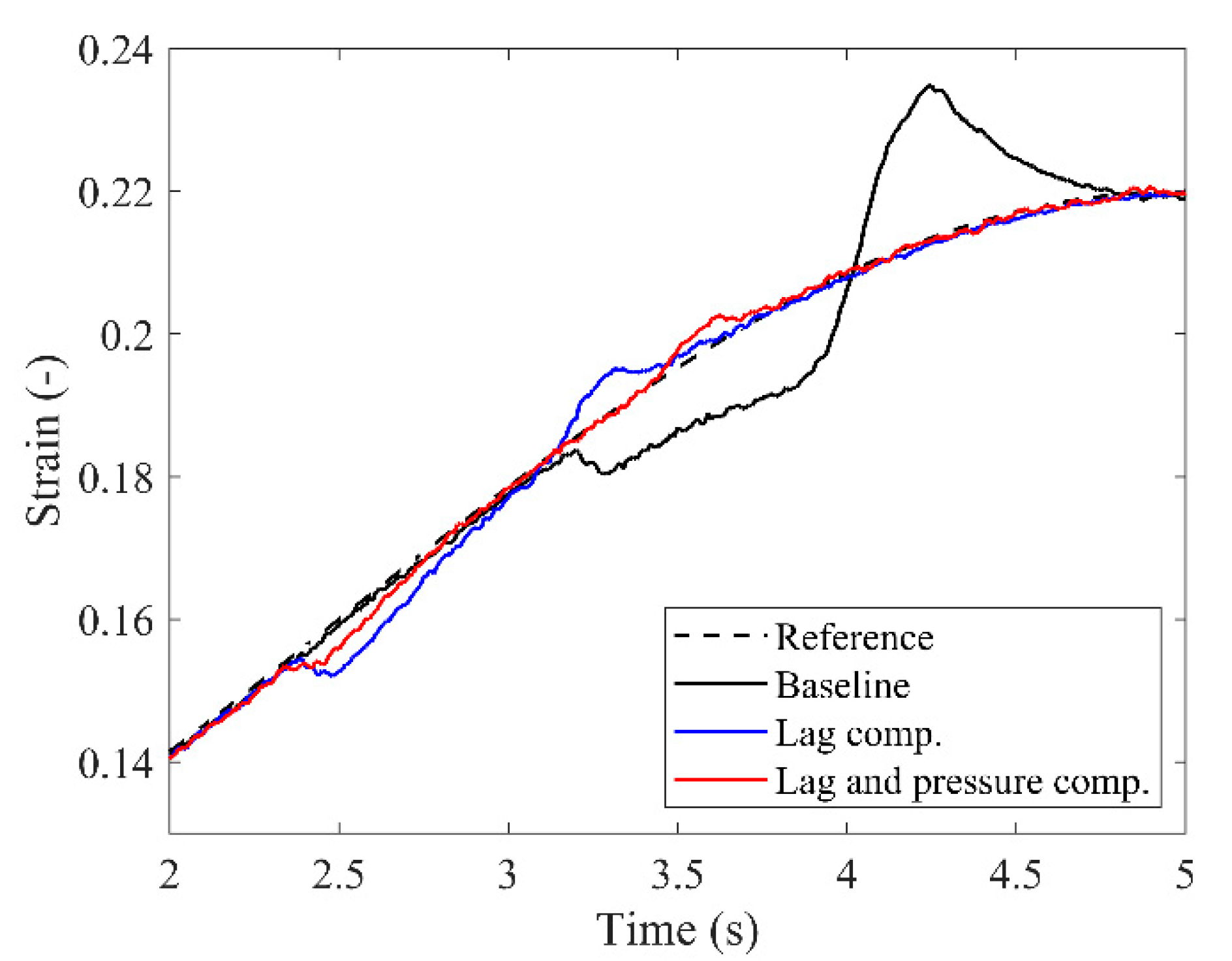
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tondu, B.; Lopez, P. Modelling and Control of McKibben Artificial Muscle Robot Actuators. IEEE Control. Syst. 2000, 20, 15–38. [Google Scholar] [CrossRef]
- Tondu, B. Modelling of the McKibben artificial muscle: A review. J. Intell. Mater. Syst. Struct. 2012, 23, 225–253. [Google Scholar] [CrossRef]
- Al-Fahaam, H.; Davis, S.; Nefti-Meziani, S. The design and mathematical modelling of novel extensor bending pneumatic artificial muscles (EBPAMs) for soft exoskeletons. Robot. Auton. Syst. 2017, 99, 63–74. [Google Scholar] [CrossRef]
- Xiao, W.; Hu, D.; Chen, W.; Yang, G.; Han, X. Modeling and analysis of bending pneumatic artificial muscle with multi-degree of freedom. Smart Mater. Struct. 2021, 30, 095018. [Google Scholar] [CrossRef]
- Zou, J.; Feng, M.; Ding, N.; Yan, P.; Xu, H.; Yang, D.; Fang, N.X.; Gu, G.; Zhu, X. Muscle-fiber array inspired, multiple-mode, pneumatic artificial muscles through planar design and one-step rolling fabrication. Natl. Sci. Rev. 2021, 8, nwab048. [Google Scholar] [CrossRef]
- Phan, P.T.; Hoang, T.T.; Thai, M.T.; Low, H.; Lovell, N.H.; Do, T.N. Twisting and Braiding Fluid-Driven Soft Artificial Muscle Fibers for Robotic Applications. Soft Robot. 2022, 9, 820–836. [Google Scholar] [CrossRef]
- Wirekoh, J.; Valle, L.; Pol, N.; Park, Y.-L. Sensorized, Flat, Pneumatic Artificial Muscle Embedded with Biomimetic Microfluidic Sensors for Proprioceptive Feedback. Soft Robot. 2019, 6, 768–777. [Google Scholar] [CrossRef]
- Yang, H.D.; Greczek, B.T.; Asbeck, A.T. Modeling and analysis of a high-displacement pneumatic artificial muscle with integrated sensing. Front. Robot. AI 2019, 5, 136. [Google Scholar] [CrossRef]
- Tiziani, L.O.; Hammond, F.L. Optical Sensor-Embedded Pneumatic Artificial Muscle for Position and Force Estimation. Soft Robot. 2020, 7, 462–477. [Google Scholar] [CrossRef]
- Legrand, J.; Loenders, B.; Vos, A.; Schoevaerdts, L.; Poorten, E.V. Integrated Capacitance Sensing for Miniature Artificial Muscle Actuators. IEEE Sens. J. 2020, 20, 1363–1372. [Google Scholar] [CrossRef]
- Jenkins, T.; Bryant, M. Pennate actuators: Force, contraction and stiffness. Bioinspiration Biomim. 2020, 15, 046005. [Google Scholar] [CrossRef] [PubMed]
- Duan, E.; Bryant, M. Implications of Spatially Constrained Bipennate Topology on Fluidic Artificial Muscle Bundle Actuation. Actuators 2022, 11, 82. [Google Scholar] [CrossRef]
- Andrikopoulos, G.; Nikolakopoulos, G.; Manesis, S. A Survey on applications of Pneumatic Artificial Muscles. In Proceedings of the 2011 19th Mediterranean Conference on Control and Automation, MED 2011, Corfu, Greece, 20–23 June 2011; pp. 1439–1446. [Google Scholar] [CrossRef]
- Ogawa, K.; Thakur, C.; Ikeda, T.; Tsuji, T.; Kurita, Y. Development of a pneumatic artificial muscle driven by low pressure and its application to the unplugged powered suit. Adv. Robot. 2017, 31, 1135–1143. [Google Scholar] [CrossRef]
- Pawar, M.V. Experimental Modelling of Pneumatic Artificial Muscle Systems Designing of Prosthetic Robotic Arm. In Proceedings of the 2018 3rd International Conference for Convergence in Technology (I2CT), I2CT 2018, Pune, India, 6–8 April 2018; pp. 18–23. [Google Scholar] [CrossRef]
- Choi, H.S.; Lee, C.H.; Baek, Y.S. Design and Validation of a Two-Degree-of-Freedom Powered Ankle-Foot Orthosis with Two Pneumatic Artificial Muscles. Mechatronics 2020, 72, 102469. [Google Scholar] [CrossRef]
- Henneman, E.; Somjen, G.; Carpenter, D.O. Excitability and inhibitibility of motoneurons of different sizes. J. Neurophysiol. 1965, 28, 599–620. [Google Scholar] [CrossRef]
- Bryant, M.; Meller, M.A.; Garcia, E. Variable recruitment fluidic artificial muscles: Modeling and experiments. Smart Mater. Struct. 2014, 23, 074009. [Google Scholar] [CrossRef]
- Jenkins, T.E.; Chapman, E.M.; Bryant, M. Bio-inspired online variable recruitment control of fluidic artificial muscles. Smart Mater. Struct. 2016, 25, 125016. [Google Scholar] [CrossRef]
- Robinson, R.M.; Kothera, C.S.; Wereley, N.M. Variable Recruitment Testing of Pneumatic Artificial Muscles for Robotic Manipulators. IEEE/ASME Trans. Mechatron. 2014, 20, 1642–1652. [Google Scholar] [CrossRef]
- Delahunt, S.A.; Pillsbury, T.E.; Wereley, N.M. Variable recruitment in bundles of miniature pneumatic artificial muscles. Bioinspiration Biomim. 2016, 11, 056014. [Google Scholar] [CrossRef]
- Chapman, E.M.; Jenkins, T.; Bryant, M. Design and Analysis of Electrohydraulic Pressure Systems for Variable Recruitment in Fluidic Artificial Muscles. Smart Mater. Struct. 2018, 27, 105024. [Google Scholar] [CrossRef]
- Mazzoleni, N.; Kim, J.Y.; Bryant, M. Motor unit buckling in variable recruitment fluidic artificial muscle bundles: Implications and mitigations. Smart Mater. Struct. 2022, 31, 035004. [Google Scholar] [CrossRef]
- Focchi, M.; Guglielmino, E.; Semini, C.; Parmiggiani, A.; Tsagarakis, N.; Vanderborght, B.; Caldwell, D.G. Water/air performance analysis of a fluidic muscle. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2010), Taipei, Taiwan, 18–22 October 2010; pp. 2194–2199. [Google Scholar] [CrossRef]
- Minh, T.V.; Tjahjowidodo, T.; Ramon, H.; Van Brussel, H. Cascade position control of a single pneumatic artificial muscle–mass system with hysteresis compensation. Mechatronics 2010, 20, 402–414. [Google Scholar] [CrossRef]
- Ganguly, S.; Garg, A.; Pasricha, A.; Dwivedy, S. Control of pneumatic artificial muscle system through experimental modelling. Mechatronics 2012, 22, 1135–1147. [Google Scholar] [CrossRef]
- Ba, D.X.; Dinh, T.Q.; Ahn, K.K. An Integrated Intelligent Nonlinear Control Method for a Pneumatic Artificial Muscle. IEEE/ASME Trans. Mechatron. 2016, 21, 1835–1845. [Google Scholar] [CrossRef]
- Zhang, Z.; Philen, M. Pressurized artificial muscles. J. Intell. Mater. Syst. Struct. 2011, 23, 255–268. [Google Scholar] [CrossRef]
- Ai, Q.; Ke, D.; Zuo, J.; Meng, W.; Liu, Q.; Zhang, Z.; Xie, S.Q. High-Order Model-Free Adaptive Iterative Learning Control of Pneumatic Artificial Muscle with Enhanced Convergence. IEEE Trans. Ind. Electron. 2019, 67, 9548–9559. [Google Scholar] [CrossRef]
- Sun, N.; Liang, D.; Wu, Y.; Chen, Y.; Qin, Y.; Fang, Y. Adaptive Control for Pneumatic Artificial Muscle Systems with Parametric Uncertainties and Unidirectional Input Constraints. IEEE Trans. Ind. Inform. 2019, 16, 969–979. [Google Scholar] [CrossRef]
- Duong, M.-D.; Pham, Q.-T.; Vu, T.-C.; Bui, N.-T.; Dao, Q.-T. Adaptive fuzzy sliding mode control of an actuator powered by two opposing pneumatic artificial muscles. Sci. Rep. 2023, 13, 8242. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Pham, B.-L.; Nguyen, T.-V.; Bui, N.-T.; Dao, Q.-T. Sliding mode control of antagonistically coupled pneumatic artificial muscles using radial basis neural network function. SN Appl. Sci. 2023, 5, 246. [Google Scholar] [CrossRef]
- Zhao, Z.; Hao, L.; Tao, G.; Liu, H.; Shen, L. Prescribed performance sliding mode control for the PAMs elbow exoskeleton in the tracking trajectory task. Ind. Robot. 2023, 51, 167–176. [Google Scholar] [CrossRef]
- Lin, C.-J.; Sie, T.-Y. Design and Experimental Characterization of Artificial Neural Network Controller for a Lower Limb Robotic Exoskeleton. Actuators 2023, 12, 55. [Google Scholar] [CrossRef]
- Meller, M.; Chipka, J.; Volkov, A.; Bryant, M.; Garcia, E. Improving actuation efficiency through variable recruitment hydraulic McKibben muscles: Modeling, orderly recruitment control, and experiments. Bioinspir. Biomim. 2016, 11, 065004. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, M.; Shim, T.; Zhang, Y. Shift dynamics and control of dual-clutch transmissions. Mech. Mach. Theory 2006, 42, 168–182. [Google Scholar] [CrossRef]
- Kahlbau, S.; Bestle, D. Optimal shift control for automatic transmission. Mech. Based Des. Struct. Mach. 2013, 41, 259–273. [Google Scholar] [CrossRef]
- Kuo, K.L. Simulation and analysis of the shift process for an automatic transmission. World Acad. Sci. Eng. Technol. 2011, 76, 341–347. [Google Scholar]
- Walker, P.; Zhu, B.; Zhang, N. Powertrain dynamics and control of a two speed dual clutch transmission for electric vehicles. Mech. Syst. Signal Process. 2017, 85, 1–15. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, X. Optimization of the Quality of the Automatic Transmission Shift and the Power Transmission Characteristics. Energies 2022, 15, 4672. [Google Scholar] [CrossRef]
- Chou, C.-P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Trans. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Sangian, D.; Naficy, S.; Spinks, G.M.; Tondu, B. The effect of geometry and material properties on the performance of a small hydraulic McKibben muscle system. Sens. Actuators A Phys. 2015, 234, 150–157. [Google Scholar] [CrossRef]
- Yu, Z.; Pillsbury, T.; Wang, G.; Wereley, N.M. Hyperelastic analysis of pneumatic artificial muscle with filament-wound sleeve and coated outer layer. Smart Mater. Struct. 2019, 28, 105019. [Google Scholar] [CrossRef]
- Kalita, B.; Leonessa, A.; Dwivedy, S.K. A Review on the Development of Pneumatic Artificial Muscle Actuators: Force Model and Application. Actuators 2022, 11, 288. [Google Scholar] [CrossRef]
- Kim, J.Y.; Mazzoleni, N.; Bryant, M. Modeling of Resistive Forces and Buckling Behavior in Variable Recruitment Fluidic Artificial Muscle Bundles. Actuators 2021, 10, 42. [Google Scholar] [CrossRef]
- Klute, G.K.; Hannaford, B. Accounting for Elastic Energy Storage in McKibben Artificial Muscle Actuators. J. Dyn. Syst. Meas. Control. 1998, 122, 386–388. [Google Scholar] [CrossRef]
- Jelali, M.; Kroll, A. Hydraulic Servo-Systems: Modeling, Identification and Control; Springer: London, UK, 2003. [Google Scholar]
- Meller, M.A.; Bryant, M.; Garcia, E. Reconsidering the McKibben muscle: Energetics, operating fluid, and bladder material. J. Intell. Mater. Syst. Struct. 2014, 25, 2276–2293. [Google Scholar] [CrossRef]
- Chipka, J.; Meller, M.A.; Volkov, A.; Bryant, M.; Garcia, E. Linear dynamometer testing of hydraulic artificial muscles with variable recruitment. J. Intell. Mater. Syst. Struct. 2017, 28, 2051–2063. [Google Scholar] [CrossRef]








| FAM dimensions | Initial inner radius | 0.0063 | |
| Initial thickness | 0.0016 | ||
| Initial braid angle | 33 | ||
| Initial length | 0.222 | ||
| Empirical-based tuning correction factors | Young’s modulus | - | 1.3 |
| Collapse moment | - | 0.75 | |
| Torsional spring constant | - | 0.9P + 1.54 | |
| Transition constant | 100 |
| Strain IAE | Max. Strain Error | |
|---|---|---|
| Baseline controller | 0.0454 | 0.0223 |
| Cascaded controller with only lag compensation | 0.0234 | 0.0075 |
| Cascaded controller with lag and pressure compensation | 0.0211 | 0.0064 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.Y.; Bryant, M. Model-Based Control Allocation During State Transitions of a Variable Recruitment Fluidic Artificial Muscle Bundle. Actuators 2025, 14, 235. https://doi.org/10.3390/act14050235
Kim JY, Bryant M. Model-Based Control Allocation During State Transitions of a Variable Recruitment Fluidic Artificial Muscle Bundle. Actuators. 2025; 14(5):235. https://doi.org/10.3390/act14050235
Chicago/Turabian StyleKim, Jeong Yong, and Matthew Bryant. 2025. "Model-Based Control Allocation During State Transitions of a Variable Recruitment Fluidic Artificial Muscle Bundle" Actuators 14, no. 5: 235. https://doi.org/10.3390/act14050235
APA StyleKim, J. Y., & Bryant, M. (2025). Model-Based Control Allocation During State Transitions of a Variable Recruitment Fluidic Artificial Muscle Bundle. Actuators, 14(5), 235. https://doi.org/10.3390/act14050235






