Inner–Outer Loop Intelligent Morphology Optimization and Pursuit–Evasion Control for Space Modular Robot
Abstract
1. Introduction
- (1)
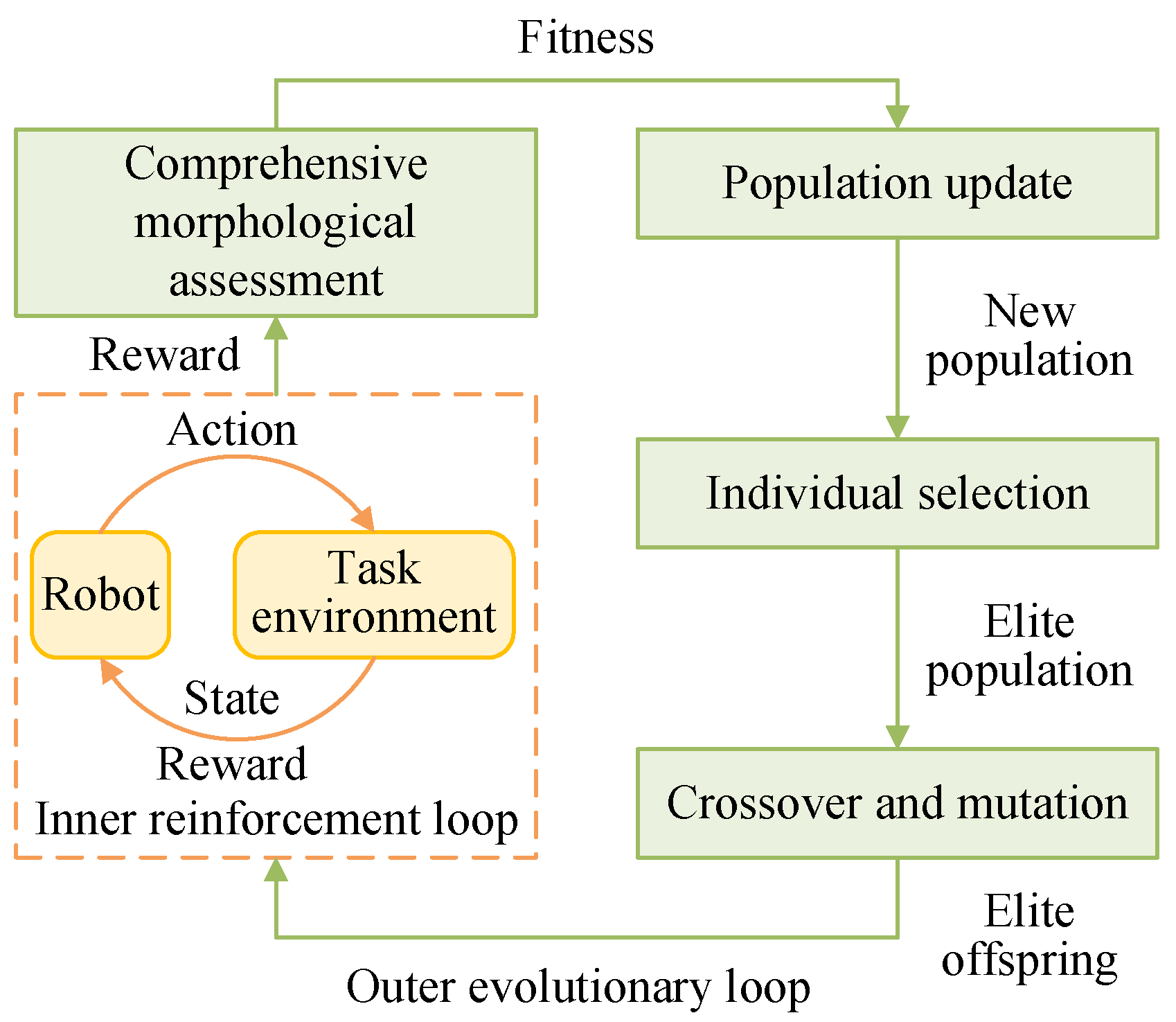
- Aninner–outer loop computational framework alternating between the evolution of morphology and the training of modular robots is built for space pursuit–evasion task for the first time. This framework is implemented on JAX to achieve efficient parallel computation, ultimately resulting in the globally approximate optimal combination of the morphology and the strategy for the space pursuit–evasion task.
- (2)
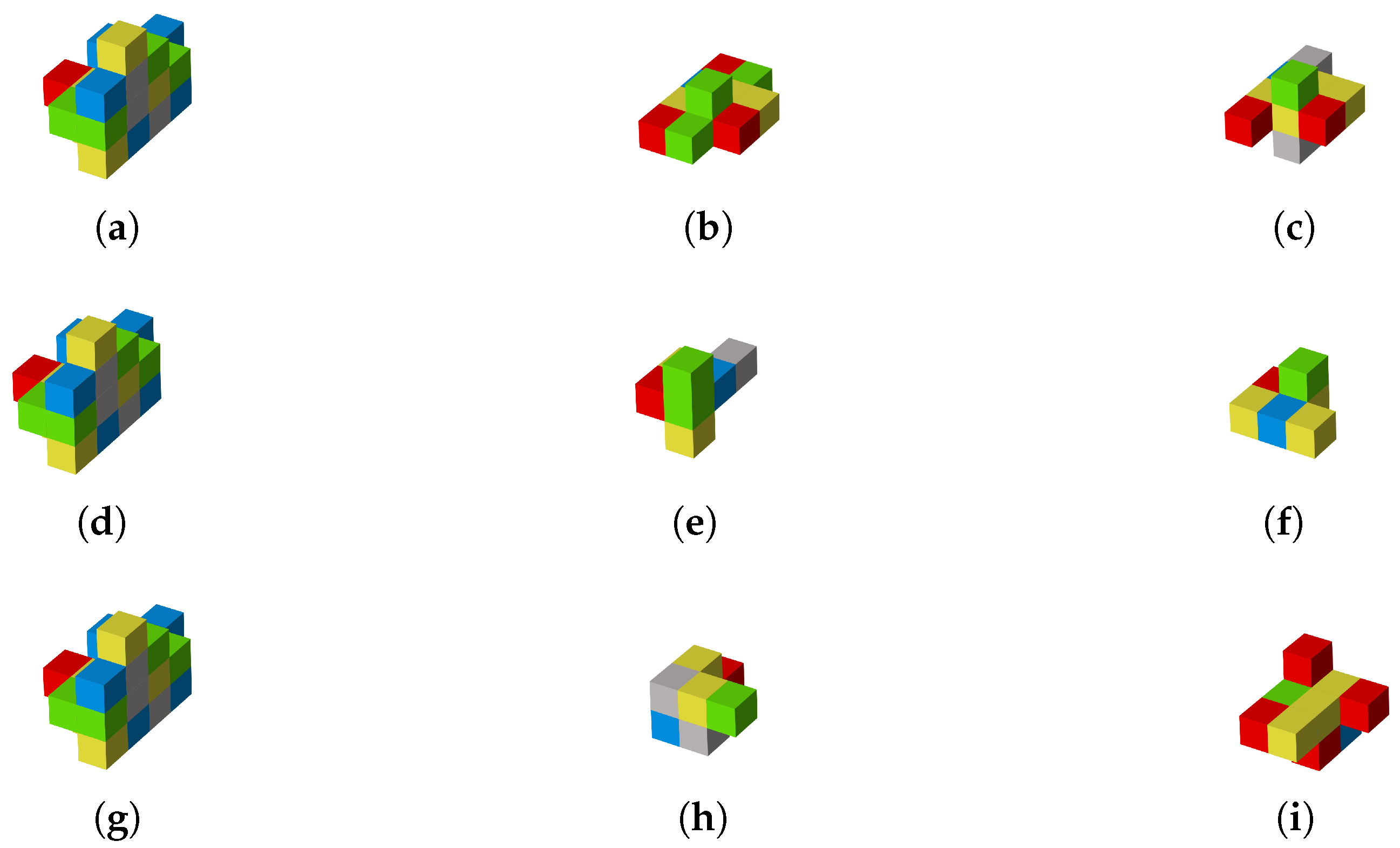
- In the outer loop, a morphological evolutionary algorithm based on the elite GA (EGA) is developed to optimize the morphology of the modular robots. Unlike most studies on modular robots that focus on modules with straightforward functions [21,22], this study investigates a modular robot with various practical module functions. Therefore, a morphological design space that considers the various module functional characteristics and a corresponding morphological encoding scheme is designed. Additionally, a comprehensive morphological assessment is proposed to guide morphological evolution and ensure the evolved morphology has good structural and control performance.
- (3)
- In the inner loop, a pursuit–evasion control approach based on the PPO algorithm is proposed for the space modular robots to pursue the free-floating and maneuvering evaders. By introducing the fuel consumption punishment into the reward function, the pursuit strategy is near fuel-optimal. The proposed approach possesses the superiority in balancing the pursuit performance and control cost.
2. Model and Problem Statement
2.1. Model of a Space Modular Robot
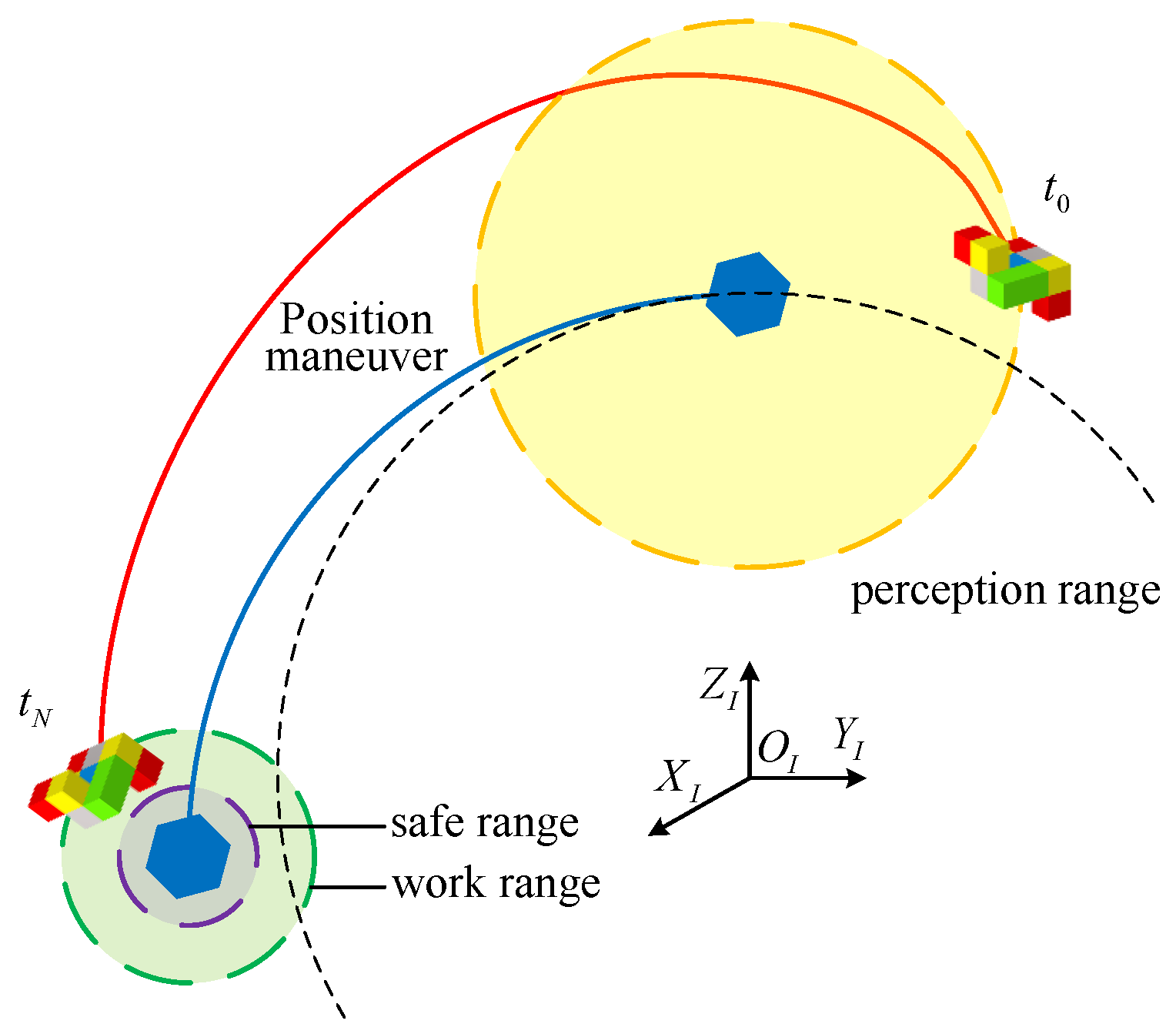
2.2. Problem Statement
3. Inner–Outer Loop Intelligent Morphology Optimization and Pursuit–Evasion Control
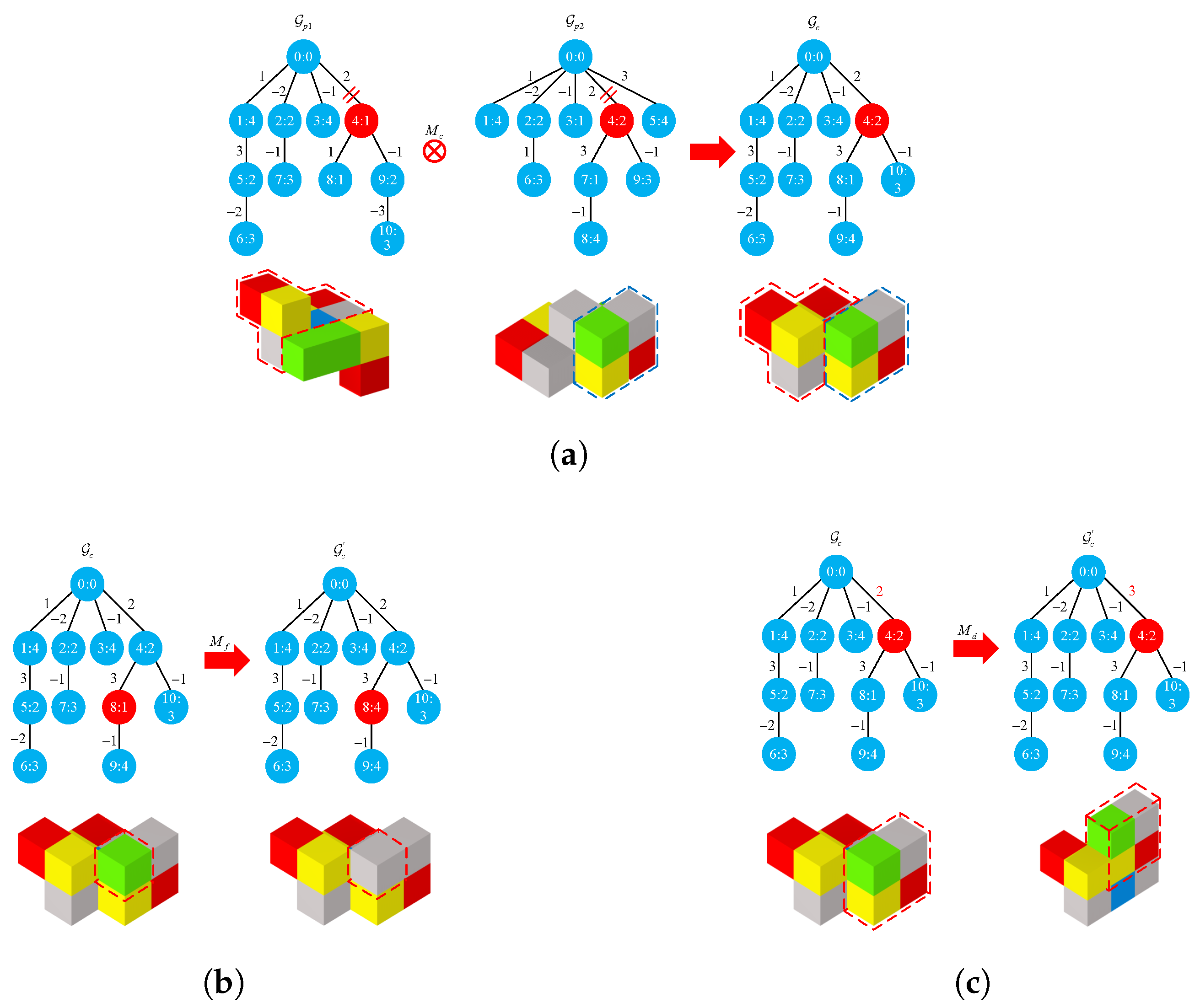
3.1. Crossover and Mutation
3.2. Comprehensive Morphological Assessment
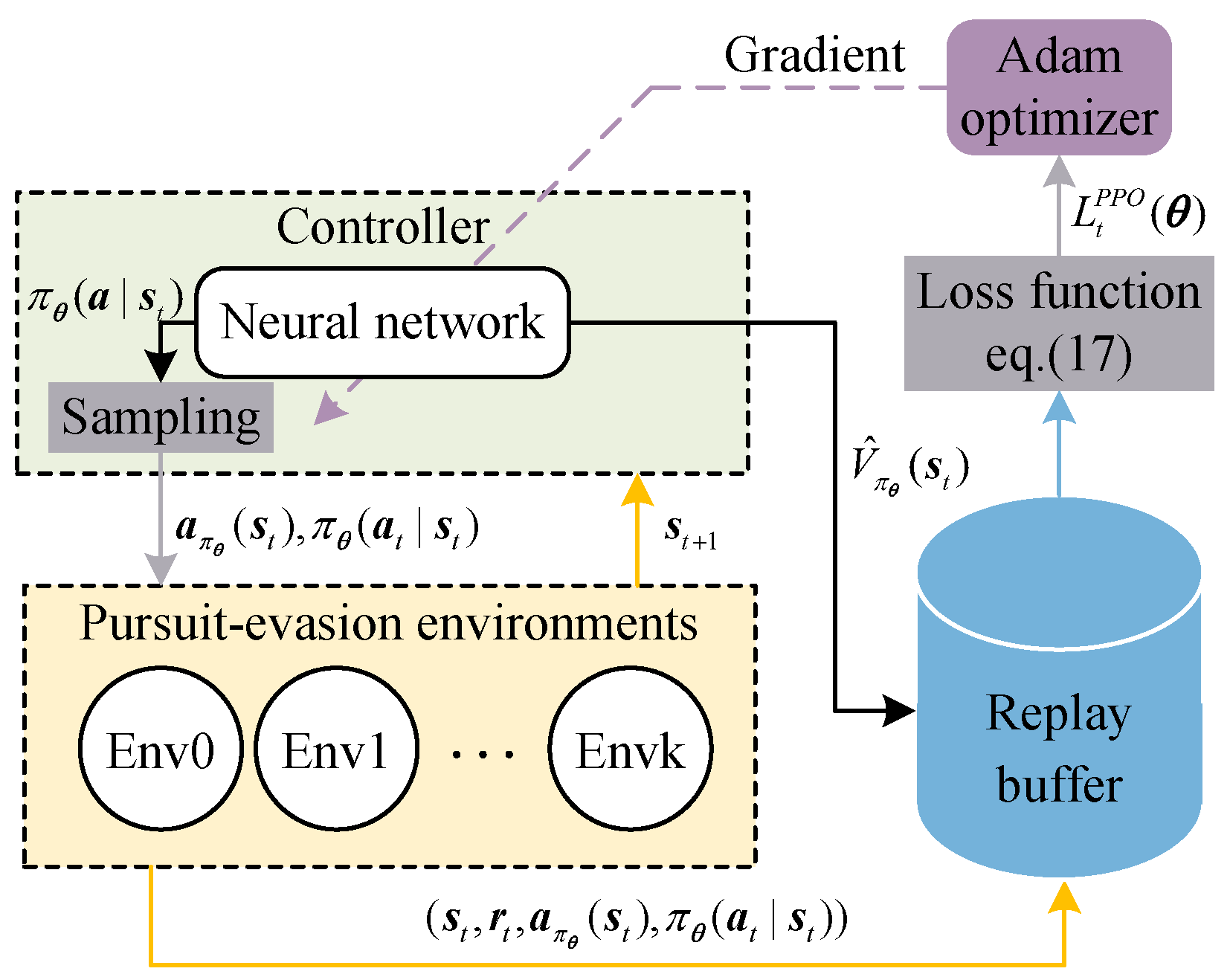
3.3. Proximal Policy Optimization Algorithm
3.4. Reward Function of the Space Pursuit–Evasion Task
3.5. Outline of the Inner–Outer Loop Computational Framework Implementation
| Algorithm 1: Inner–Outer Loop Computational Framework |
|
4. Numerical Simulation
4.1. Configuration of Task and Algorithm
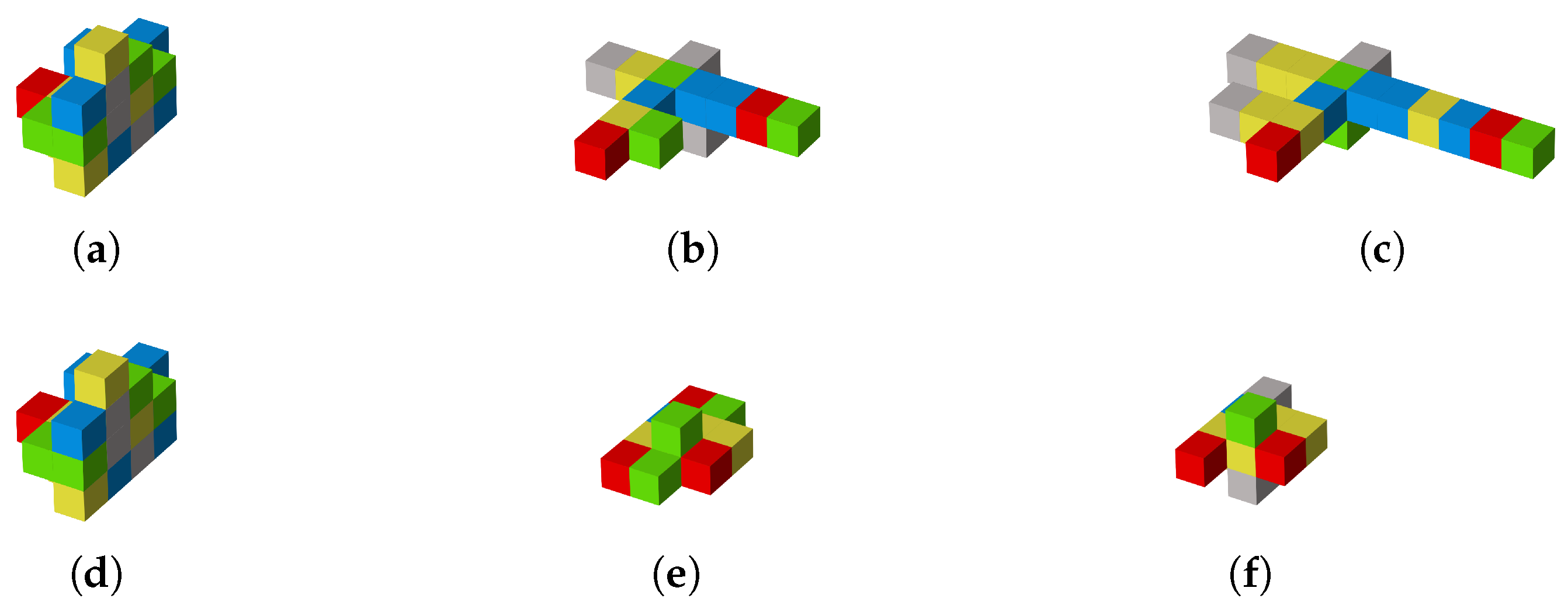
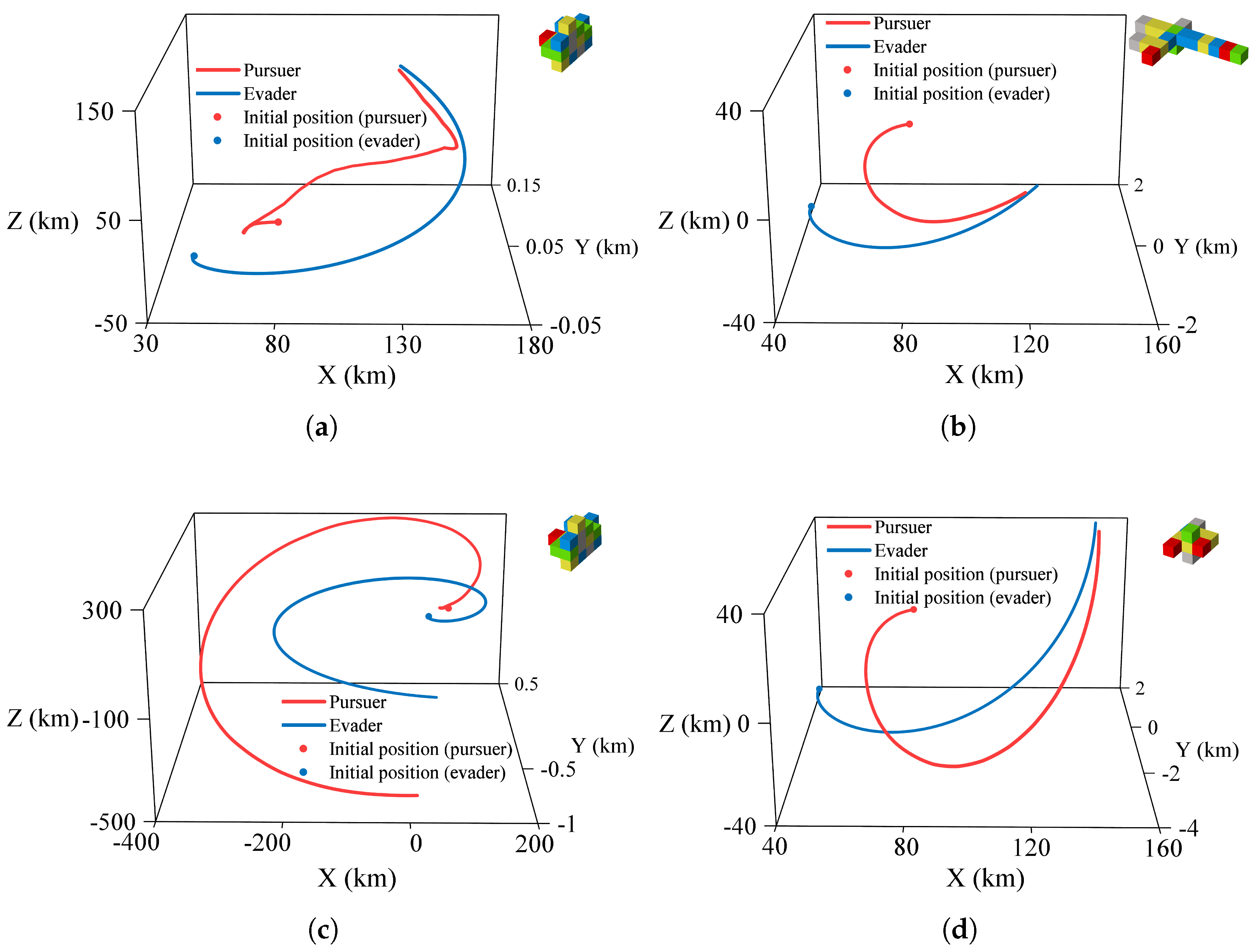
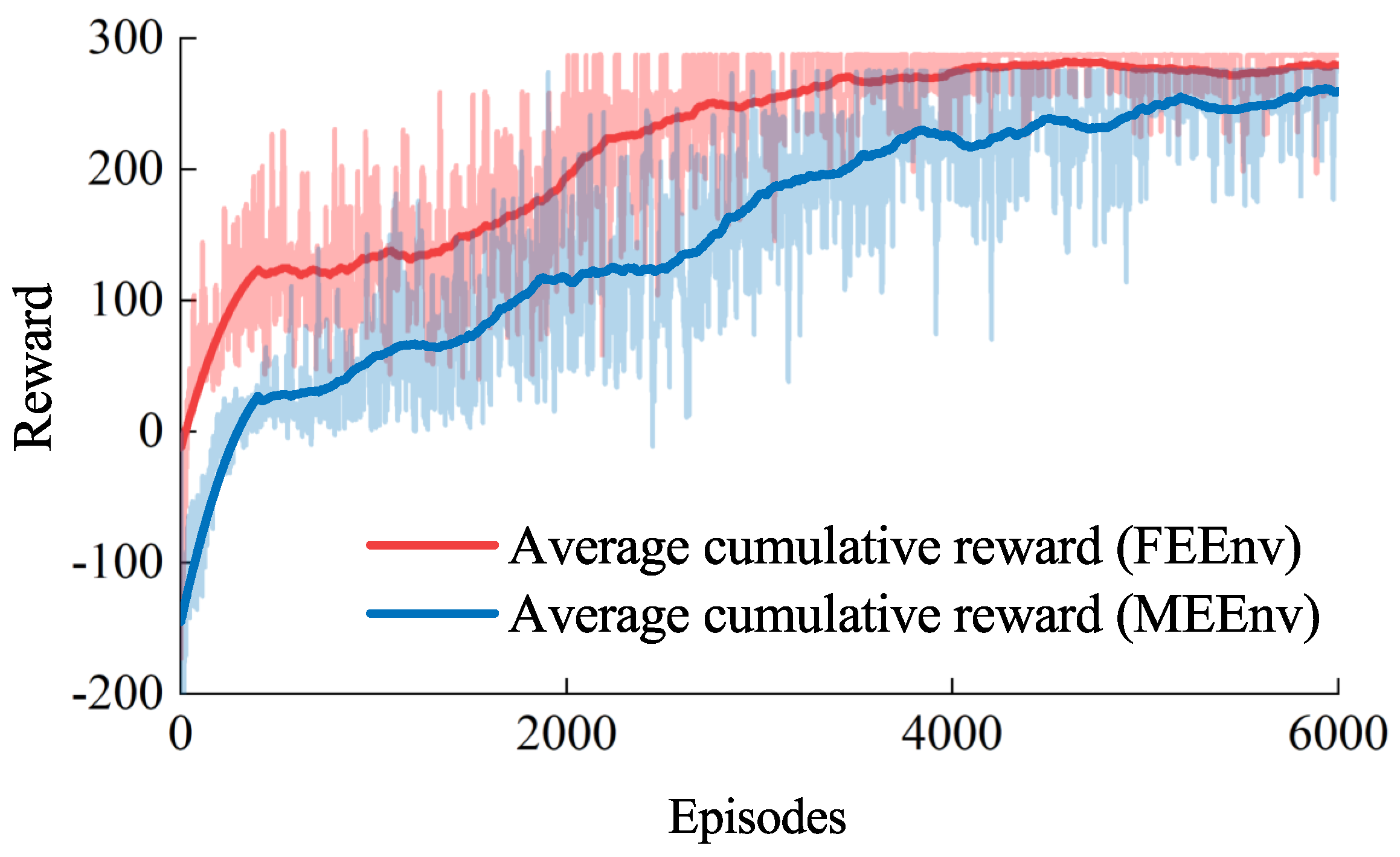
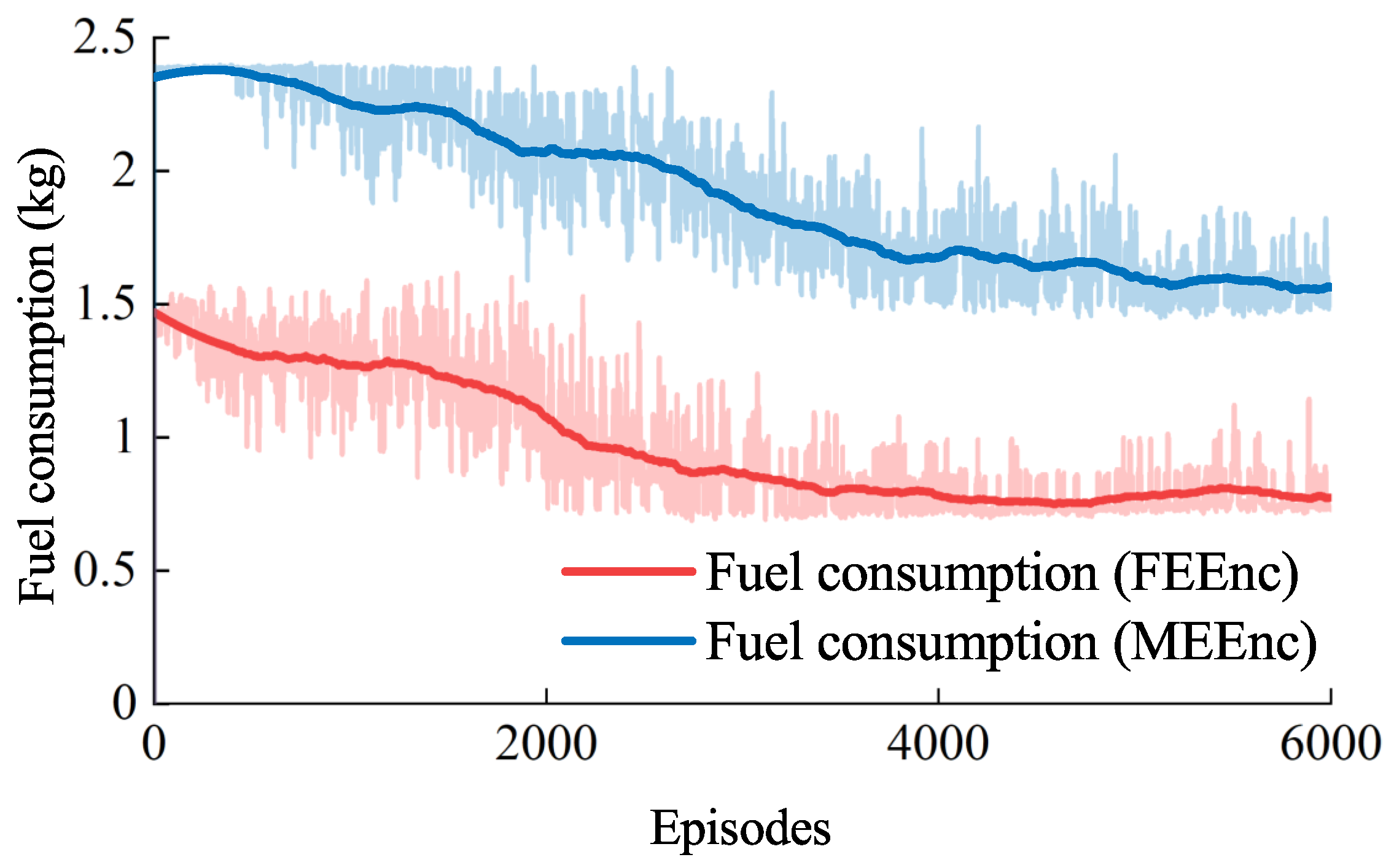
4.2. Simulation in Different Space Pursuit–Evasion Task Environments
4.3. Simulation in Different Optimization Frameworks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, N.; Luo, J.; Zong, L. Cooperative Game Method for On-Orbit Substructure Transportation Using Modular Robots. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1161–1175. [Google Scholar] [CrossRef]
- Han, N.; Luo, J.; Zheng, Z. Robust Coordinated Control for On-Orbit Substructure Transportation under Distributed Information. Nonlinear Dyn. 2021, 104, 2331–2346. [Google Scholar] [CrossRef]
- Wharton, P.; You, T.L.; Jenkinson, G.P.; Diteesawat, R.S.; Le, N.H.; Hall, E.C.; Garrad, M.; Conn, A.T.; Rossiter, J. Tetraflex: A Multigait Soft Robot for Object Transportation in Confined Environments. IEEE Robot. Autom. Lett. 2023, 8, 5007–5014. [Google Scholar] [CrossRef]
- Hu, Q.; Dong, E.; Sun, D. Soft Modular Climbing Robots. IEEE Trans. Robot. 2023, 39, 399–416. [Google Scholar] [CrossRef]
- Gerkey, B.P.; Thrun, S.; Gordon, G. Visibility-Based Pursuit-Evasion with Limited Field of View. Int. J. Robot. Res. 2006, 25, 299–315. [Google Scholar] [CrossRef]
- Tovar, B.; LaValle, S.M. Visibility-Based Pursuit-Evasion with Bounded Speed. Int. J. Rob. Res. 2008, 27, 1350–1360. [Google Scholar] [CrossRef]
- Gurumurthy, V.; Mohanty, N.; Sundaram, S.; Sundararajan, N. An Efficient Reinforcement Learning Scheme for the Confinement Escape Problem. Appl. Soft. Comput. 2024, 152, 111248. [Google Scholar] [CrossRef]
- Post, M.A.; Yan, X.T.; Letier, P. Modularity for the Future in Space Robotics: A Review. ACTA Astronaut. 2021, 189, 530–547. [Google Scholar] [CrossRef]
- Stroppa, F.; Majeed, F.J.; Batiya, J.; Baran, E.; Sarac, M. Optimizing Soft Robot Design and Tracking with and without Evolutionary Computation: An Intensive Survey. Robotica 2024, 42, 2848–2884. [Google Scholar] [CrossRef]
- Nadizar, G.; Medvet, E.; Ramstad, H.H.; Nichele, S.; Pellegrino, F.A.; Zullich, M. Merging Pruning and Neuroevolution: Towards Robust and Efficient Controllers for Modular Soft Robots. Knowl. Eng. Rev. 2022, 37, 1–27. [Google Scholar] [CrossRef]
- Hiller, J.; Lipson, H. Automatic Design and Manufacture of Soft Robots. IEEE Trans. Robot. 2012, 28, 457–466. [Google Scholar] [CrossRef]
- Atia, M.G.B.; Mohammad, A.; Gameros, A.; Axinte, D.; Wright, I. Reconfigurable Soft Robots by Building Blocks. Adv. Sci. 2022, 9, 2203217. [Google Scholar] [CrossRef] [PubMed]
- Ghoreishi, S.F.; Sochol, R.D.; Gandhi, D.; Krieger, A.; Fuge, M. Bayesian Optimization for Design of Multi-Actuator Soft Catheter Robots. IEEE Trans. Med. Robot. Bionics 2021, 3, 725–737. [Google Scholar] [CrossRef]
- Zhao, A.; Xu, J.; Konaković-Luković, M.; Hughes, J.; Spielberg, A.; Rus, D.; Matusik, W. RoboGrammar: Graph Grammar for Terrain-Optimized Robot Design. ACM Trans. Graph. 2020, 39, 1–16. [Google Scholar] [CrossRef]
- Sims, K. Evolving 3D Morphology and Behavior by Competition. Artif. Life 1994, 1, 353–372. [Google Scholar] [CrossRef]
- Kriegman, S.; Blackiston, D.; Levin, M.; Bongard, J. A Scalable Pipeline for Designing Reconfigurable Organisms. Proc. Natl. Acad. Sci. USA 2020, 117, 1853–1859. [Google Scholar] [CrossRef]
- Cheney, N.; MacCurdy, R.; Clune, J.; Lipson, H. Unshackling Evolution: Evolving Soft Robots with Multiple Materials and a Powerful Generative Encoding. ACM SIGEVOlution 2014, 7, 11–23. [Google Scholar] [CrossRef]
- Mintchev, S.; Floreano, D. Adaptive Morphology: A Design Principle for Multimodal and Multifunctional Robots. IEEE Robot. Autom. Mag. 2016, 23, 42–54. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, J.; Li, J.; Peng, Y.; Mao, Z. Large Language Models for Human–Robot Interaction: A Review. Biomim. Intell. Robot. 2023, 3, 100131. [Google Scholar] [CrossRef]
- Mao, Z.; Kobayashi, R.; Nabae, H.; Suzumori, K. Multimodal Strain Sensing System for Shape Recognition of Tensegrity Structures by Combining Traditional Regression and Deep Learning Approaches. IEEE Robot. Autom. Lett. 2024, 9, 10050–10056. [Google Scholar] [CrossRef]
- Gupta, A.; Savarese, S.; Ganguli, S.; Li, F. Embodied Intelligence via Learning and Evolution. Nat. Commun. 2021, 12, 5721. [Google Scholar] [CrossRef]
- Koike, R.; Ariizumi, R.; Matsuno, F. Simultaneous Optimization of Discrete and Continuous Parameters Defining a Robot Morphology and Controller. IEEE Trans. Neural Netw. Learning Syst. 2024, 35, 13816–13829. [Google Scholar] [CrossRef] [PubMed]
- Geng, Y.; Yuan, L.; Guo, Y.; Tang, L.; Huang, H. Impulsive Guidance of Optimal Pursuit with Conical Imaging Zone for the Evader. Aerosp. Sci. Technol. 2023, 142, 108604. [Google Scholar] [CrossRef]
- Yang, B.; Jiang, L.; Wu, W.; Zhen, R. Evolving Robotic Hand Morphology through Grasping and Learning. IEEE Robot. Autom. Lett. 2024, 9, 8475–8482. [Google Scholar] [CrossRef]
- Tao, C.; Li, M.; Cao, F.; Gao, Z.; Zhang, Z. A Multiobjective Collaborative Deep Reinforcement Learning Algorithm for Jumping Optimization of Bipedal Robot. Adv. Intell. Syst. 2024, 6, 2300352. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.; Yang, Y.; Xiao, B. Appointed-fixed-time Observer based Sliding Mode Control for A Quadrotor UAV Under External Disturbances. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7281–7294. [Google Scholar] [CrossRef]
- Liu, H.; Li, B.; Xiao, B.; Ran, D.; Zhang, C. Reinforcement Learning-Based Tracking Control for a Quadrotor Unmanned Aerial Vehicle under External Disturbances. Int. J. Robust Nonlinear Control 2023, 33, 10360–10377. [Google Scholar] [CrossRef]
- Li, B.; Liu, H.; Ahn, C.K.; Gong, W. Optimized Intelligent Tracking Control for a Quadrotor Unmanned Aerial Vehicle with Actuator Failures. Aerosp. Sci. Technol. 2024, 144, 108803. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, Y.; Fidler, S.; Ba, J. Neural Graph Evolution: Towards Efficient Automatic Robot Design. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar] [CrossRef]
- Duan, K.; Suen, C.W.K.; Zou, Z. Robot Morphology Evolution for Automated HVAC System Inspections Using Graph Heuristic Search and Reinforcement Learning. Autom. Constr. 2023, 153, 104956. [Google Scholar] [CrossRef]
- Jing, G.; Tosun, T.; Yim, M.; Kress-Gazit, H. Accomplishing High-Level Tasks with Modular Robots. Auton. Robots 2018, 42, 1337–1354. [Google Scholar] [CrossRef]
- Luck, K.S.; Amor, H.B.; Calandra, R. Data-efficient co-adaptation of morphology and behaviour with deep reinforcement learning. In Proceedings of the Conference on Robot Learning, Virtual, 16–18 November 2020; Volume 100, pp. 854–869. [Google Scholar] [CrossRef]
- Schaff, C.; Yunis, D.; Chakrabarti, A.; Walter, M.R. Jointly Learning to Construct and Control Agents Using Deep Reinforcement Learning. In Proceedings of the International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 9798–9805. [Google Scholar] [CrossRef]
- Ha, D. Reinforcement learning for improving agent design. Artif. Life 2019, 25, 352–365. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Cheng, R.; Li, Z.; Jin, Y.; Tan, K.C. EvoX: A Distributed GPU-Accelerated Framework for Scalable Evolutionary Computation. IEEE Trans. Evol. Comput. 2024, 1. [Google Scholar] [CrossRef]
- Makoviychuk, V.; Wawrzyniak, L.; Guo, Y.; Lu, M.; Storey, K.; Macklin, M.; Hoeller, D.; Rudin, N.; Allshire, A.; Handa, A.; et al. Isaac Gym: High Performance GPU Based Physics Simulation For Robot Learning. In Proceedings of the 35th Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2), Virtual, 6–14 December 2021. [Google Scholar] [CrossRef]
- Rudin, N.; Hoeller, D.; Reist, P.; Hutter, M. Learning to Walk in Minutes Using Massively Parallel Deep Reinforcement Learning. In Proceedings of the Conference on Robot Learning, Auckland, New Zealand, 14–18 December 2022; pp. 91–100. [Google Scholar] [CrossRef]
- Bradbury, J.; Frostig, R.; Hawkins, P.; Johnson, M.J.; Leary, C.; Maclaurin, D.; Necula, G.; Paszke, A.; VanderPlas, J.; Wanderman-Milne, S.; et al. JAX: Composable Transformations of Python+NumPy Programs. 2018. Available online: http://github.com/jax-ml/jax (accessed on 4 May 2025).
- Shishir, M.I.R.; Tabarraei, A. Multi-Materials Topology Optimization Using Deep Neural Network for Coupled Thermo-Mechanical Problems. Comput. Struct. 2024, 291, 107218. [Google Scholar] [CrossRef]
- Golberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Deb, K. A Comparative Analysis of Selection Schemes Used in Genetic Algorithms. In Foundations of Genetic Algorithms; Elsevier: Amsterdam, The Netherlands, 1991; Volume 1, pp. 69–93. [Google Scholar] [CrossRef]
- Lu, C.; Kuba, J.; Letcher, A.; Metz, L.; Schroeder de Witt, C.; Foerster, J. Discovered policy optimisation. Adv. Neural Inform. Process. Syst. 2022, 35, 16455–16468. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| 150 kg | |
| k | 10 kg |
| 50 N | |
| 260 s | |
| 0.47 kg | |
| 100 m | |
| 1000 m | |
| p | 100 s |
| 50,000 m | |
| R | 6,971,393 m |
| 100 N |
| Parameter | Value |
|---|---|
| Population size | 16 |
| Generations | 50 |
| Tournament groups | 16 |
| Crossover rate | 0.8 |
| Mutation rate | 0.5 |
| Total steps | 800,000 |
| Learning rate | 0.001 |
| Epochs | 10 |
| Batch size | 2048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, W.; Meng, L.; Feng, F.; Guo, P.; Li, B. Inner–Outer Loop Intelligent Morphology Optimization and Pursuit–Evasion Control for Space Modular Robot. Actuators 2025, 14, 234. https://doi.org/10.3390/act14050234
Luo W, Meng L, Feng F, Guo P, Li B. Inner–Outer Loop Intelligent Morphology Optimization and Pursuit–Evasion Control for Space Modular Robot. Actuators. 2025; 14(5):234. https://doi.org/10.3390/act14050234
Chicago/Turabian StyleLuo, Wenwei, Ling Meng, Fei Feng, Pengyu Guo, and Bo Li. 2025. "Inner–Outer Loop Intelligent Morphology Optimization and Pursuit–Evasion Control for Space Modular Robot" Actuators 14, no. 5: 234. https://doi.org/10.3390/act14050234
APA StyleLuo, W., Meng, L., Feng, F., Guo, P., & Li, B. (2025). Inner–Outer Loop Intelligent Morphology Optimization and Pursuit–Evasion Control for Space Modular Robot. Actuators, 14(5), 234. https://doi.org/10.3390/act14050234






