Fast Dynamic P-RRT*-Based UAV Path Planning and Trajectory Tracking Control Under Dense Obstacles
Abstract
1. Introduction
- (1)
- A fast bidirectional dynamic informed P-RRT* (BDIP-RRT*) algorithm is first developed for UAV in dense obstacle environments. Superior to the P-RRT* algorithm [14], the bidirectional dynamic informed structure is optimized in terms of sampling probability, sampling range, target bias, and a multi-tree structure to improve the quality and speed of initial path generation.
- (2)
- A hybrid optimized trajectory generator is proposed that significantly improves trajectory smoothness and efficiency by optimizing jerk and snap compared with the spline-based method in [30]. More specifically, an adaptive distance interpolation strategy is introduced to generate trajectory control points, further balancing control performance and trajectory deviation.
- (3)
- Two prescribed-time control laws are designed to ensure fast and accurate UAV position and attitude control. A segmented function is introduced in the prescribed-time control laws to suppress the growth of the scale function and solve the singularity-like problem [39].
2. Preliminaries and Problem Statement
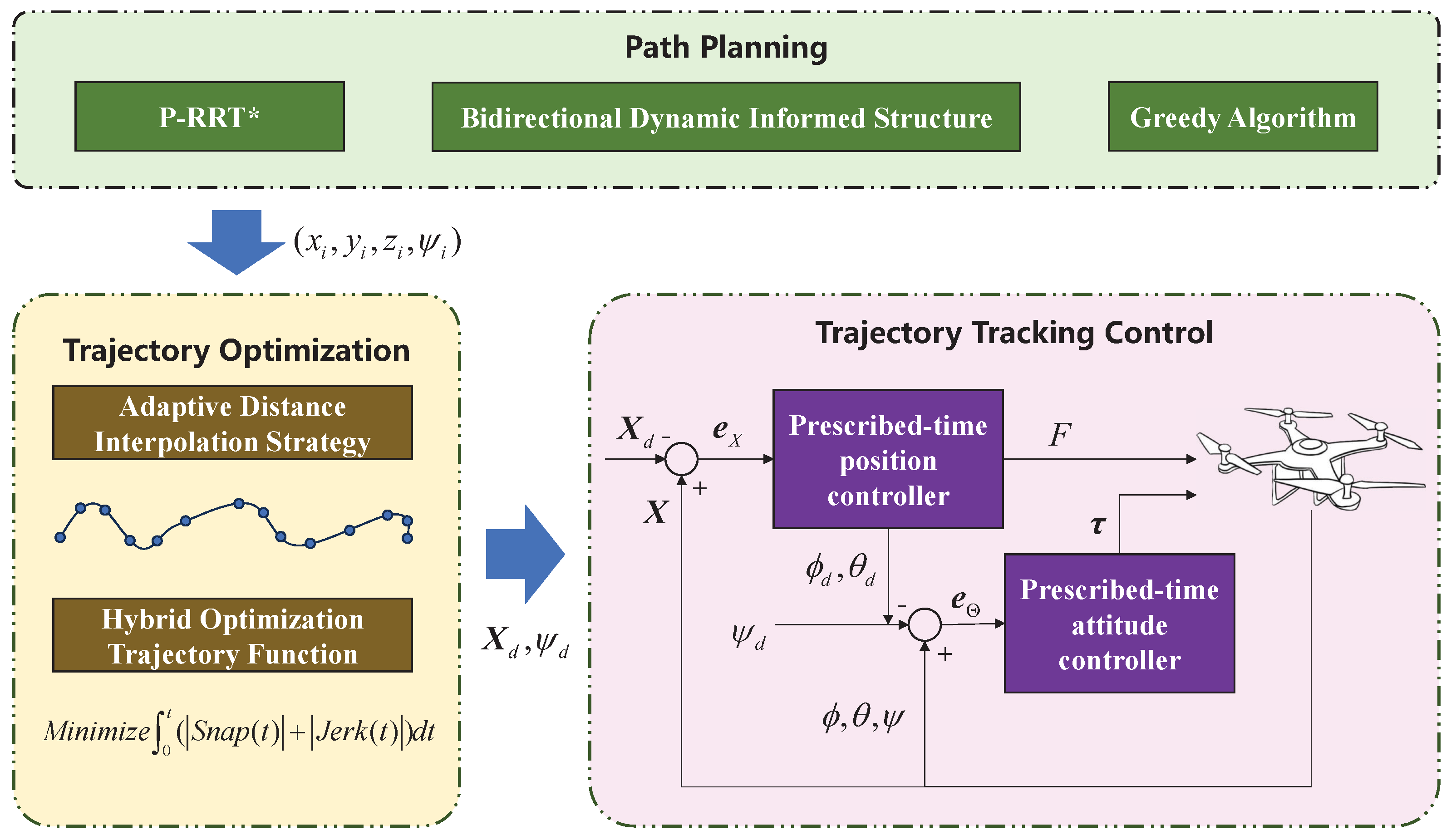
3. Integrated Planning and Control Framework and Algorithm
3.1. Advanced Path Planning
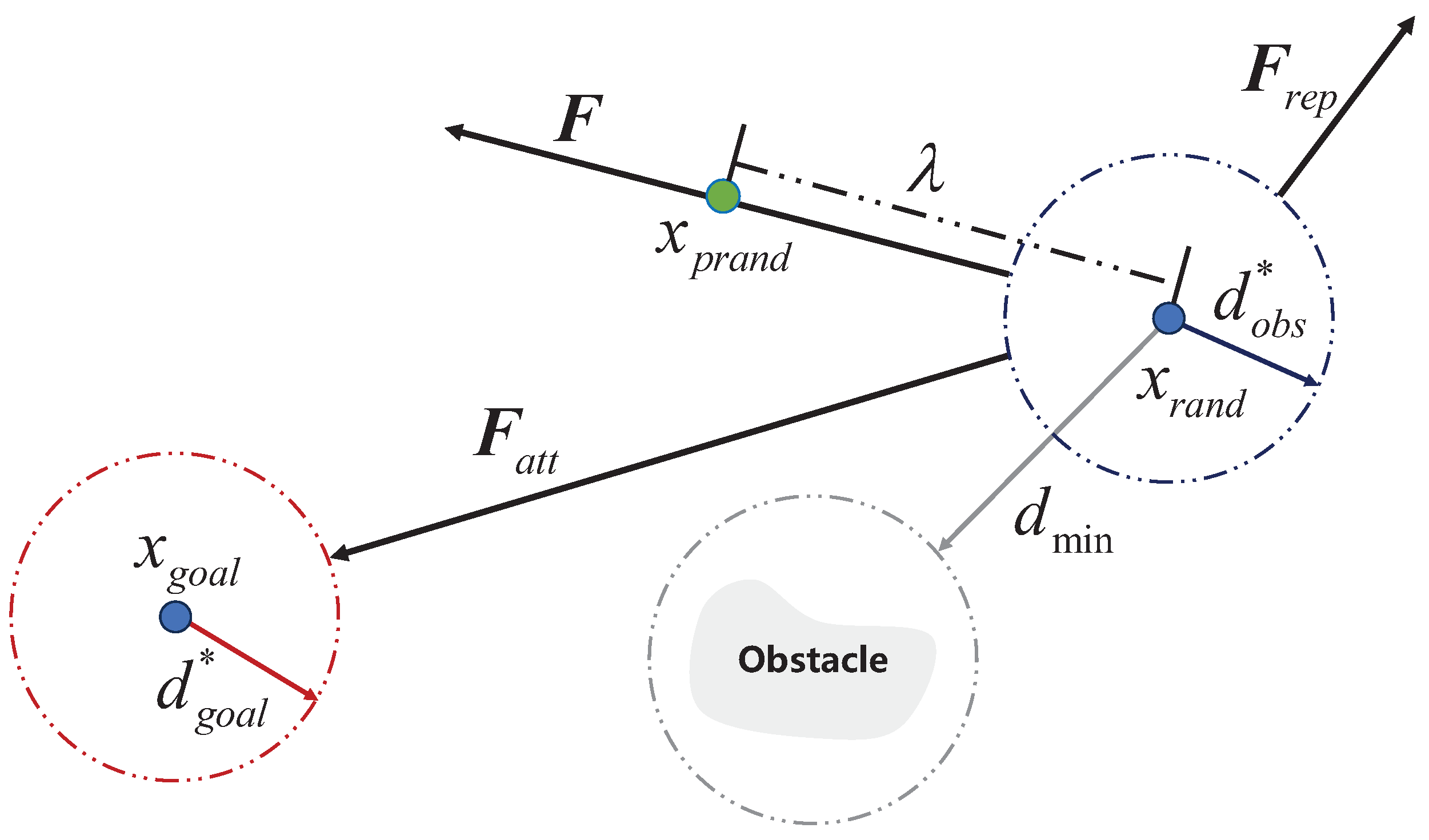
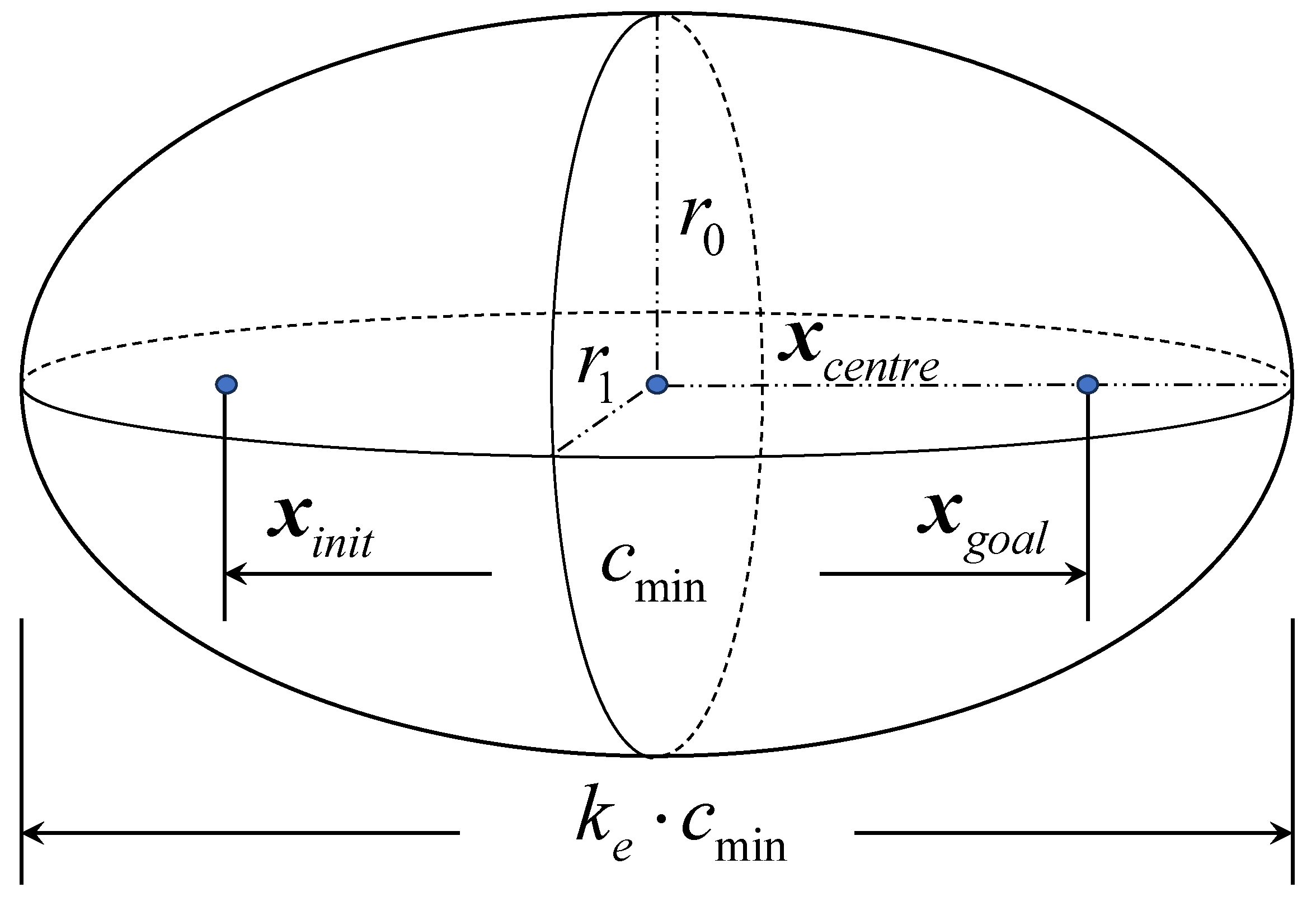
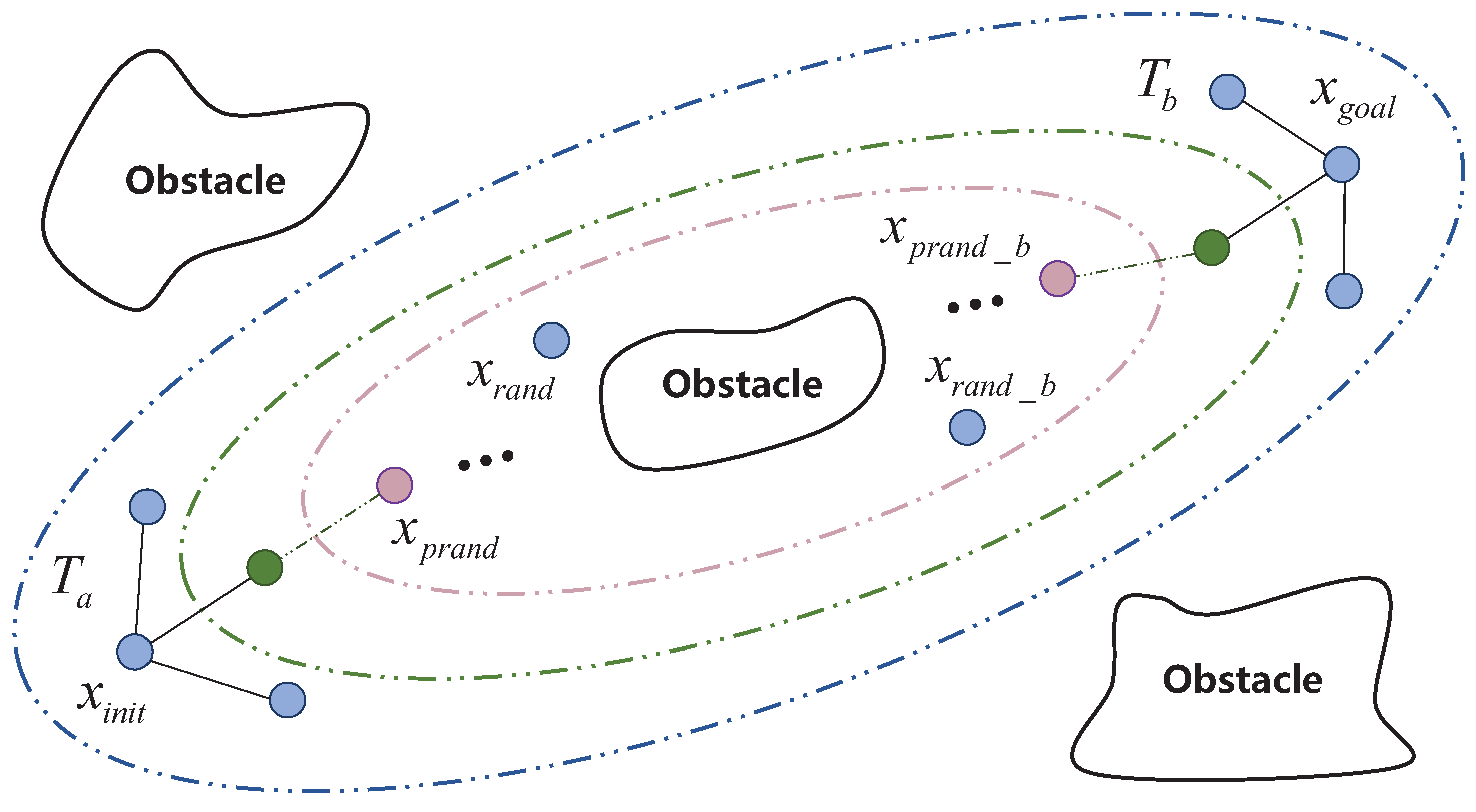
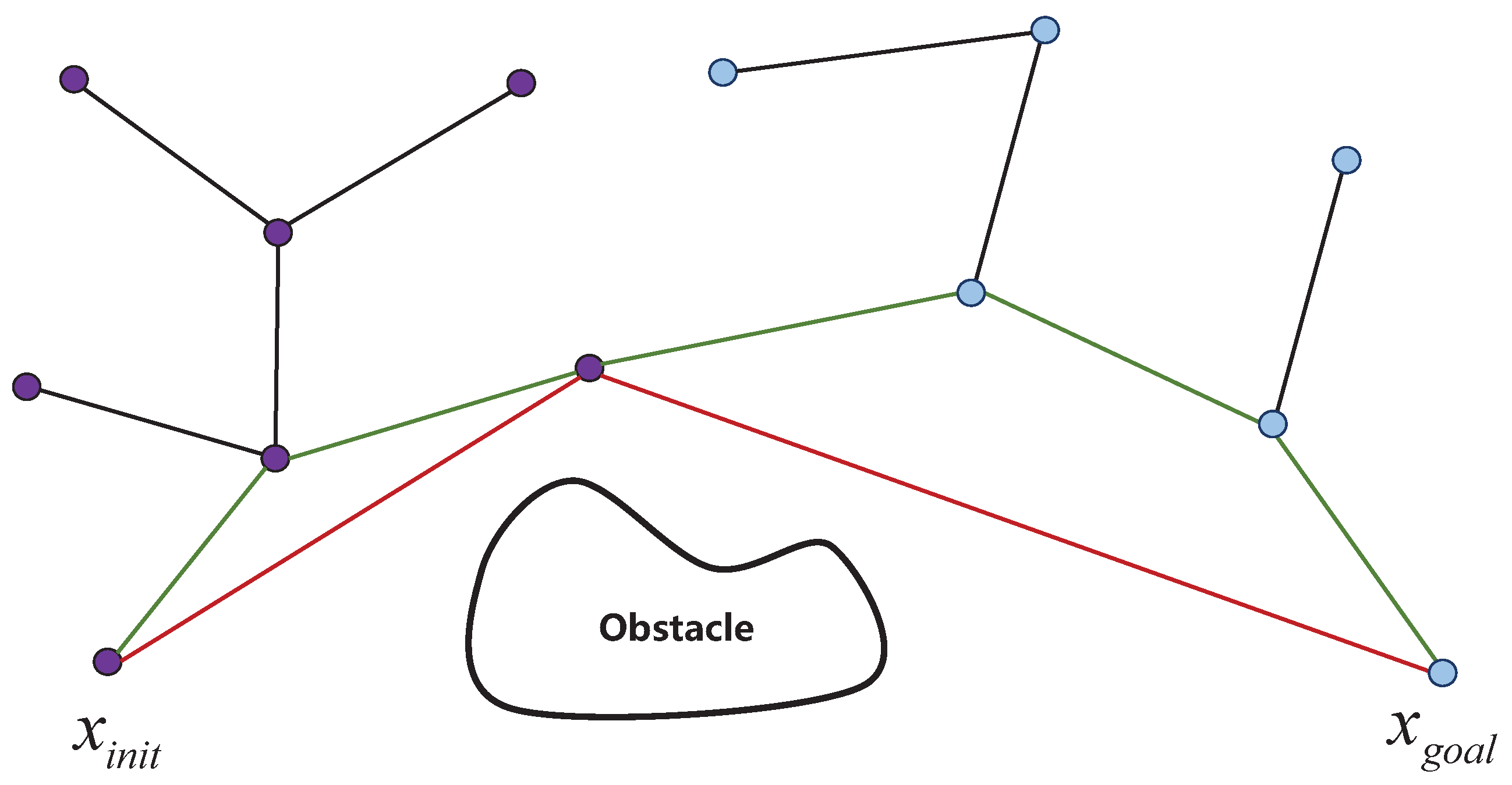
3.1.1. P-RRT* and Bidirectional Dynamic Informed Structure
3.1.2. BDIP-RRT* with Greedy Algorithm
| Algorithm 1 BDIP-RRT* with greedy (, ) |
|
3.2. Comprehensive Trajectory Optimization
3.2.1. Adaptive Distance Interpolation Strategy
3.2.2. Hybrid Optimization Trajectory Function
3.3. Prescribed-Time Trajectory Tracking Control
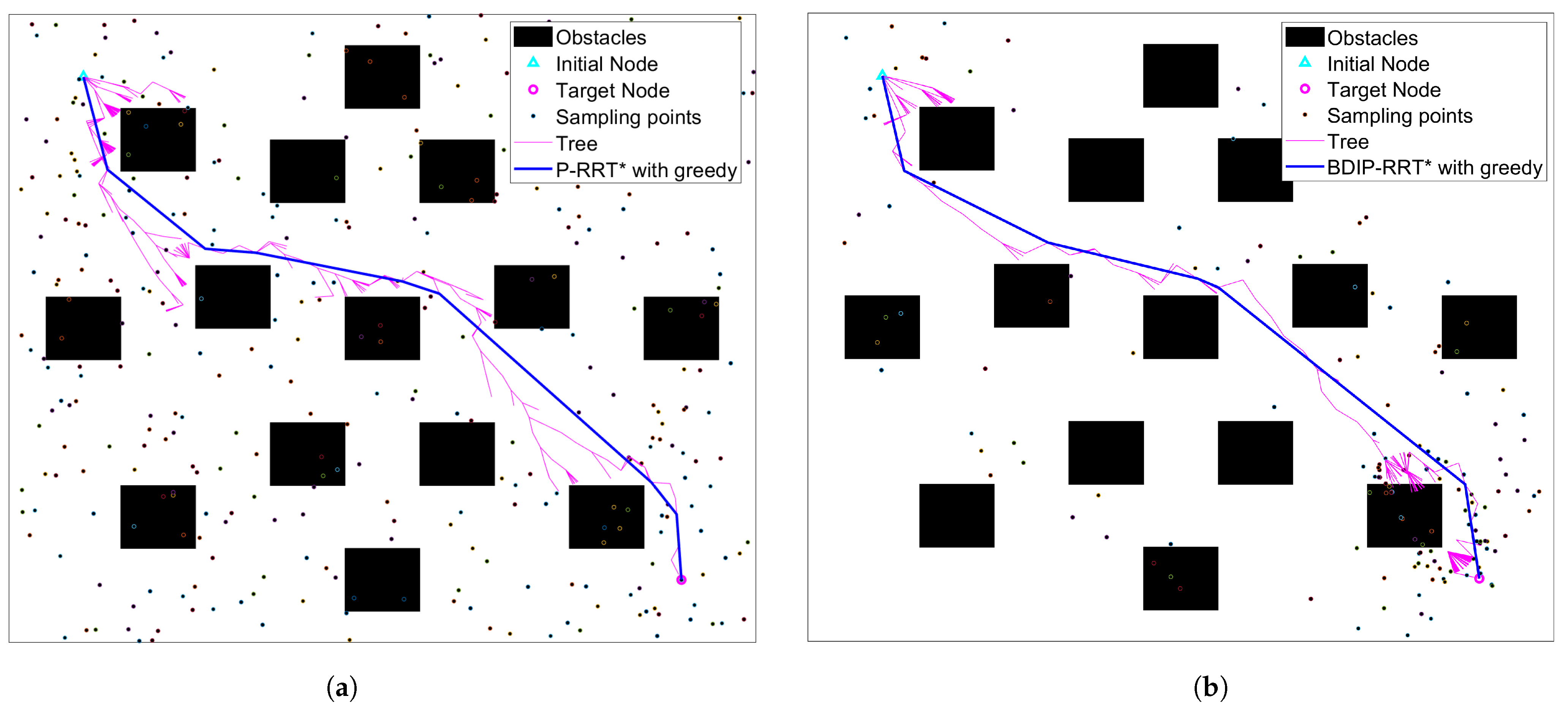
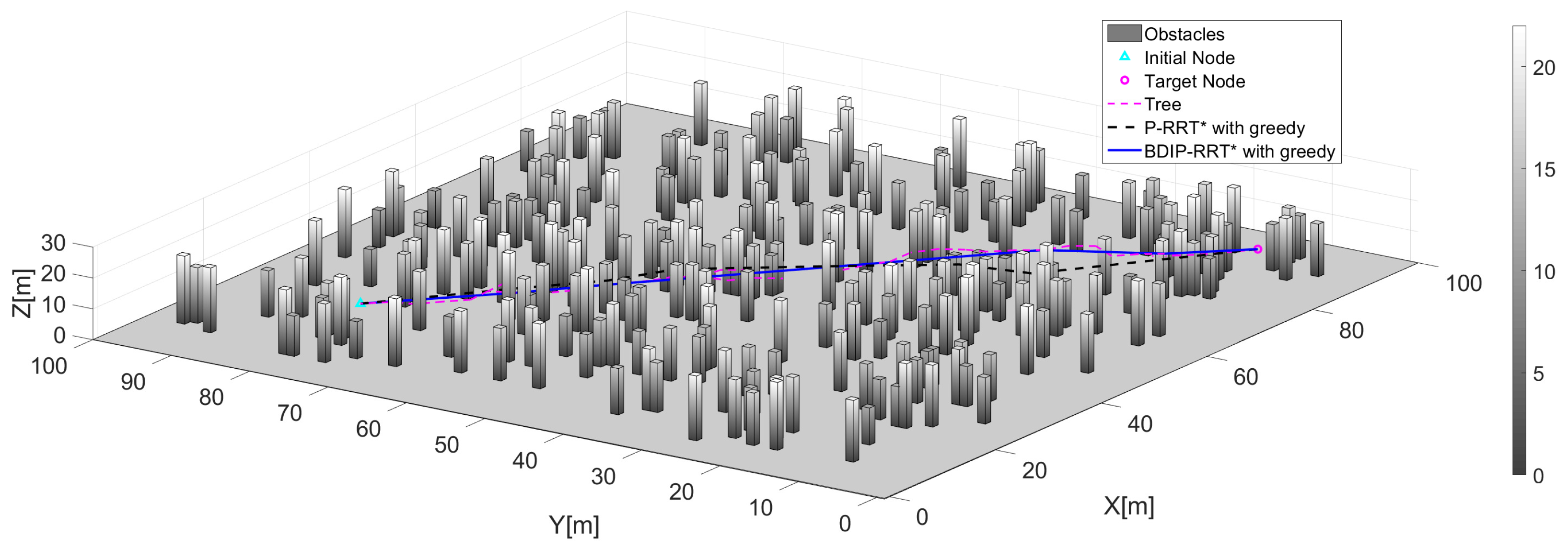
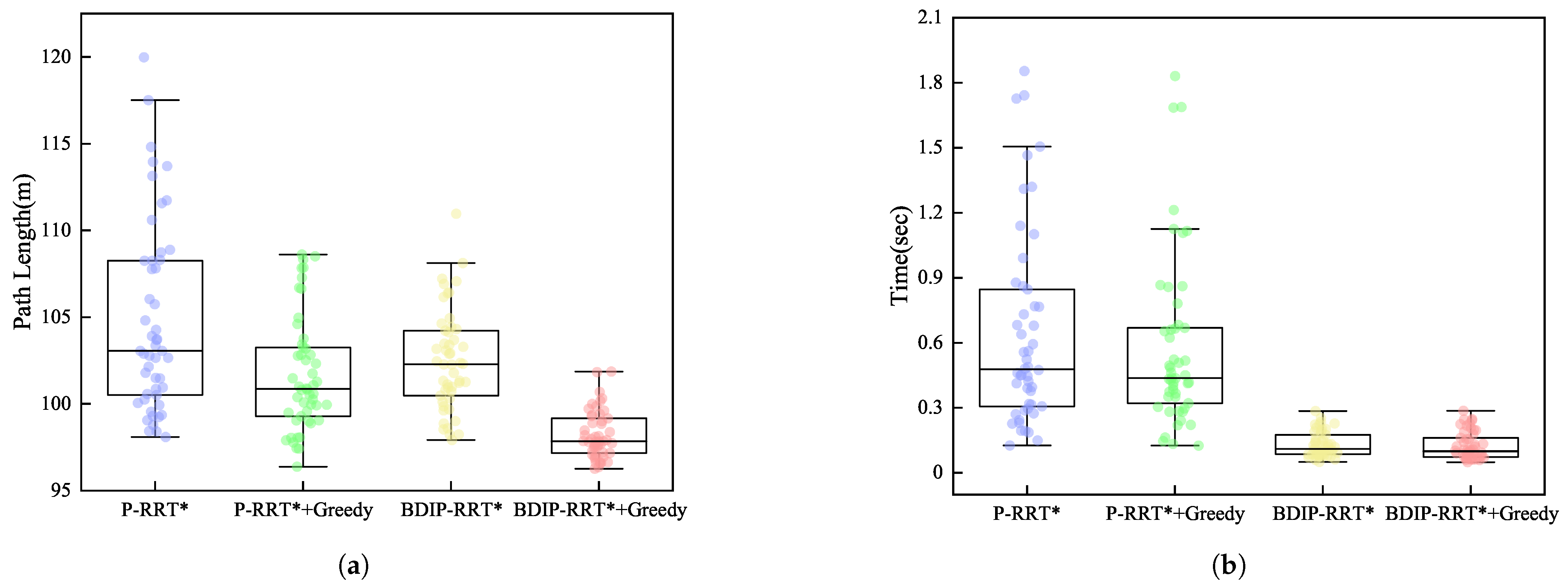
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| P-RRT* | Potential function-based Rapid-exploration Random Tree star |
| BDIP-RRT* | Bidirectional Dynamic Informed P-RRT* |
References
- Han, T.; Hu, Q.; Shin, H.-S.; Tsourdos, A.; Xin, M. Incremental twisting fault tolerant control for hypersonic vehicles with partial model knowledge. IEEE Trans. Ind. Inform. 2022, 18, 1050–1060. [Google Scholar] [CrossRef]
- Raja, A.; Njilla, L.; Yuan, J. Adversarial attacks and defenses toward AI-assisted UAV infrastructure inspection. IEEE Internet Things J. 2022, 9, 23379–23389. [Google Scholar] [CrossRef]
- Qadir, Z.; Ullah, F.; Munawar, H.S.; Al-Turjman, F. Addressing disasters in smart cities through UAVs path planning and 5G communications: A systematic review. Comput. Commun. 2021, 168, 114–135. [Google Scholar] [CrossRef]
- Badue, C.; Guidolini, R.; Carneiro, R.V.; Azevedo, P.; Cardoso, V.B.; Forechi, A.; Jesus, L.; Berriel, R.; Paixão, T.M.; Mutz, F.; et al. Self-driving cars: A survey. Expert Syst. Appl. 2021, 165, 113816. [Google Scholar] [CrossRef]
- Yao, J.; Hu, Q.; Zheng, J. Nonlinear optimal attitude control of spacecraft using novel state-dependent coefficient parameterizations. Aerosp. Sci. Technol. 2021, 112, 106586. [Google Scholar] [CrossRef]
- Xu, D.; Yang, J.; Zhou, X.; Xu, H. Hybrid path planning method for USV using bidirectional A* and improved DWA considering the manoeuvrability and COLREGs. Ocean Eng. 2024, 298, 117210. [Google Scholar] [CrossRef]
- Ganesan, S.; Ramalingam, B.; Mohan, R.E. A hybrid sampling-based RRT* path planning algorithm for autonomous mobile robot navigation. Expert Syst. Appl. 2024, 258, 125206. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhong, M.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Chang, J.; Dong, N.; Li, D.; Ip, W.H.; Yung, K.L. Skeleton extraction and greedy-algorithm-based path planning and its application in UAV trajectory tracking. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4953–4964. [Google Scholar] [CrossRef]
- Ma, G.; Duan, Y.; Li, M.; Xie, Z.; Zhu, J. A probability smoothing Bi-RRT path planning algorithm for indoor robot. Future Gener. Comput. Syst. 2023, 143, 349–360. [Google Scholar] [CrossRef]
- Cheng, X.; Zhou, J.; Zhou, Z.; Zhao, X.; Gao, J.; Qiao, T. An improved RRT-connect path planning algorithm of robotic arm for automatic sampling of exhaust emission detection in Industry 4.0. J. Ind. Inf. Integr. 2023, 33, 100436. [Google Scholar] [CrossRef]
- Karaman, S.; Walter, M.R.; Perez, A.; Frazzoli, E.; Teller, S. Anytime motion planning using the RRT*. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1478–1483. [Google Scholar]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Qureshi, A.H.; Ayaz, Y. Potential functions based sampling heuristic for optimal path planning. Auton. Robot. 2015, 40, 1079–1093. [Google Scholar] [CrossRef]
- Jeong, I.-B.; Lee, S.-J.; Kim, J.-H. Quick-RRT*: Triangular inequality-based implementation of RRT* with improved initial solution and convergence rate. Expert Syst. Appl. 2019, 123, 82–90. [Google Scholar] [CrossRef]
- Wang, J.; Li, T.; Li, B.; Meng, M.Q.-H. GMR-RRT*: Sampling-based path planning using Gaussian mixture regression. IEEE Trans. Intell. Veh. 2022, 7, 690–700. [Google Scholar] [CrossRef]
- Tahir, Z.; Qureshi, A.H.; Ayaz, Y.; Nawaz, R. Potentially guided bidirectionalized RRT* for fast optimal path planning in cluttered environments. Robot. Auton. Syst. 2018, 108, 13–27. [Google Scholar] [CrossRef]
- Li, Y.; Wei, W.; Gao, Y.; Wang, D.; Fan, Z. PQ-RRT*: An improved path planning algorithm for mobile robots. Expert Syst. Appl. 2020, 152, 113425. [Google Scholar] [CrossRef]
- Wang, X.; Wei, J.; Zhou, X.; Xia, Z.; Gu, X. AEB-RRT*: An adaptive extension bidirectional RRT* algorithm. Auton. Robot. 2022, 46, 685–704. [Google Scholar] [CrossRef]
- Tang, L.; Wang, H.; Li, P.; Wang, Y. Real-time trajectory generation for quadrotors using B-spline based non-uniform kinodynamic search. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 1133–1138. [Google Scholar]
- Richter, C.; Bry, A.; Roy, N. Polynomial trajectory planning for aggressive quadrotor flight in dense indoor environments. In Robotics Research, Proceedings of the 16th International Symposium ISRR, Singapore, 16–19 December 2013; Inaba, M., Corke, P., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 649–666. [Google Scholar]
- Gao, F.; Shen, S. Online quadrotor trajectory generation and autonomous navigation on point clouds. In Proceedings of the 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 23–27 October 2016; pp. 139–146. [Google Scholar]
- Chen, T.; Cai, Y.; Chen, L.; Xu, X. Trajectory and velocity planning method of emergency rescue vehicle based on segmented three-dimensional quartic bezier curve. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3461–3475. [Google Scholar] [CrossRef]
- Zhou, B.; Gao, F.; Wang, L.; Liu, C.; Shen, S. Robust and efficient quadrotor trajectory generation for fast autonomous flight. IEEE Robot. Autom. Lett. 2019, 4, 3529–3536. [Google Scholar] [CrossRef]
- Chai, R.; Savvaris, A.; Tsourdos, A.; Chai, S.; Xia, Y. A review of optimization techniques in spacecraft flight trajectory design. Prog. Aerosp. Sci. 2019, 109, 100543. [Google Scholar] [CrossRef]
- Tordesillas, J.; Lopez, B.T.; Everett, M.; How, J.P. FASTER: Fast and safe trajectory planner for navigation in unknown environments. IEEE Trans. Robot. 2022, 38, 922–938. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]
- Brown, A.; Anderson, D. Trajectory optimization for high-altitude long-endurance UAV maritime radar surveillance. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2406–2421. [Google Scholar] [CrossRef]
- Hu, Q.; Xie, J.; Wang, C. Dynamic path planning and trajectory tracking using MPC for satellite with collision avoidance. ISA Trans. 2019, 84, 128–141. [Google Scholar] [CrossRef] [PubMed]
- Woo, J.W.; An, J.-Y.; Cho, M.G.; Kim, C.-J. Integration of path planning, trajectory generation and trajectory tracking control for aircraft mission autonomy. Aerosp. Sci. Technol. 2021, 118, 107014. [Google Scholar] [CrossRef]
- Efe, M.O. Neural network assisted computationally simple PIλDμ control of a quadrotor UAV. IEEE Trans. Ind. Inform. 2011, 7, 354–361. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Zhang, X.; Sun, Q.; Sun, M. A novel control scheme for quadrotor UAV based upon active disturbance rejection control. Aerosp. Sci. Technol. 2018, 79, 601–609. [Google Scholar] [CrossRef]
- Lungu, M. Backstepping and dynamic inversion combined controller for auto-landing of fixed wing UAVs. Aerosp. Sci. Technol. 2020, 96, 105526. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.; Yang, Y.; Xiao, B.; Ran, D. Appointed fixed time observer-based sliding mode control for a quadrotor UAV under external disturbances. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 290–303. [Google Scholar] [CrossRef]
- Xu, L.-X.; Ma, H.-J.; Guo, D.; Xie, A.-H.; Song, D.-L. Backstepping sliding-mode and cascade active disturbance rejection control for a quadrotor UAV. IEEE-ASME Trans. Mechatron. 2020, 25, 2743–2753. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.; Yang, Y.; Xiao, B. Distributed fixed-time leader-following formation control for multiquadrotors with prescribed performance and collision avoidance. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7281–7294. [Google Scholar]
- Li, B.; Liu, H.; Ahn, C.K.; Wang, C.; Zhu, X. Fixed-time tracking control of wheel mobile robot in slipping and skidding conditions. IEEE/ASME Trans. Mechatron. 2024; early access. [Google Scholar]
- Gong, W.; Li, B.; Ahn, C.K.; Yang, Y. Prescribed-time extended state observer and prescribed performance control of quadrotor UAVs against actuator faults. Aerosp. Sci. Technol. 2023, 138, 108322. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Holloway, J.; Krstic, M. Time-varying feedback for regulation of normal-form nonlinear systems in prescribed finite time. Automatica 2017, 83, 243–251. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. A new disturbance attenuation control scheme for quadrotor unmanned aerial vehicles. IEEE Trans. Ind. Inform. 2017, 13, 2922–2932. [Google Scholar] [CrossRef]
- Jordan, M.; Perez, A. Optimal Bidirectional Rapidly-Exploring Random Trees; Technical Report MIT-CSAIL-TR-2013-021; Massachusetts Institute of Technology: Cambridge, MA, USA, 2013. [Google Scholar]
- Tal, E.; Karaman, S. Global incremental flight control for agile maneuvering of a tailsitter flying wing. J. Guid. Control Dyn. 2022, 45, 2332–2349. [Google Scholar] [CrossRef]
- Tal, E.; Karaman, S. Accurate tracking of aggressive quadrotor trajectories using incremental nonlinear dynamic inversion and differential flatness. IEEE Trans. Control Syst. Technol. 2021, 29, 1203–1218. [Google Scholar] [CrossRef]
- Li, B.; Liu, H.; Ahn, C.K.; Gong, W. Optimized intelligent tracking control for a quadrotor unmanned aerial vehicle with actuator failures. Aerosp. Sci. Technol. 2024, 144, 108833. [Google Scholar] [CrossRef]
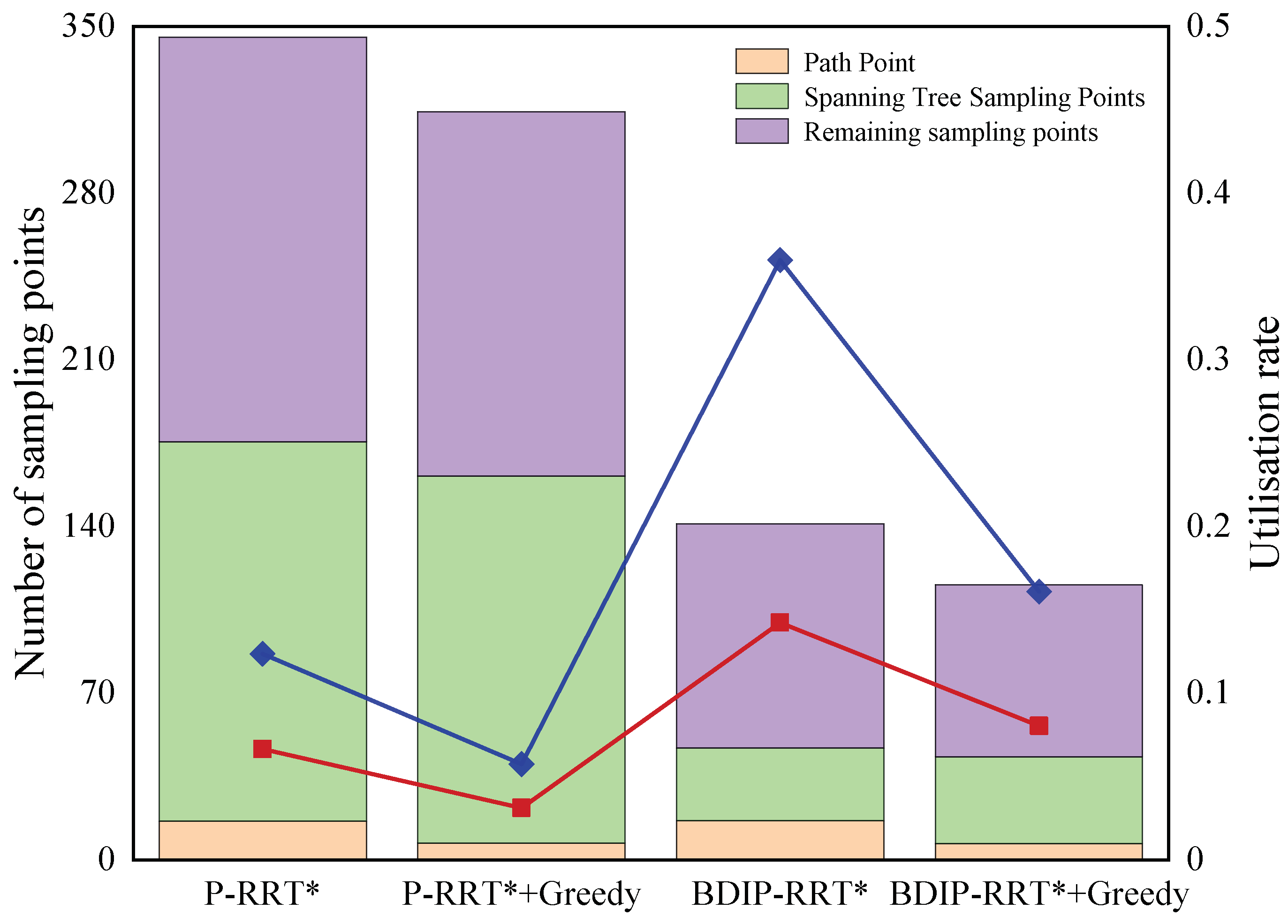
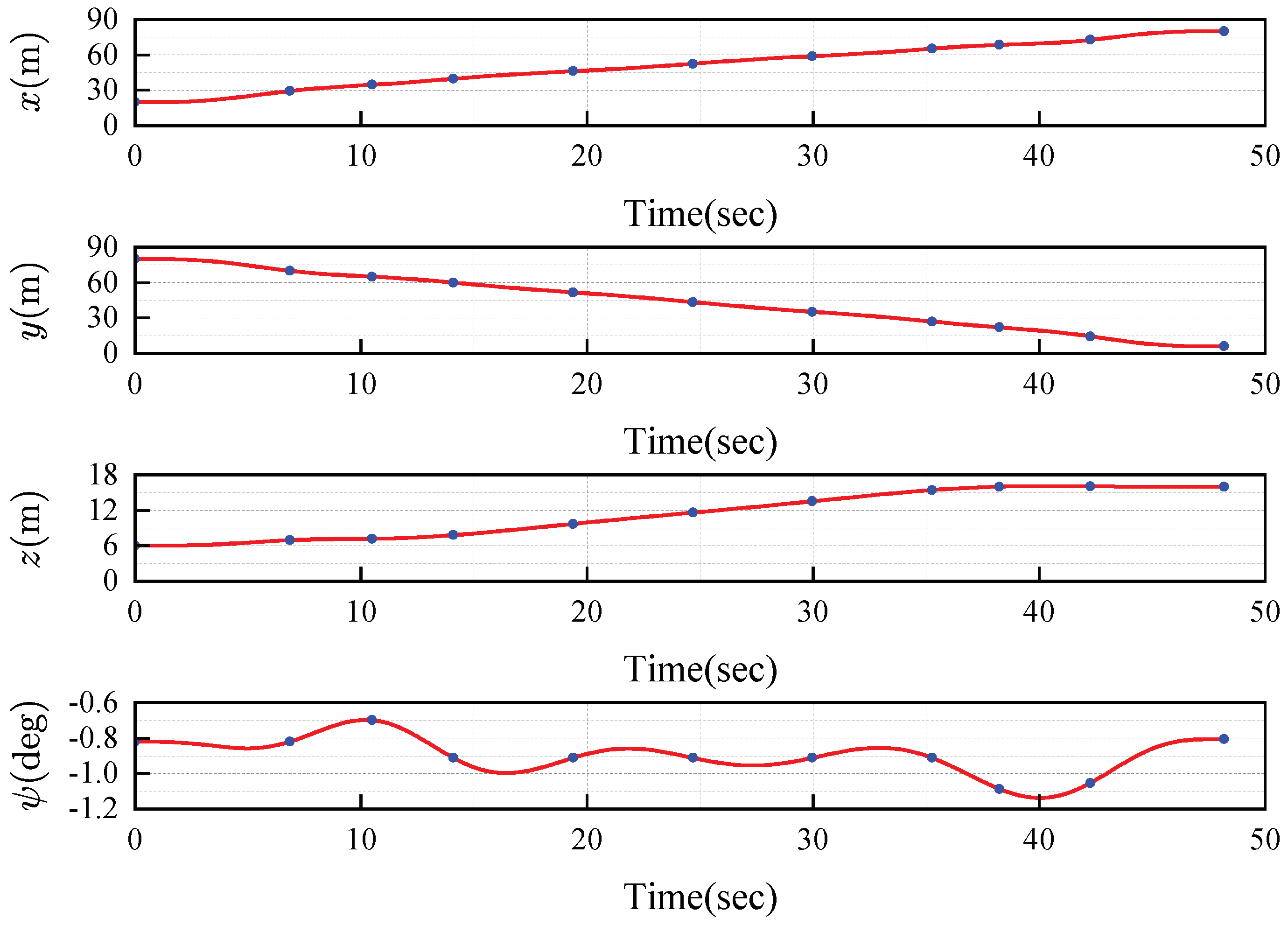
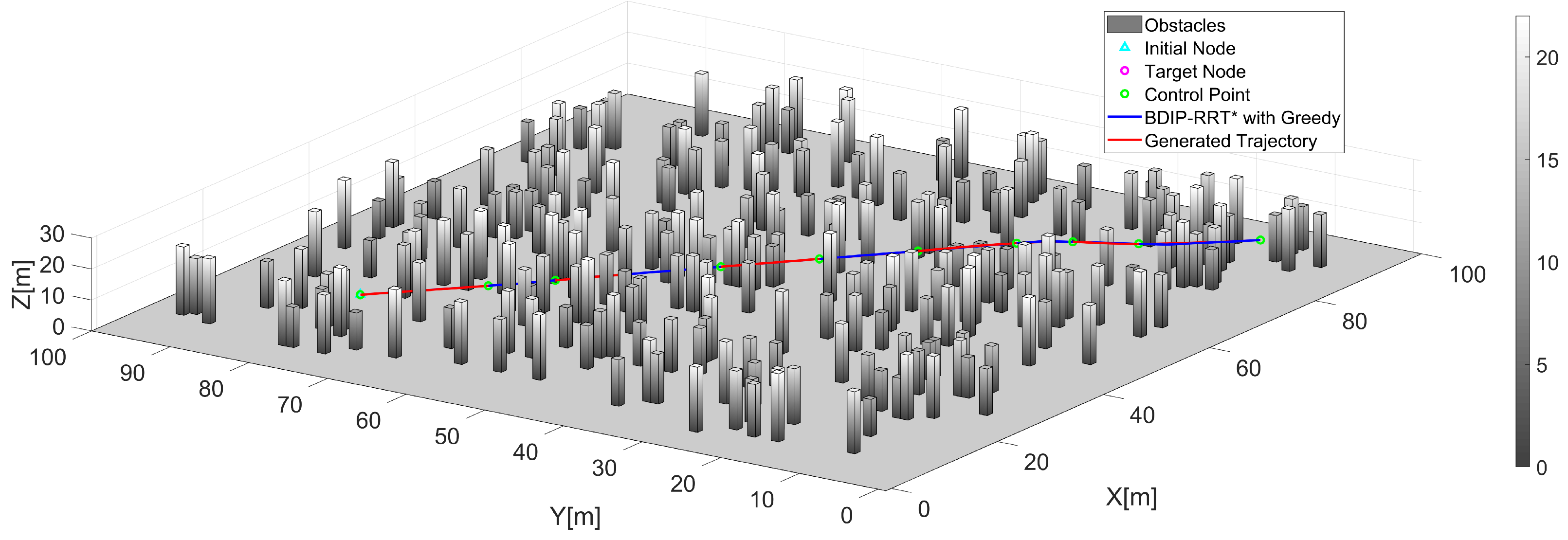

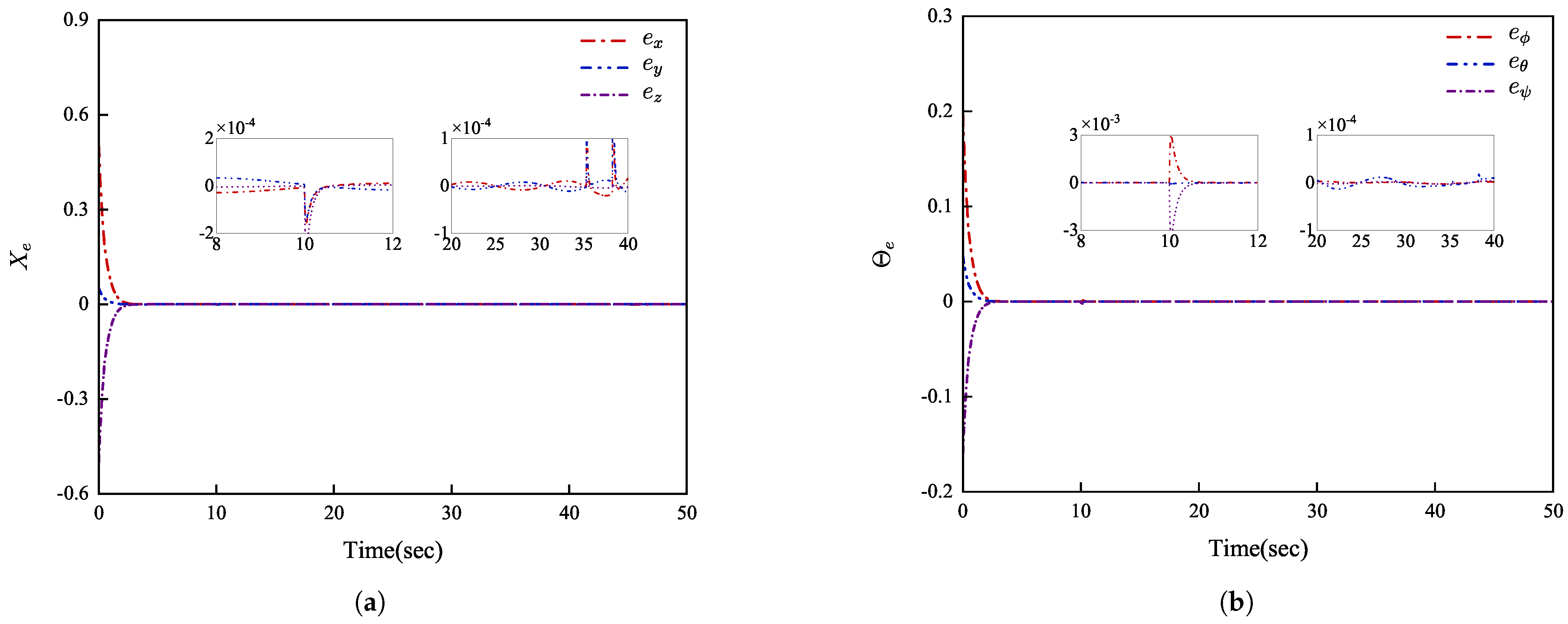
| Algorithms | Length (m) | Time (s) |
|---|---|---|
| P-RRT* | 25.385 | 0.925 |
| P-RRT* with greedy | 24.773 | 0.631 |
| BDIP-RRT* | 24.943 | 0.410 |
| BDIP-RRT* with greedy | 24.588 | 0.308 |
| Algorithms | Length (m) | Time (s) |
|---|---|---|
| P-RRT* with greedy | 99.296 | 0.133 |
| BDIP-RRT* with greedy | 96.596 | 0.049 |
| Algorithm | Metrics | Length (m) | Time (s) |
|---|---|---|---|
| P-RRT* with greedy | Mean | 101.696 | 0.575 |
| Standard deviation | 3.256 | 0.393 | |
| BDIP-RRT* with greedy | Mean | 98.202 | 0.124 |
| Standard deviation | 1.370 | 0.063 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Gao, Y.; Li, Y.; Li, B. Fast Dynamic P-RRT*-Based UAV Path Planning and Trajectory Tracking Control Under Dense Obstacles. Actuators 2025, 14, 211. https://doi.org/10.3390/act14050211
Zhu X, Gao Y, Li Y, Li B. Fast Dynamic P-RRT*-Based UAV Path Planning and Trajectory Tracking Control Under Dense Obstacles. Actuators. 2025; 14(5):211. https://doi.org/10.3390/act14050211
Chicago/Turabian StyleZhu, Xiangyu, Yufeng Gao, Yanyan Li, and Bo Li. 2025. "Fast Dynamic P-RRT*-Based UAV Path Planning and Trajectory Tracking Control Under Dense Obstacles" Actuators 14, no. 5: 211. https://doi.org/10.3390/act14050211
APA StyleZhu, X., Gao, Y., Li, Y., & Li, B. (2025). Fast Dynamic P-RRT*-Based UAV Path Planning and Trajectory Tracking Control Under Dense Obstacles. Actuators, 14(5), 211. https://doi.org/10.3390/act14050211






