Abstract
Piezoelectric (PE) micropumps are distinguished by their high precision, absence of electromagnetic radiation, and straightforward construction principles, making them vital in biomedicine and drug delivery. Integrating PE micropumps with microneedles creates a stable, accurate transdermal drug delivery device capable of finely tuning dosage, rate, and targeting. This paper proposes such a device, combining a PE micropump with a microneedle array. Initially, the internal flow dynamics of the PE micropump and the microneedle forces were analyzed through simulations. Subsequently, the optimal size for the PE micropump was established via parameter optimization experiments. Comprehensive tests were conducted to assess the device’s output performance, including frequency response, voltage characteristics, and flow resistance properties. Key performance indicators evaluated were output flow, pressure, and resolution. Experimental findings revealed that with a constant driving voltage, the PE micropump’s output flow and pressure initially increase and then decrease as the operating frequency rises. Conversely, with a fixed operating frequency, output flow and pressure positively correlate with the driving voltage, showing a near-linear relationship. Under stable working conditions, output pressure and flow are inversely proportional. The PE micropump achieves an output flow of 4.0 mL/min and a pressure of 35.7 kPa at 70 V and 80 Hz. The output flow rate and pressure of the device with the integrated microneedle array are 3.5 mL/min and 30 kPa, the minimum flow resolution is 0.28 μL, exemplifying the potential applications of PE micropumps and microneedles in the field of biomedicine.
1. Introduction
The rapid evolution of microfluidic technology, characterized by its multifunctionality, has been significantly propelled by advancements in microelectromechanical systems (MEMS) technology [1]. This progression has led to the development and continual refinement of various microfluidic devices, including micropumps [2,3,4], microvalves [5], micromixers [6,7,8], and microfluid flow sensors [9,10].
PE micropumps are a specialized type of micropump renowned for their high precision, absence of electromagnetic radiation, and uncomplicated construction principles [11,12,13,14]. These pumps are increasingly utilized in the fabrication of compact mobile devices, medical instruments, biomedicine, and other advanced technological applications. Particularly in the realm of biomedical and drug delivery systems, PE micropumps are indispensable [15,16,17,18]. Micro-administration facilitated by these pumps is pivotal for timely treatment, maintaining consistent drug levels in the body, and minimizing drug toxicity.
Furthermore, MEMS technology advancements have spurred the development of microneedle technology, essential for transdermal drug delivery [19,20]. Microneedles inflict minimal damage to living tissues, present lower infection risks, and reduce patient discomfort during treatments [21]. As such, they are perfectly suited for integration with PE micropumps, which link the storage device to the patient. This integration enables precise control over the dosage, rate, and targeting of drug infusions.
Recent research has centered on developing precise infusion systems by integrating microneedles with PE micropumps. Rao et al. [22] explored such integration by creating a micropump with an electrode, PE vibrator, PDMS film, and channels, with the whole device fixed on a glass base, achieving a flow rate of 4.67 mL/min at 10 V and 300 Hz. García et al. [23] devised an innovative transdermal drug delivery device incorporating PE micropumps and microneedle arrays, capable of delivering a volume flow rate of 2.92 × 10−5 cm3/s at 6.6 Hz, which required only 116 Pa for supply and 2560 Pa for pumping. The microneedle array enables penetration of the skin, delivering the fluid to the desired destination and minimizing pain during insertion. Haldkar et al. [24] presented an innovative design for a PE actuator. This design improves the deflection capabilities of the strip PE actuator and incorporates microneedles, resulting in enhanced performance of the micropump, making it well-suited for drug delivery applications. Karumuri et al. [25] described a MEMS technology-based drug delivery device capable of efficient microliter-scale drug administration. They analyzed the mechanical strength and flow characteristics of microneedles, demonstrating their appropriateness for use in micropump drug delivery systems. The proposed square-tip and round-tip microneedles can withstand stresses of 23 MPa and 20 kPa, respectively. Additionally, they examined microneedle materials to ensure biocompatibility and strength. Rizvi et al. [26] developed a PE insulin micropump using MEMS microneedles, designed for pumping viscous Newtonian fluids. Their research included the design and simulation of PE insulin micropumps based on MEMS, including microvalves and microneedle arrays. The micropump’s performance under human skin pressure was evaluated to align with the operational parameter range for diabetic patients.
The research report indicates that the market for precision infusion equipment is valued at several hundred billion dollars, with a robust annual growth rate. Consequently, the demand for high-performance devices is continuously escalating. This paper presents the design of a precision infusion PE micropump integrated with a microneedle array. This device achieves high output pressure, substantial flow rate, and fine flow resolution, all within a compact structure. The PE micropump and microneedle systems were rigorously analyzed through theoretical, simulation, and experimental approaches. The design’s practicality was substantiated, and the prototype’s output performance was meticulously evaluated.
2. Methods
2.1. Overall Design
Figure 1a displays the PE micropump prototype integrated with a microneedle array, as conceptualized in this paper. The prototype comprises a PE vibrator, a wheel valve, a cantilever valve, a valve plate, a pump body, and a 17 × 17 microneedle array. The valve is composed of Polyethylene Terephthalate (PET, KarDon, Baoding, China), which is laser cut, while the pump body is fabricated from Polymethylmethacrylate (PMMA, XinWang, Bianzhou, China), the sculpting of which is performed by a Computerized Numerical Control machine (CNC, Beijing JingDiao, Beijing, China). The microneedles are fabricated from high-temperature resin using the Additive Manufacturing process (BMF, Shenzhen, China). The assembly of these components is facilitated by the utilization of a two-component epoxy resin adhesive.
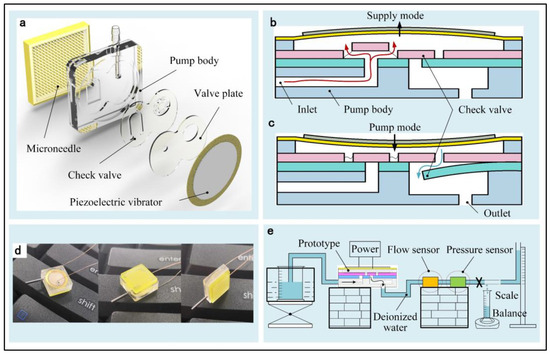
Figure 1.
(a) Precision transdermal drug delivery device featuring integrated microneedles and PE micropump. (b) Supply mode (Red arrow indicates fluid being pumped into chamber). (c) Pump mode (Blue arrow indicates fluid being pushed out of chamber). (d) Prototype photo. (e) Experimental test platform (The arrow indicates the fluid path, while the X mark denotes the shutoff clip).
Figure 1b,c delineates the operational mechanism of the PE micropump. Applying an AC signal to the PE vibrator induces radial stretching and contraction, generating internal tension and compression stresses, leading to bending deformation. The resultant upward bending of the PE vibrator increases the pump chamber’s volume, decreasing pressure and opening the inlet valve, allowing fluid to ingress into the pump chamber. Conversely, downward bending reduces the chamber volume, elevating the pressure, which closes the inlet valve and opens the outlet valve, expelling the chamber’s liquid. This cyclical process facilitates a continuous directional fluid flow.
The prototype, depicted in Figure 1d, measures 11 × 11 × 3.8 mm3. Notably, the PE vibrator dimensions are Ø10 × Ø8 mm2, and both the copper substrate and PE ceramics have a thickness of 0.1 mm. Table 1 details the performance parameters of the PE ceramics.

Table 1.
Performance parameters of PE ceramics.
2.2. Numerical Simulation
The PE micropump underwent numerical simulation using COMSOL Multiphysics 6.2. For this, the fluid-structure interaction within the MEMS module was leveraged, with a global equation tracking the cumulative flow across the inlet and outlet. The simulation integrated the PE material with fluid–solid coupling, employing a velocity-dependent formulation to replicate the valve’s dynamics at the inlet and outlet boundaries. Owing to physical symmetry, only half of the geometry was necessary for the model’s analysis, as illustrated in Figure 2a. In this model, the valve’s function is represented through a boundary condition that is predicated on K-factor pipe losses, where the loss is substantial for reverse flow and minimal for forward flow. The back pressure produced by the valve is described by the equation
where uav signifies the fluid’s velocity perpendicular to the boundary, and ρ represents the fluid’s density. At is a dimensionless constant, varying with the sign of uav. The constant for the outlet boundary is the inverse of that at the inlet, indicating the valve’s opening and closing directions.
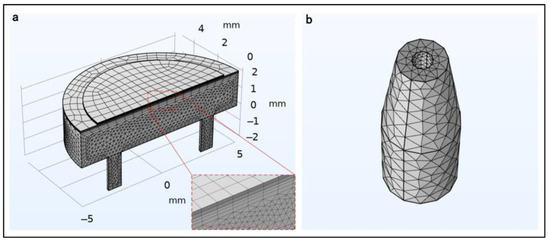
Figure 2.
(a) Depicts the geometric modeling and meshing of the PE micropump. (b) Illustrates the microneedles.
For efficiency, a relatively coarse grid was utilized. A scanning grid was established for the solid domain, a boundary layer grid for the fluid domain, and a matching pair of boundaries was created at the solid–fluid interface. The terminal voltage of the PE vibrator is expressed as
An average operator was defined to compute the average fluid velocity at the inlet and outlet, subsequently employed in the pressure analysis formula to consider the valve’s impact at these points. Pressure boundary conditions were applied at both the inlet and outlet, with the applied pressures being
Transient studies were conducted to simulate the model, tracing the evolution over five drive cycles. Stringent time stepping was adopted to minimize interpolation errors, and a fully coupled solver was utilized to enhance computational efficiency.
The study also included a fluid-structure coupling analysis of the flow field near both the wheel valve and cantilever valve. The valve was designated as the solid domain, with the remaining areas classified as the fluid domain. The interface between the valve and fluid was designated as the fluid-structure coupling surface. A water column was placed in the lower plane of the wheel valve and the upper plane of the cantilever, respectively, to simulate fluid action. The differential pressure between the inlet and outlet was applied to emulate the valve’s opening and closing mechanisms.
Concerning the microneedle’s skin penetration, if axial and lateral stresses surpass a certain threshold, it may result in breakage or buckling failure. As depicted in Figure 2b, a microneedle model was developed, applying an equivalent stress to the tip. The optimization of parameters was based on the maximum transverse stress experienced at the tip.
2.3. Valve Characteristic
The wheel valve’s plate, positioned at the geometric center, connects to the fixed component via curved arms, as depicted in Figure 3a. This plate operates with an approximate horizontal translation for opening and closing, illustrated in Figure 3b, facilitating increased flow clearance and reduced fluid resistance, thereby enhancing the micropump’s outlet flow. The backstopping effect is pronounced in the wheel valve’s closed state, making the low-strength wheel valve optimal for low-frequency operations. In this study, based on empirical and experimental optimization (with the output flow and pressure of the micropump as objective functions), the wheel valve plate has a diameter of 1.2 mm, a bent cantilever root diameter of 2.8 mm, and a thickness of 0.025 mm.
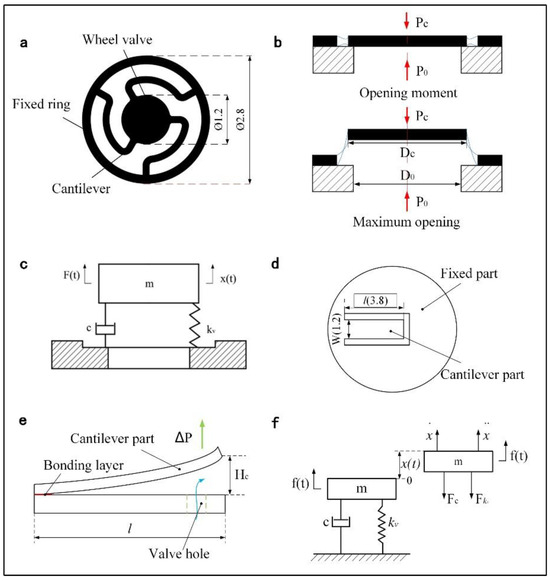
Figure 3.
(a–c) Illustrate the wheel valve structure, its operational process, and dynamic model (The red arrows point to the pressure on either side of the valve). (d–f) Display the cantilever valve structure, its operational process, and dynamic model (The blue arrow denotes the direction of fluid flow, while the green arrow indicates the direction of valve action).
The wheel valve’s movement under the pump chamber’s internal pressure resembles simple harmonic motion, similar to the damped vibration system of a mass reed, as shown in Figure 3c. Here, m represents the equivalent mass and kv represents the equivalent stiffness. The valve’s motion considers only the viscous damping c. The vibration amplitude of the wheel valve is given by [27]:
And the phase difference of the wheel valve’s response is
The cantilever valve, as shown in Figure 3d,e, oscillates up and down under differential pressure to open and close the valve hole. The instantaneous flow rate through the slot depends on the pressure difference, material, and dimensions. This cantilever beam measures 3.8 mm in length, 1.2 mm in width, and 0.025 mm in thickness.
The movement of the cantilever valve’s cantilever portion under the pump chamber pressure can be simplified to a damping oscillation system of a small mass valve spring, as illustrated in Figure 3f. In this model, m is the equivalent mass, kv is the equivalent stiffness, c is the damping factor, and f(t) is the exciting force generated in the pump chamber. The vibration amplitude of the cantilever valve is [28]
And the phase difference is
Equation (7) indicates that at low frequencies, the vibration amplitude of the cantilever valve is approximately equal to the deformation X0 when driven by force f0, implying that X, the vibration amplitude, is mainly regulated by the cantilever valve’s equivalent stiffness. As per equation (8), at frequencies lower than the first-order resonance frequency (i.e., v < 1), the higher the frequency, the greater the hysteresis. When utilizing the PE vibrator as the driving force, a damping effect is introduced, causing the valve’s motion to lag behind the PE vibrator. Hence, the theoretical resonant frequency differs from the actual operating frequency. Operating below the first-order frequency allows the lower frequency to enhance the valve’s movement in coordination with the PE element.
2.4. Experimental Setup
The performance assessment of the PE micropump primarily focuses on its output flow and pressure, as illustrated in Figure 1e. The testing apparatus includes a signal generator (RIGOL, DG4062, Suzhou, China), a power amplifier (Core Tomorrow, E00.A3, Harbin, China), and an oscilloscope (RIGOL, DS1102E). The sinusoidal signal from the signal generator is amplified and applied to the PE micropump, while the oscilloscope monitors the output signal. Real-time output flow is measured using a flow sensor (Keyence, FD-XA1, Osaka, Japan), and output pressure is gauged by a pressure sensor (FLUIGENT, EIPS7000, Le Kremlin-Bicêtre, France). The scale and piping on the right side are utilized for assessing the flow resistance characteristics of the PE micropump. Additionally, a precision electronic balance measures the volume flow under varying pulse numbers to evaluate the flow resolution of the PE micropump.
3. Results and Discussion
3.1. Simulation of the PE Micropump
The integration operator calculates the flow at the inlet and outlet, tracking the cumulative flow at these points. As seen in Figure 4a, the time-based cumulative flow exhibits alternating inflow and outflow patterns.
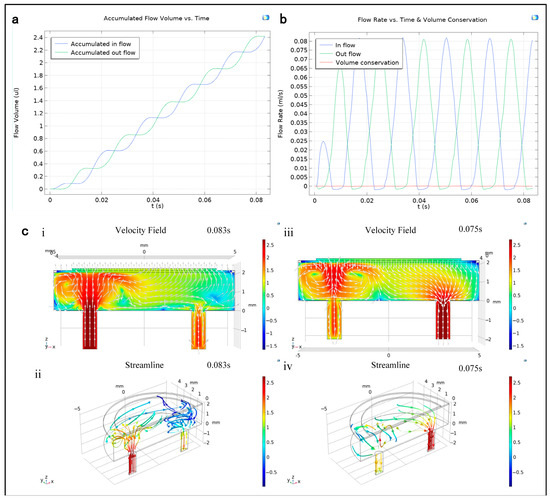
Figure 4.
(a) Shows the accumulated flow of the PE micropump over time. (b) Demonstrates the variations in inlet and outlet flow rates over time and their correlation with volume flow. (c) Depicts the velocity field and streamline during the (i,ii) supply process and (iii,iv) pumping process.
The integral operator is employed to quantify the chamber volume change resulting from the PE vibrator’s displacement. Global probes monitor the inflow and outflow. Figure 4b illustrates the fluctuating inlet and outlet flow rates relative to time and volume flow, where the sum of the velocity and the volume change rate caused by the PE vibrator is plotted, demonstrating volume conservation. The combined inlet and outlet flow rates consistently equate to zero, affirming the micropump’s adherence to volume conservation principles.
Figure 4c portrays the velocity field and flow dynamics, showing fluid movement on the symmetric plane and within the cavity. The fluid is periodically pumped in one direction by the PE vibrators and valves. During the pumping phase, the inlet pipe and adjacent chamber exhibit a higher flow rate, while the outlet’s flow rate is lower despite minimal fluid ingress. The outlet valve does not entirely prevent reverse fluid flow, a condition attributed to the micropump’s operational dynamics. Conversely, when the chamber fluid is expelled, the flow rate in the outlet pipe and nearby area significantly surpasses that of the inlet. These findings objectively reflect the micropump’s performance, with a considerable volume of fluid being expelled from the outlet, accompanied by a minor quantity from the inlet.
The deformation of the valve and the fluid domain flow field were meticulously analyzed through multiple iterations. Figure 5a,b illustrates that when fluid enters the chamber via the wheel valve, driven by a pressure differential, the movement approximates translational motion, creating substantial fluid gaps. This configuration benefits the flow rate of the micropump and enhances its reverse cutoff efficiency. Figure 5c–e depicts the fluid being expelled from the chamber through the cantilever valve’s opening and closing, passing through a narrow slit. These figures visually represent the dynamic states of the wheel and cantilever valves, as well as the chamber’s flow field.
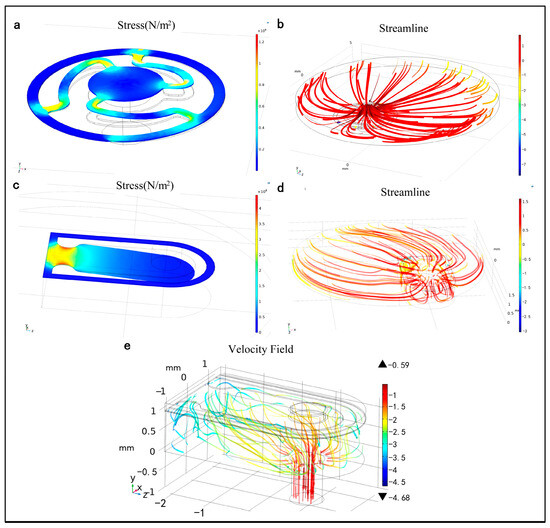
Figure 5.
(a) Deformation process of a wheel valve, (b) flow field near the wheel valve, (c) deformation process of a cantilever valve, (d) flow field near the cantilever valve, and (e) flow field near the outlet.
3.2. Simulation of the Microneedle
The design parameters for the microneedle in this study are as follows: the microneedle has a bottom diameter of 220 μm and an inner diameter of 40 μm, constructed from high-temperature-resistant resin (HTL) with an elastic modulus of 4.2 GPa and a bending strength of 120 MPa.
The analysis focused on a microneedle tip wall thickness ranging from 40 to 70 μm. Figure 6a demonstrates that an increase in the tip wall thickness enhances the maximum transverse stress the microneedle can withstand. Specifically, a tip wall thickness between 60 and 70 μm can bear a higher maximum transverse stress compared to thicknesses below 60 μm. However, considering the overall dimensions of the microneedle and the requirement for easy skin penetration, the tip wall thickness is optimally set between 60 and 70 μm, with a specific choice of 70 μm.
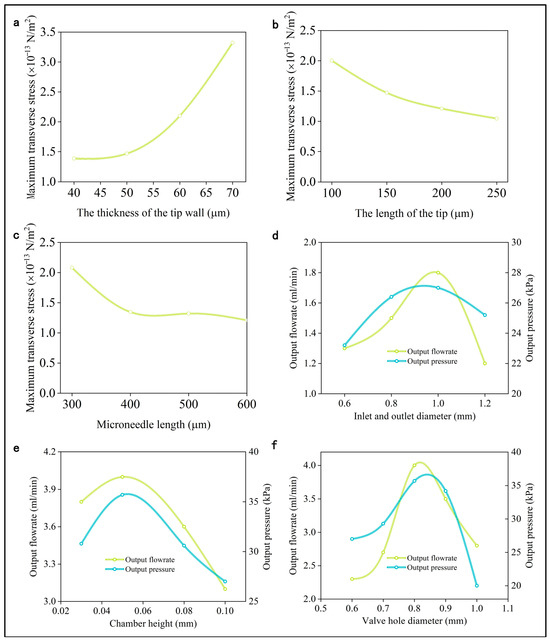
Figure 6.
Illustrates the maximum transverse stress of microneedles under various conditions: (a) thickness of the tip wall; (b) length of the tip; and (c) overall microneedle length. Output performance of the PE micropump for varying structural parameters: (d) inlet and outlet diameter; (e) chamber height; (f) valve hole diameter.
Optimization was also conducted for the microneedle tip and overall length. As shown in Figure 6b, elongating the tip reduces the maximum transverse stress the microneedle can endure. However, a tip length shorter than 150 μm, though painless for skin piercing, results in low piercing and administration efficiency. A tip length ranging from 200 μm to 250 μm maintains a relatively consistent maximum transverse stress. Thus, to ensure efficient skin penetration and high administration efficiency, a tip length of 250 μm is recommended. Figure 6c indicates that longer microneedles exhibit decreased maximum transverse stress, implying that shorter microneedles can withstand greater stress. Nonetheless, excessively short microneedles are less efficient. When the microneedle length is between 400 μm and 500 μm, the maximum transverse stress remains nearly constant. Therefore, a microneedle length of 500 μm is advised.
3.3. Optimization of Inlet and Outlet Diameters
The diameters of the inlet and outlet are pivotal in determining the output flow and pressure of the PE micropump. It is evident that if the inlet and outlet diameters are excessively large, the flow rate will be reduced. Conversely, if the diameter is too small, the flow resistance will increase, resulting in a significant decrease in efficiency. Therefore, it can be concluded that the inlet and outlet diameters must be appropriately sized to ensure optimal functionality and efficiency. Tests were conducted with inlet and outlet diameters of 0.6 mm, 0.8 mm, 1.0 mm, and 1.2 mm, with corresponding output performance at 50 V and 80 Hz depicted in Figure 6d. The micropump’s output performance initially improves with an increase in diameter but then diminishes. When the diameter is too small (0.6 mm), flow resistance in the channel escalates, thereby limiting the output pressure and flow rate. Conversely, overly large diameters (1.2 mm) reduce the flow rate, adversely impacting the micropump’s output flow. A diameter range of 0.8 to 1.0 mm is deemed optimal. The inlet diameter was set at 0.8 mm, considering the notable increase in prototype thickness with larger inlet diameters. It is advisable to select identical diameters for both the inlet and outlet.
3.4. Optimization of Chamber Height
In the context of the PE micropump’s conveyance of fluids, the pump chamber exerts a significant influence on the system’s characteristics. This, in turn, determines the output flow rate and pressure. Insufficient height of the pump chamber can impede the movement of the pump’s components, potentially leading to suboptimal performance or failure of the micropump. It is therefore recommended that the height of the pump chamber be slightly larger than the maximum displacement of the vibrator center point, thus allowing the maximum amplitude of the vibrator to be utilized while meeting the self-priming and pumping function of the micropump. Conversely, an excessively large pump chamber height can compromise the micropump’s self-priming capability, potentially diminishing its operational effectiveness. The chamber heights tested were 0.03 mm, 0.05 mm, 0.08 mm, and 0.10 mm. This parameter is vital for the PE micropump’s output performance. Figure 6e presents the output power at different chamber heights, tested at 70 V and 80 Hz. The micropump’s performance initially increases with chamber height but then decreases. Optimal output is achieved at a chamber height of 0.05 mm.
3.5. Optimization of Valve Hole Diameter
It has been established that an increase in the diameter ratio of the valve in relation to the valve hole is indicative of a greater pressure loss. Consequently, reducing the diameter ratio to the greatest extent possible can enhance the pump’s output pressure. However, if the diameter ratio is excessively reduced, it can impede the sealing between the valve and the valve hole, leading to reverse fluid leakage and a subsequent reduction in pump output pressure. Furthermore, it is important to note that the proximity of the valve and valve hole dimensions to each other has a direct impact on the difficulty of assembly. Valve holes with diameters of 0.6 mm, 0.7 mm, 0.8 mm, 0.9 mm, and 1.0 mm were examined. Figure 6f illustrates the PE micropump’s output performance at 70 V and 80 Hz for these various valve hole diameters. When the valve and valve hole are closely sized (1.0 mm), both the outlet flow rate and pressure decline, indicating suboptimal reverse cutoff performance. This suggests potential challenges in sealing the chamber inlet effectively during pumping, resulting in decreased internal pressure and energy loss during supply. Conversely, if the valve and valve hole are mismatched in size (e.g., 0.6 mm, 0.7 mm), the kinetic energy loss around the valve increases due to the difficulty in opening the valve. The micropump functions most efficiently with a valve hole diameter between 0.8 mm and 0.9 mm. However, a 0.9 mm diameter might lead to poor reverse cutoff due to improper assembly. Consequently, the valve hole diameter was set to 0.8 mm.
3.6. Output Performance Test
This section elucidates the test results for the output performance of the optimized PE micropump. Figure 7a illustrates the frequency characteristics of the micropump. Initially, both the output pressure and flow rate of the micropump rise and then decline as the operating frequency increases under a set driving voltage. Beyond the first optimal frequency point, the micropump’s pumping flow diminishes gradually within a specific frequency range. However, with further frequency increments, the pumping cycles per minute substantially increase, leading to a continuous elevation in output flow. The output pressure of the micropump chiefly depends on the synchronization level between the PE vibrator and the valve. Due to the valve’s delayed response to the PE vibrator, a phase difference occurs, resulting in decreased output pressure after the first optimal frequency. Nevertheless, with the rising working frequency, this phase difference undergoes adjustment, temporarily boosting the output pressure. At an operating frequency of 300 Hz, both output flow and pressure decrease, significantly impairing the micropump’s overall efficiency. For single-chamber PE micropumps, lower operating frequencies correlate with enhanced output performance and an extended lifespan of both the PE vibrator and valve. Consequently, the operational frequency of the micropump in this study was established at approximately 80 Hz.
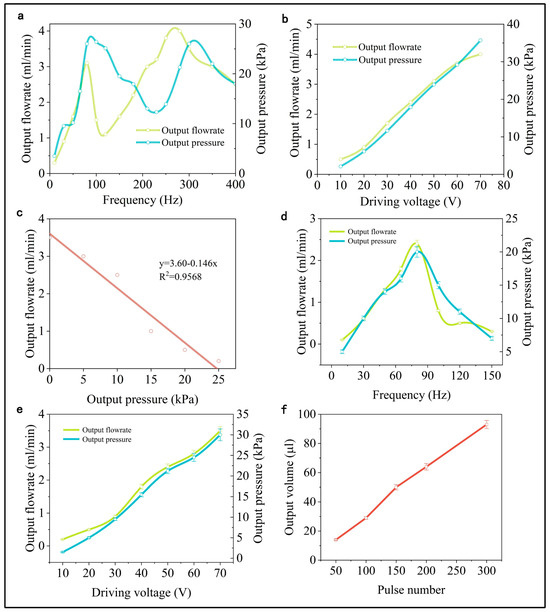
Figure 7.
The output performance of the PE micropump under various (a) frequencies, (b) voltages, and (c) the relationship between output pressure and output flow. The output performance of the PE micropump integrated with microneedles under various (d) frequencies, (e) voltages, and (f) pulse numbers.
Moreover, the PE micropump’s output pressure and flow rate exhibit a linear relationship with the driving voltage at a specific operating frequency (see Figure 7b). At 70 V and 80 Hz, the micropump can generate a maximum output pressure of 35.7 kPa and an outlet flow rate of 4.0 mL/min. Despite its compact size, the proposed micropump demonstrates superior overall output performance.
Flow resistance characteristics, indicative of the back pressure-flow relationship, are critical performance indices for PE micropumps. These characteristics assess the micropump’s output performance under certain working conditions. As shown in Figure 7c, at 50 V and 80 Hz, the output pressure declines linearly with increasing flow rate, meaning that an increase in output pressure results in a reduction in output flow.
Figure 7d,e demonstrates that the outlet performance of the PE micropump, when integrated with a microneedle array, initially rises and then falls with operating frequency. The flow rate and pressure are positively correlated with the driving voltage, exhibiting an approximately linear relationship. However, the output flow and pressure are slightly diminished compared to configurations without the integrated microneedle array. Typically, the device achieves an output performance of 3.5 mL/min and 30 kPa at 70 V and 80 Hz. The integration of the microneedle array causes the fluid to pass through the micropump outlet and disperse into multiple streams via the micro-outlet array of microneedles, which increases fluid resistance and consequently reduces the flow rate and pressure. Nonetheless, the output performance remains within the anticipated range, ensuring its practical applicability is not compromised.
Flow resolution is an essential measure of pumping accuracy in precise infusion systems. To ascertain the flow resolution of the PE micropump with integrated microneedles, various pulse numbers were tested under conditions of 50 V and 80 Hz, with the cumulative output flow being calculated. As shown in Figure 7f, a direct correlation exists between the cumulative output flow and the number of pulses. The minimum flow resolution attained is 0.28 μL.
The transdermal drug delivery device proposed in this work has an advantageous comprehensive output performance compared to previous studies, as shown in Table 2. For example, the device proposed by Cheng et al. has a high drive voltage and operating frequency (noticeable noise), and there is room for improvement in output flow rate and pressure. The devices proposed by Rao et al. and Liu et al. have improved output flow rate, which is more promising to be applied to the needs of large-dose delivery of drugs, but the output pressure is insufficient to constrain the viscosity of the drug across the viscosity range. Tseng et al. improved the output pressure of the device, but lacked the ability to deliver large doses of drugs. In contrast, the present work balances many of the device’s properties, i.e., high output flow rate and pressure at lower driving conditions. This gives the device the ability to deliver large doses of drug while accommodating a wider range of viscosities and allowing for microdosing.

Table 2.
Comparison of the present work with previous research.
4. Conclusions
This work introduces a PE micropump system with integrated microneedles, optimized for precise fluid pumping applications such as transdermal drug delivery. The structural parameters near the valve, the inner chamber of the PE micropump, and the microneedles were meticulously analyzed using COMSOL. Based on these analyses, the prototype’s structural parameters were preliminarily determined, and subsequently refined in accordance with the actual output performance. The prototype was fabricated, and its comprehensive output performance was rigorously tested. The following conclusions were drawn:
- The working principle of the PE micropump reveals that the fluid’s flow field within the chamber and channel changes due to the coordinated action of the PE vibrator and valve. This results in the fluid being pumped in and out in a staggered sequence, adhering to the principle of volume conservation.
- The chamber height can be fine-tuned to enhance self-priming capabilities without compromising the micropump’s output characteristics. The diameter ratio of the valve to the valve hole should be carefully selected to balance pressure loss, sealing efficacy, and assembly practicality. The inlet and outlet diameters must be optimized to minimize energy loss.
- The penetration of the microneedles into the skin is primarily driven by axial and lateral pressure. The mechanical characteristics of the microneedles are greatly influenced by factors such as tip wall thickness, tip length, and overall microneedle length.
- The output flow rate and pressure of the PE micropump initially increase and then decrease with rising operating frequencies. Conversely, at a constant operating frequency, both the flow rate and pressure show a positive correlation with the driving voltage, forming a nearly linear relationship. Under stable working conditions, the micropump’s output pressure is inversely related to its output flow, demonstrating a linear correlation.
- At an operating voltage of 70 V and a frequency of 80 Hz, the micropump achieves an output flow of 4.0 mL/min and a pressure of 35.7 kPa. The output flow rate and pressure of the device with the integrated microneedle array were 3.5 mL/min, 30 kPa, with a minimum flow resolution of 0.28 μL, demonstrating the effectiveness and practicality of the design.
Author Contributions
Conceptualization, S.L. and Y.Z.; Methodology, S.L. and C.W.; Software, S.L. and J.L.; Validation, J.L.; Formal analysis, S.L. and J.L.; Investigation, S.L.; Resources, C.W. and Y.Z.; Writing—original draft, S.L.; Writing—review & editing, Y.Z.; Visualization, S.L. and J.L.; Supervision, C.W. and Y.Z.; Project administration, Y.Z.; Funding acquisition, C.W. All authors have read and agreed to the published version of the manuscript.
Funding
The Natural Science Foundation of China (52475103) and Jilin Provincial Natural Science Foundation Project (20230101108JC).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lu, S.; Yu, M.; Qian, C.; Deng, F.; Zhang, Z. A Quintuple-Bimorph Tenfold-Chamber Piezoelectric Pump Used in Water-Cooling System of Electronic Chip. IEEE Access 2020, 8, 186691–186698. [Google Scholar] [CrossRef]
- Anh, P.N.; Bae, J.S.; Hwang, J.H. Computational Fluid Dynamic Analysis of Flow Rate Performance of a Small Piezoelectric-Hydraulic Pump. Appl. Sci. 2021, 11, 4888. [Google Scholar] [CrossRef]
- Woo, J.; Sohn, D.K.; Ko, H.S. Performance and flow analysis of small piezo pump—ScienceDirect. Sens. Actuators A Phys. 2020, 301, 111766. [Google Scholar] [CrossRef]
- Senjanović, I.; Vladimir, N.; Tomić, M. On new first-order shear deformation plate theories. Mech. Res. Commun. 2016, 73, 31–38. [Google Scholar] [CrossRef]
- Wu, X.; He, L.; Hou, Y.; Tian, X.; Zhao, X. Advances in passive check valve piezoelectric pumps. Sens. Actuators A Phys. 2021, 323, 112647. [Google Scholar] [CrossRef]
- Liu, G.; Wang, M.; Li, P.; Sun, X.; Dong, L.; Li, P. A micromixer driven by two valveless piezoelectric pumps with multi-stage mixing characteristics. Sens. Actuators A Phys. 2021, 333, 113225. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Wang, B.; Cai, Y.; Song, Q. An overview on state-of-art of micromixer designs, characteristics and applications. Anal. Chim. Acta 2023, 1279, 341685. [Google Scholar] [CrossRef]
- Zhou, D.; Qin, L.; Yue, J.; Yang, A.; Jiang, Z.; Zheng, S. Numerical and experimental investigations of spiral and serpentine micromixers over a wide Reynolds number range. Int. J. Heat Mass Transf. 2023, 212, 124273. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, H.; Wang, Y.; Zhao, W.; Han, M.; Zhang, H. A time sequential microfluid sensor with Tesla valve channels. Nano Res. 2023, 16, 11667–11673. [Google Scholar] [CrossRef]
- Wu, T.; Shen, J.; Li, Z.; Xing, F.; Xin, W.; Wang, Z.; Liu, G.; Han, X.; Man, Z.; Fu, S. Microfluidic-integrated graphene optical sensors for real-time and ultra-low flow velocity detection. Appl. Surf. Sci. 2021, 539, 148232. [Google Scholar] [CrossRef]
- Hu, R.; He, L.; Hu, D.; Hou, Y.; Cheng, G. Recent studies on the application of piezoelectric pump in different fields. Microsyst. Technol. 2023, 29, 663–682. [Google Scholar] [CrossRef]
- Jun, H.; Jianhui, Z.; Weidong, S.; Yuan, W. 3D FEM Analyses on Flow Field Characteristics of the Valveless Piezoelectric Pump. Chin. J. Mech. Eng. 2016, 29, 825–831. [Google Scholar]
- Zhao, D.; He, L.P.; Li, W.; Huang, Y.; Cheng, G.M. Experimental analysis of a valve-less piezoelectric micropump with crescent-shaped structure. J. Micromech. Microeng. 2019, 29, 105004. [Google Scholar] [CrossRef]
- Cheng, C.H.; Yang, A.S.; Lin, C.J.; Huang, W.J. Characteristic studies of a novel piezoelectric impedance micropump. Microsyst. Technol. 2017, 23, 1709–1717. [Google Scholar] [CrossRef]
- Yeming, S.; Junyao, W. Digitally-controlled driving power supply for dual-active-valve piezoelectric pump. Microsyst. Technol. 2019, 25, 1257–1265. [Google Scholar] [CrossRef]
- Sakuma, S.; Kasai, Y.; Hayakawa, T.; Arai, F. On-chip cell sorting by high-speed local-flow control using dual membrane pumps. Lab Chip 2017, 17, 2760–2767. [Google Scholar] [CrossRef]
- Haber, J.M.; Gascoyne, P.R.C.; Sokolov, K. Rapid real-time recirculating PCR using localized surface plasmon resonance (LSPR) and piezo-electric pumping. Lab Chip 2017, 17, 2821–2830. [Google Scholar] [CrossRef]
- Mohith, S.; Karanth, P.N.; Kulkarni, S.M. Recent trends in mechanical micropumps and their applications: A review. Mechatronics 2019, 60, 34–55. [Google Scholar] [CrossRef]
- Elahpour, N.; Pahlevanzadeh, F.; Kharaziha, M.; Bakhsheshi-Rad, H.R.; Ramakrishna, S.; Berto, F. 3D printed microneedles for transdermal drug delivery: A brief review of two decades. Int. J. Pharm. 2021, 597, 120301. [Google Scholar] [CrossRef]
- Cárcamo-Martínez, Á.; Mallon, B.; Domínguez-Robles, J.; Vora, L.K.; Anjani, Q.K.; Donnelly, R.F. Hollow microneedles: A perspective in biomedical applications. Int. J. Pharm. 2021, 599, 120455. [Google Scholar] [CrossRef]
- Ahmad, N.F.N.; Ghazali, N.N.N.; Wong, Y.H. Concept Design of Transdermal Microneedles for Diagnosis and Drug Delivery: A Review. Adv. Eng. Mater. 2021, 23, 2100503. [Google Scholar] [CrossRef]
- Rao, K.S.; Sateesh, J.; Guha, K.; Baishnab, K.L.; Ashok, P.; Sravani, K.G. Design and analysis of MEMS based piezoelectric micro pump integrated with micro needle. Microsyst. Technol. 2018, 26, 3153–3159. [Google Scholar] [CrossRef]
- Garcia, J.; Rios, I.; Fonthal Rico, F. Design and Analyses of a Transdermal Drug Delivery Device (TD(3)) dagger. Sensors 2019, 19, 5090. [Google Scholar] [CrossRef] [PubMed]
- Haldkar, R.K.; Khalatkar, A.; Gupta, V.K.; Sheorey, T. New piezoelectric actuator design for enhance the micropump flow. Mater. Today Proc. 2021, 44, 776–781. [Google Scholar] [CrossRef]
- Karumuri, S.R.; Mohammed, H.; Guha, K.; Puli, A.K.; Einsanwi, A.; Kondavitee, G.S. Design, simulation and analysis of micro electro-mechanical system microneedle for micropump in drug delivery systems. IET Nanobiotechnol. 2021, 15, 484–491. [Google Scholar] [CrossRef]
- Meshkinfam, F.; Rizvi, G. A MEMS Based Drug Delivery Device with Integrated Micro-Needle Array—Design and Simulation. J. Biomech. Eng. 2021, 143, 081010. [Google Scholar] [CrossRef]
- Dong, J.; Cao, Y.; Chen, Q.; Wu, Y.; Liu, R.G.; Liu, W.; Yang, Y.; Yang, Z. Performance of single piezoelectric vibrator micropump with check valve. J. Intell. Mater. Syst. Struct. 2019, 31, 117–126. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, X.; Chen, X.; Yang, H. A Piezoelectric Resonance Pump Based on a Flexible Support. Micromachines 2019, 10, 169. [Google Scholar] [CrossRef]
- Cheng, C.H.; Tseng, Y.P. Characteristic studies of the piezoelectrically actuated micropump with check valve. Microsyst. Technol. 2013, 19, 1707–1715. [Google Scholar] [CrossRef]
- Liu, G.; Yang, Z.; Liu, J.; Li, X.; Wang, H.; Zhao, T.; Yang, X. A low cost, high performance insulin delivery system based on PZT actuation. Microsyst. Technol. 2014, 20, 2287–2294. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).