Speed Sensorless Motion Control Scheme for a Robotic Manipulator Under External Forces and Payload Changes
Abstract
1. Introduction
2. Mathematical Model: Thermo CRS Catalyst 5-DOF Manipulator Robot
3. Problem Statement
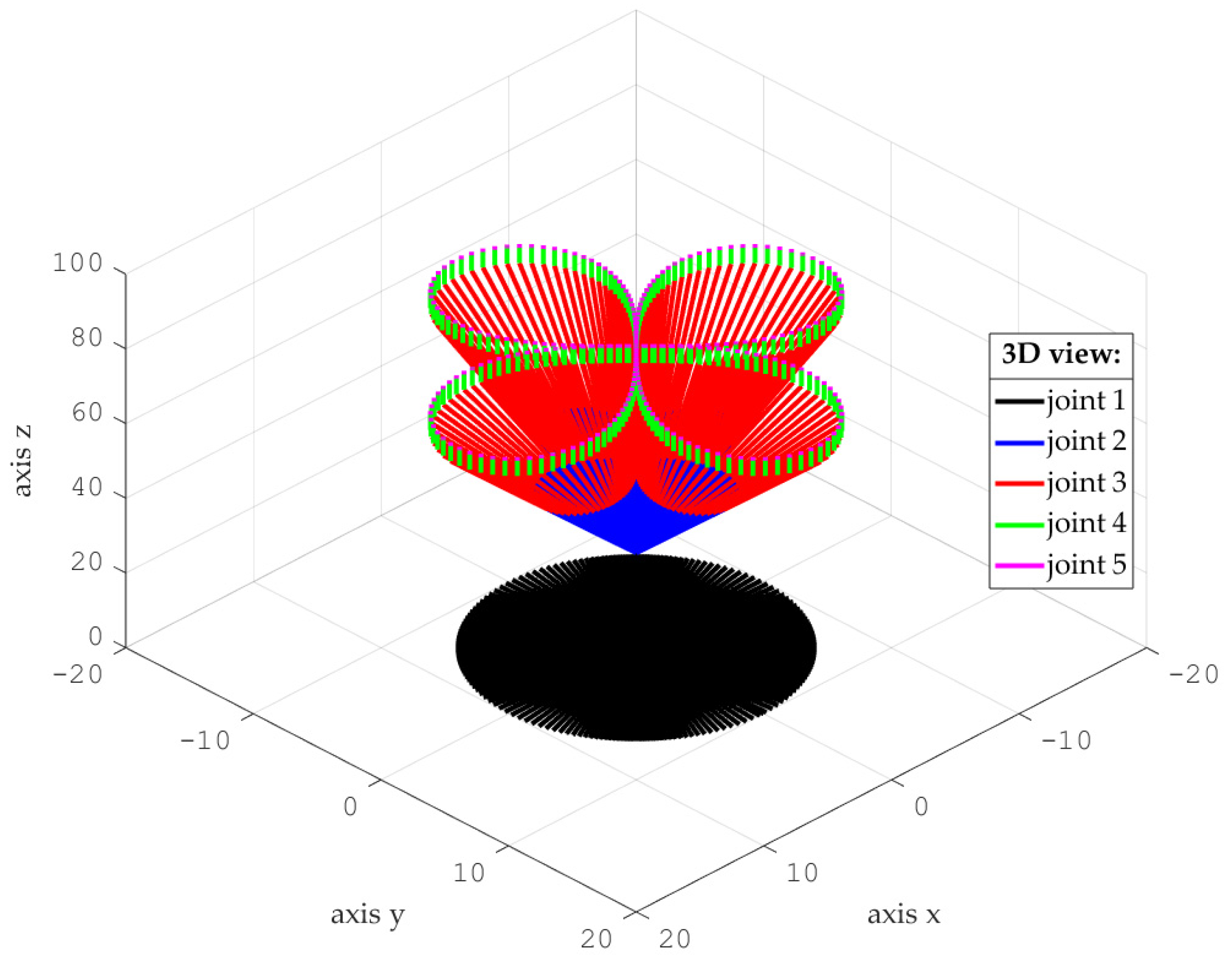
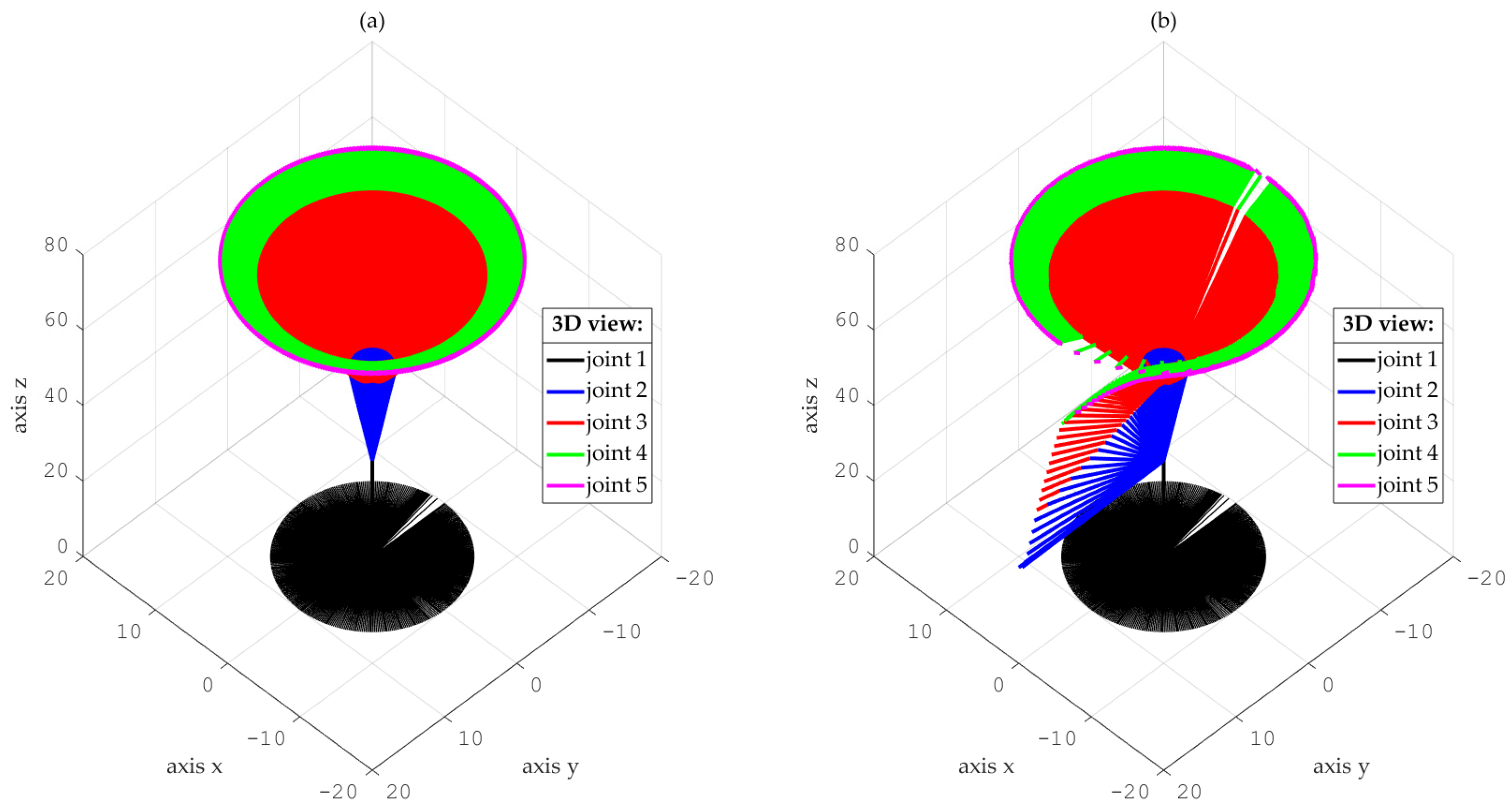
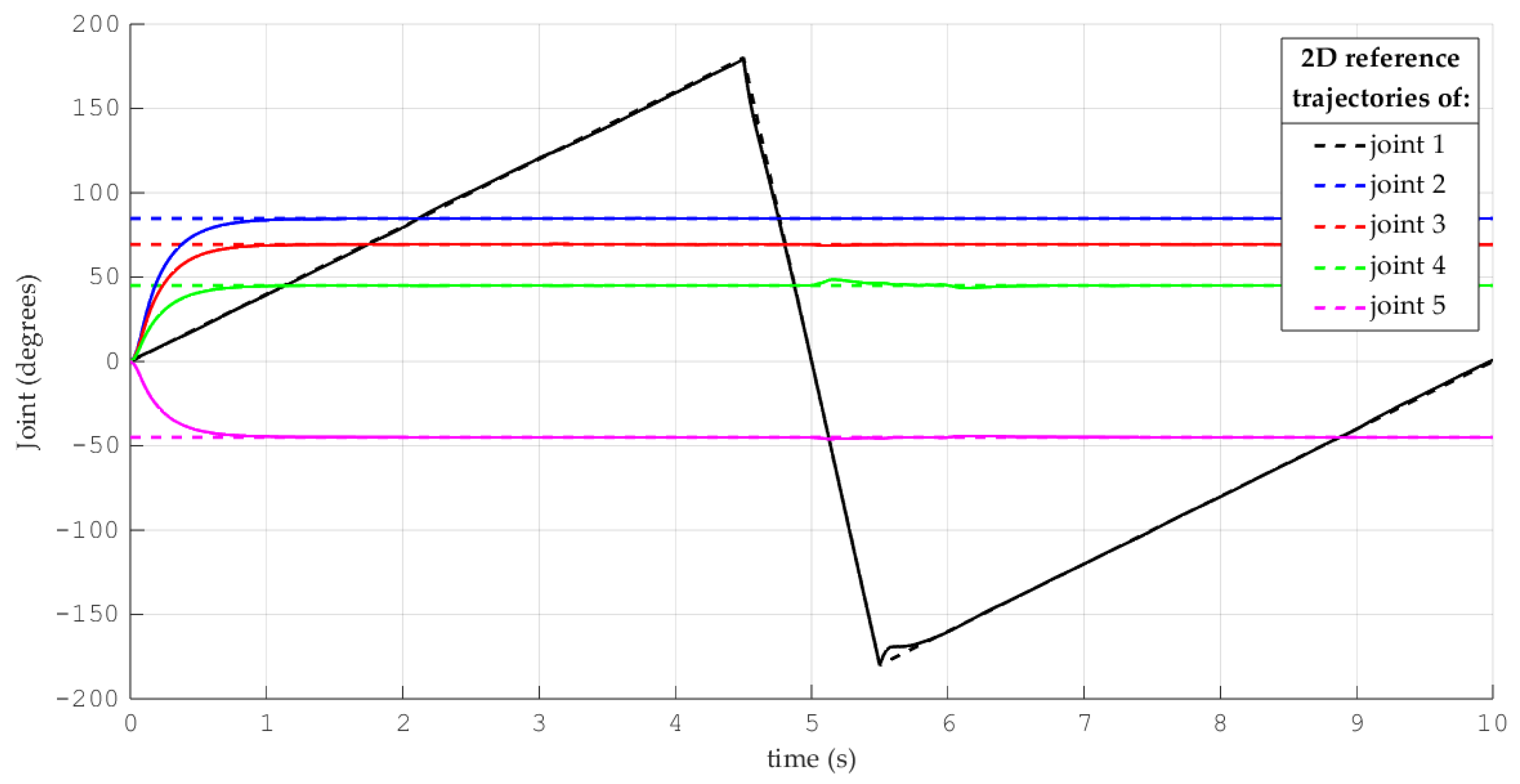
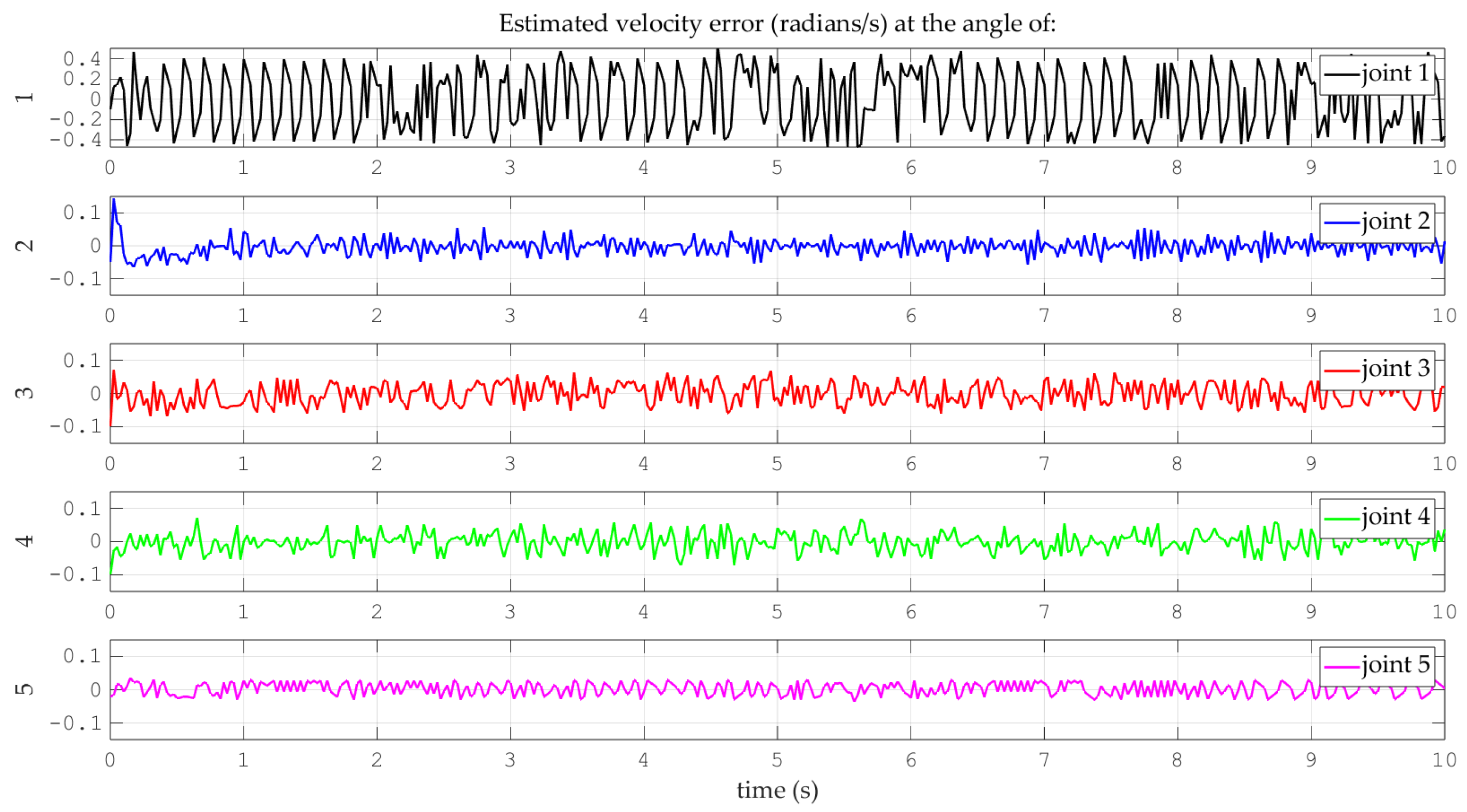
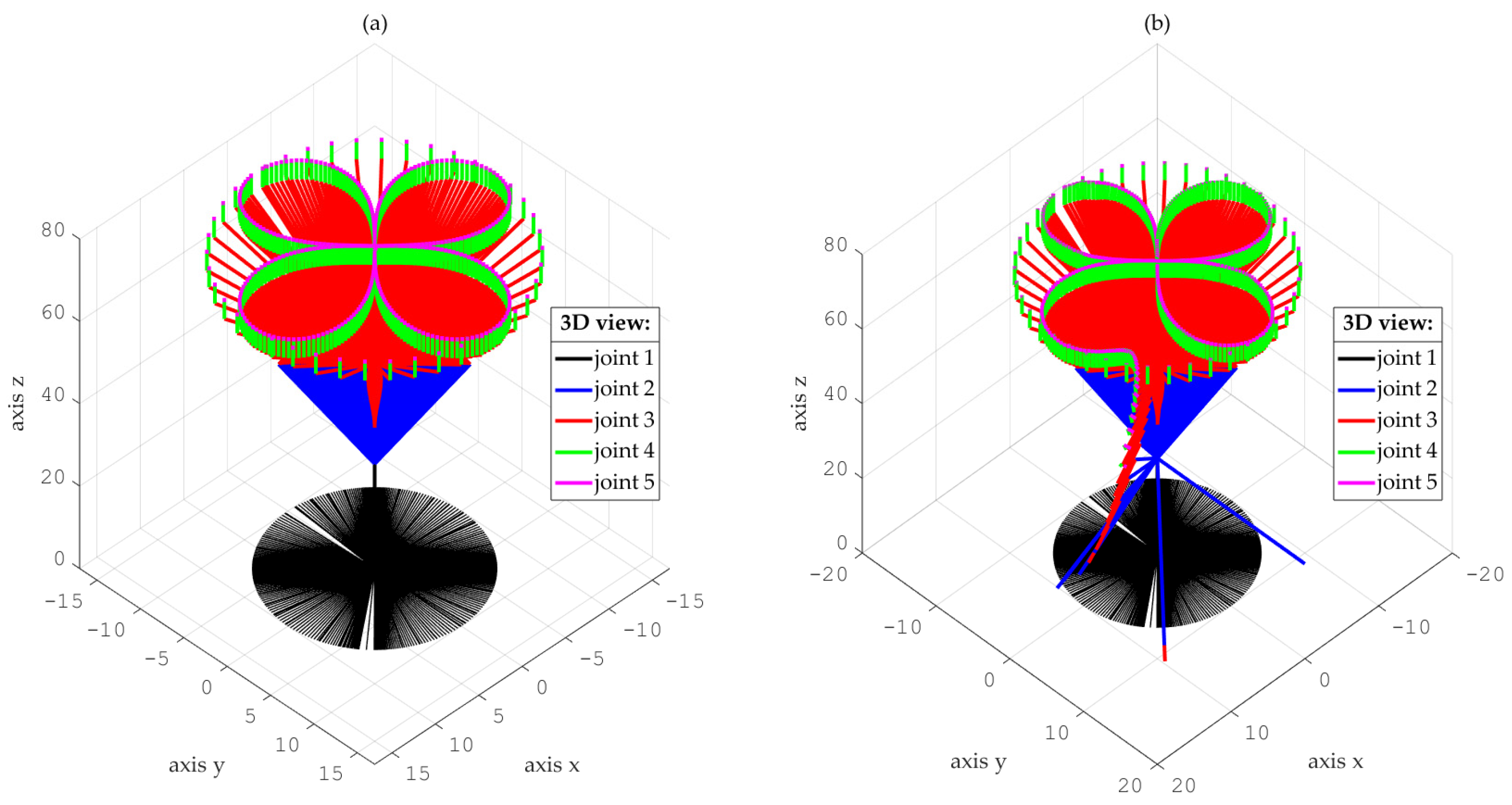
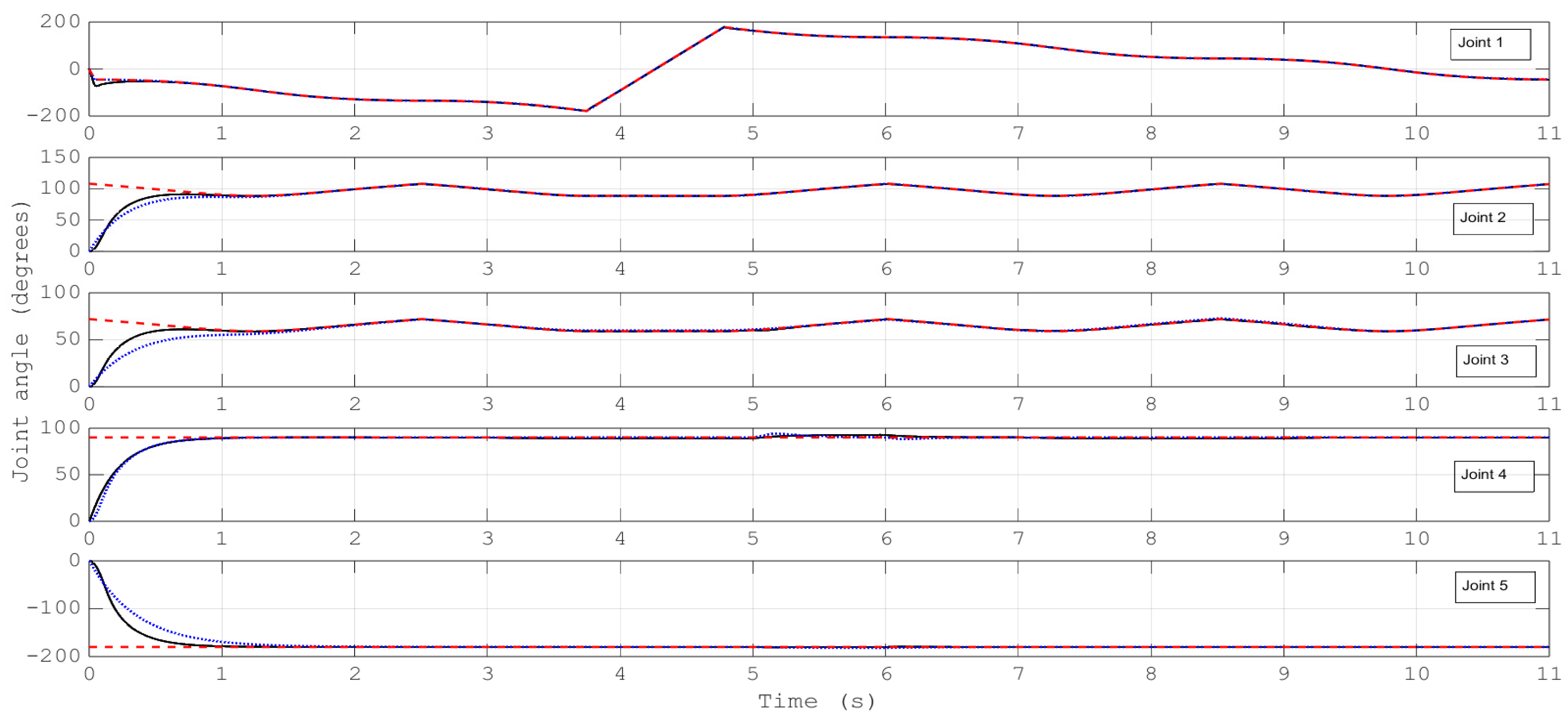
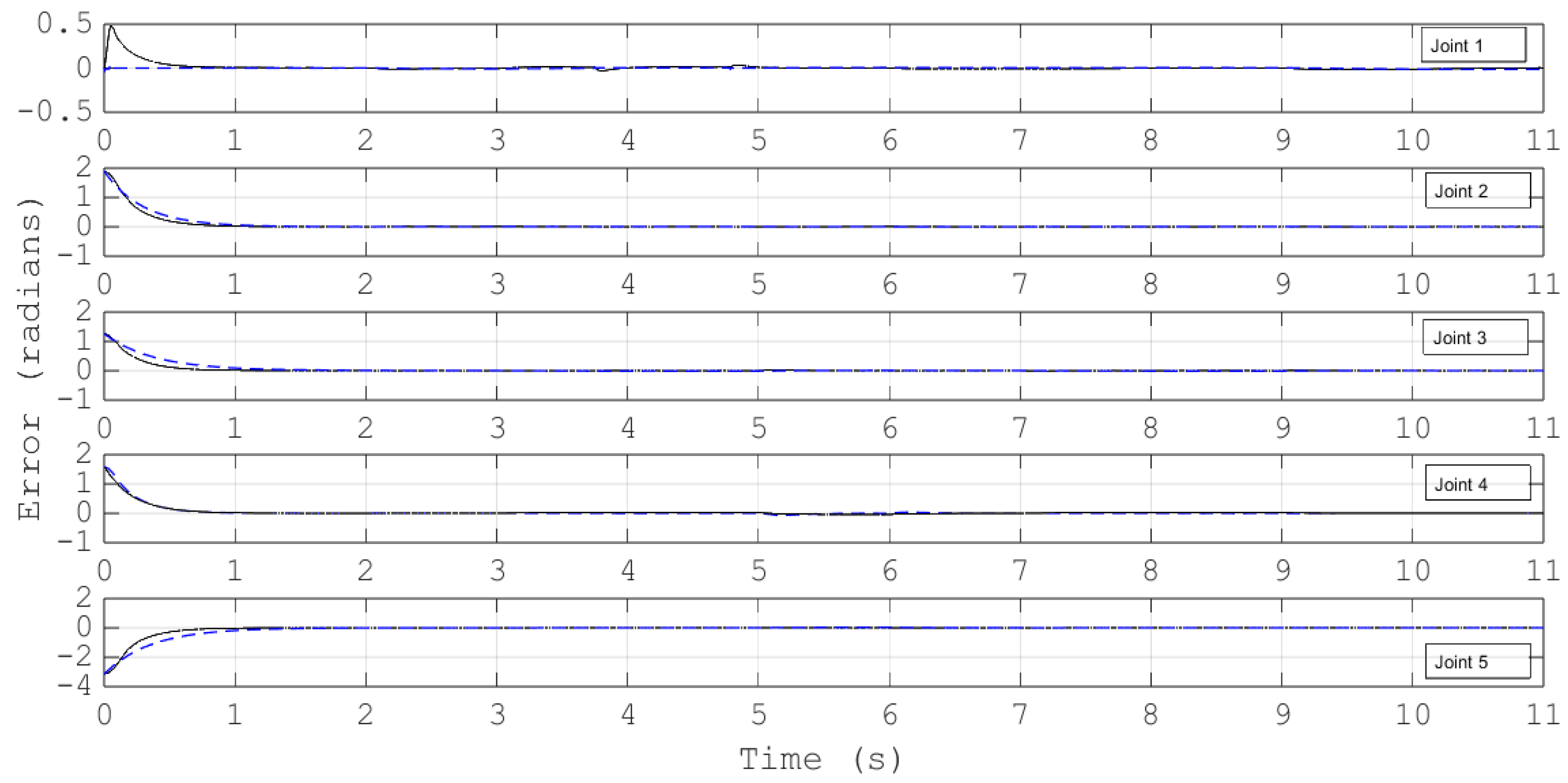
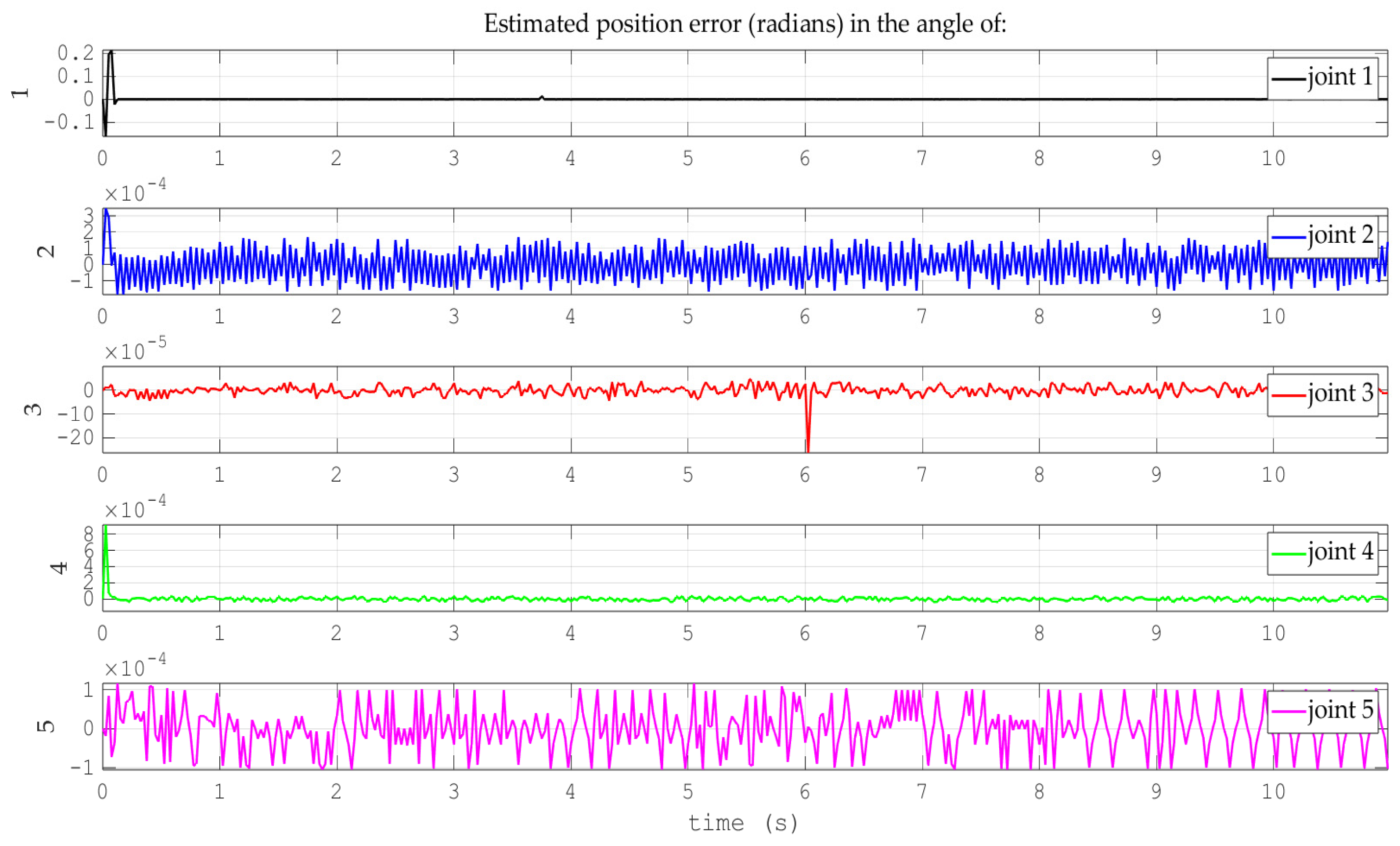
4. Results and Discussion
- (A)
- Simulations for the reference trajectory: circumference in three-dimensional space
- (B)
- Comparison of the performance of the proposed control scheme versus a disturbance observer-based control scheme
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reboucas Filho, P.P.; da Silva, S.P.P.; Praxedes, V.N.; Hemanth, J.; de Albuquerque, V.H.C. Control of singularity trajectory tracking for robotic manipulator by genetic algorithms. J. Comput. Sci. 2019, 30, 55–64. [Google Scholar] [CrossRef]
- Božek, P.; Nikitin, Y. The Development of an Optimally-Tuned PID Control for the Actuator of a Transport Robot. Actuators 2021, 10, 195. [Google Scholar] [CrossRef]
- Yilmaz, B.M.; Tatlicioglu, E.; Savran, A.; Alci, M. Self-adjusting fuzzy logic based control of robot manipulators in task space. IEEE Trans. Ind. Electron. 2021, 69, 1620–1629. [Google Scholar] [CrossRef]
- Urrea, C.; Kern, J.; Alvarado, J. Design and evaluation of a new fuzzy control algorithm applied to a manipulator robot. Appl. Sci. 2020, 10, 7482. [Google Scholar] [CrossRef]
- Bae, H.J.; Jin, M.; Suh, J.; Lee, J.Y.; Chang, P.H.; Ahn, D.S. Control of robot manipulators using time-delay estimation and fuzzy logic systems. J. Electr. Eng. Technol. 2017, 12, 1271–1279. [Google Scholar] [CrossRef]
- Chang, W.; Li, Y.; Tong, S. Adaptive fuzzy backstepping tracking control for flexible robotic manipulator. IEEE/CAA J. Autom. Sin. 2018, 8, 1923–1930. [Google Scholar] [CrossRef]
- Djelal, N.; Saadia, N.; Ramdane-Cherif, A. Adaptive force-vision control of robot manipulator using sliding mode and fuzzy logic. Autom. Control Comput. Sci. 2019, 53, 203–213. [Google Scholar] [CrossRef]
- Huang, H.L.; Cheng, M.Y.; Huang, T.Y. A Rapid Base Parameter Physical Feasibility Test Algorithm for Industrial Robot Manipulator Identification Using a Recurrent Neural Network. IEEE Access 2023, 11, 145692–145705. [Google Scholar] [CrossRef]
- Li, T.; Zhang, G.; Zhang, T.; Pan, J. Adaptive neural network tracking control of robotic manipulators based on disturbance observer. Processes 2024, 12, 499. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, L.; Yu, J.; Li, Y.; Yu, Z. Three recurrent neural networks and three numerical methods for solving a repetitive motion planning scheme of redundant robot manipulators. IEEE/ASME Trans. Mechatron. 2017, 22, 1423–1434. [Google Scholar] [CrossRef]
- Klančar, G.; Škrjanc, I. Tracking-error model-based predictive control for mobile robots in real time. Robot. Auton. Syst. 2007, 55, 460–469. [Google Scholar] [CrossRef]
- Trejo-Sosa, L.E.; Alazki, H. Control Robusto Adaptable para Sistema no inercial: Acrobot sobre un carro Robust Adaptive Control for System non-inertial: Acrobot on a cart. Diseño Innov. 2019, 3, 8–15. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Li, C.; Buss, M. Adaptive incremental sliding mode control for a robot manipulator. Mechatronics 2022, 82, 102717. [Google Scholar] [CrossRef]
- Mobayen, S.; Mofid, O.; Din, S.U.; Bartoszewicz, A. Finite-Time Tracking Controller Design of Perturbed Robotic Manipulator Based on Adaptive Second Order Sliding Mode Control Method. IEEE Access 2021, 9, 71159–71169. [Google Scholar] [CrossRef]
- Truc, L.N.; Vu, L.A.; Thoan, T.V.; Thanh, B.T.; Nguyen, T.L. Adaptive Sliding Mode Control Anticipating Proportional Degradation of Actuator Torque in Uncertain Serial Industrial Robots. Symmetry 2022, 14, 957. [Google Scholar] [CrossRef]
- Lopez-Cruz, G.; Alazki, H.; Cortes-Vega, D.; Rullán-Lara, J.L. Application of robust discontinuous control algorithm for a 5-DOF industrial robotic manipulator in real-time. J. Intell. Robot. Syst. 2021, 101, 75. [Google Scholar] [CrossRef]
- Al-Dujaili, A.Q.; Falah, A.; Humaidi, A.J.; Pereira, D.A.; Ibraheem, I.K. Optimal super-twisting sliding mode control design of robot manipulator: Design and comparison study. Int. J. Adv. Robot. Syst. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Ahmed, S.; Ahmed, A.; Mansoor, I.; Junejo, F.; Saeed, A. Output feedback adaptive fractional-order super-twisting sliding mode control of robotic manipulator. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 335–347. [Google Scholar] [CrossRef]
- Loria, A. Observers are unnecessary for output-feedback control of Lagrangian systems. IEEE Trans. Autom. Control 2015, 61, 905–920. [Google Scholar] [CrossRef]
- Stotsky, A.; Hedrick, J.K.; Yip, P.P. The use of sliding modes to simplify the backstepping control method. In Proceedings of the 1997 American Control Conference, Albuquerque, NM, USA, 6 June 1997; Volume 3, pp. 1703–1708. [Google Scholar] [CrossRef]
- Brunot, M. Comparison of Numerical Differentiation Techniques for Aircraft Identification. J. Aerosp. Eng. 2019, 32, 06019002. [Google Scholar] [CrossRef]
- Levant, A. Robust exact differentiation via sliding mode technique. Automatica 1998, 34, 379–384. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Springer: New York, NY, USA, 2014; Volume 10. [Google Scholar] [CrossRef]
- Cao, P.; Gan, Y.; Dai, X. Finite-time disturbance observer for robotic manipulators. Sensors 2019, 19, 1943. [Google Scholar] [CrossRef]
- Vo, A.T.; Truong, T.N.; Kang, H.-J. A Novel Tracking Control Algorithm with Finite-Time Disturbance Observer for a Class of Second-Order Nonlinear Systems and its Applications. IEEE Access 2021, 9, 31373–31389. [Google Scholar] [CrossRef]
- Dao, H.V.; Nguyen, M.H.; Ahn, K.K. Nonlinear functional observer design for robot manipulators. Mathematics 2023, 11, 4033. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Mei, Y.; Wu, Y. Observer-based boundary control for an asymmetric output-constrained flexible robotic manipulator. Sci. China Inf. Sci. 2022, 65, 139203. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Disturbance Observer-Based Control: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Sariyildiz, E.; Ohnishi, K. Stability and robustness of disturbance-observer-based motion control systems. IEEE Trans. Ind. Electron. 2014, 62, 414–422. [Google Scholar] [CrossRef]
- Na, G.; Jo, N.H.; Eun, Y. Performance degradation due to measurement noise in control systems with disturbance observers and saturating actuators. J. Frankl. Inst. 2019, 356, 3922–3947. [Google Scholar] [CrossRef]
- Ali, M.; Alexander, C.K. Robust tracking control of a robot manipulator using a passivity-based extended-state observer approach. IET Cyber-Syst. Robot. 2019, 1, 63–71. [Google Scholar] [CrossRef]
- Sinan, S.; Kali, Y.; Fareh, R.; Saad, M.; Bettayeb, M. Extended state observer-based synergetic control for n-DOF robot manipulators using joint position measurements only. Adv. Robot. 2023, 37, 766–778. [Google Scholar] [CrossRef]
- Lavín-Delgado, J.E.; Solís-Pérez, J.E.; Gómez-Aguilar, J.F.; Escobar-Jiménez, R.F. Trajectory tracking control based on non-singular fractional derivatives for the PUMA 560 robot arm. Multibody Syst. Dyn. 2020, 50, 259–303. [Google Scholar] [CrossRef]
- Chen, W.H. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Haselirad, A.; Neubert, J. A comparison of three trajectory planning methods for smooth motion in 5-DOF manipulators. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; Volume 60, p. 6. [Google Scholar]
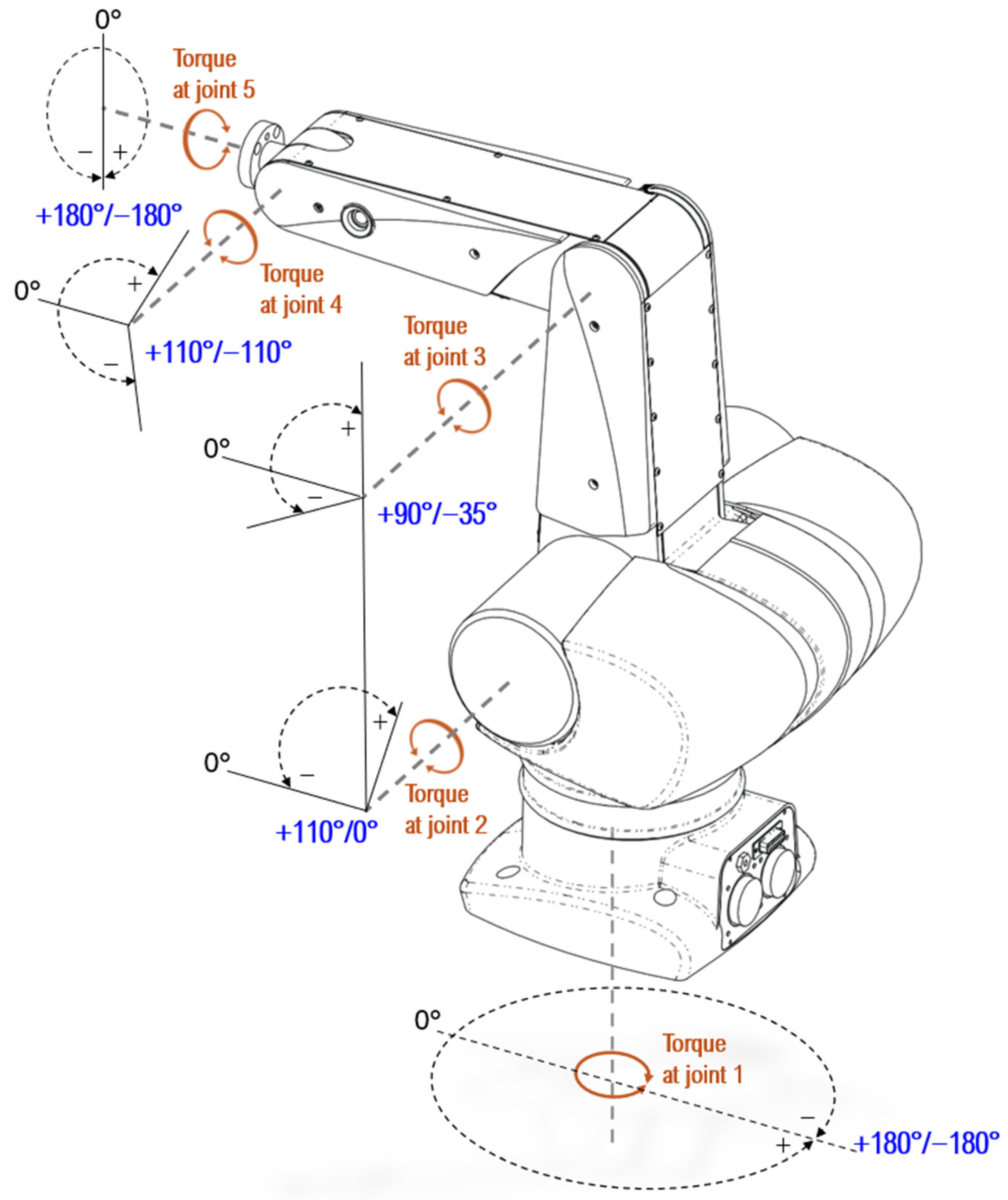


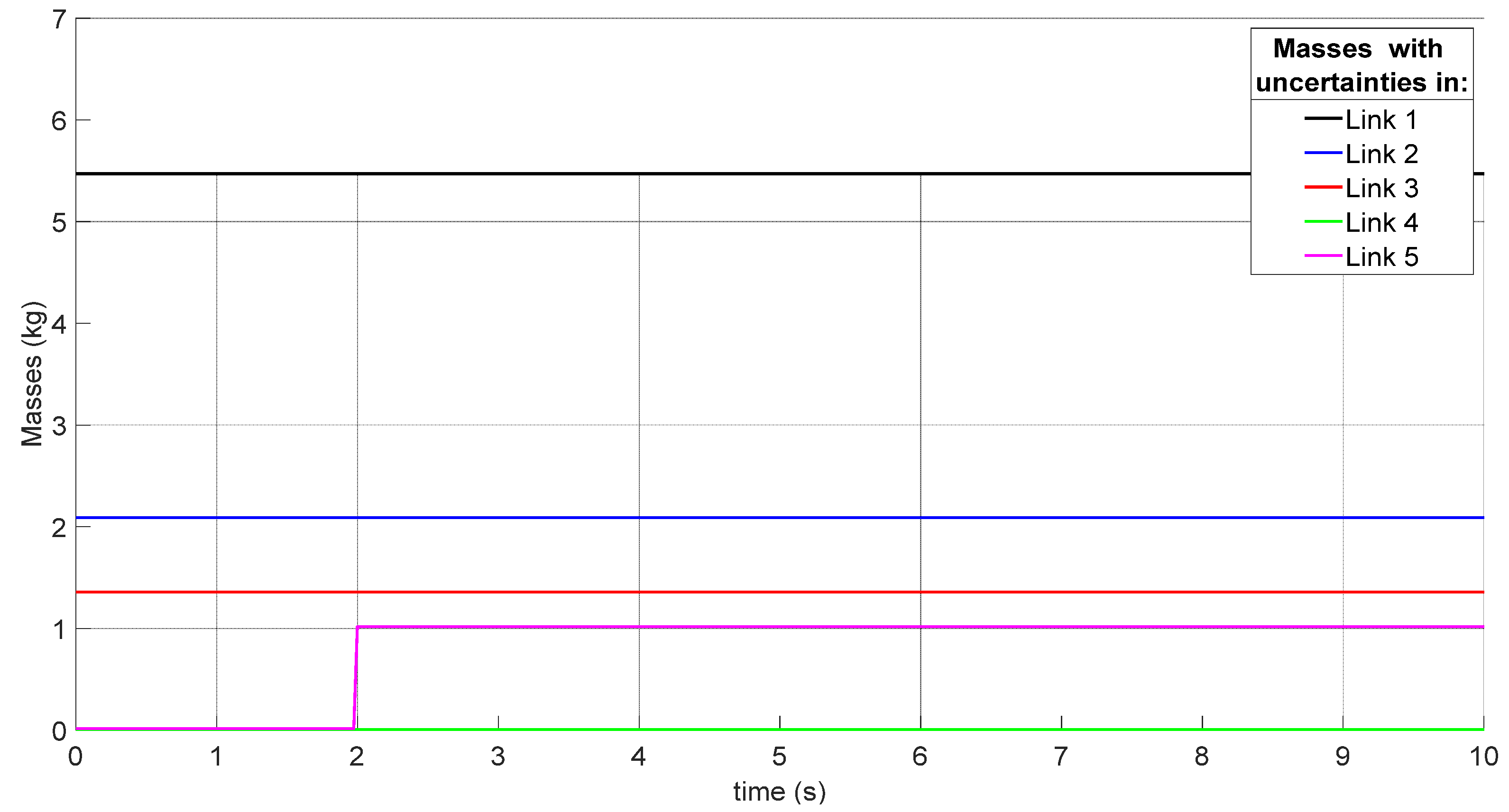
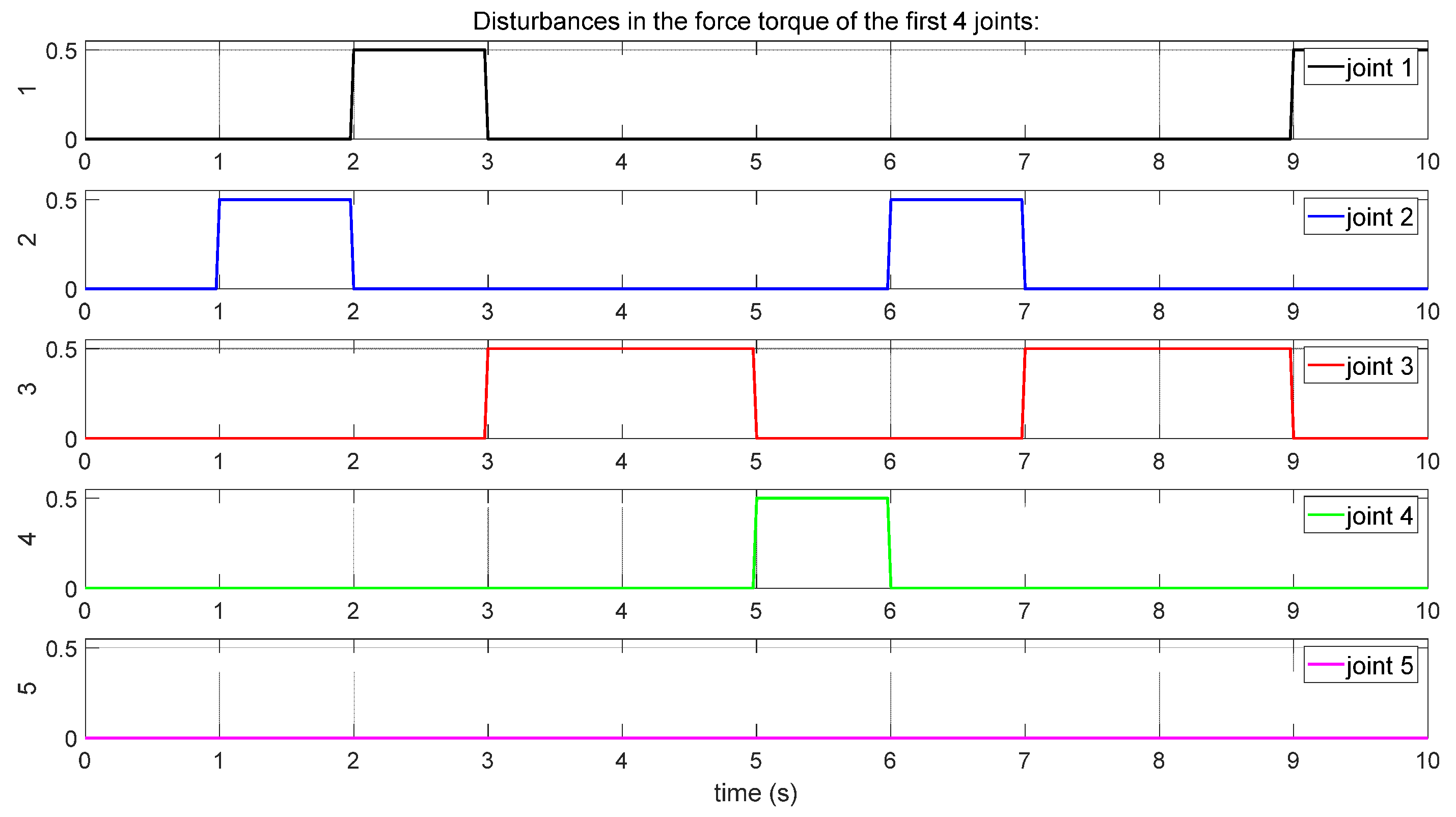
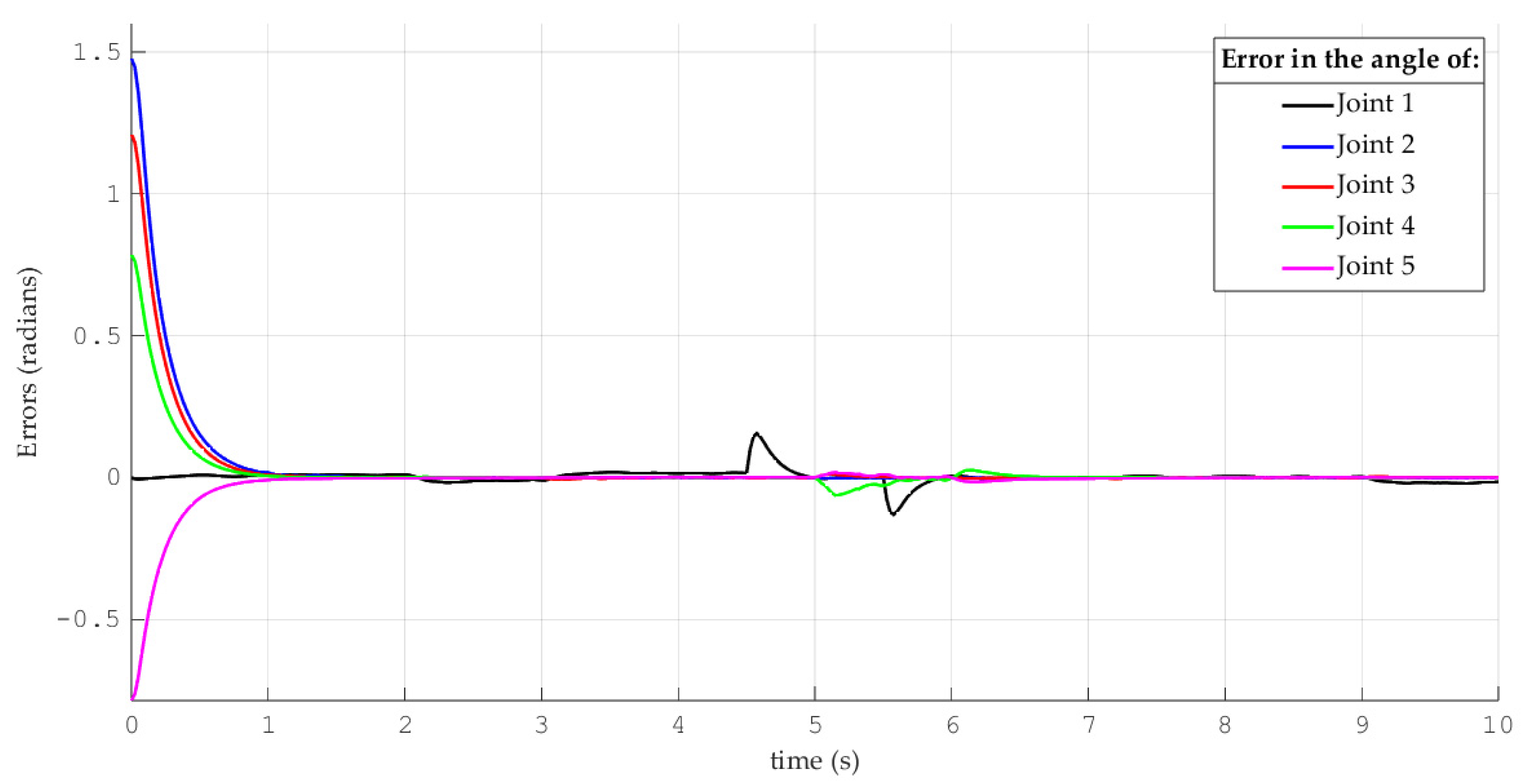
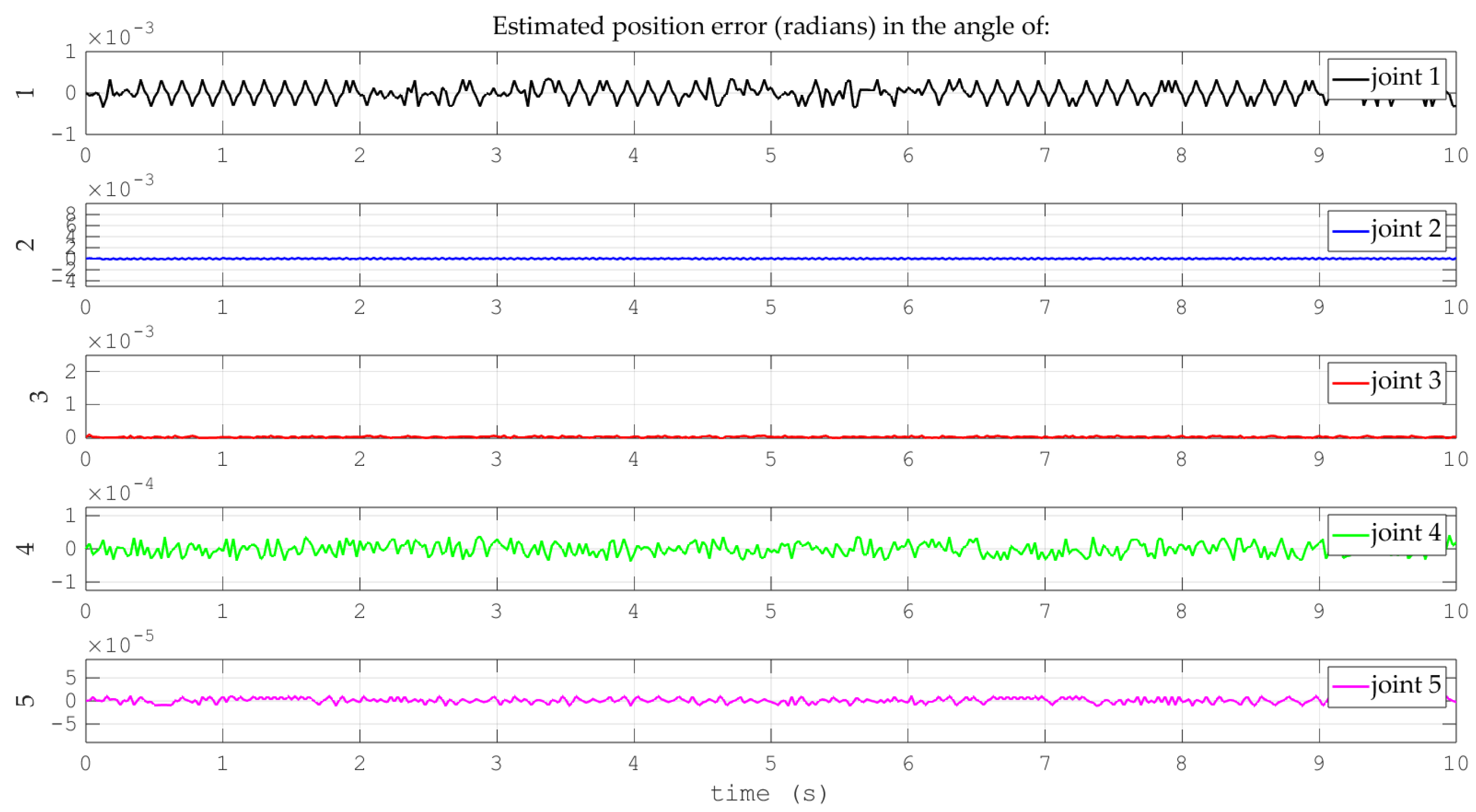

| Link Mass (kg) | Link Length (m) | Link Inertia (kg-m2) | Axis Length to Center of Mass (m) | Working Angle of Each Joint |
|---|---|---|---|---|
| m1 = 5.47 | l1 = 0.254 | I1 = 0.08822 | lc1 = 0.127 | J1: +180°/−180° |
| m2 = 2.09 | l2 = 0.254 | I2 = 0.03370 | lc2 = 0.127 | J2: +110°/0° |
| m3 = 1.36 | l3 = 0.254 | I3 = 0.02193 | lc3 = 0.127 | J3: +90°/−35° |
| m4 = 0.006 | l4 = 0.0508 | I4 = 0.02193 | lc4 = 0.0254 | J4: +110°/−110° |
| m5 = 0.6 | l5 = 0.01 | I5 = 0.00000039 | lc5 = 0.005 | J5: +180°/−180° |
| Parameter | Values Associated with the Joints | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 20 | 20 | 20 | 20 | 20 | |
| 5 | 15 | 5 | 2.5 | 5 | |
| 15 | 5 | 5 | 5 | 15 | |
| Parameter | Values Associated with the Joints | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 40 | 40 | 40 | 40 | 40 | |
| 150 | 150 | 150 | 150 | 150 | |
| 5 | 5 | 5 | 5 | 5 | |
| Performance Index | Values Associated with the Joints | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 0.1673 | 0.4728 | 0.3110 | 0.4102 | 0.7478 | |
| Ref. [35] | 0.0756 | 0.5701 | 0.5405 | 0.4599 | 1.1516 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacheco, J.; Cortés-Vega, D.; Alazki, H. Speed Sensorless Motion Control Scheme for a Robotic Manipulator Under External Forces and Payload Changes. Actuators 2025, 14, 209. https://doi.org/10.3390/act14050209
Pacheco J, Cortés-Vega D, Alazki H. Speed Sensorless Motion Control Scheme for a Robotic Manipulator Under External Forces and Payload Changes. Actuators. 2025; 14(5):209. https://doi.org/10.3390/act14050209
Chicago/Turabian StylePacheco, Jorge, David Cortés-Vega, and Hussain Alazki. 2025. "Speed Sensorless Motion Control Scheme for a Robotic Manipulator Under External Forces and Payload Changes" Actuators 14, no. 5: 209. https://doi.org/10.3390/act14050209
APA StylePacheco, J., Cortés-Vega, D., & Alazki, H. (2025). Speed Sensorless Motion Control Scheme for a Robotic Manipulator Under External Forces and Payload Changes. Actuators, 14(5), 209. https://doi.org/10.3390/act14050209






