Nonlinear Backstepping Fault-Tolerant Controllers with Extended State Observers for Aircraft Wing Failures
Abstract
1. Introduction
2. Design of Expanded State Observer for Aircraft Airflow Angle
2.1. State Observer Design
2.2. Observer Stability Analysis
3. Backstepping-Based Fault-Tolerant Controller Design
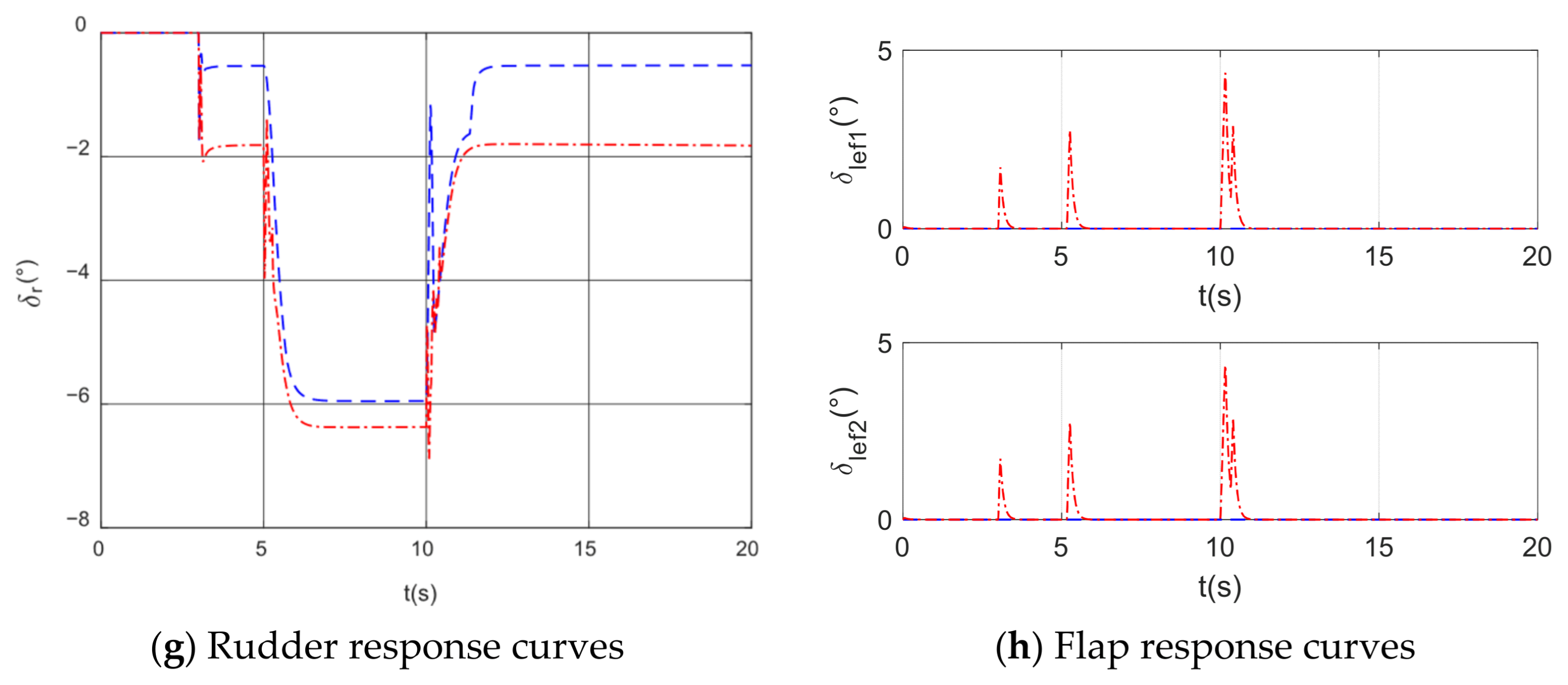
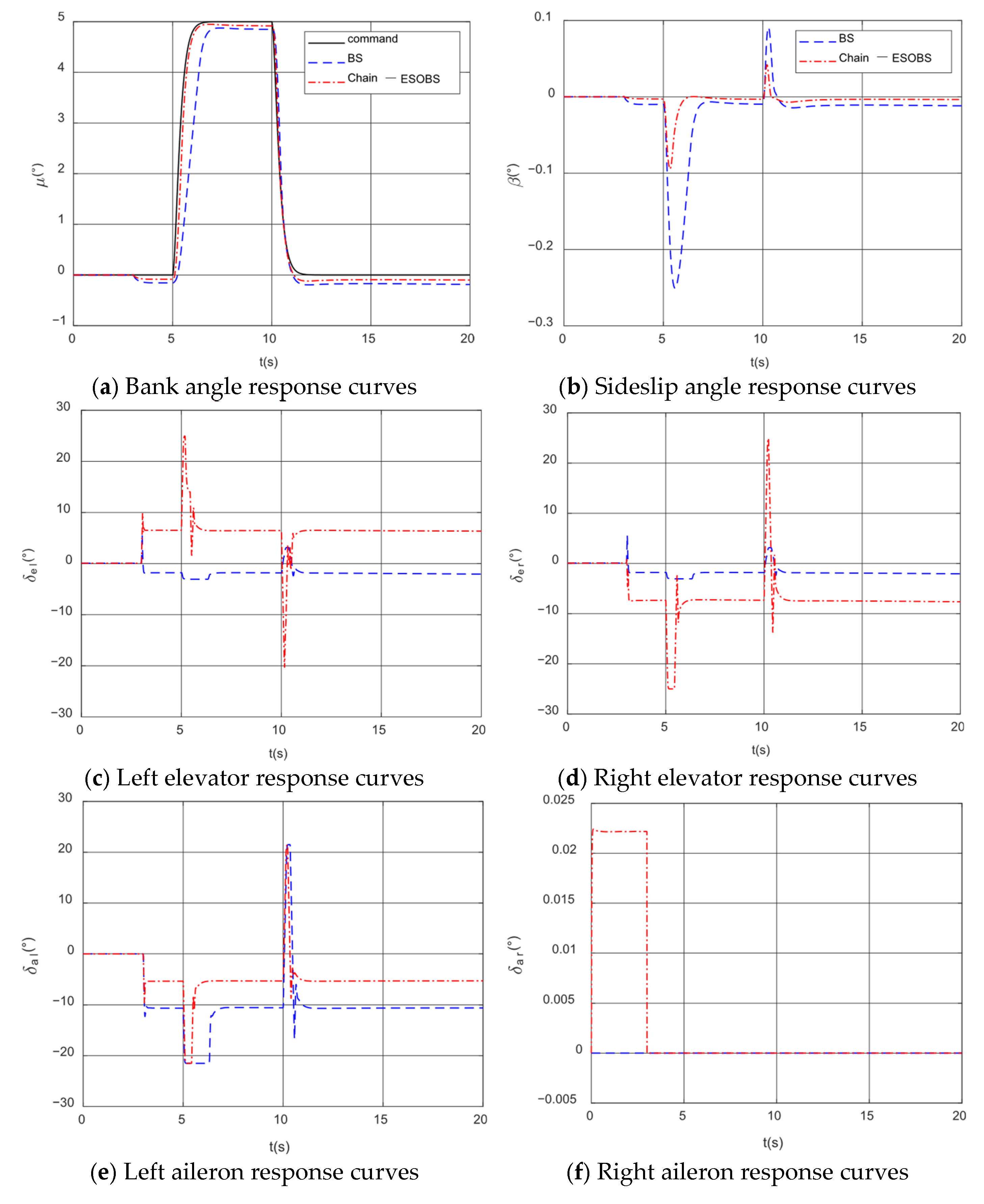
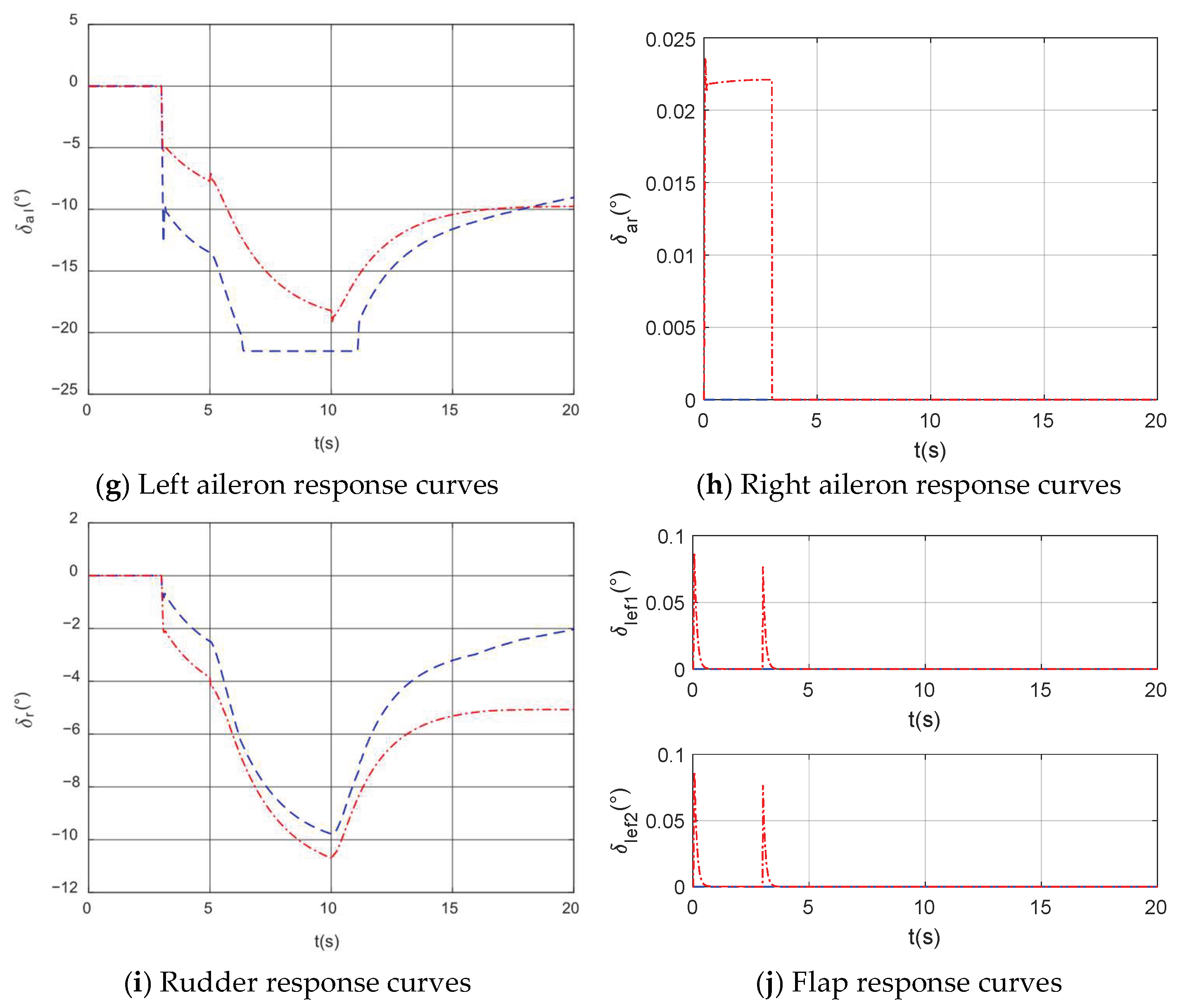
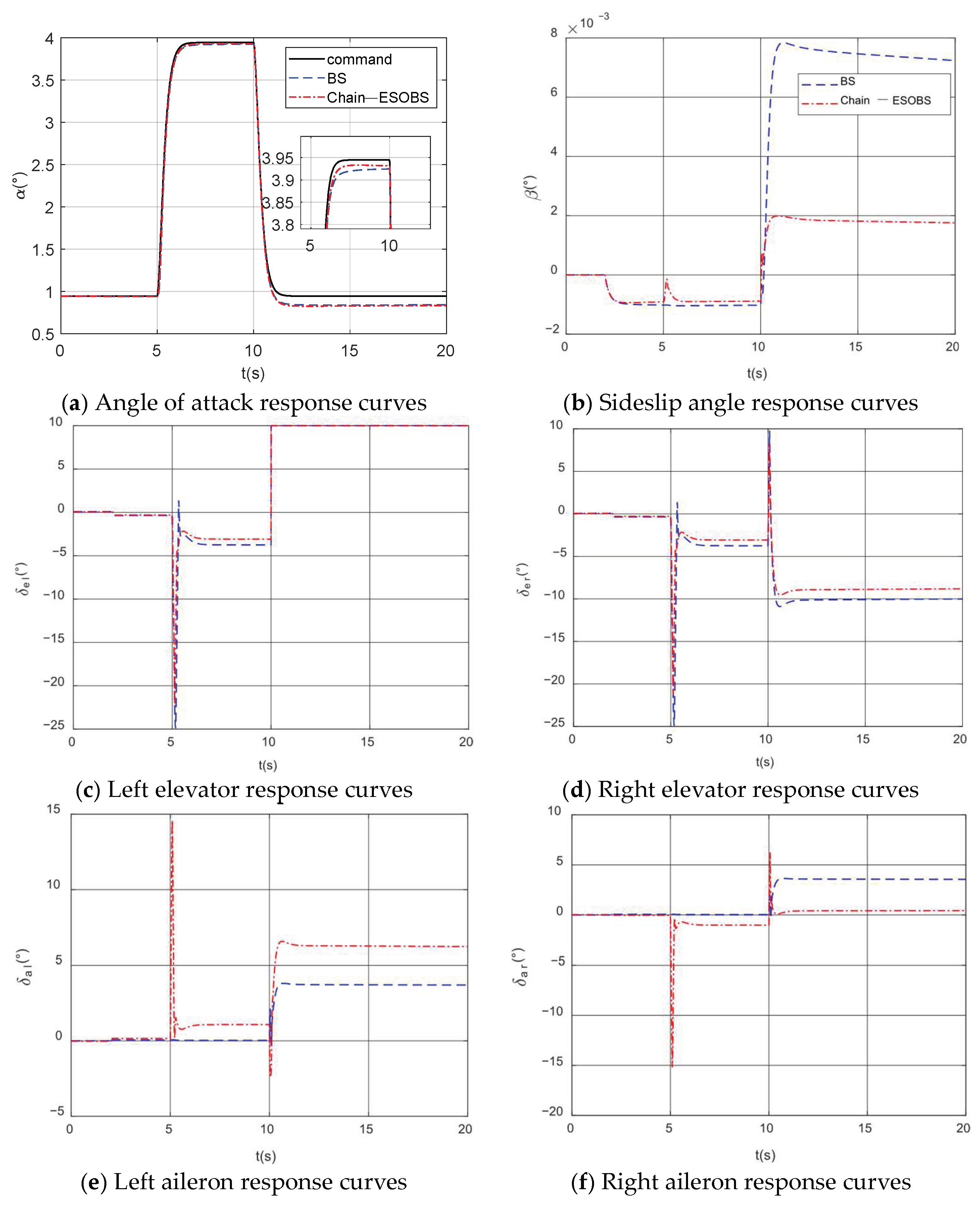
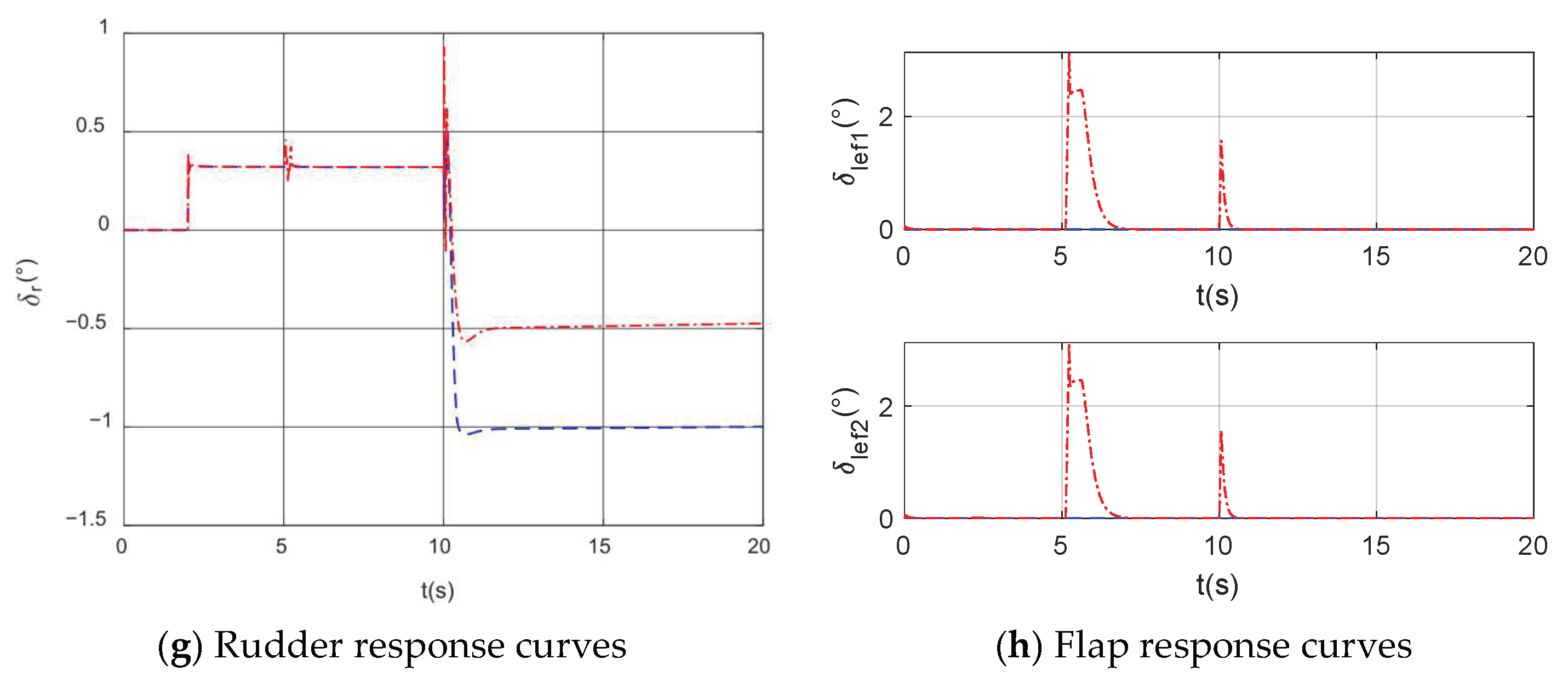
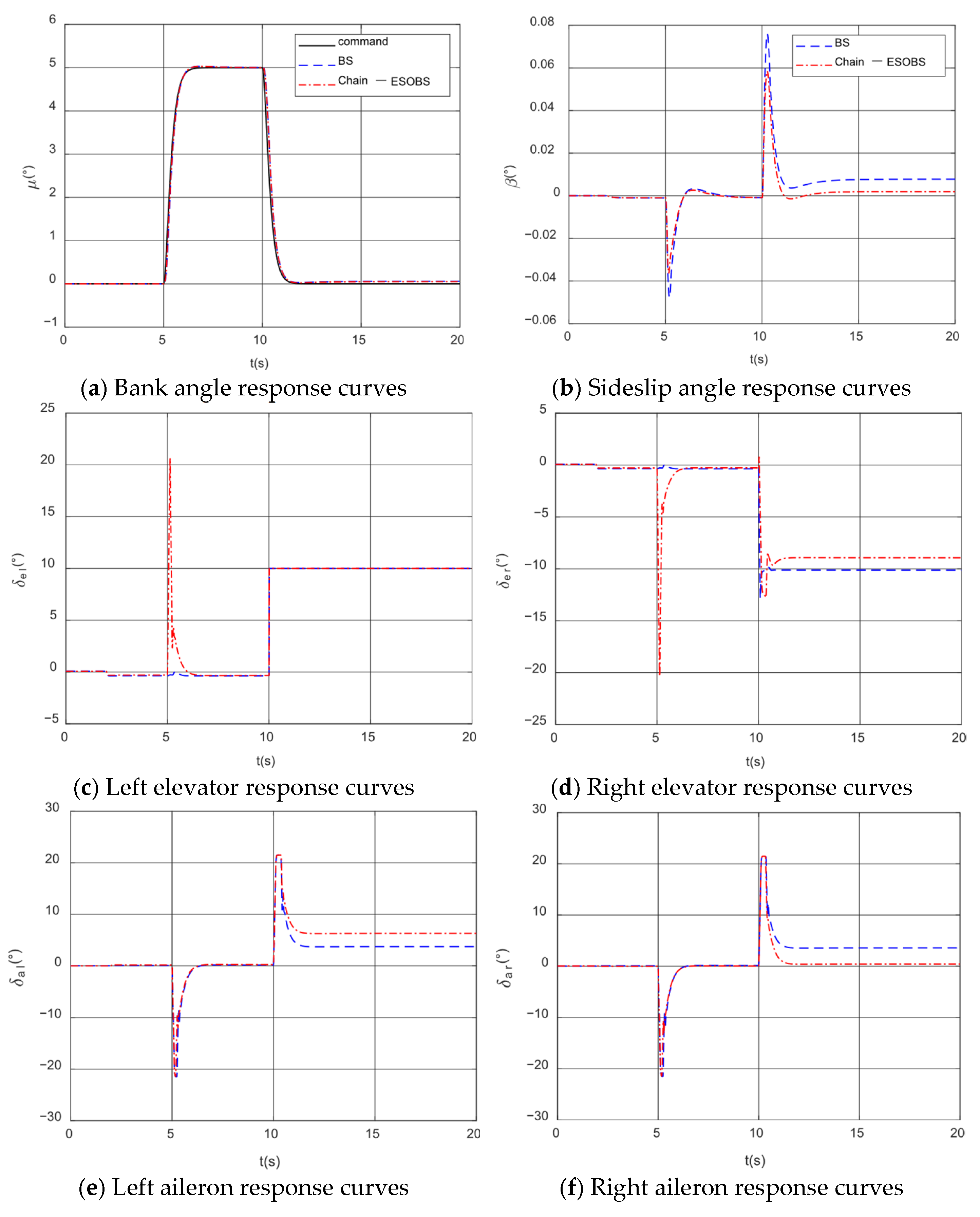
4. Simulation Analysis of Fault-Tolerant Control for Wing Surface Failure
4.1. Simulation of Fault-Tolerant Control for Wing Damage
4.2. Simulation of Fault-Tolerant Control for Elevator Failures
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Foster, J.; Cunningham, K.; Fremaux, C.; Shah, G.; Stewart, E.; Rivers, R.; Wilborn, J.; Gato, W. Dynamics modeling and simulation of large transport airplanes in upset conditions. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005; p. 5933. [Google Scholar]
- Rajagopal, K.; Balakrishnan, S.; Nguyen, N.; Krishnakumar, K. Robust adaptive control of a structurally damaged aircraft. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Shah, G. Aerodynamic effects and modeling of damage to transport aircraft. In Proceedings of the AIAA atmospheric flight mechanics conference and exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Yang, H.; Jiang, B.; Staroswiecki, M. Supervisory fault tolerant control for a class of uncertain nonlinear systems. Automatica 2009, 45, 2319–2324. [Google Scholar] [CrossRef]
- Lyu, Y.; Cao, Y.; Zhang, W. Dynamic surface control design of post-stall maneuver under unsteady aerodynamics. Aerosp. Sci. Technol. 2018, 80, 269–280. [Google Scholar] [CrossRef]
- Guerreiro, N.M.; Moutinho, A. Robust Incremental Backstepping Controller for the Attitude and Airspeed Tracking of a Commercial Airplane. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering, Brussels, Belgium, 22–25 July 2019. [Google Scholar]
- Cordeiro, R.A.; Azinheira, J.R.; Moutinho, A. Robustness of Incremental Backstepping Flight Controllers: The Boeing 747 Case Study. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3492–3505. [Google Scholar] [CrossRef]
- Safwat, E.; Zhang, W.; Kassem, M.; Mohsen, A. Robust Nonlinear Flight Controller for Small Unmanned Aircraft Vehicle based on Incremental BackStepping. In Proceedings of the AIAA SciTech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Singh, P.; Salahudden, S.; Karnam, A.; Singh, A. Flight Path Angle Control using Backstepping Dynamic Surface for Non-Strict Feedback System. In Proceedings of the AIAA Aviation Forum and ASCEND co-located Conference Proceedings, Las Vegas, NA, USA, 29 July–2 August 2024. [Google Scholar]
- Wang, X.; Van Kampen, E.J. Incremental Backstepping Sliding Mode Fault-Tolerant Flight Control. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Fei, A.L.; Li, N.; Li, S.Y. Active disturbance rejection backstepping control for UAVs. Control Theory Appl. 2016, 33, 1296–1302. [Google Scholar]
- Liu, Y. Research on Fixed-Wing UAV Control Method Based on Backstepping Adaptive; School of Automation, Harbin Engineering University: Harbin, China, 2015. [Google Scholar]
- Li, J.; Wang, N.; Hua, Y.; Song, X. Study on Disturbance Observer-Based Backstepping Control for Quadrotor. Comput. Simul. 2020, 37, 28–34. [Google Scholar]
- Zhang, Q.; Wang, C.; Xu, D. Robust adaptive backstepping control for a class of non-affine nonlinear system with full states constraints and input saturation. Control Decis. 2020, 35, 769–780. [Google Scholar]
- Zhuang, H. Research on Aircraft Attitude Control Method for Strong Disturbance and Maximum Allowable Damage; School of Artificial Intelligence, Nankai University: Tianjin, China, 2021. [Google Scholar]
- Zhang, Q.; Xu, H.; Xu, D.; Wang, C. Finite-time convergence backstepping control for a class of uncertain affine nonlinear systems based on disturbance observer. Control Theory Technol. 2020, 37, 747–757. [Google Scholar]
- Xu, H.; Yu, D.; Sui, S.; Zhao, Y.-P.; Chen, C.P.; Wang, Z. Nonsingular practical fixed-time adaptive output feedback control of MIMO nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7222–7234. [Google Scholar] [CrossRef] [PubMed]
- Al-Dujaili, A.Q.; Humaidi, A.J.; Pereira, D.A.; Ibraheem, I.K. Adaptive backstepping control design for ball and beam system. Int. Rev. Appl. Sci. Eng. 2021, 12, 211–221. [Google Scholar] [CrossRef]
- Hu, J.; Huang, J.; Gao, Z.; Gu, H. Position tracking control of a helicopter in ground effect using nonlinear disturbance observer-based incremental backstepping approach. Aerosp. Sci. Technol. 2018, 81, 167–178. [Google Scholar] [CrossRef]
- Wen, Y.; Zhou, Z.; Zhou, W.; Tang, X. Attitude Control of Quadrotor UAV Based on Extended State Observer and Backstepping Method. Meas. Control Technol. 2020, 39, 141–146. [Google Scholar] [CrossRef]
- Qin, H.; Chen, Z.; Sun, M. Longitudinal Control of Nonlinear Supercavitating Vehicle Based on Extended State Observer and Backstepping Method. Control Theory Appl. 2023, 40, 373–380. [Google Scholar]
- Zhao, M.; Wang, Y.; Wang, Y. Adaptive Backstepping Sliding Mode Control of SMA Drive System Based on Extended Observer. Mech. Electr. Eng. Technol. 2025, 1–7. [Google Scholar]
- Li, X.; Wang, C.; Guo, Y.; Li, A. Cooperative control for flight formation of tandem-rotor wheeled UAVs. Acta Aeronaut. Astronaut. Sin. 2022, 45, 1–12. [Google Scholar]
- Li, Y.; Wen, C.Y.; Liu, X.; Zhang, W.; Zheng, Y. Prescribed-Time Fault-Tolerant Flight Control for Aircraft Subject to Structural Damage. IEEE Trans. Aerosp. Electron. Syst. 2024, 61, 1848–1859. [Google Scholar] [CrossRef]
- Ming, R.; Liu, X.; Li, Y.; Zhang, W. Research on a backstepping flight control method improved by STFT in atmospheric disturbance applications. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2024, 238, 1534–1547. [Google Scholar] [CrossRef]





| State | Symbol | Unit | Trim Value |
|---|---|---|---|
| Thrust | 126,588.7576 | ||
| Left Elevator Deflection Angle | 0.074002 | ||
| Right Elevator Deflection Angle | 0.074002 | ||
| Left Aileron Deflection Angle | 0 | ||
| Right Aileron Deflection Angle | 0 | ||
| Rudder Deflection Angle | 0 | ||
| Flap Deflection Angle | 0 | ||
| Angle of Attack | 0.94483 | ||
| Sideslip Angle | 0 | ||
| Flight Altitude | 4000 | ||
| Flight Velocity | 200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, Y.; Wang, B.; Liu, X. Nonlinear Backstepping Fault-Tolerant Controllers with Extended State Observers for Aircraft Wing Failures. Actuators 2025, 14, 206. https://doi.org/10.3390/act14050206
Geng Y, Wang B, Liu X. Nonlinear Backstepping Fault-Tolerant Controllers with Extended State Observers for Aircraft Wing Failures. Actuators. 2025; 14(5):206. https://doi.org/10.3390/act14050206
Chicago/Turabian StyleGeng, Yansheng, Bo Wang, and Xiaoxiong Liu. 2025. "Nonlinear Backstepping Fault-Tolerant Controllers with Extended State Observers for Aircraft Wing Failures" Actuators 14, no. 5: 206. https://doi.org/10.3390/act14050206
APA StyleGeng, Y., Wang, B., & Liu, X. (2025). Nonlinear Backstepping Fault-Tolerant Controllers with Extended State Observers for Aircraft Wing Failures. Actuators, 14(5), 206. https://doi.org/10.3390/act14050206






