Finite-Time Control for Maneuvering Aircraft with Input Constraints and Disturbances
Abstract
1. Introduction
- A finite-time control law using a piecewise function technique was designed for controlling aircraft during flight maneuvers. In this way, the singularity issue of the backstepping-based finite-time control can be addressed.
- A HODO was designed to estimate disturbances during the maneuvering of aircraft. With this technique, the disturbance estimates can be fed forward into the control channel to effectively mitigate their adverse impacts.
- A novel FTAS was developed by introducing the control matrix into the design. By this means, this approach suppresses the adverse effects of input constraints on system performance and reduces the dependency on control parameters on the control matrix.
2. Problem Formulation
3. Design for High-Order Disturbance Observer-Based Finite-Time Control
3.1. Design for High-Order Disturbance Observer
3.2. Design for Finite-Time Control
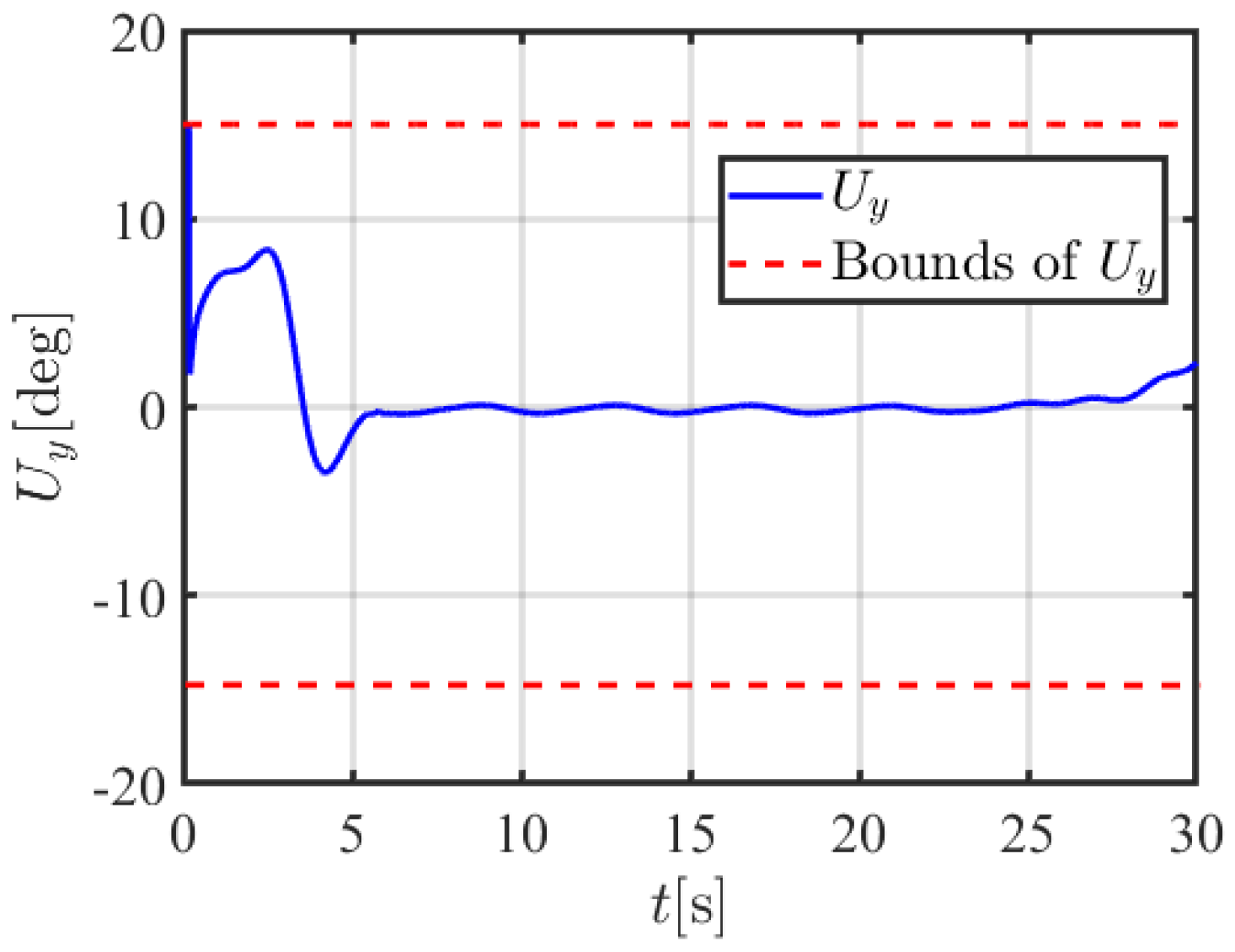
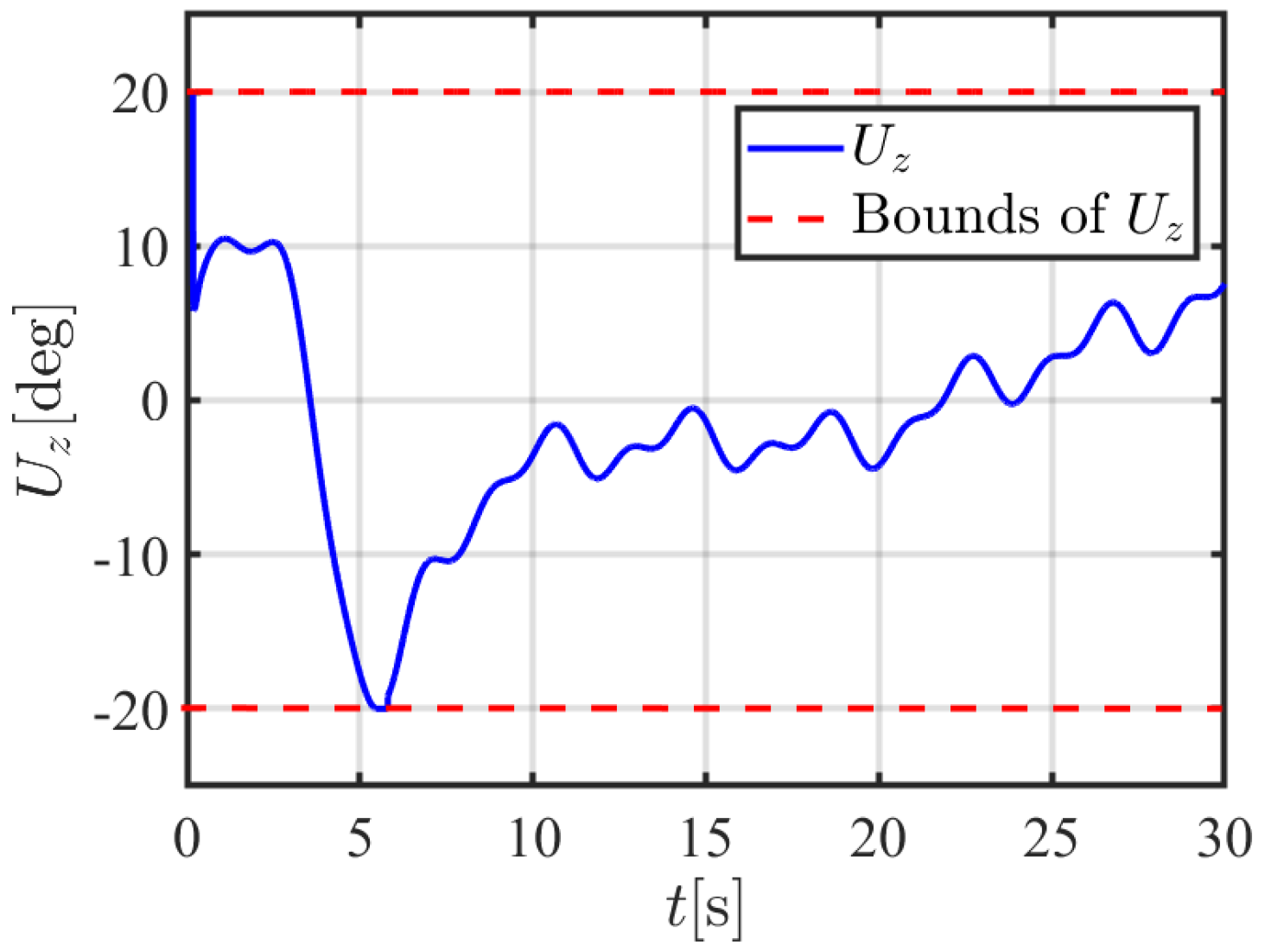
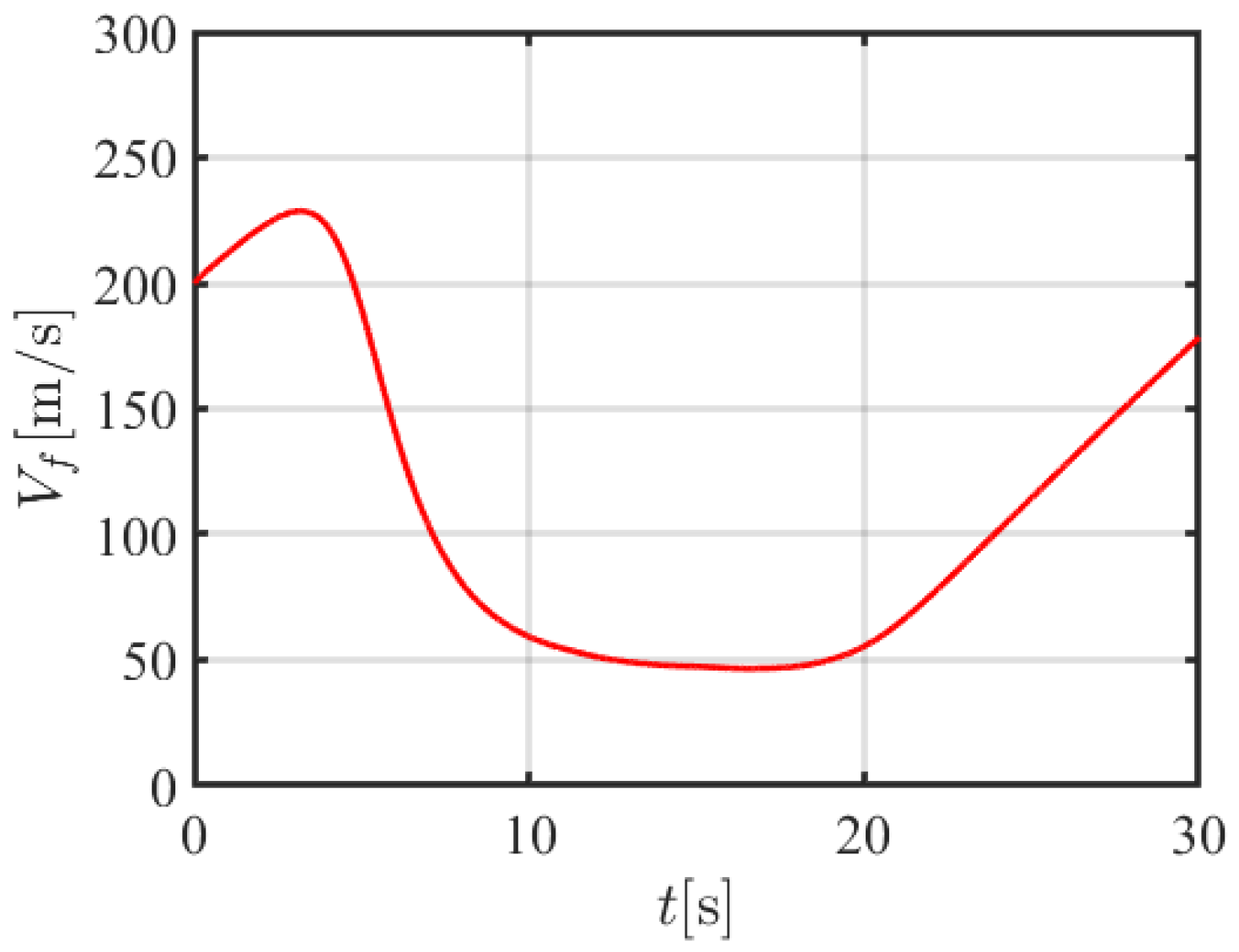
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boryaev, A.A. Parameters to assess the operation of thrust vector control systems in jet engines. Unmanned Syst. 2024, 12, 87–98. [Google Scholar] [CrossRef]
- Bai, S.; Wang, Y.; Liu, H.; Sun, X. Finite-thrust lambert transfer based on multistage constant-vector thrust control. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4947–4967. [Google Scholar] [CrossRef]
- Alkhedher, M. Comparative study of machine learning modeling for unsteady aerodynamics. CMC-Comput. Mater. Contin. 2022, 72, 1901–1920. [Google Scholar] [CrossRef]
- Wang, H.; Luo, Z.; Deng, X.; Zhou, Y.; Gong, J. Enhancement of flying wing aerodynamics in crossflow at high angle of attack using dual synthetic jets. Aerosp. Sci. Technol. 2024, 156, 109773. [Google Scholar] [CrossRef]
- Liu, J.; Ji, Y.; Xu, L.; Chen, Z. Extended state observer based generalized predictive control for aircraft at high angle of attack. Int. J. Control Autom. Syst. 2024, 22, 2578–2590. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, M. Event-triggering-learning-based ADP control for post-stall pitching maneuver of aircraft. IEEE Trans. Cybern. 2024, 54, 423–434. [Google Scholar] [CrossRef]
- Song, Y.; Tang, Y.; Ma, B.; Xu, B. A singularity-free online neural network-based sliding mode control of the fixed-wing unmanned aerial vehicle optimal perching maneuver. Optim. Control Appl. Methods 2023, 44, 1425–1440. [Google Scholar] [CrossRef]
- Goswami, S.; Kishore, G.; Kumar, N.; Saderla, S. Controller design and remote piloting training module development for unmanned cropped delta reflex wing configuration. Aerosp. Sci. Technol. 2024, 153, 109472. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, A.; Liang, X.; Zhang, X.; Qiu, J. Fixed-time stabilization of underactuated cart-pendulum system based on hierarchical sliding mode control method. Nonlinear Dyn. 2024, 112, 11187–11194. [Google Scholar] [CrossRef]
- Xu, X.; Liu, P.; Lu, S.; Wang, F.; Yang, J.; Xiao, G. Iterative learning with adaptive sliding mode control for trajectory tracking of fast tool servo systems. Appl. Sci. 2024, 14, 3586. [Google Scholar] [CrossRef]
- Geng, H.; Zhang, H.; Su, S. Asynchronously switched control With variable convergence rate for switched nonlinear Systems: A persistent dwell-time scheme. IEEE Trans. Fuzzy Syst. 2024, 32, 6695–6707. [Google Scholar] [CrossRef]
- Yuan, R.; An, Z.; Shao, S.; Chen, M.; Lungu, M. Dynamic event-triggered fault-tolerant cooperative resilient tracking control with prescribed performance for UAVs. Sci. China Inf. Sci. 2024, 67, 180205. [Google Scholar] [CrossRef]
- Chen, M.; Ma, H.; Kang, Y.; Wu, Q. Adaptive neural safe tracking control design for a class of uncertain nonlinear systems with output constraints and disturbances. IEEE Trans. Cybern. 2021, 52, 12571–12582. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Shi, D.; Lou, Y.; Zou, W.; Shi, L. Generalized multikernel maximum correntropy Kalman filter for disturbance estimation. IEEE Trans. Autom. Control 2024, 69, 3732–3747. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, Q.; Chen, B.; Ye, K.; Zhang, Q. Backstepping control based on adaptive neural network and disturbance observer for reconfigurable variable stiffness actuator. ISA Trans. 2024, 152, 318–330. [Google Scholar] [CrossRef]
- Hu, G.; Yang, W.; Pan, T.; Xu, D.; Yan, X. Observer-based hierarchical distributed model predictive control for multi-linear motor traction systems. ISA Trans. 2024, 151, 131–142. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, M. Robust backstepping control for maneuver aircraft based on event-triggered mechanism and nonlinear disturbance observer. Aircr. Eng. Aerosp. Technol. 2023, 95, 1016–1028. [Google Scholar] [CrossRef]
- Wu, D.; Chen, M.; Ye, H. High angle of attack flight control based on switched prescribed performance. Int. J. Adapt. Control Signal Process. 2020, 34, 1059–1079. [Google Scholar] [CrossRef]
- Ginoya, D.; Shendge, P.D.; Phadke, S.B. Sliding mode control for mismatched uncertain systems using an extended disturbance observer. IEEE Trans. Ind. Electron. 2014, 61, 1983–1992. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, M.; Ri, S.; Xiong, C.; Li, Z.; Kang, Y. High-order disturbance-observer-based sliding mode control for mobile wheeled inverted pendulum systems. IEEE Trans. Ind. Electron. 2020, 67, 2030–2041. [Google Scholar] [CrossRef]
- Wang, G.; Wang, X.; Li, S. Node task expansion based finite-time formation-containment control for ground-air collaboration systems. IEEE Trans. Netw. Sci. Eng. 2024, 11, 3346–3357. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, H.; Hua, C.; Li, J. Finite-time composite learning control for nonlinear teleoperation systems under networked time-varying delays. Sci. China Inf. Sci. 2024, 67, 162203. [Google Scholar] [CrossRef]
- Li, H.; Zhao, S.; He, W.; Lu, R. Adaptive finite-time tracking control of full state constrained nonlinear systems with dead-zone. Automatica 2019, 100, 99–107. [Google Scholar] [CrossRef]
- Van, M.; Do, V.T.; Khyam, M.O.; Do, X.P. Tracking control of uncertain surface vessels with global finite-time convergence. Ocean Eng. 2021, 241, 109974. [Google Scholar] [CrossRef]
- He, J.; Yang, X.; Zhang, C.; Xiao, M. Sliding mode consistency tracking control of multiple heavy haul trains under input saturation and safety distance constraints. J. Frankl. Inst.-Eng. Appl. Math. 2023, 360, 9028–9049. [Google Scholar] [CrossRef]
- Chen, M.; Yan, K.; Wu, Q. Multiapproximator-based fault-tolerant tracking control for unmanned autonomous helicopter with input saturation. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5710–5722. [Google Scholar] [CrossRef]
- Lu, S.; Pan, M.; Cheng, K.; Sun, Q. A new saturation control for uncertain system using diffeomorphism approach: Application to turbofan engine. IEEE Trans. Ind. Inform. 2024, 20, 8861–8872. [Google Scholar] [CrossRef]
- Song, M.; Zhang, F.; Huang, B.; Huang, P. Adaptive safe control for tethered aircrafts with input and output constraints. Int. J. Robust Nonlinear Control 2023, 33, 10716–10741. [Google Scholar] [CrossRef]
- Han, X.; Wang, B.; Liu, L.; Fan, H. Adaptive-critic-design based tracking controller for boost complement glide vehicle with performance constraint and input saturation. Aerosp. Sci. Technol. 2024, 145, 108839. [Google Scholar] [CrossRef]
- Li, J.; Wan, L.; Li, J.; Hou, K. Adaptive backstepping control of quadrotor aircrafts with output constraints and input saturation. Appl. Sci. 2023, 13, 8710. [Google Scholar] [CrossRef]
- Li, H.; Liu, C.; Zhang, Y.; Chen, Y. Practical fixed-Time consensus tracking for multiple Euler-Lagrange systems with stochastic packet losses and input/output constraints. IEEE Syst. J. 2022, 16, 6185–6196. [Google Scholar] [CrossRef]
- Gao, X.; Long, Y.; Li, T.; Hu, X.; Chen, C.L.P.; Sun, F. Optimal fuzzy output feedback control for dynamic positioning of vessels with finite-time disturbance rejection under thruster saturations. IEEE Trans. Fuzzy Syst. 2023, 31, 3447–3458. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, C.; Li, T.; Shen, H. Heading and velocity guidance based path following of autonomous surface vehicle with uncertainty attenuation and asymmetric saturated constraints. ISA Trans. 2023, 138, 88–105. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhao, Y.; Zhang, O.; Chen, W.; Wang, J.; Gao, Y.; Liu, J. A novel faster fixed-time adaptive control for robotic systems with input saturation. IEEE Trans. Ind. Electron. 2024, 71, 5215–5223. [Google Scholar] [CrossRef]
- Zuo, Z.; Tie, L. Distributed robust finite-time nonlinear consensus protocols for multi-agent systems. Int. J. Syst. Sci. 2016, 47, 1366–1375. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, W. Adaptive finite-time anti-disturbance fuzzy control for uncertain time-delay nonlinear systems and its application to SVC. Fuzzy Sets Syst. 2023, 472, 108699. [Google Scholar] [CrossRef]
- Yan, X.; Chen, M.; Feng, G.; Wu, Q.; Shao, S. Fuzzy robust constrained control for nonlinear systems with input saturation and external disturbances. IEEE Trans. Fuzzy Syst. 2021, 29, 345–356. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Z. Finite-time block backstepping control for rudder roll stabilization with input constraints. Ocean Eng. 2024, 295, 116989. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, M.; Lungu, M.; Guo, H. Decoupled finite-time approximation auxiliary system-based three-dimensional integrated guidance and control. IEEE Trans. Autom. Sci. Eng. 2025, 22, 6100–6112. [Google Scholar] [CrossRef]
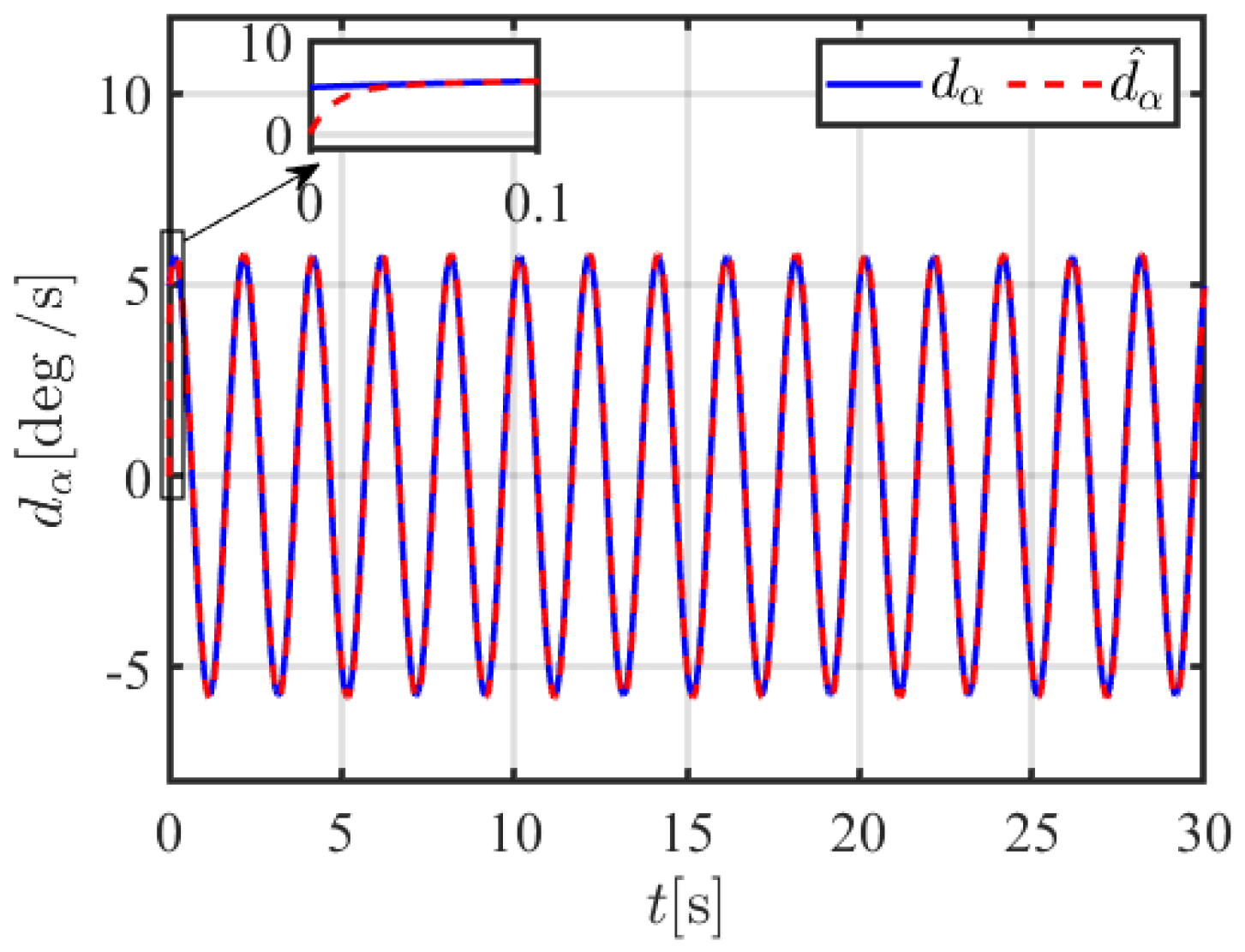
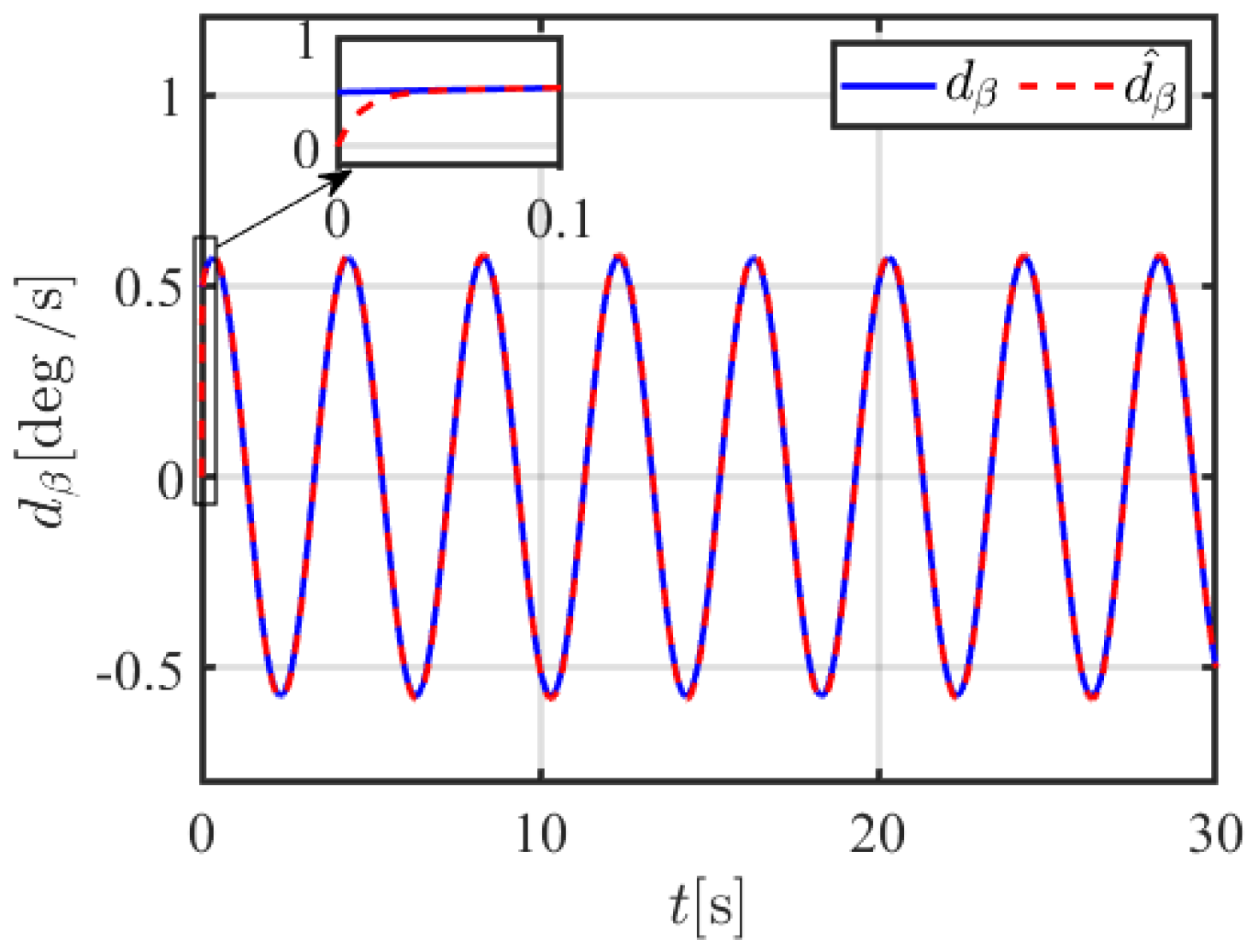




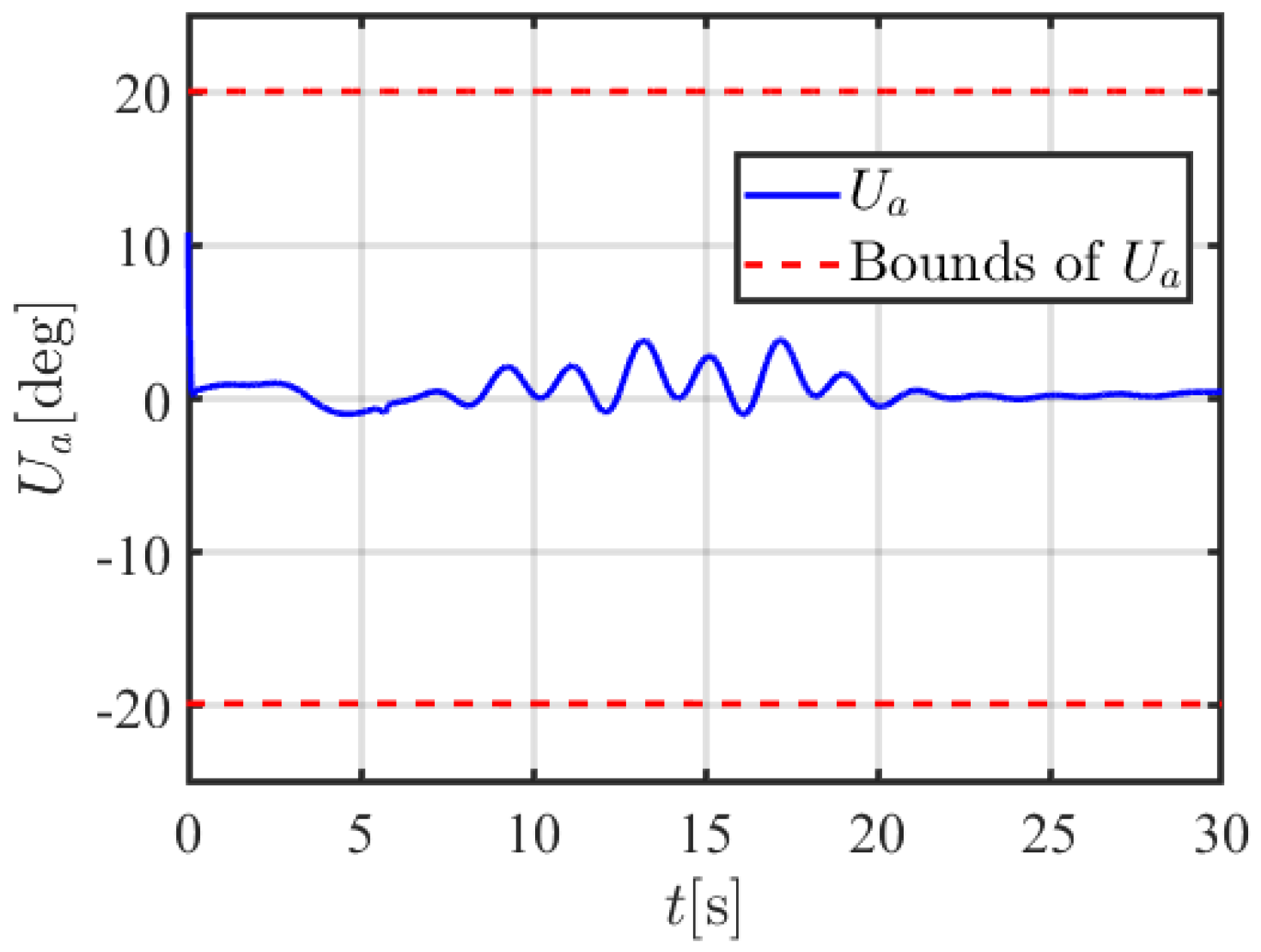
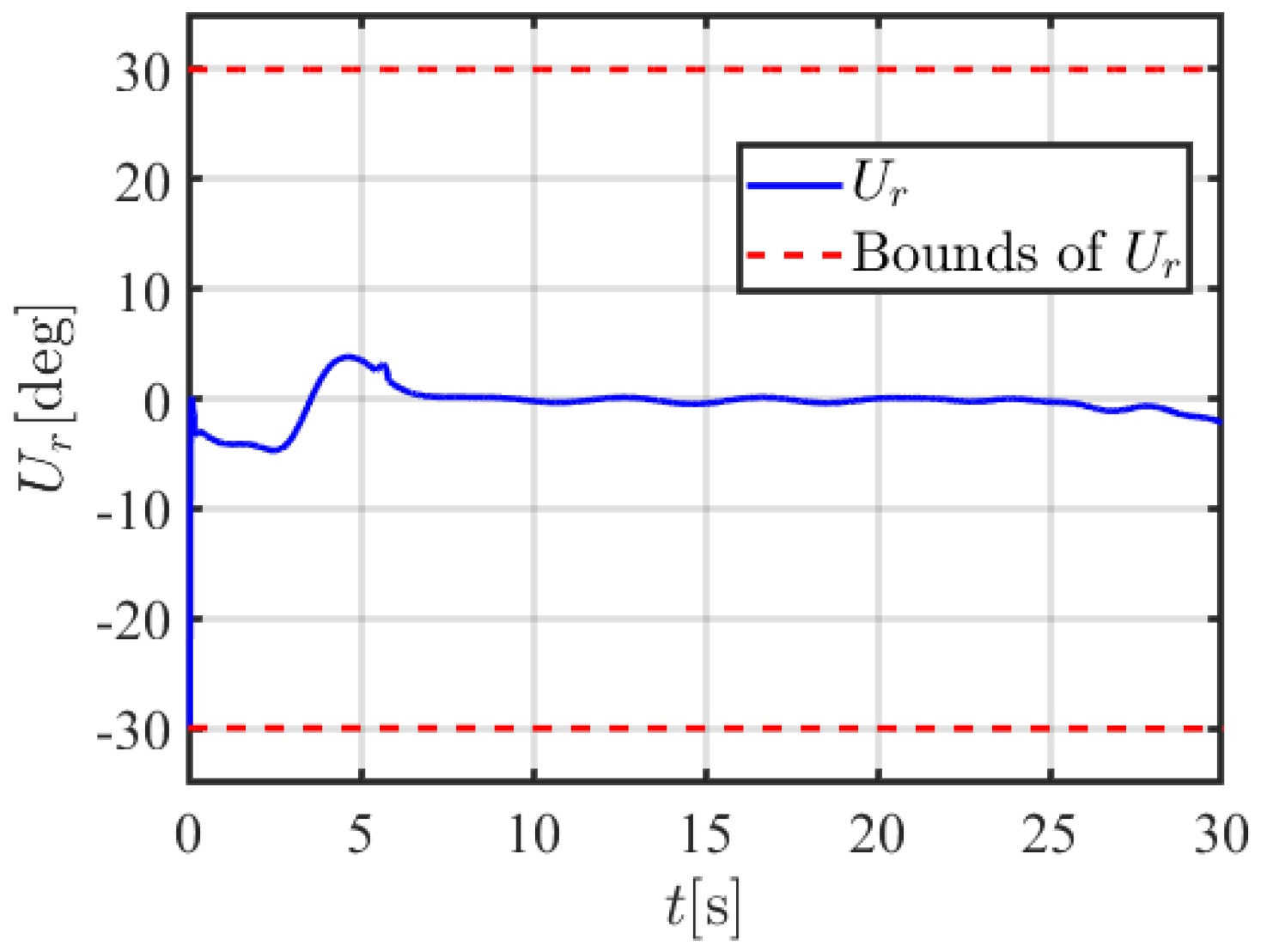




| Symbol | Value | Symbol | Value | Symbol | Value |
|---|---|---|---|---|---|
| 22,682 | 1.11164 [] | 8.5 [m] | |||
| 77,095 [] | 200 [m/s] | 146,000 [kN] | |||
| 95,561 [] | 57.7 [] | 10,617 [kg] | |||
| 1125 [] | 13.11 [m] | g | 9.8 [] |
| Symbol | Value | Symbol | Value | Symbol | Value | Symbol | Value |
|---|---|---|---|---|---|---|---|
| 3 | 4 | ||||||
| 100 | 4 | 100 | 8 | ||||
| 100 | 4 | 100 | 8 | ||||
| 100 | 100 | 8 | |||||
| 4 | 100 | 8 | |||||
| 4 | 100 | 8 | |||||
| 4 | 100 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Shen, Y.; Chen, M. Finite-Time Control for Maneuvering Aircraft with Input Constraints and Disturbances. Actuators 2025, 14, 194. https://doi.org/10.3390/act14040194
Zhou Z, Shen Y, Chen M. Finite-Time Control for Maneuvering Aircraft with Input Constraints and Disturbances. Actuators. 2025; 14(4):194. https://doi.org/10.3390/act14040194
Chicago/Turabian StyleZhou, Zhangyong, Yaohua Shen, and Mou Chen. 2025. "Finite-Time Control for Maneuvering Aircraft with Input Constraints and Disturbances" Actuators 14, no. 4: 194. https://doi.org/10.3390/act14040194
APA StyleZhou, Z., Shen, Y., & Chen, M. (2025). Finite-Time Control for Maneuvering Aircraft with Input Constraints and Disturbances. Actuators, 14(4), 194. https://doi.org/10.3390/act14040194







