A Novel Cycloid Tooth Profile for Harmonic Drive with Fully Conjugate Features

Abstract

A harmonic drive (HD) is a precision reduction device widely utilized in the core joints of high-end equipment such as spacecraft and robots. The design of an excellent tooth profile is the core challenge related to the performance of HD. This investigation aims to propose a design method of a fully conjugated cycloid tooth profile (CTP) for HD. Firstly, the rationality of CTP use for HD is analyzed, and the cycloidal characteristics of the tooth trajectory are studied by use of canonical warping distance. Then, initial CTP equations are constructed, adopting the trajectory mapping results. Presetting the addendum CTP of circular spline, the conjugate CTP of flexspline is then designed using the envelope method. Subsequently, the envelope of the designed flexspline addendum is used to reverse-design the circular spline dedendum. The backlash is calculated to evaluate the CTPs designed with different radial displacement coefficients. Research shows that the tooth trajectory has cycloidal characteristics; therefore, the HDs that use CTP can realize a fully conjugate engagement. Moreover, the variable control parameters enable the proposed CTP expression to have excellent fitting characteristics, resulting in small and uniform mesh backlash distribution. The CTP is expected to become one of the ideal tooth profiles of HD.

1. Introduction

A harmonic drive (HD) is a lightweight transmission mechanism that aligns with the stringent requirements of spacecraft reducers—namely, light weight, compact dimensions, and exceptional precision—while simultaneously offering robust load-bearing capabilities. Consequently, HD has found extensive applications across diverse fields, including robotics, aerospace systems, and medical devices [1,2,3]. A central challenge in HD research stems from the fluctuating deformations of the flexspline (FS), which has rendered the meshing theory and tooth profile (TP) design enduringly complex and pivotal areas of investigation within this domain.

Numerous research methodologies have been developed to investigate the meshing theory of HD, with the envelope method and the kinematic method being the most widely adopted. Shen et al. [4] established a generalized formula for calculating the conjugate TP of HDs using the envelope method. Building on this, Chen et al. [5] introduced a precise envelope algorithm that accounts for the elastic deformation of the FS. Recognizing the influence of the wave generator (WG) shape on the relative motion between the FS and the circular spline (CS) [6], Yang et al. [7] developed an exact solution method for determining the conjugate TP based on cam profiles. Further advancing the field, Dong et al. [8] conceptualized the FS and WG as a cam-follower mechanism, providing a rigorous analysis and detailed description of the planar kinematic model of HDs. In a comparative study, Wang et al. [9] evaluated the kinematic method and the envelope method through the design outcomes of a double circular arc TP, concluding that the envelope method offers superior accuracy.

In the context of TP design, HD initially employed a straight TP to achieve surface-to-surface contact between tooth surfaces. However, this approach failed to account for the circumferential displacement and normal deflection of the tooth rim. Consequently, the technologically mature, involute TP was later widely adopted in HDs. Maiti [10] demonstrated that an unmodified involute TP could function effectively through the strategic design of the cam. The application and refinement of involute TPs in HDs have been extensively studied [11,12]. Nevertheless, involute HDs exhibit poor conjugate characteristics, relying primarily on cusp meshing at the tooth tips to achieve multi-tooth engagement [4]. This cusp meshing condition, however, tends to disrupt the lubricant film and accelerate tooth wear, rendering the involute profile suboptimal for HD applications. Additionally, while the involute TP of the CS as an internal gear is concave, Ivanov [13] proposed that the CS TP should be convex based on an analysis of the motion characteristics of the FS teeth. This insight led Ivanov to pioneer the double-arc TP for HDs. Since its introduction, the double circular arc TP has become the dominant approach in HD profile design [14,15]. The double circular arc TP not only significantly enhances the conjugate existence interval of HDs by incorporating a convex TP for the CS [16,17] but also further improves meshing performance by synchronizing the convex and concave segments of the CS through the utilization of double-conjugate characteristics [18,19].

The distinctive characteristics of the double-arc TP have inspired the development and design of novel TPs for HD. Ishikawa et al. [20] introduced an S-shaped TP directly derived from the halved mapping of the tooth trajectory using the rack approximation method. This innovative profile incorporates both concave and convex segments. Through appropriate TP modifications [21], which address the interference caused by the normal deflection angle of the FS, the S-shaped TP achieves continuous contact with similarly designed profiles. In a comparative study, Wang et al. [22] evaluated the double-arc TP designed via the envelope method and the S-shaped TP developed using the rack approximation method, revealing that the S-shaped profile exhibits smaller and more uniform meshing backlash. As a result, both the double circular arc TP and the S-shaped TP have gained widespread adoption in HD applications.

The studies on the double-arc TP and the S-shaped TP demonstrate that it is both logical and effective to consider the motion characteristics of HD and to design TPs directly based on the motion trajectory of gear teeth. Shen et al. [4] observed that the relative motion trajectory of HD tooth approximates a cycloid. Building on this insight, Le et al. [23] proposed a cycloidal TP (CTP) composed of epicycloid and inner cycloid segments for HDs. Subsequently, the CTP was further refined through the TP angle design [24] to eliminate interference within the backlash [25]. This CTP exhibits theoretical properties akin to those of the double circular arc TP. However, the current CTP is not directly derived from the tooth trajectory, suggesting that there remains significant potential for further optimization and improvement of this profile.

The objective of this paper is to propose a novel construction and design methodology for a CTP tailored for HD, leveraging the combined advantages of trajectory mapping and the envelope method. First, canonical correlation analysis is employed to validate the cycloidal characteristics of the tooth trajectory, followed by the formulation of a CTP equation for HD with variable coefficients. While this equation is inspired by the trajectory mapping method, it is not constrained by its results; instead, the variable coefficients ensure the design flexibility of the CTP. Subsequently, the CTPs of the FS and CS are meticulously designed using the envelope method and the bidirectional conjugate design flow [16].

In addition to the Introduction section, this article is structured as follows. Section 2 analyzes the rationality of the CTP, calculates the HD tooth trajectories, and verifies their cycloidal characteristics. Section 3 constructs the initial cycloidal equations for the TP based on the trajectory mapping relationship and presents the bidirectional conjugate design process for the CTP using the envelope method. Section 4 provides an example of a TP design, discussing the designed CTP in terms of its conjugate characteristics and backlash distribution. Section 5 examines the results of the TP design under varying deformation magnitudes. Finally, Section 6 summarizes the main conclusions of this paper.

2. Rationality Analysis of Cycloid Tooth Profile

When the WG is installed, the FS undergoes deformation, forming a differential meshing relationship with the CS. As the WG rotates, a periodic “meshing in–meshing out” motion is established between the teeth of the FS and CS. This section calculates the tooth trajectory of the HD, extracts the coordinates of several points on the trajectory as the query array s₁, and compares it with a reference array s₂ extracted from a general cycloid. By employing canonical correlation analysis, the similarity between the tooth trajectory and the general cycloid is verified using the canonical time warping distance. Furthermore, a cycloidal expression for the tooth trajectory is constructed, thereby validating the rationality of applying a CTP to HDs based on tooth trajectory mapping.

2.1. Calculation of Tooth Trajectory

As illustrated in Figure 1, the neutral circle of the FS with radius r_m undergoes elliptical deformation under the influence of the WG. The coordinate system S₀-OXY is fixed to the WG, with point O at the center of rotation and the Y-axis aligned with the major axis of the WG. The coordinate system S₁-O₁X₁Y₁ is fixed to the FS tooth, with point O₁ located on the neutral line of the FS and the Y₁-axis aligned with the symmetry line of the tooth (normal at point O₁). ρ is the polar radius of point O₁. The coordinate system S₂-OX₂Y₂ is fixed to the CS tooth, with the Y₂-axis aligned with the symmetry line of the tooth space. The angle φ represents the initial position of point O₁ relative to the Y-axis, while φ₁ denotes the angle between their new positions after deformation.

Assuming negligible elongation of the FS under internal deformation forces [26], the midline non-elongation assumption is approximately satisfied. Consequently, the angles φ and φ₁ are related as follows:

$$\phi ={\displaystyle \frac{1}{r_{\mathrm{m}}}}{\displaystyle {\int }_0^{\varphi }\sqrt{{\rho }^2+{{\rho }^{\prime }}^2}\mathrm{d}{\phi }_1},$$

(1)

here, the integral limit ϕ is equal to the related angle φ₁ of the polar radius ρ.

φ₂ denotes the angle between the symmetry line of the CS tooth space and the Y-axis.

$${\phi }_2=\phi z_1/z_2,$$

(2)

here, z₁ and z₂ denote the tooth number of FS and CS, respectively. The angle between the FS tooth positioning point O₁ and the symmetry line of the corresponding CS tooth space is as follows:

$${\theta }_{\gamma }={\phi }_1-\phi z_1/z_2,$$

(3)

Additionally, θ_μ represents the deflection angle of the normal to the neutral line of the deformed FS, i.e., the angle between the tooth symmetry line and the polar diameter ρ. According to the exact algorithm [5],

$${\theta }_{\mathrm{\mu }}=-\arctan \left({\rho }^{\prime }/\rho \right),$$

(4)

θ_p represents the angle between the symmetry line of the CS tooth space and the symmetry line of the FS tooth, which form the corresponding meshing tooth pair.

$${\theta }_{\mathrm{p}}={\theta }_{\mathrm{\mu }}+{\theta }_{\mathrm{\gamma }},$$

(5)

The deflection angle θ_μ influences the trajectory of any point on the FS’s TP but does not affect the trajectory of the positioning point O₁, which lies on the neutral line. Therefore, to simplify the problem, the trajectory of point O₁ is taken as the tooth trajectory to be studied. As illustrated in Figure 1, when the FS undergoes deformation, O₁ is allocated a polar diameter ρ in the coordinate system S₀. Consequently, the coordinates of point O₁ in the coordinate system S₂ are as follows:

$$\left\{\begin{array}{c}{x}_{2O_1}=\rho \sin {\theta }_{\mathrm{\gamma }}\\ y_{2O_1}=\rho \cos {\theta }_{\mathrm{\gamma }}\end{array}\right.,$$

(6)

here, both ρ(φ₁) and θ_γ are functions of the polar angle φ₁, indicating that when φ₁ varies between 0 and π/2, the tooth trajectory expressed in coordinate system S₂ can be obtained using Equation (6). From Equation (6), it is evident that the tooth trajectory ultimately depends on the deformation shape of the neutral line of the FS, which is determined by ρ(φ₁).

2.2. Cycloid Characteristic of Tooth Trajectory

Analytically deriving formulas to demonstrate the similarity between the tooth trajectory and a general cycloid is highly challenging. Instead, a discrete point similarity analysis method can be effectively employed to study the cycloidal characteristics of the tooth movement locus. Canonical correlation analysis (CCA), a widely recognized method for identifying correlations between two sets of multidimensional variables [27], serves as a suitable tool for this purpose. During the analysis, the correlation variables s_1α and s_2β are constructed by introducing projection transformation matrices α and β for any sequence s₁ and s₂ and then used to determine the correlation coefficients, with their corresponding transformation matrices α and β adhering to the principle of maximum correlation. In CCA, the correspondence of elements in s₁ and s₂ follows the original element order.

Therefore, relying solely on canonical CCA is insufficient to accurately judge the similarity between two curves with distorted shapes. To address this limitation, canonical time warping (CTW) [28] is introduced. CTW iteratively adjusts the correspondence between the elements of sequences s₁ and s₂ and performs the projection transformations α and β to minimize the residual sum of squares (RSS) of the two sequences. The minimum RSS obtained for sequences s₁ and s₂ through two levels of optimization—CCA and CTW—is defined as the canonical warping distance (CWD).

$$J_{\mathrm{s}}={\displaystyle \sum _{i=1}^k{\left({\alpha }_i{s}_1[n_i]-{\beta }_i{s}_2[m_i]\right)}^2},$$

(7)

here, n_i and m_i represent the correspondence of sequences s₁ and s₂ after CTW, respectively; s₁[n_i] and s₂[m_i] denote the corresponding elements; α_i and β_i are the elements in the projection matrices, and k is the elements number of s₁[n_i] and s₂[m_i]. CTW demonstrates superior robustness to spatial transformations, enabling the CWD to accurately capture the similarity between two sequences, even in the presence of relative displacement, rotation, and scaling in space.

An arbitrary model with the parameters listed in

Table 1. Parameters of the trajectory calculation model.

Parameter	Symbol	Value
Gear modulus	m	0.5 mm
Tooth number of FS	z1	200
Tooth number of CS	z2	202
Radius of FS neutral circle	rm	48.75 mm
Max. radial displacement coefficient	w0*	1

is established for the tooth trajectory calculation. The maximum radial displacement coefficient w₀* in Table 1 is defined as the ratio of the designed maximum radial displacement w₀ of the FS to the modulus m, i.e., w₀* = w₀/m.

Taking the deformation of the FS under the action of the elliptical WG as an example, the polar coordinate expression of the neutral line of the FS after deformation is as follows:

$$\rho ={\displaystyle \frac{{\rho }_{\mathrm{a}}{\rho }_{\mathrm{b}}}{\sqrt{{\rho }_{\mathrm{a}}^2{\sin }^2{\phi }_1+{\rho }_{\mathrm{b}}^2{\cos }^2{\phi }_1}}},$$

(8)

here,

$${\rho }_{\mathrm{a}}=r_{\mathrm{m}}+m{w}_0^{*},$$

$${\rho }_{\mathrm{b}}=\left(1/9\right)\left[(12r_{\mathrm{m}}-7{\rho }_{\mathrm{a}})+4\sqrt{{\rho }_{\mathrm{a}}(3r_{\mathrm{m}}-2{\rho }_{\mathrm{a}})}\right],$$

represent the polar diameters of the major axis and the minor axis of the FS’s neutral line, respectively. The tooth trajectory of the model specified in Table 1 is calculated for φ₁, ranging from 0 to π/2 using Equation (6). The coordinates of 90 points on the trajectory are extracted to form the query sequence s₁.

The general expression of the cycloid formed by the trajectory of a point fixed on a circle as the circle rolls along a straight line is obtained using the following equation [29]:

$$\left\{\begin{array}{l}{x}_{\mathrm{t}}=r_{\mathrm{g}}\left(t-\sin t\right)\hfill \\ y_{\mathrm{t}}=r_{\mathrm{g}}\left(1-\cos t\right)\hfill \end{array}\right.,$$

(9)

Let the radius of the rolling circle be r_g = 1 mm, the coordinates of 90 points on the cycloid are calculated for t, ranging from 0 to π, by using Equation (9) to form the reference sequence s₂. The tooth trajectory sequence s₁ and the general cycloid sequence s₂ are illustrated in Figure 2. Perform the CWD calculation between sequences s₁ and s₂ in Mathematica. The result is as follows:

J_s = 2.61 × 10⁻⁵,

J_s is very close to zero, indicating that the tooth trajectory exhibits a high degree of similarity to the cycloid. This result demonstrates that the correlation between the tooth trajectory and the general cycloid is accurately identified after CTW, despite significant differences in the positions and angles of the tooth trajectory and the general cycloid, as shown in Figure 2.

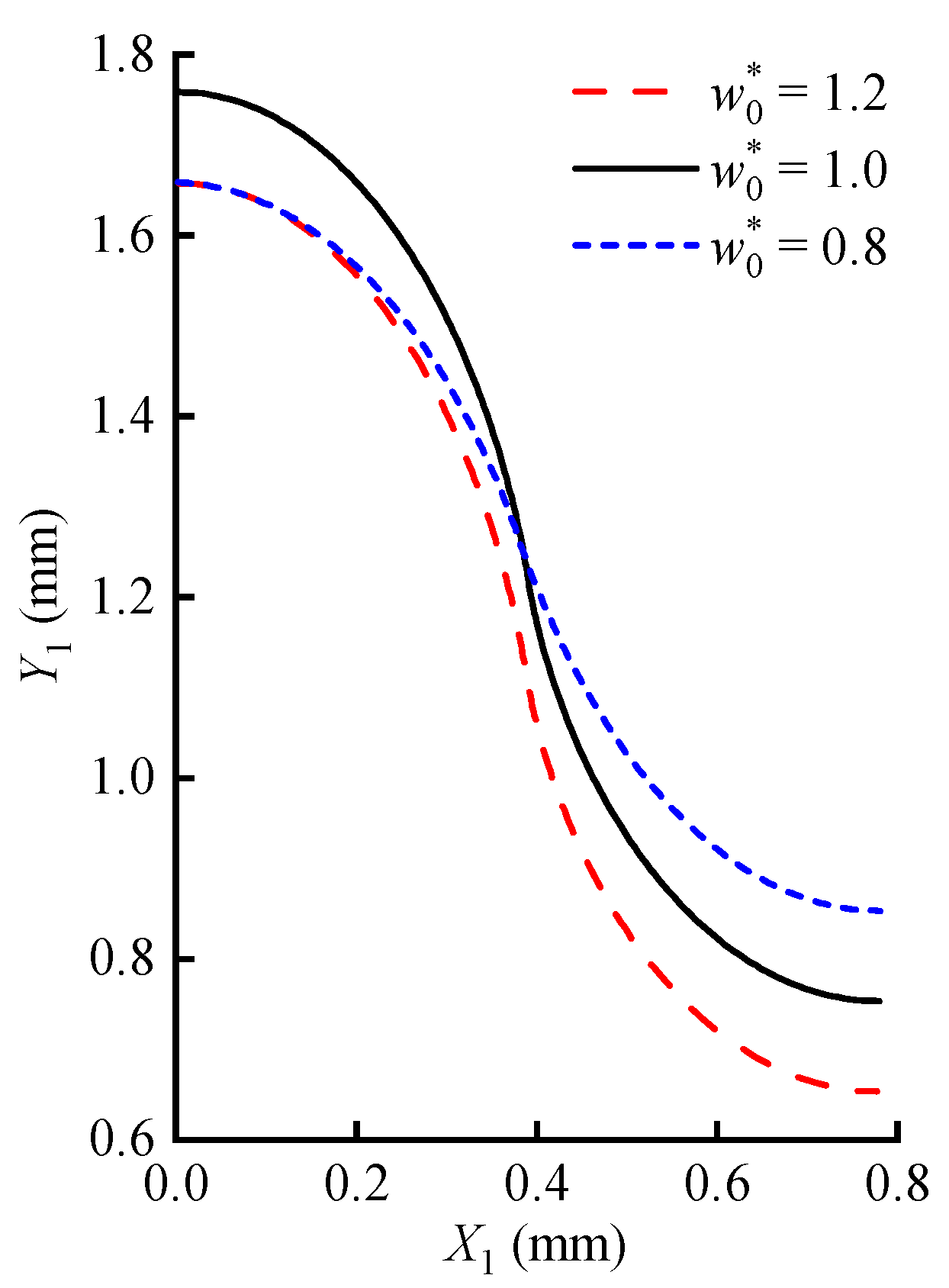
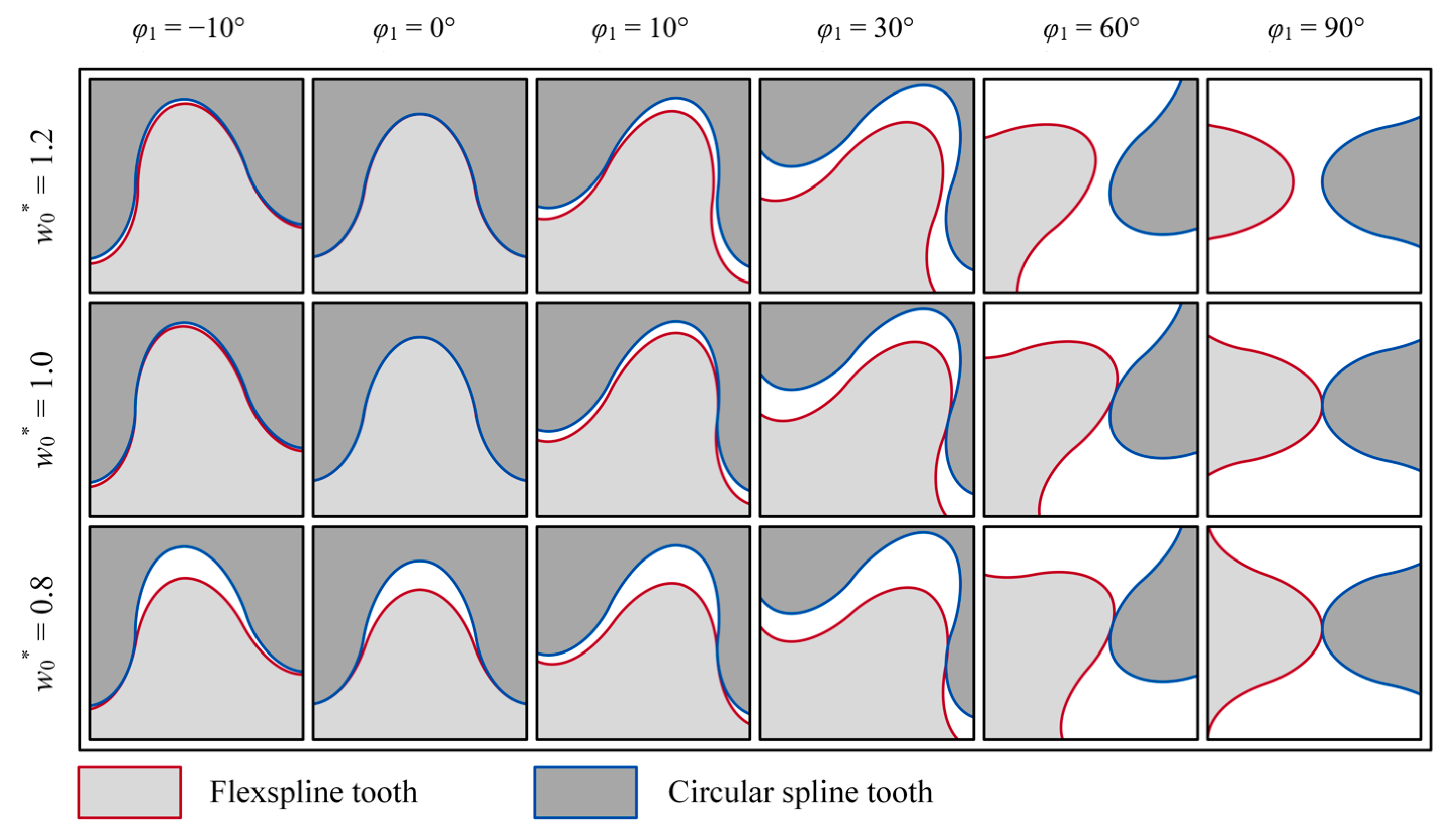
Therefore, the tooth trajectory exhibits cycloid characteristics. While the tooth trajectory can display different characteristics (see Figure 8 for details when w₀* = 1.2 and w₀* = 0.8), both prolate cycloids and curtate cycloids can effectively match these variations. However, the standard cycloid (Equation (9)), which aligns with the tooth trajectory when w₀* = 1.0, is the most convenient for curve mapping calculations.

2.3. X-Halved Cycloid Tooth Trajectory

Let the radius of the rolling circle in Equation (9) be equal to the modulus of the HD, i.e., r_g = m. A cycloid with the x-coordinate compressed by half is constructed as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{t}}=m\left(t-\sin t\right)/2\hfill \\ y_{\mathrm{t}}=-m\left(1-\cos t\right)\hfill \end{array}\right.,$$

(10)

The geometry, slope, and curvature of the tooth trajectory and the cycloid expressed in Equation (10) are calculated and illustrated in Figure 3.

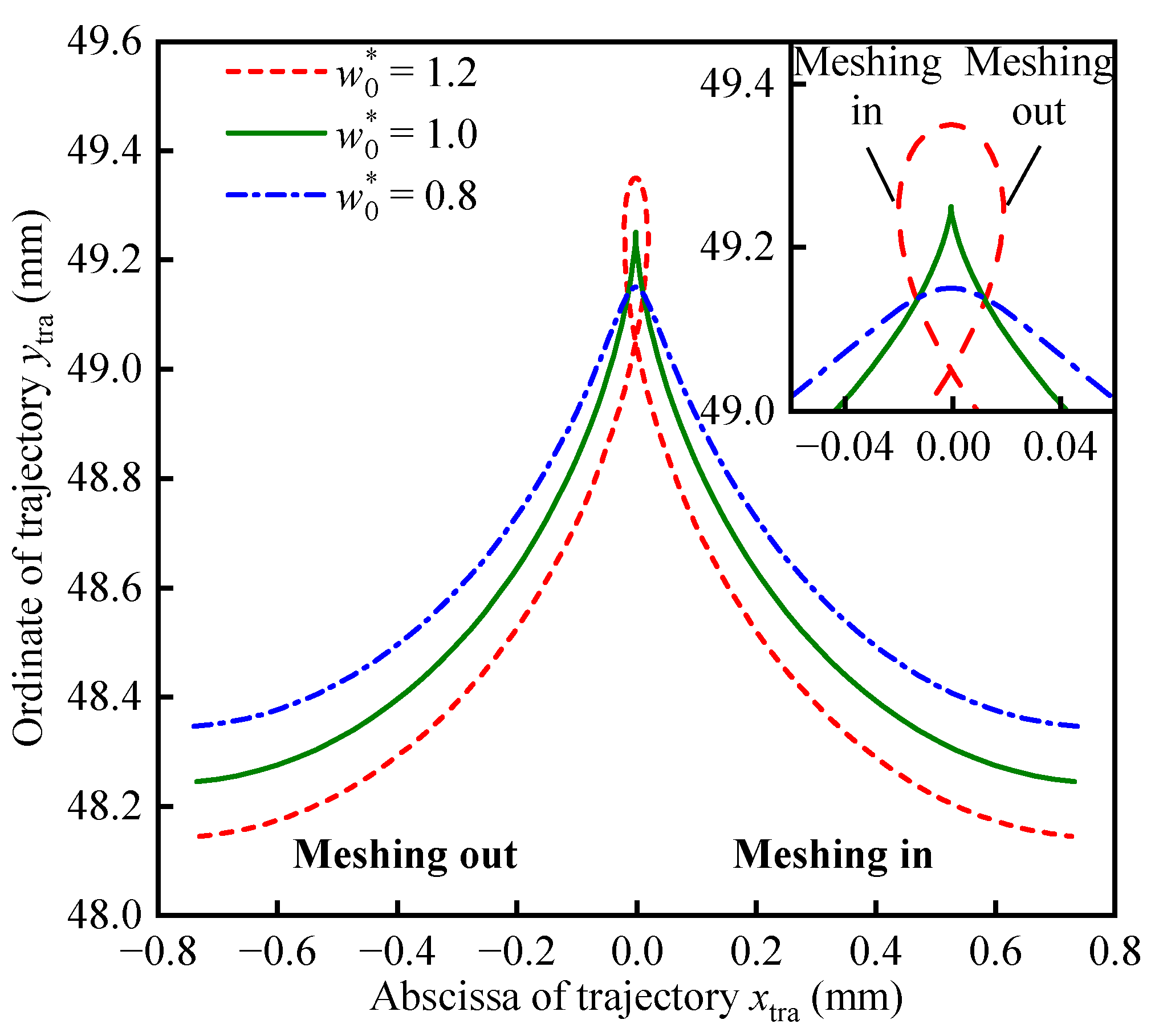
Figure 3a illustrates the trajectory (x_tra, y_tra) of a complete meshing process of the FS’s tooth as φ₁ varies from 0 to π/2, alongside the cycloid (x_cyc, y_cyc), with its x-coordinate halved as t changes from 0 to π. Although the ordinate ranges of the two curves are not consistent, the geometric shape of the tooth trajectory aligns precisely with the cycloid in which the x-coordinate is halved. Furthermore, as shown in Figure 3b,c, the slope and curvature of the tooth trajectory and the cycloid are identical.

The results in Figure 3 demonstrate that the tooth trajectory can be approximately expressed by a cycloid with its x-coordinate halved. Since the tooth trajectory is a cycloid, the TP obtained using the halved mapping of the trajectory can also be represented by a cycloid. Therefore, the application of a CTP in HD is justified. Although these results are derived from the trajectory of a specific model under the influence of an elliptical WG, they also reflect, to a certain extent, the common characteristics of the tooth trajectory in harmonic drives.

3. Method of Cycloid Tooth Profile Design

Directly constructing the meshing TPs of the CS and FS based on the trajectory mapping curve represents a fundamentally sound approach. However, to address potential TP interference caused by the normal rotation of the FS, modifications to the TPs are essential [21]. To meet the requirements of precise conjugation, the TP design can be refined using the envelope method. Additionally, the double-conjugate phenomenon in HD [15,18] can be leveraged to form viable conjugate TPs through practical design. The bidirectional conjugate design process [16] further enhances this by maximizing the double-conjugation effect between meshing tooth pairs. In this section, the addendum profile of the CS is selected as the initial TP, and its CTP equation is formulated based on cycloid mapping. Subsequently, the complete TPs of the CS and FS are achieved through the bidirectional conjugate design process.

3.1. Construction of Initial Cycloid Tooth Profile

As demonstrated in Section 2, the tooth trajectory can be approximated using the cycloid expressed in Equation (10). Consequently, the initial cycloid is constructed by halving the radius of the rolling circle in Equation (10) (i.e., r_g = m/2) as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{d}}=m\left(t-\sin t\right)/4\hfill \\ y_{\mathrm{d}}=m\left(1+\cos t\right)/2\hfill \end{array}\right.,$$

(11)

Point symmetry of Equation (11) about the point (0, 0) is as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{u}}=-m\left(t-\sin t\right)/4\hfill \\ y_{\mathrm{u}}=-m\left(1+\cos t\right)/2\hfill \end{array}\right.,$$

(12)

In the subsequent description, the cycloid expressed in Equation (11) is referred to as the D-cycloid, and the cycloid expressed in Equation (12) is referred to as the U-cycloid. According to the FS tooth coordinate system S₁ and the CS tooth coordinate system S₂ shown in Figure 1, Equations (11) and (12) can be transformed to represent the TPs of the FS and CS, respectively.

Research on the double-conjugation phenomenon [15,18] has demonstrated that the conjugate result of a convex TP is the primary consideration in TP design. Therefore, the convex TP of either the FS’s tooth addendum or the CS’s tooth addendum can be selected as the initial TP. In this case, the addendum TP of the CS is chosen as the initial TP. According to the coordinate system S₂ in Figure 1 and the D-cycloid equation expressed in Equation (11), the initial CTP {x_d2(t), y_d2(t)} of the CS’s tooth addendum has the following relationship:

$$\left[\begin{array}{c}{x}_{\mathrm{d}2}\\ y_{\mathrm{d}2}\end{array}\right]=A_{\mathrm{d}2}\left[\begin{array}{c}{x}_{\mathrm{d}}\\ y_{\mathrm{d}}\end{array}\right]+B_{\mathrm{d}2},$$

(13)

here,

$$A_{\mathrm{d}2}=\left[\begin{array}{cc}{a}_{x\mathrm{d}2}{a}_{r\mathrm{d}2}& 0\\ 0& a_{y\mathrm{d}2}{a}_{r\mathrm{d}2}\end{array}\right], B_{\mathrm{d}2}=\left[\begin{array}{c}{e}_{\mathrm{t}2}/2+b_{\mathrm{d}2}\\ R_{\mathrm{a}2}\end{array}\right]$$

A_d2 is the scaling coefficients matrix of the D-cycloid, where a_xd2 is the x-scaling coefficient, a_yd2 is the y-scaling coefficient, and a_rd2 is the scaling coefficient of the rolling circle radius; B_d2 is the coordinate translation matrix of the initial cycloid (Equation (11)) when expressing the addendum profile of CS in coordinate system S₂; e_t2 is the width of the tooth space on the reference circle of CS, b_d2 is the x-translation coefficient, and R_a2 is the addendum circle radius of CS. These coefficients allow for the adjustment of the initial cycloid from multiple perspectives, significantly enhancing the design flexibility of the cycloid.

3.2. Envelope of Initial Cycloid Tooth Profile

According to Figure 1, the transformation matrix from coordinate system S₂ to S₁ is as follows:

$$T_{21}=\left[\begin{array}{ccc}\cos {\theta }_{\mathrm{p}}& -\sin {\theta }_{\mathrm{p}}& \rho \sin {\theta }_{\mu }\\ \sin {\theta }_{\mathrm{p}}& \cos {\theta }_{\mathrm{p}}& -\rho \cos {\theta }_{\mu }\\ 0& 0& 1\end{array}\right],$$

Therefore, the addendum profile of CS shown in Equation (13) is transformed into the coordinate system S₁ as follows:

$$\left[\begin{array}{c}{x}_{\mathrm{d}21}\\ y_{\mathrm{d}21}\\ 1\end{array}\right]=T_{21}\left[\begin{array}{c}{x}_{\mathrm{d}2}\\ y_{\mathrm{d}2}\\ 1\end{array}\right],$$

(14)

here, both x_d21 and y_d21 are functions with variables t and φ₁, i.e., they represent a cluster of curves distributed along φ₁. If an envelope curve exists for this curve cluster, the points on the envelope curve satisfy the envelope condition expressed in Equation (15).

$${\displaystyle \frac{\partial x_{\mathrm{d}21}}{\partial t}}{\displaystyle \frac{\partial y_{\mathrm{d}21}}{\partial {\phi }_1}}-{\displaystyle \frac{\partial x_{\mathrm{d}21}}{\partial {\phi }_1}}{\displaystyle \frac{\partial y_{\mathrm{d}21}}{\partial t}}=0,$$

(15)

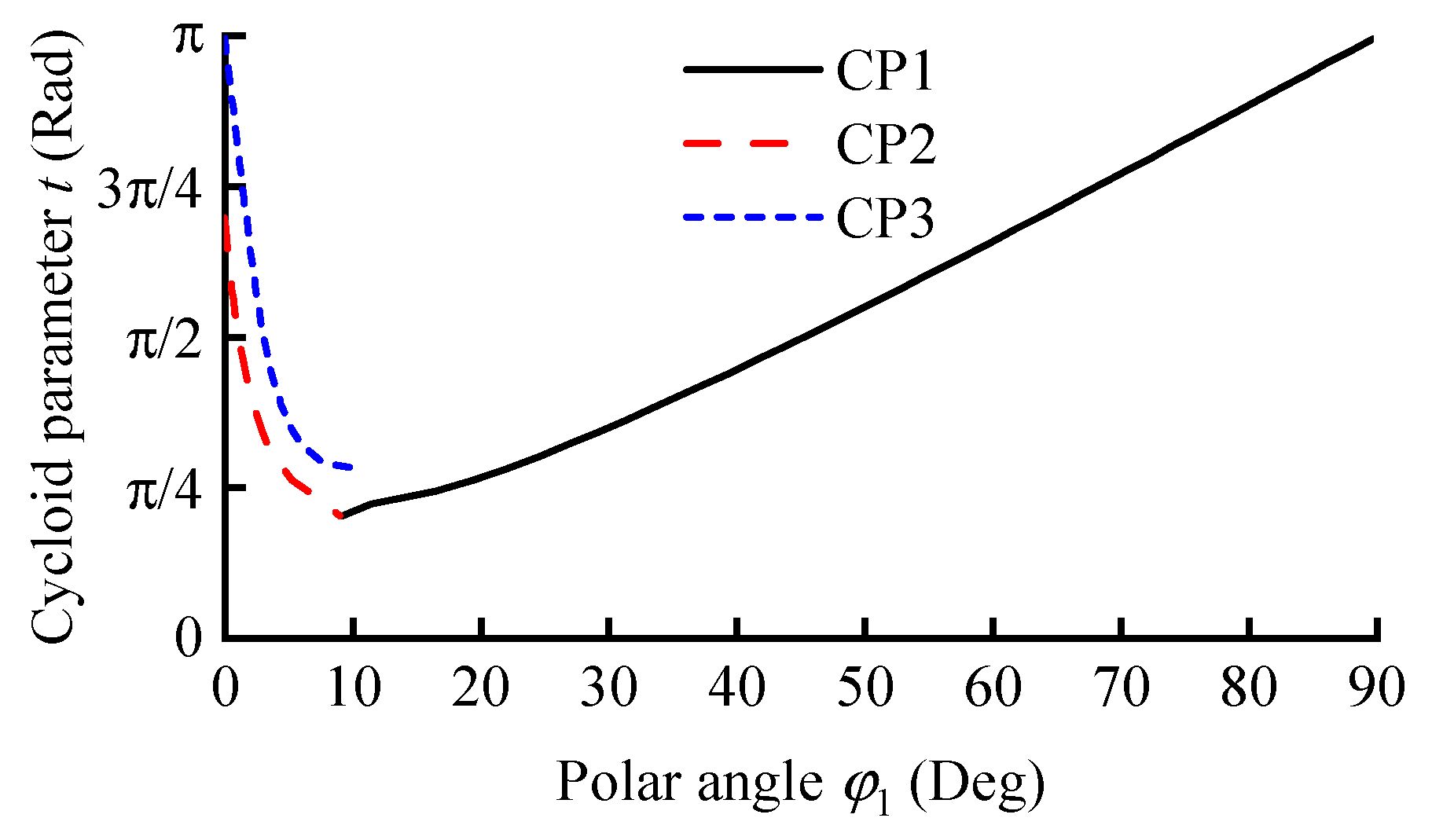
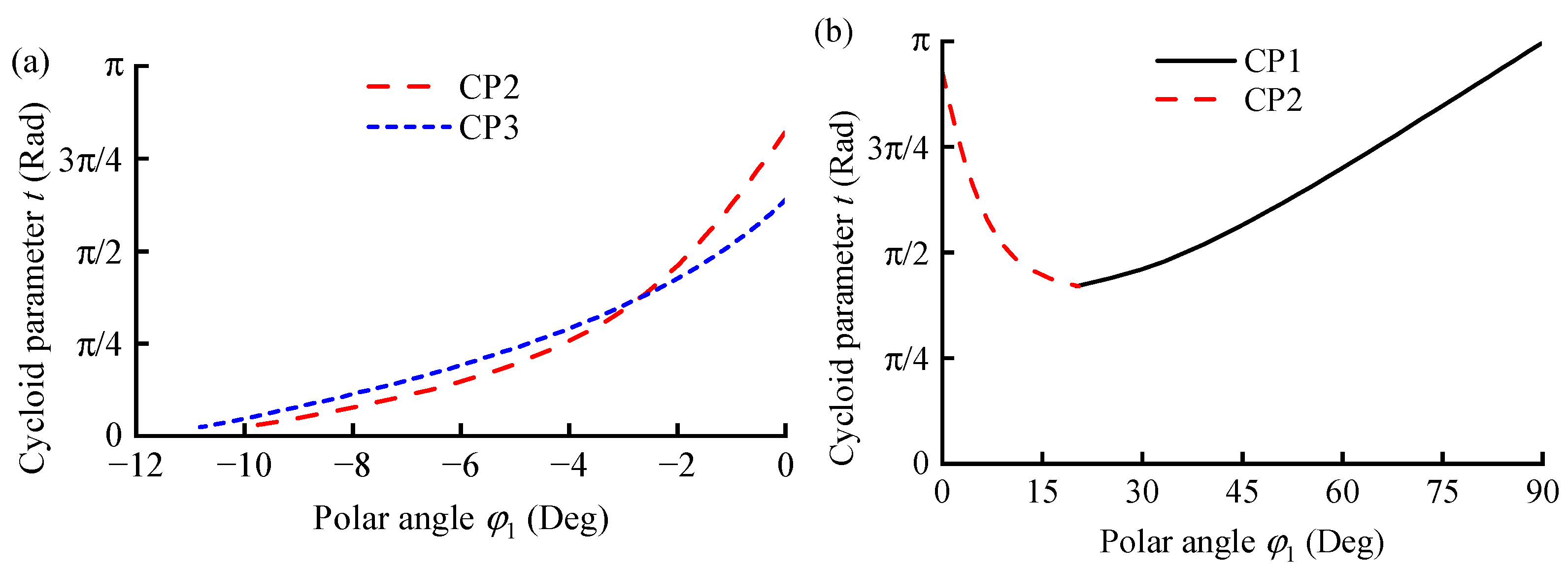
Parameter t of the TP, which satisfies the conjugate condition for any φ₁, can be determined using Equation (15). By substituting t and φ₁ into Equation (14), the discrete conjugate point of the CS’s addendum can be obtained.

3.3. Cycloid Tooth Profile Design of Flexspline

Preliminary studies on the composite cycloid [24] indicate that the conjugate points of the CTP retain a cycloidal shape and should incorporate a specific TP angle. Trial calculations of the envelope reveal that the conjugate points forming the FS TP not only appear outside the reference circle but also partially distribute within it. Consequently, a CTP with a non-zero TP angle can be constructed, as illustrated in Figure 4.

The TP angle at the joint point of the two cycloids can serve as a design variable, thereby further enhancing the design flexibility of the CTP. In Figure 4, AB represents a U-cycloid, and CD represents a D-cycloid. The tangent angle of AB at point E is α₀, and the tangent angle of CD at point F is also α₀. By translating AB, the CTP with TP angle α₀ can be obtained by smoothly connecting AB and CD at points E and F. The expression {x_d1(t), y_d1(t)} of FS’s dedendum CTP has the following relationship:

$$\left[\begin{array}{c}{x}_{\mathrm{d}1}\\ y_{\mathrm{d}1}\end{array}\right]=A_{\mathrm{d}1}\left[\begin{array}{c}{x}_{\mathrm{d}}\\ y_{\mathrm{d}}\end{array}\right]+B_{\mathrm{d}1},$$

(16)

here,

$$A_{\mathrm{d}1}=\left[\begin{array}{cc}{a}_{x\mathrm{d}1}{a}_{r\mathrm{d}1}& 0\\ 0& a_{y\mathrm{d}1}{a}_{r\mathrm{d}1}\end{array}\right], B_{\mathrm{d}1}=\left[\begin{array}{c}{s}_{\mathrm{t}1}/2+b_{\mathrm{d}1}\\ R_{\mathrm{a}2}-{\rho }_{\mathrm{a}}\end{array}\right]$$

The initial expression {x_u1(t), y_u1(t)} of the FS’s addendum CTP has the following relation:

$$\left[\begin{array}{c}{x}_{\mathrm{u}1}\\ y_{\mathrm{u}1}\end{array}\right]=A_{\mathrm{u}1}\left[\begin{array}{c}{x}_{\mathrm{u}}\\ y_{\mathrm{u}}\end{array}\right]+B_{\mathrm{u}1},$$

(17)

here,

$$A_{\mathrm{u}1}=\left[\begin{array}{cc}{a}_{x\mathrm{u}1}{a}_{r\mathrm{u}1}& 0\\ 0& a_{y\mathrm{u}1}{a}_{r\mathrm{u}1}\end{array}\right], B_{\mathrm{d}1}=\left[\begin{array}{c}{s}_{\mathrm{t}1}/2+b_{\mathrm{d}1}\\ R_{\mathrm{a}2}-{\rho }_{\mathrm{a}}\end{array}\right]$$

here, a_xd1 and a_xu1 are the x-scaling coefficients; a_yd1 and a_yu1 are the y-scaling coefficients; a_rd1 and a_ru1 are the scaling coefficients of the rolling circle radius; s_t1 is the tooth thickness of FS on the reference circle (where s_t1 = e_t2), and b_d1 and b_u1 are the x-translation coefficients.

Calculate the first-order derivatives of the U-cycloid and D-cycloid of the FS,

$${\displaystyle \frac{\mathrm{d}{y}_{\mathrm{u}1}}{\mathrm{d}{x}_{\mathrm{u}1}}}=-{\displaystyle \frac{2a_{y\mathrm{u}1}\sin t}{a_{x\mathrm{u}1}\left(1-\cos t\right)}}, {\displaystyle \frac{\mathrm{d}{y}_{\mathrm{d}1}}{\mathrm{d}{x}_{\mathrm{d}1}}}=-{\displaystyle \frac{2a_{y\mathrm{d}1}\sin t}{a_{x\mathrm{d}1}\left(1-\cos t\right)}}$$

Let the tooth angle at the connection of the U-cycloid and D-cycloid of the FS be α₀₁. The slope at this position is −cot(α₀₁). Consequently, the tooth parameters at points E and F can be determined as follows:

$$t_{E1}=2\mathrm{arccot}\left({\displaystyle \frac{a_{x\mathrm{u}1}}{2a_{y\mathrm{u}1}}}\cot {\alpha }_{01}\right), t_{F1}=2\mathrm{arccot}\left({\displaystyle \frac{a_{x\mathrm{d}1}}{2a_{y\mathrm{d}1}}}\cot {\alpha }_{01}\right)$$

The coordinates of points E and F can be determined by substituting t_E1 and t_F1 into Equations (17) and (16), respectively. By translating the U-cycloid to align point E with point F, the addendum CTP of the FS is expressed as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{u}1}=m[a_{x\mathrm{u}1}{a}_{r\mathrm{u}1}(t_{E1}-t+\sin t-\sin t_{E1})+a_{x\mathrm{d}1}{a}_{r\mathrm{d}1}(t_{F1}-\sin t_{F1})]/4+s_1/2+b_{\mathrm{d}1}\\ y_{\mathrm{u}1}=m[a_{y\mathrm{u}1}{a}_{r\mathrm{u}1}(\cos t_{E1}-\cos t)+a_{y\mathrm{d}1}{a}_{r\mathrm{d}1}(1+\cos t_{F1})]/2+R_{\mathrm{a}2}-{\rho }_{\mathrm{a}}\end{array}\right.,$$

(18)

here, the independent variable t takes values in the range from t_E1 to π.

According to Equation (16), the dedendum profile of FS is expressed as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{d}1}=a_{x\mathrm{d}1}{a}_{r\mathrm{d}1}m\left(t-\sin t\right)/4+s_1/2+b_{\mathrm{d}1}\\ y_{\mathrm{d}1}=a_{y\mathrm{d}1}{a}_{r\mathrm{d}1}m\left(1+\cos t\right)/2+R_{\mathrm{a}2}-{\rho }_{\mathrm{a}}\end{array}\right.,$$

(19)

here, the independent variable t takes values in the range from t_F1 to π.

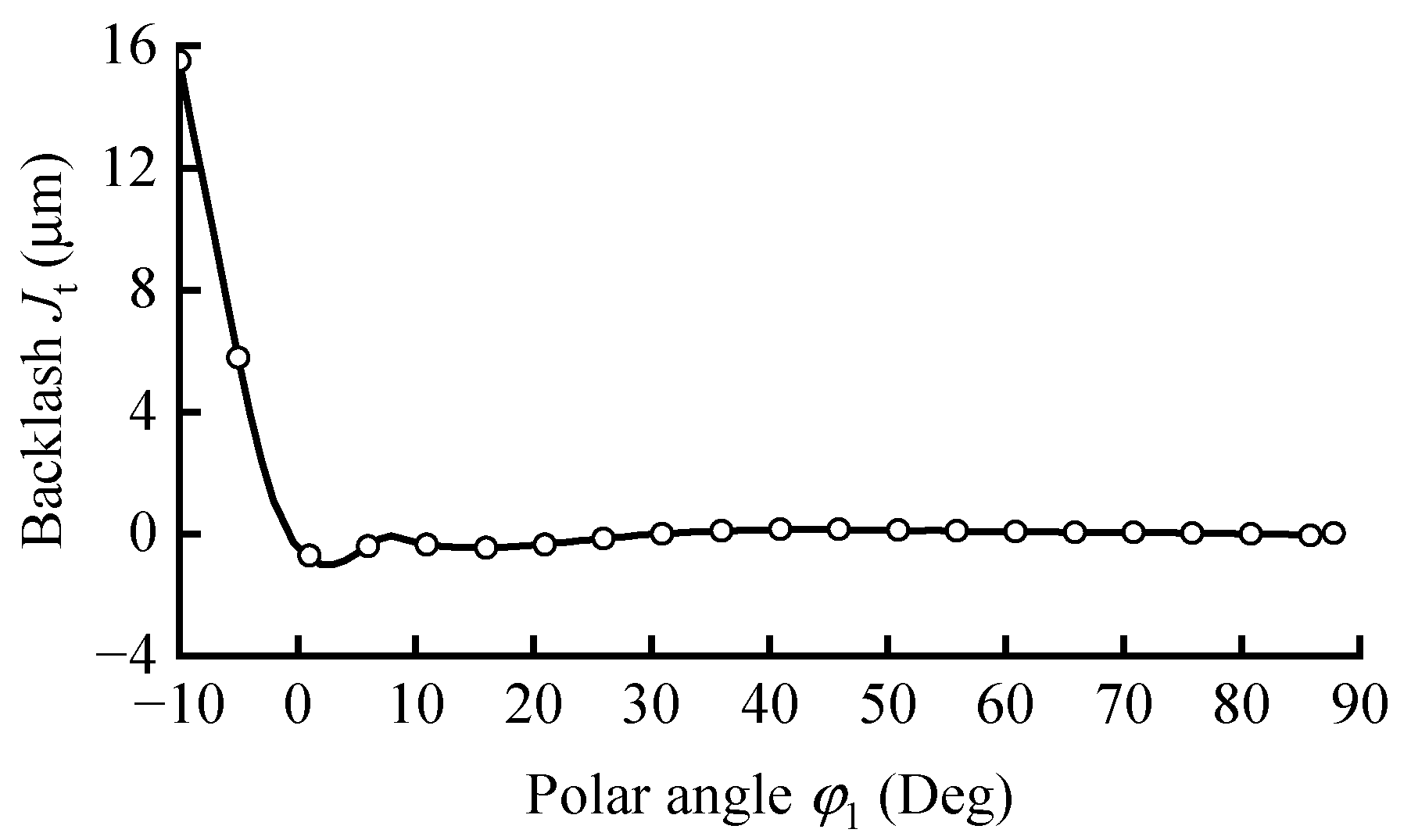
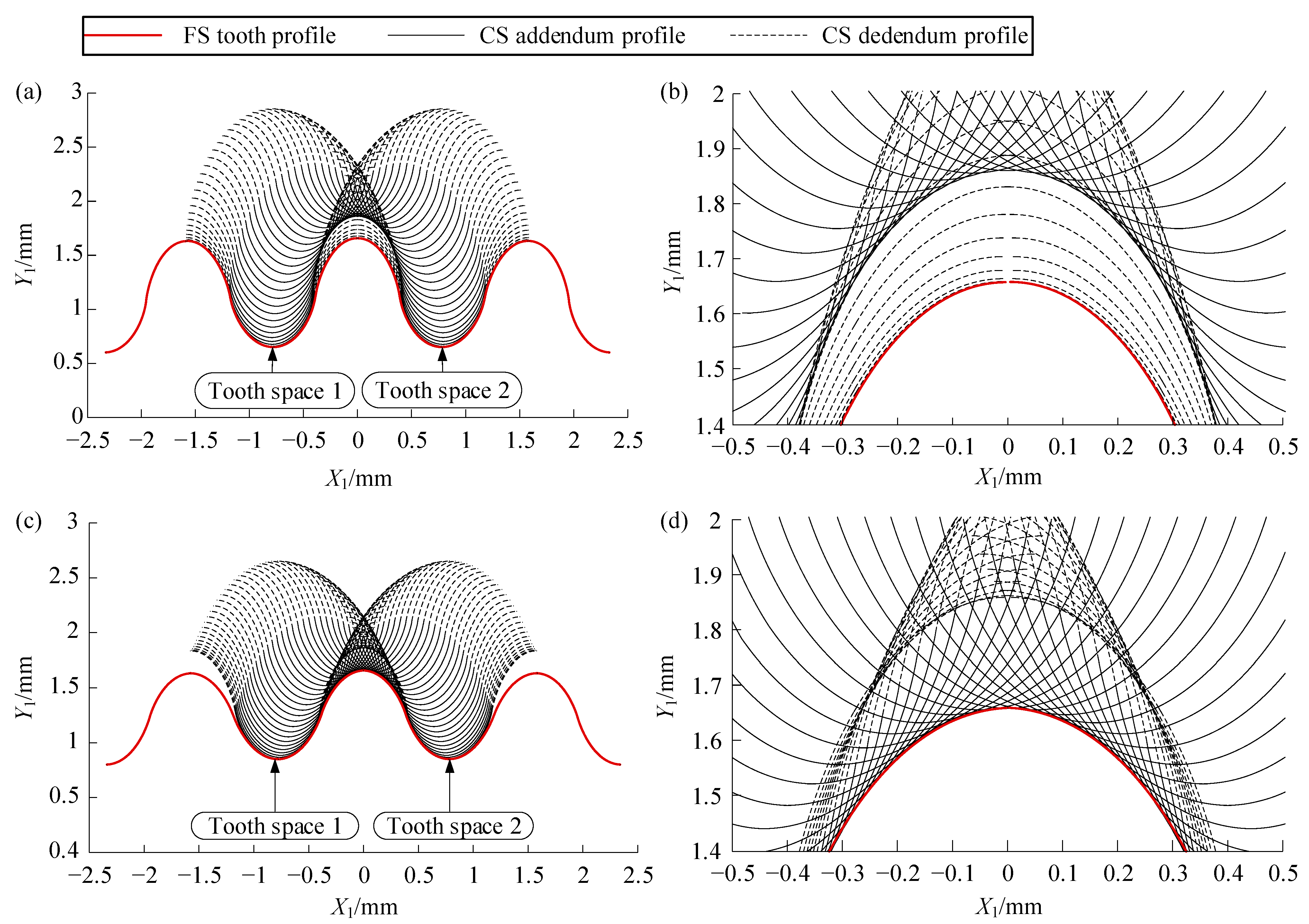
Among the discrete conjugate points of the CS’s addendum, the points located inside the FS’s reference circle are selected for least-squares fitting, using Equation (19) as the target curve, to determine the coefficient matrices A_d1 and B_d1. Subsequently, the points outside the reference circle are fitted using Equation (18) to determine the coefficient matrices A_u1, B_u1, and tooth angle α₀₁ of the addendum cycloid of FS. This completes the design of the FS’s CTP.

3.4. Cycloid Tooth Profile Design of Circular Spline

As the FS’s addendum profile design has been completed, its conjugate calculation can be performed to complete the dedendum profile design of CS, which can realize the double-conjugate meshing. This process of the reverse conjugate design of CS’s dedendum by the addendum of FS, which was previously designed by the presetting CS’s addendum, is called a bidirectional conjugate design [16].

Among the discrete conjugate points of the FS’s addendum, the points located inside the CS’s reference circle should align with the initial CTP of the CS addendum, while the points outside the CS’s reference circle can be used to design its dedendum TP. According to Figure 1, the transformation matrix from the coordinate system S₁ to S₂ is T₂₁⁻¹. According to Equation (13), the CTP of the CS’s dedendum is expressed as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{d}2}=a_{x\mathrm{d}2}{a}_{r\mathrm{d}2}m\left(t-\sin t\right)/4+e_2/2+b_{\mathrm{d}2}\\ y_{\mathrm{d}2}=a_{y\mathrm{d}2}{a}_{r\mathrm{d}2}m\left(1+\cos t\right)/2+R_{\mathrm{a}2}\end{array}\right.,$$

(20)

here, the independent variable t takes values ranging from t_F2 to π.

The expression of the CS dedendum CTP is as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{u}2}=m[a_{x\mathrm{u}2}{a}_{r\mathrm{u}2}(t_{E2}-t+\sin t-\sin t_{E2})+a_{x\mathrm{d}2}{a}_{r\mathrm{d}2}(t_{F2}-\sin t_{F2})]/4+e_2/2+b_{\mathrm{d}2}\\ y_{\mathrm{u}2}=m[a_{y\mathrm{u}2}{a}_{r\mathrm{u}2}(\cos t_{E2}-\cos t)+a_{y\mathrm{d}2}{a}_{r\mathrm{d}2}(1+\cos t_{F2})]/2+R_{\mathrm{a}2}+{\rho }_{\mathrm{a}}-{\rho }_{\mathrm{b}}\end{array}\right.,$$

(21)

here, the independent variable t takes values ranging from t_E2 to π.

4. Case Study

The feasibility of applying the CTP to HD, along with the design methodology and bidirectional conjugate process for the CTP, has been thoroughly discussed in the preceding sections. In this section, a specific example is provided to illustrate the complete design process of the CTPs for both the CS and FS.

4.1. Design Case of Cycloid Tooth Profile

Set the wall thickness of the tooth rim of FS as 1.5 mm, the design maximum radial displacement coefficient w₀* = 1.0, and the tooth addendum height coefficient h_a* = 1.0. The remaining parameters are referenced from Table 1. According to Equation (8), the diameters of the major and minor axes of the neutral line of the FS are ρ_a = 49.25 mm and ρ_b = 48.2474 mm. The radius of the CS’s addendum circle is R_a2 = m(z₂/2 − h_a*) = 50 mm. The initial parameters are set as follows:

$$s_{\mathrm{t}1}=e_{\mathrm{t}2}=\mathrm{\pi }m/2, a_{x\mathrm{d}2}=1, a_{y\mathrm{d}2}=1, a_{r\mathrm{d}2}=1, b_{\mathrm{d}2}=0$$

The design is carried out according to the method and process described in Section 3, and the resulting coefficients of the TPs are summarized in

Table 2. Design results of cycloid tooth profiles.

CS Parameter	Value	FS Parameter	Value
axd2	1	axd1	1.003
ayd2	1	ayd1	1.007
ard2	1	ard1	1.033
axu2	0.8646	axu1	0.8819
ayu2	1.18	ayu1	1.144
aru2	1.096	aru1	1.081
bd2	0	bd1	−0.0045 mm
α02	9.1°	α01	9.17°

.

By substituting the coefficients shown in Table 2 into Equations (18)–(21), the expression of addendum CTP of CS is as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{d}2}=0.125\left(t-\sin t\right)+0.3927\\ y_{\mathrm{d}2}=0.25\cos t+50.25\end{array}\right.,$$

(22)

the expression of dedendum CTP of CS is as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{u}2}=-0.1275\left(t-\sin t\right)+0.407\\ y_{\mathrm{u}2}=-0.3233\cos t+50.6852\end{array}\right.,$$

(23)

the expression of addendum CTP of FS is as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{u}1}=-0.1261\left(t-\sin t\right)+0.4\\ y_{\mathrm{u}1}=-0.3093\cos t+1.4494\end{array}\right.,$$

(24)

and the expression of the dedendum CTP of FS is as follows:

$$\left\{\begin{array}{l}{x}_{\mathrm{d}1}=0.1262\left(t-\sin t\right)+0.3872\\ y_{\mathrm{d}1}=0.2598\cos t+1.0098\end{array}\right.$$

(25)

4.2. Case Results

4.2.1. Conjugate Engagement Existence Interval

During the conjugate point calculation process, the conjugate range of the cycloid can also be obtained. The meshing of CS and FS can be divided into three states: the conjugation between CS’s tooth addendum and FS’s tooth addendum (CP1 in Figure 5), the conjugation between CS’s tooth addendum and FS’s tooth dedendum (CP2 in Figure 5), and the conjugation between CS’s tooth dedendum and FS’s tooth addendum (CP3 in Figure 5). There is no meshing relationship between CS’s tooth dedendum and FS’s tooth dedendum.

As illustrated in Figure 5, the addendum of CS and the addendum of FS mesh conjugately in the range from φ₁ = 9° to 90°; the CS’s addendum and the FS’s dedendum mesh in the range from φ₁ = 0° to 9°, while the CS’s dedendum and the FS’s addendum mesh are in the range from φ₁ = 0 to 11°. In other words, within the range from φ₁ = 0° to 10°, the teeth of FS and the CS are conjugately meshing at two points simultaneously. Therefore, φ₁ = 0° to 10° represents the double-conjugate meshing interval of the CTP. The complete conjugate existence interval, which is close to 90°, and the double-conjugate interval of approximately 10° significantly enhance the proportion of teeth involved in meshing, thereby sharing the load, reducing tooth wear, and extending the gear life.

4.2.2. Engagement Motion

Transformed by the matrix T₂₁ (as described in Section 3.2), the CS’s TP can be illustrated in coordinate system S₁ alongside the FS’s TP. By increasing φ₁ from 0° to 180° (i.e., rotating the WG by 180°) and calculating multiple positions of the CS’s TP, a complete “meshing-out to meshing-in” process with an engaged tooth pair of the CS and FS can be simulated by simultaneously displaying the CS’s TP at these positions.

Figure 6 depicts the engagement process of the CS tooth as it exits the “tooth space 1” of the FS and subsequently enters “tooth space 2”. As illustrated in Figure 6a, the CS tooth maintains excellent conjugate engagement with the FS tooth throughout the entire engagement process. The envelopes formed by the CS’s addendum and dedendum nearly coincide with the FS’s addendum (Figure 6b), achieving an ideal double-conjugate meshing state between the CS and FS.

However, it is important to note that Figure 6 also reveals a tight fit relationship between the tooth pair at the deepest meshing position, where no clearance exists, and the radial clearance between the addendums of the FS and CS approaches zero at the minor axis. This meshing condition, while ideal, imposes stringent tolerances for machining and assembly. In practical applications, an appropriate clearance must be reserved to account for manufacturing tolerances, assembly requirements, and lubrication needs. While a specific clearance can be achieved by trimming the addendum, this approach significantly reduces the conjugate engagement range. When designing the TP for an actual product, the clearance value should be meticulously studied to ensure that the CTP retains the maximum conjugate interval while simultaneously meeting transmission efficiency requirements. In this context, the clearance is discussed only in a theoretical state and will not be explored in greater detail.

4.2.3. Engagement Backlash

Theoretically, the meshing backlash would be nonexistent if the TPs were constructed solely from conjugate points. However, since the CTP represents an approximate fit to these conjugate points, the resulting profile may exhibit meshing backlash or interference due to the fitting method and precision. The quality of the fitting result and the meshing performance of the TP can be assessed by calculating the backlash between the meshing tooth pair. The clearance between the CTPs of the FS and CS can be determined using the dichotomy method, as illustrated in Figure 7.

Since there is no circumferential contact between the CS and FS near the minor axis, the backlash is calculated in the range of φ₁ = −10–88° (Figure 7). The change of φ₁ from 90° to 0° represents the meshing-in process between the teeth of CS and FS, and the change of φ₁ from 0° to −10° represents part of the meshing-out process. It can be seen from Figure 7 that, in most of the meshing-in processes (φ₁ ≈ 30–88°), the backlash varies within only 0.1 μm, which indicates a stable meshing state. During the engagement process of φ₁ ≈ 0–30°, the backlash appears negative, varying in a small range from −0.1 μm to −1 μm. The backlash distributed in the meshing-in region can be echoed with the conjugate interval distribution shown in Figure 5. When the CS’s tooth is meshing out of the FS’s tooth space (φ₁ ≈ −10–0°), the backlash increases rapidly, and the tooth pairs are no longer in an engagement state.

The backlash in the local area (φ₁ ≈ 0–30°) shows that there is a slight interference (<1 μm). This is caused by the algorithm accuracy of the TP fitting and the backlash calculation and, therefore, does not affect the evaluation of the overall excellent meshing performance of the CTP.

5. Discussion

5.1. Tooth Trajectories with Different w₀*

Based on the distinct characteristics of the tooth movement locus, the maximum radial displacement coefficient w₀* can be analyzed in three cases: w₀* = 1, w₀* > 1, and w₀* < 1. Representing these scenarios with w₀* = 1.2, w₀* = 1.0, and w₀* = 0.8, the complete trajectories of a tooth (refer to Table 1) from meshing-in to meshing-out are illustrated in Figure 8. It is evident that the amplitude of tooth motion is the largest when w₀* > 1, and a period of reverse movement occurs near the deepest position of meshing. When w₀* = 1, the tooth moves along the x-direction from meshing-in to meshing-out, exhibiting a pronounced cusp at the highest position. Conversely, when w₀* < 1, the tooth also moves along the x-direction from meshing-in to meshing-out but remains smooth at the highest position without a cusp.

Therefore, the design of the TP becomes more complex when w₀* > 1. According to the trajectory characteristics shown in Figure 8, if the envelope formed by the CS tooth during the meshing-in movement is used as the designed TP of FS, the FS tooth will interfere with the CS tooth near the deepest meshing position where the reverse motion occurs.

Therefore, when w₀* > 1, the conjugate calculation of the TP should be performed in the meshing-out interval (−π/2 ≤ φ₁ ≤ 0). However, the available motion range for conjugate calculation is so limited that the envelope of CS’s addendum can only form the FS’s dedendum profile. Consequently, the dedendum profile of the CS is required for the calculation of the FS’s addendum, implying that the entire profile of the CS must be fully established beforehand.

When w₀* < 1, there is no self-interference in the trajectory, and the quadratic conjugate design of the CS’s dedendum profile can be completed when w₀* = 1. However, to simplify the discussion, the CS’s TP is unified by Equations (22) and (23) during the design of the FS TP with different tooth trajectories.

5.2. Cycloid Tooth Profile of Flexspline with Different w₀*

Using the model described in Section 4, the FS’s TPs are calculated for w₀* = 1.2 and w₀* = 0.8, respectively. According to Equation (8), the major and minor axes of the FS’s neutral line are presented in

Table 3. Calculation model of flexspline neutral line.

Polar Diameter	w0* = 1.2	w0* = 0.8
Major axis, ρa	49.35 mm	49.15 mm
Minor axis, ρb	48.1463 mm	48.3483 mm

. Following the method and process outlined above, the coefficients of the FS TP are obtained and summarized in

Table 4. Coefficients of cycloid tooth profile.

Parameter	w0* = 1.2	w0* = 0.8
axd1	1.002	1.084
ayd1	1.007	1.076
ard1	1.022	1.268
axu1	0.8302	1.073
ayu1	1.209	1.043
aru1	1.034	1.225
bd1	−0.0077 mm	−0.066 mm
α01	8.95°	18.99°

. The TP expression can be determined by substituting these coefficients into Equations (18) and (19). The designed TPs of the FS are illustrated in Figure 9.

In Table 2 and Table 4, as well as Figure 9, the TPs of FS obtained for w₀* = 1.2 and w₀* = 1.0 are very similar to those of the CS in terms of TP parameters. However, when w₀* = 1.2, the CS tooth meshes deeper, resulting in the FS TP being positioned lower. Conversely, the small relative motion between the splines when w₀* = 0.8 leads to a reduction in the FS tooth height. Consequently, the TP parameters are significantly altered, and the TP becomes more inclined, as indicated by the notable increase in the TP angle.

5.3. Conjugate Interval of 3D Tooth Shape

During the conjugate calculation process for the CS, the distribution of conjugate solutions is extracted for w₀* = 1.2 and w₀* = 0.8, respectively, and the results are presented in Figure 10.

Figure 10a illustrates that when w₀* = 1.2, effective conjugate meshing occurs between the CS addendum and the FS dedendum in the range of φ₁ = −10–0°, and between the CS dedendum and the FS addendum in the range of φ₁ = −11–0°. No effective conjugation is observed in the remaining range of φ₁.

Figure 10b demonstrates that when w₀* = 0.8, conjugate meshing can occur between the CS addendum and the FS addendum in the range of φ₁ = 20–90°, and between the CS addendum and FS dedendum in the range of φ₁= 0–20°.

From Figure 5, Figure 7 and Figure 10, it is evident that when w₀* > 1, there is only a very small conjugate range during the meshing-out process. In contrast, when w₀* ≤ 1, a conjugate range covers almost the entire meshing-in process.

5.4. Meshing Status of 3D Tooth Pair

According to Section 4.2, a complete process of CS tooth meshing out of the FS tooth space 1 and meshing into FS tooth space 2, as the WG rotates 180°, is calculated for w₀* = 1.2 and w₀* = 0.8, as shown in Figure 11.

As illustrated in Figure 11a, when w₀* = 1.2, although the TP of CS forms a good envelope, most of the envelope is unavailable due to interference with the CS dedendum itself (Figure 11b). At the beginning of the meshing-out process, a small envelope of the CS coincides with the FS TP on the left side of tooth space 1, forming the working TP of the FS. As shown in Figure 11c, when w₀* = 0.8, the meshing depth of CS is relatively shallow. Although the CS tooth differs in height from the FS tooth, such that the CS dedendum does not contact the FS tooth throughout the entire process (Figure 11d), the CS addendum maintains excellent conjugate engagement with the FS addendum during the entire process.

An assembly model of the CS and the deformed FS was established in AutoCAD 2024. According to the conjugate intervals shown in Figure 5 and Figure 10, φ₁ is set to −10°, 0°, 15°, 30°, 60°, and 90° to observe the meshing states of the FS and the CS under different maximum radial displacement coefficients, as illustrated in Figure 12.

In Figure 12, the dark gray area represents the CS tooth, and the light gray area represents the FS tooth. Assuming the WG rotates clockwise, the right side of the FS tooth and the left side of the CS tooth are the working TPs. Near the position of φ₁ = −10° in Figure 12, although the meshing tooth pairs are in the meshing-out process, they remain in contact when w₀* = 1.2. A slight meshing backlash is observed when w₀* = 1.0, and the backlash becomes significant when w₀* = 0.8. At the position of φ₁ = 0°, the TPs of the FS and the CS nearly coincide when w₀* = 1.2 and w₀* = 1.0. However, when w₀* = 0.8, only the addendum of the CS is in contact with the FS dedendum.

The positions of φ₁ = 10°, 30°, and 60° all belong to the meshing-in process. The tooth pairs are in contact when w₀* = 1.0 and w₀* = 0.8; however, there is a noticeable backlash when w₀* = 1.2. At the position of φ₁ = 90°, although the circumferential meshing load cannot be applied, the tooth of the FS and the CS maintain a conjugate contact state when w₀* = 1.0 and w₀* = 0.8, while a significant radial clearance is observed when w₀* = 1.2.

5.5. Backlash Between Meshed 3D Tooth Pair

According to Section 4.2.3, the backlash between the meshing tooth pairs is calculated for w₀* = 1.2 and w₀* = 0.8, as illustrated in Figure 13.

When w₀* = 1.2 (Figure 13a), as the polar angle φ₁ increases, the backlash J_t between the tooth pairs decreases and then rapidly increases. Specifically, when φ₁ increases from −15° to −2°, J_t decreases from 11 μm to 1 μm. As φ₁ increases from −2° to 65°, J_t rapidly increases from 1 μm to 350 μm. For φ₁ > 65°, the position of the FS tooth tip is lower than that of the CS tooth tip, resulting in no meshing condition and, thus, no meshing backlash. In the range of φ₁ ≈ −10–0°, the backlash J_t between the working TPs is less than 3 μm, which aligns with the distribution range of the conjugate solution shown in Figure 10a.

When w₀* = 0.8 (Figure 13b), the backlash J_t between the tooth pairs initially decreases rapidly and then fluctuates as φ₁ increases. Specifically, when φ₁ increases from −15° to 1°, J_t decreases rapidly from 74 μm to 0.1 μm. However, when φ₁ varies from 1° to 88°, J_t fluctuates continuously between −5.6 μm and 3.2 μm and remains negative in most cases. This indicates that the working TP exhibits a maximum backlash of 3.2 μm and a maximum interference of 5.6 μm.

Compared with w₀* = 1.0 (Figure 7), both the backlash value and the interference amount between the TPs are larger, suggesting that the goodness of fit of the CTP deteriorates under the current fitting method (least squares method) when w₀* = 0.8. Nevertheless, for φ₁ = 0–88°, the backlash J_t remains approximately within the range of ±5 μm, which aligns with the conjugate solution distribution shown in Figure 10b.

6. Conclusions

This study comprehensively investigates the CTP of HD, encompassing its rationality, construction, design, and meshing performance. The primary conclusions are summarized as follows:

(1)

The application of the CTP used on the HD is rationality. The motion trajectory of the HD gear tooth exhibits a high degree of compatibility with cycloidal fitting, confirming its cycloidal characteristics. The initial CTP and its conjugate CTP, derived from the semi-mapping of the motion trajectory, demonstrate fully conjugate meshing properties.

(2)

The proposed CTP expression has excellent fitting performance. The CTP expression, designed with variable control coefficients, exhibits superior adaptability to the fitting requirements of conjugate points under varying deformation conditions. The resulting conjugate CTP features small and uniform meshing backlash, ensuring optimal design outcomes and enhancing HD performance.

(3)

The meshing performance of HD could be enhanced through multi-section CTP design. For HDs with the maximum radial displacement coefficient w₀* varying across different sections (from w₀* > 1 to w₀* < 1), the implementation of multi-section CTP design enables 3D CTP to achieve conjugate meshing over 90 degrees, significantly improving meshing performance.