Safe 3D Coverage Control for Multi-Agent Systems
Abstract
1. Introduction
2. Controller Design
2.1. Preliminaries: CVT and CBF
2.2. Control Problem Formalization
2.3. 3D Safe Coverage Controller Design
3. Simulation
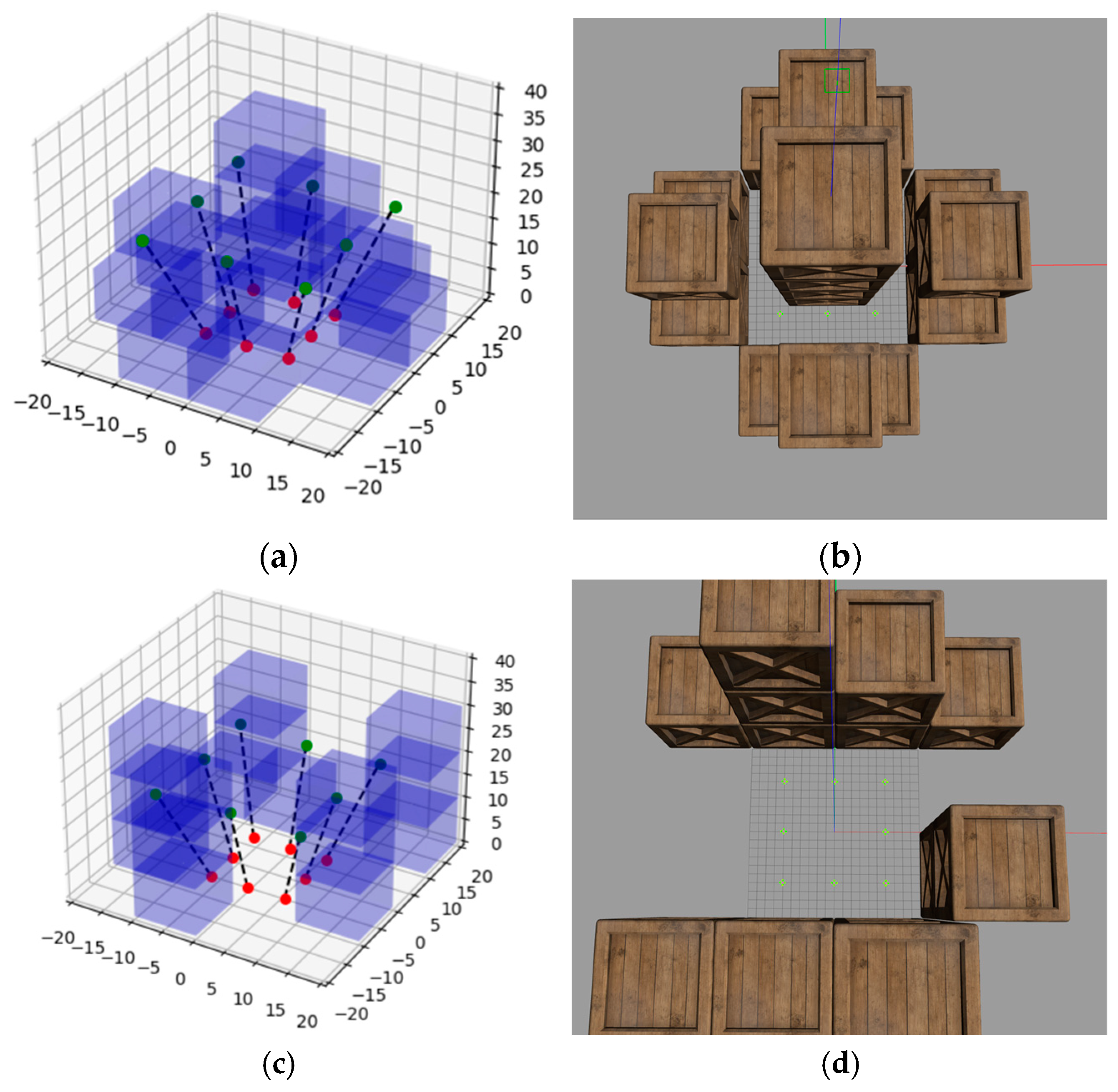
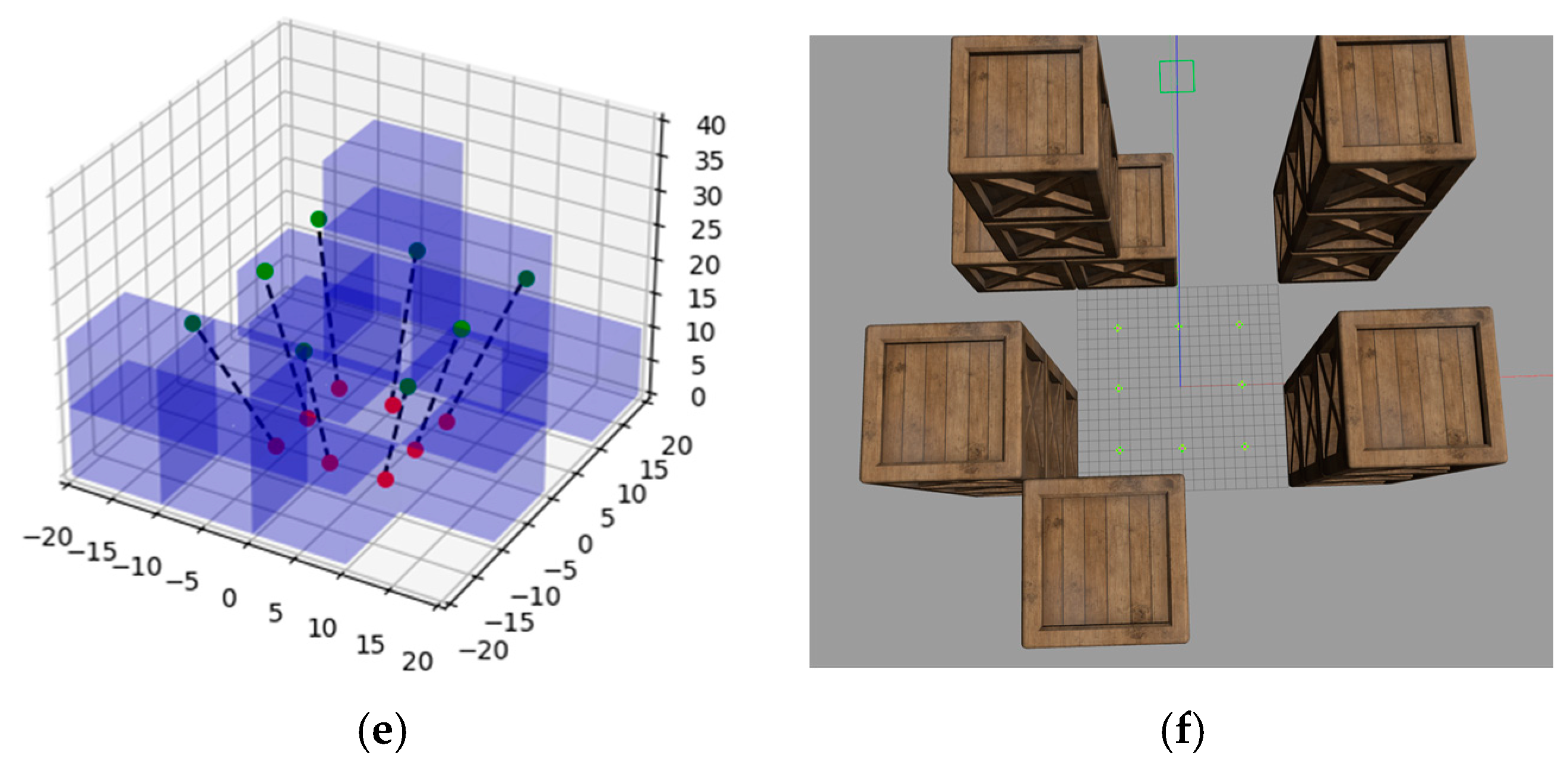
3.1. Simulation Environment
3.2. Simulation Setup
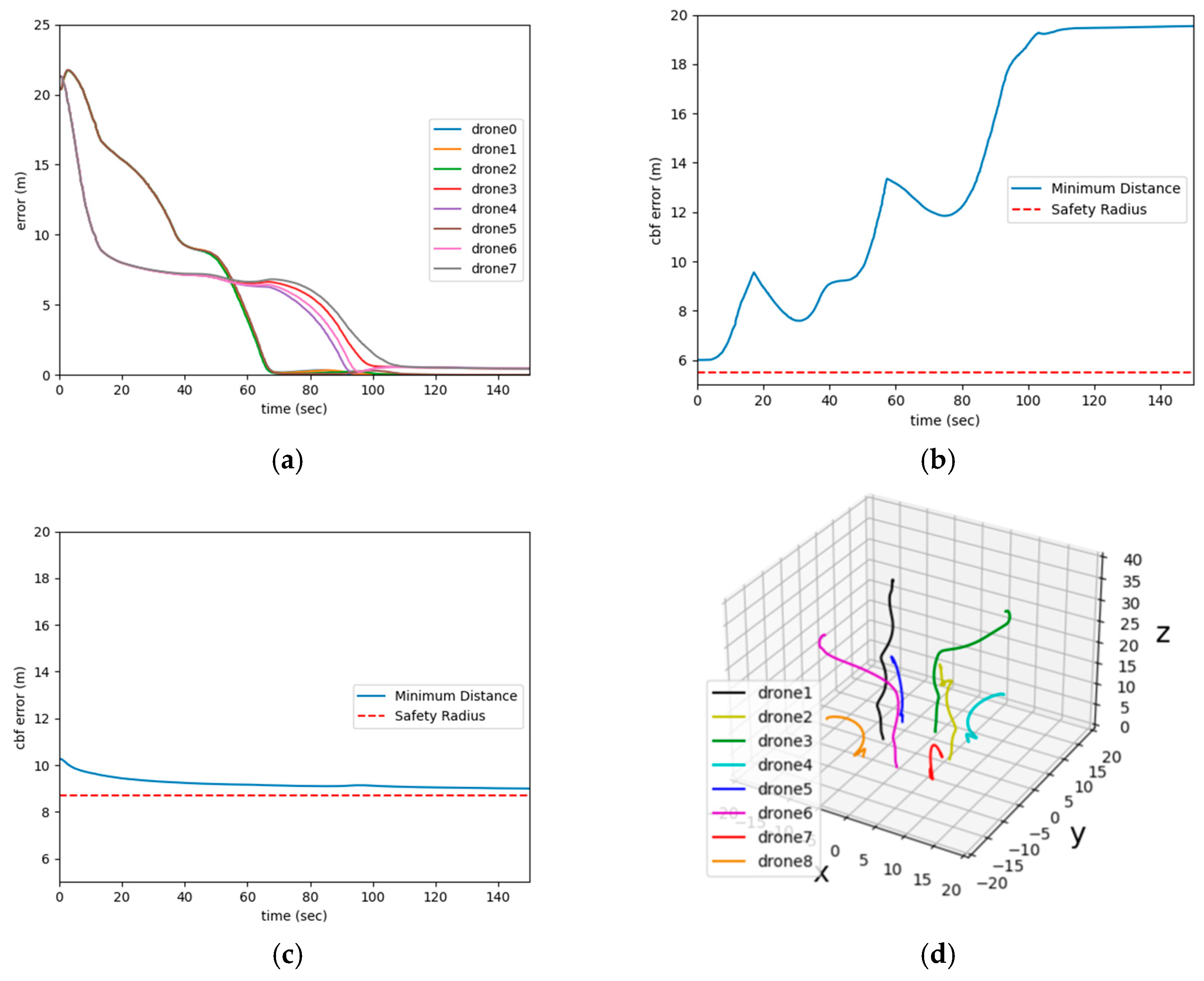
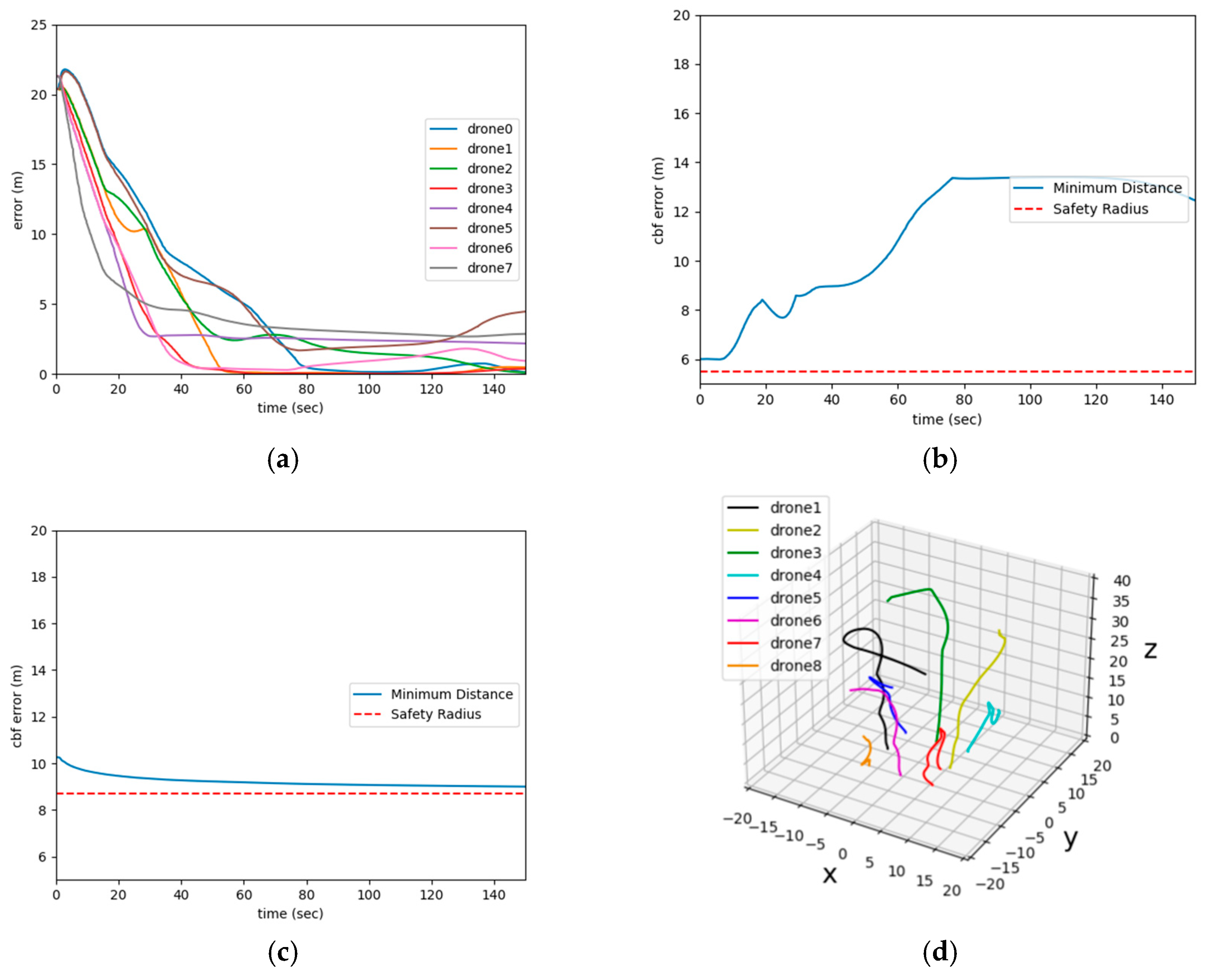
3.3. Simulation Results and Discussion
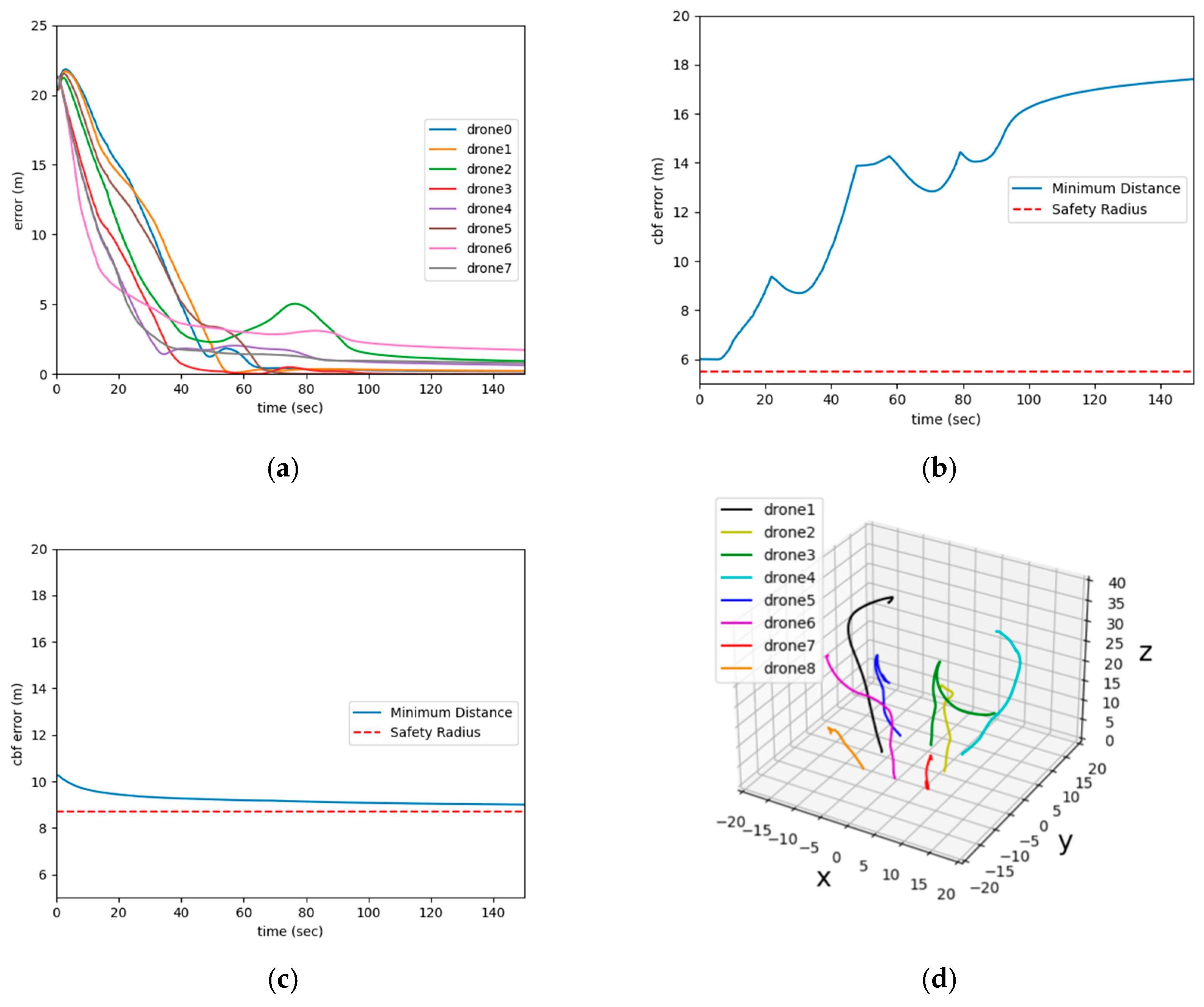
- The distance between agents and their respective goals;
- The shortest distance between agents over time;
- The shortest distance between agents and obstacles over time;
- The trajectories of the agents.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bai, Y.; Tran Ngoc, P.T.; Nguyen, H.D.; Le, D.L.; Ha, Q.H.; Kai, K.; See To, Y.X.; Deng, Y.; Song, J.; Wakamiya, N.; et al. Swarm Navigation of Cyborg-Insects in Unknown Obstructed Soft Terrain. Nat. Commun. 2025, 16, 221. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wan, J.; Zhang, D.; Li, D.; Zhang, C. Towards Smart Factory for Industry 4.0: A Self-Organized Multi-Agent System with Big Data-Based Feedback and Coordination. Comput. Netw. 2016, 101, 158–168. [Google Scholar] [CrossRef]
- Xie, J.; Liu, C. Multi-Agent Systems and Their Applications. J. Int. Counc. Electr. Eng. 2017, 7, 189–197. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, C.O. Multi-Agent Systems Applications in Manufacturing Systems and Supply Chain Management: A Review Paper. Int. J. Prod. Res. 2007, 46, 233–265. [Google Scholar] [CrossRef]
- Dorri, A.; Kanhere, S.S.; Jurdak, R. Multi-Agent Systems: A Survey. IEEE Access 2018, 6, 28573–28593. [Google Scholar] [CrossRef]
- Liang, J.; Li, Y.; Yin, G.; Xu, L.; Lu, Y.; Feng, J.; Shen, T.; Cai, G. A MAS-Based Hierarchical Architecture for the Cooperation Control of Connected and Automated Vehicles. IEEE Trans. Veh. Technol. 2022, 72, 1559–1573. [Google Scholar] [CrossRef]
- Liang, J.; Lu, Y.; Yin, G.; Fang, Z.; Zhuang, W.; Ren, Y.; Xu, L.; Li, Y. A Distributed Integrated Control Architecture of AFS and DYC Based on MAS for Distributed Drive Electric Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 5565–5577. [Google Scholar] [CrossRef]
- Cortes, J.; Martinez, S.; Karatas, T.; Bullo, F. Coverage Control for Mobile Sensing Networks. IEEE Trans. Robot. Autom. 2004, 20, 243–255. [Google Scholar] [CrossRef]
- Lee, S.G.; Diaz-Mercado, Y.; Egerstedt, M. Multi-Robot Control Using Time-Varying Density Functions. IEEE Trans. Robot. 2015, 31, 489–493. [Google Scholar] [CrossRef]
- Miah, S.; Fallah, M.M.H.; Spinello, D. Non-Autonomous Coverage Control with Diffusive Evolving Density. IEEE Trans. Autom. Control 2017, 62, 5262–5268. [Google Scholar] [CrossRef]
- Miah, S.; Panah, A.Y.; Fallah, M.M.H.; Spinello, D. Generalized Non-Autonomous Metric Optimization for Area Coverage Problems with Mobile Autonomous Agents. Automatica 2017, 80, 295–299. [Google Scholar] [CrossRef]
- Chevet, T.; Maniu, C.S.; Vlad, C.; Zhang, Y. Guaranteed Voronoi-Based Deployment for Multi-Agent Systems under Uncertain Measurements. In Proceedings of the 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019. [Google Scholar]
- Li, S.; Li, B.; Yu, J.; Zhang, L.; Zhang, A.; Cai, K. Probabilistic Threshold k-Ann Query Method Based on Uncertain Voronoi Diagram in Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3592–3602. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, Z.; Bandyopadhyay, S.; Schwager, M. Fast, Online Collision Avoidance for Dynamic Vehicles Using Buffered Voronoi Cells. IEEE Robot. Autom. Lett. 2017, 2, 1047–1054. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Z.; Paudel, S.; Schwager, M. Safe Distributed Lane Change Maneuvers for Multiple Autonomous Vehicles Using Buffered Input Cells. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 4678–4684. [Google Scholar]
- Pierson, A.; Rus, D. Distributed Target Tracking in Cluttered Environments with Guaranteed Collision Avoidance. In Proceedings of the 2017 International Symposium on Multi-Robot and Multi-Agent Systems (MRS), Cambridge, MA, USA, 4–5 December 2017; pp. 83–89. [Google Scholar]
- Pierson, A.; Schwarting, W.; Karaman, S.; Rus, D. Weighted Buffered Voronoi Cells for Distributed Semi-Cooperative Behavior. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 5611–5617. [Google Scholar]
- Garg, K.; Panagou, D. Robust Control Barrier and Control Lyapunov Functions with Fixed-Time Convergence Guarantees. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 2292–2297. [Google Scholar]
- Nguyen, Q.; Sreenath, K. Robust Safety-Critical Control for Dynamic Robotics. IEEE Trans. Autom. Control 2022, 67, 1073–1088. [Google Scholar] [CrossRef]
- Verginis, C.K.; Djeumou, F.; Topcu, U. Safety-Constrained Learning and Control Using Scarce Data and Reciprocal Barriers. arXiv 2021, arXiv:2105.06526. [Google Scholar]
- Fungtammasan, K.; Bai, Y.; Svinin, M.; Matsuno, F.; Magid, E.; Suthakorn, J. Adaptive Coverage Control for Dynamic Pattern Generation. In Proceedings of the 2022 13th Asian Control Conference (ASCC), Pusan, Republic of Korea, 4–7 May 2022; pp. 1404–1408. [Google Scholar]
- Bai, Y.; Wang, Y.; Xiong, X.; Song, J.; Svinin, M. Safe Adaptive Multi-Agent Coverage Control. IEEE Control Syst. Lett. 2023, 7, 3217–3222. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, Y.; Svinin, M.; Magid, E.; Sun, R. Function Approximation Technique Based Immersion and Invariance Control for Unknown Nonlinear Systems. IEEE Control Syst. Lett. 2020, 4, 934–939. [Google Scholar] [CrossRef]
- Bai, Y.; Svinin, M.; Yamamoto, M. Function Approximation Based-Control for Non-Square Systems. SICE J. Control Meas. Syst. Integr. 2018, 11, 477–485. [Google Scholar] [CrossRef]
- Chertovskih, R.; Ribeiro, V.M.; Gonçalves, R.; Aguiar, A.P. Sixty Years of the Maximum Principle in Optimal Control: Historical Roots and Content Classification. Symmetry 2024, 16, 1398. [Google Scholar] [CrossRef]
- Meng, X.; Houshmand, A.; Cassandras, C.G. Multi-Agent Coverage Control with Energy Depletion and Repletion. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Bonnet, B. A Pontryagin Maximum Principle in Wasserstein Spaces for Constrained Optimal Control Problems. ESAIM Control Optim. Calc. Var. 2019, 25, 52. [Google Scholar] [CrossRef]
- Segawa, K.; Hayashi, N.; Takai, S. 2D Voronoi Coverage Control with Gaussian Density Functions by Line Integration. SICE J. Control Meas. Syst. Integr. 2017, 10, 110–116. [Google Scholar]
- Xu, B.; Sreenath, K. Safe Teleoperation of Dynamic UAVs through Control Barrier Functions. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7848–7855. [Google Scholar]
- Wang, L.; Ames, A.D.; Egerstedt, M. Safe Certificate-Based Maneuvers for Teams of Quadrotors Using Differential Flatness. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3293–3298. [Google Scholar]
- Siri, F.C.; Song, J.; Svinin, M. Safe Coverage Control of Multi-Agent Systems and Its Verification in ROS/Gazebo Environment. Information 2024, 15, 462. [Google Scholar] [CrossRef]
- Siri, F.C.; Song, J.; Svinin, M. Experimental Verification of Coverage Control of Multi-Agent Systems with Obstacle Avoidance. J. Eng. 2024, 12, e70045. [Google Scholar] [CrossRef]
- Xu, X.; Tabuada, P.; Grizzle, J.W.; Ames, A.D. Robustness of Control Barrier Functions for Safety-Critical Control. IFAC—PapersOnLine 2015, 48, 54–61. [Google Scholar] [CrossRef]
- Tess. Available online: https://tess.readthedocs.io/en/latest/ (accessed on 10 May 2024).
- Open Source Robotics Foundation. Available online: https://wiki.ros.org/hector_quadrotor (accessed on 10 May 2024).
- Rafalamao/Hector-Quadrotor-Noetic: Hector Quadrotor Ported to ROS Noetic with Gazebo 11. Available online: https://github.com/RAFALAMAO/hector-quadrotor-noetic (accessed on 12 May 2024).
- Open Source Robotics Foundation. Available online: https://gazebosim.org/about (accessed on 15 May 2024).
- Open Dynamic Engine. Available online: https://ode.org (accessed on 15 May 2024).


| Experiment Layout | Average Final Error (m) | Convergence Time (s) |
|---|---|---|
| Symmetrical Layout | 0.3 | 105 |
| Asymmetrical Layout 1 | 1.8 | 80 |
| Asymmetrical Layout 2 | 0.9 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Borikarnphanichphaisal, K.; Song, J.; Vasilieva, O.; Svinin, M. Safe 3D Coverage Control for Multi-Agent Systems. Actuators 2025, 14, 186. https://doi.org/10.3390/act14040186
Liu W, Borikarnphanichphaisal K, Song J, Vasilieva O, Svinin M. Safe 3D Coverage Control for Multi-Agent Systems. Actuators. 2025; 14(4):186. https://doi.org/10.3390/act14040186
Chicago/Turabian StyleLiu, Wenbin, Kritapas Borikarnphanichphaisal, Jie Song, Olga Vasilieva, and Mikhail Svinin. 2025. "Safe 3D Coverage Control for Multi-Agent Systems" Actuators 14, no. 4: 186. https://doi.org/10.3390/act14040186
APA StyleLiu, W., Borikarnphanichphaisal, K., Song, J., Vasilieva, O., & Svinin, M. (2025). Safe 3D Coverage Control for Multi-Agent Systems. Actuators, 14(4), 186. https://doi.org/10.3390/act14040186






