Deep Reinforcement Learning-Based Enhancement of Robotic Arm Target-Reaching Performance
Abstract
1. Introduction
- Implementation of the deep deterministic policy gradient algorithm in a simulated environment to improve the target-reaching performance of a robotic arm.
- Integration of reinforcement learning with OpenAI Gym, PyBullet, and Panda Gym to create a flexible simulation framework.
- Comparison of the DDPG (off-policy) and Proximal Policy Optimization (PPO) (on-policy) algorithms to assess their efficiency, stability, and performance in robotic manipulation tasks.
- Evaluation of the performance and training behavior of the robotic agent using the DDPG and PPO algorithms in the context of a simulated target-reaching task.
2. Modeling of Robotic Arm
Direct Kinematic Model of Robotic Arm
- The rotation matrix () represents the orientation of the i-th frame relative to the -th frame.
- represents the center of the link frame with components (, , and ).
3. Deep Reinforcement Learning Algorithm Design
3.1. Policy Gradient Algorithm
- Objective function (): This represents the expected cumulative reward obtained by following the policy in the given environment. The objective function is optimized by adjusting the parameter to maximize the expected cumulative reward.
- Discounted state distribution (): This represents the probability of being in a particular state s under the policy ; mathematically,where when starting from and following policy for t time steps.
- Action–value function (): This represents the expected cumulative reward obtained by taking action a in state s and following policy thereafter.
- Policy function(): This represents the probability of taking action a in state s under the parameterized policy .
3.1.1. Derivation of the Policy Gradient Theorem
- For , and
- For , we can consider every action that might be taken and add up the probabilities of reaching the desired state:
- The goal is to move from s to x after steps by following . The agent can first move from s to intermediate state before proceeding to the final state x in the last steps after k stages. This allows us to recursively update the visitation probability as
3.1.2. Off-Policy Gradient Algorithms
3.2. Deterministic Policy Gradient (DPG)
- be the initial distribution over states,
- be the density of visitation probability in state when starting from state s after moving k steps by policy , and
- be the discounted state distribution, defined as.
3.3. Deep Deterministic Policy Gradient (DDPG)
| Algorithm 1: Deep Deterministic Policy Gradient [37] |
 |
4. Results and Discussion
4.1. Simulation Environment and Training Setup
4.2. Hyperparameter Selection and Initial Search
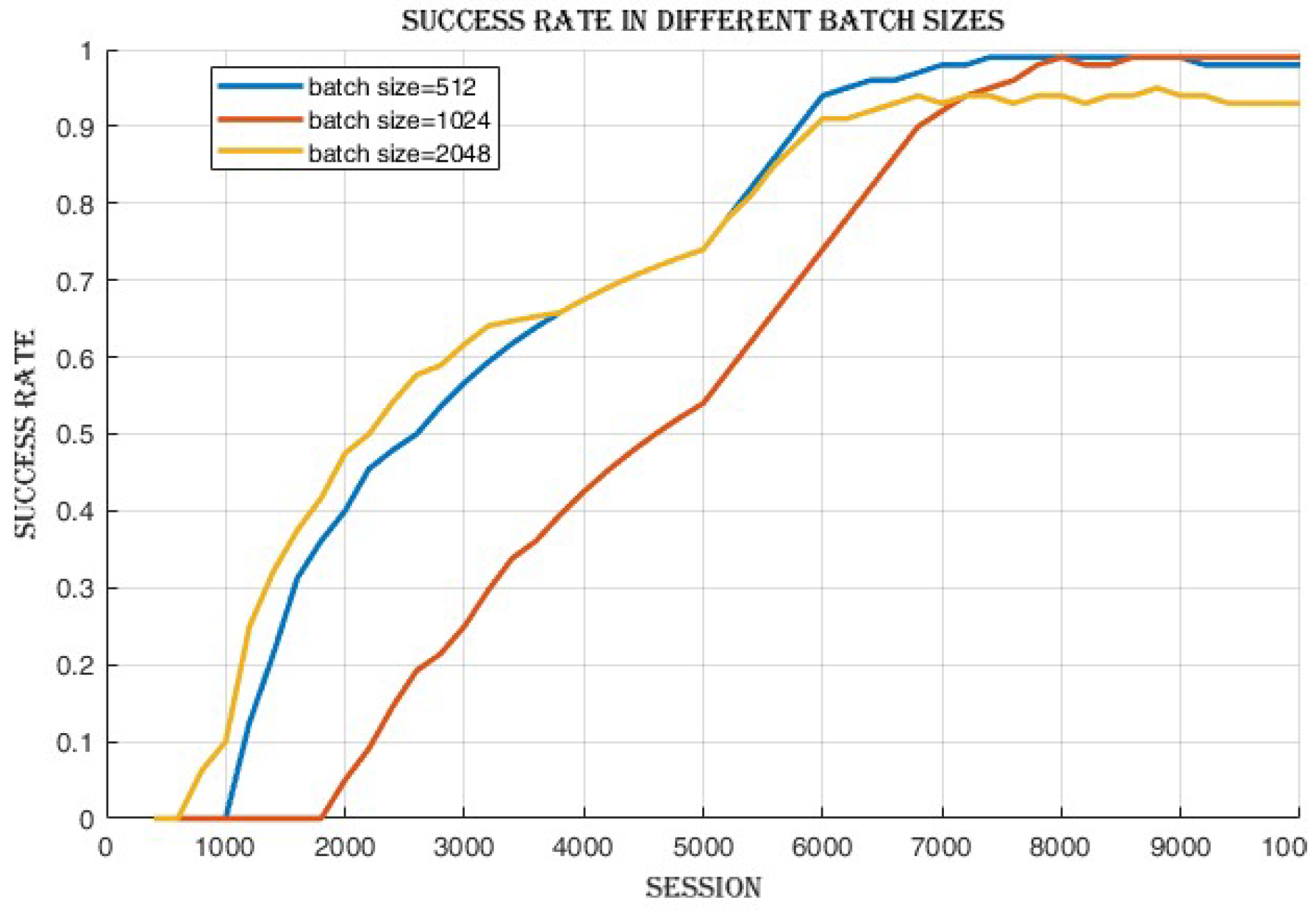
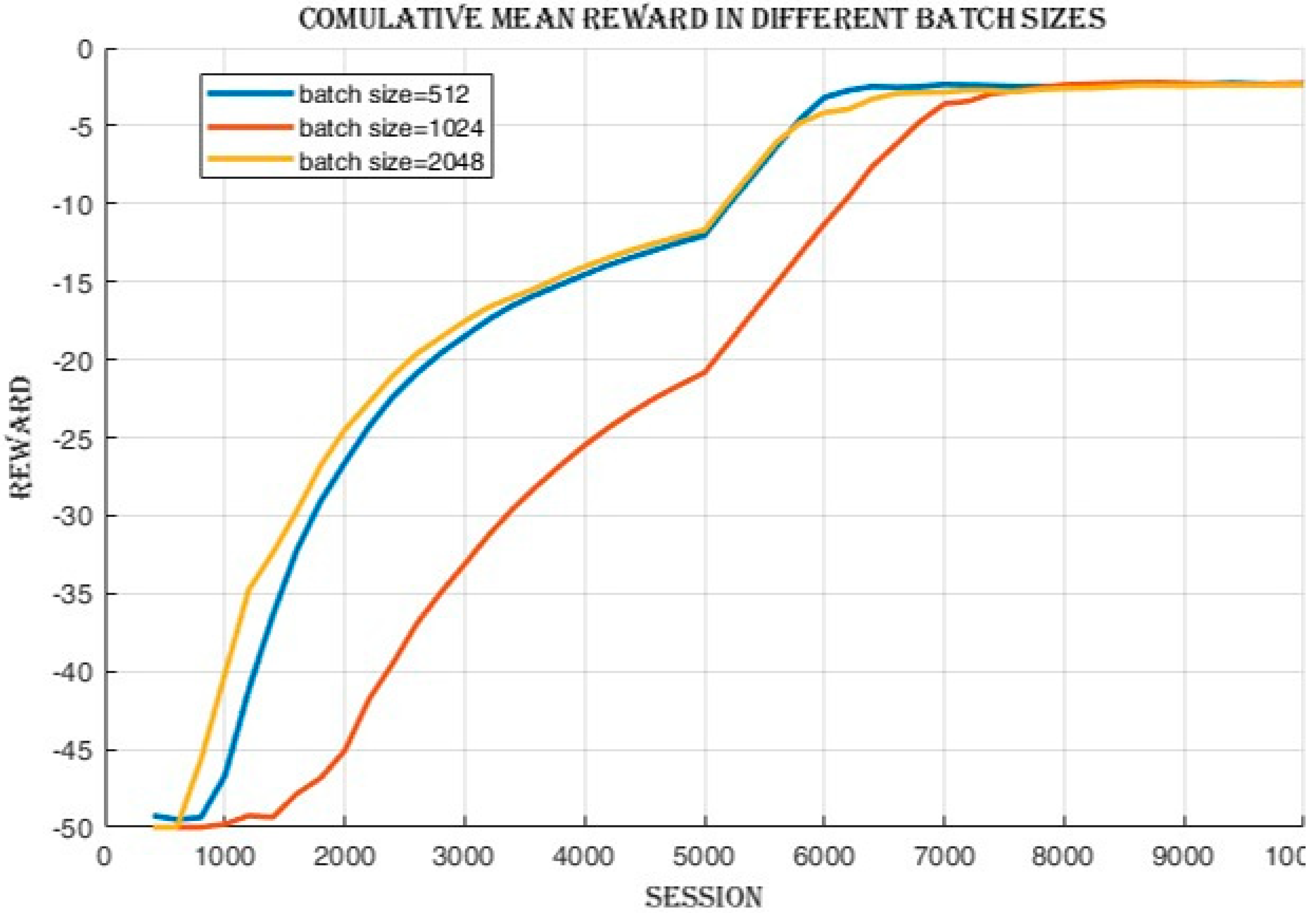
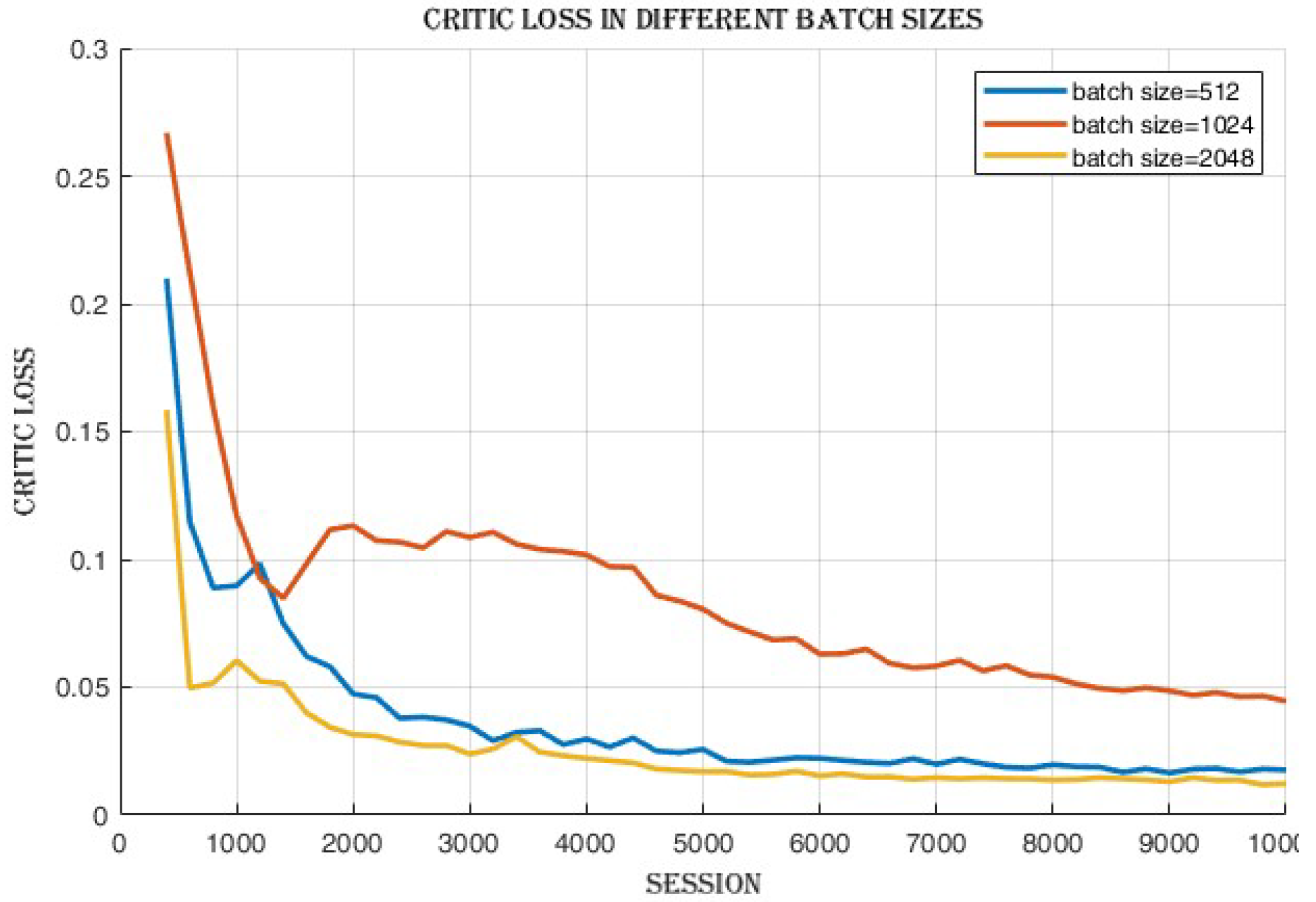
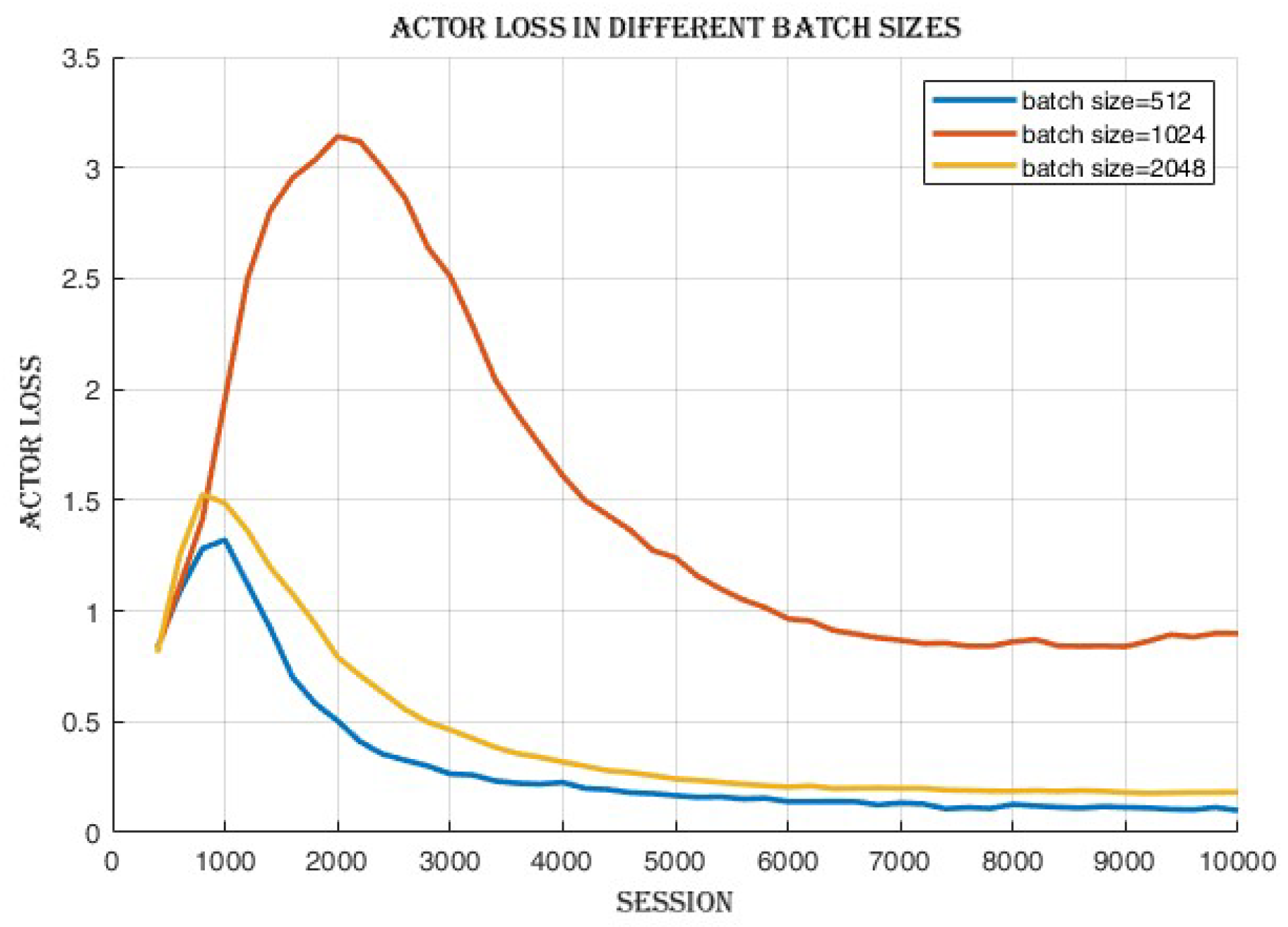
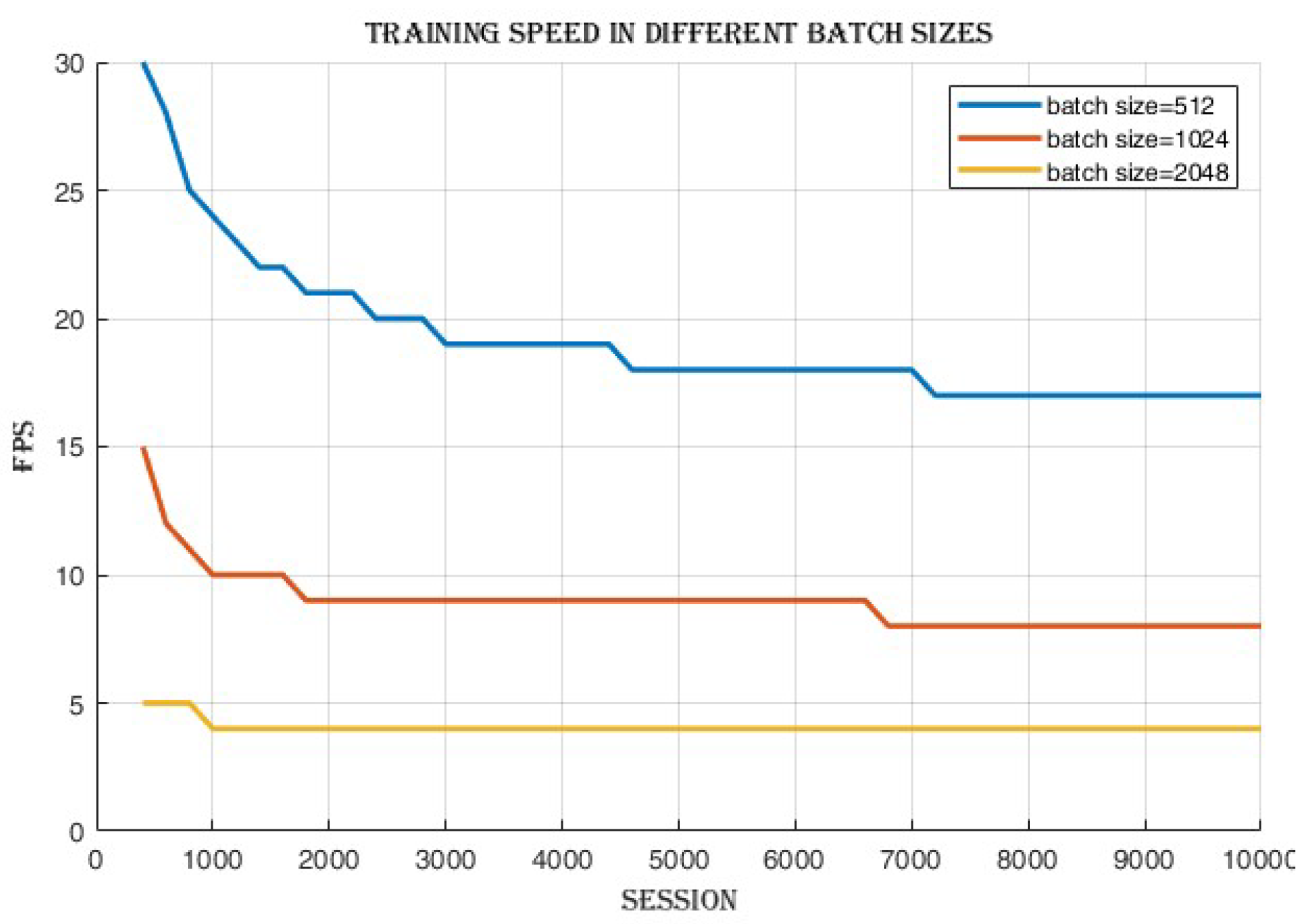
4.2.1. Batch Size Comparison
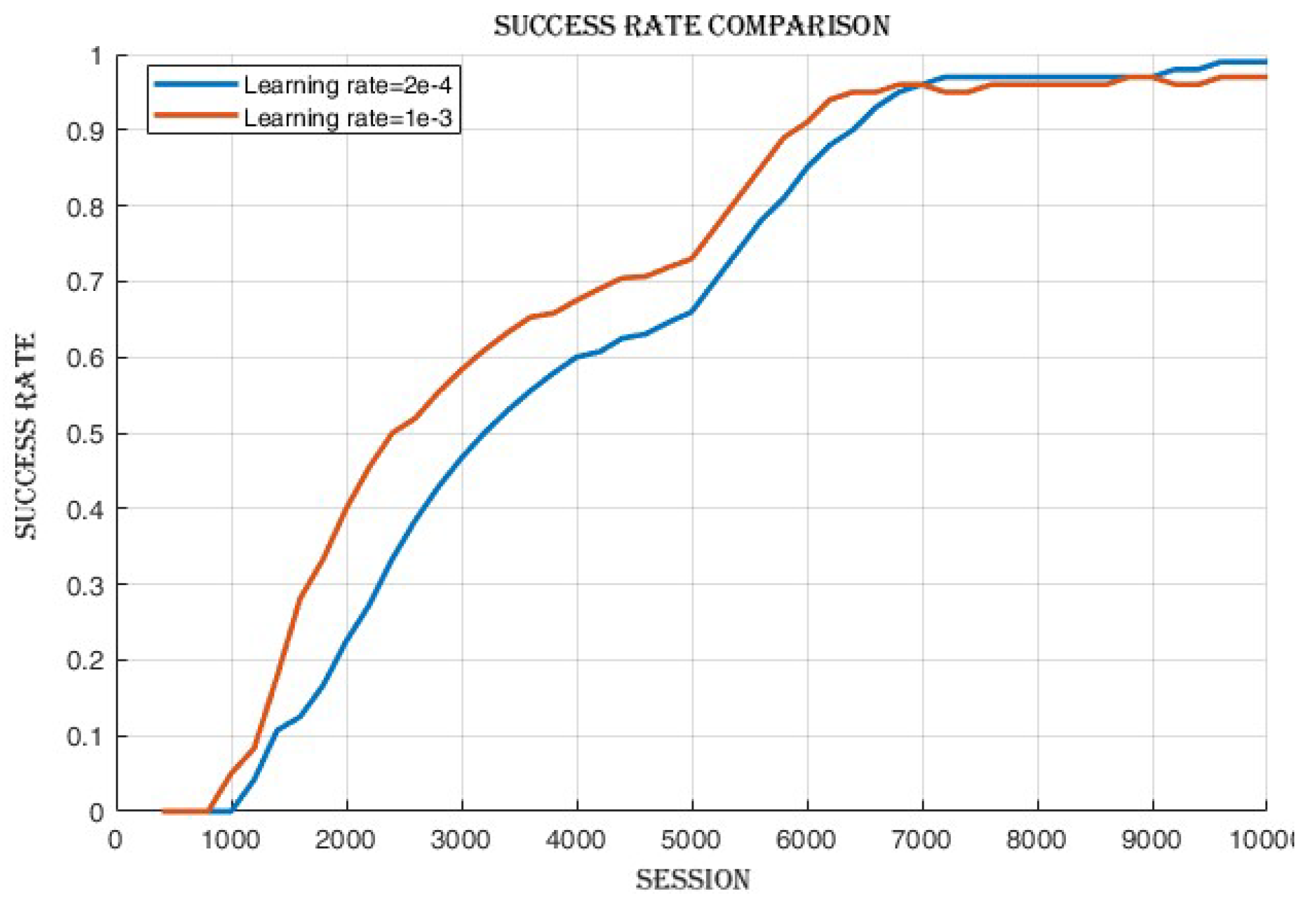
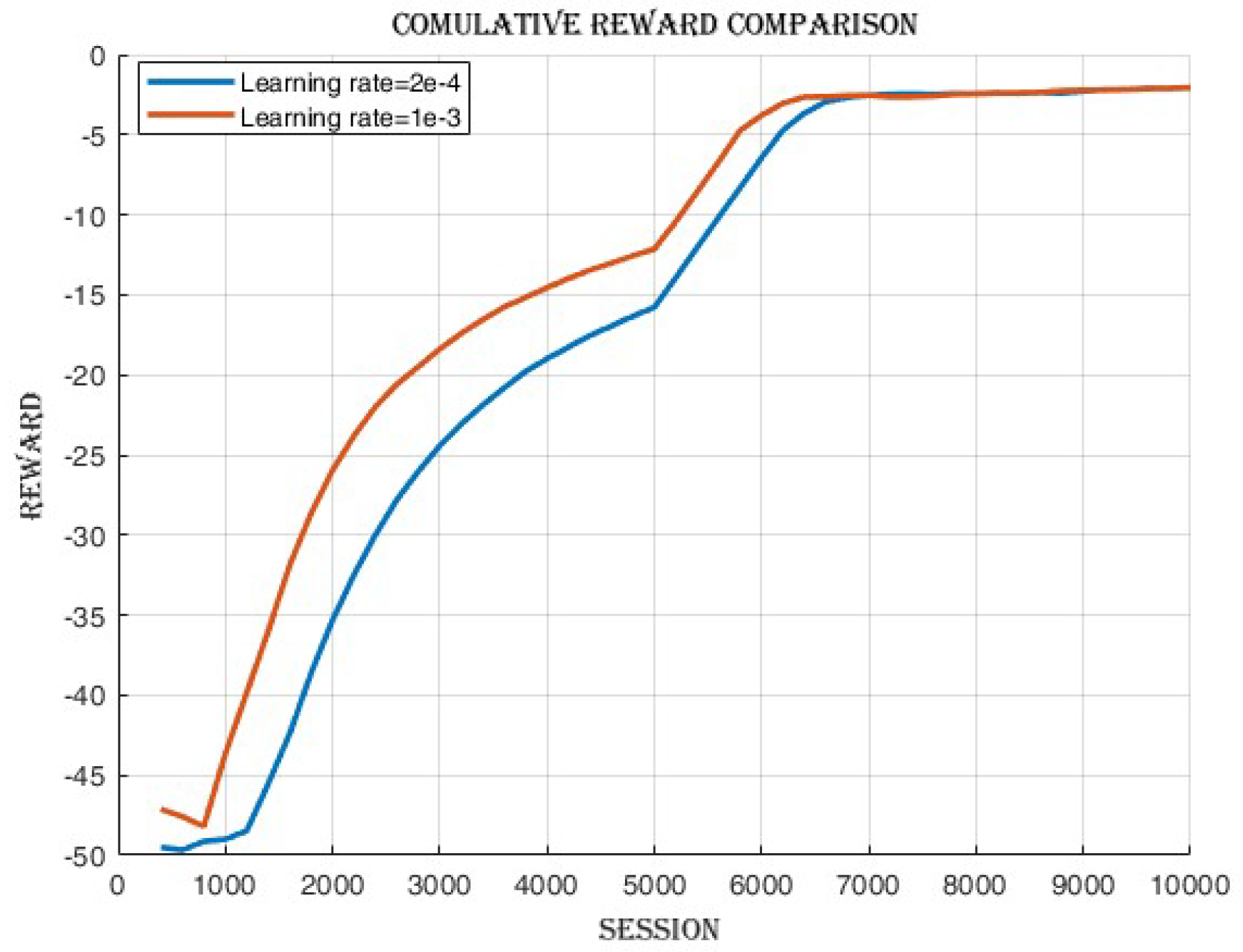
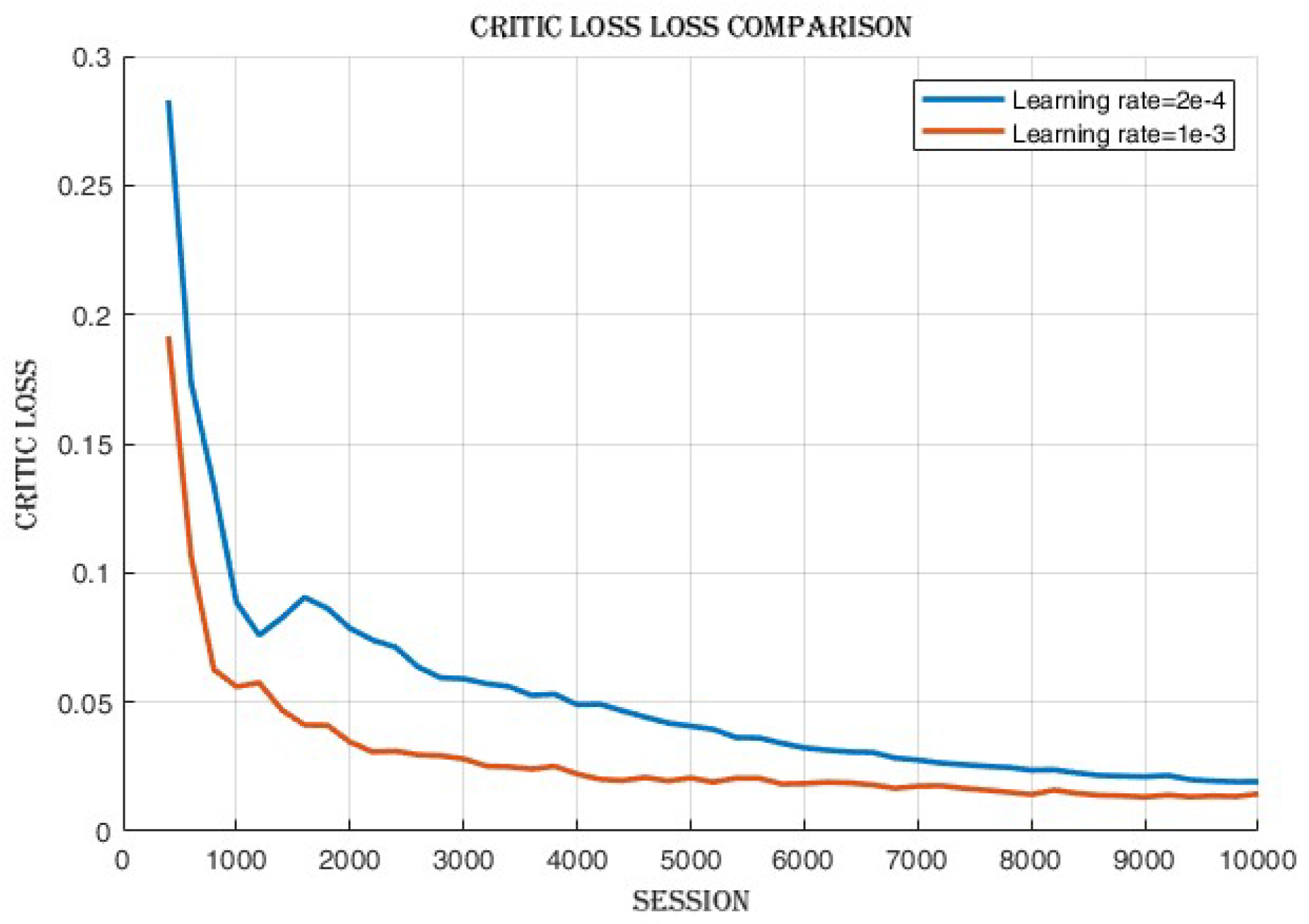
4.2.2. Learning Rate Comparison
4.3. Selection of Optimal Hyperparameters and Extended Training of DDPG Agent
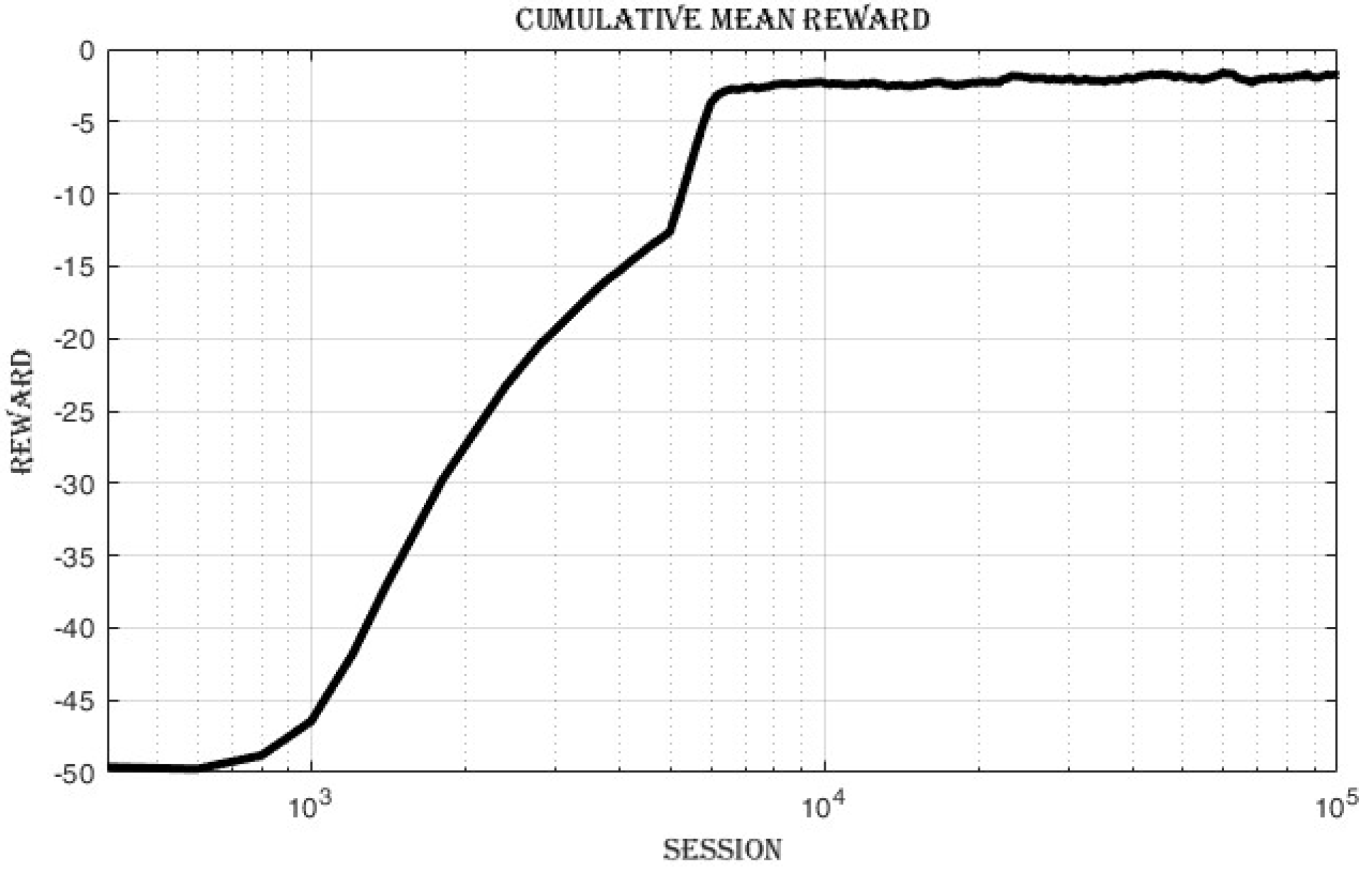
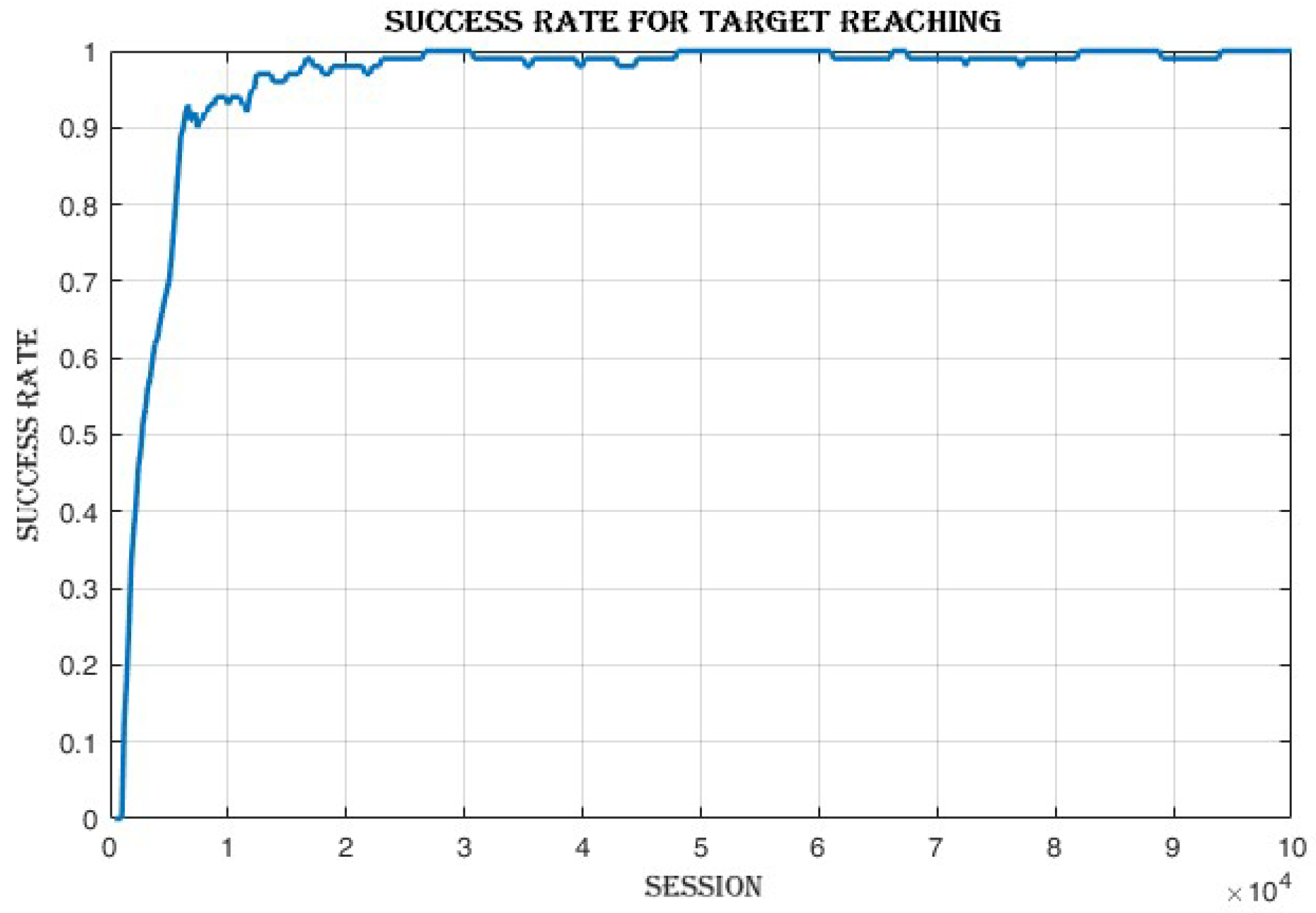
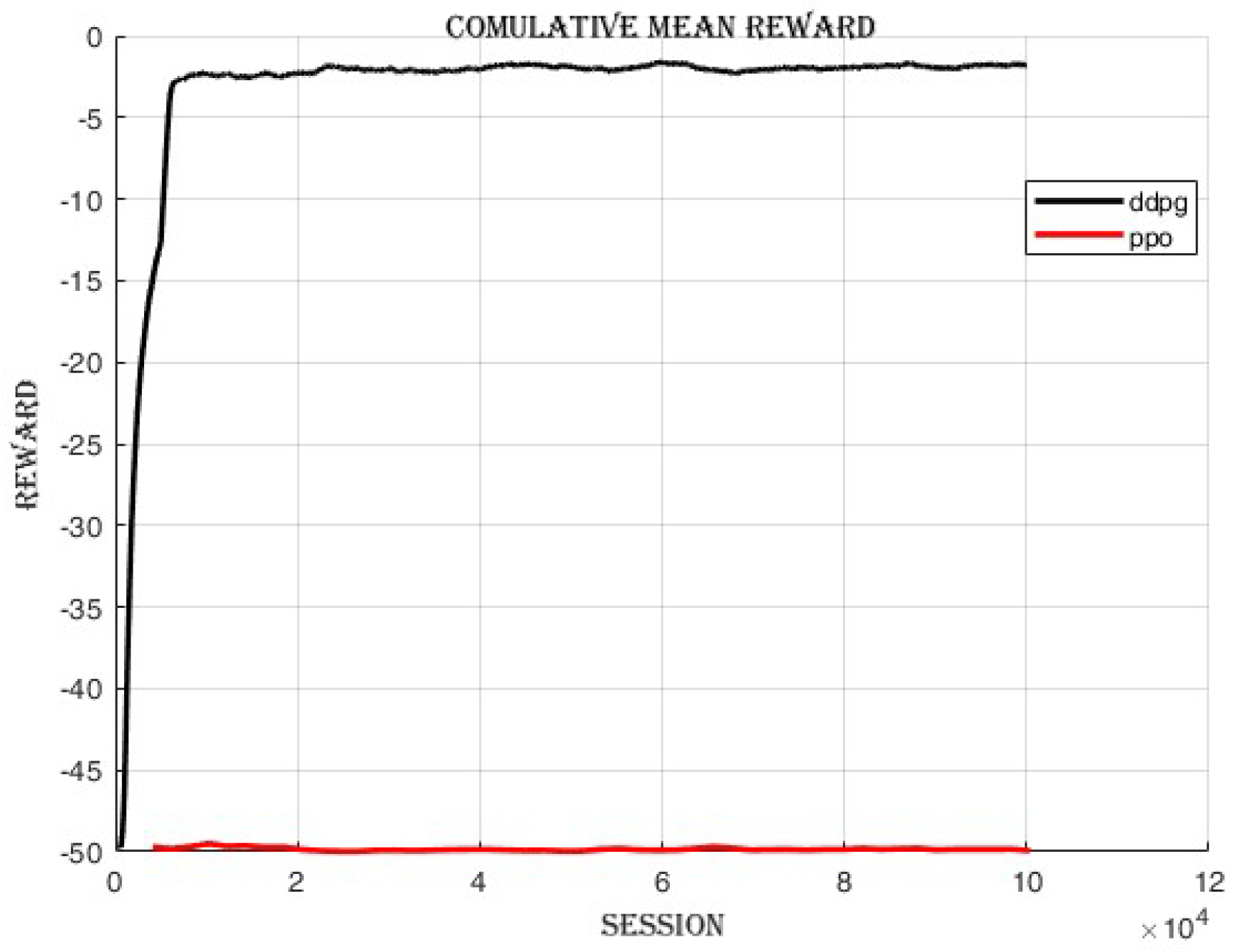
4.3.1. Improvement in Cumulative Reward and Success Rate
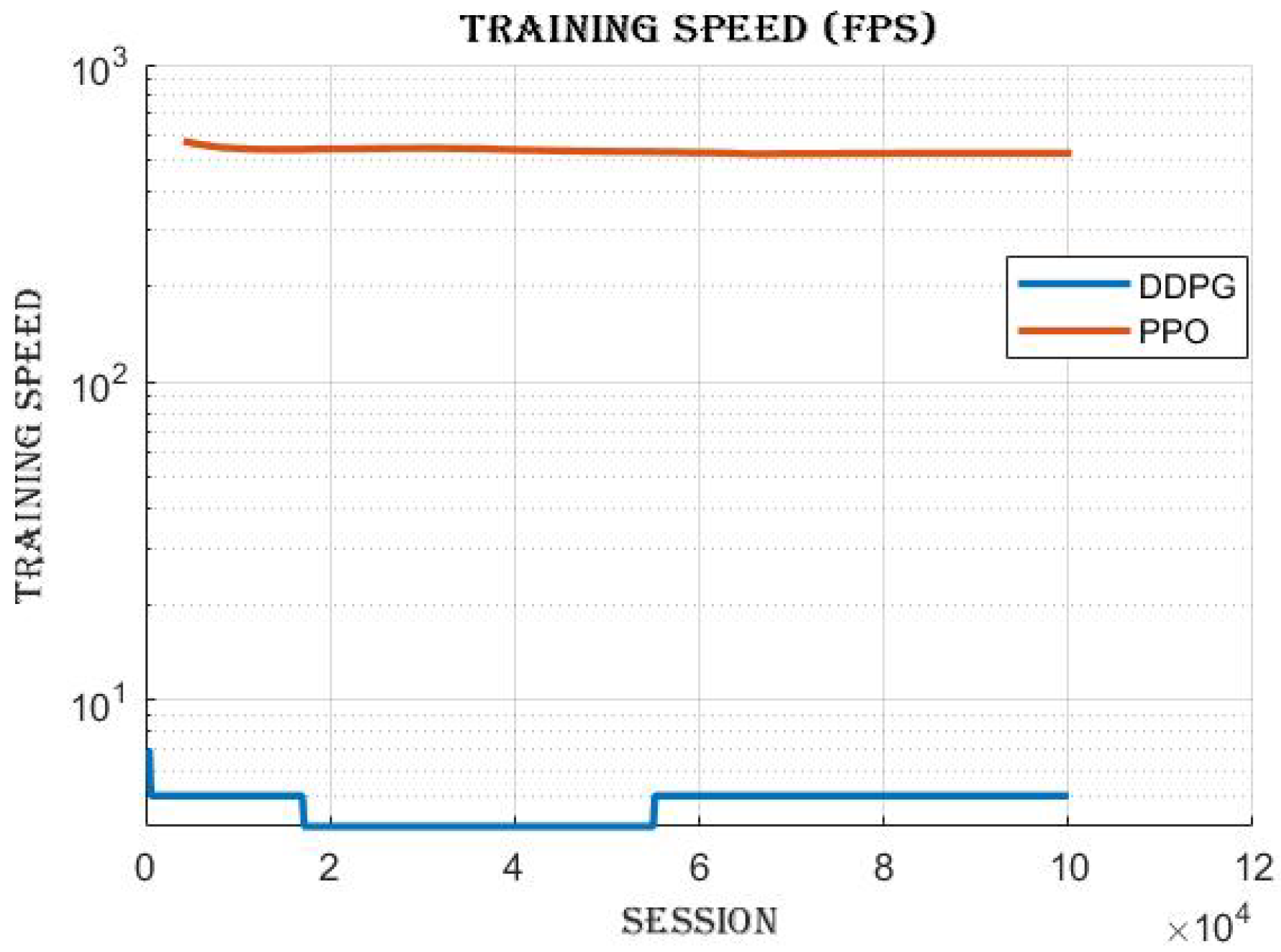
4.3.2. Frames per Second (FPS)
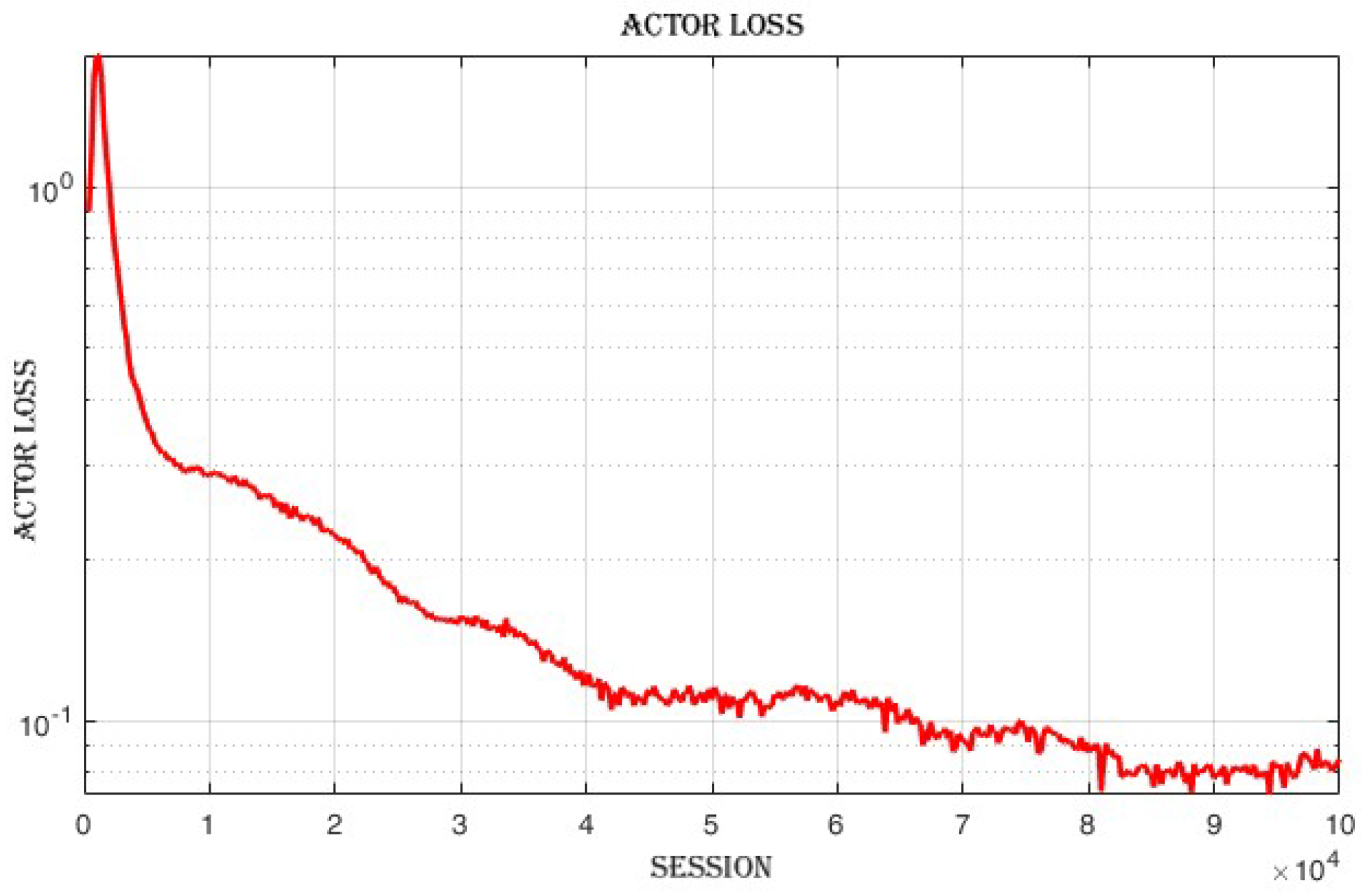
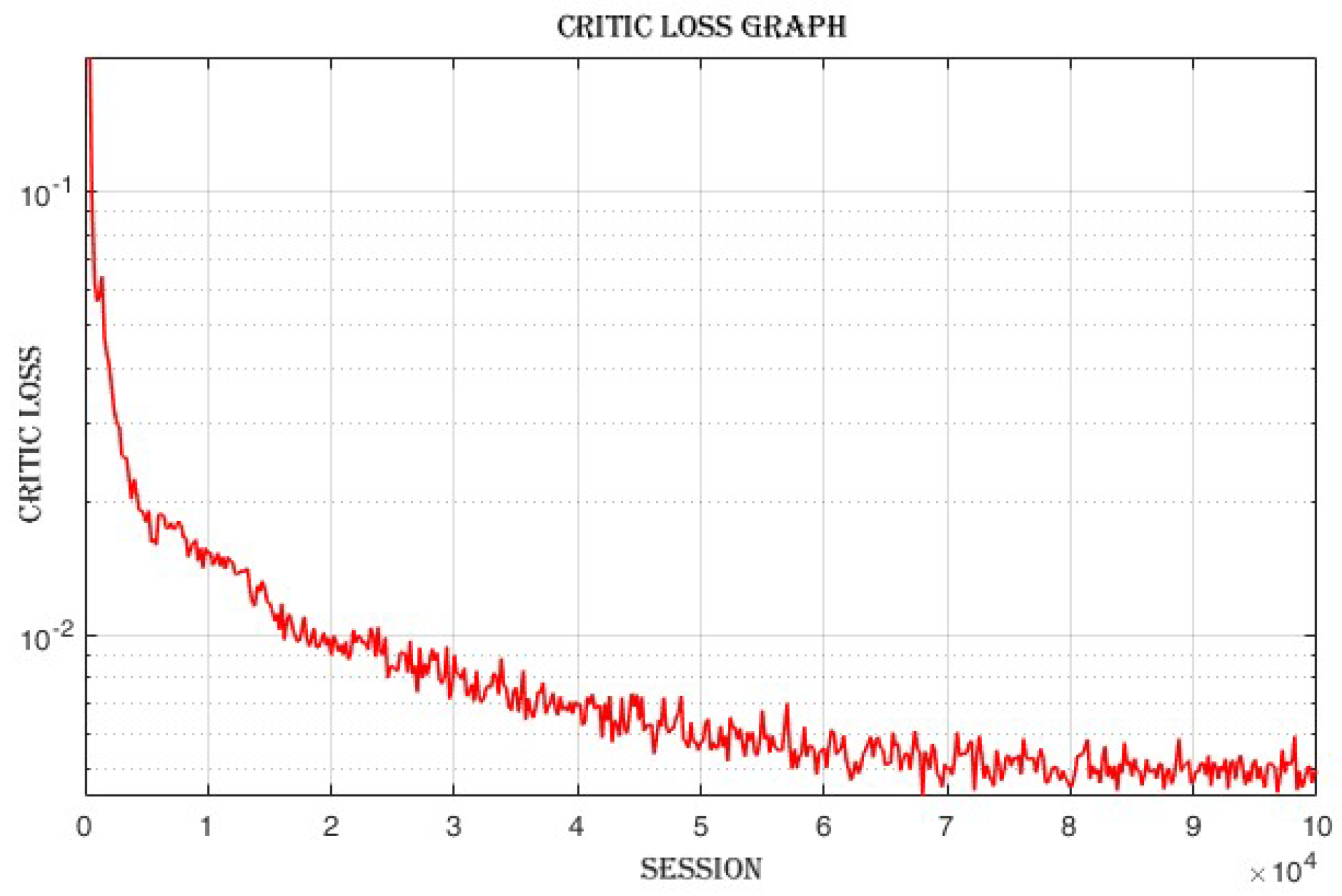
4.3.3. Improvement in Actor and Critic Losses
4.4. Comparing DDPG and PPO: Off-Policy vs. On-Policy Reinforcement Learning Algorithms
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohsen, S.; Behrooz, A.; Roza, D. Artificial intelligence, machine learning and deep learning in advanced robotics, a review. Cogn. Robot. 2023, 3, 54–70. [Google Scholar]
- Santos, A.A.; Schreurs, C.; da Silva, A.F.; Pereira, F.; Felgueiras, C.; Lopes, A.M.; Machado, J. Integration of Artificial Vision and Image Processing into a Pick and Place Collaborative Robotic System. J. Intell. Robot. Syst. 2024, 110, 159. [Google Scholar] [CrossRef]
- Xinle, Y.; Minghe, S.; Lingling, S. Adaptive and intelligent control of a dual-arm space robot for target manipulation during the post-capture phase. Aerosp. Sci. Technol. 2023, 142, 108688. [Google Scholar]
- Abayasiri, R.A.M.; Jayasekara, A.G.B.P.; Gopura, R.A.R.C.; Kazuo, K. Intelligent Object Manipulation for a Wheelchair-Mounted Robotic Arm. J. Robot. 2024, 2024, 1516737. [Google Scholar] [CrossRef]
- Yi, J.; Zhang, H.; Mao, J.; Chen, Y.; Zhong, H.; Wang, Y. Review on the COVID-19 pandemic prevention and control system based on AI. Eng. Appl. Artif. Intell. 2022, 114, 105184. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Liang, J.; Zhu, F. A comparative review on multi-modal sensors fusion based on deep learning. Signal Process. 2023, 213, 109165. [Google Scholar] [CrossRef]
- Doewes, R.I.; Purnama, S.K.; Nuryadin, I.; Kurdhi, N.A. Human AI: Social robot decision-making using emotional AI and neuroscience. In Emotional AI and Human-AI Interactions in Social Networking; Garg, M., Koundal, D., Eds.; Academic Press: Cambridge, MA, USA, 2024; pp. 255–286. [Google Scholar] [CrossRef]
- Martin, J.G.; Muros, F.J.; Maestre, J.M.; Camacho, E.F. Multi-robot task allocation clustering based on game theory. Robot. Auton. Syst. 2023, 161, 104314. [Google Scholar]
- Nguyen, M.N.T.; Ba, D.X. A neural flexible PID controller for task-space control of robotic manipulators. Front. Robot. AI 2023, 9, 975850. [Google Scholar]
- Laurenzi, A.; Antonucci, D.; Tsagarakis, N.G.; Muratore, L. The XBot2 real-time middleware for robotics. Robot. Auton. Syst. 2023, 163, 104379. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, M.; Farid, D.; Hossain, M.A. Intelligent Facial Emotion Recognition and Semantic-Based Topic Detection for a Humanoid Robot. Expert Syst. Appl. 2013, 40, 5160–5168. [Google Scholar]
- Floreano, D.; Wood, R.J. Science, Technology, and the Future of Small Autonomous Drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.D.; Kockelman, K.M.; Hanna, J.P. Operations of a Shared, Autonomous, Electric Vehicle Fleet: Implications of Vehicle & Charging Infrastructure Decisions. Transp. Res. Part Policy Pract. 2016, 94, 243–254. [Google Scholar]
- Chen, Z.; Jia, X.; Riedel, A.; Zhang, M. A Bio-Inspired Swimming Robot. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; p. 2564. [Google Scholar]
- Ohmura, Y.; Kuniyoshi, Y. Humanoid Robot Which Can Lift a 30kg Box by Whole Body Contact and Tactile Feedback. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1136–1141. [Google Scholar]
- Kappassov, Z.; Corrales, J.-A.; Perdereau, V. Tactile Sensing in Dexterous Robot Hands. Robot. Auton. Syst. 2015, 74, 195–220. [Google Scholar] [CrossRef]
- Gomes, N.; Martins, F.; Lima, J.; Wörtche, H. Deep Reinforcement Learning Applied to a Robotic Pick-and-Place Application; Springer: Berlin/Heidelberg, Germany, 2021; pp. 251–265. [Google Scholar] [CrossRef]
- Aryslan, M.; Yevgeniy, L.; Troy, H.; Richard, P. A deep reinforcement-learning approach for inverse kinematics solution of a high degree of freedom robotic manipulator. Robotics 2022, 11, 44. [Google Scholar]
- Serhat, O.; Enver, T.; Erkan, Z. Adaptive Cartesian space control of robotic manipulators: A concurrent learning based approach. J. Frankl. Inst. 2024, 361, 106701. [Google Scholar]
- Ladosz, P.; Weng, L.; Kim, M.; Oh, H. Exploration in deep reinforcement learning: A survey. Inf. Fusion 2022, 85, 1–22. [Google Scholar] [CrossRef]
- AlMahamid, F.; Grolinger, K. Reinforcement learning algorithms: An overview and classification. In Proceedings of the 2021 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Virtual, 12–17 September 2021; pp. 1–7. [Google Scholar]
- Thrun, S.; Littman, M.L. Reinforcement Learning: An Introduction. AI Mag. 2000, 21, 103. [Google Scholar]
- Smruti, A. Deep reinforcement learning for robotic manipulation-the state of the art. arXiv 2017, arXiv:1701.08878. Available online: https://api.semanticscholar.org/CorpusID:9103068 (accessed on 21 February 2024).
- Jens, K.; Bagnell, J.A.; Jan, P. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar]
- Tianci, G. Optimizing robotic arm control using deep Q-learning and artificial neural networks through demonstration-based methodologies: A case study of dynamic and static conditions. Robot. Auton. Syst. 2024, 181, 104771. [Google Scholar]
- Andrea, F.; Elisa, T.; Nicola, C.; Stefano, G. Robotic Arm Control and Task Training through Deep Reinforcement Learning. arXiv 2020, arXiv:2005.02632v1. [Google Scholar]
- Shianifar, J.; Schukat, M.; Mason, K. Optimizing Deep Reinforcement Learning for Adaptive Robotic Arm Control. arXiv 2024, arXiv:2407.02503v1. [Google Scholar]
- Roman, P.; Jakub, K.; Radomil, M.; Martin, J. Deep-Reinforcement-Learning-Based Motion Planning for a Wide Range of Robotic Structures. Computation 2024, 12, 116. [Google Scholar] [CrossRef]
- Wanqing, X.; Yuqian, L.; Weiliang, X.; Xun, X. Deep reinforcement learning based proactive dynamic obstacle avoidance for safe human-robot collaboration. Manuf. Lett. 2024, 41, 1246–1256. [Google Scholar]
- Chua, K.; Calandra, R.; McAllister, R.; Levine, S. Deep reinforcement learning in a handful of trials using probabilistic dynamics models. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Levine, S.; Pastor, P.; Krizhevsky, A.; Quillen, D. Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection. Int. J. Robot. Res. 2018, 37, 421–436. [Google Scholar]
- Kathirgamanathan, A.; Mangina, E.; Finn, D.P. Development of a Soft Actor Critic deep reinforcement learning approach for harnessing energy flexibility in a Large Office building. Energy AI 2021, 5, 100101. [Google Scholar] [CrossRef]
- Li, P.; Chen, D.; Wang, Y.; Zhang, L.; Zhao, S. Path planning of mobile robot based on improved TD3 algorithm in dynamic environment. Heliyon 2024, 10, e32167. [Google Scholar] [CrossRef]
- Salas-Pilco, S.; Xiao, K.; Hu, X. Correction: Salas-Pilco et al. Artificial Intelligence and Learning Analytics in Teacher Education: A Systematic Review. Educ. Sci. 2023, 13, 897. [Google Scholar] [CrossRef]
- Franka Emika Documentation. Control Parameters Documentation. 2024. Available online: https://frankaemika.github.io/docs/control_parameters.html (accessed on 21 February 2024).
- Weng, L. Policy Gradient Algorithms. Lil’Log. 2018. Available online: https://lilianweng.github.io/posts/2018-04-08-policy-gradient (accessed on 21 February 2024).
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Tassa, Y.; Silver, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar] [CrossRef]
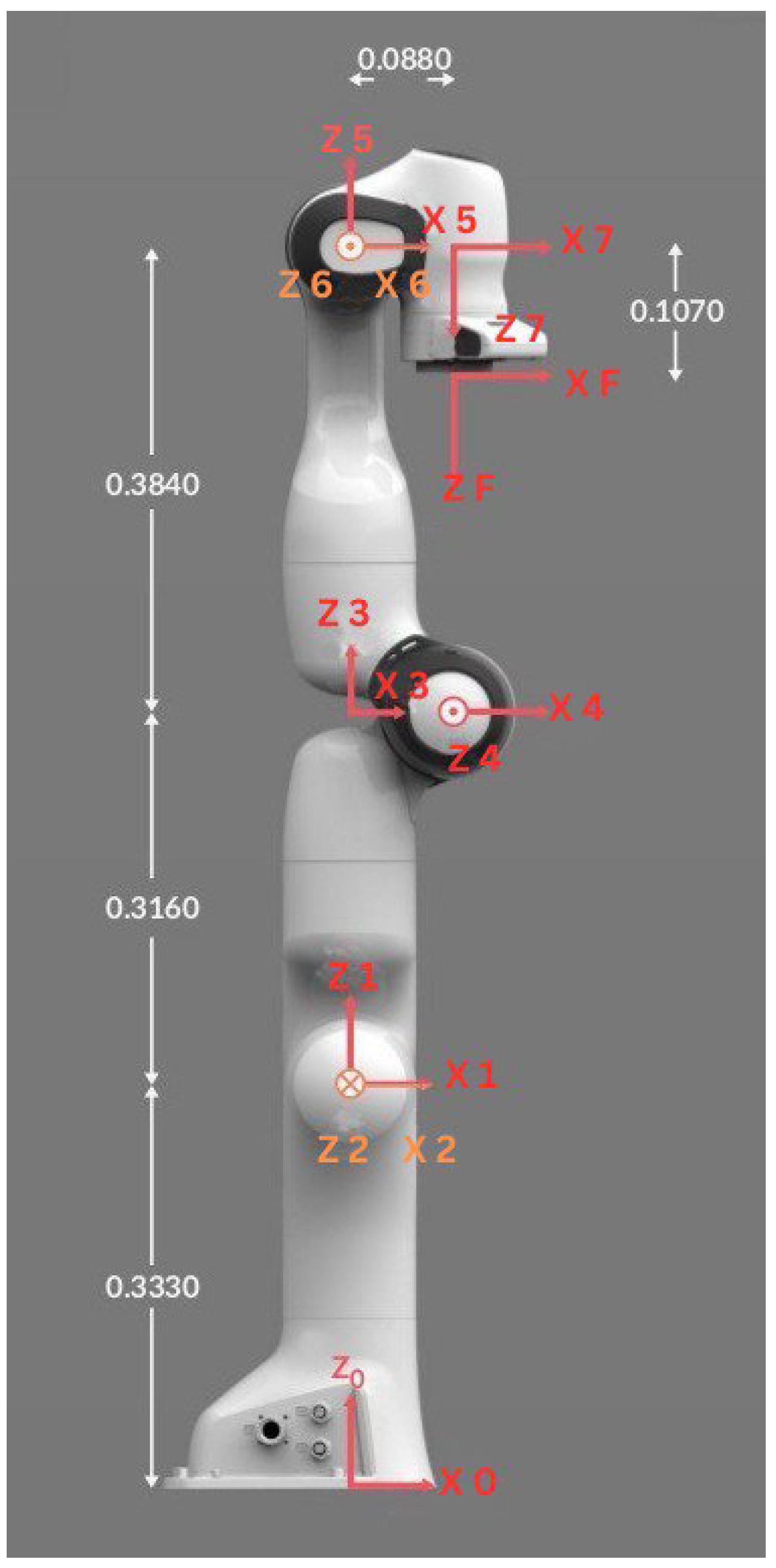


| Joint | a (m) | d (m) | (Rad) | (Rad) |
|---|---|---|---|---|
| 1 | 0 | 0.333 | 0 | |
| 2 | 0 | 0 | −90 | |
| 3 | 0 | 0.316 | 90 | |
| 4 | 0.0825 | 0 | 90 | |
| 5 | −0.0825 | 0.384 | −90 | |
| 6 | 0 | 0 | 90 | |
| 7 | 0.088 | 0 | 90 | |
| Flange | 0 | 0.107 | 0 | 0 |
| Parameter | Value |
|---|---|
| Policy | MultiInputPolicy |
| Replay buffer class | HerReplayBuffer |
| Verbose | 1 |
| Gamma | 0.95 |
| Tau () | 0.005 |
| Batch size | 512, 1024, 2048 |
| Buffer size | 100,000 |
| Replay buffer kwargs | rb kwargs |
| Learning rate | 1e-3, 2e-4 |
| Action noise | Normal action noise |
| Policy kwargs | Policy kwargs |
| Tensorboard log | Log path |
| Parameter | Value |
|---|---|
| Policy | MultiInputPolicy |
| Replay buffer class | HerReplayBuffer |
| Verbose | 1 |
| Gamma | 0.95 |
| Tau () | 0.005 |
| Batch size | 2048 |
| Buffer size | 100,000 |
| Replay buffer kwargs | rb kwargs |
| Learning rate | 1e-3 |
| Action noise | Normal action noise |
| Policy kwargs | Policy kwargs |
| Category | Value | Category | Value |
|---|---|---|---|
| rollout/ | rollout/ | ||
| Episode length | 50 | ||
| Episode mean reward | −49.2 | Episode mean reward | −1.8 |
| Success rate | 0 | Success rate | 1 |
| time/ | time/ | ||
| Episodes | 4 | Episodes | 2000 |
| FPS | 18 | FPS | 5 |
| Time elapsed | 10 | Time elapsed | 19,505 |
| Total timesteps | 200 | Total time steps | 100,000 |
| train/ | train/ | ||
| Actor loss | 0.625 | Actor loss | 0.0846 |
| Critic loss | 0.401 | Critic loss | 0.00486 |
| Learning rate | 0.001 | Learning rate | 0.001 |
| Number of updates | 50 | Number of updates | 99,850 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Honelign, L.; Abebe, Y.; Tullu, A.; Jung, S. Deep Reinforcement Learning-Based Enhancement of Robotic Arm Target-Reaching Performance. Actuators 2025, 14, 165. https://doi.org/10.3390/act14040165
Honelign L, Abebe Y, Tullu A, Jung S. Deep Reinforcement Learning-Based Enhancement of Robotic Arm Target-Reaching Performance. Actuators. 2025; 14(4):165. https://doi.org/10.3390/act14040165
Chicago/Turabian StyleHonelign, Ldet, Yoseph Abebe, Abera Tullu, and Sunghun Jung. 2025. "Deep Reinforcement Learning-Based Enhancement of Robotic Arm Target-Reaching Performance" Actuators 14, no. 4: 165. https://doi.org/10.3390/act14040165
APA StyleHonelign, L., Abebe, Y., Tullu, A., & Jung, S. (2025). Deep Reinforcement Learning-Based Enhancement of Robotic Arm Target-Reaching Performance. Actuators, 14(4), 165. https://doi.org/10.3390/act14040165









