Mechanical Design of McKibben Muscles Predicting Developed Force by Artificial Neural Networks
Abstract
1. Introduction
- Proposal of a validated methodology based on ML for predicting the mechanical behavior of MKMs;
- Realization of the MKM dataset;
- Identification of the best ML algorithm via training and result comparison of 27 different ANNs on the realized dataset.
2. Materials and Methods
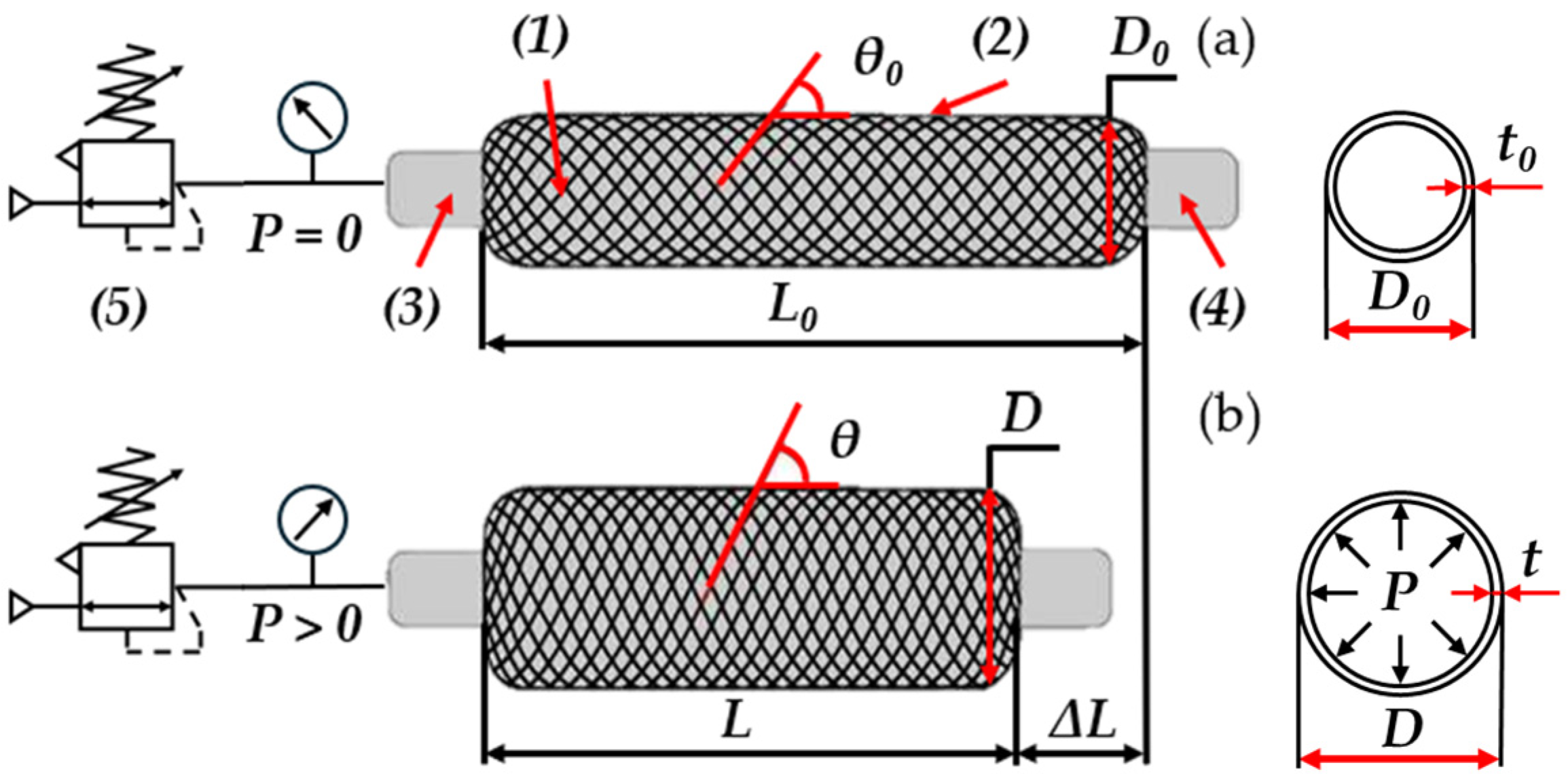
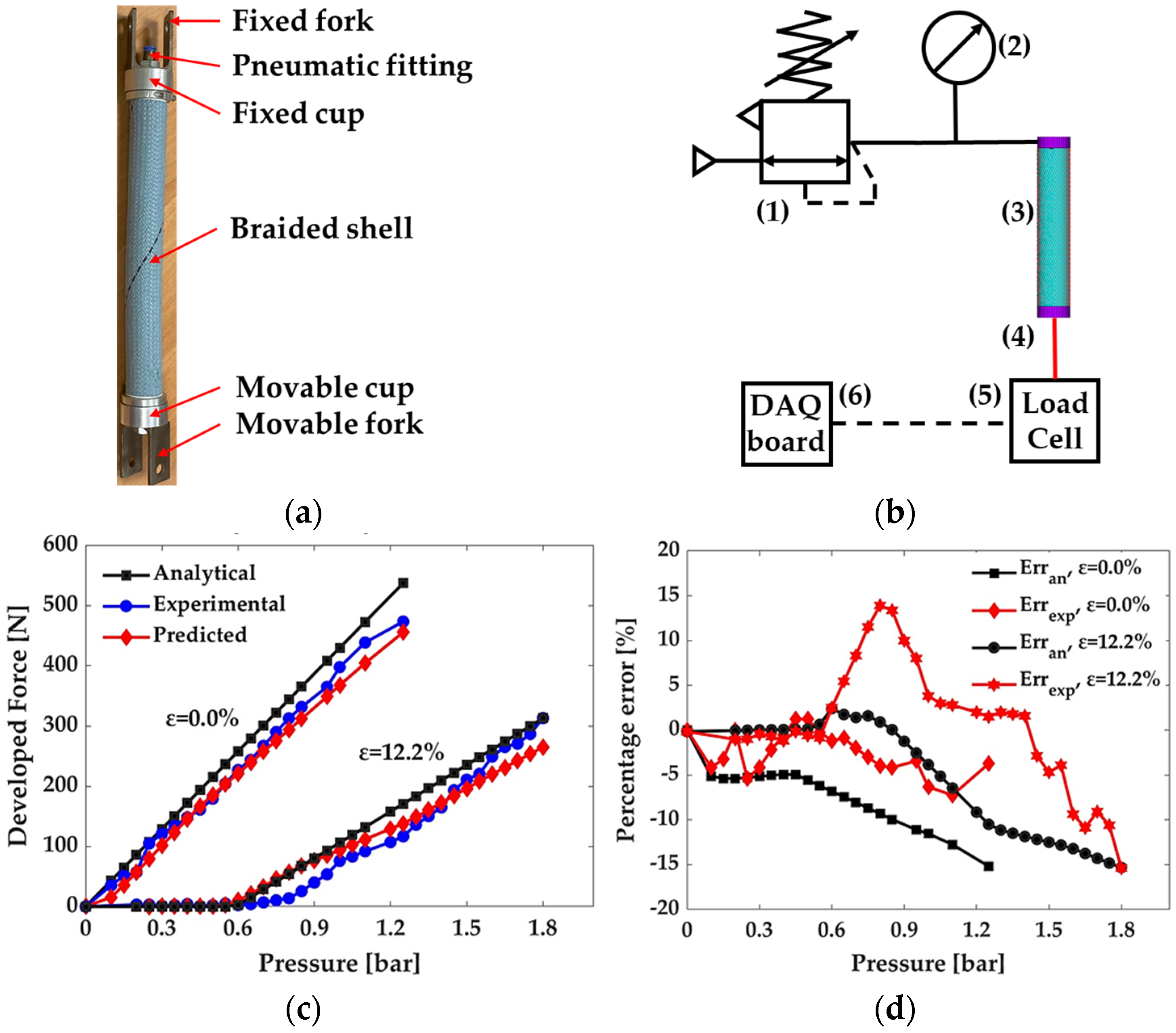
2.1. Technical Description of the MKM
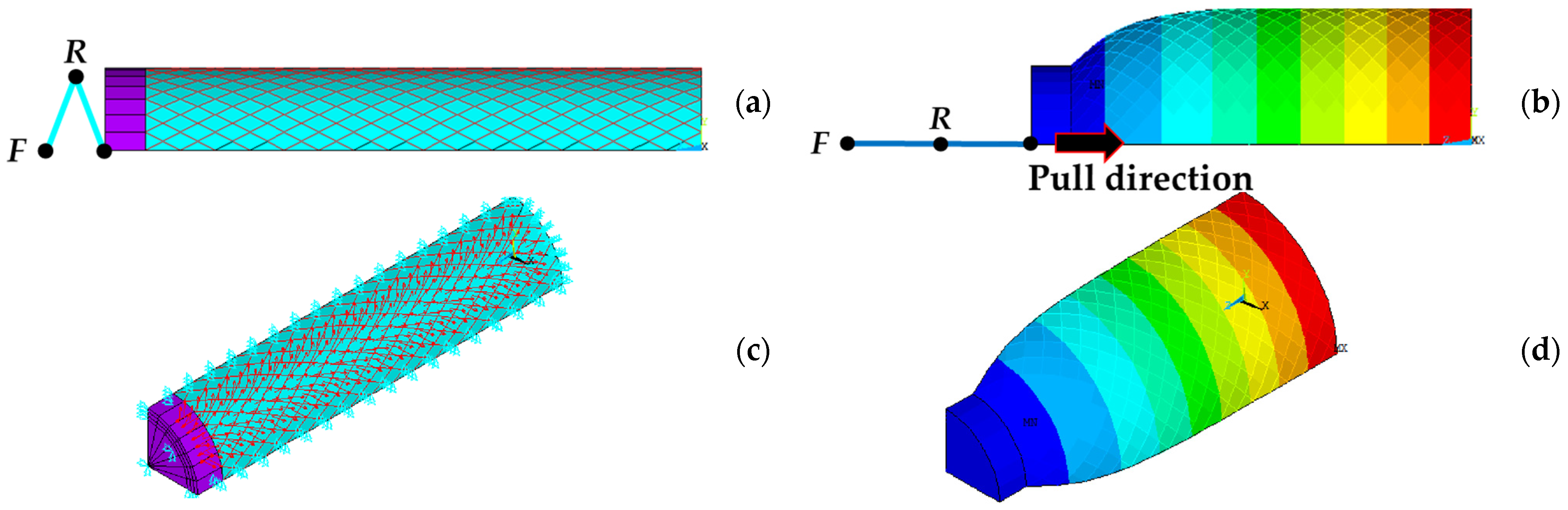
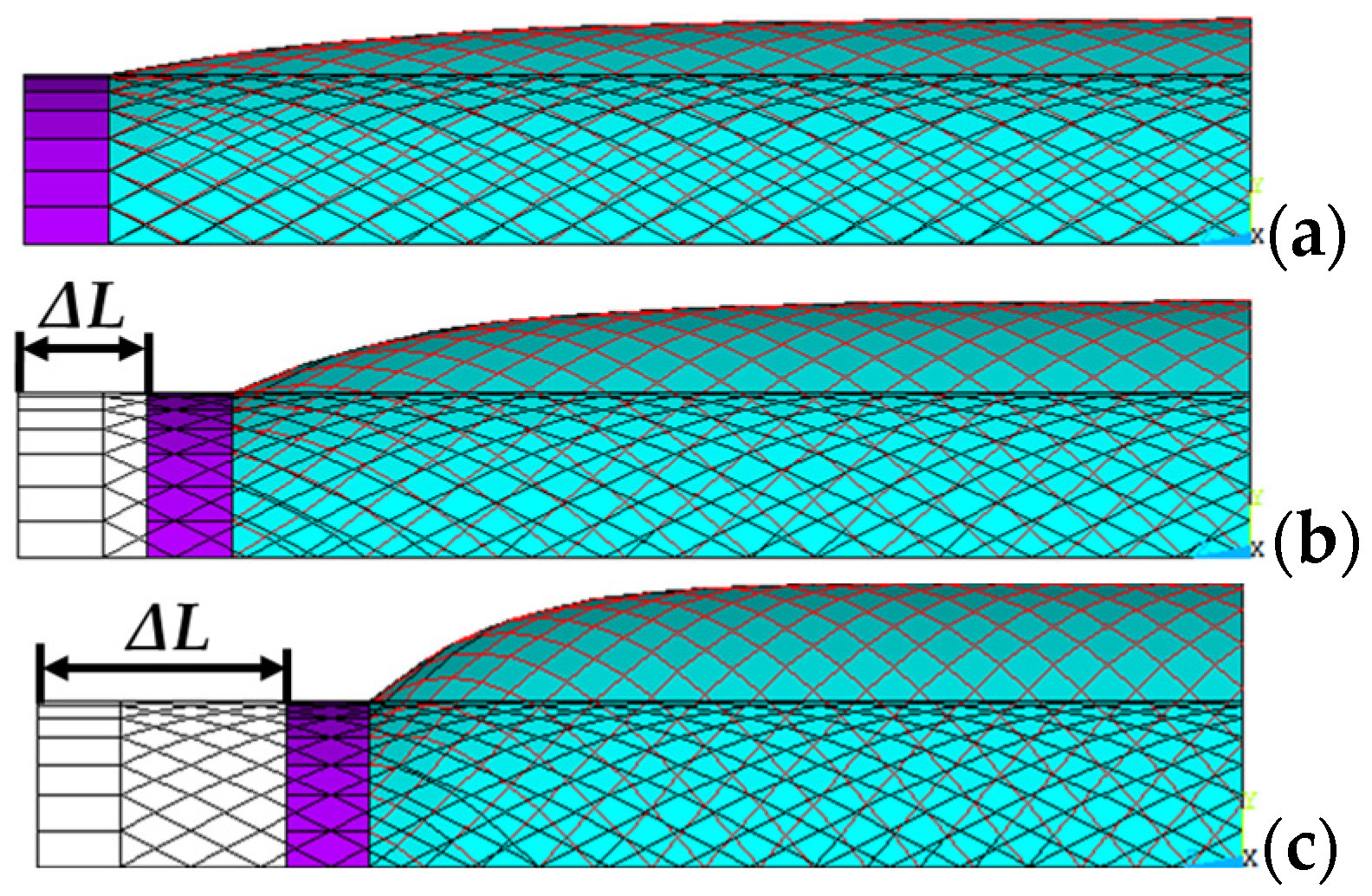
2.2. Numerical Simulations
3. Regression Algorithms
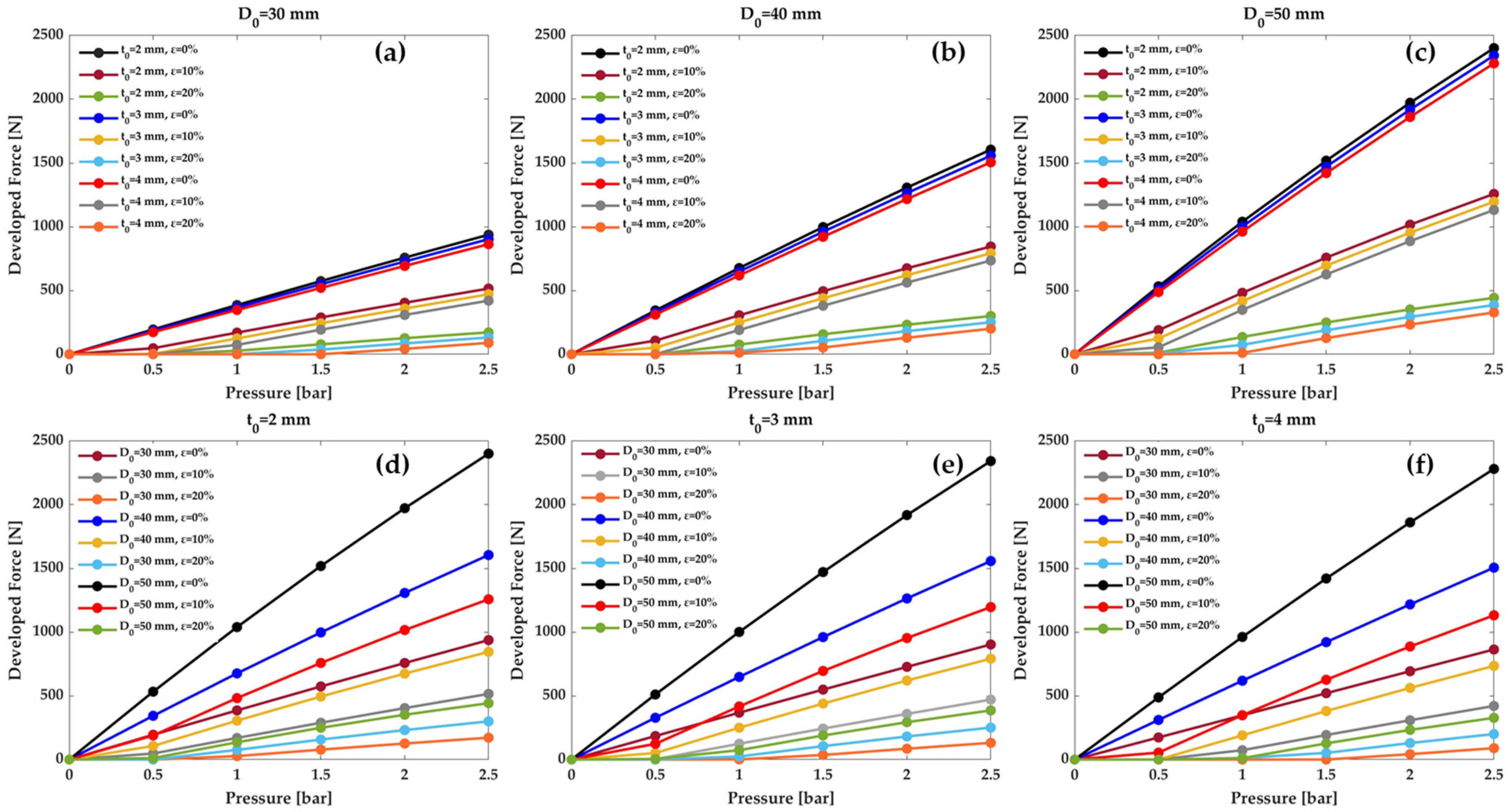
3.1. MKM Dataset Construction
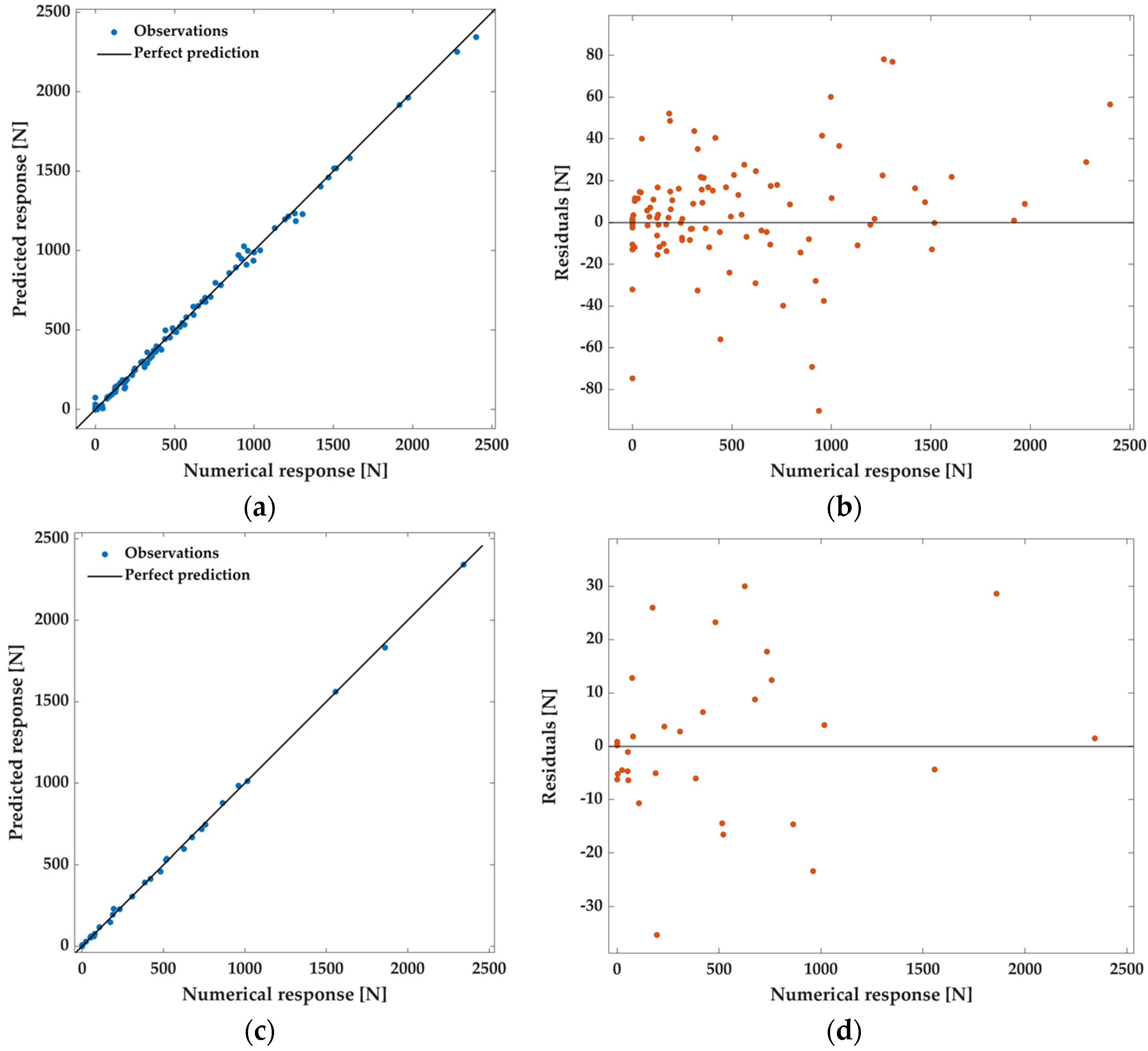
3.2. Training and Validation of the ANNs
3.3. Test
4. Experimental Validation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft Robotic Grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef] [PubMed]
- Kalita, B.; Leonessa, A.; Dwivedy, S.K. A Review on the Development of Pneumatic Artificial Muscle Actuators: Force Model and Application. Actuators 2022, 11, 288. [Google Scholar] [CrossRef]
- Antonelli, M.G.; Beomonte Zobel, P.; Mattei, E.; Stampone, N. A Methodology for the Mechanical Design of Pneumatic Joints Using Artificial Neural Networks. Appl. Sci. 2024, 14, 8324. [Google Scholar] [CrossRef]
- Antonelli, M.G.; Beomonte Zobel, P.; Mattei, E.; Stampone, N. Mechanical Design, Manufacturing, and Testing of a Soft Pneumatic Actuator with a Reconfigurable Modular Reinforcement. Robotics 2024, 13, 165. [Google Scholar] [CrossRef]
- Moreki, A. Polish artificial pneumatic muscles. In Proceedings of the 7th International Conference on Climbing and Walking Robot, Karlsruhe, Germany, 24–26 September 2001. [Google Scholar]
- Shinohara, H.; Nakamura, T. Derivation of a mathematical model for pneumatic artificial muscles. IFAC Proc. Vol. 2006, 39, 266–270. [Google Scholar] [CrossRef]
- Schulte, H. The characteristics of the McKibben artificial muscle. In The Application of External Power in Prosthetics and Orthotics; National Academy of Sciences-National Research Council: Washington, DC, USA, 1961; pp. 94–115. [Google Scholar]
- Gavrilović, M.M.; Marić, M.R. Positional servo-mechanism activated by artificial muscles. Med. Biol. Eng. 1969, 7, 77–82. [Google Scholar] [CrossRef] [PubMed]
- Yariott, J.M. Fluid Actuator. U.S. Patent 3,645,173, 29 February 1972. [Google Scholar]
- Morin, A.H. Elastic Diaphragm. U.S. Patent 2,642,091, 16 June 1953. [Google Scholar]
- Paynter, H.M. Hyperboloid of Revolution Fluid-Driven Tension Actuators and Method of Making. U.S. Patent 4,721,030, 26 January 1988. [Google Scholar]
- Han, K.; Kim, N.H.; Shin, D. A novel soft pneumatic artificial muscle with high-contraction ratio. Soft Robot. 2018, 5, 554–566. [Google Scholar] [CrossRef]
- Daerden, F.; Lefeber, D. The concept and design of pleated pneumatic artificial muscles. Int. J. Fluid Power 2001, 2, 41–50. [Google Scholar] [CrossRef]
- Daerden, F.; Lefeber, D. Pneumatic artificial muscles: Actuators for robotics and automation. Eur. J. Mech. Environ. Eng. 2002, 47, 11–21. [Google Scholar]
- Terryn, S.; Brancart, J.; Lefeber, D.; Van Assche, G.; Vanderborght, B. A pneumatic artificial muscle manufactured out of self-healing polymers that can repair macroscopic damages. IEEE Robot. Autom. Lett. 2017, 3, 16–21. [Google Scholar] [CrossRef]
- Belforte, G.; Eula, G.; Ivanov, A.; Sirolli, S. Soft Pneumatic Actuators for Rehabilitation. Actuators 2014, 3, 84–106. [Google Scholar] [CrossRef]
- Noritsugu, T.; Takaiawa, M.; Sasaki, D. Development of a pneumatic rubber artificial muscle for human support applications. In Proceedings of the 9th Scandinavia International Conference on Fluid Power, Linkoping, Sweden, 1–3 June 2005. [Google Scholar]
- Hannford, B.; Winters, J.M. Actuators properties and movement control: Biological and technological models. In Multiple Muscle Systems; Winters, J., Woo, S., Eds.; Springer: New York, NY, USA, 1990; pp. 101–120. [Google Scholar]
- Chen, C.-T.; Lien, W.-Y.; Chen, C.-T.; Wu, Y.-C. Implementation of an Upper-Limb Exoskeleton Robot Driven by Pneumatic Muscle Actuators for Rehabilitation. Actuators 2020, 9, 106. [Google Scholar] [CrossRef]
- Waycaster, G.; Wu, S.K.; Shen, X. Design and control of a pneumatic artificial muscle actuated above-knee prosthesis. J. Med. Devices 2011, 5, 031003. [Google Scholar] [CrossRef]
- Fantoni, G.; Santochi, M.; Dini, G.; Tracht, K.; Scholz-Reiter, B.; Fleischer, J.; Lien, T.K.; Seliger, G.; Reinhart, G.; Franke, J.; et al. Grasping devices and methods in automated production processes. CIRP Ann. 2014, 63, 679–701. [Google Scholar] [CrossRef]
- Giannaccini, M.E.; Georgilas, I.; Horsfield, I.; Peiris, B.; Lenz, A.; Pipe, A.G.; Dogramadzi, S. A variable compliance, soft gripper. Auton. Robot. 2014, 36, 93–107. [Google Scholar] [CrossRef]
- Verrelst, B.; Van Ham, R.; Vanderborght, B.; Lefeber, D.; Daerden, F.; Van Damme, M. Second generation pleated pneumatic artificial muscle and its robotic applications. Adv. Robot. 2006, 20, 783–805. [Google Scholar] [CrossRef]
- Martens, M.; Seel, T.; Zawatzki, J.; Boblan, I. A novel framework for a systematic integration of pneumatic-muscle-actuator-driven joints into robotic systems via a torque control interface. Actuators 2018, 7, 82. [Google Scholar] [CrossRef]
- Koter, K.; Fracczak, L.; Chojnacka, K.; Jabłoński, K.; Zarychta, S.; Podsędkowski, L. Snake robot based on McKibben Pneumatic Artificial Muscles. In Proceedings of the 15th Conference on Dynamical Systems Theory and Applications DSTA, Lodz, Poland, 2–5 December 2019. [Google Scholar]
- Iwata, K.; Suzumori, K.; Wakimoto, S. A method of designing and fabricating McKibben muscles driven by 7 MPa hydraulics. Int. J. Autom. Technol. 2012, 6, 482–487. [Google Scholar] [CrossRef]
- Kobayashi, R.; Nabae, H.; Mao, Z.; Endo, G.; Suzumori, K. Enhancement of Thin McKibben Muscle Durability Under Repetitive Actuation in a Bent State. IEEE Robot. Autom. Lett. 2024, 9, 9685–9692. [Google Scholar] [CrossRef]
- Chou, C.P.; Hannaford, B. Measurement and modeling of McKibben pneumatic artificial muscles. IEEE Trans. Robot. Autom. 1996, 12, 90–102. [Google Scholar] [CrossRef]
- Tondu, B.; Lopez, P. Modeling and control of McKibben artificial muscle robot actuators. IEEE Control. Syst. Mag. 2000, 20, 15–38. [Google Scholar]
- Marechal, L.; Balland, P.; Lindenroth, L.; Petrou, F.; Kontovounisios, C.; Bello, F. Toward a Common Framework and Database of Materials for Soft Robotics. Soft Robot. 2021, 8, 284–297. [Google Scholar] [CrossRef]
- Inada, R.; Tsuruhara, S.; Ito, K. Precise Displacement Control of Tap-Water-Driven Muscle Using Adaptive Model Predictive Control with Hysteresis Compensation. JFPS Int. J. Fluid Power Syst. 2022, 15, 78–85. [Google Scholar] [CrossRef]
- Tsuruhara, S.; Ito, K. Data-Driven Model-Free Adaptive Displacement Control for Tap-Water-Driven Artificial Muscle and Parameter Design Using Virtual Reference Feedback Tuning. J. Robot. Mechatron. 2022, 34, 664–676. [Google Scholar] [CrossRef]
- Serres, J.; Reynolds, D.; Phillips, C.; Rogers, D.; Repperger, D. Characterisation of a pneumatic muscle test station with two dynamic plants in cascade. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 11–18. [Google Scholar] [CrossRef]
- Serres, J.; Reynolds, D.; Phillips, C.; Gerschutz, M.; Repperger, D. Characterisation of a phenomenological model for commercial pneumatic muscle actuators. Comput. Methods Biomech. Biomed. Eng. 2009, 12, 423–430. [Google Scholar] [CrossRef]
- Kalita, B.; Dwivedy, S. Nonlinear dynamics of a parametrically excited pneumatic artificial muscle (PAM) actuator with simultaneous resonance condition. Mech. Mach. Theory 2019, 135, 281–297. [Google Scholar] [CrossRef]
- Kalita, B.; Dwivedy, S. Dynamic analysis of pneumatic artificial muscle (PAM) actuator for rehabilitation with principal parametric resonance condition. Nonlinear Dyn. 2019, 97, 2271–2289. [Google Scholar] [CrossRef]
- Wickramatunge, K.C.; Leephakpreeda, T. Study on mechanical behaviors of pneumatic artificial muscle. Int. J. Eng. Sci. 2010, 48, 188–198. [Google Scholar] [CrossRef]
- Wickramatunge, K.C.; Leephakpreeda, T. Empirical modeling of dynamic behaviors of pneumatic artificial muscle actuators. ISA Trans. 2013, 52, 825–834. [Google Scholar] [CrossRef]
- Antonelli, M.G.; Beomonte Zobel, P.; D’Ambrogio, W.; Durante, F.; Raparelli, T. An Analytical Formula for Designing Mckibben Pneumatic Muscles. Int. J. Mech. Technol. 2018, 9, 320–337. [Google Scholar]
- Antonelli, M.G.; Beomonte Zobel, P.; Durante, F.; Raparelli, T. Numerical modelling and experimental validation of a McKibben pneumatic muscle actuator. J. Intell. Mater. Syst. Struct. 2017, 28, 2737–2748. [Google Scholar] [CrossRef]
- Antonelli, M.G.; Beomonte Zobel, P.; De Marcellis, A.; Palange, E. Design and Characterization of a Mckibben Pneumatic Muscle Prototype with an Embedded Capacitive Length Transducer. Machines 2022, 10, 1156. [Google Scholar] [CrossRef]
- Kotkas, L.; Zhurkin, N.; Donskoy, A.; Zharkovskij, A. Design and Mathematical Modeling of a Pneumatic Artificial Muscle-Actuated System for Industrial Manipulators. Machines 2022, 10, 885. [Google Scholar] [CrossRef]
- Yang, H.D.; Greczek, B.T.; Asbeck, A.T. Modeling and Analysis of a High-Displacement Pneumatic Artificial Muscle with Integrated Sensing. Front. Robot. AI 2019, 5, 136. [Google Scholar] [CrossRef]
- Wang, G.; Wereley, N.M.; Pillsbury, T. Non-linear quasi-static model of pneumatic artificial muscle actuators. J. Intell. Mater. Syst. Struct. 2014, 26, 541–553. [Google Scholar] [CrossRef]
- Bennington, M.J.; Wang, T.; Yin, J.; Bergbreiter, S.; Majidi, C.; Webster-Wood, V.A. Design and Characterization of Viscoelastic McKibben Actuators with Tunable Force-Velocity Curves. In Proceedings of the 2023 IEEE International Conference on Soft Robotics (RoboSoft), Singapore, 3–7 April 2023; pp. 1–7. [Google Scholar]
- Slightam, J.E.; Nagurka, M.L. Modeling of Pneumatic Artificial Muscle with Kinetic Friction and Sliding Mode Control. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 3342–3347. [Google Scholar]
- Durante, F.; Antonelli, M.G.; Zobel, P.; Raparelli, T. Development of a Straight Fibers Pneumatic Muscle. Int. J. Autom. Technol. 2018, 12, 413–423. [Google Scholar] [CrossRef]
- Nunes da Silva, I.; Hernane Spatti, D.; Andrade Flauzino, R.; Bartocci Liboni, L.H.; Franco dos Reis Alves, S. Artificial Neural Networks: A Practical Course; Springer: Cham, Switzerland, 2016. [Google Scholar]
| Name | Symbol | Values | Unit |
|---|---|---|---|
| Pressure | P | 0.0–0.5–1.0–1.5–2.0–2.5 | bar |
| Diameter | D0 | 30–40–50 | mm |
| Thickness | t0 | 2–3–4 | mm |
| Shortening Ratio | ε | 0–10–20 | % |
| Number | Number of Layers | Layer Size | Activation Function | Training RMSE [N] | Validation RMSE [N] |
|---|---|---|---|---|---|
| 1 | 1 | 25 | ReLU | 66.46 | 36.51 |
| 2 | 2 | 25 | ReLU | 31.84 | 15.98 |
| 3 | 3 | 25 | ReLU | 30.57 | 14.31 |
| 4 | 1 | 50 | ReLU | 34.78 | 15.52 |
| 5 | 2 | 50 | ReLU | 25.59 | 11.84 |
| 6 | 3 | 50 | ReLU | 23.92 | 8.04 |
| 7 | 1 | 100 | ReLU | 27.37 | 13.78 |
| 8 | 2 | 100 | ReLU | 24.29 | 8.81 |
| 9 | 3 | 100 | ReLU | 21.31 | 7.30 |
| 10 | 1 | 25 | Tanh | 363.05 | 421.37 |
| 11 | 2 | 25 | Tanh | 327.30 | 381.03 |
| 12 | 3 | 25 | Tanh | 478.53 | 593.68 |
| 13 | 1 | 50 | Tanh | 329.54 | 243.02 |
| 14 | 2 | 50 | Tanh | 322.29 | 353.34 |
| 15 | 3 | 50 | Tanh | 358.68 | 738.01 |
| 16 | 1 | 100 | Tanh | 307.44 | 162.88 |
| 17 | 2 | 100 | Tanh | 285.92 | 295.67 |
| 18 | 3 | 100 | Tanh | 283.17 | 280.60 |
| 19 | 1 | 25 | Sigmoid | 119.34 | 81.380 |
| 20 | 2 | 25 | Sigmoid | 293.05 | 386.00 |
| 21 | 3 | 25 | Sigmoid | 462.55 | 448.94 |
| 22 | 1 | 50 | Sigmoid | 118.98 | 69.744 |
| 23 | 2 | 50 | Sigmoid | 258.03 | 123.71 |
| 24 | 3 | 50 | Sigmoid | 277.91 | 403.58 |
| 25 | 1 | 100 | Sigmoid | 117.57 | 79.710 |
| 26 | 2 | 100 | Sigmoid | 213.76 | 202.86 |
| 27 | 3 | 100 | Sigmoid | 241.46 | 230.19 |
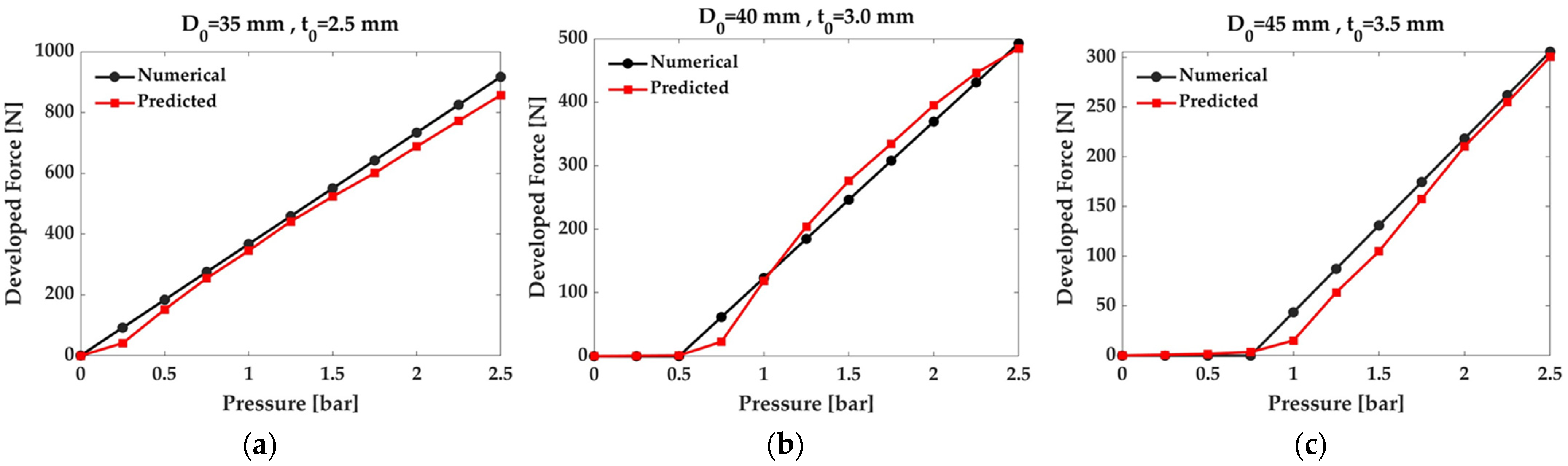
| MKM | Pressure | Numerical Force | Predicted Force | Absolute Error | Percentage Error |
|---|---|---|---|---|---|
| [bar] | [N] | [N] | [bar] | [%] | |
| I | 0.00 | 0.00 | −0.48 | 0.48 | 0.05% |
| 0.25 | 91.73 | 40.51 | 51.22 | 5.58% | |
| 0.50 | 183.46 | 151.58 | 31.88 | 3.48% | |
| 0.75 | 275.18 | 254.12 | 21.06 | 2.30% | |
| 1.00 | 366.91 | 344.84 | 22.07 | 2.41% | |
| 1.25 | 458.64 | 441.17 | 17.47 | 1.90% | |
| 1.50 | 550.37 | 523.11 | 27.26 | 2.97% | |
| 1.75 | 642.10 | 600.59 | 41.51 | 4.52% | |
| 2.0 | 733.82 | 687.79 | 46.03 | 5.02% | |
| 2.25 | 825.55 | 772.96 | 52.59 | 5.73% | |
| 2.50 | 917.28 | 857.18 | 60.10 | 6.55% | |
| II | 0.00 | 0.00 | 0.21 | −0.21 | −0.04% |
| 0.25 | 0.00 | 0.71 | −0.71 | −0.14% | |
| 0.50 | 0.07 | 1.23 | −1.16 | −0.24% | |
| 0.75 | 61.64 | 22.6 | 39.04 | 7.92% | |
| 1.00 | 123.21 | 118.54 | 4.67 | 0.95% | |
| 1.25 | 184.78 | 204.18 | −19.40 | −3.94% | |
| 1.50 | 246.35 | 276.19 | −29.85 | −6.06% | |
| 1.75 | 307.91 | 334.66 | −26.75 | −5.43% | |
| 2.0 | 369.48 | 395.04 | −25.56 | −5.19% | |
| 2.25 | 431.05 | 445.84 | −14.79 | −3.00% | |
| 2.50 | 492.62 | 484.63 | 7.99 | 1.62% | |
| III | 0.00 | 0.00 | 0.11 | −0.11 | −0.04% |
| 0.25 | 0.00 | 0.88 | −0.88 | −0.29% | |
| 0.50 | 0.00 | 1.94 | −1.94 | −0.63% | |
| 0.75 | 0.04 | 3.61 | −3.57 | −1.17% | |
| 1.00 | 43.70 | 15.14 | 28.56 | 9.34% | |
| 1.25 | 87.37 | 63.66 | 23.71 | 7.76% | |
| 1.50 | 131.03 | 104.93 | 26.10 | 8.54% | |
| 1.75 | 174.70 | 157.69 | 17.01 | 5.56% | |
| 2.00 | 218.36 | 210.4 | 7.96 | 2.60% | |
| 2.25 | 262.03 | 254.74 | 7.29 | 2.38% | |
| 2.50 | 305.69 | 300.61 | 5.08 | 1.66% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonelli, M.G.; Beomonte Zobel, P.; Sarwar, M.A.; Stampone, N. Mechanical Design of McKibben Muscles Predicting Developed Force by Artificial Neural Networks. Actuators 2025, 14, 153. https://doi.org/10.3390/act14030153
Antonelli MG, Beomonte Zobel P, Sarwar MA, Stampone N. Mechanical Design of McKibben Muscles Predicting Developed Force by Artificial Neural Networks. Actuators. 2025; 14(3):153. https://doi.org/10.3390/act14030153
Chicago/Turabian StyleAntonelli, Michele Gabrio, Pierluigi Beomonte Zobel, Muhammad Aziz Sarwar, and Nicola Stampone. 2025. "Mechanical Design of McKibben Muscles Predicting Developed Force by Artificial Neural Networks" Actuators 14, no. 3: 153. https://doi.org/10.3390/act14030153
APA StyleAntonelli, M. G., Beomonte Zobel, P., Sarwar, M. A., & Stampone, N. (2025). Mechanical Design of McKibben Muscles Predicting Developed Force by Artificial Neural Networks. Actuators, 14(3), 153. https://doi.org/10.3390/act14030153









