Modelling, Control Design and Inclusion of Articulated Robots in Cyber-Physical Factories ^†

Abstract

This paper addresses the features and limits of the principles and means that provide and support the design of motion control for industrial stationary articulated robots and their involvement in cyber-physical factories as part of the Industry 4.0 concept. The proposed methods are presented herein, from the modelling of kinematics and dynamics considering ideal rigid bodies and principles of classical mechanics, to their application in the design of conventional cascade control and advanced model-based control and use within commercial software tools. The paper demonstrates the modelling principles adapted for control design where a specific novel hierarchical control configuration is outlined. There is an introduction of possible software tools such as Simscape, Robotics Systems Toolbox, RT Toolbox, CIROS and others. It includes the specific aim of the rapid prototyping of robot motion control, which is intended for user development and tuning. In conjunction with conveyor belts, robots-manipulators are essential for cyber-physical factories built on the concept of Industry 4.0. The concept of Industry 4.0 is discussed in respect to the proposed algorithms and software means.

1. Introduction

Articulated robots belong to a class dominating today’s industrial production [1,2]. For this mass use, the control principles in control systems must continuously be subjects for testing, investigation and improvement [3,4]. This follows from a permanent effort to reduce a set of infinitesimal redundant energy inputs that lead to needless additional costs [5,6]. The full robot integration into recent cyber-physical factories (CPF) is a step on the way to the full robotisation of production. Robots are used for handling, as well as for automated manufacturing operations such as welding, painting, machining or assembly in serial and mass production. An example of CPF is shown in Figure 1.

2. Background of Analysis

There are several investigative perspectives from construction with small applications such as in [7,8], and case studies comparable with industrial applications [9]. The focus is concentrated on problems of system coordination in CPF [10] and the influence of concepts of Industry 4.0 on business operations [11]. The possible future trends are addressed towards collaborative workplaces combining human and smart production entities (machines, manipulators, sensors, etc. [12].

Unsolved research questions (continual challenges) persist in the (i) adjustment of derived ideal mathematical models and their parameters, which need to be in correspondence with the real-world robot features; (ii) which tools are suitable for the hyper prototyping of advanced control design that should reduce energy consumption in future applications; and (iii) how the robots are managed and integrated into sophisticated production procedures and systems represented by CPFs.

This article analyses specific applicable modelling software for improving model-based control design. The gap between theory and software tools used in practice is still large. This is due to the unavailability of theory sourcing and limited development and testing. It is determined by predominately separated small working groups (divisions) without regular interactions between software programmers and developers (experts and scholars) deriving basic principles and practices.

However, the number of robots grows continuously, as is demonstrated in Figure 2, i.e., a constant commissioning of new robots into industrial production every year in spite of fluctuating demand and rising input prices. In this respect, analysis of newly available software tools for industrial use is important for study [13], including the investigation of mutual relations not only within one factory, but connected suppliers using specific organising systems and digital twins in combination with real systems in CPFs [14].

The combination of physical and virtual spaces is referred as cyber-physical systems (CPSs) or CPFs, and the aim of their commissioning is to create a communication interface between the digital and physical worlds by integrating computation, networking and physical assets. It is well-understood that the interconnection between the physical world is represented by hardware (e.g., sensors, actuators, robots) and cyber software (communication, networking and internet) [15]. By using the concepts of Industry 4.0 as virtualisation, communication, smart entities, there is an estimation of the specific possibility to reach a more efficient and optimal production work flow.

Figure 2. Global industrial robot installations by industry in 2021 (grey), 2022 (red) and 2023 (blue) in thousands [16].

Figure 2. Global industrial robot installations by industry in 2021 (grey), 2022 (red) and 2023 (blue) in thousands [16].

Current modern industrial production is customer-oriented to offer customers a wide-scale portfolio of products with various properties and functions in different variants. It considers specific products such as vehicles-cars in automotive or consumer electronics for households, etc., which is customised according to customer wishes, i.e., the product is tailor-made.

Such a requirement of the market leads to high demands on the organisation and flexibility of the production but also on the timing of forwarding services, suppliers, sellers/traders, as shown in Figure 3. In this situation, Industry 4.0 was applied to pilot production that uses CPF, as shown in Figure 1. CPF, as was mentioned above, represents an approach that combines cyber space (digital twins, computer optimisation, programs, etc.) with the physical world, consisting of real factories with production lines containing real machine tools, robots and other production or manipulation machines and equipment. Both the cyber and real worlds are interconnected via specific envelope/interfaces that enable the producer to provide on-line managing and planning, thus changing and optimising production. This makes it possible to move mass standardised/unified production closer to the a more customer-oriented one.

The CPF representative depicted in Figure 1 consists of several mutually compatible modules. These modules represent self-autonomous workplaces such as drilling, pressing, heating, assembling, revolving, milling and storage (magazine) modules. They have standardised interfaces (electric and pneumatic power inputs, industrial Ethernet) and Programmable Logic Controllers (PLC), serving as local control units. Such a configuration, together using digital models in software tools RT ToolBox3 Version 2.00A (Mitsubishi) and/or CIROS Studio 7 (Festo), offers the desired production flexibility.

This paper is an extended version of the conference paper [17]. Section 3 deals with the considered representative robot topology. Section 4 deals with the mathematical model synthesis. Then, Section 5 introduces control concepts of both conventional cascade configurations and advanced model predictive procedures in a hierarchical arrangement, combining globally centralised and locally distributed designs [18]. Both concepts are graphically illustrated and compared.

Then, Section 6 and Section 7 focus on current software tools and their use in research covering both simulations and the real-run of motion control of common industrial robots. Finally, Section 8 introduces robot integration into intelligent CPFs considering conceptions of Industry 4.0. The paper concludes with a short summary of answers and possible solutions for the indicated open research questions.

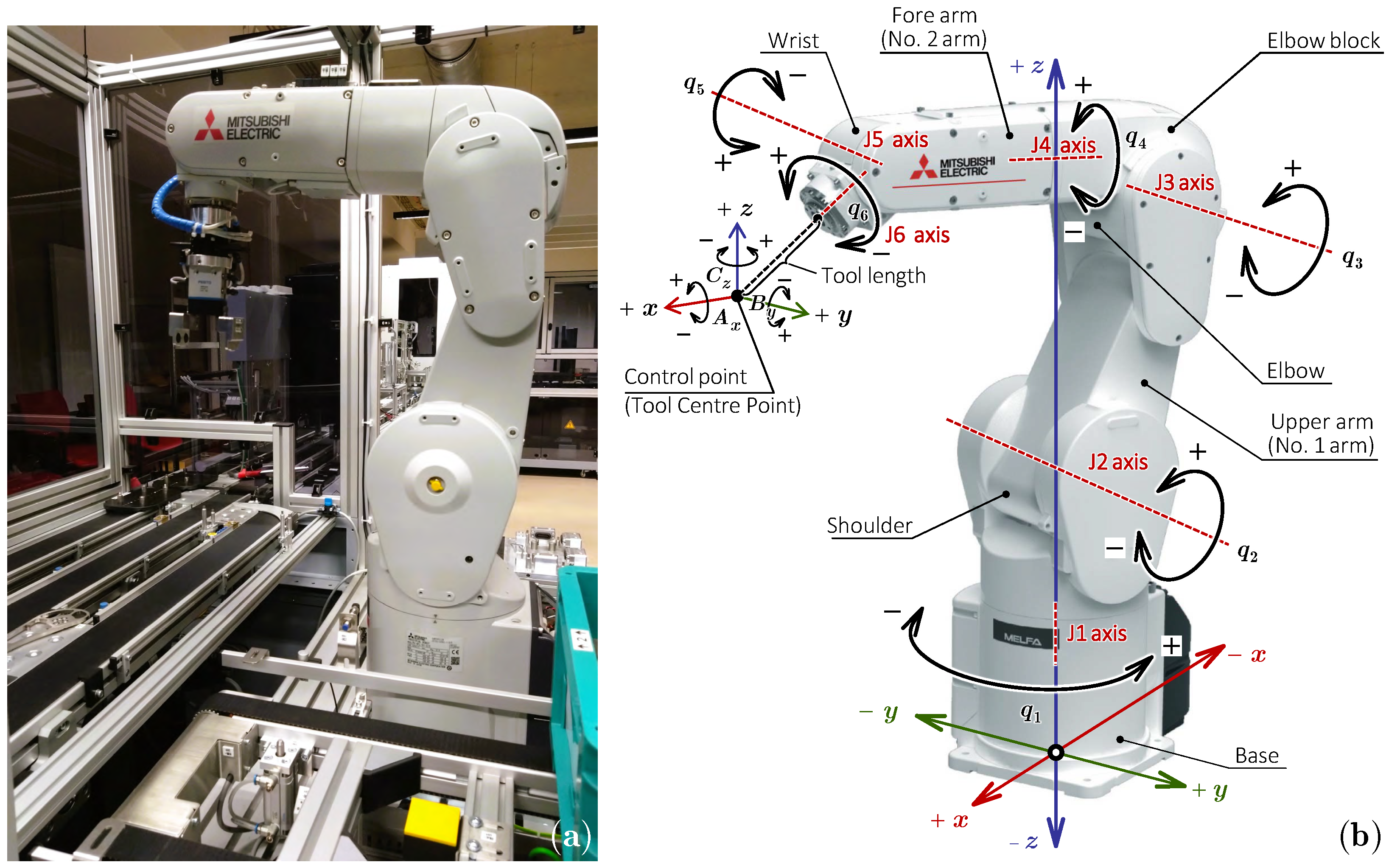
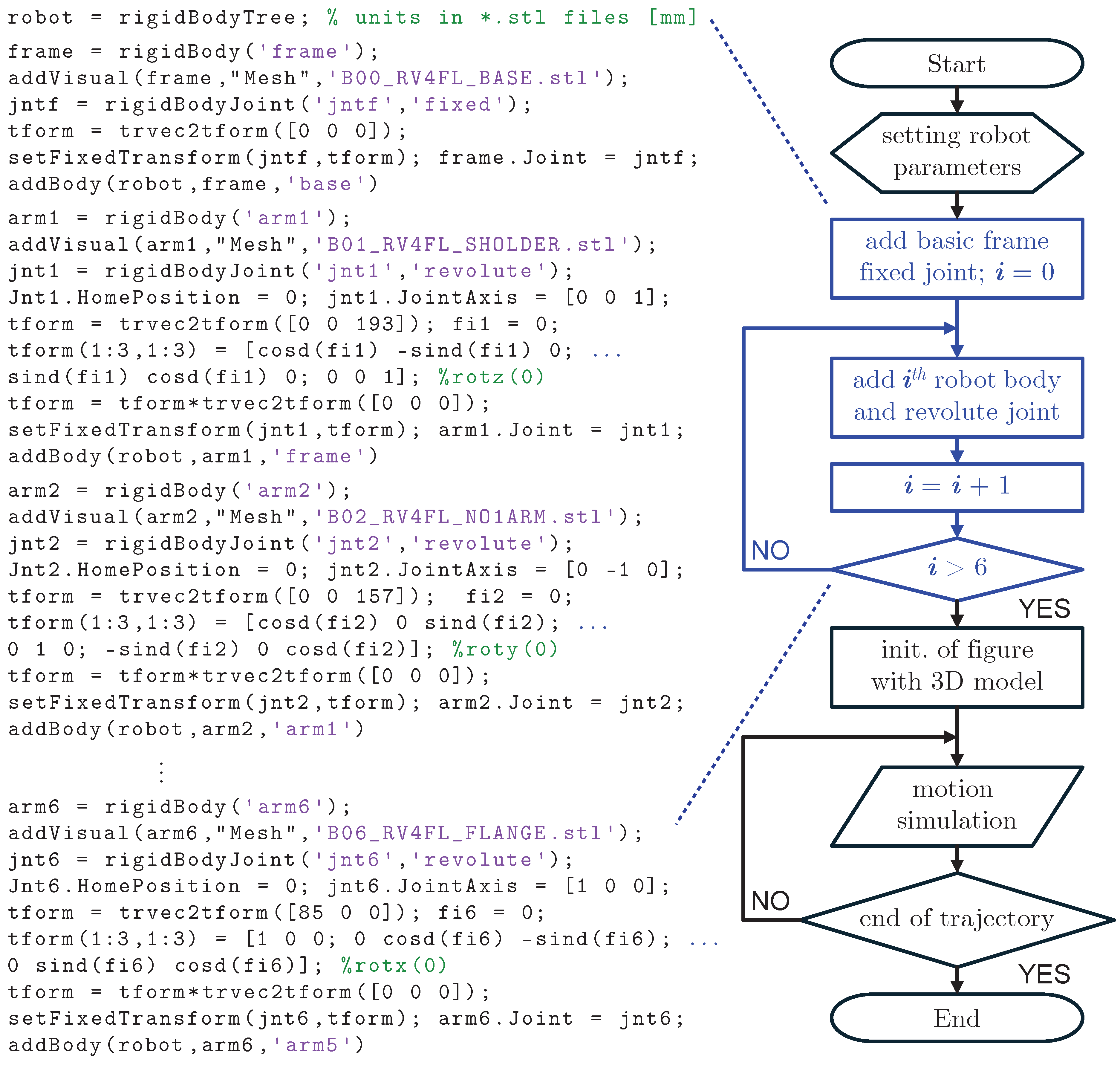
3. Considering Robot Topology

Let us consider Mitsubishi RV-4FL-D, an industrial stationary robot, situated in CPF (Figure 4a). It is considered for model synthesis, simulations and real experiments [19].

The topology of the robot has 6 degrees of freedom (DOF). The robot consists of a base and 6 arms (shoulder, upper arm, elbow, elbow block, fore arm and wrist with flange) up to the robot’s flange. It enables the user to set and control the Cartesian coordinates x, y and z for positions and $A_x$, $B_y$ and $C_z$ for the orientation of the robot tool centre point (TCP), set and control independent joint coordinates, or drive coordinates $q_{1–6}$.

4. Mathematical Model Synthesis

This section shows the synthesis of the mathematical model for simulation and as well as for the model-based control design. Ideally, rigid bodies are considered. This includes the synthesis of both forward and inverse problems for the robot kinematics and dynamics for the robot in Figure 4b. The obtained models of kinematics serve as trajectory planning, especially for the conversion of user TCP coordinates into joint coordinates, which is expected on robot drives.

4.1. Model of Robot Kinematics

To obtain the kinematic model, a Denavit–Hartenberg (DH) concept can be used. The concept defines the transformations between the joint coordinate space (drive space) and the operational coordinate space (tool centre point (TCP), robot end effector) in both directions: the forward direction ($q\to y$, joint/drive coordinates into TCP Cartesian coordinates) and the inverse direction ($y\to q$, TCP into joint/drive coordinates), where joint and operational coordinates q and y are defined for the considered robot as follows: [1]

$$\begin{array}{cc}\hfill q& ={\left[q_1,q_2,q_3,q_4,q_5,q_6\right]}^T,\hfill \\ \hfill y& ={\left[x,y,z,A_x,B_y,C_z\right]}^T.\hfill \end{array}$$

(1)

4.1.1. Forward Problem

For the 6 DOF robot, the forward problem represents a specific combination of three basic motions along axes x, y, and z, and three basic rotations around these three axes. The motions and rotations are parameters involved in the respective complex matrices. These matrices represent the individual transformations between the robot joints, i.e., they are connected to the corresponding individual robot bodies, as follows:  

$$\begin{array}{cc}\hfill F& =T_0^1{T}_1^2\left(q_1\right)T_2^3(-q_2)T_3^{\overline{3}}(-q_3)T_{\overline{3}}^4\left({90}^{\circ }\right),\hfill \\ \hfill & T_4^5\left(q_4\right)T_5^6\left(q_5\right)T_6^F\left(q_6\right)r_0,\hfill \end{array}$$

(2)

where $F={\left[x_F,y_F,z_F,1\right]}^T$ represents considered TCP and $r_0={\left[0,0,0,1\right]}^T$ represents the general origin for coordinate systems.

In (2), the first line represents TCP positioning and the second line orientation in TCP, i.e., the orientation of tool or gripper principal axis. It corresponds to a pattern from nature, as do the names in Figure 4b and

Table 1. D-H Parameters.

Robot	D-H  Parameters
Body Names	${\mathit{q}}_{\mathit{i}}$	${\mathit{d}}_{\mathit{i}}$	${\mathit{a}}_{\mathit{i}}$	${\mathit{\alpha }}_{\mathit{i}}$
Base (0–1)	$0^{\circ }$	$h_0$	0	$0^{\circ }$
Shoulder (1–2)	$q_1$	$h_1$	0	${90}^{\circ }$
Upper arm (2–3)	${90}^{\circ }-q_2$	0	${\ell }_2$	$0^{\circ }$
Elbow ver. (3–$\overline{3}$)	$-q_3$	0	$r_3$	${90}^{\circ }$
Elbow hor. ($\overline{3}$–4)	${90}^{\circ }$	${\ell }_3$	0	$0^{\circ }$
Fore arm (4–5)	$-{90}^{\circ }-q_4$	${\ell }_4$	0	$-{90}^{\circ }$
Wrist (5–6)	$q_5$	${\ell }_5$	0	${90}^{\circ }$
Flange (6–T)	$q_6$	${\ell }_6$	0	$0^{\circ }$

, which are taken from the biology of the human arm.

The individual motions and rotations, and their combinations mentioned above, are realised by transformation matrices expressed generally by one variable complex matrix, as follows:

$$\left[\begin{array}{cccc}cos{q}_i& -cos{\alpha }_{i}sin{q}_i& sin{\alpha }_{i}sin{q}_i& a_{i}cos{q}_i\\ sin{q}_i& cos{\alpha }_{i}cos{q}_i& -sin{\alpha }_{i}cos{q}_i& a_{i}sin{q}_i\\ 0& sin{\alpha }_i& cos{\alpha }_i& d_i\\ 0& 0& 0& 1\end{array}\right]$$

(3)

Figure 5. Two-dimensional views for robot kinematic analysis [17]. Individual numbers ⓪–⑥ represent numbers of robot bodies, see Figure 4b.

Figure 5. Two-dimensional views for robot kinematic analysis [17]. Individual numbers ⓪–⑥ represent numbers of robot bodies, see Figure 4b.

The matrices contain constant and/or variable parameters $q_i$, $d_i$, $a_i$ and ${\alpha }_i$—so called D-H parameters relating to the kinematic chain of the robot [1]. Their values are listed in Table 1. The number of variable rotations $q_i$ is 6 according to DOF of the considered robot. Other indicated constants $h_0$, $h_1$, ${\ell }_2$, $r_3$, ${\ell }_3$, ${\ell }_4$, ${\ell }_5$ and ${\ell }_{6-9}$ include vertical distances, axis offsets and lengths of robot arms. Moreover, the joint between ‘Elbow ver. (=Elbow vertical)’ and ‘Elbow hor. (=Elbow horizontal)’ is fixed as an immovable right-angle joint $\overline{3}$.

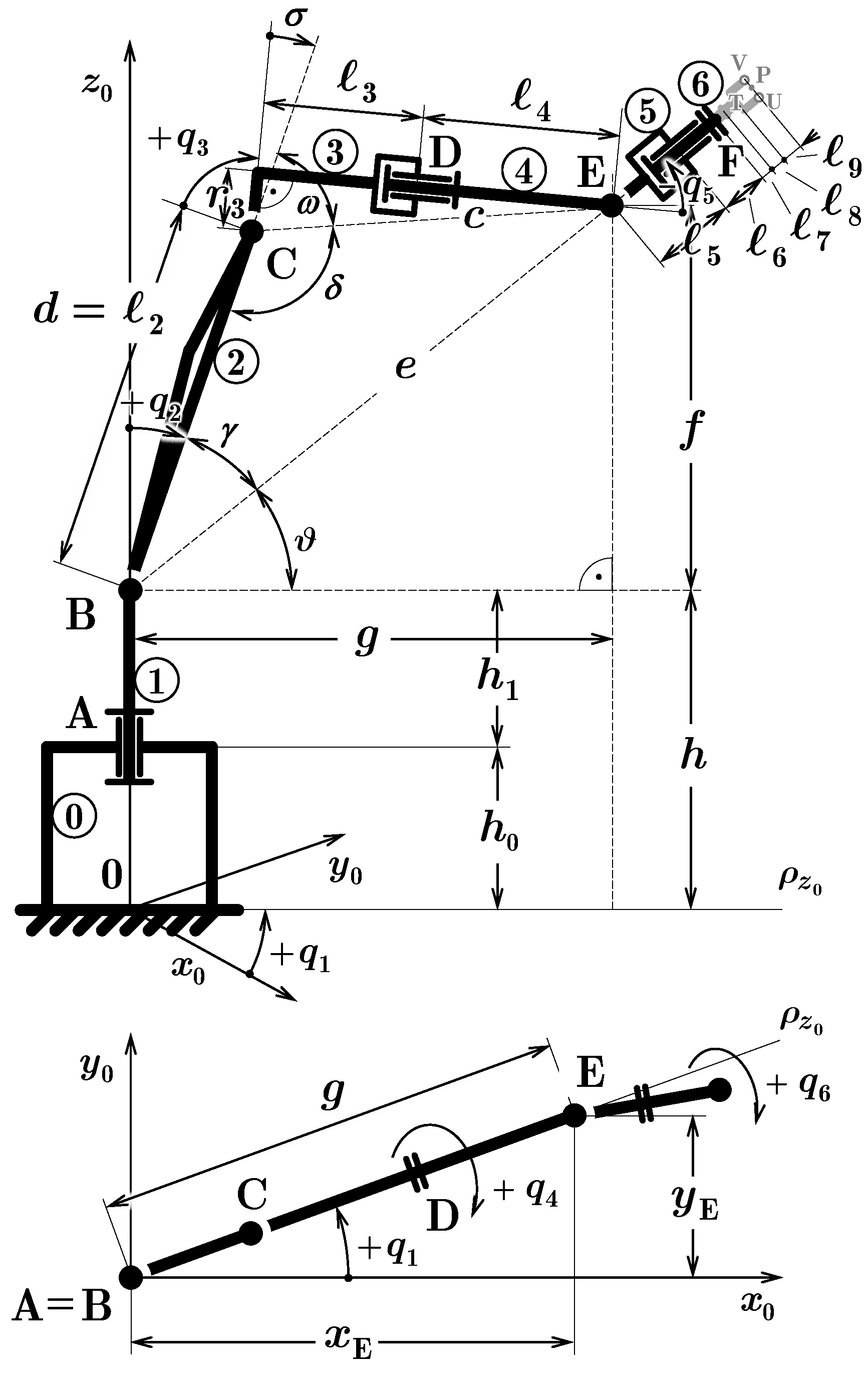
4.1.2. Inverse Problem

The inverse problem can be solved either numerically as a solution of the transformations expressed by (2) or analytically. Here, the analytical solution is demonstrated using geometrical relations depicted in Figure 5. The following expressions introduce the solution.

$$\begin{array}{cc}\hfill q_1& =\mathrm{atan}2(y_E,x_E),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill q_2& ={\displaystyle \frac{\pi }{2}}-(\gamma -\vartheta ),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill q_3& ={\displaystyle \frac{3}{2}}\pi -\beta -\gamma ,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill f& =z_E-h=z_E-(h_0+h_1),g=\sqrt{x_E^2+y_E^2},e=\sqrt{f^2+g^2},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill c& =\sqrt{r_3^2+{({\ell }_3+{\ell }_4)}^2},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \gamma & =\arccos {\displaystyle \frac{d^2+e^2-c^2}{2de}},\delta =\arccos {\displaystyle \frac{c^2+d^2-e^2}{2cd}},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \vartheta & =\mathrm{atan}2(f,g),\omega =\mathrm{atan}2({\ell }_3+{\ell }_4,r_3).\hfill \end{array}$$

(10)

To obtain the coordinates of point E for specific cases, let point E be determined using appropriate transformation chains based on orientation angles $Ax$, $By$, $Cz$ from end points, specifically F (Flange) or tool points T, U, V and P—see [20].

4.2. Model of Robot Dynamics

The model of the robot dynamics is derived using Lagrange equations of the second type:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}{\left({\displaystyle \frac{\partial \mathcal{L}}{\partial \dot{q}}}\right)}^T-{\left({\displaystyle \frac{\partial \mathcal{L}}{\partial q}}\right)}^T=\xi ,\hfill \end{array}$$

(11)

$$\begin{array}{c}\hfill \mathcal{L}=V(q,\dot{q})-P\left(q\right),\end{array}$$

(12)

$$\begin{array}{cc}\hfill \mathrm{i}.\mathrm{e}.,& {\displaystyle \frac{d}{dt}}{\left({\displaystyle \frac{\partial V}{\partial \dot{q}}}\right)}^T-{\left({\displaystyle \frac{\partial V}{\partial q}}\right)}^T+{\left({\displaystyle \frac{\partial P}{\partial q}}\right)}^T=\xi ,\hfill \end{array}$$

(13)

where $\xi$ are generalised force effects and V is kinematic energy as follows:

$$\begin{array}{cc}\hfill V& =\sum _{i=1}^n{V}_i={\displaystyle \frac{1}{2}}\sum _{i=1}^n\left(v_i^T{m}_i{v}_i+{\omega }_i^T{\mathcal{I}}_i{\omega }_i\right).\hfill \end{array}$$

(14)

The kinetic energy V in (14) for translation and rotation along the principal axes can be simply expressed as follows:

$$\begin{array}{cc}\hfill V& ={\displaystyle \frac{1}{2}}\sum _{i=1}^n\left(m_i{v}_i^2+I_i{\omega }_i^2\right),\hfill \end{array}$$

(15)

where n is a number of robot bodies and quantities $m_i$, $I_i$, $v_i$ and ${\omega }_i$ are weights, moments of inertia, translation and angular speeds, respectively. P is potential energy:

$$\begin{array}{cc}\hfill P& =\sum _{i=1}^n{P}_i=\sum _{i=1}^n{m}_{i}g{z}_i,\hfill \end{array}$$

(16)

where quantities $z_i$ represent the appropriate vertical distances of  the centres of gravity of individual bodies and g is gravitational acceleration. Expressing the terms of (13) leads to the dynamic equations of motion as follows (inverse dynamics) [1]:

$$M(q,\dot{q})\ddot{q}+N(q,\dot{q})\dot{q}+g\left(q\right)=\tau ,$$

(17)

or (forward dynamics):

$$\begin{array}{cc}\hfill \ddot{q}& =-M^{-1}N\dot{q}-M^{-1}g+M^{-1}\tau ,\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \ddot{q}& =-M^{-1}N\dot{q}+u,\hfill \end{array}$$

(19)

where modification $u=-M^{-1}g+M^{-1}\tau$ removes the effects of gravitation from the model and simplifies control design. The expression (18) can be performed in continuous or discrete state-space forms

$$\left.\begin{array}{ccc}\dot{x}=A\left(x\right)x+Bu\hfill & \to & x_{k+1}=A\left(x_k\right)x_k+u_k\\ y=Cx\hfill & \to & y_k=C{x}_k\\ \tau =Mu+g\hfill & \to & {\tau }_k=M{u}_k+g\end{array}\right\}$$

(20)

The equations in (20) are prepared for simulation and control design.

5. Control Concepts and Principles

This section introduces specific representatives of non-model and model-based control approaches used for applications in industrial stationary (not only articulated) robots. The first one presents a common approach used in industry without any optimisation for future outlook, but is proven. The second represents a strategy enabling the future development and inclusion of additional user requirements as specific constraints on motion increments, smoothing for specific horizons, and energy optimisation, i.e., better energy input distribution in multi-body systems for robots. Note that the success and accuracy of the robot motion depends on the appropriately designed reference trajectory, considering technological and geometric constraints as well.

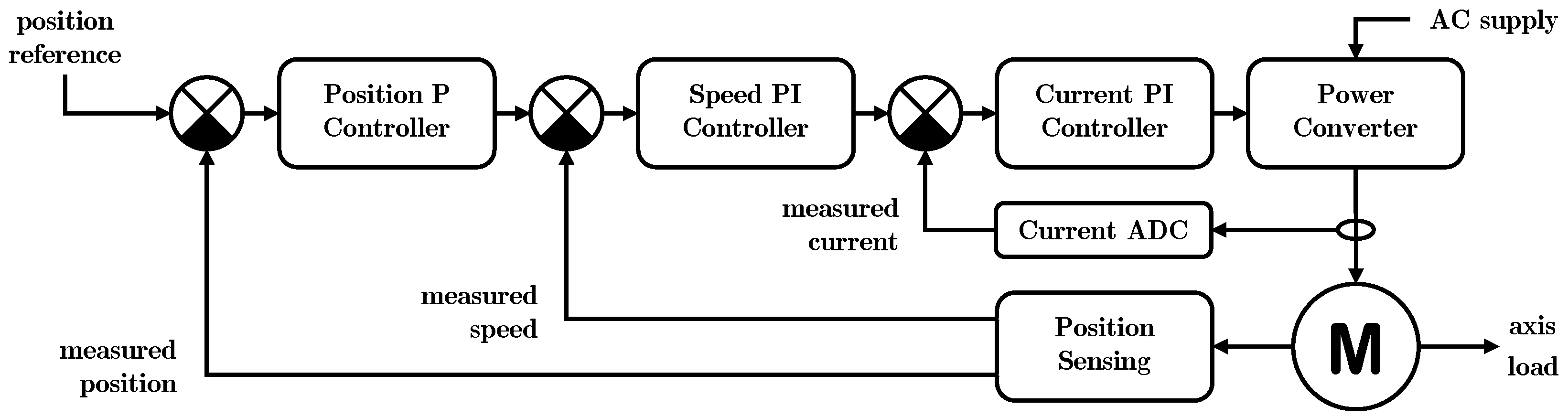
5.1. Conventional Cascade Control

Let us consider continuous and discrete PID controllers as representatives of the conventional non-model-based control approach. Their usual basic forms are as follows.

• continuous form:

$$u\left(t\right)=K_p\left(e\left(t\right)+{\displaystyle \frac{1}{T_i}}\underset{0}{\overset{t}{\int }}e\left(t\right)\mathrm{d}t+T_d\dot{e}\left(t\right)\right),$$

(21)

• discrete incremental form:

$$\begin{array}{cc}\hfill u_k& =u_{k-1}+K_p\left((e_k-e_{k-1})+{\displaystyle \frac{1}{T_i}}{e}_k{T}_s+T_d{\displaystyle \frac{e_k-2e_{k-1}+e_{k-2}}{T_s}}\right).\hfill \end{array}$$

(22)

The form (22), if applied to the drive control, i.e., the actuation of individual robot joints, is configured to the cascade configuration [21]. It consists of three interrelated loops: positional, speed and current, see Figure 6.

The mentioned concept represents still the independent (distributed, local) control approach from the robot point of view. All internal interactions given by a robot dynamic behaviour are considered as external disturbances.

5.2. Advanced Model Predictive Control

The discrete model predictive control is the representative of a model-based control with a specific optimality criterion:

$$\begin{array}{cc}\hfill \underset{\Delta U_k}{min}& J_k({\widehat{Y}}_{k+1},W_{k+1},\Delta U_k),\hfill \end{array}$$

(23)

subject to the state-space model (20) and constraints:

$y_{min}\le y_{j+1}\le y_{max}$ and $u_{min}\le u_j\le u_{max}$, where ${\widehat{Y}}_{k+1}$, $W_{k+1}$ and $\Delta U_k$ are vectors of output predictions, reference values and increments of searched control actions $u_k=u_{k-1}+\Delta u_k$, respectively; $j=k,\cdots ,k+N$ and N is a prediction horizon. The cost of the criterion (23) is usually expressed by quadratic function:

$$J_k=\left|\right|Q_{YW}({\widehat{Y}}_{k+1}-W_{k+1}){\left|\right|}_2^2+\left|\right|Q_{\Delta U}\Delta U_k{\left|\right|}_2^2.$$

(24)

Figure 7 shows the novel concept of the application of predictive control. A global slower part has online optimisation [23] and a local fast part uses pre-computed control laws [18]. The concept uses the same computation principle.

6. Software Tools

To provide adequate robot behaviour analysis and control design, it is necessary to use suitable software tools. These support users to obtain detailed robot models and simulate them, and to realise real-run control and data acquisition from the physical robot motion. Outside of the mentioned tools, other modelling software such as NX or Inventor and others should be considered. All these tools serve the determination of realistic (ideal) physical parameters such as moments of inertia, weights, lengths and positions of centres of gravity, which all are important for the construction of an adequate mathematical model.

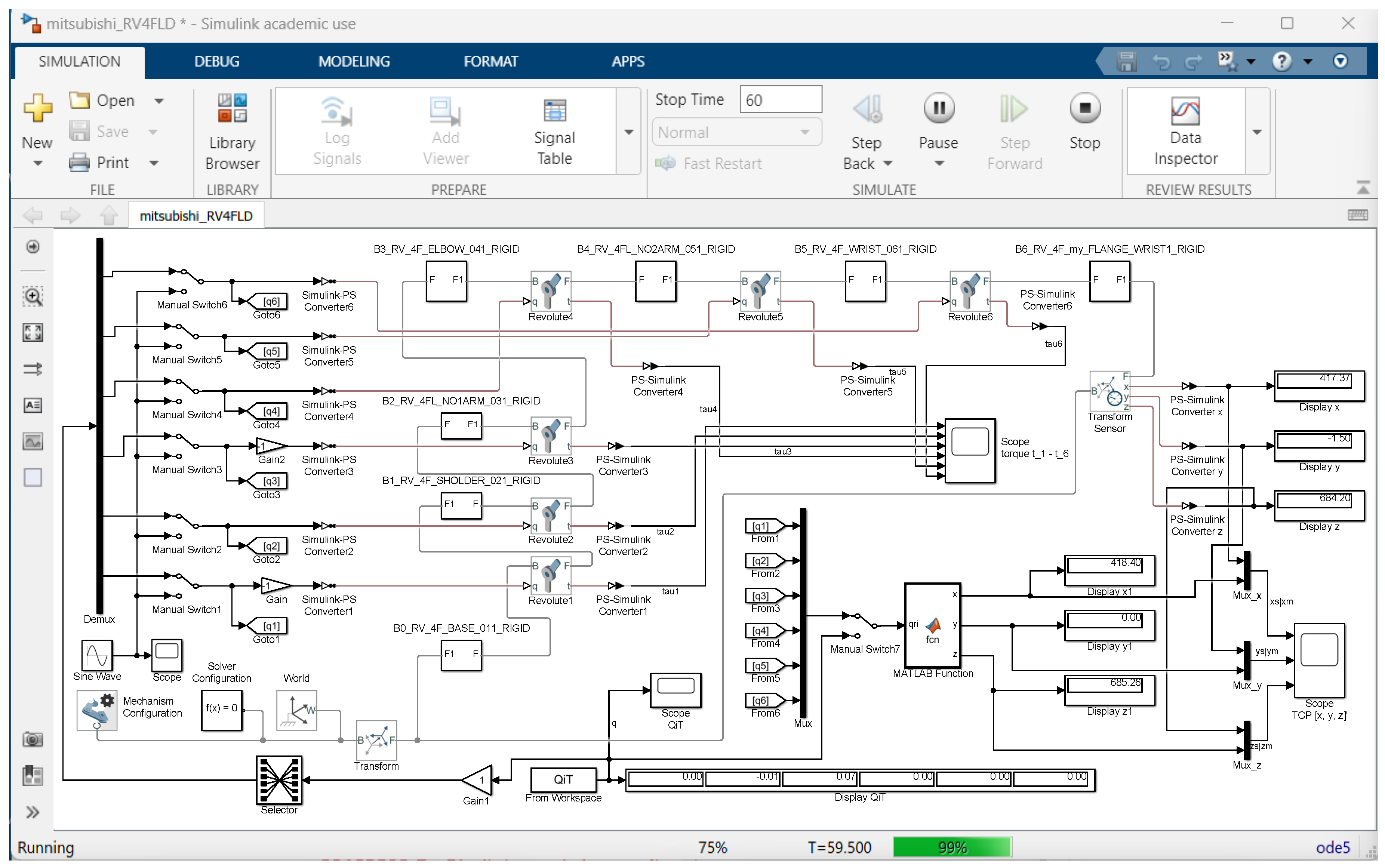
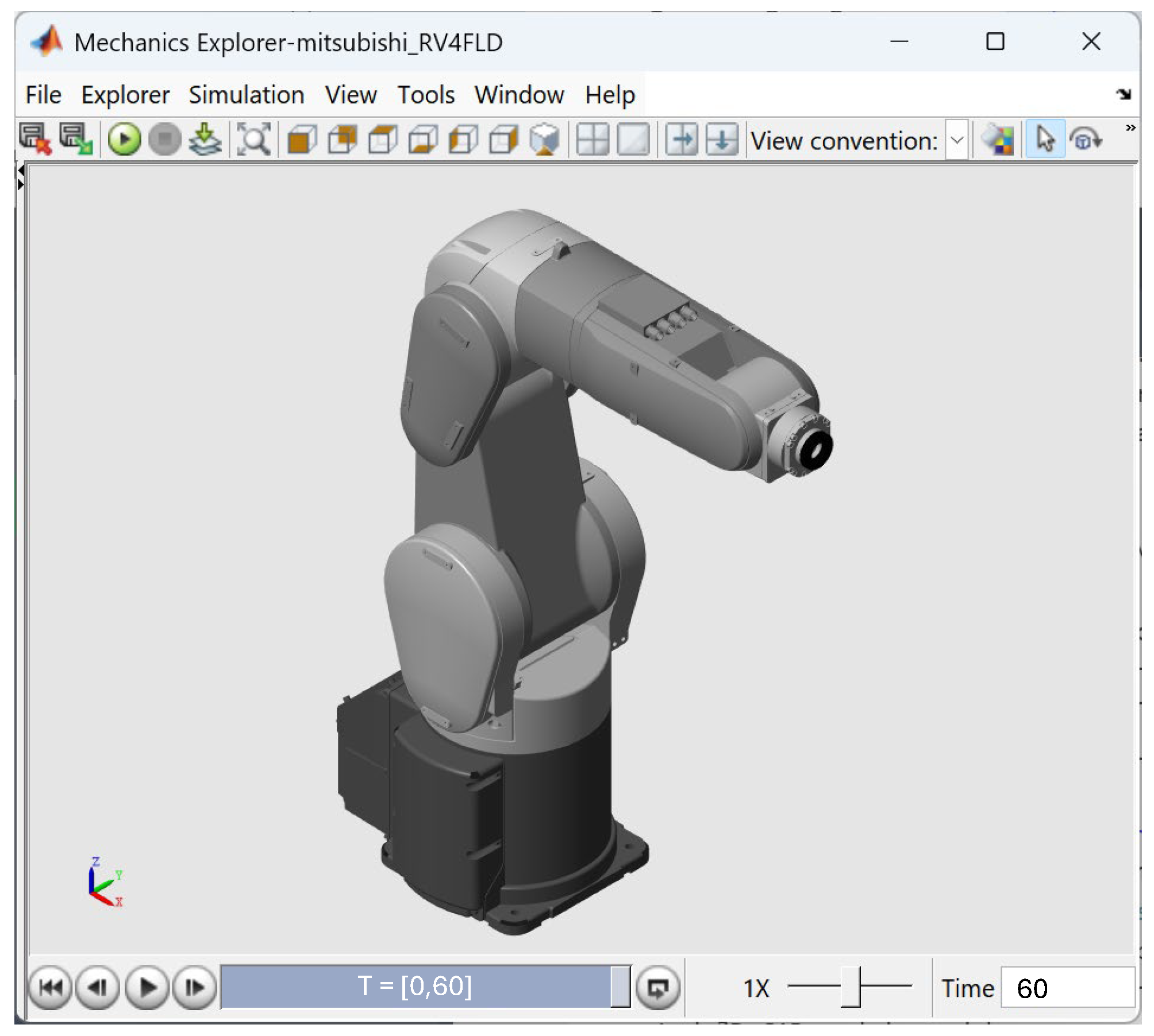
6.1. Simscape Multibody Lib—MathWorks

Simscape Libraries, specifically Simscape Multibody library [24] included in Simulink, serves to verify derived models and 3D CAD models, especially for rapid drive prototyping in the construction phase, when only the CAD model is available, but there are no equations of motion (model of robot dynamics). In this paper, the Multibody library was used for simulations of dynamic robot behaviour, see Figure 8: Simulink model based on blocks of Multibody library, and Figure 9: ‘Mechanics Explorer’ involving imported 3D CAD model, and keeping real physical parameters from used original CAD applications (NX or Inventor) as mentioned above.

6.2. Robotics System Toolbox—MathWorks

Similarly to the previous section, the plain MATLAB R2024b environment with the Robotics System Toolbox [25] is suitable for simulations with a rich function set as well. It enables users to have all procedures in hand, i.e., from trajectory planning, to control design and its verification. Toolbox is specifically suitable for the verification of kinematic transformations and collision tests for user defined trajectories. A creation of the structure describing the robot is shown in Figure 10 and the listing of the created structure in the MATLAB command line window is in Figure 11.

The model defined and used in this toolbox contains all physical parameters such as arm lengths, masses, moments of inertia, centres of gravity and geometrical envelopes of robot bodies. The motion during a simulation can be visualised, including collision analysis and motion trajectory display (Figure 12). The wireframe points were calculated using the kinematics equations in Section 4.1, as well as the figures below. They show simulated joint and TCP coordinates. In this paper, the MATLAB software environment including Simulink and its toolboxes and libraries was used due to the possible importation of a 3D CAD robot model [26]. Furthermore, for the implementation of derived models and for the processing of measured data by RT Toolbox (Mitsubishi), see the figures in the next section.

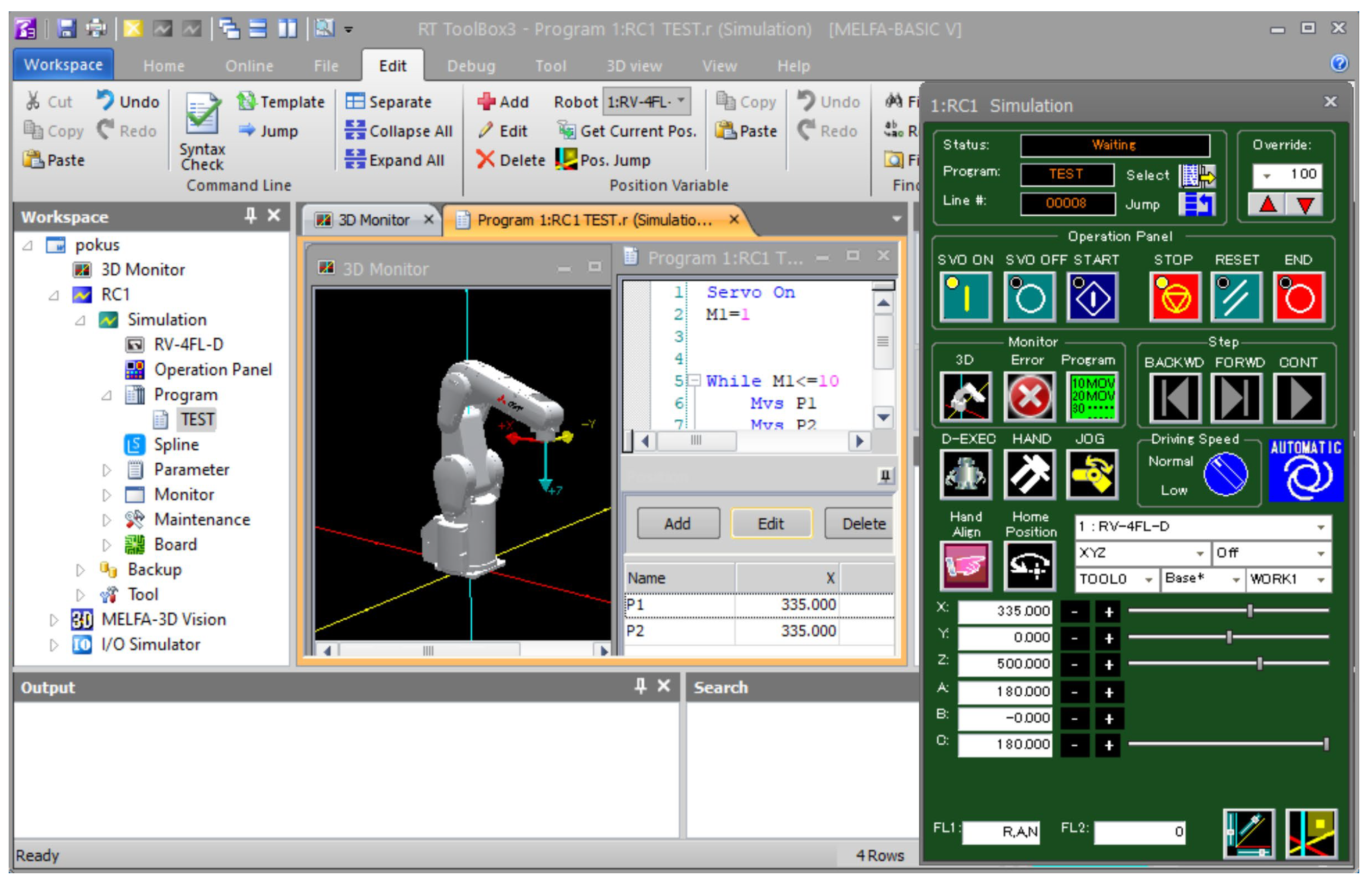
6.3. RT Toolbox—Mitsubishi Electric

RT Toolbox represents a suitable software tool that enables users to program robot motion and to verify it, including 3D visualisation and executing the real control of the specific class of industrial robots, including data acquisition options [27]. The data acquisition depends on the type of control system of the Mitsubishi robot.

In this paper, this RT Toolbox was used for the verification of the designed motion trajectory and for real experiments on the described robot Mitsubishi RV-4FL-D as shown in Figure 13. For measured data of real experimental runs tracking testing trajectory see Section 7.

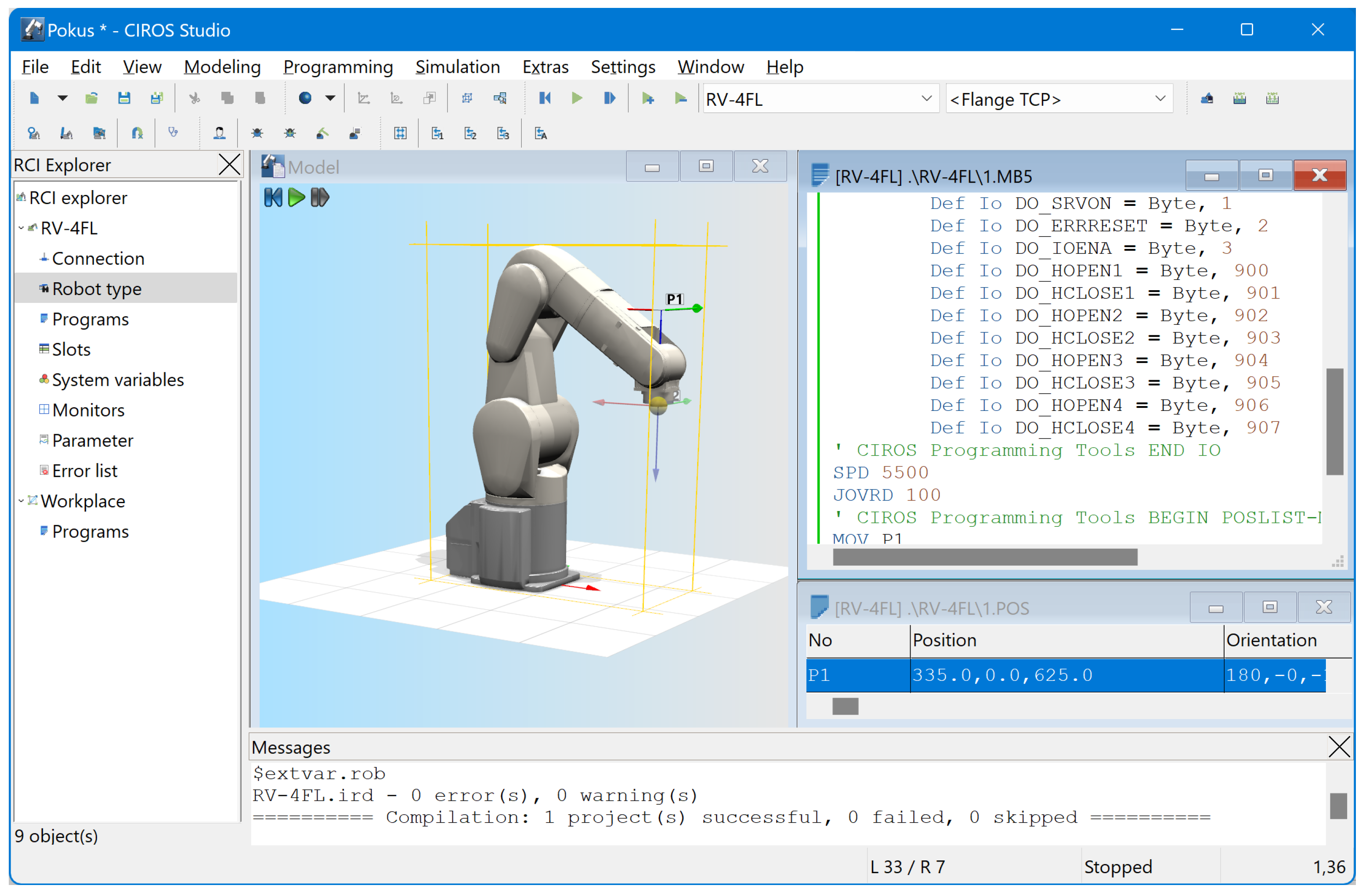
6.4. CIROS Studio—Festo

CIROS Studio is an industrially oriented software tool, containing analogous features such as RT Toolbox. It includes an environment for creating 3D simulation models and for programming with wide debugging and simulation options, see Figure 14. The data of robot statements or input commands can be managed and changed using industrial interfaces, and user-programmed with approaches via Python 3.13.1.

In this paper, CIROS Studio was considered powerful alternative to RT Toolbox for  the verification of motion trajectory and for real experiments on considered robot RV-4FL-D.

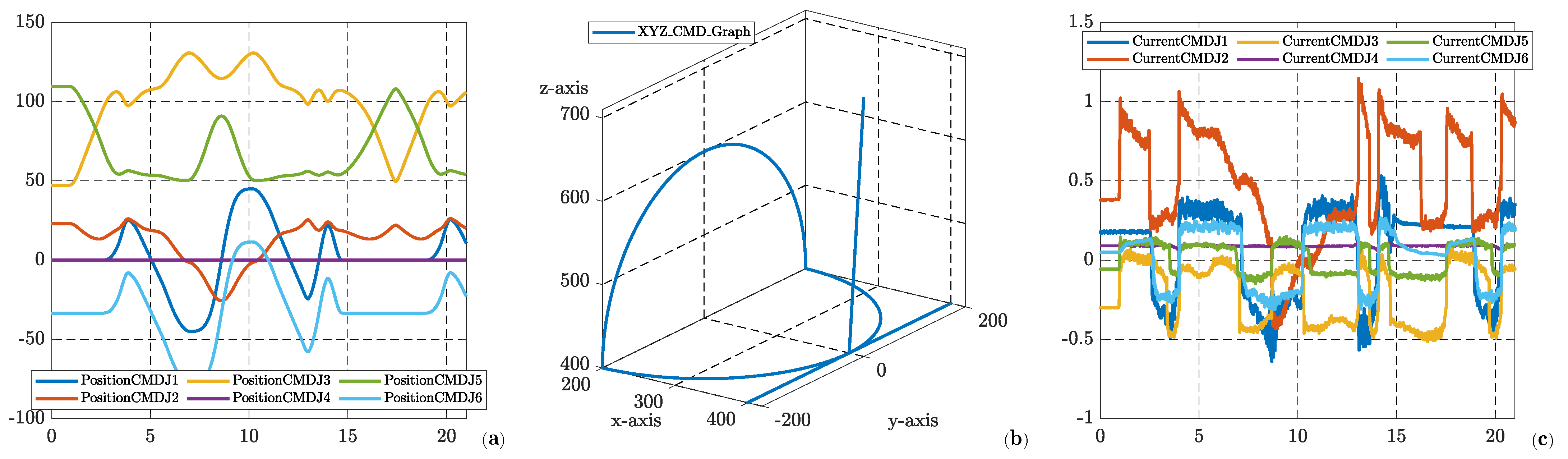
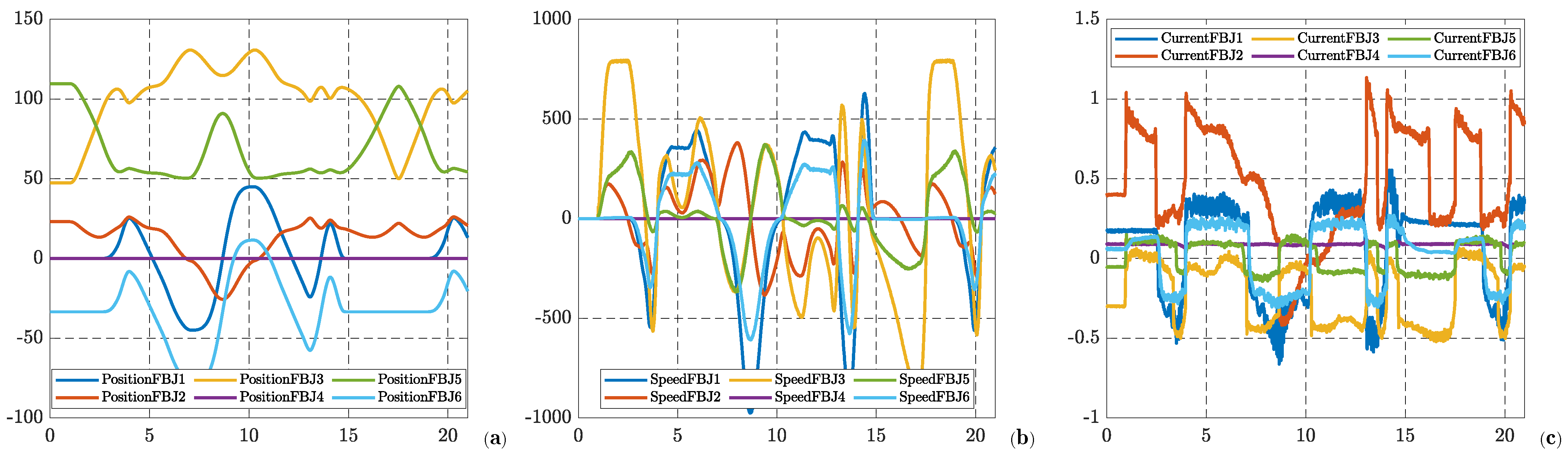
7. Simulation and Real Experiment

Modelling includes both mathematical and 3D modelling, and the planning of motion trajectories, i.e., it represents a number of complex procedures. This section show results in the form of time histories of simulated and measured physical quantities of robot motion.

7.1. Simulation

Specifically, let us first consider the definition of reference motion in Figure 15 or its equivalent code shown in Figure 16. It shows the universal description of the motion geometry in G-code for motion trajectory generation, i.e., path interpolation and time parameterisation. Using listed G-code via MATLAB user functions, the simulation runs were realised. Figure 17a–c show simulated input data processed by a robot control system intended for real experiment. A record of the simulation is shown in Figure 12 that proves the correctness of user-designed trajectory.

7.2. Real Experimental Results

For the code in Figure 16, Figure 18a–c shows measured state quantities using RT Toolbox specifically as follows: angular position, angular speed, current (torque currents) for individual joints—appropriate drives along defined trajectory, i.e., each containing 6 time histories corresponding to 6 driven joints/axes. The presented time histories were captured by RT Toolbox for sampling period $T_s=7.1$ ms [27]. Current profiles indicate load from motion and the robot arm itself from joint 1 to joint 6. The biggest load has to be covered by joint 2, which produces the main motion of the robot access system (the first three axes). On the other side, the orientation system (wrist, the last three axes) represents only a particular motion. It was reduced by the reference trajectory. Figure 18b depict x, y and z Cartesian coordinates as individual time histories of resultant 3D trajectory.

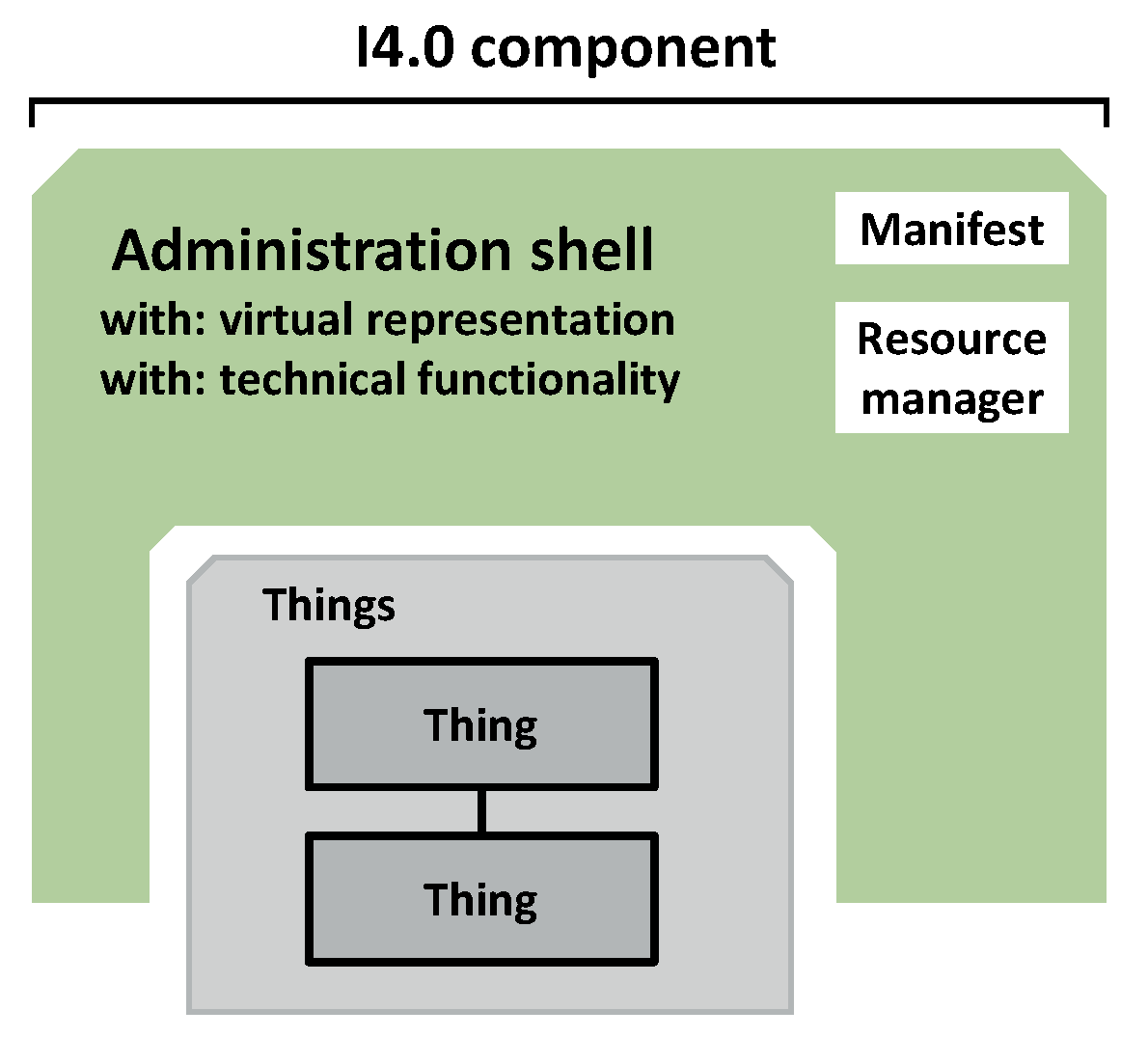
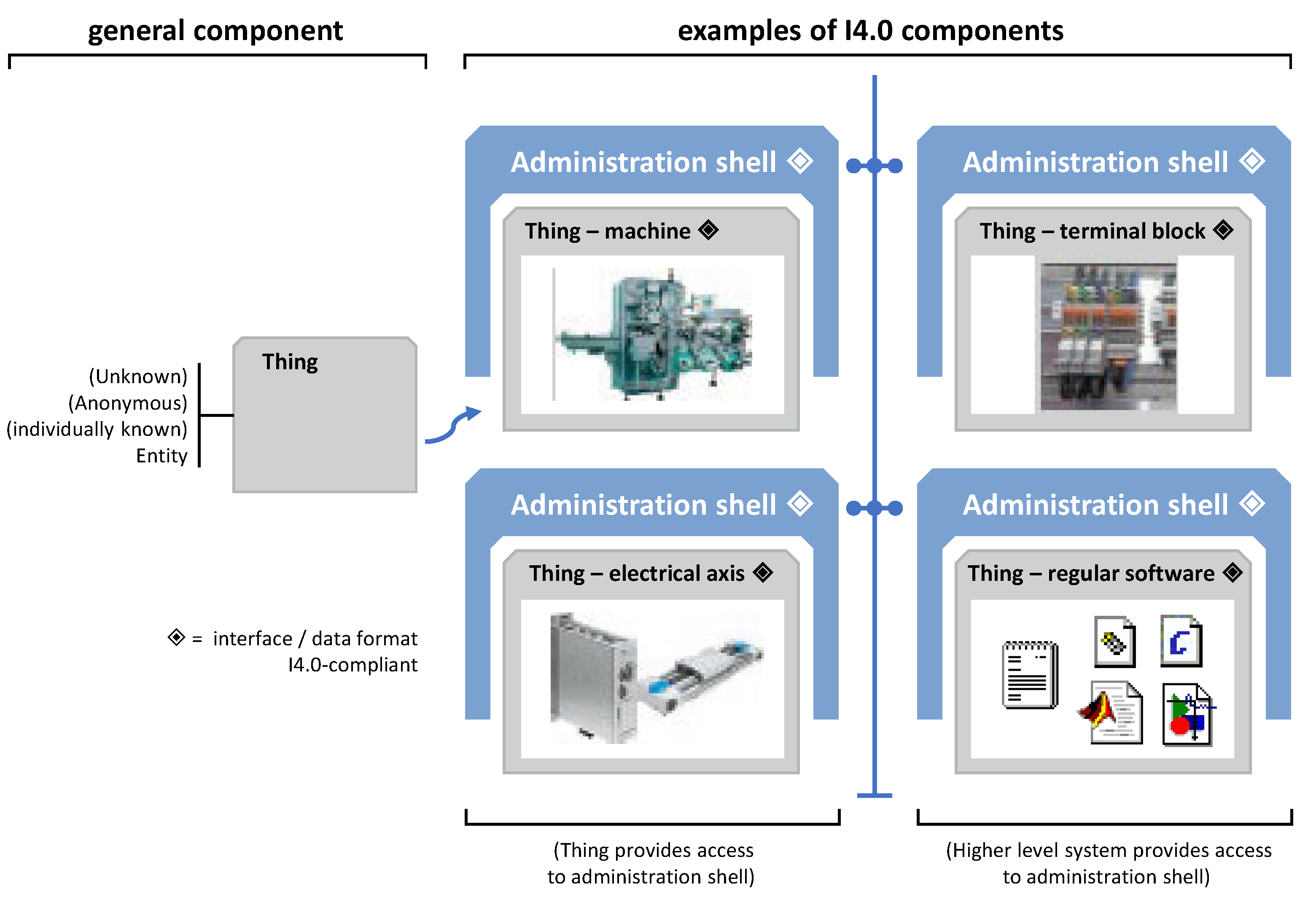
8. Robot Integration in Cyber-Physical Factories

In the previous sections, the creation of digital models was introduced. If such models, robots or other devices should be integrated into the complex production process, then such a task represents a totally different point of view. A basic element for the integration of the robot(s) (or any other unit(s)) is a digital interface providing a standardised communication between units and the outside world. However, the interface itself is not sufficient for the full integration of the robot into the production process, since full integration means both the ability to offer and request individual operations or steps of the production process as well as the ability to dynamically react to events such as error states, adding a new unit (element), changing the parameters of the production process, changing customer requirements, etc.

For such a level of integration, it is necessary to provide the surrounding system with comprehensive information about the capabilities, parameters and status of the given device (robot). This consideration leads directly to the concept of Industry 4.0 (I4.0) components, as defined in [28] and the concept of a real digital twin (full digital twin), Figure 19.

According to the I4.0 definition of a component [28], a given object becomes a component if it is equipped with a so-called administrative shell. That is, a digital envelope that contains all the above-mentioned parameters, states and information about the physical object together with a unified interface for communication with the environment. The mutual communication of the components created in this way takes place exclusively through these administrative shells (see Figure 20). The data structure of this envelope itself is not part of the definition of the I4.0 component, but the Asset Administration Shell (ASS) standard, defined in [29,30], appears to be a suitable data model for this case.

8.1. Asset Administration Shell

The specification of ASS defines common form of digital component envelope I4.0 and it is originated and still developed by the international organisations Platform Industrie 4.0, VDE/VDI and ZVEI [31]. Specifications [29,30] contain detail description of data model, design way, class description and communication ways in envelope level. The digital envelope in ASS point of view can be split in passive and active parts, where passive part is mandatory:

• passive part contains descriptions of parameters, properties and object abilities in prescribed format; this form means pieces of information and attributes that description has to contain of each parameter, but data format (XML, JSON),
• active part contains functions in any programming language used for communication for I4.0 components with their surroundings.

8.2. Application to Robots Mitsubishi—Full Digital Twin

The above-mentioned principles can be applied completely universally, for Mitsubishi industrial robots as well. The basis is the creation of the Administrative Shell in its active (more precisely, proactive) form. The passive part of AAS alone would certainly not be sufficient in the case of a robot-type device. From the principle of the production process, the robot is an active element that must be able to interact with other elements of production. The communication between the robot and its digital envelope itself is not limited by the AAS standard. We can use either the standardised OPC UA interface or one of the low-level approaches, such as C language libraries.

The specific implementation of the administrative shell always depends on the specific application of the given robot. In our CPF environment (Figure 1), robots are used both for assembling final products and for accurately loading semi-finished products into a CNC milling machine. In the case of an assembling robot, it is appropriate to create a digital envelope of the robot itself and implement functions for offering assembly operations of the robot in the active part of this envelope.

On the contrary, in the case of a robot that is used to load material into a machining centre, it turns out to be appropriate to create an administrative shell of the entire assembly. The robot itself here performs only a single-purpose operation, serving a single end device (milling machine). To offer and confirm this operation through a robust and administratively complex mechanism of administrative shells would be extremely inefficient. In this case, only the creation of a complete digital twin of the entire assembly (machining centre together with the robot) makes sense. Such a digital twin then offers comprehensive machining services in its active part, the parameters of which already include the time required to place the workpiece in and out of the machining centre.

On the other hand, from the point of view of monitoring the efficiency of robot movement or measuring energy consumption, it is appropriate to implement a passive administrative shell for both types of robots, which provides data on robot movement and the values of required quantities in a standardized manner.

A question for future research is whether the virtual model described in the previous chapters can be integrated into the thus created digital envelope. In terms of development complexity, this is a step that will require considerable effort. However, the result will be a truly full digital twin of the given robot, which will be able to serve both for internal control or optimisation of the robot’s functions, as well as for its integration into a smart production process, control of the production flow, optimisation and response to external events.

9. Conclusions

The paper deals with mathematical modelling adapted to a specific industrial robot kinematics and dynamics, conventional control and outline of novel advanced hierarchical control concept. There are representatives of possible software tools for modelling [2,15]. They provide data (both measured and simulated) for identifying and verifying model parameters of a particular robot. Each industrial robot considered in the research requires an analysis of the manufacturer’s configuration. Control design optimisation can then be designed and achieved.

The paper showed that there are many possible software tools. However, their purpose/use is different. Their use for a verification of derived models is possible, but by their combination. The use for hyper prototyping depends especially on given robot and the support in specific software tool. Key robot producers also support robots from other manufacturers, but partially. The situation is similar for the integration of robots into CPFs. Communication standards allow the user to design solutions independently of proprietary solutions.

Our future work will focus on camera vision and trajectory tracking and trajectory optimization and on further development of control based on an advanced model.

All pictured real data were captured on the assembly module (Figure 4a) involved in CPF at the College of Polytechnics Jihlava. The introduced conceptions of Industry 4.0 in Section 8 are being developed in this factory.