Fuzzy Course Tracking Control of Unmanned Surface Vehicle with Actuator Input Quantization and Event-Triggered Mechanism
Abstract
1. Introduction
- (1)
- In comparison with the existing ship course tracking control methods [39,40,41], the course tracking control of USVs with actuator input quantization and an event-triggered mechanism is considered for the first time, which also solves the computational inflation problem with dynamic surface control.
- (2)
2. Problem Formulation
3. Controller Design
- (1)
- When , , which implies that and ;
- (2)
- When , , which implies that ;
- (3)
- When , meaning that the current moment is , and .
4. Stability Analysis
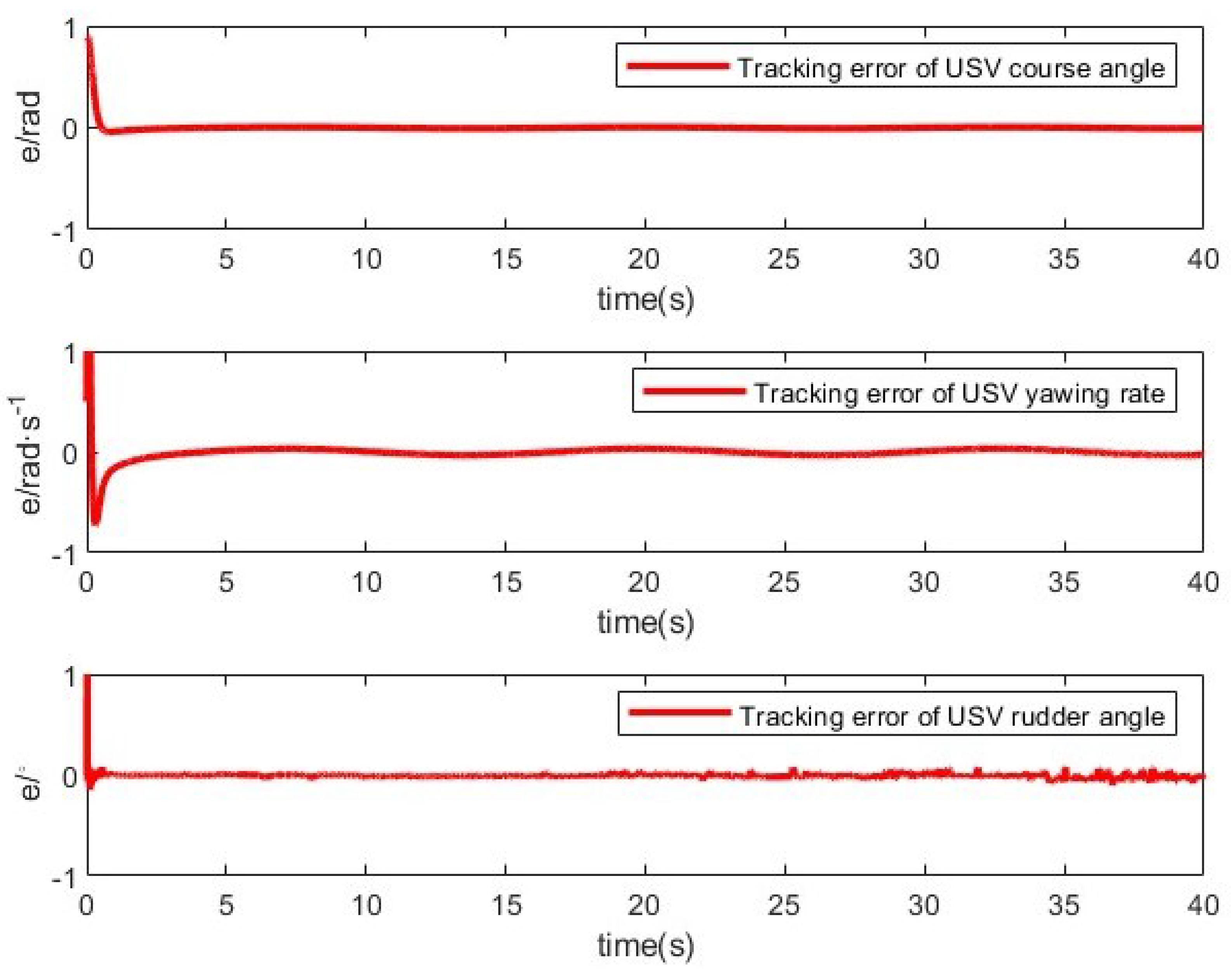
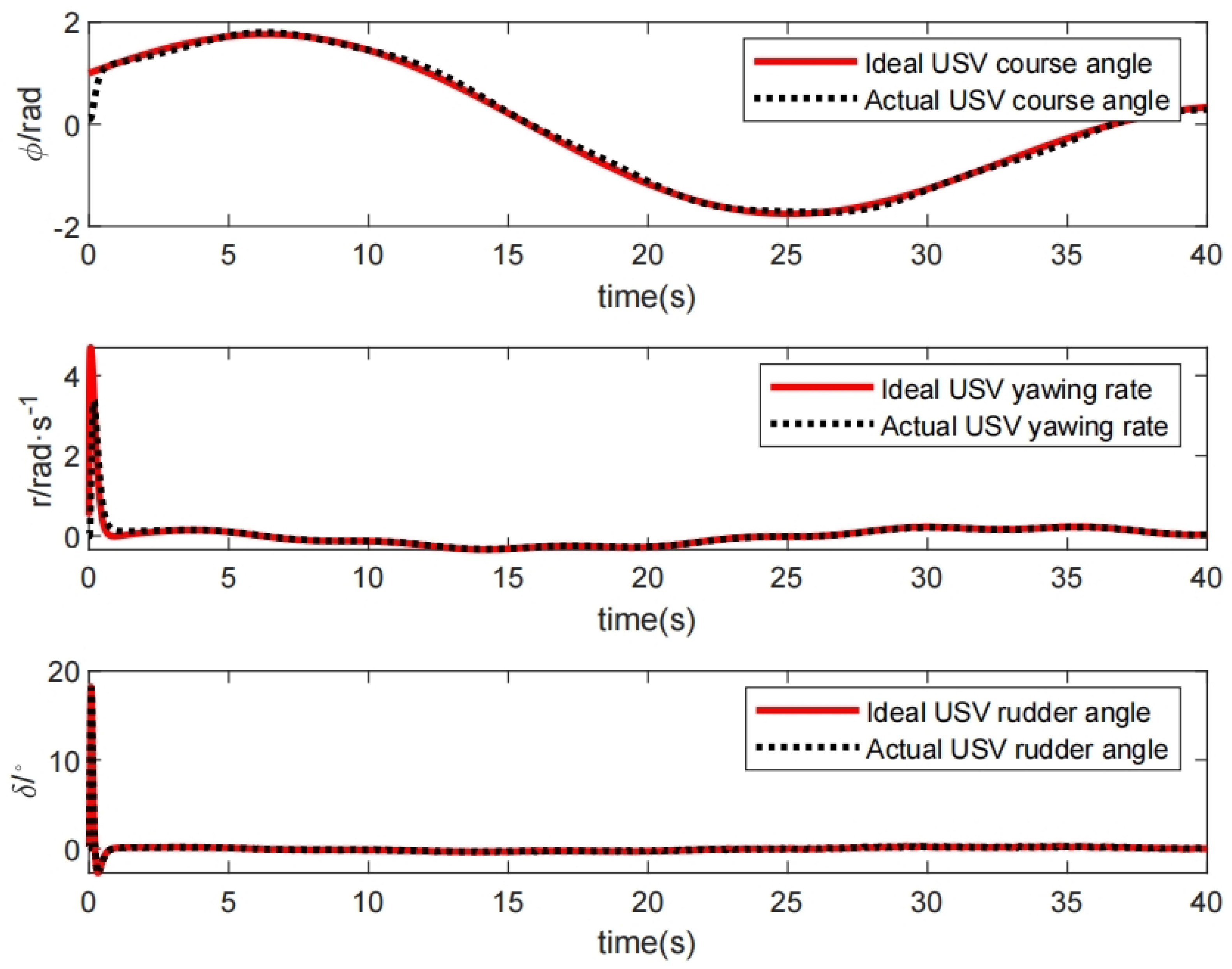
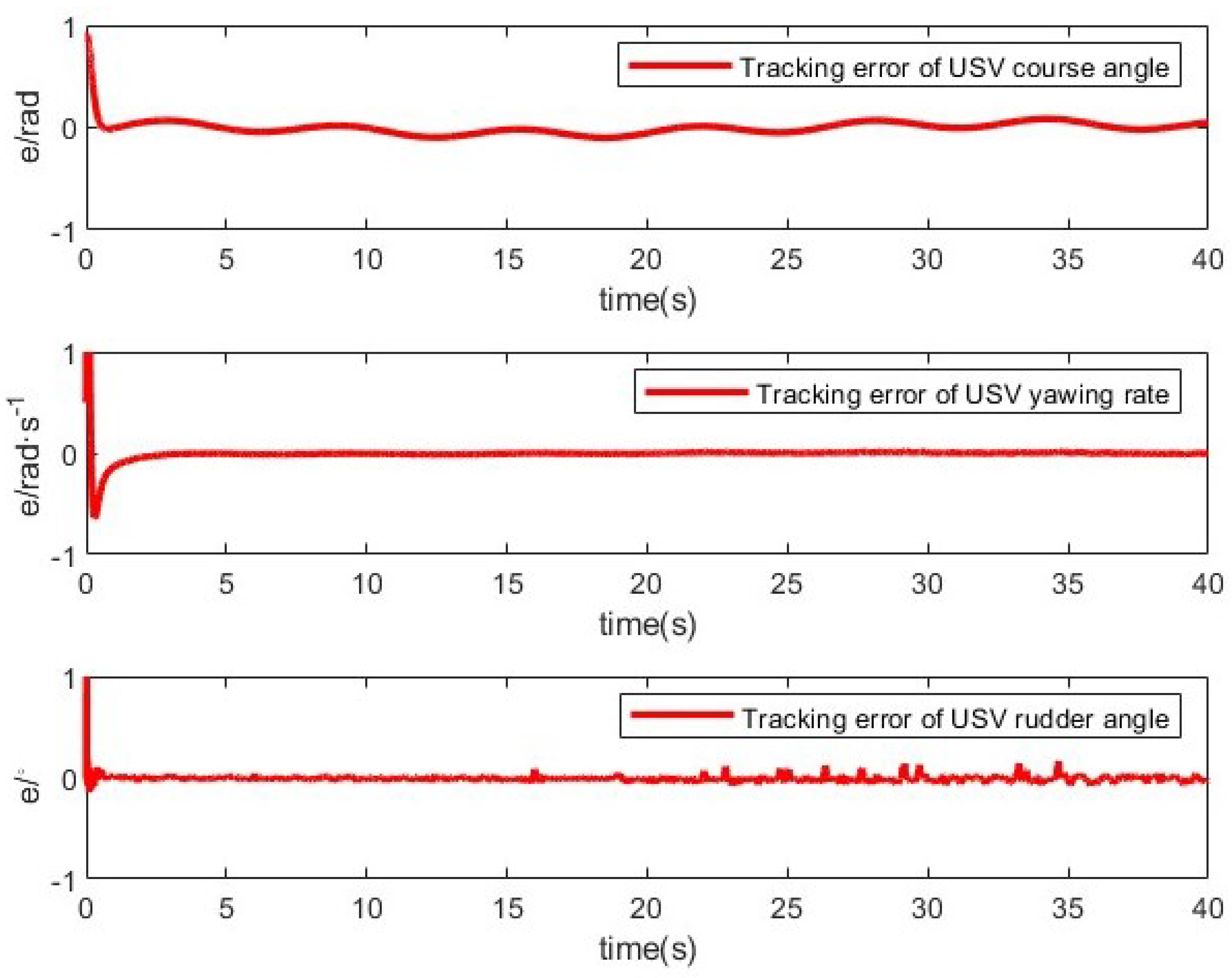
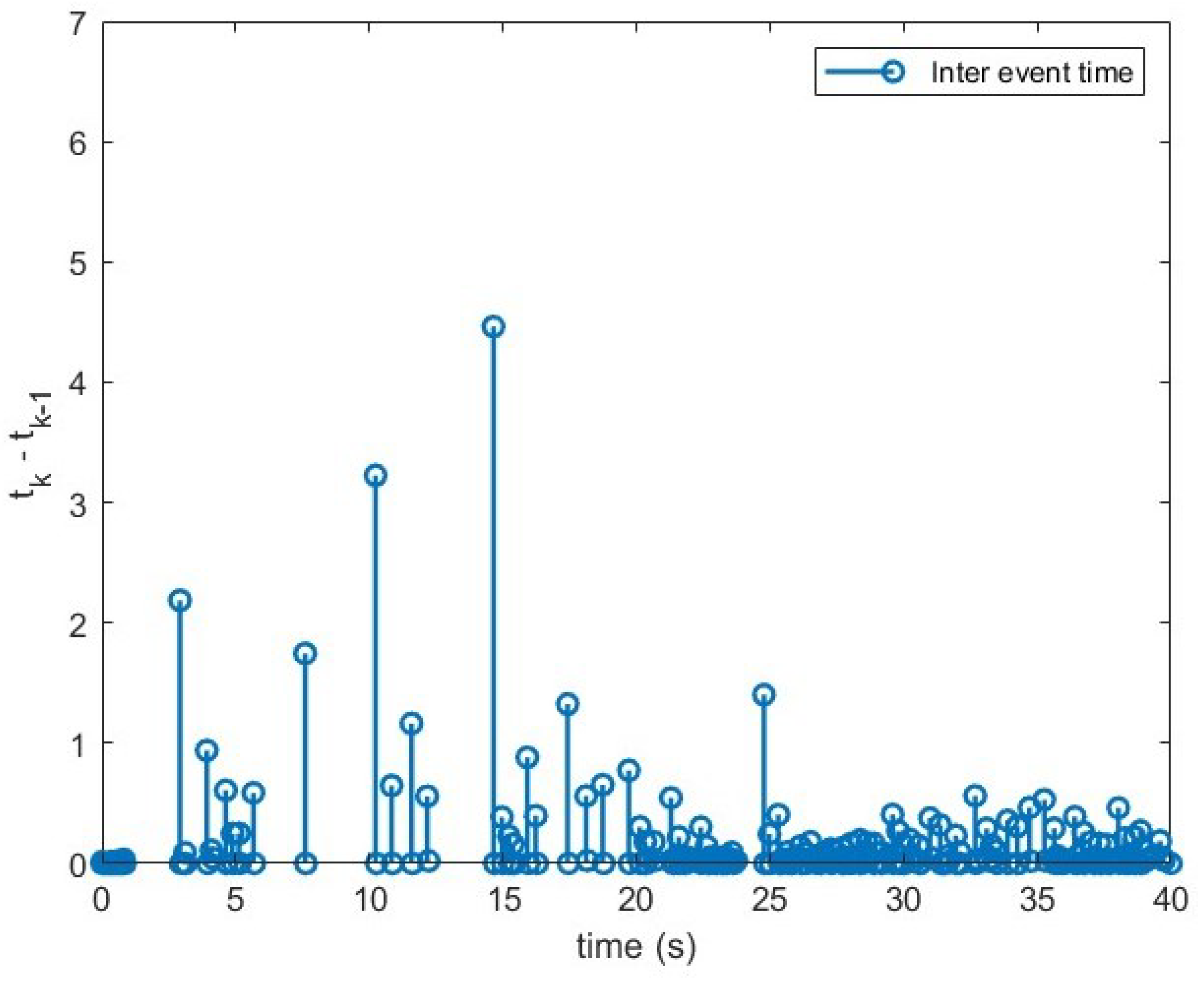
5. Simulation Result
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peng, Z.; Gu, N.; Liu, L.; Zhang, B.; Wang, D. Extended state observer design for autonomous surface vehicles using position-yaw measurements. In Proceedings of the 2017 4th International Conference on Information, Cybernetics and Computational Social Systems (ICCSS), Dalian, China, 24–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 636–641. [Google Scholar]
- Jiang, Q.; Li, Y.; Liao, Y.; Miao, Y.; Jiang, W.; Wu, H. Information fusion model-free adaptive control algorithm and unmanned surface vehicle heading control. Appl. Ocean Res. 2019, 90, 101851. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, Y.; Hao, L.Y. Nonsingular finite-time heading tracking control of marine vehicles with tracking error constraints. J. Frankl. Inst. 2024, 361, 106734. [Google Scholar] [CrossRef]
- Lv, C.; Yu, H.; Hua, Z.; Li, L.; Chi, J. Speed and heading control of an unmanned surface vehicle based on state error PCH principle. Math. Probl. Eng. 2018, 2018, 7371829. [Google Scholar] [CrossRef]
- Liu, J.; Huang, L.; Yu, D.; Xu, L.; He, Y. The control method for ship tracking when navigating through narrow and curved sections. Appl. Ocean Res. 2024, 145, 103943. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Zhang, J.; Zhou, D.; Dong, J. Adaptive sliding-mode path following control system of the underactuated USV under the influence of ocean currents. J. Syst. Eng. Electron. 2018, 29, 1271–1283. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, A.; Castañeda, H. Guidance and Control Based on Adaptive Sliding Mode Strategy for a USV Subject to Uncertainties. IEEE J. Ocean. Eng. 2021, 46, 1144–1154. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Zhang, Y.; Nie, Y.; Tang, J.; Zhu, S. Disturbance-Observer-Based Sliding Mode Control Design for Nonlinear Unmanned Surface Vessel with Uncertainties. IEEE Access 2019, 7, 148522–148530. [Google Scholar] [CrossRef]
- Cortes-Vega, D.; Alazki, H.; Rullan-Lara, J.L. Visual odometry-based robust control for an unmanned surface vehicle under waves and currents in a urban waterway. J. Mar. Sci. Eng. 2023, 11, 515. [Google Scholar] [CrossRef]
- Huayna-Aguilar, M.M.; Cutipa-Luque, J.C.; Yanyachi, P.R. Robust control and fuzzy logic guidance for an unmanned surface vehicle. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 766–772. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, A.; Castañeda, H.; Garrido, L. USV Path-Following Control Based On Deep Reinforcement Learning and Adaptive Control. In Proceedings of the Global Oceans 2020: Singapore—U.S. Gulf Coast, Biloxi, MS, USA, 5–30 October 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Yuan, C.; Luo, J. Adaptive Path Following Control of Unmanned Surface Vehicles Considering Environmental Disturbances and System Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 339–353. [Google Scholar] [CrossRef]
- Song, S.; Park, J.H.; Zhang, B.; Song, X. Event-Triggered Adaptive Practical Fixed-Time Trajectory Tracking Control for Unmanned Surface Vehicle. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 436–440. [Google Scholar] [CrossRef]
- Mu, D.; Zhao, Y.; Wang, G.; Fan, Y.; Bai, Y. Course control of USV based on fuzzy adaptive guide control. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 6433–6437. [Google Scholar] [CrossRef]
- Wenting, S.; Shaocheng, T. Fuzzy optimal tracking control for nonlinear underactuated unmanned surface vehicles. Ocean. Eng. 2023, 287, 115700. [Google Scholar]
- Ahn, J.H.; Rhee, K.P.; You, Y.J. A study on the collision avoidance of a ship using neural networks and fuzzy logic. Appl. Ocean Res. 2012, 37, 162–173. [Google Scholar] [CrossRef]
- Wrat, G.; Bhola, M.; Ranjan, P.; Mishra, S.K.; Das, J. Energy saving and Fuzzy-PID position control of electro-hydraulic system by leakage compensation through proportional flow control valve. ISA Trans. 2020, 101, 269–280. [Google Scholar] [CrossRef]
- Fang, Y.; Pang, M.; Wang, B. A course control system of unmanned surface vehicle (USV) using back-propagation neural network (BPNN) and artificial bee colony (ABC) algorithm. Procedia Comput. Sci. 2017, 111, 361–366. [Google Scholar] [CrossRef]
- Wang, R.; Li, D.; Miao, K. Optimized radial basis function neural network based intelligent control algorithm of unmanned surface vehicles. J. Mar. Sci. Eng. 2020, 8, 210. [Google Scholar] [CrossRef]
- Jia, F.; Chen, M. Design of a nonlinear heading control system for ocean going ships based on backstepping technique. J. Coast. Res. 2019, 94, 515–519. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, H.; Cheng, Z. A Heading Control Strategy Based On Neural Network PID Controller. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 940–944. [Google Scholar]
- Mu, D.; Wang, G.; Fan, Y.; Liu, Y.; Jiao, X.; Wang, T.; Li, L. A Novel Heading Control Strategy for Unmanned Surface Vehicle. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2756–2760. [Google Scholar]
- Fang, X.; Zhou, J.; Wen, G. Location game of multiple unmanned surface vessels with quantized communications. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 1322–1326. [Google Scholar] [CrossRef]
- Peng, Z.; Gu, N.; Zhang, Y.; Liu, Y.; Wang, D.; Liu, L. Path-guided time-varying formation control with collision avoidance and connectivity preservation of under-actuated autonomous surface vehicles subject to unknown input gains. Ocean. Eng. 2019, 191, 106501. [Google Scholar] [CrossRef]
- Hao, L.Y.; Zhao, Z.H. Quantized Sliding Mode Fault-Tolerant Control for Unmanned Marine Vehicles with Thruster Saturation. J. Mar. Sci. Eng. 2023, 11, 309. [Google Scholar] [CrossRef]
- Ning, J.; Huang, Y.; Liu, Z.; Li, W.; Yue, X. Adaptive Distributed Heterogeneous Formation Control for UAV-USVs with Input Quantization. J. Mar. Sci. Eng. 2024, 12, 975. [Google Scholar] [CrossRef]
- Ren, W.; Xiong, J. Quantized feedback stabilization of nonlinear systems with external disturbance. IEEE Trans. Autom. Control 2018, 63, 3167–3172. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Wu, Z.; Liu, X.; Wu, J. Adaptive NN Control of Input-Delayed Stochastic Nonlinear Systems With States and Input Quantization. IEEE Access 2022, 10, 70342–70349. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, Y.; Chen, J.; Zheng, X. A quantized set-membership estimation-based heading control method of unmanned surface vessels under unknown-but-bounded wave-induced disturbances. Asian J. Control 2023, 25, 3105–3118. [Google Scholar] [CrossRef]
- Wang, J. Quantized feedback control of discrete-time MIMO linear systems with input and output quantization over finite data rate channels. IEEE Trans. Autom. Control 2022, 68, 6277–6284. [Google Scholar] [CrossRef]
- Peng, Z.; Jiang, Y.; Wang, J. Event-triggered dynamic surface control of an underactuated autonomous surface vehicle for target enclosing. IEEE Trans. Ind. Electron. 2020, 68, 3402–3412. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, W.; Wang, D.; Peng, Z. Event-triggered extended state observers design for dynamic positioning vessels subject to unknown sea loads. Ocean Eng. 2020, 209, 107242. [Google Scholar] [CrossRef]
- Ning, J.; Ma, Y.; Li, T.; Chen, C.P.; Tong, S. Event-triggered based trajectory tracking control of under-actuated unmanned surface vehicle with state and input quantization. IEEE Trans. Intell. Veh. 2023, 9, 3127–3139. [Google Scholar] [CrossRef]
- Zhou, Z.; Rother, C.; Chen, J. Event-triggered model predictive control for autonomous vehicle path tracking: Validation using CARLA simulator. IEEE Trans. Intell. Veh. 2023, 8, 3547–3555. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, H.; Xu, D.; Yu, H. Event-triggered model-free adaptive sliding-mode heading control for unmanned surface vehicles under DoS attacks. Appl. Ocean Res. 2024, 153, 104203. [Google Scholar] [CrossRef]
- Ning, J.; Wang, Y.; Liu, L.; Li, T. Disturbance observer based adaptive heading control for unmanned marine vehicles with event-triggered and input quantization. Int. J. Robust Nonlinear Control 2024, 34, 11469–11486. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, X. Event-triggered composite adaptive fuzzy output-feedback control for path following of autonomous surface vessels. IEEE Trans. Fuzzy Syst. 2020, 29, 2701–2713. [Google Scholar] [CrossRef]
- Li, A.; Shen, Z.; Bi, H.; Yu, H. Event-triggered error-constrained switching guidance-based marine surface vessel path-following control and collision avoidance. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2024, 238, 1050–1066. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Hu, H.; Wang, L.; Dong, J. Backstepping adaptive sliding mode control for the USV course tracking system. In Proceedings of the 2017 9th International Conference on Advanced Infocomm Technology (ICAIT), Chengdu, China, 22–24 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 265–269. [Google Scholar]
- Jiang, Q.; Liao, Y.; Li, Y.; Fan, J.; Miao, Y. Heading control of unmanned surface vehicle with variable output constraint model-free adaptive control algorithm. IEEE Access 2019, 7, 131008–131018. [Google Scholar] [CrossRef]
- Ge, Y.; Zhong, L.; Qiang, Z.J. Research on usv heading control method based on kalman filter sliding mode control. In Proceedings of the 2020 Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1547–1551. [Google Scholar]
- Hao, L.Y.; Yang, X.; Zhang, Y.Q.; Atajan, H.; Liu, Y. Fault-tolerant control of unmanned marine vehicles with unknown parametric dynamics via integral sliding mode output feedback control. Asian J. Control 2024, 27, 840–851. [Google Scholar] [CrossRef]
- Wang, C.; Xie, S.; Chen, H.; Peng, Y.; Zhang, D. Course Control of Unmanned Surface Vehicle Based on Fuzzy Sliding Mode. In Proceedings of the 2019 IEEE International Conference on Advanced Robotics and its Social Impacts (ARSO), Beijing, China, 31 October–2 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 287–290. [Google Scholar]
- Bai, Y.; Zhao, Y.; Fan, Y. The unmanned surface vehicle course tracking control with input saturation. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 40–43. [Google Scholar]
- Yoo, S.J.; Park, B.S. Guaranteed performance design for distributed bounded containment control of networked uncertain underactuated surface vessels. J. Frankl. Inst. 2017, 354, 1584–1602. [Google Scholar] [CrossRef]
- Fossen, T.I.; Paulsen, M. Adaptive feedback linearization applied to steering of ships. Model. Identif. Control 1993, 14, 229–237. [Google Scholar] [CrossRef]
- Kim, Y.H.; Ahn, S.C.; Kwon, W.H. Computational complexity of general fuzzy logic control and its simplification for a loop controller. Fuzzy Sets Syst. 2000, 111, 215–224. [Google Scholar] [CrossRef]
- Qin, H.; Li, C.; Sun, Y. Adaptive neural network-based fault-tolerant trajectory-tracking control of unmanned surface vessels with input saturation and error constraints. IET Intell. Transp. Syst. 2020, 14, 356–363. [Google Scholar] [CrossRef]
- Ma, Y.; Li, W.; Ning, J.; Liu, L. Disturbance observer based adaptive heading control for unmanned surface vehicle with event-triggered and signal quantization. Int. J. Adapt. Control Signal Process. 2024, 38, 3195–3212. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y. Dynamic memory event-triggered adaptive control for a class of strict-feedback nonlinear systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3470–3474. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Jiang, C.; Ning, J.; Hao, L.; Yin, Y. Fuzzy Course Tracking Control of Unmanned Surface Vehicle with Actuator Input Quantization and Event-Triggered Mechanism. Actuators 2025, 14, 130. https://doi.org/10.3390/act14030130
Wang Q, Jiang C, Ning J, Hao L, Yin Y. Fuzzy Course Tracking Control of Unmanned Surface Vehicle with Actuator Input Quantization and Event-Triggered Mechanism. Actuators. 2025; 14(3):130. https://doi.org/10.3390/act14030130
Chicago/Turabian StyleWang, Qifu, Chenchen Jiang, Jun Ning, Liying Hao, and Yong Yin. 2025. "Fuzzy Course Tracking Control of Unmanned Surface Vehicle with Actuator Input Quantization and Event-Triggered Mechanism" Actuators 14, no. 3: 130. https://doi.org/10.3390/act14030130
APA StyleWang, Q., Jiang, C., Ning, J., Hao, L., & Yin, Y. (2025). Fuzzy Course Tracking Control of Unmanned Surface Vehicle with Actuator Input Quantization and Event-Triggered Mechanism. Actuators, 14(3), 130. https://doi.org/10.3390/act14030130






