Inverse System Decoupling Control of Composite Cage Rotor Bearingless Induction Motor Based on Support Vector Machine Optimized by Improved Simulated Annealing-Genetic Algorithm
Abstract
1. Introduction
2. Suspension Mechanism, Topology, and Mathematical Model of CCR-BIM
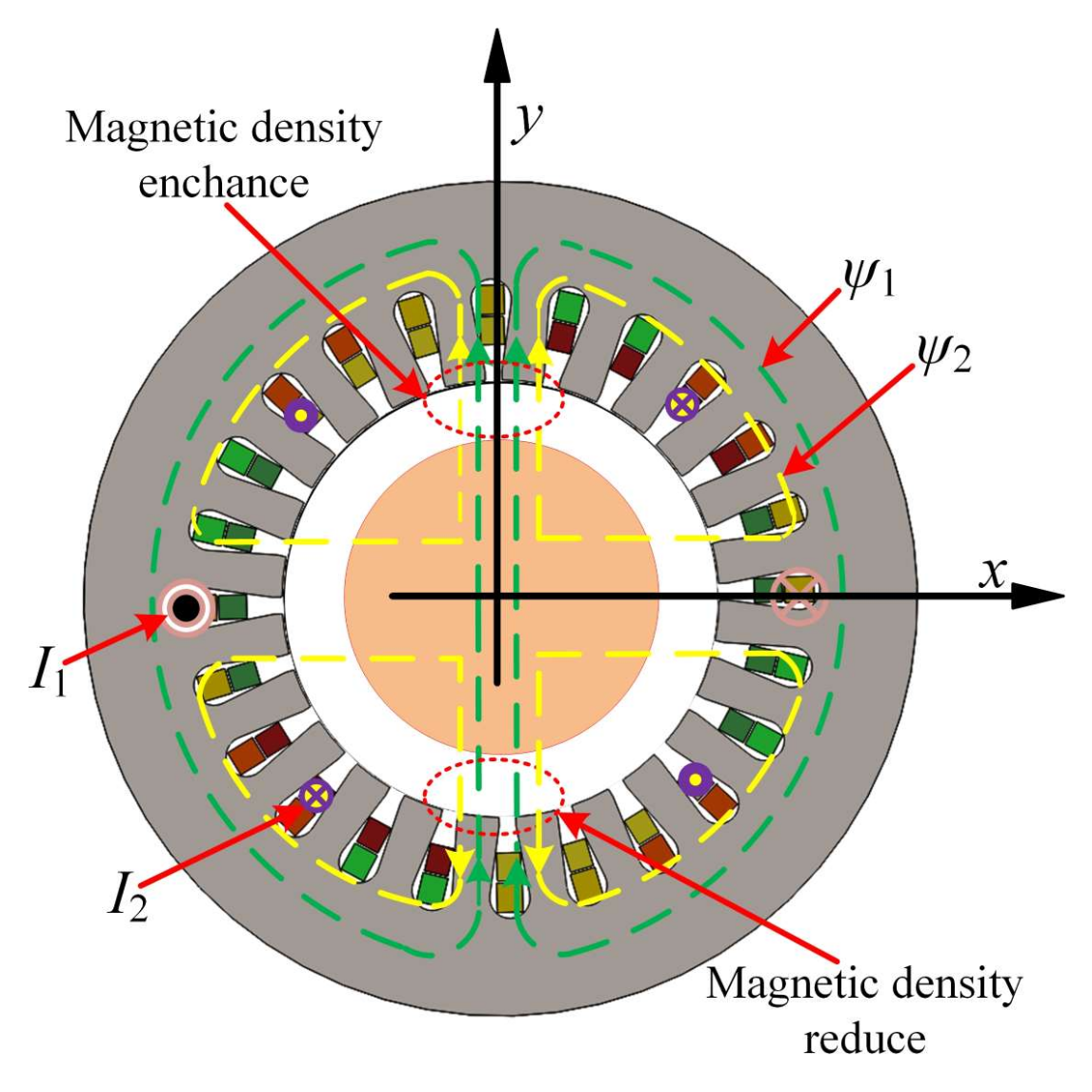
2.1. Suspension Mechanism of CCR-BIM
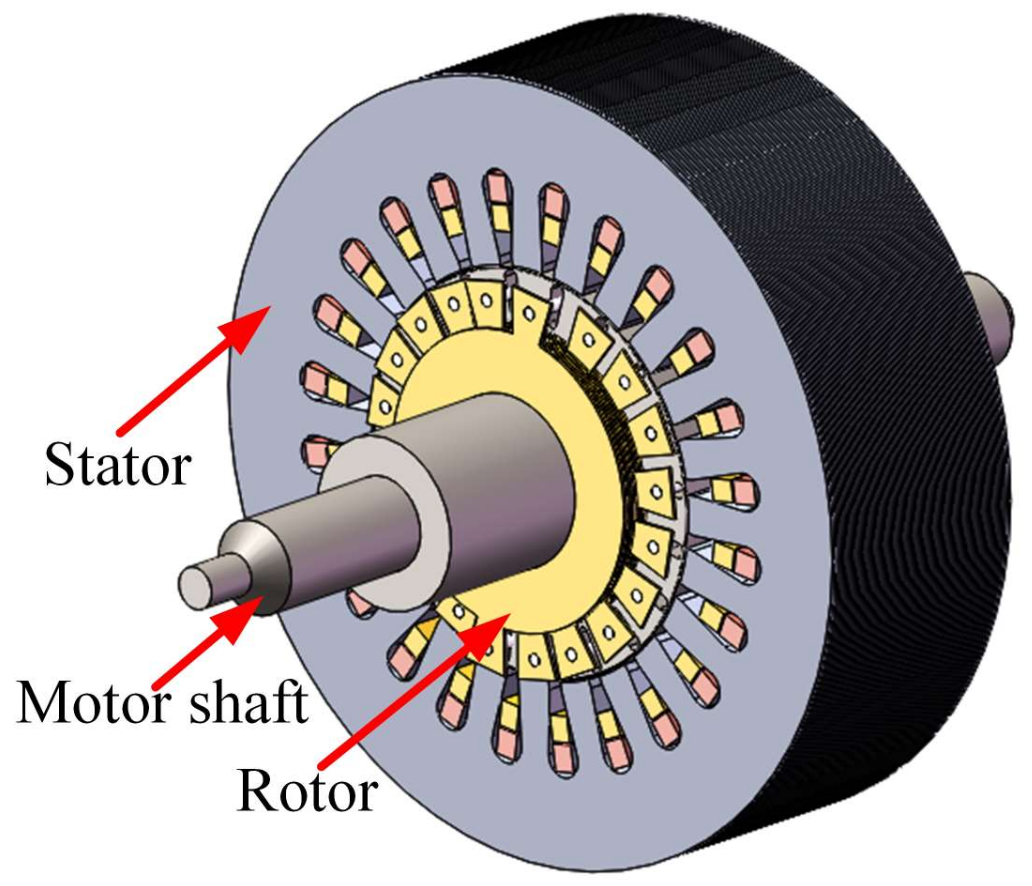
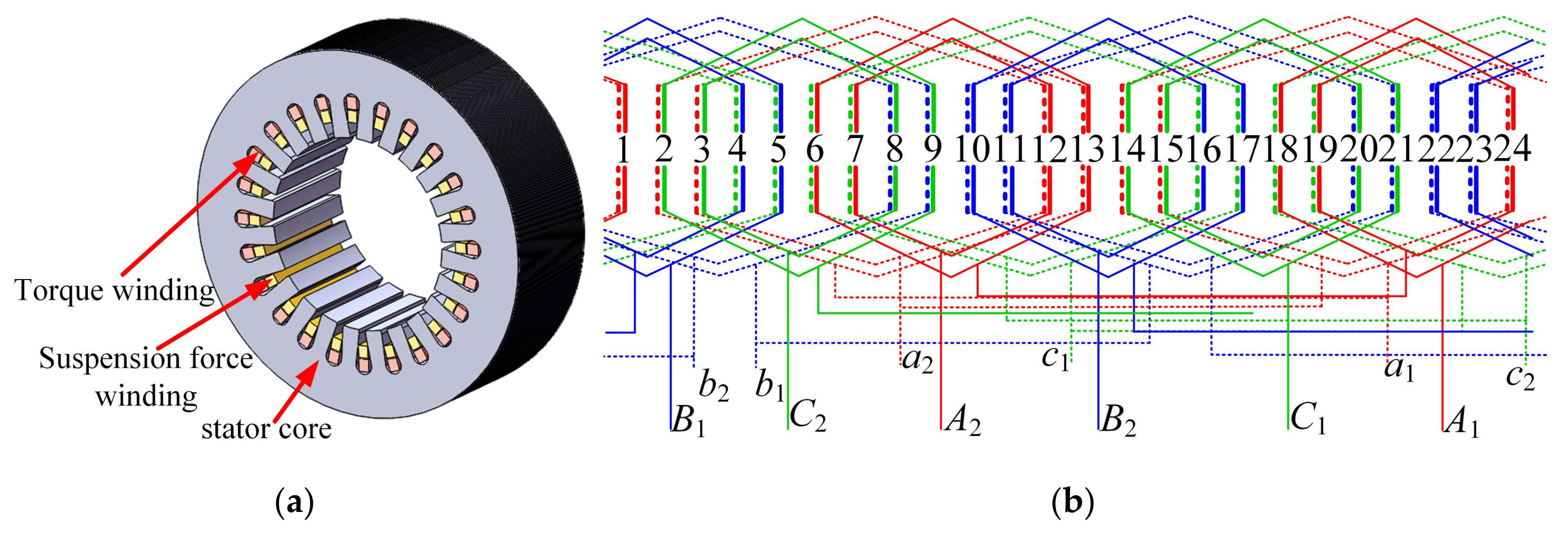
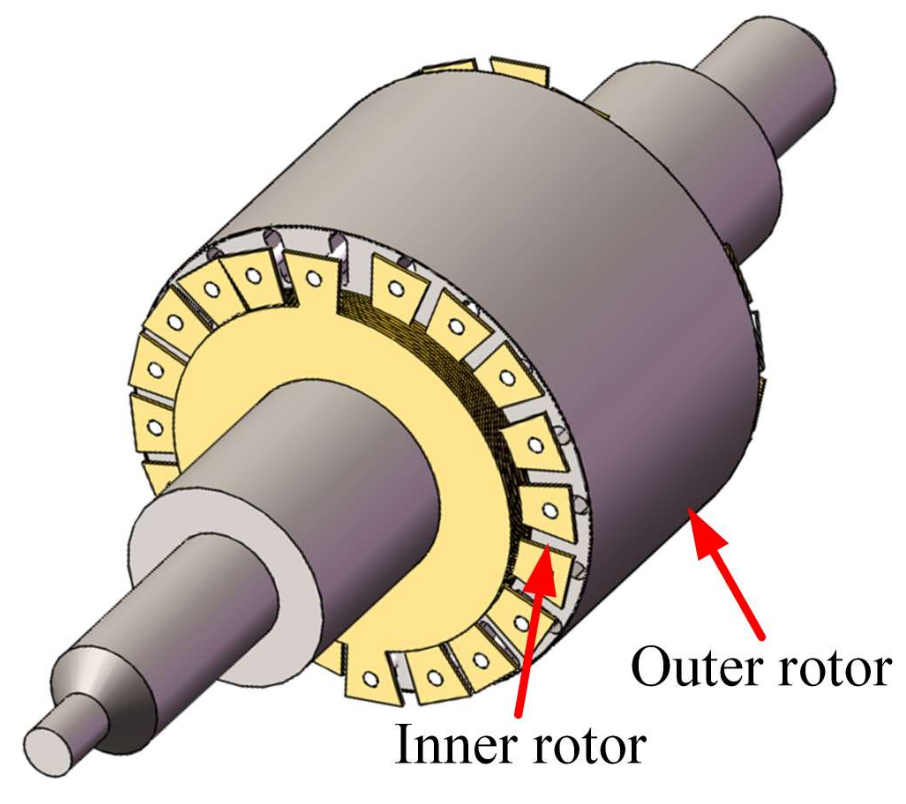
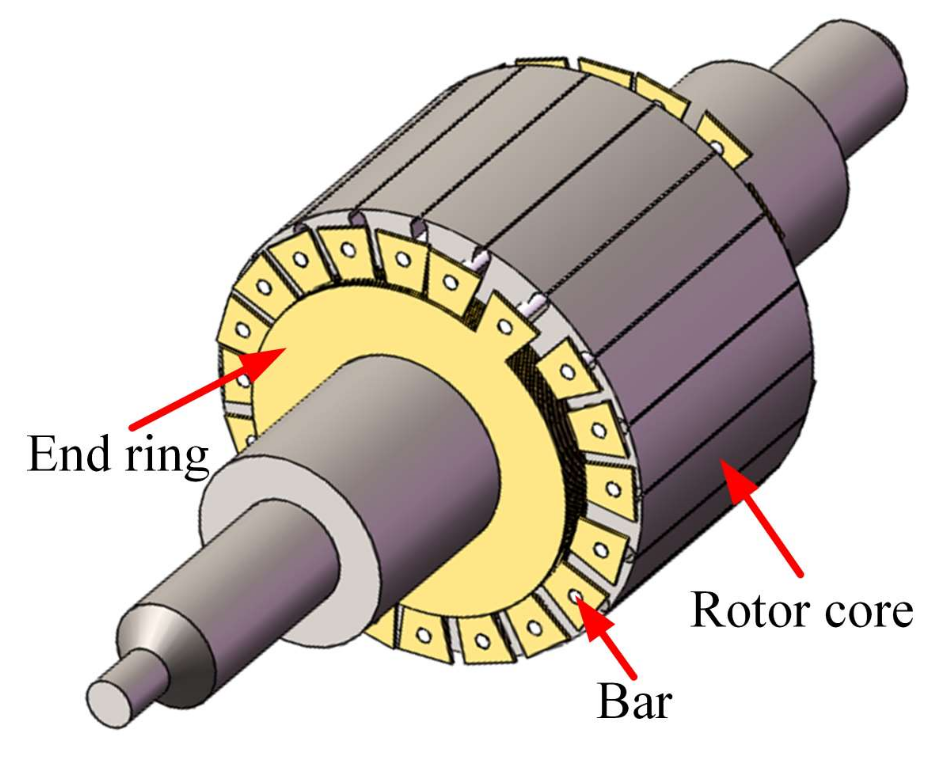
2.2. Topology of CCR-BIM
2.3. Mathematical Model of CCR-BIM
3. Establishment of SVM Inverse System Optimized by ISA-GA
3.1. Reversibility Analysis of CCR-BIM
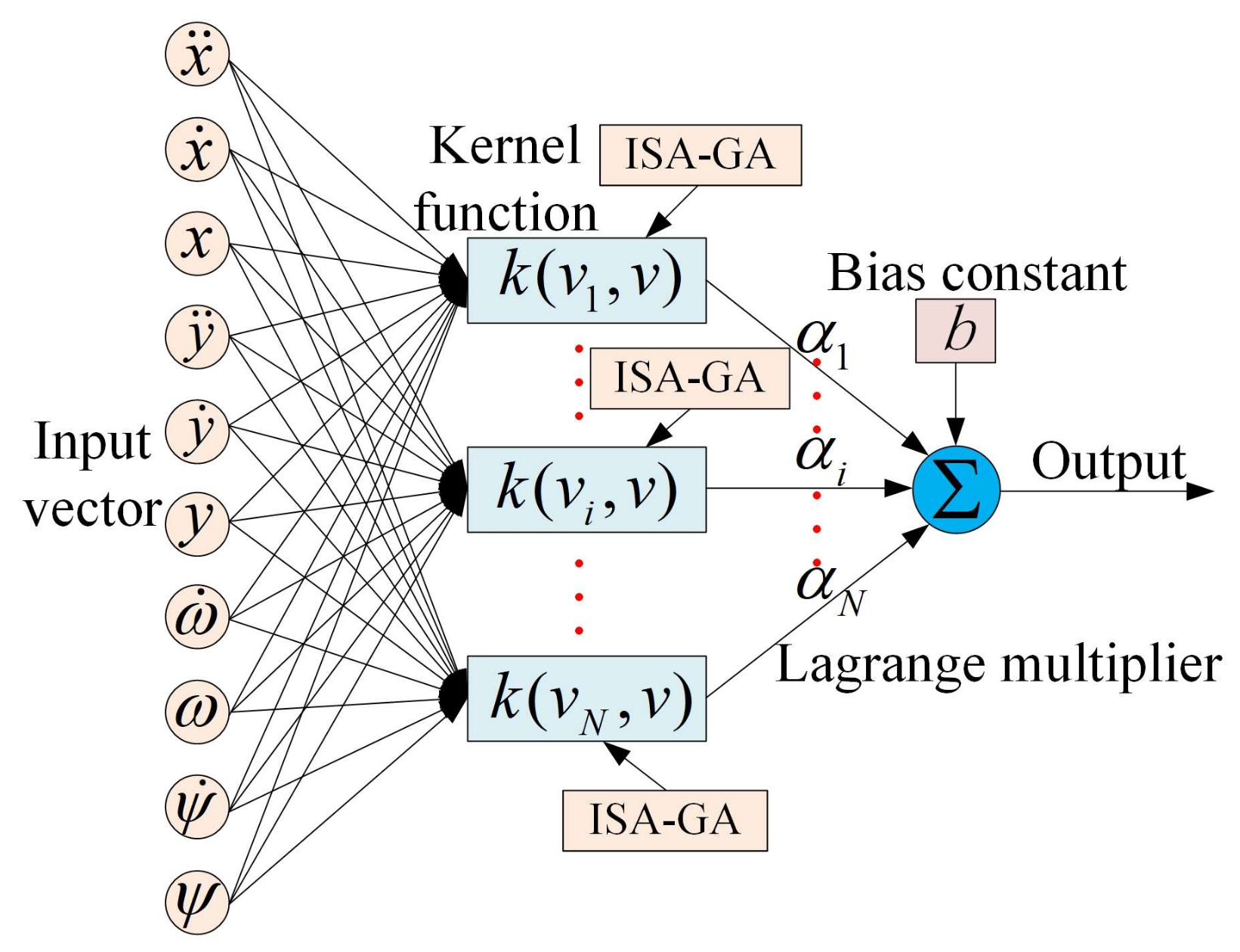
3.2. Establishment of SVM Model
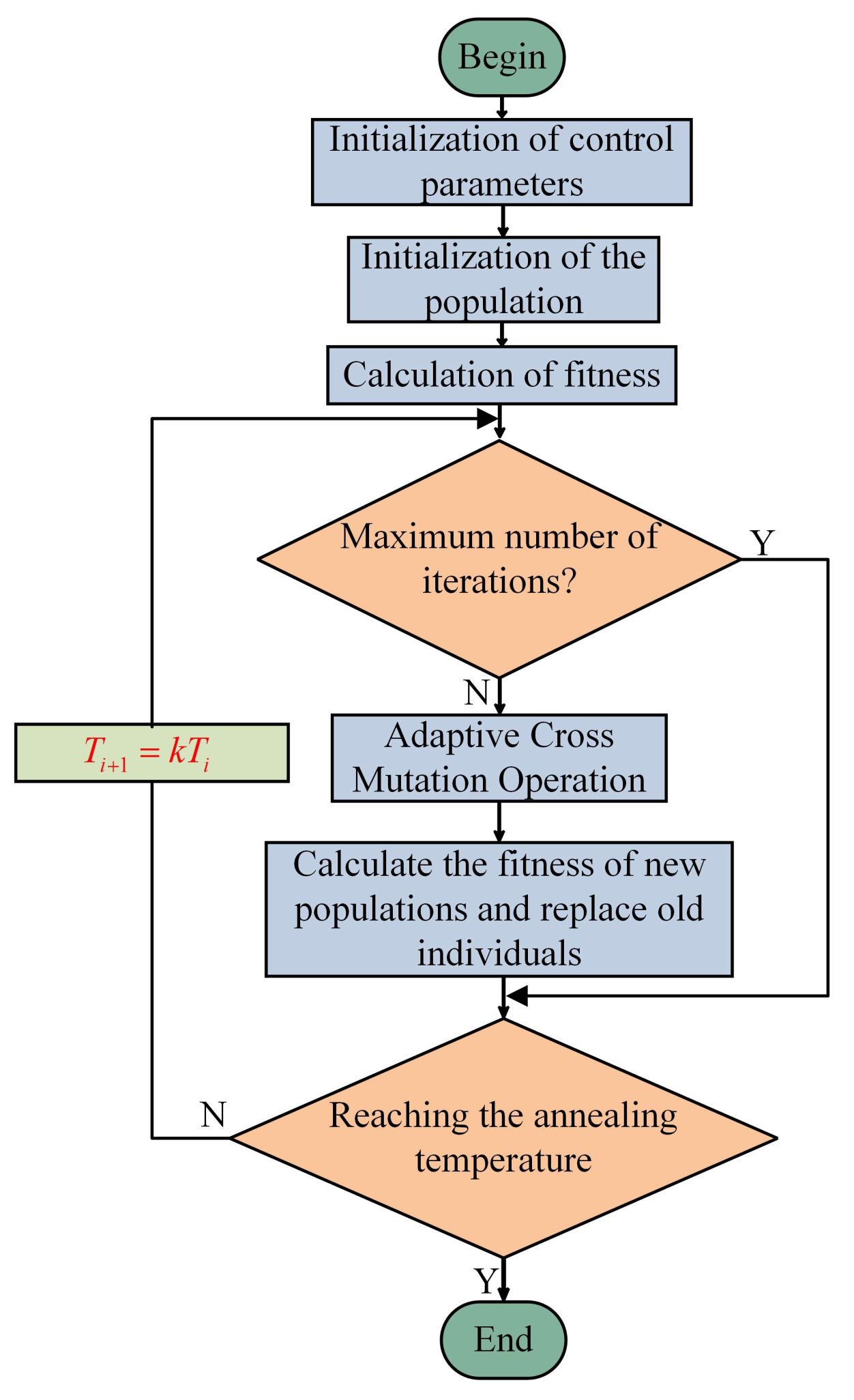
3.3. Optimal Design of Kernel Function Based on ISA-GA
- (1)
- Initialization of Population: Initialize the population by randomly generating individuals, each representing a potential solution.
- (2)
- Genetic Operations: Evolve the population using selection, adaptive crossover, and mutation operations to update the fitness of each individual.
- (3)
- Simulated Annealing Operations: Apply simulated annealing to each individual to conduct a local search for better solutions.
- (4)
- Stopping Condition Check: Check if the preset stopping conditions for iteration have been met.
- (5)
- Return Optimal Solution: Return the optimal individual as the final result.
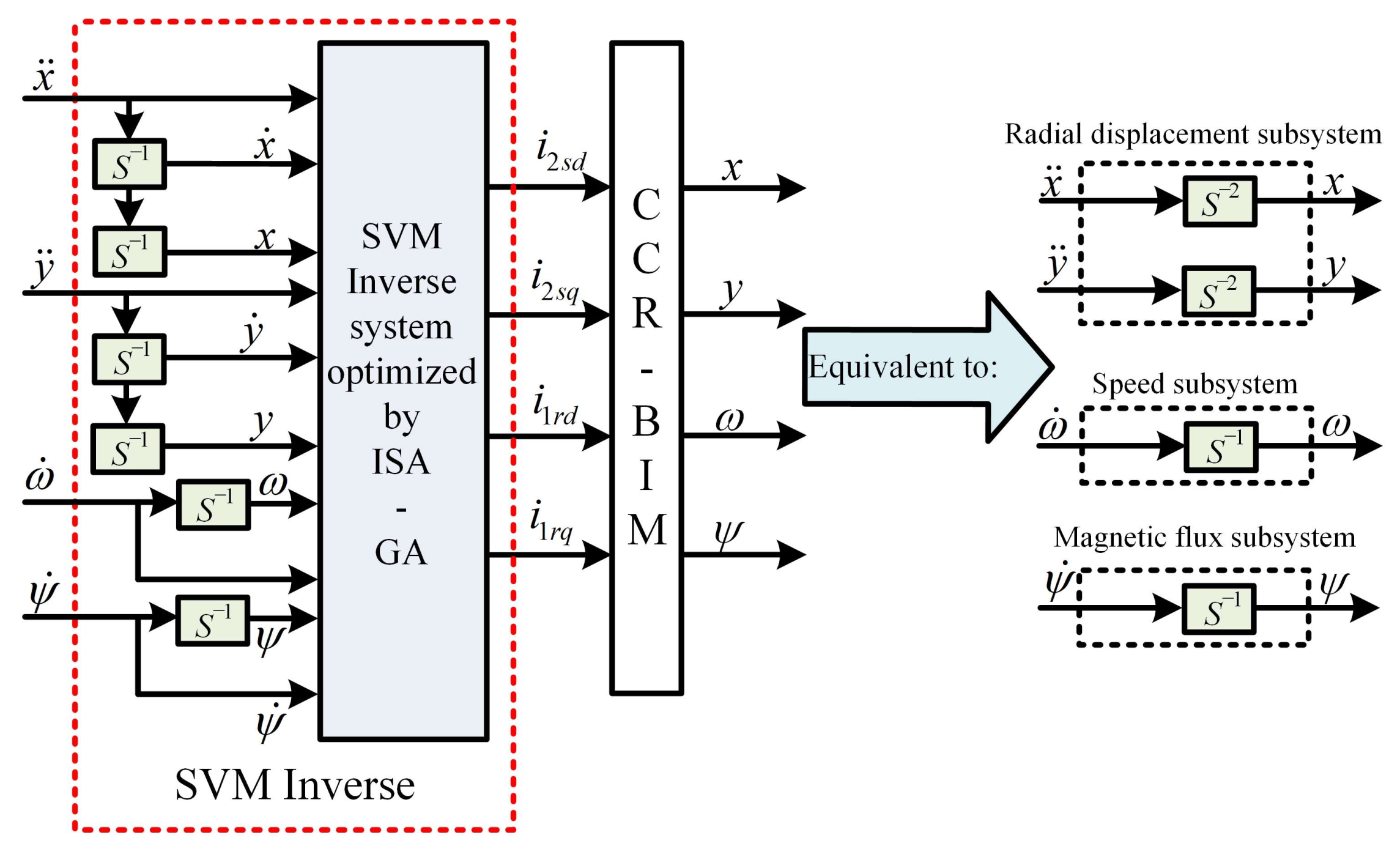
4. Decoupling Control System Based on SVM Inverse System Optimized by ISA-GA
4.1. Design of Control System
4.2. Structure of Control System
5. Analysis of Simulation and Experimental Results
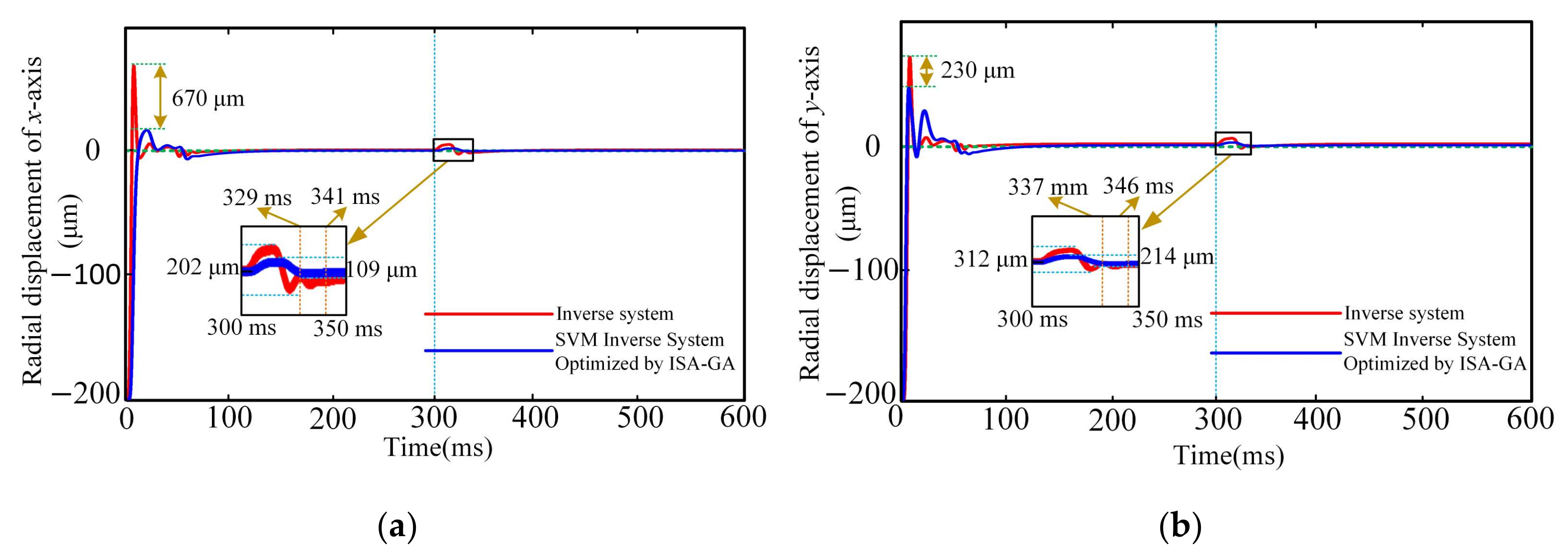
5.1. Analysis of Simulation Results
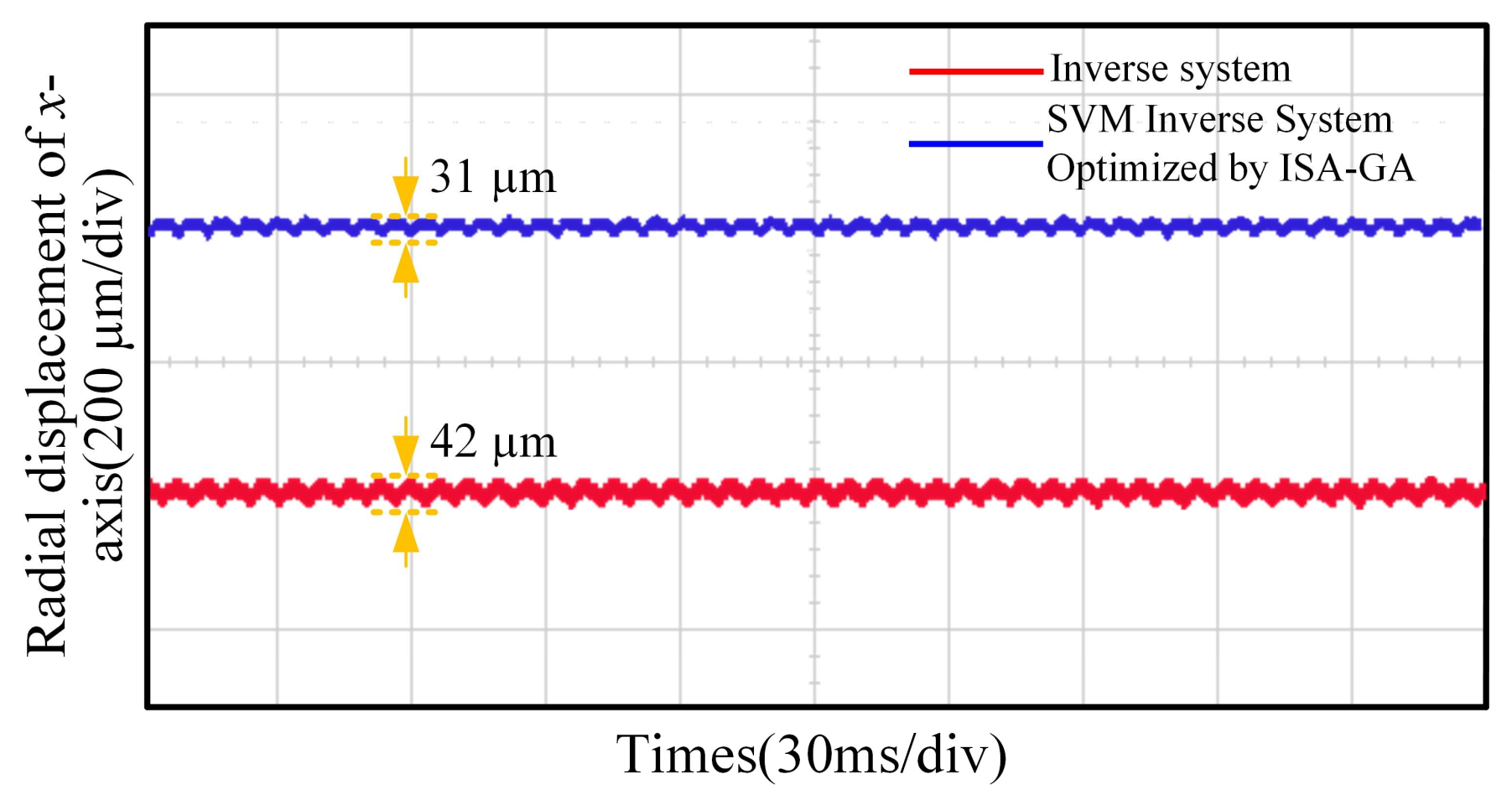
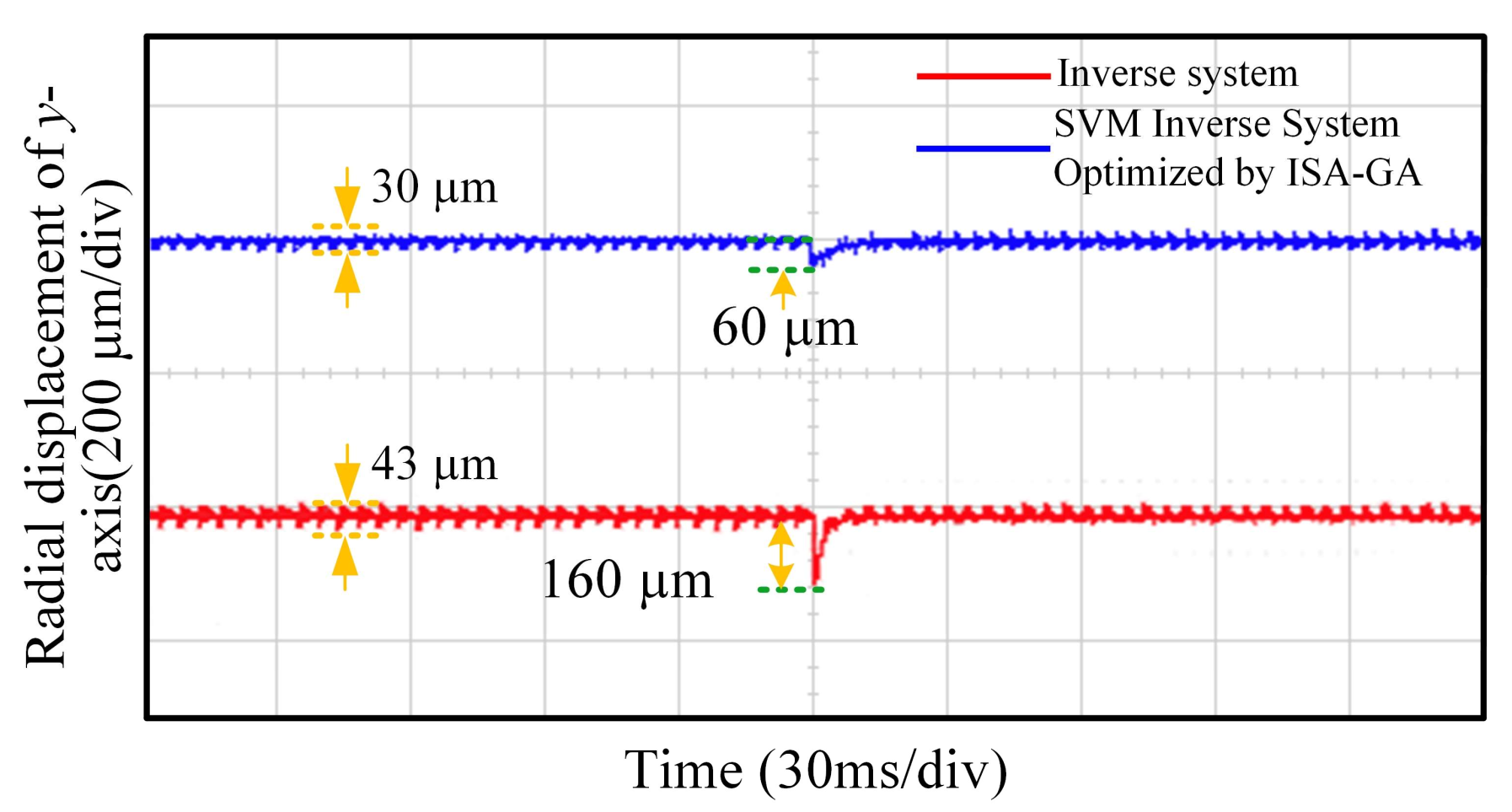
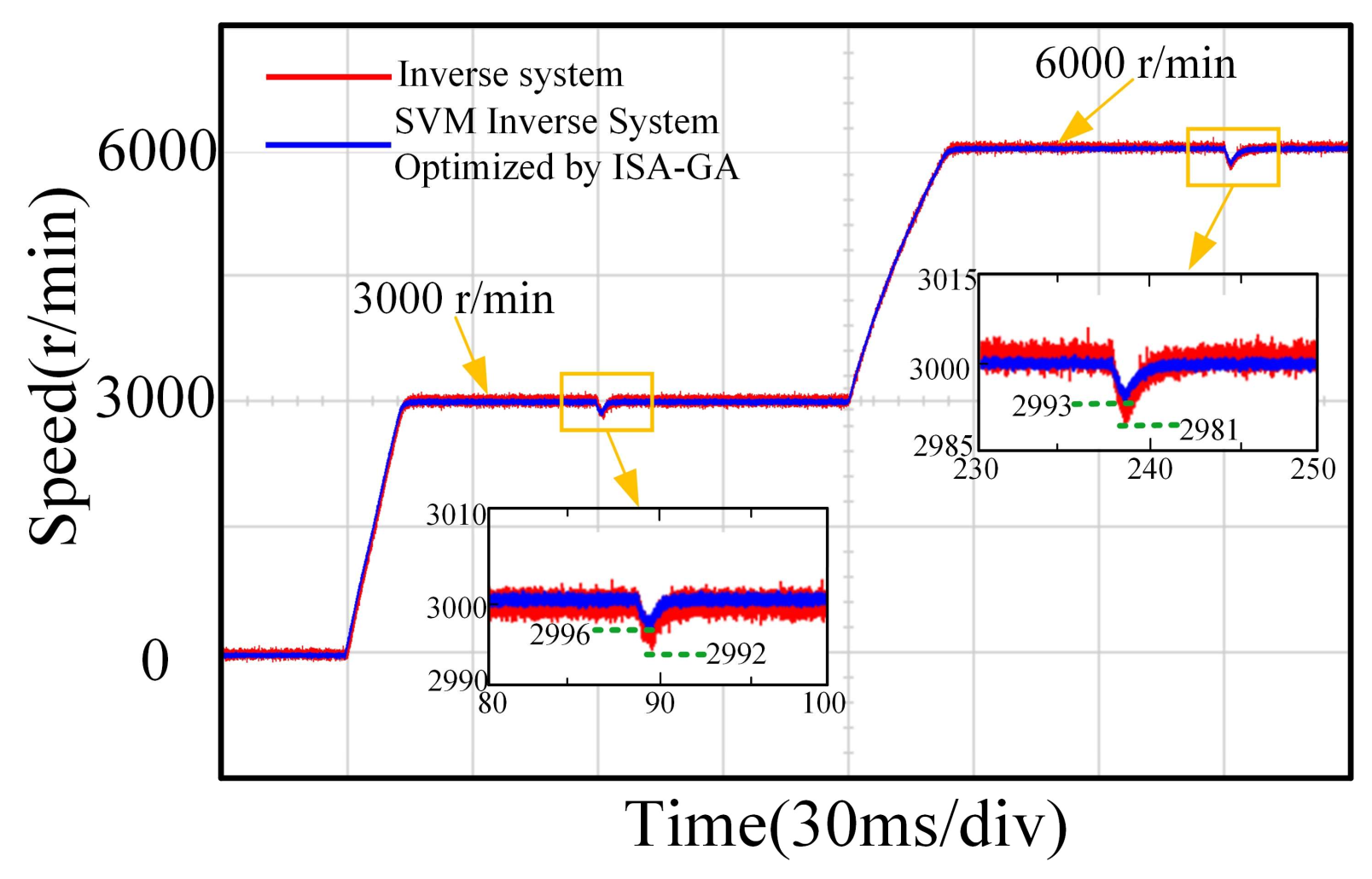
5.2. Analysis of Experimental Results
6. Conclusions
- (1)
- The ISA-GA introduces adaptive crossover and mutation operators, effectively mitigating premature convergence and improving global search efficiency. This enables precise optimization of SVM kernel parameters, resulting in a high-accuracy inverse system model.
- (2)
- By cascading the optimized SVM inverse model with the original system, the nonlinear CCR-BIM is transformed into a pseudo-linear system, achieving independent control of rotor displacement, speed, and flux linkage.
- (3)
- Simulation and experimental results demonstrated significant improvements over traditional inverse decoupling control. For instance, radial displacement deviations in the x- and y-axes were reduced by 35.5% and 43.3%, respectively, under dynamic conditions. Additionally, the speed fluctuation decreased by 50.0% and 63.2% at 3000 r/min and 6000 r/min, respectively. These metrics confirm the superior dynamic and static decoupling performance of the proposed strategy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCR-BIM | Composite Cage Rotor Bearingless Induction Motor |
| IM | Induction Motor |
| SVM | Support Vector Machine |
| ISA-GA | Improved Simulated Annealing-Genetic Algorithm |
| MMF | Magnetomotive force |
| (EMEs) | Induced Electromotive Forces |
| KKT | Karush–Kuhn–Tucker |
| SMO | Sequential Minimal Optimization |
| PWM | Pulse Width Modulation |
References
- Garcia-Calva, T.; Morinigo-Sotelo, D.; Fernandez-Cavero, V.; Romero-Troncoso, R. Early Detection of Faults in Induction Motors—A Review. Energies 2022, 15, 7855. [Google Scholar] [CrossRef]
- Yakhni, M.F.; Cauet, S.; Sakout, A.; Assoum, H.; Etien, E.; Rambault, L.; El-Gohary, M. Variable speed induction motors’ fault detection based on transient motor current signatures analysis: A review. Mech. Syst. Signal Process. 2023, 184, 109737. [Google Scholar] [CrossRef]
- Shiravani, F.; Alkorta, P.; Cortajarena, J.A.; Barambones, O. An enhanced sliding mode speed control for induction motor drives. Actuators 2022, 11, 18. [Google Scholar] [CrossRef]
- Gundewar, S.K.; Kane, P.V. Condition monitoring and fault diagnosis of induction motor. J. Vib. Eng. Technol. 2021, 9, 643–674. [Google Scholar] [CrossRef]
- Azab, M. A Review of Recent Trends in High-Efficiency Induction Motor Drives. Vehicles 2025, 7, 15. [Google Scholar] [CrossRef]
- Supreeth, D.K.; Bekinal, S.I.; Chandranna, S.R.; Doddamani, M. A review of superconducting magnetic bearings and their application. IEEE Trans. Appl. Supercond. 2022, 32, 3800215. [Google Scholar] [CrossRef]
- Lu, C.; Yang, Z.; Sun, X.; Ding, Q. Vibration compensation control strategy of composite cage rotor bearingless induction motor based on fuzzy coefficient adaptive-linear-neuron method. ISA Trans. 2024, 154, 455–464. [Google Scholar] [CrossRef]
- Lu, C.; Yang, Z.; Sun, X.; Ding, Q. Design and Multi-Objective Optimization of a Composite Cage Rotor Bearingless Induction Motor. Electronics 2023, 12, 775. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Tharwat, A. Parameter investigation of support vector machine classifier with kernel functions. Knowl. Inf. Syst. 2019, 61, 1269–1302. [Google Scholar] [CrossRef]
- Chen, P.H.; Fan, R.E.; Lin, C.J. A study on SMO-type decomposition methods for support vector machines. IEEE Trans. Neural Netw. 2024, 17, 893–908. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Sun, X.; Zhu, H. Decoupling control for bearingless synchronous reluctance motor based on support vector machine inverse. Int. J. Model. Identif. Control. 2015, 23, 24–32. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, Z.; Sun, Y. Decoupling control of single winding bearingless switched reluctance motors based on support vector machine inverse system. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 1829–1833. [Google Scholar]
- Xu, B.; Zhu, H.; Wang, X. Decoupling control of outer rotor coreless bearingless permanent magnet synchronous motor based on least squares support vector machine generalized inverse optimized by improved genetic algorithm. IEEE Trans. Ind. Electron. 2021, 69, 12182–12190. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Huang, X.L. Nonlinear decoupling control for bearingless induction motor based on support vector machines inversion. Trans. China Electrotech. Soc. 2015, 30, 164–170. [Google Scholar]
- Yang, Z.; Wang, D.; Sun, X.; Wu, J. Speed sensorless control of a bearingless induction motor with combined neural network and fractional sliding mode. Mechatronics 2022, 82, 102721. [Google Scholar] [CrossRef]
- Pei, T.; Li, D.; Liu, J.; Li, J.; Kong, W. Review of bearingless synchronous motors: Principle and topology. IEEE Trans. Transp. Electrif. 2022, 8, 3489–3502. [Google Scholar] [CrossRef]
- Hemenway, N.R.; Gjemdal, H.; Severson, E.L. New three-pole combined radial–axial magnetic bearing for industrial bearingless motor systems. IEEE Trans. Ind. Appl. 2021, 57, 6754–6764. [Google Scholar] [CrossRef]
- Sun, C.; Yang, Z.; Sun, X.; Ding, Q. An Improved Mathematical Model for Speed Sensorless Control of Fixed Pole Bearingless Induction Motor. IEEE Trans. Ind. Electron. 2023, 71, 1286–1295. [Google Scholar] [CrossRef]
- Ding, Q.; Yang, Z.; Sun, X.; Lu, C. Correction of the suspension force expression and the control compensation study in a bearingless induction motor. Electr. Eng. 2022, 104, 2457–2469. [Google Scholar] [CrossRef]
- Roy, A.; Chakraborty, S. Support vector machine in structural reliability analysis: A review. Reliab. Eng. Syst. Saf. 2023, 233, 109126. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, X.; Xing, S.; Sun, C.; Chen, X. Sparse representation theory for support vector machine kernel function selection and its application in high-speed bearing fault diagnosis. ISA Trans. 2021, 118, 207–218. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.; Bui, X.N.; Choi, Y.; Lee, C.W.; Armaghani, D.J. A novel combination of whale optimization algorithm and support vector machine with different kernel functions for prediction of blasting-induced fly-rock in quarry mines. Nat. Resour. Res. 2021, 30, 191–207. [Google Scholar] [CrossRef]
- He, F.; Ye, Q. A bearing fault diagnosis method based on wavelet packet transform and convolutional neural network optimized by simulated annealing algorithm. Sensors 2022, 22, 1410. [Google Scholar] [CrossRef]
- Okwu, M.O.; Tartibu, L.K. Metaheuristic Optimization: Nature-Inspired Algorithms Swarm and Computational Intelligence, Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2021; pp. 125–132. [Google Scholar]







| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated power (P1/P2) | 1.5/0.5 kW | Rated speed | 3000 r/min |
| Number of poles (P1/P2) | 1/2 | Wire diameter of windings | 2.5 mm |
| Number of turns (N1/N2) | 60/30 | Rotor outer diameter | 64.2 mm |
| Number of stator slots | 24 | Thickness of outer rotor | 1.8 mm |
| Number of rotor slots | 20 | Outer diameter of inner rotor | 60.6 mm |
| Voltage of torque winding | 310 V | Inner diameter of rotor | 20.5 mm |
| Current of suspension winding | 0.5 A | Inner diameter of stator | 64.6 mm |
| Rotor weight | 2.8 kg | Rotor length | 80 mm |
| Stator and rotor silicon steel | DW540_50 | Air gap length | 0.4 mm |
| Moment of inertia | 7.7 g·m2 | Outer diameter of stator | 122 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, C.; Cheng, J.; Ding, Q.; Zhang, G.; Fang, J.; Zhang, L.; Du, C.; Zhang, Y. Inverse System Decoupling Control of Composite Cage Rotor Bearingless Induction Motor Based on Support Vector Machine Optimized by Improved Simulated Annealing-Genetic Algorithm. Actuators 2025, 14, 125. https://doi.org/10.3390/act14030125
Lu C, Cheng J, Ding Q, Zhang G, Fang J, Zhang L, Du C, Zhang Y. Inverse System Decoupling Control of Composite Cage Rotor Bearingless Induction Motor Based on Support Vector Machine Optimized by Improved Simulated Annealing-Genetic Algorithm. Actuators. 2025; 14(3):125. https://doi.org/10.3390/act14030125
Chicago/Turabian StyleLu, Chengling, Junhui Cheng, Qifeng Ding, Gang Zhang, Jie Fang, Lei Zhang, Chengtao Du, and Yanxue Zhang. 2025. "Inverse System Decoupling Control of Composite Cage Rotor Bearingless Induction Motor Based on Support Vector Machine Optimized by Improved Simulated Annealing-Genetic Algorithm" Actuators 14, no. 3: 125. https://doi.org/10.3390/act14030125
APA StyleLu, C., Cheng, J., Ding, Q., Zhang, G., Fang, J., Zhang, L., Du, C., & Zhang, Y. (2025). Inverse System Decoupling Control of Composite Cage Rotor Bearingless Induction Motor Based on Support Vector Machine Optimized by Improved Simulated Annealing-Genetic Algorithm. Actuators, 14(3), 125. https://doi.org/10.3390/act14030125








