Abstract
The paper points out the growing interest in the use of composite materials for load-bearing parts, including hydraulic components. The non-negligible benefits of using composite materials in mechanical engineering are pointed out. However, applications of new materials sometimes give rise to new challenges. The strength parameters of a new structure, such as a composite cylinder for a hydraulic actuator, depend on its structure, including the number of layers and the fibre angle. This paper presents the application of a genetic algorithm to optimise the process of selecting the structure of a composite cylinder for a hydraulic actuator. The operation of the algorithm and the process of selecting global parameters (hyperparameters) are described. A block diagram of the algorithm for optimising the structure selection process is presented, and the designed structure is verified.
1. Introduction
A composite is a material obtained by combining two or more base materials with (usually) diametrically opposed properties. The resulting material has superior and/or novel properties compared to components used separately or resulting from their summation [1]. In most cases, one of the materials takes on the role of the matrix (continuous, bonding medium), while the rest become the filler (reinforcement). Among fibre composites (in which reinforcement is realised with fibres), two main types can be distinguished: chopped fibre (short)-reinforced and continuous fibre-reinforced [2]. The fibres (usually glass, carbon or aramid) have a high modulus of elasticity along their axis and high tensile strength. Properly stored and processed, they do not show a decrease in these properties during the technological process, and the differences in diameter and properties between individual fibres of the same type are negligibly small.
Many types of such fibres can be found on the market, which differ in their parameters and therefore also in their price. Figure 1 and Figure 2 show charts made available by leading carbon fibre manufacturers presenting their offerings. They show that fibres are divided into three main groups according to their Young’s modulus, with medium-modulus fibres achieving the highest strengths (even over 6000 MPa). The strength range of carbon fibres extends from about 2800 MPa to the more than 6000 MPa, as already mentioned, while the modulus range is from about 220 GPa to more than 500 GPa [3,4].
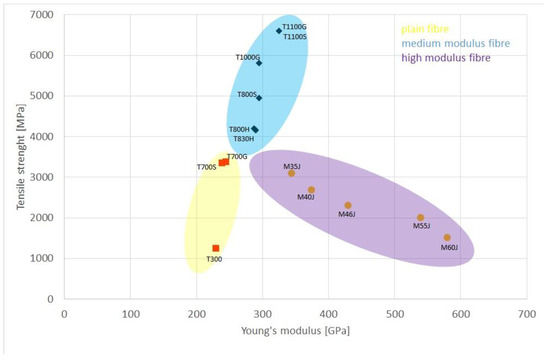
Figure 1.
Diagram showing Young’s moduli and strengths of different types of Torayca carbon fibres offered by TORAY (Tokyo, Japan) (authors’ elaboration based on [3]).
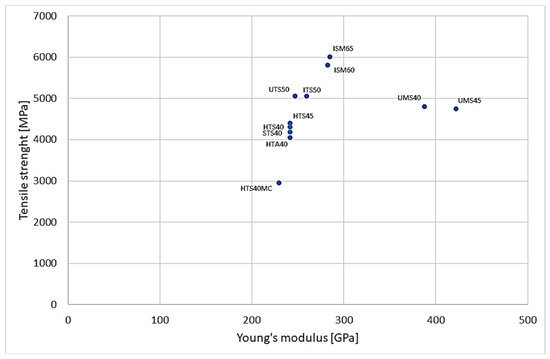
Figure 2.
Diagram showing Young’s moduli and strengths of different types of TENAX carbon fibre offered by Taijin (Tokyo, Japan) (authors’ elaboration based on [4]).
The second component of the composite material is the matrix, the purpose of which is to bind the reinforcement material together and allow load transfer between the fibres. It can also stop or slow the propagation of cracks initiated in the reinforcement and protect the fibres from adverse environmental conditions. The most commonly used matrix materials include polyester, vinylester, epoxy resins and thermoplastics (PE, PP, PA) [1,5,6].
Interest in the use of fibre-reinforced composite materials is growing every year. This is due to their high strength, low weight and corrosion resistance [1,6]. There are many ways to manufacture fibre-reinforced polymer composite materials, such as lamination (hand, spray, vacuum bag), infusion moulding, winding, weaving or pultrusion [1]. In the manufacture of high-pressure cylinders and tanks, the winding and weaving methods have mainly been used [7]. There are two main areas of application for composite materials in hydraulic components. The first is the production of accumulators [8,9], in which many analogies can be found with high-pressure, fourth-generation tanks. The second area, more widely described in the literature, is the manufacturing of cylinders or other parts of hydraulic actuators. Research [10,11] has presented a method for calculating the strength of a composite cylinder with a steel liner due to static strength and buckling. For this, the authors used the solution of the Lame problem modified for anisotropic materials. Design constraints were adopted to ensure that the strength of the cylinder as well as the circumferential deformation of the cylinder and the axial deformation of the liner were sufficiently low.
Since the cylinder under consideration would also transmit axial forces, the authors included layers in which fibres would be arranged along the axis of the element. Research [12] has conducted a static and modal finite element analysis of a composite cylinder. However, the authors do not consider issues specific to composite materials such as layering, the effect of manufacturing method on properties, or the existence of strength hypotheses different from those for conventional isotropic materials. Nowak and Schmidt [13,14,15] conducted an in-depth theoretical analysis of composite tubes with steel liners, deriving analytical formulas to calculate the stress distribution, taking into account internal pressure, axial force and temperature loads. They also conducted experimental verification using strain gauges and acoustic emission. They showed that as long as the liner operates in the elastic deformation range, the composite overwrap does not carry significant loads. However, once the liner is in the range of plastic deformation, the composite provides the necessary strength to the structure. Research [16] has also considered removing the steel liner from inside the cylinder and replacing it with a nanocomposite coating with properties that provide suitable tribological conditions at the cylinder–piston interface. The researchers presented methods for calculating stresses in the various layers of the composite, as well as a method for manufacturing nanocomposite coatings. However, the process of selecting and optimising the laminate structure was not presented in more detail. The fabricated cylinders were subjected to bench tests and the deformation as a function of internal pressure and the abrasive wear of the nanocomposite layer were determined. The authors confirmed the suitability of such a coating as a sliding material in a cylinder. Another paper [17] shows the design process of a telescopic actuator made of composite material. Material selection, basic strength calculations for isotropic material and partially also for anisotropic material, as well as finite element analysis are presented. Special emphasis was placed on preventing the buckling of the designed component. Once again, the Huber–Mises hypothesis, commonly used for metallic materials, was used to evaluate the strength of the composite material. The authors took into account the difficulties in connecting the actuator parts due to their being made of different materials, proposing a bonded connection as the best option. The authors do not mention the selected fibre angles in the paper.
In the literature, one can find papers addressing the issue of the design of hydraulic cylinders using composite materials, while signalling a number of design problems.
One of them is the change in the isotropic metallic material of the cylinder to an anisotropic material, which entails changing the methods of the strength calculations [11,13,14,15,16,18,19,20,21,22]. However, there are no attempts in the literature to optimise the structure of such a component, which can result in an unnecessary increase in weight and manufacturing costs.
Genetic algorithms have proven their usefulness in optimising elements made of composite materials. In 1995, Le Richie and Haftka [23] optimised a flat laminate for four different loading conditions with forces acting in the plane of the element. The researchers tested different types of penalty functions and obtained several variants of layer arrangement for each load case. Ref. [24] presented different methods of elitist selection and their influence on convergence and the results of laminate optimisation. They showed that retaining more than one best solution from the previous generation in subsequent generations allows for improving the algorithm’s performance, achieving convergence faster and avoiding local optima. Ref. [25] used a genetic algorithm to optimise composite patches applied to damaged steel structures. The patch application site and its shape, orientation and layer arrangement were subject to optimization. The patch orientation was expressed in a continuous manner, while the layers themselves had discrete angles. To reduce the computational cost, the memory functionality was implemented in the genetic algorithms [26,27]. Apart from the optimization of flat laminates, genetic algorithms were also used to design cylindrical elements and storage vessels. Richard and Perreux [28] presented an analysis of the testing process of composite pipes loaded with internal pressure, taking into account cracking phenomena and statistical uncertainties. Then, they optimised the elements by minimising the number of layers and searching for the optimal angle of fibre alignment. Ref. [29] optimised underwater cylindrical tanks subjected to external pressure. The optimal fibre arrangement was determined by a genetic algorithm coupled with analytical methods for calculating the strength and stability of the elements. The results were validated using FEM calculations and experimental tests. Ref. [30] presented an optimization method for the reinforcement of a type 3 composite high-pressure tank. The optimal solution allowed for semi-geodetic winding, and the progressive damage of the material was taken into account in the strength calculations. Ref. [31] proposed an adaptive algorithm that had the advantage of faster convergence and better optima finding. This was achieved by varying the mutation and crossover probabilities with the fitness function value.
Paper [32] provides a comprehensive review of optimisation methods for various composite structures, including beams and tubes. It can be seen that methods based on genetic algorithms and Particle Swarm Optimisation were the most commonly used algorithms. The combination of Particle Swarm Optimisation and Simple Cell Mapping methods allowed the authors of [33] to optimise the material distribution of functionally graded beams. The objective functions were to achieve a design with minimum total mass and maximum emitted power with upper and lower limits of the desired frequencies as constraints. Methods for optimising composite structures based on genetic algorithms in combination with numerical analysis can also be found in the literature. These studies have used composite failure criteria such as Tsai–Wu, Hashin, Maximum Stress and Puck failure criteria as material constraints and mass minimisation, deflection minimisation, buckling load maximisation, material minimisation and load-carrying capacity maximisation as objective functions [34].
2. Genetic Algorithms: Selection of Parameters
The selection of a composite cylinder structure requires an optimisation procedure. Genetic algorithms are a group of optimisation algorithms based on the Darwinian principle of “survival of the fittest” [35,36]. Their operation can be divided into several steps (Figure 3):
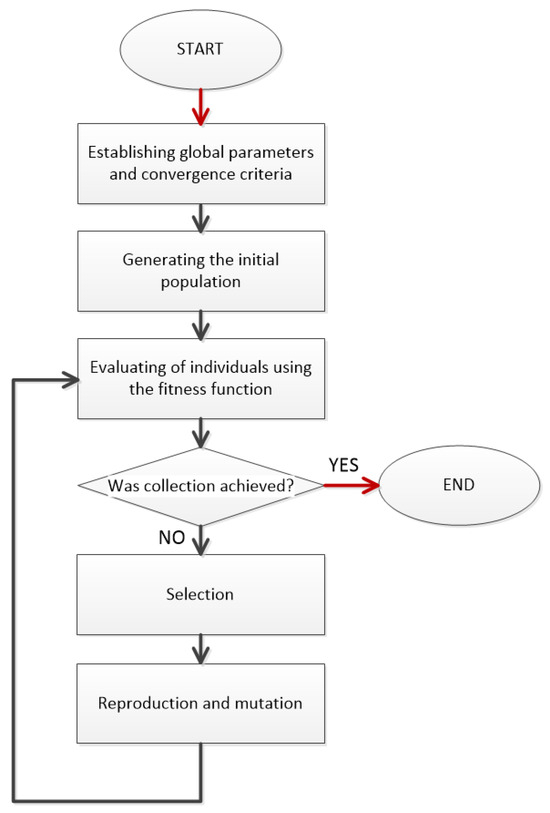
Figure 3.
Block diagram of genetic algorithm.
- The determination of the global parameters of the algorithm;
- The generation of a (mostly random) initial population;
- The evaluation of individuals for adaptation to a specific problem, according to the criteria adopted for the problem;
- The evaluation of the convergence of the algorithm;
- The selection of the best fitted individuals for further reproduction;
- Reproduction, consisting of (a) crossover and (b) mutations;
- Returning to step 3 and continuing the process until the desired convergence criteria are achieved.
In the case of laminate optimisation, a single individual reflects the arrangement of successive layers, which are treated as separate genes. Such genes, in the course of evolution, may undergo mutation, crossover and/or deletion. For the element manufactured using the filament winding method, one of the constraints is that the layers are grouped in twos [+α/−α], which forces an even number of layers. Thus, two corresponding layers [+α/−α] are treated by the algorithm as a single gene. An example of an individual with six genes is shown in Figure 4.

Figure 4.
An example of an individual representing the layering of a winding element.
The goal of the algorithm is to minimise the Ff (fitness function). After preliminary analyses of the algorithm, the fitness function for the issue under consideration was selected as follows:
where RT−H is the strength factor calculated according to the Tsai–Hill hypothesis and Nw is the number of layers.
To perform strength calculations, a numerical script based on the classical laminate theory running in Wolfram Mathematica 10.3 software was used. The calculations used an orthotropic material model described by the following relationship [37]:
where
- —Young’s modulus measured along the fibres;
- —Young’s modulus measured perpendicular to the fibres;
- —in-plane Poisson’s ratios;
- —normal stresses;
- —shear stress;
- —normal strains;
- —shear strain.
The strength coefficient was calculated based on the Tsai–Hill hypothesis [38]
where
where
- —the tensile strength in direction 1 (parallel to the fibre direction);
- —the compressive strength in direction 1 (parallel to the fibre direction);
- —the tensile strength in direction 2 (perpendicular to the fibre direction);
- —the compressive strength in direction 2 (perpendicular to the fibre direction);
- —the in-plane shear strength.
The fitness function being chosen in this way means that individuals with fewer layers will have a lower Ff value than those with a higher number of layers, and within a group with the same number of layers, those individuals with a lower value of RT−H will be “better”. To prevent an individual with fewer layers but with RT−H > 1 (suggesting failure) obtaining a lower value of the fitness function, a penalty function Fp was introduced [35,36]. Its application multiplies by 4 the Ff value of those individuals whose RT−H > 1.
The calculation of the fitness function was followed by a check to see if convergence of the algorithm had been achieved. In the presented algorithm, the invariability of the best solution with the smallest value of Ff for six consecutive generations was chosen as the convergence criterion. The invariant nature of the solution is a criterion commonly described in the literature [35,36,39,40]. If convergence was achieved, the operation of the algorithm was stopped, if not, a replication procedure followed.
Individuals in the population were sorted according to the increasing value of the fitness function and the part of the population that had the highest Ff values was removed and new individuals were created in its place by means of reproduction and mutation. The selection of parents was performed by the so-called roulette method. It involves constructing a virtual roulette wheel on which all other individuals are placed. What part of the circle a variant occupies is inversely proportional to the value of its fitness function (the lower the value, the higher the probability of becoming a “parent”). Once the two “parents” were drawn, the replication procedure involving gene crossover began. If the numbers of layers of the two “parents” was not equal, the offspring always inherited the smaller number of layers, and the angles of fibre alignment were inherited alternately from both “parents”. A randomly selected (with a certain predetermined probability) portion of the offspring was then subjected to mutation, which could act in two ways: to remove two layers at a time from the laminate, or to change the angle of fibre alignment (at once in two corresponding layers). After the whole procedure, the evaluation of individuals was carried out again. In this paper, an algorithm was developed to optimise the structure (number and angle of layers) of a composite cylinder, in which the strength evaluation was based on the classical theory of laminates. Fitness Ff and penalty Fp functions were selected, and convergence criteria as well as selection, reproduction and mutation methods were established.
The global parameters of the developed genetic algorithm, such as the number of individuals in the population, the probability and size of mutations or the number of surviving individuals in each generation, can also be subject to optimisation. This is performed to allow the algorithm to converge at the lowest computational cost and to improve the algorithm’s ability to find global optima [36].
The computational cost C is expressed as [24]
where Np is the number of generations and P is the population size.
To select the best parameters for the algorithm, simulations were performed for the following values:
- Mutation probability, pmut ∈ {0.5; 0.2; 0.1};
- The portion of the population that passes to the next generation, Nn ∈ {0.5; 0.1; 0.05};
- Population size, P ∈ {20, 100, 1000};
- Maximum layer mutation angle, αmax ∈ {5°; 15°; 30°}.
These values were chosen based on the literature analysis performed, as well as preliminary attempts by the authors to achieve convergence of the algorithm. This gave a total of 81 combinations of variables. For each combination, 50 simulations were performed to eliminate the influence of outlier results.
Figure 5 shows the simulation-derived average numbers of generations to convergence for each maximum mutation angle. Each graph shows results for three population sizes P, different percentages of best solutions passing to the next generation Nn and different values of mutation probability pmut. However, not all simulations achieved satisfactory convergence. Some stopped at local optima, which was characterised by significantly higher values of the fitness function compared to other simulations. These cases are eliminated in the charts below.
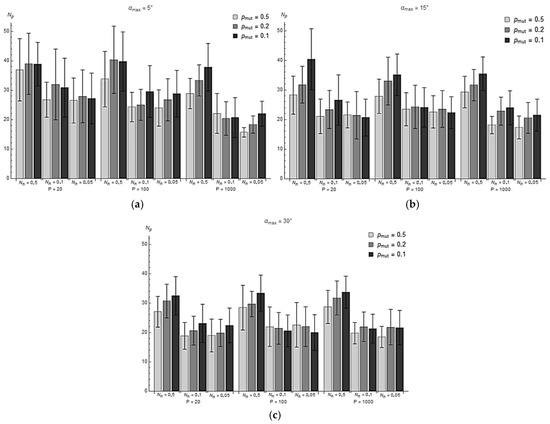
Figure 5.
Number of generations to convergence for (a) αmax = 5°; (b) αmax = 15°; (c) αmax = 30°.
It can be noted that an increase in population size in almost every case translated into a decrease in the average number of generations in the simulation. This was due to the larger gene pool undergoing optimisation in each successive generation. Reducing Nn also had a positive effect on the speed of reaching convergence in most cases. The smaller the number of “old” individuals in a generation, the greater the proportion of the population that could be filled with new, potentially better solutions.
Comparing the graphs among themselves, it can be observed that increasing the probability of mutation also leads to earlier convergence of the algorithm. A higher probability of mutation means a greater diversity of individuals in the next generation, thus increasing the chances of finding a better solution. Increasing pmut can also lead to easier lowering of local optima and finding global optima.
Moreover, as the number increases, so does the computational cost and thus the time and resource consumption. Figure 6 shows the average computational cost of achieving convergence for different algorithm parameters. It can be seen that an increase in population size spikes the cost.
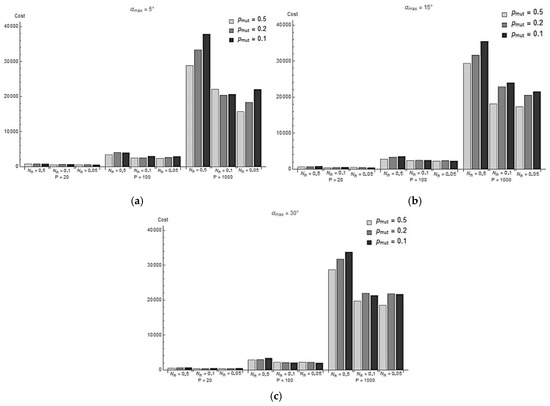
Figure 6.
Average design cost for different values of P, Nn and pmut at (a) αmax = 5°; (b) αmax = 15°; (c) αmax = 30°.
Figure 7, Figure 8 and Figure 9 show the values of the lowest Ff achieved for each run. The red line shows the Ff value corresponding to the global minimum (Ff = 8.62) The following graphs show that increasing the population size avoids the algorithm becoming stuck in the local minimum. This is because a wider initial gene pool increases the probability of finding a solution close enough to the global minimum, and in later generations, the probability of a mutation allowing the global minimum to be approached is increased. For the same reason, increasing the probability of mutation also leads to the algorithm finding global optima more easily.
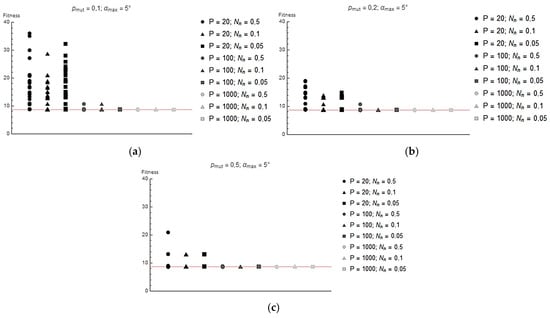
Figure 7.
Value of fitness function reached at end of each iteration for (a) pmut = 0.1 and αmax = 5°; (b) pmut = 0.2 and αmax = 5°; (c) pmut = 0.5 and αmax = 5°.
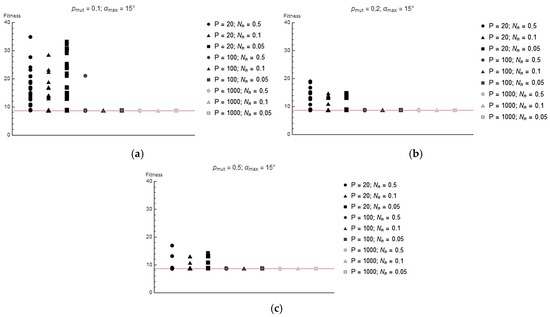
Figure 8.
Value of fitness function reached at end of each iteration for (a) pmut = 0.1 and αmax = 15°; (b) pmut = 0.2 and αmax = 15°; (c) pmut = 0.5 and αmax = 15°.
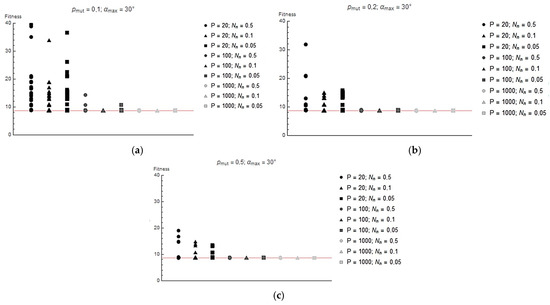
Figure 9.
Value of fitness function reached at end of each iteration for (a) pmut = 0.1 and αmax = 30°; (b) pmut = 0.2 and αmax = 30°; (c) pmut = 0.5 and αmax = 30°.
After analysing the presented simulation results, the following algorithm parameters were selected:
- The probability of mutation, pmut = 0.5;
- The portion of the population that passes to the next generation, Nn = 0.1;
- Population size, P = 100;
- The maximum mutation angle of the layer, αmax = 15°.
At these parameter values, the genetic algorithm showed 100 percent convergence, with acceptable values for the computational cost.
3. Determination of the Structure of Composite Cylinders
The number of layers and fibre angles in each layer were determined using the genetic algorithm described earlier. The calculations used the orthotropic material model presented earlier, whose properties were determined experimentally and are summarised in Table 1.

Table 1.
Material properties of the epoxy–carbon composite used.
Two solutions proposed by the algorithm that are among the top five presented in Table 2 and are structurally significantly different from each other were selected for implementation. Both had eight layers. In the first solution, the fibre arrangement was [90/90/±20]2 while in the second it was [±83/±84/±85/±83].

Table 2.
The top five solutions found by the genetic algorithm.
Using specialised equipment (winder MAW 20 LS4/1 manufactured by Mikrosam (Prilep, Macedonia) with software on-board), the designed composite cylinders 1 and 5 in Table 2 were made.
Table 3 shows the weights of the various cylinders and compares them with a reference steel cylinder with a wall thickness of 5 mm, made from commercially available pipe intended for a hydraulic actuator. As can be seen, the weight reduction with composite reinforcement is very large, ranging from 67.6% for a [±83/±84/±85/±83] cylinder with a steel liner to as much as 94.4% for a [90/90/±20/]2 cylinder.

Table 3.
Comparison of masses of made cylinders.
4. Bench Testing of a Composite Cylinder for a Hydraulic Cylinder
To verify the validity of the composite cylinder design method using a genetic algorithm, a hydraulic test rig was designed and built. Figure 10 shows a hydraulic diagram of the actuator test stand. The stand allows the cyclic extension and retraction of the tested actuator at preset speeds and under a preset load. The change in the direction of movement of the actuator is forced by overdriving the directional control valve (4), while the speed of movement can be set independently for both directions using flow regulators (5) and (6). The load is realised by a loading actuator (15) connected to a maximum valve (18), which allows the loading pressure to be maintained regardless of the flow rate (speed of actuator movement). The system allows the recording of the values of pressures in the chambers of the test actuator, flow rates, piston rod position and loading force.
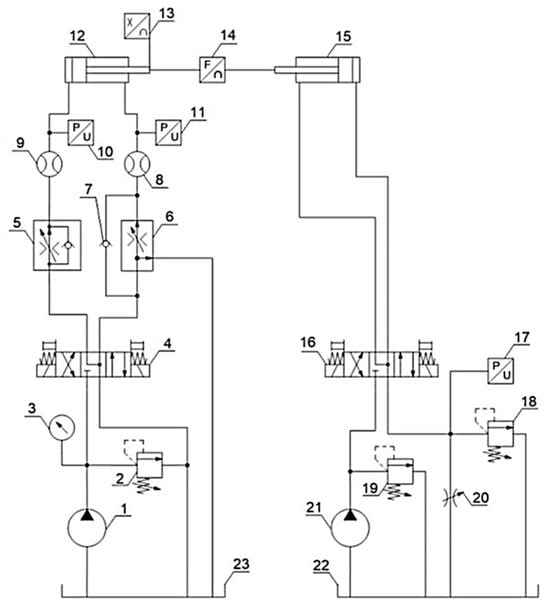
Figure 10.
Hydraulic diagram of actuator test stand: 1—pump; 2—safety valve; 3—pressure gauge; 4—4/3 directional control valve; 5—2-way flow regulator; 6—3-way flow regulator; 7—check valve; 8 and 9—flow meters; 10 and 11—pressure sensors; 12—tested actuator; 13—position sensor; 14—force sensor; 15—load actuator; 16—4/3 directional control valve; 17—pressure sensor; 18—relief valve; 19—safety valve; 20—adjustable throttle valve; 21—pump; 22 and 23—tanks.
4.1. Strain Measurements of the [±83/±84/±85/±83] Composite Cylinder Without a Liner
Figure 11 shows an actuator with a [±83/±84/±85/±83] composite cylinder mounted on a test stand. Strain gauges were placed in the middle of the cylinder’s length, allowing the measurement of the cylinder’s circumferential and axial deformations.

Figure 11.
Actuator with [±83/±84/±85/±83] composite cylinder mounted on test stand.
Figure 12 shows a graph of the cylinder’s deformation when it was loaded with internal pressure up to 200 bar. Deformations recorded experimentally, as well as values obtained computationally using classical laminate theory, are presented. The calculations were carried out in the Wolfram Mathematica package. Figure 13 and Figure 14 show the stresses in the cylinder layers and the values of the strength factor R, respectively. The strength factor R is defined as
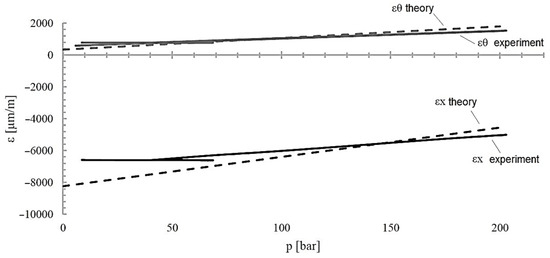
Figure 12.
Deformation of composite [±83/±84/±85/±83] cylinder during internal pressure loading.
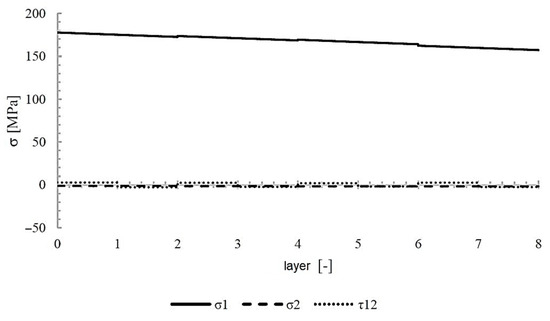
Figure 13.
Stress in individual cylinder layers of [±83/±84/±85/±83] cylinder in layer coordinate systems under internal pressure loading.
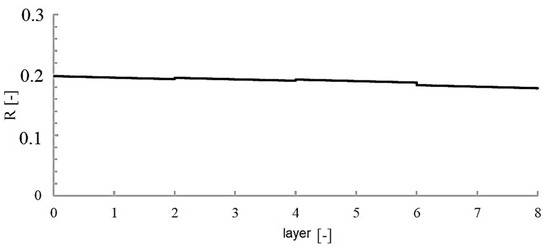
Figure 14.
Value of strength factor R in individual layers under internal pressure loading.
The strength factor defined in this way can be applied to any strain hypothesis. If R > 1 then the layer remains undamaged, and the load can be increased by a factor of R. If, on the other hand, R < 1 then the layer will be damaged, in which case the load must be reduced by a factor of R. In the case of the method of loading adopted during the tests, the maximum value of the R factor was about 0.2, which may indicate some oversizing of the structure and the existence of further room for optimisation.
Table 4 summarises the results of the strain measurements and compares them with theoretical values. There are some discrepancies between theoretical and actual values, with differences usually being greater the smaller the absolute value of the measured quantity is. The calculations carried out show agreement with experimental results as to the value and nature of changes in the determined parameters.

Table 4.
Comparison of [±83/±84/±85/±83] composite cylinder deformations measured experimentally and determined theoretically using classical laminate theory.
4.2. Deformation Measurements of [90/90/±20/]2 Composite Cylinder Without Liner
Figure 15 shows the deformation of the cylinder when loaded with internal pressure up to 200 bar. The deformations measured experimentally and those determined computationally were compared. Figure 16 and Figure 17 show, respectively, the values of stress in the composite layers and the value of the strength coefficient R. As can be seen, the value of the R coefficient during a pressure load of 200 bar reaches a value of almost 0.8 in the layers ±20°, which may indicate that the strength of the component is well utilised.
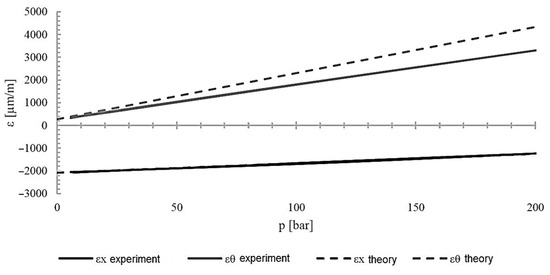
Figure 15.
Deformation of composite [90/90/±20/]2 cylinder during pressure loading.
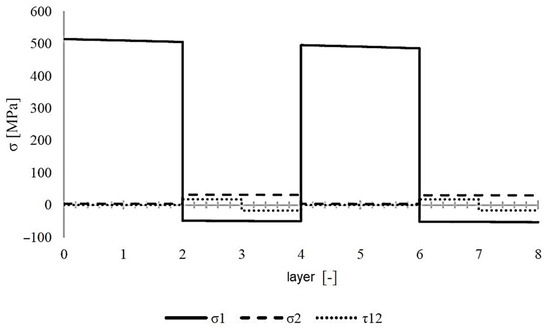
Figure 16.
Stress in individual layers of [90/90/±20/]2 cylinder in layer coordinate systems under internal pressure loading.
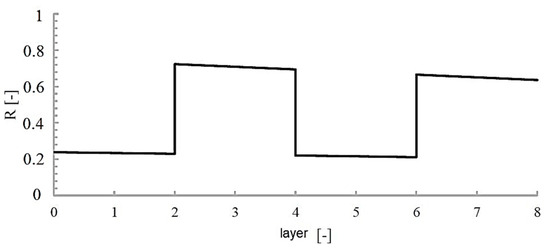
Figure 17.
Value of strength factor R in individual layers under internal pressure loading.
The results of the measurements and calculations are summarised in Table 5. As can be seen, the agreement between the experimental and theoretical results for three of the four cases is very good. A large difference (31.2%) occurred only for circumferential deformation when the cylinder’s internal pressure was loaded to a value of 200 bar. The reason for this may be the low stiffness of the bonded connection between the sensor and the cylinder surface, as the experimental values were smaller than the theoretical ones.

Table 5.
Comparison of deformations of composite [90/90/±20/]2 cylinder measured experimentally and determined theoretically using classical laminate theory.
5. Discussion
Using the experience gained in the course of the work, a method for designing a composite cylinder for a hydraulic actuator was proposed. The method consists of seven steps and is shown schematically in Figure 18.
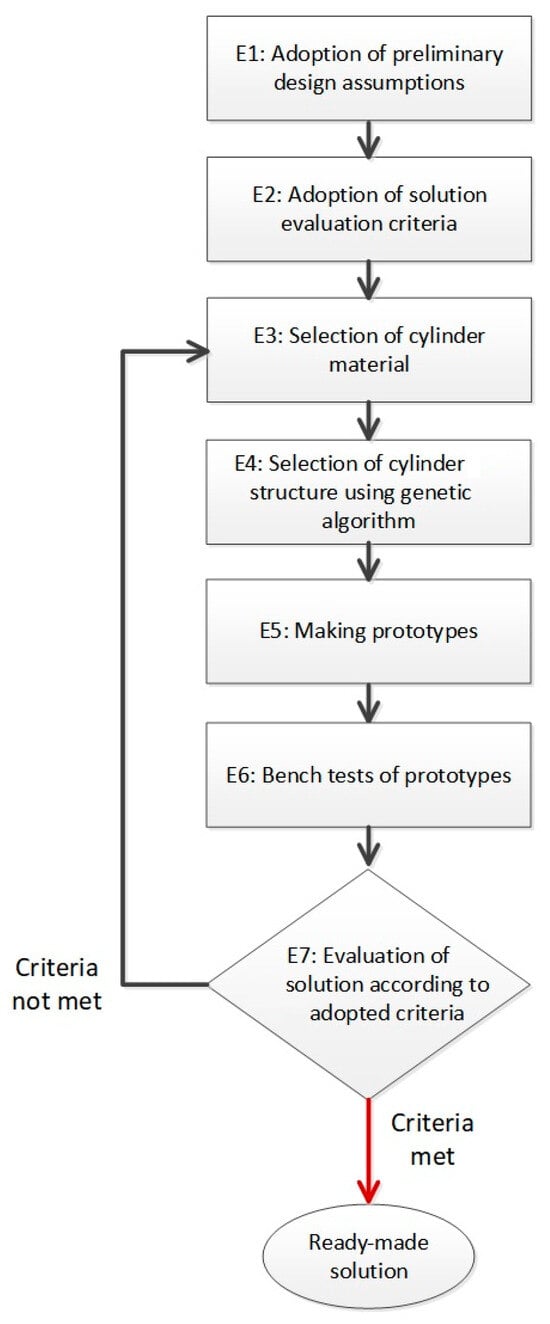
Figure 18.
Block diagram of proposed composite cylinder design method.
In the first stage, it is necessary to make preliminary assumptions about the designed cylinder. Among these assumptions are the following: diameter, stroke and type of actuator (with or without tie-rods), operating and maximum allowable pressure, type of medium, operating temperature, cost. In stage two, the criteria for evaluating the solution are adopted. In this case, they mainly refer to the agreement of the results of strength tests of prototypes with the results of theoretical analyses. In the third stage, the selection of the cylinder material is carried out. Since one is considering a cylinder made of composite material, it is necessary to make decisions on both the type of fibre and matrix (resin). Depending on the initial assumptions made, such as the cost of the solution or the temperature and operating environment, the designer has a choice of a range of fibre types (from glass to basalt to carbon and aramid) and resins (polyester, vinylester, epoxy and others). Once the material has been selected, it is necessary to determine the structure of the cylinder (number of layers and fibre angles). In stage five, it is proposed to make prototype cylinders. Prototypes should be made by available methods (in the case of cylindrical parts, this is usually the wet-winding or prepreg method) from pre-selected materials according to designated specifications. The sixth stage is bench testing of the completed prototypes. In this step, measurements are taken of the deformation of prototypes when they are loaded according to previously identified loading patterns. After bench testing comes the time to evaluate the solution. The results of the strain measurements are compared with those obtained by computational methods. Their discrepancies may be due to factors such as incorrect inputs to the theoretical model (material data or load patterns), technological errors in prototyping, and mistakes made in the installation of the strain sensors. If these discrepancies are large, it is necessary to return to the previous steps of the method and correct them.
6. Conclusions
This paper presents a method for designing a composite hydraulic cylinder using genetic algorithms. A genetic algorithm was developed using classical laminate theory and the Tsai–Hill strength hypothesis to optimise the material structure of a composite cylinder by minimising the number of layers while maintaining the required strength of the component. Optimisation can be carried out taking into account multiple load patterns. A meta-optimisation of the algorithm was carried out to determine its global parameters such as mutation probability, population size and the maximum mutation angle of the layer. Using the determined material properties, two cylinders’ reinforcement structures were selected. Cylinder prototypes were then fabricated and subjected to bench tests to measure deformation. The results of the strain measurements were compared with those calculated theoretically. Finally, a seven-step method for designing a composite hydraulic cylinder was proposed.
From the deformation measurements, it can be seen that in most cases the results obtained experimentally coincided with those calculated theoretically using classical laminate theory as to the values and direction of the changes. After pressure loading, the differences were 10.3% for εx and 18.4% for εθ. It can be noted that in both cases the actual deformations were smaller than the theoretical ones, which may indicate, for example, a higher proportion of reinforcing fibres in the cylinder material than in the flat specimens used to determine material properties.
For the [90/90/±20/]2 cylinder, the differences in axial strain in both steps were slightly more than 1%, while for circumferential strain εθ when the cylinder was loaded with internal pressure, the differences were 31.2%. This is a sizable difference, but the experimentally obtained values were smaller than the theoretical ones, which means that the designed composite cylinder structure is less stressed than the numerical calculations suggest and can be safely operated in the pressure range up to 200 bar.
In addition, based on theoretical and experimental considerations, the following conclusions can be drawn:
- The use of a composite material in the construction of a hydraulic cylinder with tie-rods makes it possible to reduce the weight of the cylinder by 94.4% compared to a steel cylinder.
- The speed of reaching convergence and the computational cost of the genetic algorithm created to optimise the structure of a composite cylinder depend on its global parameters. Increasing the probability of mutation and population size leads to faster convergence. Increasing the size and percentage of the population surviving to the next generation, however, leads to an increase in computational cost.
Author Contributions
Conceptualization, M.S. and M.L.; methodology, M.S. and M.L.; software, M.S. and M.K.; validation, M.S. and M.L.; formal analysis, M.S. and M.K.; investigation, M.S. and M.L.; resources, M.S. and M.K.; data curation, M.S. and M.L.; writing—original draft preparation, M.S., M.L. and M.K.; writing—review and editing, M.S. and M.L.; visualisation, M.S. and M.L.; supervision, M.S.; project administration, M.S. and M.K.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data included in this research are available upon request from the corresponding author.
Conflicts of Interest
Author Marek Lubecki was employed by the company Komes Group Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Bajpai, P.; Singh, I. Reinforced Polymer Composites: Processing, Characterization and Post Life Cycle Assessment; John Wiley & Sons: Hoboken, NJ, USA, 2019; 288p, ISBN 978-3-527-34599-1. [Google Scholar]
- Hwu, C. Mechanics of Laminated Composite Structures; CRC Press: Boca Raton, FL, USA, 2024; 414p, ISBN 9781032746944. [Google Scholar]
- Toray Composite Material America Inc. Torayca® Carbon Fiber Selector Guide; Toray Composite Materials America: Tacoma, WA, USA, 2021; 6p, Available online: https://www.toraycma.com/wp-content/uploads/Carbon-Fiber-Selector-Guide.pdf (accessed on 12 July 2024).
- Teijin Carbon Fiber Business. Tenax™ Filament Yarn Property; Teijin Carbon Fiber Business: Tokyo, Japan, 2021; Available online: https://www.teijincarbon.com/products/filament-yarn (accessed on 12 July 2024).
- Sachdeva, A.; Singh, P.; Rhee, H. Composite Materials; CRC Press: Boca Raton, FL, USA, 2024; 278p, ISBN 9780367531379. [Google Scholar]
- Altenbach, H.; Altenbach, J.; Kissing, W. Mechanics of Composite Structural Elements; Springer Nature: Singapore, 2018; 503p. [Google Scholar] [CrossRef]
- Błażejewski, W.; Barcikowski, M.; Stosiak, M.; Warycha, J.; Stabla, P.; Smolnicki, M.; Bury, P.; Towarnicki, K.; Lubecki, M.; Paczkowska, K. A novel design of a low-pressure composite vessel with inspection opening—Design, manufacturing and testing. Alex. Eng. J. 2024, 91, 442–456. [Google Scholar] [CrossRef]
- HYDAC. Hydraulic Accumulators; HYDAC: Sulzbach/Saar, Germany, 2025; Available online: https://www.hydac.com/de-en/products/hydraulic-accumulators/special-accumulators.html (accessed on 2 January 2025).
- Steelhead Composites. Combined Propellant/Pressurant Vessel (CPPV) Concept. Available online: https://steelheadcomposites.com/news/combined-propellantpressurant-vessel-cppv-concept (accessed on 23 July 2024).
- Mantovani, S.; Costi, D.; Strozzi, A.; Bertocchi, E.; Dolcini, E. Double Acting Composite Tube Cylinder for Fluid Power Applications: A Design Procedure. In Proceedings of the International Conference on Mechanical, Automotive and Aerospace Engineering, Kuala Lumpur, Malaysia, 17–19 May 2011. [Google Scholar]
- Mantovani, S. Feasibility Analysis of a Double-Acting Composite Cylinder in High-Pressure Loading Conditions for Fluid Power Applications. Appl. Sci. 2020, 10, 826. [Google Scholar] [CrossRef]
- Upendra, N.; Moulali, P.; Reddy, K.V. Static and Modal Analysis of Laminated Composite Hydraulic Cylinder. Int. J. Eng. Res. 2014, 3, 140–143. [Google Scholar]
- Nowak, T.; Schmidt, J. Non-linear Mechanical Analysis of the Composite Overwrapped Cylinder for Hydraulic Applications. Adv. Manuf. Sci. Technol. 2014, 37, 31–48. [Google Scholar] [CrossRef][Green Version]
- Nowak, T.; Schmidt, J. Prediction of Elasto-Plastic Behavior of Pressurized Composite Reinforced Metal Tube by Means of Acoustic Emission Measurements and Theoretical Investigation. Compos. Struct. 2014, 118, 49–56. [Google Scholar] [CrossRef]
- Nowak, T.; Schmidt, J. Theoretical, Numerical and Experimental Analysis of Thick Walled Fiber Metal Laminate Tube under Axisymmetric Loads. Compos. Struct. 2015, 131, 637–644. [Google Scholar] [CrossRef]
- Scholz, S.; Kroll, L. Nanocomposite Glide Surfaces for FRP Hydraulic Cylinders—Evaluation and Test. Compos. Part B Eng. 2014, 61, 207–213. [Google Scholar] [CrossRef]
- Solazzi, L.; Buffoli, A. Telescopic Hydraulic Cylinder Made of Composite Material. Appl. Compos. Mater. 2019, 26, 1189–1206. [Google Scholar] [CrossRef]
- Solazzi, L. Feasibility Study of Hydraulic Cylinder Subject to High Pressure Made of Aluminum Alloy and Composite Material. Compos. Struct. 2019, 209, 739–746. [Google Scholar] [CrossRef]
- Solazzi, L. Design and Experimental Tests on Hydraulic Actuator Made of Composite Material. Compos. Struct. 2020, 232, 111544. [Google Scholar] [CrossRef]
- Solazzi, L. Stress Variability in Multilayer Composite Hydraulic Cylinder. Compos. Struct. 2021, 259, 113249. [Google Scholar] [CrossRef]
- Solazzi, L.; Buffoli, A. Fatigue Design of Hydraulic Cylinder Made of Composite Material. Compos. Struct. 2021, 277, 114647. [Google Scholar] [CrossRef]
- Solazzi, L.; Buffoli, A.; Formicola, R. The Multi-Parametric Weight Optimization of a Hydraulic Actuator. Actuators 2020, 9, 60. [Google Scholar] [CrossRef]
- Le Riche, R.; Haftka, R. Improved genetic algorithm for minimum thickness composite laminate design. Compos. Eng. 1995, 5, 143–161. [Google Scholar] [CrossRef]
- Soremekun, G.; Gürdal, Z.; Haftka, R.; Watson, L. Composite laminate design optimization by genetic algorithm with generalized elitist selection. Comput. Struct. 2001, 79, 131–143. [Google Scholar] [CrossRef]
- Mathias, J.; Balandraud, X.; Grediac, M. Applying a genetic algorithm to the optimization of composite patches. Comput. Struct. 2006, 84, 823–834. [Google Scholar] [CrossRef]
- Park, C.; Lee, W.; Han, W.; Vautrin, A. Improved genetic algorithm for multidisciplinary optimization of composite laminates. Comput. Struct. 2008, 86, 1894–1903. [Google Scholar] [CrossRef]
- Kogiso, N.; Watson, L.; Gürdal, Z.; Haftka, R. Genetic algorithms with local improvement for composite laminate design. Struct. Optim. 1994, 7, 207–218. [Google Scholar] [CrossRef]
- Richard, F.; Perreux, D. Reliability method for optimization of [+φ, -φ]n fiber reinforced composite pipes. Reliab. Eng. Syst. Saf. 2000, 68, 53–59. [Google Scholar] [CrossRef]
- Messager, T.; Pyrz, M.; Gineste, B.; Chauchot, P. Optimal laminations of thin underwater composite cylindrical vessels. Compos. Struct. 2002, 58, 529–537. [Google Scholar] [CrossRef]
- Kim, C.; Hong, C.; Kim, C.; Kim, J. Optimal design of filament wound type 3 tanks under internal pressure using a modified genetic algorithm. Compos. Struct. 2005, 71, 16–25. [Google Scholar] [CrossRef]
- Xu, P.; Zheng, J.; Chen, H.; Liu, P. Optimal design of high pressure hydrogen storage vessel using an adaptive genetic algorithm. Int. J. Hydrogen Energy 2010, 35, 2840–2846. [Google Scholar] [CrossRef]
- Nikbakht, S.; Kamarian, S.; Shakeri, M. A Review on optimization of composite structures Part I: Laminated composites. Compos. Struct. 2018, 195, 158–185. [Google Scholar] [CrossRef]
- He, M.; Sun, J. Multi-objective structural-acoustic optimization of beams made of functionally graded materials. Compos. Struct. 2018, 185, 221–228. [Google Scholar] [CrossRef]
- Henrichsen, S. Optimization of Laminated Composite Structures; Aalborg Universitetsforlag: Aalborg, Denmark, 2015; 59p. [Google Scholar] [CrossRef]
- Ventura, S.; Luna, J.; Moyano, J. Genetic Algorithms; IntechOpen: London, UK, 2022; 174p, ISBN 9781803551777. [Google Scholar]
- Kramer, O. Genetic Algorithm Essentials; Springer International Publishing: Cham, Switzerland, 2017; 92p. [Google Scholar] [CrossRef]
- Datoo, M. Mechanics of Fibrous Composites; Springer: Dordrecht, The Netherlands, 1991; 636p. [Google Scholar] [CrossRef]
- Kaw, A. Mechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 2005; 490p, ISBN 9780429125393. [Google Scholar] [CrossRef]
- Wei, R.; Pan, G.; Jiang, J.; Shen, K.; Lyu, D. An Efficient Approach for Stacking Sequence Optimization of Symmetrical Laminated Composite Cylindrical Shells based on a Genetic Algorithm. Thin-Walled Struct. 2019, 142, 160–170. [Google Scholar] [CrossRef]
- Almeida, F.; Awruch, A. Design Optimization of Composite Laminated Structures using Genetic Algorithms and Finite Element Analysis. Compos. Struct. 2009, 88, 443–454. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).