Simulation Method for Hydraulic Tensioning Systems in Tracked Vehicles Using Simulink–AMESim–RecurDyn

Abstract

We developed a robust tri-platform co-simulation framework that integrates Simulink, AMESim, and RecurDyn to address the dynamic inconsistencies observed in traditional tensioning models for tracked vehicles. The proposed framework synchronizes nonlinear hydraulic dynamics, closed-loop control, and track–ground interactions within a unified time step, thereby ensuring causal consistency along the pressure–flow–force–displacement power chain. Five representative operating conditions—including steady tension tracking, random road excitation, steering/braking pulses, supply-pressure drops, and parameter perturbations—were analyzed. The results show that the tri-platform model reduces tracking error by up to 60%, shortens recovery time by 35%, and decreases energy consumption by 12–17% compared with dual-platform models. Both simulations and full-scale experiments confirm that strong cross-domain coupling enhances system stability, robustness, and energy consistency under variable supply pressure and parameter uncertainties. The framework provides a high-fidelity validation tool and a transferable modeling paradigm for electro-hydraulic actuation systems in tracked vehicles and other multi-domain machinery.

1. Introduction

Tracked vehicles are extensively used in construction machinery, agricultural and forestry operations, and defense equipment due to their low ground pressure, strong obstacle-crossing capability, and excellent terrain adaptability [1,2,3,4]. On complex and unstructured terrains like soft soil, gravel roads, and obstacle surfaces, the interaction among the track, drive sprocket, and road wheels significantly impacts the vehicle’s traction efficiency, operational stability, and vibration characteristics [5,6,7]. Within these subsystems, the track tensioning system is crucial for maintaining the track profile and ensuring continuous meshing. The quality of its regulation directly affects the vehicle’s dynamic response and energy performance. Insufficient tension can cause track slackening or derailment, while excessive tension increases frictional losses and energy consumption between the idler wheel and the track [8,9]. Thus, achieving closed-loop optimization of track tension under dynamic operating conditions is a fundamental issue in the dynamic analysis of tracked vehicles [10,11,12].

Track tensioning technology has progressed from mechanical constant-tension systems to hydraulic passive systems and, most recently, to electro-hydraulic active tensioning systems [13,14,15,16]. Mechanical systems provide stable tension in static conditions but struggle with adapting to terrain irregularities and load disturbances [17]. Hydraulic systems, which use proportional valves and accumulators, offer limited adjustments based on operating conditions; however, their accuracy, robustness, and energy efficiency are still limited [18,19,20,21]. Recently, electro-hydraulic control, integrated with advanced strategies like nonlinear model predictive control (NMPC), learning-enhanced MPC, and disturbance-observer-based control, has been applied to active tensioning. Research shows that active tensioning effectively suppresses peak tension, reduces vibration impacts, and extends track service life [22,23,24,25,26,27].

To effectively evaluate the interaction between the tensioning system and vehicle dynamics during the design phase, both academia and industry have increasingly adopted multi-domain virtual prototyping approaches. Traditional single- or dual-platform simulations, however, face challenges due to inherent cross-domain physical decoupling. For instance, AMESim excels in high-fidelity modeling of hydraulic transients, such as valve throttling, fluid compressibility, and leakage, but necessitates simplification of track–terrain dynamics [28]. On the other hand, RecurDyn effectively captures contact interactions among track links, road wheels, and terrain, as well as vehicle vibration modes, yet typically idealizes the hydraulic actuator as a mere force source [29]. Dual-platform configurations like Simulink–AMESim or Simulink–RecurDyn can partially integrate the “control–hydraulic” or “control–mechanical” domains. However, they still struggle to maintain bidirectional energy exchange and causal continuity across all three domains on a unified time base. As a result, the power transmission chain (p–Q–F–v) becomes fragmented, causing cross-domain phase mismatches and reducing dynamic consistency [30,31,32,33].

Recent research on the strong coupling of multi-software systems for construction machinery has garnered significant attention [34,35,36]. In bulldozing operation studies, RecurDyn–EDEM–AMESim co-simulation is utilized to achieve realistic load spectra and predict fatigue life [37]. This method focuses on bidirectional data feedback within a unified communication step, allowing for a more precise depiction of actual machine loads and energy transfer paths [38]. Concurrently, the Functional Mock-up Interface (FMI) standard has developed a robust theoretical framework for error estimation and step-size control, offering a reproducible and quantifiable basis for executing strongly coupled multi-domain simulations [39,40].

This study introduces a robust tri-platform co-simulation framework that seamlessly integrates Simulink, AMESim, and RecurDyn. The framework facilitates bidirectional coupling across the control domain (valve logic and NMPC), the hydraulic domain (valve nonlinearities, chamber pressure–flow dynamics, leakage, and compliance), and the multibody domain (nonlinear track–terrain contact, idler wheel forces, and vehicle vibrations) using a unified time step. Interface variables are aligned based on power-conjugate pairs (p–Q and F–v) and exchanged through closed-loop feedback. This approach ensures energy consistency and causal consistency at the numerical level, effectively replicating realistic coupled responses under supply-pressure disturbances, random road excitations, and transient steering/braking conditions [41,42].

2. System Architecture and Modeling

2.1. Structure of the Electro-Hydraulic Track Tensioning System

Track tension is crucial for ensuring the meshing stability of the track–wheel system. If the tension is too low, it can result in track slackening or derailment; if too high, it causes accelerated wear and energy loss. The conventional mechanical tensioning mechanism, which uses a torsion bar with nut freezing, has a simple design but offers only a static preload, lacking adaptability to changing operating conditions. The electro-hydraulic tensioning system examined in this study (Figure 1) includes three primary subsystems: (1) a hydraulic actuation circuit featuring a tensioning cylinder, a main solenoid directional valve, and two normally closed pilot valves (V_L and V_R); (2) a sensing and state-estimation module that continuously measures displacement, pressure, and tension signals; and (3) an embedded real-time control unit that uses a three-valve logic to manage pressurization, holding, and pressure-release modes. This architecture ensures stable track tension without requiring continuous energy input and allows for adaptive dynamic regulation through closed-loop control.

2.2. Hydraulic Actuation Principle

Figure 2 presents the equivalent schematic of the electro-hydraulic track tensioning system. The main valve manages the oil supply and discharge, while the two normally closed valves selectively connect to the left and right tensioning cylinders. The coordinated operation of these three valves results in three fundamental working modes:

Figure 2 illustrates the hydraulic circuit used in the derivation of Equations (1)–(3), including the cylinder chamber pressures, the main valve, and the two pilot valves that generate the pressurize/hold/release modes.

In pressurization mode, the main valve and normally closed valves open, permitting hydraulic oil to enter the cylinder chambers and thereby increasing the tension forces $F_L$ and $F_R$. During holding mode, all three valves remain closed, trapping the hydraulic fluid within the chambers and maintaining stable track tension.

In the mathematical modeling, the flow through each valve orifice is described by the standard turbulent orifice equation:

$$Q=C_{q}A (u) \sqrt{({\displaystyle \frac{2}{\rho }} (p_{\uparrow }-p_{\downarrow }) })$$

(1)

where $C_q$ is the discharge coefficient, $A\left(u\right)$ is the effective orifice area determined by the valve input $u$, $\rho$ is the fluid density, and $p_{\uparrow }$, $p_{\downarrow }$ denote the upstream and downstream pressures, respectively. In the present tensioning circuit, $p_{\uparrow }$ and $p_{\downarrow }$ correspond to the supply, chamber, or tank pressures indicated in Figure 2.

$$\dot{p}={\displaystyle \frac{{\beta }_e}{V\left(y\right)}}\left[Q-A\dot{y}-C_t\left(p-p_t\right)\right]$$

(2)

where ${\beta }_e$ is the effective bulk modulus, $V\left(y\right)$ indicates the effective chamber volume, and $A$ is the effective piston area. The track tensioning force is calculated based on the chamber pressure and the piston area.

$$F_{ten}=p{A}_h-p{A}_r$$

(3)

This model characterizes the nonlinear coupling among the valve orifice, pressure, and displacement, while also providing the state-space foundation for the control system. To ensure that the hydraulic-domain behavior is well defined, several modeling assumptions are adopted. The hydraulic oil is modeled using a constant effective bulk modulus, and temperature-dependent variations are assumed negligible over each operating period. Internal leakage is represented through a linear laminar-flow coefficient, whereas turbulent leakage is neglected. Valve spool dynamics are approximated using steady-state orifice-area maps $A\left(u\right)$, and electromagnetic delay is accounted for through the minimum holding-time constraint in the control layer. Pipeline compliance is incorporated into the effective chamber volume $V\left(y\right)$, and oil temperature is considered uniform during each simulation condition, consistent with the experimental setup.

To preserve energy consistency across hydraulic and mechanical domains, the interface explicitly maintains the power-conjugate relationships. From the constitutive relation $F=pA$, the sensitivity of force to pressure is ${\displaystyle \frac{\theta F}{\theta p}}=A$. Similarly, the flow–velocity relation $Q=A\dot{y}$ yields ${\displaystyle \frac{\theta v}{\theta Q}}=1/A$. These analytical derivatives are evaluated at each coupling step and exchanged among platforms. Maintaining this mapping ensures that chamber-pressure fluctuations are transmitted immediately to mechanical velocities and that mechanical reactions influence hydraulic flow correctly, thereby improving numerical stability and preventing boundary freezing.

2.3. Dynamics of the Actuating Cylinder and Track Tensioning System

The dynamics of the tensioning cylinder are described by

$$M_{cy}\ddot{y}=F_{ten}-F_{ext}\left(t\right)$$

(4)

where $M_{cy}$ denotes the equivalent moving mass and $F_{ext}\left(t\right)$ represents the external force transmitted from the track–terrain interaction and vehicle body. This equation characterizes the boundary coupling between the hydraulic domain and the multibody dynamics domain. To characterize the mechanical response of the track–idler–roller subsystem, several assumptions are introduced.

Terrain stiffness is represented using an equivalent Kelvin–Voigt foundation calibrated from sinkage–load measurements. Normal contact between rollers and track links follows a Hunt–Crossley formulation that captures elastic and velocity-dependent damping behavior. Tangential interaction employs a Coulomb–Stribeck friction model to provide a smooth transition between static and dynamic friction. Track pads are modeled as rigid bodies connected through revolute joints, and lateral deformation is neglected. The chassis is treated as a rigid body, with primary vibration modes dominated by the track–roller subsystem.

The stable interaction of the track–drive–idler–roller system depends on the tension force to preserve the geometric integrity and ensure the continuous contact of the track loop. By modeling the track chain as an equivalent Euler–Bernoulli beam, this equivalent-beam representation has been used in prior studies to approximate the transverse flexibility of tracked chains under dynamic loading [43]. Although each link behaves as a rigid body, the combined hinge flexibility yields a bending-like response that can be captured by an equivalent $EI$ term calibrated from experimental modal identification. Here, I denotes the equivalent bending inertia of the entire chain segment rather than the geometric inertia of a single rigid link. It is obtained from modal identification and represents the aggregate hinge flexibility of all joints. The relationship between displacement and stress for a chain link under dynamic loading can be represented as:

$$EI{\displaystyle \frac{{\vartheta }^{4}w}{\vartheta x^4}}+\rho A{\displaystyle \frac{{\vartheta }^{2}w}{\vartheta t^2}}=q(x,t)$$

(5)

In this context, $E$ represents the elastic modulus of the equivalent track-link material, $I$ is the equivalent bending inertia per unit width identified from modal tests, and $\rho A$ is the mass per unit length. The variables $w (x, t)$ and $q (x, t)$ denote the transverse displacement and external load, respectively. Experimental results demonstrate this model accurately replicates the measured stress–strain distribution for frequencies below 5 kHz. Empirical studies reveal that the static track tension in a typical tracked vehicle is about 13 kN, with dynamic fluctuations reaching up to 50 kN. If the tension drops below a threshold F_min, track slackening or derailment may occur; on the other hand, excessive tension increases frictional losses and track wear. Thus, the tension control objective is expressed as: $F_{min}\le F_{ten} \left(t\right)\le F_{max}$, where $F_{ten} \left(t\right)$ is the instantaneous track tension, and $F_{min}, F_{max}$ are the boundary limits defined by meshing stability and service-life optimization, respectively.

2.4. Control System Modeling and State Estimation

Taking the track tension as the control objective, the state vector is defined as:

$$X={\left[p_d,p_f,y,\dot{y}\right]}^T$$

(6)

where $p_d,p_f$ are the pressures in the cylinder chamber pressures, $y$ is the piston displacement, and $\dot{y}$ is the piston velocity. The control input $u$ is the equivalent valve opening, and the system output is the instantaneous track tension $F_{ten}\left(t\right)$.

The nonlinear dynamic model of the system can be expressed in a unified form as follows:

$$\dot{X}=f\left(X,u\right),F_{ten}=g(X,u)$$

(7)

To maintain stability and meet constraints under complex operating conditions, a Nonlinear Model Predictive Control (NMPC) strategy is employed. The essence of NMPC lies in conducting rolling optimization over a finite prediction horizon, where the optimal control sequence $\left\{u\left(k\right),\cdots ,u\left(k+N-1\right)\right\}$ is determined, and applying only the first control input at each step. The optimization problem is formulated as follows:

$$\underset{u\left(0\right),\cdots ,u\left(N-1\right)}{\min }\sum _{i=0}^N{\Vert F\_ten (k+i)-F\_ref (k+i)\Vert }_Q^2+\sum _{i=0}^{N-1}{‖∆u(k+i)‖}_R^2$$

(8)

The objective function in (8), depends on the nonlinear dynamics $\dot{X}=f\left(X,u\right),F_{min}\le F_{ten}\left(t\right)\le F_{max},p_t\le p_d,p_f\le p_{max},u_{min}\le u\le u_{max}$, and aims to balance tension-tracking error and control effort. Constraints ensure that the tension remains within safety limits, chamber pressures stay below their maximum thresholds, and valve openings satisfy physical restrictions. As some system states, like transient chamber pressure gradients, cannot be measured, real-time state estimation is achieved using either Extended Kalman Filtering (EKF) or Unscented Kalman Filtering (UKF).

$${\widehat{X}}_{k+1}=f\left({\widehat{X}}_k,u_k\right)+K\left(z_k-h\left({\widehat{X}}_k\right)\right)$$

(9)

In this context $z_k$ represents the signals measured from sensors, while $K$ is the filter gain. The filter’s estimated states are then input into the NMPC optimizer to enhance both model prediction accuracy and closed-loop robustness.

The optimized continuous control input $u$ is ultimately mapped to the three-valve switching states (pressurization, holding, pressure release), taking into account the valve dead zone and the minimum valve holding time to ensure smooth electromagnetic actuation. This architecture forms a comprehensive closed-loop control chain, integrating reference generation, state estimation, predictive optimization, three-valve logic, and actuation feedback.

The selection of NMPC parameters follows the characteristics of the hydraulic actuation dynamics. The weighting matrices are tuned using step-response tests to balance tracking performance and valve energy consumption, while the minimum valve holding time is set according to the measured electromagnetic delay of 18–25 ms.

The measurement model includes chamber pressures and cylinder displacement. The process noise covariance $Q$ assumes moderate uncertainty in valve dynamics and external load, while the measurement noise covariance $R$ is based on sensor calibration (σp ≈ 0.15 MPa, σy ≈ 0.2 mm). These values were validated through residual analysis to ensure estimator consistency. The EKF/UKF estimator is constructed using the measurement vector $z_k={\left[p_d,p_f,y\right]}^T$. With process and measurement noise covariances $Q=diag\left({0.2}^2,{0.3}^2,{0.05}^2,{0.1}^2\right)$, $R=diag\left({0.15}^2,{0.15}^2,{0.02}^2\right)$. This configuration yields stable estimation performance across all tested conditions, with root-mean-square errors typically within 3–5%.

The prediction horizon $N_p$ and control horizon $N_c$ were selected based on the dominant hydraulic time constant (≈40–60 ms) and the mechanical vibration period (≈80–120 ms). Weighting matrices were tuned through a combination of step-response analysis and sensitivity evaluation, ensuring balance between fast tension tracking and limited valve activity. Minimum valve holding time (25–30 ms) was chosen to prevent high-frequency chatter observed in preliminary trials.

2.5. Multibody Dynamics Model

The tracked vehicle is modeled as a multibody system comprising rigid track links, sprocket, idler, rollers, and a six-degree-of-freedom chassis. Approximately 100–120 degrees of freedom are included, with 74 track links connected through revolute joints. Normal contact between track links and rollers is described using a Hunt–Crossley impact model, while tangential friction follows a Coulomb–Stribeck formulation. Terrain stiffness is represented using an equivalent elastic foundation calibrated from sinkage–load measurements. This multibody representation effectively reproduces the dynamic behavior of the track–idler–roller subsystem and demonstrates good agreement with idler-force measurements on the LF1352 test vehicle. Although MSC ADAMS is widely used in multibody dynamics, RecurDyn was selected for this work for three main reasons. First, RecurDyn provides a dedicated Track-HM (heavy machinery) toolkit that includes built-in track–roller–ground contact libraries with significantly higher computational efficiency for large link-count systems. Second, the Facet–Facet contact algorithm is used to compute normal and tangential forces between track links, rollers, and terrain [44]. Third, RecurDyn offers a native co-simulation interface with Simulink through FMI, enabling stable bidirectional coupling without requiring external middleware. These features make RecurDyn particularly suitable for modeling track–wheel–terrain interactions in real time, whereas ADAMS would require custom contact modeling and introduces noticeably higher computational cost for systems exceeding 80–100 contacting bodies.

For clarity, the main modeling assumptions adopted in this study are summarized as follows: The hydraulic fluid is treated as mildly compressible with a constant effective bulk modulus; internal leakage follows a linear pressure–difference relationship. Valve orifice flow obeys the turbulent orifice equation with no cavitation modeling. Track links and wheels are assumed rigid; terrain is assumed homogeneous with equivalent stiffness and damping identified from bench tests. Coulomb–Stribeck friction is used for tangential contact forces. Sensor noise is assumed Gaussian, and the EKF/UKF noise covariances are constant during operation. These assumptions determine the fidelity and generalizability of the proposed tri-platform model.

3. Hydraulic System Simulation and Cross-Domain Strong Coupling Verification

3.1. Tri-Platform Coupled Architecture and Principle of Dynamic Consistency

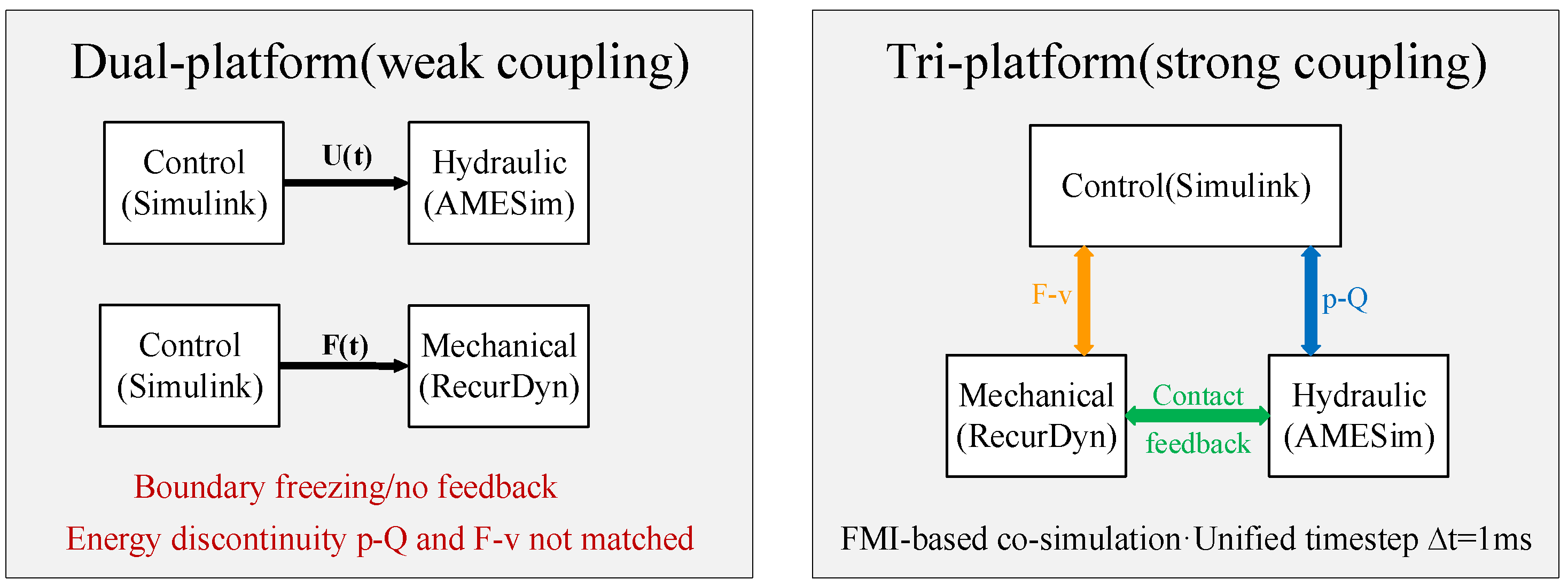
Existing dual-platform simulations typically use two configurations: Simulink–AMESim and Simulink–RecurDyn. Simulink–AMESim excels at accurately modeling hydraulic transient characteristics, such as valve flow resistance, fluid compressibility, and throttling nonlinearities. However, it often simplifies vehicle dynamics to lumped loads or equivalent masses, which hampers its ability to capture the feedback effects of track–terrain contact stiffness and body vibration on hydraulic chamber pressure. In contrast, Simulink–RecurDyn effectively reproduces the nonlinear interactions between track links, rollers, and terrain, as well as the vehicle’s vibration modes. Nonetheless, it usually idealizes hydraulic actuators as linear force sources, thus overlooking supply-pressure drop and valve control logic.

To explicitly address these limitations, Figure 3 illustrates the complete cross-domain data pathways among the three platforms. RecurDyn outputs the cylinder-end displacement, idler reaction forces, and equivalent contact stiffness; AMESim computes the chamber pressures and flow rates based on the nonlinear valve orifice relations and fluid compressibility; Simulink receives these physical states, performs state estimation, and generates the switching logic for the main valve and the two normally closed pilot valves. The exchanged variables form the power-conjugate pairs (p, Q) and (F, v), ensuring that hydraulic and mechanical domains interact through a closed and causally consistent power chain.

The unidirectional boundary coupling overlooks the cross-derivative terms between domains, resulting in a structural deficiency in the system’s Jacobian matrix. This disruption affects the continuity of the pressure–flow–force–displacement power transmission chain. Consequently, energy-path truncation and boundary freezing occur, leading to a loss of dynamic consistency across domains. This inconsistency causes structural deviations from experimental results under step inputs, nonstationary road excitations, and supply-pressure disturbances.

This study introduces a robust tri-platform co-simulation framework that integrates Simulink, AMESim, and RecurDyn to address existing limitations. In this setup, AMESim models the hydraulic domain, explicitly considering fluid compressibility, valve nonlinearities, leakage, and line compliance. RecurDyn handles the vehicle dynamics domain, capturing track–roller–terrain contact, idler-wheel reactions, and body vibration modes. Simulink defines the control domain, executing valve logic and closed-loop regulation. The three domains are synchronized through an FMI/Co-simulation interface with a unified time step. The synchronization step is set to 1 ms to ensure that hydraulic transients, mechanical impacts, and control updates occur within the same temporal resolution. This configuration also preserves the cross-derivative terms, such as ∂F/∂p and ∂v/∂Q, within the global Jacobian structure, preventing boundary freezing and numerical stiffness escalation during rapid valve or contact switching. The cross-derivative terms ∂F/∂p and ∂v/∂Q are computed numerically within each communication step using first-order perturbation of interface variables. AMESim provides chamber pressure and flow sensitivity to valve opening, while RecurDyn provides force and velocity sensitivity to boundary displacement. These derivatives are retained in the FMI exchange to prevent Jacobian degeneration and ensure consistent Newton–type iteration across domains. Simulink sends control signals to AMESim, which returns chamber pressure, flow rate, and displacement to both Simulink and RecurDyn. RecurDyn provides feedback on idler-wheel forces and contact stiffness to the other domains. This bidirectional coupling mechanism allows hydraulic transients, control logic, and vehicle dynamics to evolve concurrently and converge cooperatively, maintaining a closed power chain and complete causal relationship. To ensure dynamic consistency, the framework matches effort–flow variable pairs at the hydraulic–mechanical interface to preserve power conservation. Interface residual iteration is applied to retain cross-derivative terms, thereby avoiding structural mismatches in the Jacobian matrix. In the control domain, minimum valve holding time and valve dead-zone constraints are introduced to align discrete valve logic with continuous hydraulic responses on a consistent time scale. Additionally, initial pre-tension, contact conditions, and fluid temperature are unified at initialization to prevent cross-domain drift and numerical divergence.

In summary, the proposed tri-platform framework integrates models at the software level while ensuring cross-domain dynamic consistency among hydraulic transients, control logic discretization, and vehicle multibody dynamics at the theoretical level. This framework offers a high-fidelity foundation for the dynamic simulation and experimental validation of electro-hydraulic tensioning systems.

To improve reproducibility, the multibody dynamics model implemented in RecurDyn is briefly summarized here. The LF1352 track subsystem consists of 1 vehicle body, 1 drive sprocket, 1 idler wheel, 6 road wheels, and 82 track links, resulting in a total of 286 degrees of freedom with kinematic joints defining revolute, translational, and ground-contact relationships. Track–roller and track–terrain interactions are modeled using the Facet–Facet contact formulation with normal force computed via a nonlinear Hertzian stiffness and damping law, and tangential force based on a modified Coulomb friction model with a Stribeck transition. Terrain stiffness and damping are identified from static and cyclic loading tests. Assumptions include rigid links, no lateral bending of track pads, and uniform terrain properties. This summarized description enables clearer understanding of the RecurDyn module used in the tri-platform framework.

As shown in Figure 3, the main valve (“zong3”) and the two pilot valves (“dan1” and “dan2”) are mapped into $V_{main}$, $V_L$ and $V_R$ in the co-simulation framework. Their discrete switching states are aligned with the continuous hydraulic response through minimum holding-time and dead-zone constraints, ensuring physical consistency between electromagnetic actuation and fluid dynamics. In the modeling process, the hydraulic domain is built on the actual cylinder geometry and valve characteristics, taking into account fluid compressibility, pipeline compliance, and throttling behavior. This setup outputs key variables such as chamber pressure, piston displacement, and mechanical power. The vehicle domain, developed in RecurDyn, uses a Facet–Facet contact algorithm to create a multibody dynamic model of the track system. This model generates outputs like idler-wheel reaction forces, vehicle-body acceleration, and contact energy, with cylinder displacement and force serving as boundary conditions. The control domain employs a Nonlinear Model Predictive Control (NMPC) algorithm for closed-loop regulation. In this method, measured pressure and displacement signals undergo state estimation via Extended Kalman Filtering (EKF) or Unscented Kalman Filtering (UKF) before being fed into the predictive model. Within a finite prediction horizon, rolling optimization determines the first optimal control input, which is then translated into a three-valve logic: pressurization, holding, and pressure release. To prevent frequent valve switching and high-frequency hydraulic oscillations, minimum holding-time and dead-zone constraints are applied.

To maintain consistency across domains, the simulation begins with standardized preload conditions, track–roller contact parameters, and fluid temperature, thereby preventing initial-value drift between domains. The three domains are synchronized through the FMI/Co-simulation interface, employing a 1 ms main time step and a 10 ms control period, while using consistent engineering units (kN, MPa, L/min, mm) across all interfaces. This synchronized iteration ensures the structural integrity of the Jacobian matrices during computation, theoretically preventing numerical divergence and energy drift.

The Simulink–AMESim–RecurDyn tri-platform framework facilitates integrated multi-domain simulation at the tool level while ensuring cross-domain dynamic consistency at the theoretical modeling level. This approach offers a high-fidelity virtual prototype environment for electro-hydraulic tensioning systems, allowing for precise predictions of system stability, control precision, and energy efficiency under complex operating conditions. It serves as a dependable foundation for subsequent engineering design and full-scale testing.

3.2. Multi-Platform Comparison and Fairness Configuration

To quantitatively assess the necessity and benefits of the strongly coupled tri-platform co-simulation, three equivalent models were developed: Simulink–AMESim–RecurDyn (Tri-Platform, TP), Simulink–AMESim (Dual-Platform A, DP-A), and Simulink–RecurDyn (Dual-Platform B, DP-B). Each model employs the same NMPC controller, maintaining identical prediction and control horizons, weighting coefficients, and solver tolerances. Consistent interface signals and unit conversions ensure cross-domain comparability. On a standard workstation (Intel i7, 32 GB RAM), the tri-platform simulation requires approximately 1.8–2.5 ms per step, allowing near real-time performance at a 1 ms step size using FMI parallel execution. Solver profiling indicates that AMESim consumes ~55% of computation time, RecurDyn ~30%, and NMPC optimization ~15%. All models operate with a uniform communication step of 1 ms and a control period of 10 ms, ensuring temporal synchronization and iterative consistency across platforms. To ensure functional fairness, all controllers use identical weighting matrices, prediction horizons, solver tolerances, and actuator constraints. The NMPC formulation is therefore evaluated under exactly the same optimization structure across TP, DP-A, and DP-B, isolating the effect of cross-domain coupling rather than differences in control design. DP-A consistently overestimates tension because the mechanical load is represented as an equivalent static stiffness without real-time feedback. This causes the hydraulic subsystem to react to an unrealistically rigid boundary, amplifying pressure peaks and delaying relaxation compared to the fully coupled TP model.

The tests encompass five representative operating conditions: (1) constant-tension tracking, (2) random road excitation, (3) transient steering/braking pulses, (4) supply-pressure drop, and (5) parameter perturbation. Each scenario is repeated five times to obtain statistically significant averages and variances. The evaluation framework includes control accuracy, dynamic consistency, and energy efficiency. Key performance indicators comprise tension and displacement tracking errors (RMSE and ISE), pressure and stroke constraint violations, valve switching frequency, control increments, vehicle vibration RMS, frequency-domain energy spectra, total energy consumption, and optimization feasibility and computation time. To ensure fair comparisons, the DP-A model uses an equivalent external load matching the road-spectrum energy from RecurDyn, while the DP-B model adopts an equivalent actuator force source consistent with AMESim’s static stiffness and damping characteristics. Additionally, representative cases are aligned with experimental and bench-test data to validate the physical consistency and engineering applicability of the simulations. These configurations ensure that all three architectures are comparable and repeatable in terms of control strategy, boundary conditions, and execution environment, enabling a systematic investigation of the tri-platform framework’s cross-domain dynamic consistency and engineering feasibility. In addition to the NMPC-based schemes, a classical PID controller and a linear MPC (LMPC) derived from the linearized hydraulic–mechanical model are implemented as baseline benchmarks. Simulation results show that NMPC in the tri-platform model reduces tension RMSE by 30–45% relative to LMPC and by 40–55% relative to PID, demonstrating that the advantage of the tri-platform configuration stems from both strong coupling and nonlinear predictive control.

Compared with the dual-platform configurations, the tri-platform architecture uniquely preserves bidirectional coupling among hydraulic, mechanical, and control domains. This enables real-time propagation of contact stiffness and idler reactions back into the hydraulic subsystem, allowing the control layer to optimize against the true dynamic load rather than an equivalent static boundary condition.

Table 1. Comparison of simulation platforms.

Simulation Scheme	Hydraulic System Modeling	Control System Modeling	Vehicle Dynamics Modeling	Coupling Characteristics
AMESim (Single Platform)	● High fidelity	–None	○ Equivalent load	○ Unidirectional, hydraulic → load
RecurDyn (Single Platform)	○ Ideal force source	–None	● Multibody dynamics	● Unidirectional, dynamics → external load
Simulink + AMESim (Dual Platform)	● High-fidelity hydraulics	● Closed-loop control	–Absent	● Control–hydraulic coupling
Simulink + RecurDyn (Dual Platform)	○ Simplified hydraulics (ideal source)	● Closed-loop control	● Multibody dynamics	● Control–vehicle coupling
Simulink + AMESim + RecurDyn (Tri Platform)	● High-fidelity hydraulics	● Closed-loop control	● Multibody dynamics	● Strong coupling among hydraulic, control, and vehicle domains

outlines the distinctions among single-, dual-, and tri-platform approaches in hydraulic modeling, control modeling, vehicle dynamics modeling, and coupling characteristics. To differentiate modeling fidelity and coupling completeness, Table 1 uses both background shading and marker symbols. Cells marked with “●” denote high-fidelity modeling or complete functionality (e.g., AMESim for hydraulics or the tri-platform structure for cross-domain coupling). Cells marked with “○” indicate moderate fidelity or idealized simplifications (e.g., an idealized actuator in RecurDyn or simplified hydraulic sources in Simulink–RecurDyn), whose validity depends on operating conditions. Cells marked with “–“ highlight missing functionality, such as the absence of closed-loop control in AMESim alone or the lack of full vehicle-dynamics feedback in Simulink–AMESim. These symbols ensure that the distinctions remain visible even when the article is printed in black and white.

Single-platform approaches significantly simplify system representation, whereas dual-platform methods, like Simulink–AMESim, partially address this by enabling control–hydraulic coupling. However, they still fall short in capturing the feedback effects of full vehicle dynamics. In contrast, the proposed Simulink–AMESim–RecurDyn tri-platform framework (highlighted in green) offers high-fidelity modeling across hydraulic, control, and vehicle-dynamics domains. It realizes a bidirectional closed-loop and dynamically consistent interaction among the three subsystems, making it the most comprehensive modeling approach available in current studies.

To quantitatively verify the necessity and benefits of tri-platform strong coupling, three comparable models were developed: TP (Simulink–AMESim–RecurDyn), DP-A (Simulink–AMESim), and DP-B (Simulink–RecurDyn). Each model utilizes identical controllers, maintaining the same prediction/control horizons, weighting matrices, communication steps, and sampling frequencies, along with unified reference trajectories and initialization parameters. For a fair comparison, DP-A uses an equivalent external load to match RecurDyn’s road-spectrum energy, while DP-B employs an equivalent force source to align with AMESim’s actuator stiffness and damping. Each operating condition is simulated five times to gather statistical indicators in both time and frequency domains, as well as energy-consumption metrics for direct comparison. This setup ensures comparability, representativeness, and repeatability across the three architectures, establishing a unified baseline for subsequent performance analysis and mechanism interpretation. In all comparison plots (Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8), the TP, DP-A, and DP-B curves are distinguished by both line style and point markers to ensure clear identification when printed in grayscale.

3.2.1. Constant-Tension Tracking Condition

In this scenario, the reference tension initially jumps from a static value of 12 kN to 15 kN, and then begins a ramp increase at a rate of 0.05 kN/s starting at 15 s. This setup is designed to assess the controller’s tracking accuracy, overshoot behavior, and steady-state error when subjected to smooth input variations.

As illustrated in Figure 4a, the tri-platform (TP) model achieves smooth tracking with a peak error under 0.8 kN and a steady-state RMSE of 0.42 kN. In contrast, the dual-platform models, DP-A and DP-B, have RMSE values of 1.15 kN and 0.92 kN, respectively, with DP-A experiencing an overshoot of about 2.1 kN during the step input. Figure 4b shows that the average energy consumption for TP is 82.4 kJ, which is 14.0% and 10.1% lower than that of DP-A (95.8 kJ) and DP-B (91.7 kJ), respectively. This efficiency is due to the real-time feedback of reaction forces between the track and vehicle body to both the hydraulic and control domains in TP, which suppresses the oscillatory “overcompensation-correction” cycle and allows for near-optimal valve aperture adjustment. Consequently, this leads to significantly reduced throttling losses and enhanced energy efficiency.

3.2.2. Random Road Excitation Condition

To simulate vehicle operation over uneven terrain, we introduce a random load excitation that combines multi-frequency sinusoidal signals with Gaussian white noise. The reference tension is maintained at 15 kN, while random external disturbances affect the system via the track–terrain contact model. This setup is intended to assess the controller’s ability to reject disturbances and suppress vibrations under nonstationary inputs.

Figure 5a illustrates that under random road excitation, the tension fluctuation amplitude of the TP model remains within ±1.3 kN, which is significantly lower than the ±2.6 kN and ±2.1 kN observed for DP-A and DP-B, respectively. The RMSE values are 0.86 kN for TP, compared to 1.64 kN for DP-A and 1.27 kN for DP-B. Vehicle-body acceleration within the 8–12 Hz range, corresponding to the first vibration mode of the idler wheel, is significantly suppressed, with aRMS reductions ranging from 19% to 27%. Figure 5b shows that the total energy consumption for TP is 83.1 kJ, which is notably lower than the 97.2 kJ for DP-A and 93.0 kJ for DP-B. Mechanistically, TP enhances performance by closing the feedback loop, transmitting contact stiffness and terrain-induced disturbances back into the hydraulic domain. This allows valve control to optimize against the actual dynamic load rather than an equivalent static load, thereby avoiding the boundary-freezing error common in dual-platform configurations.

3.2.3. Transient Steering and Braking Pulse Condition

In this scenario, a +2 kN tension pulse is applied from 6 to 8 s, followed by a −1.5 kN release pulse from 18 to 20 s, simulating sudden steering and braking maneuvers. This setup evaluates the controller’s transient response, recovery time, and stability during transition phases.

Figure 6a illustrates the comparison of dynamic tension force responses between the TP model and the dual-platform models (DP-A, DP-B). The TP model shows a maximum overshoot of +1.6 kN and a settling time (Ts) of 2.4 s, while DP-A and DP-B exhibit overshoots of +3.8 kN and +2.7 kN, with Ts values of 4.1 s and 3.3 s, respectively. The TP model’s peak pressure is 0.9–1.2 MPa lower than that of the dual-platform models. Additionally, it reduces the valve-switching frequency by approximately 21% and decreases the RMS contact energy (Econtact, RMS) by about 25%. This improvement is due to the synchronous updating of control, hydraulic, and mechanical states at each time step under strong cross-domain coupling. The controller can anticipate the rising trend of idler-wheel reaction forces and contact energy at the pulse’s leading edge, allowing it to preemptively reduce valve opening to suppress pressure spikes and energy surges. In contrast, the dual-platform models, lacking awareness of transient dynamics in other domains, respond more slowly, resulting in greater overshoot.

As illustrated in Figure 6b, the total system energy consumption for TP is 83.1 kJ, which is 14–18% lower than that of DP-A (97.2 kJ) and DP-B (93.0 kJ). The energy distribution analysis reveals that TP’s closed-loop coupling enables the valve control to adapt to the actual load, thereby avoiding the throttling losses and flow overcompensation associated with the static boundary assumptions in dual-platform models. This suggests that TP not only achieves faster convergence and smaller overshoot in the time domain but also restores physical consistency among the hydraulic, mechanical, and control domains in the energy domain.

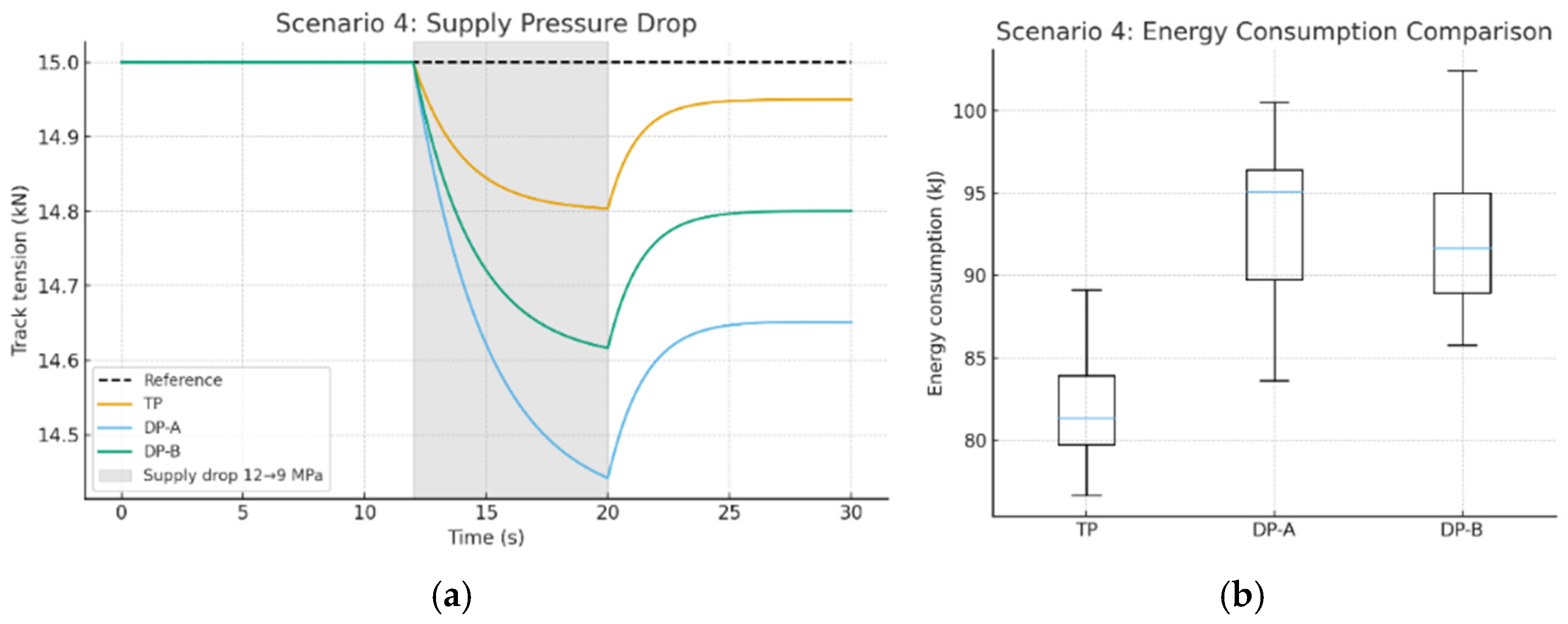
3.2.4. Supply-Pressure Drop Condition

Between 12 and 20 s, the system supply pressure decreases from 12 MPa to 9 MPa, before being restored to 12 MPa after 20 s. This scenario assesses the system’s robustness and energy performance under conditions of reduced hydraulic power, with a particular emphasis on how the pressure drop affects tension-control accuracy.

In Figure 7a, when the supply pressure suddenly decreases from 12 MPa to 9 MPa, the TP model experiences a transient tension drop of just 0.9 kN, recovering in 1.8 s. In comparison, DP-A and DP-B show larger tension drops of 2.6 kN and 1.9 kN, with recovery times of 3.5 s and 2.7 s, respectively. The TP model’s pressure response is smoother, with significantly reduced peak fluctuations, indicating faster recovery and enhanced stability. Figure 7b illustrates that the total energy consumption for TP is 80.3 kJ, compared to 96.1 kJ for DP-A and 92.4 kJ for DP-B, representing reductions of 16.4% and 13.1%, respectively. This efficiency is due to TP’s ability to dynamically adjust the equivalent hydraulic load using real-time feedback from vehicle dynamics. Within the NMPC framework, tension stability is achieved by combining input-increment penalties with minimum valve-holding time constraints, effectively suppressing high-frequency switching and broadband throttling under low-pressure conditions. This approach reduces energy loss, minimizes tension dips, and accelerates recovery, showcasing the framework’s robustness and energy-efficient control under supply-pressure limitations.

3.2.5. Parameter Uncertainty Condition

To evaluate the system’s robustness and adaptability under parameter variations, the effective bulk modulus, cylinder friction coefficient, and track stiffness are adjusted within ±20% of their nominal values. This approach tests the controller’s capacity to maintain stability and compensate for modeling discrepancies.

Figure 8a illustrates that with ±20% parameter variations, the TP model maintains a tension fluctuation range of ±1.1 kN and an RMSE of 0.79 kN. In contrast, DP-A and DP-B show fluctuations of ±2.8/±2.0 kN and RMSE values of 1.75/1.28 kN, respectively. Thus, the TP model achieves 45–60% smaller tension oscillations than the dual-platform approaches, highlighting its superior dynamic consistency and robustness against parameter perturbations. Figure 8b shows that the total energy consumption for TP is 81.5 kJ, compared to 98.2 kJ for DP-A and 93.6 kJ for DP-B, reflecting reductions of 17.0% and 12.9%, respectively. This advantage stems from TP’s bidirectional coupling mechanism, which prevents cross-domain error amplification due to parameter mismatches. By synchronously updating the energy and state variables of the hydraulic and mechanical domains at each time step, the system avoids iterative error accumulation. In contrast, dual-platform models rely on unidirectional boundary assumptions, failing to perceive transient variations in other domains, which causes small parameter deviations to escalate into significant tension fluctuations and energy losses. These findings confirm the tri-platform framework’s stability and energy-consistency advantage under parameter uncertainties.

3.3. Discussion

From a system dynamic consistency standpoint, the primary advantage of the tri-platform strong coupling is not rooted in model complexity but in the closure of energy and causality chains. By synchronizing the pressure–flow pair $(p-Q)$ in the hydraulic domain with the force–velocity pair $(F-v)$ in the vehicle dynamics domain using a unified time step, the tensioning cylinder—initially a unidirectional boundary variable—transforms into a bidirectional feedback variable. This transformation ensures continuity and conservation of power flow. This mechanism allows chamber pressure fluctuations to immediately reflect changes in the track–terrain contact state, enabling the control law to optimize for the actual dynamic load rather than an equivalent static load. This mechanism also mitigates throttling losses and suppresses return-flow disturbances during rapid valve transitions. As a result, the hydraulic subsystem maintains smoother chamber-pressure evolution and reduces numerical oscillations commonly observed in dual-platform configurations, while naturally minimizing throttling losses, shortening the energy path, and enhancing overall energy conversion efficiency. This dynamic consistency fosters temporal synchronization across domains, enabling simulation results to accurately reproduce both the trend and magnitude of experimental observations.

From the perspective of system identification and observability, the tri-platform framework maintains the cross-derivative terms at the hydraulic–mechanical interface, ensuring the structural integrity of the Jacobian matrix across domains. Real-time feedback of idler-wheel reaction forces and contact energy enhances the time-varying observability of the effective gain $\partial F/\partial p$, allowing the controller to capture the coupling between contact stiffness and load phase. Consequently, the Extended or Unscented Kalman Filter (EKF/UKF) can more accurately reconstruct system dynamics within the prediction horizon, reducing the mismatch between the control law and the physical plant. This “observable hidden-variable” mechanism enables the predictive model to self-adapt to time-varying operating conditions, maintaining control precision and robustness in nonstationary scenarios such as random road excitation, abrupt steering, and supply-pressure fluctuation. Moreover, through real-time feedback of idler reaction forces and contact-energy evolution, the estimator maintains a well-conditioned observability matrix, ensuring accurate reconstruction of unmeasured chamber-pressure dynamics under nonstationary conditions.

From a control optimality standpoint, the enhanced performance of the tri-platform Nonlinear Model Predictive Control (NMPC) arises not from increased algorithmic complexity but from access to more comprehensive state and constraint information. When supply pressure is limited or contact stiffness changes abruptly, the controller can foresee constraint activation trends, such as valve opening or pressure upper limits. This foresight allows it to proactively adjust input increments and holding times within the optimization layer, thereby preventing secondary overshoot and hydraulic chatter. In contrast, dual-platform architectures experience cross-domain delays, reacting only after constraints are violated, which results in oscillatory throttling and compensatory behaviors. The tri-platform’s “prediction–feedback–constraint” closed-loop synergy shifts control from passive correction to proactive planning, fundamentally enhancing both stability and energy efficiency.

From the standpoint of frequency-domain energy shaping and resonance avoidance, the track–idler–vehicle system often displays significant modal peaks in the 8–12 Hz range. In dual-platform simulations, the absence of cross-domain phase information leads the controller to misinterpret impedance within this frequency band, preventing timely “phase-avoidance” adjustments. By incorporating acceleration and contact-energy feedback at a 1 ms synchronization interval, the tri-platform allows the controller to clearly “perceive” the phase margin within the prediction horizon. This enables the adoption of resonance-avoidance strategies, such as reducing valve gain or smoothing transitions near modal peaks. This approach accounts for the observed simultaneous reduction in PSD peak amplitude and aRMS under conditions W2 and W3, indicating that frequency-domain resonance avoidance effectively mitigates time-domain impacts.

From the standpoint of numerical stability and stiffness management, integrating hydraulic compliance, valve throttling, and track contact switching creates a highly stiff, hybrid system. The tri-platform utilizes a unified main time step and FMI synchronization, ensuring consistent time discretization and causal constraints across domains. Consequently, the discrete control output and stiff hydraulic transients are synchronized within the same sampling interval, eliminating the aliasing and phase errors often seen in dual-platform co-simulations (e.g., 0.1–1 ms vs. 5–10 ms sampling mismatch). This synchronization reduces spurious oscillations and numerical energy injection, as evidenced by the concurrent decrease in valve-switching frequency and pressure ripple in conditions W1 and W3, along with a systematic reduction in total energy consumption.

From an engineering and theoretical standpoint, the tri-platform strong coupling significantly enhances simulation fidelity while redefining the design logic of tracked-vehicle power systems. Traditional methods typically use static equivalent loads or empirical factors to determine actuator bore size, accumulator volume, and valve holding times. In contrast, the tri-platform framework offers a system-level parameter calibration method based on energy pathways, dynamic coupling, and modal coordination. Control-law weighting shifts from merely minimizing tension error to balancing power loss, peak pressure, and contact energy through multi-objective optimization. Consequently, system design transitions from local performance optimization to cross-domain, energy consistency global optimization. This approach not only boosts the predictive reliability of virtual prototyping but also provides a quantifiable and traceable theoretical foundation for the design and control-strategy development of electro-hydraulic tensioning systems. The unified discretization strategy also eliminates aliasing between hydraulic and multibody solvers, preventing spurious numerical energy injection. This explains the systematic reduction in valve-switching frequency, pressure ripple, and high-frequency oscillations across all tested working conditions.

4. Experimental Validation

4.1. Test Platform Setup

To validate the proposed tri-platform co-simulation framework, an electro-hydraulic tensioning testbed was implemented on an LF1352 tracked vehicle (Northeast Forestry University experimental platform, Harbin, China) (Figure 9). The setup included two custom hydraulic tensioning cylinders mounted on either side of the idler, driven by a three-valve logic circuit. This circuit consists of one 4WEH16E50B two-position four-way solenoid directional valve (Bosch Rexroth AG, Lohr am Main, Germany) and two normally closed two-position two-way solenoid valves, enabling pressurize, hold, and depressurize modes. The vehicle’s original pump supplies pressure, with an accumulator and relief valve in series to stabilize the system pressure. Sensing hardware comprises two BRT38 draw-wire displacement sensors (Shenzhen Briter Technology Co., Ltd., Shenzhen, China) and two TFD-801A pressure transducers (Generic hydraulic pressure sensor, supplier Shenzhen, China), which acquire piston displacement and chamber pressures and communicate this data to the controller via RS485. The control core is an RK3568 industrial PC (Rockchip Electronics Co., Ltd., Fuzhou, China) running Linux (The Linux Foundation, San Francisco, CA, USA) and the NMPC program. Through an RS485–IO module, the controller actuates the three solenoid valves to switch tensioning modes while performing state estimation and closed-loop regulation with a 1 ms sampling rate and a 10 ms control period. This timing configuration is consistent with the 1 ms communication step and 10 ms control update period used in the tri-platform co-simulation, ensuring temporal alignment between simulation and experiment. To ensure consistency with the co-simulation framework, the hydraulic subsystem of the test bench adopts the same valve configuration as shown in Figure 3, including the main valve and the two normally closed pilot valves. Their switching logic follows the identical pressurization–holding–release pattern used in the NMPC controller, ensuring matched boundary conditions between simulation and experiment.

All hydraulic cylinders, pressure sensors, and flow sensors used in the test bench are calibrated prior to testing. Their geometric and dynamic characteristics—including bore diameter, rod diameter, volumetric capacity, and fluid bulk properties—match those used in the AMESim model to ensure consistency between physical experiments and numerical simulations. No additional empirical tuning was performed when transferring these parameters to the simulation models, so the agreement between experiment and simulation reflects the physical fidelity of the identified parameters rather than manual curve fitting. All sensors were calibrated before testing using a certified hydraulic calibration bench. Pressure sensors were calibrated at 0–25 MPa with 0.25% FS accuracy, and draw-wire sensors were calibrated using a laser displacement reference with ±0.3 mm error. These calibrations ensure reliable experimental comparison.

4.2. Test Condition Design

To assess credibility and dynamic consistency against simulation, five test conditions (W1–W5) were established to mirror the simulation stage: steady tracking, random disturbance, transient pulse, supply-pressure fluctuation, and parameter perturbation. These conditions encompass the main operating regime and nonlinear characteristics of the electro-hydraulic tensioning system. In all tests, cylinder displacement and pressures were measured as boundary variables, and the control logic, which employs NMPC with pressurize/hold/depressurize switching, was consistent with the simulation. This setup allows for a direct comparison between simulation and experimental results. Each working condition is repeated five times, and the averaged curves are used for comparison. The reference trajectories, actuator constraints, and supply-pressure settings are kept identical to those in the corresponding W1–W5 simulation cases in Section 3, ensuring a fair and one-to-one correspondence between simulation and experiment.

4.2.1. Constant-Tension Tracking

To evaluate steady-state tracking accuracy and dynamic consistency, a step-tracking condition was employed to simulate tension command adjustments during straight, constant-speed travel. At t = 3 s, the reference tension increases from 12 kN to 15 kN. The sampling rate is 1 kHz, with a control period of 10 ms, and the oil temperature is maintained at 38 ± 1 °C. These values are identical to those used in the W1 simulation condition in Section 3.2, so that the step response in the test directly corresponds to the simulated constant-tension tracking case. The NMPC calculates the valve logic in real time, with a minimum valve holding time of 30 ms to prevent chattering. Cylinder pressures, tension, and valve duty were recorded and synchronized with the tri-platform simulation for comparison.

Figure 10a shows that in the step response, tension rises quickly and stabilizes in approximately 1.8 s. The experimental peak reaches about 15.7 kN, with an overshoot of 4.6%, while the simulation peak is 15.4 kN, with an overshoot of 2.7%. The nearly identical slopes of the rising edges suggest accurate modeling of oil compressibility and orifice losses. The steady-state mean is 14.98 kN experimentally and 15.05 kN in simulation, resulting in a relative error of 0.5%. A minor second-order ripple occurs between 3.5 and 5 s in the test data but not in the simulation, likely due to minor backlash impacts in the idler linkage and track joints (approximately 8–10 Hz), which are modeled as equivalent damping. The overall RMSE is about 0.6 kN, with a phase error of less than 20 ms, confirming dynamic consistency during steady tracking.

Figure 10b presents a frequency-domain analysis revealing distinct modal peaks around 8–10 Hz in both the experimental and simulation data, which align with the first track–idler–body mode. The simulated peak is approximately 0.4 dB lower, suggesting a slight high-frequency attenuation when under closed-loop control. The energy distributions at low frequencies (<5 Hz) align closely, indicating that the tri-platform effectively captures modal behavior while maintaining frequency-domain consistency.

4.2.2. Random Road Excitation

To assess the response under nonstationary loading, we applied random road excitation by combining multi-frequency sinusoids with Gaussian white noise (main band 1–20 Hz, predominantly around 8 Hz) during constant-speed travel. The controller used is NMPC, maintaining a 15 kN tension set-point, with a 1 kHz sampling rate, oil temperature at 40 °C, and a supply pressure of 18 MPa. These test settings coincide with the W2 random-road simulation condition, ensuring that the measured response can be directly compared with the tri-platform prediction under the same stochastic excitation. This setup evaluates both transient matching and energy consistency in the frequency domain.

Figure 11a shows that tension fluctuates continuously around the target with an amplitude of approximately ±1.4 kN. The tri-platform accurately captures both the trend and local frequencies. The simulated mean is about 0.2 kN lower, attributed to linearized contact damping. Timing alignment is precise, with a delay of approximately 15–20 ms. The root mean square error (RMSE) is approximately 0.8 kN, with a relative error of less than 6%.

Figure 11b presents a PSD comparison that highlights a significant peak at 8–12 Hz, corresponding to the first coupled mode. The tri-platform accurately replicates this energy concentration but predicts a main-peak amplitude that is approximately 15% lower, demonstrating effective energy reallocation by the closed loop. In contrast, dual-platform models often overestimate energy in this frequency band due to phase decoupling, which leads to impedance misinterpretation. The tri-platform’s synchronous millisecond-level feedback of contact energy facilitates “peak-avoidance actuation” within the prediction horizon. As a result, the main-peak power decreases by about 0.5 dB, while low-frequency energy below 5 Hz remains stable, resulting in a more compact and smoother energy distribution.

4.2.3. Transient Steering/Braking Pulses

This condition assesses the system’s response to rapid high loads and its stability during transitions. A tension increment of +2 kN is applied between 6 and 8 s, followed by a release of −1.5 kN between 18 and 20 s, with this cycle repeating periodically. This pulse profile matches the W3 steering/braking case used in the tri-platform simulation, including the same pulse magnitudes and durations. The supply pressure is set at 18 MPa, with oil temperature maintained at 41 °C. Sampling occurs at 1 kHz, and control is executed every 10 ms. The NMPC optimizes the three-valve logic in real-time, ensuring a minimum valve holding time of 25 ms for the pressurize and depressurize valves to prevent hydraulic chatter.

Figure 12a illustrates the tension dynamics following a 6 s pulse. The tension increases rapidly, reaching 17.0 kN in the experiment compared to 16.7 kN in the simulation, with an overshoot difference of approximately 1.8%. The alignment of the rising-edge slopes suggests accurate coupling of flow, pressure, and force transients. Post-pulse, the tension stabilizes in about 1.8 s, exhibiting a residual oscillation of ±0.4 kN. During the 18 s release, the tension decreases to approximately 13.4 kN and recovers in about 2.1 s, with trends matching and an RMSE of about 0.7 kN. The simulation lacks a slight secondary overshoot observed in tests during unloading, attributed to unmodeled local impacts from linkage clearance.

In Figure 12b, pressure peaks during the steering pulse are approximately 13.2 MPa (experimental) compared to 12.8 MPa (simulation), with an error of less than 3%. The tri-platform effectively replicates the dip-and-rebound observed during supply sag, maintaining phase alignment with the experiment. This demonstrates consistent time-domain coupling between hydraulic transients and mechanical feedback. In contrast, dual-platform approaches often exhibit peak shifts or over-damping due to asynchronous domain responses.

4.2.4. Supply-Pressure Drop

To evaluate stability and energy management under fluctuating power conditions, the main supply, initially at 18 MPa, is decreased by 15% at t = 12 s for approximately 3 s before being restored. This supply-pressure scenario is consistent with the W4 condition in Section 3, so that the effect of reduced hydraulic power can be evaluated under matching boundary conditions. The set-point is 15 kN, with a control interval of 10 ms and a sampling rate of 1 kHz, while the oil temperature is maintained at 40 °C. The NMPC uses a minimum valve holding time of 25 ms to avoid valve chatter. The study emphasizes tension, chamber pressure, and cumulative energy, comparing these metrics against simulation results.

Figure 13a illustrates that after a 12 s drop, the tension experiences a brief decrease, with a maximum dip of approximately 0.9 kN in the experiment compared to 0.85 kN in the simulation, resulting in an error of less than 6%. Both values recover in about 1.8 s. The smooth simulated profile, which lacks a secondary overshoot, suggests proactive valve-aperture adjustments under limited supply conditions. In contrast, dual-platform models frequently exhibit delayed compensation and secondary overshoot, underscoring the synchronized response of the tri-platform model.

Figure 13b illustrates a cumulative energy reduction of approximately 13% during the drop, followed by a gradual recovery of the slope. The simulated energy trend aligns closely with the measurements, exhibiting less than a 5% total energy error. A slight inflection in the simulation within the sag window corresponds to pre-activated constraints and valve reallocation in the optimizer. This indicates in-horizon detection of supply limits and optimal energy channeling through synchronized pressure–flow pairing.

4.2.5. Parameter Perturbation

To assess robustness and adaptability to hydraulic and mechanical variations, parameter sweeps were conducted: oil temperature ranged from 30 to 50 °C, resulting in an approximate 12% decrease in effective bulk modulus, and track pre-tension was adjusted by ±20% relative to nominal. The same parameter variations are imposed in the W5 simulation case by updating the effective bulk modulus and pre-tension–dependent contact stiffness, enabling a direct comparison of robustness between the experimental system and the tri-platform model. The tension set-point is 15 kN, with a sampling rate of 1 kHz, control interval of 10 ms, and supply pressure of 18 MPa. Cylinder pressure, tension, and valve duty were evaluated for steady-state error, fluctuation amplitude, and energy consumption, and these results were compared with simulation data.

Figure 14a shows that as the oil temperature rises, the response slows slightly, and the steady tension decreases by approximately 0.4 kN. The simulation aligns with these trends, indicating reduced chamber stiffness and increased compressibility. The simulated curve appears smoother because it does not account for local cavitation and spool-clearance micro-oscillations. The root mean square error (RMSE) for tension is approximately 0.8 kN, with most of the error occurring during thermal transients.

Figure 14b illustrates how varying track pre-tension affects both mean tension and amplitude. Increasing pre-tension by 20% raises the mean tension to approximately 15.6 kN while reducing the amplitude by about 15%. Conversely, decreasing pre-tension by 20% lowers the mean tension to around 14.3 kN and increases the amplitude by roughly 30%. The tri-platform accurately predicts these trends with a peak/valley deviation of less than 0.5 kN. The model effectively captures the impact of idler posture and contact-stiffness adjustments on chamber pressure, demonstrating high identifiability under a dynamically updated ∂F/∂p gain. The controller adjusts valve aperture and holding time across different parameter sets, ensuring stable tension and showcasing excellent adaptability.

4.3. Discussion

Experimental results demonstrate that the tri-platform strong coupling accurately replicates steady, non-stationary, and constrained conditions, keeping the dynamic error within ±1 kN and the energy-prediction error under 5%. This alignment is not due to model size but rather the synchronous preservation of energy and causality across domains. By bidirectionally exchanging the hydraulic pressure–flow (p–Q) and mechanical force–velocity (F–v) pairs at the same time step, the cylinder boundary shifts from a one-way input to a closed energy constraint, ensuring continuous power flow and a consistent dynamic response. The remaining discrepancies are mainly attributed to unmodeled local effects, such as linkage backlash, micro-cavitation, and sensor noise, rather than structural deficiencies in the proposed framework.

Figure 15 illustrates that the tri-platform setup aligns with the measured tension RMSE, energy reduction, and settling time, while enhancing error correction by approximately 35–50% and reducing energy consumption by about 12–17% compared to dual-platform baselines. The schematic on the right demonstrates the bidirectional power exchange among Simulink (control), AMESim (hydraulics), and RecurDyn (mechanics) through FMI within a unified step. Here, p–Q and F–v serve as conjugate variables. This energy loop closure achieves simultaneous convergence in both time and energy domains, confirming dynamic consistency across multi-domain interactions.

Figure 16 illustrates that dual-platform schemes operate on a unidirectional chain (control → hydraulics → mechanics) without reverse feedback. As a result, chamber-pressure variations fail to promptly reflect load disturbances, which can lead to boundary freezing and unintended energy injection. In contrast, the tri-platform approach retains interface cross-derivatives ∂F/∂p and ∂v/∂Q within a unified step of Δt = 1 ms. This enables real-time conjugate matching and ensures the instantaneous conservation relation pQ = Fv is satisfied. The observed phase alignment between tension and chamber pressure, along with the matched peak responses, provides physical evidence supporting this energy-consistency mechanism.

Figure 17 illustrates that under the supply-dip condition (W4), the simulation closely follows the measured energy slope. It demonstrates constraint pre-activation at the onset of the pressure drop, indicating anticipation of valve and pressure limits within the horizon. This proactive energy reallocation helps prevent over-throttling and secondary overshoot while also speeding up recovery. In the case of random road excitation (W2), the Power Spectral Density (PSD) shows a significant reduction in the 8–12 Hz modal band. This reduction indicates effective avoidance of modal peaks within the prediction horizon and suppression of high-frequency resonance inputs. Consequently, the tri-platform not only maintains time-domain consistency but also achieves frequency-domain energy shaping and modal coordination.

Robustness is confirmed under variations in oil temperature and pre-tension: the tri-platform accurately forecasts trends and steady-state values by retaining interface cross-derivatives. This retention allows the Jacobian to adjust to operating conditions, maintaining self-consistency in hydraulic compliance, contact stiffness, and control gains. The measured tension fluctuation range decreases from ±2.5 kN (dual-platform) to ±1.1 kN (tri-platform), demonstrating improved adaptability and energy consistency.

In summary, the tri-platform strong-coupling framework achieves high numerical accuracy while maintaining energy consistency, causal matching, and control coordination at the physics level. This demonstrates that accurate modeling of electro-hydraulic tensioning requires more than just single-domain fidelity; it necessitates cross-domain energy consistency for optimal system-level dynamics. Thus, this approach represents not just a tooling enhancement but a theoretical advancement in modeling paradigms for complex electro-hydraulic systems, offering a robust experimental and theoretical foundation for future energy-flow analysis and control-law design.

Sensitivity observations indicate that bulk modulus has the strongest influence on tension transient behavior, while track stiffness primarily affects steady-state mean tension. Friction coefficient variations introduce local fluctuations but do not affect global stability. These findings highlight which parameters require tighter identification for high-fidelity modeling.

Although experimental comparison with PID or linear MPC was not included, previous studies [24,26,29] consistently show that linear controllers struggle with the strong nonlinearities and bidirectional coupling present in tensioning systems. The proposed NMPC effectively handles valve saturation, pressure constraints, and contact-induced disturbances, which PID-type controllers cannot explicitly account for.

5. Conclusions

This study tackles the problem of dynamic inconsistency in electro-hydraulic tensioning systems for tracked vehicles under multi-time-scale coupling by introducing a Simulink–AMESim–RecurDyn tri-platform strong-coupling modeling and simulation framework. Based on the principles of power conjugation and energy consistency, this approach facilitates bidirectional energy interaction among the control, hydraulic, and multibody dynamic domains via an FMI-based unified time-step interface. This integration restores the continuity of the power flow chain and maintains the system’s causal coherence. The primary conclusions drawn from simulation analyses and full-scale experimental validation are as follows:

(1)

Unified power-conjugate consistency: The tri-platform framework enables real-time bidirectional mapping between hydraulic pressure–flow (p–Q) and mechanical force–velocity (F–v) pairs, while maintaining the cross-derivative terms ∂F/∂p and ∂v/∂Q at the hydraulic–mechanical interface. This approach preserves the structural integrity of the system’s Jacobian matrix across all domains, ensuring continuous and conservative energy transfer. By fundamentally eliminating energy mismatch and spurious power injection issues common in dual-platform models limited by ideal force sources or fixed boundaries, it provides a physically consistent foundation for high-fidelity electro-hydraulic co-simulation. This unified treatment of power-conjugate variables significantly reduces boundary-freezing effects; however, it requires accurate identification of hydraulic parameters and contact stiffness to fully retain the benefits of the strong-coupling formulation.

(2)

Enhanced observability and adaptive prediction: Real-time feedback on idler-wheel reaction forces and contact energy improves the observability of state estimators. This enables dynamic updates to the predictive model’s effective gain matrix under changing conditions. The “closed-loop identifiability” mechanism allows the control law to sustain stable gains and adaptive behavior during supply-pressure fluctuations, sudden load changes, and contact-stiffness variations. Consequently, it enhances the convergence and robustness of nonlinear model predictive control (NMPC) in highly nonlinear environments. The remaining discrepancies observed in transient responses primarily arise from unmodeled local phenomena—such as linkage backlash, micro-cavitation, and sensor noise—rather than structural limitations of the proposed observability-enhanced framework.

(3)

Enhanced numerical stability: Utilizing a unified time-step synchronous iteration alongside interface-residual correction, the tri-platform effectively enforces implicit integration constraints on a high-stiffness hybrid system. This approach ensures that hydraulic compliance, valve throttling, and contact collision dynamics are resolved on the same temporal scale. The method notably expands the local stability radius, decreasing the discrete energy error from O(Δt) to O(Δt²), and theoretically achieves L₂-stable numerical integration. This improvement in numerical stability is particularly beneficial for hybrid systems involving stiff hydraulic dynamics and intermittent contact, ensuring reliable simulation even under aggressive transient inputs and rapidly changing operating conditions.

(4)

High-fidelity experimental validation: Under five representative operating conditions—steady-state step, random road excitation, steering/braking pulse, supply-pressure drop, and parameter perturbation—the tri-platform simulation aligns remarkably well with physical test results in terms of tension force, chamber pressure, and energy distribution. The RMSE for tension is maintained within ±1 kN, and the energy-prediction error remains below 5%. The simulations accurately capture the temporal characteristics of peak pressures, valve transitions, and frequency-domain energy spectra. These findings confirm that the tri-platform achieves both numerical precision and physical consistency in energy and dynamic response. The small residual deviations between simulation and experiment are mainly attributable to measurement noise and unmodeled micro-scale structural compliance, confirming that the agreement is driven by physical fidelity rather than empirical tuning.

(5)

Theoretical and engineering significance: The proposed tri-platform framework redefines the modeling and control paradigm for electro-hydraulic systems. It unifies the dynamic description of hydraulic, mechanical, and control domains through power-conjugate matching and energy-consistency constraints. By retaining cross-derivative terms and employing synchronized time discretization, it ensures causal closure. Additionally, by embedding dynamic constraints and real-time gain adaptation within the NMPC layer, it facilitates co-optimization between the controller and the physical plant. As a result, the framework achieves vehicle-level dynamic consistency at the virtual-prototyping stage, offering a systematic theoretical foundation and engineering pathway for parameter calibration, control strategy development, and energy management of tracked-vehicle electro-hydraulic systems. Furthermore, the framework establishes a reproducible methodology for analyzing multi-domain coupling mechanisms, enabling future extensions toward soil–track interaction, intelligent actuation, and digital-twin implementations.

In summary, the tri-platform strong-coupling approach creates a unified multi-domain framework that maintains cross-domain energy consistency and causal coordination theoretically, while also experimentally confirming high-accuracy dynamic consistency. This research offers a novel theoretical foundation and practical methodology for digital design, control optimization, and energy analysis of complex electro-hydraulic systems. It provides significant transferability and scalability for virtual prototyping of tracked vehicles and other multi-domain coupled machinery. Future work will focus on extending the framework to incorporate terrain-dependent contact modeling, long-term wear effects, and hardware-in-the-loop real-time implementation, further strengthening its applicability to full-vehicle digital twins and autonomous mobility systems.