A Three-Stage Amplification Mechanism for a Compact Piezoelectric Actuator

Abstract

Mechanical amplifiers can enhance the travel range of piezoelectric actuators, thereby expanding the applications of these actuators. Various amplification mechanisms have been proposed for piezoelectric actuators with different design requirements. For instance, rhombus- and bridge-type amplification mechanisms are compact and can therefore be applied in many applications with size restrictions. However, the amplification ratio of a single-stage rhombus- or bridge-type mechanism is limited. In this study, a novel three-stage amplifier was developed to achieve a high amplification ratio while keeping the device compact. A piezoelectric actuator integrated with this amplifier had a travel range of 207.5 μm, an amplification ratio of 13.7, and dimensions of 33.5 mm × 34.2 mm × 10 mm. Moreover, this actuator was used to construct a compact jetting dispenser with dimensions of 69 mm × 72 mm × 20 mm. Experimental results suggested that this dispenser can generate uniform and stable droplets, confirming the practical utility of the developed piezoelectric actuator.

1. Introduction

Piezoelectric actuators have high precision, respond quickly, and are easy to control; therefore, they have been widely used in many fields, such as precision measurement and positioning [1,2,3]. A piezoelectric stack consists of multilayer piezoelectric plates, and its length can be modified to meet various displacement requirements [4]. The ratio between the maximum displacement and length of the piezoelectric stack is approximately 1 μm/mm [5]. For instance, a piezoelectric stack with a length of 10 mm can achieve a maximum displacement of approximately 10 μm. However, in applications that require a travel distance of hundreds of micrometers, a long piezoelectric stack must be employed, making it difficult to achieve a compact design.

Mechanical amplifiers have been widely adopted to enhance the displacement of piezoelectric stacks [6,7]. Commonly used mechanical amplifiers include those with lever, Scott Russell, rhombus-type, and bridge-type mechanisms, which are shown in Figure 1a–d, respectively. The amplification ratio of lever-type amplifiers can be modulated by adjusting the lever length [8,9]. However, a longer lever structure also increases the total width of the actuator. Moreover, an angular displacement is coupled with the linear displacement output because of the rotational motion of the lever. The Scott Russell mechanism is a mechanical linkage that can perform straight-line output motion [10,11]. However, the linkage structure of the Scott Russell mechanism requires a relatively large space. In the rhombus- and bridge-type mechanisms, a piezoelectric stack is surrounded by flexure structures, resulting in a compact configuration [12,13,14]. The amplification ratio is mainly controlled by the inclination angle of the flexures. Because the possible amplification ratios of single-stage rhombus- and bridge-type mechanisms are limited, three-dimensional, double-stage mechanisms have been proposed [15,16,17]. Moreover, diverse multistage amplifiers have been proposed for several purposes. Such amplifiers can include a series connection of the same type of amplifiers or a hybrid mechanism [18,19,20,21,22,23]. However, most multistage amplifiers are too bulky for applications such as jetting dispensers and large-range scanning probe microscopes [8,9,12,24,25,26,27].

In this study, we developed a novel three-stage amplifier to achieve a high amplification ratio while keeping the device compact. The aforementioned amplifier has an amplification ratio of 13.7. Thus, it enables a piezoelectric actuator to achieve a travel range of 207.5 μm while having small dimensions of 33.5 mm × 34.2 mm × 10 mm. This compact actuator was used to construct a jetting dispenser, which demands a travel range exceeding 200 μm.

2. Instrumentation

This section describes the proposed three-stage amplifier. The static and dynamic properties of this amplifier were examined through finite-element analysis (FEA). Moreover, displacement and force measurement setups were constructed to investigate the performance of a piezoelectric actuator containing the developed amplifier.

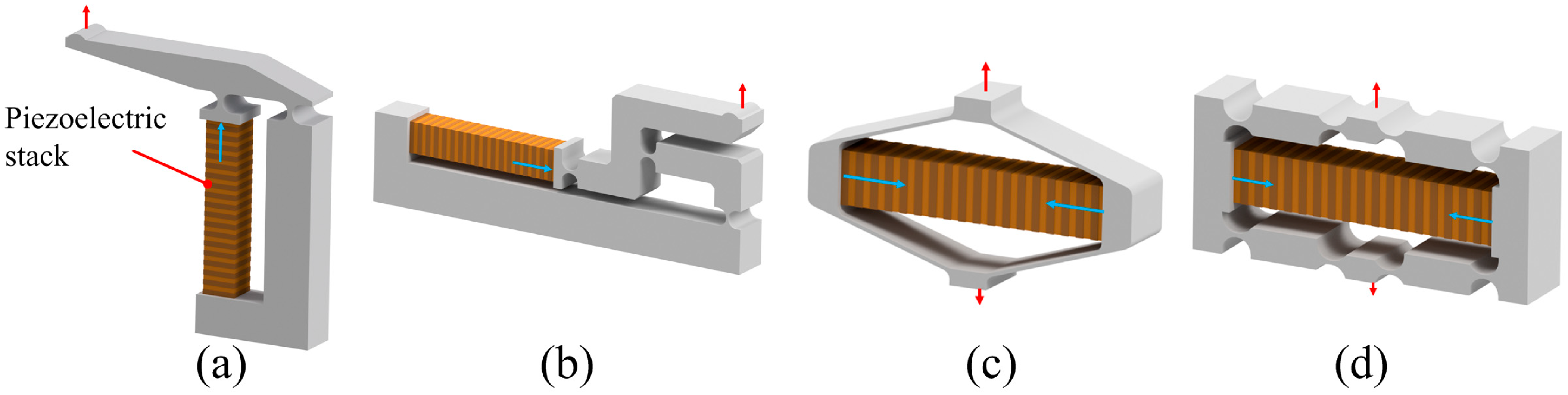
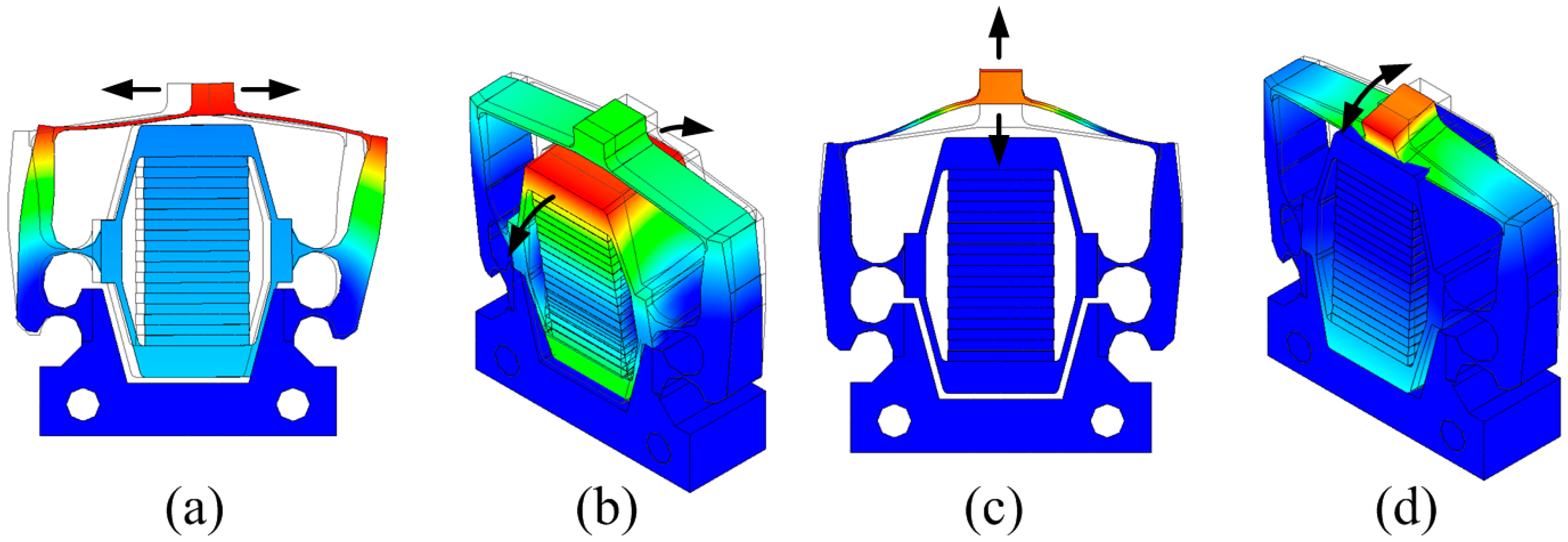
2.1. Mechanism of Three-Stage Amplification

The configuration and a photograph of a piezoelectric actuator with the developed three-stage amplifier are shown in Figure 2a,b, respectively. The amplification mechanism comprised three stages consisting of rhombus-, lever-, and semibridge-type mechanisms, respectively. The amplifier structure was made of stainless steel and fabricated through electrical discharge machining. An 18 mm-long piezoelectric stack (PSt 150/10 × 10/20, Piezomechanik GmbH) was clamped in the three-stage amplifier. The displacement of this stack was first amplified by the rhombus-type mechanism, which had an inclination angle of 15°. The rhombus structure was arranged at the center of the actuator to ensure a compact device.

FEA was employed to evaluate the amplification ratio of the proposed three-stage amplifier. The piezoelectric stack had a free-stroke displacement (D_max) of 21.2 μm at a driving voltage of 150 V, which was measured by a laser displacement sensor. According to the specification, a blocking force (F_max) of 5800 N was evaluated with a driving voltage range of 0–150 V. The relationship between the output force and displacement of the piezoelectric stack under a driving voltage of 150 V is illustrated as a dashed line in Figure 2c according to the specification of the manufacturer. To estimate the actual displacement (D_in) and force (F_in) of the piezoelectric stack clamped in the three-stage amplifier, the spring constant (k) of the amplifier had to be considered [slope of the solid red line in Figure 2c]. The FEA was performed using the Autodesk Inventor 2023 software program. In the simulation, the density, Young’s modulus, and Poisson’s ratio of the steel used to create the amplification mechanisms were set as 8 g/cm³, 193 GPa, and 0.3, respectively. Figure 2d displays the deformation of the amplifier structure, and the estimated spring constant (k) was 26.7 N/μm. Since the internal space of the rhombus structure was designed to be slightly shorter than the length of the piezoelectric stack, installation of the piezoelectric stack induced a deformation of approximately 50 μm of the rhombus structure, thereby generating a preload (F_pre) of roughly 1300 N on the piezoelectric stack. From the intersection of the dashed black line and the solid red line, the D_in [arrows 1a + 1b in Figure 2d] and F_in values were determined to be 15.0 μm and 1700 N, respectively. In the first stage of amplification, the rhombus-type mechanism converted the vertical displacement (D_in) into horizontal shrinkage. Under an amplification ratio of 1.92, the total shrinkage on the left and right sides was 28.8 μm [arrows 2a + 2b in Figure 2d]. The two levers in the second-stage amplification mechanism further amplified the displacement into 59.0 μm [arrows 3a + 3b in Figure 2d], with the amplification ratio of 2.05. These levers pushed the semibridge-type mechanism, which had an inclination angle of 8°, in the third amplification stage to generate the final output of 206.0 μm [arrow 4 in Figure 2d], with an amplification ratio of 3.49. The total amplification ratio of the three stages was 13.7.

The dynamic properties of the developed three-stage amplifier were also evaluated through FEA. Since the piezoelectric stack can influence the resonant frequencies of the amplifier structure, it was included in the simulation with PZT material properties including a density of 8 g/cm³, a Young’s modulus of 65 GPa, and a Poisson’s ratio of 0.3. Figure 3a–d display the first four resonant modes of the piezoelectric actuator, which occurred at 0.90, 1.36, 1.93, and 2.09 kHz, respectively. The third resonant mode at 1.93 kHz limited the bandwidth of the actuator; however, this frequency is higher than the required operating frequency of a jetting dispenser (i.e., 1 kHz). Moreover, the load mass may further reduce the resonant frequency of the actuator, and the actual response speed depends on the specific applications.

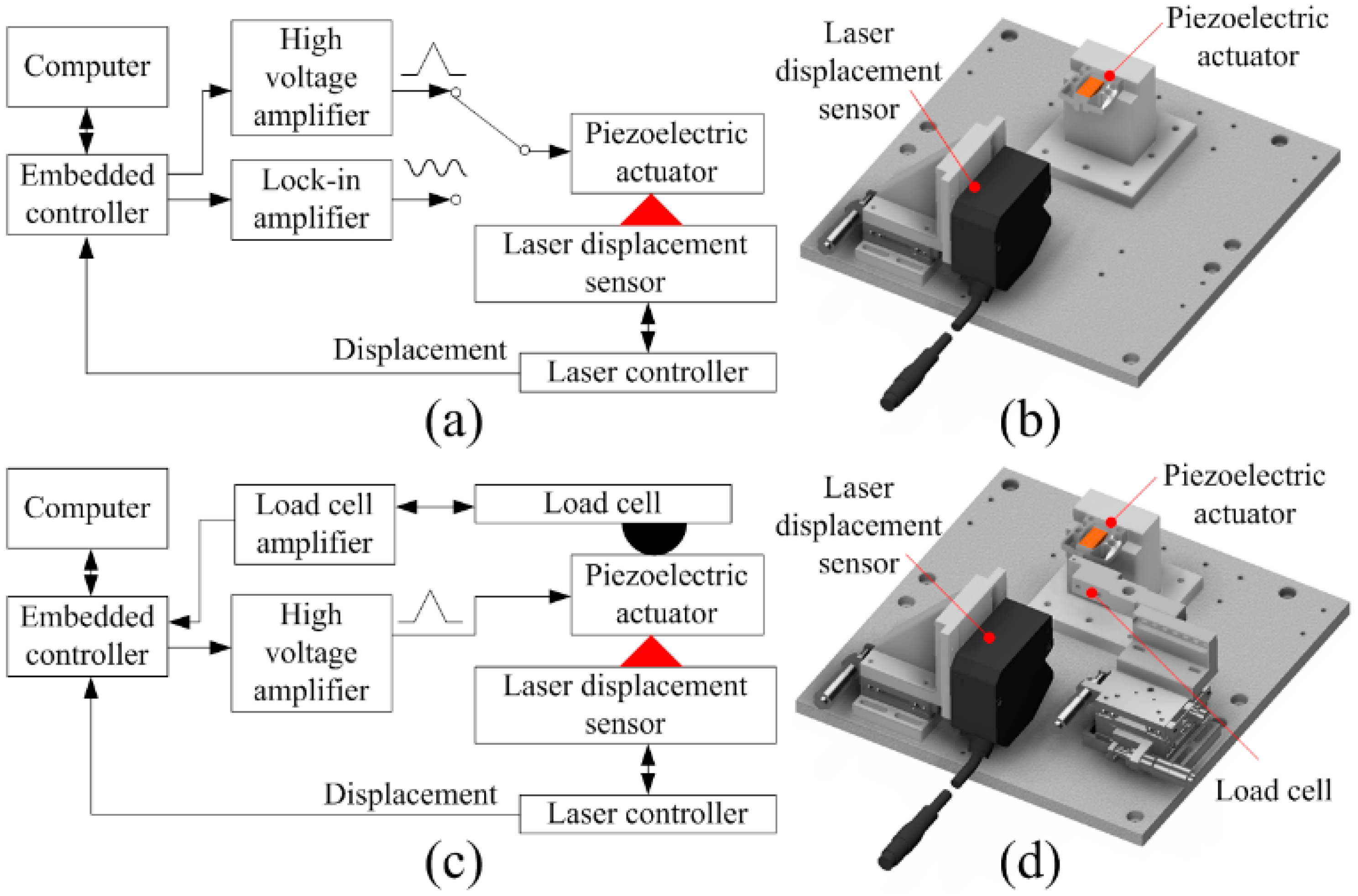
2.2. Setup for Displacement and Force Measurements

Figure 4a,b display the system configuration and mechanical design, respectively, of the test setup for examining the travel range and dynamic property of the constructed piezoelectric actuator. To measure the travel range, an embedded controller (myRIO-1900, National Instruments, Austin, TX, USA) was programmed to generate a triangular waveform, which was magnified by a high-voltage amplifier (SVR 350-3 bip, Piezomechanik GmbH, Munich, Germany) to drive the piezoelectric actuator. The displacement of the piezoelectric actuator was measured using a laser displacement sensor (LK-H052S, Keyence, Osaka, Japan), and the output displacement signal from its controller (LK-G5001, Keyence) was acquired by the embedded controller. To investigate the dynamic property, a lock-in amplifier (SR830, Stanford Research Systems, Sunnyvale, CA, USA) was employed to generate a sinusoidal signal to drive the piezoelectric actuator. The frequency of the driving signal was controlled by tracking a digital reference signal from the embedded controller. The displacement signal from the laser controller was detected at a sampling rate of 500 kHz by the embedded controller. The displacement spectrum was obtained by sweeping the driving frequency. At each driving frequency, 100,000 samples were captured to calculate the displacement amplitude of the piezoelectric actuator.

Figure 4c,d depict the test configuration and mechanical design, respectively, of the test setup for measuring the output force. During the force measurement, the piezoelectric actuator pressed against a precalibrated load cell (YZC131-05KG, TCT Electronics, Shenzhen, China), and a homemade amplifier was used to amplify the force signal. The displacement of the actuator was also measured simultaneously using the laser displacement sensor. Both force and displacement signals were recorded by the embedded controller to obtain the relationship between the output force and the displacement.

2.3. Test Setup for the Jetting Dispenser

To demonstrate an application of the developed piezoelectric actuator, it was employed to construct a jetting dispenser [Figure 5a]. The piezoelectric actuator was mounted within a frame that connected to a fluid chamber. The internal structure of the constructed jetting dispenser is depicted in Figure 5b. The overall dimensions of the jetting dispenser were 69.5 mm × 72.7 mm × 20 mm. A syringe was attached to the fluid inlet to supply the jetting fluid. The jetting dispenser operated by driving a needle to dispense droplets through the nozzle, while a spring maintained contact between the needle and the piezoelectric actuator.

To evaluate the performance of the jetting dispenser, a test system was assembled [Figure 5c]. A sample holder was mounted on a motorized Y-stage (EZSM3D030AZAK and AZDKD, Oriental Motor, Taipei, Taiwan) to facilitate sample positioning. The jetting dispenser was installed on a Z-stage (C-ZMBS650-L-A-2 and C-DR42A, Misumi, Taipei, Taiwan) for precise control of the vertical distance between the sample and the jetting dispenser. Moreover, an X-stage (EZSM3D030AZAK and AZDKD, Oriental Motor) was used to adjust the horizontal position of the jetting dispenser. The jetting dispenser was actuated using a commercial driver (VC1245, VIEWEG GmbH, Kranzberg, Germany), and a line-scan camera (PA4KGV, Hefei I-TEK, Hefei, China) was employed to monitor the size of droplets.

3. Results and Discussion

3.1. Static Displacement of the Three-Stage Amplifier

The static output displacement of the piezoelectric actuator was examined using the setup shown in Figure 4a,b. The piezoelectric actuator was driven using a triangular waveform with a voltage range of 0 to 150 V at 0.1 Hz. Two steel chips were fixed on the rhombus structure adjacent to the two ends of the piezoelectric stack clamped in the three-stage amplifier; this allowed the laser displacement sensor to measure the displacements at both ends of the stack [arrows 1a and 1b in Figure 2d, respectively]. The solid blue line and dashed red line in Figure 6a represent the displacements of the two ends, respectively, of the clamped piezoelectric stack. Furthermore, the dotted green line in this figure indicates the calculated total displacement D_in (arrow 1a + arrow 1b). The maximum forward, backward, and total displacements were 7.4, 7.8, and 15.2 μm, respectively. To measure the final output displacement of the piezoelectric actuator, the laser displacement sensor was aligned to detect the surface of the output end [arrow 4 in Figure 2d]. Figure 6b displays the relationship between the output displacement and the driving voltage, with the solid blue line and dashed red line corresponding to the extension and retraction movements of the piezoelectric actuator, respectively. The curves for extension and retraction are not coincident because of piezoelectric hysteresis. The maximum travel range was 207.5 μm under a driving voltage of 150 V, with the amplification ratio being 13.7. Both the travel range and total amplification ratio in the experiment were consistent with the results obtained in the FEA simulation.

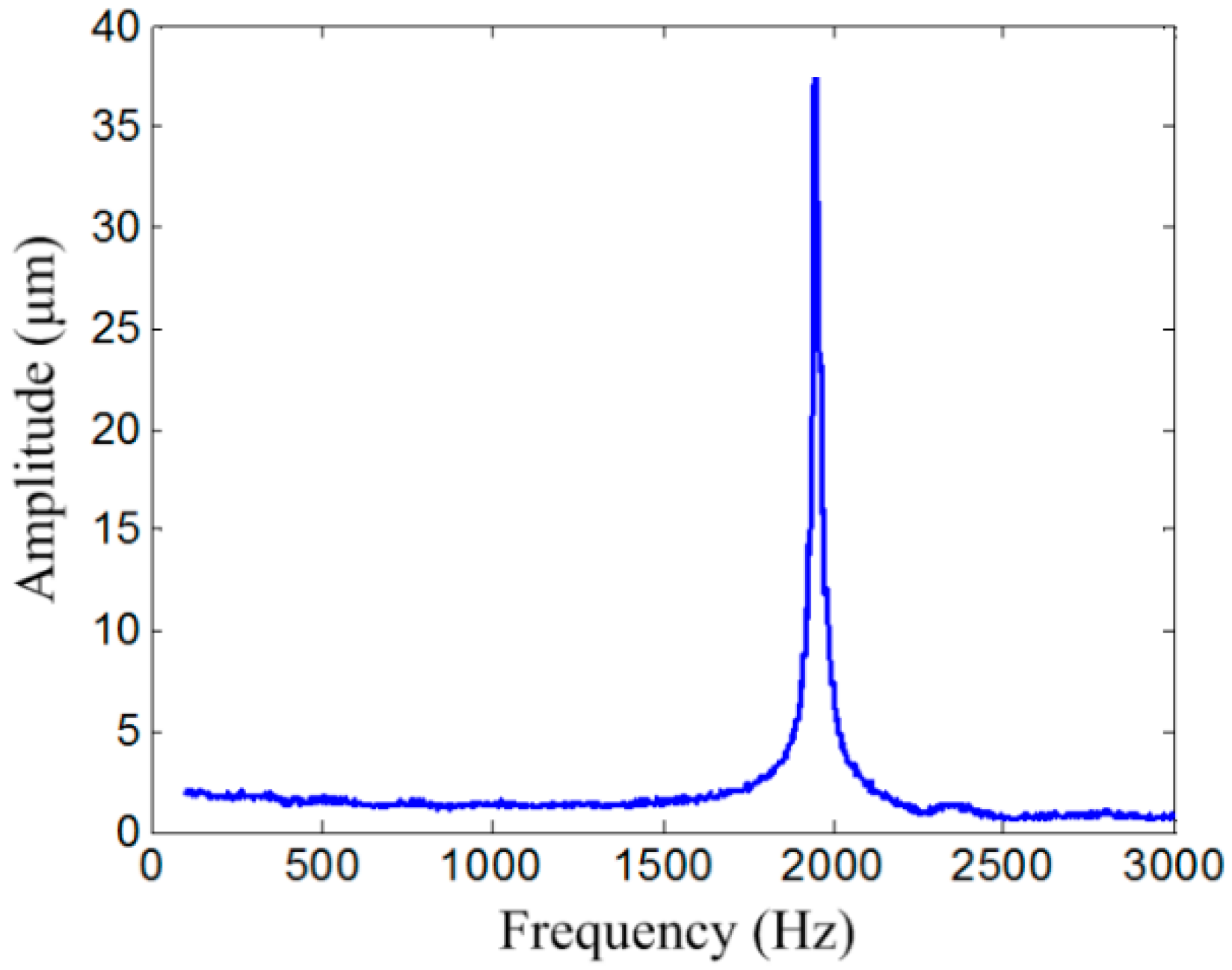
3.2. Dynamic Property of the Three-Stage Amplifier

To examine the dynamic property of the proposed three-stage piezoelectric actuator, it was driven with a sinusoidal signal by using the setup shown in Figure 4a,b. The driving frequency ranged from 0.1 to 3.0 kHz, with the driving voltage being 2.5 V. Figure 7 displays the variation in the output displacement amplitude with the driving frequency. The resonant frequency was found to be 1.95 kHz, with a corresponding output amplitude of 37.4 μm, which is consistent with the third resonant frequency of 1.93 kHz in the simulation. Since the excitation direction of the piezoelectric stack does not align with the first and second resonant modes, these modes exist but weakly coupled to the excitation. The first and second resonant modes were not observed, indicating that resonances would not be induced under the normal operation of the constructed jetting dispenser, which operates at frequencies below 1 kHz.

3.3. Output Force of the Three-Stage Amplifier

The output force of the three-stage piezoelectric actuator was examined using the setup illustrated in Figure 4c,d. The output displacement and force were measured simultaneously by the laser displacement sensor and load cell, respectively. Figure 8a shows the variation in the output displacement with the driving voltage. The maximum displacement of the piezoelectric actuator was only 76.6 μm because of the resisting force from the load cell. The solid blue line and dashed red line represent the results obtained under extension and retraction movements, respectively. Figure 8b displays the variation in the output force with the driving voltage. The maximum force of 14.6 N was achieved at a driving voltage of 150 V. Figure 8c shows the relationship between the output force and output displacement. This relationship was linear, and its slope indicated that the equivalent spring constant of the load cell was 0.19 N/μm. Under the assumption that the piezoelectric actuator had properties similar to the piezoelectric stack [Figure 2c], the relationship between the output force and output displacement under a fixed driving voltage could be determined from the dotted green lines in Figure 8c. A large resistant force reduced the output displacement of the piezoelectric actuator, and the estimated blocking force was approximately 23 N.

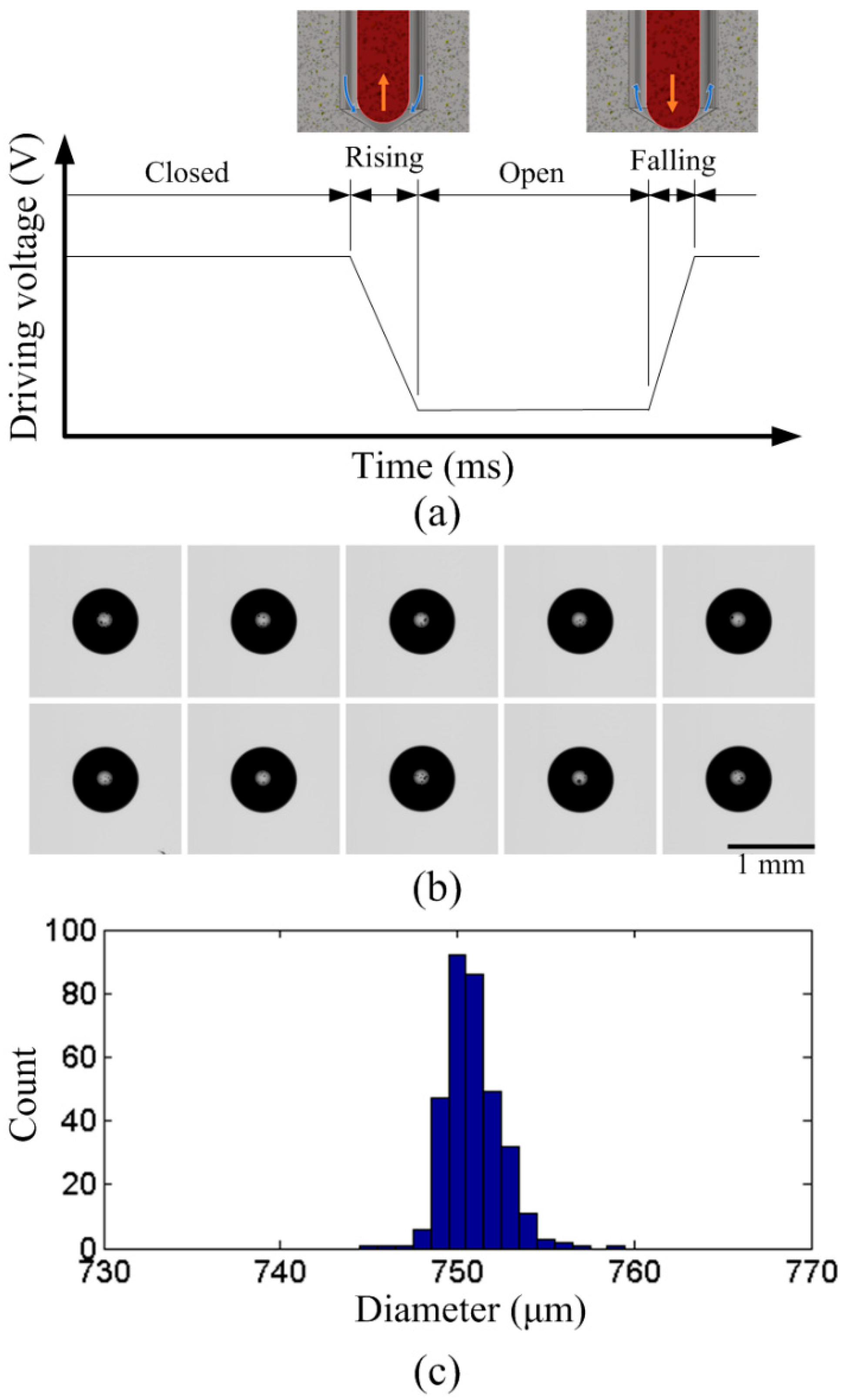
3.4. Performance of the Jetting Dispenser

To evaluate the performance of the constructed jetting dispenser [Figure 5c], the developed piezoelectric actuator was operated using a periodic driving signal [Figure 9a]. Initially, the driving voltage was maintained at 150 V; this caused the actuator to press the needle downward to keep the nozzle closed. Subsequently, the driving voltage rapidly decreased to 0 V, lifting the needle upward within 0.8 ms. The elevated needle position was maintained for 15 ms to allow fluid to fill the open space in the nozzle. The driving voltage was then restored to 150 V within 0.1 ms, generating high pressure to dispense a droplet. The nozzle then remained closed for 150 ms before the next operation cycle began.

Silicone oil (Emperor Chemical Co., Ltd., Taipei, Taiwan) with a viscosity of 1000 cP was dispensed onto a silica wafer substrate. An air pressure of 2 kgf/cm² was applied to the syringe to drive the silicone oil into the fluid chamber. Figure 9b presents optical images captured using the scan-line camera, and Figure 9c shows the size distribution of the dispensed droplets. The optical images were obtained at a resolution of 3.5 μm/pixel. Droplet profiles were extracted and analyzed using Python 3.11.11 software to determine their diameters. The mean droplet diameter was 750.9 μm, with a standard deviation of 1.6 μm, indicating that the droplet size was uniform.

4. Conclusions

In this study, a novel three-stage amplification mechanism was developed, integrating rhombus-, lever-, and semibridge-type stages to achieve a high amplification ratio of 13.7 while maintaining a compact piezoelectric actuator design with dimensions of 33.5 mm × 34.2 mm × 10 mm. The FEA simulation validated the mechanism, predicting stage-specific amplifications of 1.92, 2.05, and 3.49, yielding a total output of 206.0 μm; experimental static testing confirmed a travel range of 207.5 μm. Dynamic characterization revealed a primary resonant frequency of 1.95 kHz (matching FEA’s 1.93 kHz third mode), ensuring suitability for jetting applications.

This actuator enabled the construction of a compact jetting dispenser (69.5 mm × 72.7 mm × 20 mm), which dispensed silicone oil droplets with a mean diameter of 750.9 μm and standard deviation of 1.6 μm using a periodic driving signal. These results demonstrate uniform, stable droplet generation, confirming the actuator’s practical utility in precision dispensing and its potential for applications such as scanning probe microscopy, precision valve systems, and precision manipulation [8,27,28].