RM-Act 2.0: A Modular Harmonic Actuator Towards Improved Torque Density
Abstract
1. Introduction
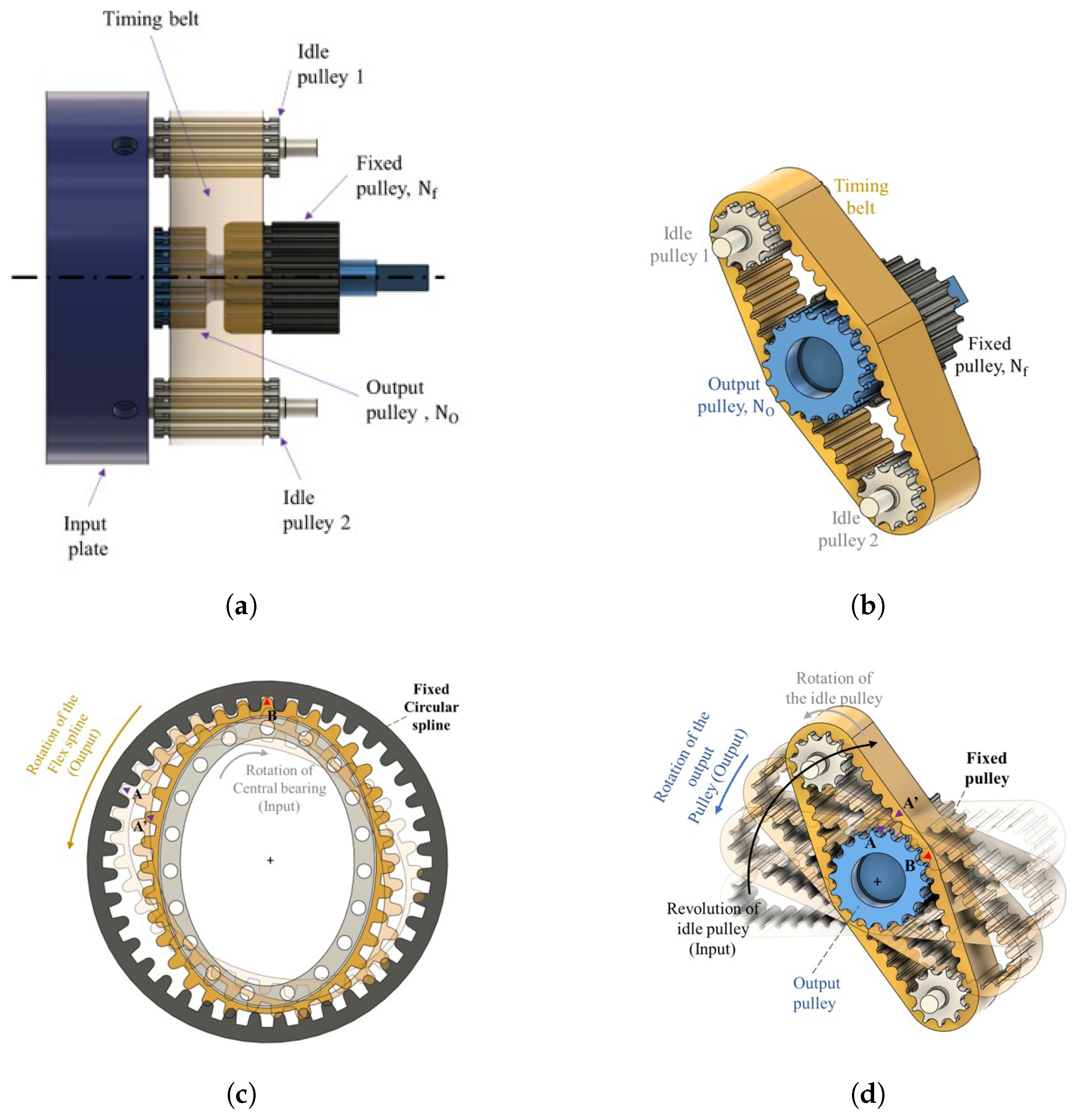
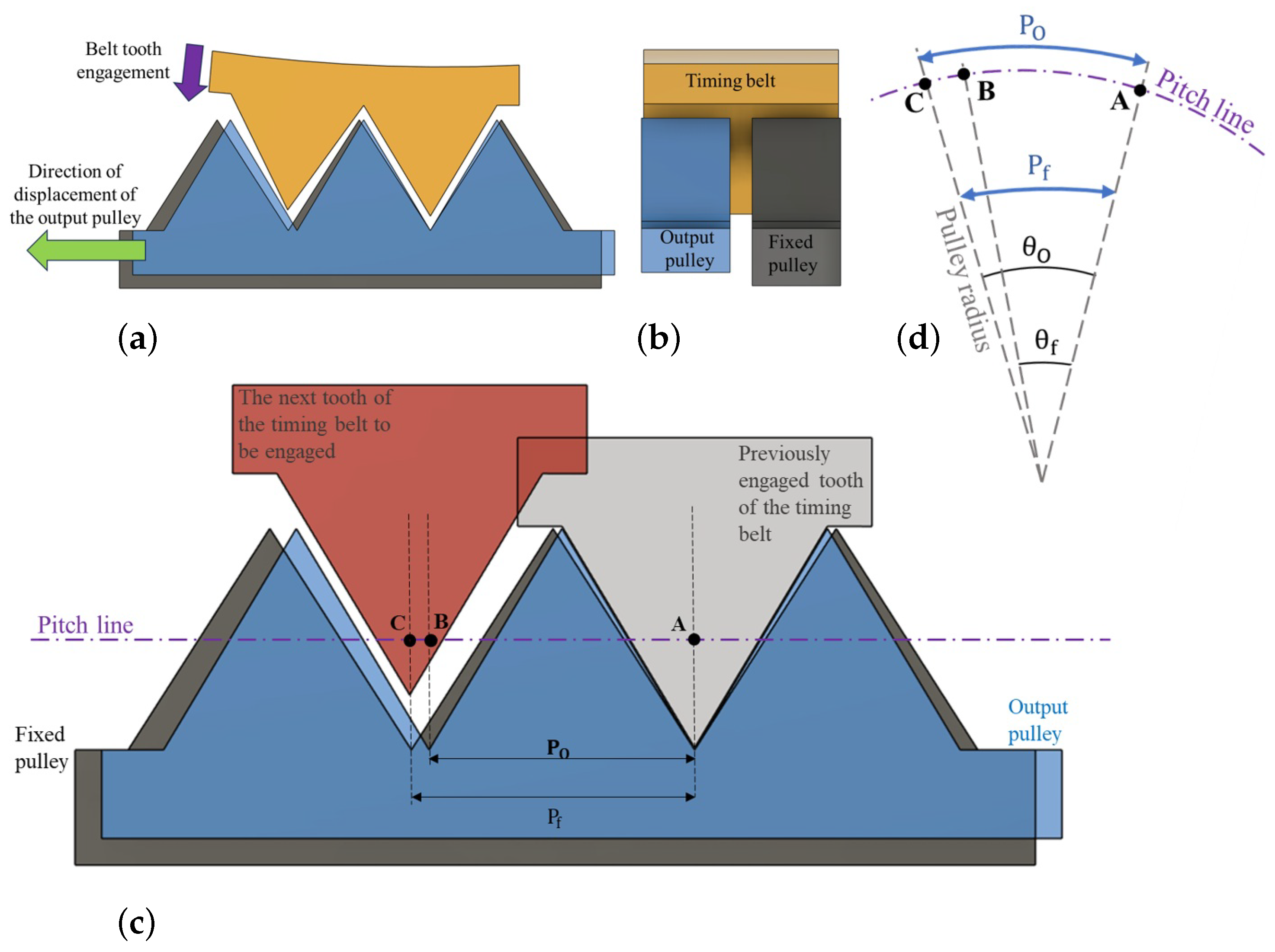
2. Concept of the Design
3. RM-Act 2.0—Final Design
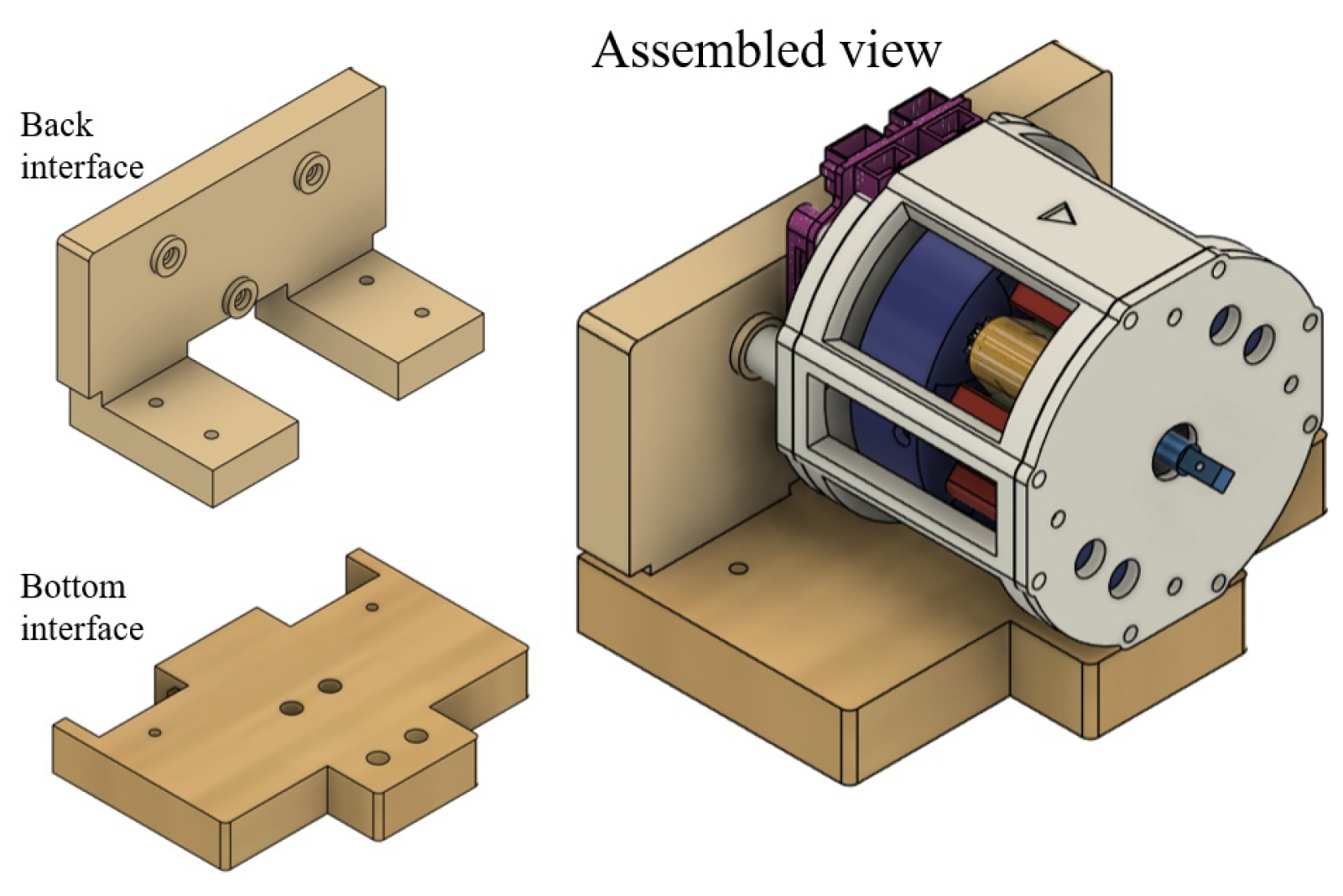
3.1. CAD Model
3.2. Parts and Material Specification
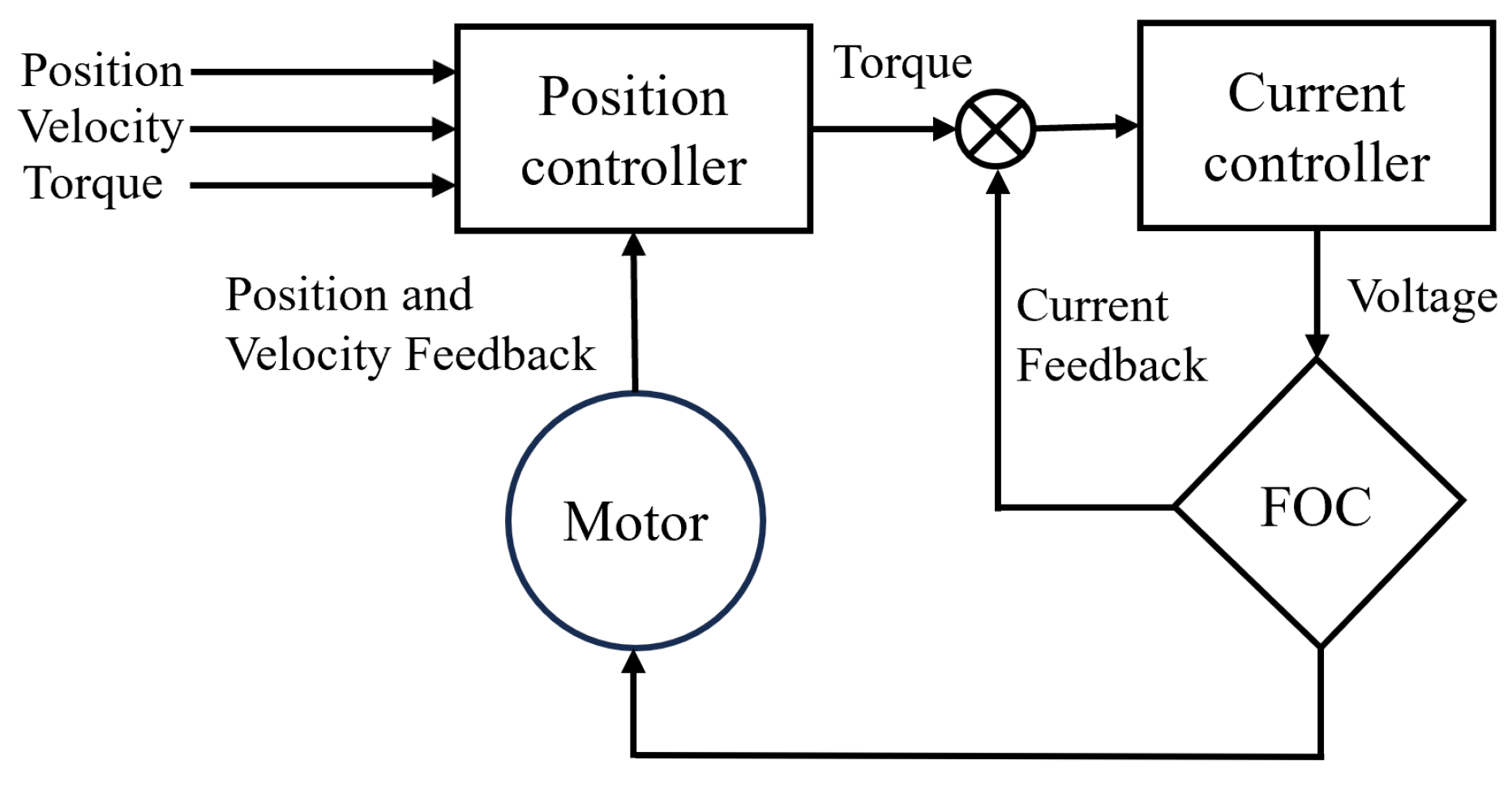
3.3. Electronics and Control
4. Testing and Results
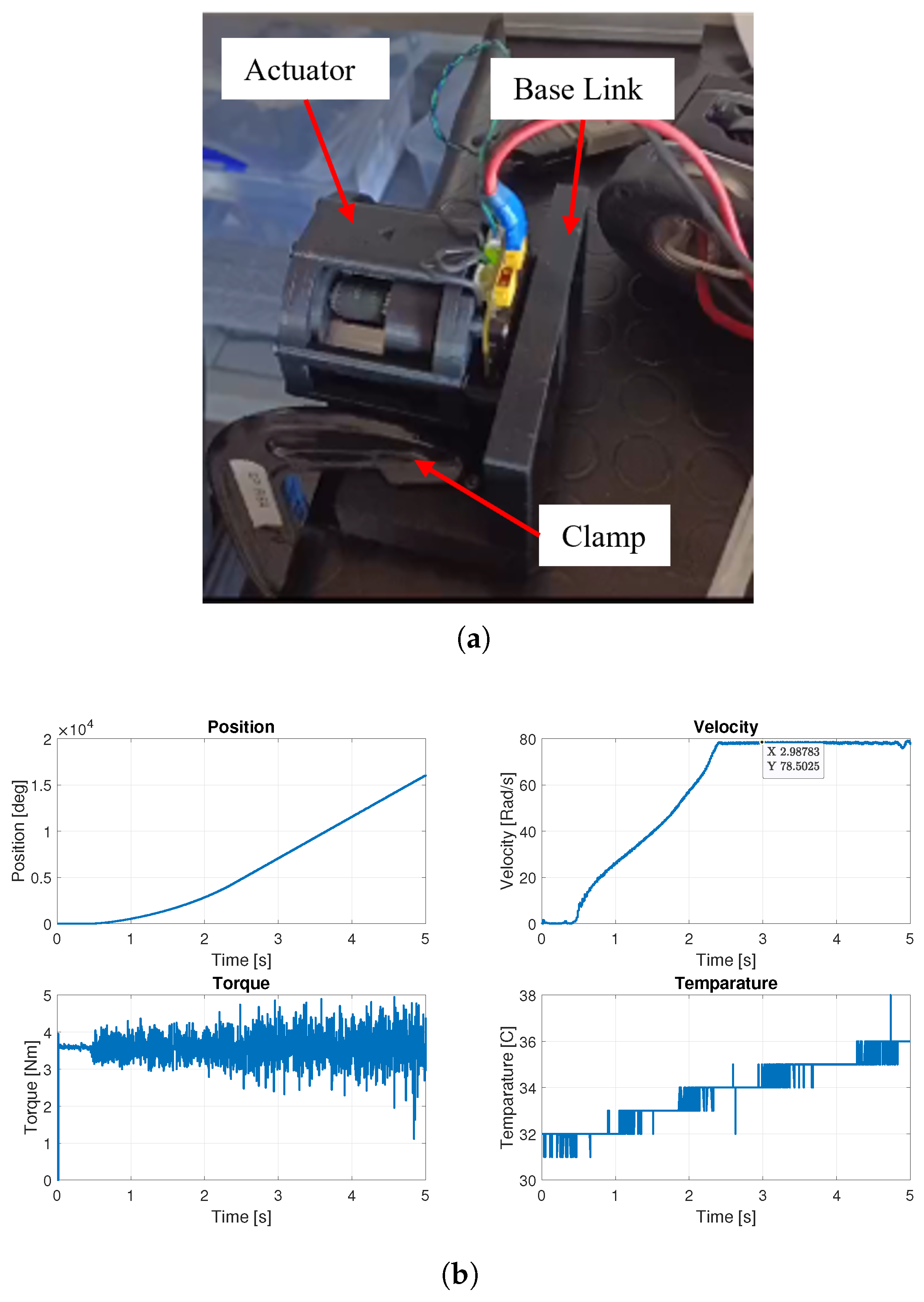
4.1. Static Tests
4.2. Dynamic Tests
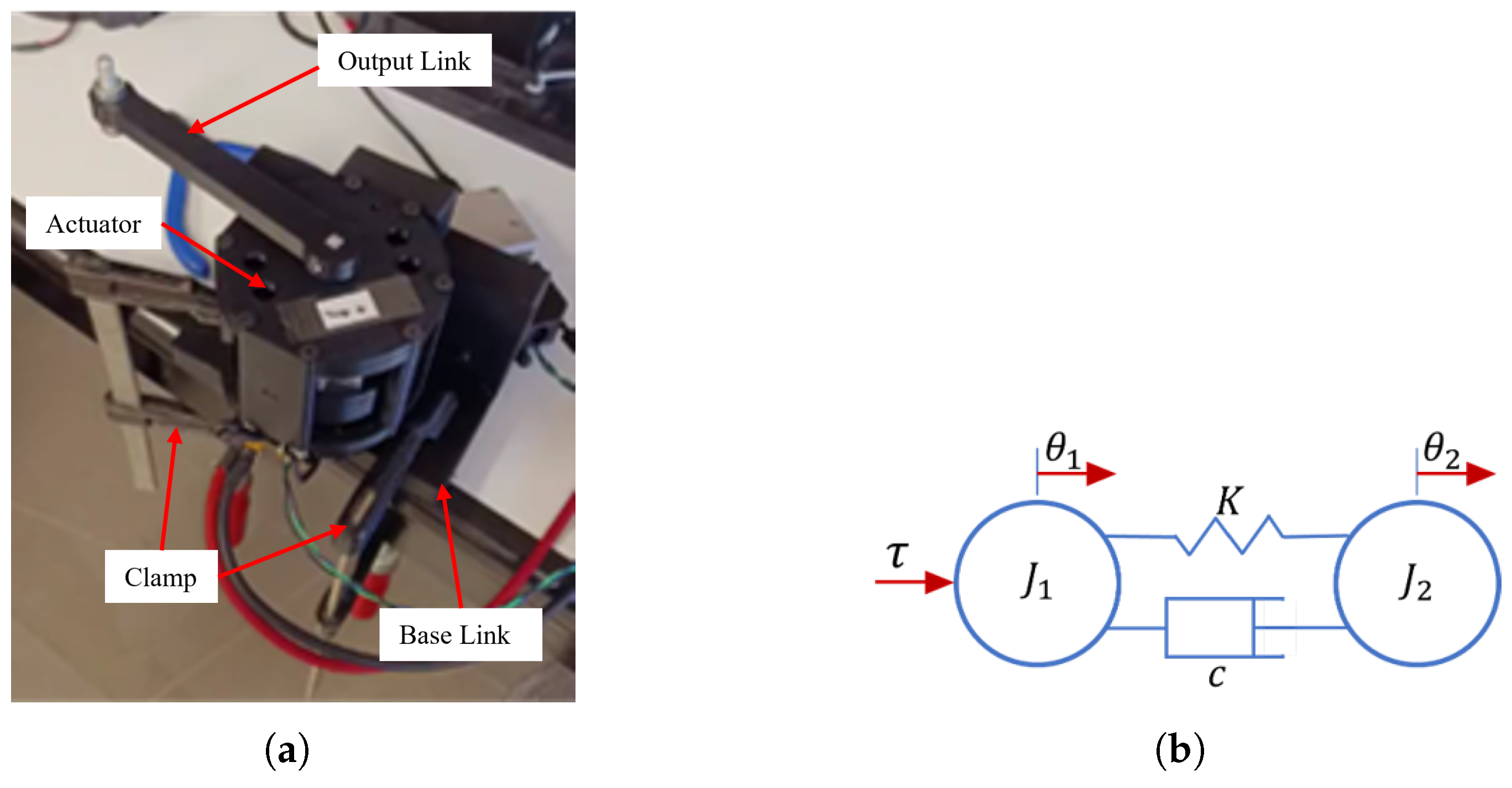
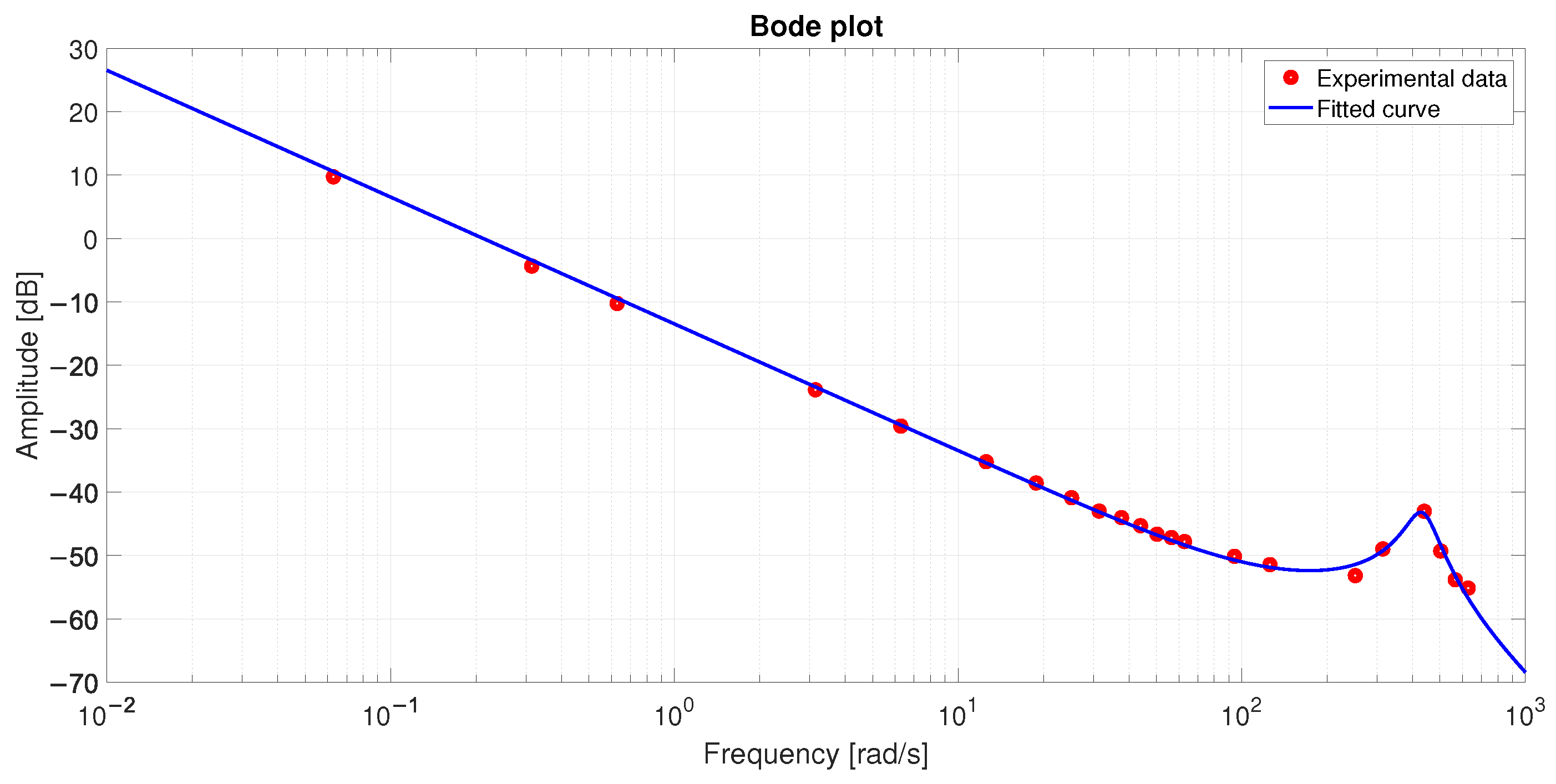
5. Model Identification
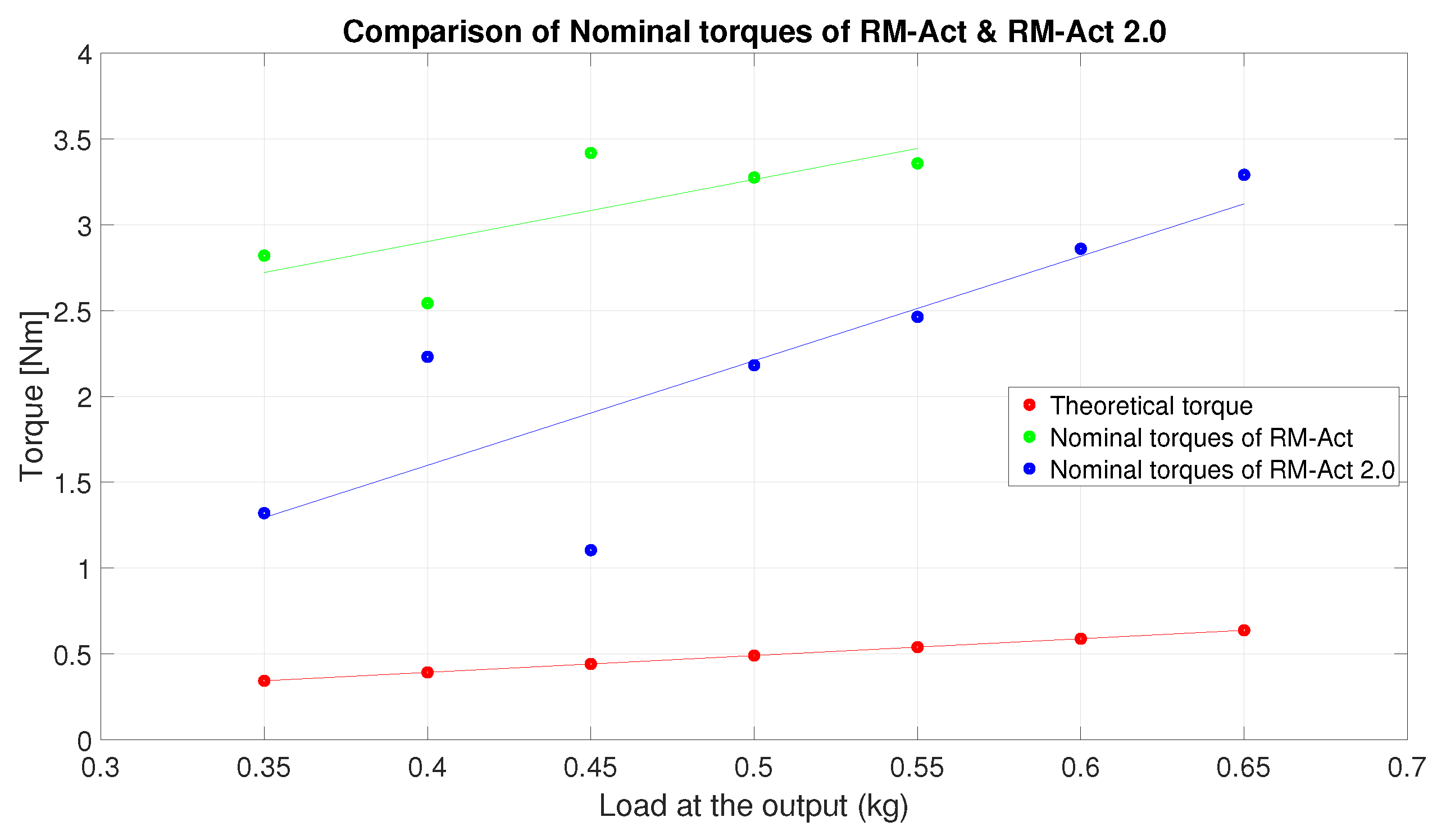
6. Quick Comparison Between the RM-Act & RM-Act 2.0 Actuators
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HG | Harmonic Gearboxes |
| WG | Wave Generator |
| FS | Flex Spline |
| CS | Circular Spline |
| HD | Harmonic Drive |
| CAD | Computer Aided Design |
| 3D | Three Dimensional |
| FDM | Fused Deposition Modeling |
| DOF | Degree of Freedom |
References
- Scheinman, V.; McCarthy, J.M.; Song, J.B. Mechanism and actuation. In Springer Handbook of Robotics; Springer International Publishing: Cham, Switzerland, 2016; pp. 67–90. [Google Scholar]
- Al Kouzbary, M.; Al Kouzbary, H.; Liu, J.; Khamis, T.; Al-Hashimi, Z.; Shasmin, H.N.; Arifin, N.; Abu Osman, N.A. Robotic Knee Prosthesis with Cycloidal Gear and Four-Bar Mechanism Optimized Using Particle Swarm Algorithm. Actuators 2022, 11, 253. [Google Scholar] [CrossRef]
- Yadav, V.; Kumar, D.; Srivastav, A.; Sarangi, S. Modelling and FEM simulation of a rotating hyperelastic spherical balloon actuator. Aust. J. Mech. Eng. 2024, 22, 37–48. [Google Scholar] [CrossRef]
- Laffranchi, M.; Tsagarakis, N.; Caldwell, D.G. A compact compliant actuator (CompAct™) with variable physical damping. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 4644–4650. [Google Scholar]
- Arnaudov, K.; Karaivanov, D.P. Planetary Gear Trains; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Arm, P.; Zenkl, R.; Barton, P.; Beglinger, L.; Dietsche, A.; Ferrazzini, L.; Hampp, E.; Hinder, J.; Huber, C.; Schaufelberger, D.; et al. Spacebok: A dynamic legged robot for space exploration. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 6288–6294. [Google Scholar]
- Wensing, P.M.; Wang, A.; Seok, S.; Otten, D.; Lang, J.; Kim, S. Proprioceptive actuator design in the mit cheetah: Impact mitigation and high-bandwidth physical interaction for dynamic legged robots. IEEE Trans. Robot. 2017, 33, 509–522. [Google Scholar] [CrossRef]
- Bjelonic, M.; Klemm, V.; Lee, J.; Hutter, M. A survey of wheeled-legged robots. In Proceedings of the Climbing and Walking Robots Conference, Ponta Delgada, Portugal, 12–14 September 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 83–94. [Google Scholar]
- Iotti, F.; Ranjan, A.; Angelini, F.; Garabini, M. OmniQuad: A wheeled-legged hybrid robot with omnidirectional wheels. Mech. Mach. Theory 2025, 214, 106125. [Google Scholar] [CrossRef]
- Ranjan, A.; Iotti, F.; Angelini, F.; Garabini, M. TraQuad: A Modular Tracked Legged Multimodal Quadrupedal Robot. IEEE/ASME Trans. Mechatron. 2025, 1–13. [Google Scholar] [CrossRef]
- Slatter, R. Weiterentwicklung eines Präzisionsgetriebes für die Robotik; Antriebstechnik: St. Leonard, France, 2000. [Google Scholar]
- Sensinger, J.W.; Lipsey, J.H. Cycloid vs. harmonic drives for use in high ratio, single stage robotic transmissions. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 4130–4135. [Google Scholar]
- Schorsch, J. Compound Planetary Friction Drive. Patent No. 2013496, 20 September 2016. [Google Scholar]
- Schreiber, H.; Schmidt, M. Getriebe. Patent No. DE 10 2015105 525 A1, 10 April 2015. [Google Scholar]
- Kanai, Y.; Fujimoto, Y. Torque-sensorless control for a powered exoskeleton using highly back-drivable actuators. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 5116–5121. [Google Scholar]
- Fankhauser, P.; Hutter, M. Anymal: A unique quadruped robot conquering harsh environments. Res. Featur. 2018, 126, 54–57. [Google Scholar]
- Kang, I.; Peterson, R.R.; Herrin, K.R.; Mazumdar, A.; Young, A.J. Design and Validation of a Torque-Controllable Series Elastic Actuator-Based Hip Exoskeleton for Dynamic Locomotion. J. Mech. Robot. 2022, 15, 021007. [Google Scholar] [CrossRef]
- Font-Llagunes, J.M.; Lugrís, U.; Clos, D.; Alonso, F.J.; Cuadrado, J. Design, Control, and Pilot Study of a Lightweight and Modular Robotic Exoskeleton for Walking Assistance After Spinal Cord Injury. J. Mech. Robot. 2020, 12, 031008. [Google Scholar] [CrossRef]
- Sun, Z.; Li, Y.; Zi, B.; Chen, B. Development and dynamic state estimation for robotic knee–ankle orthosis with shape memory alloy actuators. J. Mech. Des. 2024, 146, 013302. [Google Scholar] [CrossRef]
- Li, R.; Zhou, G.; Huang, J.; Li, J. Lightweight design and verification of space harmonic drive. Int. J. Mech. Sci. 2025, 296, 110302. [Google Scholar] [CrossRef]
- Kondo, K.; Takada, J. Study on tooth profiles of the harmonic drive. J. Mech. Des. 1990, 112, 131–137. [Google Scholar] [CrossRef]
- Maiti, R. A novel harmonic drive with pure involute tooth gear pair. J. Mech. Des. 2004, 126, 178–182. [Google Scholar] [CrossRef]
- Yao, Y.; Lu, L.; Chen, X.; Xie, Y.; Yang, Y.; Xing, J. A Novel Cycloid Tooth Profile for Harmonic Drive with Fully Conjugate Features. Actuators 2025, 14, 187. [Google Scholar] [CrossRef]
- Chang, J.; Chang, I. Design of high ratio gear reducer using vernier differential theory. J. Mech. Des. 2021, 143, 023401. [Google Scholar] [CrossRef]
- Megalingam, R.K.; Vadivel, S.R.R.; Manoharan, S.K.; Pula, B.T.; Sathi, S.R.; Gupta, U.S.C. Reduced Kinematic Error for Position Accuracy in a High-Torque, Lightweight Actuator. Actuators 2024, 13, 218. [Google Scholar] [CrossRef]
- Ling, Z.; Zhao, L.; Xiao, D.; Zhou, Y.; Ma, C.; He, K.; Liu, G. A Novel Strain Wave Gear Reducer with Double Flexsplines. Actuators 2023, 12, 313. [Google Scholar] [CrossRef]
- Muttathil Gopanunni, R.K.; Martignetti, L.; Iotti, F.; Ranjan, A.; Angelini, F.; Garabini, M. EM-Act: A Modular Series Elastic Actuator for Dynamic Robots. IEEE Open J. Ind. Electron. Soc. 2024, 5, 468–480. [Google Scholar] [CrossRef]
- Galea, M.; Hamiti, T.; Gerada, C. Torque density improvements for high performance machines. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 1066–1073. [Google Scholar]
- Lin, X.; Wu, Y.; Olson, G.F.; Liu, J.; Wu, L.; Peretti, L. Optimal Pole-Transition Current Distribution for Constant Torque Maintenance and Stator Copper Loss Minimization in Variable-Pole Machines. IEEE Trans. Transp. Electrif. 2025, 11, 10573–10582. [Google Scholar] [CrossRef]
- Lin, X.; Liu, J.; Liu, Z.; Gao, Y.; Peretti, L.; Wu, L. Model-Free Current Predictive Control for PMSMs With Ultra-Local Model Employing Fixed-Time Observer and Extremum-Seeking Method. IEEE Trans. Power Electron. 2025, 40, 10682–10693. [Google Scholar] [CrossRef]
- Xu, R.; Shen, X.; Lin, X.; Liu, Z.; Xu, D.; Liu, J. Robust Model Predictive Control of Position Sensorless Driven IPMSM Based on Cascaded EKF-LESO. IEEE Trans. Transp. Electrif. 2025, 11, 8824–8832. [Google Scholar] [CrossRef]
- Uppalapati, K.K.; Calvin, M.D.; Wright, J.D.; Pitchard, J.; Williams, W.B.; Bird, J.Z. A magnetic gearbox with an active region torque density of 239 N· m/L. IEEE Trans. Ind. Appl. 2017, 54, 1331–1338. [Google Scholar] [CrossRef]
- Shin, W.; Ahn, B.; Kwon, S. A low backlash and highly efficient gearbox for robot actuator. In Proceedings of the 2024 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 15–19 July 2024; pp. 224–229. [Google Scholar]
- Zhou, G.; Yang, Y.; Xie, R.; Chang, L.; Gao, B. A novel harmonic movable tooth drive with almost surface contact conjugate tooth profiles: Parametric design, modification and analysis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 9032–9048. [Google Scholar] [CrossRef]
- Buleandra, D.; Băneasă, A.; Donca, R. 3D Printed Harmonic Drive for Legged Mobile Robots. In Proceedings of the International Conference on Robotics in Alpe-Adria Danube Region, Cluj-Napoca, Romania, 5–7 June 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 597–605. [Google Scholar]
- Pacana, J.; Pacana, A.; Oliwa, R. Possibilities of Using Selected Additive Methods for the Production of Polymer Harmonic Drive Prototypes. Materials 2023, 16, 4073. [Google Scholar] [CrossRef] [PubMed]
- Dini, M. Harmonic Drive with Compact Structure Made by Plastic Material. Patent No. US20250012348A1, 9 January 2025. [Google Scholar]
- Muttathil Gopanunni, R.K.; Martignetti, L.; Angelini, F.; Garabini, M. RM-Act: A Novel Modular Harmonic Actuator. Actuators 2025, 14, 492. [Google Scholar] [CrossRef]
- Pettersson, M.; Ölvander, J. Drive train optimization for industrial robots. IEEE Trans. Robot. 2009, 25, 1419–1424. [Google Scholar] [CrossRef]
- Scaldaferri, A.; Tolomei, S.; Iotti, F.; Gambino, P.; Pierallini, M.; Angelini, F.; Garabini, M. Otto-Design and Control of an 8-DoF SEA-driven Quadrupedal Robot. IEEE Open J. Ind. Electron. Soc. 2025, 6, 820–839. [Google Scholar] [CrossRef]
- Yunfei, L.; Chengning, Z. A comparative experimental analysis of PMSM between deadbeat prediction current control and field-oriented control. Energy Procedia 2019, 158, 2488–2493. [Google Scholar] [CrossRef]







| Component | Specification/Model | Qty. | Source/Manufacturing | Type |
|---|---|---|---|---|
| Motor | Antigravity 5006 KV 450 | 1 | T-Motor, Jiangxi, China | Commercial |
| Timing belt | Poggi® 120-3MGT-15 | 1 | Casa del Cuscinetto S.P.A., Livorno, IT | Commercial |
| Idler pulley | Poggi GT® 11-3MR-80-AL | 2 | Casa del Cuscinetto S.P.A., Livorno, IT | Commercial + In-house machining |
| Output pulley | Poggi GT® 18-3MR-125-AL | 1 | Casa del Cuscinetto S.P.A., Livorno, IT | Commercial + In-house machining |
| Fixed pulley | Poggi GT® 20-3MR-125-AL | 1 | Casa del Cuscinetto S.P.A., Livorno, IT | Commercial + In-house machining |
| Snap rings | Sizes 9, 16, and 18 | 4,1,1 | RS Components S.r.l., Milan, IT | Commercial |
| Bearing A | SKF W-638-4-2Z | 1 | MISUMI, Frankfurt am Main, DE | Commercial |
| Bearing B | SKF W-628-6-2Z | 1 | MISUMI, Frankfurt am Main, DE | Commercial |
| Bearing C (and E) | SKF W-627-3-2Z | 16 | MISUMI, Frankfurt am Main, DE | Commercial |
| Bearing D | SKF W-61705 | 1 | MISUMI, Frankfurt am Main, DE | Commercial |
| Fasteners | Ø3 mm pins, M2/M3 screws | Various | Casa del Cuscinetto S.P.A., Livorno, IT | Commercial |
| tensioners | N/A | 1 sets | Aluminum | In-house |
| supports, covers | N/A | 1 each | 3D printed using ABS (FDM) | In-house |
| Moteous microcontroller | r4.8 32-bit | 1 | Mjbots, Cambridge, MA, USA | Commercial |
| Sl. No | Load (kg) | ||
|---|---|---|---|
| 1 | 0.350 | 0.3433 | 1.3202 |
| 2 | 0.400 | 0.3924 | 2.2310 |
| 3 | 0.450 | 0.4414 | 1.1047 |
| 4 | 0.500 | 0.4905 | 2.1817 |
| 5 | 0.550 | 0.5395 | 2.4637 |
| 6 | 0.600 | 0.5886 | 2.8606 |
| 7 | 0.650 | 0.6376 | 3.2913 |
| 8 | 0.700 | 0.6867 | – |
| Parameter | Symbol | Value |
|---|---|---|
| Motor inertia | 2.1 × 10−3 kg·m2 | |
| Link inertia | 1.2 × 10−2 kg·m2 | |
| Total stiffness | K | 360.29 Nm/rad |
| Friction | c | 3.4 × 10−1 Nm·s2/rad |
| Parameter | Unit | RM-Act | RM-Act 2.0 | Relative Change (%) |
|---|---|---|---|---|
| Size (Diameter × Length) | mm | −21.05 (Length) | ||
| Weight | kg | 0.333 | 0.329 | −1.2 |
| Reduction ratio | – | 9:1 | 9:1 | 0.0 |
| Number of stages | – | 1 | 1 | 0.0 |
| Total stiffness | Nm/rad | 130.4 | 360.3 | +176.4 |
| Continuous output power | W | 450 | 450 | 0.0 |
| Max. nominal torque (Load) | Nm (kg) | 3.36 (0.55) | 3.29 (0.65) | −2.1 |
| Max. peak torque | Nm | 3.96 | 5.41 | +36.6 |
| Max. speed | rad/s | 86.0 | 78.5 | −8.7 |
| Active rotation angle | – | Continuous | Continuous | 0.0 |
| Angular resolution | Deg | 360/16,384 | 360/16,384 | 0.0 |
| Nominal voltage | V | 24 | 24 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muttathil Gopanunni, R.K.; Ranjan, A.; Martignetti, L.; Angelini, F.; Garabini, M. RM-Act 2.0: A Modular Harmonic Actuator Towards Improved Torque Density. Actuators 2025, 14, 538. https://doi.org/10.3390/act14110538
Muttathil Gopanunni RK, Ranjan A, Martignetti L, Angelini F, Garabini M. RM-Act 2.0: A Modular Harmonic Actuator Towards Improved Torque Density. Actuators. 2025; 14(11):538. https://doi.org/10.3390/act14110538
Chicago/Turabian StyleMuttathil Gopanunni, Ramesh Krishnan, Alok Ranjan, Lorenzo Martignetti, Franco Angelini, and Manolo Garabini. 2025. "RM-Act 2.0: A Modular Harmonic Actuator Towards Improved Torque Density" Actuators 14, no. 11: 538. https://doi.org/10.3390/act14110538
APA StyleMuttathil Gopanunni, R. K., Ranjan, A., Martignetti, L., Angelini, F., & Garabini, M. (2025). RM-Act 2.0: A Modular Harmonic Actuator Towards Improved Torque Density. Actuators, 14(11), 538. https://doi.org/10.3390/act14110538






