Study and Optimization of Shore-to-Ship Underwater Capacitive Power Transfer System Considering Parasitic Coupling
Abstract
1. Introduction
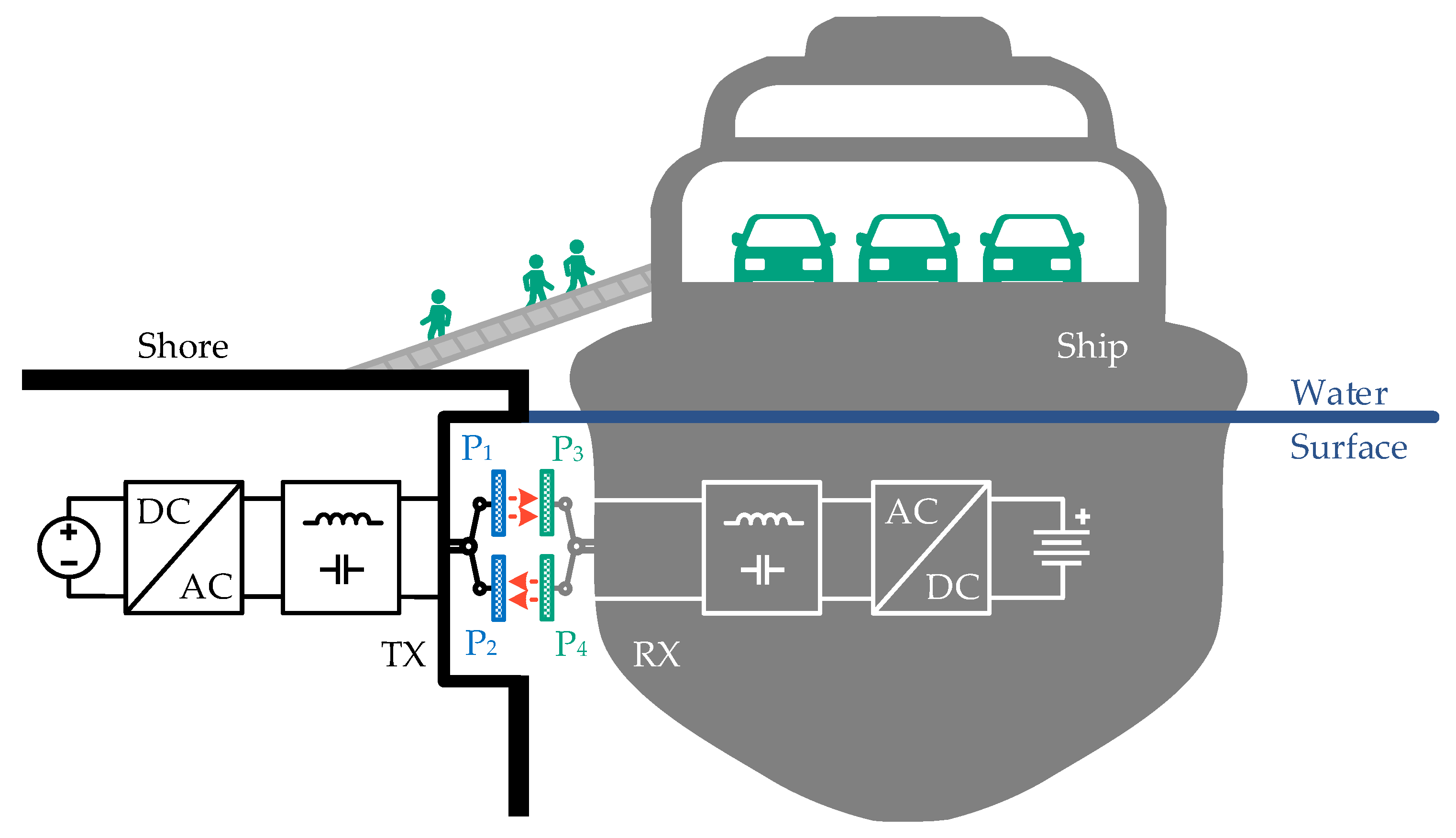
2. Underwater Capacitive Power Transfer System for Electric Ships
3. UCPT System for Electric Ships
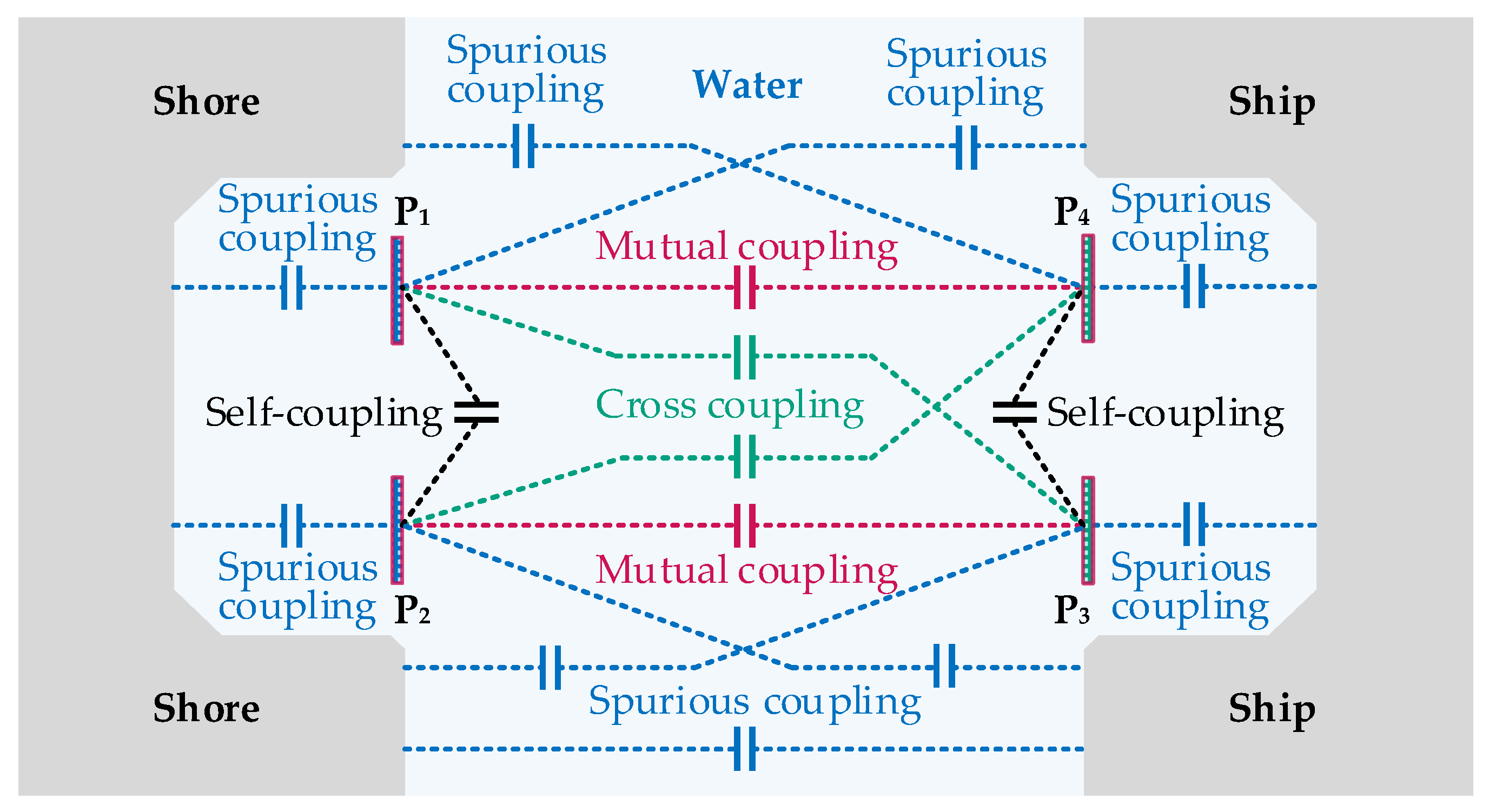
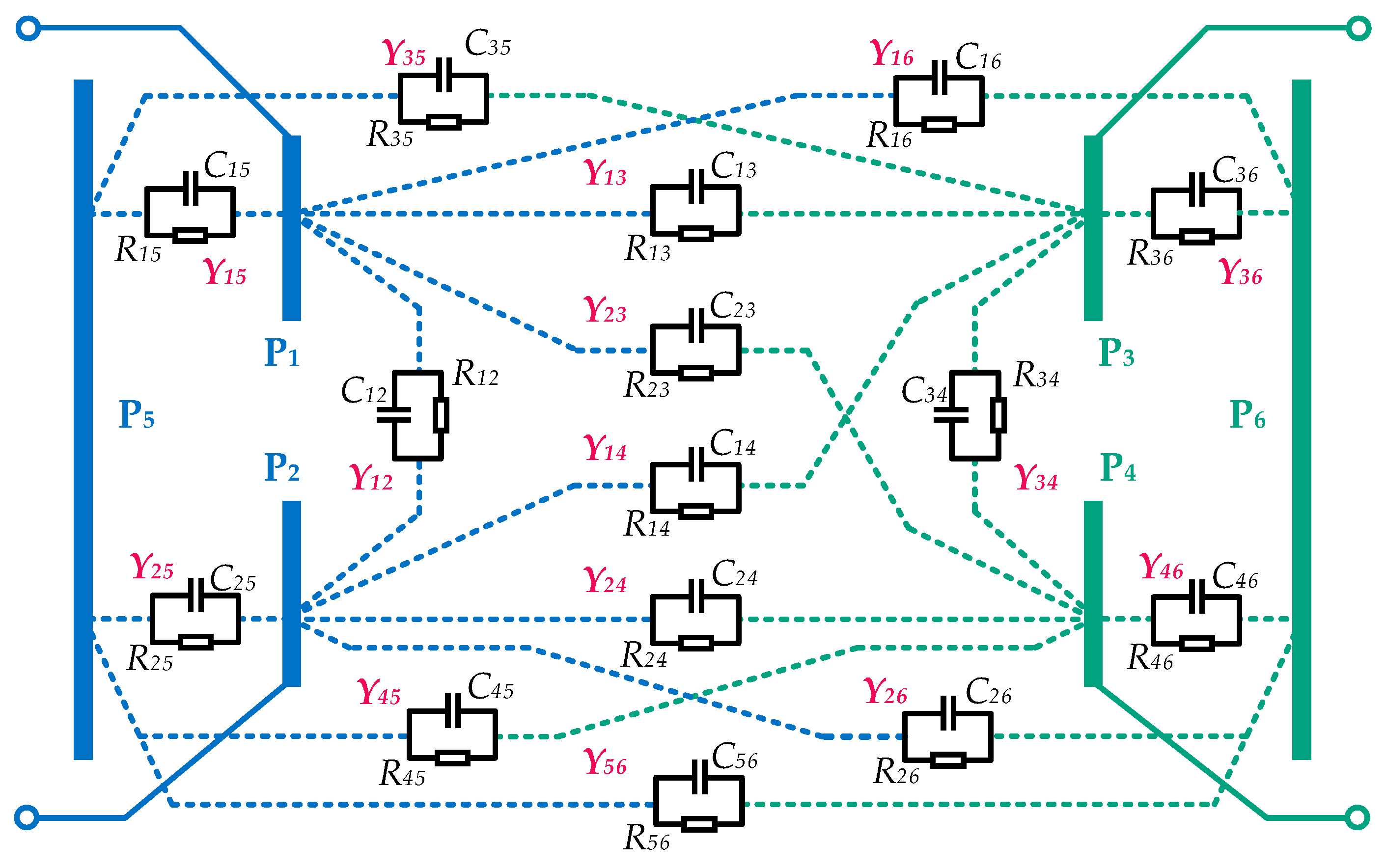
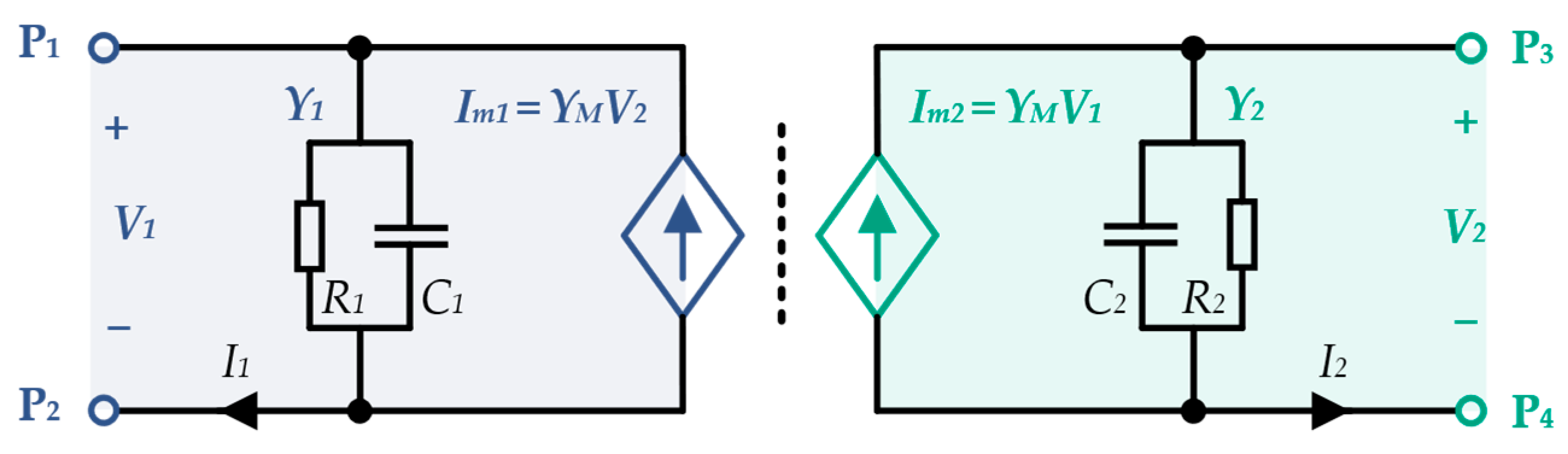
3.1. Simplification and Equivalence of the Coupler Model
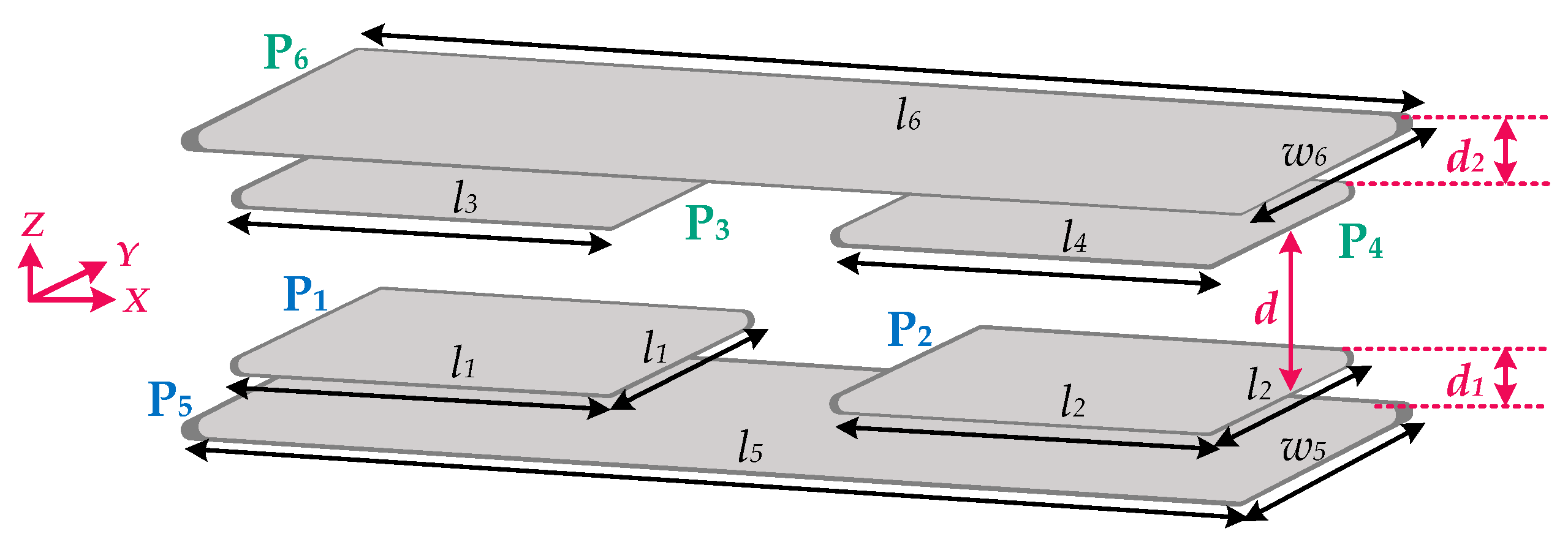
3.2. Coupler Dimension Configuration
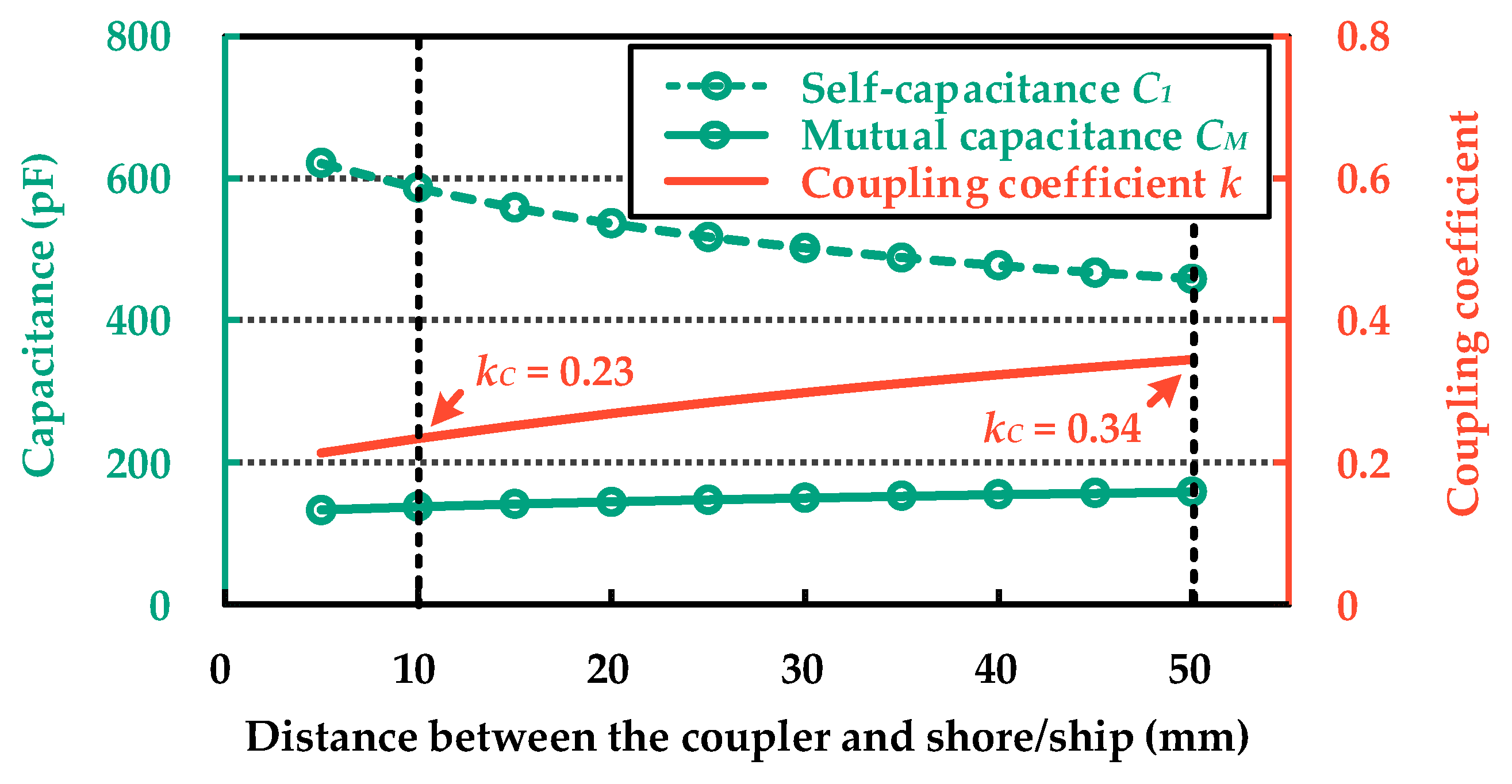
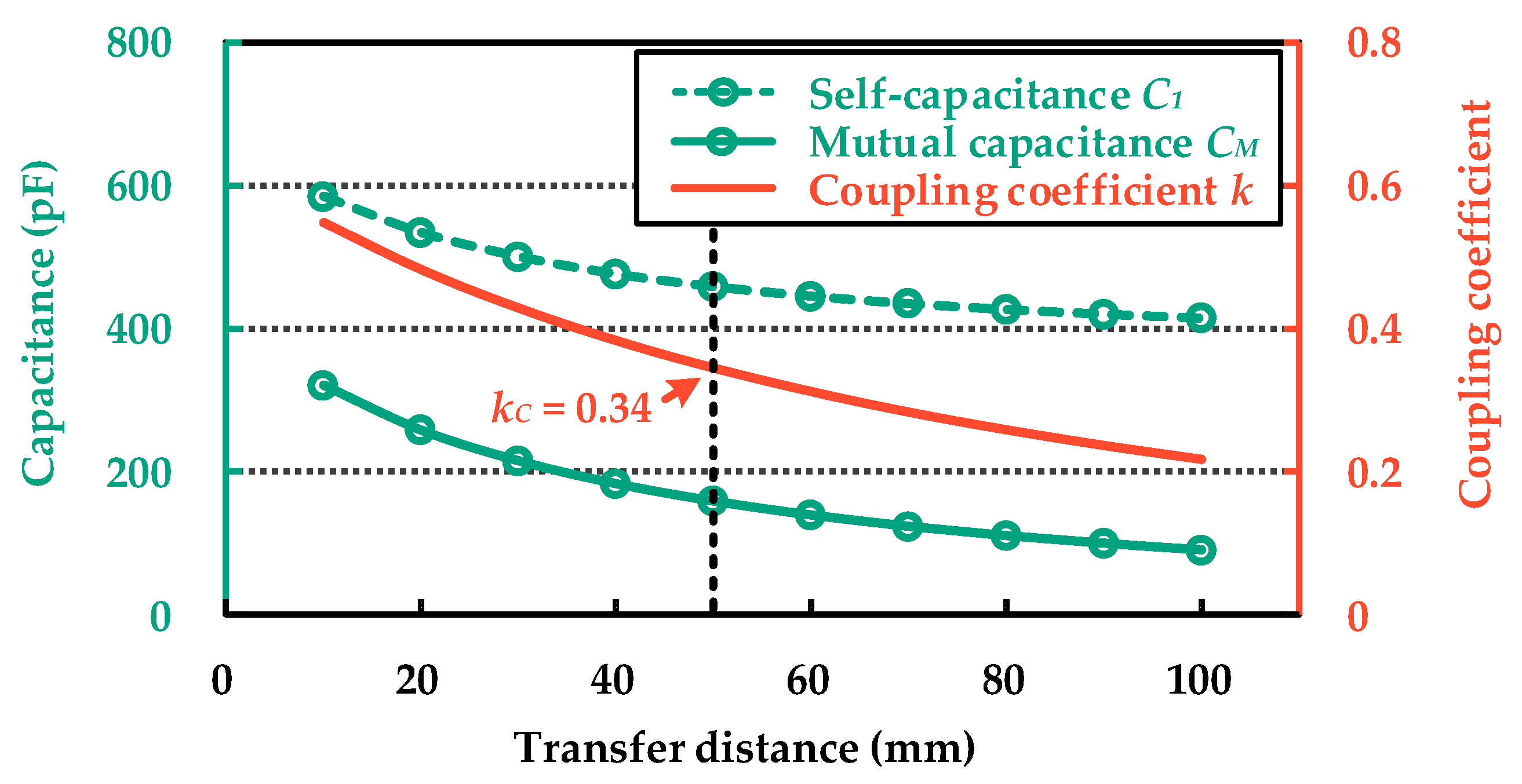
3.3. Characteristics Analysis of Coupler
4. Compensation Network Design
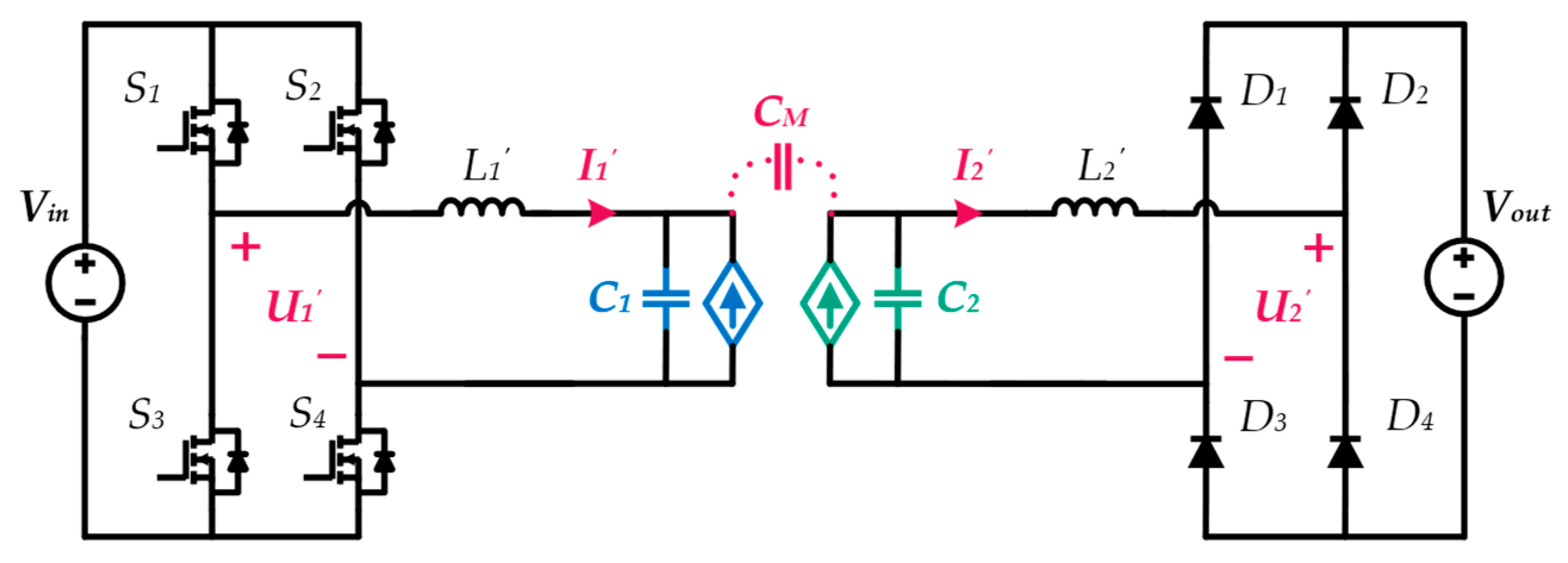
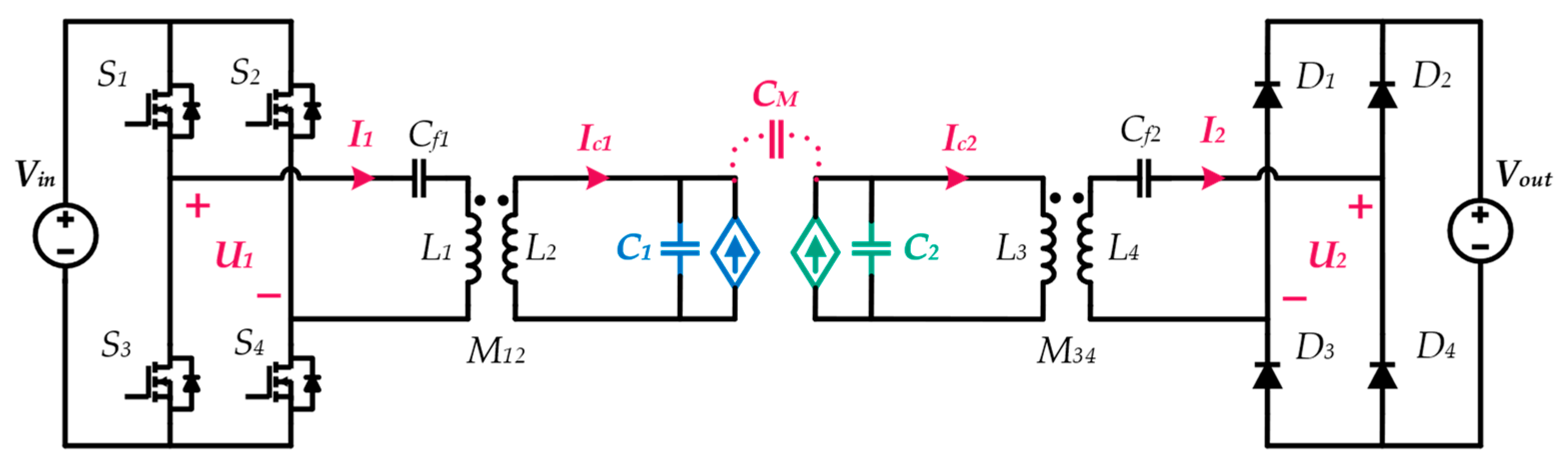
4.1. Compensation Network Structure
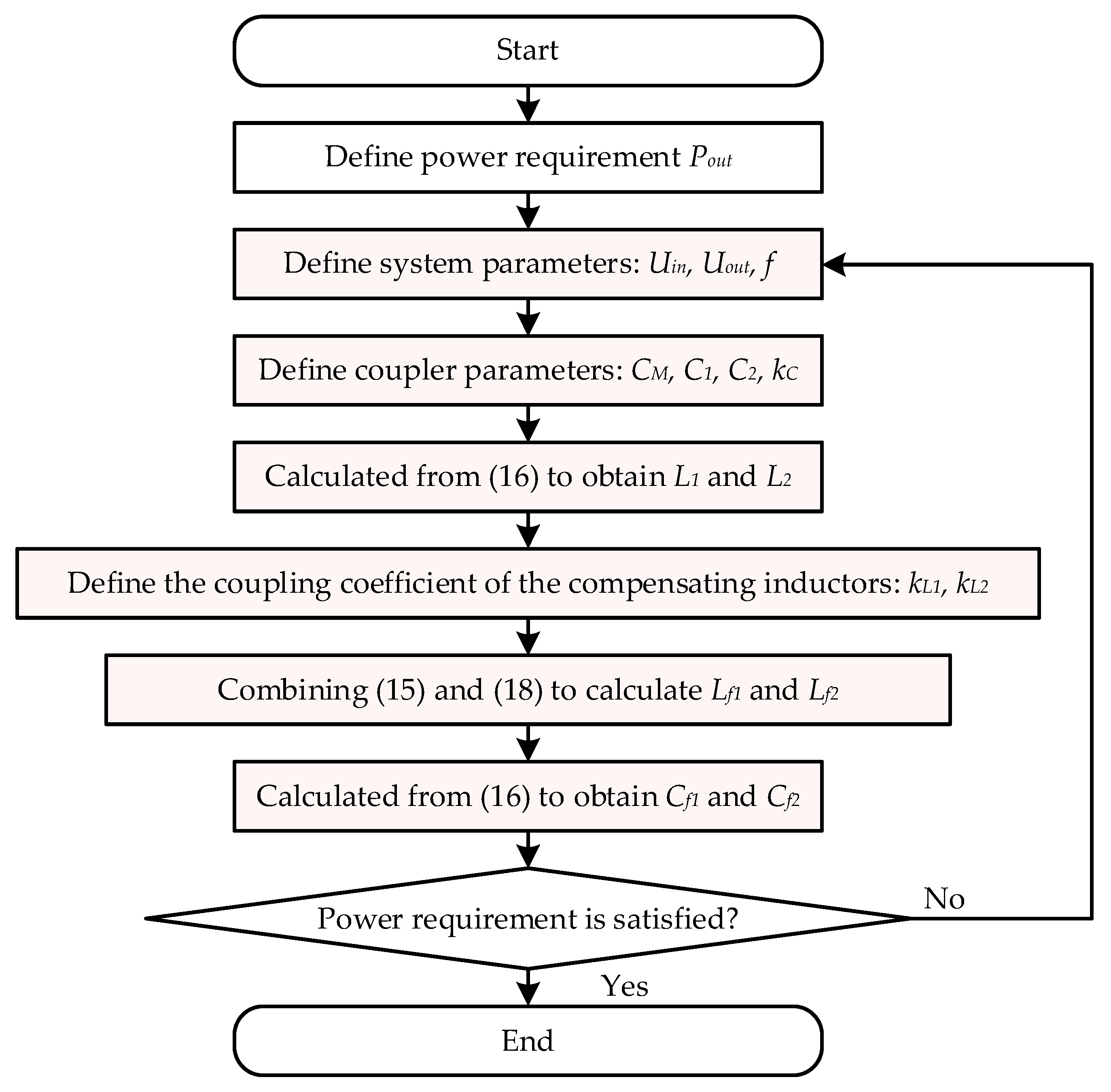
4.2. Parameter Design
5. Experimental Verification
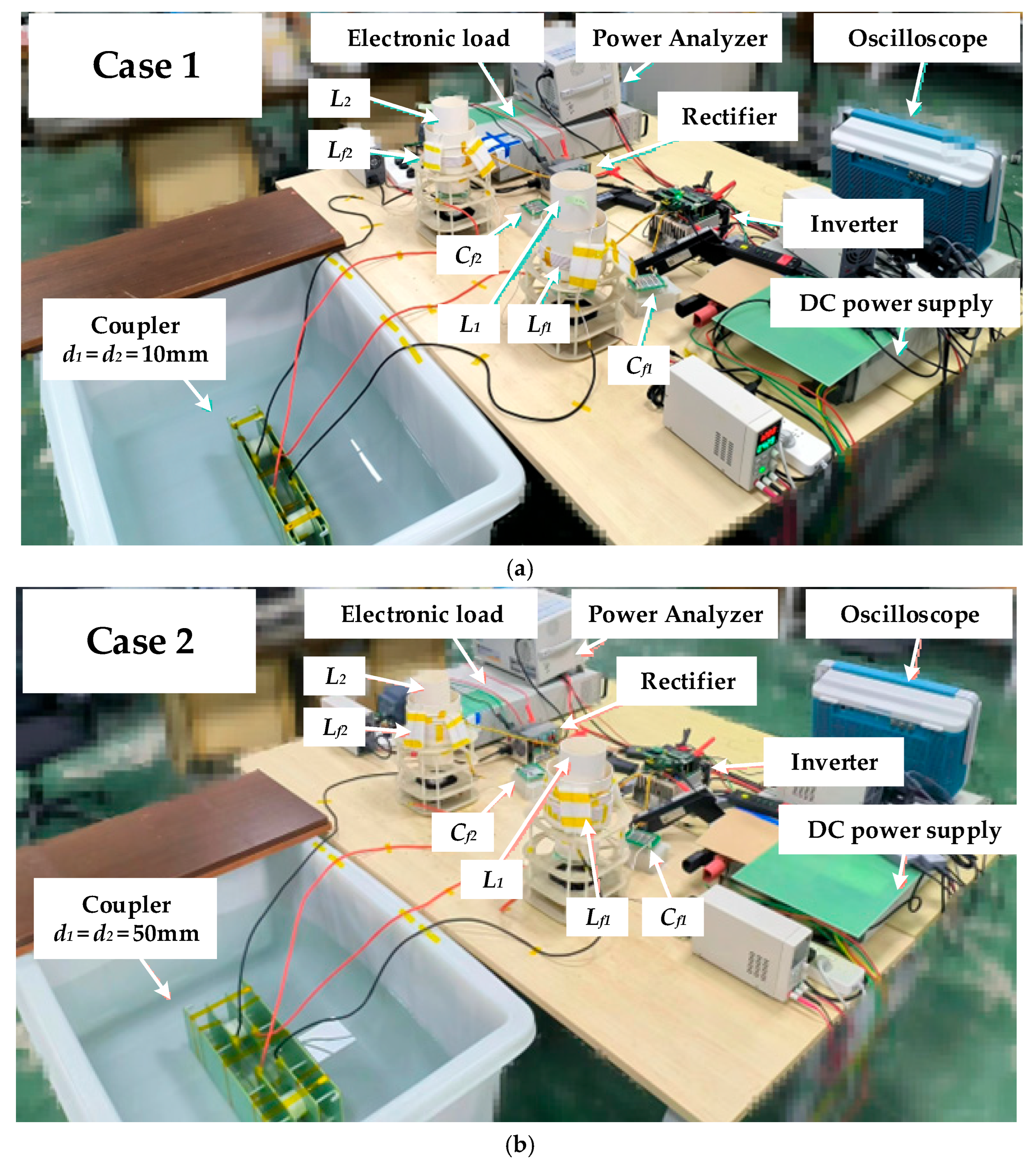
5.1. Experimental Platform
5.2. Experimental Results
6. Conclusions and Discussions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, G.-h.; You, Y.-m. Optimal Design for Torque Ripple Reduction in a Traction Motor for Electric Propulsion Vessels. Actuators 2025, 14, 314. [Google Scholar] [CrossRef]
- Liu, Y.; He, Y.; Liang, J.; Cao, Y.; Liu, Z.; Song, C.; Zhu, N. Progress on Research and Application of Energy and Power Systems for Inland Waterway Vessels: A Case Study of the Yangtze River in China. Energies 2025, 18, 4636. [Google Scholar] [CrossRef]
- Roberts, T.; Williams, I.; Preston, J.; Clarke, N.; Odum, M.; O’Gorman, S. Ports in a Storm: Port-City Environmental Challenges and Solutions. Sustainability 2023, 15, 9722. [Google Scholar] [CrossRef]
- Yu, X.; Xie, R.; Tu, Y.; Zhuang, Y.; Cheng, X.; Yin, F.; Zhang, Y. Compact Wireless Power Transfer with Enhanced Misalignment Tolerance via Independent Secondary PWM Control. IEEE Trans. Power Electron. 2025, 40, 11998–12002. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, P.; Wu, X.; Wang, L.; Rong, E.; Li, Y.; Deng, Q. Multi-Parameter Identification Method for IPT System Based on Bipolar SPWM Technology. IEEE J. Emerg. Sel. Top. Power Electron. 2025, 13, 6753–6767. [Google Scholar] [CrossRef]
- Rahman, A.; Mizuno, T.; Takasaki, M.; Ishino, Y. An Equivalent Circuit Analysis and Suspension Characteristics of AC Magnetic Suspension Using Magnetic Resonant Coupling. Actuators 2020, 9, 52. [Google Scholar] [CrossRef]
- Cai, C.; Chen, T.; Ren, X.; Jiao, Y.; Liu, X.; Li, C.; Yu, J.; Wu, S. Modeling and Design of a Transcutaneous Resonant Capacitive Power Transfer Link for Biomedical Implants. IEEE Trans. Power Electron. 2024, 2, 3726–3737. [Google Scholar] [CrossRef]
- Liang, Y.; Sun, P.; Wu, X.; Wang, L.; Sun, J.; Rong, E.; Deng, Q. Input-Series Output-Series Multichannel IPT System for High-Voltage and High-Power Wireless Power Transfer. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 5509–5523. [Google Scholar] [CrossRef]
- Karimi, S.; Zadeh, M.; Suul, J.A. Shore Charging for Plug-In Battery-Powered Ships: Power System Architecture, Infrastructure, and Control. IEEE Electrif. Mag. 2020, 8, 47–61. [Google Scholar] [CrossRef]
- Mahdi, H.; Hoff, B.; Østrem, T. A Review of Power Converters for Ships Electrification. IEEE Trans. Power Electron. 2023, 38, 4680–4697. [Google Scholar]
- Qiao, K.; Rong, E.; Sun, P.; Zhang, X.; Sun, J. Design of LCC-P Constant Current Topology Parameters for AUV Wireless Power Transfer. Energies 2022, 15, 5249. [Google Scholar] [CrossRef]
- Sun, P.; Wu, X.; Cai, J.; Wang, X.; Zhang, X.; Liang, Y.; Xiong, Q.; Rong, E. Eddy Current Loss Analysis and Frequency Optimization Design of Double-Sided LCC-IPT System in Seawater Environment. Sci. China Technol. Sci. 2021, 65, 407–418. [Google Scholar] [CrossRef]
- Qiao, K.; Sun, P.; Rong, E.; Sun, J.; Zhou, H.; Wu, X. Anti-Misalignment and Light-Weight Magnetic Coupler with H-Shaped Receiver Structure for AUV Wireless Power Transfer. IET Power Electron. 2022, 15, 1843–1857. [Google Scholar] [CrossRef]
- Shafiq, Z.; Li, T.; Xia, J.; Li, S.; Yang, X.; Zhao, Y. Addressing EMI and EMF Challenges in EV Wireless Charging with the Alternating Voltage Phase Coil. Actuators 2024, 13, 324. [Google Scholar] [CrossRef]
- Li, Y.; Sun, P.; Liang, Y.; Wu, X.; Sun, J.; Rong, E.; Liu, Y.; Deng, Q. Research on Rectifier Fault Diagnosis and Self-Protecting for Inductive Power Transfer System with Constant-Current Output. IEEE Trans. Power Electron. 2025, 40, 3750–3769. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, Y.; Yang, L. An LCC-LCC Compensated WPT System with Inherent CC-CV Transition Function for Battery Charging Applications. Wirel. Power Transf. 2024, 11, e002. [Google Scholar] [CrossRef]
- Xie, R.; Liu, Q.; Chen, Y.; Shi, J.; Yue, J.; Lin, G.; Chen, X.; Zhang, Y. A Simple Integrated Solution of Reconfigurable Wired and Wireless Vehicle-to-Vehicle (V2V) Charging System. Wirel. Power Transf. 2024, 11, e011. [Google Scholar] [CrossRef]
- Cai, J.; Sun, P.; Ji, K.; Wu, X.; Ji, H.; Wang, Y.; Rong, E. Constant-Voltage and Constant-Current Controls of the Inductive Power Transfer System for Electric Vehicles Based on Full-Bridge Synchronous Rectification. Electronics 2024, 13, 1686. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, Z.; Zhang, Q.; Li, Z.; Huang, L.; Mai, R.; He, Z. Design and Analysis of CPT System with Wide-Range ZVS and Constant Current Charging Operation Using 6.78 MHz Class-E Power Amplifier. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 3211–3225. [Google Scholar] [CrossRef]
- Yang, G.; Sun, P.; Rong, E.; Zhang, X.; Wu, X.; Deng, Q. Universal Design Method of Load-Independent Constant Voltage and Constant Current Outputs for Capacitive Power Transfer System. IET Power Electron. 2025, 18, e70016. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Lu, F. Review, Analysis, and Design of Four Basic CPT Topologies and the Application of High-Order Compensation Networks. IEEE Trans. Power Electron. 2022, 37, 6181–6193. [Google Scholar] [CrossRef]
- Liang, C.; Liu, M.; Zhao, F.; Wang, D.; Wang, X.; Yuan, H.; Rong, M. A Multi-Cell SCC Capacitive Coupler with Strong Lateral, Longitudinal and Rotational Anti-Offset Performance. IEEE Trans. Power Electron. 2024, 4, 6230–6247. [Google Scholar]
- Lian, J.; Qu, X. Design of a Double-Sided LC Compensated Capacitive Power Transfer System with Capacitor Voltage Stress Optimization. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 715–719. [Google Scholar] [CrossRef]
- Liu, Y.; Li, B.; Pan, L.; Yao, S.; Dong, Z.; Zhang, J.; Zhu, C.; Cui, S. Review on Development and Research of Underwater Capacitive Power Transfer. Energies 2024, 17, 6496. [Google Scholar] [CrossRef]
- Rong, E.; Sun, P.; Wu, X.; Cai, J.; Qiao, K.; Zhang, X.; Wang, L.; Liang, Y. Capacitive Wireless Power Transfer Coupler and Application Thereof. U.S. Patent Application No. 18/814,214, 1 July 2025. [Google Scholar]
- Rong, E.; Sun, P.; Zhang, X.; Yang, G.; Wu, X. 3.3 kW Underwater Capacitive Power Transfer System for Electric Ship Charging Application. In Proceedings of the 2023 IEEE International Conference on Power Science and Technology (ICPST), Kunming, China, 5–7 May 2023; pp. 1052–1057. [Google Scholar]
- Urano, M.; Takahashi, A. Study on Underwater Wireless Power Transfer via Electric Coupling. In Proceedings of the IEEE International Meeting on Future Electronics Devices, San Francisco, CA, USA, 3–7 December 2016; pp. 1–2. [Google Scholar]
- Urano, M.; Ata, K.; Takahashi, A. Study on Underwater Wireless Power Transfer via Electric Coupling with a Submerged Electrode. In Proceedings of the IEEE International Meeting on Future Electronics Devices, Kyoto, Japan, 29–30 June 2017; pp. 36–37. [Google Scholar]
- Tamura, M.; Naka, Y.; Murai, K.; Nakata, T. Design of a Capacitive Wireless Power Transfer System for Operation in Fresh Water. IEEE Trans. Microw. Theory Tech. 2018, 66, 5873–5884. [Google Scholar] [CrossRef]
- Tamura, M.; Naka, Y.; Murai, K. Design of Capacitive Coupler for Wireless Power Transfer under Fresh Water Focusing on kQ Product. In Proceedings of the MTTS International Microwave Symposium, Philadelphia, PA, USA, 10–15 June 2018; pp. 1257–1260. [Google Scholar]
- Bang, K.; Park, S. Design and Characteristics of Underwater Stacked Capacitive Power Transfer Coupler and Analysis of Propagation in Water Medium. Appl. Sci. 2025, 15, 1901. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, F. Insulated Coupler Structure Design for the Long-Distance Freshwater Capacitive Power Transfer. IEEE Trans. Ind. Inform. 2020, 16, 5191–5201. [Google Scholar] [CrossRef]
- Li, H.; Li, G.; Jin, X.; Li, J.; Xu, G. A LC-CLL Compensated Capacitive Wireless Power Transfer System in Fresh Water. In Proceedings of the International Conference on Power and Energy Applications, Guangzhou, China, 18–20 November 2022; pp. 130–137. [Google Scholar]
- Zhang, X.; Lian, J. A Novel Coupler of Capacitive Power Transfer for Enhancing Underwater Power Transfer Characteristics. Electronics 2024, 13, 74. [Google Scholar] [CrossRef]
- Yang, L.; Tian, L.; Chen, X.; Bu, Z.; Xing, D.; Zhang, A.; Tong, X. Three-Phase High Power Underwater Capacitive Wireless Power Transfer System for Autonomous Underwater Vehicles. J. Mar. Sci. Eng. 2025, 13, 989. [Google Scholar] [CrossRef]
- Yang, G.; Sun, P.; Rong, E.; Zhang, X.; Wu, X.; Deng, Q.; Li, S. High-Power Capacitive Power Transfer System with Integrated Multi-Channel Coupler. IEEE Trans. Power Electron. 2025, in press. [CrossRef]
- Sinha, S.; Kumar, A.; Regensburger, B.; Afridi, K.K. A New Design Approach to Mitigating the Effect of Parasitics in Capacitive Wireless Power Transfer Systems for Electric Vehicle Charging. IEEE Trans. Transport. Electrific. 2019, 5, 1040–1059. [Google Scholar] [CrossRef]
- Regensburger, B.; Sinha, S.; Kumar, A.; Maji, S.; Afridi, K.K. High-Performance Multi-MHz Capacitive Wireless Power Transfer System for EV Charging Utilizing Interleaved-Foil Coupled Inductors. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 35–51. [Google Scholar] [CrossRef]
- Rong, E.; Sun, P.; Qiao, K.; Zhang, X.; Yang, G.; Wu, X. Six-Plate and Hybrid-Dielectric Capacitive Coupler for Underwater Wireless Power Transfer. IEEE Trans. Power Electron. 2024, 39, 2867–2881. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, F.; Hofmann, H.; Liu, W.; Mi, C.C. A Four-Plate Compact Capacitive Coupler Design and LCL-Compensated Topology for Capacitive Power Transfer in Electric Vehicle Charging Application. IEEE Trans. Power Electron. 2016, 31, 8541–8551. [Google Scholar]
- Zhang, H.; Lu, F.; Hofmann, H.; Liu, W.; Mi, C.C. Six-Plate Capacitive Coupler to Reduce Electric Field Emission in Large Air-Gap Capacitive Power Transfer. IEEE Trans. Power Electron. 2018, 33, 665–675. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Cao, Y.; Lu, F. Remaining Opportunities in Capacitive Power Transfer Based on Duality with Inductive Power Transfer. IEEE Trans. Transp. Electrif. 2023, 9, 2902–2915. [Google Scholar] [CrossRef]
- Rong, E.; Sun, P.; Yang, G.; Xia, J.; Liu, Z.; Li, S. 5-kW, 96.5% Efficiency Capacitive Power Transfer System with a Five-Plate Coupler: Design and Optimization. IEEE Trans. Power Electron. 2025, 40, 2542–2555. [Google Scholar] [CrossRef]
- Mahdi, H.; Hoff, B.; Østrem, T. Optimal Solutions for Underwater Capacitive Power Transfer. Sensors 2021, 21, 8233. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, F. Feasibility Study of the High-Power Underwater Capacitive Wireless Power Transfer for the Electric Ship Charging Application. In Proceedings of the 2019 IEEE Electric Ship Technologies Symposium (ESTS), Washington, DC, USA, 14–16 August 2019; pp. 231–235. [Google Scholar]
- Ji, H.; Sun, P.; Xiang, Y.; Hou, Y.; Zhang, X.; Rong, E. Groove Disk Capacitive Coupler for Wireless Rotor Excitation in Wound Field Synchronous Machines. In Proceedings of the 2025 IEEE International Conference on Industrial Technology, Wuhan, China, 26–28 March 2025; pp. 1–6. [Google Scholar]
- Liu, Z.; Zuo, C.; Li, S.; Lu, S.; Xia, J.; Zhao, Y.; Rong, E.; Li, T. A Large-Area Free-Positioning SCC-WPT System for Movable Receivers. IEEE Trans. Power Electron. 2025, 40, 8911–8916. [Google Scholar] [CrossRef]


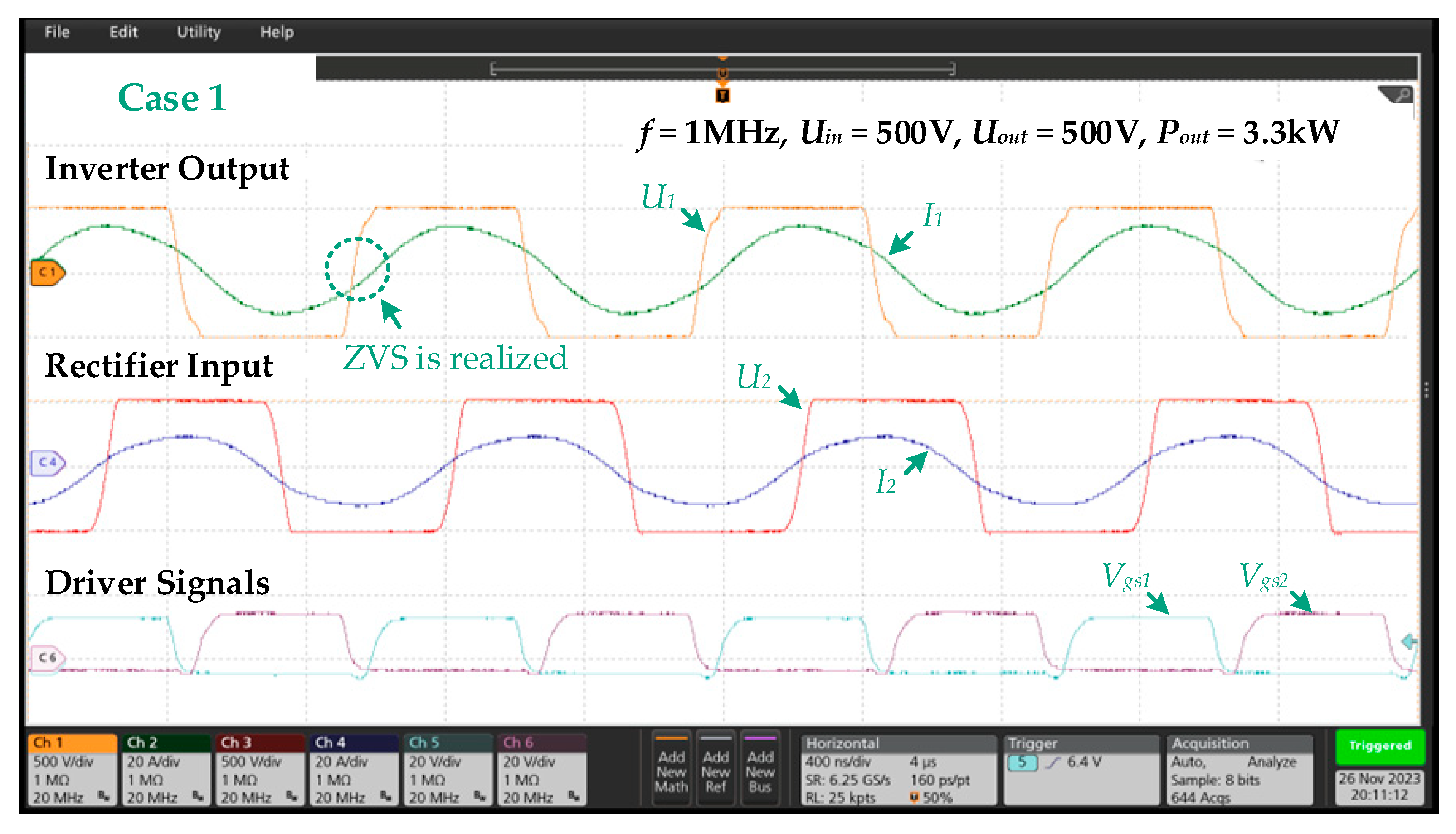
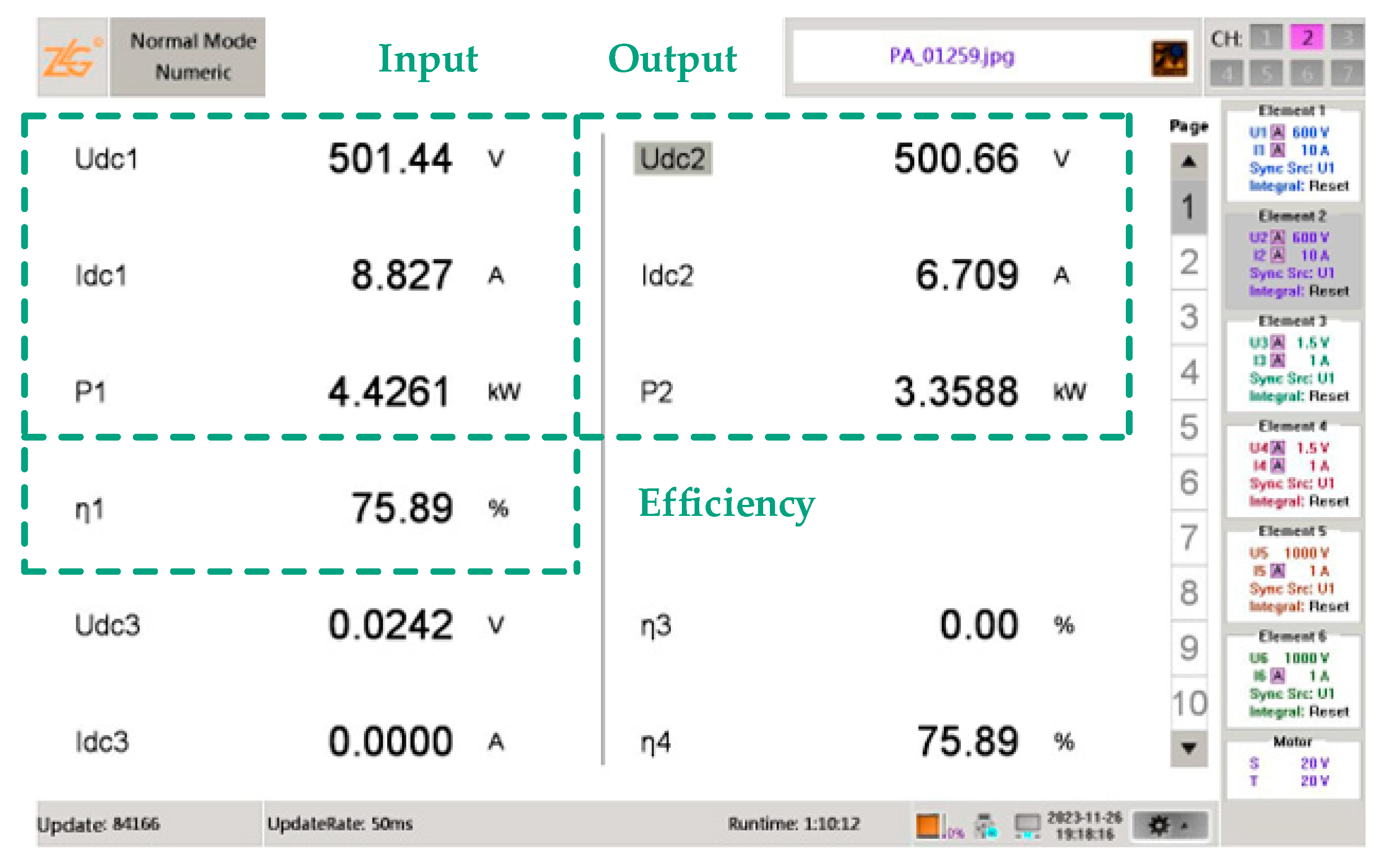
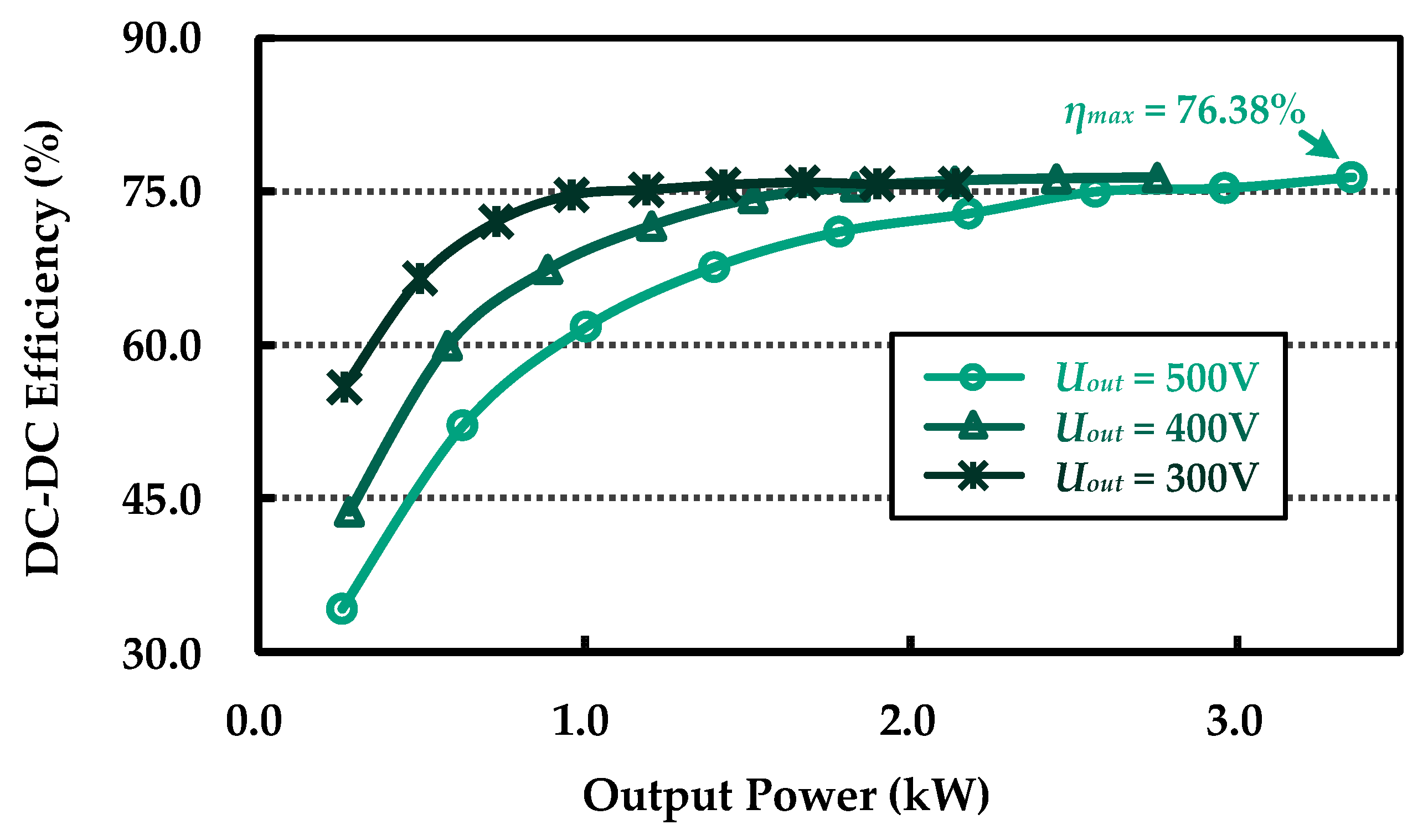

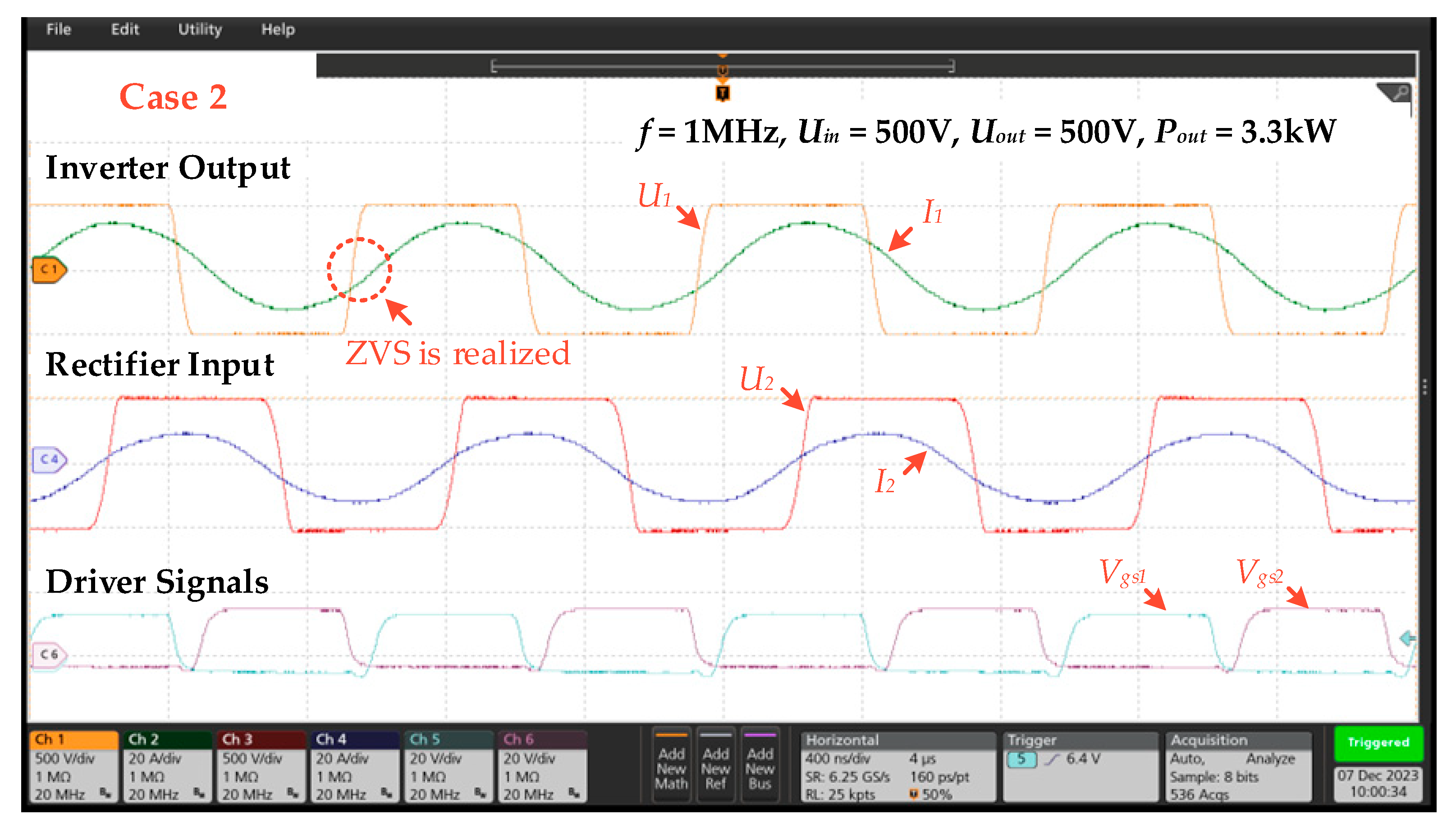
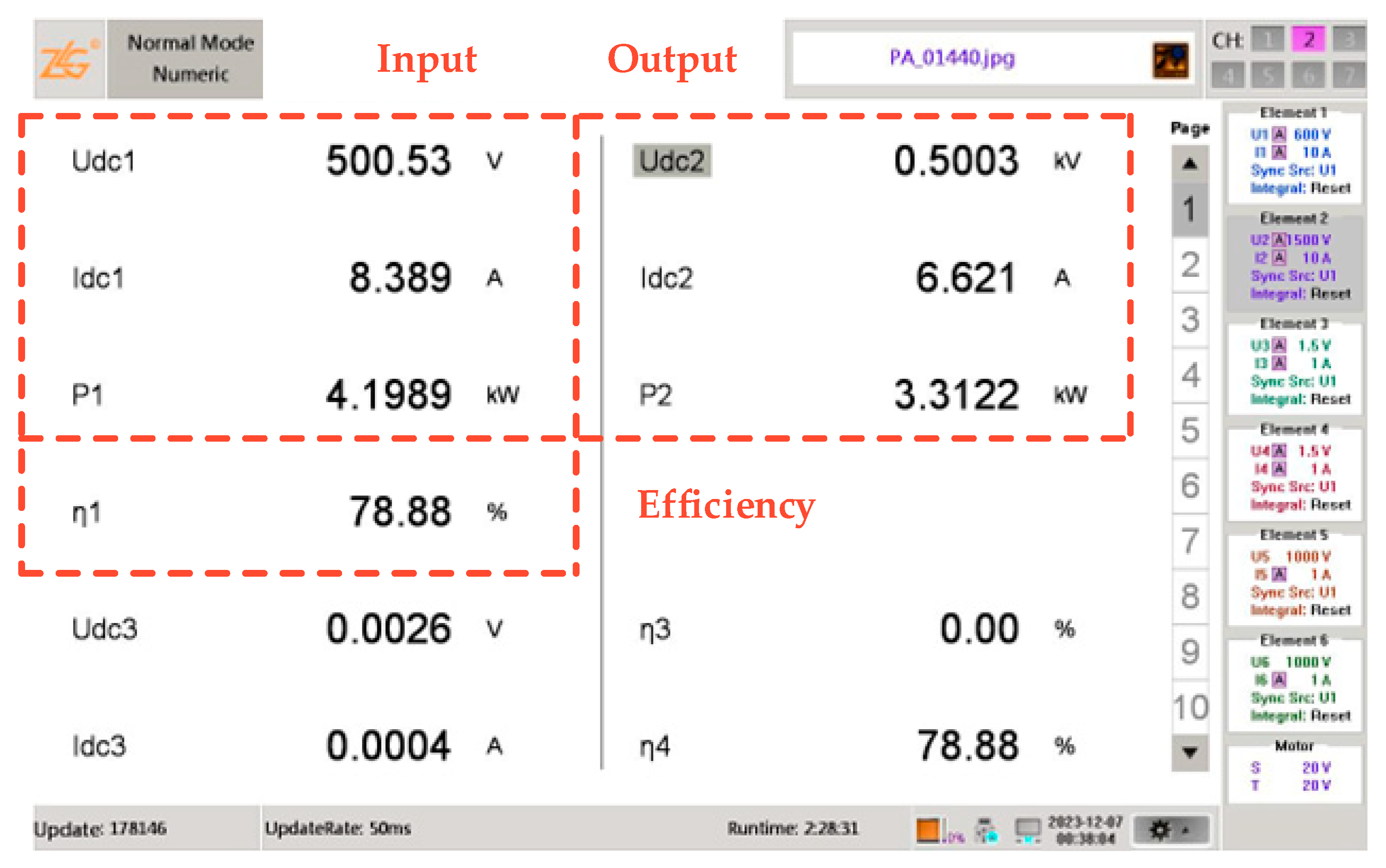
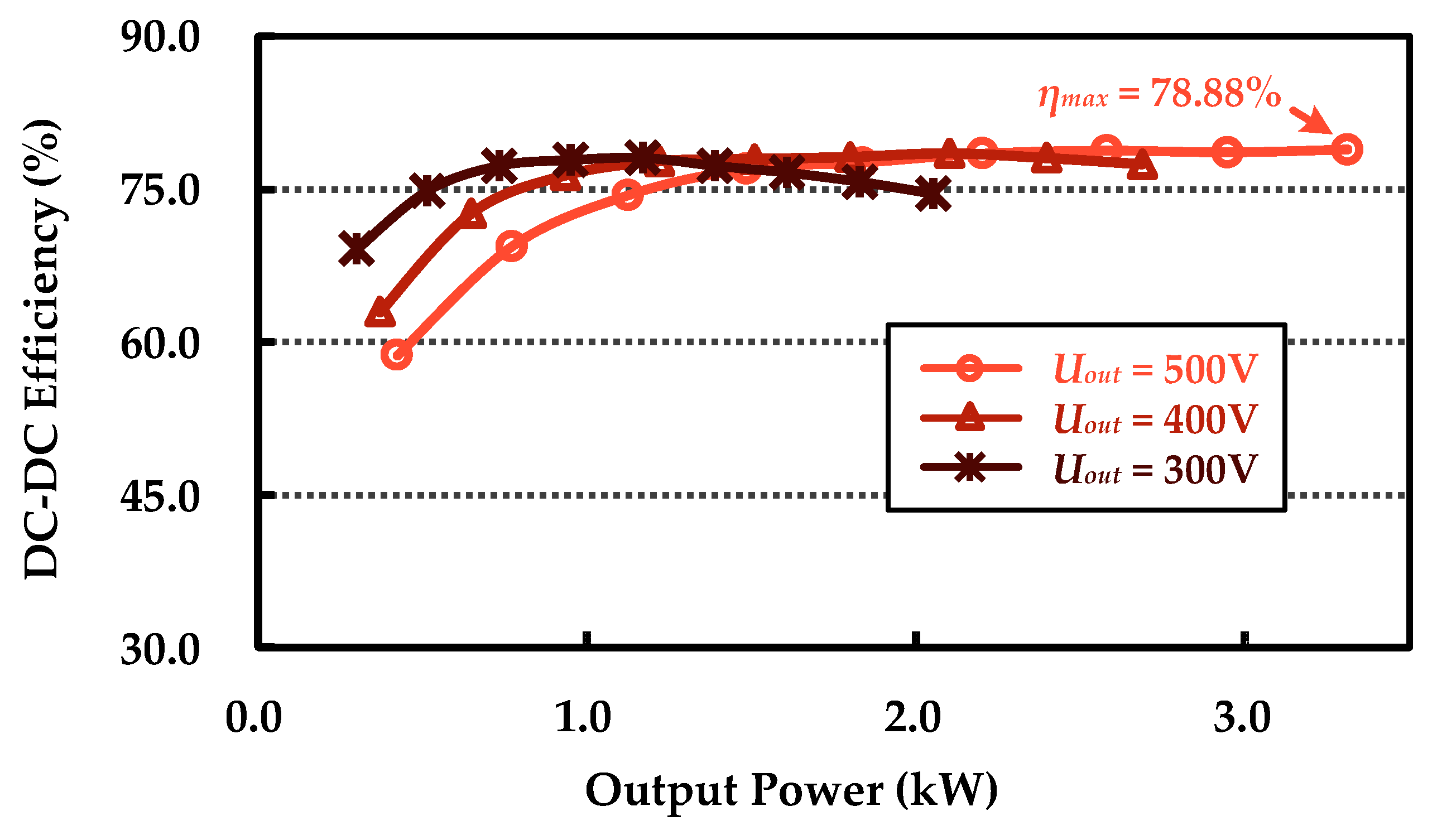
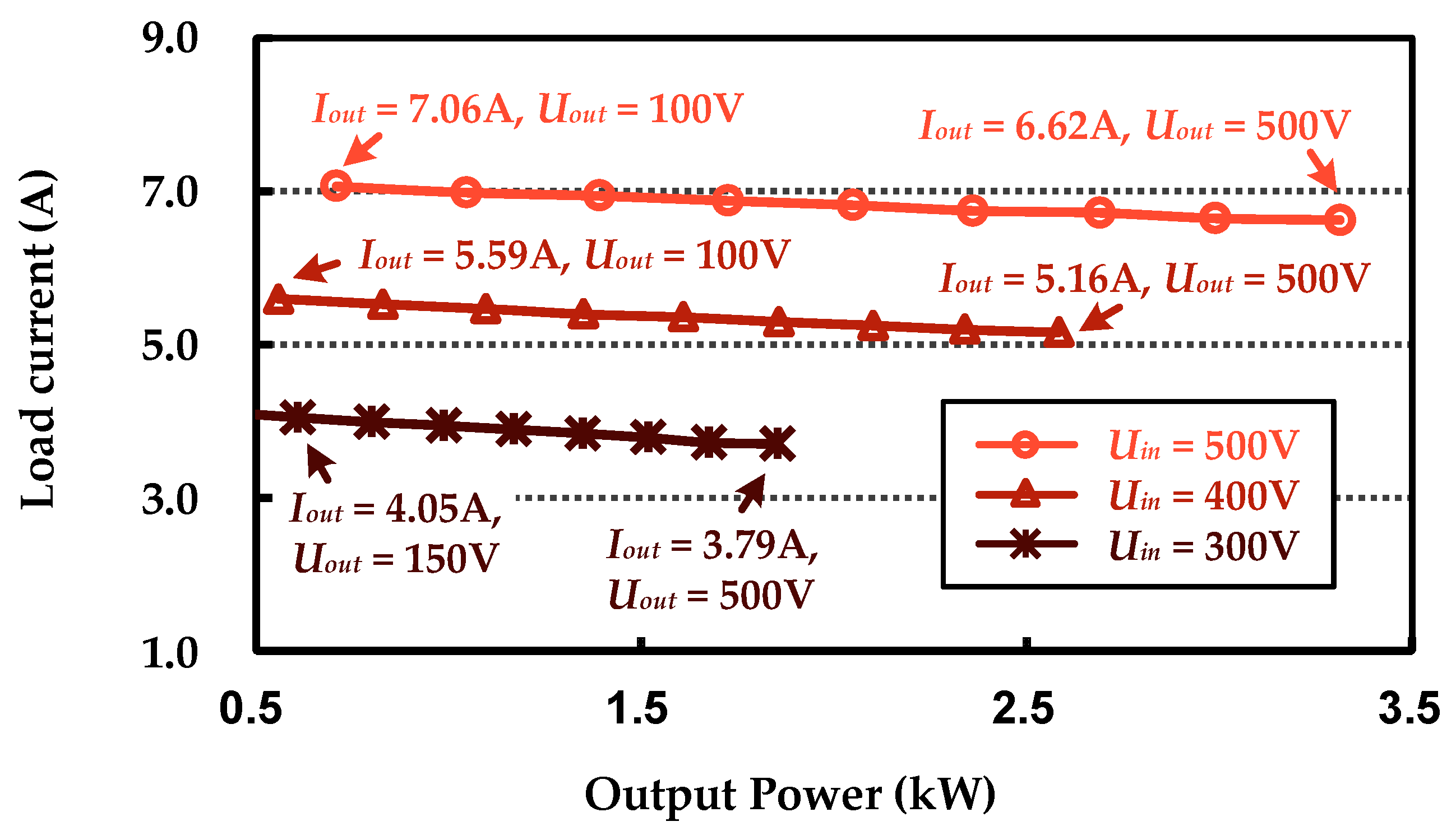
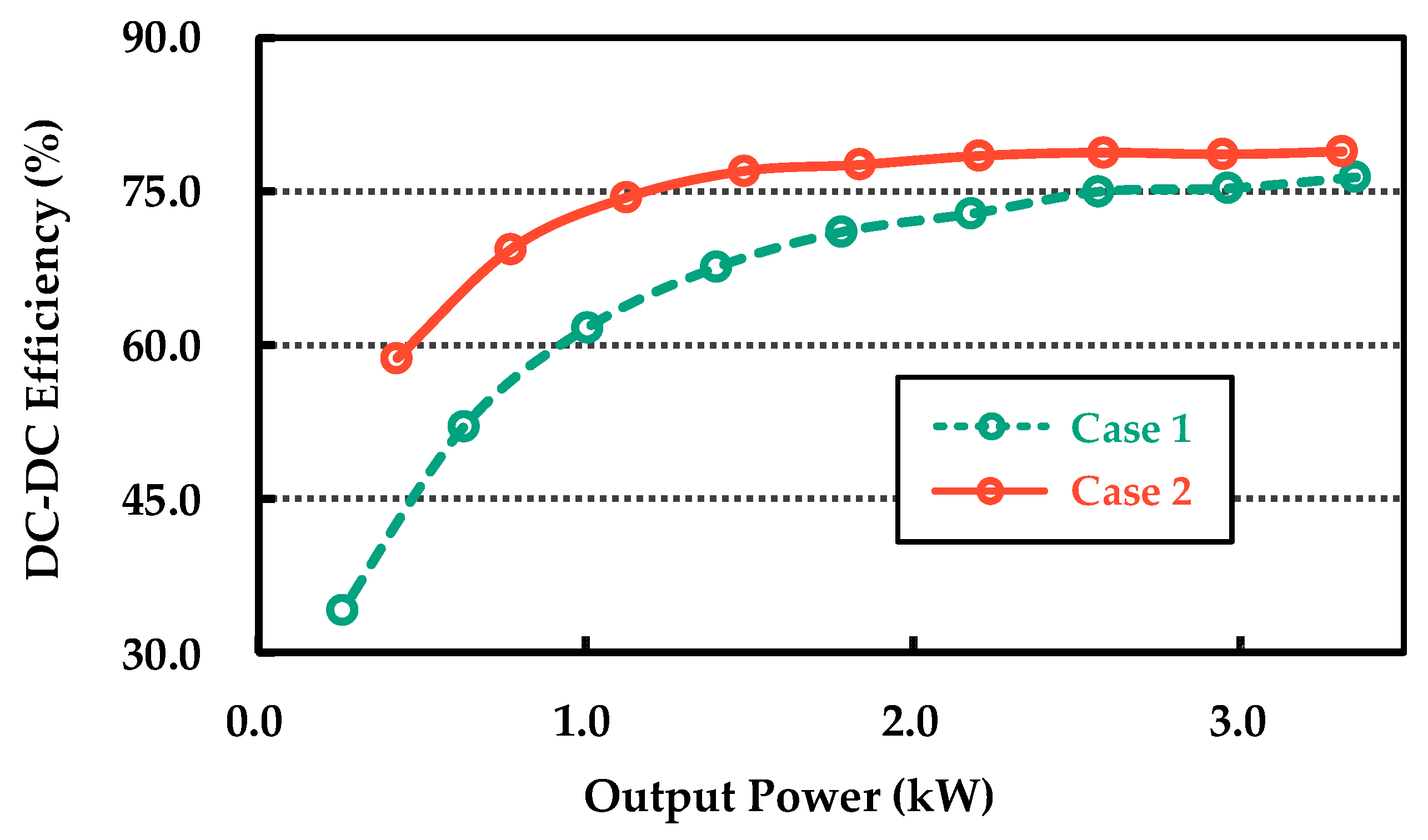

| Designator | Parameter | Case 1 (d1 = 10 mm) | Case 2 (d1 = 50 mm) |
|---|---|---|---|
| Cf1 | Source side capacitance | 2.53 nF | 1.71 nF |
| Cf2 | Load side capacitance | 2.53 nF | 1.71 nF |
| Lf1 | Source side inductance | 9.99 uF | 14.79 uH |
| Lf2 | Load side inductance | 9.99 uF | 14.79 uH |
| L1 | Primary side inductance | 45.63 uF | 62.65 uH |
| L2 | Secondary side inductance | 45.63 uF | 62.65 uH |
| kL1 | Inductive coupling coefficient | 0.4 | 0.4 |
| kL2 | Inductive coupling coefficient | 0.4 | 0.4 |
| C1 | Primary side capacitance | 587.01 pF | 458.85 pF |
| C2 | Secondary side capacitance | 587.01 pF | 458.85 pF |
| CM | Coupling capacitance | 136.79 pF | 158.22 pF |
| kC | Capacitive coupling coefficient | 0.23 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, X.; Zeng, H.; Feng, G.; Wang, S.; Rong, E. Study and Optimization of Shore-to-Ship Underwater Capacitive Power Transfer System Considering Parasitic Coupling. Actuators 2025, 14, 534. https://doi.org/10.3390/act14110534
Pan X, Zeng H, Feng G, Wang S, Rong E. Study and Optimization of Shore-to-Ship Underwater Capacitive Power Transfer System Considering Parasitic Coupling. Actuators. 2025; 14(11):534. https://doi.org/10.3390/act14110534
Chicago/Turabian StylePan, Xin, Haiyan Zeng, Guoli Feng, Shudan Wang, and Enguo Rong. 2025. "Study and Optimization of Shore-to-Ship Underwater Capacitive Power Transfer System Considering Parasitic Coupling" Actuators 14, no. 11: 534. https://doi.org/10.3390/act14110534
APA StylePan, X., Zeng, H., Feng, G., Wang, S., & Rong, E. (2025). Study and Optimization of Shore-to-Ship Underwater Capacitive Power Transfer System Considering Parasitic Coupling. Actuators, 14(11), 534. https://doi.org/10.3390/act14110534








