Adaptive Prediction of Compressor Cylinder Pressure Dynamics Using a Physics-Guided VAE-CNN State Space Model
Abstract
1. Introduction
2. Problem Statement
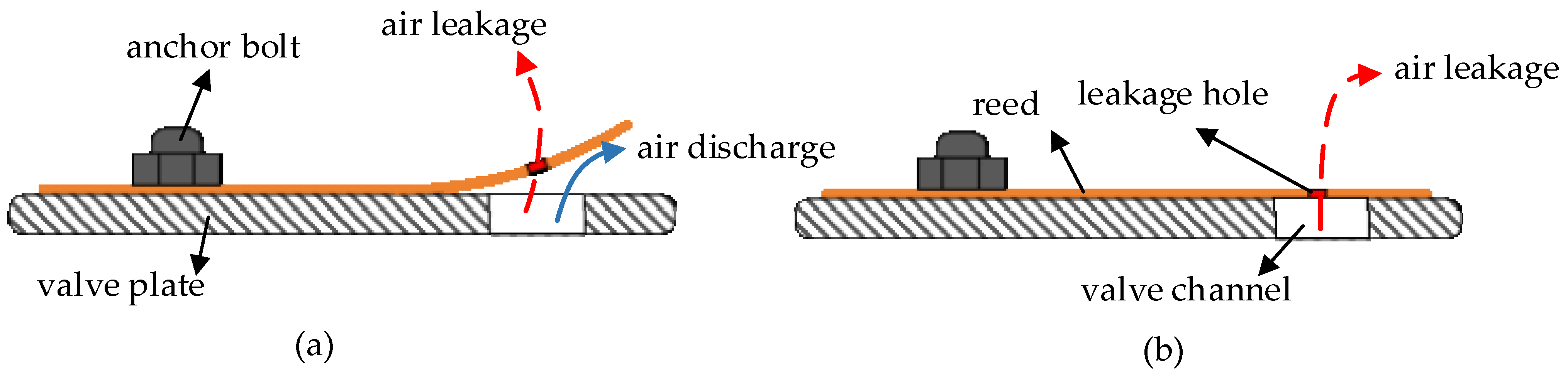
2.1. Problem Analysis
2.2. Mathematical Model
3. Proposed Model
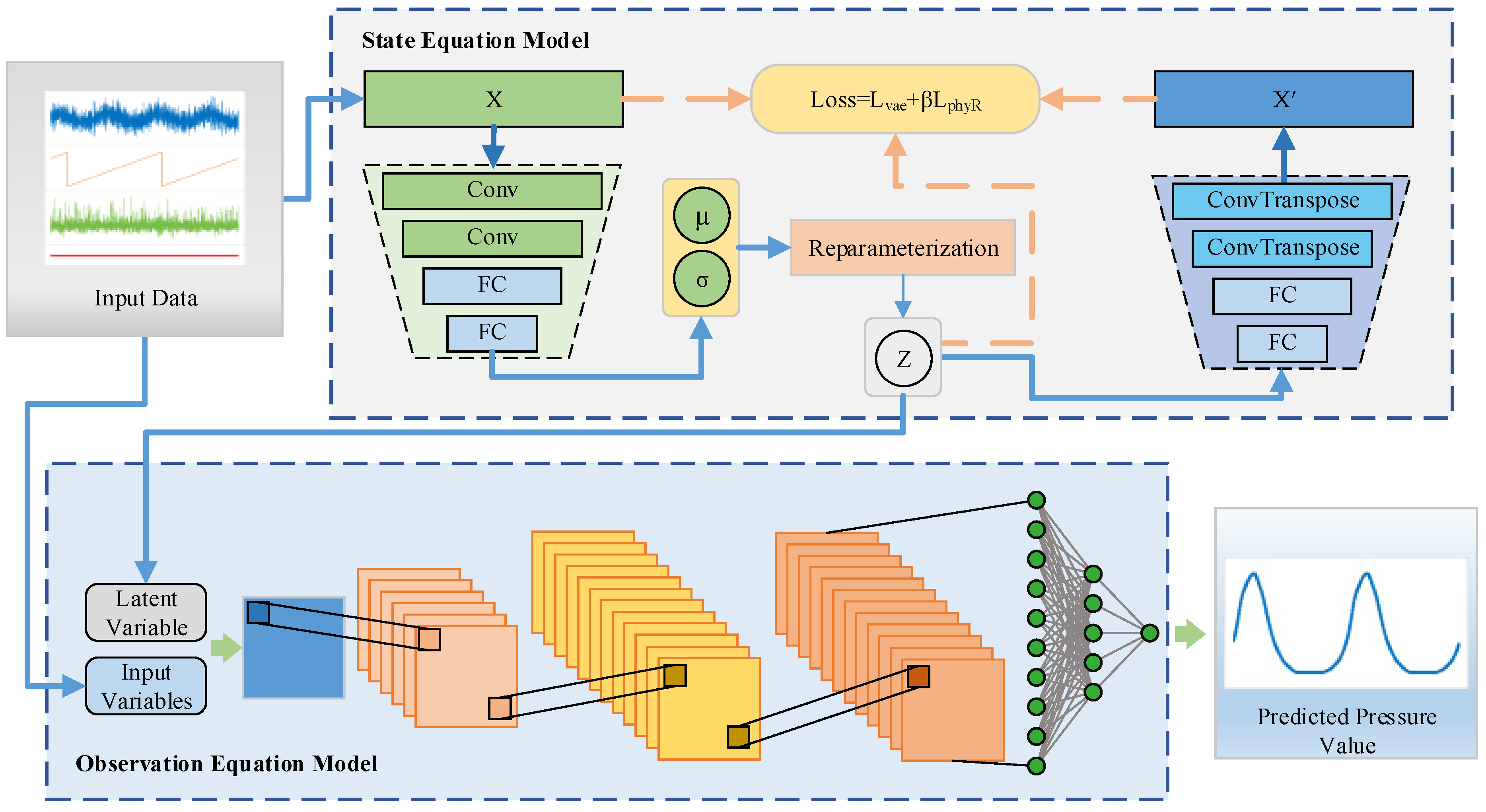
3.1. Framework
3.2. Dynamic System Based on State Space Model
3.3. State Equation Model Based on VAE
3.3.1. Loss Function Design
3.3.2. VAE Structure
3.4. Observation Equation Model Based on CNN
4. Experimental Details
4.1. Experimental Setup
4.2. Model Parameter Settings
4.3. Evaluation Indicators
5. Results Analysis
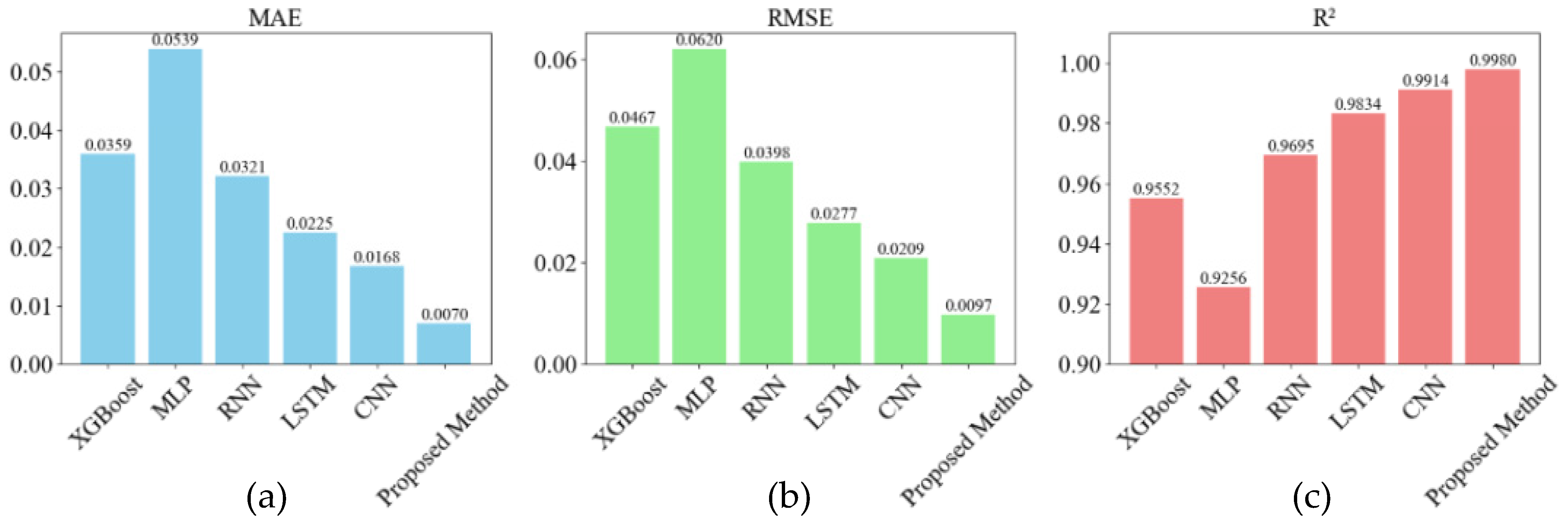
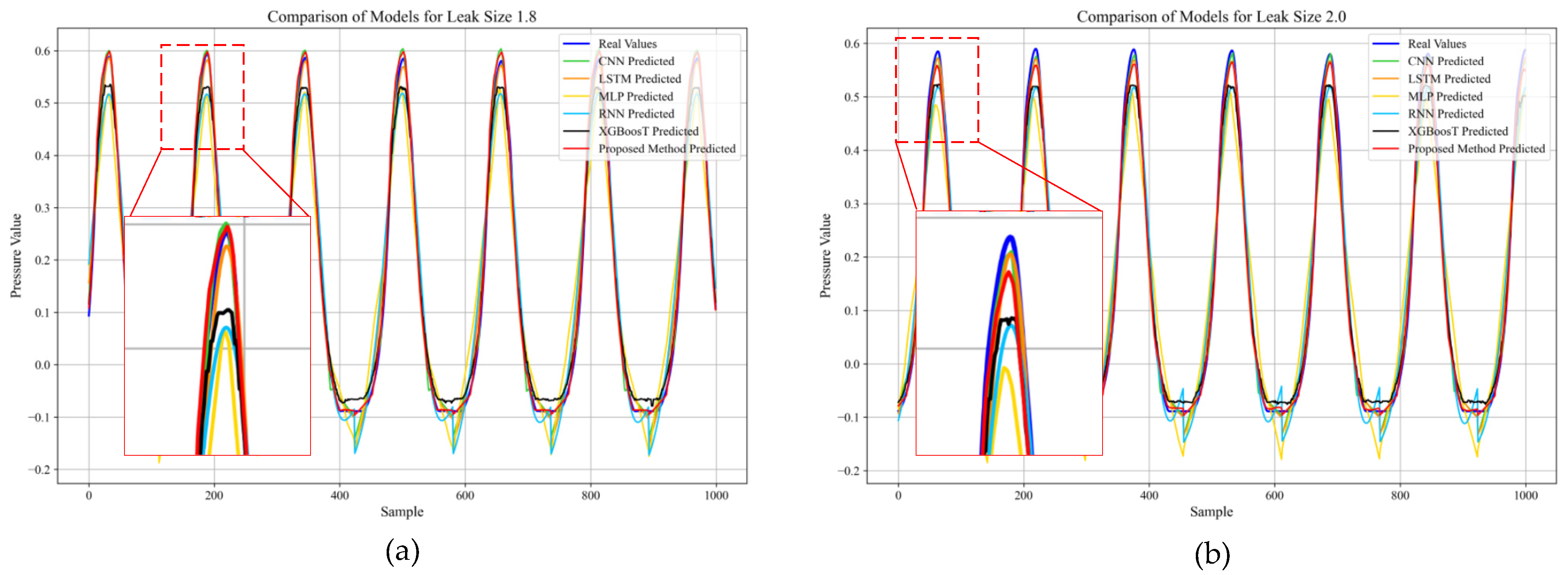
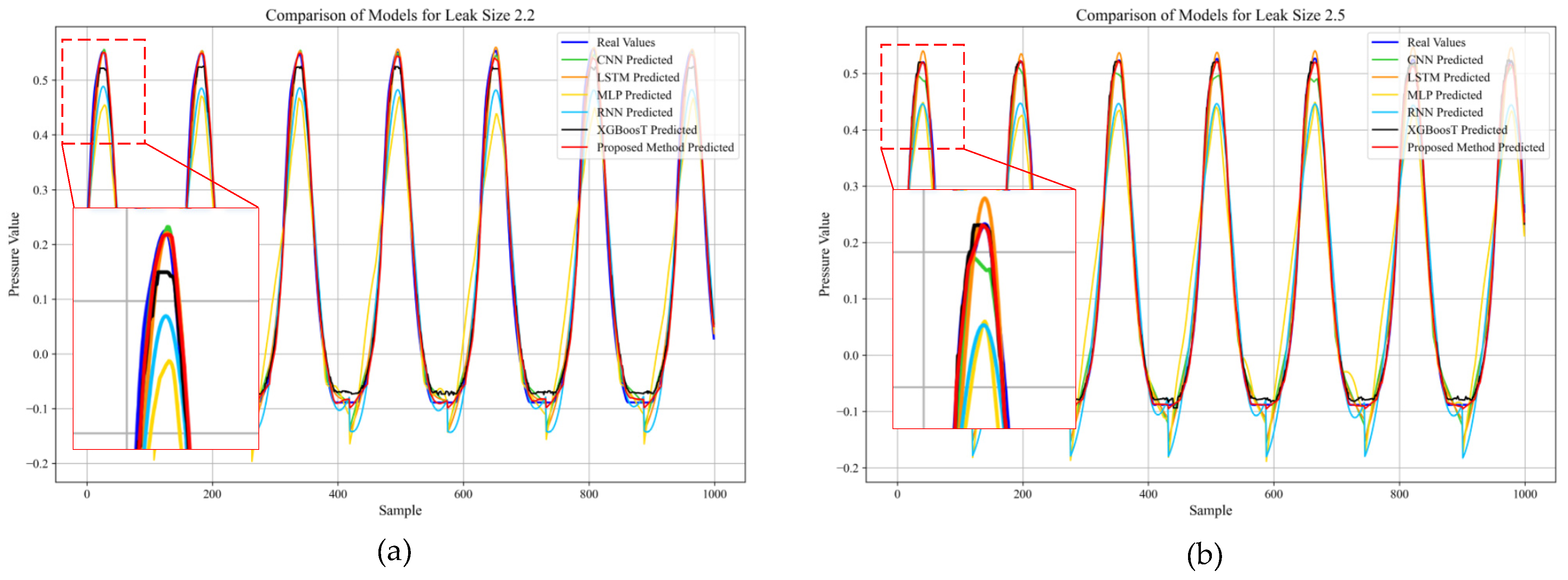
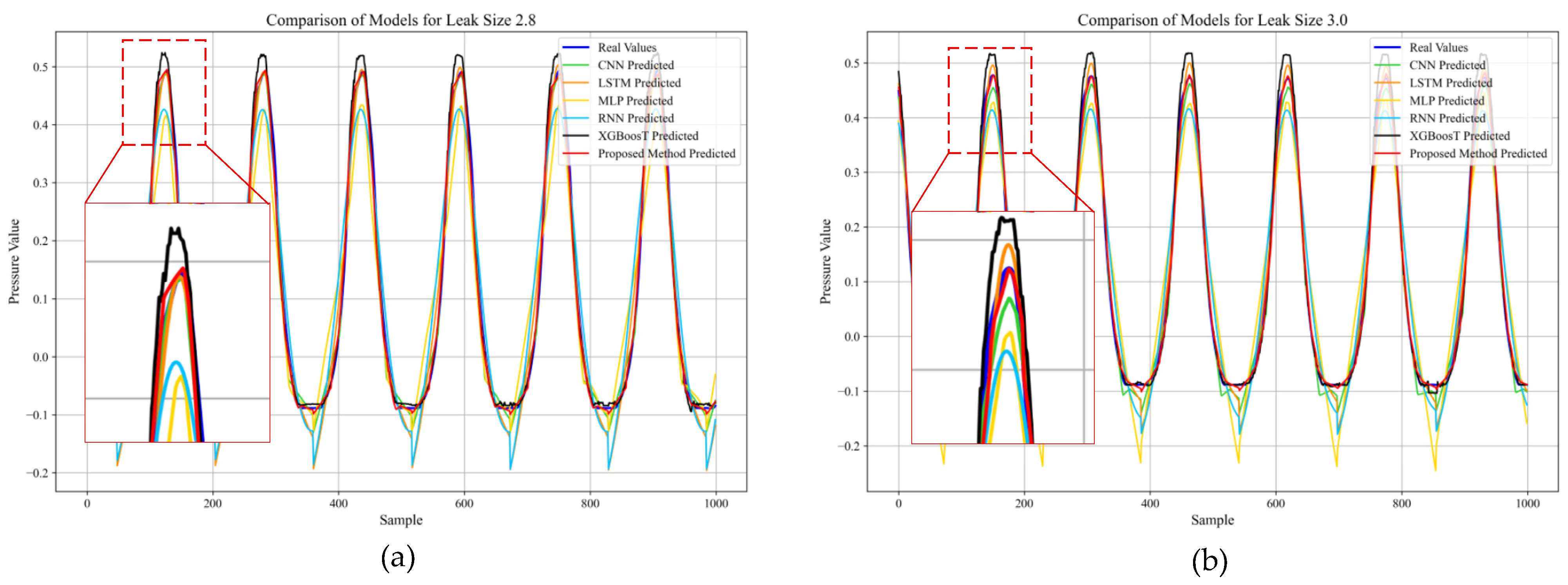
5.1. Prediction Accuracy Evaluation
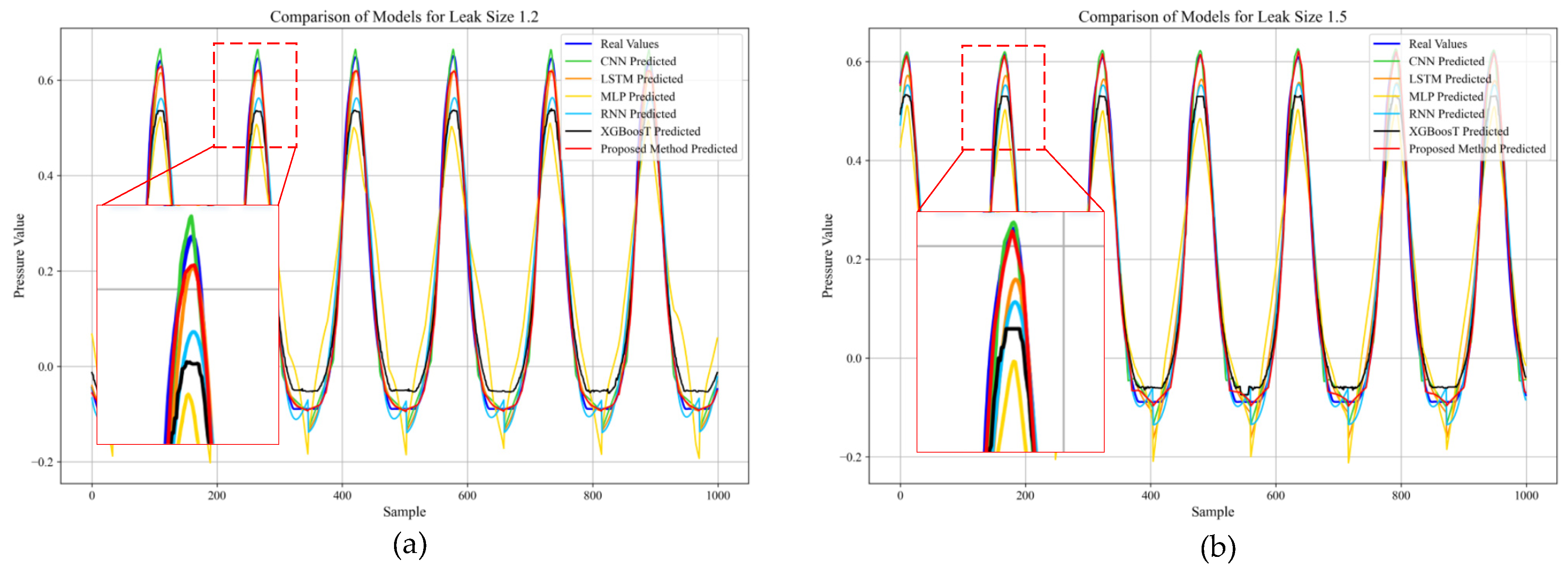
5.2. Generalization Evaluation
5.3. Ablation Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, W.; Su, H.; Liu, H.; Zhang, Y.; Qiu, N.; Gao, B. Leakage and Rotordynamic Performance of a Semi-Y Labyrinth Seal Structure for Centrifugal Pump Based on Multifrequency Whirl Method. J. Eng. Gas Turbines Power 2025, 147, 101022. [Google Scholar] [CrossRef]
- Cui, W.; Wang, D.; Hong, X.; Liu, D.; Cao, X. Automated multi-functional system for the characterization of plate valves in reciprocating compressors. Instrum. Sci. Technol. 2024, 52, 494–515. [Google Scholar] [CrossRef]
- Mu, G.; Wang, F.; Mi, X.; Gao, G. Dynamic modeling and analysis of compressor reed valve based on movement characteristics. Appl. Therm. Eng. 2019, 150, 522–531. [Google Scholar] [CrossRef]
- Rigola, J.; Pérez-Segarra, C.D.; Oliva, A. Parametric studies on hermetic reciprocating compressors. Int. J. Refrig. 2005, 28, 253–266. [Google Scholar] [CrossRef]
- Govindan, N.; Jayaraman, V.; Venkatasamy, R.; Ramasamy, M. Mathematical modeling and simulation of a reed valve reciprocating air compressor. Therm. Sci. 2009, 13, 47–58. [Google Scholar] [CrossRef]
- Farzaneh-Gord, M.; Khoshnazar, H. Valve fault detection for single-stage reciprocating compressors. J. Nat. Gas Sci. Eng. 2016, 35, 1239–1248. [Google Scholar] [CrossRef]
- Silva, L.R.; Deschamps, C.J. Modeling of gas leakage through compressor valves. Int. J. Refrig. 2015, 53, 195–205. [Google Scholar] [CrossRef]
- Elhaj, M.; Gu, F.; Ball, A.D.; Albarbar, A.; Al-Qattan, M.; Naid, A. Numerical simulation and experimental study of a two-stage reciprocating compressor for condition monitoring. Mech. Syst. Signal Process. 2008, 22, 374–389. [Google Scholar] [CrossRef]
- Damle, R.; Rigola, J.; Pérez-Segarra, C.D.; Castro, J.; Oliva, A. Object-oriented simulation of reciprocating compressors: Numerical verification and experimental comparison. Int. J. Refrig. 2011, 34, 1989–1998. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; He, Z.; Sun, J.; Wang, T.; Liu, C. Investigation on Dynamic Characteristics of the Reed Valve in Compressors Based on Fluid-Structure Interaction Method. Appl. Sci. 2021, 11, 3946. [Google Scholar] [CrossRef]
- Hwang, I.S.; Park, S.J.; Oh, W.; Lee, Y.L. Linear compressor discharge valve behavior using a rigid body valve model and a FSI valve model. Int. J. Refrig. 2017, 82, 509–519. [Google Scholar] [CrossRef]
- Zhao, B.; Jia, X.; Sun, S.; Wen, J.; Peng, X. FSI model of valve motion and pressure pulsation for investigating thermodynamic process and internal flow inside a reciprocating compressor. Appl. Therm. Eng. 2018, 131, 998–1007. [Google Scholar] [CrossRef]
- Tao, W.; Guo, Y.; He, Z.; Peng, X. Investigation on the delayed closure of the suction valve in the refrigerator compressor by FSI modeling. Int. J. Refrig. 2018, 91, 111–121. [Google Scholar] [CrossRef]
- Wu, W.; Guo, T.; Peng, C.; Li, X.; Li, X.; Zhang, Z.; Xu, L.; He, Z. FSI simulation of the suction valve on the piston for reciprocating compressors. Int. J. Refrig. 2022, 137, 14–21. [Google Scholar] [CrossRef]
- Bacak, A.; Pınarbaşı, A.; Dalkılıç, A.S. A 3-D FSI simulation for the performance prediction and valve dynamic analysis of a hermetic reciprocating compressor. Int. J. Refrig. 2023, 150, 135–148. [Google Scholar] [CrossRef]
- Fu, J.; Zhang, G.; Sun, X.; He, T.; Li, H. A combinatorial prediction model for the performance of fuel cell air compressor with air bearings considering accelerated decay characteristics. Appl. Therm. Eng. 2024, 253, 123784. [Google Scholar] [CrossRef]
- Belman-Flores, J.M.; Ledesma, S.; Barroso-Maldonado, J.M.; Navarro-Esbrí, J. A comparison between the modeling of a reciprocating compressor using artificial neural network and physical model. Int. J. Refrig. 2015, 59, 144–156. [Google Scholar] [CrossRef]
- Ledesma, S.; Belman-Flores, J.M.; Barroso-Maldonado, J.M. Analysis and modeling of a variable speed reciprocating compressor using ANN. Int. J. Refrig. 2015, 59, 190–197. [Google Scholar] [CrossRef]
- Kumar, A.; Patil, S.; Kovacevic, A.; Ponnusami, S.A. Performance prediction and Bayesian optimization of screw compressors using Gaussian Process Regression. Eng. Appl. Artif. Intell. 2024, 133, 108270. [Google Scholar] [CrossRef]
- Ghorbanian, K.; Gholamrezaei, M. An artificial neural network approach to compressor performance prediction. Appl. Energy 2009, 86, 1210–1221. [Google Scholar] [CrossRef]
- Wang, Y.; Du, Q.; Li, Y.; Zhang, D.; Xie, Y. Field reconstruction and off-design performance prediction of turbomachinery in energy systems based on deep learning techniques. Energy 2022, 238, 121825. [Google Scholar] [CrossRef]
- Li, H.; Zhou, S.; Kan, H.; Cong, M. Milling cutter condition reliability prediction based on state space model. J. Vibroengineering 2016, 18, 4312–4328. [Google Scholar] [CrossRef]
- Pedregal, D.J.; Carmen Carnero, M. State space models for condition monitoring: A case study. Reliab. Eng. Syst. Saf. 2006, 91, 171–180. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L. Intelligent fault detection of reciprocating compressor using a novel discrete state space. Mech. Syst. Signal Process. 2022, 169, 108583. [Google Scholar] [CrossRef]
- Yao, Y.; Wang, W.; Huang, M. A state-space dynamic model for vapor compression refrigeration system based on moving-boundary formulation. Int. J. Refrig. 2015, 60, 174–189. [Google Scholar] [CrossRef]
- Skordilis, E.; Moghaddass, R. A Double Hybrid State-Space Model for Real-Time Sensor-Driven Monitoring of Deteriorating Systems. IEEE Trans. Autom. Sci. Eng. 2020, 17, 72–87. [Google Scholar] [CrossRef]
- Liu, H.T.; Liu, C.J.; Jiang, X.M.; Chen, X.; Yang, S.; Wang, X. Deep probabilistic time series forecasting using augmented recurrent input for dynamic systems. Mech. Syst. Signal Process. 2022, 177, 16. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, B.; Zio, E.; Wen, G.; Liu, Z.; Su, Y.; Chen, X. Hybrid system response model for condition monitoring of bearings under time-varying operating conditions. Reliab. Eng. Syst. Saf. 2023, 239, 109528. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Q.; Wang, K. Revealing the degradation patterns of lithium-ion batteries from impedance spectroscopy using variational auto-encoders. Energy Storage Mater. 2024, 69, 103394. [Google Scholar] [CrossRef]
- Jing, T.; Zheng, P.; Xia, L.; Liu, T. Transformer-based hierarchical latent space VAE for interpretable remaining useful life prediction. Adv. Eng. Inform. 2022, 54, 101781. [Google Scholar] [CrossRef]
- Mou, M.; Zhao, X.; Liu, K.; Hui, Y. Variational autoencoder based on distributional semantic embedding and cross-modal reconstruction for generalized zero-shot fault diagnosis of industrial processes. Process Saf. Environ. Prot. 2023, 177, 1154–1167. [Google Scholar] [CrossRef]
- Guo, F.Y.; Zhang, Y.C.; Wang, Y.; Wang, P.; Ren, P.-J.; Guo, R.; Wang, X.-Y. Fault Detection of Reciprocating Compressor Valve Based on One-Dimensional Convolutional Neural Network. Math. Probl. Eng. 2020, 2020, 10. [Google Scholar] [CrossRef]






| Model | Parameters |
|---|---|
| XGBOOST | Max_depth = 5, colsample_bytree = 0.3, learning_rate = 0.1, alpha = 10, n_estimators = 100 |
| MLP | Neuron = 64, epoch = 500, loss function = MSE, learning rate = 0.01, activation function is ReLU |
| RNN | Neuron = 64, epoch = 500, loss function = MSE, learning rate = 0.01, activation function is ReLU |
| LSTM | Neuron = 64, epoch = 500, loss function = MSE, learning rate = 0.01, activation function is ReLU |
| CNN | Neuron = 32, epoch = 500, loss function = MSE, learning rate = 0.01, activation function ReLU, convolution kernel 3 × 3 |
| Proposed Method | Neuron = 32, epoch = 500, loss function = MSE, learning rate = 0.01, activation function ReLU, convolution kernel 3 × 3 |
| Leakage Size | 0 | 1.2 | 1.5 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3 | 3.2 | 3.5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| XGBOOST | MAE | 0.0638 | 0.0543 | 0.0477 | 0.0491 | 0.0409 | 0.0319 | 0.0261 | 0.0237 | 0.0140 | 0.0159 | 0.0273 |
| RMSE | 0.0788 | 0.0660 | 0.0571 | 0.0830 | 0.0487 | 0.0377 | 0.0303 | 0.0284 | 0.0282 | 0.0193 | 0.0360 | |
| R2 | 0.9159 | 0.9355 | 0.9483 | 0.8814 | 0.9596 | 0.9735 | 0.9813 | 0.9819 | 0.9811 | 0.9906 | 0.9578 | |
| MLP | MAE | 0.0781 | 0.0632 | 0.0541 | 0.0505 | 0.0563 | 0.0511 | 0.0514 | 0.0463 | 0.0491 | 0.0511 | 0.0421 |
| RMSE | 0.0893 | 0.0705 | 0.0601 | 0.0571 | 0.0652 | 0.0586 | 0.0600 | 0.0557 | 0.0571 | 0.0590 | 0.0499 | |
| R2 | 0.8891 | 0.9249 | 0.9440 | 0.9456 | 0.9279 | 0.9381 | 0.9294 | 0.9284 | 0.9216 | 0.9149 | 0.9182 | |
| RNN | MAE | 0.0481 | 0.0411 | 0.0383 | 0.0348 | 0.0359 | 0.0319 | 0.0266 | 0.0233 | 0.0227 | 0.0214 | 0.0288 |
| RMSE | 0.0616 | 0.0505 | 0.0469 | 0.0432 | 0.0448 | 0.0390 | 0.0330 | 0.0311 | 0.0271 | 0.0261 | 0.0346 | |
| R2 | 0.9468 | 0.9612 | 0.9658 | 0.9689 | 0.9658 | 0.9726 | 0.9787 | 0.9779 | 0.9824 | 0.9833 | 0.9607 | |
| LSTM | MAE | 0.0326 | 0.0279 | 0.0250 | 0.0197 | 0.0223 | 0.0199 | 0.0164 | 0.0193 | 0.0174 | 0.0176 | 0.0289 |
| RMSE | 0.0393 | 0.0323 | 0.0296 | 0.0233 | 0.0262 | 0.0256 | 0.0201 | 0.0242 | 0.0217 | 0.0226 | 0.0403 | |
| R2 | 0.9784 | 0.9841 | 0.9864 | 0.9909 | 0.9883 | 0.9882 | 0.9920 | 0.9867 | 0.9887 | 0.9875 | 0.9465 | |
| CNN | MAE | 0.0197 | 0.0191 | 0.0185 | 0.0161 | 0.0170 | 0.0180 | 0.0130 | 0.0162 | 0.0158 | 0.0142 | 0.0173 |
| RMSE | 0.0246 | 0.0230 | 0.0230 | 0.0196 | 0.0206 | 0.0228 | 0.0168 | 0.0196 | 0.0202 | 0.0180 | 0.0214 | |
| R2 | 0.9915 | 0.9919 | 0.9918 | 0.9936 | 0.9928 | 0.9906 | 0.9944 | 0.9913 | 0.9902 | 0.9921 | 0.9850 | |
| Proposed Method | MAE | 0.0066 | 0.0053 | 0.0068 | 0.0062 | 0.0073 | 0.0098 | 0.0044 | 0.0087 | 0.0084 | 0.0058 | 0.0076 |
| RMSE | 0.0098 | 0.0075 | 0.0093 | 0.0086 | 0.0100 | 0.0127 | 0.0059 | 0.0120 | 0.0112 | 0.0082 | 0.0114 | |
| R2 | 0.9986 | 0.9991 | 0.9986 | 0.9988 | 0.9983 | 0.9971 | 0.9993 | 0.9967 | 0.9970 | 0.9984 | 0.9957 | |
| Leakage Size | 0 | 1.2 | 1.5 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3 | 3.2 | 3.5 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | Proposed Method | 0.0066 | 0.0053 | 0.0068 | 0.0062 | 0.0073 | 0.0098 | 0.0044 | 0.0087 | 0.0084 | 0.0058 | 0.0076 | 0.0070 |
| VAECNNSSM | 0.0183 | 0.0155 | 0.0149 | 0.0139 | 0.0151 | 0.0156 | 0.0129 | 0.0157 | 0.0147 | 0.0135 | 0.0164 | 0.0151 | |
| VAEBPSSM | 0.0175 | 0.0143 | 0.0140 | 0.0131 | 0.0160 | 0.0166 | 0.0165 | 0.0219 | 0.0190 | 0.0206 | 0.0220 | 0.0174 | |
| CNN | 0.0197 | 0.0191 | 0.0185 | 0.0161 | 0.0170 | 0.0180 | 0.0130 | 0.0162 | 0.0158 | 0.0142 | 0.0173 | 0.0168 | |
| RMSE | Proposed Method | 0.0098 | 0.0075 | 0.0093 | 0.0086 | 0.0100 | 0.0127 | 0.0059 | 0.0120 | 0.0112 | 0.0082 | 0.0114 | 0.0097 |
| VAECNNSSM | 0.0222 | 0.0187 | 0.0187 | 0.0168 | 0.0175 | 0.0194 | 0.0158 | 0.0198 | 0.0180 | 0.0163 | 0.0203 | 0.0185 | |
| VAEBPSSM | 0.0207 | 0.0183 | 0.0185 | 0.0157 | 0.0189 | 0.0200 | 0.0189 | 0.0259 | 0.0216 | 0.0232 | 0.0254 | 0.0206 | |
| CNN | 0.0246 | 0.0230 | 0.0230 | 0.0196 | 0.0206 | 0.0228 | 0.0168 | 0.0196 | 0.0202 | 0.0180 | 0.0214 | 0.0209 | |
| R2 | Proposed Method | 0.9986 | 0.9991 | 0.9986 | 0.9988 | 0.9983 | 0.9971 | 0.9993 | 0.9967 | 0.9970 | 0.9984 | 0.9957 | 0.9980 |
| VAECNNSSM | 0.9931 | 0.9946 | 0.9946 | 0.9953 | 0.9948 | 0.9932 | 0.9951 | 0.9910 | 0.9922 | 0.9935 | 0.9865 | 0.9931 | |
| VAEBPSSM | 0.9940 | 0.9949 | 0.9947 | 0.9959 | 0.9939 | 0.9928 | 0.9930 | 0.9847 | 0.9888 | 0.9868 | 0.9788 | 0.9908 | |
| CNN | 0.9915 | 0.9919 | 0.9918 | 0.9936 | 0.9928 | 0.9906 | 0.9944 | 0.9913 | 0.9902 | 0.9921 | 0.9850 | 0.9914 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Sheng, B.; Li, Y.; Fu, G.; Jiang, S.; Jiang, Z. Adaptive Prediction of Compressor Cylinder Pressure Dynamics Using a Physics-Guided VAE-CNN State Space Model. Actuators 2025, 14, 535. https://doi.org/10.3390/act14110535
Lu Y, Sheng B, Li Y, Fu G, Jiang S, Jiang Z. Adaptive Prediction of Compressor Cylinder Pressure Dynamics Using a Physics-Guided VAE-CNN State Space Model. Actuators. 2025; 14(11):535. https://doi.org/10.3390/act14110535
Chicago/Turabian StyleLu, Yingkang, Buyun Sheng, Yanfei Li, Gaocai Fu, Shan Jiang, and Zeyang Jiang. 2025. "Adaptive Prediction of Compressor Cylinder Pressure Dynamics Using a Physics-Guided VAE-CNN State Space Model" Actuators 14, no. 11: 535. https://doi.org/10.3390/act14110535
APA StyleLu, Y., Sheng, B., Li, Y., Fu, G., Jiang, S., & Jiang, Z. (2025). Adaptive Prediction of Compressor Cylinder Pressure Dynamics Using a Physics-Guided VAE-CNN State Space Model. Actuators, 14(11), 535. https://doi.org/10.3390/act14110535






