Multi-Objective Optimization of Torque Motor Structural Parameters in Direct-Drive Valves Based on Genetic Algorithm
Abstract
1. Introduction
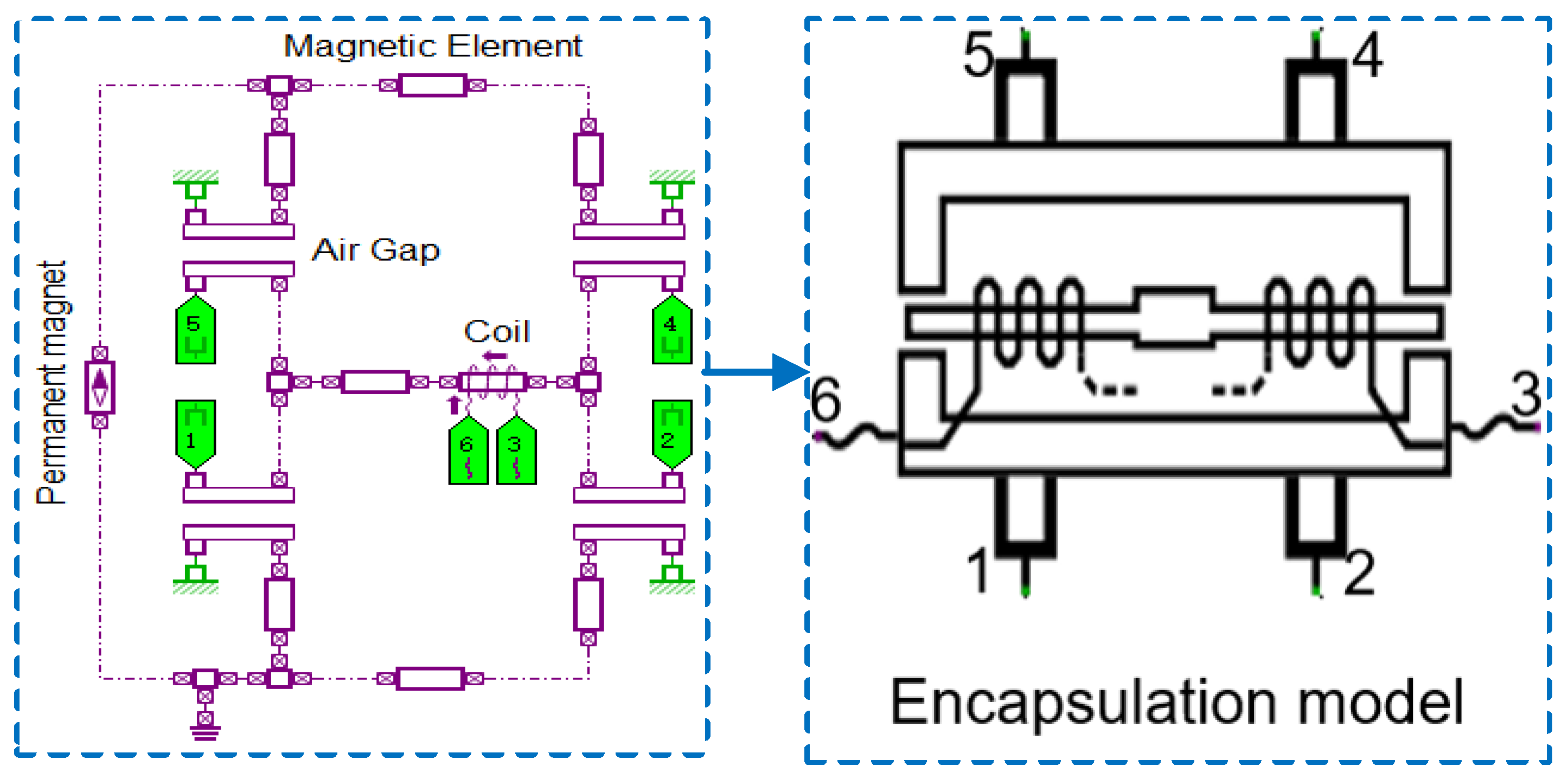
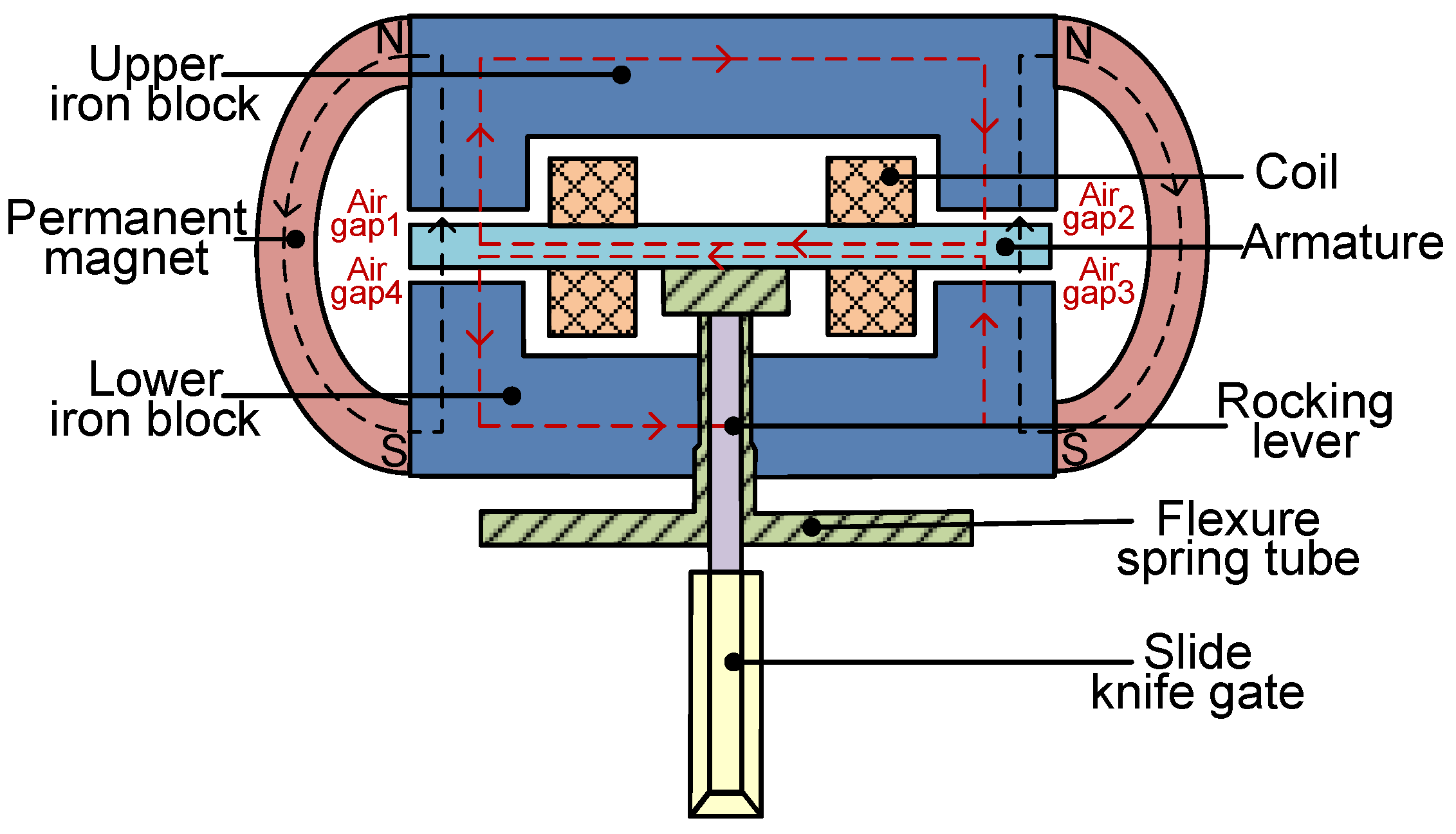
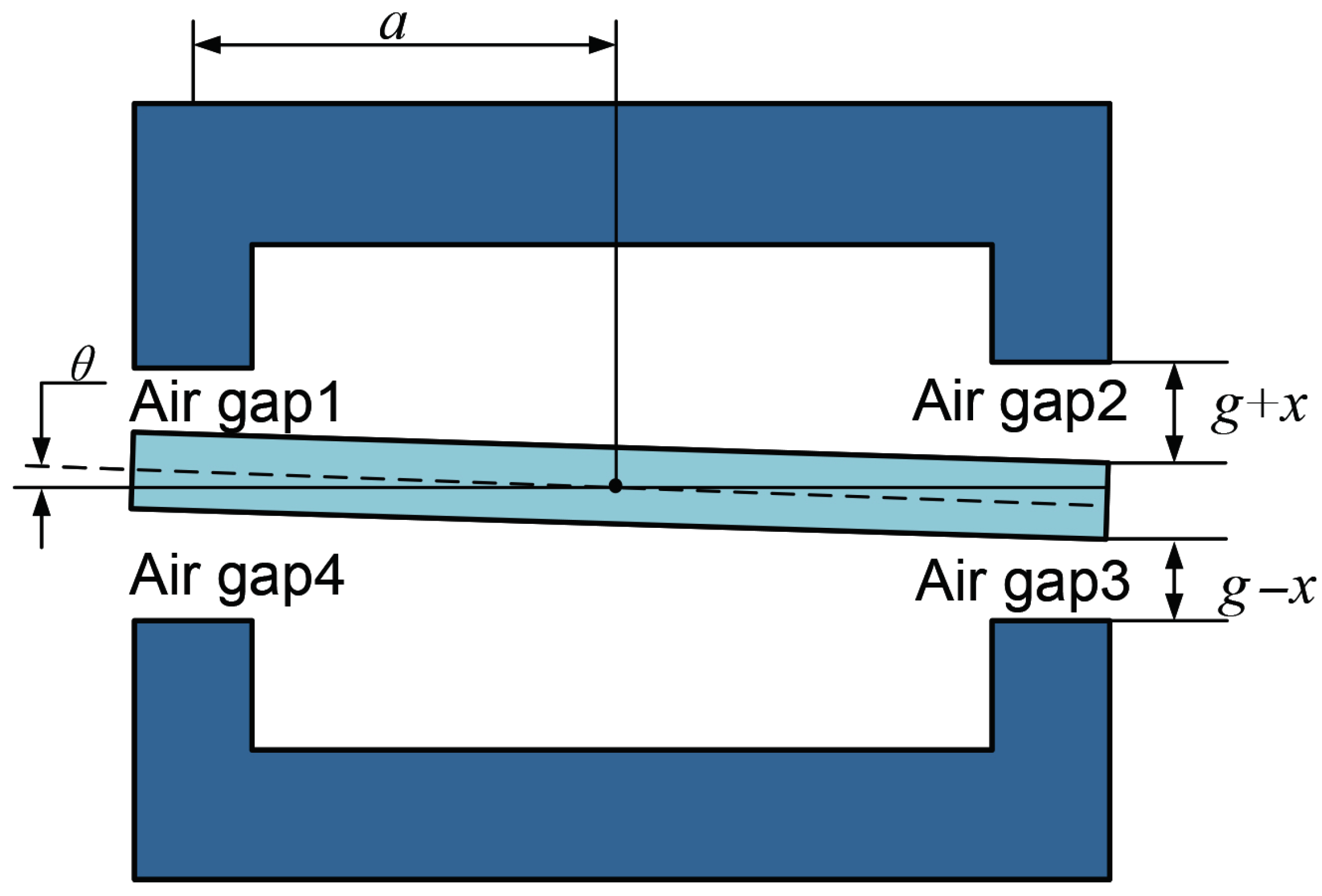
2. Mathematical Model of the Torque Motor
3. Simulation Analysis of the Torque Motor
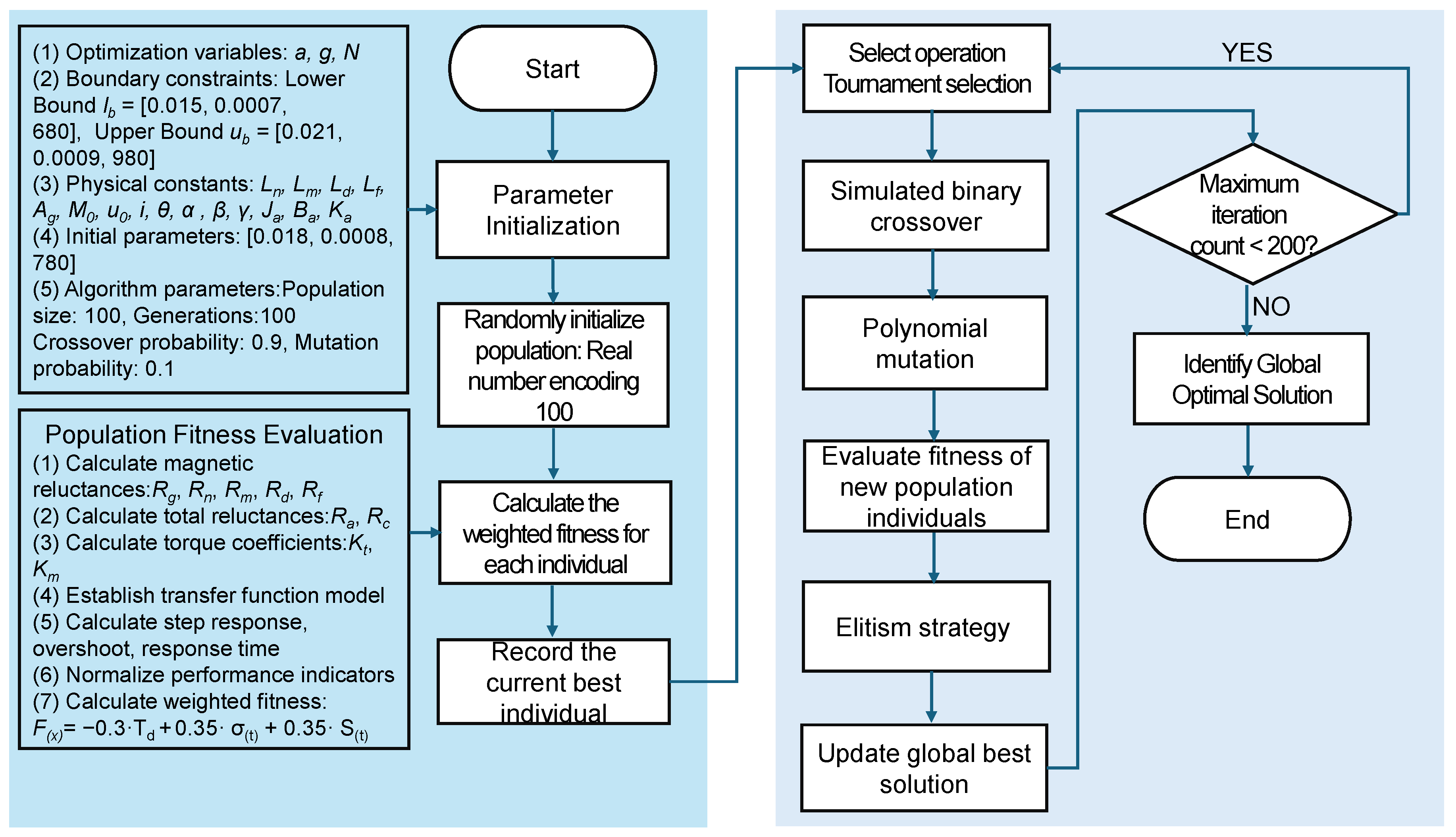
4. Analysis of Optimization Based on the GA
4.1. Multi-Objective GA
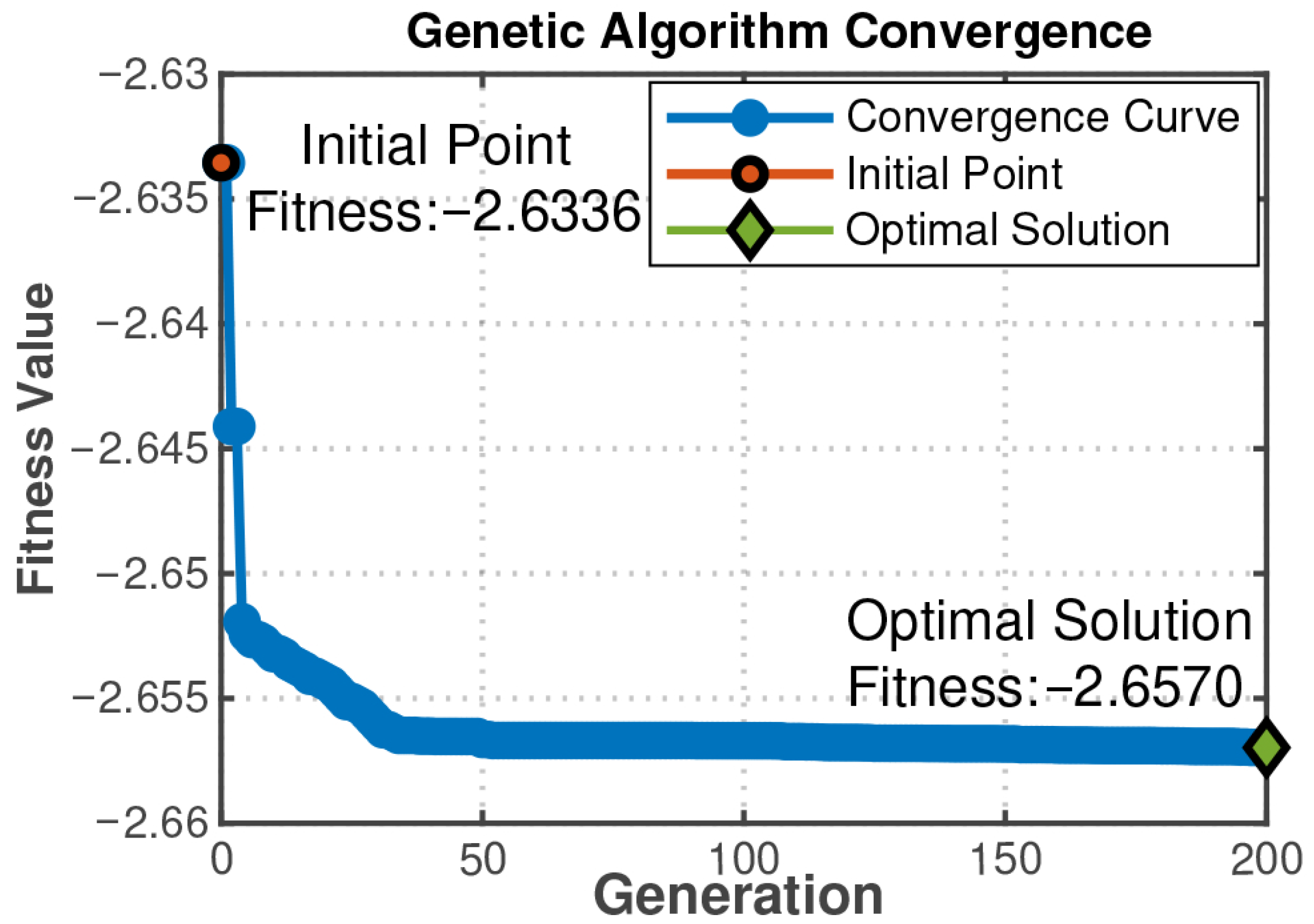
4.2. Simulation Analysis of Optimization
5. Influence of Optimization on the Valve
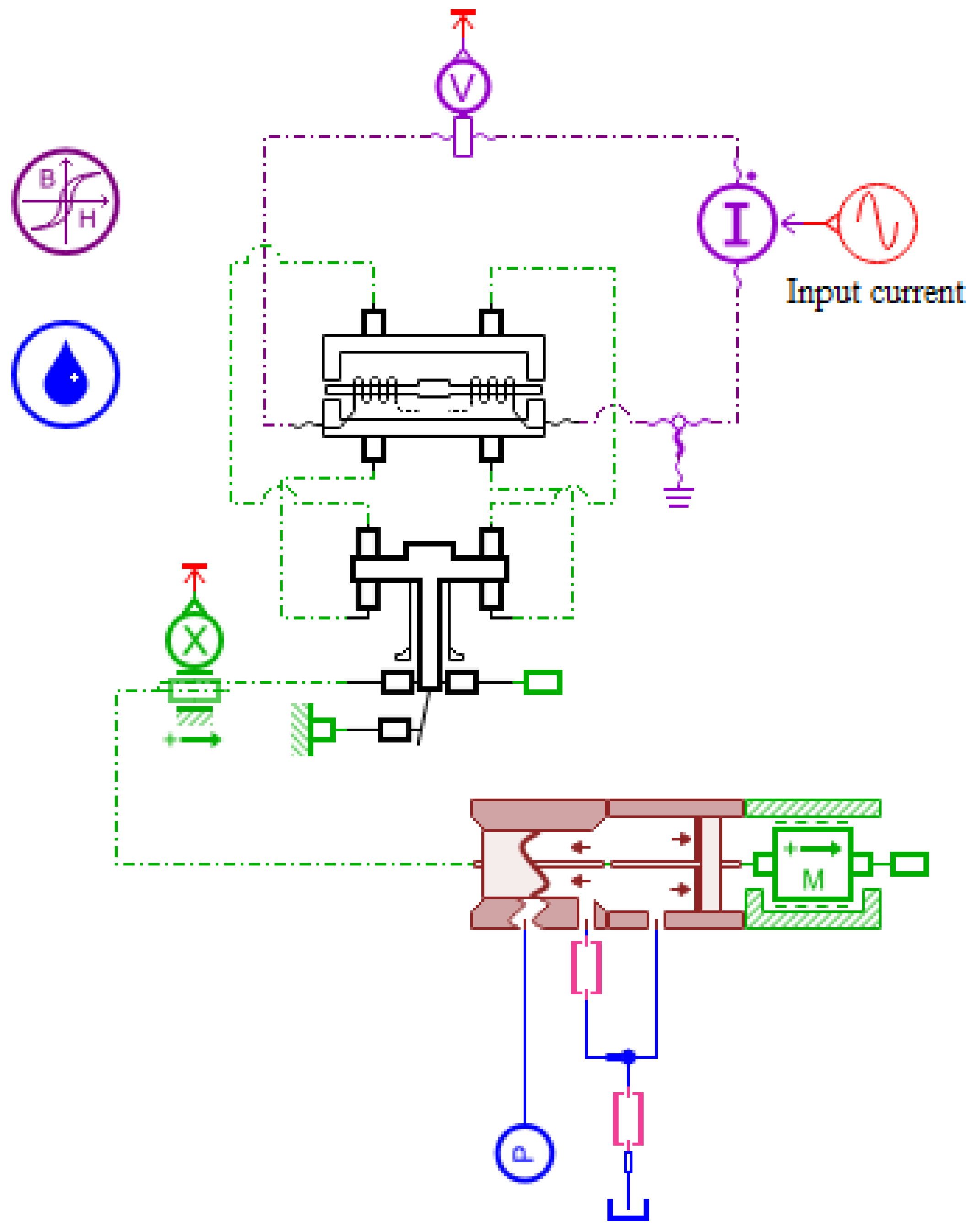
6. Experimental Verifications
6.1. Static Test
6.2. Dynamic Test
7. Conclusions
- (1)
- Based on FEA results, this paper reveals that the structural parameters of the torque motor are inherently coupled with its static and dynamic performance, where improving one metric often compromises others. Thus, torque motor design is inherently a multi-objective optimization problem requiring systematic trade-offs among output torque, response time, and overshoot.
- (2)
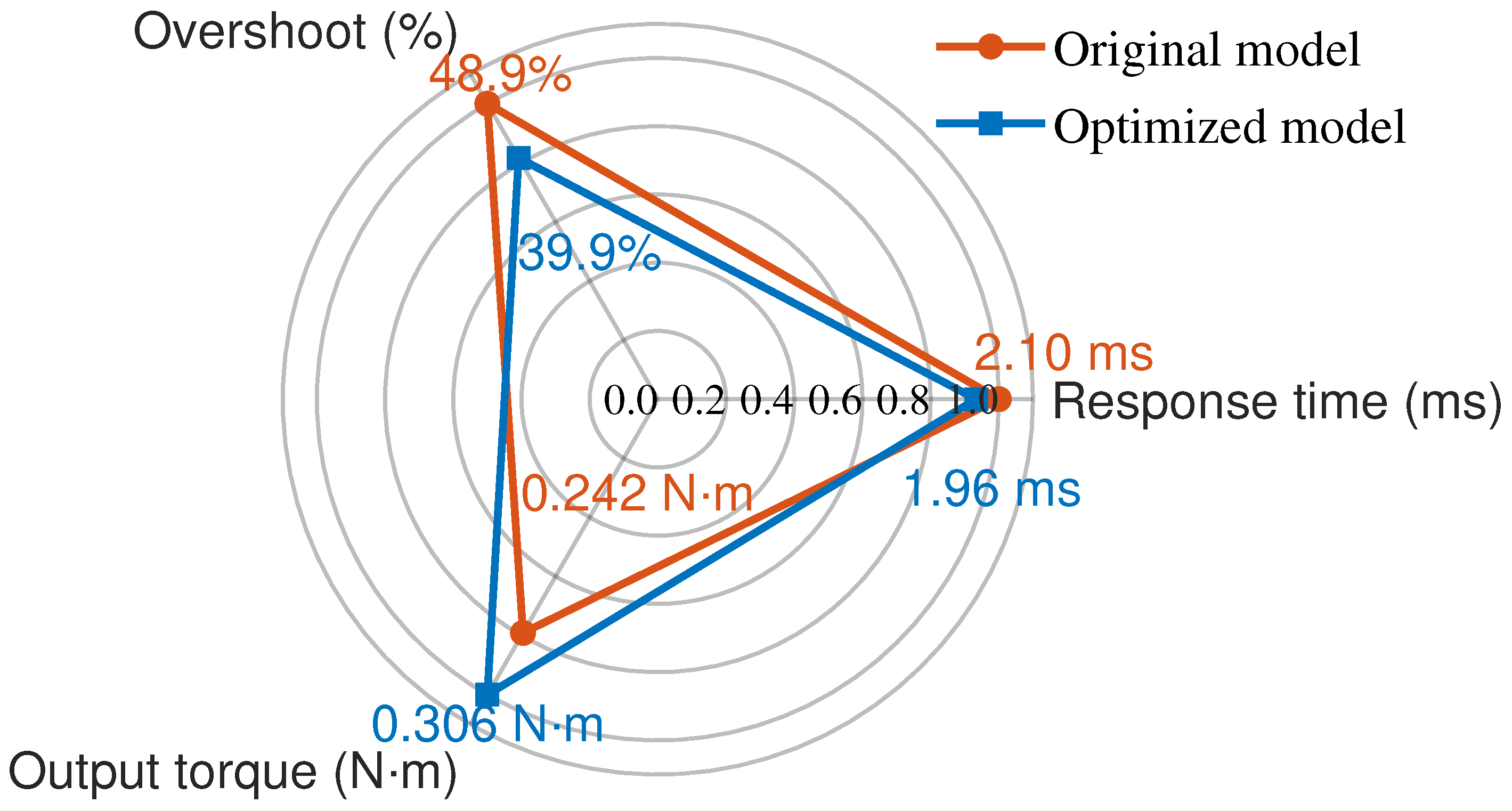
- The multi-objective GA is used to optimize the torque arm, air gap, and coil turns, resulting in a 20 mm arm, a 0.71 mm gap, and 980 turns. The output torque increases by 26.4%, the overshoot is reduced by 9%, and the response time decreases by 0.14 ms. Significant effectiveness is achieved.
- (3)
- AMESim simulations show that the optimized torque motors improve valve control precision and response speed, which accelerates the stabilization of flow rate. Consistent flow output is observed in high-current regions, suggesting reduced sensitivity to pressure fluctuations.
- (4)
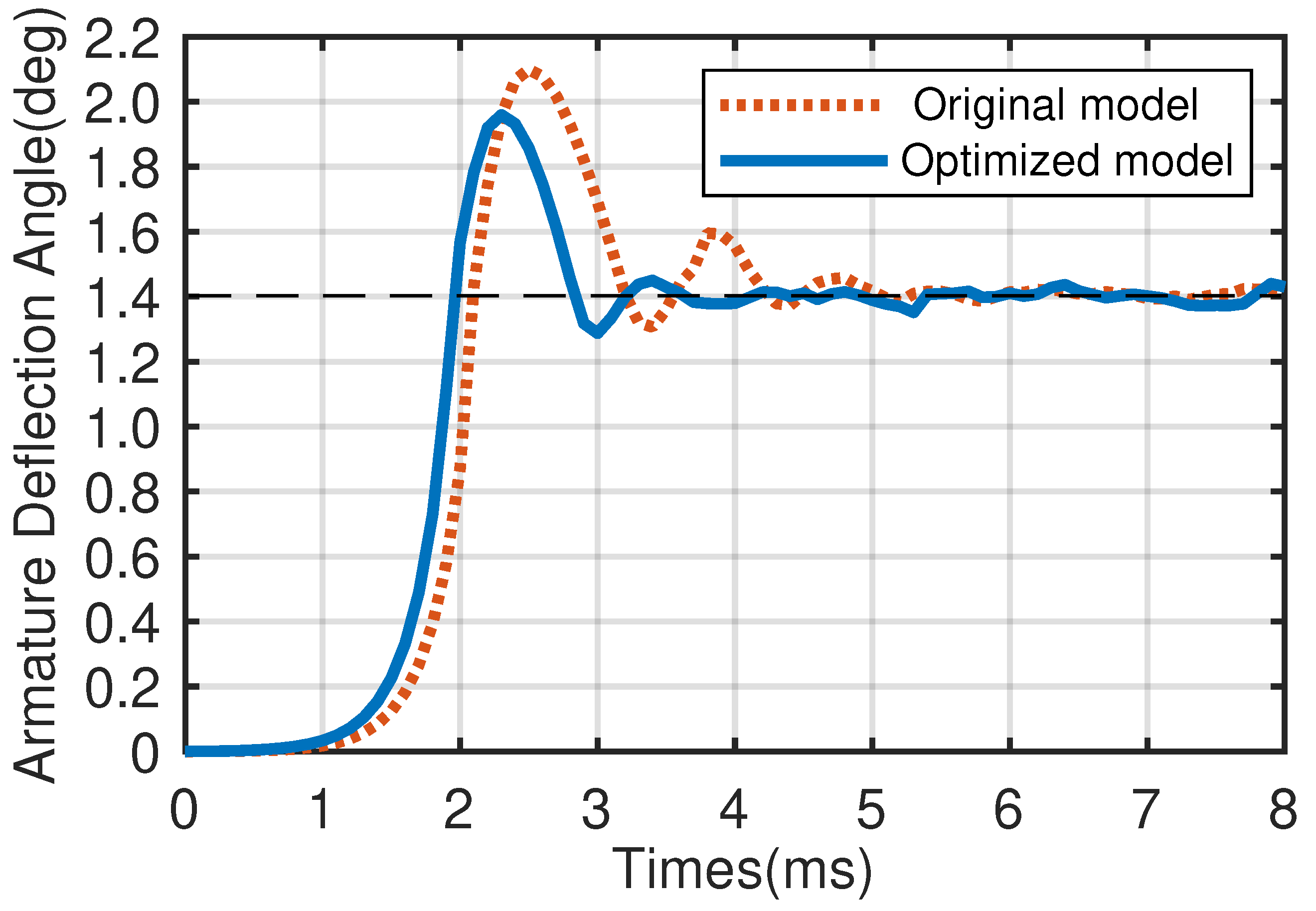
- Experimental results conclusively demonstrate that the optimized model significantly enhances both the static and dynamic characteristics of the torque motor, quantified by a 26% increase in output torque and an average 7.1% reduction in response time. The strong agreement between the experimental data and simulation results further validates the accuracy of the theoretical models. Consequently, this paper provides insights into the design of torque motors for aerospace servo valves and the optimization of high-frequency servo valve performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Magnetic flux in air gap 1 | |
| Magnetic flux in air gap 2 | |
| Magnetic flux in air gap 3 | |
| Magnetic flux in air gap 4 | |
| Magnetic flux in the upper iron block | |
| Magnetic flux in the control coil | |
| Magnetic flux in the lower iron block | |
| Magnetic flux in the permanent magnet | |
| Magnetic flux in the permanent magnet | |
| Permanent magnet | |
| N | Number of turns in the control coil |
| Reluctance of air gap 1 | |
| Reluctance of air gap 2 | |
| Reluctance of air gap 3 | |
| Reluctance of air gap 4 | |
| Reluctance of the permanent magnet | |
| Reluctance of the armature | |
| Horizontal reluctance of the magnetic conductor | |
| Vertical reluctance of the magnetic conductor | |
| Reluctance of the leakage flux path in permanent magnet | |
| Reluctance of the leakage flux path in the control coil | |
| Reluctance of the leakage flux path in air gap | |
| Leakage coefficient of the permanent magnet | |
| Leakage coefficient of the coil | |
| Leakage coefficient of the air gap |
Appendix A
| Parameter | Value |
|---|---|
| Hydraulic oil density (kg/m3) | 778 |
| Initial air gap (mm) | 0.8 |
| Magnetic induction (T) | 0.15 |
| Minimum coercive field (A/m) | −20,000 |
| Spool mass (g) | 3.5 |
| Coil turns (turns) | 780 |
| Moment of inertia (kg·m2) | |
| Spring rate of feedback spring (N/m) | 3400 |
| Inlet pressure (MPa) | 0.402/0.598 |
| Armature assembly rotational damping (N·m/(rad/s)) | 0.002 |
| Armature assembly translational damping (N·s/m) | 10 |
References
- Deng, X. Modeling and Simulation Research of Fuel Metering Device Based on Rotary Direct Drive Valve. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2020. [Google Scholar]
- Mi, J. Life Prediction Method of Direct-Drive Electro-Hydraulic Servo Valve Spool Valve Sleeve. Master’s Thesis, Chongqing University, Chongqing, China, 2023. [Google Scholar]
- Tu, F.; Shi, L.; Li, S.; Chen, C.; Wei, S.; Su, Z.; Wei, J. Research progress of direct drive electro-hydraulic servo valve. Fluid Mach. 2022, 50, 61–70. [Google Scholar]
- Huh, J.Y.; Park, C.S. An Analysis of Static and Dynamic Characteristics of Torque Motor. J. Drive Control 2015, 12, 9–14. [Google Scholar] [CrossRef]
- Manring, N.D.; Fales, R.C. Hydraulic Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Wang, M.; Li, D.; Qu, R. An overview on developments and research of limited angle torque motor. Trans. China Electrotech. Soc. 2023, 38, 1486–1505. [Google Scholar]
- Wang, Z.; Li, J.; Hu, C.; Li, X.; Zhu, Y. Hybrid energy storage system and management strategy for motor drive with high torque overload. J. Energy Storage 2024, 75, 109432. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, L.; Duan, Z.; Jiao, Z.; Gerada, C.; Chen, I.-M. High torque density torque motor with hybrid magnetization pole arrays for jet pipe servo valve. IEEE Trans. Ind. Electron. 2019, 67, 2133–2142. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, Q.; Duan, Z.; Jiao, Z. Modeling and analysis of servo valve torque motor based on FEM. In Proceedings of the 2017 IEEE International Conference on Cybernetics and Intelligent Systems (CIS) and IEEE Conference on Robotics, Automation and Mechatronics (RAM), Ningbo, China, 19–21 November 2017; pp. 791–796. [Google Scholar]
- Rao, D. Analysis of Influencing Factors of Output Torque on Fuel-Oil Servo Valve Torque Motor. Ph.D. Thesis, Yanshan University, Qinhuangdao, China, 2025. [Google Scholar]
- Hao, Z.; Ma, Y.; Wang, P.; Luo, G.; Chen, Y. A review of axial-flux permanent-magnet motors: Topological structures, design, optimization and control techniques. Machines 2022, 10, 1178. [Google Scholar] [CrossRef]
- Sharan, A.S.; Hiremath, S.S.; Venkatesha, C.S.; Venkatesha, C.S. Investigation on the critical parameters affecting the working design dynamics of a torque motor employed in an electro-hydraulic servovalve. Simulation 2019, 95, 31–49. [Google Scholar]
- Sun, X.; Xu, N.; Yao, M. Sequential subspace optimization design of a dual three-phase permanent magnet synchronous hub motor based on NSGA III. IEEE Trans. Transp. Electrif. 2023, 9, 622–630. [Google Scholar] [CrossRef]
- Sun, X.; Hu, C.; Lei, G.; Guo, Y.; Zhu, J. State feedback control for a PM hub motor based on gray wolf optimization algorithm. IEEE Trans. Power Electron. 2020, 35, 1136–1146. [Google Scholar] [CrossRef]
- Tian, W.; Zhang, C.; Mao, Z.; Cheng, B. Optimization of a dual-channel water-cooling heat dissipation system for PMSM in underwater unmanned vehicles using a multi-objective genetic algorithm. J. Mar. Sci. Eng. 2024, 12, 2133. [Google Scholar] [CrossRef]
- Oh, J.-A.; Sarbajit, P.; Kim, D.-J.; Bang, D.; Lee, K.-W.; Yoon, B.-K.; Jang, G.-W.; Kang, J.-H.; Chang, J. Design and performance testing of a large direct-drive generator for low speed and high torque applications. J. Mech. Sci. Technol. 2025, 39, 1641–1651. [Google Scholar] [CrossRef]
- Xie, F.; Wang, H.; Ni, S.; Xu, J.; Zheng, Z. Multi-objective optimization design of external rotor permanent magnet synchronous motor for robot arm. J. Mech. Sci. Technol. 2024, 38, 803–814. [Google Scholar] [CrossRef]
- Salarian, M.; Azari, M.N.; Hajiaghaee-Keshteli, M. Using multi-objective optimization and finite element method to reduce cogging torque in a brushless DC motor. IETE J. Res. 2024, 70, 6350–6360. [Google Scholar] [CrossRef]
- Chai, J.; Zhao, T.; Gui, X. Multi-objective optimization design of permanent magnet torque motor. World Electr. Veh. J. 2021, 12, 131. [Google Scholar] [CrossRef]
- Cen, Y.; Shen, H.; Wang, X.; Wu, Y.; Du, J. Multi-objective optimization analysis of electromagnetic performance of permanent magnet synchronous motors based on the PSO algorithm. Energies 2024, 17, 4637. [Google Scholar] [CrossRef]
- Ni, X.; Li, Y.; Sun, R.; Xu, Y. Multiparameter optimization analysis of permanent magnet couplings using response surface methodology and genetic algorithm. J. Mech. Sci. Technol. 2024, 38, 6279–6286. [Google Scholar] [CrossRef]
- Zhang, J.; Shan, W.; Chen, K.; Chen, Y. Research and optimization of demagnetization performance of permanent magnet synchronous motorized spindle. Mach. Tool Hydraul. 2025, 53, 24–31. [Google Scholar]
- Feng, L.; Liu, W.; Ding, Y.; Li, H. Optimal design and analysis of high-speed permanent magnet synchronous motor based on genetic algorithm and TOPSIS method. J. Electr. Eng. Technol. 2025, 20, 1463–1473. [Google Scholar] [CrossRef]
- Fan, D.; Quan, L.; Zhu, X.; Xiang, Z. Design and optimization of double-stator Vernier permanent magnet motor with improved torque characteristics based on flux modulation theory. IEEE Trans. Magn. 2022, 58, 8202707. [Google Scholar] [CrossRef]
- Stosiak, M.; Lubecki, M.; Karpenko, M. Designing a Composite Hydraulic Cylinder Using Genetic Algorithms. Actuators 2025, 14, 77. [Google Scholar] [CrossRef]
- Li, Y. Modeling and Simulink Simulation of Electrohydraulic Servo Valve; Mechanical Industry Press: Beijing, China, 2020. [Google Scholar]
- Li, H. Hydraulic Control Systems; National Defense Industry Press: Beijing, China, 1990. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Qiu, F.Y.; Mo, L.P.; Jiang, B.; Wang, L.P. Multi-Objective particle swarm optimization algorithm using large scale variable decomposition. Chin. J. Comput. 2016, 39, 2598–2613. [Google Scholar]
- Chen, J. Dynamic Simulation and Optimal Design and Control Method of Jet Pipe Servo Valve. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2017. [Google Scholar]

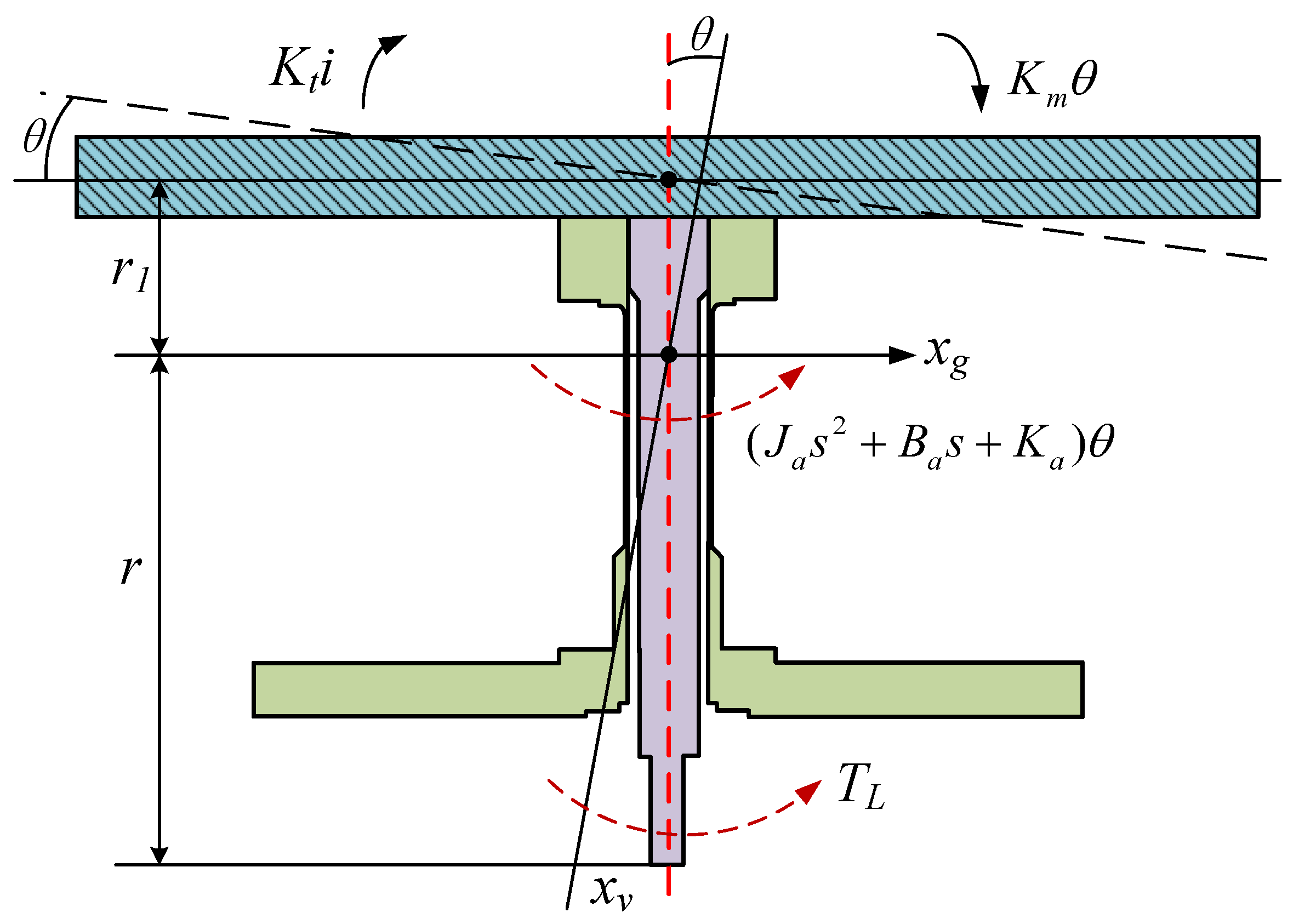
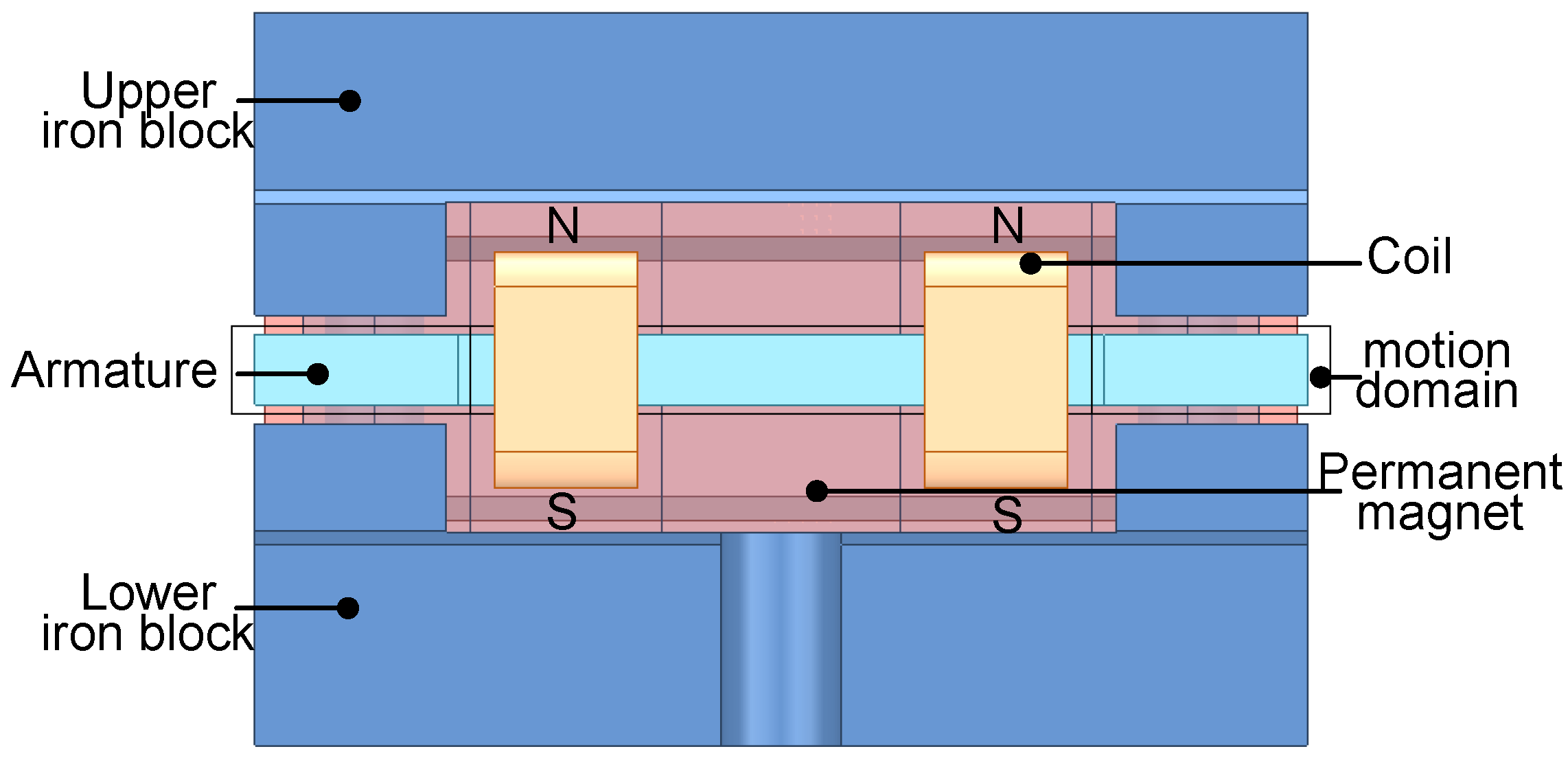

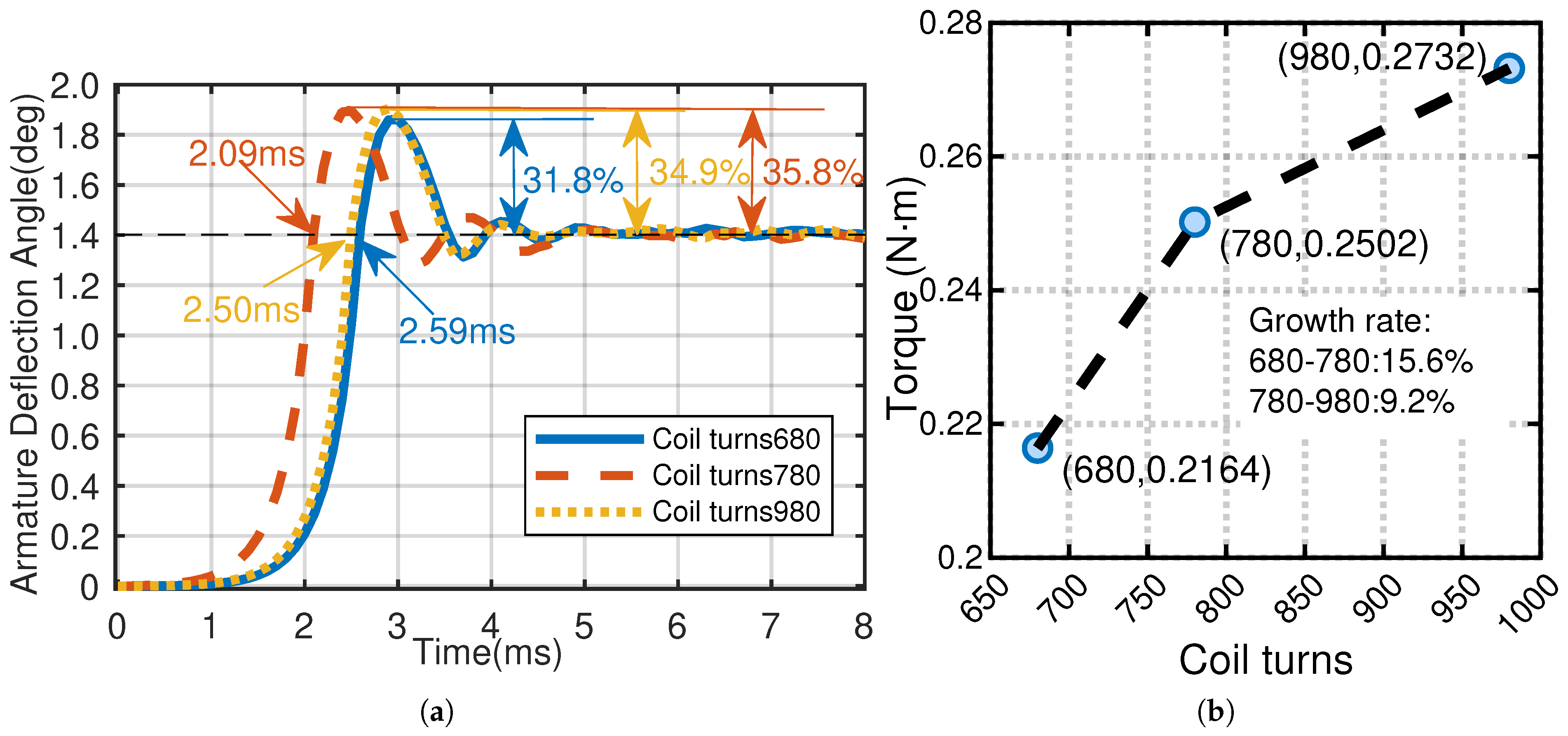
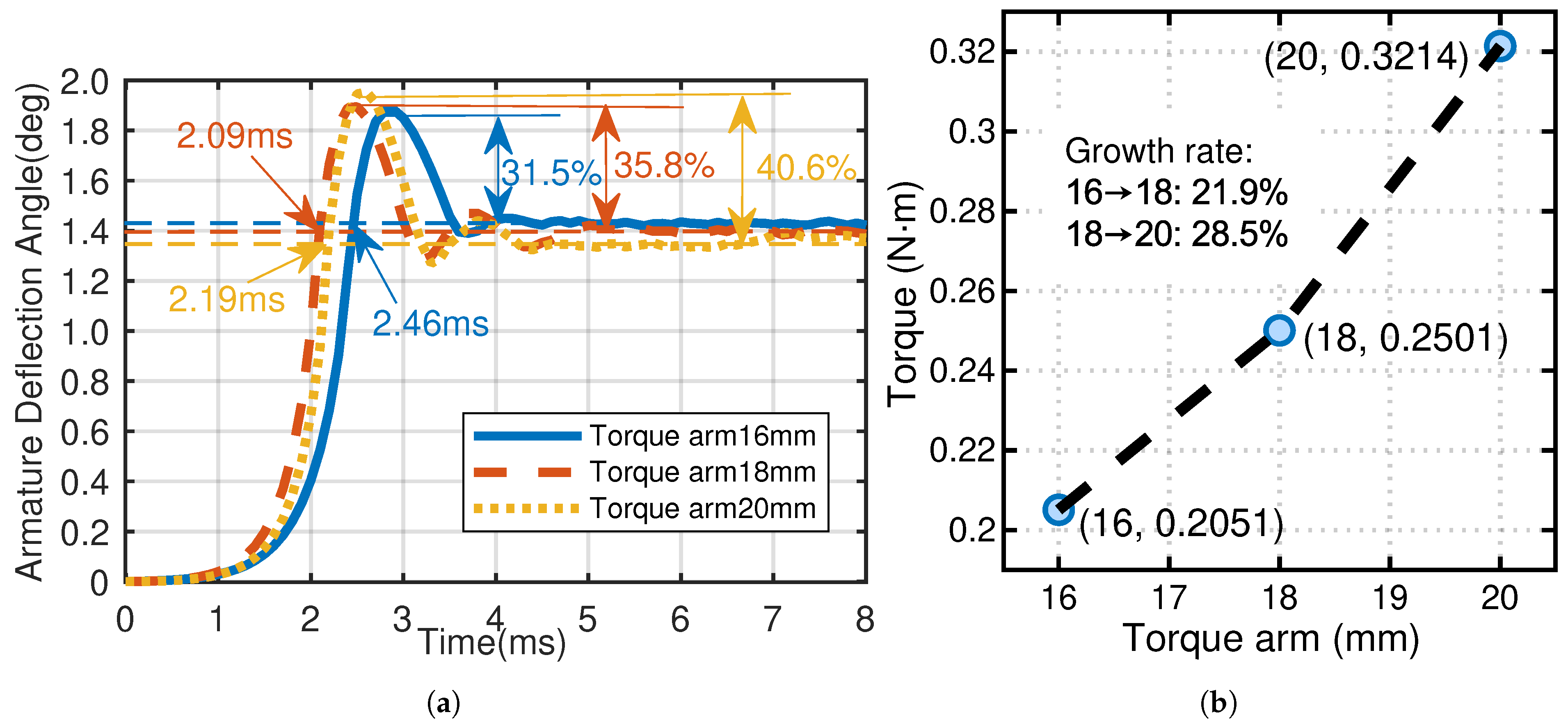
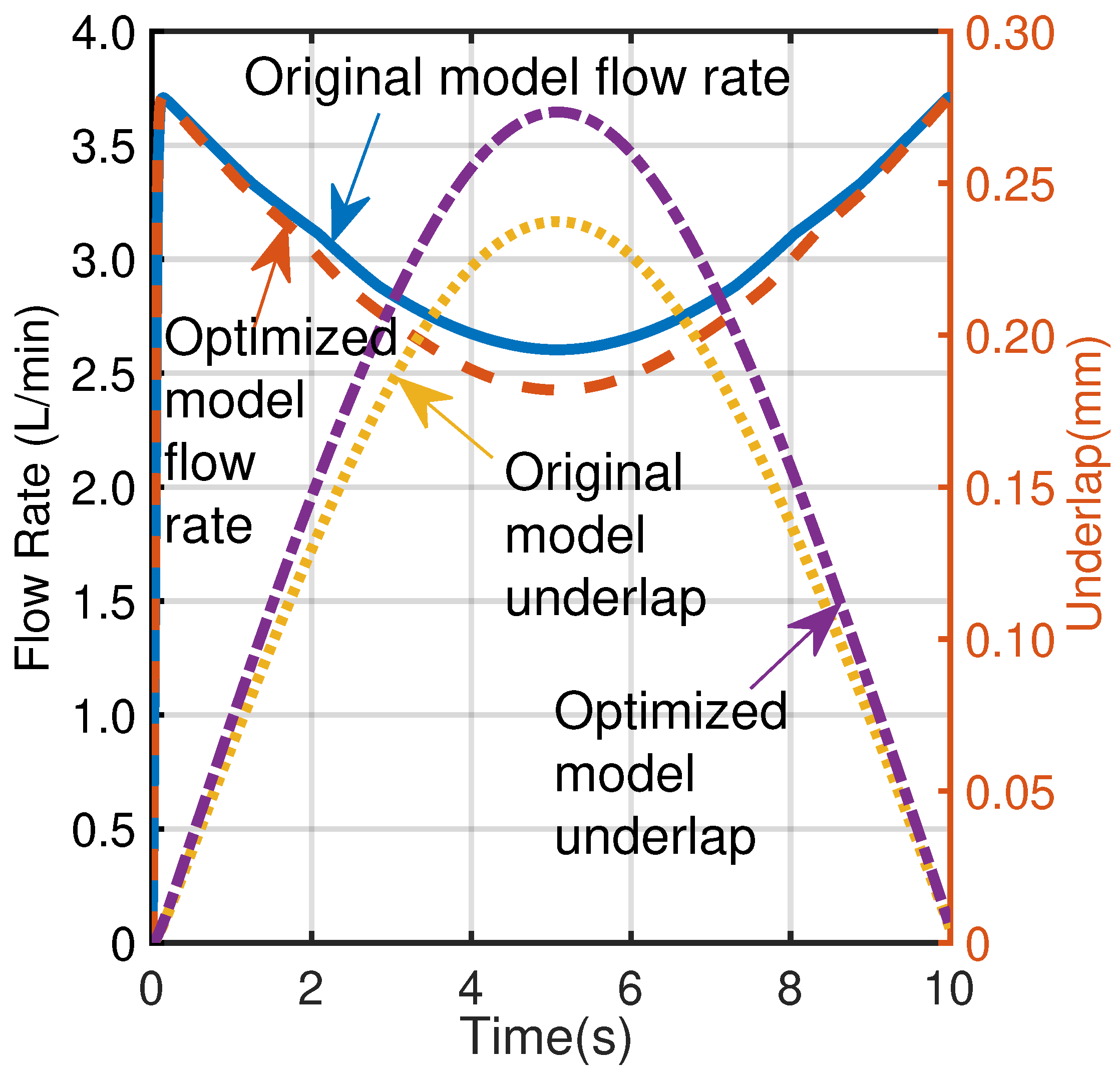


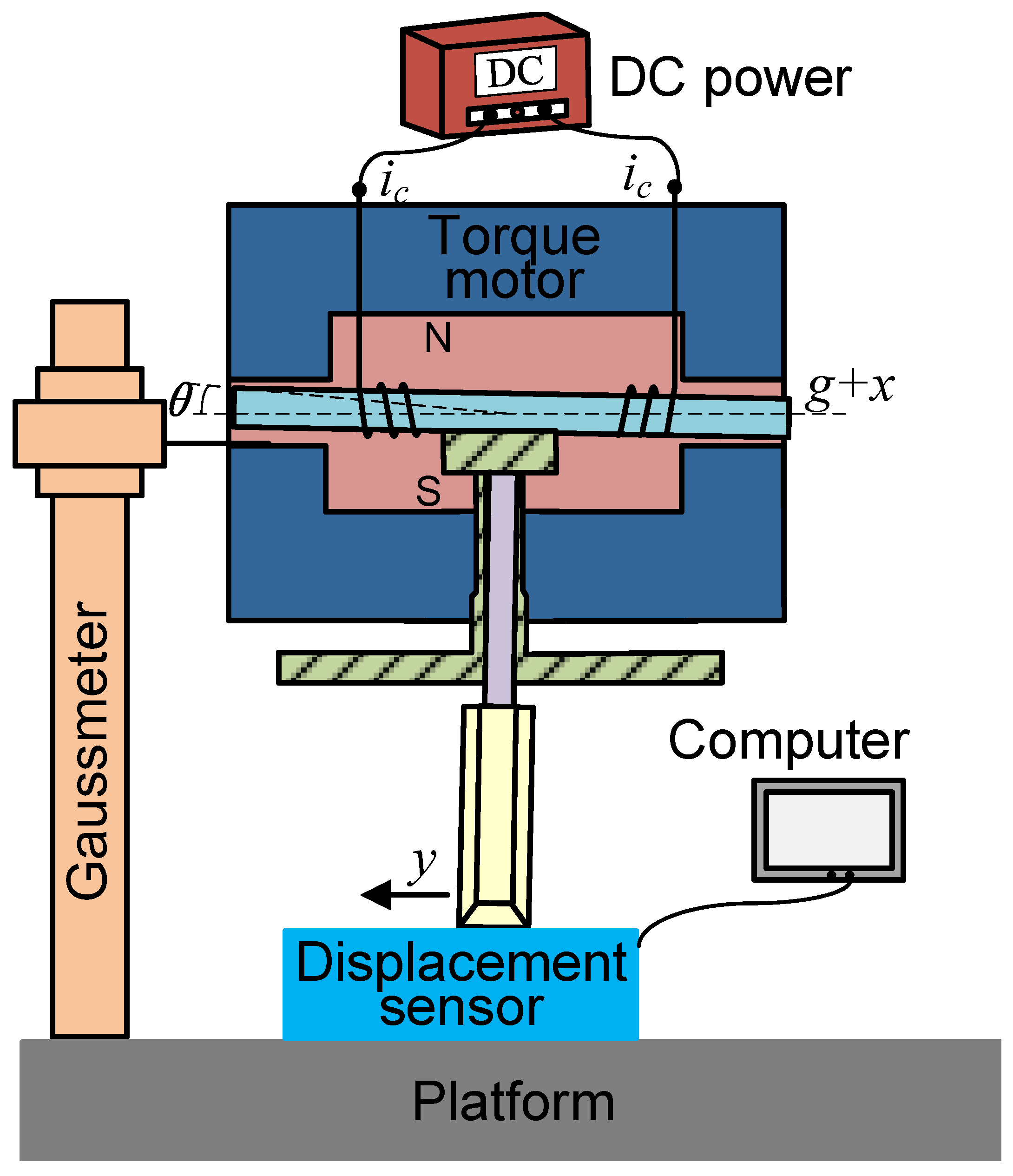

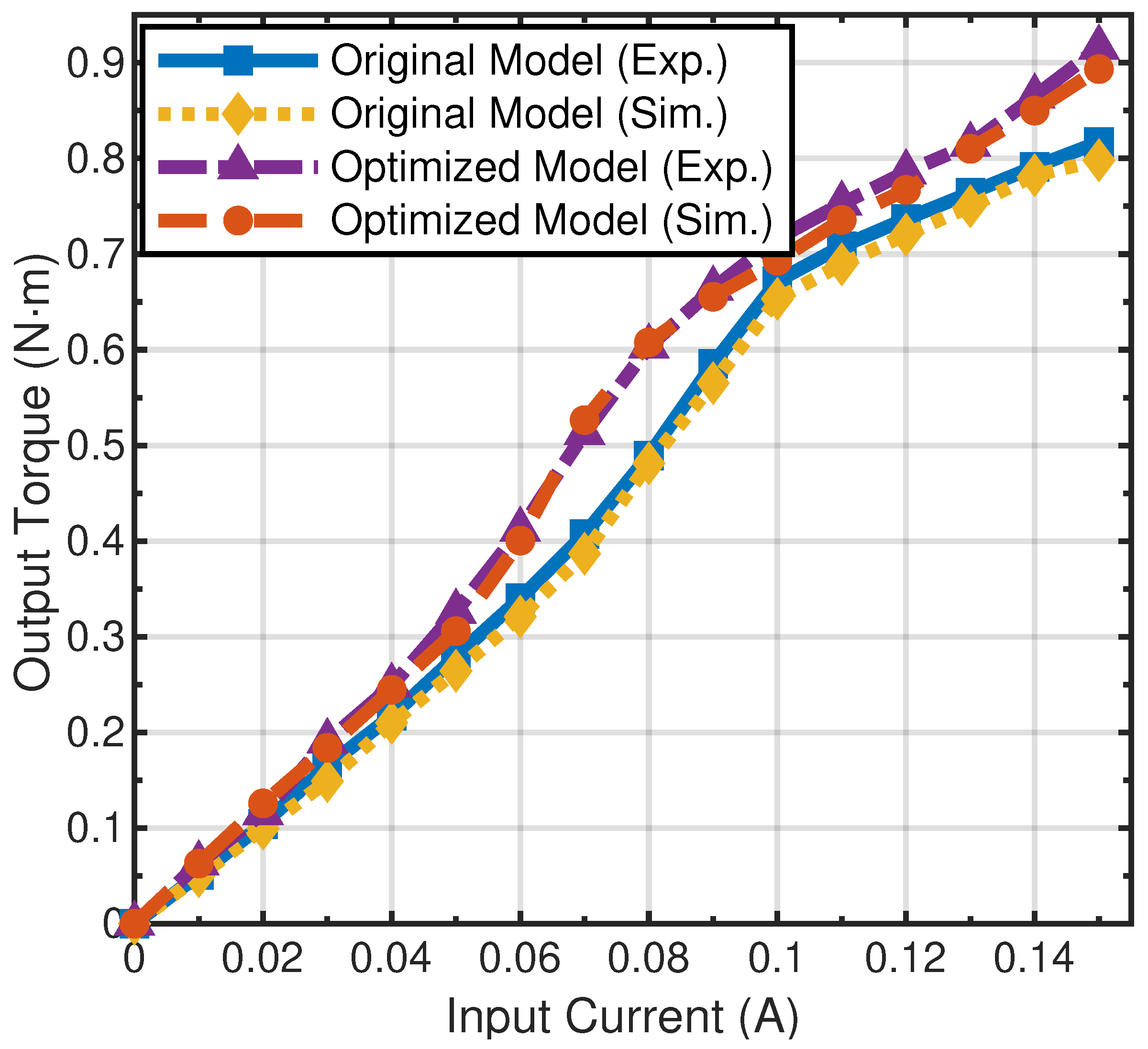

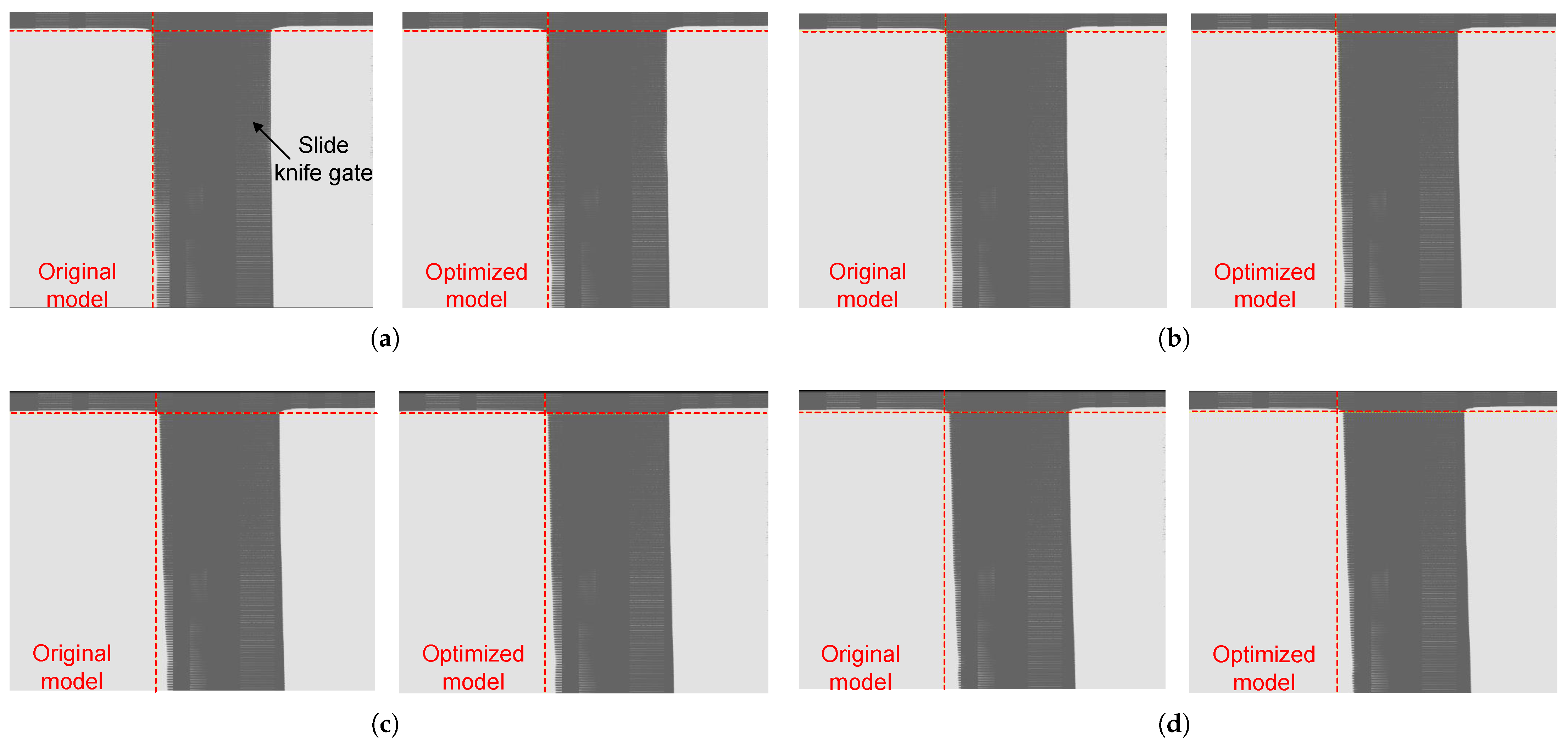
| Parameter | Initial Value | Variable Range |
|---|---|---|
| Torque arm (mm) | 18 | 15–21 |
| Air gap (mm) | 0.8 | 0.7–0.9 |
| Coil turns (turns) | 780 | 600–1000 |
| Parameter | Optimized Value |
|---|---|
| Torque arm (mm) | 20 |
| Air gap (mm) | 0.71 |
| Coil turns (N) | 980 |
| Input Current (A) | Model | Response Time (ms) |
|---|---|---|
| 0.05 | Original | 2.12 |
| Optimized | 1.96 | |
| 0.10 | Original | 2.09 |
| Optimized | 1.94 | |
| 0.15 | Original | 2.05 |
| Optimized | 1.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Liang, Q.; Sun, J.; Yan, B.; Hu, Z.; Sun, W. Multi-Objective Optimization of Torque Motor Structural Parameters in Direct-Drive Valves Based on Genetic Algorithm. Actuators 2025, 14, 527. https://doi.org/10.3390/act14110527
Zhang J, Liang Q, Sun J, Yan B, Hu Z, Sun W. Multi-Objective Optimization of Torque Motor Structural Parameters in Direct-Drive Valves Based on Genetic Algorithm. Actuators. 2025; 14(11):527. https://doi.org/10.3390/act14110527
Chicago/Turabian StyleZhang, Jian, Qiusong Liang, Jipeng Sun, Baosen Yan, Zhidong Hu, and Wei Sun. 2025. "Multi-Objective Optimization of Torque Motor Structural Parameters in Direct-Drive Valves Based on Genetic Algorithm" Actuators 14, no. 11: 527. https://doi.org/10.3390/act14110527
APA StyleZhang, J., Liang, Q., Sun, J., Yan, B., Hu, Z., & Sun, W. (2025). Multi-Objective Optimization of Torque Motor Structural Parameters in Direct-Drive Valves Based on Genetic Algorithm. Actuators, 14(11), 527. https://doi.org/10.3390/act14110527






