Dynamic Modeling of a Three-Phase BLDC Motor Using Bond Graph Methodology
Abstract
1. Introduction
- Development of a complete bond graph model for a 3-phase BLDC motor used in differential-drive serving robot.
- Cross-domain modeling of electromechanical and structural components in a unified framework.
- Analysis of motor performance to support future controller design and task planning.
2. Bond Graph
Causality
3. System Description
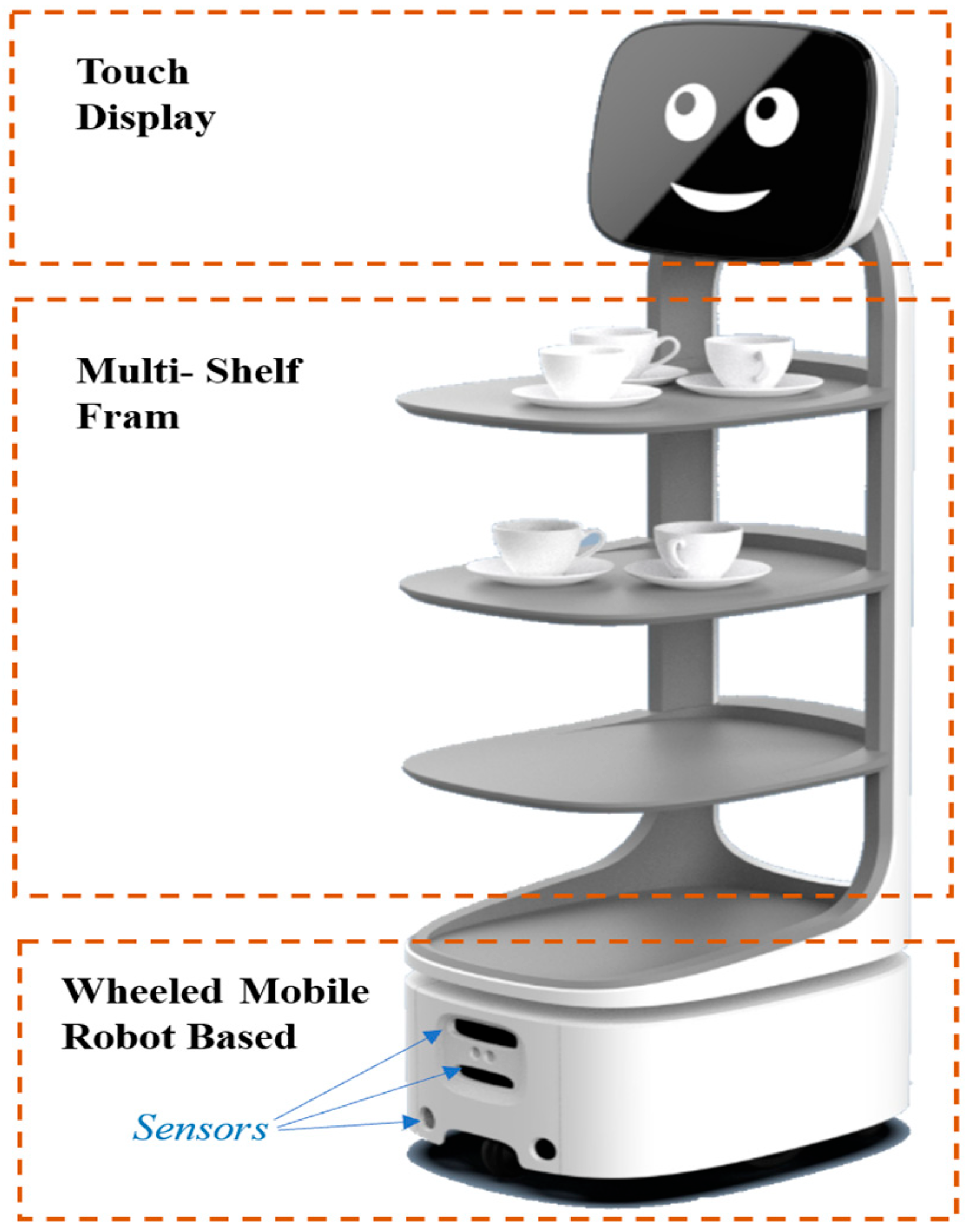
3.1. Kinematic Configuration and Wheel Layout
- Move forward or backward by setting = ;
- Rotate in place by setting = ;
- Turn with a defined radius by setting .
3.2. Bond Graph Modeling
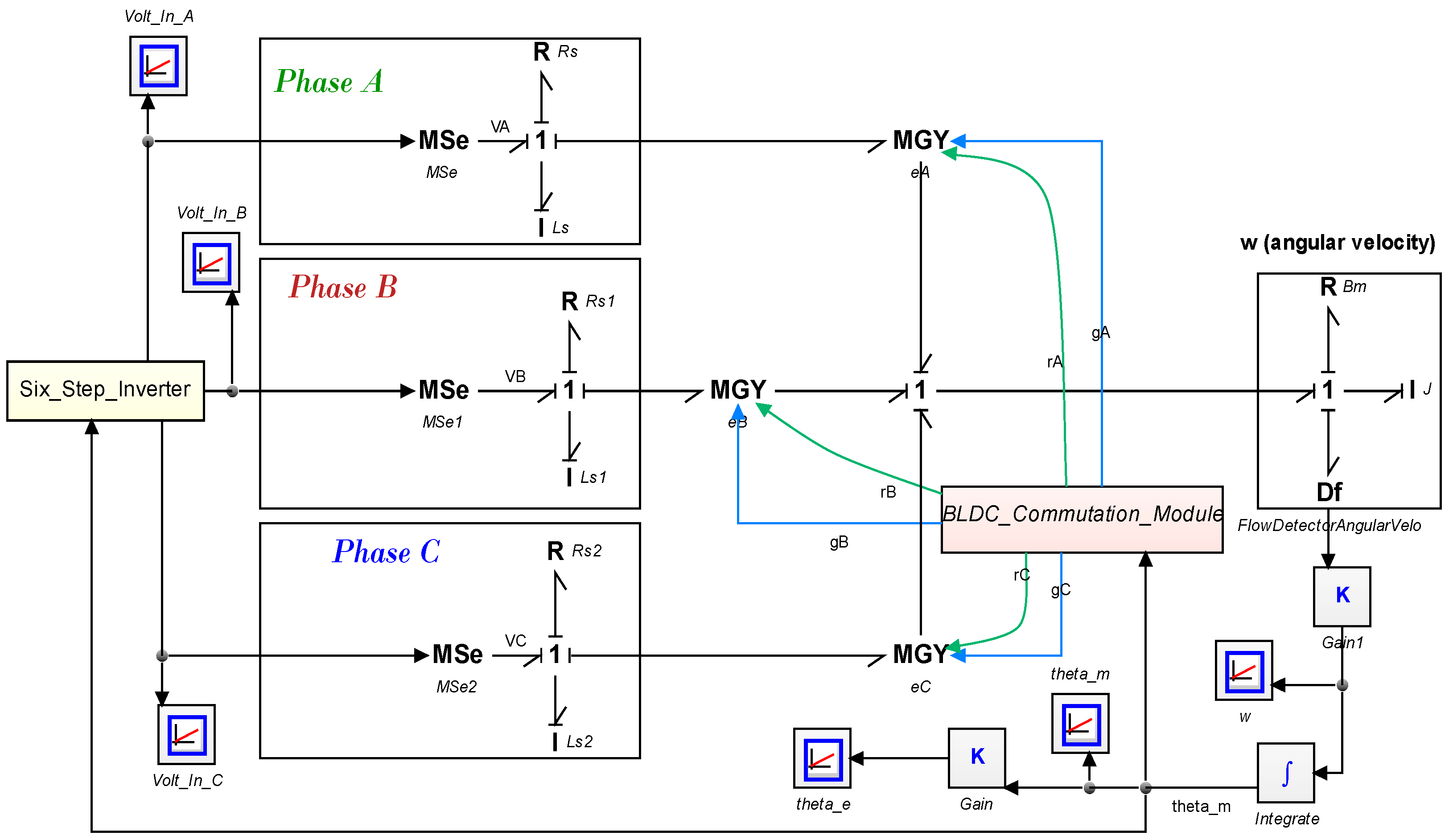
3.2.1. Modeling of the Electromechanical System
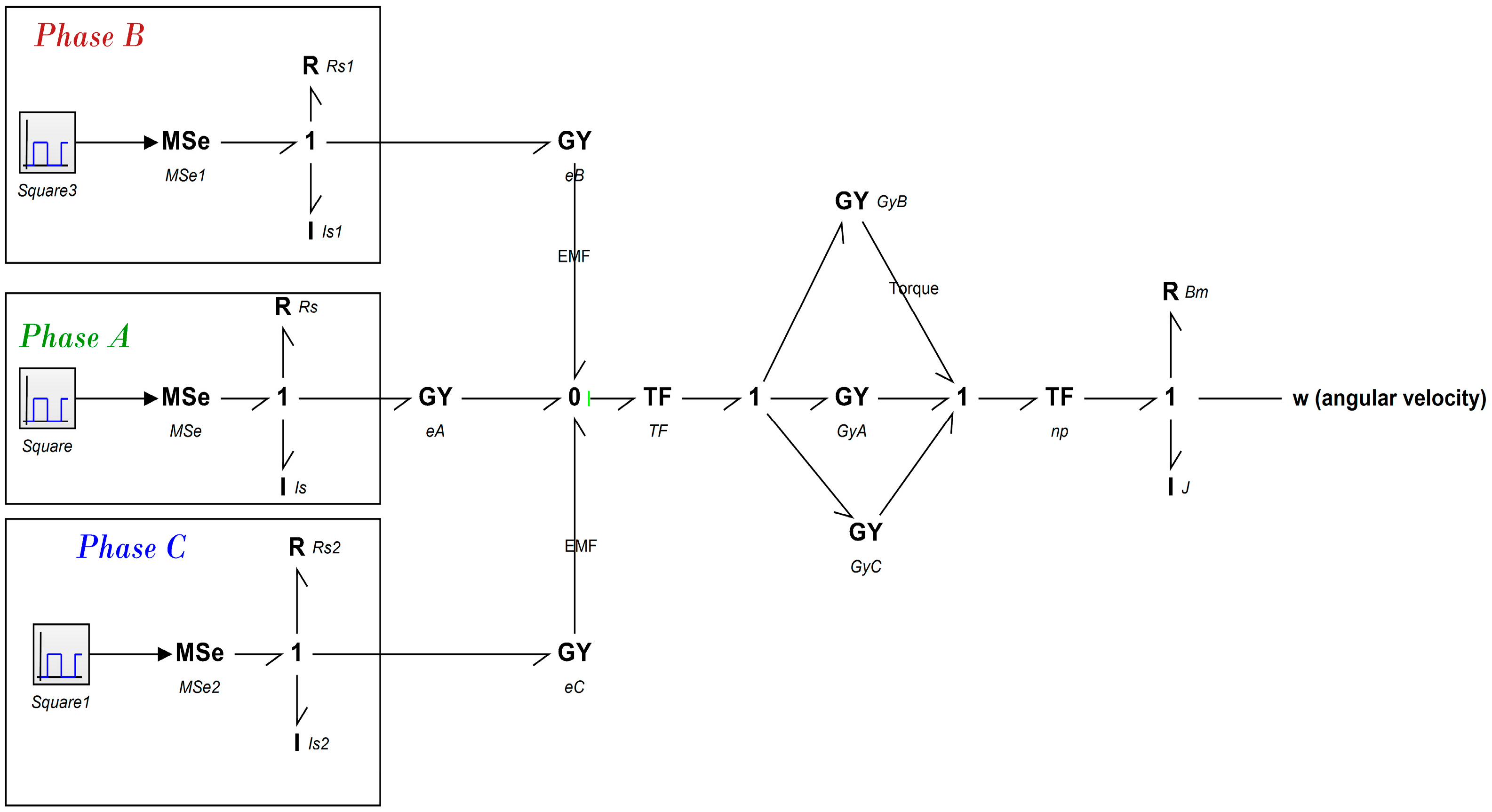
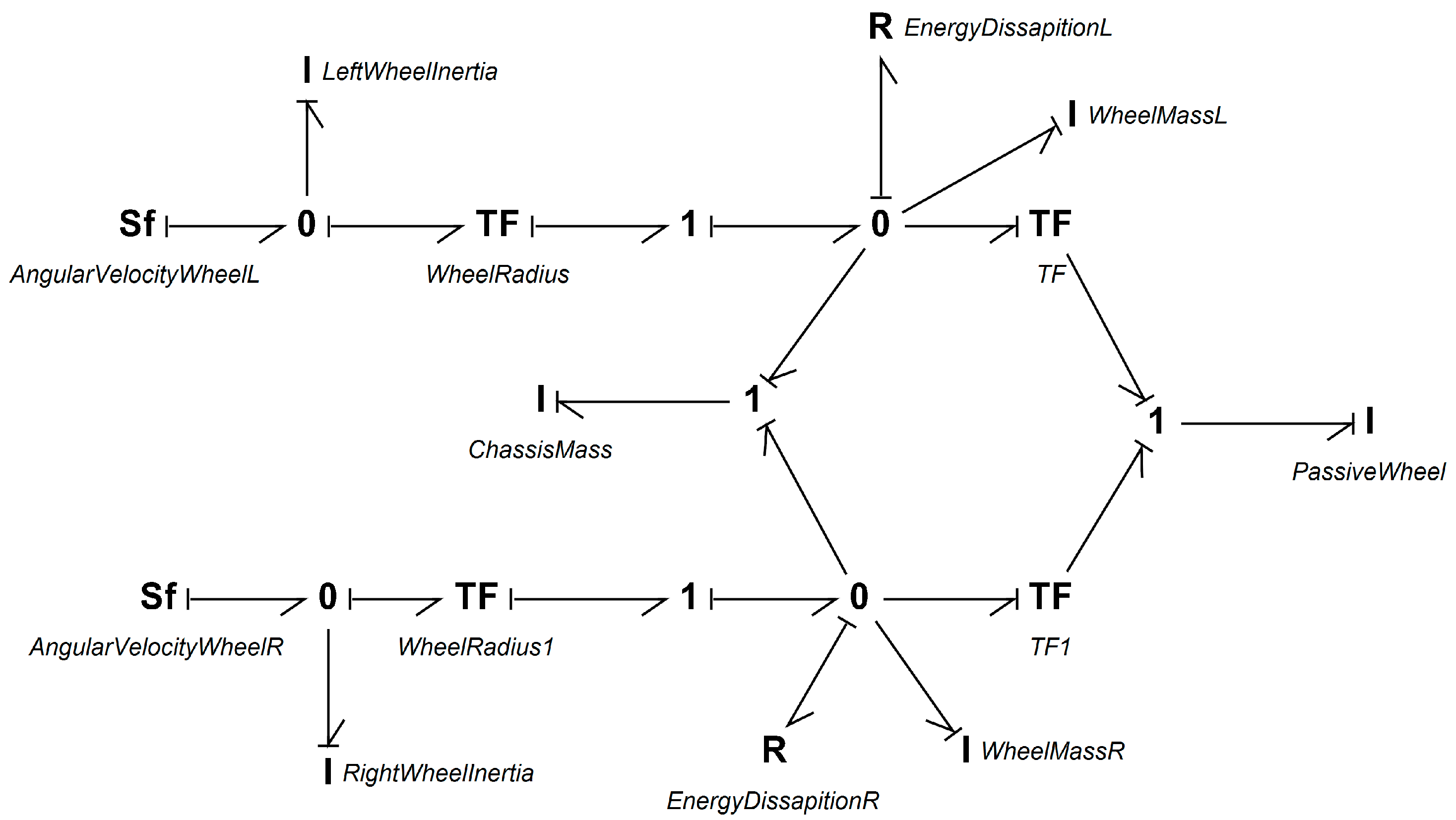
3.2.2. Modeling of the Mobile Robot
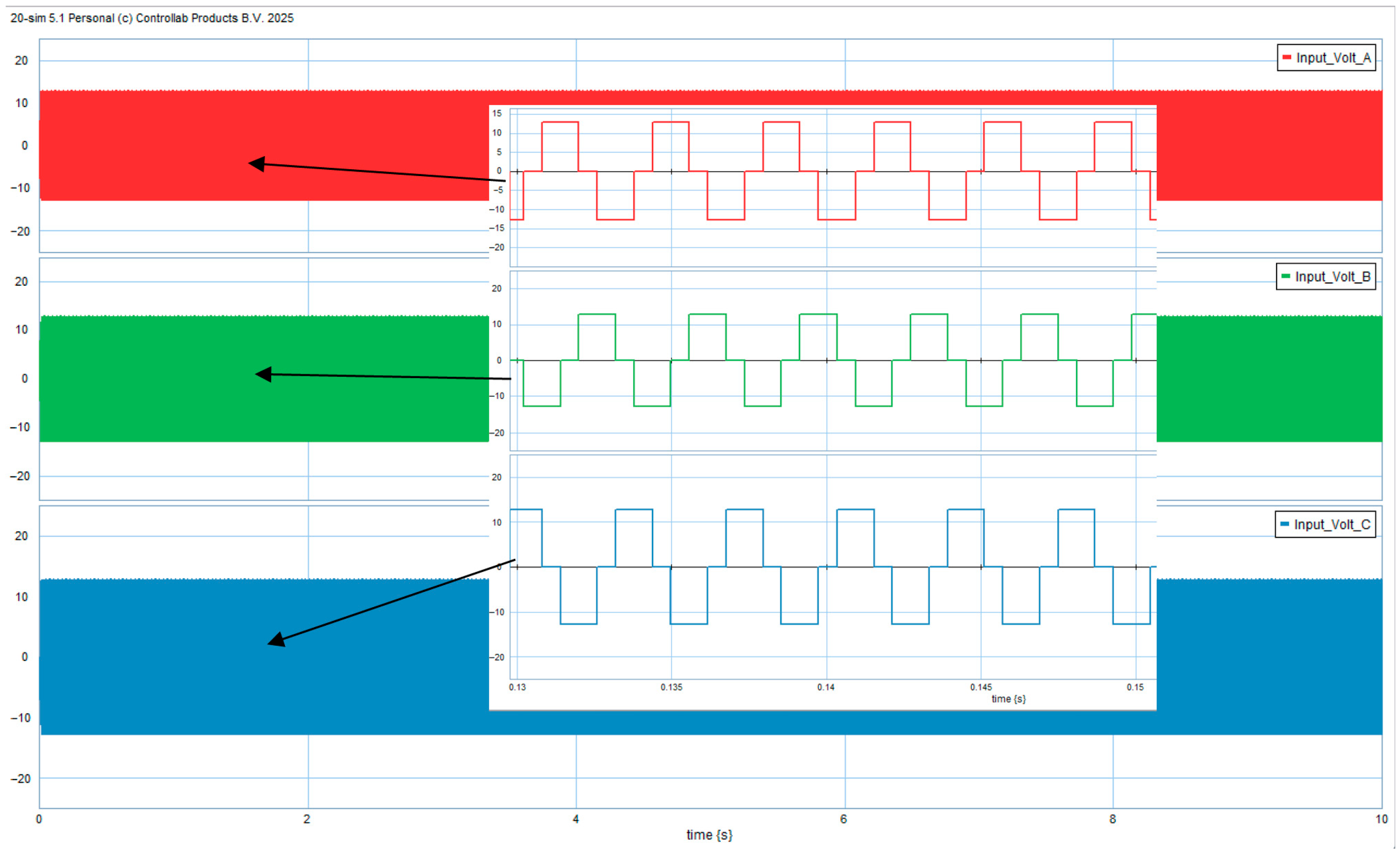
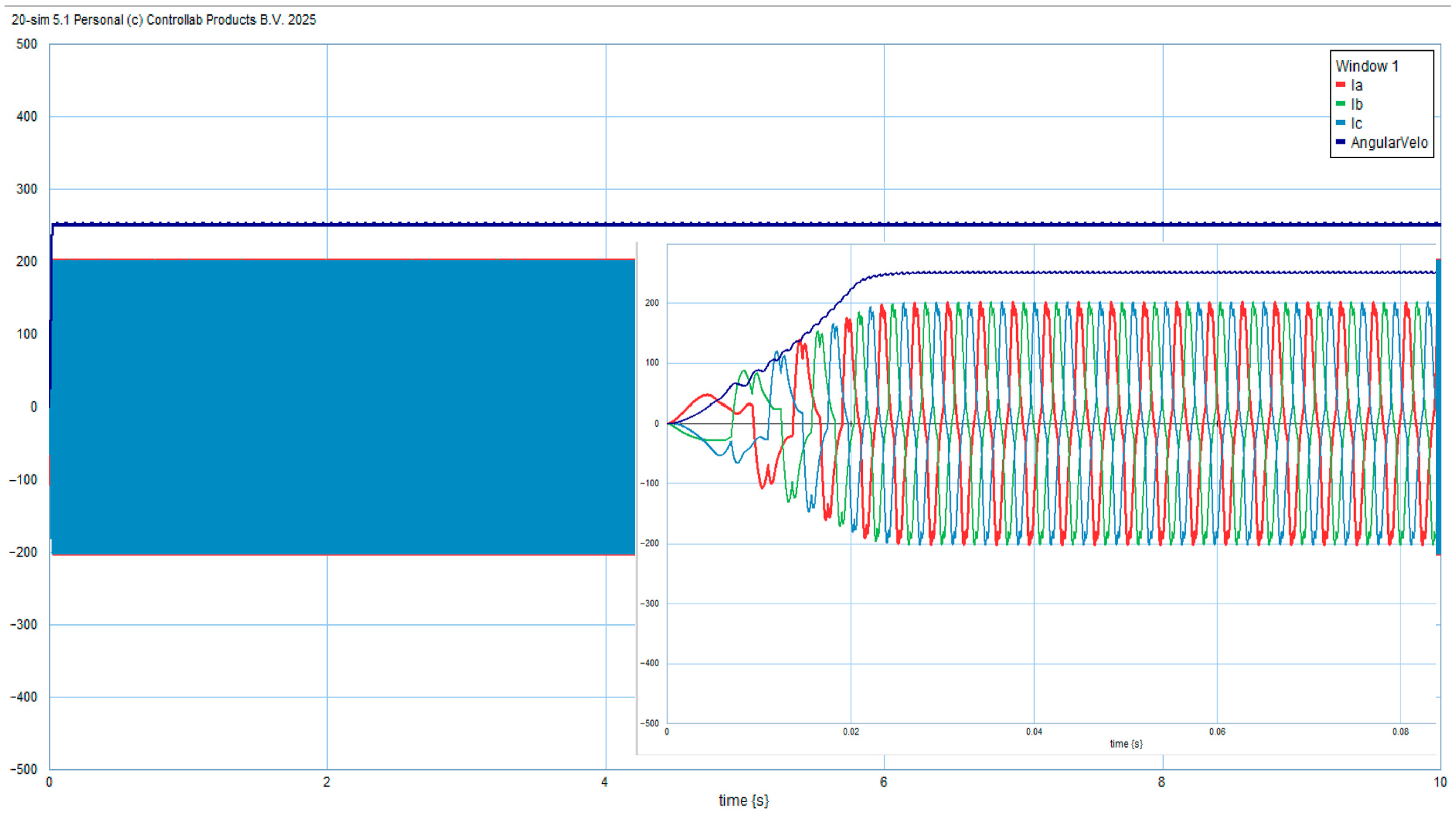
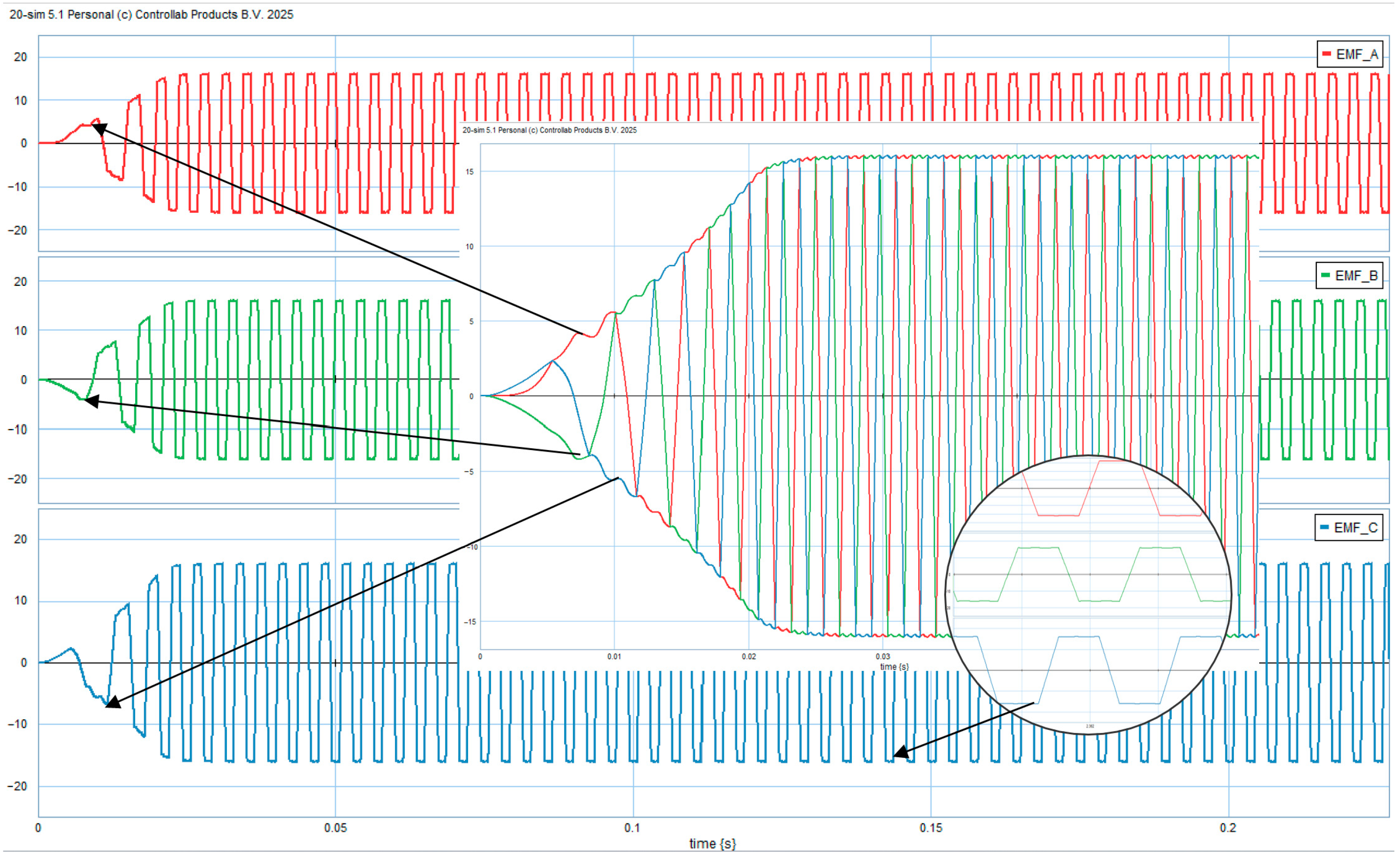
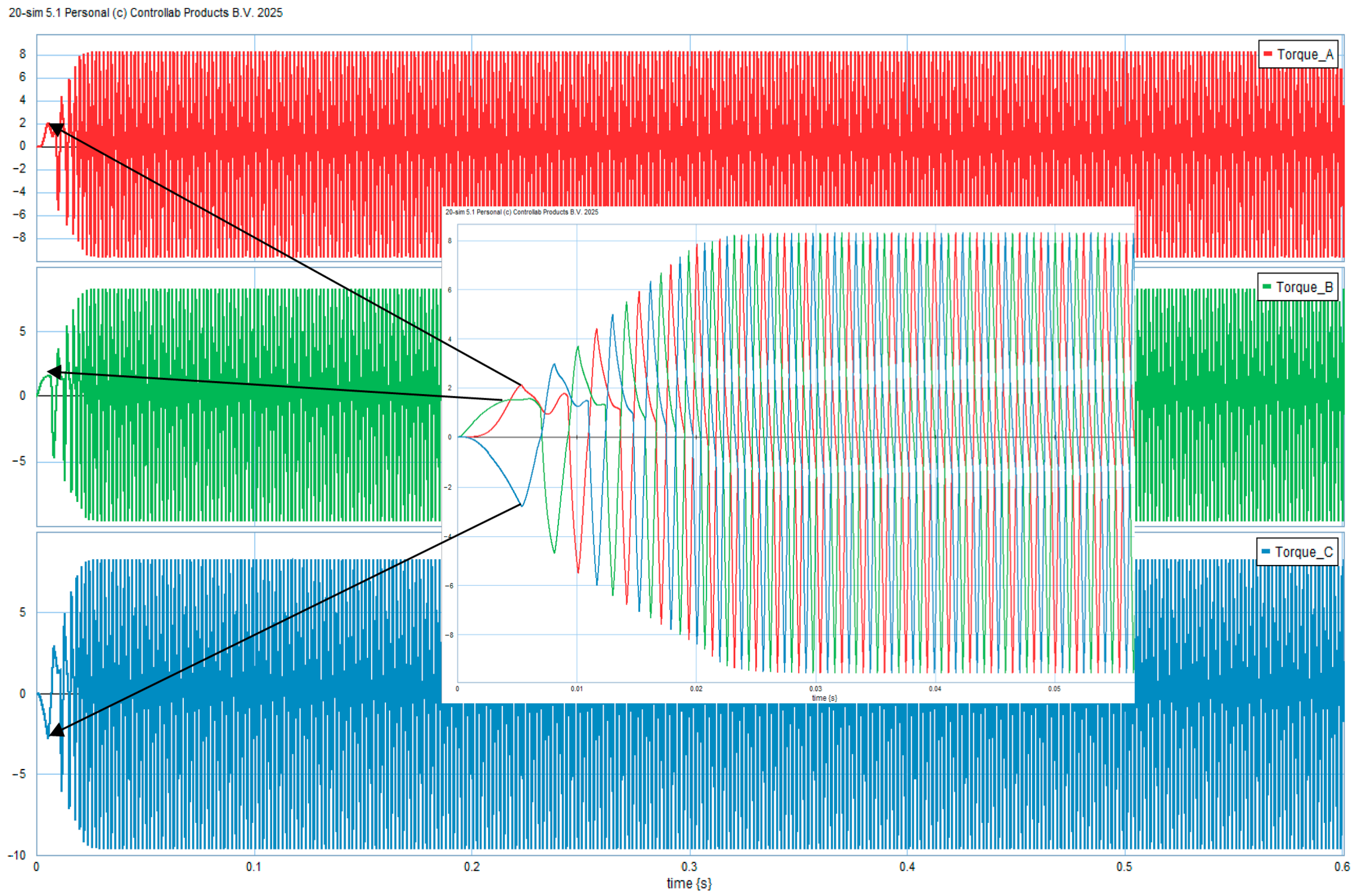
4. Simulation and Validation
Model Validation Using Datasheet Benchmark
5. Discussion
6. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IFR International Federation of Robotics. Available online: https://ifr.org/wr-service-robots (accessed on 2 June 2025).
- Li, L.; Li, Y.; Song, B.; Shi, Z.; Wang, C. How Human-like Behavior of Service Robot Affects Social Distance: A Mediation Model and Cross-Cultural Comparison. Behav. Sci. 2022, 12, 205. [Google Scholar] [CrossRef] [PubMed]
- Lee, I. Service Robots: A Systematic Literature Review. Electronics 2021, 10, 2658. [Google Scholar] [CrossRef]
- Garcia-Haro, J.M.; Oña, E.D.; Hernandez-Vicen, J.; Martinez, S.; Balaguer, C. Service Robots in Catering Applications: A Review and Future Challenges. Electronics 2021, 10, 47. [Google Scholar] [CrossRef]
- Samantaray, A.K.; Dasgupta, S.S.; Bhattacharyya, R. Bond Graph Modeling of an Internally Damped Nonideal Flexible Spinning Shaft. J. Dyn. Syst. Meas. Control 2010, 132, 061502. [Google Scholar] [CrossRef]
- Karnopp, D.C.; Margolis, D.L.; Rosenberg, R.C. System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-0-470-88908-4. [Google Scholar]
- Li, Y.; Ma, Y.; Huo, X.; Wu, X. Remote Object Navigation for Service Robots Using Hierarchical Knowledge Graph in Human-Centered Environments. Intel. Serv. Robot. 2022, 15, 459–473. [Google Scholar] [CrossRef]
- Kim, H.; So, K.K.F.; Wirtz, J. Service Robots: Applying Social Exchange Theory to Better Understand Human–Robot Interactions. Tour. Manag. 2022, 92, 104537. [Google Scholar] [CrossRef]
- Gao, J.; Wang, H.; Li, W.; Li, G.; He, S. Research on the Effect of the Empathy Ability of AI Service Robots on Consumer Well-Being: The Chain Mediating Model. Int. J. Hum. Comput. Interact. 2025, 41, 6716–6728. [Google Scholar] [CrossRef]
- Satya Durga Manohar Sahu, V.; Samal, P.; Kumar Panigrahi, C. Modelling, and Control Techniques of Robotic Manipulators: A Review. Mater. Today Proc. 2022, 56, 2758–2766. [Google Scholar] [CrossRef]
- Mughal, A.M. Introduction to Bond Graph Modeling. In Real Time Modeling, Simulation and Control of Dynamical Systems; Mughal, A.M., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 35–45. ISBN 978-3-319-33906-1. [Google Scholar]
- Broenink, J. Introduction to Physical Systems Modelling with Bond Graphs. SiE Whitebook Simul. Methodol. 1999, 31, 1–31. [Google Scholar]
- Wang, X.; Wu, H.; Yang, J.; Deng, X.; Piao, Z.; Yao, X. Modeling and Prediction Method for Inherent Energy Consumption of CNC Machine Tool Spindle Systems. J. Mech. Sci. Technol. 2025, 39, 4129–4145. [Google Scholar] [CrossRef]
- Massarotti, G.P.; Filippini, G.; Alviach, G.R.; Gamez-Montero, P.J.; Macia, E.C. A New Dual Steering System in a Compact Tractor. Actuators 2025, 14, 35. [Google Scholar] [CrossRef]
- Borutzky, W. Bond Graph Modelling for Control, Fault Diagnosis and Failure Prognosis; Springer International Publishing: Cham, Switzerland, 2021; ISBN 978-3-030-60966-5. [Google Scholar]
- Guo, Z.; Korondi, P.; Szemes, P.T. Bond-Graph-Based Approach to Teach PID and Sliding Mode Control in Mechatronics. Machines 2023, 11, 959. [Google Scholar] [CrossRef]
- Zaidi, A.; Barambones, O.; Zanzouri, N. Implementation of a Cascade Fault Tolerant Control and Fault Diagnosis Design for a Modular Power Supply. Actuators 2023, 12, 135. [Google Scholar] [CrossRef]
- Dash, B.M.; Bouamama, B.O.; Boukerdja, M.; Pekpe, K.M. Bond Graph-CNN Based Hybrid Fault Diagnosis with Minimum Labeled Data. Eng. Appl. Artif. Intell. 2024, 131, 107734. [Google Scholar] [CrossRef]
- Kypuros, J. System Dynamics and Control with Bond Graph Modeling; CRC Press: Boca Raton, FL, USA, 2013; ISBN 978-0-429-10006-2. [Google Scholar]
- Ibănescu, R. Bond Graphs in System Modelling. In Graph-Based Modelling in Engineering; Zawiślak, S., Rysiński, J., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 3–23. ISBN 978-3-319-39020-8. [Google Scholar]
- Felszolgáló Robotok. Available online: https://enjoyrobotics.com/ (accessed on 2 June 2025).
- Chu, Y.; AEsoy, V.; Zhang, H.; Bunes, O. Modelling and Simulation of an Offshore Hydraulic Crane. In Proceedings of the 28th European Conference on Modelling and Simulation, Brescia, Italy, 27–30 May 2014; Squazzoni, F., Baronio, F., Archetti, C., Castellani, M., Eds.; pp. 87–93. [Google Scholar]
- Sahoo, S.R.; Chiddarwar, S.S. Mobile Robot Control Using Bond Graph and Flatness Based Approach. Procedia Comput. Sci. 2018, 133, 213–221. [Google Scholar] [CrossRef]
- Joshi, J.; Kumar, P.; Manral, A.R.; Makkar, M. Bond Graph Model-Based Control of a Wheeled Mobile Robot. In Proceedings of the 2023 5th International Conference on Power, Control & Embedded Systems (ICPCES), Allahabad, India, 6–8 January 2023; pp. 1–6. [Google Scholar]
- Kumar, P.; Bensekrane, I.; Singh, M.; Merzouki, R. Bond Graph Based Power Consumption Estimation of a Non-Holonomic Wheeled Mobile Robot with Multiple Driving Modes. In Proceedings of the 2018 7th International Conference on Systems and Control (ICSC), Valencia, Spain, 24–26 October 2018; pp. 441–446. [Google Scholar]
- Kumar, P.; Othman, L.; Merzouki, R. Bond Graph Modeling of a Holonomic Mobile Platform with Four Mecanum Wheels. In Proceedings of the 13th International Conference on Bond Graph Modeling (ICBGM 2018); Society for Modeling & Simulation International (SCS), Bordeaux, France, 16 July 2018; Volume 50. [Google Scholar]
- Sahoo, S.R.; Chiddarwar, S.S.; Alakshendra, V. Dynamic Modelling and Simulation of a Three-Wheeled Omnidirectional Mobile Robot: Bond Graph Approach. In Proceedings of the 2017 3rd International Conference on Advances in Robotics, New York, NY, USA, 28 June 2017; Association for Computing Machinery: New York, NY, USA; pp. 1–6. [Google Scholar]
- Qian, Y.; Rahmani, A. Bond Graph Modeling and Simulation of a Dual-Arm Mobile Manipulator. In Proceedings of the 1st International and 16th National Conference on Machines and Mechanisms, Roorkee, India, 18–20 December 2013; pp. 62–69. [Google Scholar]
- Daigle, M.; Koutsoukos, X.; Biswas, G. Distributed Diagnosis of Coupled Mobile Robots. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 3787–3794. [Google Scholar]
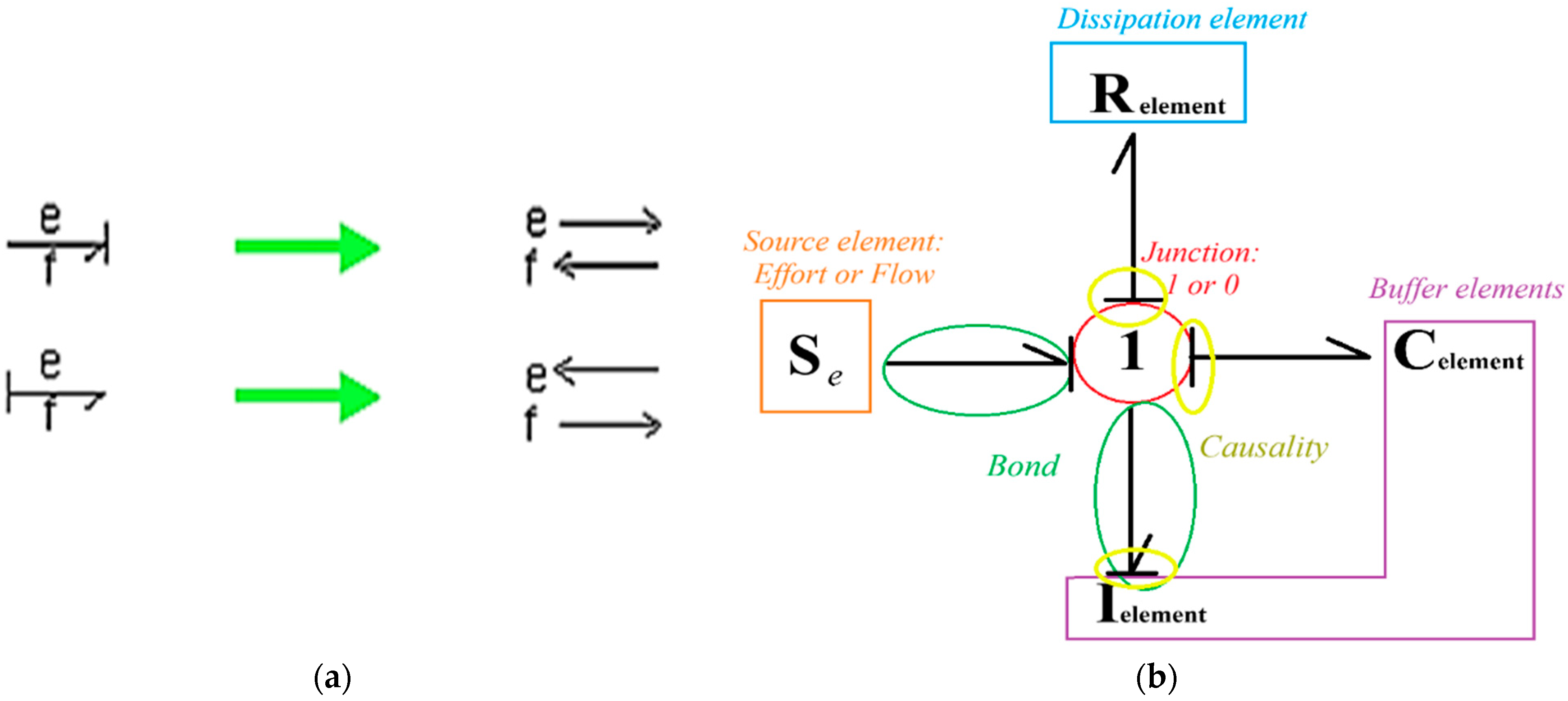


| Element Type | Bond-Graph Class | Function |
|---|---|---|
| 1-Junctions | Power-conserving junction | Common flow |
| 0-Junctions | Common effort | |
| R-element | 1-Port Elements | Dissipate energy |
| C-element | Store potential energy | |
| I-element | Store kinetic energy | |
| Source of Effort () | Impose a prescribed effort regardless of flow. | |
| Source of Flow () | Impose a prescribed flow regardless of effort. | |
| Transformer (TF) | 2-Port Elements | Scales effort and flow by a fixed ratio |
| Gyrator (GY) | Converts effort ↔ flow between ports |
| Specification | Value | Unit |
|---|---|---|
| Speed Constant | 150 | RPM/V [1] |
| Torque Constant | 0.055 | Nm/A [2] |
| Speed/Torque Gradient | 159.54 | RPM/Nm |
| Pole Pairs | 7 | |
| Phase Resistance | 39 → Phase-neutral | mΩ |
| Phase Inductance | 24 → Phase-neutral | uH |
| Continuous Current | 50 → Free Air 70 → Forced Air | A A |
| Peak Current | 90 → 3-second | A |
| Thermistor | NTC 10k 3435 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taleb, M.A.; Husi, G. Dynamic Modeling of a Three-Phase BLDC Motor Using Bond Graph Methodology. Actuators 2025, 14, 523. https://doi.org/10.3390/act14110523
Taleb MA, Husi G. Dynamic Modeling of a Three-Phase BLDC Motor Using Bond Graph Methodology. Actuators. 2025; 14(11):523. https://doi.org/10.3390/act14110523
Chicago/Turabian StyleTaleb, Mayar Abdullah, and Géza Husi. 2025. "Dynamic Modeling of a Three-Phase BLDC Motor Using Bond Graph Methodology" Actuators 14, no. 11: 523. https://doi.org/10.3390/act14110523
APA StyleTaleb, M. A., & Husi, G. (2025). Dynamic Modeling of a Three-Phase BLDC Motor Using Bond Graph Methodology. Actuators, 14(11), 523. https://doi.org/10.3390/act14110523







