Optimization of Soft Actuator Geometry and Material Modeling Using Metaheuristic Algorithms
Abstract
1. Introduction
2. Problem Statement
2.1. Hyperelastic Models for Soft Actuators
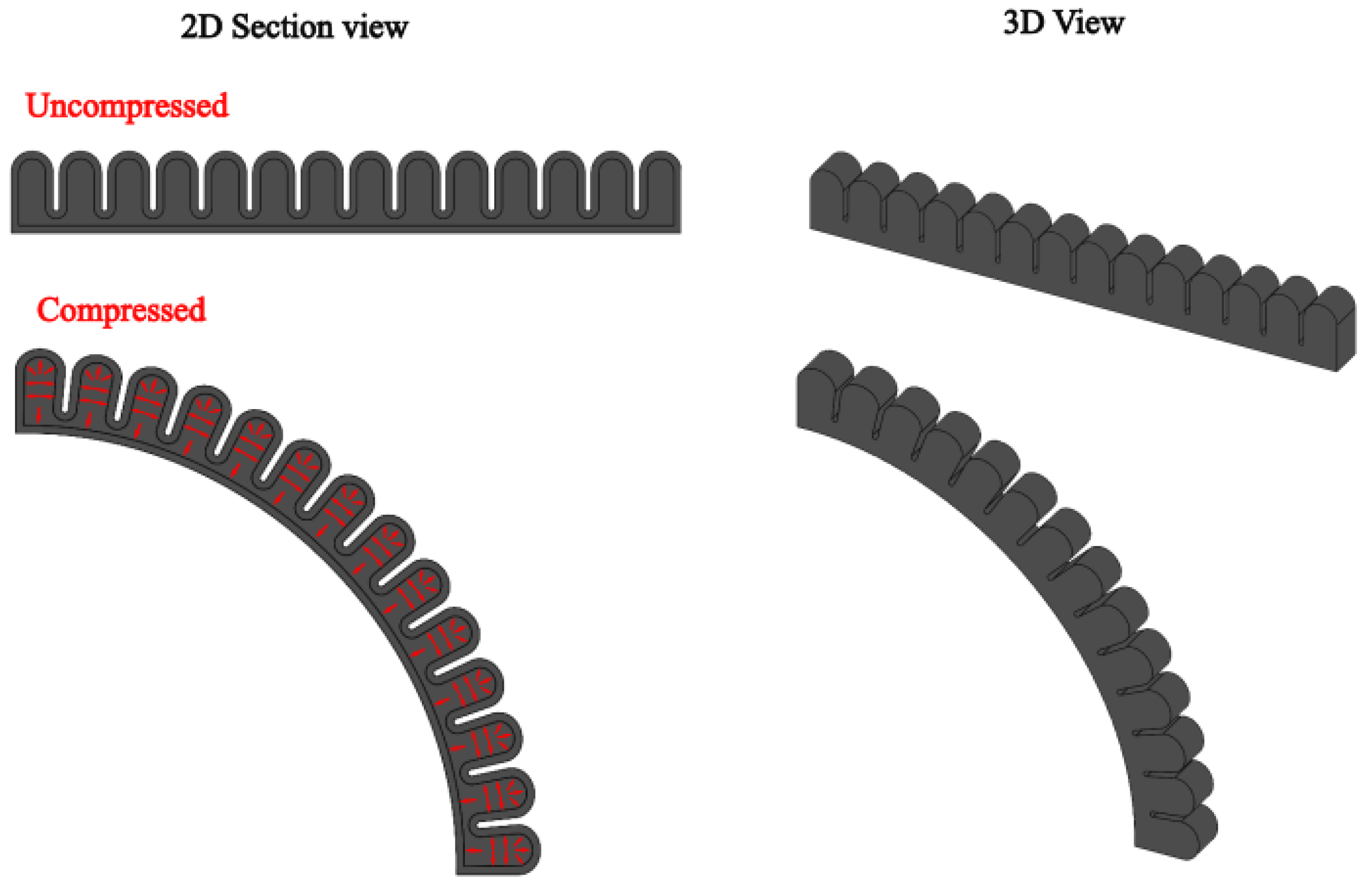
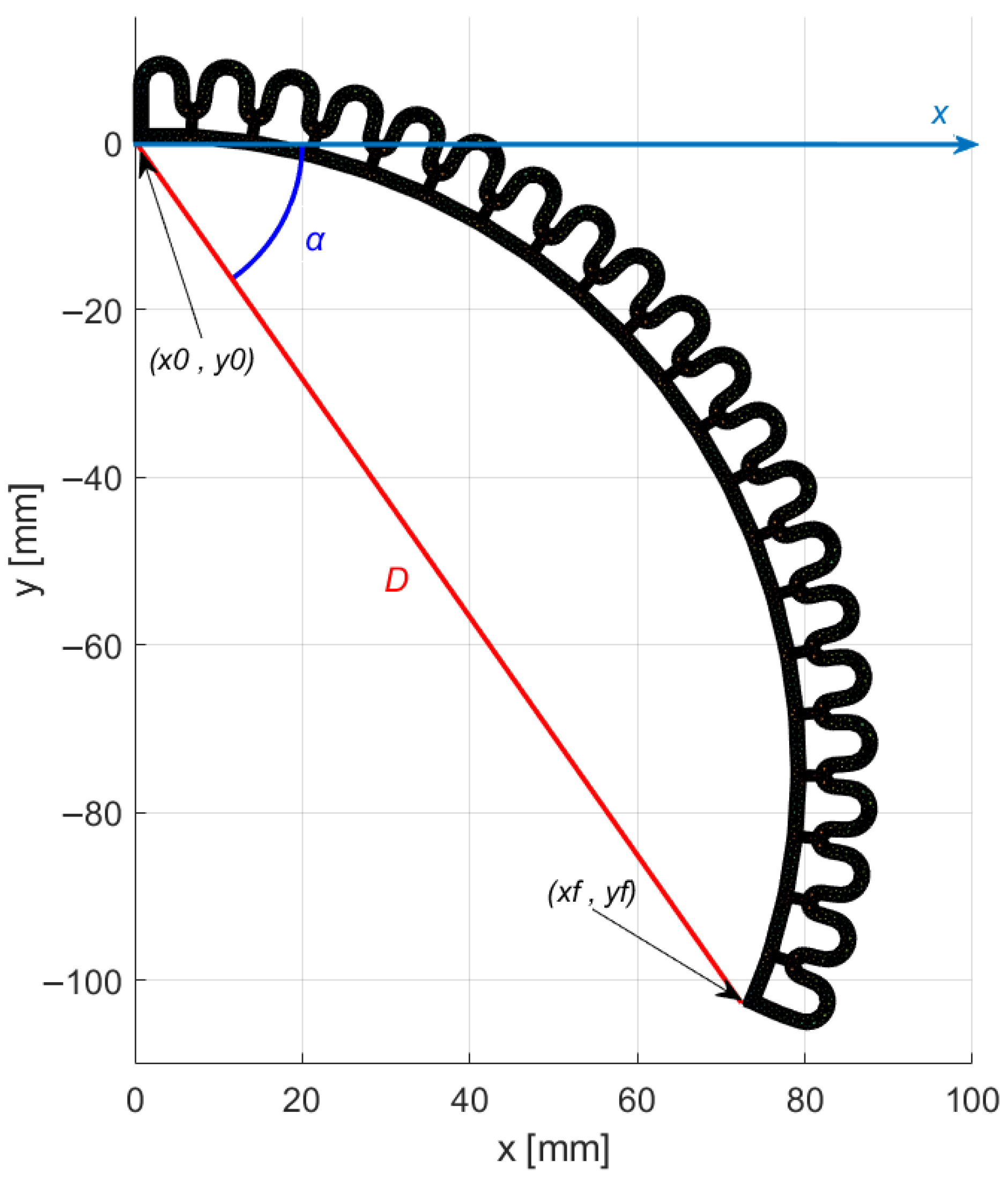
2.2. Parametric Design of the Actuator
3. Methodology
3.1. Finite Element Analyses for Optimization
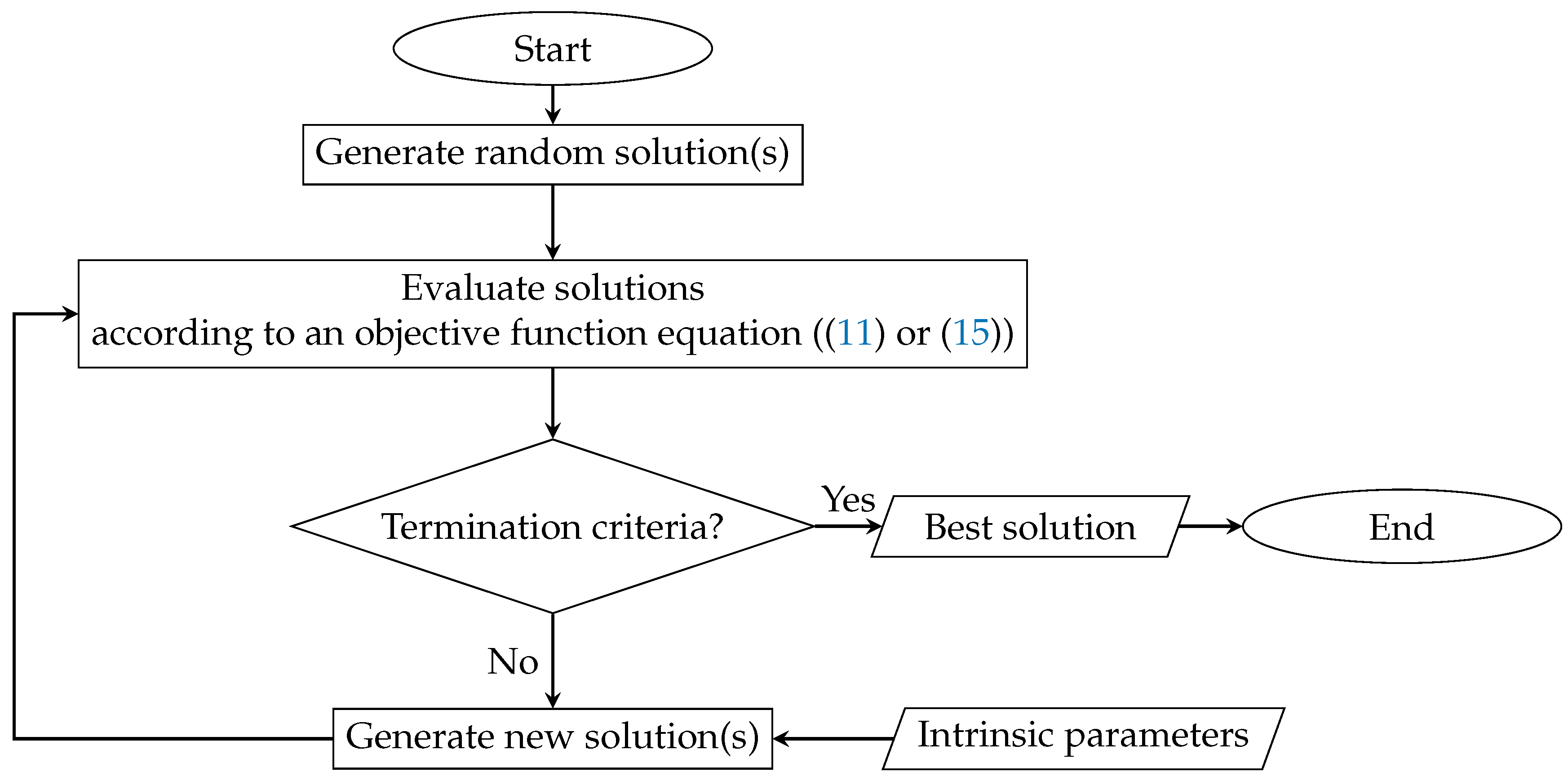
3.2. Metaheuristic Optimization Algorithms
4. Results and Discussion
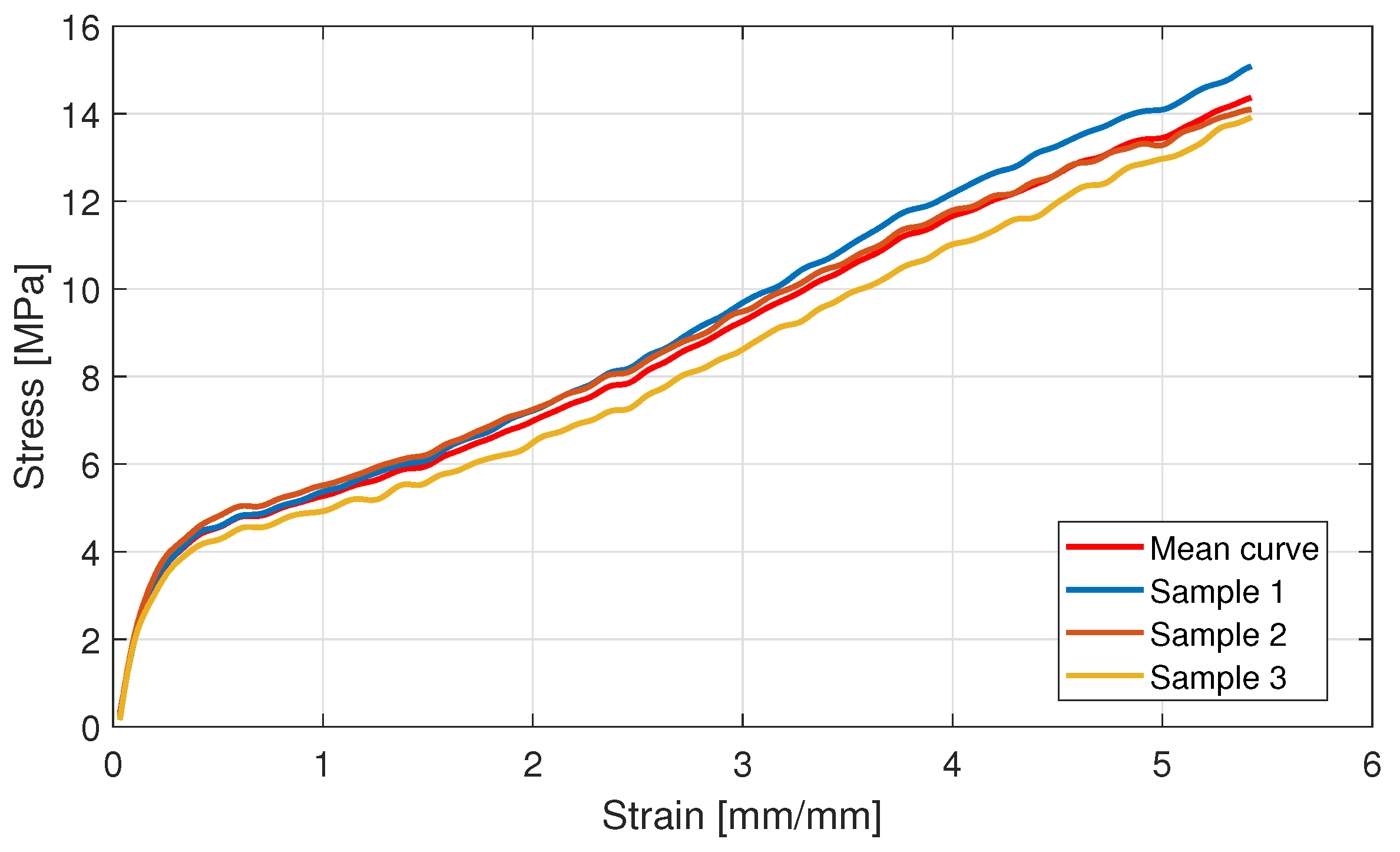
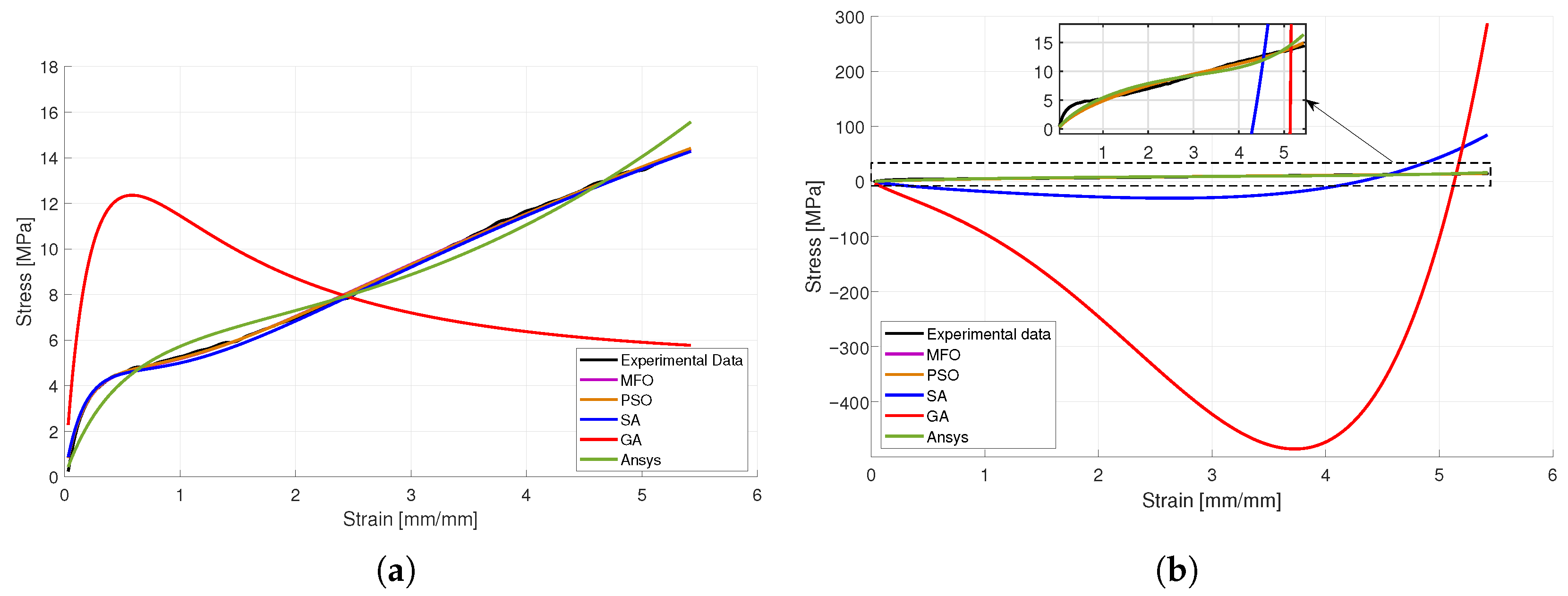
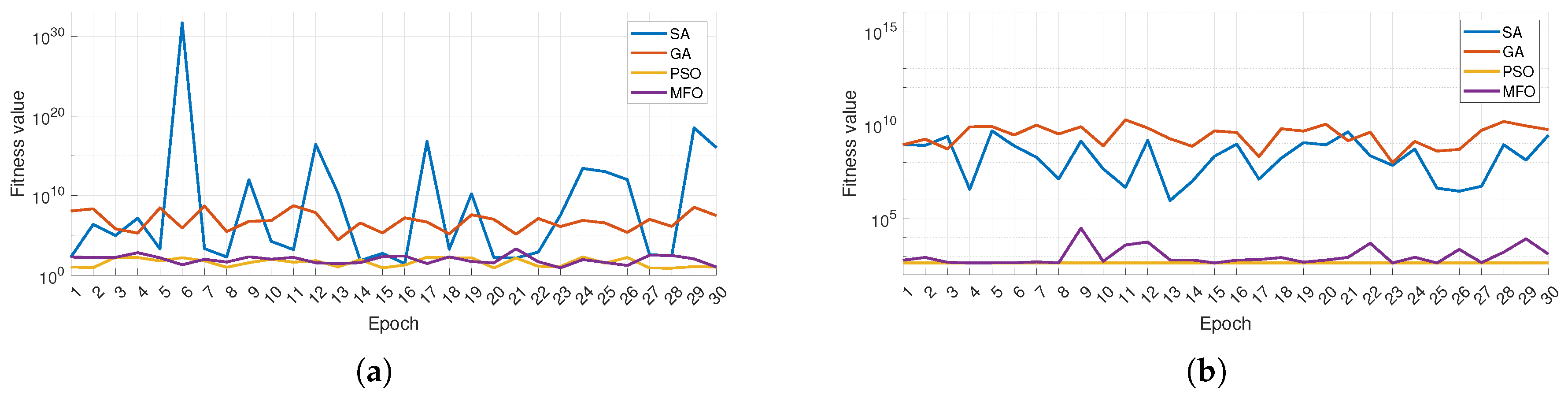
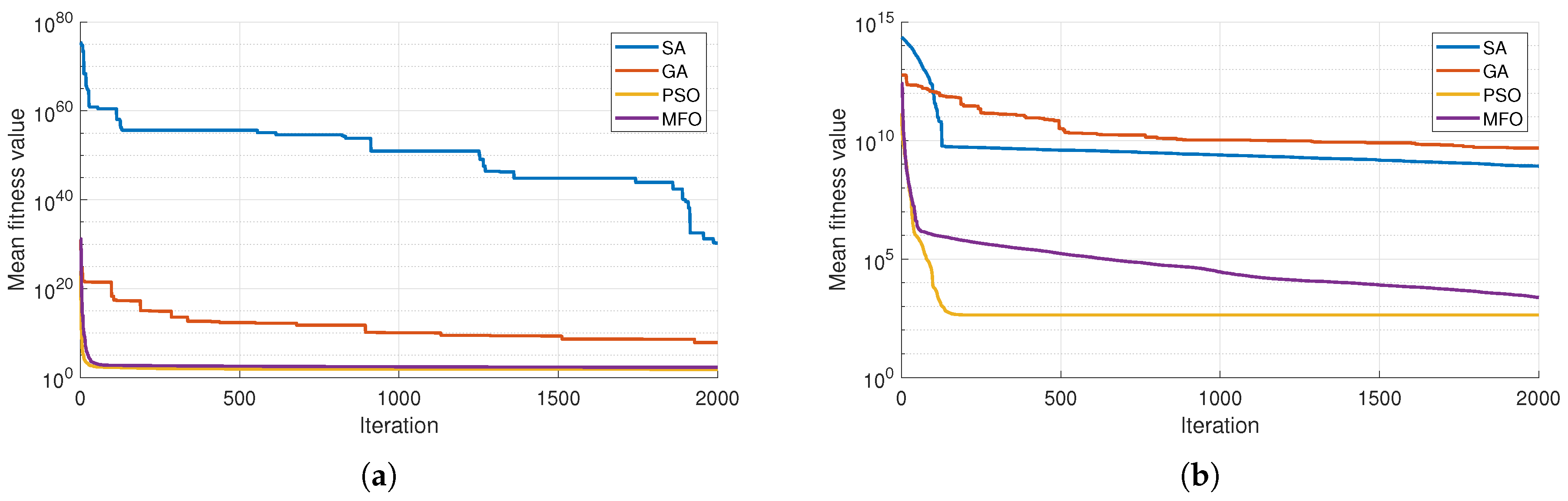
4.1. Material Modeling
- : The statistical significance of the observed differences. A small p-value (e.g., <0.05) indicates that the differences are unlikely to be due to random chance, supporting the conclusion that one algorithm outperforms the other;
- : The sum of positive ranks. calculated based on the differences between paired observations in two datasets;
- : The sum of negative ranks. calculated based on the differences between paired observations in two datasets.
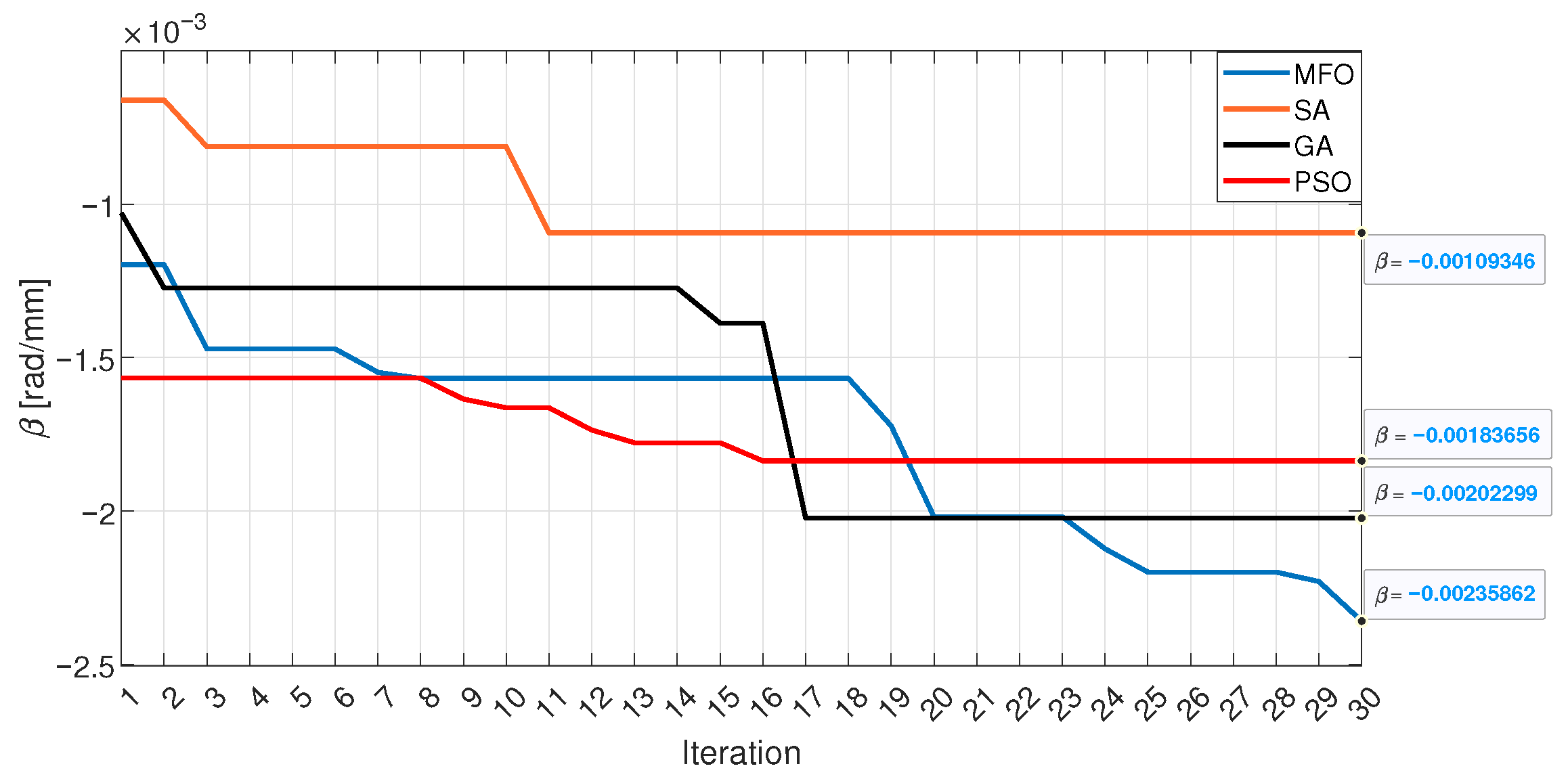
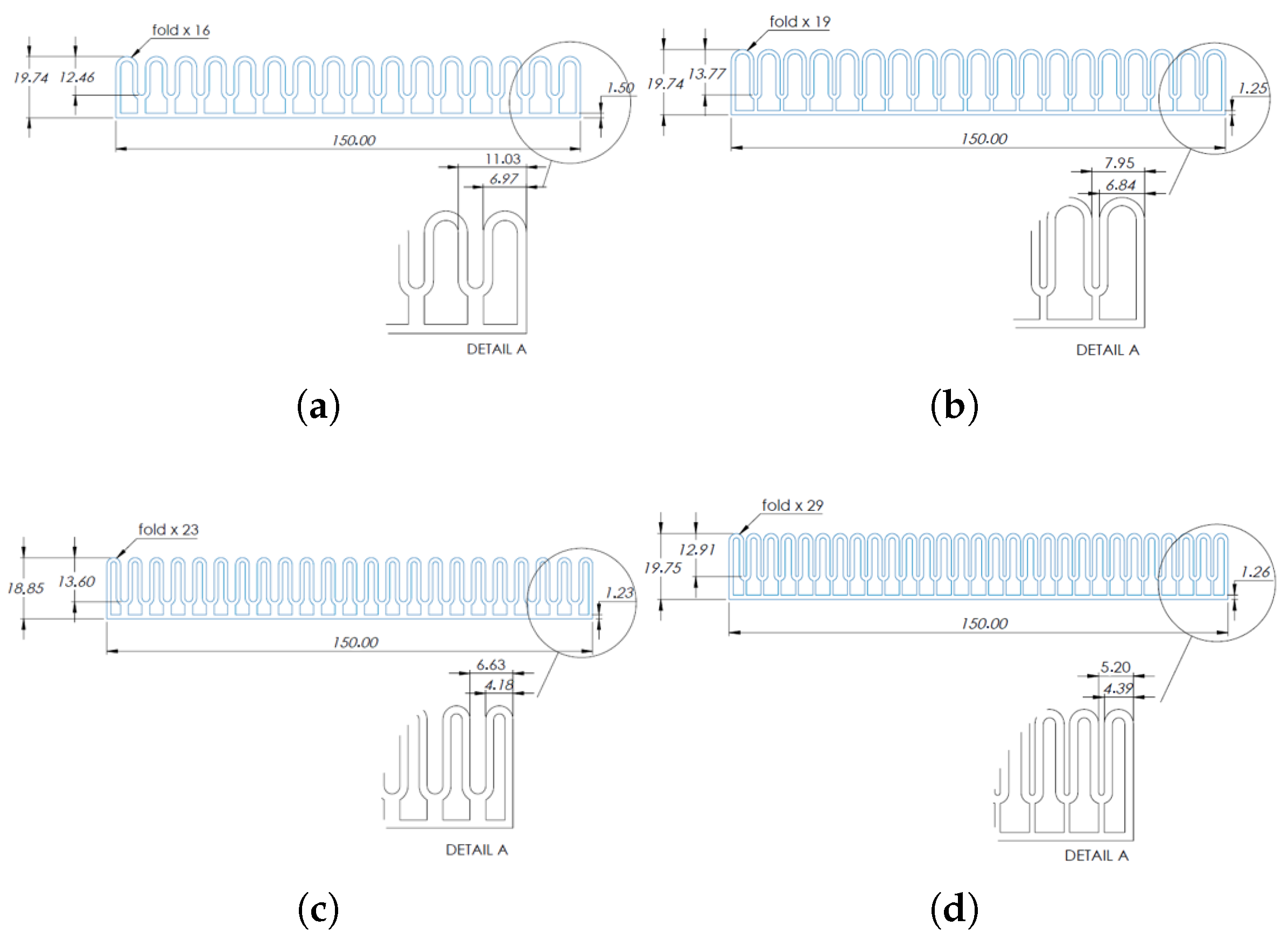
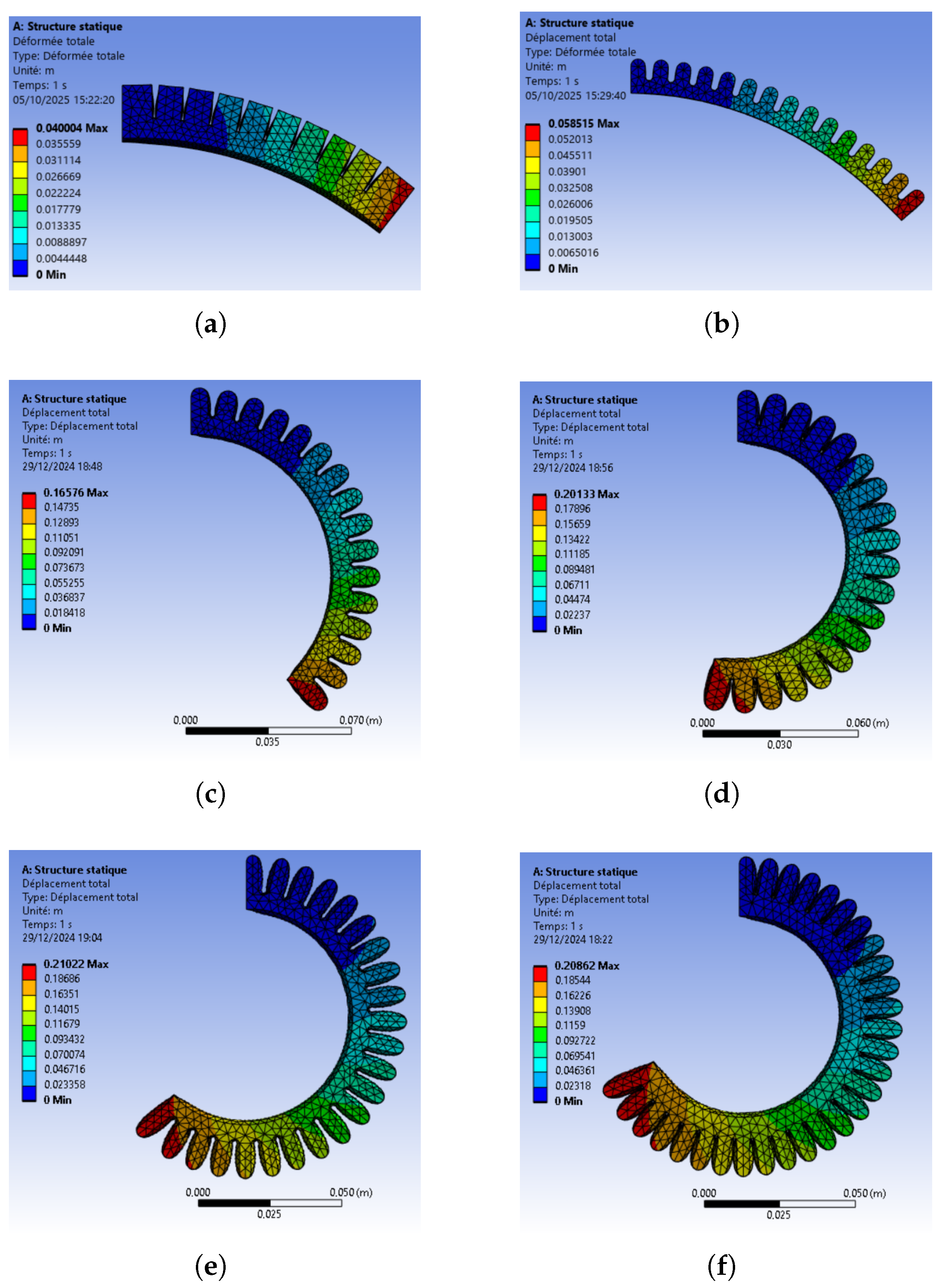
4.2. Design Optimization
- Material propriety: inserting the fittest Ogden parameters presented in Table 5, , , , , , and into engineering data;
- Model import: a .step file of the 3D cad model of the actuator, according to the algorithm’s resulting geometry, is imported to ANSYS “Design Modeler”;
- Assign material: assign the Ogden parameters presented to the imported model;
- Named selections: prepare selections for the inner walls of the actuator to be selected for applied load, and outer walls (surfaces between each bellow) for contact interactions definition;
- A nonlinear mechanical mesh with quadratic tetrahedral elements and an element size of 0.3 mm was used. This size provided approximately four elements across the actuator wall thickness (1.2 mm), ensuring sufficient accuracy in capturing the strain distribution while maintaining computational efficiency. The mesh density was also limited by the maximum number of cells (512,000) supported by the available computational resources.
- Contact interaction: a friction-less contact interaction between two juxtaposed outer surfaces of each bellow of the actuator;
- Analysis settings: A single analysis step was used, with a step end time of 1 s, an initial time step of 0.1 s, a minimum time step of 0.0001 s, and a maximum time step of 1 s. The large deflection option was activated.
- Input boundary conditions and loads: Select a fixed support for the actuator and apply a pressure load of 900 kPa on the inner walls of the actuator;
- Solve and evaluate results: Job execution and results visualization.
4.3. Experimental Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Debije, M.G.; Schenning, A.P.H.J. Stimuli-Responsive Liquid Crystalline Materials. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Hughes, J.; Culha, U.; Giardina, F.; Guenther, F.; Rosendo, A.; Iida, F. Soft Manipulators and Grippers: A Review. Front. Robot. AI 2016, 3, 69. [Google Scholar] [CrossRef]
- Marchese, A.D.; Katzschmann, R.K.; Rus, D. A Recipe for Soft Fluidic Elastomer Robots. Soft Robot. 2015, 2, 7–25. [Google Scholar] [CrossRef]
- Low, F.Z.; Tan, H.H.; Lim, J.H.; Yeow, C.H. Development of a Soft Pneumatic Sock for Robot-Assisted Ankle Exercise. J. Med. Devices 2016, 10, 014503. [Google Scholar] [CrossRef]
- Haghshenas-Jaryani, M.; Carrigan, W.; Wijesundara, M.B.J.; Patterson, R.M.; Bugnariu, N.; Niacaris, T. Kinematic Study of a Soft-and-Rigid Robotic Digit for Rehabilitation and Assistive Applications. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Al-Ibadi, A.; Nefti-Meziani, S.; Davis, S. Design, Kinematics and Controlling a Novel Soft Robot Arm with Parallel Motion. Robotics 2018, 7, 19. [Google Scholar] [CrossRef]
- Tang, X.; Li, H.; Ma, T.; Yang, Y.; Luo, J.; Wang, H.; Jiang, P. A Review of Soft Actuator Motion: Actuation, Design, Manufacturing and Applications. Actuators 2022, 11, 331. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, P.; Lin, Y.; Tang, W.; Jiao, Z.; Yang, H.; Zou, J. Fluid-driven artificial muscles: Bio-design, manufacturing, sensing, control, and applications. Bio-Des. Manuf. 2021, 4, 123–145. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, X.J.; Dong, X.; Zhou, J.; Zhao, H. Enhancing the Universality of a Pneumatic Gripper via Continuously Adjustable Initial Grasp Postures. IEEE Trans. Robot. 2021, 37, 1604–1618. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Ren, T.; Li, Y.; Choi, S.h. Precharged Pneumatic Soft Actuators and Their Applications to Untethered Soft Robots. Soft Robot. 2018, 5, 567–575. [Google Scholar] [CrossRef] [PubMed]
- Shan, W.; Diller, S.; Tutcuoglu, A.; Majidi, C. Rigidity-tuning conductive elastomer. Smart Mater. Struct. 2015, 24, 065001. [Google Scholar] [CrossRef]
- Rich, S.; Jang, S.H.; Park, Y.L.; Majidi, C. Liquid Metal-Conductive Thermoplastic Elastomer Integration for Low-Voltage Stiffness Tuning. Adv. Mater. Technol. 2017, 2, 1700179. [Google Scholar] [CrossRef]
- Wang, Q.; Tian, X.; Li, D. Multimodal soft jumping robot with self-decision ability. Smart Mater. Struct. 2021, 30, 085038. [Google Scholar] [CrossRef]
- Yuan, X.; Zhou, X.; Liang, Y.; Wang, L.; Chen, R.; Zhang, M.; Pu, H.; Xuan, S.; Wu, J.; Wen, W. A stable high-performance isotropic electrorheological elastomer towards controllable and reversible circular motion. Compos. Part B Eng. 2020, 193, 107988. [Google Scholar] [CrossRef]
- Yin, L.J.; Zhao, Y.; Zhu, J.; Yang, M.; Zhao, H.; Pei, J.Y.; Zhong, S.L.; Dang, Z.M. Soft, tough, and fast polyacrylate dielectric elastomer for non-magnetic motor. Nat. Commun. 2021, 12, 4517. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Bi, C.; Cappelleri, D.J.; Ciuti, G.; Conn, A.T.; Faivre, D.; Habibi, N.; Hošovský, A.; Iacovacci, V.; Khalil, I.S.M.; et al. Magnetic Actuation Methods in Bio/Soft Robotics. Adv. Funct. Mater. 2021, 31, 2005137. [Google Scholar] [CrossRef]
- Maeda, S.; Hara, Y.; Yoshida, R.; Hashimoto, S. Self-Oscillating Gel Actuator for Chemical Robotics. Adv. Robot. 2008, 22, 1329–1342. [Google Scholar] [CrossRef]
- Hu, W.; Mutlu, R.; Li, W.; Alici, G. A Structural Optimisation Method for a Soft Pneumatic Actuator. Robotics 2018, 7, 24. [Google Scholar] [CrossRef]
- Keong, B.A.W.; Hua, R.Y.C. A Novel Fold-Based Design Approach toward Printable Soft Robotics Using Flexible 3D Printing Materials. Adv. Mater. Technol. 2018, 3, 1700172. [Google Scholar] [CrossRef]
- Wang, Z.; Hirai, S. Chamber dimension optimization of a bellow-type soft actuator for food material handling. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 382–387. [Google Scholar] [CrossRef]
- Pagoli, A.; Chapelle, F.; Corrales-Ramon, J.A.; Mezouar, Y.; Lapusta, Y. Review of soft fluidic actuators: Classification and materials modeling analysis. Smart Mater. Struct. 2021, 31, 013001. [Google Scholar] [CrossRef]
- Pagoli, A.; Chapelle, F.; Ramon, J.A.C.; Mezouar, Y.; Lapusta, Y. Design and Optimization of a Dextrous Robotic Finger: Incorporating a Sliding, Rotating, and Soft-Bending Mechanism While Maximizing Dexterity and Minimizing Dimensions. IEEE Robot. Autom. Mag. 2020, 27, 56. [Google Scholar] [CrossRef]
- Decroly, G.; Mertens, B.; Lambert, P.; Delchambre, A. Design, characterization and optimization of a soft fluidic actuator for minimally invasive surgery. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 333–340. [Google Scholar] [CrossRef] [PubMed]
- Xavier, M.S.; Tawk, C.D.; Fleming, A.; Zolfagharian, A.; Pinskier, J.; Howard, D.; Young, T.; Lai, J.; Harrison, S.M.; Yong, Y.K.; et al. Soft Pneumatic Actuators: A Review of Design, Fabrication, Modeling, Sensing, Control and Applications; Open Research Newcastle: Callaghan, Australia, 2022. [Google Scholar]
- Peng, X.; Zhang, N.; Ge, L.; Gu, G. Dimension Optimization of Pneumatically Actuated Soft Continuum Manipulators. In Proceedings of the 2019 2nd IEEE International Conference on Soft Robotics (RoboSoft), Seoul, Republic of Korea, 14–18 April 2019; pp. 13–18. [Google Scholar] [CrossRef]
- Runge, G.; Peters, J.; Raatz, A. Design optimization of soft pneumatic actuators using genetic algorithms. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 393–400. [Google Scholar] [CrossRef]
- Jin, L.; Zhai, X.; Xue, W.; Zhang, K.; Jiang, J.; Bodaghi, M.; Liao, W.H. Finite element analysis, machine learning, and digital twins for soft robots: State-of-arts and perspectives. Smart Mater. Struct. 2025, 34, 033002. [Google Scholar] [CrossRef]
- Raeisinezhad, M.; Pagliocca, N.; Koohbor, B.; Trkov, M. Design Optimization of a Pneumatic Soft Robotic Actuator Using Model-Based Optimization and Deep Reinforcement Learning. Front. Robot. AI 2021, 8, 639102. [Google Scholar] [CrossRef]
- Yao, J.; Fang, Y.; Yang, X.; Wang, P.; Li, L. Design optimization of soft robotic fingers biologically inspired by the fin ray effect with intrinsic force sensing. Mech. Mach. Theory 2024, 191, 105472. [Google Scholar] [CrossRef]
- Caasenbrood, B.J.; Pogromsky, A.Y.; Nijmeijer, H. Sorotoki: A Matlab Toolkit for Design, Modeling, and Control of Soft Robots. IEEE Access Pract. Innov. Open Solut. 2024, 12, 17604–17638. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A Math. Phys. Sci. 1997, 326, 565–584. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Haghshenas-Jaryani, M.; Manvar, M.; Wijesundara, M.B.J. Torque Characterization of a Novel Pneumatic Soft-and-Rigid Hybrid Actuator; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Kanyanta, V.; Ivankovic, A. Mechanical characterisation of polyurethane elastomer for biomedical applications. J. Mech. Behav. Biomed. Mater. 2010, 3, 51–62. [Google Scholar] [CrossRef] [PubMed]
- Dilibal, S.; Sahin, H.; Celik, Y. Experimental and numerical analysis on the bending response of the geometrically gradient soft robotics actuator. Arch. Mech. 2018, 70, 391–404. [Google Scholar] [CrossRef]
- Xu, Y.X.; Juang, J.Y. Measurement of Nonlinear Poisson’s Ratio of Thermoplastic Polyurethanes under Cyclic Softening Using 2D Digital Image Correlation. Polymers 2021, 13, 1498. [Google Scholar] [CrossRef]
- Ogden, R.W.; Saccomandi, G.; Sgura, I. Fitting hyperelastic models to experimental data. Comput. Mech. 2004, 34, 484–502. [Google Scholar] [CrossRef]
- Vinod Chandra, S.S.; Anand, H.S. Nature inspired meta heuristic algorithms for optimization problems. Computing 2022, 104, 251–269. [Google Scholar] [CrossRef]
- Rahman, M.A.; Sokkalingam, R.; Othman, M.; Biswas, K.; Abdullah, L.; Abdul Kadir, E. Nature-Inspired Metaheuristic Techniques for Combinatorial Optimization Problems: Overview and Recent Advances. Mathematics 2021, 9, 2633. [Google Scholar] [CrossRef]
- Rajwar, K.; Deep, K.; Das, S. An exhaustive review of the metaheuristic algorithms for search and optimization: Taxonomy, applications, and open challenges. Artif. Intell. Rev. 2023, 56, 13187–13257. [Google Scholar] [CrossRef] [PubMed]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95, Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Rokbani, N.; Kumar, R.; Alimi, A.M.; Thong, P.H.; Priyadarshini, I.; Nhu, V.H.; Ngo, P.T.T. Impacts of heuristic parameters in PSO inverse kinematics solvers. Int. J. Nonlinear Sci. Numer. Simul. 2022, 23, 833–858. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, H.; Zhou, A. A particle swarm optimization algorithm for mixed-variable optimization problems. Swarm Evol. Comput. 2021, 60, 100808. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1992. [Google Scholar] [CrossRef]
- The Binary Genetic Algorithm. In Practical Genetic Algorithms; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003; pp. 27–50. [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Nikolaev, A.G.; Jacobson, S.H. Simulated Annealing. In Handbook of Metaheuristics; Gendreau, M., Potvin, J.Y., Eds.; Springer: Boston, MA, USA, 2010; pp. 1–39. [Google Scholar] [CrossRef]
- Guilmeau, T.; Chouzenoux, E.; Elvira, V. Simulated Annealing: A Review and a New Scheme. In Proceedings of the 2021 IEEE Statistical Signal Processing Workshop (SSP), Online, 11–14 July 2021; pp. 101–105. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Shehab, M.; Abualigah, L.; Al Hamad, H.; Alabool, H.; Alshinwan, M.; Khasawneh, A.M. Moth–flame optimization algorithm: Variants and applications. Neural Comput. Appl. 2020, 32, 9859–9884. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Mirjalili, S.; Soleimanian Gharehchopogh, F.; Oliva, D. A Critical Review of Moth-Flame Optimization Algorithm and Its Variants: Structural Reviewing, Performance Evaluation, and Statistical Analysis. Arch. Comput. Methods Eng. 2024, 31, 2177–2225. [Google Scholar] [CrossRef]
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM: Conshohocken, PA, USA, 2022. [CrossRef]
- Perry, S.; Rafael, R.; Huayamave, V.; Gonzalez, B.; Dae-Won, K.; Nadeau, Z. Tensile Testing of 3D Printed TPU Samples for Pediatric Biomaterial Applications. In Proceedings of the 1st International Conference of the Panamerican Society of Modeling, Methods in Engineering and Applied Sciences, PanaSoMM, Galapagos Islands, Ecuador, 22–25 May 2022. [Google Scholar]
- Raise3D Technologies Inc. Powerful 3D Slicer Software—ideaMaker®|Raise3D; Raise3D Technologies, Inc.: Irvine, CA, USA; Available online: https://www.raise3d.com/ideamaker/ (accessed on 20 October 2025).
- Tawk, C.; Alici, G. Finite Element Modeling in the Design Process of 3D Printed Pneumatic Soft Actuators and Sensors. Robotics 2020, 9, 52. [Google Scholar] [CrossRef]
- Xavier, M.S.; Fleming, A.J.; Yong, Y.K. Finite Element Modeling of Soft Fluidic Actuators: Overview and Recent Developments. Adv. Intell. Syst. 2021, 3, 2000187. [Google Scholar] [CrossRef]
- Wilcoxon, F. Probability Tables for Individual Comparisons by Ranking Methods. Biometrics. J. Int. Biom. Soc. 1947, 3, 119–122. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. In Breakthroughs in Statistics: Methodology and Distribution; Kotz, S., Johnson, N.L., Eds.; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar] [CrossRef]
- Manns, M.; Morales, J.; Frohn, P. Additive manufacturing of silicon based PneuNets as soft robotic actuators. Procedia CIRP 2018, 72, 328–333. [Google Scholar] [CrossRef]
- Hiremath, S.; Mathias, K.A.; Kim, T.W. 3D-Printed soft pneumatic actuators: Enhancing flexible gripper capabilities. Robomech. J. 2025, 12, 26. [Google Scholar] [CrossRef]







| Algorithm | Key Parameters | Solution Generation Technique |
|---|---|---|
| PSO [41,42,43] | Inertia weight, w Cognitive factor, Social factor, | New solutions are generated by updating particle velocities V and positions X using social and cognitive guidance : , |
| GA [44,45] | Number of bit, Selection rate, Mutation probability, | Normalize variables X between 0 and 1 relative to bounds then convert them to binary using Apply crossover operator to parent chromosomes Apply mutation operator by flipping bits with probability Decode new solutions for evaluation the following equation then scale them to original bounds Select fittest solutions with rate for next generation |
| SA [46,47,48] | Cooling rate, | New generations are generated using the following equation, where indicates a Gaussian perturbation: Evaluate energy (fitness) difference between new solution and current solution using the objective function : Accept if or with probability Decrease the temperature by a cooling rate factor : |
| MFO [49,50,51] | Spiral constant, b | Moths represent candidate solutions M, while flames F store the best positions found. Each moth updates its position using logarithmic spiral flight around its assigned flame: , where is the distance to the flame, b controls the spiral shape, and is a random parameter. To balance exploration and exploitation, the number of flames decreases adaptively each iteration: , where is the current iteration and T the maximum iterations. |
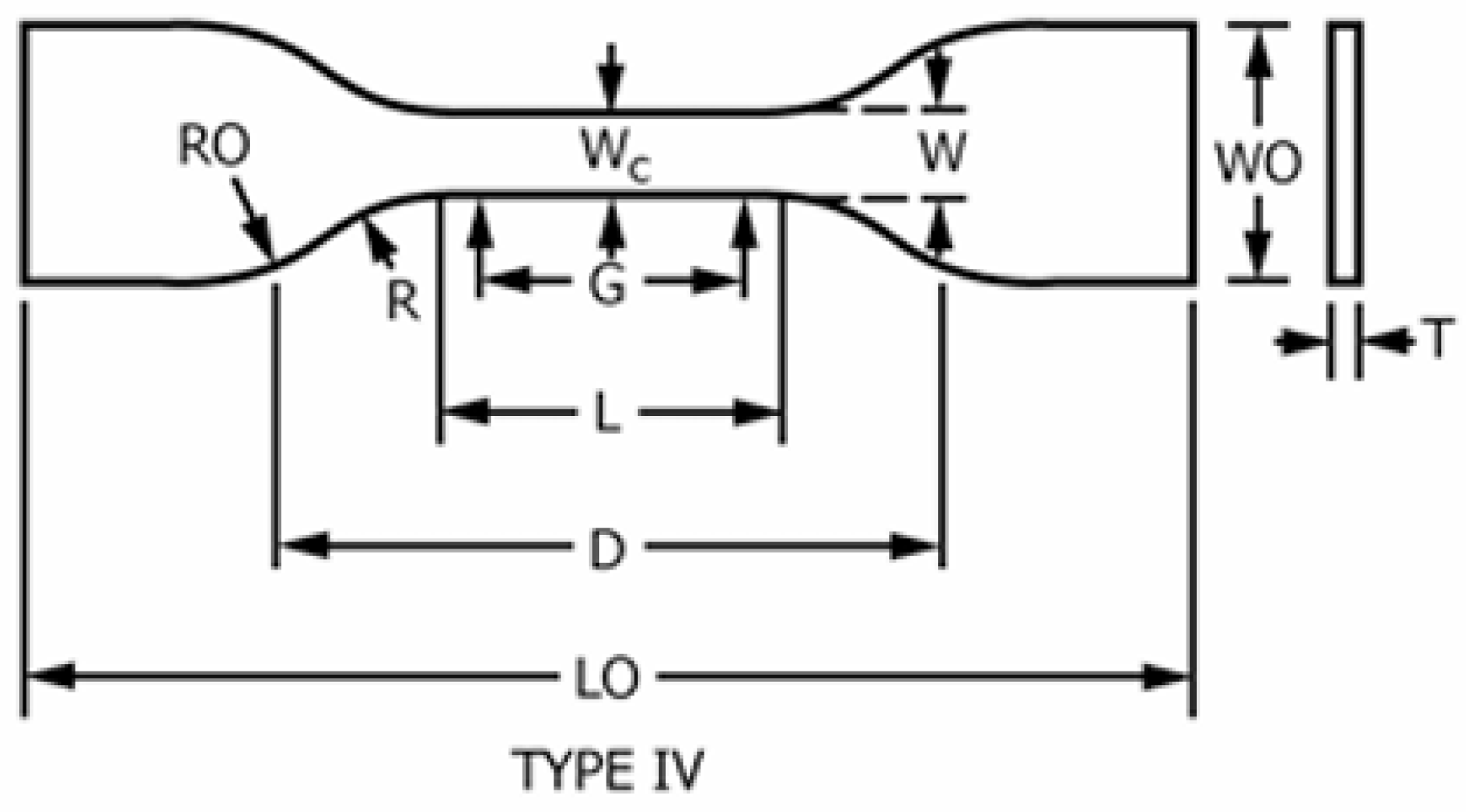
| Dimension | Value (mm) |
|---|---|
| Width (W) | |
| Cross Sectional Width (Wc) | |
| Length (L) | |
| Outer Width (WO) | |
| Outer Length (LO) | 115 no max |
| Gauge Length (G) | |
| Grip Distance (D) | |
| Inner Radius (R) | |
| Outer Radius (RO) | |
| Thickness (T) |
| Settings | Parameter | Value/Type |
|---|---|---|
| Layer | Layer height | 0.1 mm |
| Shell | 2 mm | |
| Maximum Percentage of Shell Overlaps | 50% | |
| Extruder | Line width | 0.4 mm |
| Retraction speed | 20 mm/s | |
| Quantity of the retracted material | 1 mm | |
| Infilling | Filling density | 100% |
| Infill overlap | 100% | |
| Filling flow rate | 100% | |
| Infill pattern | Gyroid | |
| Full infilling | Base solid fill layers | 2 |
| Solid fill layers | 2 | |
| Base solid fill flowrate | 100% | |
| Solid fill flowrate | 100% | |
| Temperature | Heated bed temperature | 100 deg |
| Primary extruder | 230 deg | |
| Speed | Default printing speed | 50 mm/s |
| Inner shell speed | 40 mm/s | |
| Outer shell speed | 25 mm/s |
| Algorithm | Intrinsic Parameter | Value |
|---|---|---|
| GA | Selection rate, | 0.5 |
| Mutation probability, | 0.7 | |
| Number of bits, | 10 | |
| Population size, N | 20 | |
| PSO | Global acceleration factor, | 1.43 |
| Personal acceleration factor, | 1.43 | |
| Weight factor, w | 0.6 | |
| Population size, N | 20 | |
| SA | Cooling rate, c | 0.95 |
| MFO | Population size, N | 20 |
| logarithmic spiral shape constant, c | 1 |
| Model | Parameters | Solutions | ||||
|---|---|---|---|---|---|---|
| MFO | PSO * | GA | SA | Ansys | ||
| Ogden | 0.5632 | −2.5697 | −2.8809 | −2.2784 | 3.4144 | |
| −0.7566 | 0.5502 | 1.3184 | 0.5784 | 0.3061 | ||
| −2.4900 | −0.2173 | −2.3926 | −0.6989 | 0.2913 | ||
| [MPa] | −38.5910 | −17.3404 | −12.8418 | −27.5857 | 0.121202 | |
| [MPa] | 9.9714 | −40.8435 | −33.5449 | −37.5099 | 15.4935 | |
| [MPa] | −19.4755 | 13.1420 | −24.8535 | 30.0426 | 15.5351 | |
| Fitness | 8.1431 | 7.4753 | 27.2570 | 260.7055 | ||
| Yeoh | [MPa] | 1.4261 | 1.4246 | −18.4082 | −5.2330 | 1.6337 |
| [MPa] | −0.0106 | −0.0105 | −2.2949 | 0.0043 | −0.0234 | |
| [MPa] | 0.0488 | 0.0026 | ||||
| Fitness | 434.7180 | 434.7078 | 665.8216 | |||
| Algorithm | Model | Best Value | Worst Value | Median | Mean | Std |
|---|---|---|---|---|---|---|
| MFO | Ogden | 8.1431 | 98.8142 | 192.9934 | 374.3590 | |
| Yeoh | 434.7180 | 622.8308 | ||||
| PSO | Ogden | 7.4753 | 189.4057 | 38.7020 | 69.0326 | 66.5322 |
| Yeoh | 434.7078 | 434.7078 | 434.7078 | 434.7078 | ||
| GA | Ogden | |||||
| Yeoh | ||||||
| SA | Ogden | 27.2570 | 5.6701 | |||
| Yeoh |
| Compared Algorithms | Wilcoxon Metrics | Best Algorithm | |||
|---|---|---|---|---|---|
| Algorithm 1 | Algorithm 2 | ||||
| MFO | PSO | 0.0230 | 343 | 122 | PSO |
| MFO | GA | 1.7344 | 0 | 465 | MFO |
| MFO | SA | 1.2381 | 20 | 445 | MFO |
| PSO | GA | 1.7344 | 0 | 465 | PSO |
| PSO | SA | 2.6033 | 4 | 461 | PSO |
| GA | SA | 0.1589 | 164 | 301 | −− |
| Compared Algorithms | Wilcoxon Metrics | Best Algorithm | |||
|---|---|---|---|---|---|
| Algorithm 1 | Algorithm 2 | ||||
| MFO | PSO | 1.7344 | 465 | 0 | PSO |
| MFO | GA | 1.7344 | 0 | 465 | MFO |
| MFO | SA | 1.7344 | 0 | 465 | MFO |
| PSO | GA | 1.7344 | 0 | 465 | PSO |
| PSO | SA | 1.7344 | 0 | 465 | PSO |
| GA | SA | 1.9729 | 440 | 25 | SA |
| Algorithm | Intrinsic Parameter | Value |
|---|---|---|
| GA | Selection rate, | 0.5 |
| Mutation probability, | 0.7 | |
| Number of bits, | 10 | |
| Population size, N | 6 | |
| PSO | Global acceleration factor, | 1.43 |
| Personal acceleration factor, | 1.43 | |
| Weight factor, | 0.6 | |
| Population size, | 6 | |
| SA | Cooling rate, | 0.95 |
| MFO | Population size, N | 6 |
| logarithmic spiral shape constant, c | 1 |
| Settings | Parameter | Value/Type |
|---|---|---|
| Layer | Layer height | 0.3 mm |
| Shell | 2 mm | |
| Maximum Percentage of Shell Overlaps | 50% | |
| Extruder | Line width | 0.4 mm |
| Retraction speed | 20 mm/s | |
| Quantity of the retracted material | 1 mm | |
| Infilling | Filling density | 100% |
| Infill overlap | 100% | |
| Filling flow rate | 100% | |
| Infill pattern | Rectilinear | |
| Full infilling | Base solid fill layers | 2 |
| Solid fill layers | 2 | |
| Base solid fill flowrate | 100% | |
| Solid fill flowrate | 100% | |
| Temperature | Heated bed temperature | 100 deg |
| Primary extruder | 230 deg | |
| Speed | Default printing speed | 50 mm/s |
| Inner shell speed | 40 mm/s | |
| Outer shell speed | 25 mm/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slim, M.; Rokbani, N.; Terres, M.A.; Watelain, E.; Ben Khelifa, M.M. Optimization of Soft Actuator Geometry and Material Modeling Using Metaheuristic Algorithms. Actuators 2025, 14, 520. https://doi.org/10.3390/act14110520
Slim M, Rokbani N, Terres MA, Watelain E, Ben Khelifa MM. Optimization of Soft Actuator Geometry and Material Modeling Using Metaheuristic Algorithms. Actuators. 2025; 14(11):520. https://doi.org/10.3390/act14110520
Chicago/Turabian StyleSlim, Mohamed, Nizar Rokbani, Mohamed Ali Terres, Eric Watelain, and Mohamed Moncef Ben Khelifa. 2025. "Optimization of Soft Actuator Geometry and Material Modeling Using Metaheuristic Algorithms" Actuators 14, no. 11: 520. https://doi.org/10.3390/act14110520
APA StyleSlim, M., Rokbani, N., Terres, M. A., Watelain, E., & Ben Khelifa, M. M. (2025). Optimization of Soft Actuator Geometry and Material Modeling Using Metaheuristic Algorithms. Actuators, 14(11), 520. https://doi.org/10.3390/act14110520







