Nonlinear Dynamic Modeling of Flexible Cable in Overhead Bridge Crane and Trajectory Optimization Under Full-Constraint Conditions
Abstract
1. Introduction
- (1)
- A nonlinear dynamic model of flexible cables in overhead bridge cranes is established based on continuum mechanics which accurately captures the distributed mass, bending stiffness, and damping effects that are often neglected in conventional rigid link models.
- (2)
- A novel trajectory optimization framework named reverse angle enumeration reasoning (RAER) is proposed. By discretizing the continuous dynamics and systematically enumerating candidate trajectories, RAER ensures full-state constraint satisfaction while effectively suppressing load swing.
- (3)
- The effectiveness and robustness of the proposed model and optimization strategy are validated through both numerical simulations and experiments on a self-built crane platform, demonstrating significant improvements in swing suppression and motion smoothness compared to existing methods. Compared with existing methods, the predicted and measured responses of the flexible cable exhibit high similarity. The RAER algorithm satisfies all state constraints while achieving the lowest energy consumption, and it provides significant improvements in swing suppression and motion smoothness.
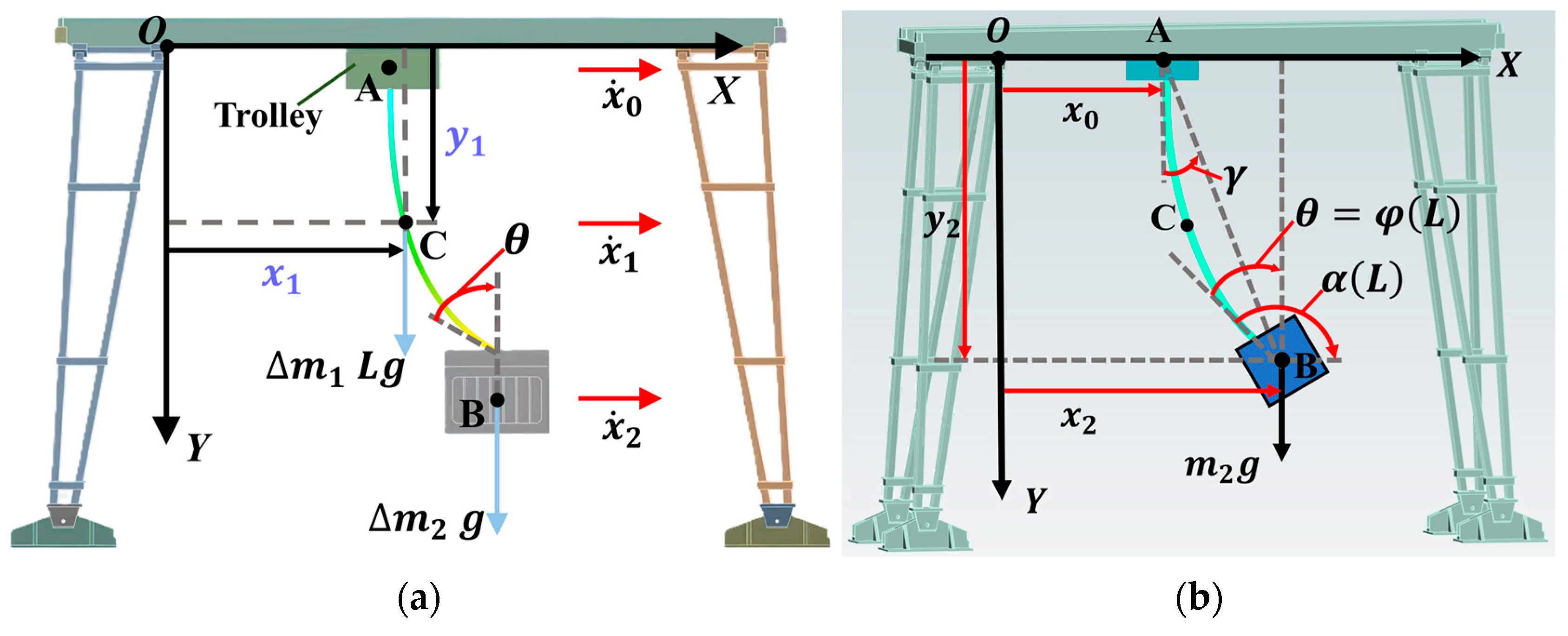
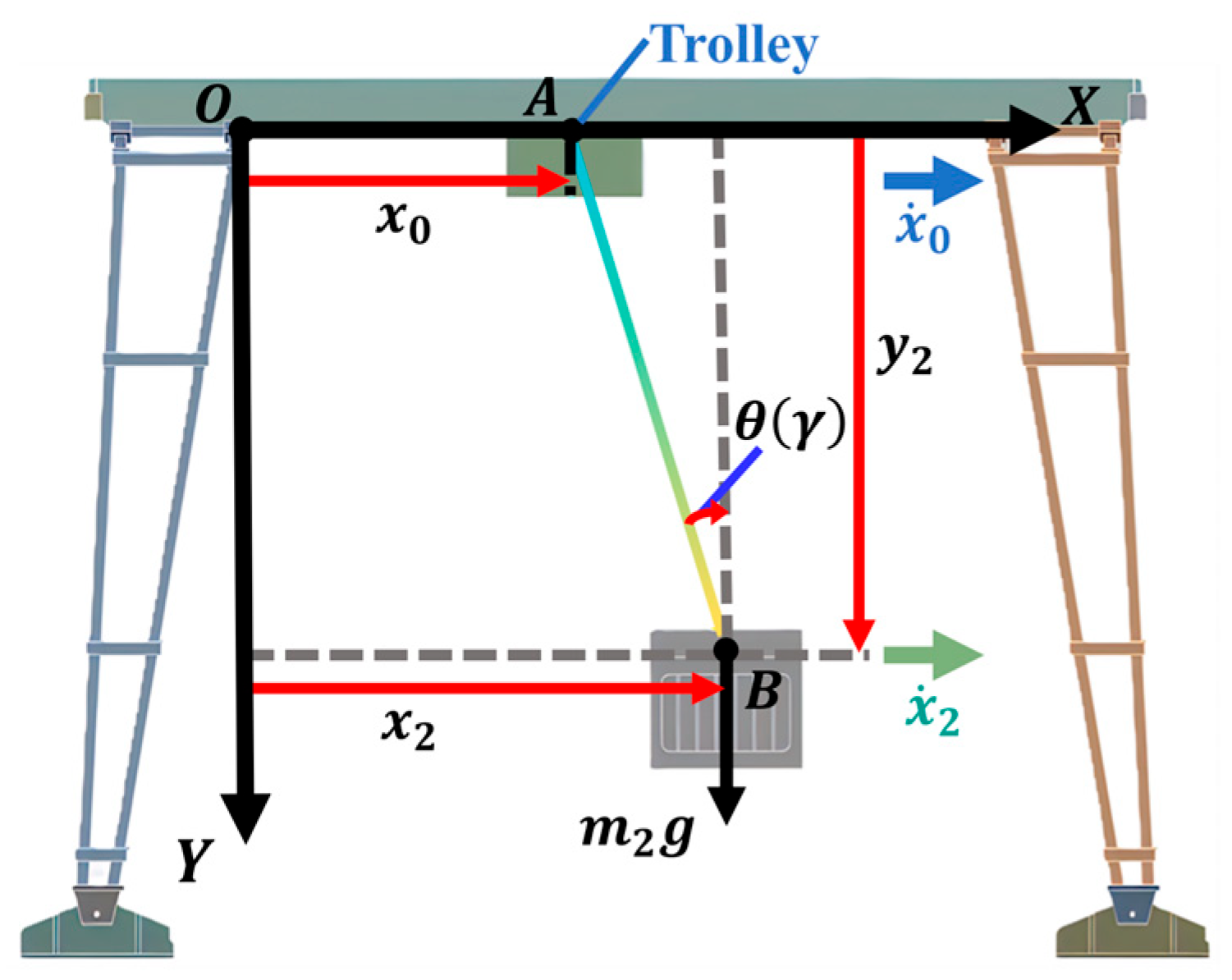
2. Dynamics and Motion Trajectory Modeling of the Flexible Cable System in Bridge Cranes
2.1. Dynamic Modeling of Flexible Cable
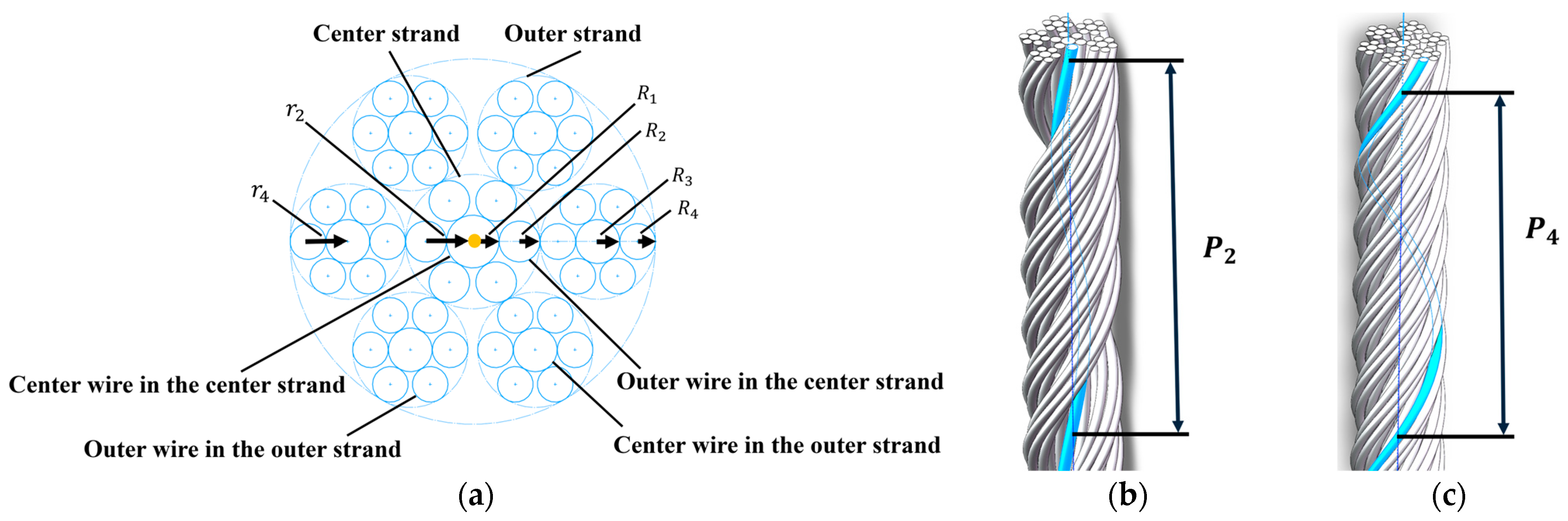
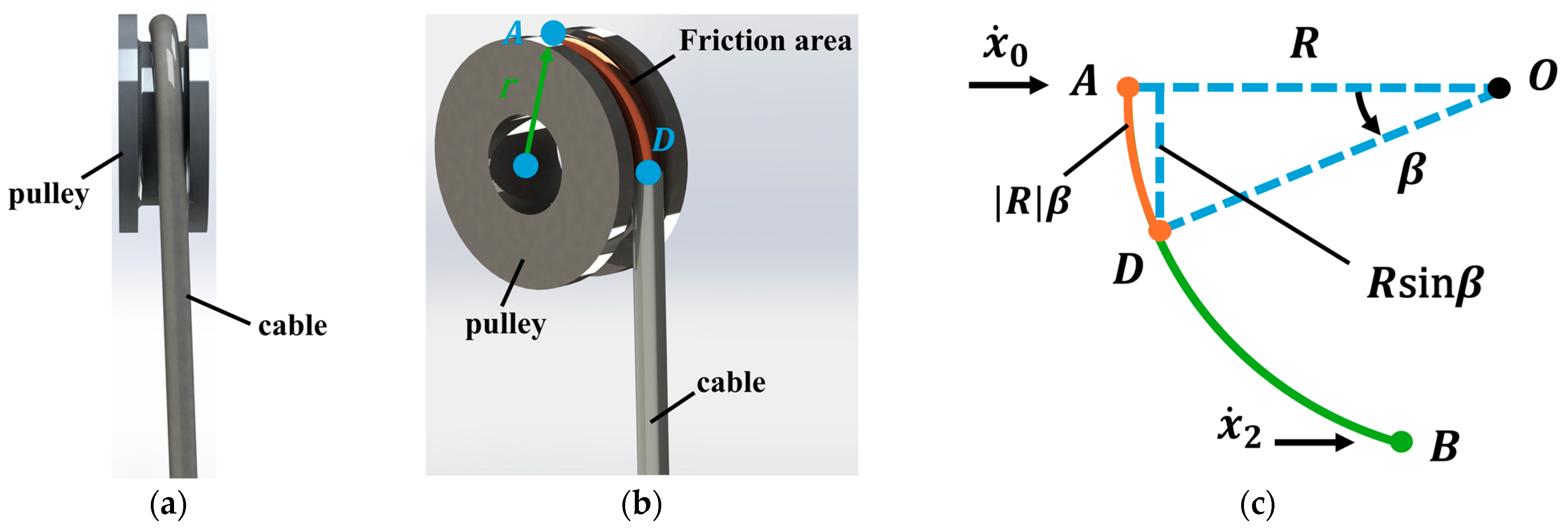
2.2. Analysis and Modeling of Internal Forces and Friction Forces in Flexible Cable
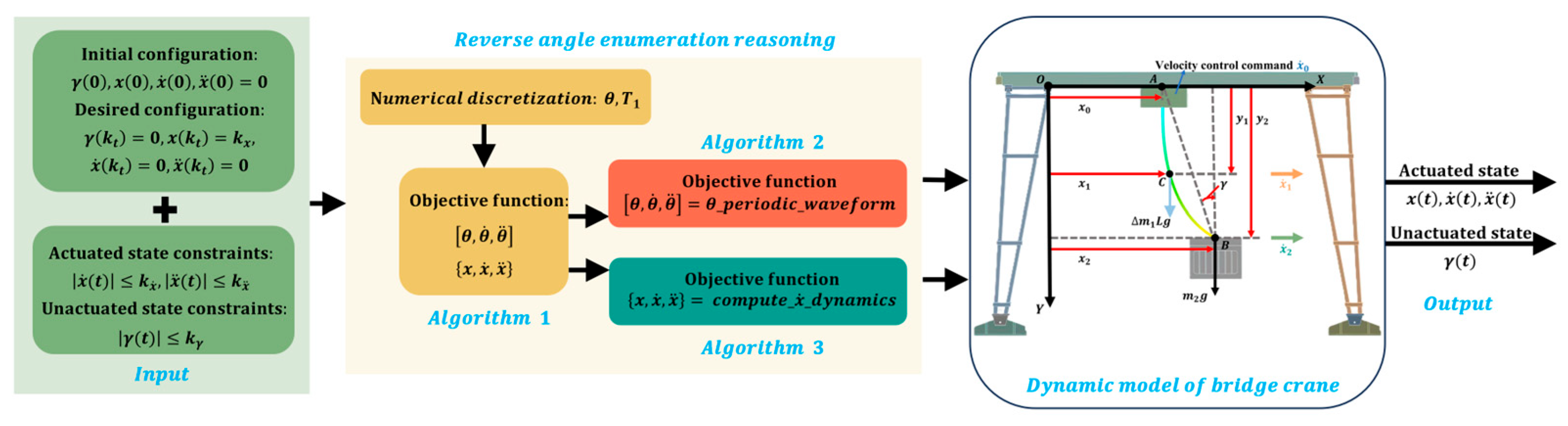
3. Numerical Discretization and Dynamic Optimization for Cable Motion Control Systems
3.1. Discretization Scheme and Trajectory Planning
3.2. Algorithmic Implementation for Dynamic Optimization
| Algorithm 1. The enumeration–verification method generates the current optimal solution of the system |
| Input: . |
Output: .
|
4. Simulation Verification and Analysis
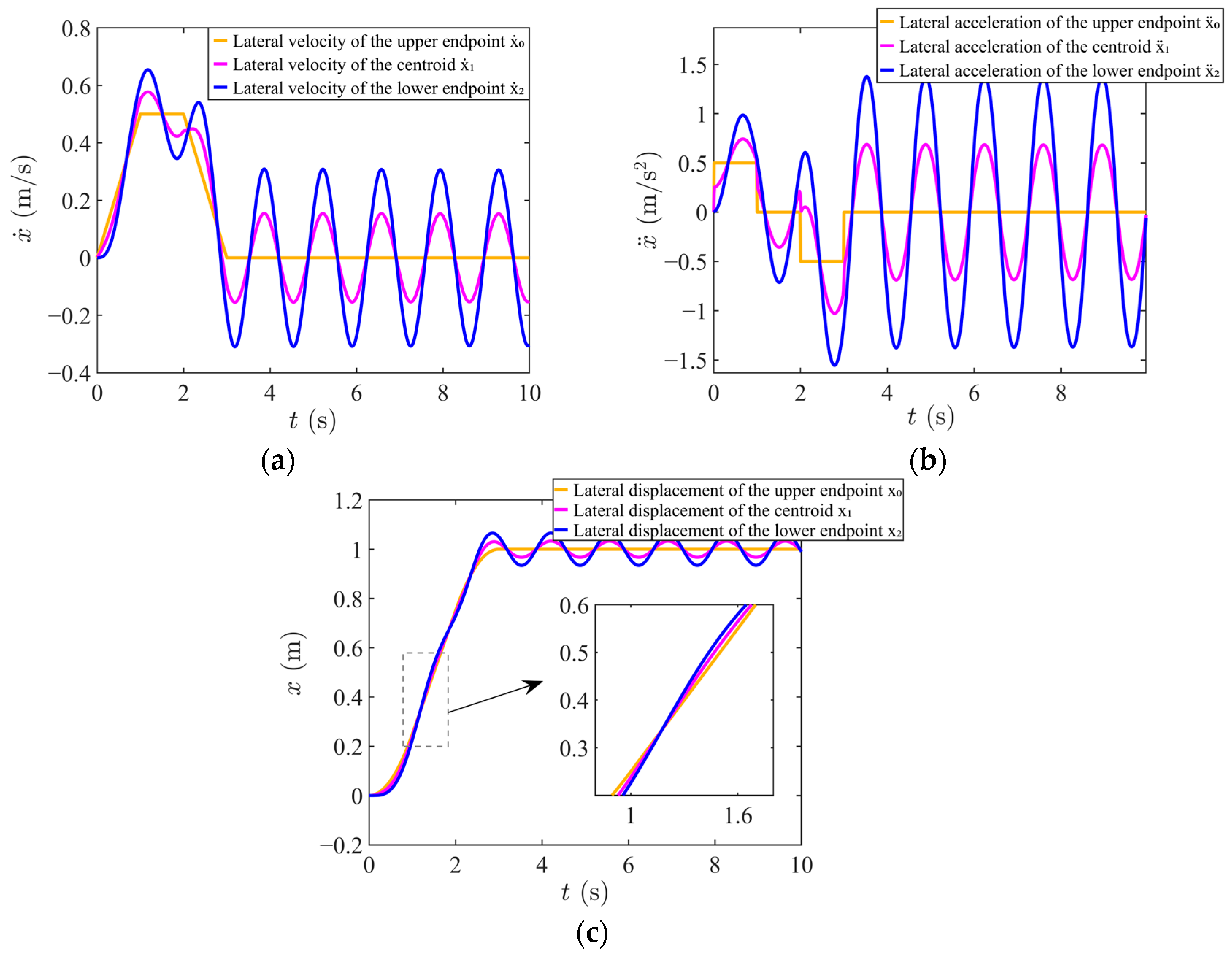
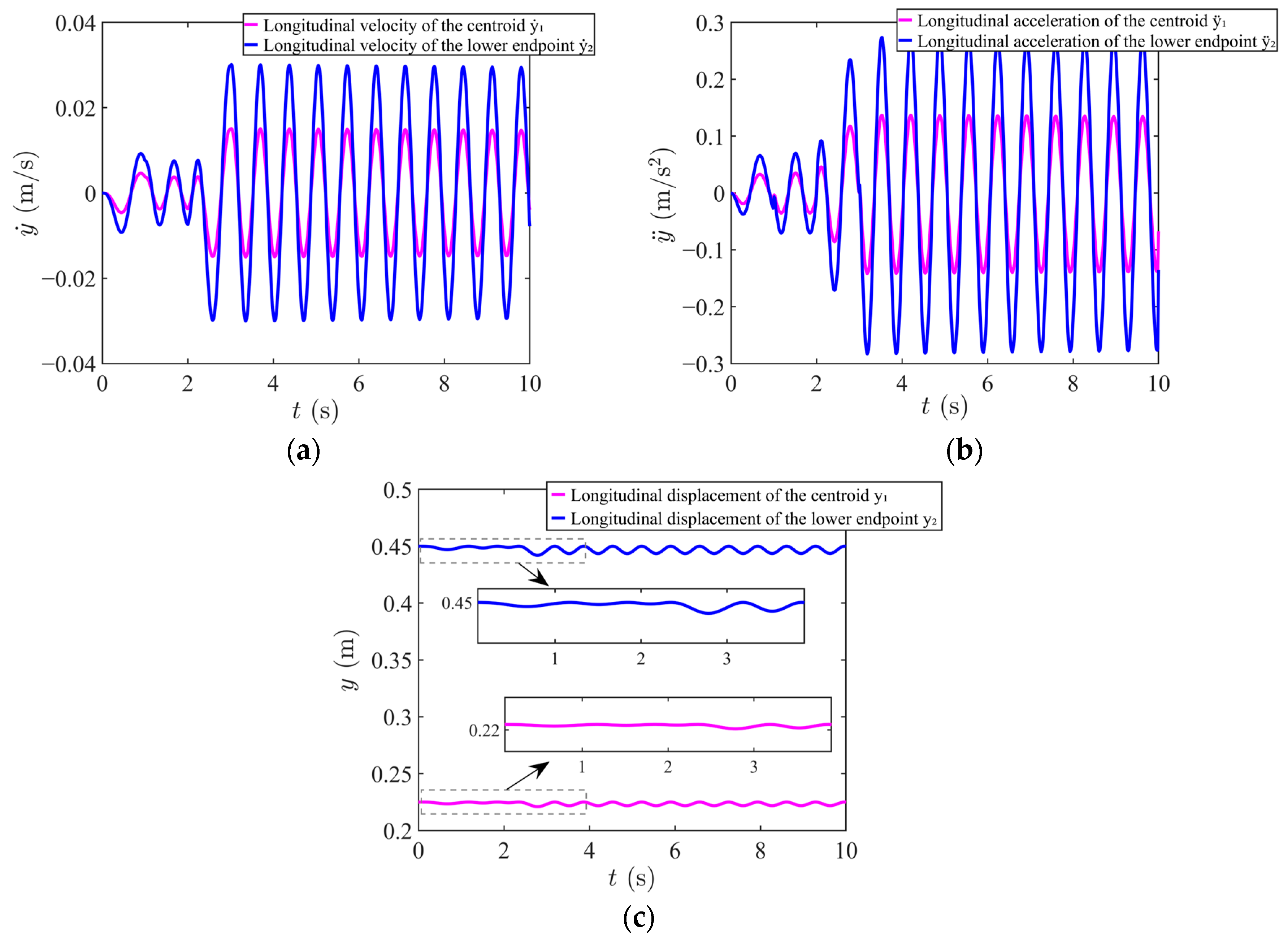
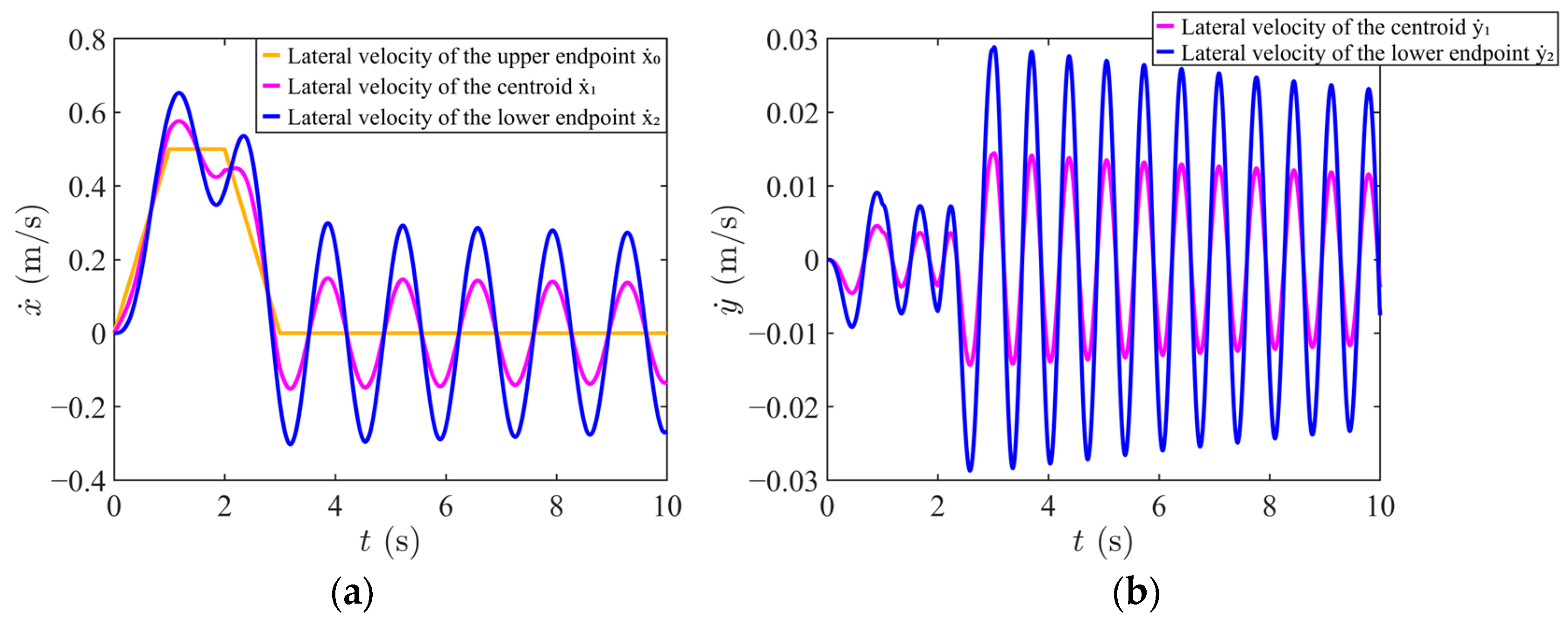
4.1. Flexible Cable Kinematics Simulation
4.2. Validation of Speed Optimization Simulation and Comparative Analysis of Performance
- (1)
- is the maximum angle between the line connecting the upper and lower endpoints of the flexible cable and the vertical direction in the optimal result, where ;
- (2)
- is the time taken to reach the target distance in the optimal result;
- (3)
- is the residual swing angle between the line connecting the upper and lower endpoints of the flexible cable and the vertical direction when reaching the target distance in the optimal result, where ;
- (4)
- is the maximum velocity of the upper endpoint of the flexible cable in the optimal result, where ;
- (5)
- is the maximum acceleration of the upper endpoint of the flexible cable in the optimal result, where ;
- (6)
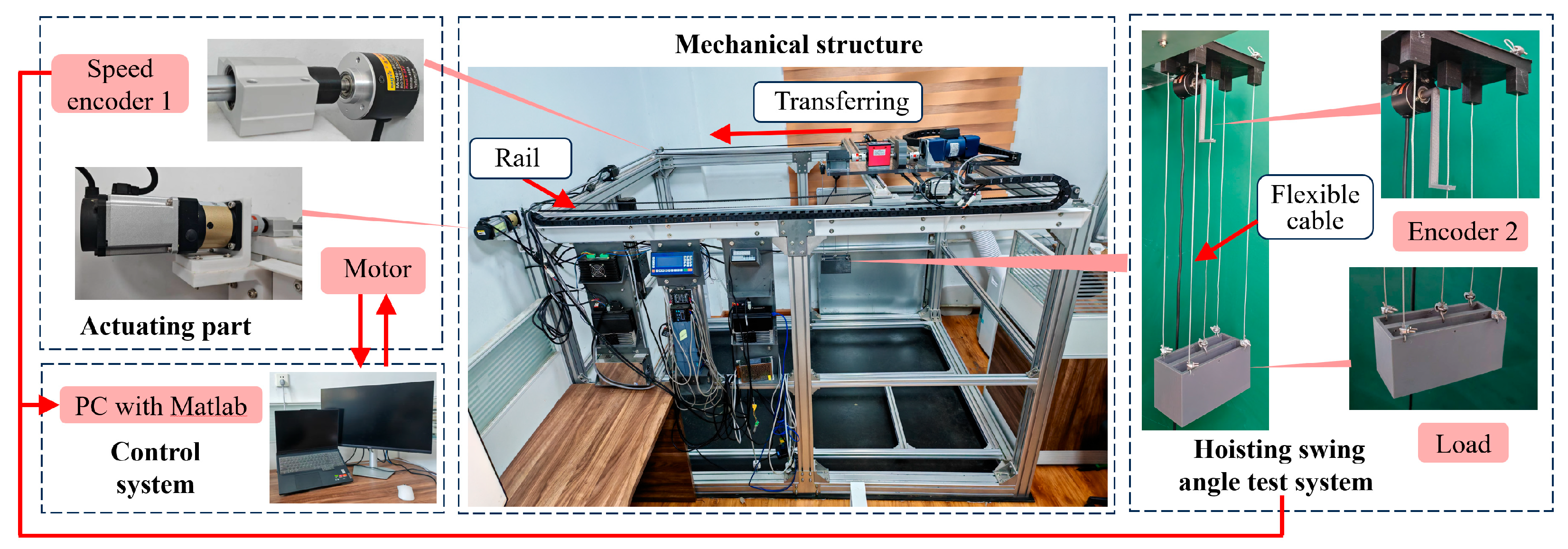
4.3. Experiments and Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | alternating current |
| ARBTS | Active Rider Block Tagline System |
| DMB | double-pendulum crane model with a distributed mass beam |
| MCAS | Multi-Cable Anti-Sway System |
| OFB | novel amplitude-saturated output feedback |
| PSO | Particle Swarm Optimization |
| RAER | reverse angle enumeration reasoning |
| SA | Simulated Annealing |
| SIRMs | single-input rule module |
| ZV | Zero Vibration |
| ZVD | Zero Vibration Derivative |
Appendix A
Appendix A.1
| Symbol | Meaning | Unit |
|---|---|---|
| Cable bending stiffness | ||
| Quintic polynomial coefficients (trajectory planning) | - | |
| Elastic modulus of cable material | ||
| Intermediate function in trajectory planning | - | |
| Friction force component | ||
| Gravitational acceleration | ||
| Rotational inertia of the cable | ||
| Air damping torque coefficient | ||
| Maximum swing angle constraint | ||
| The shortest time to reach the target displacement | ||
| Target displacement constraint | ||
| Maximum motion speed constraint | ||
| Maximum motion acceleration constraint | ||
| Total cable length | ||
| Cable mass per unit length | ||
| Mass of end load | ||
| Total number of discretization steps | - | |
| Number of cable strands | - | |
| Pitch of cable strands | ||
| Radius of cable wires | ||
| Pulley radius | ||
| Cable arc length parameter | ||
| Continuous time variable | ||
| Discrete time node | ||
| Time to complete target displacement | ||
| Control period of trajectory planning | ||
| Coordinates of cable upper endpoint | ||
| Coordinates of cable centroid | ||
| Coordinates of cable lower endpoint | ||
| Discrete time step | ||
| Swing angle at cable lower endpoint | ||
| Cable curvature | ||
| Angle between cable endpoints connection line and y-axis | ||
| Residual swing angle | ||
| Cable–pulley friction coefficient | - | |
| Poisson’s ratio | - | |
| Cable tangential angle | ||
| Helical angle of cable strands | ||
| Arc angle of the contact line between the cable and the pulley | ||
| Tangential angle distribution of the cable |
Appendix A.2
| Algorithm A1. Generate the angle trajectory of the current time based on the discretized angle |
| Input: . |
Output: .
|
| Algorithm A2. Determine constraints based on dynamics model |
| Input: . |
Output: .
|
References
- Lee, H.-H.; Cho, S.-K. A New Fuzzy-Logic Anti-Swing Control for Industrial Three-Dimensional Overhead Cranes. In Proceedings of the 2001 ICRA IEEE International Conference on Robotics and Automation (Cat. No.01CH37164), Seoul, Republic of Korea, 21–26 May 2001; Volume 3, pp. 2956–2961. [Google Scholar]
- Liu, F.; Zhu, L.; Wang, G.; Li, Z.; Wu, L.; Hao, Y.; Cao, H. Experimental Study on Anti-Swing Control Strategy of Portal Crane. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 3755–3759. [Google Scholar]
- Cao, Y.; Li, T. Review of Antiswing Control of Shipboard Cranes. IEEE CAA J. Autom. Sin. 2020, 7, 346–354. [Google Scholar] [CrossRef]
- Abdullahi, A.M.; Mohamed, Z.; Selamat, H.; Pota, H.R.; Zainal Abidin, M.S.; Ismail, F.S.; Haruna, A. Adaptive Output-Based Command Shaping for Sway Control of a 3D Overhead Crane with Payload Hoisting and Wind Disturbance. Mech. Syst. Signal Process. 2018, 98, 157–172. [Google Scholar] [CrossRef]
- Singhose, W. Command Shaping for Flexible Systems: A Review of the First 50 Years. Int. J. Precis. Eng. Manuf. 2009, 10, 153–168. [Google Scholar] [CrossRef]
- Smith, O.J.M. Posicast Control of Damped Oscillatory Systems. Proc. IRE 1957, 45, 1249–1255. [Google Scholar] [CrossRef]
- Maleki, E.; Singhose, W. Swing Dynamics and Input-Shaping Control of Human-Operated Double-Pendulum Boom Cranes. J. Comput. Nonlinear Dyn. 2012, 7, 031006. [Google Scholar] [CrossRef]
- Fujioka, D.; Singhose, W. Performance Comparison of Input-Shaped Model Reference Control on an Uncertain Flexible System. IFAC-Pap. 2015, 48, 129–134. [Google Scholar] [CrossRef]
- Maghsoudi, M.J.; Mohamed, Z.; Sudin, S.; Buyamin, S.; Jaafar, H.I.; Ahmad, S.M. An Improved Input Shaping Design for an Efficient Sway Control of a Nonlinear 3D Overhead Crane with Friction. Mech. Syst. Signal Process. 2017, 92, 364–378. [Google Scholar] [CrossRef]
- Martin, I.A.; Irani, R.A. Evaluation of Both Linear and Non-Linear Control Strategies for a Shipboard Marine Gantry Crane. In Proceedings of the OCEANS 2019 MTS/IEEE SEATTLE, Washington, DC, USA, 27–31 October 2019; pp. 1–10. [Google Scholar]
- Maghsoudi, M.J.; Mohamed, Z.; Tokhi, M.O.; Husain, A.R.; Abidin, M.S.Z. Control of a Gantry Crane Using Input-Shaping Schemes with Distributed Delay. Trans. Inst. Meas. Control 2017, 39, 361–370. [Google Scholar] [CrossRef]
- Xing, B.; Huang, J. Control of Pendulum-Sloshing Dynamics in Suspended Liquid Containers. IEEE Trans. Ind. Electron. 2021, 68, 5146–5154. [Google Scholar] [CrossRef]
- Kang, C.-G. Impulse Vectors for Input-Shaping Control: A Mathematical Tool to Design and Analyze Input Shapers. IEEE Control Syst. Mag. 2019, 39, 40–55. [Google Scholar] [CrossRef]
- Sorensen, K.L.; Hekman, K.; Singhose, W.E. Finite-State Input Shaping. IEEE Trans. Control Syst. Technol. 2010, 18, 664–672. [Google Scholar] [CrossRef]
- Singhose, W.; Porter, L.; Kenison, M.; Kriikku, E. Effects of Hoisting on the Input Shaping Control of Gantry Cranes. Control Eng. Pract. 2000, 8, 1159–1165. [Google Scholar] [CrossRef]
- Li, H.; Hui, Y.-B.; Wang, Q.; Wang, H.-X.; Wang, L.-J. Design of Anti-Swing PID Controller for Bridge Crane Based on PSO and SA Algorithm. Electronics 2022, 11, 3143. [Google Scholar] [CrossRef]
- Sun, N.; Fang, Y.; Chen, H.; Fu, Y.; Lu, B. Nonlinear Stabilizing Control for Ship-Mounted Cranes with Ship Roll and Heave Movements: Design, Analysis, and Experiments. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1781–1793. [Google Scholar] [CrossRef]
- Sun, N.; Yang, T.; Chen, H.; Fang, Y. Dynamic Feedback Antiswing Control of Shipboard Cranes Without Velocity Measurement: Theory and Hardware Experiments. IEEE Trans. Ind. Inform. 2019, 15, 2879–2891. [Google Scholar] [CrossRef]
- Jensen, K.J.; Ebbesen, M.K.; Hansen, M.R. Anti-Swing Control of a Hydraulic Loader Crane with a Hanging Load. Mechatronics 2021, 77, 102599. [Google Scholar] [CrossRef]
- Yu, Z.; Dong, H.-M.; Liu, C.-M. Research on Swing Model and Fuzzy Anti Swing Control Technology of Bridge Crane. Machines 2023, 11, 579. [Google Scholar] [CrossRef]
- Yi, J.; Yubazaki, N.; Hirota, K. Anti-Swing and Positioning Control of Overhead Traveling Crane. Inf. Sci. 2003, 155, 19–42. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Hua, L.; Xia, M. Dynamic Analysis and Time Optimal Anti-Swing Control of Double Pendulum Bridge Crane with Distributed Mass Beams. Mech. Syst. Signal Process. 2020, 144, 106968. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Li, Z.; Li, Y. Time-Polynomial-Based Optimal Trajectory Planning for Double-Pendulum Tower Crane with Full-State Constraints and Obstacle Avoidance. IEEE ASME Trans. Mechatron. 2023, 28, 919–932. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Li, Y. Adaptive Anti-Swing Control for 7-DOF Overhead Crane with Double Spherical Pendulum and Varying Cable Length. IEEE Trans. Autom. Sci. Eng. 2024, 21, 5240–5251. [Google Scholar] [CrossRef]
- Sun, N.; Fang, Y.; Chen, H.; Lu, B. Amplitude-Saturated Nonlinear Output Feedback Antiswing Control for Underactuated Cranes with Double-Pendulum Cargo Dynamics. IEEE Trans. Ind. Electron. 2017, 64, 2135–2146. [Google Scholar] [CrossRef]
- Sun, N.; Fang, Y.; Zhang, X. Energy Coupling Output Feedback Control of 4-DOF Underactuated Cranes with Saturated Inputs. Automatica 2013, 49, 1318–1325. [Google Scholar] [CrossRef]
- Hong, K.-S.; Ngo, Q.H. Dynamics of the Container Crane on a Mobile Harbor. Ocean Eng. 2012, 53, 16–24. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, X.; Gao, Y.; Chen, Y. An Anti-Swing Control Method Combining Deep Learning Prediction Models with a Multistate Fractional-Order Terminal Sliding Mode Controller for Wave Motion Compensation Devices. Mech. Syst. Signal Process. 2025, 223, 111819. [Google Scholar] [CrossRef]
- Wang, Y.; Yan, F.; Jiang, S.; Chen, B. Time Delay Control of Cable-Driven Manipulators with Adaptive Fractional-Order Nonsingular Terminal Sliding Mode. Adv. Eng. Softw. 2018, 121, 13–25. [Google Scholar] [CrossRef]
- Qian, Y.; Fang, Y.; Lu, B. Adaptive Robust Tracking Control for an Offshore Ship-Mounted Crane Subject to Unmatched Sea Wave Disturbances. Mech. Syst. Signal Process. 2019, 114, 556–570. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Li, Y. Adaptive Sliding Mode Control Based on Time-Delay Estimation for Underactuated 7-DOF Tower Crane. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 2277–2288. [Google Scholar] [CrossRef]
- Yuan, G.H.; Hunt, B.R.; Grebogi, C.; Ott, E.; Yorke, J.A.; Kostelich, E.J. Design and Control of Shipboard Cranes. In Proceedings of the ASME 1997 Design Engineering Technical Conferences, Sacramento, CA, USA, 14 September 1997; Volume 1D. [Google Scholar]
- Parker, G.; Graziano, M.; Leban, F.; Green, J.; Bird, J.D. Reducing Crane Payload Swing Using a Rider Block Tagline Control System. In Proceedings of the OCEANS 2007-Europe, Aberdeen, Scotland, 18–21 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–5. [Google Scholar]
- Sun, M.; Wang, S.; Han, G.; Jin, G.; Li, J.; Chen, H.; Sun, Y. Multi-Cable Anti-Swing System for Cranes Subject to Ship Excitation and Wind Disturbance: Dynamic Analysis and Application in Engineering. Ocean Eng. 2023, 281, 114518. [Google Scholar] [CrossRef]
- Patel, M.H.; Brown, D.T.; Witz, J.A. Operability Analysis for a Monohull Crane Vessel. R. Inst. Nav. Archit. Trans. 1987, 129, 103–113. [Google Scholar]
- Hu, Y.; Tao, L.; Lv, W. Anti-Pendulation Analysis of Parallel Wave Compensation Systems. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2016, 230, 177–186. [Google Scholar] [CrossRef]
- Kimiaghalam, B.; Homaifar, A.; Bikdash, M.; Hunt, B.R. Feedforward Control Law for A Shipboard Crane with Maryland Rigging System. J. Vib. Control 2002, 8, 159–188. [Google Scholar] [CrossRef]
- Costello, G.A. Theory of Wire Rope; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 978-1-4612-1970-5. [Google Scholar]
- Kaneshige, A.; Kaneshige, N.; Hasegawa, S.; Miyoshi, T.; Terashima, K. Model and Control System for 3D Transfer of Liquid Tank with Overhead Crane Considering Suppression of Liquid Vibration. Int. J. Cast Met. Res. 2008, 21, 293–298. [Google Scholar] [CrossRef]
- Kaneshige, A.; Miyoshi, T.; Terashima, K. The Development of an Autonomous Mobile Overhead Crane System for the Liquid Tank Transfer. In Proceedings of the 2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 630–635. [Google Scholar]
- Hamaguchi, M. Damping Control of Sloshing in Liquid Container in Cart with Active Vibration Reducer: The Case of a Curved Path on a Horizontal Plane. IEEE ASME Trans. Mechatron. 2019, 24, 361–372. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Li, Z.; Li, Y. Optimal Trajectory Planning Strategy for Underactuated Overhead Crane with Pendulum-Sloshing Dynamics and Full-State Constraints. Nonlinear Dyn. 2022, 109, 815–835. [Google Scholar] [CrossRef]
- Sung, Y.-G.; Singhose, W.E. Robustness Analysis of Input Shaping Commands for Two-Mode Flexible Systems. IET Control Theory Appl. 2009, 3, 722–730. [Google Scholar] [CrossRef]
- Hu, G.; Makkar, C.; Dixon, W.E. Energy-Based Nonlinear Control of Underactuated Euler–Lagrange Systems Subject to Impacts. IEEE Trans. Autom. Control 2007, 52, 1742–1748. [Google Scholar] [CrossRef]
- Zhang, M.; Jing, X.; Zhu, Z. Disturbance Employment-Based Sliding Mode Control for 4-DOF Tower Crane Systems. Mech. Syst. Signal Process. 2021, 161, 107946. [Google Scholar] [CrossRef]


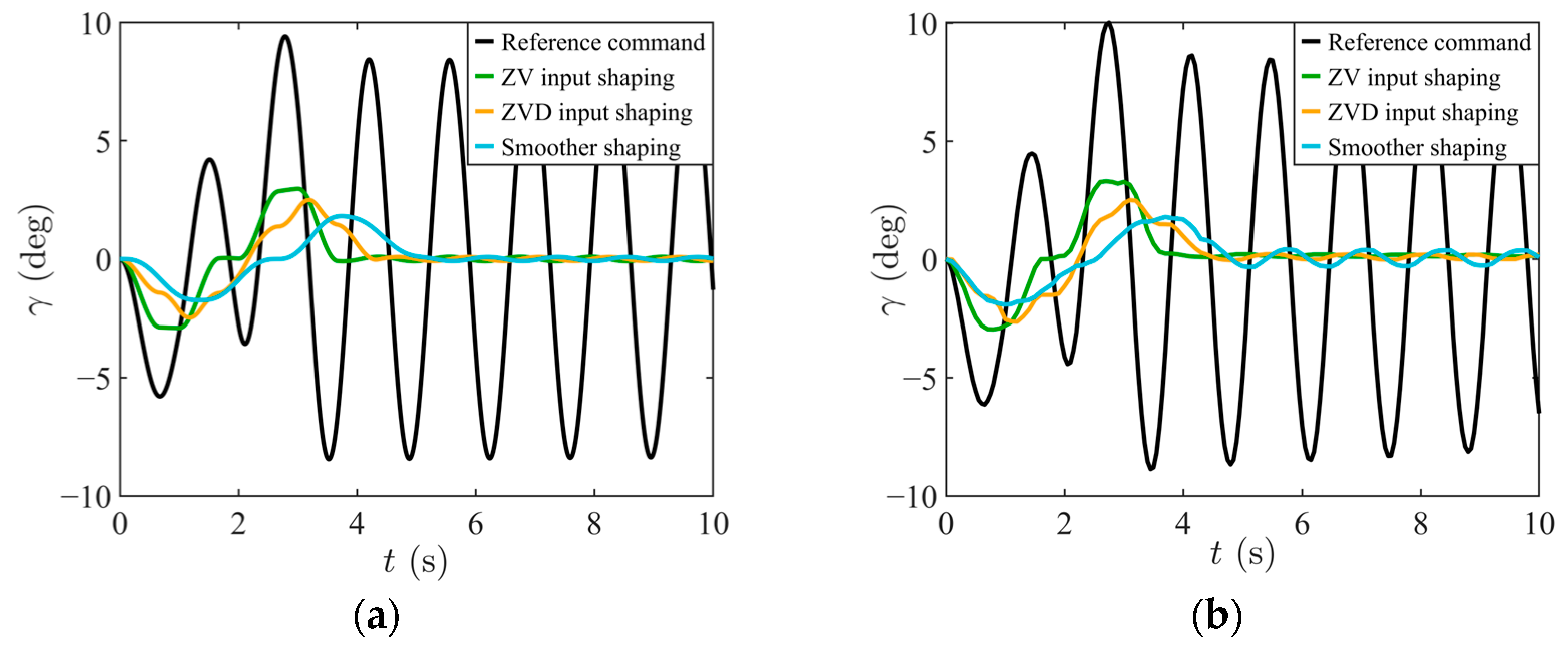

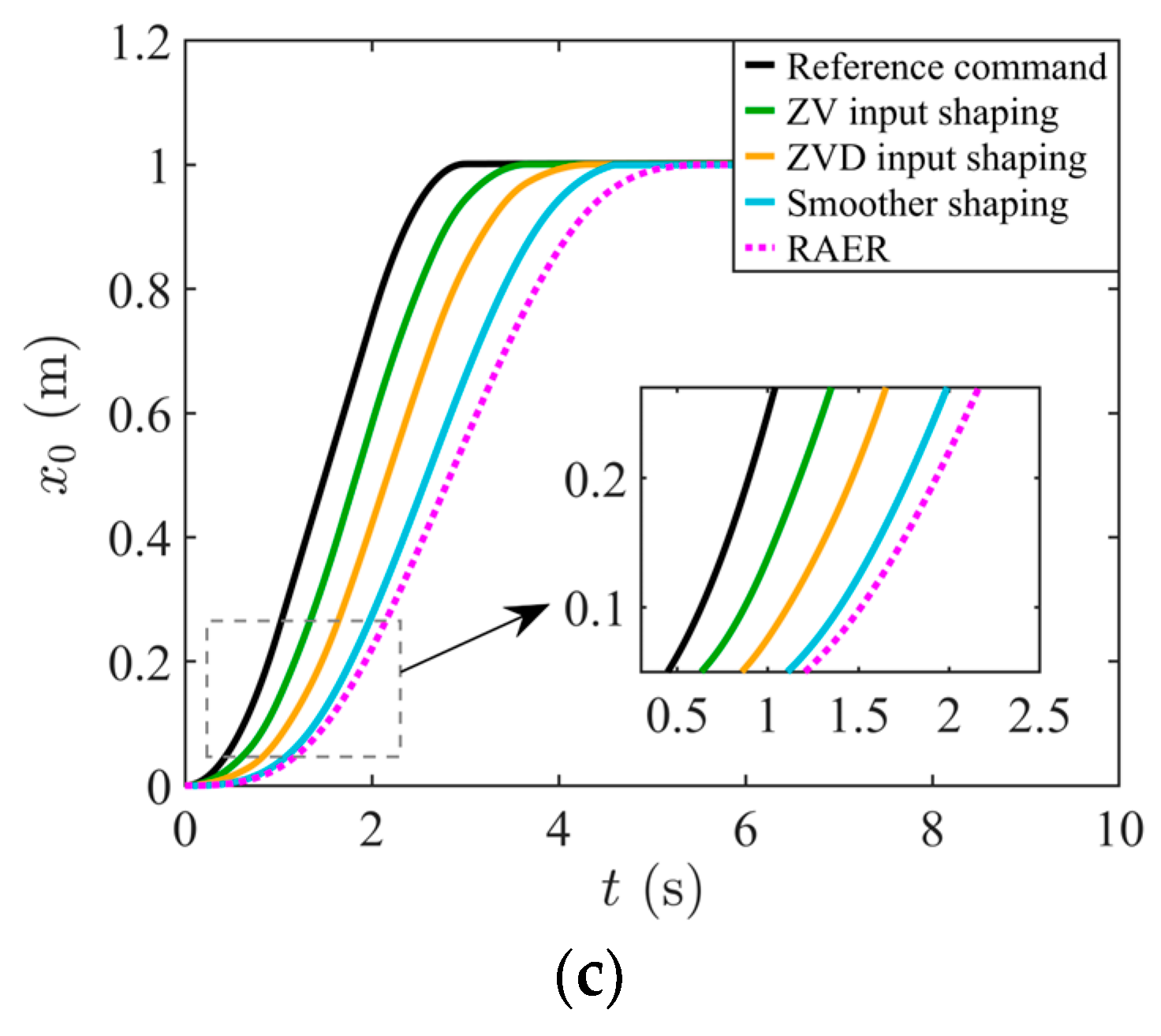
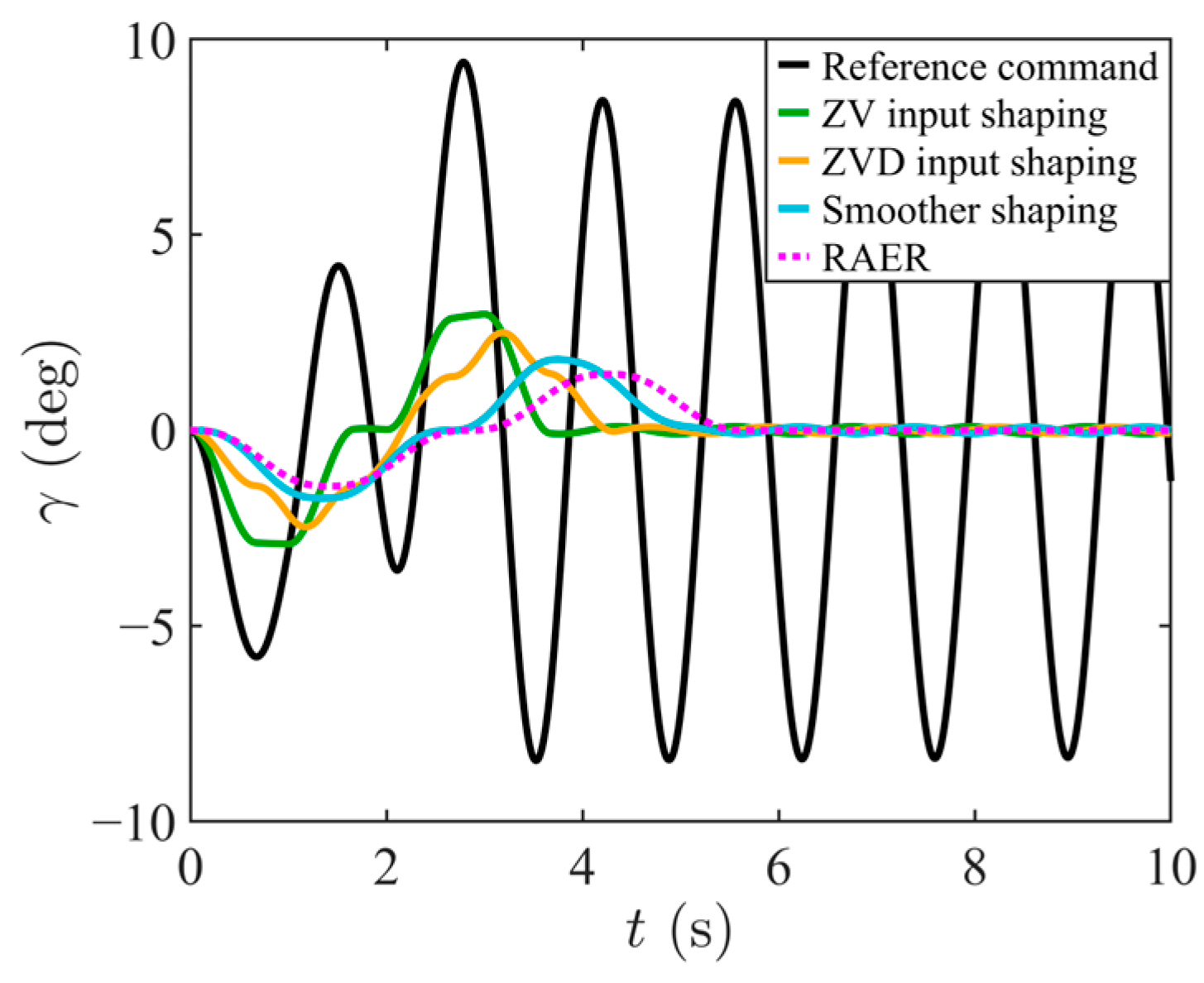
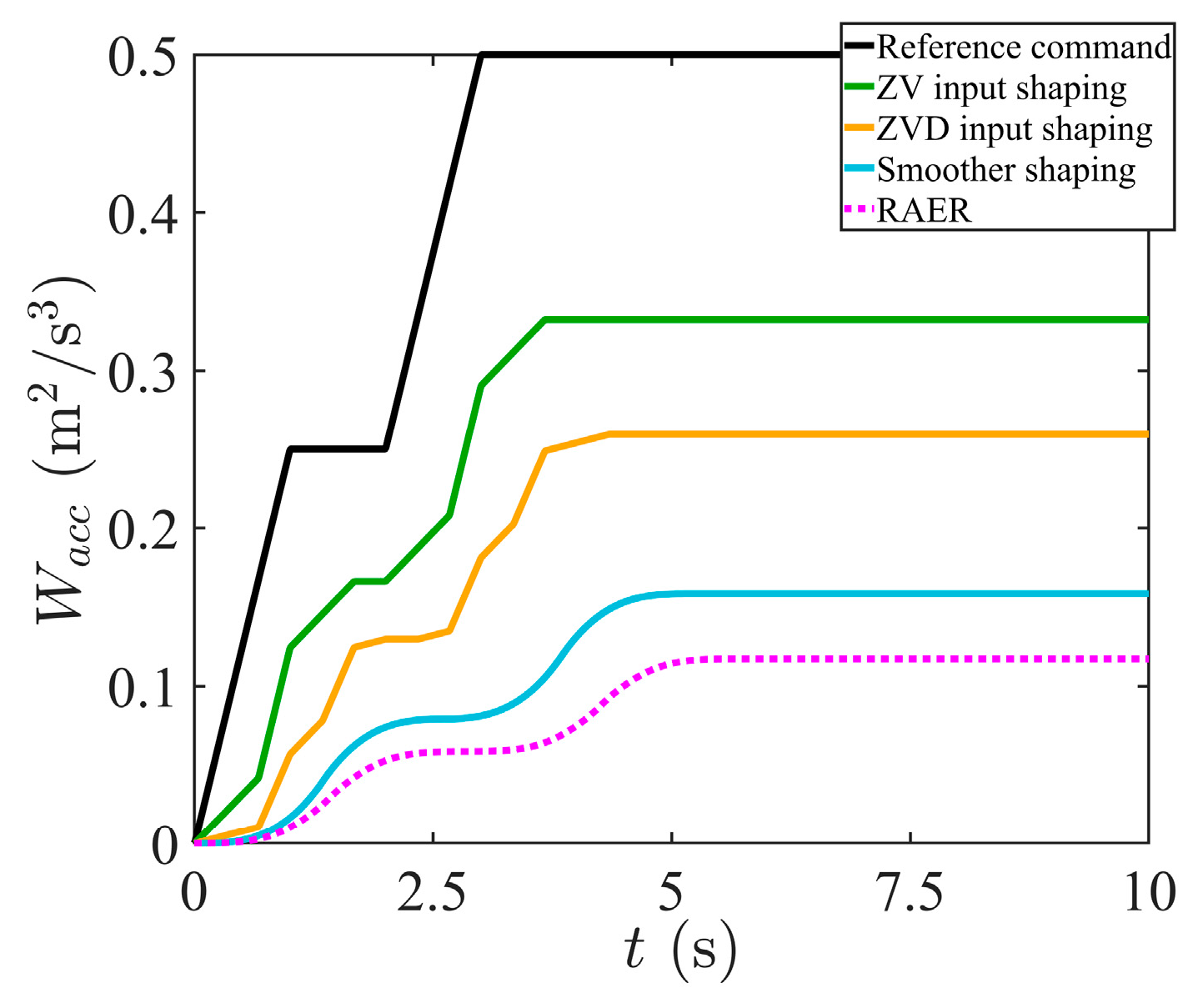
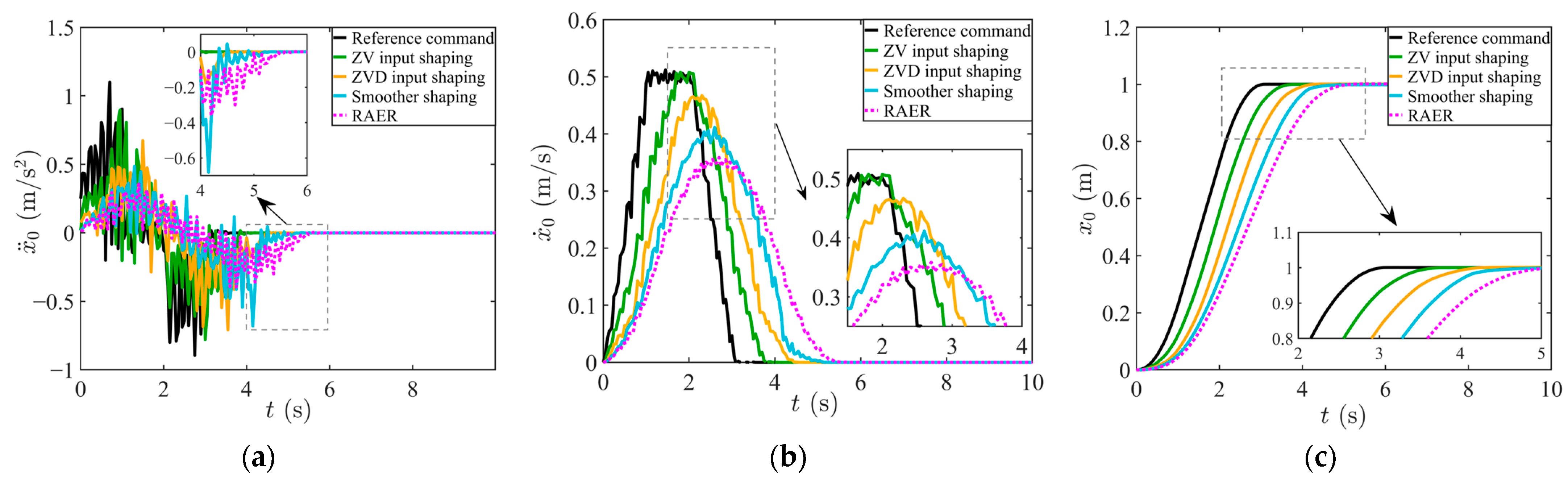
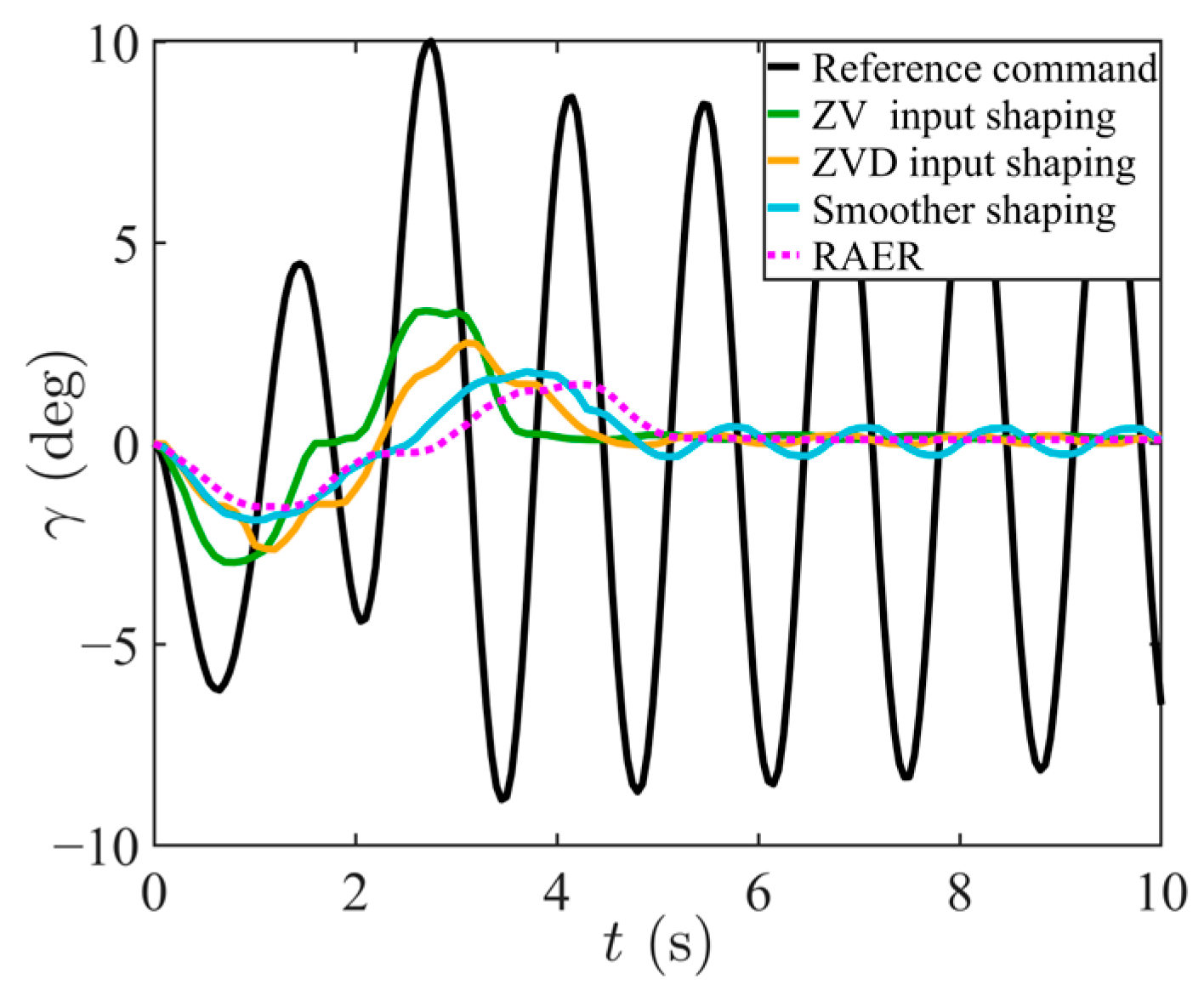
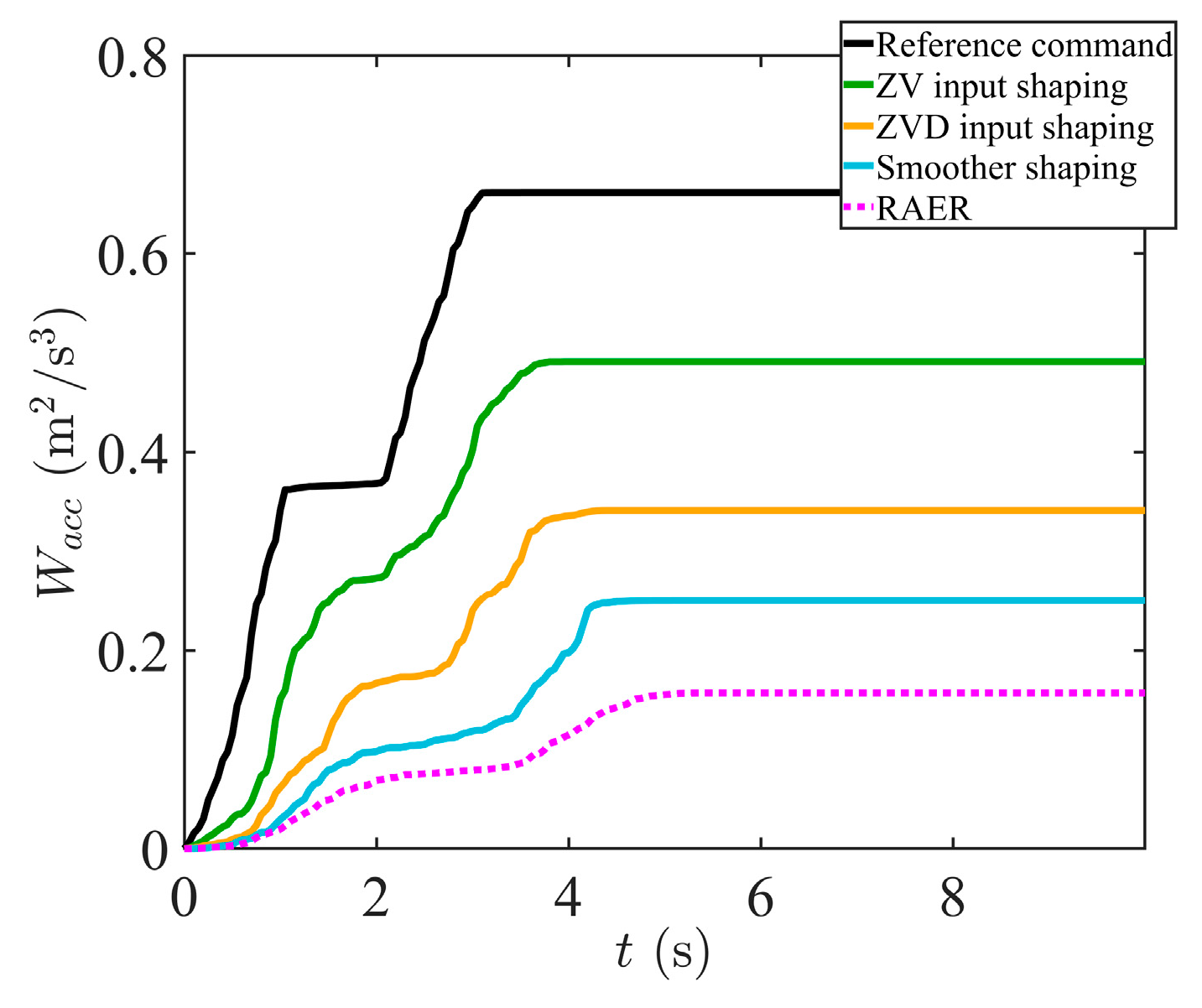
| Control Methods | (deg) | (deg) | (s) | (m/s) | (m/s2) | (m2/s3) |
|---|---|---|---|---|---|---|
| Reference common | 9.42 | 8.45 | 2.93 | 0.50 | 0.50 | 0.50 |
| ZV input shaping | 2.97 | 0.10 | 3.59 | 0.50 | 0.50 | 0.33 |
| ZVD input shaping | 2.49 | 0.03 | 4.26 | 0.46 | 0.38 | 0.26 |
| Smoother shaping | 1.81 | 0.08 | 4.60 | 0.40 | 0.30 | 0.16 |
| RAER | 1.43 | 0 | 5.58 | 0.35 | 0.25 | 0.12 |
| Control Methods | (deg) | (deg) | (s) | (m/s) | (m/s2) | (m2/s3) |
|---|---|---|---|---|---|---|
| Reference Command | 10.00 | 8.96 | 3.05 | 0.51 | 1.10 | 0.66 |
| ZV input shaping | 3.30 | 0.31 | 3.90 | 0.50 | 0.89 | 0.49 |
| ZVD input shaping | 2.64 | 0.13 | 4.25 | 0.47 | 0.71 | 0.34 |
| Smoother shaping | 1.91 | 0.42 | 4.90 | 0.41 | 0.68 | 0.25 |
| RAER | 1.60 | 0.03 | 5.58 | 0.36 | 0.39 | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Wu, J.; Lei, Y.; Cui, Y.; Liu, Y.; Wan, L.; Li, G.; Long, C.; Zhang, Y.; Chen, Z. Nonlinear Dynamic Modeling of Flexible Cable in Overhead Bridge Crane and Trajectory Optimization Under Full-Constraint Conditions. Actuators 2025, 14, 513. https://doi.org/10.3390/act14110513
Yang G, Wu J, Lei Y, Cui Y, Liu Y, Wan L, Li G, Long C, Zhang Y, Chen Z. Nonlinear Dynamic Modeling of Flexible Cable in Overhead Bridge Crane and Trajectory Optimization Under Full-Constraint Conditions. Actuators. 2025; 14(11):513. https://doi.org/10.3390/act14110513
Chicago/Turabian StyleYang, Guangwei, Jiayang Wu, Yutian Lei, Yanan Cui, Yifei Liu, Lin Wan, Gang Li, Chunyan Long, Yonglong Zhang, and Zehua Chen. 2025. "Nonlinear Dynamic Modeling of Flexible Cable in Overhead Bridge Crane and Trajectory Optimization Under Full-Constraint Conditions" Actuators 14, no. 11: 513. https://doi.org/10.3390/act14110513
APA StyleYang, G., Wu, J., Lei, Y., Cui, Y., Liu, Y., Wan, L., Li, G., Long, C., Zhang, Y., & Chen, Z. (2025). Nonlinear Dynamic Modeling of Flexible Cable in Overhead Bridge Crane and Trajectory Optimization Under Full-Constraint Conditions. Actuators, 14(11), 513. https://doi.org/10.3390/act14110513






