Numerical Investigation of a Morphing Wing Section Controlled by Piezoelectric Patches
Abstract
1. Introduction
2. Materials and Methods
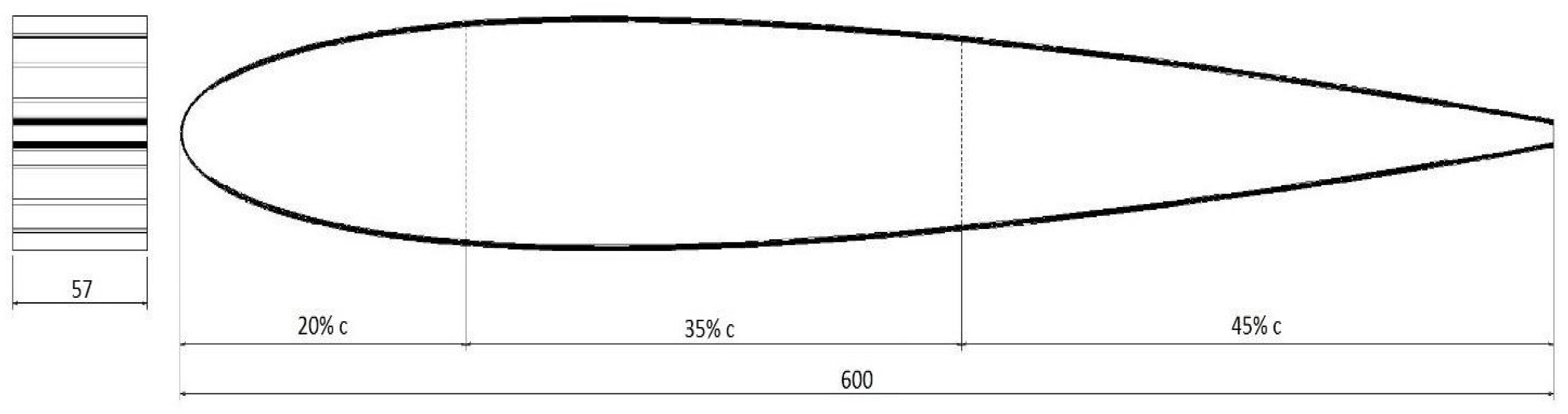
2.1. Numerical Model of a Piezo-Controlled NACA0012 Wing Section
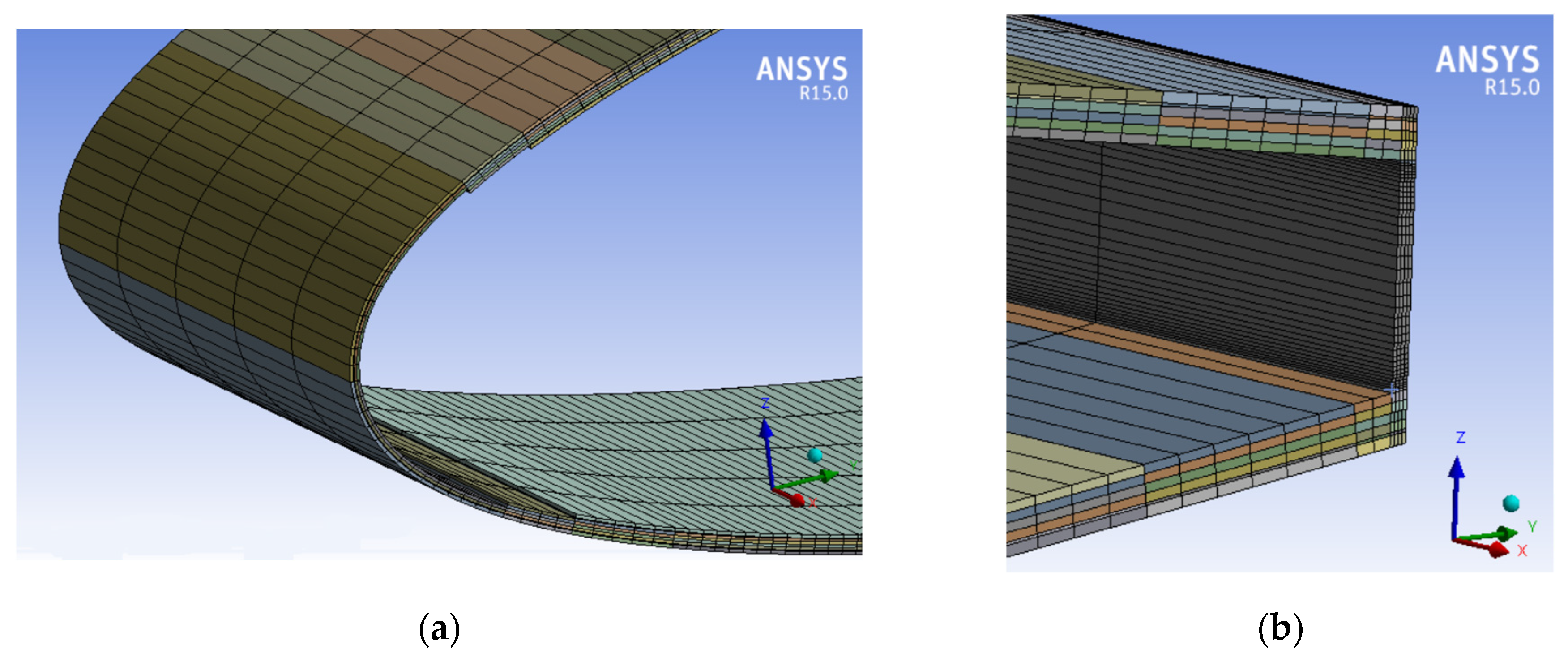
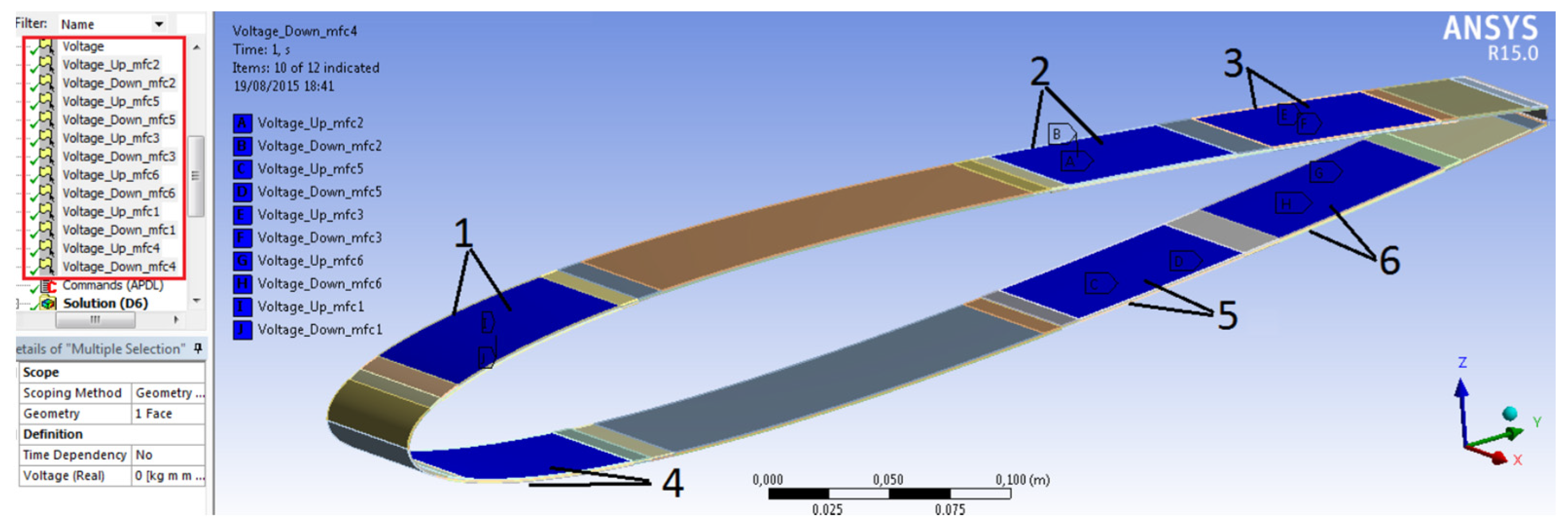
2.1.1. Finite Element Structural Model of the Wing Section
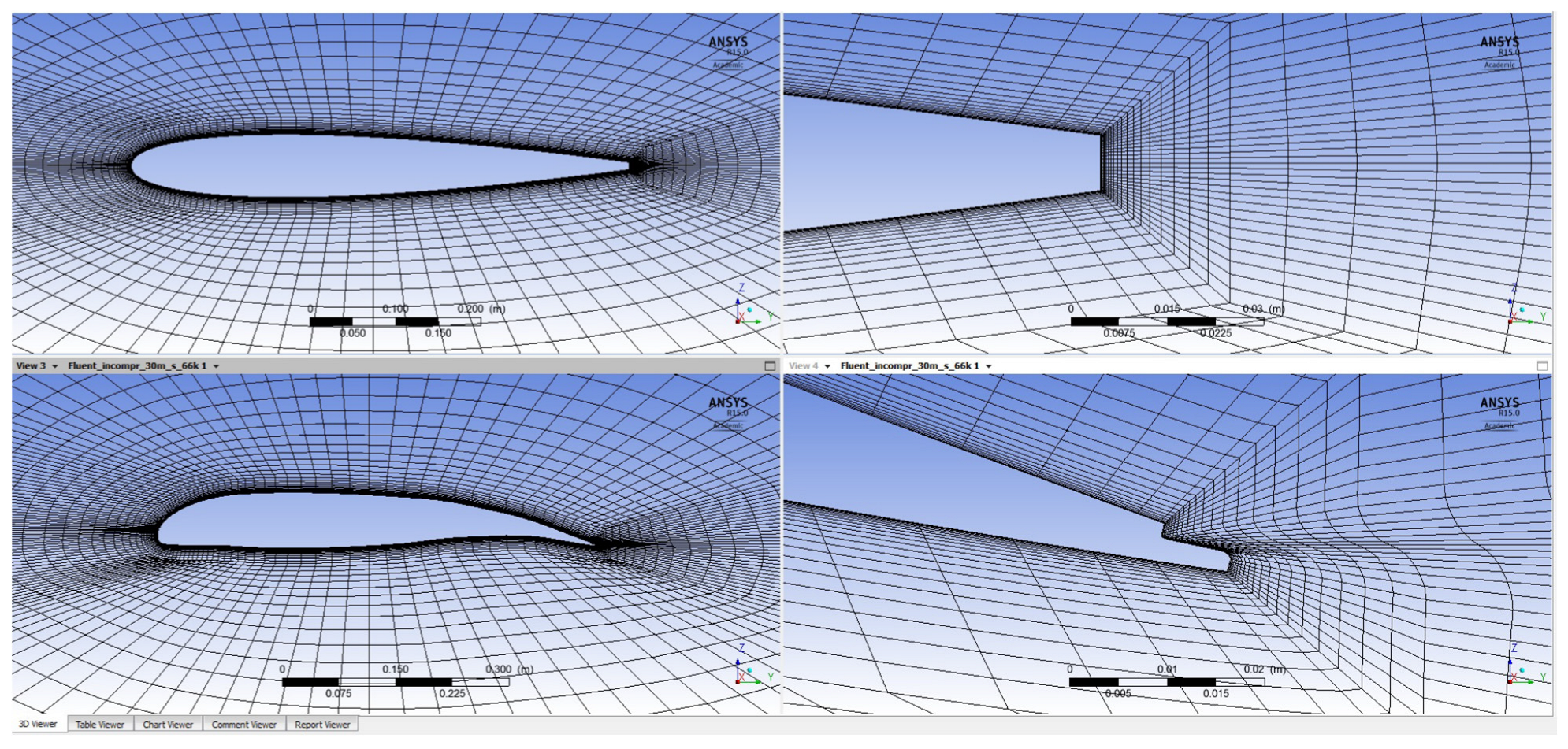
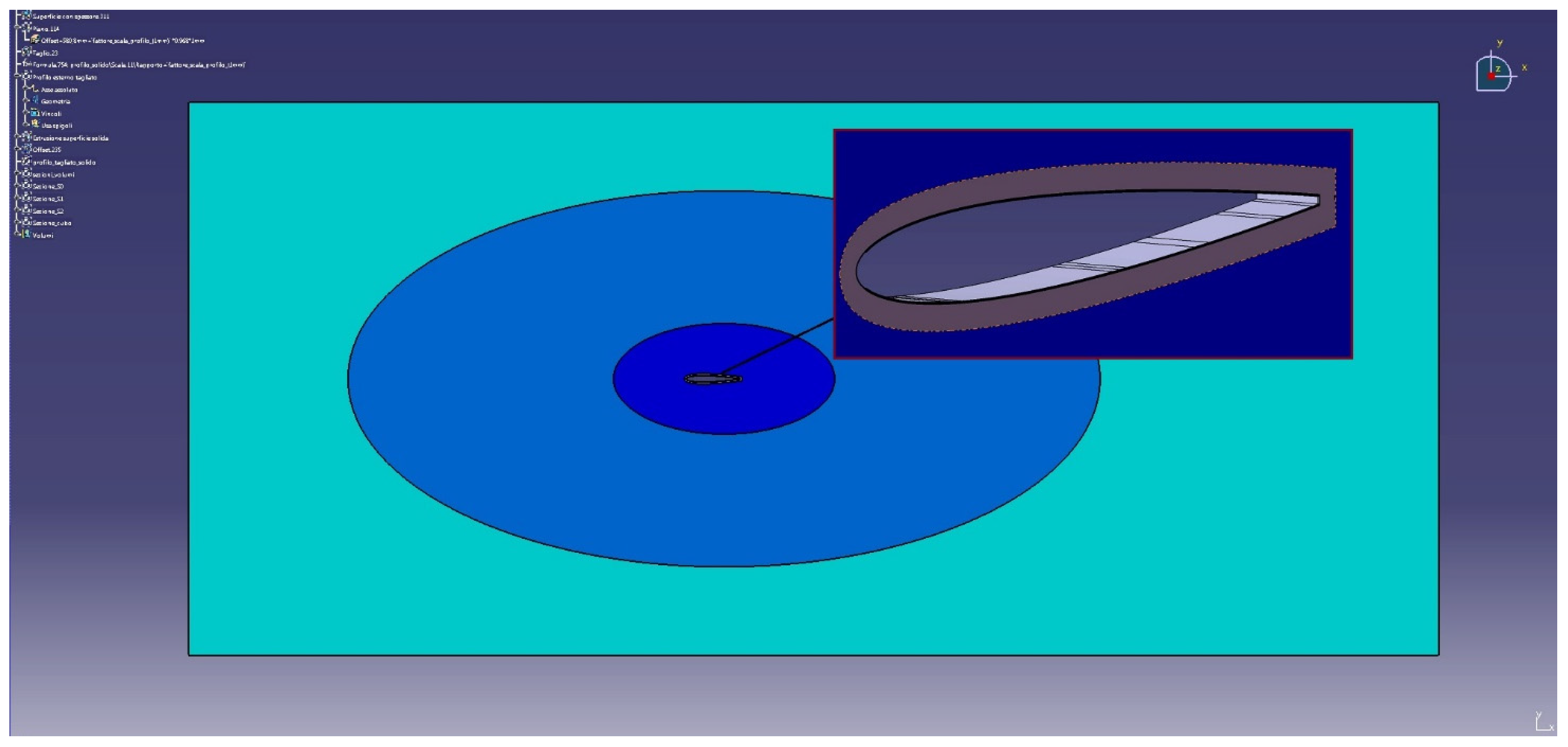
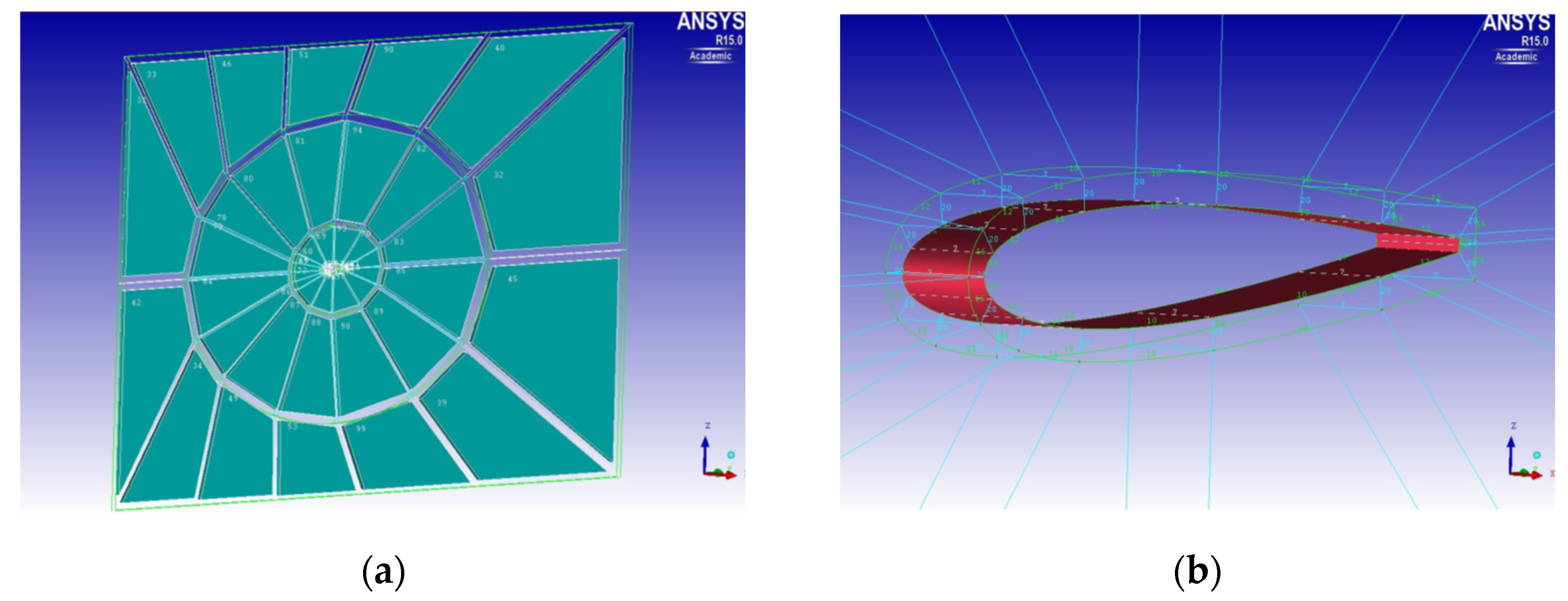
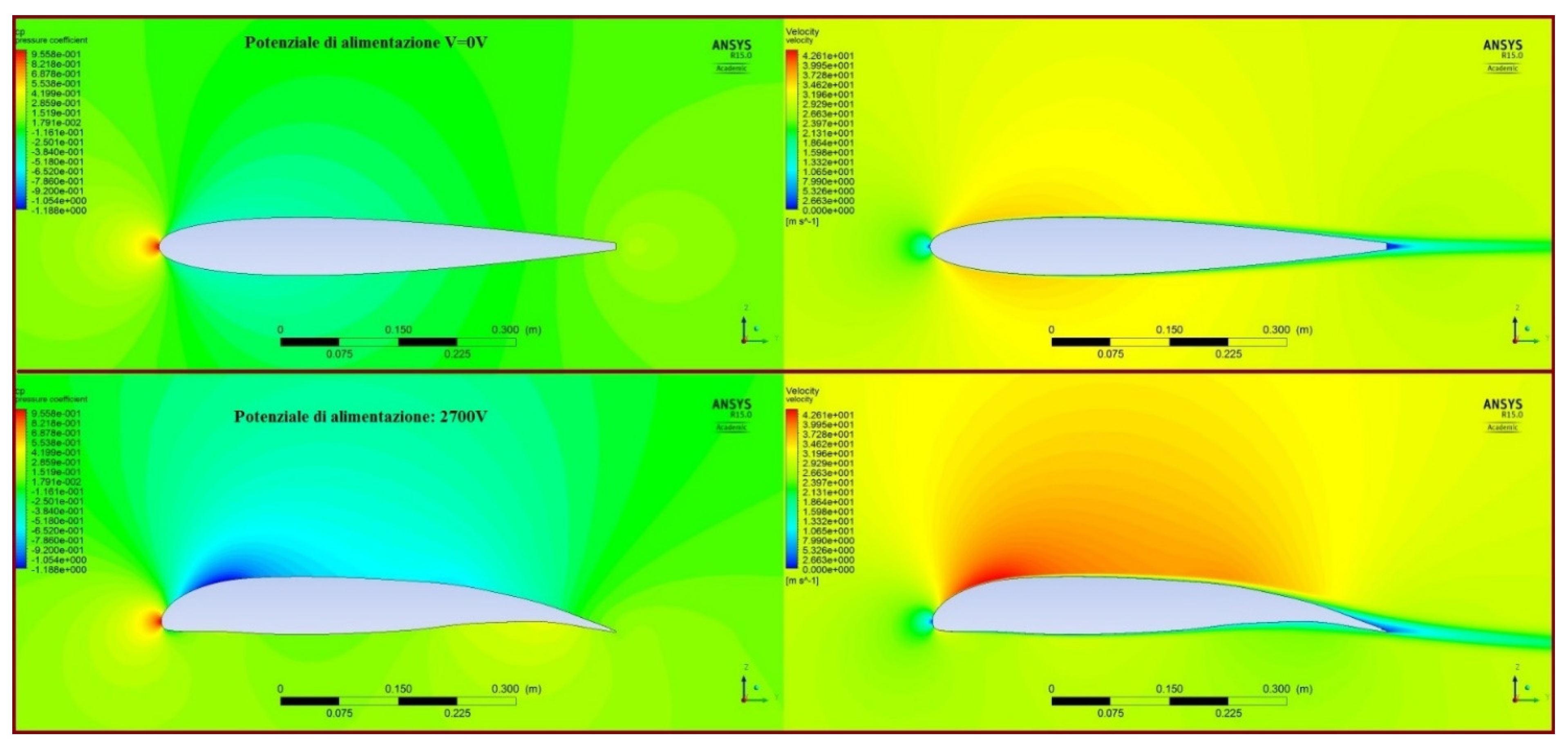
2.1.2. Fluid Dynamic Model of the Wing Section
3. Results
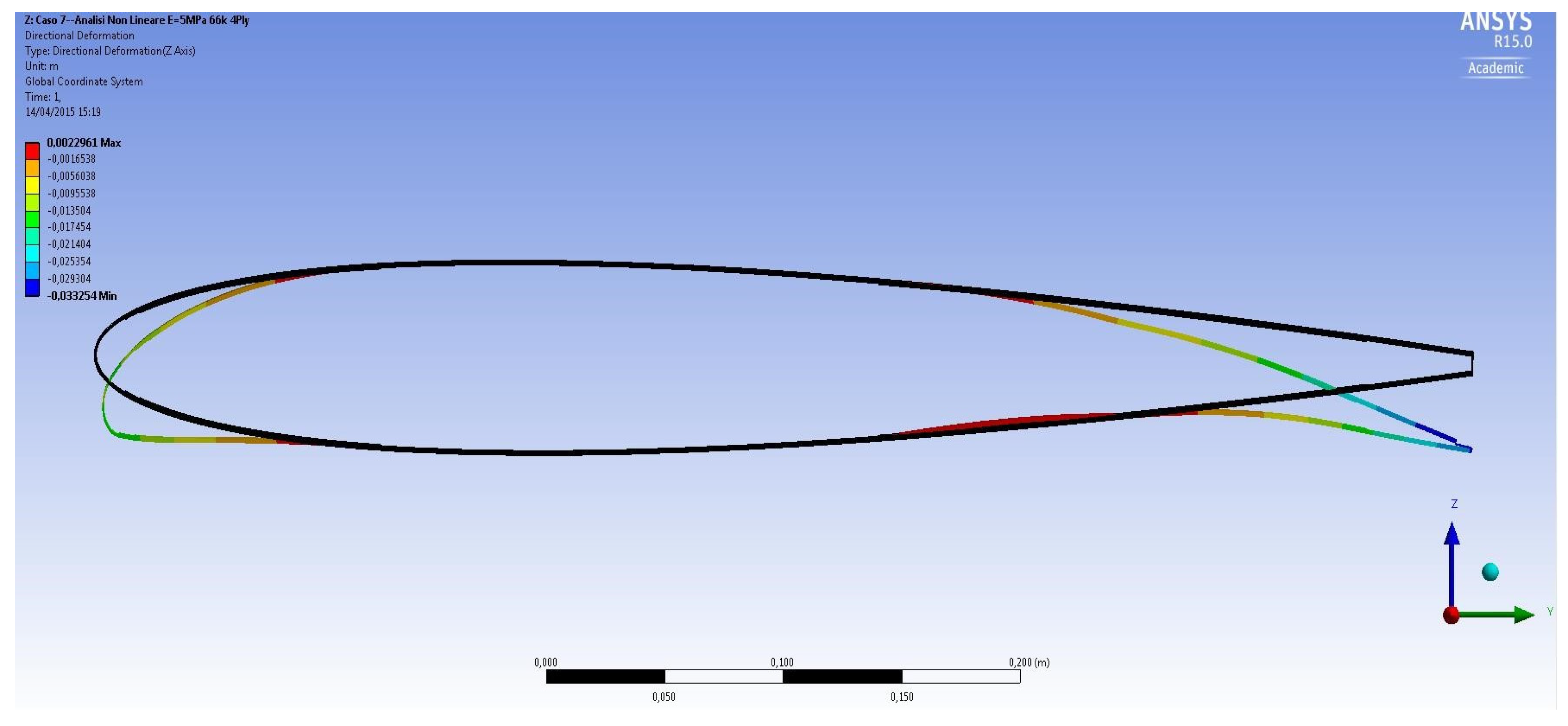
3.1. Deformations and Aerodynamic Coefficients of the Morphing Profile
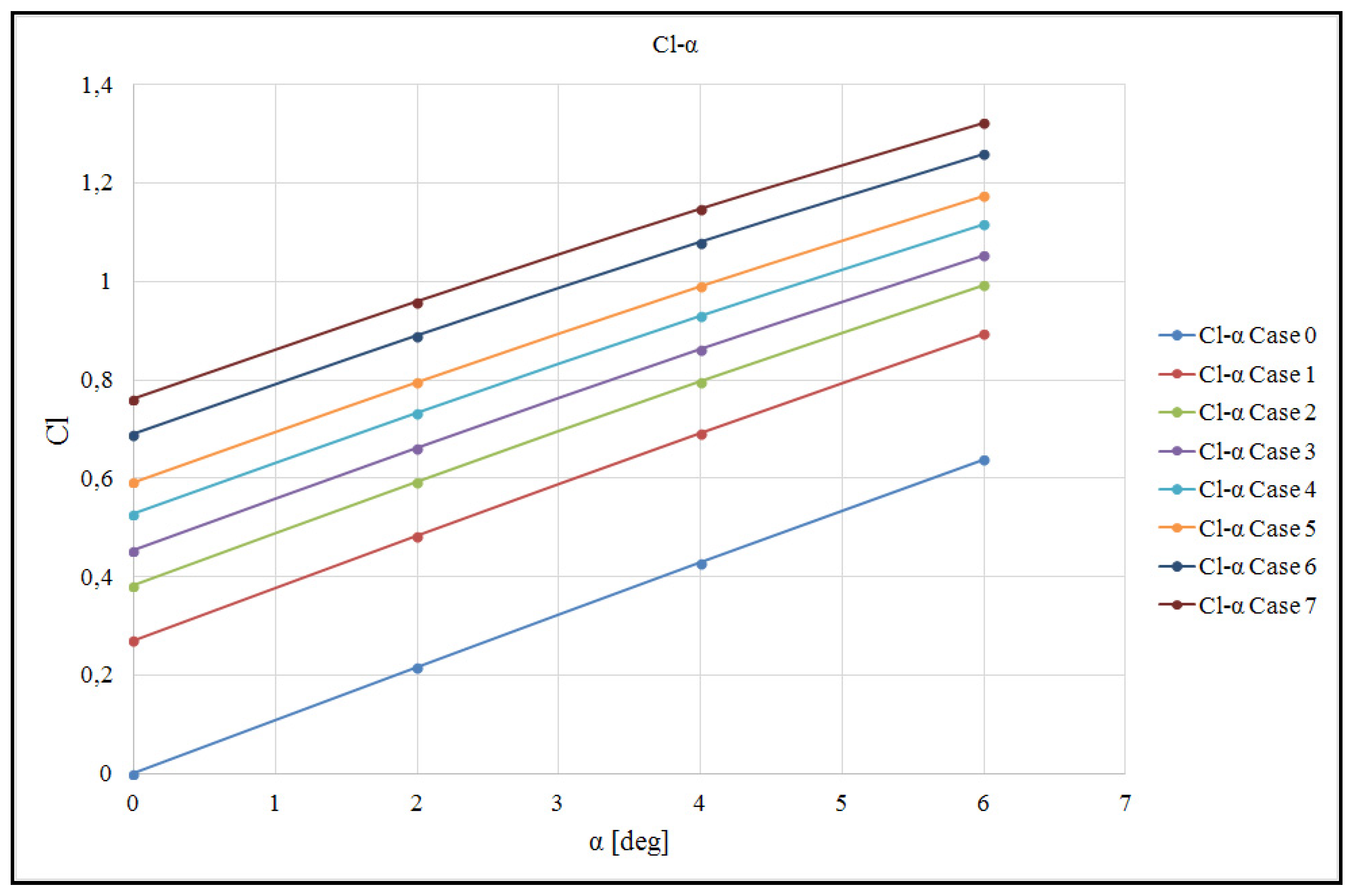
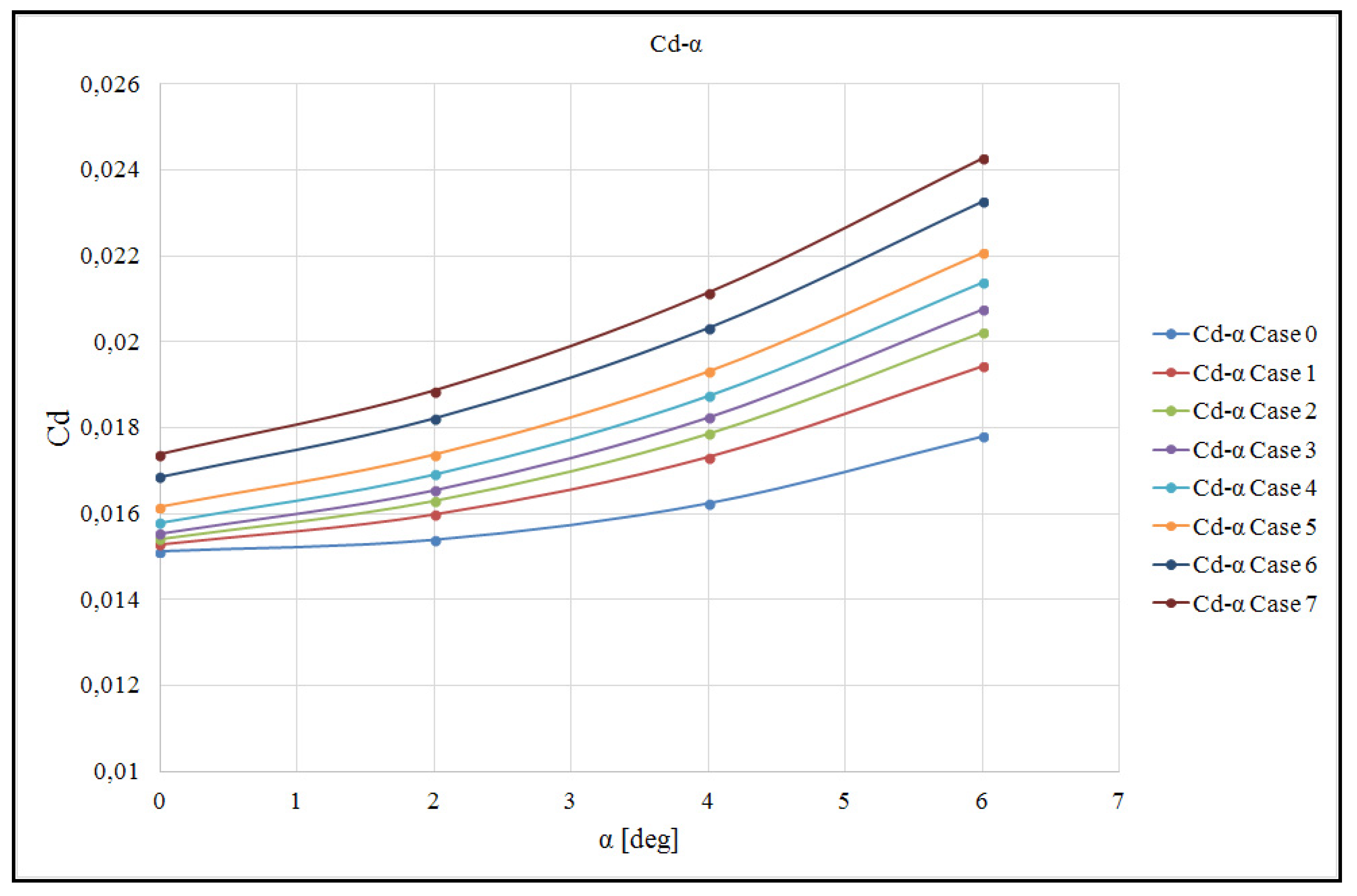
3.2. Comparison of Results in Terms of Calculated Aerodynamic Coefficients
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MFC | Macro Fiber Composite |
| FishBAC | Fish Bone Active Camber Concept |
| FSI | Fluid–Structure Interaction |
| EMC | Elastomeric Matrix Composite |
| SMA | Shape-Memory Alloy |
| UAV | Unmanned Aerial Vehicle |
| CFD | Computational Fluid Dynamics |
| TE | Trailing Edge |
| LE | Leading Edge |
References
- Kaygan, E. Aerodynamic Analysis of morphing winglets for improved commercial aircraft performance. J. Aviat. 2020, 4, 31–44. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A review of morphing aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Li, D.; Zhao, S.; Da Ronch, A.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P.; et al. A review of modelling and analysis of morphing wings. Prog. Aerosp. Sci. 2018, 100, 42–62. [Google Scholar] [CrossRef]
- Santos, P.; Sousa, J.; Gamboa, P. Variable-span wing development for improved flight performance. J. Intell. Mater. Syst. Struct. 2017, 28, 961–978. [Google Scholar] [CrossRef]
- Eguea, J.P.; Pereira Gouveia da Silva, G.; Martini Catalano, F. Fuel efficiency improvement on a business jet using a camber morphing winglet concept. Aeros. Sci. Tech. 2020, 96, 105542. [Google Scholar] [CrossRef]
- Weisshaar, T.A. Morphing aircraft systems: Historical perspectives and future challenges. J. Aircr. 2013, 50, 337–353. [Google Scholar] [CrossRef]
- FlexSys Inc. 2025. Available online: https://www.flxsys.com (accessed on 1 January 2025).
- Wlezien, R.W.; Homer, G.C.; McGowan, A.R.; Padula, S.L.; Scott, M.A.; Silcox, R.J.; Simpson, J.O. The aircraft morphing program. In Proceedings of the 39th Structures, Structural Dynamics, and Materials Conference and Exhibit, Long Beach, CA, USA, 20–23 April 1998; AIAA Paper 98-1927. Available online: https://ntrs.nasa.gov/citations/19980053567 (accessed on 6 September 2013).
- Concilio, A.; Dimino, I.; Lecce, L.; Pecora, R. Morphing Wing Technologies: Large Commercial Aircraft and Civil Helicopters; Butterworth-Heinemann, an Imprint of Elsevier: Oxford, UK, 2018; ISBN 978-0-08-100964-2. [Google Scholar]
- Parancheerivilakkathil, M.S.; Ajaj, R.M.; Khan, K.A. A compliant polymorphing wing for small UAVs. Chin. J. Aeronaut. 2020, 33, 2575–2588. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, J.; Zhang, W.; Gu, X.; Zhou, H. Design and applications of morphing aircraft and their structures. Front. Mech. Eng. 2023, 18, 34. [Google Scholar] [CrossRef]
- Jo, B.W.; Majid, T. Enhanced Range and Endurance Evaluation of a Camber Morphing Wing Aircraft. Biomimetics 2023, 8, 34. [Google Scholar] [CrossRef]
- Fasel, U.; Keidel, D.; Baumann, L.; Cavolina, G.; Eichenhofer, M.; Ermanni, P. Composite additive manufacturing of morphing aerospace structures. Manuf. Lett. 2020, 23, 85–88. [Google Scholar] [CrossRef]
- Majid, T.; Jo, B.W. Comparative aerodynamic performance analysis of camber morphing and conventional airfoils. Appl. Sci. 2021, 11, 10663. [Google Scholar] [CrossRef]
- Bishay, P.L.; Finden, R.; Recinos, S.; Alas, C.; Lopez, E.; Aslanpour, D.; Flores, D.; Gonzalez, E. Development of an SMA-based camber morphing UAV tail core design. Smart Mater. Struct. 2019, 28, 075024. [Google Scholar] [CrossRef]
- Fincham, J.H.S.; Friswell, M.I. Aerodynamic optimisation of a camber morphing aerofoil. Aerosp. Sci. Technol. 2015, 43, 245–255. [Google Scholar] [CrossRef]
- Yokozeki, T.; Sugiura, A.; Hirano, Y. Development and wind tunnel test of variable camber morphing wing. In Proceedings of the 22nd AIAA/ASME/AHS Adaptive Structures Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- Woods, B.K.S.; Friswell, M.I. Preliminary investigation of a Fishbone Active Camber concept. In Proceedings of the ASME 2012 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, SMASIS 2012, Stone Mountain, GA, USA, 19–21 September 2012. [Google Scholar] [CrossRef]
- Jo, B.W.; Majid, T. Aerodynamic analysis of camber morphing airfoils in transition via computational fluid dynamics. Biomimetics 2022, 7, 52. [Google Scholar] [CrossRef]
- Schlup, A.; Bishay, P.; Mclennan, T.; Barajas, C.; Talebian, B.; Thatcher, G.; Flores, R.; Perez-Norwood, J.; Torres, C.; Kibret, K.; et al. MataMorph 2: A new experimental UAV with twist-morphing wings and camber-morphing tail stabilizers. In Proceedings of the AIAA SciTech Forum, Virtual Event, 19–21 January 2021. [Google Scholar] [CrossRef]
- Thill, C.; Downsborough, J.D.; Lai, S.J.; Bond, I.P.; Jones, D.P. Aerodynamic study of corrugated skins for morphing wing applications. Aeronaut. J. 2010, 114, 237–244. [Google Scholar] [CrossRef]
- Ahmad, D.; Ajaj, R.M. Multiaxial mechanical characterization of latex skin for morphing wing application. Polym. Test. 2022, 106, 107408. [Google Scholar] [CrossRef]
- Wang, M.; Xu, M.; Shen, X.; Lai, Z.; Zhao, Y.; Wang, C.; Hu, Q. Conceptual design and analysis of a trans-domain aircraft based on the camber morphing wing. Machines 2025, 13, 428. [Google Scholar] [CrossRef]
- Kumar, T.R.S.; Venugopal, S.; Ramakrishnananda, B.; Vijay, S. Aerodynamic performance estimation of camber morphing airfoils for small unmanned aerial vehicle. J. Aerosp. Technol. Manag. 2020, 12, e1420. [Google Scholar] [CrossRef]
- Woods, B.K.; Bilgen, O.; Friswell, M.I. Wind tunnel testing of the fish bone active camber morphing concept. J. Intell. Mater. Syst. Struct. 2014, 25, 772–785. [Google Scholar] [CrossRef]
- Ozbek, E.; Ekici, S.; Karakoc, T.H. Unleashing the Potential of Morphing Wings: A Novel Cost Effective Morphing Method for UAV Surfaces, Rear Spar Articulated Wing Camber. Drones 2023, 7, 379. [Google Scholar] [CrossRef]
- Albuquerque, P.F.; Gamboa, P.V.; Silvestre, M.A. Mission-based multidisciplinary aircraft design optimization methodology tailored for adaptive technologies. J. Aircr. 2018, 55, 755–770. [Google Scholar] [CrossRef]
- Dharmdas, A.; Patil, A.Y.; Baig, A.; Hosmani, O.Z.; Mathad, S.N.; Patil, M.B.; Kumar, R.; Kotturshettar, B.B.; Fattah, I.M.R. An Experimental and Simulation Study of the Active Camber Morphing Concept on Airfoils Using Bio-Inspired Structures. Biomimetics 2023, 8, 251. [Google Scholar] [CrossRef]
- Li, S.; Chen, X.; Wang, Z.; Liang, Y. Ground Strength Test Technique of Variable-Camber Wing Leading Edge. Biomimetics 2024, 9, 467. [Google Scholar] [CrossRef]
- Prabhakar, M.; Murugan, S. Dynamic stability and response of morphing wing structure with time-varying stiffness. Smart Mater. Struct. 2024, 33, 105024. [Google Scholar] [CrossRef]
- Grohmann, B.; Maucher, C.; Prunhuber, T.; Janker, P.; Dieterich, O.; Enenkl, B.; Bauer, M.; Ahci, E.; Altmikus, A.; Baier, H. Multidisciplinary Design and Optimization of Active Trailing Edge for Smart Helicopter Rotor Blade. Mech. Adv. Mater. Struct. 2008, 15, 307–324. [Google Scholar] [CrossRef]
- Wright, C.; Bilgen, O. Induced-Strain Actuators for Morphing of Multi-Element Airfoils. J. Aircr. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Chiarelli, M.R.; Binante, V.; Botturi, S.; Massai, A.; Kunzmann, J.; Colbertaldo, A.; Romano, D.G. On the Active Deformations of Hybrid Specimens. Aircr. Eng. Aerosp. Technol. Int. J. 2016, 88, 676–687. [Google Scholar] [CrossRef]
- Di Rito, G.; Luciano, B.; Chiarelli, M.R.; Galatolo, R. Condition monitoring of a morphing laminate with MFC piezoelectric patches via model-based approach. In Proceedings of the 2019 IEEE International Workshop on Metrology for AeroSpace, MetroAeroSpace 2019, Torino, Italy, 19–21 June 2019. [Google Scholar] [CrossRef]
- Di Rito, G.; Chiarelli, M.R.; Luciano, B. Dynamic Modelling and Experimental Characterization of a Self-Powered Structural Health-Monitoring System with MFC Piezoelectric Patches. Sensors 2020, 20, 950. [Google Scholar] [CrossRef]
- Doddahosahalli Nagarajaiah, N.K.; Neri, G.; Chaliyath, A.J.; Chiarelli, M.R.; Di Rito, G. Use of piezoelectric actuators for thrust vectoring in ion engines: Conceptual design and preliminary analysis. In Proceedings of the 2020 IEEE International Workshop on Metrology for AeroSpace, MetroAeroSpace 2020, Virtual Event, 22–24 June 2020. [Google Scholar] [CrossRef]
- Chiarelli, M.R.; Di Rito, G.; Luciano, B.; Miralles Irles, I.J.; Liberatori, E.; Bancallari, L. Use of piezoelectric patches in Health Usage and Monitoring Systems: A preliminary assessment. In Proceedings of the 2022 IEEE International Workshop on Metrology for AeroSpace, MetroAeroSpace 2022, Pisa, Italy, 27–29 June 2022. [Google Scholar] [CrossRef]
- Werner, J.M.; Engelmann, M.; Schmidt, M.; Titsch, C.; Dix, M.; Drossel, W.-G. Comparison of Structural Integrated Piezoceramics, Piezoelectric Patches and Strain Gauges for Condition Monitoring. Sensors 2022, 22, 8847. [Google Scholar] [CrossRef]
- Tommasino, D.; Moro, F.; Bernay, B.; De Lumley Woodyear, T.; de Pablo Corona, E.; Doria, A. Vibration Energy Harvesting by Means of Piezoelectric Patches: Application to Aircrafts. Sensors 2022, 22, 363. [Google Scholar] [CrossRef]
- Darleux, R.; Lossouarn, B.; Giorgio, I.; dell’Isola, F.; Deü, J.F. Electrical analogs of curved beams and application to piezoelectric network damping. Math. Mech. Solids 2022, 27, 578–601. [Google Scholar] [CrossRef]
- Chróścielewski, J.; Schmidt, R.; Eremeyev, V.A. Nonlinear finite element modeling of vibration control of plane rod-type structural members with integrated piezoelectric patches. Contin. Mech. Thermodyn. 2019, 31, 147–188. [Google Scholar] [CrossRef]
- He, Z.; Fan, S.; Wang, C.; Li, S.; Zhao, Y.; Shen, X.; Zhang, J. Conceptual Design of Compliant Structures for Morphing Wingtips Using Single-Row Corrugated Panels. Aerospace 2024, 11, 682. [Google Scholar] [CrossRef]
- Ameduri, S.; Galasso, B.; Noviello, M.C.; Dimino, I.; Concilio, A.; Catalano, P.; D’Aniello, F.A.; Carossa, G.M.; Pinazo, L.; Derry, J.; et al. Design and Optimization of a Compliant Morphing Trailing Edge for High-Lift Generation. Appl. Sci. 2025, 15, 2529. [Google Scholar] [CrossRef]
- Abu Salem, K.; Palaia, G.; Quarta, A.A.; Chiarelli, M.R. Preliminary Analysis of the Stability and Controllability of a Box-Wing Aircraft Configuration. Aerospace 2023, 10, 874. [Google Scholar] [CrossRef]
- Abu Salem, K.; Palaia, G.; Chiarelli, M.R.; Bianchi, M. A Simulation Framework for Aircraft Take-Off Considering Ground Effect Aerodynamics in Conceptual Design. Aerospace 2023, 10, 459. [Google Scholar] [CrossRef]
- Ellis, J.D.; Balatti, D.; Khodaparast, H.H.; Jiffri, S.; Friswell, M.I. Active Hinged Wingtip Control for Reducing Wing Root Bending Moment. J. Aircr. 2025, 62, 847–856. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, H.; Guo, Y.; Wang, Y.; Deng, Z. Design and Aerodynamic Analysis of Leading Edge for Morphing Wing. J. Aircr. 2025, 62, 1–12. [Google Scholar] [CrossRef]
- Somnic, J.; Jo, B.W. Status and Challenges in Homogenization Methods for Lattice Materials. Materials 2022, 15, 605. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Wang, Z.; Yang, Y.; Lu, Y.; Shi, X.; Bao, P. Research on compliant wing design technology based on mechanical metamaterials. J. Phys. Conf. Ser. 2025, 2956, 012029. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Wang, C.; Qiu, J. The Application of Negative Poisson’s Ratio Metamaterials in the Optimization of a Variable Area Wing. Aerospace 2025, 12, 125. [Google Scholar] [CrossRef]
- Islam, M.A.; Rahman, A.; Saha, A.; Jo, B.W. Design, Implementation, and Test Flight of a Lightweight Camber Morphing Wing Aircraft. In Proceedings of the AIAA AVIATION FORUM and ASCEND 2025, Las Vegas, NV, USA, 21–25 July 2025. [Google Scholar] [CrossRef]
- Li, C.; Xiao, H.; Guo, H.; Tao, J.; Liu, C.; Yang, G. The mechanical characteristics analysis of the telescopic wing with adaptive driving mechanism. Adv. Mech. Eng. 2025, 17, 1–10. [Google Scholar] [CrossRef]
- Bilgen, O.; Friswell, M.I.; Kochersberger, K.B.; Inman, D.J. Surface actuated variable-camber and variable-twist morphing wings using piezocomposites. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Denver, CO, USA, 4–7 April 2011. [Google Scholar] [CrossRef][Green Version]
- Bilgen, O.; Friswell, M.I. Implementation of a Continuous-Inextensible-Surface Piezocomposite Airfoil. J. Aircr. 2013, 50, 508–518. [Google Scholar] [CrossRef]
- Bilgen, O.; Butt, L.M.; Day, S.R.; Sossi, C.A.; Weaver, J.P.; Wolek, A.; Mason, W.H.; Inman, D.J. A novel unmanned aircraft with solid-state control surfaces: Analysis and flight demonstration. J. Intell. Mater. Syst. Struct. 2013, 24, 147–167. [Google Scholar] [CrossRef]
- Bilgen, O.; Friswell, M.I. Piezoceramic composite actuators for a solid-state variable-camber wing. J. Intell. Mater. Syst. Struct. 2014, 25, 806–817. [Google Scholar] [CrossRef]
- Zhang, K.; Shah, B.; Bilgen, O. Low-Reynolds-Number Aerodynamic Characteristics of Airfoils with Piezocomposite Trailing Surfaces. AIAA J. 2022, 60, 2701–2706. [Google Scholar] [CrossRef]
- Chanzy, Q.; Keane, A.J. Analysis and experimental validation of morphing UAV wings. Aeronaut. J. 2018, 122, 390–408. [Google Scholar] [CrossRef]
- FutureWings Project, Wings of the Future, 7th Framework Programme of the European Union, Call Identifier: FP7-AAT-2012-RTD-L0, G.A. 335042, 1 June 2013–31 July 2015. Available online: https://cordis.europa.eu/project/id/335042 (accessed on 1 January 2016).
- Smart Material GmbH. Available online: https://smart-material.com/ (accessed on 31 July 2002).
- Baykar Piaggio Aerospace S.p.A. Available online: http://www.piaggioaerospace.it/ (accessed on 30 June 2025).
- IChrome. Available online: http://ichrome.com/ (accessed on 1 January 2009).
- SADE Project, Smart High Lift Devices for Next Generation Wings, 7th Framework Programme of the European Union, Call identifier: FP7-AAT-2011-RTD-1, G.A. 213442, 1 May 2008–31 October 2012. Available online: https://cordis.europa.eu/project/id/213442 (accessed on 1 January 2013).
- NOVEMOR Project, Novel Air Vehicles Configurations: From Fluttering Wings to Morphing Flight, 7th Framework Programme of the European Union, Call identifier: FP7-AAT-2011-RTD-1, G.A. 285395, 1 September 2011–28 February 2015. Available online: https://cordis.europa.eu/project/id/285395 (accessed on 1 January 2016).
- Vasista, S.; De Gaspari, A.; Ricci, S.; Riemenschneider, J.; Monner, H.P.; van de Kamp, B. Compliant structures-based wing and wingtip morphing devices. Aircr. Eng. Aerosp.Technol. Int. J. 2016, 88, 311–330. [Google Scholar] [CrossRef]
- SARISTU Project, Smart Intelligent Aircraft Structures, 7th Framework Programme of the European Union, Call identifier: FP7-AAT-2011-RTD-1, G.A. 284562, 1 September 2011–31 August 2015. Available online: https://cordis.europa.eu/project/id/284562 (accessed on 1 January 2016).
- Yang, F.; Xiao, H.; Yang, G.; Guo, H.; Liu, R.; Deng, Z. Large Deflection Model and Optimal Design for a Morphing Wing Leading-Edge Skin. J. Aircr. 2024, 61, 1–11. [Google Scholar] [CrossRef]
- Trotec Laser GmbH. Cutting Technique for Bending Applications. 2025. Available online: https://www.troteclaser.com/en/helpcenter/materials/application-techniques/bending-technique (accessed on 1 January 2025).
- ANSYS Workbench User’s Guide, Release 15.0, November 2013. Available online: https://www.ansys.com (accessed on 1 November 2013).
- Giani, L.; Botturi, S. Numerical Study of a Morphing Wing Activated by Means of Piezoelectric Patches. Master’s Thesis, Università di Pisa, Pisa, Italy, 2015. Available online: https://etd.adm.unipi.it/theses/available/etd-09102015-175331/ (accessed on 29 September 2015).
- CATIA V5R20, 2002–2025 Dassault Systèmes. Available online: https://www.3ds.com/products/catia/catia-v5 (accessed on 1 January 2002).
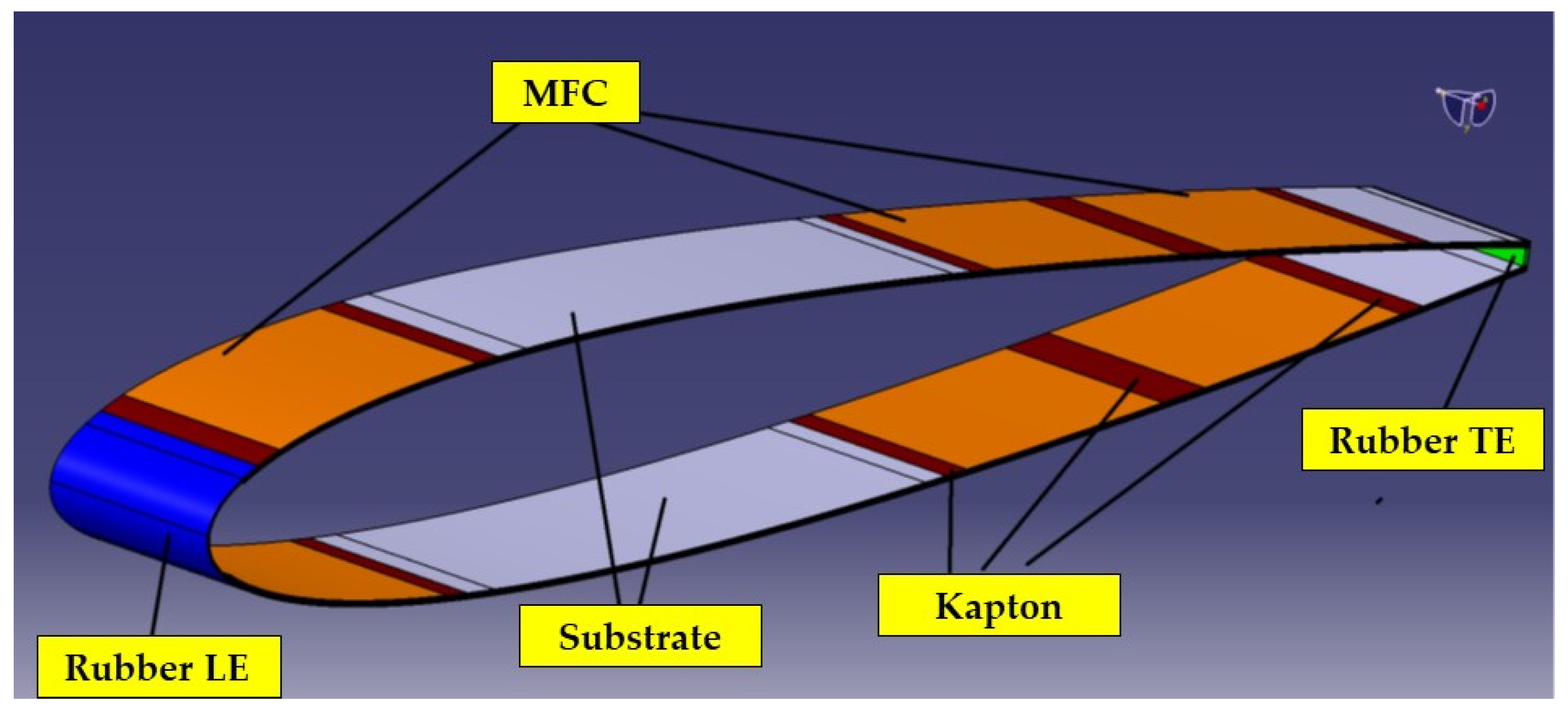

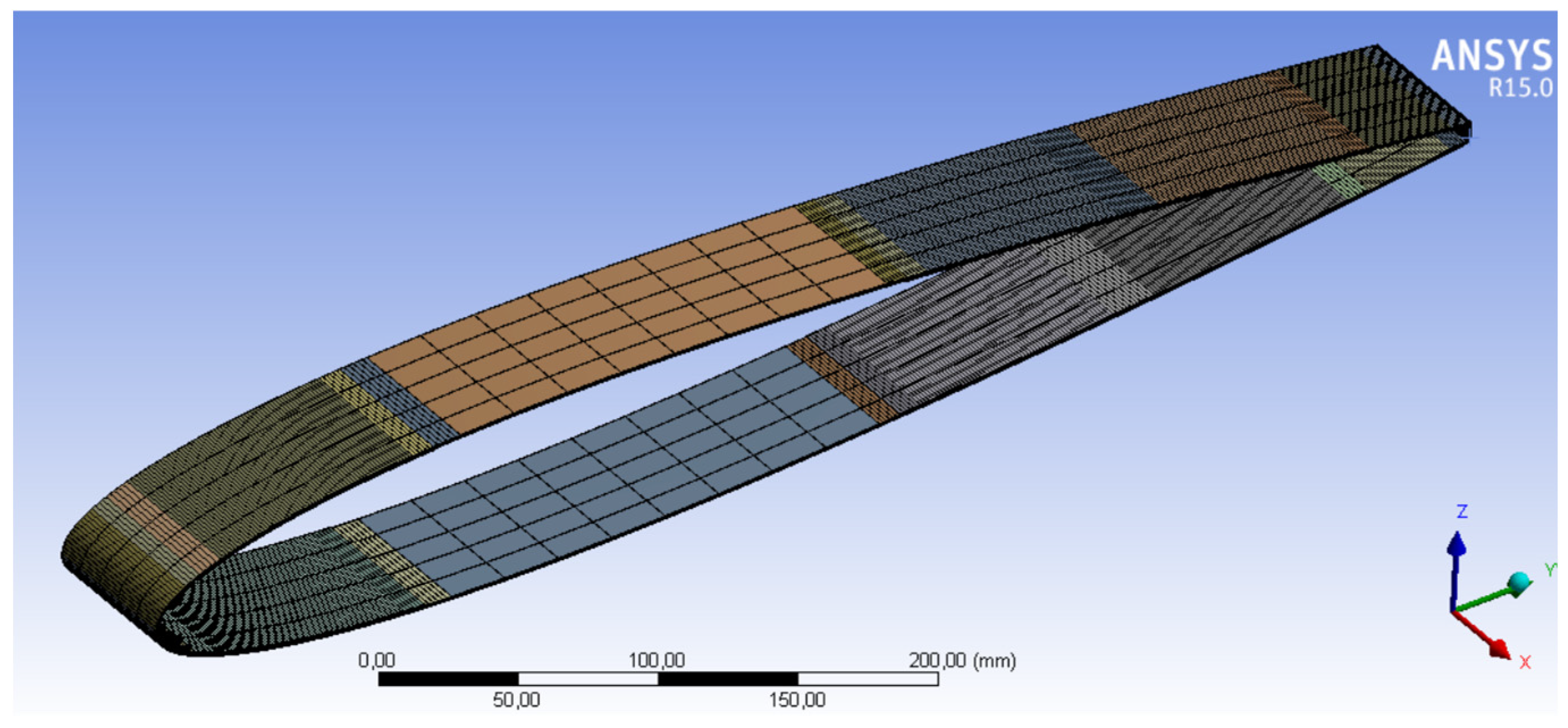





| Material | Thickness [mm] |
|---|---|
| MFC | 0.3 |
| Resin | 0.075 |
| Graphite/Epoxy | 1 (4 × 0.25) |
| Kapton | 0.3 |
| Rubber TE | 0.875 |
| Rubber LE | 0.5 |
| Engineering Constant | Substrate Graphite/Epoxy | Rubber TE | Resin | MFC | Kapton | Rubber LE |
|---|---|---|---|---|---|---|
| E1 [GPa] | 67.07 | 5 × 10−3 | 10 | 30.34 | 2.5 | 0.8 |
| E2 [GPa] | 67.07 | 15.86 | ||||
| E3 [GPa] | 67.07 | 15.86 | ||||
| ν12 | 0.042 | 0.34 | 0.31 | 0.34 | 0.4 | |
| ν13 | 0.042 | 0.16 | ||||
| ν23 | 0.042 | 0.16 | ||||
| G12 [GPa] | 4.78 | 5.51 | ||||
| G13 [GPa] | 4.78 | 5.51 | ||||
| G23 [GPa] | 4.78 | 5.51 | ||||
| C10 = C01 [Pa] | 416,670 | |||||
| Dielectric [F/m] | ε = 1.64 × 10−8 | |||||
| Piezoelectric [m/V] | d31 = −4.6 × 10−10 |
| Case | Patches | Voltage [V] |
|---|---|---|
| 0 | MFC 1/2/3 | 0/0 |
| MFC 4/5/6 | 0/0 | |
| 1 | MFC 1/2/3 | 600/−200 |
| MFC 4/5/6 | 600/−200 | |
| 2 | MFC 1/2/3 | 900/−300 |
| MFC 4/5/6 | 900/−300 | |
| 3 | MFC 1/2/3 | 1200/−400 |
| MFC 4/5/6 | 1200/−400 | |
| 4 | MFC 1/2/3 | 1800/−600 |
| MFC 4/5/6 | 1800/−600 | |
| 5 | MFC 1/2/3 | 2400/−800 |
| MFC 4/5/6 | 2400/−800 | |
| 6 | MFC 1/2/3 | 2700/−900 |
| MFC 4/5/6 | 3300/−1100 | |
| 7 | MFC 1/2/3 | 2700/−900 |
| MFC 4/5/6 | 3900/−1300 |
| [14] | Present Results | [14] | Present Results | [14] | Present Results | |
|---|---|---|---|---|---|---|
| Basic Airfoil: NACA 0012 | Flap | Realistic Voltage | Flap | Realistic Voltage | ||
| Figures 7 and 8 | Figure 15 | Figure 8 | Figure 15 | Figure 8 | Figure 15 | |
| Re | 77,000 | 1,200,000 | 77,000 | 1,200,000 | 77,000 | 1,200,000 |
| α [°] | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 | 4.0 |
| β [°] | 4.5 | 9.5 | ||||
| Case (Table 3) | 1 | 3 | ||||
| Cl | 0.4 | 0.42 | 0.67 | 0.70 | 0.89 | 0.86 |
| [14] | Present Results | [14] | Present Results | |
|---|---|---|---|---|
| Morphing | Realistic Voltage | Morphing | Hypothetical Voltage | |
| Figure 10 | Figure 15 | Figure 10 | Figure 15 | |
| Re | 77,000 | 1,200,000 | 77,000 | 1,200,000 |
| α [°] | 4.0 | 4.0 | 4.0 | 4.0 |
| Airfoil | 5412 | 6412 | ||
| Case (Table 3) | 3 | 4 | ||
| Cl | 0.86 | 0.86 | 0.93 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiarelli, M.R.; Binante, V.; Bonomo, S.; Botturi, S.; Giani, L.; Kunzmann, J.; Cozzolino, A.; Romano, D.G. Numerical Investigation of a Morphing Wing Section Controlled by Piezoelectric Patches. Actuators 2025, 14, 499. https://doi.org/10.3390/act14100499
Chiarelli MR, Binante V, Bonomo S, Botturi S, Giani L, Kunzmann J, Cozzolino A, Romano DG. Numerical Investigation of a Morphing Wing Section Controlled by Piezoelectric Patches. Actuators. 2025; 14(10):499. https://doi.org/10.3390/act14100499
Chicago/Turabian StyleChiarelli, Mario Rosario, Vincenzo Binante, Salvatore Bonomo, Stefano Botturi, Luca Giani, Jan Kunzmann, Aniello Cozzolino, and Diego Giuseppe Romano. 2025. "Numerical Investigation of a Morphing Wing Section Controlled by Piezoelectric Patches" Actuators 14, no. 10: 499. https://doi.org/10.3390/act14100499
APA StyleChiarelli, M. R., Binante, V., Bonomo, S., Botturi, S., Giani, L., Kunzmann, J., Cozzolino, A., & Romano, D. G. (2025). Numerical Investigation of a Morphing Wing Section Controlled by Piezoelectric Patches. Actuators, 14(10), 499. https://doi.org/10.3390/act14100499