Abstract
This article presents a method for the optimal design of actuators for electric vessels that utilize DC motors. Typically, these vessels are small, unmanned craft that can be Unmanned Surface Vessels (USVs) or Unmanned Underwater Vessels (UUVs). The propulsion systems for these vessels are currently hindered because most propulsion system research targets large, open ocean vessels. These vessels are either low-speed Diesel or Diesel-electric craft that turn propellers at slow speeds, in the tens or hundreds of revolutions per minute. The smaller vessels, on the other hand, utilize DC motors that operate at thousands or tens of thousands of revolutions per minute. Therefore, there is limited research on the design of propellers that considers the difference in speed and performance of these DC motors. This paper will demonstrate a series of use cases for where traditional propeller performance analysis fails and will demonstrate a method to integrate propeller design and motor performance. The focus of this paper will be on the well-studied Wageningen B-Series propellers due to their known performance characteristics. MATLAB R2022b models will be utilized to demonstrate the performance of the actuator systems.
1. Introduction
In modern naval architecture, a propeller is determined based on the vessel information, and a motor is selected based on that propeller. However, this can build inefficiencies into the systems through these underwater actuators. Specifically, unless a custom motor is built [1], the motor will not run at its designed operating point. This can lead to losses as the propellers are spun at higher speeds or torques than intended, and leave the region of maximum efficiency. This can also lead to a change in hull speeds, which either incur additional drag losses from excess speed or hulls that cannot meet the target speeds. For standard vessels and boats, this is not a concern as the propulsion unit will likely be designed and tailored for the individual vessel due to the costs involved. For smaller vessels, like Unmanned Surface Vessels (USVs) and Unmanned Underwater Vessels (UUVs) that are used as research platforms, this will not be the case, as they must use Commercial-Off-The-Shelf (COTS) motors. This paper looks to incorporate pre-selected motors into the calculations of efficiency of propeller designs to determine the benefits this may bring.
A complete guide to propeller design can be found in [2], but a brief introduction to the concepts will be provided here. The propeller moves a vessel through the water by “screwing” through the fluid, using the aft, or pressure, side of the blade to press against it. This leads to a pressure drop on the forward, or suction, side of the propeller. In pressing against the fluid, the propeller no longer moves in a perfect screwing motion but instead “slips” slightly. The thrust produced is tied to the amount of slip incurred, but the relationship is non-linear. At a certain point, too much slip leads to the propeller “recutting” the same water. In this case, instead of a laminar flow entering the propeller from the open water ahead of the vessel, each blade of the propeller encounters water that was pressed upon by the previous blade. This causes performance to degrade exponentially. Another physical phenomenon that can cause performance degradation is cavitation. This occurs when the drop in pressure on the suction side of the blade is large enough to cause the water to transition into a vapor state. This leads to a sudden drop in thrust due to the compressible nature of water vapor, and can lead to propeller damage from the formation of the water vapor bubbles
1.1. Wageningen B-Series Propeller Modeling
The typical propeller design process for a marine propeller is detailed below, following standard outlines [3,4]. This process utilizes a Wageningen Propeller B-Series as a standardized propeller shape. It is commonly used in naval architecture and has been studied extensively [3,5,6,7]. An example of a typical B-Series propeller is shown in Figure 1.

Figure 1.
An example propeller generated in CAESES by [8] using the parameters from the verification case discussed further in this document.
The designer will utilize a series of charts, equations, or existing generators to determine the optimal geometry to fully define the propeller. A B-Series propeller is fully defined using five key variables: the pitch to diameter ratio (PD ratio), the diameter in m (), the expanded area ratio (EAR or ), and the number of blades (). The speed of advance coefficient () is also used to determine the performance of the propellers. The propeller blade thickness in m () can be included, but standard values exist based on the diameter of the propeller [3]. However, this process is independent of the driver behind the propeller shaft.
The PD ratio is the ratio of the pitch—the distance the propeller moves forward in one revolution—and the diameter. Since this ratio is dependent on the diameter, the pitch in m () will be used instead for this work. The EAR is the projected area of all blades () divided by the area of a circle with diameter D (). Since this ratio is dependent on the diameter, the projected area of all blades—called the expanded area in m2 (Ae)—will be used instead for this work. The speed of advance coefficient is the fluid velocity at the propeller divided by the rotational speed of the motor in revolutions per second () and the diameter of the propeller. This equation is shown below, where () is the speed of advance, or the fluid velocity at the propeller.
Utilizing these parameters, existing Wageningen Propeller B-Series experimental data can be used to determine the thrust coefficients () and torque coefficients () for the propeller. These are represented by the black and red curves in Figure 2. These coefficients can, in turn, be used to determine the thrust generated by the propeller in N () and the shaft torque in N-m () that would be needed to drive the propeller at that speed. These are shown in the equations below, where the density of seawater () is given in kg/m3 following standard data [9].
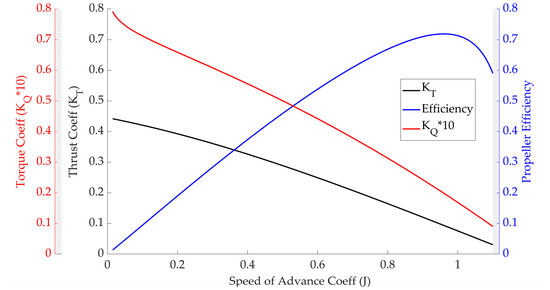
Figure 2.
Plot showing the speed of advance coefficient vs. the thrust coefficient, torque coefficient, and efficiency for the calculated exhaustive propeller in Table 6 with scaled by a factor of 10.
With the shaft torque () and speed () known, the mechanical shaft power in kW () can be calculated through multiplication and unit conversions.
The open-water efficiency of the propeller () can be determined through the equation below based on the relationship between the output thrust coefficient and the input torque coefficient, along with a scaling factor built on the speed of advance coefficient.
Utilizing Equations (2)–(5), the efficiency of a given propeller can be obtained for any combination of vessel and motor speed. This is shown in the blue curve of Figure 2. This then defines the objective function for the optimization problem. However, this is a source of losses for actuator design. As the drive characteristics of the shaft are not included in Equation (5), the result of any propeller optimization may not optimize the complete system efficiency.
With the objective function defined, the constraints can be considered. The three main constraints are thrust, cavitation, and strength. Simply, the thrust generated in N (T) must meet or exceed the minimum thrust necessary to drive the vessel in N (), the propeller blades must not cause the water around the propeller to cavitate, and the propeller blades must be thick enough to avoid failing. The thrust constraint is given in Equation (6), the cavitation constraint is given in Equation (7) assuming there are no more than 2 propellers, and the strength constraint is given in Equation (8). These are listed as negative semi-definite inequality constraints to set up for future optimization methods.
The pressure terms in pascals ( and ) are the water pressure at the midline of the propeller and the vapor pressure. The vapor pressures are taken from standard values [9]. Common practice is for the propeller to be assumed to be located at a depth equal to the maximum allowable diameter of the propeller [2]. The term () is the number of propellers in the design. The term () is the maximum allowable stress for the propeller’s material. Depending on the application, this will be the yield strength or endurance limit of the material with a factor of safety applied.
The standard approach in naval architecture is to select the number of blades based on vibratory interactions around the vessel, to select the maximum propeller diameter allowed by the design of the hull, and then select the lowest EAR that does not cause cavitation according to Equation (7) [2]. With three of the five design parameters defined, either the pitch or the speed of advance is optimized while the other is calculated as an output. Often, the point of maximum efficiency is tied to the maximum viable pitch value [2], so the process can be simplified further in some cases. Variations on this approach are prevalent. Some prefer this to be performed through an iterative process, selecting the pitch based on empirical graphs and backing out the appropriate motor speed [2], while others prefer optimization of the diameter [10]. Research has also been done with engine propeller matching, but these are for large vessels, such as a 60-m patrol boat [7].
The limits on the allowable design parameters may also be dictated by definitions and the limitations on production. As the speed of advance coefficient is a ratio of speeds, it can be limited to between 0 and 1, though it can exceed this [11]. For this application, the propellers will be targeted for manufacture utilizing a standard desktop 3D printer, so the minimum diameter of the propeller will be dictated by generating a sufficiently strong hub, and the maximum will be dictated by the available build volume. The propellers will be generated through an online tool that limits the PD Ratio to between 0.4 and 1.4 and limits the EAR to between 0.35 and 1.05 [8]. This corresponds to the limits of the defining experimental data [11]. The number of blades is technically any integer greater than or equal to 2, but the propeller generation tool allows between 3 and 5 blades, defining the limits on Z. These constraints will be converted into negative semi-definite inequality constraints as shown in the equations below.
Following the previous propeller design process, these values indicate that an optimal propeller would be expected to have three blades, a diameter of 0.215 m, an EAR of 0.35, a high value for pitch, and a very low speed. The actuators for USVs and UUVs under investigation in the rest of this paper are not expected to follow these rules, as the motor inefficiencies at low speeds will be significant.
1.2. Optimization Method Applicability
Before getting into the motor influence, the design and optimization of propellers without an iterative process and without following these rules of thumb can be discussed. A nonlinear optimization problem can be generated in a standard form to maximize the efficiency of the propeller in a manner that can be analyzed through Karush-Kuhn-Tucker (KKT) conditions and Augmented Lagrange Multipliers (ALM). The formulation is shown below, including the performance function along with the eleven constraint equations. The maximum condition previously discussed is inverted and used as a minimization for computational ease.
Minimize
subject to
where
It should be noted that for ALM methods, the variables are assumed to be continuous [12]. While this may be acceptable for the first four design parameters, the number of blades is discrete. To account for this without loss of mathematical rigor, the number of blades can be treated as a constant for an iteration of the solution. That is, it can be set to a value of 3, and then the problem can be optimized. Afterwards, it can be set to 4 and optimized again. This can be repeated for all reasonable values of . Since there are very few options regarding the number of blades and because increasing the number of blades will degrade the overall efficiency due to increased blade edges cutting through the water, it will be assumed that the solution can be found close to the minimum allowed. Alternatively, all of the design parameters can be treated as discrete and evolutionary, or genetic algorithms can be utilized [13,14,15,16].
The above is relatively straightforward mathematically, but the relationships for the thrust and torque coefficients are modeled from curve fits of experimental data. Proper modeling of these utilizes Equations (26) and (27) for the thrust and torque coefficients. The following is drawn from [11] following the work of [17], and is valid while the fluid at the characteristic distance has a Reynolds number below 2 × 106. Higher values for the Reynolds number will be discussed momentarily.
and
The first and second order derivatives for these equations are still continuous and fully defined, meaning the system of equations is technically solvable through analytical techniques such as Augmented Lagrange Multipliers. However, due to the size of the problem, this may not be feasible. After accounting for Z as a discrete parameter, there are a total of 4 continuous design parameters, 11 Lagrange multipliers (λ terms), and 11 augmentation or slack parameters (s terms). Taking the partial derivatives with respect to each of these terms generates 27 equations. The differentiation with respect to alone generates an equation with 2123 terms and is 17 pages of 12-pt font. This can be simplified somewhat by breaking the problem into subsets and solving them multiple times [4], but the overall computational load is substantial.
The inclusion of the Reynolds number adjustment complicates the issue further due to both length and an added discontinuity at the critical Reynolds number. Extensive empirical work has been performed in this region to evaluate propellers at the limits of performance [17,18,19], though it can still break down at the extreme limits. For the application in this work, small vessels, the propeller speeds can end up being extremely high relative to traditional designs. In this instance, an adjustment must be made to the thrust and torque. As previously mentioned, this occurs when the Reynolds number is above 2 × 106 at a distance from the propeller’s rotational axis of 75% the radius. This distance is called the characteristic distance for the B-Series propeller (). Note that some authors, such as [19], prefer to use 70% of the radius for the Reynolds number, and corrections must be included if this value is to be used. The Reynolds number at the characteristic distance () is calculated as
where the constant term () is the chord length at the characteristic radius and can be determined from [3]. The kinematic viscosity of the water is () and can be determined from standard sources [9]. If required, the adjustment factor for the thrust coefficient () and the adjustment factor for torque coefficient () are given below.
And
Because these factors are only added to the thrust and torque coefficients when the is above 2 × 106, the derivatives of the thrust and torque coefficients have a discontinuity at that point. To account for this, the optimization techniques that require smooth derivatives can be solved twice: once using the unadjusted thrust and torque coefficients plus a constraint that the Reynolds number must be below the critical value, and once using the adjusted thrust and torque coefficients plus a constraint that the Reynolds number must be above the critical value.
The first iteration would be as follows:
Minimize
subject to
where
The second iteration would be as follows:
Minimize
subject to
where
A numerical KKT approach can be beneficial in situations such as this, where problems are complex and the gradients are defined, but it can be a poor choice here because it provides necessary but not sufficient conditions for optimality. Because the problem is highly variable, there are many local maxima and minima and discontinuous feasibility regions. This leads to the algorithms often getting stuck outside the global maximum, indicating that a method with randomization included may be necessary, such as multiple starting points, simulated annealing, genetic algorithms, or random sampling. Alternatively, an analytical solution could potentially be determined.
Additionally, the algorithms for the computation of the propeller thrust and torque coefficients can generate negative results unexpectedly. For example, the motor torque can become negative if the speed of advance coefficient goes too high, indicating that the motor is operating as a generator. A constraint can be added to eliminate conditions where the shaft torque is negative, but it adds complexity. This constraint is labeled with a subscript of () and is added here for completeness.
One approach for a situation such as this, where the optimization calculation could be troublesome, is to conduct an exhaustive search. Manufacturing precision means there is a finite resolution on propeller diameter, pitch, and areas. Motor controllers are also digital machines, meaning they also provide a finite resolution for the speed of advance coefficient given a target fluid velocity at the propeller. In that case, all different combinations of the design parameters can be tested. Since this can be done through simulation and analysis utilizing standardized B-Series propeller data, the exhaustive search is a valid approach. It should be noted that, as an exhaustive search, this is both slow and energy-intensive.
1.3. Vessel Considerations in Optimization
Given these challenges, it is unsurprising that adding the additional complexity of motor performance characteristics is often not done. However, they significantly impact the feasibility and efficiency of the design for USVs. In general, the best solutions mimic those of large cargo vessels; large propellers spinning at speeds of tens or hundreds of RPM to provide immense amounts of thrust. Small DC motors often cannot produce these torque–speed combinations or cannot do so effectively.
Commonly seen exceptions to these values are vessels designed to ride up and glide over the water, as many RC boats do. These utilize a planing hull design rather than a displacement hull design. In a planing design, the vessels exert a significant amount of energy to get up on top of the bow wave, with water pushed out in front of the boat as it moves. Once up on the bow wave, the overall drag coefficient of the vessel decreases drastically, leading to higher maximum speeds. The vessel characteristic that defines whether a vessel should use a planing hull or a displacement hull is the speed-to-length ratio. The details are beyond the scope of this paper, but as the speed of the vessel increases, it will eventually start to try to ride up the bow wave it creates if the hull shape allows it [3].
Many small personal watercraft, like jet-skis and bass boats, incorporate elements of a planing hull design. While significantly faster, these are not the most efficient from a power, weight, and energy perspective since significant amounts of thrust must be generated to get up on the bow wave. For smaller USVs like RC boats, planing hulls are often an excellent choice since they can be lightweight, and they must have high speeds relative to their short length, and they need short durations. But for vessels used as long-term research platforms, it is not viable. In addition, planing vessels struggle in waters that are not flat. Due to the size of oceanic waves relative to the size of the vessels, the water is virtually guaranteed not to be flat.
This means these USVs will be small, displacement hulls that will be battery-powered, sometimes with solar power regeneration. This leads to the requirement of the use of brushed or brushless DC motors. These motors typically operate in the tens of thousands of RPM and struggle to produce high torque at the low speeds dictated by the propeller design. The most common solutions are to utilize a custom or manufacturer-supplied gearbox or use a mismatched propeller and motor from available COTS sources. Both approaches introduce additional and unnecessary inefficiency to the system.
In contrast, this paper looks to combine the expected or known performance characteristics of motors into the design of propellers. This will increase the computational complexity of the problem, but this paper hopes to demonstrate that this will improve overall performance for the vessel.
The consideration of electric motor performance along with propeller characteristics has begun to be studied in industry, but it is in its early stages [20]. These designs are highly variable and have yet to come towards standardized solutions like the B-Series propellers. One major consideration for this is that there are few electric vessels currently in use or under construction, roughly 0.3% of the global fleet [21]. Propeller manufacturers are designing their products towards the majority of vessels, which utilize internal combustion engines. However, that is not to say that no designers are looking at this. A few are beginning to consider this market and are developing propellers that must be designed with the output of the drive systems in mind. The scientific community is working to validate these designs through CFD modeling as well as physical experimentation [22].
As an example, the BlueNav Whale Design uses an internal, rim-driven propeller design with blade shapes derived from biomimicry of humpback whale fins, including tubercles [23]. However, the rim-driven propeller’s nozzle shape, the tubercles, and even surface conditions of the blades need to be optimized for each use case [20]. Surface protrusions are an area of study that leads to promising gains in efficiency [24] and CFD studies have been performed to indicate the benefits of these tubercles [25]. This reinforces the need for the propeller to be designed with the motor in mind.
These actuators often see high thrust requirements due to the relative sizes of the actuators on UUVs and USVs. Thus, propeller designs that incorporate high-thrust principles over high-speed principles are more common, such as the Hydro Impulse HI-RF 11 Mitek [26]. While this propeller is not designed specifically for electric motors, the principles it uses are more suitable for electric motors than traditional internal combustion engines. This can lead designers towards a trend of selecting and designing propellers that match the drive system.
One designer who is considering electric motors in their propeller designs is Sharrow Marine. The Sharrow Marine toroidal propeller has a twisting loop design, a highly innovative approach [27], that the inventor claims will be able to operate at 30% higher efficiency at the high-torque regions of electric motors [20]. It should be noted that this design is not dedicated to only electric motor applications, as it claims to produce up to 40% higher efficiency than traditional designs, regardless of the driving source [28]. Current academic research is attempting to properly model and validate these designs, such as in [22].
As an alternative approach from the UUV perspective, many manufacturers. In this space, they prefer to maximize bollard test ratings where the actuator is held stationary and the efficiency is measured as the thrust output per Watt consumed. BlueRobotics pioneered a flooded brushless DC motor that allows high efficiency while being essentially depth-unrestricted [1]. However, this approach is entirely focused on the performance under conditions where the speed of advance coefficient is zero and the thruster is stationary [29]. Data is unavailable for varying speed of advance coefficients, i.e., when the vessel is underway. While this is an acceptable assumption for UUVs due to their relatively slow speed, it may not be acceptable in higher-speed USV applications or for long-duration missions where the thrusters are run continuously.
1.4. Motor Performance Modelling
Between the brushed and brushless DC motor, this work will begin with the brushed motor since it can be used to model part of the brushless motor’s performance. The typical torque-speed performance curve for a brushed DC motor is shown in Figure 3. This motor will be used in the case study done later in this work.
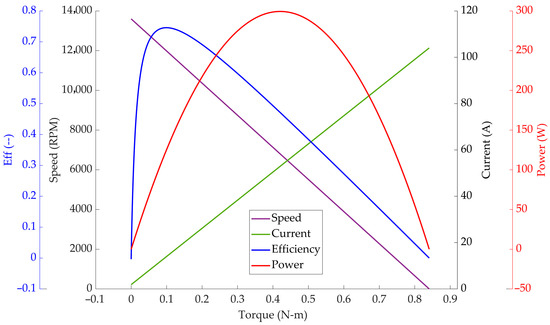
Figure 3.
Plot showing torque vs. speed, power, current, and efficiency for a brushed DC motor.
The relationship between torque and speed can be modeled as a linear relationship with a form of
where () represents the torque generated by the motor and () represents the speed of the motor in RPM. The stall torque () serves as the y-intercept of the linear equation. Connecting this to the previous conversations, the required shaft torque () will be equal to the motor output torque at steady state. The parameter () is the torque coefficient of the motor and provides a constant value slope.
The relationship between torque and current is also a linear relationship with a form of
where () is the current draw of the motor under the torque load. The no-load current draw of the motor () serves as the y-intercept of the linear equation and the parameter () is the motor torque constant, and is another constant linear slope.
The efficiency of the motor is the mechanical output power—torque multiplied by speed—divided by the electrical input power—current multiplied by voltage.
Note that the speed of the motor here is generally represented with () for a speed in radians per second, while the motor performance coefficients are often provided in revolutions per minute. For consistency, the speed will be represented in revolutions per minute throughout, with the unit conversion occurring only here. It must be stressed that the motor speed () is in revolutions per minute (RPM) while the propeller speed () is in revolutions per second (RPS). Substituting in the previous equations provides a single equation for motor efficiency based on speed.
Since the speed of the motor can be connected to the propeller design parameters through the definition of the speed of advance, the efficiency equation can be rewritten in terms of the design parameters as
For a brushless DC motor (BLDC), the performance limits are broken into two regions: a constant or semi-constant speed region and a constant or semi-constant torque region. In either case, performance decays if the torque exceeds an operating point where the motor is rated, and it performs similarly to a brushed DC motor. Below this point, the torque available at the speed is constant or semi-constant, depending on the motor’s construction. This is represented by the torque-speed curve shown in Figure 4. The following estimate of performance is rough, as the true values will be more continuously differentiable instead of showing a sharp peak at the rated torque.
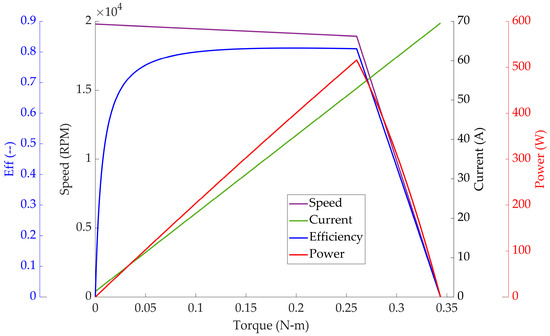
Figure 4.
Plot showing torque vs. speed, power, current, and efficiency for a hobby-grade brushless DC motor.
The motor begins intermittent operation if it is overloaded and the required torque is outside of this boundary. In Figure 4, overloading the motor would look like a shift to the right. This can become perilous with the motor potentially overheating. In practice, therefore, if the desired speed is below the rated speed, then the torque output should be kept at or below the rated torque. Above the rated torque, the motor will have a torque-speed curve like that of a brushed DC motor with a linearly decreasing relationship. Note that the winding methods inside the motor can be represented as either a true BLDC or a permanent magnet synchronous motor (PMSM). This difference may only be detectable by disassembling the motor or measuring the back-EMF from the motor to judge whether the waveform is sinusoidal or trapezoidal. Due to the variability involved, the relationship for the torque to the voltage constant will be modeled as a PMSM and is defined by the equation below where () is a constant, () is the current draw, () is the no-load current draw, and () is the motor’s voltage constant [30].
The constant C is based on conversion factors for three-phase PMSM and has a theoretical value of but a value of 8.1 is more conservative based on experimental motor performance due to losses [31].
Combining the two theoretical torque regions for those above and below the rated speed produces a piece-wise function for the available motor torque, as shown below.
Here again, it should be noted that this approach is an estimation of the performance of the motor, as the BLDC motors and PMSM have slight performance variations and can be significantly impacted by the control methodology used, such as pulse frequency modulation for the BLDC and field-oriented control for the PMSM. However, these are considered beyond the scope of this paper.
In this paper, the conservative semi-constant relationships will be used, so the torque-speed curve will be defined by
and the current draw of the motor at the required torque will be
These are the relationships used to generate the curves shown in Figure 4.
1.5. Combining Propeller Performance and Motor Performance
To incorporate these equations into the system of inequality constraints previously given, a different set of equations will need to be satisfied, depending on the type of motor used. If a brushed DC motor is used, one additional constraint can be added using Equation (46) as shown below. An index of () is used here as the implementation will need to be changed for different conditions.
For a brushless DC motor, the piece-wise function in Equation (53) can be converted into two separate constraints that must be satisfied. Indices of () and () are used here as the implementation will need to be changed for different conditions listed in the Materials and Methods section.
and
Motor efficiency can be combined with propeller efficiency by multiplication to generate a performance function to capture system-wide efficiency (). An additional term for gearbox efficiency () can be added for completeness for designs that wish to pursue including a gearbox. For this work, the gearbox efficiency will be unity for all but the brushed DC motor with the gearbox. Thus, the system-wide efficiency is
Or, more completely
The research question posed in this paper is whether including the motor efficiency in the performance function and/or constraint equations for the optimization algorithm improves the overall performance of the system. For this paper, the available motors will be constrained to a finite set to represent a range of motors available at a manufacturer’s website. First, the propeller efficiency problem will be solved through exhaustive searches without considering the motors’ limitations (Equations (55)–(57)). Then, a second round of exhaustive searches will be repeated, but this time considering the performance limits of each motor. The most appropriate motor(s) for the propeller will be selected, and the system efficiency will be calculated utilizing the relationship in Equation (59). Lastly, the system will be optimized using a third round of exhaustive searches, considering the motor limitations and the overall system efficiency. It is expected that the overall performance will increase in these final iterations, with the efficiency greater than during these trials than during the others.
1.6. Limitations of Considered Approach
This paper will not address the complete vessel optimization and will solely focus on the optimization of the actuator itself. The performance of a particular vessel hull has been studied extensively in general terms [32], relative to destroyers [33,34], relative to conventional reefer ships [35], and relative to bulkers [36].
Similarly, this paper will not address final design validation under real-world conditions. This area of study will be a critical portion of future work that will need to be completed. However, the process of propeller validation is well studied through the Wageningen B-series propeller data generated from the Netherlands Ship Model Basin and is considered requisite for any theory or mathematical model [37]. Any model is compared to this data set, as it is the most exhaustive and comprehensive data available for marine propellers.
Initial validation will need to be performed through Computational Fluid Dynamics (CFD). This is an active area of research [37,38,39,40]. A particularly challenging aspect is the modeling of cavitation [37,41,42]. Some authors prefer a two-equation k-ω model for a Reynolds-averaged Navier–Stokes equation [43] while others prefer the three-equation k-ε version [42] or a hybrid 2.5D numerical approach [44]. The details of this CFD approach are beyond the scope of this paper, but a calibration study is provided in [45] which will be the guiding document for future work. It should be noted that the generally accepted variation is 10% [46]. The efficiency improvements for larger propellers may not be sufficiently significant to register changes within that band, but the values for smaller propellers may. The difference will depend on the motors and constraints selected for future work. Once an appropriate CFD model has been generated, the results of this paper will be validated or corrected, and prototype testing will commence. However, as noted in [24,45], the surface roughness can have a significant impact on performance and would need to be included in the model if FDM fabrication is used.
2. Materials and Methods
2.1. Exhaustive Search Algorithm Methodology
The exhaustive search began with the minimum values for the number of blades and the diameter. The pitch and expanded area values are dependent on the diameter, so the minimum values for the pitch and expanded area were calculated from constraints in Equation (20) and Equation (22), respectively. The remaining values for pitch and expanded area were found by increasing them by a predetermined step size until the maximum allowable value was reached, as given by Equation (21) and Equation (23), respectively. These values were stored and associated with the minimum diameter. The diameter was increased by the step size, and values for pitch and expanded area were calculated again, stored, and assigned to this new diameter. This process was repeated for all allowable values of the diameter.
Once all possible combinations of the design parameters were generated, the values for the thrust and torque coefficient were calculated for each configuration along with the efficiency. The constraints were evaluated for each configuration as well. This was performed through a series of nested for loops in MATLAB. If the efficiency of the solution is better than the previous best solution and the constraints are satisfied, it replaces the previous best solution in a separate storage variable.
2.2. Exhaustive Search Algorithm Verification
The Wageningen B-Series Propeller Generator, utilized to generate the propellers, allows limited resolutions, leading to fixed step sizes on the design parameters [8]. These are shown in Table 1. The resolution on the speed of advance coefficient was selected to be 0.001 to match the values for the other parameters for this verification stage. An existing case study for a similar exhaustive search was utilized to verify the model used for this paper [47]. The upper and lower bounds shown in the table are drawn from this source.

Table 1.
Step size and bounds for verification test case [8,47].
That work utilizes a comparison between a simple exhaustive search and the results from commercial nonlinear equation software (LINGO). In that work, the thrust required for a given propeller is governed by a large cargo ship’s overall resistance, the number of propellers, and an additional parameter for a thrust deduction (). The vessel parameters are provided in Table 2. With these parameters, each of the two propellers will need to provide half of the force to overcome the total ship resistance and will have a thrust efficiency of 85% to incorporate the thrust deduction. Thus, each propeller must produce 20,600 N.

Table 2.
Vessel parameters for the verification test.
2.3. Vessel Model and Design Parameters
With the model having been verified, the performance for actuators in non-standard vessels can be addressed. The performance requirements for the actuator in this case are dictated by the desired speed of a small USV. This speed will be selected to be 1.79 m/s (3.48 kts). This value roughly represents transiting a local 2.4 km (1.5 mi) coastline on one battery charge. However, because it is low compared to traditional vessels, it can cause many rule-of-thumb relationships for propeller design to break down. While beyond the scope of this paper, the breakdown of these relationships is a secondary driving factor for this paper. The vessel will have a weight of roughly 22.7 kg (50 lbs.), leading to an expected thrust requirement of 44.7 N following Gerr’s displacement speed formula [2]. Since the speed of advance is the speed of the propeller through the water, not the speed of the vessel, a typical Taylor wake factor of 0.20 will be assumed [48], meaning that the water at the propeller is at 80% the speed of the vessel or 1.432 m/s. The propeller will be designed for fabrication through finite deposition manufacturing (FDM) on a desktop 3D printer, an Ultimaker 2 Extended+. The strength of the plastic used for the propeller is estimated to be 8 MPa. This is a common value of strength for propellers and is used in the propeller generator for this work [8]. The strength of the 3D printed part compared to an injection molded part is considered beyond the scope of this paper. The propeller will have an assumed depth equal to the maximum allowable diameter of the propeller to minimize the likelihood of propeller ventilation. These parameters are summarized as shown in Table 3.

Table 3.
Vessel parameters for the USV.
The motors selected for this work are a motor for a cordless drill (for the brushed DC motor) and an off-the-shelf motor for an RC boat (for the brushless DC motor). The brushed DC motor will include a gearbox. Performance characteristics for these motors can be found in the referenced links below, with key parameters summarized in Table 4. It should be noted that, in a previous project, Motor B was selected as a COTS motor that would be suitable to drive the vessel under consideration.

Table 4.
Summary of motor specifications.
The cordless drill motor is a 281 W Mabuchi RZ-735VA-9517 [49]. This motor also includes the option of a 2-stage planetary 12:1 reduction gearbox. The gearbox efficiency will be assumed to be 98% per gear mesh, resulting in an overall gearbox efficiency of 92%. This is a conservative estimation, as specialized industrial planetary gearboxes can have efficiencies of 95% [50], though this can vary with customization between 97.3% to 92.31% [51]. This also does not consider that spur gear mesh losses can be reduced by up to 65% when the operating point is not at peak loads [52]. The brushless DC motor is a 1819 W Turnigy XK3674-1650KV [53]. The brushed DC motor will be called Motor A. The brushed DC motor with the gearbox will be called Motor B. The brushless DC motor will be called Motor C. All motors will be driven by a 12 V power source, as this is the available power source that is below their maximum voltage.
With the FDM equipment, the maximum diameter is controlled by the build volume allowed [54]. Since the printer has a maximum build area of 223 mm by 223 mm, a maximum diameter was selected to be 215 mm (8.5 in). The lower limit on the diameter was selected to be 25 mm (0.98 in) to allow for a small hub for an existing 3 mm shaft. Since the motors selected have very high speeds, up to 20,000 RPM, the step size for the speed of advance coefficient was reduced by an order of magnitude to 0.0001. These values are summarized in Table 5.

Table 5.
Step size and bounds for further testing [8].
2.4. Algorithm Conditions
With these parameters defined, the algorithm can be run for fourteen different conditions. The first five trials look to demonstrate the need for motor performance limits to be included in propeller design, or an actuator may be designed that cannot function at the desired operating point. Trials 6 through 14 look to show the improvement that can be achieved by considering the complete actuator rather than the propeller and motor independently. Three trials are done to investigate the shortcomings of traditional design methodologies, even when the motor limitations are included. That is, when the motor efficiency is considered, is the best actuator going to be designed through the same method as the best propeller?
- 1.
- Maximize propeller efficiency without thrust performance cap.
- 2.
- Maximize propeller efficiency with the thrust performance cap.
- 3.
- Maximize propeller efficiency with Motor A performance limits.
- 4.
- Maximize propeller efficiency with Motor B performance limits.
- 5.
- Maximize propeller efficiency with Motor C performance limits.
- 6.
- Maximize system efficiency without the thrust performance cap with Motor A.
- 7.
- Maximize system efficiency with the thrust performance cap with Motor A.
- 8.
- Maximize system efficiency with Motor A performance limits.
- 9.
- Maximize system efficiency without the thrust performance cap with Motor B.
- 10.
- Maximize system efficiency with the thrust performance cap with Motor B.
- 11.
- Maximize system efficiency with Motor B performance limits.
- 12.
- Maximize system efficiency without the thrust performance cap with Motor C.
- 13.
- Maximize system efficiency with the thrust performance cap with Motor C.
- 14.
- Maximize system efficiency with Motor C performance limits.
As the first five trials do not reflect the total system efficiency, the system efficiency will need to be calculated. This is done by using the required shaft torque and speed in the models of the motors to determine their efficiencies. This is reflected in Equation (50) for Motors A and B and Equation (59) for Motor C.
3. Results
3.1. Exhaustive Search Algorithm Verification Results
When the exhaustive search is performed with the model to be verified, a slight variation is found between the calculated values and the values presented by the original authors. The solutions for the two approaches are shown in Table 6.

Table 6.
Reference and calculated results from the verification test case.
The variation between the reference exhaustive and reference analytical results is discussed in the original paper, but the difference between those values and the output of this paper’s exhaustive algorithm is initially of concern. Through investigation, it was determined that the original source erroneously applied the adjustment factors. While the Reynolds number is above the critical point, the original authors applied the adjustment factor to the torque coefficient but not to the thrust coefficient. Based on these results, it was determined that the algorithm generated for this paper correctly identifies the appropriate solution. The results justifying this conclusion are shown in Table 7. The values show that while the referenced paper included the Reynolds number adjustment for the torque coefficient, they did not do so for the thrust coefficient. This led to erroneous calculations for the efficiency and thrust provided.

Table 7.
Discrepancies between thrust and torque coefficients for the referenced paper and the calculated results. Dashes indicated the data was not provided.
3.2. Propeller Efficiency Optimization
The calculated results from the first five trials are shown in blue in Figure 5. These efficiencies are low, but reasonable in comparison to the verification trial. Since they do not reflect the total system efficiency, the system efficiency will need to be calculated by using the required shaft torque and required speed in the models of the motors to determine the efficiencies. Equation (50) was used for Motors A and B and Equation (59) was used for Motor C. The results are shown in red in the same figure. Since trials 1 and 2 were motor agnostic, the best viable motor is shown. The numerical results as well as the propeller parameters are shown in Table A1 and Table A2.
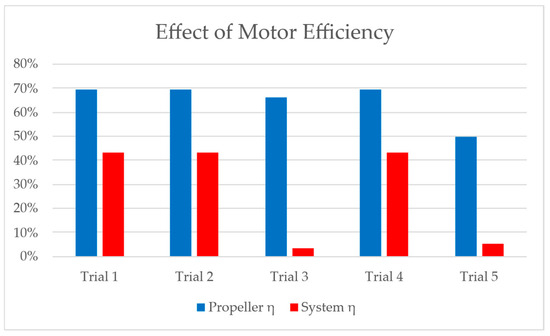
Figure 5.
Plot showing theoretical propeller efficiencies (blue) and maximum system efficiencies for trials 1 through 5.
The figure highlights the effect motor performance can have on the actuator. By disregarding the efficiency of the motor, the actuator could end up with an acceptable propeller efficiency that is unable to drive the system for the desired duration because the motor efficiency is so low, or one that is unable to drive the system at all.
3.3. System Efficiency Optimization
The results for the next nine trials are summarized in Table 8. Trials 6 through 8 represent the performance when Motor A is being considered. Trials 9 through 11 represent the performance when Motor B is being considered. Trials 12 through 14 represent the performance when Motor C is being considered. Within the propellers designed for any given motor, identical results arise if the limits on motor torque and current are not active at the optimum condition. Primarily, the similarity between rows, particularly Motor A and Motor C, is due to the constraints active while optimizing efficiency. For both motors, the active constraints are based on thrust, while Motor B was constrained primarily by the maximum propeller diameter. This will be further addressed in the results

Table 8.
Optimal parameters and efficiencies for trials 6 through 14.
The results for the different motor configurations in this section show little visual difference between them. A representative propeller from Trial 8 is shown in Figure 6. These propeller parameters have values that would be considered typical except for low area ratio () values and small diameters.

Figure 6.
Propeller generated in CAESES by [8] using parameters identified in Trial 8.
3.4. Comparison of Efficiencies
This work seeks to evaluate the importance of including the performance of motors in the design of propellers. To visualize this, the system efficiency of all trials can be shown in a single plot. This is done in Figure 7.
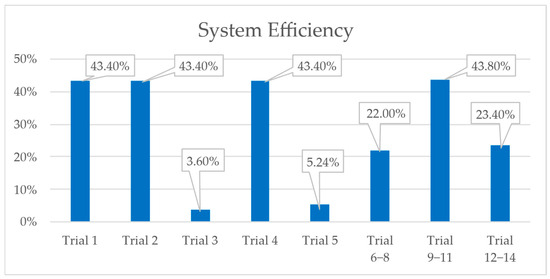
Figure 7.
Plot of all system efficiencies with duplicate values combined for trials that produced zero variation.
4. Discussion
4.1. Propeller Efficiency
The propeller efficiencies are high, but as discussed in the introduction, they require a very low propeller speed. Trial 3 has the highest speed (2442 RPM) and the lowest efficiencies, while trials 1, 2, and 4 have the lowest speed (568 RPM) and some of the highest efficiencies. When utilizing a COTS DC motor, which will have rated speeds in the tens of thousands of RPM, the performance degrades quickly and potentially reaches infeasible regions. The infeasible examples are indicated by the X entries in Table A2. As an example, the torque required for the propeller in Trial 1 is 0.392 N-m, which is above the stall torque of Motor C (0.344 N-m). Thus, the result is infeasible. This justifies the need to include the motor performance in the design process for the propeller in some manner.
One option to create a viable actuator for the infeasible combinations would be to generate a gearbox to make the motors capable of operating closer to this required setpoint. Based on the shaft torque (1.02 N-m) and speed (568 RPM) for trial 1, the motor power is only 60.9 W. The selected motors could all easily supply the power required for this propeller, but not at the necessary torque and speed combination. Hence, a gearbox could be utilized to adjust the speeds. However, the gearbox efficiency will be non-negligible because these would need to be multi-stage gearboxes due to the significant drop in speed. Assuming a rough 5:1 ratio per non-planetary gear stage, Motor A would require a 21.1:1 ratio, approximately four stages, leading to an efficiency loss equal to that of Motor B. Motor C would require a 31.8:1 ratio, approximately six stages, resulting in an efficiency of 88.6%. While brushless DC motors are slightly more power efficient than brushed motors, the loss from additional gearing may negate the benefit.
The utilization of either slow-speed Diesel engines or gearboxes is the current industrial best practice for large vessel designs. However, it is rare in the smaller vessel realm due to expense and the availability of affordable motors and gearboxes at this size. Most suppliers of reduction gearing systems have maximum input speeds of 5000 to 10,000 RPM. Thus, the focus of this work is on addressing designs that do not utilize these gearboxes despite the benefits.
4.2. System Efficiency
When motor performance is considered in the efficiency calculation, the propeller efficiencies will drop as can be seen in the blue series of Figure 5. However, the overall system efficiency increases, sometimes significantly, due to the increased motor efficiency. This is seen by comparing trials 3, 4, and 5 to their corresponding system efficiency optimizations, trials 6–8, trials 9–11, and trials 12–14, respectively. This can be done visually by inspecting Figure 7.
The most important note here is that the optimal design for the propeller is one that includes motor efficiency rather than just the feasible region of the motors. If the motor and propeller are already well-matched, such as Motor B, the efficiency gain is minor. Trials 9–11 have an optimal efficiency of 43.8%, which is only slightly higher than the 43.4% achieved by designs that considered only motor constraints. This is an improvement of only 0.92%. However, for the less-well-matched motors, the improvements are 510% and 350% for Motors A and B, respectively.
Based on this information, the process by which a propeller would normally be designed results in an extremely inefficient actuator. Instead, the complete actuator needs to be considered during the optimization process.
4.3. Trends Regarding Inactive Motor Constraints
As expected, the overall system efficiency is best when the motor is slowed down to a speed closer to that of a traditional boat motor. This can be seen through Motor B being the most efficient motor while also rotating at the lowest speed.
One unexpected relationship was the similarity of the brushed and brushless DC motors seen in trials 8 and 14, and the similarity across trials for a given motor, trials 6 through 8 giving identical results, for example. In these cases, the optimal efficiency point for these propellers is constrained by factors other than the motor performance constraints, leading to the similarities.
In the first case, the peak efficiency points for the brushed and brushless DC motors are at nearly identical J values because they operate at such high speeds. This leads the algorithm to find very similar solutions when the active constraints are thrust and minimum allowable diameters to create that thrust. Because diameter and thrust are the active constraint sets, the motor constraints are inactive.
Considering an extreme case, the active constraint sets can change to include the motor limits if the vessel speed is increased. For demonstration purposes, the traditional naval architecture approach can be used if the motor is selected and the speed of the vessel is to be maximized. Assuming a cubic relationship between required power and speed, a 65% efficient propeller, and an appropriate 2-stage planetary gearbox design with 92% efficiency, Motor A could operate at its rated maximum efficiency point to output 281 W. This would generate a speed of roughly 6.0 m/s. This would be a rare situation where the system would be optimized for a given motor.
The key factor is that beyond 6.0 m/s, the performance would be constrained by the motor’s performance limits since both motor torque and speed would need to increase. At this point, the results for trials including motor limits would give different results than trials that only attempted to optimize efficiency.
4.4. Other Connections
The results all indicate that, for this vessel, the upper limit on thrust does not come into play. For example, the first trial and second trial look at the effect of including the upper limit on thrust independent of motor selection and show zero variation. As discussed previously, the lower limit on thrust is one of the active constraints rather than the upper limit. This depends on the parameters of the vessel. A more accurate model would include a dynamic equation for the resistance of the vessel based on speed. Increasing the vessel speed would decrease the thrust and torque generated by the propeller but moderately increase the efficiency of both the propeller and the motor. However, the drag on the vessel would increase in linear proportion to the square of the speed, and the power required would increase by the cube of the speed. Thus, the overall system efficiency would be expected to drop. Different hull forms can modify this situation and produce slightly different response curves, as was previously mentioned in the introduction. Future work will explore incorporating drag models into the propeller design calculations to discover whether an optimal point may exist at a higher speed than required under certain motor performance conditions.
For demonstration purposes, if the speed was increased to the same values as those of the verification test (10.289 m/s), the maximum thrust limit comes into play. The maximum actuator efficiency for Motor C when allowing excess thrust is 57.7% but with the upper limit on thrust, it is 43.5%.
5. Conclusions
This paper attempts to address the question of whether motor performance should be included in propeller design. A model was developed to evaluate the performance of propeller-motor combinations as a complete system. While this model can be evaluated through modern optimization techniques in future work, a simple exhaustive search algorithm was developed to justify the inclusion of motor performance. The model demonstrated accuracy when applied to a test case. This model was then applied to propellers for small DC motors and successfully demonstrated the need to incorporate motor performance into propeller design.
For propeller designers, this paper demonstrates the potentially significant performance gains that can be achieved when motor efficiency is included. Any gain to system efficiency results in a nearly identical gain in range and duration for a vessel. For the UUVs and USVs in consideration of this paper, that can mean the difference between completing a mission and not. In larger applications, this can begin to address the single largest inhibiting factor to the implementation of electric cargo vessels: range.
Future Work
Future work will take several approaches: improvements to the optimization algorithm, Computational Fluid Dynamics (CFD) evaluation, performance evaluation of FDM propellers, and experimental verification.
Optimization improvements will focus on speeding up the optimization by performing a global optimization through methods like Augmented Lagrange Multipliers, evaluating whether an iterative method should be used to select an initial motor and then adjusting the propeller, and determining what minimum constraints need to be considered for the propeller design. In addition, expanding the algorithm to include the drag for the vessel and different hull form characteristics could be considered at this stage.
In the future, CFD may be used to check whether the propellers generated by this work are able to produce the outputs as expected. This problem is non-trivial as the CFD solutions currently available are targeted toward low-speed Diesel applications or high-speed impellers inside of ducted systems, and will need to be evaluated and then modified or rebuilt for this application. Of particular concern are situations where the Reynolds number adjustments needed to be included in the propeller design. The process laid out in Section 1.6 will be followed here.
Empirical testing in this application will be difficult as the performance of FDM-generated propellers must first be benchmarked in comparison to machined or injection-molded propellers. Due to the tessellation that occurs between vertical layers in FDM parts, the propellers are not smooth. Roughness has a significant impact on propeller performance [18,20]. Thus, it is expected that the efficiencies of these propellers are significantly below the theoretical values provided. However, many concepts, such as the relationship between FDM layer height, propeller pitch, and propeller speed, are not currently known. Thus, the decrease in efficiency is unknown.
A two-prong approach will be taken for empirical testing. Firstly, existing propellers with known parameters will be modeled and generated through FDM. These propellers will be tested to identify the performance drops that are incurred by using 3D printed propellers. At the same time, the second prong will be to attempt to fabricate the desired propellers through a sand-casting process followed by a polishing process. Between these two approaches, it is hoped that one will be able to generate propellers with sufficient smoothness to allow accurate empirical testing. Once complete, a dynamometer and tachometer will allow the measurement of shaft torque and speed, while a strain gauge will be used to measure the output thrust for varying water speeds inside a flow channel. This will allow the results to be experimentally validated.
Defining these relationships and validating the efficiency of these designs requires specific testing facilities. The local facilities currently available do not have the ability to simultaneously measure motor torque and propeller thrust. Work is ongoing to expand this infrastructure, so experimental evaluation will be done as future work.
Funding
This research received no external funding.
Data Availability Statement
All data generated through this work, including propeller parameters and propeller performance plots, will be published at: https://github.com/bokidd/propeller-opt-with-motors (accessed on 27 July 2025).
Acknowledgments
The author would like to thank Dave Gerr for his extensive contributions to further the knowledge of naval architecture among mechanical engineers.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DC | Direct Current |
| USV | Unmanned Surface Vessel |
| UUV | Unmanned Underwater Vessel |
| RC | Remote Control |
| EAR | Expanded Area Ratio |
| PD Ratio | Pitch Diameter Ratio |
| RPM | Revolutions Per Minute |
| RPS | Revolutions Per Second |
| COTS | Commercial-Off-The-Shelf |
| BLDC | Brushless DC Motor |
| PMSM | Permanent Magnet Synchronous Motor |
| KKT | Karush–Kuhn–Tucker |
| ALM | Augmented Lagrange Multipliers |
| FDM | Finite Deposition Modelling |
| CFD | Computational Fluid Dynamics |
Appendix A

Table A1.
Optimal parameters and efficiencies for conditions 1 through 5.
Table A1.
Optimal parameters and efficiencies for conditions 1 through 5.
| Trial | ||||||
|---|---|---|---|---|---|---|
| 1 (No Thrust) | 3 | 0.215 | 0.9628 | 0.350 | 0.703 | 69.3% |
| 2 (Thrust) | 3 | 0.215 | 0.9628 | 0.350 | 0.703 | 69.3% |
| 3 (Motor A limits) | 3 | 0.192 | 0.8062 | 0.350 | 0.5855 | 66.3% |
| 4 (Motor B limits) | 3 | 0.215 | 0.9628 | 0.350 | 0.703 | 69.3% |
| 5 (Motor C limits) | 3 | 0.106 | 0.6075 | 0.350 | 0.332 | 49.7% |

Table A2.
System efficiencies for propeller designs in configurations 1 through 5. Infeasible values are indicated by an X. The entries with the “sys” subscripts indicate overall system efficiencies, while the motor and propeller efficiencies are indicated by the appropriate subscript.
Table A2.
System efficiencies for propeller designs in configurations 1 through 5. Infeasible values are indicated by an X. The entries with the “sys” subscripts indicate overall system efficiencies, while the motor and propeller efficiencies are indicated by the appropriate subscript.
| Trial | |||||||
|---|---|---|---|---|---|---|---|
| 1 (No Thrust) | 69.3% | X | X | 62.65% | 43.4% | X | X |
| 2 (Thrust) | 69.3% | X | X | 62.65% | 43.4% | X | X |
| 3 (Motor A limits) | 66.3% | 5.39% | 3.6% | -- | -- | -- | -- |
| 4 (Motor B limits) | 69.3% | -- | -- | 62.65% | 43.4% | -- | -- |
| 5 (Motor C limits) | 49.7% | -- | -- | -- | -- | 10.6% | 5.24% |
References
- BlueRobotics Inc. T200 Thruster. Available online: https://bluerobotics.com/store/thrusters/t100-t200-thrusters/t200-thruster-r2-rp/ (accessed on 5 September 2025).
- Gerr, D. The Propeller Handbook: The Complete Reference for Choosing, Installing, and Understanding Boat Propellers; International Marine/Ragged Mountain Press: Camden, ME, USA, 2001. [Google Scholar]
- Comstock, J. (Ed.) Principles of Naval Architecture; Society of Naval Architects and Marine Engineers: New York, NY, USA, 1967; Volume 2. [Google Scholar]
- Bernitsas, M.M.; Ray, D. Optimal Revolution B-Series Propellers; University of Michigan: Ann Arbor, MI, USA, 1982. [Google Scholar]
- Windyandari, A.; Haryadi, G.D.; Suharto, S. Design and Performance Analysis of B-Series Propeller for Traditional Purse Seine Boat in the North Coastal Region of Central Java Indonesia. J. Appl. Eng. Sci. 2018, 16, 494–502. [Google Scholar] [CrossRef]
- Tadros, M.; Boulougouris, E. Performance Assessment of B-Series Marine Propellers with Cupping and Face Camber Ratio Using Machine Learning Techniques. J. Mar. Sci. Eng. 2025, 13, 1345. [Google Scholar] [CrossRef]
- Kusuma, C.; Ariana, I.M.; Nugroho, W.H.; Indiaryanto, M.; Ali, B. Development of Optimum Design B-Series Propeller with Engine Propeller Matching, A Case Study 60-Meters Patrol Boat. Int. J. Mar. Eng. Innov. Res. 2022, 7, 116–125. [Google Scholar] [CrossRef]
- Friendship Systems AG. Wageningen B-Series Propeller Generator. 2021. Available online: https://www.wageningen-b-series-propeller.com/ (accessed on 1 July 2025).
- Nayar, K.G.; Sharqawy, M.H.; Banchik, L.D.; Lienhard, J.H. Thermophysical Properties of Seawater: A Review and New Correlations. Desalination 2016, 390, 1–24. [Google Scholar] [CrossRef]
- Bernitsas, M.M.; Ray, D. Optimal Diameter B-Series Propellers; University of Michigan: Ann Arbor, MI, USA, 1982. [Google Scholar]
- Bernitsas, M.M.; Ray, D.; Kinley, P. KT, KQ and Efficiency Curves for the Wageningen B-Series Propellers; The University of Michigan: Ann Arbor, MI, USA, 1981. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. A Globally Convergent Augmented Langrangian Algorithm for Optimization with General Constraints and Simple Bounds. SIAM J. Numer. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef]
- Benini, E. Multiobjective Design Optimization of B-Screw Series Propellers Using Evolutionary Algorithms. Mar. Technol. SNAME News 2003, 40, 229–238. [Google Scholar] [CrossRef]
- Chen, J.-H.; Shih, Y.-S. Basic design of a series propeller with vibration consideration by genetic algorithm. J. Mar. Sci. Technol. 2007, 12, 119–129. [Google Scholar] [CrossRef]
- Suen, J.-B.; Kouh, J.-S. Genetic Algorithms for Optimal Series Propeller Design. WIT Trans. Built Environ. 1999, 45, 237–246. [Google Scholar]
- Karim, M.; Ikehata, M. A Genetic Algorithm (GA) Based Optimization Technique for the Design of Marine Propeller. In Proceedings of the SNAME 9th Propeller and Shafting Symposium, Virginia Beach, VA, USA, 20–21 September 2000. [Google Scholar]
- Oosterveld, M.W.C.; van Oossanen, P. Further Computer-analyzed data of the Wageningen B-screw series. Int. Shipbuild. Prog. 1975, 22, 251–262. [Google Scholar] [CrossRef]
- Lerbs, H.W. On the Effects of Scale and Roughness on Free Running Propellers. J. Am. Soc. Nav. Eng. 1951, 63, 58–94. [Google Scholar] [CrossRef]
- Heinke, H.-J.; Hellwig-Rieck, K.; Lubke, L. Influence of the Reynolds Number on the Open Water Characteristics of Propellers with Short Chord Lengths. In Proceedings of the Sixth International Symposium on Marine Propulsors, Rome, Italy, 26–30 May 2019. [Google Scholar]
- Marley, J. Exclusive Feature: How Are the Latest Developments in Propeller Design Optimizing Electric and Hybrid Vessels? Electr. Hybrid Mar. Technol. Int. 2024, 34–38. Available online: https://www.electrichybridmarinetechnology.com/features/exclusive-feature-how-are-the-latest-developments-in-propeller-design-optimizing-electric-and-hybrid-vessels.html (accessed on 1 September 2025).
- Medina, M.A. The Future of Maritime Transport: Electric Ships That Can Carry Hundreds of Containers and Thousands of People. El Pais, 4 October 2024. Available online: https://english.elpais.com/climate/2024-10-04/the-future-of-maritime-transport-electric-ships-that-can-carry-hundreds-of-containers-and-thousands-of-people.html (accessed on 1 September 2025).
- Wu, J.; Wang, Q.; Deasy, H.; Hang, J. A Study on the Effect of Toroidal Propeller Parameters on Efficiency and Thrust. Energies 2024, 17, 5938. [Google Scholar] [CrossRef]
- Frouin, H. BlueNav Whale Design Embodies the Sophistication of Nature’s Influence. 31 May 2004. Available online: https://bluenav.com/en/bluenav-whale-design/ (accessed on 1 September 2025).
- Song, Y.; Yu, H.; Chen, C.-C.; Liu, C.-Y.; Yang, Y.; Chi, C. Performance Analysis of a Propeller with Surface Protrusions. Sens. Mater. 2022, 34, 3857–3868. [Google Scholar] [CrossRef]
- Arifin, M.D.; Felayati, F.M.; Muhammad, A.H. Flow Separation Evaluation on Tubercle Ship Propeller. CFD Lett. 2022, 14, 43–50. [Google Scholar] [CrossRef]
- Hydro Impulse Systems GmbH. 2024. Available online: https://www.hydroimpulse.com/hi-rf-11-mitek-high-efficiency-propeller-replacement (accessed on 1 September 2025).
- Sharrow, G.C. Propeller. US Patent US9926058B2, 27 March 2018. [Google Scholar]
- Friedman, M. Sharrow Engineering Granted Additional 42 Patents for Groundbreaking Propeller Design. 16 May 2022. Available online: https://www.businesswire.com/news/home/20220516005558/en/Sharrow-Engineering-Granted-Additional-42-Patents-For-Groundbreaking-Propeller-Design (accessed on 1 September 2025).
- BlueRobotics Inc. T200 Public Performance Data 10-20V September 2019. Available online: https://cad.bluerobotics.com/T200-Public-Performance-Data-10-20V-September-2019.xlsx (accessed on 5 September 2025).
- Mevey, J.R. Sensorless Field Oriented Control of Brushless Permanent Magnet Synchronous Motors; Kansas State University: Manhattan, KS, USA, 2006. [Google Scholar]
- Parsons, R. How to Estimate the Torque of a BLDC (PMSM) Electric Motor Using Only Its Kv and Current Draw. 25 December 2018. Available online: https://things-in-motion.blogspot.com/2018/12/how-to-estimate-torque-of-bldc-pmsm.html (accessed on 25 July 2025).
- Bales, N.K.; Cummins, W.E. The Influence of Hull Form on Seakeeping; Society of Naval Architects and Marine Engineers: Jersey City, NJ, USA, 1970. [Google Scholar]
- Walden, D.A.; Grundmann, P. Seakeeping Optimization; US Department of the Navy: Bethesda, MD, USA, 1985. [Google Scholar]
- Serani, A.; Diez, M. Hydrodynamic Shape Optimization of a Naval Destroyer by Machine Learning Methods. J. Mar. Sci. Eng. 2024, 12, 1979. [Google Scholar] [CrossRef]
- Grigoropoulos, G. Hull Form Optimization for Hydrodynamic Performance. Mar. Technol. SNAME News 2004, 41, 167–182. [Google Scholar] [CrossRef]
- Deng, R.; Wang, S.; Hu, Y.; Wang, Y.; Wu, T. The Effect of Hull Form Parameters on the Hydrodynamic Performance of a Bulk Carrier. J. Mar. Sci. Eng. 2021, 9, 373. [Google Scholar] [CrossRef]
- Vázquez-Santos, A.; Camacho-Zamora, N.; Hernández-Hernández, J.; Herrera-May, A.; Santos-Cortes, L.; Tejeda-del-Cueto, M. Numerical Analysis and Validation of an Optimized B-Series. J. Mar. Sci. Eng. 2024, 2, 12. [Google Scholar]
- Arapakopoulos, A.; Abt, C.; Hauschulz, S.; Harries, S. Optimization and Surrogate Modeling of Tip-Rake Propellers. In Proceedings of the Eighth International Symposium on Marine Propulsors, Berlin, Germany, 17–20 March 2024. [Google Scholar]
- Tan, Q.; Yu, D.; Liu, J.; Sui, C. CFD-based hull-engine-propeller matching study after retrofitting propeller boss-cap-fin (PBCF). Ocean. Eng. 2023, 285, 115364. [Google Scholar] [CrossRef]
- Ristea, M.; Popa, A.; Volintiru, O.-N. CFD Design Performance Analysis for a High-Speed Propeller. Appl. Sci. 2025, 15, 8754. [Google Scholar] [CrossRef]
- Yusvika, M.; Prabowo, A.; Tjahjana, D.; Sohn, J. Cavitation Prediction of Ship Propeller Based on Temperature and Fluid Properties of Water. J. Mar. Sci. Eng. 2020, 8, 465. [Google Scholar] [CrossRef]
- Benoumessad, K.; Fourar, F.Z.; Fourar, A.; Massouh, F. Modeling Turbulent Flow Velocity Profiles in Irregularly shaped Open Channels: A 3D Approach. Eng. Technol. Appl. Sci. Res. 2025, 15, 22203–22208. [Google Scholar] [CrossRef]
- Seok, W.; Lee, S.; Rhee, S. Computational simulation of turbulent flows around a marine propeller by solving the partially averaged Navier–Stokes equation. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6357–6366. [Google Scholar] [CrossRef]
- Bakhtiari, M.; Ghassemi, H. Numerical analysis on effects of blade number on hydrodynamic performance of low-pitch marine cycloidal propeller. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2019, 234, 490–501. [Google Scholar]
- Krasilnikov, V.; Skjefstad, V.; Koushan, K.; Rambech, H. A Calibration Study with CFD Methodology for Self-Propulsion Simulations at Ship Scale. J. Mar. Sci. Eng. 2023, 11, 1342. [Google Scholar] [CrossRef]
- Maupin, K.A.; Swiler, L.P.; Porter, N.W. Validation Metrics for Deterministic and Probabilistic Data. J. Verif. Valid. Uncertain. Quantif. 2018, 3, 031002. [Google Scholar] [CrossRef]
- Gaafary, M.M.; El-Kilani, H.; Moustafa, M.M. Optimum design of B-series marine propellers. Alex. Eng. J. 2011, 50, 13–18. [Google Scholar] [CrossRef]
- Taylor, D.W. The Speed and Power of Ships; Ranskell Incorporated: Washington, DC, USA, 1933. [Google Scholar]
- Motor, M. Standard Specifications: RZ-735VA-9517. Available online: https://product.mabuchi-motor.com/detail.html?id=131. (accessed on 1 July 2025).
- Qin, Z.; Wu, Y.-T.; Eizad, A.; Lee, K.-H.; Lyu, S.-K. Design and Evaluation of Two-Stage Planetary Gearbox for Special Purpose Industrial Machinery. J. Mech. Sci. Technol. 2019, 33, 5943–5950. [Google Scholar] [CrossRef]
- Du, Q.; Yang, G.; Wang, W.; Chen, C.-Y.; Fang, Z. Modeling and Analysis of Transmission Efficiency for 3K Planetary Gearbox with Flexure-Based Carrier for Backdrivable Robot Joints. Actuators 2025, 14, 173. [Google Scholar] [CrossRef]
- Anderson, N.E.; Loewenthal, S.H. Spur-Gear-System Efficiency at Part and Full Load; National Aeronautics and Space Administration: Washington, DC, USA, 1980. [Google Scholar]
- Turnigy Power Systems. Turnigy XK3674-1650KV 2400W Inrunner. 2023. Available online: https://hobbyking.com/en_us/turnigy-xk3674-1650kv-2400w-inrunner.html (accessed on 1 July 2025).
- UltiMaker. The Ultimaker 2 Specifications. 20 February 2023. Available online: https://support.makerbot.com/s/article/1667337895715 (accessed on 1 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).