Optimization of Inlet Flow Pattern and Performance Enhancement in Oil-Gas Multiphase Pumps Using Helical Static Mixer

Abstract

With increasing global energy demand and depletion of onshore oil–gas resources, deep-sea hydrocarbon exploration and development have become strategically vital. As core subsea transportation equipment, the performance of helico-axial multiphase pumps directly determines the efficiency and economic feasibility of deep-sea extraction. However, non-uniform inflow patterns caused by uneven gas–liquid distribution in pipelines degrade pressure-boosting capability and reduce pump efficiency under actual operating conditions. To address this, an optimization method employing helical static mixers was developed. A mixer with a 180° helical angle was designed and installed upstream of the pump inlet. Numerical simulations demonstrate that the mixer enhances gas-phase distribution uniformity in stratified flow, improving efficiency and head across varying gas void fractions (GVFs). At a stratification height ratio (Ψ) of 0.32, efficiency increased by 15.41% and head rose by 15.64 m, while turbulent kinetic energy (TKE) at the impeller outlet decreased by up to 50%. For slug flow conditions, the mixer effectively suppressed gas volume fraction fluctuations, consistently improving efficiency under different slug flow coefficients (φ) with a maximum head increase of 9.82%. The optimized flow field exhibits uniform gas–liquid velocity distribution, stable pressure boosting, and significantly reduced TKE intensity within impeller passages.

1. Introduction

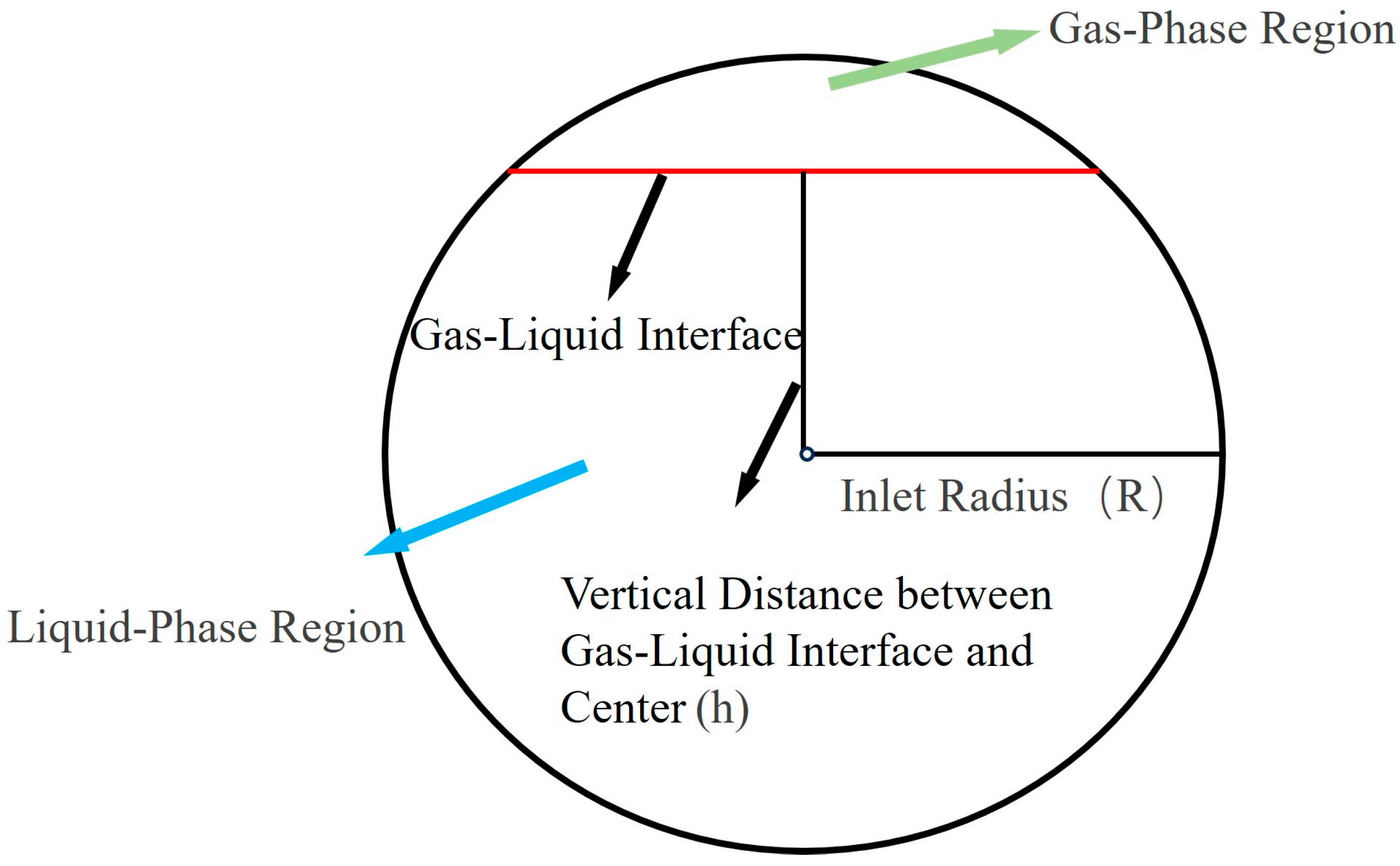
In actual operating conditions, the inlet of the helical-axial multiphase pump often experiences non-uniform inflow due to factors such as pipeline layout, flow pattern evolution, and interphase interactions. Among these, stratified flow and slug flow, which are most common in actual operating conditions, can lead to phase distribution imbalance in the impeller region, aggravate the gas blockage phenomenon, induce hydraulic pulsation, efficiency degradation, and head fluctuation, and even cause cavitation and mechanical vibration in severe cases, thereby affecting the efficient and safe operation of the multiphase transport system [1,2,3,4]. Studies have shown that flow pattern change and non-uniform phase distribution of the flow medium at the inlet are among the main factors affecting the multiphase pump. The internal flow resistance caused by turbulent dissipation in the multiphase flow pipeline and the off-design condition pressure drop caused by pressure gradient fluctuation result in non-ideal flow, which can severely affect the efficient, safe, and reliable operation of multiphase pumps. In [5,6,7,8,9], the authors investigated the effect of non-uniform inflow on the performance of a water-jet propulsion pump, finding that non-uniformity at the suction inlet led to a significant decrease in the pump head. Luo X [10] studied the mechanism of energy loss and pressure fluctuation caused by non-uniform inflow in a water-jet propulsion pump, demonstrating that non-uniform inflow reduces head and efficiency while increasing impeller axial force fluctuation, resulting in large pulsations in unsteady energy performance.

Traditional improvement methods mainly focus on pump body structure optimization or operation parameter adjustment. Zhang et al. [11] proposed three modification methods, namely, adding a splitter blade to the blade trailing edge, blade perforation, and adding a T-shaped blade, all of which were verified by numerical calculation. The results showed that all three modification methods can improve the boosting capacity of the multiphase pump. Han Wei’s research group [12,13,14,15] proposed modification schemes including slotting treatment of the blades, modifying the leading edge of the blades with bionics, installing a turbulence generator on the blades, and adding a flap, achieving considerable progress. However, regulation ability remained limited in the face of complex and variable inlet conditions.

In recent years, static mixers, as flow field homogenization devices without moving parts, have shown significant advantages in the process industry due to their simple structure, low energy consumption, and ease of integration. In the Poseidon multiphase pump test, it was found that by setting a homogenizer at the front end of the pump, the flow at the multiphase pump inlet was more stable after the buffer mixing effect of the buffer while maintaining the rotational speed [16]. The FRAMO Company designed a buffer homogenizer at the inlet. Experimental studies have found that after the incoming flow passes through the buffer homogenizer, the gas holdup is more stable than before, which greatly alleviates the harsh conditions at the pump inlet [17]. Zhang Jinya et al. [18] conducted gas–liquid two-phase visualization experiments at the impeller inlet and installed a buffer homogenization device at the front end of the multiphase pump. This device reduced the uneven gas–liquid conditions at the pump inlet [19]. Among them, the helical static mixer, with its unique swirl shear mechanism, can efficiently break up gas-phase clusters and promote interphase mixing, providing a new approach for optimizing inlet flow patterns. Static mixers are mainly classified into plate, helical, helical blade, and grid mixers, among others, according to their structure and working principle. Different types of mixers have different advantages in specific applications and are suitable for different fluid mixing requirements. Wang’s team [20] first systematically conducted experiments on gas–liquid two-phase helical flow in horizontal pipes. They used a high-speed camera to study the flow pattern of gas–liquid two-phase helical flow in horizontal pipes and found that the distribution of two-phase flow was more complex in helical flow, making the gas and liquid phases more evenly distributed in the pipe. Therefore, helical static mixers are the preferred solution for gas–liquid two-phase flow mixing problems thanks to their excellent fluid disturbance capability, low flow resistance, and outstanding bubble breakup effect [21].

This paper proposes an innovative scheme integrating a helical static mixer in the front stage of a helical axial-flow multiphase pump, aiming to actively intervene in the flow field through a pre-mixing section in order to achieve homogenization reconstruction of non-uniform inflow (stratified flow and slug flow). The optimal structural parameters of the mixer are obtained through a Box–Behnken design. The influence of the helical static mixer on the head, efficiency, and internal flow characteristics of the multiphase pump after optimizing the non-uniform inflow is investigated using computational fluid dynamics (CFD) multiphase flow simulation, which provides a new solution for the efficient and stable operation of multiphase pumps under non-uniform inflow conditions.

2. Optimization Design of Helical Static Mixers

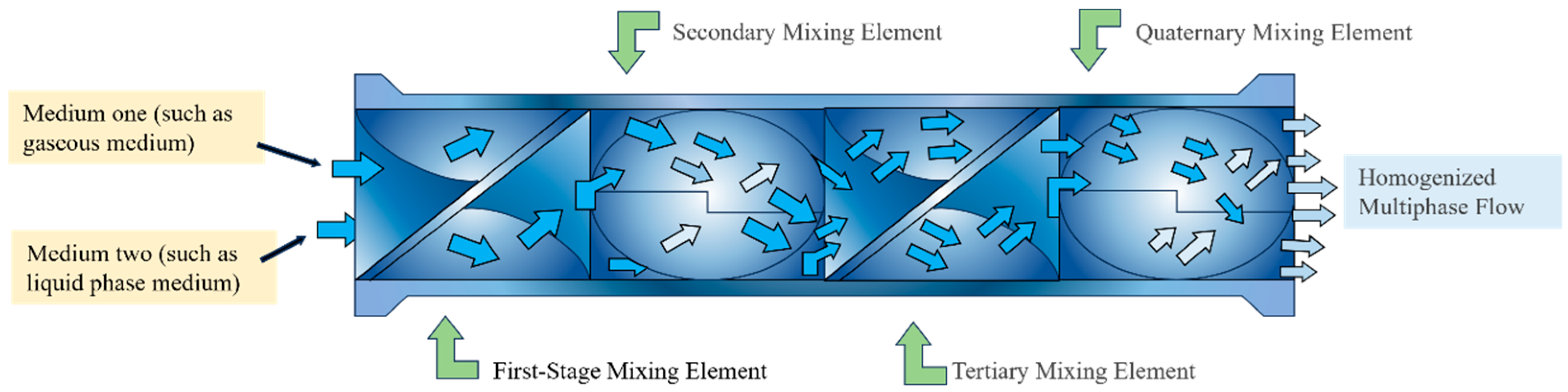
Unlike traditional mechanical mixers that rely on moving parts, this static mixer is based on fixed helical blade disturbance elements, inducing rotational motion and enhancing turbulence intensity as fluid flows through. The core mechanism lies in the strong shear force generated by the helical flow channel; as shown in Figure 1, this efficiently breaks gas bubbles and liquid droplet clusters, while the fluid rotation enhancement promotes sufficient contact between the gas and liquid phases. Furthermore, the helix angle and number of blades can be optimized to adapt to flow rate variations, thereby improving mixing efficiency while minimizing flow resistance.

When designing a helical static mixer, the primary task is to rationally determine its various design parameters. These parameters largely dictate the mixer’s actual working capacity and mixing efficiency in gas–liquid two-phase flows. For the structure of a helical static mixer, four factors are crucial to its mixing ability: the helix angle of the front, the helix angle of the rear, the unit length, and the blade thickness.

Therefore, this paper employs the Box–Behnken Design (BBD) experimental design method in Design-Expert software to optimize the mixing design of the helical static mixer with respect to these four influencing factors. The results of the experimental design are presented in

Table 1. Levels of factors in BBD.

Factor	Structural Parameter	Low Level	High Level
A	Front Helical Angle (°)	90	180
B	Rear Helical Angle (°)	45	135
C	Unit length (mm)	90	225
D	blade thickness (mm)	7.5	22.5

.

The design points and corresponding simulation results derived from the BBD methodology are presented in

Table 2. Different design schemes and results.

No.	Front Helix Angle (°)	Rear Helix Angle (°)	Unit Length (mm)	Blade Thickness (mm)	Efficiency (%)	Head (m)
1	180	90	150	15	58.97	27.14
2	180	90	225	7.5	59.32	27.03
3	180	45	90	15	58.46	26.71
4	180	135	90	15	58.88	26.95
5	225	90	90	15	58.25	26.63
6	180	90	225	22.5	59.45	27.08
7	180	90	150	15	58.97	27.14
8	180	90	90	7.5	58.81	26.92
9	180	45	150	7.5	58.52	26.77
10	180	135	150	7.5	58.95	27.06
11	180	135	150	22.5	59.18	27.12
12	90	90	150	7.5	58.43	26.68
13	180	90	150	15	58.97	27.14
14	180	45	225	15	58.37	26.61
15	90	90	150	22.5	58.56	26.83
16	225	45	150	15	58.22	26.58
17	90	45	150	15	58.31	26.65
18	180	135	225	15	58.76	26.98
19	90	90	225	15	58.49	26.79
20	225	90	225	15	58.66	26.91
21	180	90	150	15	58.97	27.14
22	180	45	150	22.5	58.89	27.01
23	180	90	90	22.5	59.06	27.09
24	225	135	150	15	58.61	26.87
25	90	90	90	15	58.27	26.59
26	90	135	150	15	58.53	26.81
27	180	90	150	15	58.97	27.14

.

The regression equation fitted for efficiency is expressed in Equation (1).

$$\begin{array}{c}\eta =60.02+3.54A+1.55B+2.15C+0.983D+1.03AB-0.2487AC+1.3AD+1.78BC+0.5275BD\\ +0.0922CD-16.71A^2-12.55B^2-11.31C^2-3.97D^2\end{array}$$

(1)

Analysis of variance was performed on the fitted regression equation for efficiency, with the results presented in

Table 3. Analysis of variance for efficiency regression model.

Source	Sum of Squares	Mean Square	F	p
Model	2857.14	204.08	14.28	<0.0001
A-front helix	147.91	147.91	10.35	0.0062
B-rear helix	24.82	24.82	1.74	0.2088
C-unit length	48.81	48.81	3.41	0.0859
D-blade thickness	10.04	10.04	0.7021	0.4162
AB	4.58	4.58	0.3204	0.5803
AC	0.2679	0.2679	0.0187	0.8931
AD	7.21	7.21	0.5047	0.4891
BC	12.78	12.78	0.8943	0.3603
BD	1.11	1.11	0.0779	0.7843
CD	0.0343	0.0343	0.0024	0.9616
A2	1349.93	1349.93	94.43	<0.0001
B2	1022.08	1022.08	71.5	<0.0001
C2	804.29	804.29	56.26	<0.0001
D2	102.32	102.32	7.16	0.0181

. The model’s p-value is substantially less than 0.05, indicating that these four independent variables significantly impact pump efficiency. Significance testing of the p-value and t-value reveals a large F-statistic coupled with a small p-value, demonstrating that the derived regression equation is statistically significant. Furthermore, the coefficient of determination reaches 98.52%, approaching unity, confirming its accuracy in predicting changes in the dependent variable relative to variations in the independent variables.

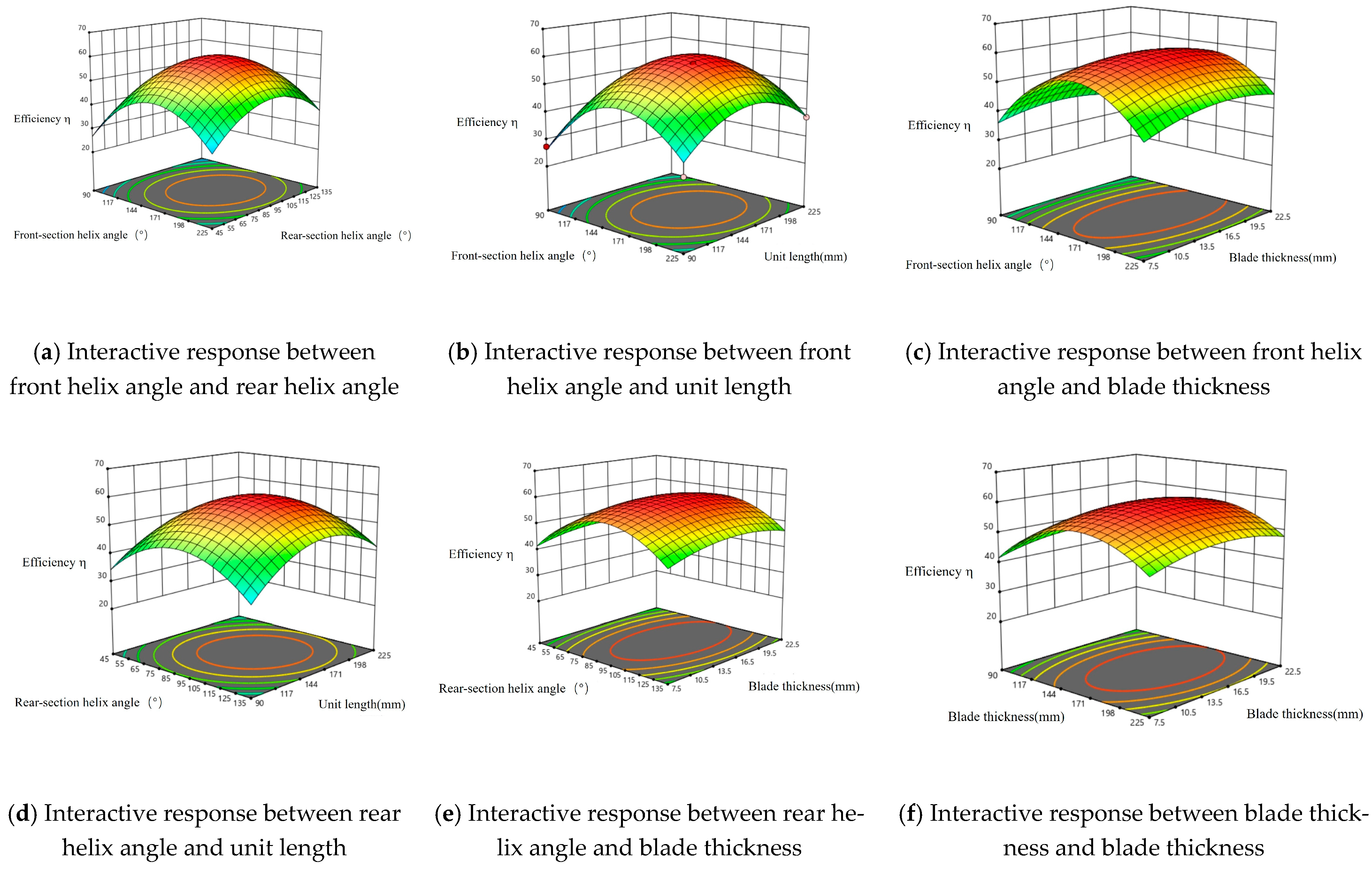
The interaction between the four variables was analyzed using three-dimensional response surface graphs. As shown in Figure 2, when the unit length is 150 mm and the blade thickness is 15 mm, with the front helix angle fixed, the efficiency first increases and then decreases as the rear helix angle increases; the same trend is observed when the rear helix angle is fixed. When the front helix angle is 150° and the rear helix angle is 90°, with the unit length kept constant, increasing the blade thickness has little effect on efficiency. However, when the blade thickness is fixed, the efficiency first increases and then decreases as the unit length increases.

The fitted regression equation for the pump head is given by Equation (2).

$$\begin{array}{c}H=27.7+1.51A+0.8801B+0.9998C+0.2128D+0.6394AB-0.1116AC+0.5628AD+0.063BC\\ -0.1325BD+0.3083DC-8.02A^2-5.83B^2-5.33C^2-2.18D^2\end{array}$$

(2)

As shown in

Table 4. Significance analysis of efficiency.

Source	Sum of Squares	Degrees of Freedom	Mean Square	F	p
Model	626.74	14	44.77	16.26	<0.0001
A-Front helix angle	26.81	1	26.81	9.73	0.0075
B-Rear helix angle	8.04	1	8.04	2.92	0.1095
C-Unit length	10.55	1	10.55	3.83	0.0705
D-Blade thickness	0.4701	1	0.4701	0.1707	0.6857
AB	1.76	1	1.76	0.6377	0.4379
AC	0.054	1	0.054	0.0196	0.8907
AD	1.36	1	1.36	0.4942	0.4936
BC	0.016	1	0.016	0.0058	0.9403
BD	0.0702	1	0.0702	0.0255	0.8754
CD	0.3833	1	0.3833	0.1392	0.7147
A2	310.73	1	310.73	112.85	<0.0001
B2	220.09	1	220.09	79.93	<0.0001
C2	178.47	1	178.47	64.82	<0.0001
D2	30.93	1	30.93	11.23	0.0047

. Its p-value is also less than 0.0001, which proves that the four independent variables have a significant impact on the head. Meanwhile, the coefficient of determination R² = 96.52%, indicating that the model has a good fitting effect on the data. Additionally, the p-value of the model is much less than 0.05, which indicates that these four independent variables have a significant impact on the pump efficiency. Moreover, through the significance test based on p-values and T-values, the large F-value and small p-value further confirm that the obtained regression equation is significant.

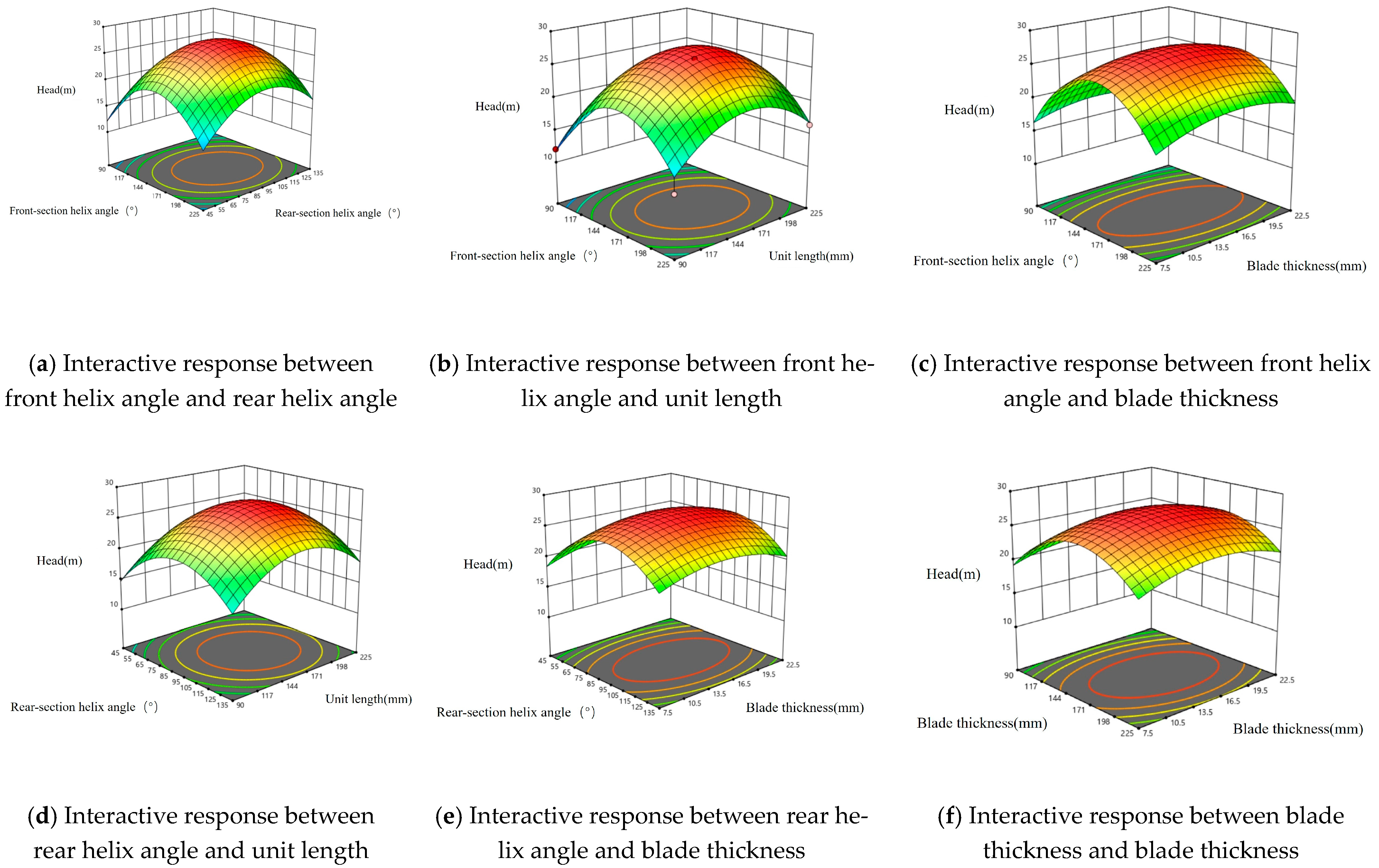
The interaction effects among the four variables were analyzed using three-dimensional response surface graphs, as illustrated in Figure 3.

Similar to the effect of variable interactions on efficiency, when the unit length is 150 mm and the blade thickness is 15 mm, with the front helix angle fixed, increasing the rear helix angle will cause the head to first increase and then decrease; the same trend applies when the rear helix angle is fixed. However, when the front helix angle is 150° and the rear helix angle is 90°, with the unit length kept constant, increasing the blade thickness has little impact on efficiency. Nevertheless, when the blade thickness is fixed, the efficiency shows< a trend of first increasing and then decreasing as the unit length increases.

To enhance both the head and efficiency of the multiphase pump, a mathematical model is established with the maximum head and maximum efficiency as the objective functions; the value ranges of the four factors are set as constraints, as follows.

$$\left\{\begin{array}{c}90<\alpha <225\\ 90<\beta <135\\ 150<\lambda <225\\ \begin{array}{c}7.5<t_b<22.5\\ f(\alpha ,\beta ,\lambda ,t_b)=max(H)\\ f(\alpha ,\beta ,\lambda ,t_b)=max()\end{array}\end{array}\right.$$

(3)

Precise optimization was conducted based on the regression equation and the imposed constraint conditions, finally obtaining the parameter combination shown in

Table 5. Structural parameters of helical static mixer.

Parameter Item	Design Value
Nominal Diameter (DN)	150 mm
Front Helix Angle(α)	180°
Rear Helix Angle (β)	90°
Unit Length (λ)	150 mm
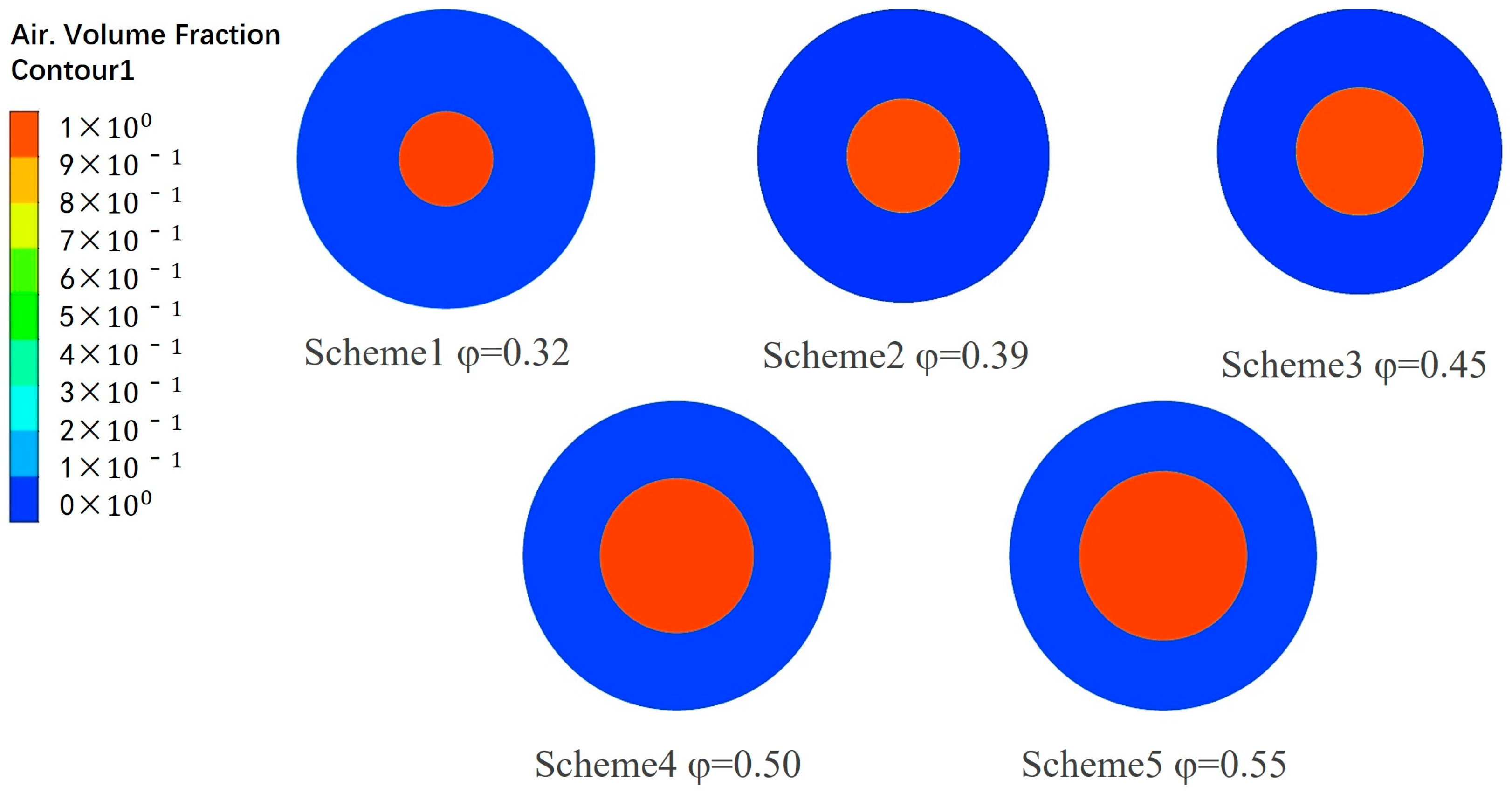
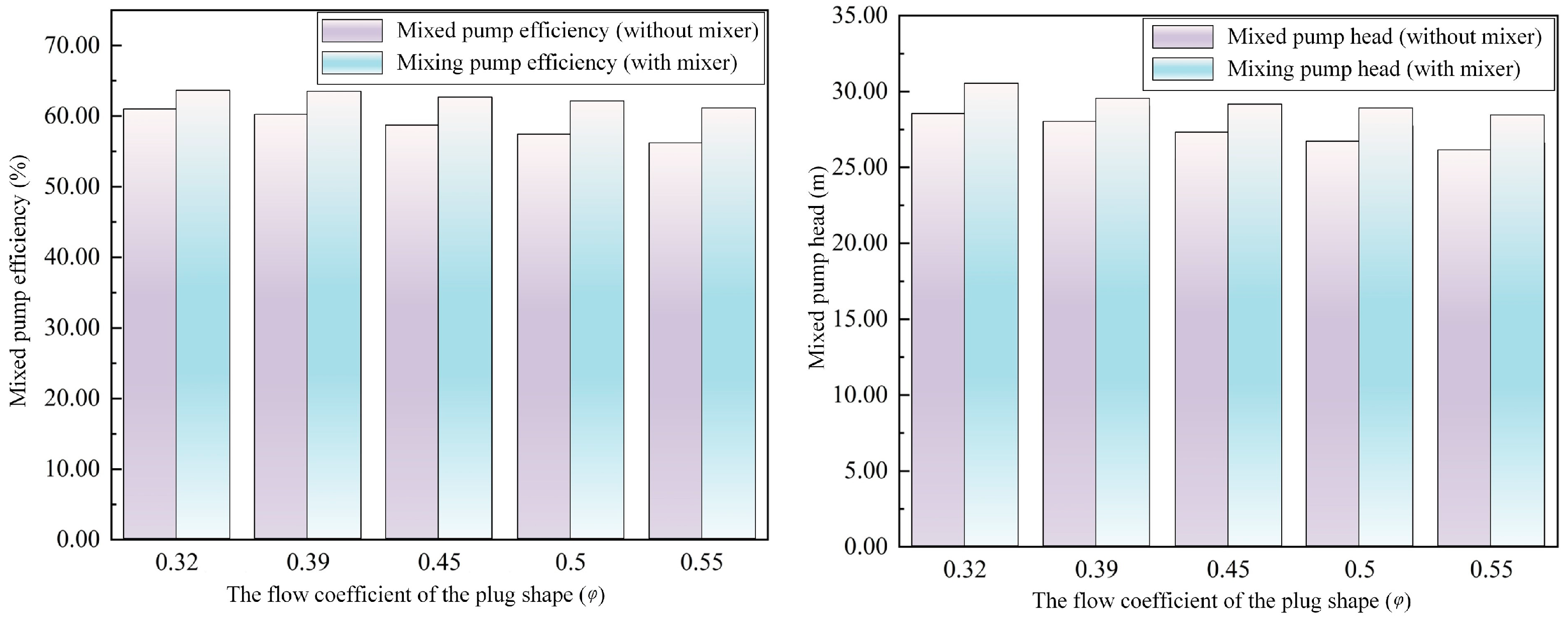
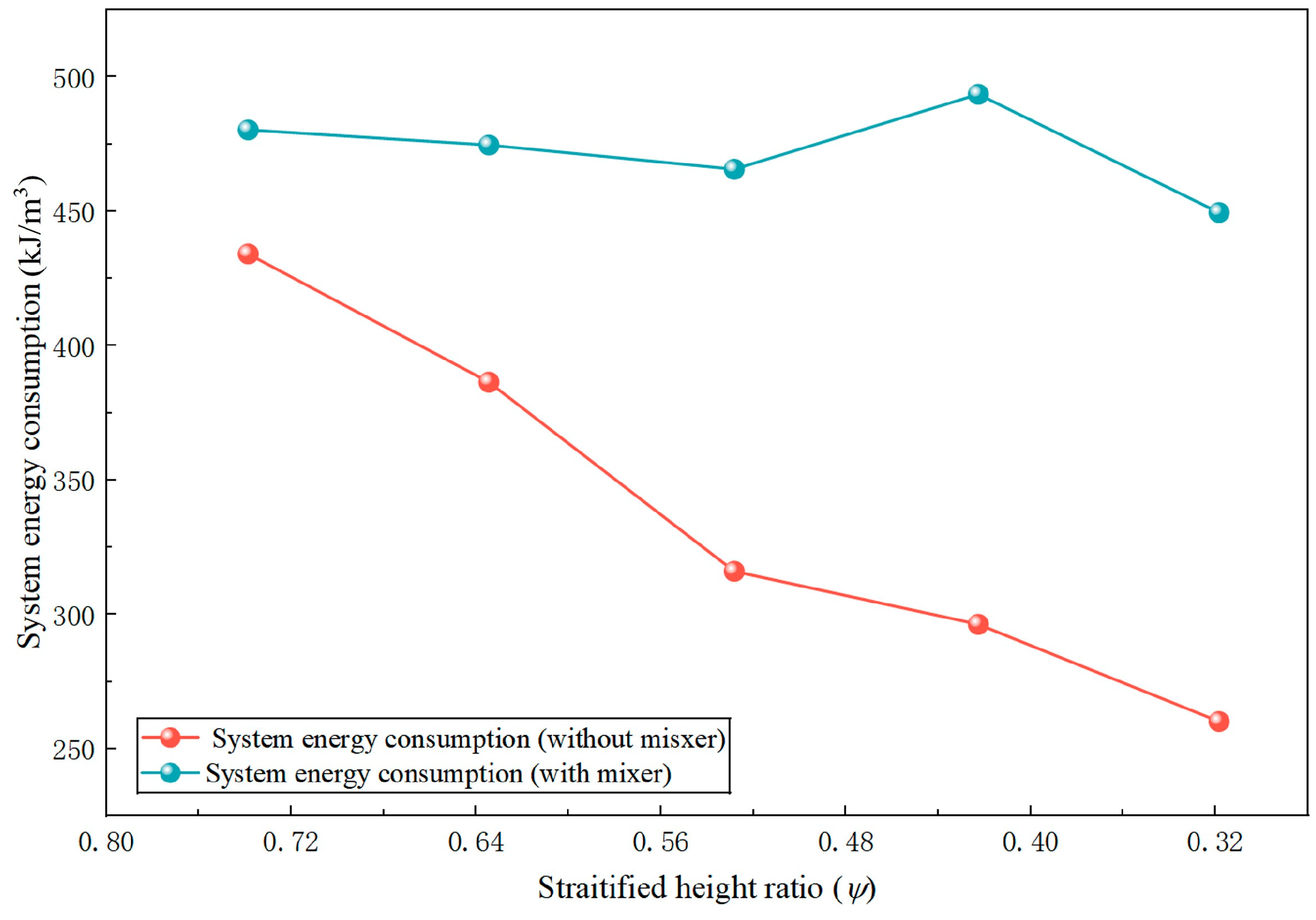
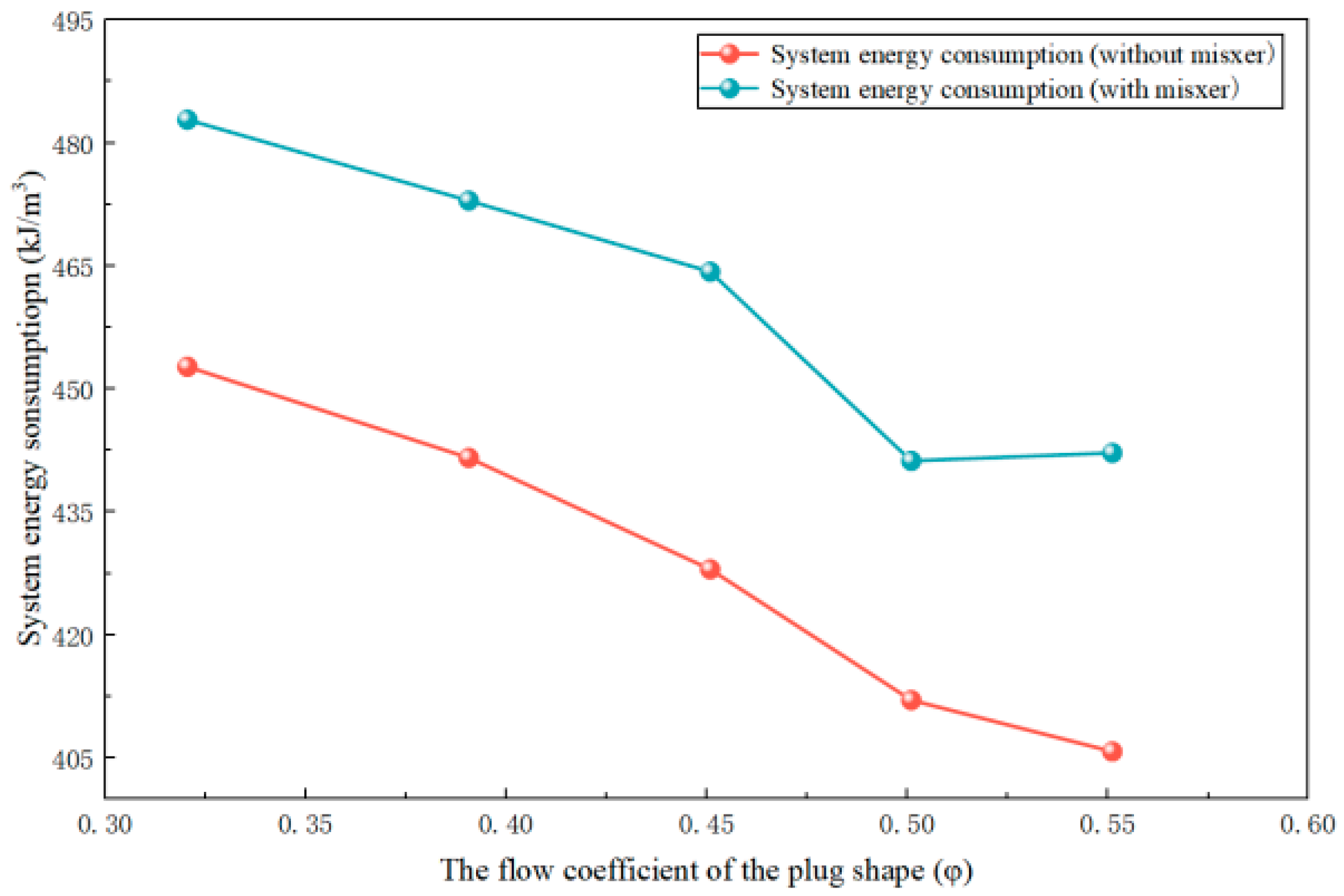
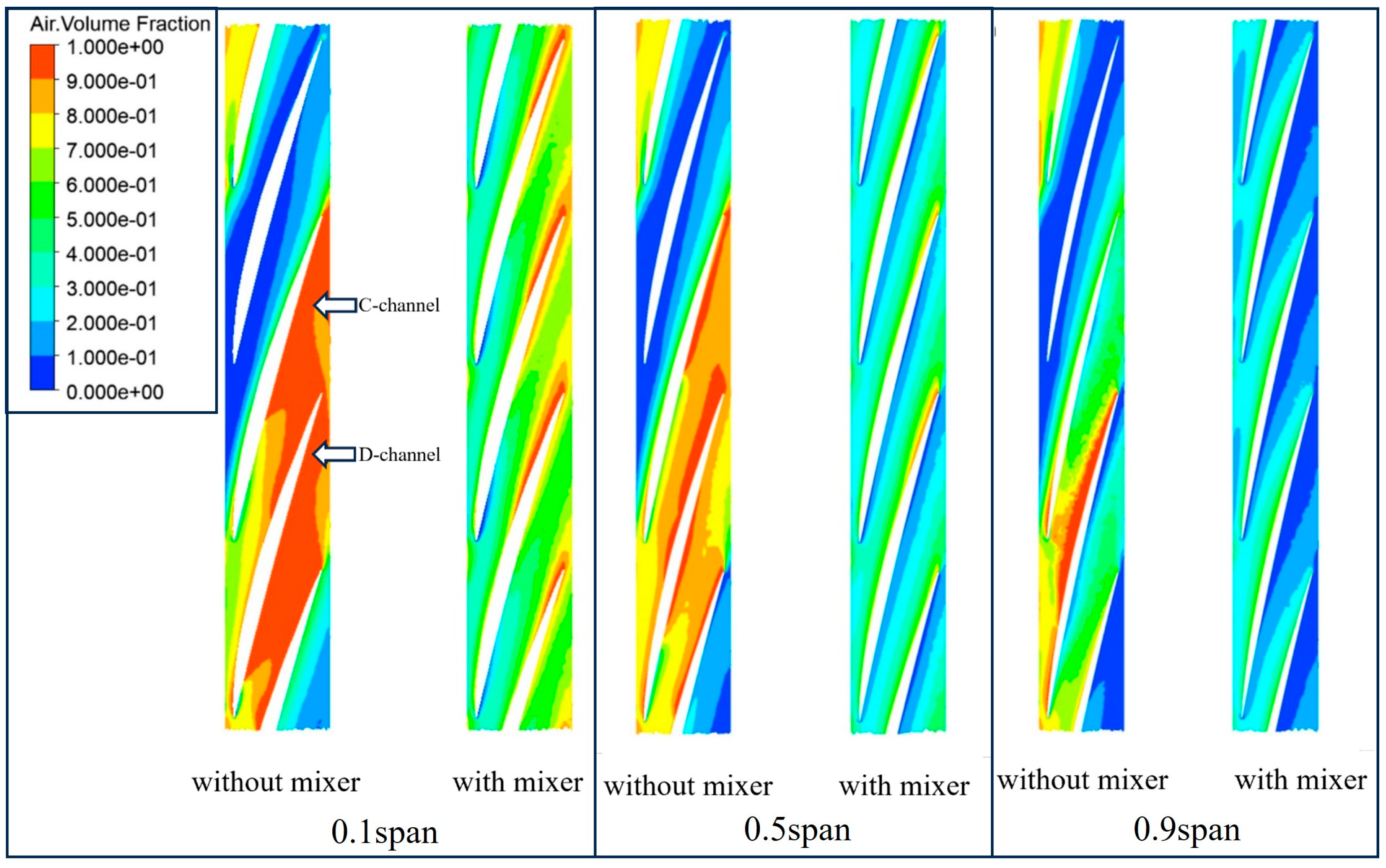
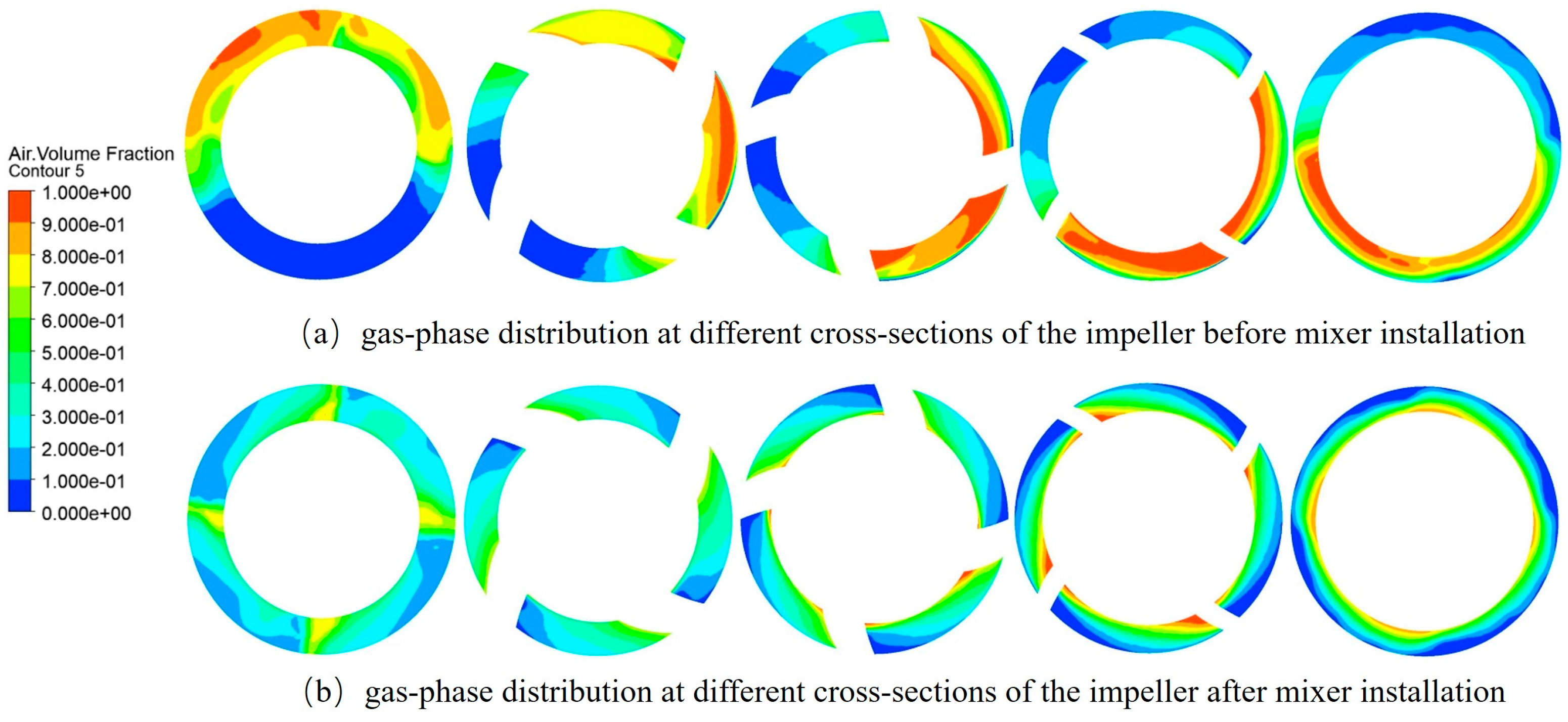
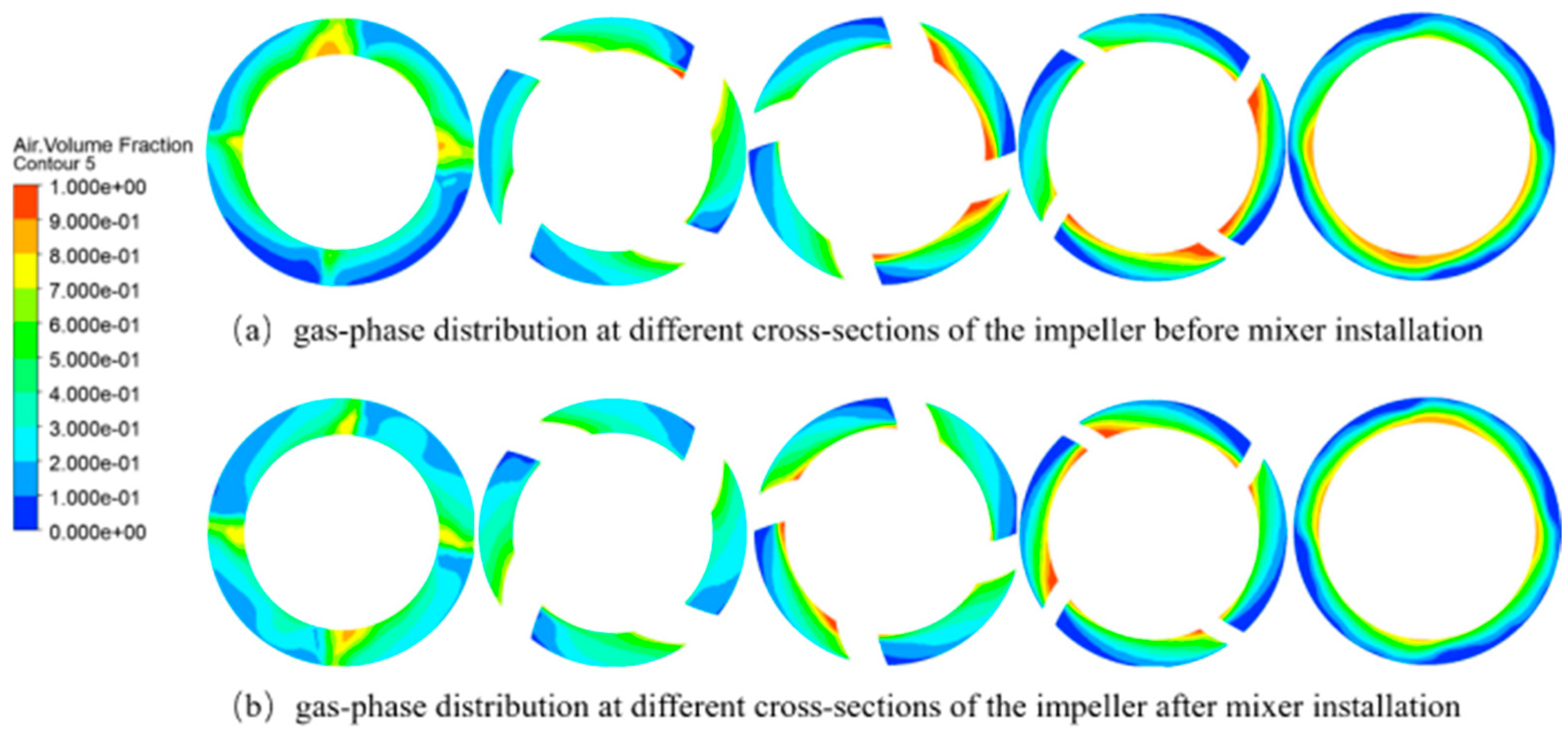
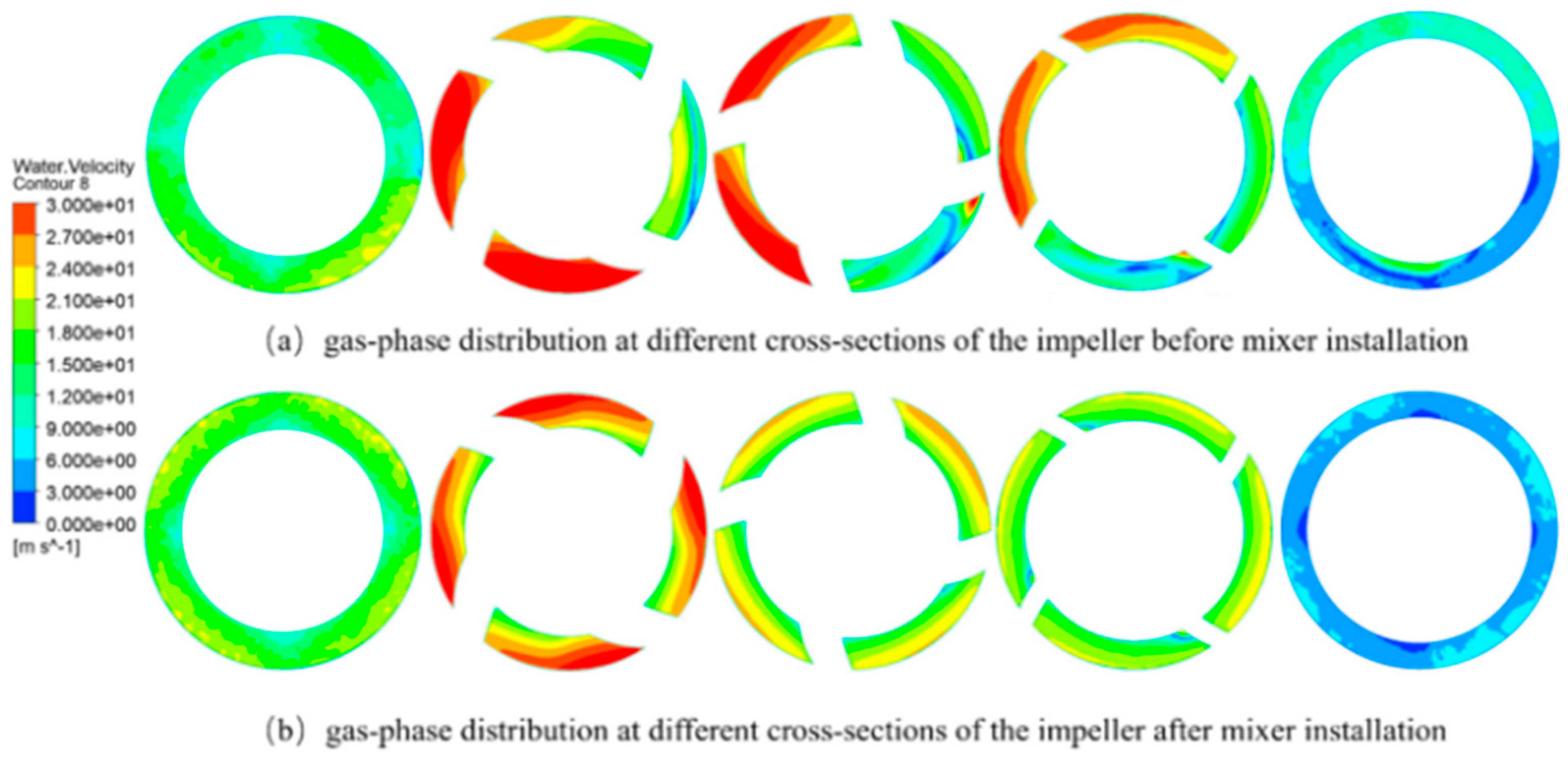
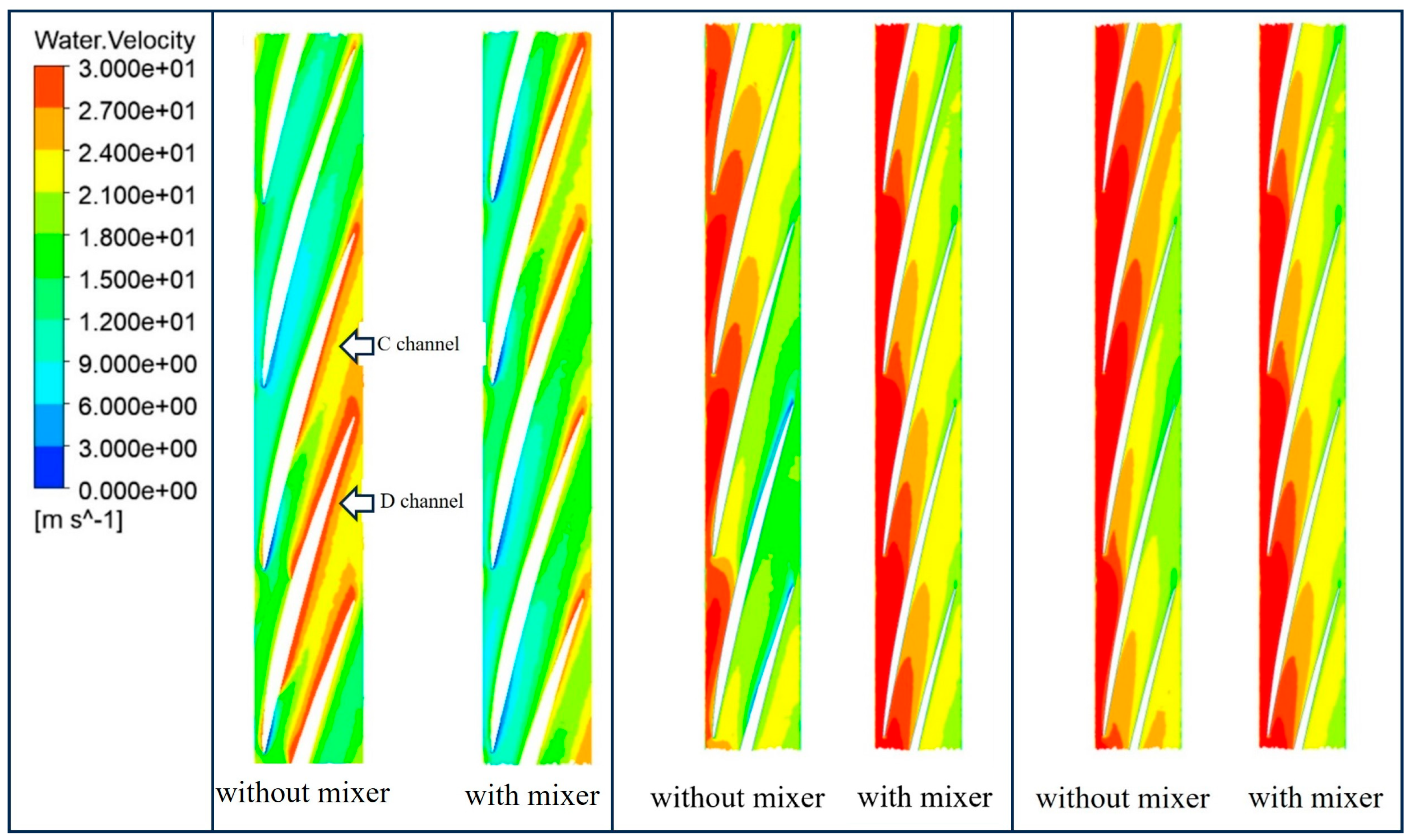
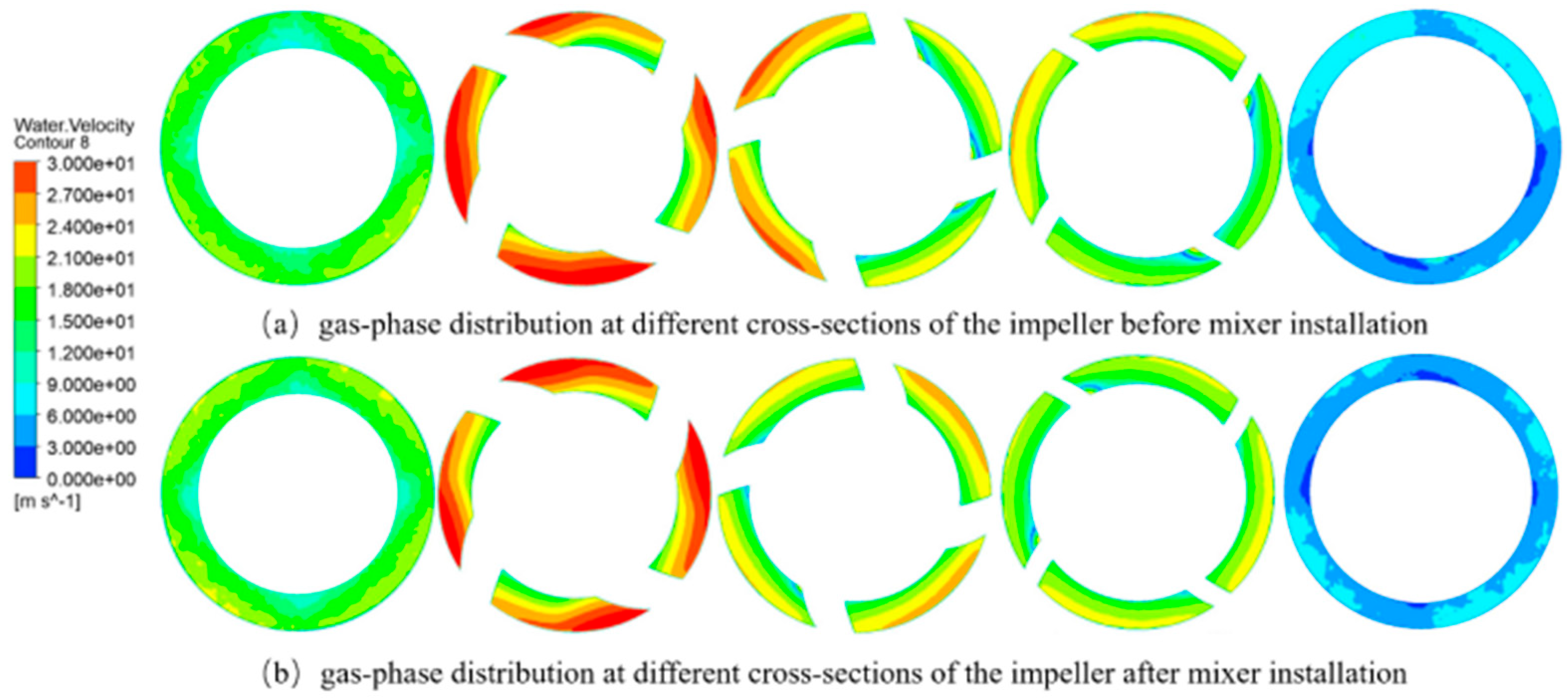
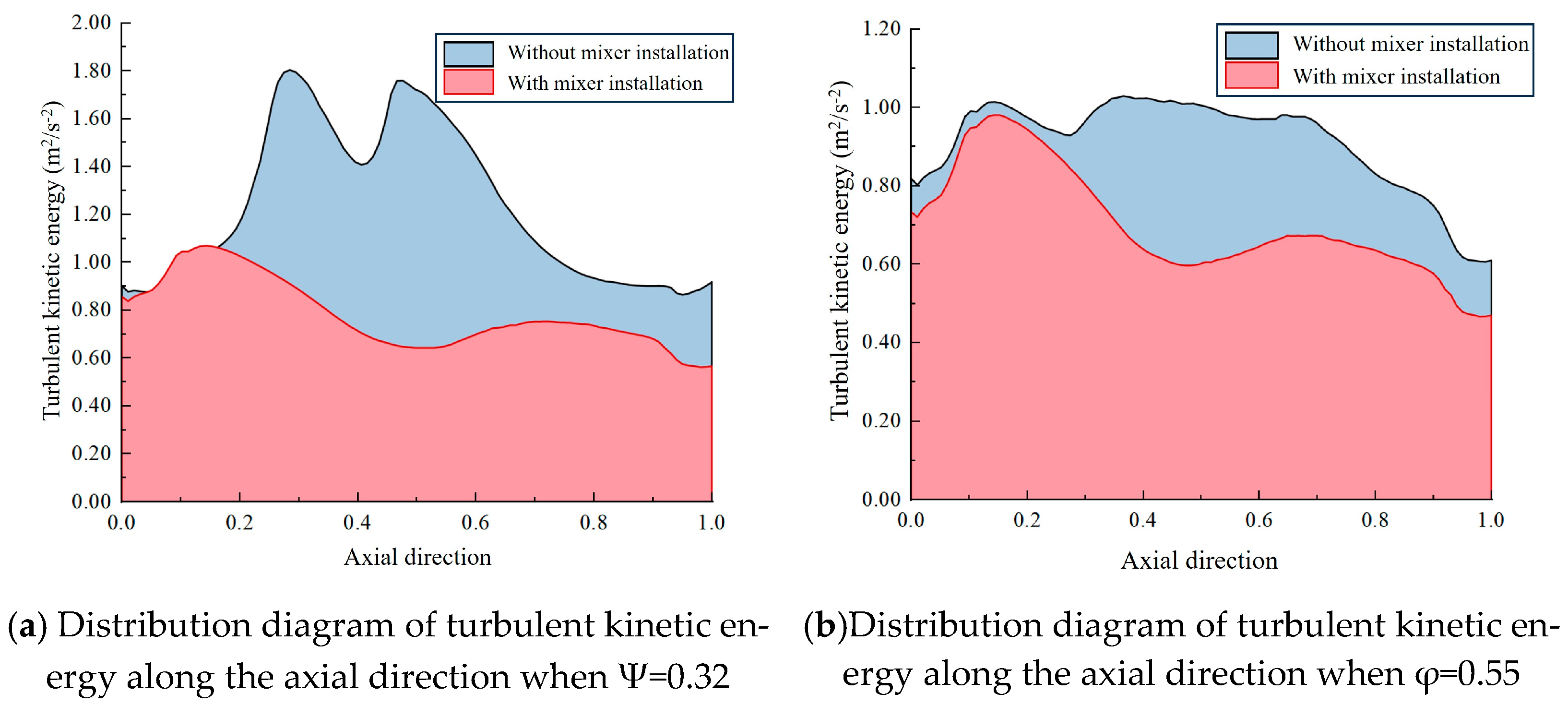
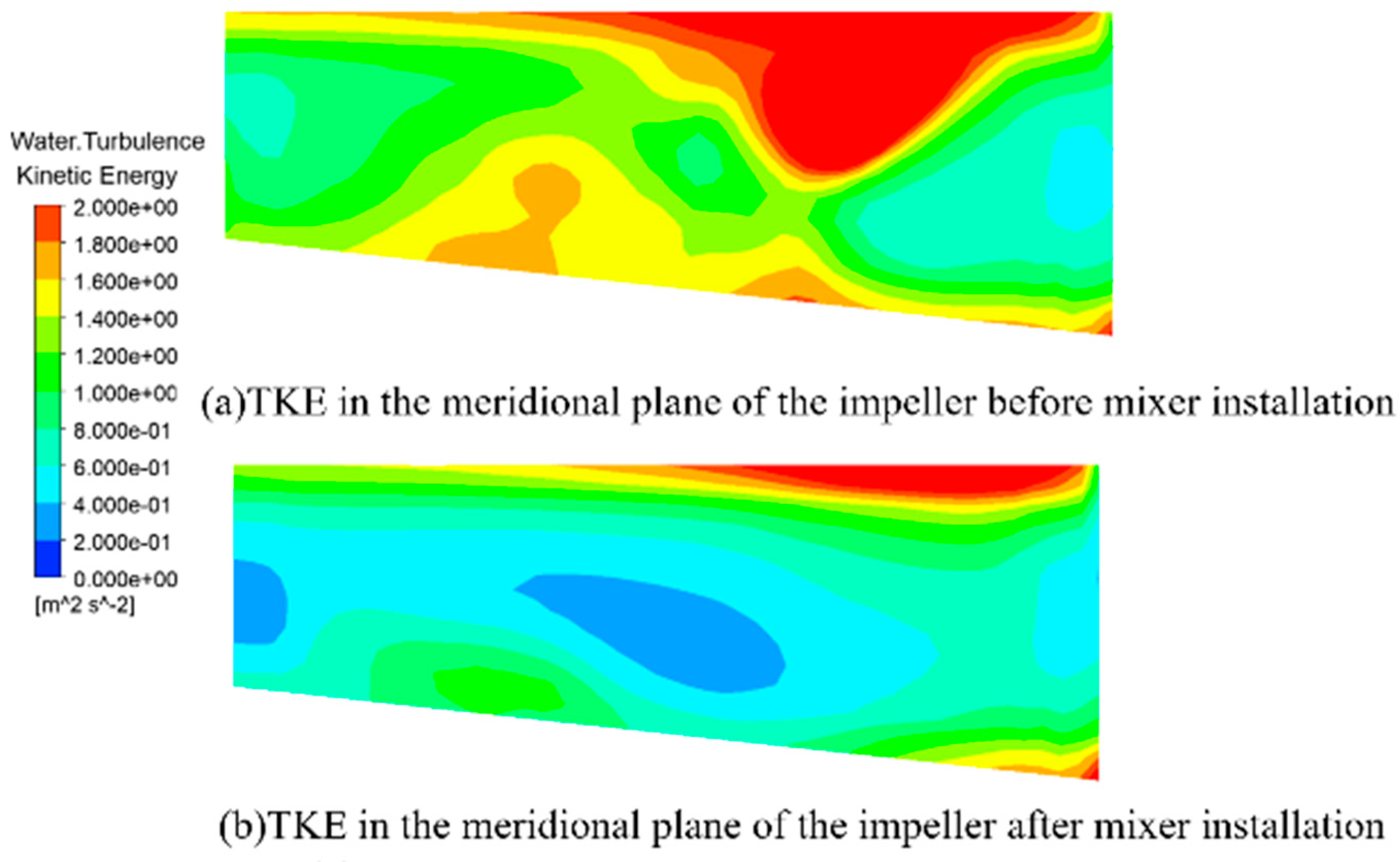
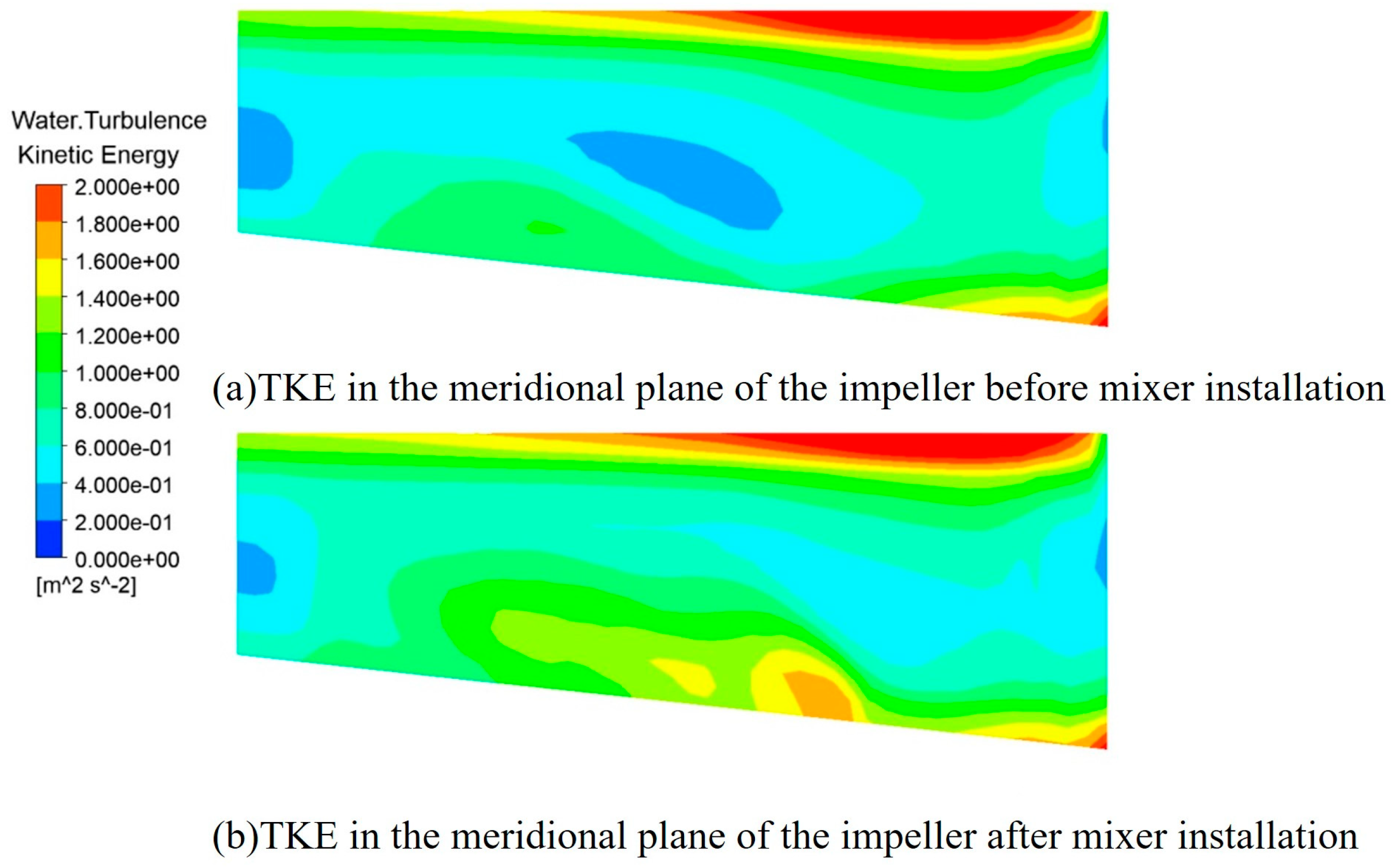
Blade Thickness (tb)	15 mm

. To further illustrate the good improvement effect on non-uniform flow of the mixer designed under these parameters, the internal flow fields of the multiphase pump before and after adding the mixer are compared and analyzed below.

In the design of static mixers, the pressure drop generated during design directly reflects the energy loss when fluid passes through the mixer. If the pressure drop is too high, the pump will need to do extra work to maintain the flow rate, resulting in increased energy consumption. Therefore, it is necessary to calculate the pressure drop and compare the calculated pressure drop ΔP with the allowable pressure drop ΔP_allow. If ΔP ≤ ΔP_allow, the design is feasible; if ΔP > ΔP_allow, the design needs to be optimized. First, the allowable pressure drop ΔP_allow is calculated as follows.

$$\Delta P_{\mathrm{allow}}=\rho gH$$

(4)

The calculation result shows that the allowable pressure drop ΔP_allow is 294.3 kPa. The pressure drop calculation formula for the helical static mixer is given in Equation (5). The calculated result is ΔP = 32.6 kPa, which is much smaller than the value of ΔP_allow. Therefore, the design is reasonable.

$$\Delta P=0.5\times \rho U^2\times ({\displaystyle \frac{L}{D}}{)}^{0.5}\times N^{1.2}\times ({\displaystyle \frac{t}{D}}{)}^{0.3}$$

(5)

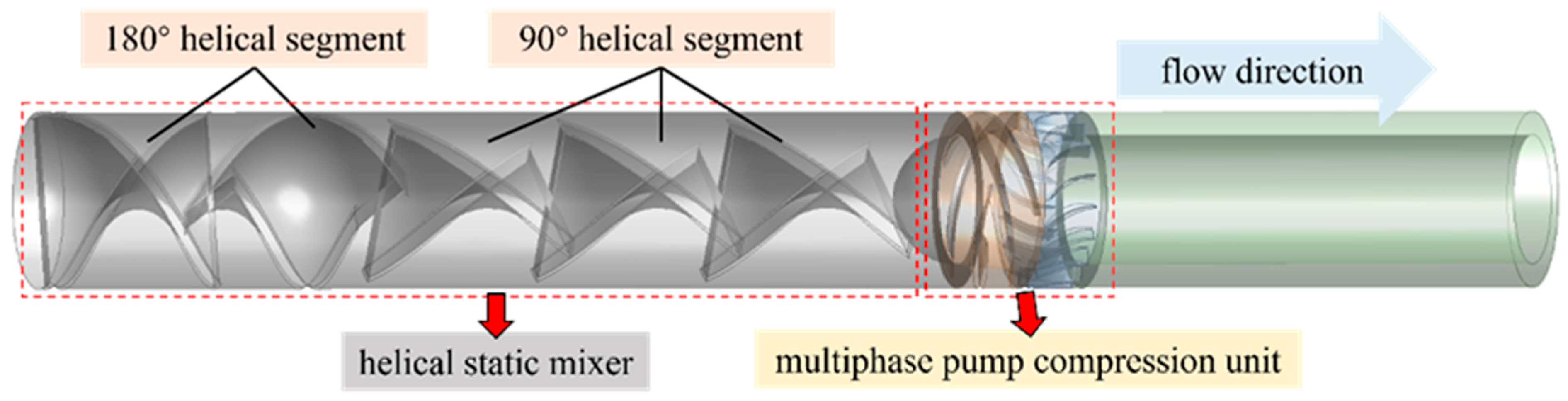
Based on the above parameters, three-dimensional modeling and design of the helical static mixer structure were carried out using SolidWorks2024 software. An inlet extension section was added at the inlet of the mixer to ensure that the two-phase medium enters in a non-uniform form. Finally, it was assembled with the impeller, guide vane, and inlet/outlet water bodies. The numerical calculation model is shown in Figure 4.

The fluid model was mainly meshed using ANSYS 2022 ICEM CFD software. Due to the complex structure of the mixer, impeller, and guide vane components, which require high mesh adaptability, tetrahedral unstructured meshes were selected [22,23,24,25,26,27]. Unstructured meshes can overcome node structure limitations, and are extremely flexible when dealing with complex boundaries and meshing. They can adapt well to the irregular shapes of the mixer, impeller, and guide vanes, and can accurately simulate internal flow. Finally, the mesh model was evaluated by combining the grid convergence index (GCI), ultimately demonstrating that the mesh model with 14.54 million units is superior in numerical calculation, as shown in Figure 5.

This study employed the ANSYS 2022 Fluent CFD software platform for numerical simulation. The simulation was set as a transient calculation to accurately capture the dynamic interface changes and unstable flow characteristics in the multiphase flow field. The SST k-ω turbulence model, which is widely used in the simulation of internal flows in fluid machinery, was selected. This model can effectively handle near-wall flow and core separation flow, making it suitable for simulating the complex turbulent phenomena within the mixed transport pump. The high-order scheme was adopted for numerical discretization, and the coupled algorithm was used for pressure–velocity coupling to ensure calculation accuracy and stability.

3. Optimization Effect of Helical Static Mixer on Non-Uniform Inflow

3.1. Dimensionless Characterization of Inlet Flow Regime and Operating Condition Design

3.1.1. Dimensionless Definition of Stratified Flow

To quantitatively characterize the geometric features of gas–liquid stratification at the inlet cross-section, a dimensionless parameter, namely, the stratified height ratio (denoted as Ψ), is defined to quantify the geometric position of the stratified interface. Its specific expression is given in Equation (6):

$$\psi ={\displaystyle \frac{h}{R}}$$

(6)

where h is the vertical distance between the gas–liquid interface and the center of the circle and R is the radius of the inlet extension, as shown in Figure 6. This paper defines the operating conditions between 10% and 30%. Refer to

Table 6. Design scheme for stratified height ratio (Ψ).

Scheme	Vertical Distance Between Gas-Liquid Interface and Center h	Radius of Inlet R	Stratified Height Ratio Ψ
I (10% GVF)	55.70 (mm)	75.00 (mm)	0.74
II (15% GVF)	49.50 (mm)	75.00 (mm)	0.66
III (20% GVF)	43.80 (mm)	75.00 (mm)	0.58
IV (25% GVF	38.50 (mm)	75.00 (mm)	0.51
V (30% GVF)	24.00 (mm)	75.00 (mm)	0.32

for specific parameter settings.

When the flow is stratified inflow, the gas volume distribution at the inlet of the multiphase pump is shown in Figure 7.

3.1.2. Dimensionless Definition of Slug Flow

By adjusting the gas–liquid distribution of the incoming flow, large bubbles generated in the flow are treated as gas columns with diameters centered on the flow channel, continuously entering the incoming flow. The specific setting conditions are as follows: the inlet flow has gas volume fractions (GVF) of 10%, 15%, 20%, 25%, and 30%, respectively; for bubble diameters under different gas volume fractions, the calculation method is uniform, and the calculation process for a 15% gas volume fraction is taken as an example here.

In a uniform gas–liquid flow, a 15% gas volume fraction indicates that gas occupies 15% of the total volume of the inlet flow cross-section. Therefore, when this gas volume fraction is suddenly concentrated at the center to form a large bubble, the diameter can be estimated as follows.

First, assume that the cross-section of the flow field is a circle with a total area of A_total and that the gas-containing part accounts for 15% of this area, i.e.,

$$A_{air}=0.15\times A_{total}.$$

(7)

Because the bubble is concentrated in the central region, this 15% area can be regarded as the area of a small circle, and its diameter is

$$A_{air}=0.15\times A_{total}=0.15\times \pi ({\displaystyle \frac{D_{total}}{2}}{)}^2.$$

(8)

Combining the above two equations, the diameter of the central large bubble can be derived as

$$D_b=D_{total}\times \sqrt{0.15}=150\times \sqrt{0.15}\approx 58.1mm.$$

(9)

According to the above formula, when the flow has gas volume fractions of 10%, 15%, 20%, 25%, and 30%, the diameters of the central gas column transformed in the flow channel are 47.4 mm, 58.1 mm, 67.1 mm, 75 mm, and 82.0 mm, respectively.

For convenience of description, a dimensionless coefficient φ is defined as a parameter to characterize the slug flow under different inlet gas volume fractions, and its specific expression is shown in Equation (10). In the equation, D_b is the diameter of the inlet gas column after the flow undergoes a sudden change, while D_inlet is the inlet diameter at the inlet extension section of the assembled water body.

$$\phi ={\displaystyle \frac{D_b}{D_{inlet}}}$$

(10)

Based on the above formula, the operating conditions with inlet gas volume fractions ranging from 10% to 30% studied in this paper are defined; the specific parameter settings are shown in

Table 7. Research schemes for different slug flow coefficients φ.

Scheme	Diameter of Inlet Gas Column Db	Inlet Diameter at Inlet Extension Section Dinlet	Slug Flow Coefficient φ
I (10% GVF)	47.40 mm	150.00 mm	0.32
II (15% GVF)	58.10 mm	150.00 mm	0.39
III (20% GVF)	67.10 mm	150.00 mm	0.45
IV (25% GVF)	75.00 mm	150.00 mm	0.50
V (30% GVF)	82.00 mm	150.00 mm	0.55

.

When the flow is slug flow, the gas volume distribution at the inlet of the multiphase pump is shown in Figure 8:

Different stratified flows and slug flows are controlled by writing a user-defined function (UDF) program combined with Fluent software, and the incoming flow is set at the inlet section before the impeller. Through program control, it can be ensured that the fluid enters the pump in different flow states.

3.2. Influence of Inlet Flow Regime Optimization on External Characteristics of Multiphase Pump

Under stratified flow and slug flow, respectively, the external characteristics of the impeller with and without a helical static mixer added at the front end were compared under different stratified height ratio conditions. As shown in Figure 9, when the inlet flow is stratified flow, after adding the mixer, both the efficiency and head of the multiphase pump are higher than those without the mixer. Under the same stratified height ratio, the efficiency only slightly decreases from 63.39% to about 58.97%, for a decrease of only 5.4%, and the head decreases by only 4 m. The efficiency also maintains a high level of 60% when the stratified height ratio Ψ is 0.58 and 0.51. The efficiency-increasing effect of the mixer becomes more significant as the stratified height ratio decreases. Under the condition of stratified height ratio Ψ = 0.32, the efficiency is 15.41% higher than that without the mixer, and the head is increased by 57.32%; at Ψ = 0.74, the efficiency increase is only 1.5%, and the head is increased by only 3%. Although the impeller efficiency also decreases with the increase of gas content, under the condition of low stratified height ratio, the optimization of efficiency and head is obviously higher than that without the mixer. The static mixer breaks the gas–liquid stratified flow, promotes the uniform mixing of gas and liquid, and reduces the uneven distribution of the two phases in the flow channel. Thus, it can effectively optimize the flow state of the gas–liquid phases, reduce the adverse effects caused by stratified inflow conditions, and significantly improve the efficiency of the pump. Especially under the condition of stratified height ratio Ψ > 0.66, the helical static mixer can provide more efficiency growth for the impeller under stratified inflow. This indicates that the addition of the mixer effectively optimizes the mixing of the gas–liquid phases and improves the working efficiency of the pump. As shown in Figure 10, when the inlet flow is slug flow, the addition of the helical static mixer significantly optimizes the ability of the impeller to transport the gas–liquid phases. Under the same working condition, the efficiency only slightly decreases from 62.66% to 59.84%, for a decrease of 4.5%, and the head decreases by only 3.86 m. At the same time, the research results show that the efficiency-increasing effect of the static mixer is closely related to the change of gas content. When the slug flow coefficient φ is 0.45, the efficiency is only increased by 0.5% and the head is increased by 2.12%; under the condition of φ = 0.55, the efficiency is increased by 1.01%, and the head is increased by 9.82%. Under the condition of φ > 0.45, the mixer can increase the pump efficiency by more than 1.5% and the head by more than 8% (relatively). This indicates that the mixer can effectively break the persistent gas column in the slug flow through forced mixing, thereby improving the working capacity of the multiphase pump.

After the static mixer is added, it can optimize the mixing of the front-end flow. However, due to the flow resistance generated by its structure, excessive energy consumption will be caused in the entire system. In this paper, the specific energy consumption is uniformly used as a direct judgment on the energy consumption of the system. System energy consumption refers to the total energy consumed by the gas–liquid multiphase pump to transport a specific volume or mass of gas–liquid two-phase medium per unit time, and its core characterization parameter is the specific energy consumption (SEC), which is defined as shown in the following formula. In the formula, g is the gravitational acceleration, H is the pump head, and η is the total efficiency of the pump. To further illustrate the impact of the static mixer on the energy consumption of the multiphase pump system, the system energy consumption before and after adding the mixer is extracted as shown in Figure 11 and Figure 12.

$$SEC={\displaystyle \frac{gH}{\eta }}$$

(11)

It can be seen that after adding the mixer, the system energy consumption of the multiphase pump increases, especially under the condition of low stratified height ratio. For example, when Ψ = 0.32, the system energy consumption after adding the mixer increases by approximately 42.24% compared with that without the mixer; when φ = 0.55, the system energy consumption after adding the mixer increases by about 8.29% compared with that without the mixer. This indicates that although the mixer can optimize different non-uniform flows, the additional energy dissipation caused by its structural resistance still makes the total energy consumption of the system show an upward trend. Therefore, when designing for different working conditions, it is necessary to balance the relationship between flow uniformity and energy efficiency optimization.

3.3. Influence of Inlet Flow Regime Optimization on Internal Flow Characteristics of Multiphase Pump

3.3.1. Optimization Results of Gas Volume Distribution in Flow Channel

Under stratified inlet flow conditions, without a mixer, the gas–liquid phases are not effectively mixed and the gas volume distribution presents an obvious stratified flow structure. Gas forms continuous high-concentration zones in flow channels C and D, where the gas volume fraction even exceeds 0.9, with a clear gas–liquid interface. This uneven distribution leads to flow instability. However, after adding a static mixer, the distribution of the gas–liquid phases changes significantly. The mixer generates rotational shear force and turbulence, enabling sufficient mixing of gas and liquid, resulting in a more uniform gas distribution in the flow channels. As can be seen in Figure 13, the gas volume fraction range is reduced to 0.1~0.6 and the gas–liquid phases in the flow channels show a continuous gradient distribution. In various cross-sections of the impeller (as shown in Figure 14), the internal gas volume fraction is significantly improved compared to that without the mixer. The mixer effectively breaks the gas aggregation structure, reduces bubble coalescence, and allows gas to be more uniformly distributed throughout the flow process. Such optimization greatly reduces the risk of unstable flow and improves the working state of the pump.

As shown in Figure 15 and Figure 16, the optimization effect of the helical mixer on slug flow is also obvious. Without a mixer, under the flow state with a gas content of 30% at the inlet, the gas volume distribution is concentrated in the flow channel to form an obvious gas column. The gas volume fraction in the center of the flow channel remains at 80~90% and its radial coverage reaches 60~70% of the flow channel diameter, causing the liquid phase to be squeezed to both sides of the flow channel, where the gas volume fraction is at a low level. At this time, there is a large velocity difference between the gas and water flows, resulting in uneven gas–liquid mixing in the flow channel which causes flow instability and local flow stagnation. However, after adding the helical mixer, the flow field is significantly reconstructed and the gas volume distribution is obviously optimized.

Compared with the flow channels without a mixer, the area with high gas content in flow channels C and D is significantly reduced. The addition of the mixer effectively breaks the concentration of gas columns, promotes effective mixing of the gas–liquid phases, reduces the difference at the gas–liquid interface, and allows the gas volume fraction to be more uniformly distributed in the flow channel. This is especially the case near the blade area, where the distribution of the gas–liquid phases becomes more uniform. With the improvement of gas–liquid flow uniformity, the water flow velocity and pressure distribution in the flow channel tend to be uniform, reducing local flow stagnation and instability. This change not only improves the working efficiency of the pump but also enhances the energy transfer efficiency of the fluid in the pump.

3.3.2. Optimization of Flow Velocity Distribution

According to the comparison of water flow velocity distributions in Figure 17, it can be seen that the helical static mixer has an obvious optimization effect on the flow velocity in the impeller. Without the mixer, the water flow velocity distribution shows significant inhomogeneity. The flow presents a typical stratified structure, with the gas and liquid not effectively mixed. The regions with higher water flow velocity are mainly concentrated in the upper part of the flow channel, with an obvious velocity peak in the inlet area, while in the lower liquid phase region the water flow velocity is lower. After adding the static mixer, the water flow velocity distribution is significantly optimized.

Compared with the change in water flow velocity distribution in the blades under stratified inflow, the mixer enables more uniform mixing of the water flow and gas phase by generating rotational shear force and turbulence. As can be seen in Figure 18, the water flow velocity distribution tends to be gentle, the velocity fluctuation is reduced, and the water flow velocity distribution in the entire flow channel is relatively uniform. The dominant flow velocity in the flow channel becomes more uniformly concentrated, the area of high-velocity regions (red) decreases, and the proportion of low-velocity regions (blue) drops, which makes the flow of the liquid phase smoother. This improvement helps to reduce the energy loss of the pump, improve the pump efficiency, and mitigate the impact caused by flow instability. By comparing the flow velocity distributions of the two cases, it is obvious that the static mixer plays a significant role in optimizing the water flow velocity distribution.

When the inlet flow is slug flow and no mixer is added, as shown in Figure 19, the water flow velocity distribution in the blade flow channel is extremely uneven due to the presence of gas columns in the flow channel. A high-velocity region is formed in the central area of the flow channel, while blue low-velocity regions appear in the near-wall areas of channels C and D. At this time, the water flow undergoes obvious local changes under the influence of the gas column, resulting in a strong gradient change and unevenness in the velocity distribution. After adding the mixer, the presence of gas columns is effectively optimized, the gas distribution tends to be uniform, the water flow velocity distribution in the flow channel becomes more uniform, and velocity peaks emerge. By disturbing the fluid, the mixer makes the water flow velocity distribution in the blade flow channel more uniform, significantly reduces the gradient of water flow velocity in the channel, makes the water flow distribution tend to be symmetrical, effectively reduces local velocity differences, and improves the stability and uniformity of the flow.

In Figure 20, the velocity distribution across the cross-section of the impeller is more regular and gentle, and the velocity distribution at the outlet cross-section is symmetric and reasonable. The addition of the static mixer significantly optimizes the velocity distribution of the water flow in the flow channel.

3.3.3. Optimization Effect of Turbulent Kinetic Energy in Flow Channel

Figure 21a shows the axial distribution of turbulent kinetic energy in the impeller under a stratified ratio Ψ = 0.32 with and without a static mixer. Without the static mixer, the axial distribution presents an obvious asymmetric bimodal pattern. The first peak appears at an axial position of 0.3 in the initial region along the streamline direction, which is the inlet of the impeller, where the water turbulent kinetic energy is approximately 1.8 m²/s². This is due to the presence of gas–liquid stratified flow, which causes instability at the interface between gas and liquid. Although the gas–liquid stratified flow can remain stable before entering the impeller, the liquid and gas begin to interact in the flow channel inlet region. Due to the uneven flow, intense turbulence forms near the gas–liquid interface, ultimately leading to a sharp increase in turbulent kinetic energy. The second peak appears at an axial position of 0.5 in the middle of the flow channel, approximately 1.6 m²/s². When the stratified flow enters the rotating impeller, the liquid phase migrates to the outer edge of the blade under the action of centrifugal force, while the gas phase locally accumulates on the hub side. This uneven distribution of the two phases in the circumferential direction results in a significant velocity difference between the gas accumulation area and the main liquid flow area, intensifying the turbulent motion of the shear layer. Additionally, at the impeller outlet, near the axial position of 0.8, the accumulation of gas weakens the axial momentum of the fluid, causing local backflow, which also leads to an increase in turbulent kinetic energy. After adding the mixer, the variation trend of the turbulent kinetic energy is the same as without the mixer. However, compared with the black curve, the turbulent kinetic energy does not fluctuate significantly and the turbulent kinetic energy at the two peaks decreases sharply, with a decrease of approximately 50% at the second peak. The addition of the mixer effectively promotes mixing of the gas–liquid phases by increasing the shear force and turbulence between them, making the flow more uniform. As the instability of the gas–liquid interface is alleviated, the distribution of turbulent kinetic energy becomes more uniform, reducing the fluctuation of local turbulence. Therefore, the variation curve of turbulent kinetic energy is relatively smooth and the turbulent kinetic energy at the outlet is low, indicating that the flow is more stable and uniform.

Figure 21b shows the axial distribution of turbulent kinetic energy in the impeller under a slug flow coefficient φ = 0.55 with and without a static mixer. Without the static mixer, the variation of the turbulent kinetic energy distribution along the axial direction is more uniform than that of stratified flow. A peak appears in the axial position range of 0.2–0.4, which is approximately 1.0 m²/s². This peak results from the strong shear effect of the gas–liquid phases in the inlet section of the impeller. When the large gas column flow with a slug flow coefficient φ = 0.55 enters the rotating impeller, the gas phase migrates to the hub side due to centrifugal force and the liquid phase accumulates on the pressure surface of the blade, forming a significant gas–liquid stratified interface. This uneven phase distribution leads to instability of the gas–liquid distribution, making the turbulent kinetic energy reach a peak at 0.4. Then, at the axial position of 0.6, a second small peak appears, where the turbulent kinetic energy rises to 0.9 m²/s². The reason for this peak is similar to that of the second peak in stratified flow mentioned earlier. As the fluid medium moves toward the outlet, the gas phase further accumulates on the hub side under the continuous action of centrifugal force, while the liquid phase migrates to the rim, resulting in an increase in the intensity of turbulent kinetic energy. Adding the static mixer forces mixing through the guide vanes, making the gas phase distribution more uniform. This reduces the peak value of turbulent kinetic energy at the axial position of 0.3 to 0.85 m²/s², a decrease of approximately 15%. In the outlet section (axial position > 0.6), the suppression of flow unevenness by the mixer stabilizes the turbulent kinetic energy in the range of 0.72–0.78 m²/s², compared with the range of 0.82–0.88 m²/s² without the mixer. In the entire axial region, the average value of turbulent kinetic energy decreases by 12.8%. Figure 21b shows that the turbulent kinetic energy in the blade meridian decreases after adding the mixer under a slug flow coefficient φ = 0.55, confirming that the static mixer eliminates non-uniformity of the phase distribution and concentration of the velocity gradient; thus, the mixer enables the impeller to operate more efficiently.

In the meridional plane contour map of the stratified flow with Ψ = 0.32, shown in Figure 22, the high turbulent kinetic energy region of the impeller is significantly reduced. The addition of the static mixer significantly optimizes the distribution and variation trend of turbulent kinetic energy. To sum up, in the entire impeller flow channel, the average value of turbulent kinetic energy decreases from 1.32 m²/s² to 0.89 m²/s², with an overall decrease of 32.57%.

Figure 23 shows that the turbulent kinetic energy in the blade meridian decreases after the mixer is added under a slug flow coefficient φ = 0.55, confirming that the static mixer eliminates non-uniformity of the phase distribution and concentration of the velocity gradient, enabling the impeller to operate more efficiently with the mixer. This is because the static mixer does not simply superimpose disturbances on the original flow but fundamentally changes the distribution pattern of the gas–liquid phases, making the system cross the stability threshold of gas-liquid flow and enter a uniformly mixed flow state. This phase transition effectively promotes the mixing of the gas–liquid phases, reduces the loss of turbulent kinetic energy, and improves the stability and efficiency of the flow. Therefore, application of the static mixer significantly optimizes the uniformity of the flow and the transfer of turbulent kinetic energy, which is one of the main internal factors for the efficiency improvement of oil–gas multiphase pumps.

4. Conclusions

This paper mainly studies the changes in external characteristics and internal flow characteristics of the impeller flow field before and after adding a helical static mixer. Firstly, the helical static mixer was designed, then the external characteristics and internal flow characteristics of the impeller with and without the mixer were analyzed under stratified flow and slug flow, respectively. The specific research results are as follows:

(1)

A suitable static mixer was selected for the studied stratified flow and slug flow. By optimizing key parameters such as the helix angle and unit length, efficient gas–liquid mixing was achieved under low pressure drop conditions.

(2)

The addition of the helical static mixer has a significant effect on improving the efficiency and head of the axial-flow multiphase pump. Under stratified flow conditions, the introduction of the mixer increases the impeller efficiency from 43.56% to 58.97% and the head from 11.58 m to 27.14 m at a stratified height ratio of 0.32. Compared with the state under uniform mixed flow, the efficiency drop rate is significantly reduced from 30.13% (before adding the helical static mixer) to 5.4%, while the head drop rate is significantly reduced from 58.17% to 11.24%. Under slug flow conditions, when the slug flow coefficient is 0.55, the mixer increases the impeller efficiency from 58.84% to 59.84%. Compared with the state under uniform mixed flow, the efficiency drop rate decreases from 7.62% (before adding the helical static mixer) to 4.5%, while the head drop rate decreases from 17.22% to 12.5%.

(3)

The helical static mixer reduces the negative impact caused by uneven flow. Analysis of the internal flow field shows that under stratified flow conditions, the mixer eliminates the high gas-containing regions dominated by gas phase in the flow channel, improving the uniformity of both the gas volume distribution in each impeller flow channel and the velocity distribution of the two-phase medium. From the axial direction of the impeller, the average turbulent kinetic energy decreases from 1.32 m²/s² to 0.89 m²/s², the turbulent kinetic energy in the outlet section drops by 50%, and the axial bimodal distribution disappears. Under slug flow conditions, in the impeller flow channel with the mixer added, the coverage range of the gas column is significantly reduced, the gas volume fraction is decreased, and the velocity distribution in the impeller is more uniform. The turbulent kinetic energy distribution in the impeller tends to be flat along the axial direction, the peak intensity is weakened by 15%, and the turbulent kinetic energy in the outlet section is stable between 0.72 and 0.78 m²/s², which is a decrease of 12.8% compared to the condition without the static mixer.