Optimal Design of 3D-Printed Flexible Fingers for Robotic Soft Gripping of Agricultural Products
Abstract
1. Introduction
2. Flexible Finger Topology Optimization
3. Case Study and Numerical Results
3.1. Analyzed Finger Topologies
3.2. Material Properties
3.3. Simulation Results
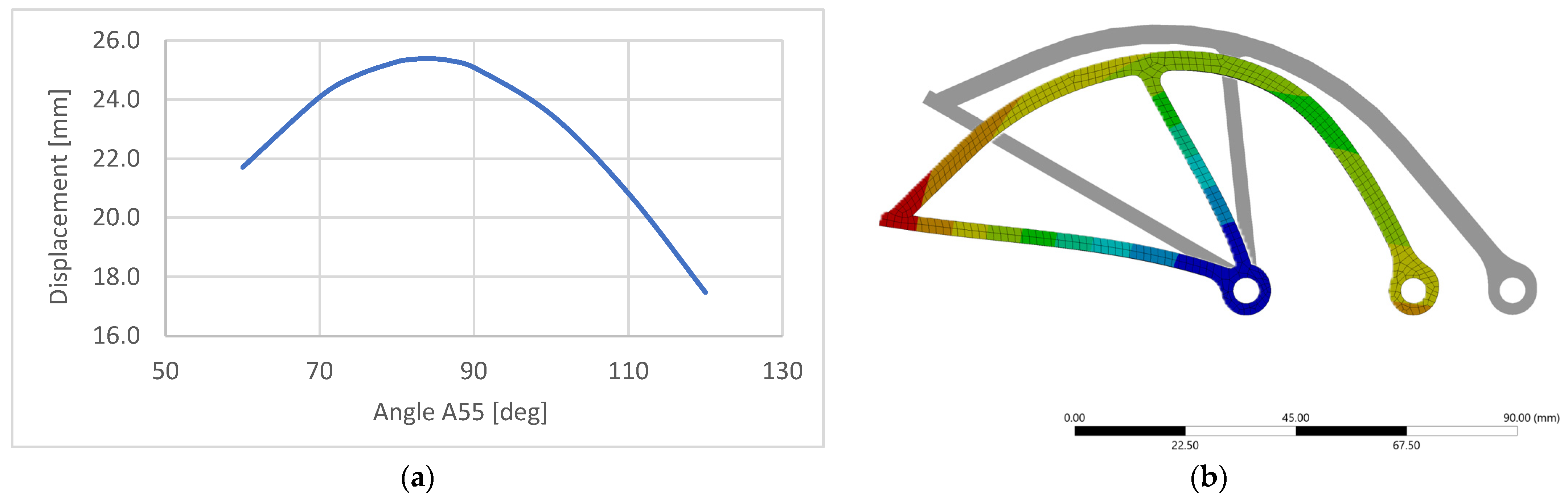
3.4. Simulation Data Analysis
- Model 1 provided the largest fingertip displacement, reaching 25.39 mm for a 20 mm actuator stroke. This wide deformation range makes it the most adaptable when handling objects of different sizes. The drawback is that it demands the highest actuation force of 12.41 N and also shows the greatest stress level of 3.41 MPa when in contact with a soft object;
- Model 2, in contrast, is highly energy-efficient. It requires only 3.58 N of force, much less than the other models, and has the lowest stress of 1.61 MPa. These values make it ideal for low-power applications. Its main drawback is the reduced fingertip displacement of 22.72 mm, which restricts the gripper’s range and makes it less adaptable to smaller fruits;
- Model 3 offers balanced performance in comparison with the first two models. With a displacement of 23.74 mm and improved stability from its dual-reinforcement design, it ensures a more consistent grip and potentially better stiffness control for precision tasks. In this case, the actuation force required was 11.09 N, similar to Model 1, and had the equivalent stress of 3.12 MPa.
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEA | Finite Element Analysis |
| TPE | Thermoplastic elastomer |
| AP | Average Precision |
References
- Vos, R.; Bellù, L.G. Global trends and challenges to food and agriculture into the 21st century. In Sustainable Food and Agriculture; Campanhola, C., Pandey, S., Eds.; Elsevier Inc.: Amsterdam, Netherlands, 2019; pp. 11–30. [Google Scholar] [CrossRef]
- Calicioglu, O.; Flammini, A.; Bracco, S.; Bellù, L.; Sims, R. The future challenges of food and agriculture: An integrated analysis of trends and solutions. Sustainability 2019, 11, 222. [Google Scholar] [CrossRef]
- Botta, A.; Cavallone, P.; Baglieri, L.; Colucci, G.; Tagliavini, L.; Quaglia, G. A review of robots, perception, and tasks in precision agriculture. Appl. Mech. 2022, 3, 830–854. [Google Scholar] [CrossRef]
- Rahmadian, R.; Widyartono, M. Autonomous robotic in agriculture: A review. In Proceedings of the 2020 Third International Conference on Vocational Education and Electrical Engineering, Surabaya, Indonesia, 3–4 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Pearson, S.; Camacho-Villa, T.C.; Valluru, R.; Gaju, O.; Rai, M.C.; Gould, I.; Sklar, E. Robotics and autonomous systems for net zero agriculture. Curr. Robot. Rep. 2022, 3, 57–64. [Google Scholar] [CrossRef]
- Boursianis, A.D.; Papadopoulou, M.S.; Diamantoulakis, P.; Liopa-Tsakalidi, A.; Barouchas, P.; Salahas, G.; Goudos, S.K. Internet of things (IoT) and agricultural unmanned aerial vehicles (UAVs) in smart farming: A comprehensive review. Internet Things 2022, 18, 100187. [Google Scholar] [CrossRef]
- Marinoudi, V.; Lampridi, M.; Kateris, D.; Pearson, S.; Sørensen, C.G.; Bochtis, D. The future of agricultural jobs in view of robotization. Sustainability 2021, 13, 12109. [Google Scholar] [CrossRef]
- Vrochidou, E.; Tsakalidou, V.N.; Kalathas, I.; Gkrimpizis, T.; Pachidis, T.; Kaburlasos, V.G. An overview of end effectors in agricultural robotic harvesting systems. Agriculture 2022, 12, 1240. [Google Scholar] [CrossRef]
- Rad, C.; Hancu, O.; Lapusan, C. Aspects regarding “soft” grasping in smart agricultural harvesting tasks. Acta Tech. Napoc.-Ser. Appl. Math. Mech. Eng. 2020, 63, 389–394. [Google Scholar]
- Russo, M.; Ceccarelli, M.; Corves, B.; Hüsing, M.; Lorenz, M.; Cafolla, D.; Carbone, G. Design and test of a gripper prototype for horticulture products. Robot. Comput.-Integr. Manuf. 2017, 44, 266–275. [Google Scholar] [CrossRef]
- Armanini, C.; Junge, K.; Johnson, P.; Whitfield, C.; Renda, F.; Calisti, M.; Hughes, J. Soft robotics for farm to fork: Applications in agriculture & farming. Bioinspiration Biomim. 2024, 19, 021002. [Google Scholar] [CrossRef]
- Navas, E.; Fernández, R.; Sepúlveda, D.; Armada, M.; Gonzalez-de-Santos, P. Soft grippers for automatic crop harvesting: A review. Sensors 2021, 21, 2689. [Google Scholar] [CrossRef]
- Wang, X.; Kang, H.; Zhou, H.; Au, W.; Wang, M.Y.; Chen, C. Development and evaluation of a robust soft robotic gripper for apple harvesting. Comput. Electron. Agric. 2023, 204, 107552. [Google Scholar] [CrossRef]
- Rad, C.; Hancu, O.; Lapusan, C. Data-driven kinematic model of PneuNets bending actuators for soft grasping tasks. Actuators 2022, 11, 58. [Google Scholar] [CrossRef]
- Visentin, F.; Castellini, F.; Muradore, R. A soft, sensorized gripper for delicate harvesting of small fruits. Comput. Electron. Agric. 2023, 213, 108202. [Google Scholar] [CrossRef]
- Șerdean, M.; Șerdean, F.; Mândru, D. An Overview of Grippers in Agriculture Robotic Systems. In New Advances in Mechanisms, Mechanical Transmissions and Robotics; MTM&Robotics 2020; Lovasz, E.C., Maniu, I., Doroftei, I., Ivanescu, M., Gruescu, C.M., Eds.; Springer: Cham, Switzerland, 2021; pp. 212–225. [Google Scholar] [CrossRef]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft robotic grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef]
- Rad, C.; Hancu, O.; Lapusan, C. Aspects regarding the modelling and design of 3D-printed bending soft pneumatic actuators. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2022; Volume 1268, p. 012012. [Google Scholar] [CrossRef]
- Xie, B.; Jin, M.; Duan, J.; Li, Z.; Wang, W.; Qu, M.; Yang, Z. Design of adaptive grippers for fruit-picking robots considering contact behavior. Agriculture 2024, 14, 1082. [Google Scholar] [CrossRef]
- Liu, C.H.; Chiu, C.H.; Chen, T.L.; Pai, T.Y.; Chen, Y.; Hsu, M.C. A soft robotic gripper module with 3D printed compliant fingers for grasping fruits. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; pp. 736–741. [Google Scholar] [CrossRef]
- Crooks, W.; Vukasin, G.; O’Sullivan, M.; Messner, W.; Rogers, C. Fin ray® effect inspired soft robotic gripper: From the robosoft grand challenge toward optimization. Front. Robot. AI 2016, 3, 70. [Google Scholar] [CrossRef]
- Varghese, F.; Cheein, F.A.; Koskinopoulou, M. Finite element optimization of a flexible fin-ray-based soft robotic gripper for scalable fruit harvesting and manipulation. Smart Agric. Technol. 2025, 11, 100899. [Google Scholar] [CrossRef]
- Vale Filho, E.; Alves, D.; Alves, A.M.; Zardini, E.; Cordeiro, V.; Galvão, M.; de Aguiar, M.L.; Antunes, R.; Pereira, N.; Gaspar, P.D. Fusion of Computer Vision Method and Fin Ray Effect Soft Robotic Gripper for Fruit Harvesting. In Proceedings of the 2024 20th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Genova, Italy, 2–4 September 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Shin, J.H.; Park, J.G.; Kim, D.I.; Yoon, H.S. A Universal Soft Gripper with the Optimized Fin Ray Finger. Int. J. Precis. Eng. Manuf.-Green Technol. 2021, 8, 3. [Google Scholar] [CrossRef]
- An, B.; Choi, T.; Kim, U. Linkage integrated fin ray gripper capable of safe adaptive grasping for tomato harvesting. Comput. Electron. Agric. 2025, 232, 110118. [Google Scholar] [CrossRef]
- Xu, Q. Design and development of a novel compliant gripper with integrated position and grasping/interaction force sensing. IEEE Trans. Autom. Sci. Eng. 2015, 14, 1415–1428. [Google Scholar] [CrossRef]
- Llanos, E.H.; Corves, B.; Huesing, M.; Saxena, A. Systematic mapping of synthesis methods for compliant grippers using PRISMA. Mech. Mach. Theory 2025, 206, 105900. [Google Scholar] [CrossRef]
- Dong, H.; Guo, H.; Yang, S.; Qiu, C.; Dai, J.; Chen, I. Theoretical Model Construction of Deformation-Force for Soft Grippers Part I: Co-rotational Modeling and Force Control for Design Optimization. arXiv 2023, arXiv:2303.12987. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, X.; Iida, F.; Howard, D. Fin-qd: A computational design framework for soft grippers: Integrating map-elites and high-fidelity fem. In Proceedings of the 2024 IEEE 7th International Conference on Soft Robotics (RoboSoft), San Diego, CA, USA, 14–17 April 2024; pp. 692–697. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Zhang, H.; Liang, J.; Zang, H.; Li, H.; Wang, R. Design of compliant mechanisms using continuum topology optimization: A review. Mech. Mach. Theory 2020, 143, 103622. [Google Scholar] [CrossRef]
- Dao, T.P.; Le, H.G.; Ho, N.L. Topology-Shape-Size Optimization Design Synthesis of Compliant Grippers for Robotics: A Comprehensive Review and Prospective Advances. Robot. Auton. Syst. 2025, 193, 105106. [Google Scholar] [CrossRef]
- Hernandez, J.; Sunny, M.S.H.; Sanjuan, J.; Rulik, I.; Zarif, M.I.I.; Ahamed, S.I.; Ahmed, H.U.; Rahman, M.H. Current designs of robotic arm grippers: A comprehensive systematic review. Robotics 2023, 12, 5. [Google Scholar] [CrossRef]
- ISO527-2:2012; Plastics—Determination of Tensile Properties, Part 2: Test Conditions for Moulding and Extrusion Plastics. International Organization for Standardization: Geneva, Switzerland, 2012.
- Kultongkham, A.; Kumnon, S.; Thintawornkul, T.; Chanthasopeephan, T. The design of a force feedback soft gripper for tomato harvesting. J. Agric. Eng. 2021, 52. [Google Scholar] [CrossRef]
- Hao, Y.; Liu, Z.; Liu, J.; Fang, X.; Fang, B.; Nie, S.; Guan, Y.; Sun, F.; Wang, T.; Wen, L. A soft gripper with programmable effective length, tactile and curvature sensory feedback. Smart Mater. Struct. 2020, 29, 035006. [Google Scholar] [CrossRef]
- Webster, R.J., III; Jones, B.A. Design and kinematic modeling of constant curvature continuum robots: A review. Int. J. Robot. Res. 2010, 29, 1661–1683. [Google Scholar] [CrossRef]






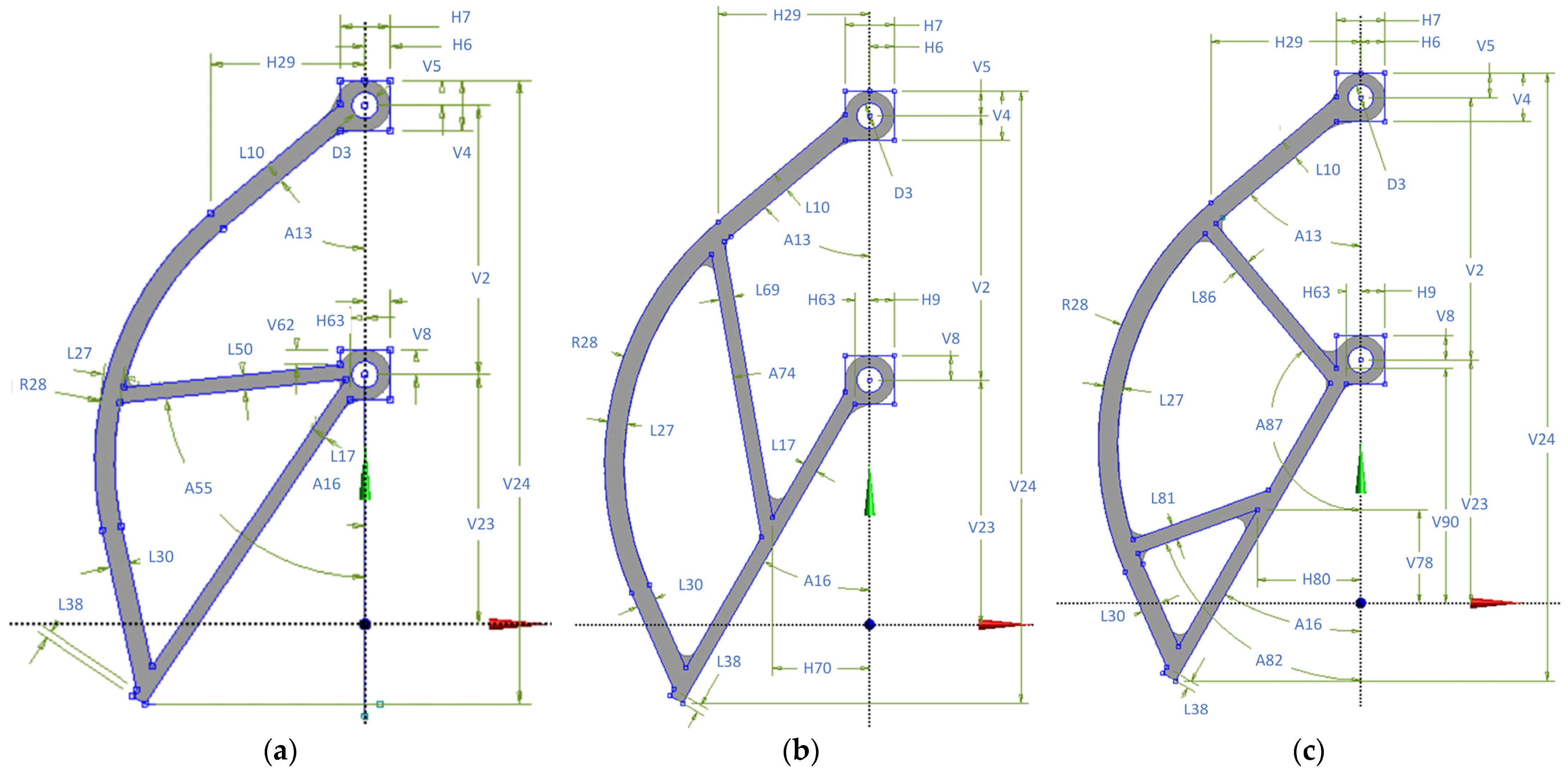








| Parameter | Description | Value | Measurement Unit |
|---|---|---|---|
| l0 | Base offset between joints | 34 | mm |
| l1 | Length of link 1 | 75.98 | mm |
| l2 | Length of link 2 | 51.51 | mm |
| lc | Contact length of the finger | 75 | mm |
| cmin/cmax | Min./Max. slider displacement | 0/20 | mm |
| Wrap angle around the object | 1.31 | rad | |
| C | Design adjustment constant | 25.8 | mm |
| Actuation Force [N] | Equivalent Stress [MPa] | |
|---|---|---|
| Model 1 | 12.41 | 3.41 |
| Model 2 | 3.58 | 1.61 |
| Model 3 | 11.09 | 3.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lapusan, C.; Chiorean, R.S.; Matis, R. Optimal Design of 3D-Printed Flexible Fingers for Robotic Soft Gripping of Agricultural Products. Actuators 2025, 14, 468. https://doi.org/10.3390/act14100468
Lapusan C, Chiorean RS, Matis R. Optimal Design of 3D-Printed Flexible Fingers for Robotic Soft Gripping of Agricultural Products. Actuators. 2025; 14(10):468. https://doi.org/10.3390/act14100468
Chicago/Turabian StyleLapusan, Ciprian, Radu Stefan Chiorean, and Radu Matis. 2025. "Optimal Design of 3D-Printed Flexible Fingers for Robotic Soft Gripping of Agricultural Products" Actuators 14, no. 10: 468. https://doi.org/10.3390/act14100468
APA StyleLapusan, C., Chiorean, R. S., & Matis, R. (2025). Optimal Design of 3D-Printed Flexible Fingers for Robotic Soft Gripping of Agricultural Products. Actuators, 14(10), 468. https://doi.org/10.3390/act14100468







